Research on Energy-Saving Performance of Intermittent Heating for Rooms in Hot Summer & Cold Winter Zone

Nomenclature

1  Introduction

In the hot summer & cold winter zone of China, intermittent space heating for buildings is widely used. Compared with continuous space heating systems, intermittent heating is supposed to reduce energy consumption. However, how much energy can be saved under various intermittent heating conditions remains to be further studied.

Scholars all over the world have studied the factors influencing energy consumption of intermittent space heating systems through experimental researches and simulation analysis. Badran et al. [1] found that if the use time of residential buildings is less than 14 h, as for residential building, under the condition of good thermal insulation performance of the envelope, intermittent operation heating system is more energy-efficient than continuous heating. Tanasiev et al. [2] have studied a passive energy-saving house with intermittent heating in Romania. Compared with the continuous heating, the intermittent heating with optional temperature and time could save about 18% of energy. Yuan et al. [3] studied thermal performance in buildings with insulated external walls and intermittently operated air-conditioning systems. The results showed that the heat dissipation and storage of the inner wall during non-working hours had the greatest influence on thermal performance. Whether the north or south orientations, the energy saving effect of the internal insulation room is at least 18% higher than that of the external insulation room. Ge et al. [4] took some typical residential buildings in Hangzhou as the research object, and found that when intermittent heating was applied, by improving the thermal performance of the envelope, the energy for space heating could be reduced by 37.3%. Ling et al. [5] took Tianjin as an example to study the optimization of the operation strategy of ASHP heating system. They found a good intermittent heating operation mode, the energy saving ratio during the entire heating season was about 17%. Li et al. [6] used EnergyPlus software to study the influence of the composite-PCW on the indoor thermal environment and energy consumption of intermittent heating under the weather condition of Chengdu, and provided an optimization strategy for heating operation time.

In the rural area of Northwest China where the outdoor daily average temperature is 0°C, Dong et al. [7] tested the air source heat pump heating system by setting different indoor temperature ranges and control operation strategies. They found that the optimal control strategy was intermittent operation. Kim et al. [8] presented the switch control method based on dynamic simulation program, using this control could make the indoor temperature fluctuation value within 2°C. Mottet et al. [9] studied two slab-type buildings, located in the hot summer and cold winter region of China, and proposed two natural ventilation-based solutions to improve indoor thermal comfort in hot summers. Cho et al. [10] proposed a predictive control strategy to improve the energy efficiency of the radiant floor heating system during intermittent heating. The result showed that in the cold winter, the use of predictive control strategies could save 10% to 12% of energy. Ling et al. [5] took Tianjin as an example to study the optimization of the operation strategy of ASHP heating system. They found a good intermittent heating operation mode, the energy saving ratio during the entire heating season was about 17%. Deng et al. [11] used the state space method to develop model and found that in order to easily control the thermal comfort of buildings and save energy, the high thermal quality of the exterior walls was even more advantageous. Lechowska et al. [12] proposed a mathematical model suitable for unstable heat transfer in light-weight envelopes by intermittent heating, and the PMV value was taken into consideration. Vytchikov et al. [13] developed an approximate analysis method in order to estimate the time and energy consumption for heating the multi-layer envelope, and suggested using this method to determine the design scheme of intermittent heating buildings. Pupeikis et al. [14] evaluated buildings with long time constant and intermittent heating from the perspective of economic benefits, and the results showed that the economic benefits were the best when the time constant of the building and the additional power of the heating system was 144 h and 50%, respectively.

In this study, a representative office located in Shanghai was selected for case. Furthermore, a dynamic thermal model of intermittent heating was setup for this room and verified by experiment, then the amount and ratio of energy saving were studied under different occupation hours, heating system temperatures, air change rates, window heat transfer coefficient, adjacent room heating modes and different types of envelopes. Moreover, the “energy saving” in this paper was actually the difference of heat load. As a result of that the heat load is closely related to the energy requirement for heating, the difference of heat load between the intermittent heating and continuous heating is called “amount of energy saving” in this study.

2  Thermal Process Analysis Model of the Heating Room

2.1 Physical Model of the Heating Room for Case Study

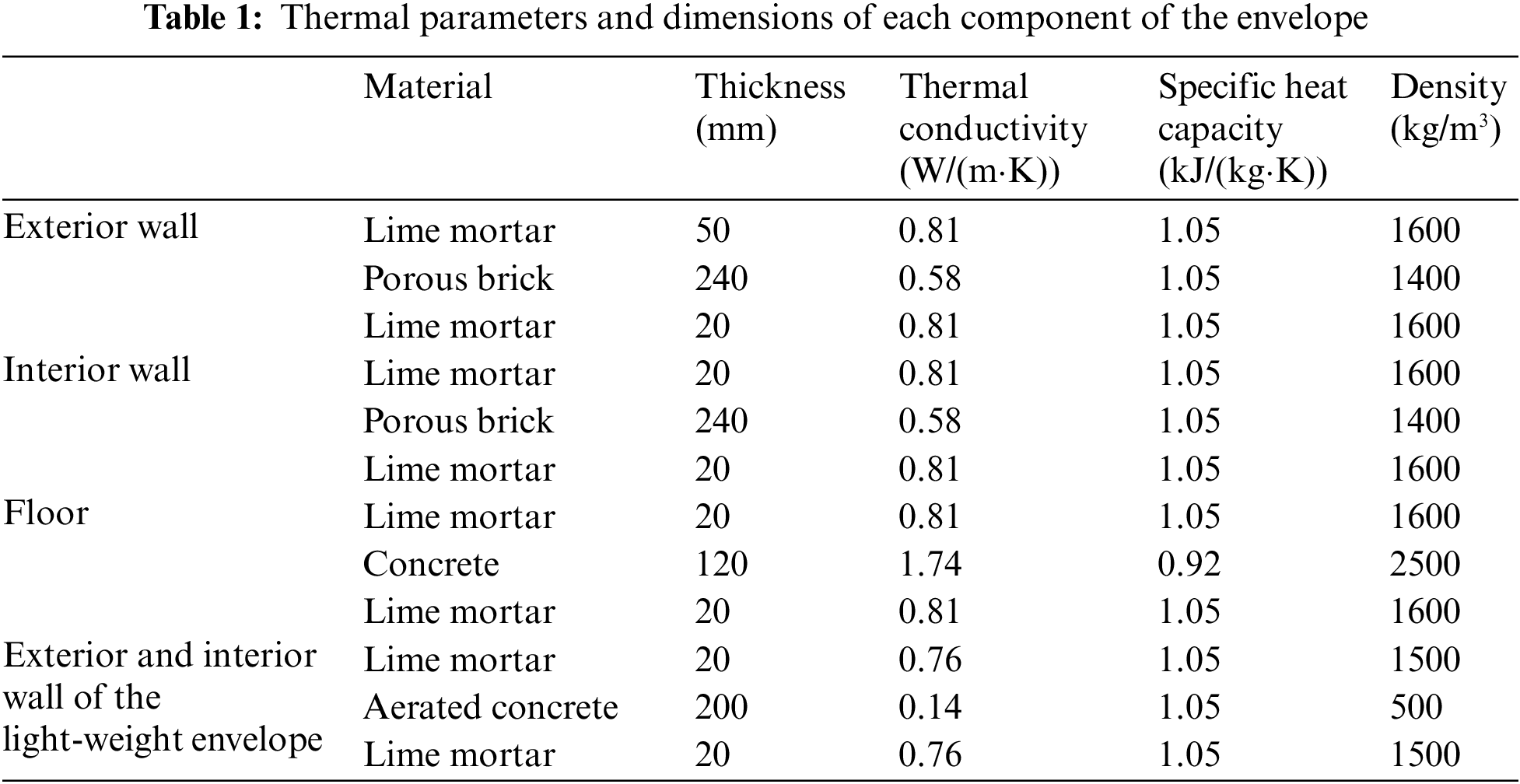
As shown in Fig. 1, the object studied was a representative north-facing office, and the adjacent rooms and corridors were not heated. Furthermore, the temperature of the internal surfaces of the envelope are shown in Fig. 2. The size of the room was 3.4 m × 3.4 m × 6 m. There was a door on the south inside wall and a double sash window on the north external wall. As shown in Table 1, there were the thermal parameters and dimensions of the envelope, and the U-value of the window and the door are 3.5 and 2.5 W/(m2·°C), respectively.

Figure 1: Schematic diagram of the typical heating room

Figure 2: Temperature of the internal surfaces

2.2 The Heat Balance Equation

2.2.1 The Heat Balance Equation of the Envelopes

The factors that affects the hourly heating load in winter is divided into two categories: one is the heat gain or heat loss that directly affects the air temperature of the room, that is, the convective part of the heat gain, such as the heat load caused by air permeation. And the second is the heat gain or heat loss that indirectly affects the air temperature of the room, that is, the radiation part of each heat gain. The radiant heat gain of the room is first absorbed by the inner surfaces of the envelope, causing changes in the temperature of each surface, and then transferred to the indoor air through convective heat transfer, thereby affecting the heat load of the room.

According to Fig. 3, The sum of the heat conducting through the inside surface of the room enclosure, the convective heat exchange with the indoor air, the radiative heat exchange with other surfaces, and the directly radiant heat gain is 0 according to heat balance of a surface [15]. So for the i-th surface, there is the heat balance equation at time n:

Figure 3: Heat transfer schematic diagram of the envelope

qi(n)+aic[tr(n)−ti(n)]+∑k=1Niaikr[tk(n)−ti(n)]+qir(n)=0

For the envelopes whose heat storage capacity could not be ignored, the inside surface can be calculated by the following equation:

qi(n)=∑j=0NsYi(j)toi(n−j)−∑j=0NsZi(j)ti(n−j)(i=1,2,…,m)(1)

For doors, windows and other envelope whose heat storage capacity could be ignored, the inside surface can be calculated by the following equation:

qi(n)=Kiaiai−KItoi(n)−Kiaiai−KIti(n)(i=m+1,m+2,…,Ni)(2)

2.2.2 The Heat Balance Equation of Indoor Air

For the heating rooms, the indoor air temperature was influenced by the convective heat transfer between each inside surface of the envelopes (including indoor furniture and equipment) and indoor air, as well as air infiltration. The heat balance equation of the indoor air was given as follows:

∑k=1NiFkakc[tk(n)−tr(n)]+[q1c(n)−q2c(n)]+La(n)(cρ)a[ta(n)−tr(n)]/3.6−HA(n)=V(cρ)r(tr(n)−tr(n−1))3.6Δτ(3)

2.3 Mathematical Model of the Heating Room

2.3.1 Mathematical Model of the Continuous Heating

In continuous heating, the indoor air temperature was usually kept constant and known. Since the heat load is the heat required for the indoor air to keep the air temperature at a certain baseline value, tr(n) is the known value which represented as tr. So according to Eqs. (1) and (2), the heat balance equations of the inside surface under continuous heating can be obtained as follows:

For the interior walls:

−[a1+Z1(0)]t1(n)+a1,2rt2(n)+a1,3rt3(n)+a1,4rt4(n)+a1,5rt5(n)+a1,6rt6(n)+a1,7rt7(n)+a1,8rt8(n)=−∑j=0NsY1(j)tz(n−j)+∑j=1NsZ1(j)t1(n−j)−q1r(n)−a1ctr(4)

a2,1rt1(n)−[a2+Z2(0)]t2(n)+a2,3rt3(n)+a2,4rt4(n)+a2,5rt5(n)+a2,6rt6(n)+a2,7rt7(n)+a2,8rt8(n)=−∑j=0NsY2(j)tc(n−j)+∑j=1NsZ2(j)t2(n−j)−q2r(n)−a2ctr(5)

⋮

a5,1rt1(n)+a5,2rt2(n)+a5,3rt3(n)+a5,4rt4(n)−[a5+Z5(0)]t5(n)+a5,6rt6(n)+a5,7rt7(n)+a5,8rt8(n)=−∑j=0NsY5(j)tc(n−j)+∑j=1NsZ5(j)t5(n−j)−q5r(n)−a5ctr(6)

a6,1rt1(n)+a6,2rt2(n)+a6,3rt3(n)+a6,4rt4(n)+a6,5rt5(n)−[a6+Z6(0)]t6(n)+a6,7rt7(n)+a6,8rt8(n)=−∑j=0NsY6(j)tl(n−j)+∑j=1NsZ6(j)t6(n−j)−q6r(n)−a6ctr(7)

For the window:

a7,1rt1(n)+a7,2rt2(n)+a7,3rt3(n)+a7,4rt4(n)+a7,5rt5(n)+a7,6rt6(n)−[a7+K7a7a7−K7]t7(n)+a7,8rt8(n)=−K7a7a7−K7ta(n)−q7r(n)−a7ctr(8)

For the door:

a8,1rt1(n)+a8,2rt2(n)+a8,3rt3(n)+a8,4rt4(n)+a8,5rt5(n)+a8,6rt6(n)+a8,7rt7(n)−[a8+K8a8a8−K8]t8(n)=−K8a8a8−K8tl(n)−q8r(n)−a8ctr(9)

The above heat balance equations can be written in matrix form as follows:

A Ti(n)=B (10)

In this formula:

A=[−[a1+Z1(0)]a1,2ra1,3ra1,4ra1,5ra1,6ra1,7ra1,8ra2,1r−[a2+Z2(0)]a2,3ra2,4ra2,5ra2,6ra2,7ra2,8ra3,1ra3,2r−[a3+Z3(0)]a3,4ra3,5ra3,6ra3,7ra3,8ra4,1ra4,2ra4,3r−[a4+Z4(0)]a4,5ra4,6ra4,7ra4,8ra5,1ra5,2ra5,3ra5,4r−[a5+Z5(0)]a5,6ra5,7ra5,8ra6,1ra6,2ra6,3ra6,4ra6,5r−[a6+Z6(0)]a6,7ra6,8ra7,1ra7,2ra7,3ra7,4ra7,5ra7,6r−[a7+K7a7a7−K7]a7,8ra8,1ra8,2ra8,3ra8,4ra8,5ra8,6ra8,7r−[a8+K8a8a8−K8]]

B=[−∑j=0NSY1(j)tZ(n−j)+∑j=1NSZ1(j)t1(n−j)−q1r(n)−a1ctr−∑j=0NSY2(j)tc(n−j)+∑j=1NSZ2(j)t2(n−j)−q2r(n)−a2ctr−∑j=0NSY3(j)tc(n−j)+∑j=1NSZ3(j)t3(n−j)−q3r(n)−a3ctr−∑j=0NSY4(j)tc(n−j)+∑j=1NSZ4(j)t4(n−j)−q4r(n)−a4ctr−∑j=0NSY5(j)tc(n−j)+∑j=1NSZ5(j)t5(n−j)−q5r(n)−a5ctr−∑j=0NSY6(j)tl(n−j)+∑j=1NSZ6(j)t6(n−j)−q6r(n)−a6ctr−K7a7a7−K7ta(n)−q7r(n)−a7ctr−K8a8a8−K8tl(n)−q8r(n)−a8ctr]

The temperature of each inside surface of the room at time n can be calculated by the following matrix equation:

Ti(n)=A −1B (11)

For continuous heating room, the heating load was primarily consisted of the heat used for heating cold air infiltrated into room, lighting and equipment, the heat released from human body, and the convection heat exchange between indoor air and inside surfaces. The hourly heating load was obtained as follows:

HL(n)=HA(n)=∑k=1NiFkakc[tk(n)−tr(n)]+q1c(n)−q2c(n)+La(n)(cρ)a[ta(n)−tr(n)]/3.6(12)

2.3.2 Mathematical Model of the Intermittent Heating

When the room is intermittently heated, due to the significant change of room temperature during the intermittent period, the surface temperature of the envelope will also change with the fluctuation of room temperature, resulting in a certain amount of heat storage. Therefore, when the room temperature is restored to a given value, the heat that should be provided to the room cannot be equal to the heat load under the design conditions. So intermittent heating is considered in three periods, occupation period, intermittent period and warm-up period.

During the occupation period, the room is heated to the indoor design air temperature. The heat storage load of the room means the heat that would transfer into envelops and should be considered. The heating load of the room during the occupation period was equal to the sum of the heating load of the room and the heat storage load at the same time.

HA(n)=HL(n)+HS(n)(13)

For the heating room, the heat storage load is able to be calculated by the heat storage reaction coefficient of the room, which means the heat at the current time and subsequent time stored into or released from the envelope when the indoor air temperature was impacted by the change of one unit of isosceles triangle wave.

The room heat storage reaction coefficient means the heat stored or released by the envelope at the time of the temperature wave and the subsequent moments when a sudden isosceles triangle change occurs in the air temperature of the room. Therefore, RS(j) can be obtained by using the heat balance equation of the envelopes and the heat balance equation of indoor air. According to Fig. 2, if tr(n−1) and tr(n) was known, the thermal balance of the whole room can be presented by the following matrix equation:

CXn=D(14)

In this formula:

C=[000A00000F1a1cF2a2cF3a3cF4a4cF5a5cF6a6cF7a7cF8a8c−1]

D=[B∑k=1NiFkakc[tk(n)−tr(n)]+q1c(n)−q2c(n)+La(n)(cρ)a[ta(n)−tr(n)]/3.6]

Due to the changes of the indoor air temperature before a certain time and at the current time, the heat storage load is the amount of heat released to the room air at that moment. Then, the room heat storage load at a certain time can be calculated.

HS(n)=−∑j=0∞RS(j)Δtr(n−j)(15)

The minus indicates that the envelope absorbs heat from indoor air.

HA(n)=HL(n)−∑j=0∞RS(j)Δtr(n−j)(16)

According to the above equation, if the changes of the indoor air temperature before time n is known, then the changes of the indoor air temperature at time n can be obtained by Eq. (17):

tr(n)=1RS(0)[HL(n)−HA(n)−∑j=0∞RS(j)Δtr(n−j)](17)

If the heating stops at time n during the intermittent period, that is, HA(n)=0, then the changes of the indoor air temperature at time n can be obtained by Eq. (18):

Δtr(n)=1RS(0)[HL(n)−∑j=0∞RS(j)Δtr(n−j)](18)

Counting from the first hour after the stop of heating, the changes of the indoor air temperature and the indoor air temperature can be calculated by Eq. (17). Then the heating load during heating period HA(n) can be obtained by Eq. (13).

3  Experimental Verification of the Dynamic Thermal Model

3.1 Experimental Systems

The room selected in this experiment was introduced in the previous section. During the intermittent heating period, the room was occupied from 8 am to 6 pm. An electric heater was used as a heater to heat the room, and a digital electric power meter was connected to the electric heater to measure the heating power. The temperature of the envelope and the indoor air were measured by thermocouples, and heat flux sensors were used to measure the heat flux on the interior walls. The measured data was automatically recorded by a data acquisition instrument (Keithley).

As shown in the Fig. 4, there were the specific positions of thermocouples and heat flux sensors. There were five thermocouples used for measuring the indoor temperature distributed in the room. Two thermocouples were arranged in the two adjacent rooms on the left and right to measure their air temperature. Thermocouples were arranged in the corridor and the outdoor air.

Figure 4: Layout of measuring points

3.2 Experimental Results and Validation

The heater was placed in the center of the room and maintained the heating power of the heater at 1500 W. Gas tracing method was used in the experiment, and the air change rate was determined by determining the concentration of carbon dioxide. Moreover, the air change rate of the room was tested before the heating process. For intermittent heating, the heater was turned on at 8 am and turned off at 18 pm. The temperature of the indoor air, corridor, adjacent room and outdoor was recorded for five consecutive days, and brought them into the intermittent heating mathematical model as known conditions. As shown in the Fig. 5, there was the outdoor temperature of the last two days, and the indoor air temperature of the last two days was compared with the experimental values and the comparison results were shown in Fig. 6.

Figure 5: Outdoor temperature of the last two days

Figure 6: Comparison of simulated values and experimental values

From Fig. 6, it was obvious that the indoor air temperature calculated by the mathematical model of intermittent heating rooms agreed with the curve of the indoor air temperature measured by experiments on the whole. On the first day, the maximum and minimum difference of the value between the experiment and simulation on the first day were 0.59°C and 0.02°C, respectively. The maximum and minimum difference of the value between the experiment and simulation on the first day were 1.27°C and 0.07°C. The maximum differences between the first and second day both appeared in the first hour of heating. The differences between the values of the experiment and simulation was within 4%, which verified the accuracy of the proposed mathematical model.

4  Thermal Performance of Intermittent Heating Rooms on a Typical Day

The room and its envelopes were the same as shown in Section 2. The meteorological data of Shanghai’s typical meteorological winter day were used for calculation. The outdoor temperature on typical day is sinusoidal temperature curve assumed based on average winter temperature change in Shanghai in recent years, and outdoor temperature on typical day was shown in Fig. 7. The initial values of temperatures of the internal surfaces and the outdoor solar-air temperature were both 18°C. The indoor temperature of adjacent rooms and the air temperature of the corridor were maintained at 10°C and 8°C, respectively. During the intermittent heating period, the room was used from 8:00 to 18:00. The indoor design temperature was 18°C during occupation. The warm-up period lasted for 2 h, which started from 6:00 to 8:00. After the warm-up period, the indoor air temperature should reach 18°C. Besides, the room was used as an office in which the heat released from human bodies, lighting and equipment was usually not large, so this part of the heat was roughly regarded as part of the heat provided by the heating equipment in this research. And the air change rate of the room was assumed as 0.5. Under this condition, simulations had been conducted.

Figure 7: Outdoor air temperature on typical day

In continuous heating, the total load is the sum of 24 h heating loads of the whole day. In intermittent heating, the total load is the sum of the heat supply during the warm-up period and the occupation period. The amount of energy saving is defined as the difference between the total load of continuous heating and intermittent heating, and energy saving ratio will be defined as the ratio of the total amount of energy saving to the total room heating load of continuous heating.

4.1 Heating Load Comparison

As shown in the Fig. 8, there is the heating load comparison between intermittent heating and continuous heating. The total load of the continuous heating and intermittent heating were 39363 and 27118 W · h, respectively. Compared with the continuous heating, the amount of energy saving and the energy saving ratio of the intermittent heating were 12245 W·h and 31.11%, respectively. However, the maximum hourly heating power for intermittent heating was 3978 W, which was more than two time of that for continuous heating, 1722 W. The higher preheating power means larger heating capacity of heating source and terminals.

Figure 8: Hourly heating load of intermittent heating and continuous heating

4.2 The Impact of Preheating Time

The impact of preheating time was studied by simulations in this section. The basic analysis conditions were the same as those in Section 4.1. At the end point of preheating, it was assumed that the indoor air temperature was 18°C, and the preheating power at each time of preheating period was assumed to be consistent. Four preheating time were calculated as 1, 2, 3, 4 h. The simulated results were shown in Fig. 9.

Figure 9: Energy saving effect under different preheating time

As shown in Fig. 9, when the indoor air temperature was the same at the end of the preheating period, the longer the preheating time, the smaller the preheating power, and the smaller the energy saving ratio. The preheating power and the energy saving ratio were 1930.31 W and 17.91% respectively when the preheating time was 1 h. The preheating power and the energy saving ratio were 1451.55 W and 10.73% respectively when the preheating time was 4 h. The differences of preheating power and energy saving ratio were 478.77 W and 7.18%, respectively. When the preheating time increased from 1 to 4 h, the preheating power decreased insignificantly, while the energy saving ratio decrease greatly. Therefore, the preheating time of 1 h was usually enough and should not exceed 2 h for most cases.

4.3 The Impact of Occupation Hours

In this simulation, except for the changes in occupation hours, all the other conditions for the calculation were same as the calculation conditions of in Section 4.1. The influence of the occupation hours on the heating load was studied. Four occupation hours were calculated as 4, 6, 8 and 10 h. The simulated results were shown in Fig. 10.

Figure 10: Energy saving conditions under different occupation hours

As shown in Fig. 10, as for the intermittent heating, the longer the occupation time, the higher the total load, and the lower energy saving and energy saving ratio. The total load, the amount of energy saving and energy saving ratio of intermittent heating were 18095, 21269 W· h and 54.03% respectively when the operating time was 4 h. It was obvious that when the occupation time was reduced, the amount of energy saving and the energy saving ratio were greatly increased. When the occupation time was 4 h, the preheating load is 8995 W⋅h, accounting for 49.71% of the total load, and when the occupation time was 10 h, the preheating load was 7956 W⋅h, accounting for 29.34% of the total load. It should be noted that the energy saving ratio by intermittent heating was much lower than unoccupied period ratio (the ratio of the unoccupied period hours to the 24).

4.4 Influence of Required Room Temperature during Occupation

The influence of required room temperature on the heating load was studied. Three conditions of required room temperature of 15°C, 18°C and 21°C during occupation were calculated. Except for the different required room temperature, other calculation conditions were same as the thermal analysis in the Section 4.1.

As shown in Fig. 11, the higher required room temperature, the higher the total load and the amount of energy saving of intermittent heating, and the lower energy saving ratio. When the required room temperature was 15°C, the total load of intermittent heating and continuous heating and the amount of energy saving were the smallest, which were respectively 17967, 26292 and 8325 W⋅h, and the energy saving ratio was highest, 31.66%. When the temperature was 21°C, the total load of intermittent heating and continuous heating and the energy saving ratio increased by 18303, 26144 and 7085 W⋅h, respectively, and the energy saving ratio decreased to 31.83%, which was slightly lower than that at 15°C.

Figure 11: Energy saving conditions under different room temperature

Therefore, the total load increased obviously with the rise of heating temperature, but the amount of energy saving of intermittent heating was increased nearly with the same proportion, thereby resulting in a slightly lower energy saving ratio.

4.5 The Effect of Air Change Rates

The influence of air change rates on the heating load was studied in this section. Three air change rates of 0.5, 1 and 2 were calculated, in other words, three cold air flowrates 34.68, 69.36 and 138.72 m3/h were used. Except for the different heating temperature, other calculation conditions were same as the thermal analysis of the Section 4.1.

As shown in Fig. 12, when air change rates was 0.5 h−1, the total load, the amount of energy saving and energy saving ratio were the lowest, which were 27118, 12245 W⋅h and 31.11%, respectively. When air change rates was 2 h−1, the three indicators increased by 6380, 4852 W⋅h and 2.86%, respectively. It was obvious that the total load of continuous and intermittent heating increased with increase of air change rates, and the energy saving ratio was slightly increased.

Figure 12: Energy saving conditions under different air change rates

4.6 Influence of U-Value of Window

The influence of U-value of exterior window was studied in this section. Three U-values of 2, 3.5 and 6 W/(m2·K) were calculated. Except for the different U-vales of exterior window, other calculation conditions were same as the thermal analysis in Section 4.1.

As shown in Fig. 13, as the U-value of the window increased, the total load of intermittent heating and continuous heating, the amount of energy saving and energy saving ratio are all increased. When, the values of the indicators were the lowest, which were 37753, 26193, 11559 W⋅h and 30.62%, respectively. When the window U-value was increased from 2 to 6 W/(m2·K), the total load of continuous and intermittent heating, the amount of energy saving and energy saving ratio increased by 4297, 2426, 1843 W⋅h and 1.27%, respectively.

Figure 13: Energy saving conditions under different U-values of window

4.7 Influence of Heating Conditions in Adjacent Rooms

The influence of heating conditions in adjacent rooms was studied in this section. The heating and non-heating of adjacent rooms were calculated, respectively. In the previous cases, for facilitating the simulation calculation, the adjacent rooms (the left room, the right room, the room in the upper floor, the room in the lower floor) without heating is assumed to keep at lower temperature, (e.g., 8°C). Except for the different heating conditions in adjacent rooms, other calculation conditions were same as the thermal analysis in Section 4.1.

As shown in Fig. 14, the total load of intermittent heating, the amount of energy saving and energy saving ratio when the adjacent rooms were heated as the room in question were 11380, 1051 W⋅h and 8.46%, respectively in heating condition, which were far lower than these indicators in non-heating condition. Therefore the whether the adjacent rooms are heated will significantly affect the energy-saving performance.

Figure 14: Energy saving conditions under different adjacent rooms heating conditions

4.8 Influence of Wall Material

The influence of wall material was studied. The heavy-weight envelope and light-weight envelopes were calculated, respectively. Except for the different materials of the exterior and interior walls, other calculation conditions were same as the thermal analysis in Section 4.1. The thermal properties of the exterior and interior wall of the light-weight envelopes were shown in the Table 1.

As shown in Fig. 15, when using the light envelope, the total load of intermittent heating, the amount of energy saving and energy saving ratio were 23787, 8506 W⋅h and 28.87%, respectively. It was obvious that these values were obviously smaller than that when the heavy envelope was adopted under the same working condition.

Figure 15: Energy saving conditions under different wall material

5  Conclusions

This study selected a representative office in Shanghai as the objective. Under typical winter weather days in Shanghai, the thermal process of intermittently heating for rooms was analyzed and compared with continuous heating.

The following conclusions were drawn:

(1) Compared with the continuous heating, as for the room with intermittent heating, the amount of energy saving and energy saving ratio were 12245 W·h and 31.11%, respectively. When the occupation period was reduced from 10 to 4 h, compared with continuous heating, the energy saving ratio increased from 31% to 54%. It should be noted that, the energy saving ratio was much lower than the unoccupied period ratio.

(2) The maximum hourly heating load for intermittent heating during preheating could be higher than twice of the hourly heating load for continuous heating. Furthermore, the preheating power decreased insignificantly when the preheating time increased from 1 to 4 h, while the energy saving ratio decrease greatly. Therefore, the preheating time of 1 h was usually enough and should not exceed 2 h for most cases.

(3) When the required room temperature during occupation period was increased from 15°C to 21°C, the total load of intermittent heating and continuous heating and the amount of energy saving increased, but the energy saving ratio was reduced only by 0.83%. When the air change rates of the room increased from 0.5 to 2 h−1, the energy saving ratio increased by 2.86%. When the U-value of the windows increased from 2 to 6 W/(m2·K), the total load of continuous and intermittent heating increased. However, the energy saving ratio only increased by 1.27%.

(4) Whether the adjacent rooms were heated or not would significantly affect energy saving ratio of intermittent heating. When the adjacent rooms were all heated in the same manner as the room in question, the energy saving ratio was also greatly reduced from 31% to 8.46%.

(5) Compared with the room with heavy envelope, the energy saving ratio for light envelope room was reduced by 2.24%. Whether the envelopes belong to heavy or light types, it had no significant effect on energy saving ratio of intermittent heating.

Funding Statement: The research is supported by the National Natural Science Foundation of China (No. 71974129).

Availability of Data and Materials: All measurement data on which the diagrams presented in this study are based can be found in the main text.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Badran, A. A., Jaradat, A. W., Bahbouh, M. N. (2013). Comparative study of continuous versus intermittent heating for local residential building: Case studies in Jordan. Energy Conversion and Management, 65(9), 709–714. https://doi.org/10.1016/j.enconman.2011.12.036 [Google Scholar] [CrossRef]

2. Tanasiev, V., Necula, H., Costinas, S., Sava, G., Badea, A. (2015). Achieving energy savings and thermal comfort through intermittent heating in very low energy buildings. 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), pp. 2183–2188. Rome, Italy. [Google Scholar]

3. Yuan, L., Kang, Y., Wang, S., Zhong, K. (2017). Effects of thermal insulation characteristics on energy consumption of buildings with intermittently operated air-conditioning systems under real time varying climate conditions. Energy and Buildings, 155, 559–570. https://doi.org/10.1016/j.enbuild.2017.09.012 [Google Scholar] [CrossRef]

4. Ge, J., Li, S., Chen, S., Wang, X., Jiang, Z. et al. (2021). Energy-efficiency strategies of residential envelope in China’s hot summer-cold winter zone based on intermittent thermal regulation behaviour. Journal of Building Engineering, 44, 103028. https://doi.org/10.1016/j.jobe.2021.103028 [Google Scholar] [CrossRef]

5. Ling, J., Tong, H., Xing, J., Zhao, Y. (2020). Simulation and optimization of the operation strategy of ASHP heating system: A case study in Tianjin. Energy and Buildings, 226(1), 110349. https://doi.org/10.1016/j.enbuild.2020.110349 [Google Scholar] [CrossRef]

6. Li, Y., Long, E., Zhang, L., Dong, X., Wang, S. (2020). Energy-saving potential of intermittent heating system: Influence of composite phase change wall and optimization strategy. Energy Exploration & Exploitation, 39(1), 426–443. https://doi.org/10.1177/0144598720969217 [Google Scholar] [CrossRef]

7. Dong, Z., Boyi, Q., Chunlong, W. (2019). Energy-saving evaluation and control optimization of an ASHP heating system based on indoor thermal comfort. Solar Energy, 194(5), 913–922. https://doi.org/10.1016/j.solener.2019.11.042 [Google Scholar] [CrossRef]

8. Kim, M. S., Kim, Y., Chung, K. S. (2010). Improvement of intermittent central heating system of university building. Energy and Buildings, 42(1), 83–89. https://doi.org/10.1016/j.enbuild.2009.07.014 [Google Scholar] [CrossRef]

9. Mottet, L., Song, J., Short, C. A., Chen, S., Wu, J. et al. (2020). The hot summer-cold winter region in China: Challenges in the low carbon adaptation of residential slab buildings to enhance comfort. Energy and Buildings, 223(8), 110181. https://doi.org/10.1016/j.enbuild.2020.110181 [Google Scholar] [CrossRef]

10. Cho, S. H., Zaheer-uddin, M. (2003). Predictive control of intermittently operated radiant floor heating systems. Energy Conversion and Management, 44(8), 1333–1342. https://doi.org/10.1016/S0196-8904(02)00116-4 [Google Scholar] [CrossRef]

11. Deng, J., Yao, R., Yu, W., Zhang, Q., Li, B. (2019). Effectiveness of the thermal mass of external walls on residential buildings for part-time part-space heating and cooling using the state-space method. Energy and Buildings, 190(8), 155–171. https://doi.org/10.1016/j.enbuild.2019.02.029 [Google Scholar] [CrossRef]

12. Lechowska, A., Guzik, A. (2014). Model of unsteady heat exchange for intermittent heating taking into account hot water radiator capacity. Energy and Buildings, 76, 176–184. https://doi.org/10.1016/j.enbuild.2014.02.062 [Google Scholar] [CrossRef]

13. Vytchikov, Y. S., Belyakov, I. G., Saparev, M. E. (2016). Investigation of the thermal effect of building envelopes of individual building under intermittent heating. Procedia Engineering, 153(21), 856–861. https://doi.org/10.1016/j.proeng.2016.08.186 [Google Scholar] [CrossRef]

14. Pupeikis, D., Burlingis, A., Stankevičius, V. (2010). Required additional heating power of building during intermitted heating. Journal of Civil Engineering and Management, 16(1), 141–148. https://doi.org/10.3846/jcem.2010.13 [Google Scholar] [CrossRef]

15. Yan, Q., Zhao, Q. (1986). Thermal processes in building. China: China Architecture & Building Press. [Google Scholar]