 Open Access
Open Access
ARTICLE
An Optimization Capacity Design Method of Wind/Photovoltaic/Hydrogen Storage Power System Based on PSO-NSGA-II
1 Yinchuan University of Energy, Wangtaibao, Yinchuan, 750100, China
2 Qingdao University of Technology, Qingdao, 266520, China
3 State Key Laboratory of Electrical Insulation and Power Equipment, Xi’an Jiaotong University, Xi’an, 710049, China
* Corresponding Author: Yakui Liu. Email:
Energy Engineering 2023, 120(4), 1023-1043. https://doi.org/10.32604/ee.2023.025335
Received 30 July 2022; Accepted 09 October 2022; Issue published 13 February 2023
Abstract
The optimal allocation of integrated energy system capacity based on the heuristic algorithms can reduce economic costs and achieve maximum consumption of renewable energy, which has attracted many attentions. However, the optimization results of heuristic algorithms are usually influenced by the choice of hyperparameters. To solve the above problem, the particle swarm algorithm is introduced to find the optimal hyperparameters of the heuristic algorithms. Firstly, an integrated energy system consisting of the photovoltaic, wind turbine, electrolysis cell, hydrogen storage tank, and energy storage is established. Meanwhile, the minimum economic cost, the maximum wind and PV power consumption rate, and the minimum load shortage rate are considered to be the objective functions. Then, a hybrid method combined the particle swarm combined with non-dominated sorting genetic algorithms-Ⅱ is proposed to solve the optimal allocation problem. According to the optimal result, the economic cost is 6.3 million RMB, and the load shortage rate is 9.83%. Finally, four comparative experiments are conducted to verify the superiority-seeking ability of the proposed method. The comparative results indicate that the proposed method possesses a stronger merit-seeking ability, resulting in a solution satisfaction rate of 87.37%, which is higher than that of the unimproved non-dominated sorting genetic algorithms-Ⅱ.Keywords
Nomenclatures
| Acronyms | description |
| PSO | particle swarm optimization |
| NSGA-II | non-dominated sorting genetic algorithms-Ⅱ |
| PV | photovoltaic |
| Ppv,t | actual power output of the PV system at time t, kw |
| Ppv,N | rated output power of the PV system, kw |
| fpv | photovoltaic system power drop factor |
| Gt | solar intensity at time t, W/m2 |
| k | temperature coefficient of the PV system power, %/°C |
| Pcell,t | actual temperature of the PV panel at time t, °C |
| Tref | reference test temperature, °C |
| Tcell,t | actual temperature of photovoltaic panels at time t, °C |
| Ta,t | ambient temperature at time t, °C |
| Ww,t | actual wind speed at time t, m/s |
| PM | mechanical power of wind turbines, kW |
| ρair | air density, kg/m³ |
| R | wind turbine impeller radius, m |
| γ | leaf tip speed ratio |
| γi | intermediate variable |
| β | pitch angle |
| Cp | wind energy conversion efficiency factor for blades |
| vw | wind speed, m/s |
| ω | angular speed of fan rotation, rad/s |
| Ebat | stored energy of the battery, kW |
| δ | self-discharge rate of batteries |
| Pbat_ch | charging power of the battery, kW |
| Pbat_dh | discharging power of the battery, kW |
| ηch | battery charging efficiency |
| ηdh | battery discharging efficiency |
| ηbat_DC-DC | conversion efficiency of battery-connected converters |
| Δt | time step |
| AEC,t | real-time hydrogen production, kg |
| PEC,t | real-time operating power of the electrolytic cell |
| ηEC | electrical to gas conversion efficiency |
| b | energy conversion factor |
| nsto | hydrogen storage tank storage capacity, kg |
| net hydrogen storage rate in hydrogen storage tanks | |
| hydrogen feed rate to hydrogen storage tanks | |
| hydrogen output rate from hydrogen storage tanks | |
| PFC | output power of hydrogen fuel cells, kW |
| nH2 | hydrogen consumption of hydrogen fuel cells |
| HHHV | hydrogen calorific value |
| ηFC | conversion efficiency of hydrogen fuel cells |
| Cic | investment cost of the system |
| Coc | maintenance cost of the system |
| Cre | replacement cost of the system |
| kic,i | investment cost per unit of capacity |
| ηi | inflation rate |
| Lsf,i | remaining useful life of the equipment |
| βi | replacement cost |
| T | expected operation time of the energy storage system |
| Pwind | power generated by wind turbines, kW |
| Ppv | power generated by PV, kW |
| Pload | customer power consumption, kW |
| PBat | battery power, kW |
| PFC | output of hydrogen fuel cells, kW |
| c1, c2 | learning factor |
| r1, r2 | random numbers between zero and one |
| λ1 | Crossover rate |
| λ2 | Variation rate |
The development of renewable energy is fundamental to accelerating the green and low-carbon transition scheme. Consequently, the issue of optimization capacity design of an integrated new power system has received considerable critical attention.
Recently, several types of renewable energy systems have been studied. Reference [1] designed an integrated charging station for photovoltaic (PV) and hydrogen storage. Reference [2] proposed a biogas-dominated energy hub that can supply heat, cooling, and electricity to users simultaneously. An energy storage system containing a flywheel and a lithium battery was proposed in [3], which can better help in the frequency modulation of wind farms. Reference [4] proposed a novel energy system, which consists of two sub-systems: the power generation sub-system includes an alkaline fuel cell, photovoltaic system, electrolysis tank, Stirling engine, and absorption chiller; the energy storage sub-system includes pumped-hydro-compressed air system. In [5], the authors proposed an industrial multi-energy scheduling framework consisting of PV, electric boilers, energy storage devices, energy trading platforms, and thermal energy storage. In [6], excess electricity would be converted to natural gas and generated revenue. Gas turbines also were adopted in a power-to-gas system, which can supply heat and electric power to the system [7]. In [8], a photovoltaic microgrid energy storage system was established to provide electricity to consumers. In [9], a hybrid energy storage system was established to supply energy by using electricity generated from wind turbines. A multi-energy coordination model was developed in [10], and the model includes three components: wind power generation, heat-gas coupling, and power to gas. As the technology of hydrogen production by electrolysis of water has matured and the price of related equipment has become more acceptable, more and more small-scale energy systems are considering the installation of electrolysis cell devices. Reference [11] proposed a comprehensive and tractable yet multi-energy microgrid model, including multiple sub-systems for power generation, natural gas, and hydrogen. Reference [12] proposed a microgrid model in the island mode through hydrogen fuel cells.
To make the above microgrid model more stable and reliable, the optimization of the microgrid is essential. In [13], the authors analyzed the impact of power cost and deficiency of power supply probability on the system and establish an objective function: the renewable factor. Then the objective function was solved by a hybrid Particle Swarm Optimization-Grey Wolf Optimizer (PSO-GWO). In [14], an improved particle swarm algorithm was proposed to optimize the operating cost of a grid-connected microgrid, and the results indicated eighteen percent less expensive compared to the traditional PSO. To improve the reliability of the microgrid, a nondominated sorting genetic algorithm (NSGA-II) was adopted to optimize the grid-connected microgrid model through two objective functions: average peak load (APL) and operating cost [15]. In [16], the authors designed three objective functions: the net present cost, the penalty cost of emission, and greenhouse gas emissions. Then the microgrid hybrid system is made to balance reliability and availability by the strength Pareto evolutionary algorithm (SPEA2). Reference [17] established three objective functions: initial investment cost, transaction cost, and load loss rate. Then the capacity allocation of the comprehensive energy system is optimate based on an improved NSGA-II to meet. Reference [18] established three objective functions: the integrated demand of a comprehensive energy system economic cost, renewable energy utilization, and energy supply reliability. Then an improved multiple objective particle swarm optimization (MOPSO) is adopted to reduce the impact of uncertainty on the multi-energy hub. Reference [19] established three objective functions: average annual cost, energy storage power deviation, and load peak-to-valley difference. Reference [20] presented a hybrid probabilistic optimization algorithm combining a discretization approach with MOPSO and NSGA-II to form a hybrid probabilistic optimization algorithm (HPOA) that can find the optimal location and size of an energy storage system with expected cost, voltage deviation, and expected carbon emissions as the objective function, fully taking into account the uncertainty of the wind farm output power. Reference [21] proposed a multi-level microgrid model consisting of energy demand schedulers, energy storage systems, and photovoltaic systems, as well as optimizes the above model level by level by using convex programming, game-theoretic framework, and genetic algorithms. Reference [22] proposed a new hybrid probabilistic optimization algorithm combining the advantages of probabilistic discretizing methods, multi-objective particle swarm optimization, and NSGA-II. Reference [23] established two objective functions: ESS investment cost and network power loss. Meanwhile, the improved simulated annealing PSO algorithm (ISAPSO) was proposed to solve the optimal capacity allocation problem. The results show that the above method can effectively reduce investment costs with a small power loss. In [24], PSO is used to minimize the combined cost of the electricity market, and it is reasonable and effective in a two-tier simulation model. The stochastic optimization approach is used in [25] to establish a tri-objective residential smart electrical distribution grid, and the model is solved using the epsilon-constraint method. Reference [26] established a smart energy hub system (SEHS) that includes multiple energy forms with electrical, thermal, wind, solar, and natural gas. The optimization of the system was performed using GAMS software to reduce operating costs and energy waste. Expansion of the above SEHS system to include a hydrogen storage component. The new model is optimized using the shuffled frog leaping algorithm (SFLA) to provide optimal decisions for the system thereby increasing flexibility [27]. The smart microgrid model developed in [28] considered demand-side management strategies. Reference [29] accomplished the optimization of techno-economic and socio-environmental indicators of the PV-wind-diesel generator-battery storage system using the HOMER PRO software. Reference [30] proposed a two-layer collaborative optimization method with the objective function of the upper layer objective function and the under layer objective function. The upper layer objective function includes the primary energy-saving rate (PESR), the annual cost-saving rate (ACSR), and the equivalent emission reduction rate (EERR). The upper layer objective function includes the primary energy rate (PER) and the annual ACSR. In [31], a wind-PV hybrid power system was developed then the levelized cost of energy and loss of power supply probability of the model were optimized using the multi-objective evolutionary algorithm for supplying energy. The optimization of the model was accomplished in [32] by using a predatory parasitic algorithm (PPA) to improve the system efficiency and reduce hydrogen consumption. In [33], a railroad power system was developed, and the possible investment cost was used as the objective function to optimize the proposed model using a genetic algorithm (GA).
For the sake of clarity, the proposed model is compared with the other studies reported in the literature in Table 1. Based on the previous studies, several multi-energy complementary modes have been established. However, a model of completely using clean energy to be the power generation units and simultaneously using hydrogen and batteries for energy storage has not been established. Furthermore, less research considers the influence of the community load. The model optimization results tend to be for the rated capacity or real-time power, with fewer relevant results for the optimum number of devices to work. Nevertheless, in the actual construction of energy storage systems, the number of devices is more instructive than the real-time power of the devices.

The contributions of this work can be summarized as follows:
1. The presented paper establishes a hydrogen system consisting of the electrolysis cell, hydrogen storage tank, and hydrogen fuel cell, and thus constructs a wind/PV/hydrogen storage power system for community energy supply. The power generation unit is completely composed of renewable energy, which avoids dependence on thermal power generation and greatly reduces carbon emissions.
2. Minimizing the economic cost, maximizing renewable energy consumption rate, and minimizing the load shortage rate are regarded as the objective functions of the wind-photovoltaic-hydrogen-storage DC microgrid model.
3. The allocation result will be influenced by the hyperparameters of NSGA-II. To solve the above problem, PSO is introduced to find the optimal value of the hyperparameters. Furthermore, the comparison results indicate that the proposed algorithm outperformed the traditional method.
The presented paper is organized as follows. Section 2 presents the mathematical model, objective function, and constraints of the wind/PV/hydrogen power system. Section 3 describes the basic theory of PSO and NSGA-II, and then proposes the hybrid algorithm that is used in the optimization capacity design. Section 4 analyses the optimization results of the proposed algorithm.
2 Wind/Photovoltaic/Hydrogen Storage Power System Model
The topology of the wind-photovoltaic-hydrogen-storage DC micro-grid model is shown in Fig. 1. The model consists of six key components: wind turbine, photovoltaic array, electrolytic cell, hydrogen storage tank, battery, and hydrogen fuel cell. During the operation of the model, the wind and photovoltaic power generation will be prioritized to meet the demand of the customer’s electrical load. The generated power will be used for hydrogen production or stored temporarily in batteries [34].

Figure 1: Model topology diagram
The distributed photovoltaic system mainly consists of the photovoltaic modules and the inverter. The photovoltaic modules convert light energy into electricity. The inverter converts direct current into alternating current. The principle of photovoltaic systems for generating electricity is the photovoltaic effect of semiconductors. When photons hit the surface of a metal, energy is absorbed by electrons, until the electrons escape from the metal surface and form photoelectrons. The theoretical output of photovoltaic power generation can be expressed as [35],
where Ppv,t is the actual power output of the PV system at time t, and the unit is kW. Ppv,N is the rated output power of the PV system, and the unit is kW. fpv is the photovoltaic system power drop factor. It indicates the ratio of the actual output power to the rated power under the reference conditions of the PV system, and its value reflects the degree of power reduction caused by aging, stains, rain, and so on [36]. Gt is the solar intensity at time t, and the unit is W/m2. k is the temperature coefficient of the PV system power, and the value is −0.47%/°C. Pcell,t is the actual temperature of the PV panel at time t, and the unit is °C. Tref is the reference test temperature, and the value is 25°C. Tcell,t is the actual temperature of photovoltaic panels at time t. The actual temperature of photovoltaic panels can be expressed as [37],
where Ta,t is the ambient temperature at time t, and the unit is °C. Ww,t is actual wind speed at time t, and the unit is m/s.
From Eqs. (1) and (2), it is known that the efficiency of photovoltaic power generation is affected by the ambient temperature, the intensity of radiation, and the wind speed. When the temperature is too high, the open circuit voltage of the PV cell decreases, the short circuit current increases, and thus the overall output power decreases. When solar radiation increases, the number of photons per unit of time falling on the PV module increases, which ultimately leads to an increase in the power generated by the PV. When the wind speed is high, the surface temperature of the PV module decreases, which indirectly affects the efficiency of PV power generation [38].
2.1.2 Wind-Driven Generators Unit
Wind turbines mainly consist of wind turbine blades, generators, and inverters. The wind turbine blades are driven by the wind to start rotating and transfer the mechanical energy through the wind turbine shaft to the generator for the final generation of electricity. Wind-driven generators convert wind energy into mechanical energy and finally into electricity thus achieving fuel-free and pollution-free power generation, and their power generation efficiency can be expressed as [39],
where PM is the mechanical power of wind turbines. ρair is the air density. R is the wind turbine impeller radius. γ is the leaf tip speed ratio. γi is the intermediate variable. β is the pitch angle. Cp is the wind energy conversion efficiency factor for blades. vw is the wind speed. ω the angular speed of fan rotation.
From Eqs. (3)–(6), it is known that the output power of a wind turbine is related to several parameters. When the wind speed is too low, the wind turbine increases the blade tip speed ratio and reduces the pitch angle thus increasing the wind energy utilization. When the wind speed is too fast, the corresponding parameters are adjusted to avoid damage to itself due to excessive angular velocity.
The power generated by wind and PV should maintain the normal work of the electrolytic cell, and meet the load demand. Besides, the excess portion will be stored in the battery. Once the power cannot meet the load, the battery can be discharged to play a temporary power supply. The inclusion of storage batteries in an integrated energy system can improve the reliability of supply and reduce the rate of wind and solar abandonment in the system. The formula for calculating the stored energy when charging and discharging the battery are as follows [40]:
where Ebat(t) is the stored energy of the battery. δ is the self-discharge rate of batteries. Pbat_ch and Pbat_dh are charging and discharging power of the battery. ηch and ηdh are battery charging and discharging efficiency. ηbat_DC-DC is the conversion efficiency of battery-connected converters. Δt is the time step.
In the presented paper, electrolytic cell device is chosen to meet the hydrogen load of the fuel cell. Electrolytic cell device has a high energy conversion efficiency and a low cost of hydrogen production, making it the most common method for industrial hydrogen production. The real-time hydrogen production of the electrolysis cell can be expressed as [41],
where AEC,t is the real-time hydrogen production. PEC,t is the real-time operating power of the electrolytic cell. ηEC is the electrical to gas conversion efficiency (generally taken as 75%). b is the energy conversion factor (generally taken as 39.65 kWh/kg).
2.1.5 Hydrogen Storage Tank Unit
When the hydrogen production capacity of the electrolytic cell is greater than the hydrogen load, the excess hydrogen will be stored in a hydrogen storage tank. The hydrogen stored in the tank can be replenished when the electrolytic cell cannot produce enough hydrogen for the normal operation of the hydrogen fuel cell. The presence of hydrogen storage tanks can improve the overall system’s renewable energy utilization as well as the reliability of the energy supply and the real-time hydrogen storage capacity of a hydrogen storage tank can be expressed as [42],
where nsto(t0) is the hydrogen storage tank storage capacity at time t.
Hydrogen fuel cells can convert chemical energy into electrical energy, and this paper uses a Proton Exchange Membrane Fuel Cell (PEMFC). PEMFC has the advantage of long continuous operation with low operating temperature and high-power density. The output power of a hydrogen fuel cell can be described as [43],
where PFC is the output power of hydrogen fuel cells. nH2 is the hydrogen consumption of hydrogen fuel cells. HHHV is the hydrogen calorific value, generally taken as 39 KWh/kg. ηFC is the conversion efficiency of hydrogen fuel cells, generally taken as 65%.
The presence of the battery and the hydrogen storage tank reduces the instability of the wind and PV power output, and the excess portion can be converted into hydrogen. If the system wants to increase revenue, the number of devices or the capacity of the devices should be increased. However, it inevitably leads to an increase in the economic cost, so the capacity of the individual units of the system need to be optimized. In order to solve for the optimal allocation of capacity, three objective functions are define, economic cost of the system, the rate of wind and photovoltaic power consumption, and the rate of load shortage. The first objective function f1 is to minimize the economic cost of the system [44], which includes the investment cost of the system (Cic), the operation and maintenance cost of the system (Coc) and the replacement cost of the system (Cre). The function can be expressed as,
where Pimaxis equipment capacity of PV, wind turbines, batteries, and electrolytic cells. N is the total amount of equipment. kic,i is the investment cost per unit of capacity. ηi is the inflation rate (taken as 5%). Lsf,i is the remaining useful life of the equipment [45].
The operation and maintenance costs can be expressed as [46],
where Pi,t is the operation power of the i-th device.
The replacement cost can be described as [47],
where βi is the replacement cost. T is the expected operation time of the energy storage system (30 years). ti is the useful life of the i-th device.
The second objective function f2 is to maximize the power consumption rate of PV and wind. The system output is consumed by customers and the electrolysis cell, so increasing the hydrogen production of the electrolysis cell after satisfying the customers’ demand can achieve the purpose of improving the consumption rate. The function can be expressed as [48],
where Pwind is the power generated by wind turbines. Ppv is the power generated by PV. Pload is the customer power consumption. PBat is the battery power.
The third objective function f3 is to minimize the loss of load probability. The loss of load probability related to the stable of the system. The objective function can be calculated as [49],
where PFC is the output of hydrogen fuel cells.
In order to better solve the proposed multi-objective planning problem and arrive at the optimal and realistic capacity optimization configuration, two constraints are applied, namely the power balance constraint and the equipment unit constraint [50]. The following formula for the power balance constraint can be derived from the principle of conservation of energy:
where Pele is the output of the electrolytic tank. Paba is the abandoned portion.
The unit constraints mainly restrict the output and capacity of devices, which can be described as,
where
3 Improved Multi-Objective Genetic Algorithm
NSGA-II introduces elite strategies, crowding comparison operators, and fast non-dominated sorting compared to the first generation of genetic algorithms. For non-dominated sorting, the calculation of the congestion distance is briefly described below:
(1) Non-dominant sorting
For each solution x in the population, two values need to be calculated: one is the domination number nx, which means the number of solutions that dominate x; and the other is Sx, which means the set of solutions dominated by x. Since the dominance of a solution on the first non-dominated level is equal to 0, for each solution of nx = 0, each member of the solution q is visited and its dominance is subtracted by 1. If the dominance of x is 0, it will be placed in a list Q, which therefore contains solutions belonging to the second non-dominated level. The process is then repeated for the solutions in this set until a third non-dominated hierarchy is found. The above process continues until all non-dominated layers have been found [52].
(2) Calculation of congestion
First, the populations are sorted according to the order of each objective function value from smallest to largest. Next, for each objective function, the boundary solutions are assigned an infinite distance value and each intermediate solution is assigned a distance value that is equal to the absolute value of the difference between the two neighboring solutions. The process is repeated for the different objective functions, and the distance value of the congestion is the sum of the distances on each objective.
In the multi-objective optimization problems, the objective functions are contradictory to each other and cannot be optimal at the same time, so the final result is a Pareto-optimal set of solutions. In practical engineering, it is often necessary to select a solution from the Pareto-optimal set of solutions based on three indicators (the cost, the wind and PV power consumption rate, and the loss of load probability) as the model optimization result [53].
In order to give full play to the advantages of NSGA-Ⅱ, PSO is introduced to optimize the two hyperparameter (the crossover ratio and the probability of variation) of NSGA-Ⅱ. PSO is inspired by and modeled on the predatory behavior of birds. The search space of the optimization problem is analogous to the flight space of a bird, with each bird abstracted as a particle, and the optimal solution to the optimization problem is equivalent to the food source sought by the bird. PSO formulates simple behavioral rules for each particle that are similar to the movement of a bird, so that the movement of the whole swarm exhibits similar properties to those of a bird feeding, allowing complex optimization problems to be solved.
At each iteration, each particle will record the individual optimal position and the particle swarm will record the global optimal position. When these two optima are found, the velocity and position of the particles are updated using the following expressions [54]:
where c1 and c2 are the learning factor. r1 and r2 are the random numbers between zero and one. vij is the velocity of particles. pij is the individual particle values. pgj is the global optimal value. xij is the position of the particles.
The detailed process for finding the number of devices in the microgrid model using NSGA-II after hyperparameter optimization can be seen in Fig. 2, which can be summarized as:
Step 1: The number of devices is first optimized using a traditional NSGA-II.
Step 2: An evaluation scheme is established to assess the optimization results.
Step 3: Sensitivity analysis of the relevant hyperparameters is performed in NSGA-II.
Step 4: The relevant hyperparameters are optimized based on PSO.
Step 5: The Pareto optimal solution set obtained from the optimization is brought into the evaluation function to calculate the satisfaction of the various solutions, and finally the best solution is selected as the solution for the model to optimize the number of devices according to the satisfaction size.
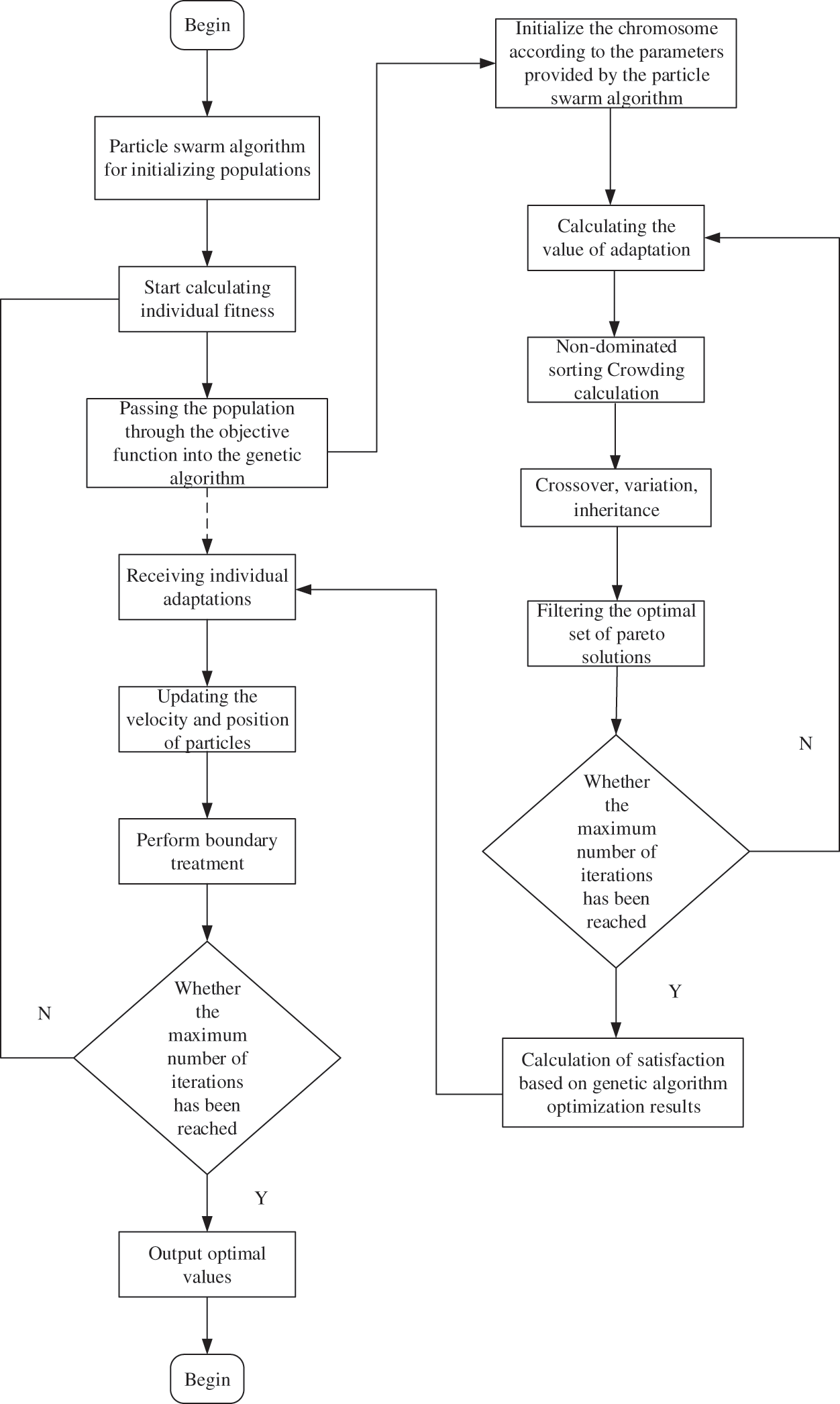
Figure 2: Optimization flow chart
In the presented paper, the construction of an evaluation function is used to calculate the satisfaction of each solution in the solution set. The comparison of satisfaction allows the superiority of solutions to be compared with each other, and serves as a criterion for optimizing the hyperparameters of the genetic algorithm by PSO. The expression for the evaluation function can be expressed as [55],
where ω(f1) denotes the normalization of the value of the objective function one.
A typical community is used as a case study to verify the validity and effectiveness of the model and methodology proposed in this paper. The data used in the case study is shown in Fig. 3. As can be seen in Figs. 3a and 3b, the solar radiation and temperature are higher at around 12 noon than at other times of the day, so the PV output during this time in Fig. 3d is higher than at other times of the day. In Fig. 3e the turbine output is more volatile due to that the parameters are adjusted at any time with the wind speed. The experimental measurements for the daily selected community load are shown in Fig. 3f.
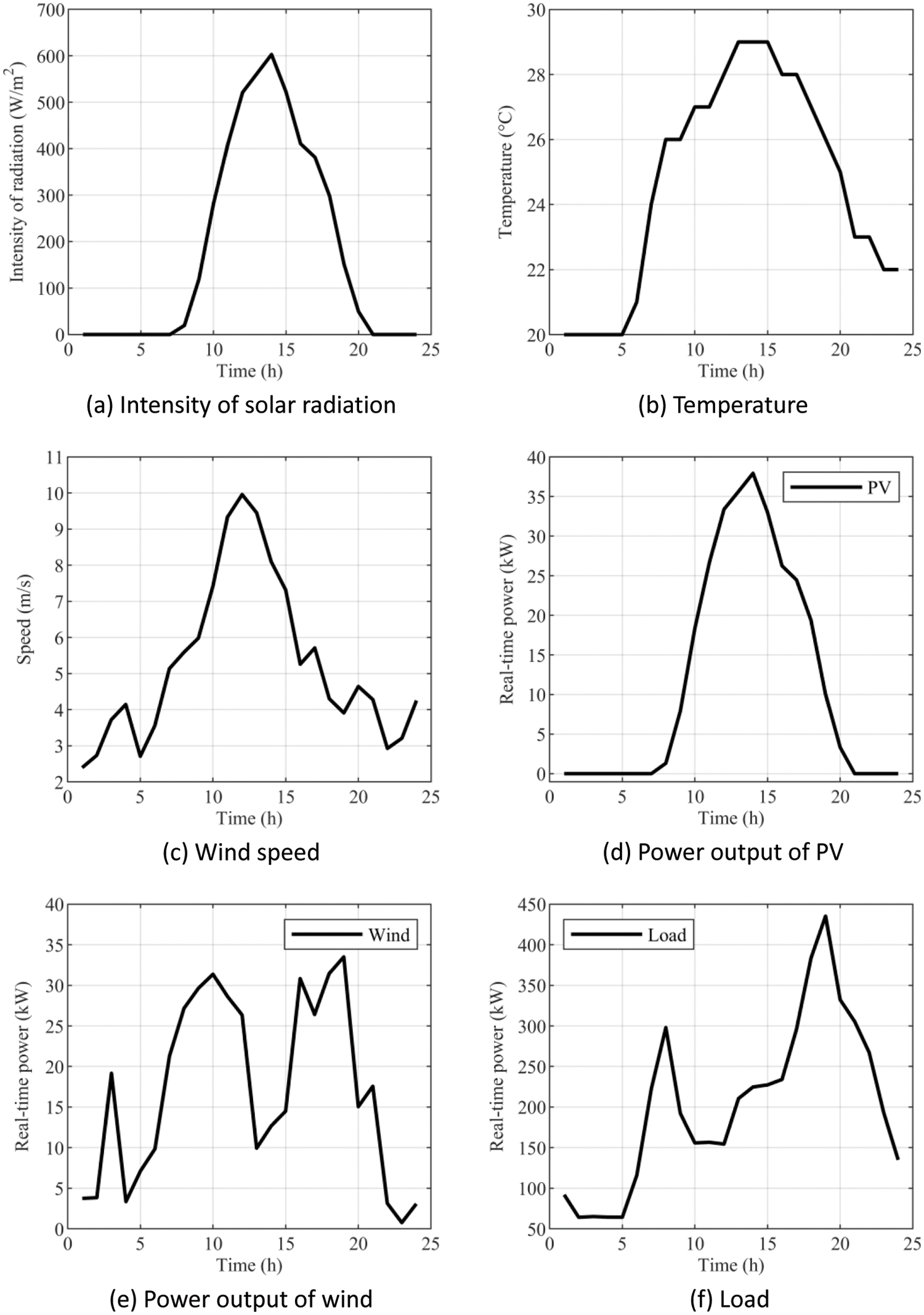
Figure 3: Data of the typical community in 24 h
Based on the above data, the results of the optimization search of the model using the unmodified NSGA-II are shown in Table 2, where the cross-ratio and variance probability hyperparameters of the algorithm are taken to be 0.8 and 0.05, respectively. The results of the sensitivity analysis are shown in Figs. 4 [56]. It is clear from the results that the selection of the crossover ratio and the probability of variation in NSGA-II has a certain influence on the optimization results.

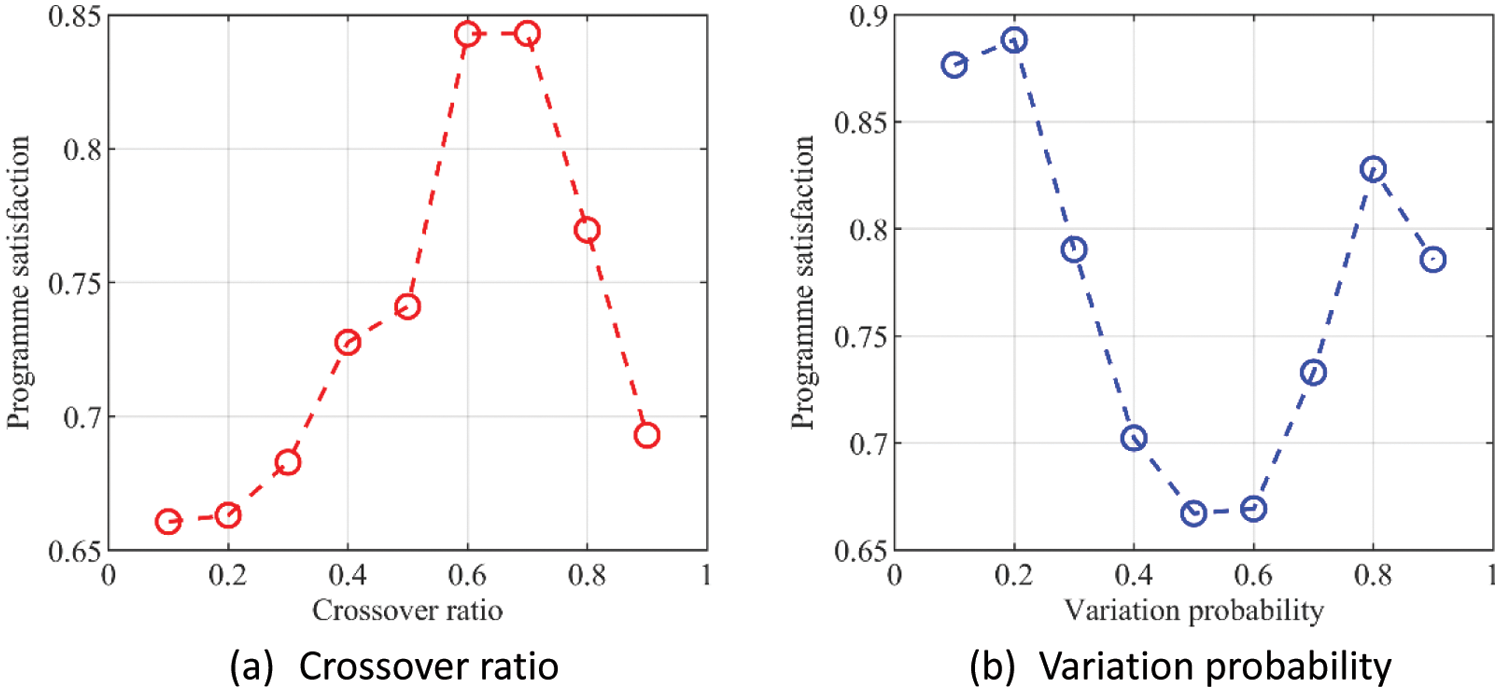
Figure 4: Influence of hyperparameters on the optimization results
Based on the proposed method, PSO is used to find the optimization of the crossover ratio and the probability of variation in NSGA-II. The mathematical model for the optimization of NSGA-II hyperparameters is shown as follows:
The evaluation function is used as the objective function of PSO. Therefore, two independent variables, the crossover ratio and the probability of variation are added to the objective function to indicate that the evaluation function is influenced by three factors: the number of devices, the crossover ratio, and the probability of variation. The PSO result indicates that the crossover ratio is 0.8831 and the probability of variation is 0.2403. When the objective function is 0.8738, the best solution for the number of settings can be obtained with 87.38% satisfaction. Furthermore, the proposed method is compared with the traditional NSGA-II in program satisfaction, and the comparison results can be seen in Table 3.

As Table 3 illustrates, the best crossover ratio and variation probabilities in NSGA-II are obtained by PSO, and the application of the above hyperparameter yielded a solution for the number of devices with a satisfaction rate of 87.38%. The solution result is shown in Table 4.

According to the allocation result. the system economic cost is 6.3 million RMB, the wind and PV power consumption rate is 89.03%, and the load shortage rate is 9.83%. Combined with the objective functions, the result indicates that most of the wind and PV power output can be consumed.
In the presented paper, a wind/PV/hydrogen power system is established, which relies entirely on renewable energy for power generation and has no carbon emissions. Minimizing the economic cost, renewable power consumption rate, and minimizing the load shortage rate are considered to be the objective functions. An energy system optimization model based on a hybrid algorithm is proposed: PSO is used to find the optimal variance rate and crossover ratio of NSGA-II; NSGA-II is applied to solve the optimization number of units. A typical community is used as a case study to verify the validity and effectiveness of the proposed model. Based on the optimization result, the proposed method improves solution satisfaction by 4.1% compared with the traditional NSGA-Ⅱ algorithm. The optimal solution improves the wind and PV power consumption rate to 89.03%. While the economic cost is reduced to 6.3 million RMB, and the load shortage rate is decreased to 9.83%.
Funding Statement: This work was supported in part by the Natural Science Foundation of Shandong Province (ZR2021QE289), and in part by State Key Laboratory of Electrical Insulation and Power Equipment (EIPE22201).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Wang, M., Dong, X., Zhai, Y. (2021). Optimal configuration of the integrated charging station for PV and hydrogen storage. Energies, 14(21), 7087. DOI 10.3390/en14217087. [Google Scholar] [CrossRef]
2. Zhang, K., Zhou, B., Li, C., Voropai, N., Li, J. et al. (2021). Dynamic modeling and coordinated multi-energy management for a sustainable biogas-dominated energy hub. Energy, 220(1), 119640. DOI 10.1016/j.energy.2020.119640. [Google Scholar] [CrossRef]
3. Yuan, M., Tian, L., Jiang, T., Hu, R., Cui, X. (2022). Research on the capacity configuration of the “flywheel + lithium battery” hybrid energy storage system that assists the wind farm to perform a frequency modulation. Journal of Physics: Conference Series, 2260(1), 012026. DOI 10.1088/1742-6596/2260/1/012026. [Google Scholar] [CrossRef]
4. Li, D., Guo, J., Zhang, J., Zhan, L., Alizadeh, M. (2021). Numerical assessment of a hybrid energy generation process and energy storage system based on alkaline fuel cell, solar energy and Stirling engine. Journal of Energy Storage, 39(1), 102631. DOI 10.1016/j.est.2021.102631. [Google Scholar] [CrossRef]
5. Xu, Z., Han, G., Liu, L., Martinez-Garcia, M., Wang, Z. (2021). Multi-energy scheduling of an industrial integrated energy system by reinforcement learning-based differential evolution. IEEE Transactions on Green Communications and Networking, 5(3), 1077–1090. DOI 10.1109/TGCN.2021.3061789. [Google Scholar] [CrossRef]
6. Zhang, R., Jiang, T., Li, F., Li, G., Chen, H. et al. (2021). Bi-level strategic bidding model for P2G facilities considering a carbon emission trading scheme-embedded LMP and wind power uncertainty. International Journal of Electrical Power and Energy Systems, 128(1), 106740. DOI 10.1016/j.ijepes.2020.106740. [Google Scholar] [CrossRef]
7. Cui, D., Ge, W., Zhao, W., Jiang, F., Zhang, Y. (2022). Economic low-carbon clean dispatching of power system containing P2G considering the comprehensive influence of multi-price factor. Journal of Electrical Engineering and Technology, 17(1), 155–166. DOI 10.1007/s42835-021-00877-4. [Google Scholar] [CrossRef]
8. Li, C., Zhu, C., Wu, K., Song, L., Wu, Q. et al. (2021). Multi-objective capacity optimal allocation of photovoltaic microgrid energy storage system based on time-sharing energy complementarity. 2021 International Conference on Power System Technology (POWERCON), pp. 1123–1129. Haikou, China. [Google Scholar]
9. Gao, X., Wang, L., Sun, H., Tian, J., Wang, Z. et al. (2021). Research on optimal configuration of hybrid energy storage system based on improved CEEMDAN. Energy Reports, 7(2), 1308–1318. DOI 10.1016/j.egyr.2021.09.133. [Google Scholar] [CrossRef]
10. Chen, J. J., Qi, B. X., Rong, Z. K., Peng, K., Zhao, Y. L. et al. (2021). Multi-energy coordinated microgrid scheduling with integrated demand response for flexibility improvement. Energy, 217(1), 119387. DOI 10.1016/j.energy.2020.119387. [Google Scholar] [CrossRef]
11. Tostado-Véliz, M., Arévalo, P., Jurado, F. (2021). A comprehensive electrical-gas-hydrogen Microgrid model for energy management applications. Energy Conversion and Management, 228, 113726. DOI 10.1016/j.enconman.2020.113726. [Google Scholar] [CrossRef]
12. Xiang, Y., Cai, H., Liu, J., Zhang, X. (2021). Techno-economic design of energy systems for airport electrification: A hydrogen-solar-storage integrated microgrid solution. Applied Energy, 283(1), 116374. DOI 10.1016/j.apenergy.2020.116374. [Google Scholar] [CrossRef]
13. Suman, G. K., Guerrero, J. M., Roy, O. P. (2021). Optimisation of solar/wind/bio-generator/diesel/battery based microgrids for rural areas: A PSO-GWO approach. Sustainable Cities and Society, 67(10), 102723. DOI 10.1016/j.scs.2021.102723. [Google Scholar] [CrossRef]
14. Hossain, M. A., Chakrabortty, R. K., Ryan, M. J., Pota, H. R. (2021). Energy management of community energy storage in grid-connected microgrid under uncertain real-time prices. Sustainable Cities and Society, 66(2), 102658. DOI 10.1016/j.scs.2020.102658. [Google Scholar] [CrossRef]
15. Teo, T. T., Logenthiran, T., Woo, W. L., Abidi, K., John, T. et al. (2021). Optimization of fuzzy energy-management system for grid-connected microgrid using NSGA-II. IEEE Transactions on Cybernetics, 51(11), 5375–5386. DOI 10.1109/TCYB.2020.3031109. [Google Scholar] [CrossRef]
16. Kharrich, M., Mohammed, O. H., Alshammari, N., Akherraz, M. (2021). Multi-objective optimization and the effect of the economic factors on the design of the microgrid hybrid system. Sustainable Cities and Society, 65, 102646. DOI 10.1016/j.scs.2020.102646. [Google Scholar] [CrossRef]
17. Zhang, Y., Sun, H., Tan, J., Li, Z., Hou, W. et al. (2022). Capacity configuration optimization of multi-energy system integrating wind turbine/photovoltaic/hydrogen/battery. Energy, 252(7), 124046. DOI 10.1016/j.energy.2022.124046. [Google Scholar] [CrossRef]
18. Hou, H., Liu, P., Xiao, Z., Deng, X., Huang, L. et al. (2021). Capacity configuration optimization of standalone multi-energy hub considering electricity, heat and hydrogen uncertainty. Energy Conversion and Economics, 2(3), 122–132. DOI 10.1049/enc2.12028. [Google Scholar] [CrossRef]
19. Zhao, J., Zhang, S., Zhang, Y., Zhang, Z. (2021). Optimal capacity configuration of hybrid energy storage system for photovoltaic plant. Proceedings-2021 IEEE Sustainable Power and Energy Conference: Energy Transition for Carbon Neutrality, pp. 1183–1188. Nanjing, China. [Google Scholar]
20. Al Ahmad, A. K., Sirjani, R. (2020). Optimal allocation of energy storage system in transmission system considering wind power. 2020 7th International Conference on Electrical and Electronics Engineering, pp. 181–187. Antalya, Turkey. [Google Scholar]
21. Lim, K. Z., Lim, K. H., Wee, X. B., Li, Y., Wang, X. (2020). Optimal allocation of energy storage and solar photovoltaic systems with residential demand scheduling. Applied Energy, 269, 115116. DOI 10.1016/j.apenergy.2020.115116. [Google Scholar] [CrossRef]
22. Ahmad, A. A. L., Sirjani, R., Daneshvar, S. (2020). New hybrid probabilistic optimisation algorithm for optimal allocation of energy storage systems considering correlated wind farms. Journal of Energy Storage, 29(2), 101335. DOI 10.1016/j.est.2020.101335. [Google Scholar] [CrossRef]
23. Zhang, S., Bai, X., Ge, L., Yan, J. (2020). Optimal configuration of energy storage system considering uncertainty of load and wind generation. IEEE Power and Energy Society General Meeting, Montreal, QC, Canada. DOI 10.1109/PESGM41954.2020.9281577. [Google Scholar] [CrossRef]
24. Ren, Z., Guo, H., Yang, P., Zuo, G., Zhao, Z. (2020). Bi-level optimal allocation of flexible resources for distribution network considering different energy storage operation strategies in electricity market. IEEE Access, 8, 58497–58508. DOI 10.1109/ACCESS.2020.2983042. [Google Scholar] [CrossRef]
25. Chamandoust, H., Derakhshan, G., Hakimi, S. M., Bahramara, S. (2020). Tri-objective scheduling of residential smart electrical distribution grids with optimal joint of responsive loads with renewable energy sources. Journal of Energy Storage, 27, 101112. DOI 10.1016/j.est.2019.101112. [Google Scholar] [CrossRef]
26. Chamandoust, H., Derakhshan, G., Hakimi, S. M., Bahramara, S. (2020). Multi-objectives optimal scheduling in smart energy hub system with electrical and thermal responsive loads. Environmental and Climate Technologies, 24(1), 209–232. DOI 10.2478/rtuect-2020-0013. [Google Scholar] [CrossRef]
27. Chamandoust, H., Derakhshan, G., Bahramara, S. (2020). Multi-objective performance of smart hybrid energy system with Multi-optimal participation of customers in day-ahead energy market. Energy and Buildings, 216(3), 109964. DOI 10.1016/j.enbuild.2020.109964. [Google Scholar] [CrossRef]
28. Chamandoust, H., Bahramara, S., Derakhshan, G. (2020). Day-ahead scheduling problem of smart micro-grid with high penetration of wind energy and demand side management strategies. Sustainable Energy Technologies and Assessments, 40(1), 100747. DOI 10.1016/j.seta.2020.100747. [Google Scholar] [CrossRef]
29. Khan, F. A., Pal, N., Saeed, S. H. (2021). Optimization and sizing of SPV/Wind hybrid renewable energy system: A techno-economic and social perspective. Energy, 233(9), 121114. DOI 10.1016/j.energy.2021.121114. [Google Scholar] [CrossRef]
30. Guo, J., Zhang, P., Wu, D., Liu, Z., Ge, H. et al. (2021). A new collaborative optimization method for a distributed energy system combining hybrid energy storage. Sustainable Cities and Society, 75(10), 103330. DOI 10.1016/j.scs.2021.103330. [Google Scholar] [CrossRef]
31. He, Y., Guo, S., Zhou, J., Wu, F., Huang, J. et al. (2021). The quantitative techno-economic comparisons and multi-objective capacity optimization of wind-photovoltaic hybrid power system considering different energy storage technologies. Energy Conversion and Management, 229(8), 113779. DOI 10.1016/j.enconman.2020.113779. [Google Scholar] [CrossRef]
32. Fathy, A., Yousri, D., Alanazi, T., Rezk, H. (2021). Minimum hydrogen consumption based control strategy of fuel cell/PV/battery/supercapacitor hybrid system using recent approach based parasitism-predation algorithm. Energy, 225(35), 120316. DOI 10.1016/j.energy.2021.120316. [Google Scholar] [CrossRef]
33. Roch-Dupré, D., Gonsalves, T., Cucala, A. P., Pecharromán, R. R., López-López, Á. J. et al. (2021). Determining the optimum installation of energy storage systems in railway electrical infrastructures by means of swarm and evolutionary optimization algorithms. International Journal of Electrical Power and Energy Systems, 124(2), 106295. DOI 10.1016/j.ijepes.2020.106295. [Google Scholar] [CrossRef]
34. He, H., Lu, Z., Guo, X., Shi, C., Jia, D. et al. (2022). Optimized control strategy for photovoltaic hydrogen generation system with particle swarm algorithm. Energies, 15(4), 1472. DOI 10.3390/en15041472. [Google Scholar] [CrossRef]
35. Hassan, Q., Jaszczur, M., Abdulateef, A. M., Abdulateef, J., Hasan, A. et al. (2022). An analysis of photovoltaic/supercapacitor energy system for improving self-consumption and self-sufficiency. Energy Reports, 8(3), 680–695. DOI 10.1016/j.egyr.2021.12.021. [Google Scholar] [CrossRef]
36. Ceran, B., Mielcarek, A., Hassan, Q., Teneta, J., Jaszczur, M. (2021). Aging effects on modelling and operation of a photovoltaic system with hydrogen storage. Applied Energy, 297(58), 117161. DOI 10.1016/j.apenergy.2021.117161. [Google Scholar] [CrossRef]
37. Hassan, Q. (2021). Evaluation and optimization of off-grid and on-grid photovoltaic power system for typical household electrification. Renewable Energy, 164, 375–390. DOI 10.1016/j.renene.2020.09.008. [Google Scholar] [CrossRef]
38. Bani Salim, M., Hayajneh, H. S., Mohammed, A., Ozcelik, S. (2019). Robust direct adaptive controller design for photovoltaic maximum power point tracking application. Energies, 12(16), 3182. DOI 10.3390/en12163182. [Google Scholar] [CrossRef]
39. Gajewski P., Pieńkowski K. (2021). Control of the hybrid renewable energy system with wind turbine, photovoltaic panels and battery energy storage. Energies, 14(6), 1595. DOI 10.3390/en14061595. [Google Scholar] [CrossRef]
40. Zhu, X., Shi, H., Xu, W., Pan, J., Zhang, T. et al. (2022). An improved air supply scheme for battery energy storage systems. Bulletin of the Polish Academy of Sciences: Technical Sciences, 70(2), 1–10. [Google Scholar]
41. Zhao, J. F., Liang, Q. C., Liang, Y. F. (2022). Simulation and study of PEMFC system directly fueled by ammonia decomposition gas. Frontiers in Energy Research, 10, 1–13. DOI 10.3389/fenrg.2022.819939. [Google Scholar] [CrossRef]
42. Luo, H., Xiao, J., Bénard, P., Chahine, R., Yang, T. (2022). Multi-objective optimization of cascade storage system in hydrogen refuelling station for minimum cooling energy and maximum state of charge. International Journal of Hydrogen Energy, 47(20), 10963–10975. DOI 10.1016/j.ijhydene.2022.01.059. [Google Scholar] [CrossRef]
43. Pirom, W., Srisiriwat, A. (2022). Electrical energy-based hydrogen production via PEM water electrolysis for sustainable energy. Proceedings of the 2022 International Electrical Engineering Congress, pp. 9–12. Khon Kaen, Thailand. [Google Scholar]
44. Fazelpour, F., Bakhshayesh, A., Alimohammadi, R., Saraei, A. (2022). An assessment of reducing energy consumption for optimizing building design in various climatic conditions. International Journal of Energy and Environmental Engineering, 13(1), 319–329. DOI 10.1007/s40095-021-00461-6. [Google Scholar] [CrossRef]
45. Li, J., Zhang, Z., Shen, B., Gao, Z., Ma, D. et al. (2020). The capacity allocation method of photovoltaic and energy storage hybrid system considering the whole life cycle. Journal of Cleaner Production, 275, 122902. DOI 10.1016/j.jclepro.2020.122902. [Google Scholar] [CrossRef]
46. Melo, F. M., Magnani, F. S., Carvalho, M. (2022). Optimization of an integrated combined cooling, heat, and power system with solar and wind contribution for buildings located in tropical areas. International Journal of Energy Research, 46(2), 1263–1284. DOI 10.1002/er.7244. [Google Scholar] [CrossRef]
47. Kommula, B. N., Song, H., Chen, L., Xu, C. (2021). Efficient energy management of hybrid renewable energy sources-based smart-grid system using a hybrid IDEA-CFA technique. International Transactions on Electrical Energy Systems, 31(5), 1–25. DOI 10.1002/2050-7038.12833. [Google Scholar] [CrossRef]
48. Alanazi, A., Alanazi, M., Arabi Nowdeh, S., Abdelaziz, A. Y., El-Shahat, A. (2022). An optimal sizing framework for autonomous photovoltaic/hydrokinetic/hydrogen energy system considering cost, reliability and forced outage rate using horse herd optimization. Energy Reports, 8(3), 7154–7175. DOI 10.1016/j.egyr.2022.05.161. [Google Scholar] [CrossRef]
49. Khezri, R., Mahmoudi, A., Aki, H. (2022). Resiliency-oriented optimal planning for a grid-connected system with renewable resources and battery energy storage. IEEE Transactions on Industry Applications, 58(2), 2471–2482. DOI 10.1109/TIA.2021.3133340. [Google Scholar] [CrossRef]
50. Jaszczur, M., Hassan, Q., Palej, P., Abdulateef, J. (2020). Multi-objective optimisation of a micro-grid hybrid power system for household application. Energy, 202, 117738. DOI 10.1016/j.energy.2020.117738. [Google Scholar] [CrossRef]
51. Chamandoust, H., Derakhshan, G., Hakimi, S. M., Bahramara, S. (2019). Tri-objective optimal scheduling of smart energy hub system with schedulable loads. Journal of Cleaner Production, 236(4), 117584. DOI 10.1016/j.jclepro.2019.07.059. [Google Scholar] [CrossRef]
52. Li, B., Deng, Y., Li, Z., Xu, J., Wang, H. (2022). Thermal-economy optimization for single/dual/triple-pressure HRSG of gas-steam combined cycle by multi-objective genetic algorithm. Energy Conversion and Management, 258(11), 115471. DOI 10.1016/j.enconman.2022.115471. [Google Scholar] [CrossRef]
53. Petchrompo, S., Coit, D. W., Brintrup, A., Wannakrairot, A., Parlikad, A. K. (2022). A review of Pareto pruning methods for multi-objective optimization. Computers and Industrial Engineering, 167(1), 108022. DOI 10.1016/j.cie.2022.108022. [Google Scholar] [CrossRef]
54. Wang, H., Wang, J., Piao, Z., Meng, X., Sun, C. et al. (2020). The optimal allocation and operation of an energy storage system with high penetration grid-connected photovoltaic systems. Sustainability, 12(15), 6154. DOI 10.3390/su12156154. [Google Scholar] [CrossRef]
55. Weerasuriya, A. U., Zhang, X., Wang, J., Lu, B., Tse, K. T. et al. (2021). Performance evaluation of population-based metaheuristic algorithms and decision-making for multi-objective optimization of building design. Building and Environment, 198(1364), 107855. DOI 10.1016/j.buildenv.2021.107855. [Google Scholar] [CrossRef]
56. Liao, X., Zhang, M., Le, J., Zhang, L., Li, Z. (2022). Global sensitivity analysis of static voltage stability based on extended affine model. Electric Power Systems Research, 208(4), 107872. DOI 10.1016/j.epsr.2022.107872. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools