 Open Access
Open Access
ARTICLE
Optimization of a Single Flash Geothermal Power Plant Powered by a Trans-Critical Carbon Dioxide Cycle Using Genetic Algorithm and Nelder-Mead Simplex Method
1 Department of Electric Engineering and Computation, Autonomous University of Ciudad Juárez, Ciudad Juárez, Chihuahua, México
2 Department of Industrial Engineering and Manufacturing, Autonomous University of Ciudad Juárez, Ciudad Juárez, Chihuahua, México
* Corresponding Authors: Yashar Aryanfar. Email: ,
Energy Engineering 2023, 120(2), 263-275. https://doi.org/10.32604/ee.2023.022587
Received 16 March 2022; Accepted 16 September 2022; Issue published 29 November 2022
Abstract
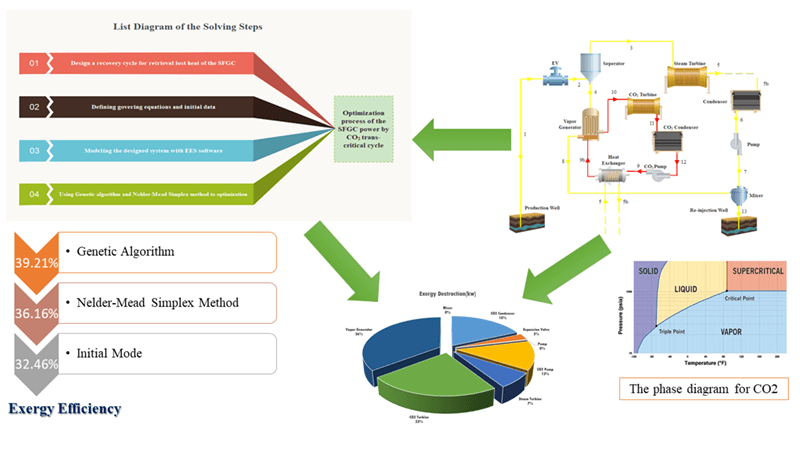
The usage of renewable energies, including geothermal energy, is expanding rapidly worldwide. The low efficiency of geothermal cycles has consistently highlighted the importance of recovering heat loss for these cycles. This paper proposes a combined power generation cycle (single flash geothermal cycle with trans-critical CO2 cycle) and simulates in the EES (Engineering Equation Solver) software. The results show that the design parameters of the proposed system are significantly improved compared to the BASIC single flash cycle. Then, the proposed approach is optimized using the genetic algorithm and the Nelder-Mead Simplex method. Separator pressure, steam turbine output pressure, and CO2 turbine inlet pressure are three assumed variable parameters, and exergy efficiency is the target parameter. In the default operating mode, the system exergy efficiency was 32%, increasing to 39% using the genetic algorithm and 37% using the Nelder-Mead method.Graphic Abstract
Keywords
In recent years, renewable energy sources have received considerable attention due to the environmental impact of fossil fuels. Geothermal energy has received more attention among renewable energies due to its reliability, stability, and high capacity [1–4]. Due to the high potential of geothermal energy worldwide, only a limited part of this resource is used [5,6]. However, electricity generation has increased in recent years using geothermal power plants, and in some countries, more than 10% of total electricity generation is due to these power plants [7,8]. In recent years, many studies have been conducted on the study and optimization of cycles of geothermal power plants [9–11].
The utilization of combined cycles and the recovery of thermal energy released to the environment is one of the suggested options for optimizing and enhancing the efficiency of geothermal systems, and the organic Rankine cycle is one of the most popular approaches. However, most organic working fluids, including water ammonia, have one or more drawbacks, including toxicity, flammability, explosiveness, and high price. Therefore, finding a better working fluid is important; for example, CO2 is easily derived from the environment, is non-toxic, non-flammable, and non-explosive, and has no adverse effects on the ecosystem, and it is suggested to be used as a fluid to produce electricity. CO2 can easily enter the supercritical state because of its low critical temperature. The most important feature of carbon dioxide is its low critical temperature, and as a result, its use in the compression cycle leads to a reduction in system dimensions. Because the trans-critical compression cycle of carbon dioxide operates at high pressures, the strength of the materials used in the components increases, which is offset by a reduction in component size and leads to significant heat dissipation in the gas cooling unit. It has high latent heat, thermal conductivity, thermal resistance and low viscosity compared to other refrigerants [12].
In this research, a power generation system’s energy efficiency and exergy efficiency have been calculated using a combined single flash geothermal source with a trans-critical carbon dioxide cycle. Separator pressure, the inlet pressure of the carbon dioxide turbine and steam turbine outlet pressure parameters will be examined to determine the optimum operating point and Fig. 1 shows the list diagram of the research steps. The novelty of the present work is to present a combined geothermal single flash system whose waste heat is recovered by a trans-critical carbon dioxide cycle. An auxiliary heat exchanger is also added to the trans-critical carbon dioxide cycle to improve the exergy efficiency of the system. Using a genetic algorithm and the Nelder-Mead simplex method, the exergy efficiency of the entire system has been optimized to determine the effectiveness of these two methods in the optimization process. In the following, the amount of exergy destruction of different system components is calculated and presented as a column chart and a pie chart. The main goals of this research are:
• Designing and modeling a combined single flash geothermal system with a trans-critical carbon dioxide cycle in the EES software environment.
• Optimizing the proposed system using a genetic algorithm and Nelder-Mid simplex method to maximize the exergy efficiency of the system.
• Investigating the amount of exergy destruction of different components of the system.
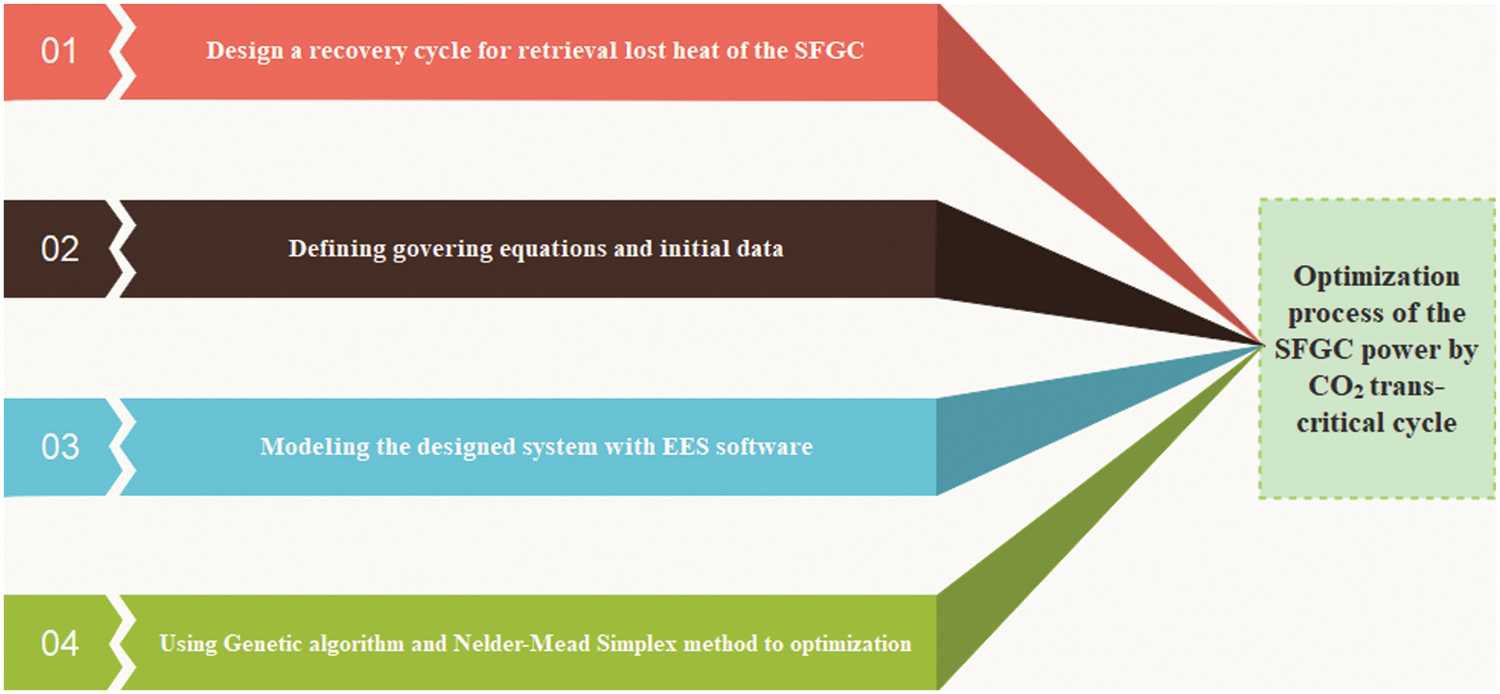
Figure 1: List diagram of the problem-solving process
According to Fig. 1, in the present work, the basic single flash geothermal cycle and recovery trans-critical CO2 cycle are designed to recover dissipated heat in the first step. In the second step, the initial data, and governing equations of the systems under study are defined using the research literature. In the third step, the proposed recovery system is simulated in the EES software environment, and in the last step, the results are optimized using genetic algorithms and the Nelder-Mead Simplex method.
The proposed basic single flash and single flash geothermal systems powered with the trans-critical carbon dioxide cycle are shown in Figs. 2 and 3. The system was simulated using engineering equation solver software (EES) [13–15]. Each system component is utilized as a control volume engineering in the simulation approach, and the first and second laws of thermodynamics are applied to it.
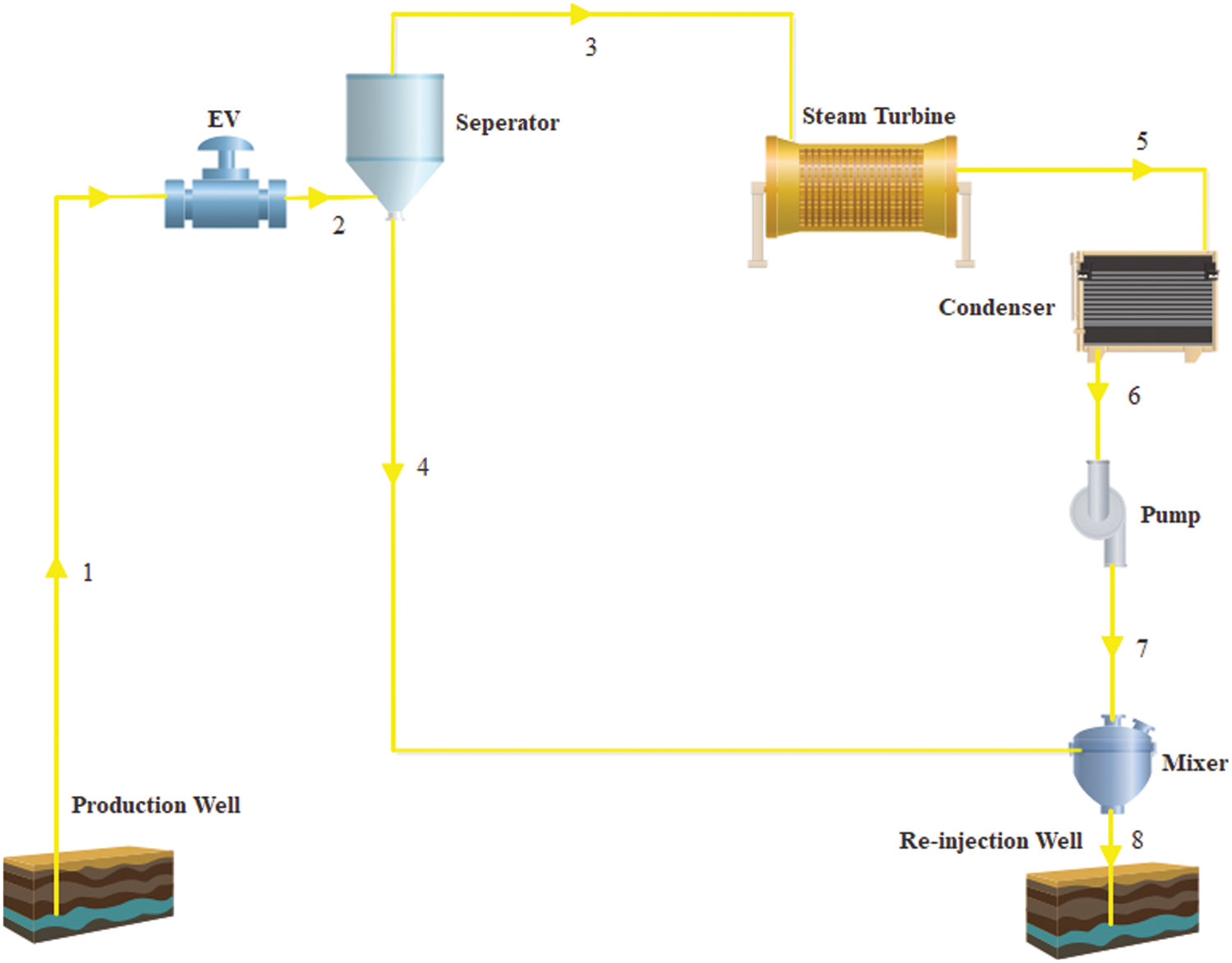
Figure 2: Schematic of basic single flash geothermal power plant
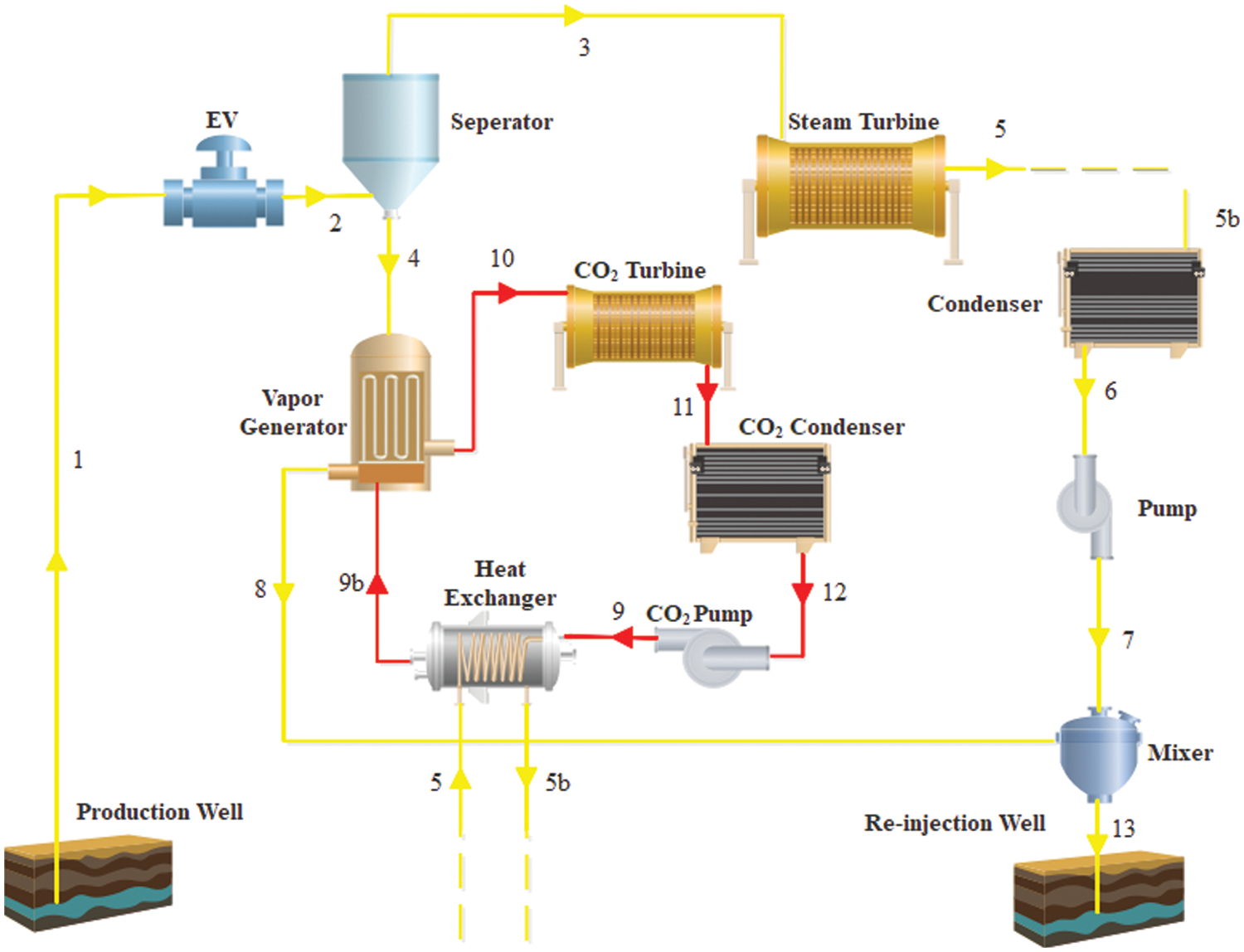
Figure 3: Schematic of single flash geothermal power plant powered by a trans-critical CO2 cycle
According to Fig. 3, after entering the system, a certain amount of geothermal fluid is converted to two-phase fluid during the decompression process, in which the pressure drop occurs at a constant enthalpy, and the two-phase fluid enters the separator, where the saturated vapor part of the fluid produces power in the steam turbine. The saturated liquid section of the separator also goes into the vapor generator (VG), which raises the temperature of carbon dioxide gas, before the heat exchanger’s outlet fluid returns to the ground. It passes through the gas turbine at the proper pressure and temperature, generating greater power for the entire system. The heat exchanger incorporated in the carbon dioxide cycle sets this research apart from earlier investigations. This heat exchanger uses the heat of the output fluid from the single-cycle steam turbine to warm the incoming gas to the vapor generator, improving the overall system performance. After passing through the heat exchanger, the steam turbine’s output fluid is cooled by a condenser before being sent to the re-injection well by the pump. Table 1 shows the input parameters needed to perform the plant’s energy and exergy analyses. The parameters are displayed in the order that they are needed.
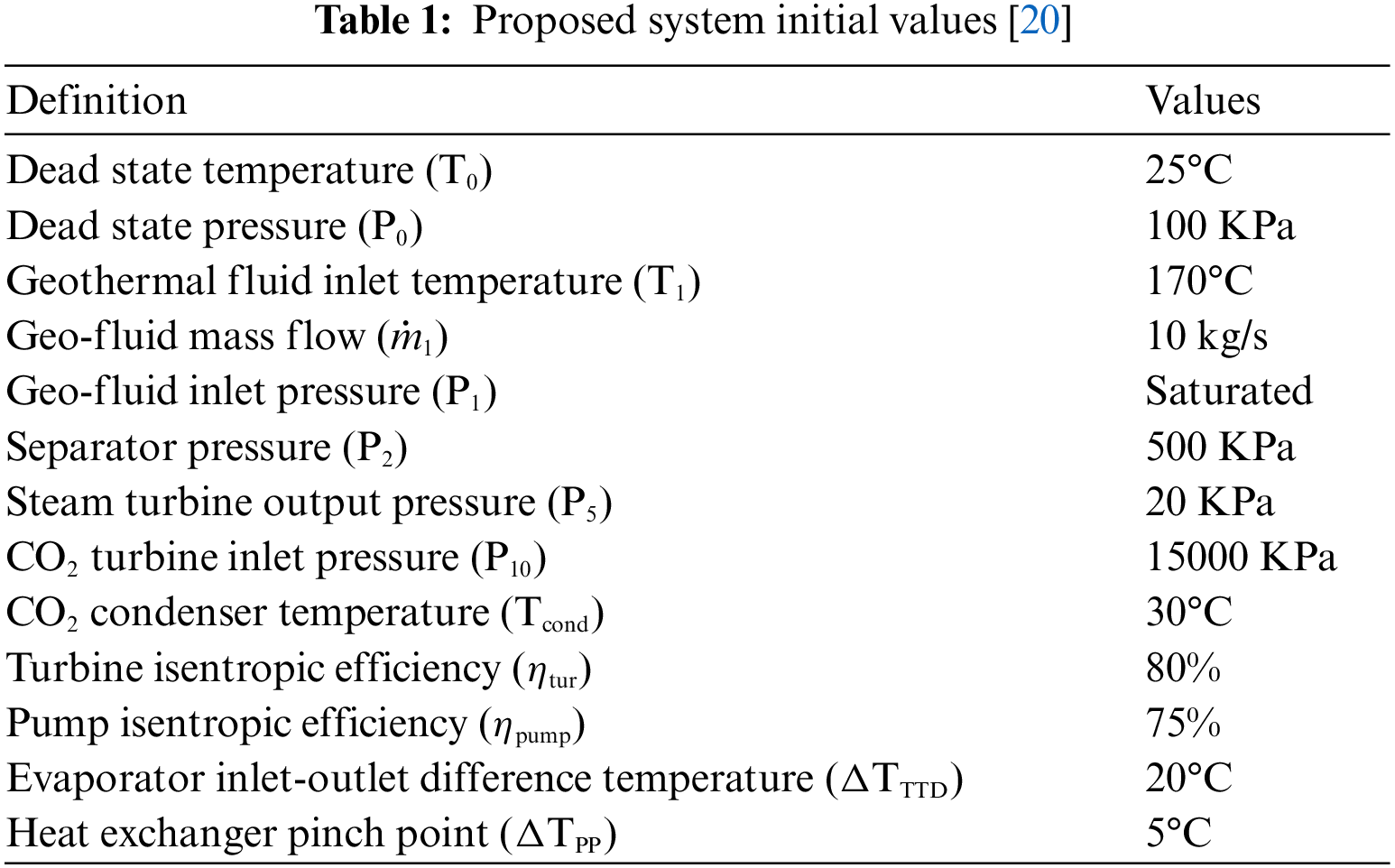
In a trans-critical cycle where carbon dioxide gas is rising in temperature inside heat exchangers such as an evaporator, the slope of the temperature change varies, so locating the congestion point is complicated. For simplicity to solve the problem, the temperature difference at the beginning and end is considered constant.
The desired cycle is written taking into account the control volume, mass and energy balance and for each component of the system according to Eqs. (1) and (2) [6,16–19]:
E is exergy; furthermore, subscript en means energy, ex means exergy, and net means network. Exergy analysis is obtained by merging the first and second laws of thermodynamics, in which the desired thermodynamic processes of a system are identified by the optimal analysis method of energy systems, as well as a clear knowledge of energy levels. The following hypotheses are considered in the present study [12,22,23]:
• All cycle components (as a control volume) work in steady-state conditions.
• Pressure drop and heat loss in pipelines can be ignored, and changes in kinetic energy and potential in all components are negligible.
• Turbines have isotropic efficiency of 80%, and pumps have isotropic efficiency of 75%.
• For the presented analysis, the ambient temperature is 25 degrees Celsius, and the ambient pressure is 100 kPa.
Definition of dead condition:
1. Be in thermal equilibrium with the environment (be at the same temperature as the environment).
2. Be in mechanical equilibrium (be at the same pressure as the environment).
3. Its kinetic energy is equal to the kinetic energy of the environment.
4. Its potential is equal to the internal energy of the environment.
5. Be chemically neutral to the environment.
6. It is magnetically and electronically balanced with the environment.
The performance of the proposed system is evaluated and analyzed in this section, and the results of energy optimization and exergy are presented in the tables. To investigate the effect of different parameters on the system performance, the values of the input parameters are given in Table 1. For the studied cycles, the net output power, thermal efficiency and exergy efficiency depend on the pressure of the separators and the difference between the evaporator tightening point temperature and the evaporator temperature.
A search heuristic that imitates the genetic processes of living things is called a genetic algorithm (GA). This heuristic is frequently employed to investigate practical answers to optimization and search problems. Genetic algorithms use stochastic direct optimization techniques and are a subset of the larger class of evolutionary algorithms (EA). The term stochastic denotes the use of random operators by GA, which could lead to a different (set of) solutions every time it is used. Additionally, because they are direct, they only operate on the value of the objective function itself, not its derivatives. GA creates an effective, all-encompassing tool that solves nearly any optimization problem, including restricted and unconstrained, single and multi-variable, linear, and nonlinear issues with continuous or discrete variables [24]. Fig. 4 shows the genetic algorithm flowchart.
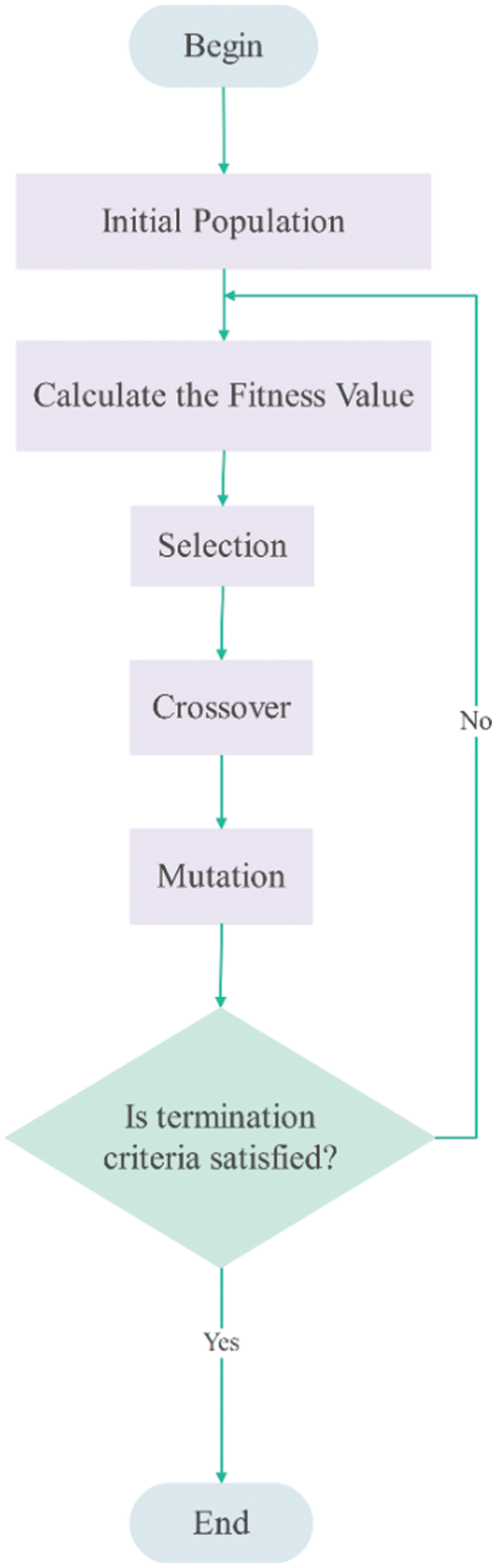
Figure 4: Flowchart of genetic algorithm [25]
Nelder and Mead first proposed the Nelder-Mead method in 1965, and the purpose of presenting this method was to solve unconstrained optimization problems; Although a long time has passed since the invention of the Nelder-Mead method, today, this method is still the right choice for solving optimization problems in the fields of statistics, engineering, physics, and medical and pharmaceutical sciences due to its ease of use and coding in the computer. This algorithm is a fast method to find the local minimum solution in optimization problems and is also used for multi-dimensional optimization problems. Also, unlike the gradient method, this method does not use the derivative of functions to find the answer. The Nelder-Mead algorithm converges to the local minimum value by forming a unique structure. Using this unique structure, the search is performed in directions with high potential to minimize the objective function. The unique structure in the Nelder-Mead method is defined as a geometric shape composed of N+1 corners, where N is the number of variables of the objective function of the optimization problem. In each iteration, the Nelder-Mead algorithm calculates the image of the worst point (the corner with the highest value of the best objective function) in line with the central point (the corner with the average good value).
Based on the value calculated in the first step, the algorithm performs expansion and contraction operations in a form with a new structure. In other words, the values of the objective function for each iteration are evaluated in the corners of the created structure. The highest value of the objective function for each corner of the structure in each iteration replaces the worst value calculated from the previous step. Otherwise, the structure moves to the best point (the corner with the lowest objective function value) and shrinks. This process is repeated until the desired error is obtained. The convergence speed of the algorithm is affected by three parameters
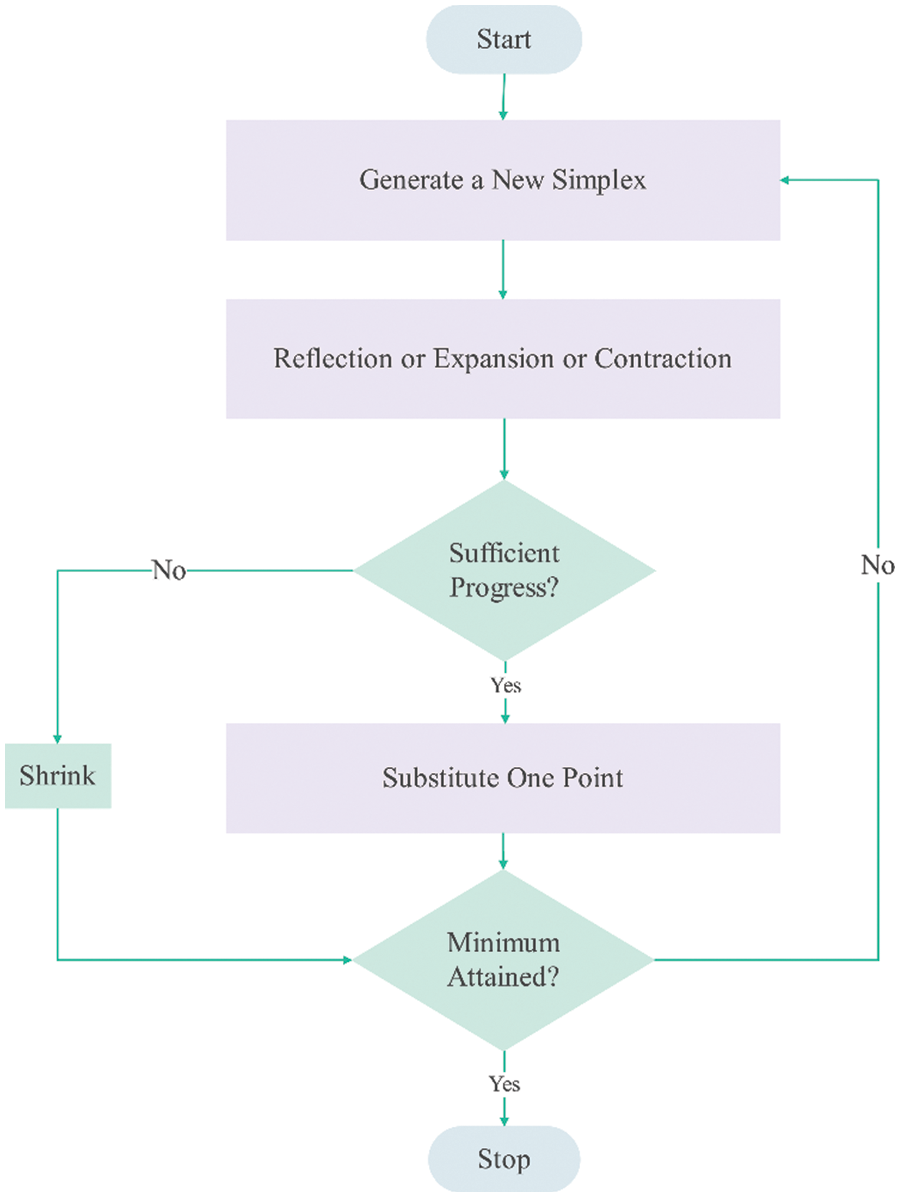
Figure 5: Flowchart of Nelder-Mead simplex method [28]
Researchers have recently become interested in global optimization, particularly when the fitness function depends on many variables or is strongly constrained by certain restrictions. As long as using only one search algorithm produces subpar results, hybridizing is the only drive that restores hope for achieving this objective. If properly executed, a combination of two algorithms in which one investigates a potential region containing global minima and the other exploits the region to discover the required point is promising. While they are renowned as effective search engines to locate and localize areas containing global minima, global methods like simulated annealing, tabu search, genetic algorithms, etc., take a very long time to converge to a particular point (if not get trapped in local minimum). On the other hand, local techniques like Nelder-Mead Simplex, climbing hills, etc., effectively utilize the search domain.
The genetic algorithm (GA) is a popular metaheuristic technique for optimizing stated functions in a confined area. According to the algorithm’s inheritance, past information is retrieved and employed in the search process. In 1989, Goldberg invented the principles of the genetic algorithm. An Evolutionary Guideline is the simulation approach described below. The Evolutionary Guideline simulation technique is a neighborhood search strategy that works the same way as a gene does [29].
Furthermore, The Nelder–Mead method, first published in, is a commonly used DS optimization approach that has been used to various unconstrained problems. NM uses an iterative technique to generate a series of simplexes that converge to the best answer. When solving an n-dimensional optimization issue, the NM approach requires n+1 vertices to define the beginning location of the simplex. To alter the simplex shape, you must do the following operations in a single iteration: reflection, expansion, contraction, and reduction. These processes cause the simplex in the decision space to evolve, and it should finally converge to the best solution. This evolution may continue in an unanticipated fashion, for example, with fewer iterations for a higher number of choice variables, depending on the original simplex’s starting position, shape, and orientation [30]. Table 2 shows the results of optimization of the proposed system using genetic algorithm and Nelder-Mead simplex method.
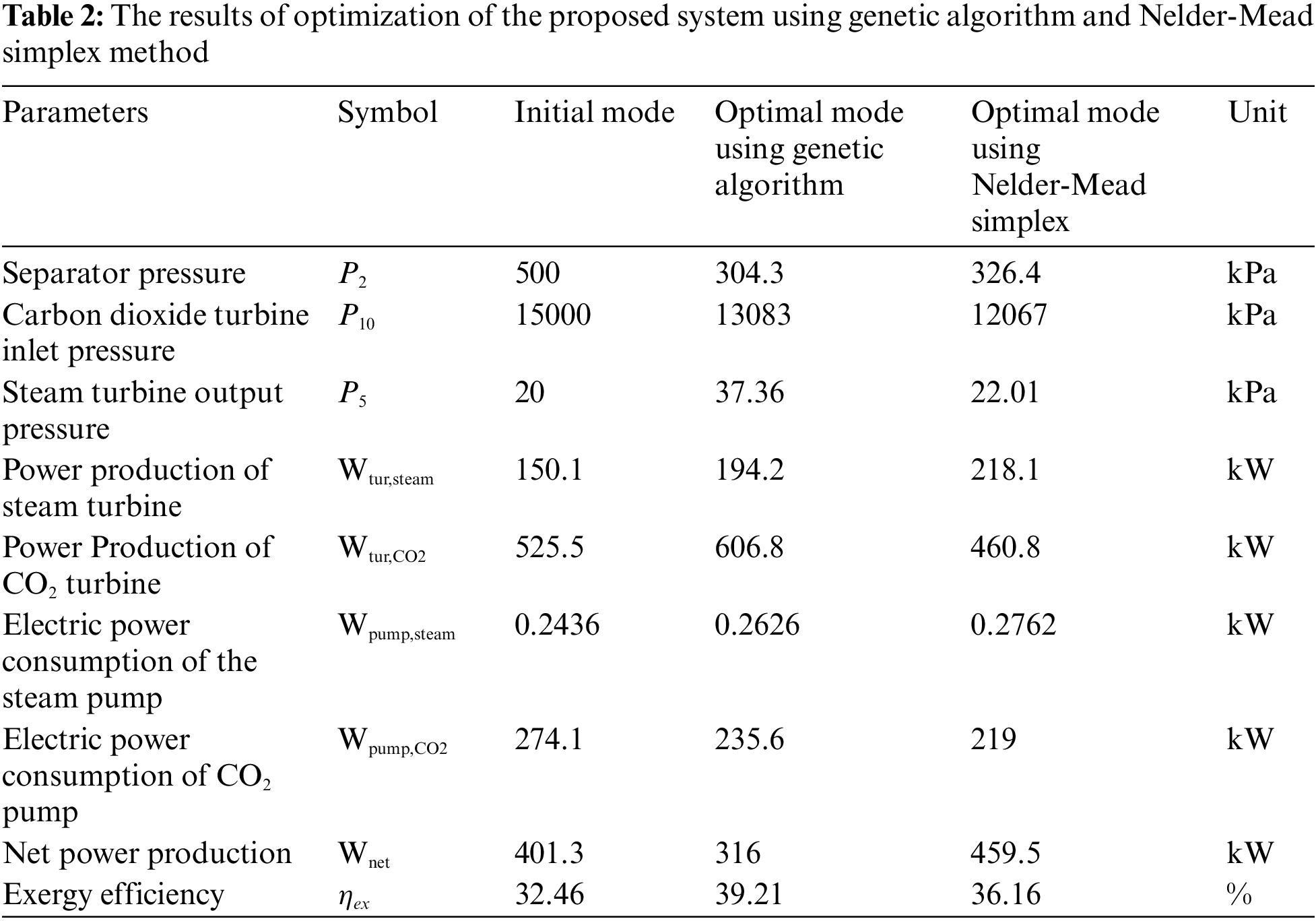
The total output of the output is 401.3 kW in BASIC mode, which after adding the recovery cycle, this value reaches 316 kW in the optimized state with the genetic algorithm and 459.5 kW in the optimized state with the Nelder-Mead simplex method. Therefore, if the goal is to increase the net output work, the working conditions obtained by the simplex method have a better result.
Exergy analysis, derived from the second law of thermodynamics, is used to analyze, upgrade energy systems, and perform new cycles [31]. Fig. 6 shows the amounts of exergy destruction of the various components of the recovery system. Fig. 7 is also a pie chart of the exergy destruction percentages of the various components. Most exergy destruction occurs in the Vapor Generator, with about 167 kW of exergy destruction, which includes almost 36% of the total exergy destruction of the proposed system, indicating a large temperature difference between the fluids in this component. CO2 turbine and CO2 condenser are in the next positions of the most exergy destruction of the system. Exergy destruction in the single flash cycle condenser and the separator is negligible and considered zero here. Also, the amount of exergy destruction in the single flash cycle pump and mixer is insignificant compared to other components, which can be seen in both diagrams. As it turns out, the exergy destruction of the carbon dioxide cycle part’s component is much more severe than the single flash cycle’s component, which can be due to the carbon dioxide cycle operating in a trans-critical state.
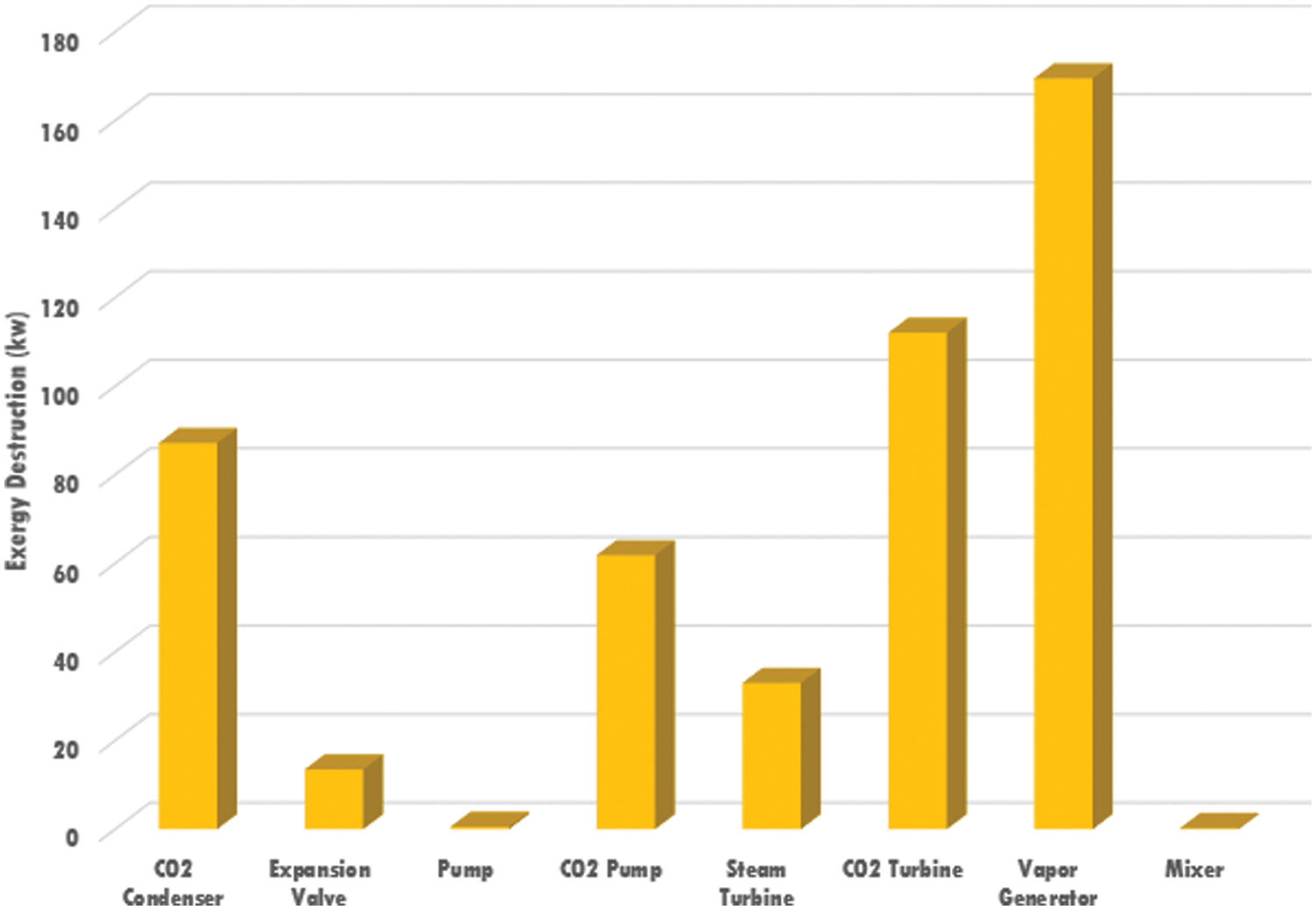
Figure 6: Exergy destruction amounts of the components of the system
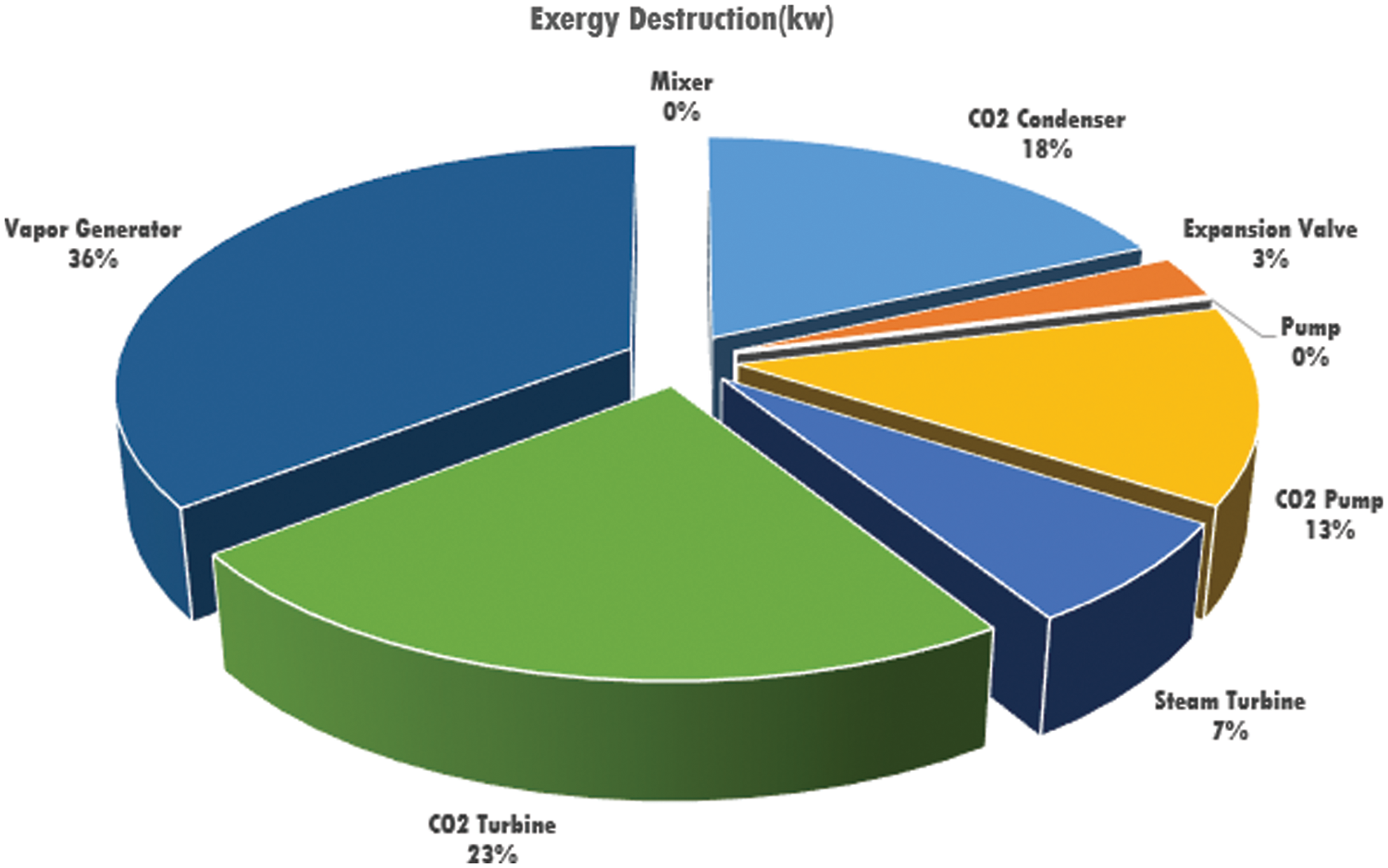
Figure 7: Exergy destruction ratio of the components of the system
The simplicity and computational efficiency of the simplex search approach make it advantageous from an algorithmic perspective. However, because they only take into account local information, there is no assurance that the global optimum will be discovered when they reach a stationary point unless the domain in which the global minimum is located is given. A GA approach, on the other hand, searches the whole search space without relying on local knowledge of possible search directions. However, it has a relatively significant computational cost. Finding global minima in various situations might be possible using a hybrid algorithm combining both traits (exploration and exploitation). It is very significant to note that none of these algorithms, along with the novel hybrid approach given in this study, call for the computation of gradient or hessian matrices; therefore, they are free from the drawbacks of traditional optimization techniques. The following will be the primary objectives of the upcoming hybrid algorithm:
- Reliability: A suitable operation of the search domain’s exploration and exploitation (also known as “diversification” and “intensification”) to locate the real global minima.
- Efficiency: Reducing the overall quantity of function evaluation using a straightforward yet effective combination.
One way to improve the performance of power generation cycles is to combine different but thermodynamically compatible cycles. Compared to other power generation units, as combined cycles with other cycles, trans-critical Carbon Dioxide cycles have certain strengths.
In this research, a combined power generation system (combined single-flash geothermal system with trans-critical carbon dioxide cycle) in energy and exergy in both optimal and primary states have been investigated and researched. Exergy efficiency in the initial state was equal to 32.46%, and after the genetic algorithm, this value increased to 39.21%. In the case of the Nelder-Mead Simplex method, the exergy efficiency has been increased from 32.46% to 36.16%. Using a genetic algorithm is more efficient than the Nelder-Mead Simplex method.
The proposed cycle was then examined from the component exergy destruction rate perspective. The exergy destruction on the carbon dioxide side was greater than in the single flash cycle. Vapor generator with 36%, CO2 turbine with 23% and CO2 condenser with 17% exergy destruction of the whole system had the highest exergy destruction among the system components. Exergy destruction in the single flash geothermal cycle condenser and the separator is negligible and is considered zero here. Also, the amount of exergy destruction in the single flash geothermal cycle’s pump and mixer is insignificant compared to other components.
Funding Statement: Yashar Aryanfar is receiving a scholarship from the National Council of Science and Technology (CONACYT) of Mexico to pursue his doctoral studies at the Universidad Autonoma de Ciudad Juarez under Grant No. 1162359.
Conflicts of Interest: The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
1. Aneke, M., Agnew, B., Underwood, C. (2011). Performance analysis of the Chena binary geothermal power plant. Applied Thermal Engineering, 31(10), 1825–1832. DOI 10.1016/j.applthermaleng.2011.02.028. [Google Scholar] [CrossRef]
2. Fan, G., Gao, Y., Ayed, H., Marzouki, R., Aryanfar, Y. et al. (2021). Energy and exergy and economic (3E) analysis of a two-stage organic Rankine cycle for single flash geothermal power plant exhaust exergy recovery. Case Studies in Thermal Engineering, 28(10), 101554. DOI 10.1016/j.csite.2021.101554. [Google Scholar] [CrossRef]
3. Mohtaram, S., Sun, Y., Omidi, M., Lin, J. (2021). Energy-exergy efficiencies analyses of a waste-to-power generation system combined with an ammonia-water dilution Rankine cycle. Case Studies in Thermal Engineering, 25(80), 100909. DOI 10.1016/j.csite.2021.100909. [Google Scholar] [CrossRef]
4. Mohtaram, S., Sun, Y., Sun, H., Abrishami, A., Omidi, M. et al. (2021). A comprehensive design, optimization and development methodology of a wasted heat recovery boiler using serrated fins and extensive surface in a bulky CCPP. Case Studies in Thermal Engineering, 23(12–17), 100808. DOI 10.1016/j.csite.2020.100808. [Google Scholar] [CrossRef]
5. Li, J., Zhu, T., Li, F., Wang, D., Bu, X. et al. (2021). Performance characteristics of geothermal single well for building heating. Energy Engineering, 118(3), 517–534. DOI 10.32604/EE.2021.014464. [Google Scholar] [CrossRef]
6. Pambudi, N. A., Wibowo, S., Ranto, Saw, L. H. (2021). Experimental investigation of organic rankine cycle (ORC) for low temperature geothermal fluid: Effect of pump rotation and R-134 working fluid in scroll-expander. Energy Engineering, 118(5), 1565–1576. DOI 10.32604/EE.2021.016642. [Google Scholar] [CrossRef]
7. Chamorro, C. R., Mondéjar, M. E., Ramos, R., Segovia, J. J., Martín, M. C. et al. (2012). World geothermal power production status: Energy, environmental and economic study of high enthalpy technologies. Energy, 42(1), 10–18. DOI 10.1016/j.energy.2011.06.005. [Google Scholar] [CrossRef]
8. Pishkariahmadabad, M., Ayed, H., Xia, W. F., Aryanfar, Y., Almutlaq, A. M. et al. (2021). Thermo-economic analysis of working fluids for a ground source heat pump for domestic uses. Case Studies in Thermal Engineering, 27(22), 101330. DOI 10.1016/j.csite.2021.101330. [Google Scholar] [CrossRef]
9. Rudiyanto, B., Bahthiyar, M. A., Pambudi, N. A., Widjonarko, Hijriawan, M. (2021). An update of second law analysis and optimization of a single-flash geothermal power plant in Dieng, Indonesia. Geothermics, 96, 102212. DOI 10.1016/j.geothermics.2021.102212. [Google Scholar] [CrossRef]
10. Budiardjo, B., Pambudi, N. A., Efendi, A. (2021). Digital energy literacy: The need for android-geofinder application based on geographic information system (GIS) to enhance student’s geothermal energy literacy in Indonesia. International Journal of Progressive Sciences and Technologies, 26(2). DOI 10.52155/ijpsat.v26.2.3119. [Google Scholar] [CrossRef]
11. Pambudi, N. A., Itoi, R., Jalilinasrabady, S., Gürtürk, M. (2018). Sustainability of geothermal power plant combined with thermodynamic and silica scaling model. Geothermics, 71(2), 108–117. DOI 10.1016/j.geothermics.2017.09.003. [Google Scholar] [CrossRef]
12. El Haj Assad, M., Aryanfar, Y., Javaherian, A., Khosravi, A., Aghaei, K. et al. (2021). Energy, exergy, economic and exergoenvironmental analyses of transcritical CO2 cycle powered by single flash geothermal power plant. International Journal of Low-Carbon Technologies, 16(4), 1504–1518. DOI 10.1093/ijlct/ctab076. [Google Scholar] [CrossRef]
13. Klein, S., Alvarado, F. (1999). EES manual. Middleton, Wisconsin, USA. [Google Scholar]
14. Klein, S. (2013). F-chart software, engineering equation solver, EES manual; Chapter 1: Getting started. Madison, WI, USA: Solar Energy Laboratory, University of Wisconsin-Madison. [Google Scholar]
15. de Oliveira, G. L.,Oliveira, A. C., Dutra, J. C. (2008). Numerical simulation of a cogeneration plant with micro gas turbine using computational tool EES; Simulacao numerica de uma planta de cogeracao com microturbina a gas natural utilizando ferramenta computacional EES. [Google Scholar]
16. Parikhani, T., Delpisheh, M., Haghghi, M. A., Holagh, S. G., Athari, H. (2021). Performance enhancement and multi-objective optimization of a double-flash binary geothermal power plant. Energy Nexus, 2(3), 100012. DOI 10.1016/j.nexus.2021.100012. [Google Scholar] [CrossRef]
17. Melzi, B., Kefif, N., Assad, M. E. H., Delnava, H., Hamid, A. (2021). Modelling and optimal design of hybrid power system photovoltaic/solid oxide fuel cell for a Mediterranean city. Energy Engineering, 118(6), 1767–1781. DOI 10.32604/EE.2021.017270. [Google Scholar] [CrossRef]
18. Yazarlou, T., Saghafi, M. D. (2021). Investigation of plans shape and glazing percentage for the energy efficiency of residential buildings. Energy Engineering, 118(6), 1783–1797. DOI 10.32604/EE.2021.017282. [Google Scholar] [CrossRef]
19. Saengsikhiao, P., Taweekun, J., Maliwan, K., Sae-ung, S., Theppaya, T. (2021). Development of environmentally friendly and energy efficient refrigerants for refrigeration systems. Energy Engineering, 118(2), 411–413. DOI 10.32604/EE.2021.012860. [Google Scholar] [CrossRef]
20. Wang, J., Wang, J., Dai, Y., Zhao, P. (2015). Thermodynamic analysis and optimization of a flash-binary geothermal power generation system. Geothermics, 55, 69–77. DOI 10.1016/j.geothermics.2015.01.012. [Google Scholar] [CrossRef]
21. Chen, L., Wang, Y., Xie, M., Ye, K., Mohtaram, S. (2021). Energy and exergy analysis of two modified adiabatic compressed air energy storage (A-CAES) system for cogeneration of power and cooling on the base of volatile fluid. Journal of Energy Storage, 42(8), 103009. DOI 10.1016/j.est.2021.103009. [Google Scholar] [CrossRef]
22. Aali, A., Pourmahmoud, N., Zare, V. (2017). Exergoeconomic analysis and multi-objective optimization of a novel combined flash-binary cycle for Sabalan geothermal power plant in Iran. Energy Conversion and Management, 143, 377–390. DOI 10.1016/j.enconman.2017.04.025. [Google Scholar] [CrossRef]
23. Sun, H., Dong, Q., Zhang, C., Chen, J. (2020). An energy efficiency improvement method for manufacturing process based on ECRSR. Energy Engineering, 117(3), 153–164. DOI 10.32604/EE.2020.010706. [Google Scholar] [CrossRef]
24. Rahami, H., Kaveh, A., Aslani, M., Najian Asl, R. (2011). A hybrid modified genetic-nelder mead simplex algorithm for large-scale truss optimization. International Journal of Optimization in Civil Engineering, 1, 29–46. [Google Scholar]
25. Albadr, M. A., Tiun, S., Ayob, M., Al-Dhief, F. (2020). Genetic algorithm based on natural selection theory for optimization problems. Symmetry, 12(11), 1758. DOI 10.3390/sym12111758. [Google Scholar] [CrossRef]
26. Cheng, B. (2005). The application of ant colony optimization algorithm in industrial process control. North China Electric Power University, China. [Google Scholar]
27. Duan, H., Wang, D., Huang, X. H., Zhu, J. Q. (2004). Research and realization on parameters optimization of PID controller based on ant colony algorithm. Engineering Journal of Wuhan University, 37(5), 97–100. [Google Scholar]
28. Barati, R. (2014). Analysis and evaluation of optimization algorithms application for parameter estimation of muskingum flood routing models in rivers. DOI 10.13140/RG.2.2.20181.86244. [Google Scholar] [CrossRef]
29. Ehyaei, M. A., Ahmadi, A., Rosen, M. A., Davarpanah, A. (2020). Thermodynamic optimization of a geothermal power plant with a genetic algorithm in two stages. Processes, 8(10), 1277. DOI 10.3390/pr8101277. [Google Scholar] [CrossRef]
30. Niegodajew, P., Marek, M., Elsner, W., Kowalczyk, Ł. (2020). Power plant optimisation—Effective use of the Nelder-Mead approach. Processes, 8(3), 357. DOI 10.3390/pr8030357. [Google Scholar] [CrossRef]
31. Yari, M., Mehr, A. S., Zare, V., Mahmoudi, S. M. S., Rosen, M. A. (2015). Exergoeconomic comparison of TLC (trilateral Rankine cycleORC (organic Rankine cycle) and Kalina cycle using a low grade heat source. Energy, 83(2), 712–722. DOI 10.1016/j.energy.2015.02.080. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools