Research of Electric Cable Path Planning Based on Heuristic Optimization Algorithm in Mixed-Land Scenario

1  Introduction

Due to the advantages of low maintenance cost, higher reliability of power supply and burying underground to beautify the city, the cable loop network has become the main objective of urban distribution network planning and reconstruction [1]. At the same time, factors such as corridor construction, power balance, load distribution, and connection mode need to be considered in the planning process [2–4]. Obviously, the cable loop path planning of a distribution network is a complex optimization problem with multi-objective, nonlinear and uncertain characteristics [5]. Although mathematical optimization algorithms theoretically guarantee the optimal solution, with the model’s increased variables and constraints increase, the path planning problem becomes more complex, making it difficult to search for the optimal solution in the feasible region. Therefore, it is necessary to explore a more efficient and intelligent solution method.

The commonly used solving algorithms for path-planning problems include mathematical optimization and heuristic intelligent algorithms [6]. With the improvement of computing resources and capability, heuristic intelligent algorithms, such as tabu search (TS) [7], simulated annealing (SA), particle swarm(PS), ant colony optimization(ACO) [8], and genetic algorithm(GA) [9], have become a better choice for distribution network path planning problems.

At present, a lot of research is committed to enhancing search speed and efficiency by improving or combining the original heuristic algorithm, in order to obtain better optimization results in a short time. To solve the problem of falling into local optima and slow convergence speed when existing algorithms are applied to the 3D design of cable laying, an artificial bee colony algorithm is proposed to be applied to the 3D design of cable laying in [10]. The adaptive probability of optional nodes matches their degree of adaptation during peak employment and observation bee search, improving the optimal search speed of the algorithm. In [11], a path-planning algorithm combining GA and ACO was proposed. GA was added to each generation of the ACO, which accelerated the convergence speed. And through selection, crossover and mutation operations, the ability of ACO to avoid falling into local optimum is improved. These researches have broadened the thinking of solving the problem, indicating that heuristic algorithms can be considered in solving the cable path planning problem. It should be noted that these methods are only applicable to special cases, and the original algorithm needs to be improved according to the actual situation.

With the improvement of geographic information platforms, the path planning of distribution network is developing toward refinement, and many articles have established a grid-based distribution network path planning model. Aiming at the transmission line selection problem with the characteristics of multi-source information, multi-objective and multi-constraint conditions, an intelligent transmission line selection algorithm combining multi-source geographic information and an improved genetic algorithm is proposed in [12] by considering the constraints of path length, geographic comprehensive cost, path continuity and obstacle avoidance. The proposed transmission line routing scheme can not only shorten the total length of the line, but also effectively reduce the comprehensive geographical cost of the route. In [13], the authors improved the ACO, and designed and simulated the power line erection scheme in Tibet with the help of the big data processing of geographic information. Compared with traditional simulation methods, the convergence speed of the algorithm is greatly improved. The planning results of these methods are more refined, which benefits from the grid processing method of the land parcel. It can be found that the smaller the divided grid, the more accurate the planning path results will be. At the same time, it is necessary to consider the problem of computation, and control the number of grids within a certain range to ensure that the model operation results can be obtained in a short time.

In short, for the distribution network path planning problem, the research mainly focuses on two aspects, planning scenarios and solving algorithms. Some researchers tend to consider more comprehensively and establish a more realistic investment model, while others are committed to improving the algorithm to speed up the operation and get better solutions.

2  Literature Review

Authors in [14] proposed a techno-economic optimization tool, which incorporates the key features such as the representative maintenance cost of cables and equipment into the mathematical model, analyzes the impact of the historical performance of electrical projects on investment decisions, in order to enhance the investment decision-making process, minimize the subsequent costs of network restructuring, and make power system expansion decisions in a more economical and effective way. In [15], a path optimization method based on improved ACO and a method based on greedy clustering to select the inspection stop point are proposed. The model considers the mutual restriction between the optimal path and the optimal temperature measurement stop point, and establishes a path planning model with the goal of minimizing time consumption. The optimal inspection path and inspection stop point sequence of the robot is obtained through the ACO iterations. The planning results are used for robot substation patrol inspection. In [16], aiming at the refinement requirements of unmanned aerial vehicle (UAV) PV inspection path planning, authors analyzed the shortcomings of the previous overlay algorithm path planning, and an adaptive method is proposed from the vertical and horizontal dimensions. For the inspection orders problem between different zones, GA is used to solve this variant of the traveling salesman problem. In [17], a new hybrid meta-heuristic method was proposed to solve the path planning problem of UAVs at multiple stations in power inspection. The algorithm adds a variable neighborhood descent to subordinate strategy under the framework of adaptive large neighborhood search, strengthens the neighborhood searchability, and increases the possibility of finding a better solution. It is verified with other meta-heuristic algorithms that the algorithm in this paper can effectively reduce the number and time cost of UAVs used in inspection. In [18], by analyzing the constraints of the observation window, the road network, and the time consumption of the attitude adjustment of the head, taking the total time of the robot to complete the inspection task as the cost, the robot path planning model was established for meter reading-oriented, and an ACO algorithm based on pheromone utilization was proposed to solve the inspection path and the parking scheme of the robot. The simulation results show that the inspection path obtained by the method in this paper is 66% less than the initial time cost, which verifies the effectiveness of the model and the feasibility of the algorithm. In [19], the antibody gene parameters were introduced, an improved immune ACO was proposed, and the optimal path selection model is established by combining the fuzzy neural network. The three-dimensional results of the calculation of the optimal path are displayed by using the substation electric field distribution map and the electric field simulation results of the electric equipment and patrol robot. The case analysis results show that the path selection model established in this paper can effectively calculate the optimal safe inspection path of the inspection robot, and has fewer iteration times than the traditional intelligent algorithm.

The above literature review shows that heuristic algorithms have several advantages over other algorithms in solving path-planning problems. Firstly, the heuristic algorithm does not require the objective function to have continuous differentiable conditions, and does not need to calculate the gradient function. Its random search features help to obtain a higher global optimal probability. Secondly, with the improvement of computer resources, the problem-solving speed of the heuristic algorithm has been greatly improved. Thirdly, for path planning problems, heuristic algorithms have many options, such as particle swarm optimization, ant optimization, fish swarm, bee swarm, etc. These heuristic algorithms are easy to understand, mature in theory, widely used, and can achieve better planning results after improvement according to actual needs. In particular, ACO and GA are insensitive to the complexity of the problem and have strong global search ability, which is suitable for solving the path planning problems in this paper.

In [20–23], ACO is used to solve typical path planning problems, such as searching the path of mobile robots, reasonably planning the distribution path of cold chain transportation, determining the effective route of public transport, and optimizing tourism routes. In [24,25], ACO minimizes the cost of assigning personnel to the factory, and optimizes the energy management and control of photovoltaic (PV), battery and supercapacitor (SC), which improves the overall efficiency of the system. In [26–28], ACO has played an important role in the intelligent security detection system based on the IoT and blockchain, the service function detection mechanism between multiple edge computing servers, and the authentication of data on the Internet of vehicles. In [29,30], ACO plays a key role in optimizing the allocation of communication resources in the design of appropriate and shortest routes in wireless sensor networks and the differentiated routing strategy of information center networks. In [31–33], ACO can help to find the optimal parameters in solving the optimal parameter set of electromagnetic problems, solving the benchmark electromagnetic problems, and finding high-quality approximate solutions. In [34,35], the immune genetic algorithm was studied, and the genetic algorithm is introduced to solve computer game problems. In [36], authors took the optimal solution searched by the genetic algorithm as the initial pheromone value of the ant colony algorithm, and add the crossover operation of the genetic algorithm to the ant colony algorithm to optimize the search speed. In [37], the MINLP problem was transformed into a linear programming problem by using Chu-Beasley genetic algorithm (CBGA), and the TNEP problem considering active power loss is solved.

In short, ACO and GA are popular with heuristic algorithms. Through the above research, it can be concluded that ACO can reach the global minimum faster than GA because it avoids falling into the local minimum. At the same time, due to the advantages of simple implementation and a small number of parameters, it can have few control parameters and can save more debugging time in the calculation process of the case. The most important thing is that the execution of different tasks of the ACO can be completed by individuals at the same time, which has the characteristics of parallelism, flexibility, robustness, scalability, and self-organization. Based on the above analysis, for the path planning problem in the paper, the ACO is more suitable for the actual scene with many grid plots. In the process of tie lines planning, the number of tie lines is far less than the number of grid plots, which requires less computation. GA can have a faster convergence speed through the coding of decision variables, and can also display the planning results more intuitively [38–40]. Therefore, the GA method is adopted for the planning of the tie line.

Given that existing research has taken little account of differences in construction costs among different types of land, this paper proposes a path planning method for cable loop network based on a heuristic optimization algorithm in the mixed-land scenario. Firstly, the plots of the power supply unit are rasterized with the help of GIS, and are divided into 6 different types according to the properties of land uses, such as residential, commercial, industrial, green space, roads, and public, in order to obtain the spatial distribution of different plots in the mixed-land scenario. Secondly, the kernel density estimation (KDE) is carried out for different plot samples, respectively, and the typical value of the construction cost is obtained, in order to quantify the unit grid cost by the analytic hierarchy process (AHP). Then, the path planning model of the cable loop network is established, and the objective function is to minimize the construction investment and operation cost, and the constraints are power balance, safe operation and connectivity, etc. In addition, the transition probability function and pheromone update formula of the ACO are improved by integrating the pheromone weight factor, the search direction and the elite ant thought, which are used to solve the cable loop network planning model in order to minimize the construction cost. And based on the path planning results, the GA is used to plan the tie line, so that the operation cost is minimized. Finally, compared with the traditional method the case analysis part, the objective quantification method of cable corridor construction cost for different plots is realized, and the solving speed of the model and the quality of the optimal solution are improved.

3  Rasterization Method of Mixed-Land Plots and Unit Construction Cost Analysis

3.1 Rasterization of Mixed-Land Plots for Power Supply Unit Based on GIS

With the development of Geographic information systems (GIS), distribution network path planning methods begin to be associated with geographic information and spatial characteristics [41]. At present, path planning methods based on GIS are mainly presented in the form of a vector or raster grid, as shown in Fig. 1.

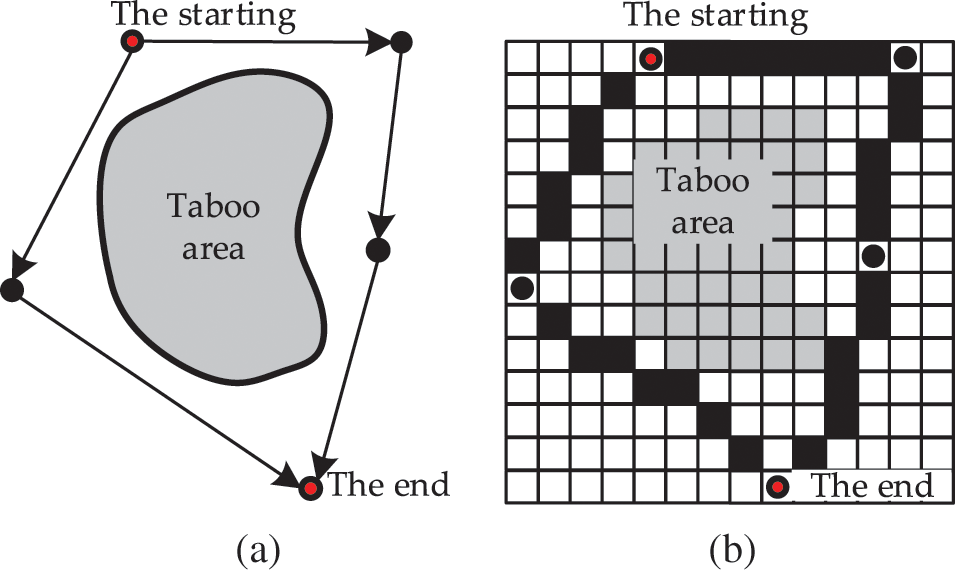
Figure 1: Two typical forms of path planning: (a) Vector method and (b) raster grid method

The vector method finds the optimal path between two nodes according to the topology structure of the network, which is not computationally intensive and is easy to solve, but it is too dependent on the actual constraints, and it is difficult to achieve refined planning results. Different from the vector method of graph theory, the raster grid method builds a grid map, searches for adjacent grids in sequence from the starting grid, and reaches the end grid after continuous optimization, and finally forms a connected path. With the improvement of computing resources, as well as the advancement of big data processing technology, distribution network path planning based on massive GIS raster data becomes possible, and the fineness of path planning results can be improved by adjusting the pixel size.

Land use types can be divided into residential, commercial, industrial, green space, transportation, public management and services, etc. For cable loop network path planning, it is necessary to build corridors to lay cables. For land plots with different properties, the cost of corridor construction varies significantly. Therefore, it is necessary to rasterize various land grids to achieve a refined effect. The process is as follows:

•   Determine the power supply area of the planned cable loop network and draw the geographical boundary with GIS;

•   Select a pixel small enough to distinguish between land plots of different properties, calculate the number of rows and columns of raster grids in the power supply area, and establish a grid matrix expressed as NR×C;

•   Combined with the land property information in GIS, the land type of each grid is filled as follows:

1.    When the proportion of the effective land area in a single grid is greater than 1/2, it needs to be filled; otherwise, no filling is required.

2.    If a single grid contains multiple land types, the entire grid is covered by the object with the largest proportion.

3.2 Quantification of Unit Raster Grid Construction Costs on Cable Paths

3.2.1 Cable Corridor Construction Cost Estimation Based on KDE

The non-parametric kernel density estimation (KDE) method does not use prior knowledge or attach any assumptions to the data distribution [42]. Instead, it studies data distribution characteristics from the samples themselves. Therefore, it is suitable for estimating the corridor construction cost of various types of land plots.

Assume that the number of a certain type of land plot in the power supply area is n, and the corridor construction cost are x1,x2,…,xn. Then, the corresponding KDE model is as follows:

fh=1nh∑i=1nK(x−xih)(1)

where n is the number of samples, x is the estimated value of corridor construction cost, fh is the probability density function, h is the bandwidth, and K is the kernel function. In addition, his closely related to the flatness of the function curve. The larger h is, the smaller proportion of sample data points in the final curve shape, so the curve is flatter. Conversely, the KDE curve is steeper.

In order to ensure the continuity of the function fh, the kernel function K is generally a nonlinear function with a single peak and is symmetrical about the y-axis. In summary, the K(x) satisfies the following properties:

{∫K(x)dx=1∫x⋅K(x)dx=0∫x2⋅K(x)dx=c>0(2)

The common kernel functions include the uniform function, Epanechikov function, Gaussian function and Quartic function. In this paper, the Gaussian function is chosen, and when h is 0.5, fh can be expressed as follows:

fh=2n∑i=1n12πe−2(x−xi)2(3)

Combined with the change of the KDE curve, the x corresponding to the maximum value of fh can be defined as the typical value xtp of the corridor construction cost for this type of land plot.

xtp=argmaxfh(x)(4)

The estimation methods for other types of plots are similar. Thus, the set of typical values of the corridor construction cost for each land plot is obtained as {xtp|xtp,i,0<i≤m}, where m is the number of land types.

3.2.2 Quantification of Unit Raster Grid Construction Costs Based on AHP and xtp

The set of typical values {xtp|xtp,i,0<i≤m} is used to construct the judgment matrix Am×m for the unit raster grid, and the matrix elements are as follows:

aij=xtp,i/xtp,j(5)

Obviously, Am×m satisfies the following characteristics:

{aij=1i=jaji=1/aiji≠j(6)

Since the Am×m conforms to the consistency test, the AHP method can be directly applied to calculate the weight ci of each type of unit raster grid, as follows:

{bij=aij/∑k=1nakjci¯=∑j=1nbijci=ci¯/∑j=1ncj¯(7)

Combined with the number of raster grid samples N, the number of land types m, and the total construction cost E, the estimated corridor construction cost Ci for the unit raster grid is as follows:

Ci=cimEN(8)

According to different land types, the above values are assigned to each raster grid of the power supply area NR×C, and the unit corridor construction cost matrix CR×C is obtained.

4  Establishment of Path Model for Planning Medium Voltage Cable Loop Network

4.1 Typical Structure of Medium Voltage Cable Loop Network

The cable loop network is the trend of urban distribution network construction and renovation. In order to improve the reliability of the power supply, the medium-voltage cable distribution network mainly adopts single or double-loop network modes. At the same time, new distribution network structures can be derived from the combination of single and double-loop networks. For example, a “diamond” cable loop distribution network has just been applied in Shanghai [43], and the structure is shown in Fig. 2.

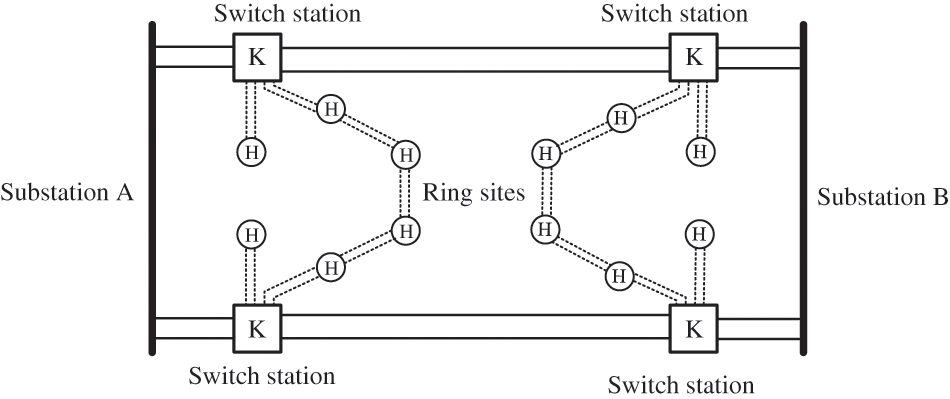
Figure 2: The structure of the “diamond” cable loop distribution network

The medium voltage “diamond” cable loop network can be divided into a backbone network and a secondary network. In short, the backbone network takes the switch station as the core node, and is powered by the substations on both sides to form a double-loop network. The secondary network takes the loop sites as the core node to form a single or double-loop network by relying on the upper switch stations. This structure can flexibly change the operation mode by adjusting the tie lines, and has better load transfer and balance ability between power stations.

4.2 The Objective Function of the Path Planning Model

For the cable loop network, the comprehensive cost of the path planning model mainly includes the cost of construction investment and operation cost. The objective function is to minimize the comprehensive cost, as follows:

minf=finv+fope(9)

where f is the annual comprehensive cost, finv is the annual construction investment of the cable loop network, and fope is the annual operating cost.

4.2.1 The Annual Construction Cost

The annual construction investment finv includes the cost of cable materials and corridor construction, and the total costs should be amortized over the entire life cycle. The annual construction cost finv is as follows:

finv=∑i=1n∑j=2k[αi⋅ri,(j−1,j)+(Ci,j−1+Ci,j)/2]⋅r0(1+r0)s(1+r0)s−1(10)

where n is the number of feeders in the cable loop network, i is the ordinal number of the feeder, k is the raster grid number of the feeder path, αi is the cost per unit length for the cable material, ri,(j−1,j) is the distance between two adjacent raster grids of the feeder, Ci,j−1 and Ci,j are the corridor construction costs of two corresponding grids, r0 is the return rate on investment, and s is the economic service life of the cable loop network.

For the distance between two adjacent raster grids, ri,(j−1,j) can be obtained as follows:

ri,(j−1,j)=(xi,j−xi,j−1)2+(yi,j−yi,j−1)2(11)

where xi,j and yi,j are the position coordinates of the jth raster grid on the path of the ith feeder.

Since the raster grids on the route are adjacent to each other, each step has 8 search directions in the process of cable path planning, as shown in Fig. 3.

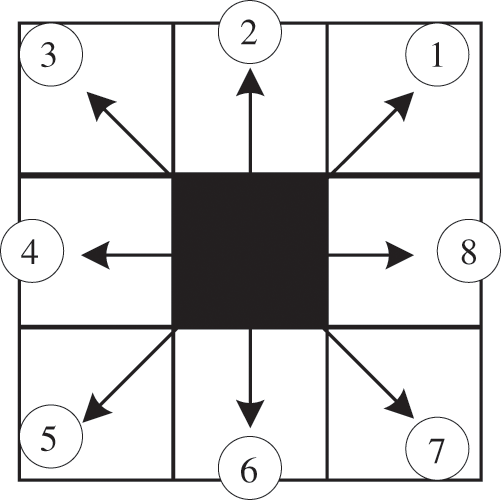
Figure 3: The search direction of the raster grid in the process of path planning

If d is the side length of the raster grid, then ri,(j−1,j) can be expressed as:

ri,(j−1,j)={dWhen the direction is 2,4,6or8.2dWhen the direction is 1,3,5or7.(12)

4.2.2 The Annual Operating Cost fope

The annual operating cost fope includes two parts: network operation loss and maintenance cost. Since the maintenance cost of the cable loop network is much less than the construction cost, the impact on the model is extremely limited. So, only the network operation loss is considered in this paper, as follows:

fope=λτmax∑i=1npi2+qi2ui2ρiLi(13)

Li=∑j=2kri,(j−1,j)(14)

where λ is the comprehensive electricity price, τmax is the maximum utilization hours per year, pi and qi are the active and reactive power of the ith feeder branch, ui is the terminal voltage, ρi is the resistance value of the cable per unit length, and Li is the total length of the ith feeder branch.

4.3 Constraints of Path Planning Model for Cable Loop Networks

For the cable loop network where the locations of power stations and switch stations in the distribution network have been limited, the path planning is mainly determined by the following constraints:

4.3.1 Power Balance

{∑Pi=Ui∑j∈ΨUj(Gijcos⁡θij+Bijsin⁡θij)∑Qi=Ui∑j∈ΨUj(Gijsin⁡θij−Bijcos⁡θij)(15)

where Pi and Qi are the active and reactive power of the node i, Ui is the node voltage, Gij and Bij are the elements in the admittance matrix corresponding to the cable loop network, and θij is the phase difference between node i and node j.

4.3.2 Safety of Operation

{Sl,min≤Sl≤Sl,maxUi,min≤Ui≤Ui,max(16)

The safety operation constraints include power flow and node voltage limits, where Sl, Sl,max and Sl,min are the feeder power flow and its upper and lower value, and Ui, Ui,max and Ui,min are the node voltage and its upper and lower value.

4.3.3 Path Search Direction

There is a constraint on the search direction between adjacent raster grids in the path of the cable loop network, which requires that the same raster grid cannot be selected repeatedly in the next steps. Combined with Fig. 3, the constraint of search direction Di,j,k can be obtained:

{Di,j,1≠Di,j−1,5,Di,j,3≠Di,j−1,7Di,j,2≠Di,j−1,6,Di,j,4≠Di,j−1,8(17)

where when the search direction of the ith feeder and its jth grid is marked as k, denote Di,j,k=1, otherwise Di,j,k=0.

4.3.4 Number of Feeders

The constraint on the number of feeders means that each substation and switch station node must be connected by feeders, and the number of feeders for each node needs to meet the capacity.

{nK,m=2,single ring networknK,m=4,double ring network1≤nP,n≤npow,lim(18)

where nK,m is the number of feeders for the mth switch station, np,n is the number of feeders for the nth substation, and npow,lim is the limit on the number of feeders that meets the requirements.

4.3.5 Connectivity of Raster Grid

Assuming that the raster grid set of the cable path lij between stations i and j is {eij}, and the raster grid set of the typical taboo area is ∏, such as lakes and mountains. There is no intersection between {eij} and ∏, and the relationship is as follows:

{eij}∩∏=∅(19)

4.3.6 Radius of Power Supply

Even if the construction cost of some raster grids is lower, the total length of the feeder branch which is formed by the raster grid is not allowed to exceed the power supply radius.

0<Li≤Lmax(20)

where Lmax is the maximum length value corresponding to the power supply radius of the feeder branch.

5  Solution of Path Planning Model Based on Heuristic Optimization Algorithm

5.1 The Path Planning Process of the Cable Loop Network

The cable loop network path planning for medium voltage distribution network has the characteristics of complex constraints, multi-objective, nonlinear, and belongs to mixed integer nonlinear programming problems. The process is shown in Fig. 4.

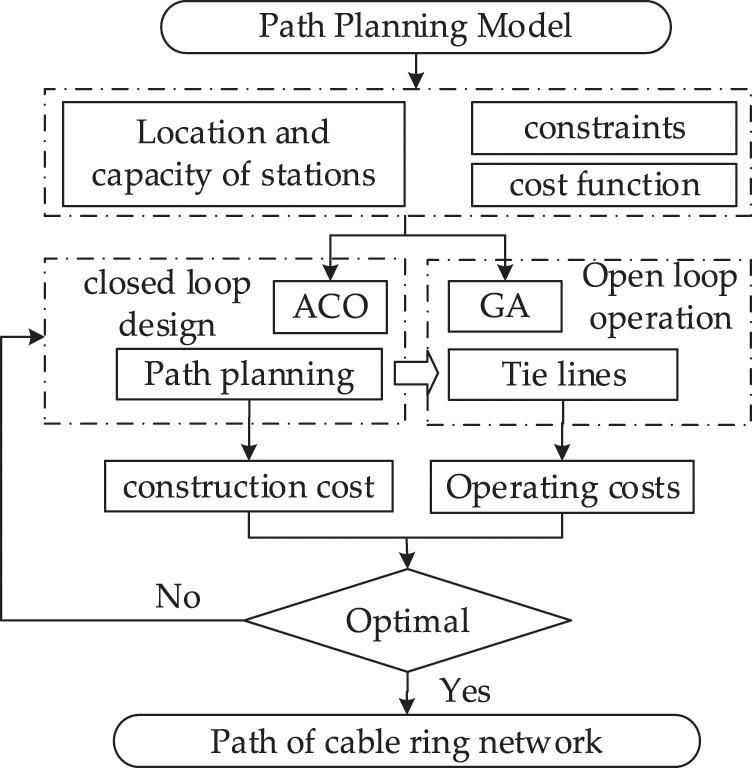
Figure 4: The path planning process of the cable loop network

After determining the locations of substations and switching stations, the ACO is selected as the path-planning method of the cable loop network to connect the raster grids between stations, and the planning result determines the annual construction cost finv.

Under the condition of minimizing the construction cost of the cable loop network and following the idea of “closed-loop design and open-loop operation”, the GA is used to plan the tie lines of the feeder, so that the operating cost fope is minimized, and the minimum comprehensive investment f is finally guaranteed.

5.2 Cable Loop Network Path Planning Based on Improved ACO

5.2.1 Characteristics of ACO

The Italian scholar Dorigo M. proposed ant colony optimization (ACO) in the 1990s, and it was successfully applied to solve the traveling salesman problem (TSP) [44]. The algorithm simulates the foraging behavior of ants to solve the optimization problem, which mainly includes two stages: calculating the probability of path selection and updating the path pheromone. The probability of path selection between nodes i and j is as follows:

pij(t)={τijα(t)⋅ηijβ(t)∑τikα(t)⋅ηikβ(t)j∈Ak(t)0j∉Ak(t)(21)

where t is the iteration order, Ak is the set of nodes to be selected by the ant k, τij is the pheromone concentration corresponding to the path Lij, and ηij is the heuristic function, which is often taken as 1/Lij. In addition, α and β are the weighting factors of pheromone concentration and the weighting factors of heuristic function. The former indicates the degree to which the amount of information left on each node is valued, and the latter indicates the degree to which the heuristic information is valued.

The pheromone concentration on the path Lij is updated according to the following equation:

τij(t+1)=(1−ρ)⋅τij(t)+∑k=1mΔτijk(22)

where ρ is the pheromone evaporation rate, Δτijk is the pheromone increment of ant k on the path Lij in every iteration process, and m is the number of ants.

Therefore, ACO is essentially a heuristic self-organization algorithm with parallel computation and a positive feedback mechanism. However, similar to other heuristic algorithms, there is a contradiction between the quality of the model solution and the speed of convergence. Generally, the larger the population, the easier it is to get the global optimum, and the longer the searching time is. Therefore, the ACO needs to be improved according to the actual situation.

5.2.2 Improved ACO Integrating Multiple Strategies

In order to improve the path planning efficiency of the cable loop network, an improved ACO is proposed which integrates the dynamic pheromone weight factor, the search direction guide factor and the elite ant thought. The improved algorithm mainly improves the state transition probability Eq. (21) and the pheromone update Eq. (22).

•   Dynamic pheromone weighting factor λ

The original ACO uses a fixed value α as the pheromone weighting factor. Considering the phenomenon that the results differ greatly at the beginning of iteration but tend to be consistent at the later stage, a larger fault-tolerant space can be used to improve the convergence speed of the algorithm at the early stage and avoid rapid local convergence in the subsequent process. The dynamic pheromone weight factor λ is used to modify α as follows:

λ(t)=α(1+e−εt)(23)

where ε is a real number and satisfies ε∈(0,1). Compared with α, the initial value of λ is larger and the convergence speed is faster. With the increase in iteration times, the λ becomes smaller, which makes the convergence gradually slow down. Therefore, the improvement is more suitable for the actual requirements of the convergence speed.

•   Search direction factor μ

In the process of ant optimization, the search direction has a great influence on the convergence speed and complexity of the algorithm. The search direction specification can greatly improve the iteration speed and the quality of feasible solutions.

Assume that the coordinate of the ith raster grid through which the feeder line passes is (xi,yi), the coordinate of the next raster grid to be linked is (xj,yj), and the coordinate of the destination power station is (Cx ,Cy), the search direction factor μij can be defined as follows:

μij=(1−cos⁡θij)/2(24)

cos⁡θij=(xi−xj)(Cx−xj)+(yi−yj)(Cy−yj)(xi−xj)2+(yi−yj)2⋅(Cx−xj)2+(Cy−yj)2(25)

where θij is the radian of ∠ABC. The range of θij is [0,π], the value of μij is [0,1], and their relationship is as follows:

According to Fig. 5, the closer θij is to π, the bigger μij is to be 1, indicating that the next search direction of the ant tends to a more ideal direction, and the convergence effect of the algorithm is better.

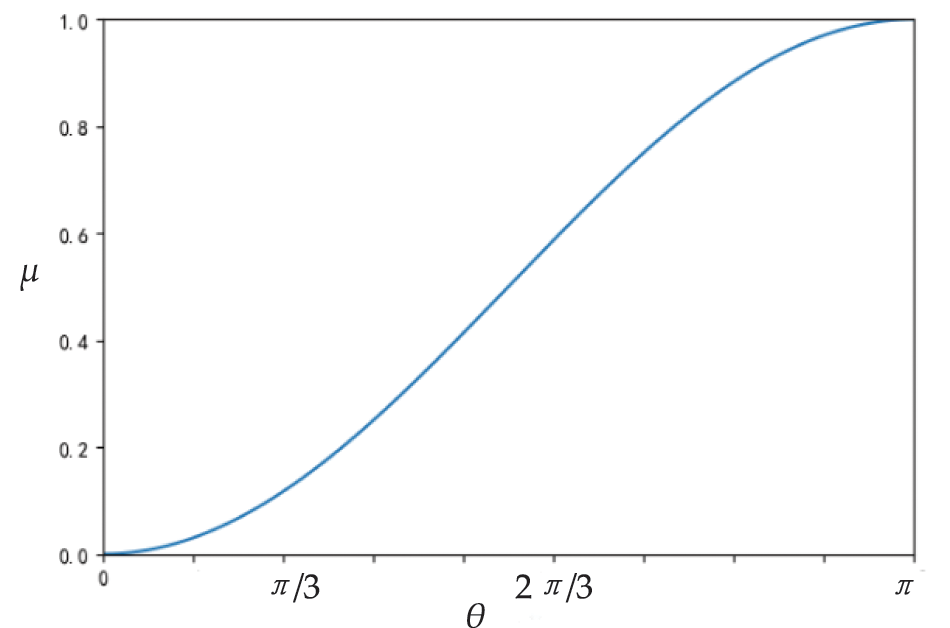
Figure 5: The Relationship between μij and θij

•   Pheromone update strategy based on elite ants Δτbestk

The pheromone on each path of the original ACO tends to be consistent in the later period of iteration, which leads to slowing down the optimization speed and even falling into a local optimum. In the iterative process of improving ACO, the elite ants in the current iteration are used to add more pheromones to the optimal path, and reduce fewer pheromones to the non-optimal path, so as to improve the guidance effect of the ants in the next iteration [45].

In the tth iteration, the pheromone increments Δτbestk of elite ants k can be expressed as:

Δτbest(t)={Q⋅[Lk−1(t)−Llow−1(t)]Lk is optimal path Q⋅[Lave−1(t)−Lk−1(t)]Lk is non-optimal path(26)

where Q is the initial pheromone concentration, Lk is the path length of ant k, Llow is the path length of the worst ant, and Lave is the average path length of ants.

Compared with the original ACO, the improved algorithm based on the idea of the elite ants pays more attention to the ants on the optimal path, forming a stronger positive feedback mechanism, which accelerates the convergence speed in the middle and late stages.

Combining the above strategies, the path selection probability function of the improved ACO and the pheromone concentration update equation are obtained as follows:

pij(t)={τijλ(t)⋅ηijβ(t)⋅μijγ(t)∑τikλ(t)⋅ηikβ(t)⋅μijγ(t)j∈Ak(t)0j∉Ak(t)(27)

τij(t+1)=(1−ρ)⋅τij(t)+∑k=1mΔτijk+Δτbest(t)(28)

where γ is the weight of the search direction factor μ, with a value range of (0,1), and Δτbestk is the pheromone increment of the elite ants.

5.3 The Tie Line Planning of Cable Loop Network Based on GA

Genetic Algorithm (GA) is a computational model that simulates the process of natural selection and biological evolution [46]. The algorithm adaptive searches the solution space through operations such as parameter encoding, population evolution, and genetic variation. In addition, it has a strong global search capability, which is suitable for the planning of tie lines in the cable loop network.

Therefore, based on the path planning results of the improved ACO and the “hand-in-hand” contact rules, the tie lines can be coded and processed by constructing a contact matrix between nodes. Taking the minimum operation and maintenance cost as the fitness function objective, the optimal contact scheme is obtained after a genetic operation. The main steps are as follows:

•   Combined with the cable loop network path, screen out the appropriate inter-station tie lines for each loop, and determine the corresponding switch station location.

•   It is stipulated that each loop has only one tie line, and the GA is used to randomly generate the tie line traversal sequence. After the formation of multiple chromosomes, the initial population is constructed to form a set of alternative solutions.

•   Open-loop operation is performed according to the selected tie line position, and the fitness function is calculated according to the different contact point configuration schemes of each chromosome and operation cost fope.

•   Whether the termination condition for iteration is reached. If so, record the optimal planning tie lines. Otherwise, perform genetic operations on each chromosome to obtain the next generation population, and return to the previous step until the iteration converges.

6  Case Analysis

The case analysis takes a power supply unit in Shanghai Pudong New Area as the object. In the whole life cycle of the planned cable loop network, the unit includes 3,110 kV substations, 2 35 kV substations, 17 original 10 kV switch stations, and 6 backup 10 kV switch stations (GCD1~GCD6). In addition, the related data are got from project engineering materials and municipal planning information, and sufficient land samples are obtained for statistics.

6.1 Estimation of Corridor Construction Cost of Raster Grid for Power Supply Unit

According to the data samples of land plots in the power supply unit, such as green space, traffic, residential, public, commercial, and industry, the probability density distribution of the corridor construction cost of 6 types of raster grids is estimated based on KDE. When the bandwidth coefficient h is equal to 2, the probability density distribution of the corridor construction cost is shown in Fig. 6.

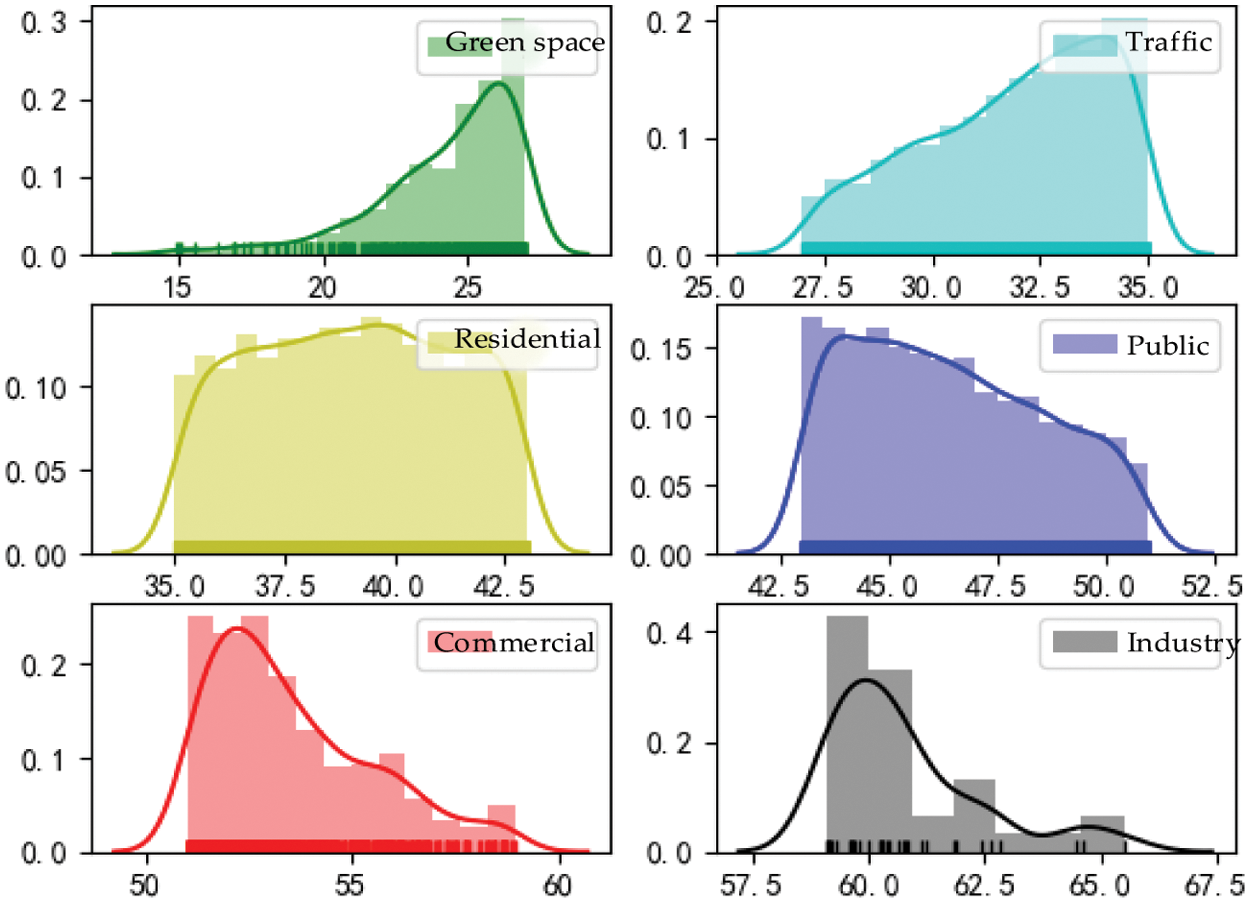
Figure 6: Probability density distribution of corridor construction costs for different land plots

It can be seen from the figure that the probability density distribution curves of the above 6 types of land plots have the characteristics of “wave and peak”, and the peak corresponds to the typical value of the unit corridor construction cost for each type. According to the different “peak” coordinates in Fig. 6, the typical corridor construction cost of green space is ¥262 thousand, traffic is ¥341 thousand, residential is ¥395 thousand, public is ¥438 thousand, commercial is ¥527 thousand, and industry is ¥601 thousand.

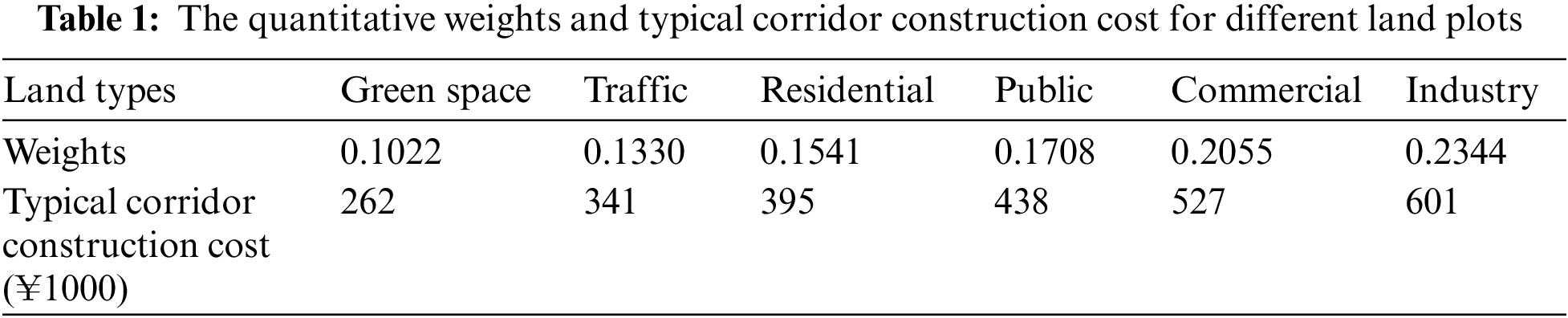
With the typical value of the corridor construction cost for different land plots, the quantitative weights of each type in the mixed-land scenario are obtained by the analytic hierarchy process, and the unit of typical corridor construction cost is ¥1000, as shown in Table 1.

The side length of the raster grid is taken as 200 meters, and then the rectangle area of 32 * 34 grids in the power supply unit is intercepted. According to Eq. (8), each grid is assigned to obtain the corridor construction cost matrix for the whole area. Finally, the distribution map of corridor construction cost in a mixed-land scenario is obtained.

As shown in Fig. 7, there are obvious differences in the corridor construction cost between adjacent raster grids in the power supply unit. Therefore, in the next step of the cable loop network path planning process, the search direction should be adjusted to connect to the next raster grid, so as to obtain the optimal path.

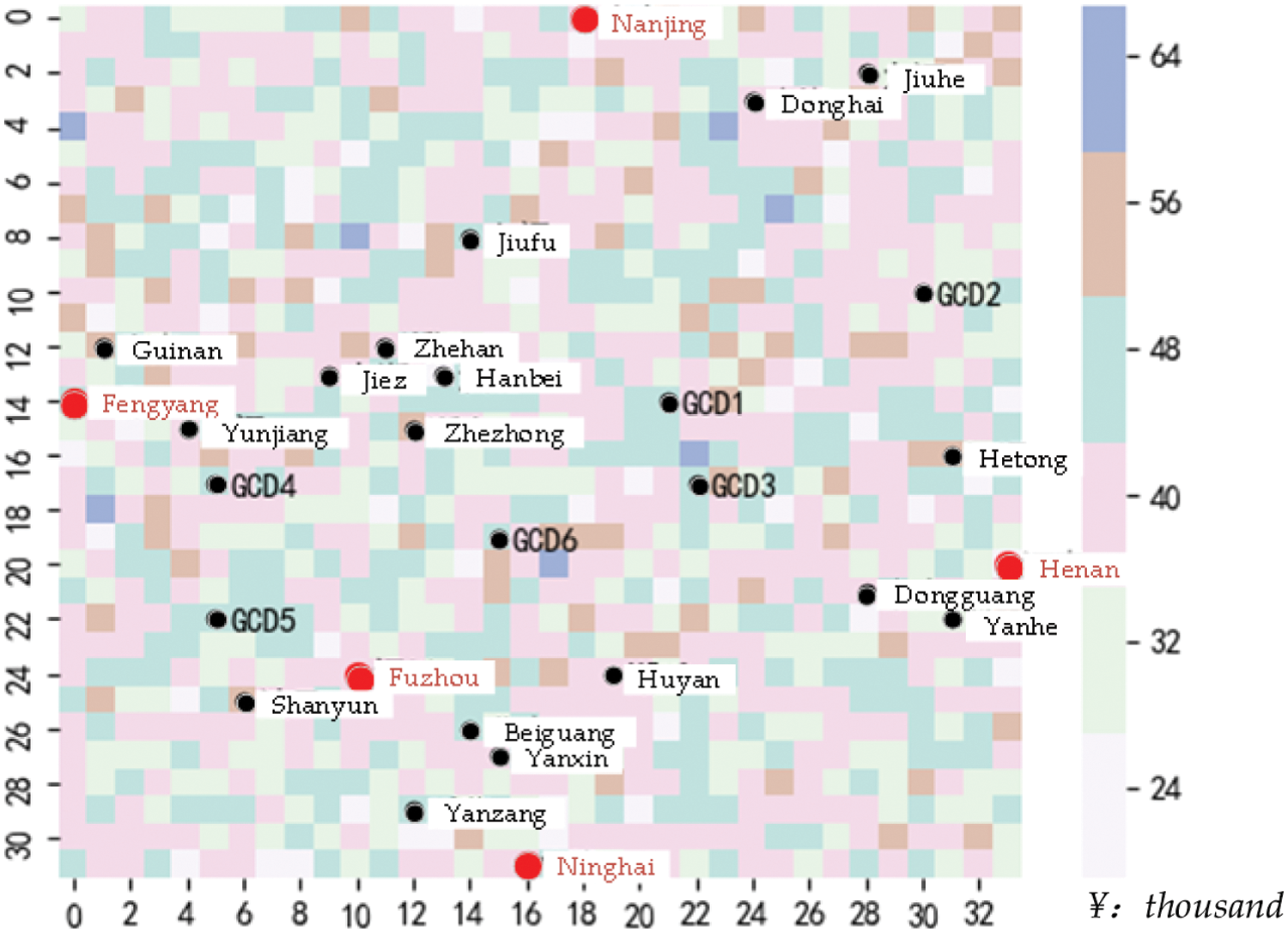
Figure 7: The distribution map of corridor construction cost in a mixed-land scenario

6.2 Result of Path Planning for Cable Loop Network Based on Improved ACO

In the power supply unit, there are 5 power stations and 23 switch stations. The voltage grades of Fengyang Station, Fuzhou Station and Nanjing Station are 110 kV, and Henan Station and Ninghai Station are 35 kV.

Since Nanjing Station, Fengyang Station and Ninghai Station are located at the boundary of the power unit area, only half of the capacity is left to supply this unit. In addition, for 10 kV switch stations, the power transmitted by each loop cannot exceed the maximum capacity, and only 4 switch stations can be connected at most.

According to the improved ACO, the number of initial ants is set to 30, the dynamic pheromone weight factor is expressed as λ(t)=1+e−t, the heuristic function factor β is 1, the pheromone evaporation rate ρ is 0.1, and the weight of the search direction factor μ satisfies γ=0.5. The definition and initial values of parameters are shown in Table 2.

Combined with material cost and corridor construction cost, aiming at the minimum annual investment cost of construction, the planned cable loop network path is obtained after considering all constraints. The result is shown in Fig. 8.

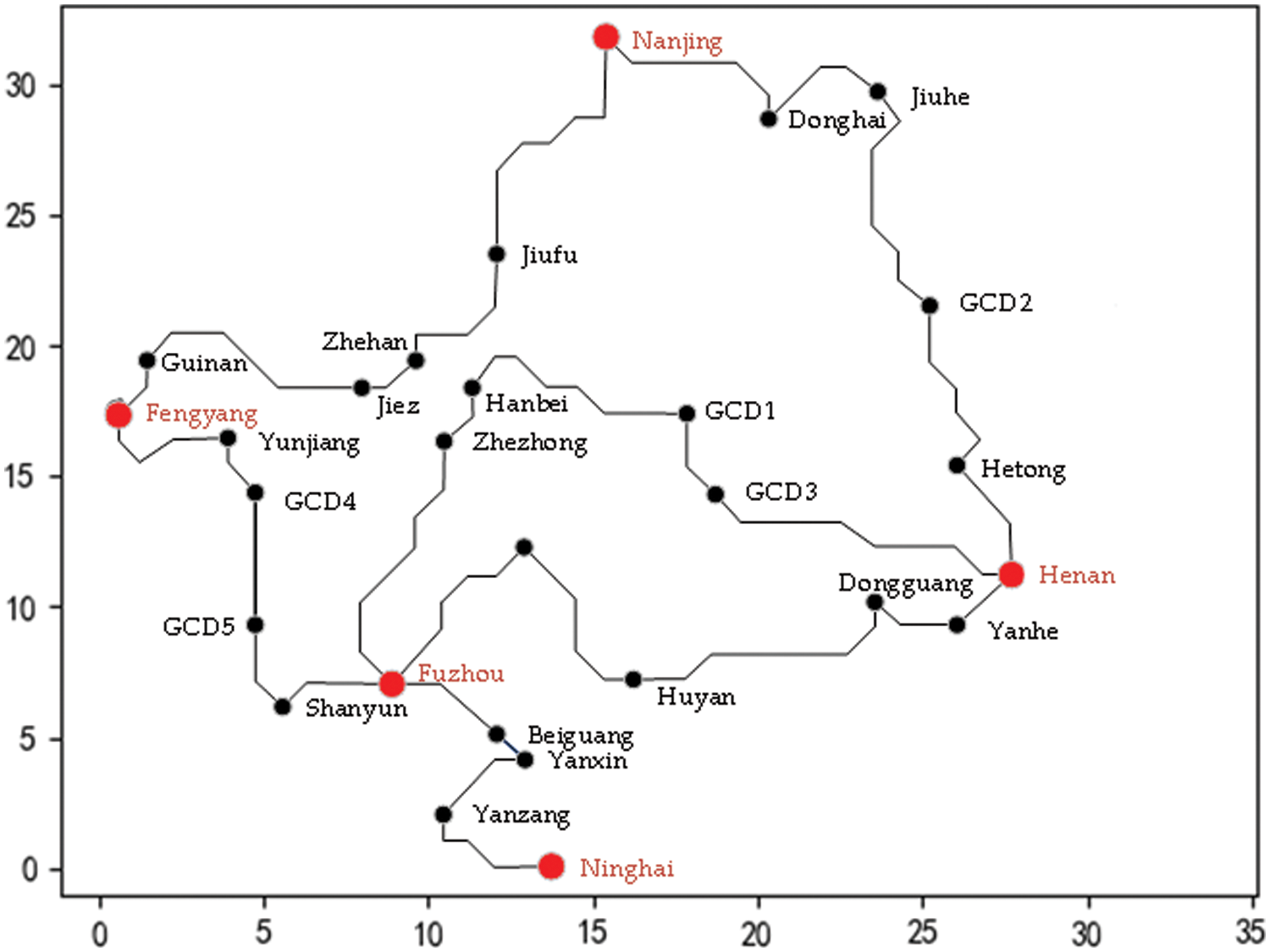
Figure 8: Path planning result of cable loop network based on improved ACO

As shown in Fig. 8, the power supply unit has planned a total of 6 loops, and each loop is connected with no more than 4 switch stations. For the 5 substations, Fuzhou Station supplies 4 loops, Henan Station supplies 3 loops, Fengyang Station and Nanjing Station each supply 2 loops, and Ninghai Station supplies 1 loop, which meets the capacity requirements.

In the process of 200 iterations, the annual investment cost of construction gradually converges. Compared with the original ACO, the convergence process of the improved ACO is shown in Fig. 9.

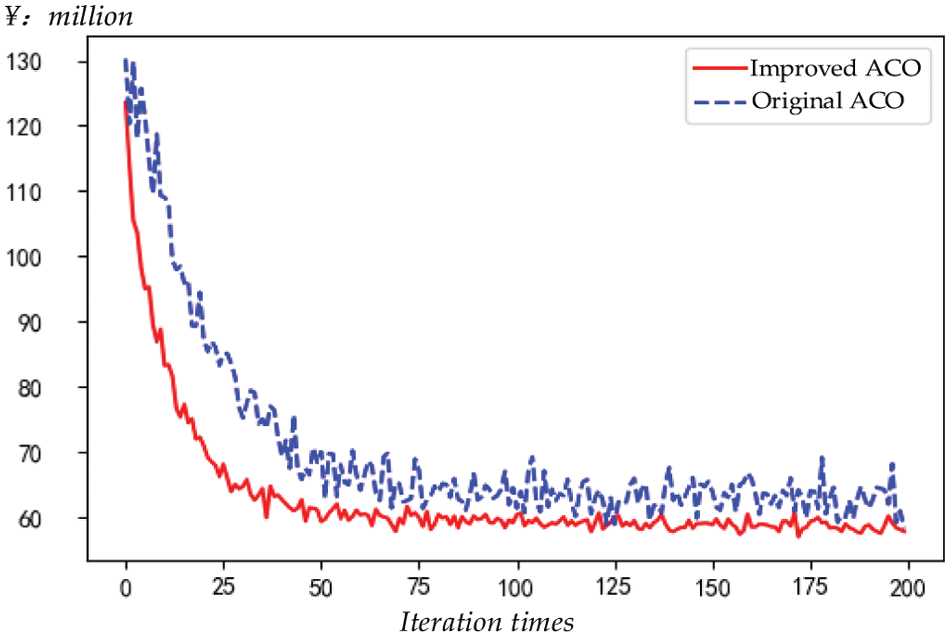
Figure 9: Comparison of improved ACO and original ACO

It can be seen from Fig. 9 that the minimum annual investment cost obtained after the convergence of the two algorithms is about ¥60 million. In the initial stage, the improved algorithm has a faster convergence speed than the original algorithm, and the value of the objective function decreases steadily. In the convergence stage, the fluctuation of the objective function value for the improved algorithm is less, and the original algorithm is difficult to fully converge.

Therefore, the improved ACO has better path planning ability than the original algorithm, which is manifested in faster convergence speed and more stable iterative results.

6.3 Results of Tie Line Planning for Cable Loop Network Based on GA

On the basis of the closed-loop design of the cable loop network, the inter-station lines of each loop are digitally encoded. In order to meet the open-loop operation mode, only one inter-station line is allowed to be a tie line. Besides, to ensure sufficient reserve capacity, a single substation can supply up to 6 switch stations when the open-loop operation is specified.

Aiming at the minimum operating cost, the ACO algorithm is applied to obtain the planning result of the tie line, as shown in Fig. 10.

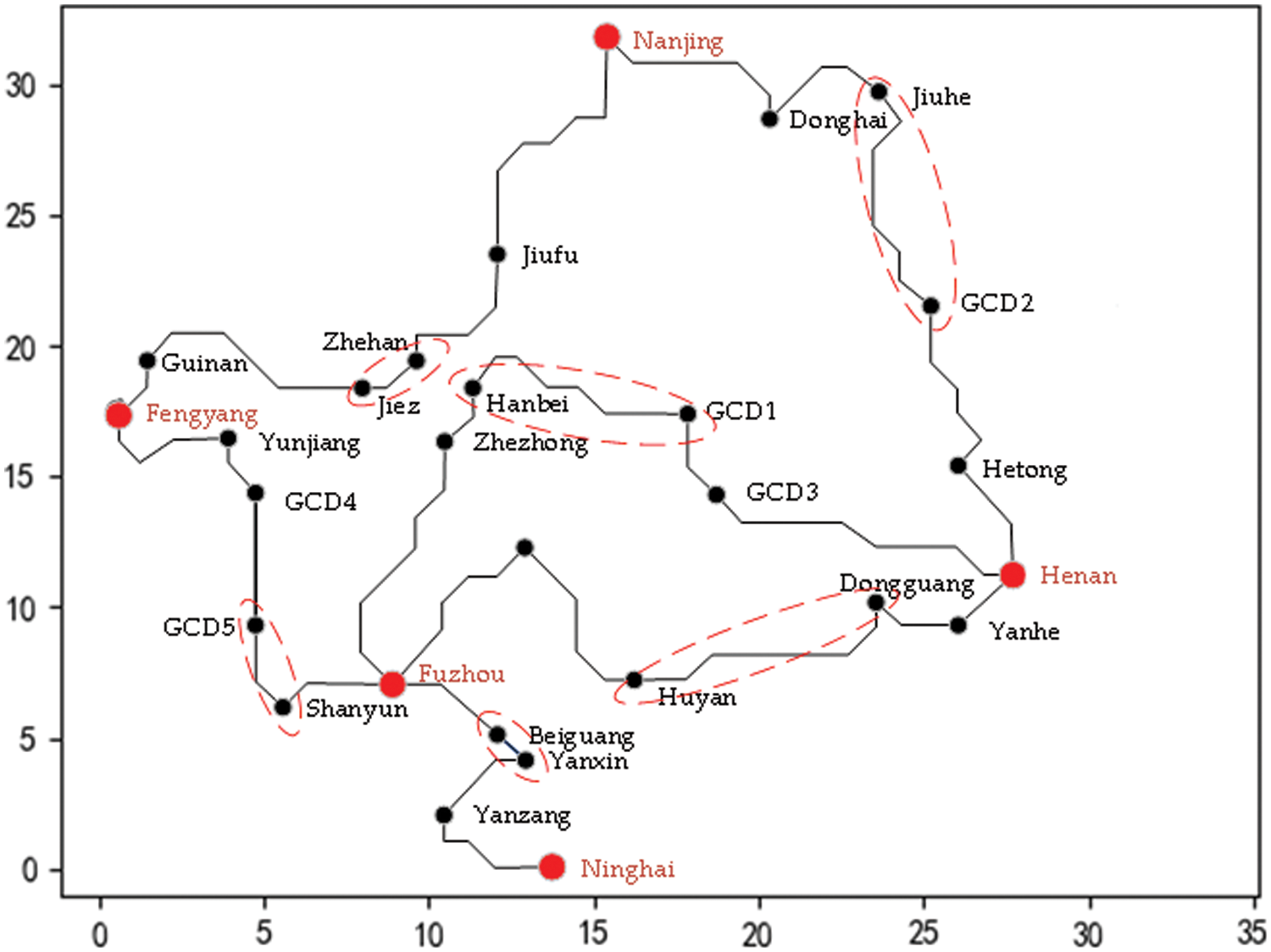
Figure 10: Planning results of tie line based on ACO algorithm

As shown in Fig. 10, when the tie lines surrounded by dotted lines are open-loop, the operating cost of the cable loop network is optimal, and the total investment also achieves the minimum cost.

According to the planning results, Fuzhou belongs to the central station and supplies power to 6 switch stations. Henan, Fengyang, Nanjing and Haining are border stations with fewer switch stations to support. In short, the capacity of the above power stations and inter-station lines all meet the requirements for safe operation, and the Haining Station has a large remaining capacity to meet the needs of future load growth.

6.4 Work Limitations and Future Scope

6.4.1 The Limitations

The findings of this paper have to be seen in light of some limitations. Firstly, the limitation of the power supply area. For the current pilot project, the area of the power supply unit in this paper is not large enough. In the future, we can try to expand the scope of power supply, or divide the entire power supply area into smaller grids to get a more accurate investment estimate. Secondly, the KDE method is used to estimate the construction cost of different types of land, which can reflect the overall data rules and find the typical value of the construction cost of each type of land, but the differences between the same types of land cannot be reflected in detail. Although the actual total construction cost tends to be the current result, there may be a small deviation. Thirdly, although the proposed method can well solve the current cable path planning problem, it does not fully consider the future load changes, the impact of distributed power generation and other factors, and the application scenarios are not universal enough.

6.4.2 The Future Scope

With the development of new power system and the application of intelligent power electronic equipment, the operation characteristics of urban distribution networks will change to some extent. For example, increased penetration of distributed power sources and access to renewable energy sources will be important factors to consider in future grid planning. At the same time, with the saturation of power grid construction, the future cable path planning model also needs to consider the problem of easy expansion. Therefore, collaborative expansion planning considering new energy injection will be the main research direction in the future. In addition, it will be optimized for more application scenarios and technical methods to make it more universal and efficient.

7  Conclusions

In this paper, a refined path planning model of cable loop networks in mixed-land scenarios is proposed, and the solution is achieved through a combination of heuristic algorithms. The main conclusions are as follows:

1.    Through the study of data samples, the corridor construction costs for different types of land are classified and estimated, which effectively avoids the interference of subjective factors, and helps to obtain a more accurate path planning result.

2.    Based on the rasterization of land plots, the estimation of corridors construction cost for different types of raster grids is realized, and the cost matrix of the global area is constructed, which can make the comprehensive investment model more precise.

3.    The ACO is improved from the aspects of the dynamic pheromone weight factor, search direction factor and elite ant thought, which can significantly improve the convergence speed and solution quality of the model.

Acknowledgement: We would like to thank the reviewers and the editor for their valuable comments and suggestions.

Funding Statement: This research was funded by the Science and Technology Project (Project No. kj2020-065) of State Grid Hebei Electric Power Co., Ltd.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Tianfeng Xu, Tao Wang and Gengwu Zhang; data collection: Peng Xi and Yunhui Chen; analysis and interpretation of results: Tianfeng Xu, Tao Wang and Chengming Ye; draft manuscript preparation: Tianfeng Xu, Tao Wang, Chengming Ye, Jing Zhang and Peng Xi. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available on request from the authors, upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Wei, Y., Zhang, J., Li, G., Hu, K., Nie, Y. et al. (2023). Material properties and electric-thermal–stress multiple fields coupling simulation of power distribution cable accessories. IEEE Transactions on Dielectrics and Electrical Insulation, 30(1), 359–367. https://doi.org/10.1109/TDEI.2022.3225694 [Google Scholar] [CrossRef]

2. Golla, M., Thangavel, S., Simon, S. P., Padhy, N. P. (2023). A novel control scheme using UAPF in an integrated PV grid-tied system. IEEE Transactions on Power Delivery, 38(1), 133–145. https://doi.org/10.1109/TPWRD.2022.3180681 [Google Scholar] [CrossRef]

3. Sandoval, N., Gong, Y., Chung, C. Y. (2023). Three-phase second-order analytic probabilistic load flow with voltage-dependent load. IEEE Transactions on Power Systems, 38(1), 229–241. https://doi.org/10.1109/TPWRS.2022.3159392 [Google Scholar] [CrossRef]

4. Shi, F., Hou, S., Tang, Q., Chen, Y., Wang, S. (2022). Evaluation and selection of typical connection modes for world-class urban distribution network. Power System Technology, 46(6), 2249–2259. [Google Scholar]

5. Zhao, F., Di, S., Cao, J., Tang, J., Jonrinaldi, J. (2021). A novel cooperative multi-stage hyper-heuristic for combination optimization problems. Complex System Modeling and Simulation, 1(2), 91–108. https://doi.org/10.23919/CSMS.2021.0010 [Google Scholar] [CrossRef]

6. Zhang, M., Ren, H., Zhou, Y. (2023). Research on global ship path planning method based on improved ant colony algorithm. IEEE Open Journal of Intelligent Transportation Systems, 4, 143–152. https://doi.org/10.1109/OJITS.2023.3247377 [Google Scholar] [CrossRef]

7. Bosisio, A., Berizzi, A., Lupis, D., Morotti, A., Lannarelli, G. et al. (2023). A tabu-search-based algorithm for distribution network restoration to improve reliability and resiliency. Journal of Modern Power Systems and Clean Energy, 11(1), 302–311. https://doi.org/10.35833/MPCE.2022.000150 [Google Scholar] [CrossRef]

8. Khedr, A. M., Aghbari, Z. A., Khalifa, B. E. (2022). Fuzzy-based multi-layered clustering and ACO-based multiple mobile sinks path planning for optimal coverage in WSNs. IEEE Sensors Journal, 22(7), 7277–7287. https://doi.org/10.1109/JSEN.2022.3150065 [Google Scholar] [CrossRef]

9. Ren, Y., Zhang, L. (2023). An adaptive evolutionary multi-objective estimation of distribution algorithm and its application to multi-UAV path planning. IEEE Access, 11, 50038–50051. [Google Scholar]

10. Guo, F., Chen, C., Mi, Y., Song, X., Bai, P. et al. (2023). Cable laying path planning based on artificial bee colony algorithm. Control Engineering of China, 30(3), 570–576. [Google Scholar]

11. Chen, X., Dai, Y. (2020). Research on an improved ant colony algorithm fusion with genetic algorithm for route planning. 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), pp. 1273–1278. Chongqing, China. [Google Scholar]

12. Peng, J., Wang, L., Yang, S., Liu, P., Wang, C. et al. (2023). Coupling multi-source geographic information and improved GA for intelligent transmission line selection. Surveying and Mapping Science, 48(2), 237–246. [Google Scholar]

13. Liu, X., Zhang, J., Chen, L., Gong, Z., Zhang, F. et al. (2019). Application research of artificial intelligence algorithm in path planning of distribution network in Tibet region. Power Supply, 36, 7–12. [Google Scholar]

14. Bordin, C., Mishra, S., Palu, I. (2021). A multihorizon approach for the reliability oriented network restructuring problem, considering learning effects, construction time, and cables maintenance costs. Renewable Energy, 168(2), 878–895. https://doi.org/10.1016/j.renene.2020.12.105 [Google Scholar] [CrossRef]

15. Lu, H., Chen, Y., Wu, H., Cheng, L. (2021). Path planning of substation inspection robot under road network and measurement constraints. China Mechanical Engineering, 32(16), 1972–1982. [Google Scholar]

16. Xi, N. (2022). Optimization of UAV patrol path for photovoltaic power station (Master Thesis). Zhejiang University, China. [Google Scholar]

17. Li, X., Zhang, L., Liu, C., Zhao, Y., Dong, Y. (2022). Path planning algorithm in power inspection. Computer System & Application, 31(3), 241–247. [Google Scholar]

18. Tong, X., Chen, Y., Lu, H., Xiong, L., Cheng, L. (2022). Path planning of substation inspection robot for meter reading. Journal of Electronic Measurement and Instrumentation, 36(8), 167–177. [Google Scholar]

19. Tang, B., Shen, Y., Huang, X., Xiao, D., Zhang, Z. et al. (2022). Research on substation robot path planning and equipment recognition based on improved ant colony algorithm and image recognition. Manufacturing Automation, 44(2), 46–52. [Google Scholar]

20. Chen, L., Su, Y., Zhang, D., Leng, Z., Qi, Y. et al. (2021). Research on path planning for mobile robots based on improved ACO. 36th Youth Academic Annual Conference of Chinese Association of Automation (YAC), pp. 379–383. Nanchang, China. [Google Scholar]

21. Wu, T. (2022). Transportation economic management strategy of cold chain transportation industry based on ABC-ACO algorithm. 2022 International Conference on Data Analytics, Computing and Artificial Intelligence (ICDACAI), pp. 57–60. Zakopane, Poland. [Google Scholar]

22. Armond, A. M., Prasetyo, Y. D., Ediningrum, W. (2022). Application of ant colony optimization (ACO) algorithm to optimize trans banyumas bus routes. 2022 IEEE International Conference on Cybernetics and Computational Intelligence (CyberneticsCom), pp. 132–137. Malang, Indonesia. [Google Scholar]

23. Niu, W. (2022). A novel multiobjective optimization for tourism route based on improvement ACO method and topology optimization. 6th International Conference on Intelligent Computing and Control Systems (ICICCS), pp. 701–704. Madurai, India. [Google Scholar]

24. Anas, E. A., Hami, N. E. (2022). Assignment problem solved by two metaheuristic algorithms ACO and HHO. 2022 8th International Conference on Optimization and Applications (ICOA), pp. 1–4. Genoa, Italy. [Google Scholar]

25. Robandi, I., Ajiatmo, D., Muhlasin, M. (2021). Optimization PI-ACO for photovoltaic system battery and supercapacitor on electric vehicle. 2021 International Seminar on Intelligent Technology and Its Applications (ISITIA), pp. 370–375. Surabaya, Indonesia. [Google Scholar]

26. Ali, M. A., Balamurugan, B., Sharma, V. (2022). IoT and blockchain based intelligence security system for human detection using an improved ACO and heap algorithm. 2022 2nd International Conference on Advance Computing and Innovative Technologies in Engineering (ICACITE), pp. 1792–1795. Greater Noida, India. [Google Scholar]

27. Bu, C., Zhang, X., Lv, J. (2022). Improved ACO inspired service functions detection over edge computing scenarios. 2022 Asia Conference on Algorithms, Computing and Machine Learning (CACML), pp. 472–476. Hangzhou, China. [Google Scholar]

28. Safavat, S., Rawat, D. B. (2021). On the elliptic curve cryptography for privacy-aware secure ACO-AODV routing in intent-based internet of vehicles for smart cities. IEEE Transactions on Intelligent Transportation Systems, 22(8), 5050–5059. https://doi.org/10.1109/TITS.2020.3008361 [Google Scholar] [CrossRef]

29. Lv, J., Li, Q., Jiang, Y., Wang, X., Ma, L. (2021). Adaptive ACO- driven ICN routing mechanism with network status analysis. 2021 IEEE 6th International Conference on Computer and Communication Systems (ICCCS), pp. 458–462. Chengdu, China. [Google Scholar]

30. Jemin, V. M., Kumar, A. S., Thirunavukkarasu, V., Kumar, D. R., Manikandan, R. (2022). Dynamic key management based ACO routing for wireless sensor networks. 2022 6th International Conference on Computing Methodologies and Communication (ICCMC), pp. 194–197. Erode, India. [Google Scholar]

31. Duca, A. (2021). RSM enhanced ACOR algorithm for electromagnetic optimization. 2021 International Conference on Applied and Theoretical Electricity (ICATE), pp. 1–5. Craiova, Romania. [Google Scholar]

32. Hajewski, J., Oliveira, S., Stewart, D. E., Weiler, L. (2021). Exploring trade-offs in parallel beam-ACO. 2021 IEEE 11th Annual Computing and Communication Workshop and Conference (CCWC), pp. 1525–1534. NV, USA. [Google Scholar]

33. Duca, A. (2021). Adaptive ACOR for solving the TEAM22 benchmark problem. 2021 International Conference on Applied and Theoretical Electricity (ICATE), pp. 1–4. Craiova, Romania. [Google Scholar]

34. Ghorab, A. S. (2021). An improved immune genetic algorithm and its application on TSP. 2021 International Conference on Promising Electronic Technologies (ICPET), pp. 84–88. Deir El-Balah, Palestine. [Google Scholar]

35. Tao, J., Wu, G., Yi, Z., Zeng, P. (2021). Innovative application of genetic algorithms in the computer games. 2021 33rd Chinese Control and Decision Conference (CCDC), pp. 2197–2200. Kunming, China. [Google Scholar]

36. Hu, W., Zhao, T., Cheng, X., Li, C. (2022). Improved genetic-ant colony fusion algorithm. 2022 4th International Conference on Robotics and Computer Vision (ICRCV), pp. 314–319. Wuhan, China. [Google Scholar]

37. Huamannahui Huanca, D., Gallego Pareja, L. A. (2021). Chu and beasley genetic algorithm to solve the transmission network expansion planning problem considering active power losses. IEEE Latin America Transactions, 19(11), 1967–1975. https://doi.org/10.1109/TLA.2021.9475851 [Google Scholar] [CrossRef]

38. Jiang, X., Wang, Y., Dong, J. (2023). Speed regulation method using genetic algorithm for dual three-phase permanent magnet synchronous motors. CES Transactions on Electrical Machines and Systems. http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=10032058&isnumber=9885156 [Google Scholar]

39. Wang, F., Xu, G., Wang, M. (2023). An improved genetic algorithm for constrained optimization problems. IEEE Access, 11, 10032–10044. https://doi.org/10.1109/ACCESS.2023.3240467 [Google Scholar] [CrossRef]

40. Ito, T. (2023). Improved evolution performance for genetic programming with method to search numbers of trees. 2023 17th International Conference on Ubiquitous Information Management and Communication (IMCOM), pp. 1–6. Seoul, Korea. [Google Scholar]

41. Tarife, R. P., Nakanishi, Y., Bondaug, J. V. S., Irosido, R. V., Tahud, A. P. et al. (2020). Optimization of electric transmission line routing for a renewable energy based micro-grid system using geographic information system (GIS) spatial analysis. 2020 9th International Conference on Renewable Energy Research and Application (ICRERA), pp. 215–220. Glasgow, UK. [Google Scholar]

42. Huang, P., Qiang, X., Xue, R. (2021). Improved particle filter based on kernel density estimation. 2021 IEEE 4th International Conference on Electronics Technology (ICET), pp. 1015–1019. Chengdu, China. [Google Scholar]

43. Ruan, Q., Xie, W., Zhang, Z., Zhu, R., Shi, F. (2020). Research and practice on the upgrading for diamond distribution network. China Electric Power, 53(6), 1–7. [Google Scholar]

44. Kumar, A. (2020). Improved genetic algorithm to solve small scale travelling salesman problem. 2020 4th International Conference on Intelligent Computing and Control Systems (ICICCS), pp. 516–520. Madurai, India. [Google Scholar]

45. Wang, Z., Lin, D., Zeng, G., Yu, T. (2020). A practical large-scale distribution network planning model based on elite Ant-Q. IEEE Access, 8, 58912–58922. https://doi.org/10.1109/ACCESS.2020.2981825 [Google Scholar] [CrossRef]

46. Deb, K., Pratap, A., Agarwal, S., Meyarivan, T. (2002). A fast and elitist multiobejective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2), 182–197. [Google Scholar]