 Open Access
Open Access
ARTICLE
Research on Equivalent Modeling Method of AC-DC Power Networks Integrating with Renewable Energy Generation
1 Central China Branch of State Grid Corporation of China, Wuhan, 430077, China
2
School of Electrical Engineering and Automation, Wuhan University, Wuhan, 430072, China
* Corresponding Author: Lei Chen. Email:
(This article belongs to the Special Issue: Renewable Energy Technologies for Sustainable Energy Production)
Energy Engineering 2023, 120(11), 2469-2487. https://doi.org/10.32604/ee.2023.043021
Received 19 June 2023; Accepted 04 August 2023; Issue published 31 October 2023
Abstract
Along with the increasing integration of renewable energy generation in AC-DC power networks, investigating the dynamic behaviors of this complex system with a proper equivalent model is significant. This paper presents an equivalent modeling method for the AC-DC power networks with doubly-fed induction generator (DFIG) based wind farms to decrease the simulation scale and computational burden. For the AC-DC power networks, the equivalent modeling strategy in accordance with the physical structure simplification is stated. Regarding the DFIG-based wind farms, the equivalent modeling based on the sequential identification of multi-machine parameters using the improved chaotic cuckoo search algorithm (ICCSA) is conducted. In light of the MATLAB simulation platform, a two-zone four-DC interconnected power grid with wind farms is built to check the efficacy of the proposed equivalent modeling method. From the simulation analyses and comparative validation in different algorithms and cases, the proposed method can precisely reflect the steady and dynamic performance of the demonstrated system under N-1 and N-2 fault scenarios, and it can efficiently achieve the parameter identification of the wind farms and fulfill the equivalent modeling. Consequently, the proposed approach’s effectiveness and suitability are confirmed.Keywords
Nomenclature
| REG | Renewable energy generation |
| LCC | Line commutated converter |
| DFIG | Doubly-fed induction generator |
| PSO | Particle swarm optimization |
| PCC | Point of common coupling |
| HVDC | High-voltage direct-current |
| ICCSA | Improved chaotic cuckoo search algorithm |
With the continuous improvement of renewable energy generation (REG) technology and power electronic equipment level, the installed capacity of REG in the AC-DC power networks has increased substantially [1,2]. Analyzing the impact on safety and stability caused by large-scale REG connected to the power grid is critical, and there is an urgent need to establish proper models that accurately reflect the dynamic characteristics of the complex AC-DC power systems with multiple REGs [3]. However, taking the wind farm (WF) as a representative of RES, detailed modeling of tens or even hundreds of wind turbines in wind farms simultaneously will face the problem of dimensional disaster [4]. Studying the equivalence modeling method for the AC-DC power networks containing multiple wind farms to decrease the simulation scale and the computational burden is of great theoretical significance and practical value.
At present, scholars have carried out some fundamental work on the equivalent modeling of the AC-DC power systems with REGs, and a literature review is implemented below. In reference [5], a methodology was presented to model the hybrid AC-DC grids to investigate the system-level control interactions, where fundamental transfer functions are considered. In reference [6], a modified nodal analysis method was suggested to construct the equivalent multiport model of a hybrid AC-DC system, in which multiport network parameters are appropriately applied. In reference [7], a modeling method based on the average dynamic phasor was proposed for a hybrid AC-DC distribution system, and the modeling goal is to realize the high-precision stability assessment and time-domain simulation analyses. In reference [8], an aggregated equivalence model was proposed for the VSC-HVDC interconnected electric power systems for the investigation of system frequency stability. In reference [9], a review of the large electrical network equivalent methods was carried out, and the findings confirmed the importance of obtaining the time-domain simulation results with reasonable accuracy. While the abovementioned studies offer some helpful values, their suitability for large-scale and complex AC-DC power systems should be checked further. In a sense, studying the equivalent modeling strategy following the physical structure simplification of the AC-DC power systems could be a potential solution.
In reference [10], the equivalent modeling of wind farms was conducted based on their natural properties, and the main objective is to analyze sub-synchronous oscillations. In reference [11], an overall identification strategy of wind farm parameters was designed, and the parameter identification was realized based on the particle swarm optimization algorithm for completing the equivalent modeling. In reference [12], a WF equivalent model based on a new clustering algorithm and high-voltage ride-through action was proposed, and the outcomes show that the equivalent accuracies are increased by introducing the multi-view clustering indexes. In reference [13], a quantitative assessment method was proposed for addressing the error of a WF equivalent model, where the grid-connection features are specifically considered. In reference [14], the equivalent modeling for large-scale offshore WT based on multi-thread parallel computing was implemented, and the WT’s dynamic characteristics with large speedup factors are well demonstrated. In reference [15], a modified WT parameterization was realized by considering the sub-grid interactions between turbines, and the output power prediction of turbine cells is updated. The key to building a WF equivalent model is accurately identifying the wind farm parameters, and the methods based on intelligent optimization algorithms may have good application prospects [16–18]. For such parameter identification methods to establish a WF equivalent model, two main problems must be solved.
On the one hand, there are many parameters for wind generators coupled to the AC-DC power networks. It is challenging to identify all parameters of wind generators simultaneously and accurately, and adopting the concept of sequential identification is a feasible technical solution. On the other hand, when a wind farm adopts a multi-machine equivalent model, the converter control parameters of different wind generators should be effectively distinguished, and it puts higher requirements on the performance of intelligent optimization algorithms.
This paper proposes an equivalent modeling method for the AC-DC power networks with doubly-fed induction generator (DFIG) based wind farms to decrease the simulation scale and computational burden. The main novelty and contributions of this paper are summarized as follows:
(1) Elaborate the equivalent modeling philosophy of the AC-DC power networks based on the physical structure simplification and recognizing coherent generator groups.
(2) Design the sequential parameter identification strategy of the DFIG-based wind farms based on the improved chaotic cuckoo search algorithm (ICCSA).
(3) Verify the effectiveness of the proposed approach in the two-zone four-DC interconnected power grid with the DFIG-based wind farms through the N-1 and N-2 fault scenarios.
(4) Confirm the suitability of the proposed method by the comparison of the particle swarm optimization (PSO), the traditional CSA, and the ICCSA.
The remaining sections of this paper are arranged as follows. Section 2 is devoted to the equivalent modeling of the AC-DC power networks. Section 3 describes the equivalent modeling of the DFIG based on wind farms using the improved chaotic cuckoo search algorithm. Section 4 focuses on implementing the simulation validation of the proposed method, and a two-zone four-DC interconnected power grid with wind farms is chosen to check the efficacy of the proposed method. In Section 5, some significant conclusions are drawn, and future research tasks are explored.
2 Equivalent Modeling of the AC-DC Power Networks
Fig. 1 shows the connection diagram of a two-zone four-DC interconnected power grid with wind farms. Herein, the line commutated converter (LCC) based high-voltage direct-current (HVDC) systems are introduced [19], and this study selects this two-zone four-DC interconnected power grid to describe the equivalent modeling strategy of the AC-DC power networks. Since the equivalent model should be able to reflect the dynamic behaviors, the treatment for the HVDC systems follows the two principles: 1) An average modeling philosophy of the HVDC systems is adopted to preserve the interaction characteristics between the AC and HVDC systems. 2) The nodes close to the HVDC systems are kept to consider the influence of possible commutation failures.
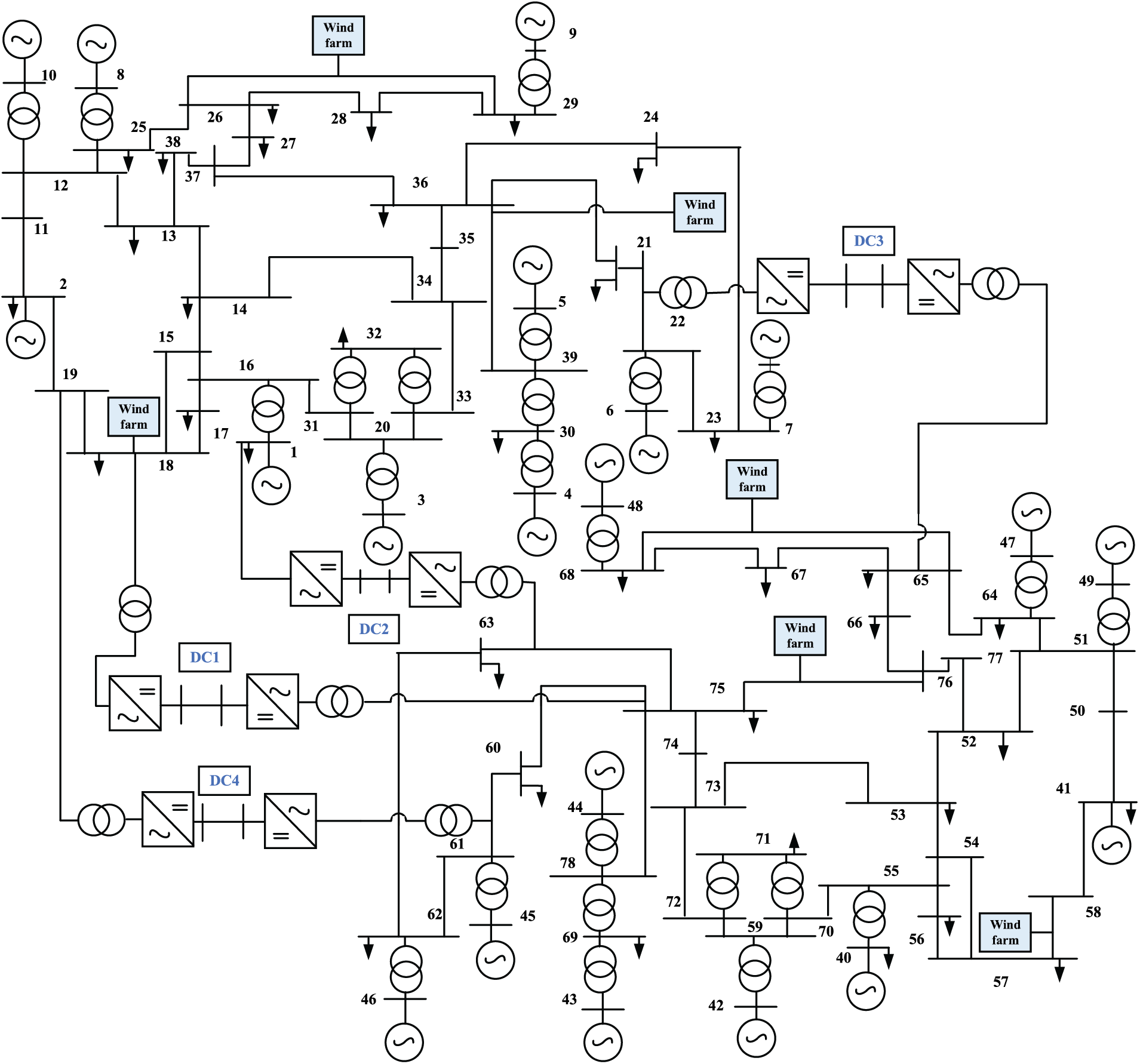
Figure 1: Connection diagram of a two-zone four-DC interconnected power grid with wind farms
In view of the dynamic characteristics of the AC-DC power networks principally depend on the main network frame, and the interaction between the middle- and low-voltage networks and the HVDC systems can be adequately ignorable. In this regard, the simplified modeling of the middle- and low-voltage networks should be given more attention. Regarding the physical structure of the AC-DC power networks, the middle- and low-voltage networks connected via separate 500 kV buses are called separate supply areas. In addition, some middle- and low-voltage networks coupled via different 500 kV buses are conducted as joint supply areas. As displayed in Fig. 2, it indicates the topological classification of the middle- and low-voltage networks [20].
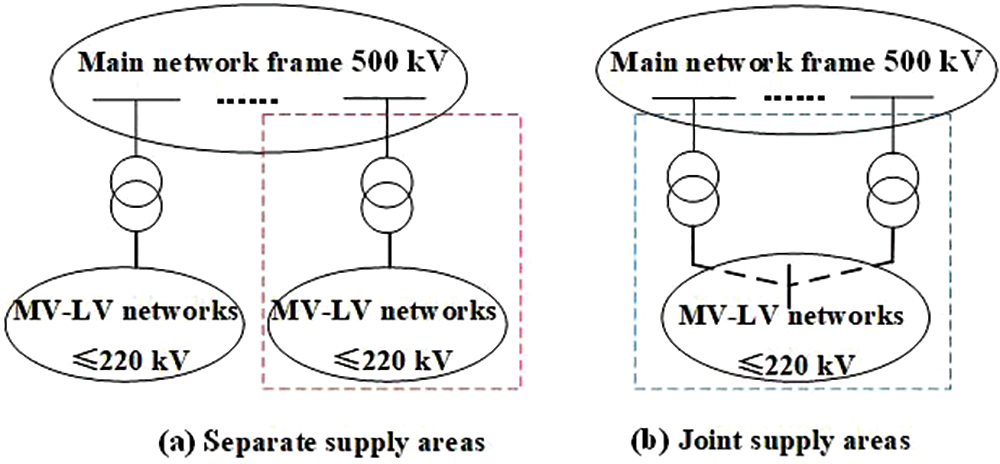
Figure 2: Topological classification of the middle- and low-voltage networks. (a) Separate supply areas, and (b) joint supply areas
Concerning the separate supply areas, the node-voltage equation is written as:
where I denotes the current vector. U indicates the load node voltage vector. Y represents the nodal admittance matrix. The subscripts r, b, and c indicate the reserved networks, boundary network, and reductive networks, respectively.
In the case of that the boundary network meets a metallic three-phase fault, Ub = 0 can be obtained, and the node-voltage equation is changed to [20]:
where
where
From Eq. (4), it is found that the boundary network can be represented as a current source Ibm with a conductance of
Concerning the joint supply areas, there will be multiple boundary networks, and the node-voltage equation can be deduced by:
where
For the equivalent modeling of conventional generators in the AC-DC power networks, recognizing coherent generator groups is employed. It means that the generators coupled to the same middle- and low-voltage networks are considered a group of coherent generators, which can be reflected by one generator with the corresponding equivalent load. This treatment is done by adjusting the parameters of the equivalent generators and transformer resistances so that the fault current levels of the detailed and equivalent models are the same.
Generally speaking, the equivalent modeling method of the AC-DC power networks preserves the 500 kV main networks, the HVDC systems, and the AC links between them during the equivalence process. It ensures that the fault currents supported by the equivalent generators are identical to the original complex power networks. The equivalent modeling of the AC-DC power networks preserves the HVDC systems, where the power electronic-based inverters adopt the average modeling manner to reflect the dynamic behaviors and control performance. The equivalent modeling method does not require unraveling the electromagnetic loops in the AC-DC power networks, and the equivalence model can be used to study the interaction characteristics under the electromagnetic transient simulation platform.
3 Equivalent Modeling of the DFIG-Based Wind Farms
Regarding the demonstrated DFIG-based wind farms, it is designed that all DFIGs connect to the point of common coupling (PCC) through a collector impedance, which can reflect the complicated configuration of the wind farm collector system, including feeder lines, trunk lines, and transformers [21]. Herein, the rotor-side converter (RSC) of the DFIG adopts the electromagnetic torque control and reactive power-terminal voltage control strategy, and the grid-side converter (GSC) uses the voltage and current double closed-loop control strategy [22].
The equivalent modeling method for the DFIG-based wind farms refers to a multi-machine modeling philosophy that divides the DFIGs into several groups. It aggregates each group into one DFIG connected with one equivalent collector impedance. During the equivalent process, the power electronic-based inverters of DFIGs are divided and aggregated; thus, each of the equivalent DFIG groups has an inverter. A detailed modeling manner of the DFIG inverter is used, and the control parameters of the inverter are tuned using the proposed parameter identification method. The controls for each turbine are the same, and this design aims to decrease the impact of the turbine controls on the number of equivalent DFIG groups. In the study, the differences in the turbine capacity, stator resistance, stator inductance, rotor resistance, rotor inductance, magnetizing inductance, and wind speed are the main criteria for determining the number of equivalent DFIG groups. Fig. 3 indicates the detailed and equivalent model of the DFIG-based wind farms, and the multi-machine equivalence is gained. It should be noted that, the equivalent model is established mainly for electromagnetic transient simulation. Since the transient simulation time is commonly short (from several hundred milliseconds to a few seconds), it can be approximatively considered that the wind speed is time-invariant. In this context, the large power uncertainties in wind farms are not taken into account.
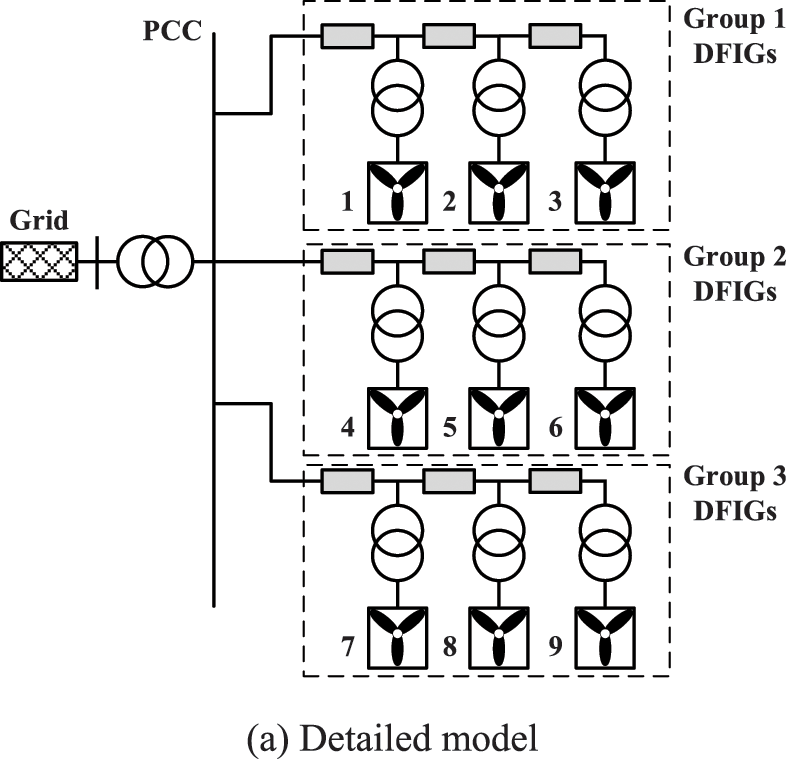
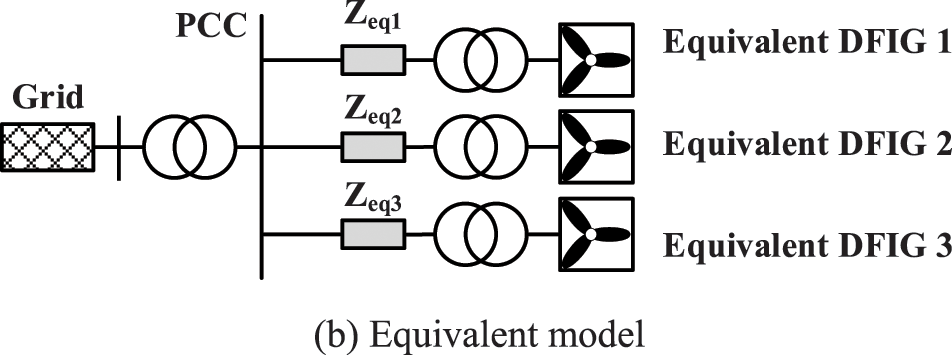
Figure 3: Detailed and equivalent model of the DFIG-based wind farms. (a) Detailed model, and (b) equivalent model
3.1 Parameter Identification Using Analytical Method
This section applies the analytical method to reduce the parameter identification difficulty by solving the initial parameters of each DFIG-based wind farm.
1) Equivalent rated capacity Seq
where Si represents the i-th DFIG’s rated capacity in a wind farm. n is the number of the DFIGs divided into the same group.
2) Equivalent DFIG parameter Xeq
where Xi represents the parameter of the i-th DFIG, including inertia time constant, stator resistance, stator inductance, rotor resistance, rotor inductance, and magnetizing inductance.
3) Equivalent wind speed veq
where vi represents the wind speed of the i-th DFIG.
3.2 Parameter Identification Using the Improved Chaotic Cuckoo Search Algorithm
The DFIG parameter identification is a two-stage process. In the first stage, the stator inductance, rotor inductance, magnetizing inductance, and converter control parameters of each equivalent DFIG are selected for identification. In common, the chosen parameters are easier to be identified with higher sensitivity [23]. Sequential identification is carried out according to the rated capacity of each equivalent DFIG. In the second stage, the equivalent collector impedance is selected for identification, considering that the value of the equivalent collector impedance significantly influences the accuracy of the equivalent model.
The objective function of the identification process can be written as:
where Porigin and Qorigin are the active and reactive power of the detailed wind farm model, respectively. Pidentify and Qidentify are the active and reactive power obtained by the parameter identification method. t is the simulation time, and T represents the total simulation time.
An optimal solution should be determined for the parameter identification process, and the improved chaotic cuckoo search algorithm (ICCSA) is selected explicitly to fulfill accurate parameter identification. The traditional cuckoo search algorithm (CSA) is based on the brood parasitism of some cuckoo species by laying their eggs in the nests of host birds of other species [24], and it generates the initial solutions randomly, which may cause the algorithm to be trapped in a local optimum. In this section, some improvements are applied to increase the algorithm’s performance in this context. On the one hand, the logistic chaotic mapping is introduced into the CSA. The randomly generated initial solutions can be updated as:
where X0 represents the initial solutions. X0,min and X0,max are the minimum and maximum values of X0, respectively. Xc denotes the updated initial solutions. The intermediate quantities generated by the chaotic mapping are x and y. In addition, μ represents the control parameter of the chaotic mapping.
On the other hand, it is designed that the step size parameter of Levy flights α and the probability of every cuckoo egg to be discovered by the host bird pa can be adaptively adjusted to accelerate the convergence speed in the iteration process. The adjustment can be expressed as:
where iter is the number of iterations. MaxIT is the maximum iteration number.
Fig. 4 shows the flowchart of the improved chaotic cuckoo search algorithm (ICCSA). The population initialization is completed first. After the updation of the logistic chaotic mapping, the initial solutions are evaluated based on the goals and restrictions. Then, considering the adaptive adjustment, the Levy flights and random walks are implemented to create an offspring population. This process iterates until the stopping condition is met and the desired optimal outcomes are obtained.
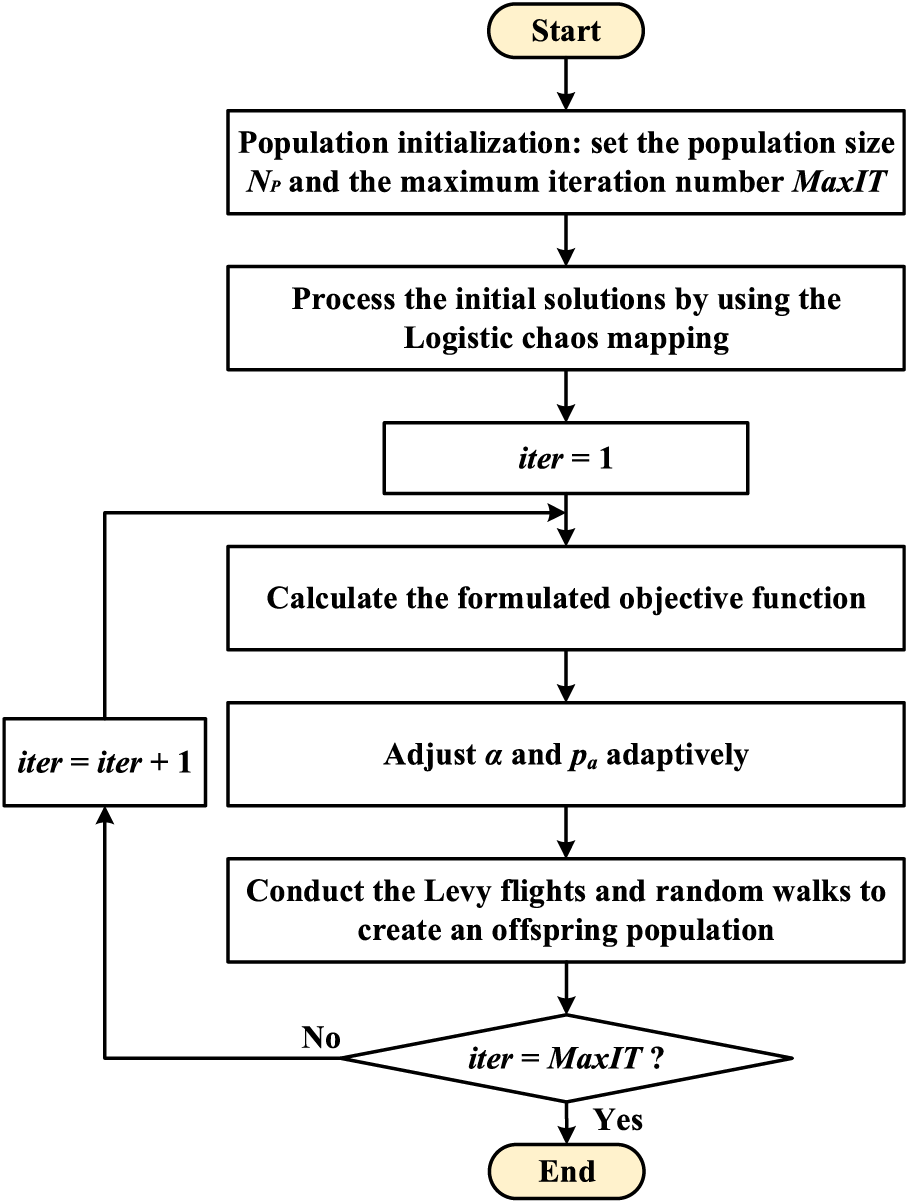
Figure 4: Flowchart of the improved chaotic cuckoo search algorithm
4 Simulation Validation and Discussion
To validate the effectiveness and adaptability of the proposed approach, the two-zone four-DC interconnected power grid with wind farms, as shown in Fig. 1, is modeled in MATLAB/SIMULINK, and different fault scenarios are considered for performance comparison. The testing environment is MATLAB 2022a, and the test case is built on a personal computer with Intel Core i5-9300 CPU running at 2.40 GHz and 8 G of memory. The simulation parameters of the two-zone four-DC interconnected power grid can refer to reference [25]. In addition, the model has six wind farms, and each wind farm has nine DFIG-based wind turbines with a total capacity of 20.4 MW. The parameters of the improved chaotic cuckoo search algorithm are listed in Table 1, and the tunning of the ICCSA parameters can mainly refer to reference [26].

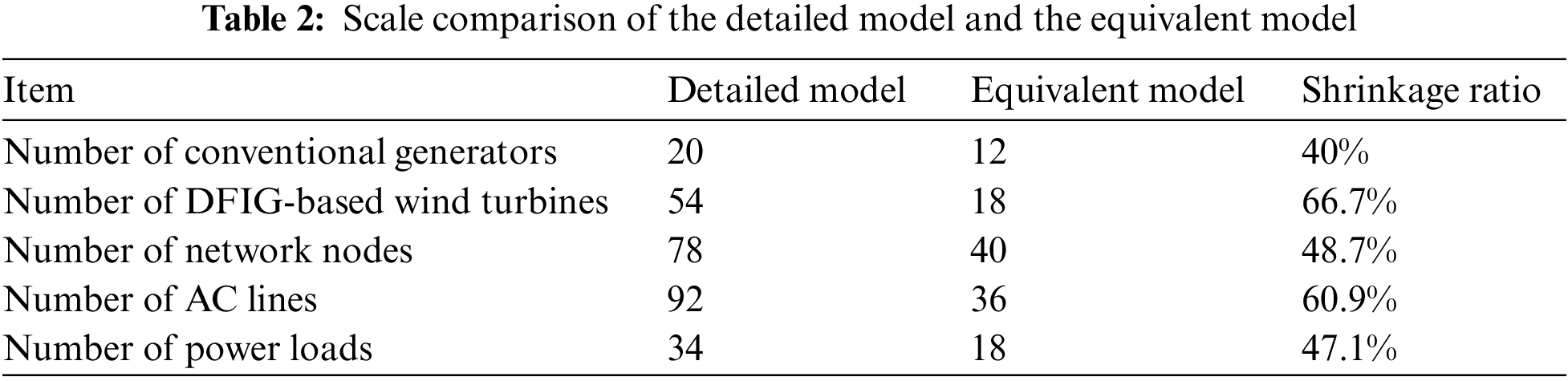
In terms of the proposed approach, the simplification of the AC-DC power networks is achieved, and the scale comparison of the detailed model and the equivalent model is listed in Table 2. The table shows that the proposed approach can visibly reduce the model scale and increase the simulation efficiency. In particular, the shrinkage ratio for the number of DFIG-based wind turbines is the most prominent. After using the presented multi-machine equivalence strategy, an original wind farm with nine DFIGs can be replaced by that with three equivalent DFIGs.
To assess the dynamic behaviors of the AC-DC power networks, the N-1 and N-2 fault scenarios are both simulated, and the specific performance comparison of the equivalent model as well as the detailed model is stated below.
The N-1 fault scenario in the demonstrated system is Node 11 meeting a three-phase short-circuit fault, which occurs at t = 2 s and lasts for 1/12 s. The operation time of the simulation model is 3 s, and Figs. 5 and 6 display the active and reactive power characteristics of different branches under the N-1 fault scenario. Herein, branches 12–23 and 2–19 are specially selected since these two are near the N-1 fault. The figures show that the demonstrated system will experience pronounced dynamics, and the active and reactive power fluctuations of the equivalent model coincide with that of the detailed model. Therefore, the proposed method ensures the consistency of the power flow property between the equivalent model as well as the detailed model.

Figure 5: Active power characteristics of different branches under the N-1 fault scenario. (a) Branches 12–23, and (b) branches 2–19
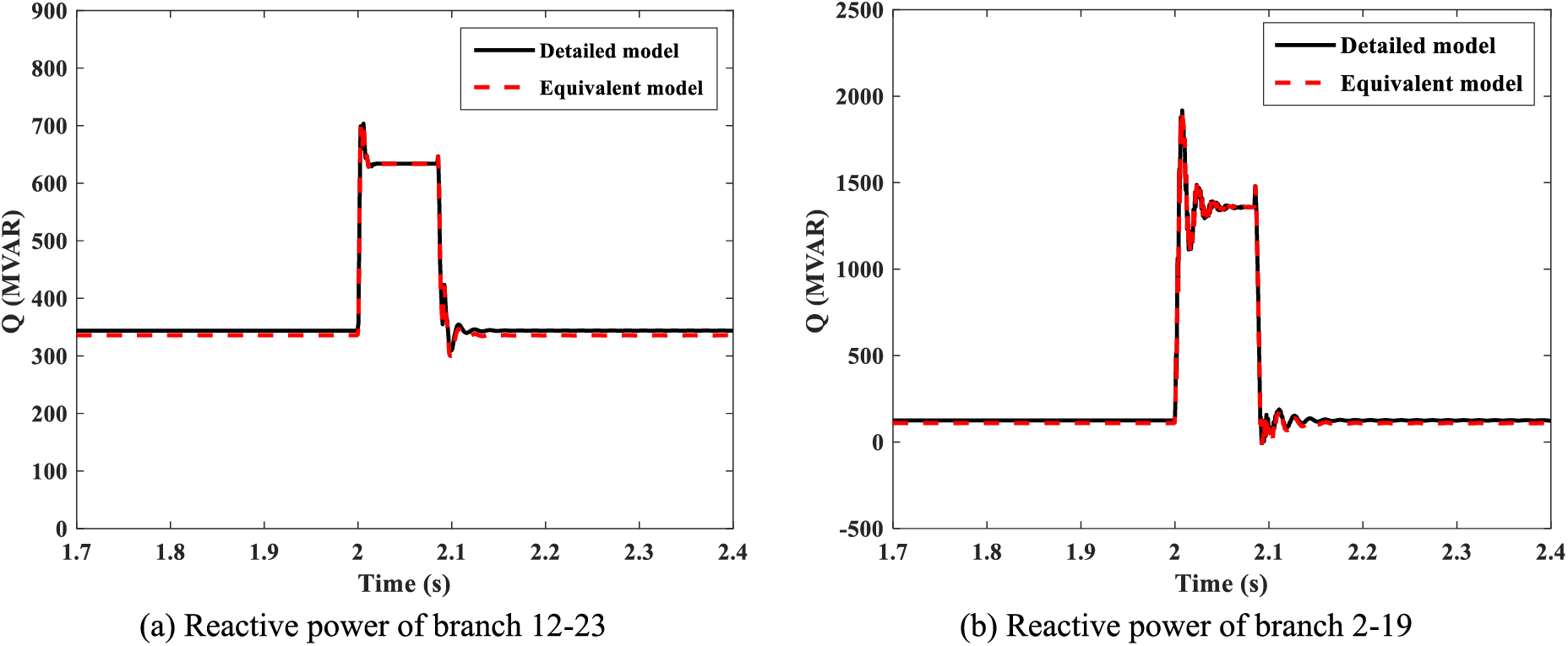
Figure 6: Reactive power characteristics of different branches under the N-1 fault scenario. (a) Branches 12–23, and (b) branches 2–19
By referring to references [27,28], Fig. 7 displays the voltage change characteristics of different nodes, and Fig. 8 shows the current change characteristics of different branches under the N-1 fault scenario. The fault node 11 and node 13 are chosen to reflect the equivalent model’s voltage performance, and branches 12–23 and 2–19 are selected to indicate the equivalent model’s current performance. For fault node 11, the voltage will drop to zero under the fault feeding process, and after the fault is cleared, the voltage can fast recover to its rated level. Both the detailed model and the equivalent model can express this dynamic property. Concerning node 13, the voltage will decline to ~0.89 p.u., and moderate voltage fluctuations are caused and exactly imitated by the equivalent model. In regards to branches 12–23 and 2–19, the fault current level will reach ~4.79 and ~2.35 p.u., respectively. When the fault is removed, the branch current can return to the normal level. In a sense, the proposed equivalent modeling method accurately performs the voltage and current change characteristics.
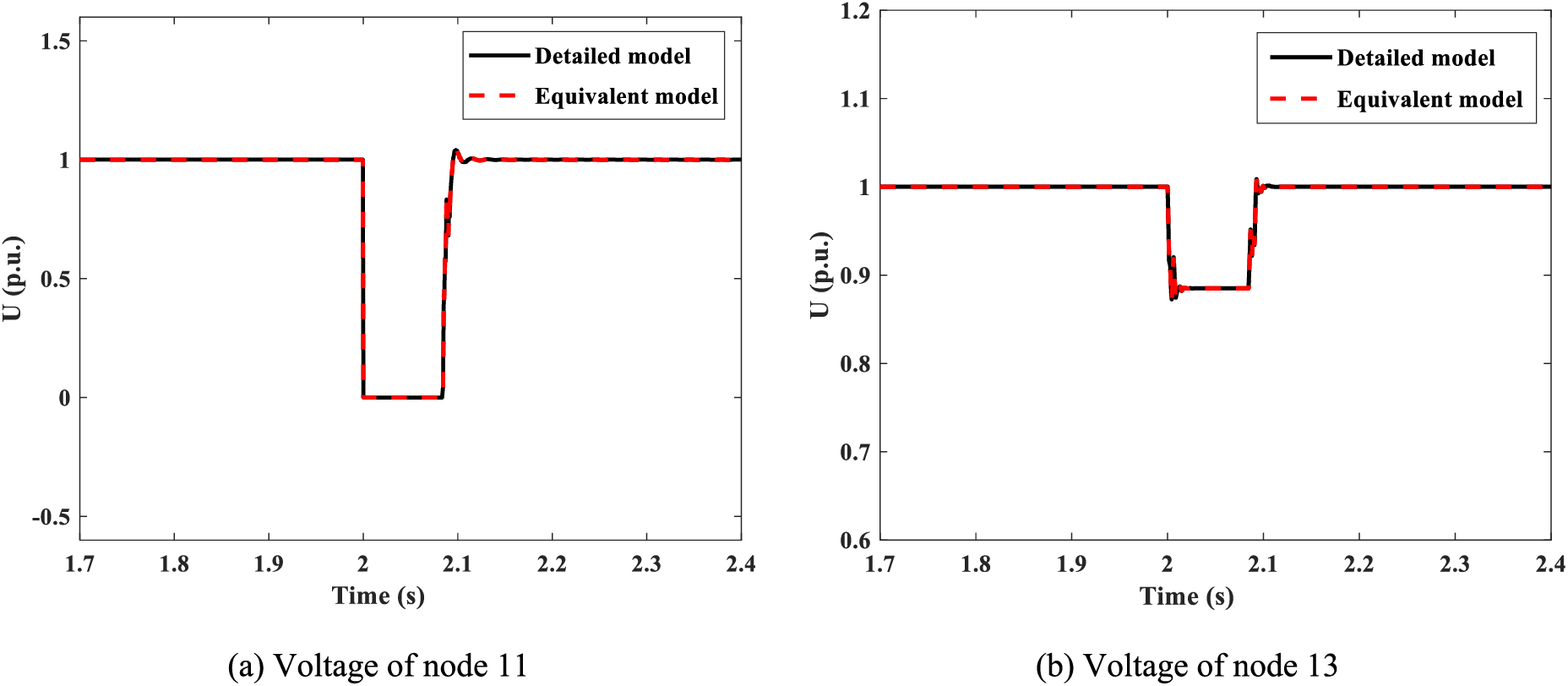
Figure 7: Voltage change characteristics of different nodes under the N-1 fault scenario. (a) Node 11, and (b) node 13
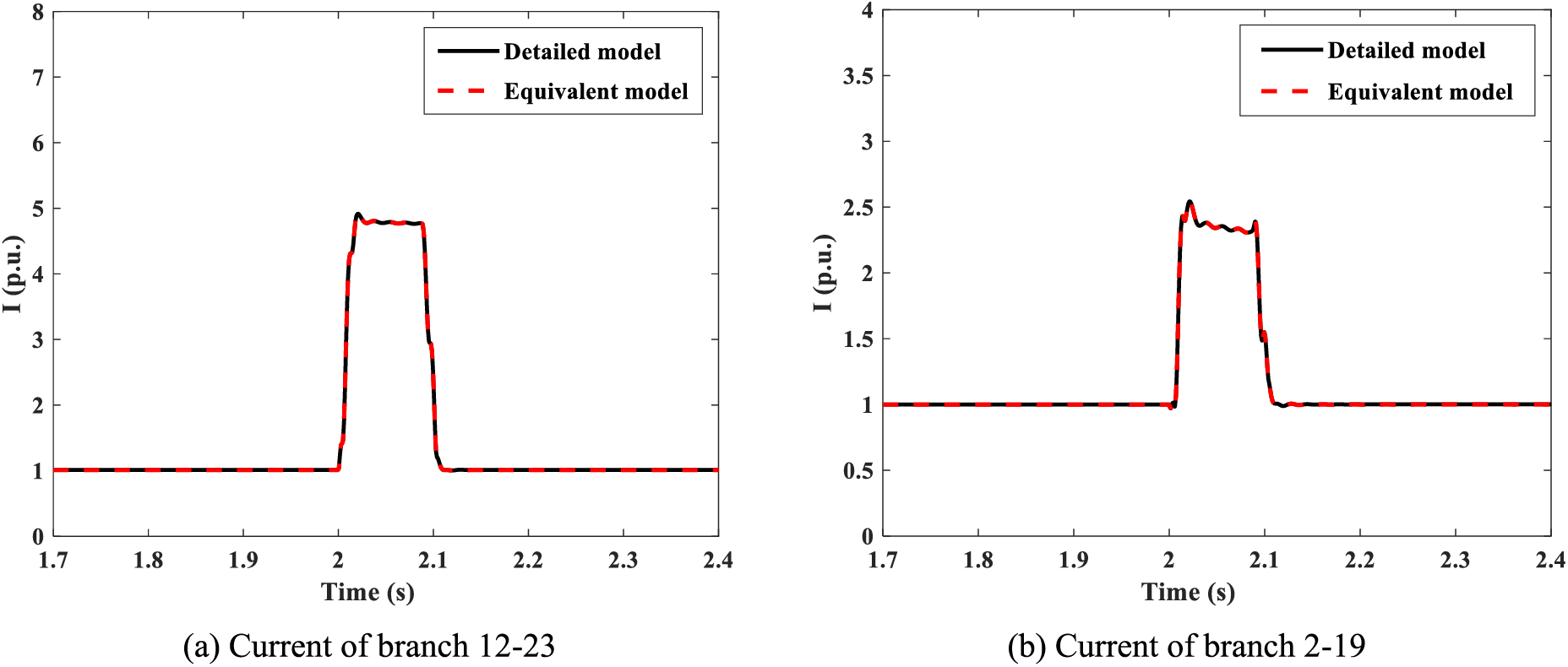
Figure 8: Current change characteristics of different branches under the N-1 fault scenario. (a) Branches 12–23, and (b) branches 2–19
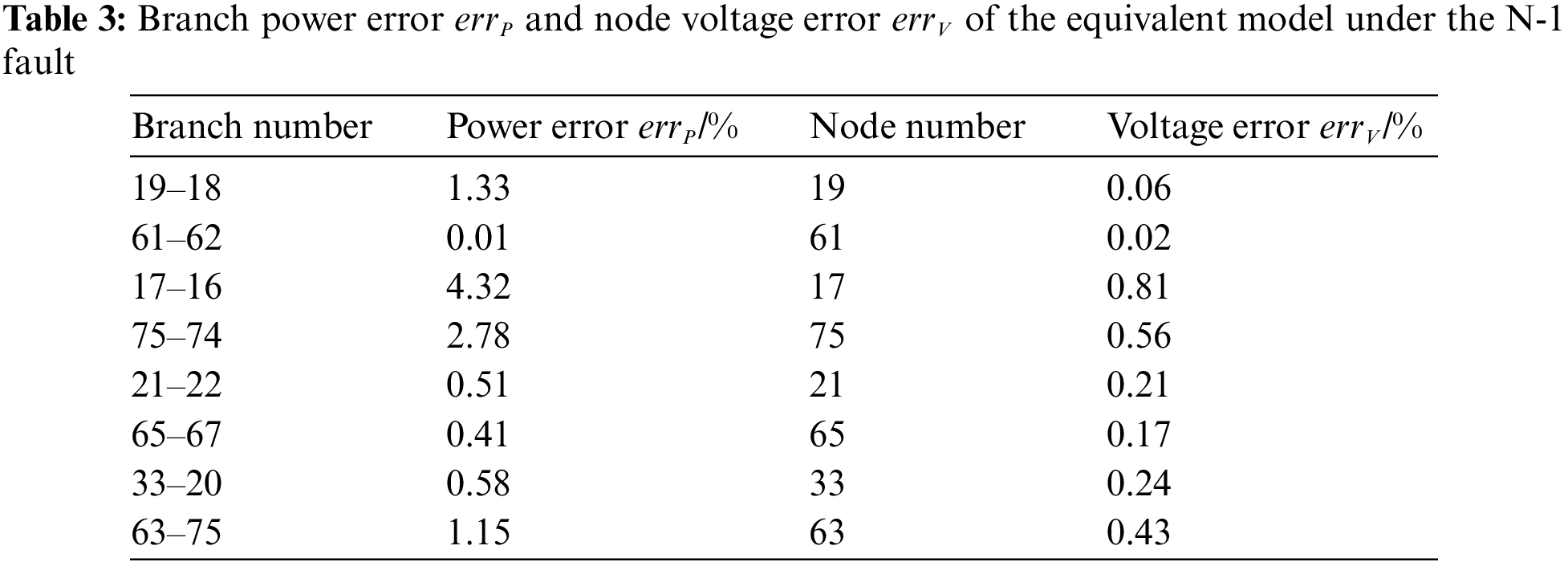
In addition, the equivalent model’s branch power and node voltage errors are appreciatively calculated. The error analysis results are enumerated in Table 3. The maximum and minimum of the branch power error will be 4.32% and 0.01%, respectively. The node voltage error’s variation range will be about [0.02%, 0.81%]. Overall, the model error is within the acceptable level, and the correctness of the equivalent model can be well confirmed.
The N-2 fault scenario in the demonstrated system is nodes 11 and 78 meeting the three-phase short-circuit faults, which occur at t = 2 s and last for 1/12 s. Fig. 9 displays the demonstrated system’s branch power and node voltage characteristics under the N-2 fault scenario. Considering branches 63–75 and node 53 are near the faults and will directly afford the dynamic influence, they are selected for comparing the performances of the detailed and equivalent models.
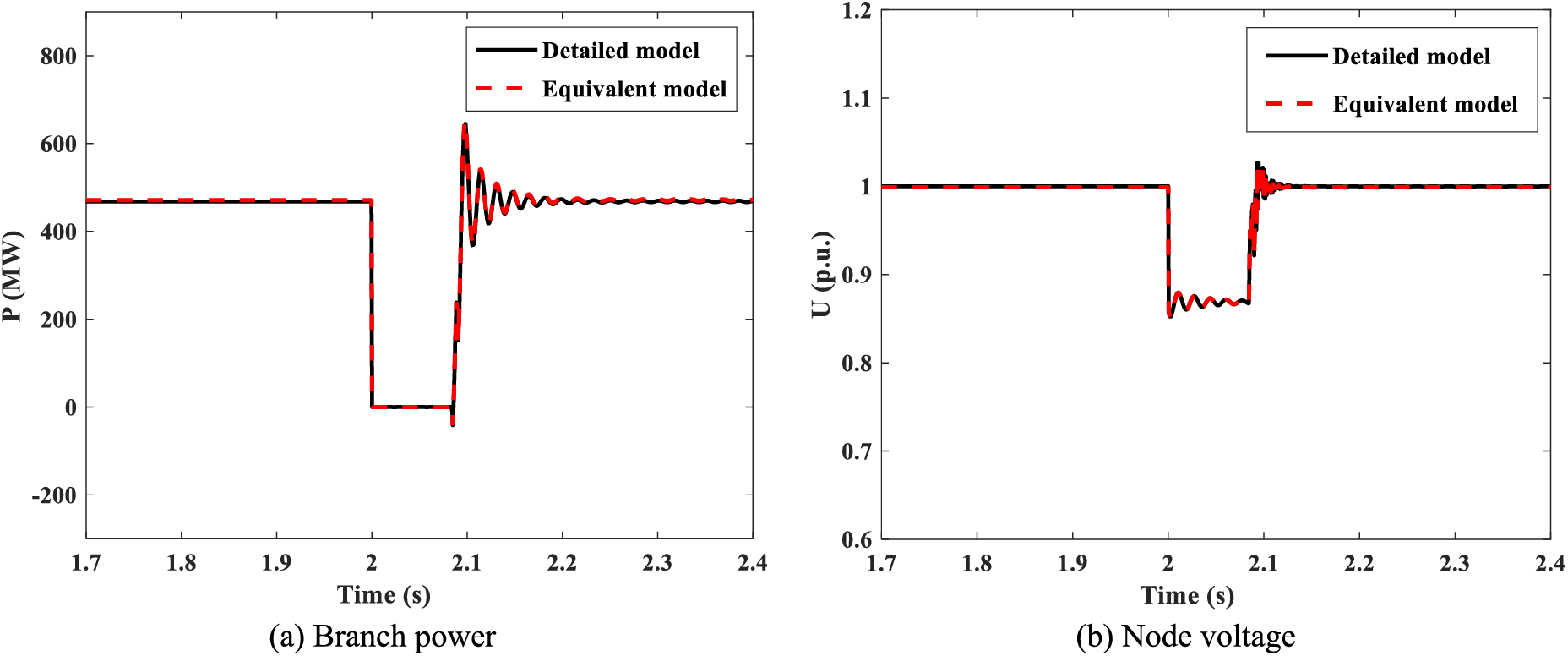
Figure 9: Branch power and node voltage of the system under the N-2 fault scenario. (a) Branches 63–75, and (b) node 53
From Fig. 9, it is found that the demonstrated system under the N-2 fault scenario will experience more obvious dynamics than the N-1 fault. The active power transmission of branch 63–75 will be interrupted under the faults, and the voltage at node 53 will drop to ~0.86 p.u. Concerning the N-2 fault scenario, the proposed method can still ensure consistency between the equivalent and detailed models.
The error analysis is carried out to verify the equivalent model’s accuracy regarding the branch power fluctuations and the node voltage in the transient state. Table 4 shows the power error errP on different branches and the voltage error errV on different nodes under the N-2 fault scenario. The chosen nodes are the endpoints of the four HVDC systems, and the selected branches have close relations to the desired nodes.
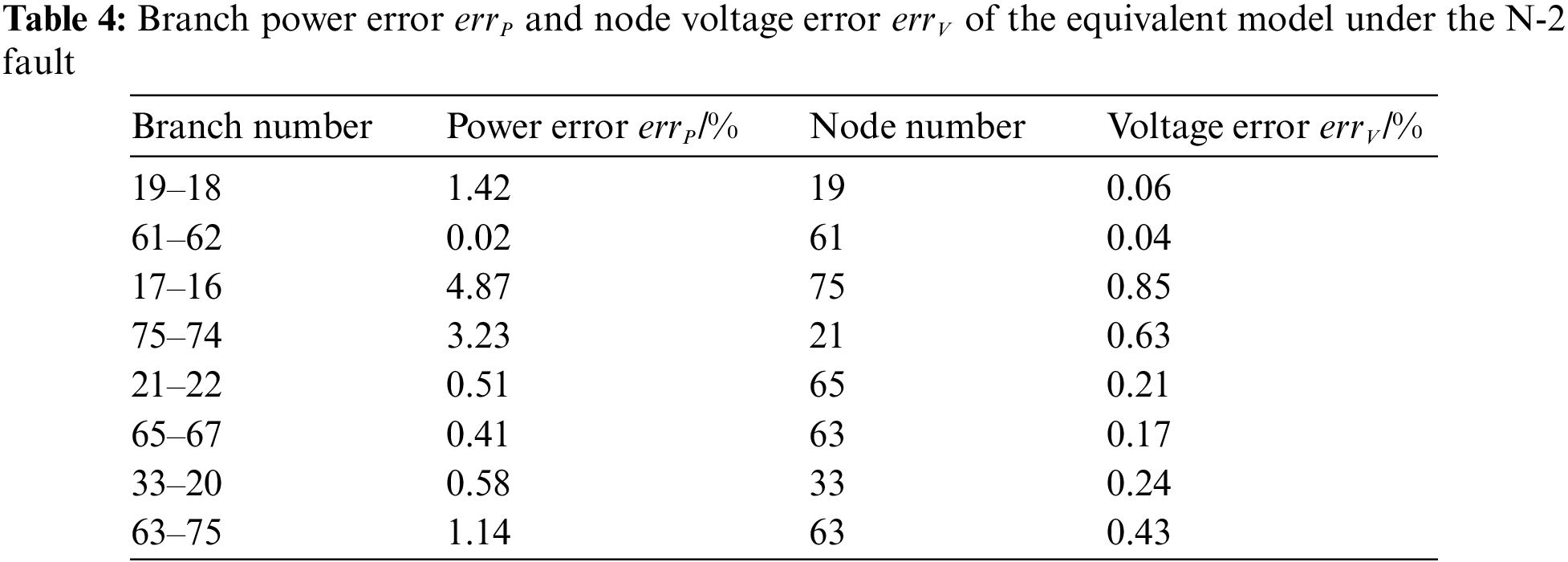
From Table 4, the maximum errP is 4.87%, which occurs at branch 17–16, and the maximum errV is 0.85%, which happens at node 75. The average value of errP is 1.52%, and the average level of errV is about 0.33%. Consequently, the proposed method can favorably simplify the AC-DC power networks and ensure that the dynamic characteristics are accurately imitated.
To further assess the performance of the proposed approach in the equivalence of the DFIG-based wind farms, the N-2 fault scenario is applied, and the following four cases are compared.
Case 1: Using the detailed model of the wind farms.
Case 2: Using the equivalent model of the wind farms based on the particle swarm optimization (PSO).
Case 3: Using the equivalent model of the wind farms based on the traditional CSA.
Case 4: Using the equivalent model of the wind farms based on the ICCSA.
The parameters of the PSO and the traditional CSA are listed in Tables 5 and 6. The tunning of the PSO parameters can refer to reference [29], and the tunning of the traditional CSA can refer to that of the ICCSA.


Fig. 10 displays the active and reactive power characteristics of the wind farm connected to node 18 under the four cases. Before the N-2 fault occurs, Case 4 is closer to Case 1 in the steady state. During the fault feeding period, Cases 2~4 have similar transient performances to show the DFIG-based wind farm’s active and reactive power changes, and possess the mind error compared with Case 1 in t = 2~2.1 s. After the fault recovery, Case 4 outperforms Case 2 and Case 3 with a tinier power error, and the equivalent model is closer to the delated model.
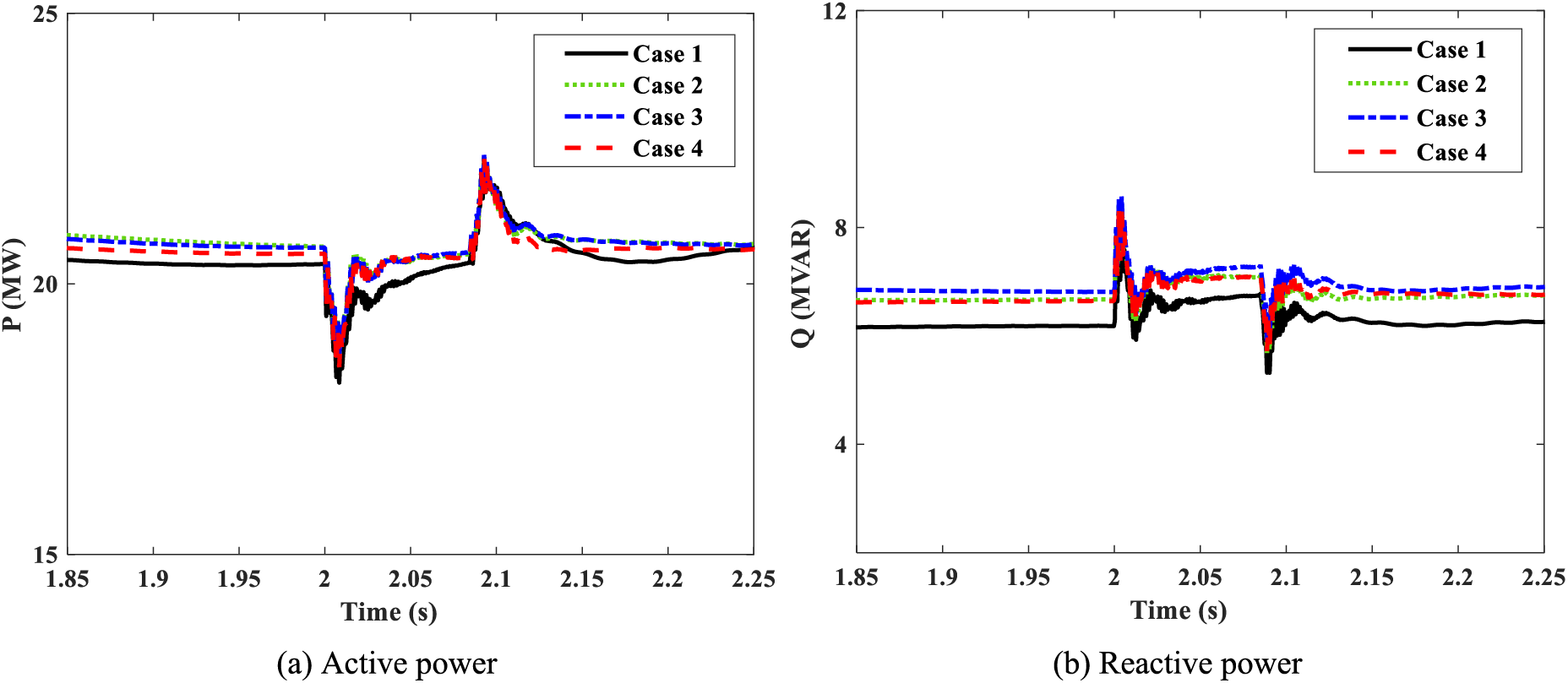
Figure 10: Power characteristics of the wind farm connected to node 18 under the four cases. (a) Active power, and (b) reactive power
In this section, the active power of the wind farm is pointedly considered, and the model error’s computation results are listed in Table 7.

To check the credibility of the suggested ICCSA method further, the comparison of the particle swarm optimization (PSO), the traditional CSA, and the ICCSA in the parameter identification of the wind farm has been carried out, and the performance differences of these three algorithms are shown in Fig. 11.
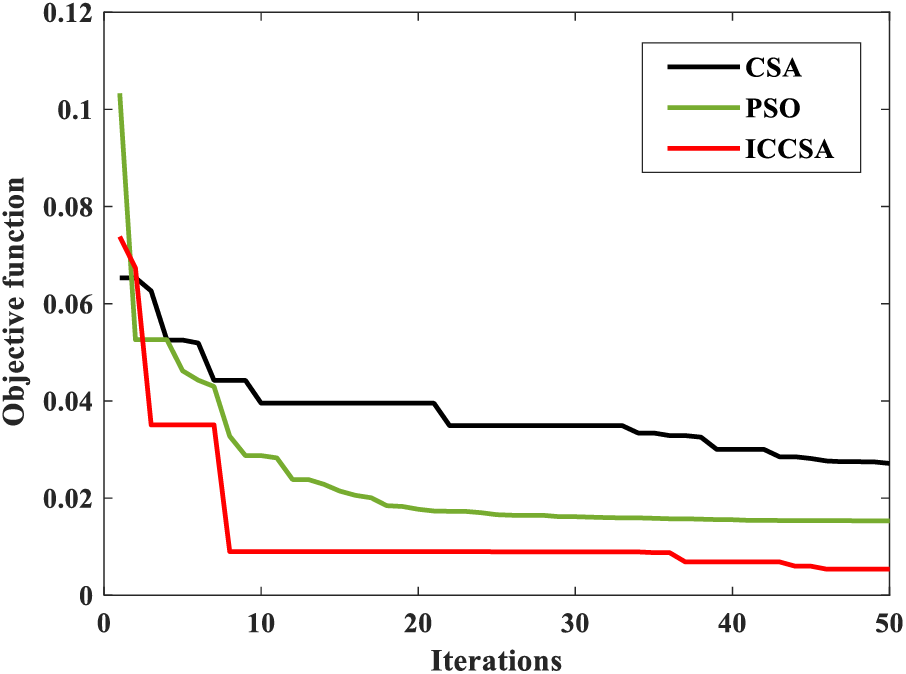
Figure 11: Optimization performance differences of the PSO, traditional CSA, and ICCSA
For the traditional CSA, the size parameter of Levy flights is fixed at 0.45, and the probability of every cuckoo egg to be discovered by the host bird is set to 0.5. From Fig. 11, it is concluded that the suggested ICCSA outperforms the PSO and the traditional CSA in the parameter identification of the wind farm. The suggested ICCSA has the lowest number of iterations and the best objective function value, and it is more suitable for addressing the equivalent modeling issue of renewable generation. Table 8 indicates the specific performance data of the PSO, traditional CSA, and ICCSA.
At the end of the simulation analysis, the scalability of the proposed equivalent modeling method is validated in a larger wind farm containing eighteen DFIG-based wind turbines with a total capacity of 40.8 MW. Table 9 lists the results of the model error in imitating the larger wind farm’s active power under the four cases. As the number of turbines in the wind farm doubles, there is a very slight decrease in the accuracy of the proposed equivalent modeling approach. Regarding Case 4, it is evident that the active power error of the equivalent model is increased from 0.42% to 0.65% during the fault, but this error change is within the acceptable level. Thus, the scalability of the proposed equivalent modeling method can be confirmed.
This paper puts forward a methodology for the equivalent modeling of the AC-DC power networks with doubly-fed induction generator (DFIG) based wind farms, and the goal is to decrease the simulation scale and computational burden while reflecting the dynamic behaviors. The equivalent modeling strategies for the AC-DC power networks and the wind farms are presented, respectively, and considering different intelligence algorithms and fault scenarios, the comparative verification of the proposed approach in the two-zone four-DC interconnected power grid with wind farms is carried out. The major findings of this work are summarized below:
(1) The proposed approach can considerably reduce the model size and increase the simulation efficiency. Regarding the number of conventional generators, DFIG-based wind turbines, network nodes, AC lines, and power loads, the equivalent model offers more than 40% shrinkage ratio compared to the detailed model.
(2) The proposed approach can well show the dynamic behaviors of the AC-DC power networks under the N-1 and N-2 fault scenarios. The errors of branch power and node voltage are calculated, and the proposed approach’s efficacy is demonstrated.
(3) The proposed approach can efficiently achieve the parameter identification of the wind farms and fulfill the equivalent modeling. The equivalent model has nice consistency with the detailed model from the wind farm power outputs in a steady state, during the fault, and after the fault clearance.
As a result, the efficacy and applicability of the proposed approach are verified. Noting that, the equivalent modeling of the AC-DC power networks preserves the 500 kV main networks, the HVDC systems, and the AC links between them during the equivalence process. As the model of the multiple HVDC systems is considered, the model complexity of the AC-DC power networks is certainly increased, and it is regarded as the main limitation of the proposed modeling. The equivalent model can be used to investigate the stability issues of the AC-DC power networks with DFIG-based wind farms in light of favorable simulation speed and accuracy. In addition, the equivalent model can be used for assessing the hosting capacity of renewable energy in the AC-DC power systems from the stability perspective. Shortly, our research team plans to test the equivalent model’s functions further and explore the application of the proposed method in the multi-region interconnected AC-DC power systems with different types of renewable energy generation. The research findings will be reported in other articles.
Acknowledgement: The authors acknowledge the support of the Central China branch of State Grid Corporation of China.
Funding Statement: This work was supported by the Science and Technology Project of Central China Branch of State Grid Corporation of China under 5214JS220010.
Author Contributions: The authors confirm their contribution to the paper as follows: The study conception and design: W. J, L. Chen, Y. Li, S. Zheng, and H. Chen. Data collection: W. J, L. Chen, Y. Li, S. Zheng, and Y. Jiang. Analysis and interpretation of results: L. Chen, Y. Li, S. Zheng, and Y. Jiang. Draft manuscript preparation: W. J, L. Chen, Y. Li, and S. Zheng. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data supporting this study are included within the article.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Zhuo, Z. Y., Zhang, N., Yang, J. W., Kang, C. Q., Smith, C. et al. (2020). Transmission expansion planning test system for AC/DC hybrid grid with high variable renewable energy penetration. IEEE Transactions on Power Systems, 35(4), 2597–2608. [Google Scholar]
2. Wu, Y. Y., Fang, J. K., Ai, X. M., Xue, X. Z., Cui, S. C. et al. (2023). Robust co-planning of AC/DC transmission network and energy storage considering uncertainty of renewable energy. Applied Energy, 339, 120933. [Google Scholar]
3. Gu, M., Meegahapola, L., Wong, K. L. (2022). Enhancing dynamic stability performance of hybrid ac/dc power grids using decentralised model predictive control. Electric Power Systems Research, 213, 108668. [Google Scholar]
4. Wang, Y., Yan, G., Mu, G., Yang, C. (2022). Research on aggregation modeling of grid connected VSC under AC current control scale. Proceedings of the CSEE, 42(8), 2900–2910. [Google Scholar]
5. Agbemuko, A. J., Domínguez-García, J. L., Prieto-Araujo, E., Gomis-Bellmunt, O. (2023). Interconnection of hybrid AC/DC grids of arbitrary strengths using supplementary bus-voltage feedforwards. International Journal of Electrical Power and Energy Systems, 147, 108803. [Google Scholar]
6. Sakinci, Ö. C., Lekić, A., Beerten, J. (2022). Generalized impedance-based AC/DC power system modeling for harmonic stability analysis. International Journal of Electrical Power and Energy Systems, 143, 108456. [Google Scholar]
7. Cheng, L., Li, B., Li, G., Wang, Z. (2022). A modeling approach for AC/DC distribution systems based on average dynamic phasor method. Energy Reports, 8, 1921–1934. [Google Scholar]
8. Yan, K., Li, G., Zhang, R., Li, F., Jiang, T. et al. (2023). Aggregated SFR model for VSC-HVDC interconnected power systems with high penetration of wind power. Electric Power Systems Research, 216, 109018. [Google Scholar]
9. Campello, T. M., Dicler, F. N. F., Varricchio, S. L., Barros, H. M. D., Costa, C. O. et al. (2023). Reviewing the large electrical network equivalent methods under development for electromagnetic transient studies in the Brazilian interconnected power system. International Journal of Electrical Power and Energy Systems, 151, 109033. [Google Scholar]
10. Xu, Y., Gao, T. (2022). Sub-synchronous frequency domain-equivalent modeling for wind farms based on rotor equivalent resistance characteristics. Global Energy Interconnection, 5(3), 293–300. [Google Scholar]
11. Pan, X., Qi, X., Liang, W., Yong, C., Ding, X. et al. (2022). Multi-machine equivalence and global identification of wind farms by combining model aggregation and parameter estimation. Electric Power Automation Equipment, 42(1), 124–132. [Google Scholar]
12. Han, J., Miao, S., Chen, Z., Liu, Z., Li, Y. et al. (2022). A novel wind farm equivalent model for high voltage ride through analysis based on multi-view incremental transfer clustering. International Journal of Electrical Power and Energy Systems, 135, 107527. [Google Scholar]
13. Zhu, Q. (2023). Quantitative evaluation method for error of wind farm equivalent model based on multiscale entropy-greedy Gaussian segmentation. Electric Power Systems Research, 220, 109270. [Google Scholar]
14. Zou, M., Zhao, C., Xu, J. (2023). Modeling for large-scale offshore wind farm using multi-thread parallel computing. International Journal of Electrical Power and Energy Systems, 148, 108928. [Google Scholar]
15. Wu, C., Wang, Q., Luo, K., Fan, J. (2023). A coupled turbine-interaction wind farm parameterization in the weather research and forecasting model. Energy Conversion and Management, 283, 116919. [Google Scholar]
16. Zhang, J., Cui, M., He, Y. (2020). Robustness and adaptability analysis for equivalent model of doubly fed T induction generator wind farm using measured data. Applied Energy, 261, 114362. [Google Scholar]
17. Zhu, L., Zhang, J., Zhong, D. T., Wang, B., Li, Q. (2020). A study of dynamic equivalence using the similarity degree of the equivalent power angle in doubly fed induction generator wind farms. IEEE Access, 8, 88584–88593. [Google Scholar]
18. Li, J., Song, Z., Wang, X., Wang, Y., Jia, Y. (2022). A novel offshore wind farm typhoon wind speed prediction model based on PSO-Bi-LSTM improved by VMD. Energy, 251, 123848. [Google Scholar]
19. Chen, L., Li, G., He, H., Chen, H., Li, Y. et al. (2020). Study on coordination of resistive SFCLs and hybrid-type circuit breakers to protect a HVDC system with LCC and VSC stations. IEEE Transactions on Applied Superconductivity, 30(4), 5600806. [Google Scholar]
20. Kang, Y., Lu, S., Cheng, L., Cheng, G., Xu, Z. (2017). A reduction method of large power systems for electromagnetic transient simulation and its application in China southern grid. Electric Power Construction, 38(1), 31–38. [Google Scholar]
21. Gupta, A. P., Mohapatra, A., Singh, S. N. (2021). Measurement based parameters estimation of large scale wind farm dynamic equivalent model. Renewable Energy, 168, 1388–1398. [Google Scholar]
22. Priyamvada, I. R. S., Das, S., Chaudhuri, B. (2022). Method to quantify modal interactions between converter interfaced generators and synchronous generators. IEEE Transactions on Power Systems, https://doi.org/10.1109/TPWRS.2022.3228940 [Google Scholar] [CrossRef]
23. Chao, P., Li, W., Liang, X., Xu, S., Shuai, Y. (2021). An analytical two-machine equivalent method of DFIG-based wind power plants considering complete FRT processes. IEEE Transactions on Power Systems, 36(4), 3657–3667. [Google Scholar]
24. Cui, Z., Xu, X., Xue, F., Cai, X., Cao, Y. et al. (2020). Personalized recommendation system based on collaborative filtering for IoT scenarios. IEEE Transactions on Services Computing, 13(4), 685–695. [Google Scholar]
25. Yang, R., He, J., Xu, Y., Shu, Z. (2020). Determination method of dynamic equivalent boundary for AC-DC power system considering security control actions. Electric Power Automation Equipment, 40(4), 56–62. [Google Scholar]
26. Saida, I. B., Nadjet, K., Omar, B. (2018). A new quantum chaotic cuckoo search algorithm for data clustering. Expert Systems with Applications, 96, 358–372. [Google Scholar]
27. Wang, R., Sun, Q., Ma, D., Liu, Z. (2019). The small-signal stability analysis of the droop-controlled converter in electromagnetic timescale. IEEE Transactions on Sustainable Energy, 10(3), 1459–1469. [Google Scholar]
28. Wang, R., Sun, Q., Zhang, P., Gui, Y., Qin, D. et al. (2020). Reduced-order transfer function model of the droop-controlled inverter via Jordan continued-fraction expansion. IEEE Transactions on Energy Conversion, 35(3), 1585–1595. [Google Scholar]
29. Jin, W., Chen, L., Chen, H., Zheng, S. (2023). A novel evaluation method of the hosting capacity of multiple renewable energy stations accessed into a power system. Energy Reports, 9, 56–65. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools