 Open Access
Open Access
ARTICLE
Dynamic Response Analysis of Semi-Submersible Floating Wind Turbine with Different Wave Conditions
1 School of Mechanical Engineering, Shandong University of Technology, Zibo, 255049, China
2 Testing Center, Lianyungang Zhongfulianzhong Composite Material Group Co., Ltd., Lianyungang, 222000, China
3 Engineering and Technology Department, Sinoma Sci & Tech Co., Ltd., Funing, 224400, China
4 Testing Center, Shandong Provincial Key Laboratory of Precision Manufacturing and Special Processing, Zibo, 255049, China
* Corresponding Author: Xuemei Huang. Email:
Energy Engineering 2023, 120(11), 2531-2545. https://doi.org/10.32604/ee.2023.029702
Received 04 March 2023; Accepted 28 June 2023; Issue published 31 October 2023
Abstract
To address the problem of poor wave resistance of existing offshore floating wind turbines, a new type of semi-submersible platform with truncated-cone-type upper pontoons is proposed by combining the characteristics of offshore wind turbine semi-submersible floating platforms. Based on the coupled hydrodynamic, aerodynamic, and mooring force physical fields of FAST, the surge, heave, pitch, and yaw motions responses of the floating wind turbine under different wave heights and periods are obtained, and the mooring line tension responses are also obtained; and compare the dynamic response of the new semi-submersible platform with the OC4-DeepCwind platform at six degrees of freedom. The results show that different wave conditions have obvious effects on the heave and pitch motions of the new floating wind turbine, and fewer effects on the surge and yaw motions; the tensegrity response of the mooring system is more affected by the wave conditions; compared with the OC4-DeepCwind floating wind turbine, the pitch and roll response of the new floating wind turbine has been significantly reduced and has good stability.Keywords
In today’s new era of green energy, wind power has become a new type of green energy that can meet the needs of people’s practical life. Although the use of wind energy is still mainly onshore wind power, onshore wind power has the disadvantages of occupying land resources, less storage capacity, power transmission difficulties, and affecting the living environment, compared to offshore wind power has more potential [1–3].
At present, there are mainly two types of offshore wind turbines, fixed and floating. Among them, the fixed foundation is generally used in offshore waters and has certain limitations; in contrast, the floating type has the advantages of good mobility, easy disassembly, and can obtain stable and high-quality wind resources in deep waters without affecting near-shore fisheries and other related industrial activities. Floating wind turbine platforms can be divided into three categories according to the different ways of obtaining stability: spar platforms [4], semi-submersible platforms [5], and tension-leg platforms [6–8]. Among them, the spar platform has a simple structure, low vertical wave excitation force, and better stability, but its roll and pitch motions are larger, while its column length is generally longer and more difficult to install; the semi-submersible platform applies to a wide range of water depths and less difficult to install, but its stability is lower than that of the single-post foundation structure; the tension-leg platform has good stability and light structural mass, but its mooring system installation process is complex and costly, and its tension is greatly affected by wind and waves. In summary, the semi-submersible platform has a wide application prospect in the design and demonstration projects of floating platforms because of its advantages of good stability, strong wind and wave resistance, easy installation, and a wide range of applicable water depth [9–12].
Currently, offshore floating platforms are subjected to complex and variable environmental loads such as wind and wave loads, resulting in more complex excitation movements of the platform. In addition, the harsh marine environment also poses a threat to its survivability [13]. Therefore, it is important to study wind turbine platforms with good stability and to analyze the dynamic response under different wind and wave conditions. To reduce the motion response of floating platforms and guarantee the smooth operation of wind turbines, a series of studies on new platform forms and their dynamic response have been conducted by domestic and foreign scholars. The U.S. Renewable Energy Laboratory [14] proposed the OC4-DeepCwind platform, whose triangular arrangement of pontoons is divided into two parts: the upper pontoon and the lower pontoon, and the lower pontoon not only plays a role in reducing the heave motion, but also reduces the center of gravity and improves the stability of the system, but the platform still suffers from relatively large wave loads, which exacerbate the problem of the platform’s swing motion; Roddier et al. [15] proposed a new eccentric offshore floating wind turbine WindFloat, and studied the free decay motion of the platform under steady-state wind conditions and the dynamic response of different operating conditions with the aerodynamic servo elastic package FAST, and verified its high agreement with the hydrodynamic numerical simulation results through model tests. Zhang et al. [16] proposed a new steel lattice foundation for offshore wind turbines, and used the coupled hydrodynamic-aerodynamic-control system-mooring system approach to analyze the dynamic response of the new offshore floating wind turbine under the combined wind and wave action, and the results showed that the roll, pitch, and yaw responses of the steel lattice foundation were smaller and had better stability; Zhang et al. [17] designed a new semi-submersible platform with inclined columns, and analyzed and optimized the parameters of the semi-submersible platform structure and mooring system, and the results showed that the new platform could effectively prevent the resonance phenomenon.
This paper proposes a new type of semi-submersible platform, which uses FAST software [18] to analyze the comprehensive effects of coupled physical fields of hydrodynamic, aerodynamic, and mooring force, to obtain the dynamic response and mooring line tension response of floating wind turbines under different wave conditions, and compare the dynamic response of the new semi-submersible platform with the OC4-DeepCwind platform at six degrees of freedom. The study shows that the platform has good kinematic performance, higher stability and better wave resistance, which can provide some reference for the development of floating platforms for offshore wind turbines.
2 The New Floating Wind Turbine
Referring to the OC4-DeepCwind semi-submersible wind turbine platform released by the National Renewable Energy Laboratory (NREL) in the United States, this paper designs a semi-submersible floating wind turbine platform with truncated-cone-type upper pontoons. The new semi-submersible platform is composed of upper pontoons, lower pontoons, central pontoon, support bars, and anchor chains, as shown in Fig. 1. Different from the OC4 floating platform, the upper pontoon is designed as a truncated-cone-type, which increases the buoyancy difference when the platform is tilted, thus effectively increasing the restoring torque and thus increasing the stability of the system; the lower pontoon is arranged below the truncated-cone-type pontoon, which increases the platform vertical damping and effectively reduces the platform wave load. The wind turbine is installed on the central pontoon, and the combination of the truncated-cone-type upper pontoon and the large cross-section lower pontoon is in an equilateral triangular array as the buoyancy unit, which is connected with the central column through the support bar. The relevant parameters of the platform are detailed in Table 1.
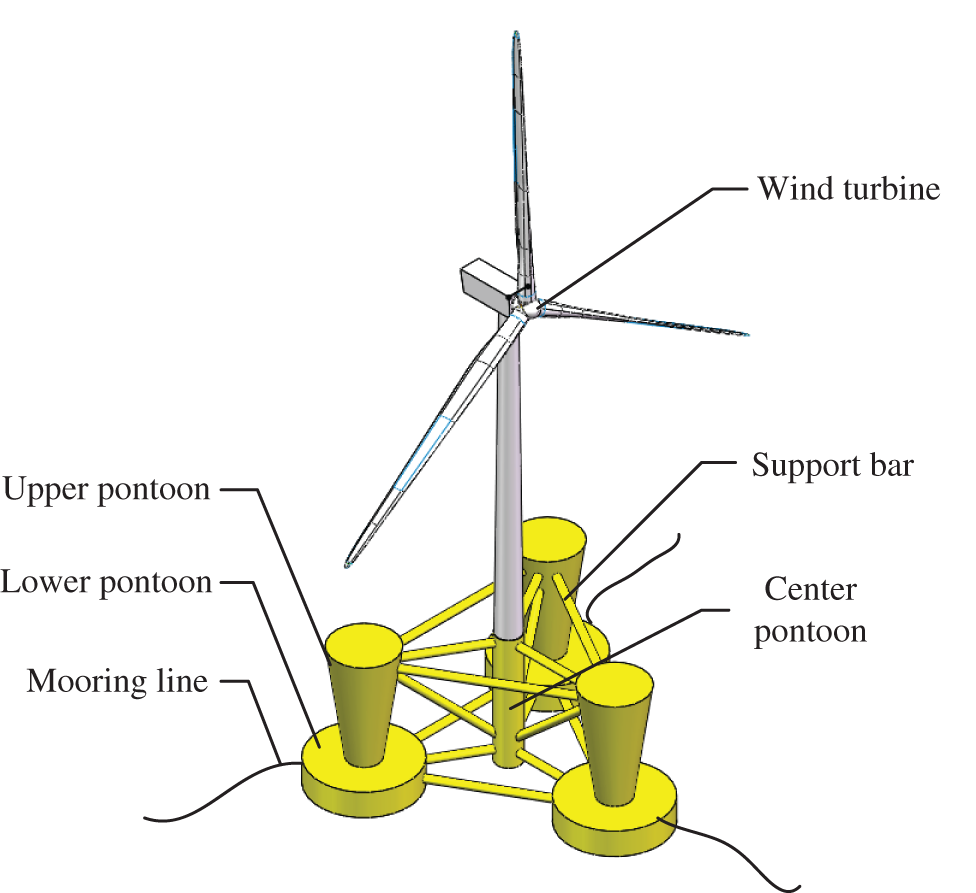
Figure 1: New semi-submersible floating wind turbine

2.2 Wind Turbine and Mooring System Parameters
For offshore wind turbines, choosing the wind turbine with the best wind energy utilization and power generation efficiency is an important indicator for selection. At present, the wind turbine researched by the National Renewable Energy Laboratory (NREL) [19] has been unanimously recognized and widely used in the verification of offshore wind farms at home and abroad. Therefore, the wind turbine in this paper adopts the 5 MW wind turbine model of this laboratory source, and its relevant parameters are detailed in Table 2.

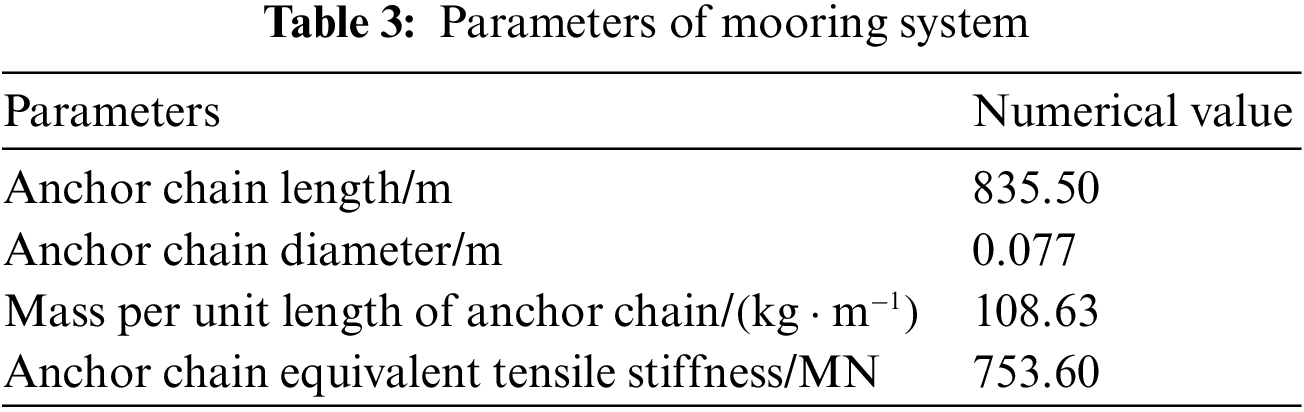
The new floating wind turbine platform consists of three suspended mooring chains distributed around the Z-axis with an angle of 120° between the mooring chains, and the origin is the triangular center O formed by three connected support bars of the lower float. The mooring chains are connected to the platform through the cable guide holes on the top of the lower float. The arrangement of the mooring system is shown in Fig. 2, and the relevant parameters are detailed in Table 3.
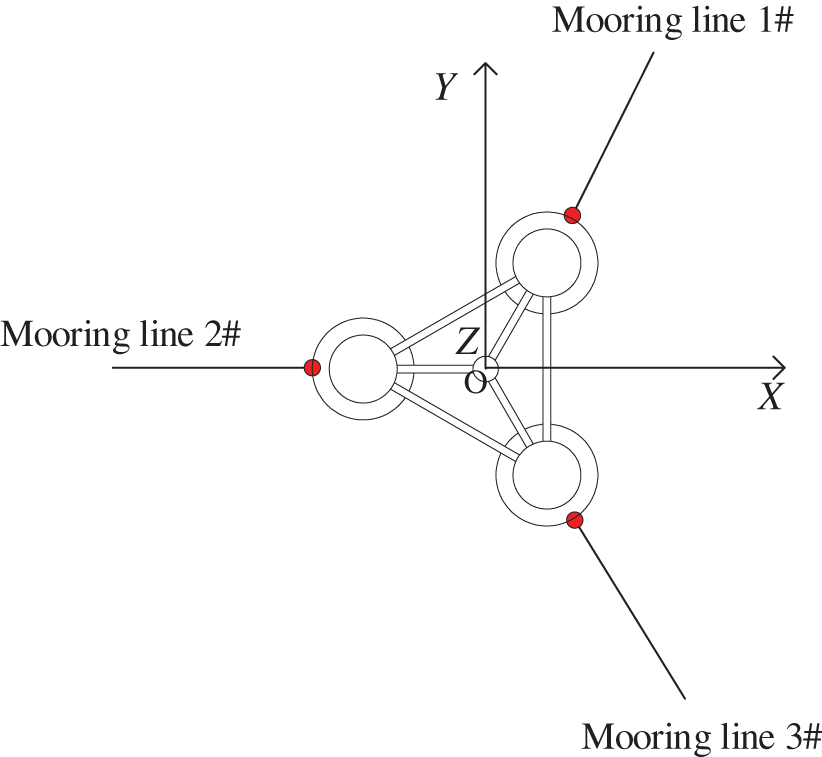
Figure 2: Layout of mooring system
Wave loads are important environmental loads for the design of offshore semi-submersible floating platforms, so the wave loads on the floating foundation of semi-submersible offshore wind turbines play a decisive role in the motion response of semi-submersible floating platforms. The new semi-submersible platform mainly consists of relatively large size pontoons (D/L > 0.2, D is the equivalent diameter of the member, m; L is the wavelength, m) and relatively small size of the support bars (D/L ⩽ 0.2). And the wave load on the platform structure mainly includes drag force, inertia force, and rounding force.
The support bars, as small-size members, are only subjected to drag force and inertia force, and the wave loads are calculated by Morison’s formula [20]. The wave load
where
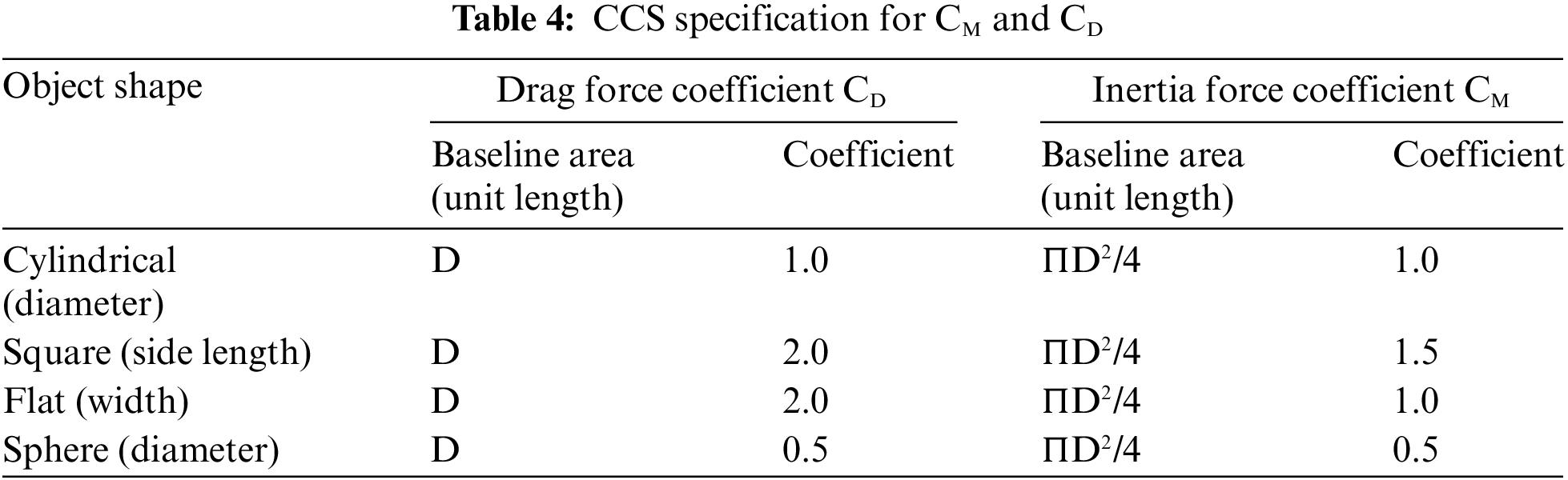
The drag force coefficient
For large-size pontoons with D/L > 0.2, they are subjected to drag force, inertia force, and diffraction force at the same time. The current methods for calculating load by linear diffraction of waves are mainly: Green’s function method, singularity distribution method, and source-sink distribution method. Among them, the Green's function method can deal with a variety of mathematical physics equations in a unified way, and its results, once derived, can calculate the field of any source. Therefore, this paper adopts the Green's function method to calculate and analyze the wave load on the platform, and firstly, the velocity potential function
Under the boundary condition of the deep-water sea, it is written as:
where
In the shallower sea boundary conditions are noted as:
where
Decompose the velocity potential into three components
where
The magnitude of the wave load on the platform is related to the water depth, shape, and size of the platform, and also to the wave spectrum selected according to the platform design criteria.
This paper applies the spectral analysis method to simulate the JONSWAP wave spectrum for a new semi-submersible platform in waves with significant wave heights of 2.5, 3, 3.6, 4.2, and 5.9 m, spectral peak periods of 9.8, 10, 10.2, 10.5, and 11.3 s, and a wave direction angle of 0°. The form of the spectrum is shown in the following equation:
where
The concentrated mass method is used for the mooring system load calculation, based on the MAP++ module of the FAST software, the mooring loads were obtained using the dynamic analysis method [21], which can be expressed as follows:
where
3.3 System Time Domain Equation of Motion
The time domain equations of motion for the coupled wind turbine, semi-submersible platform, and anchor chain are as follows:
where
4.1 Calculated Working Conditions
In this paper, FAST software coupled with hydrodynamic, aerodynamic, and other physical fields is used to simulate the offshore floating wind turbine under the same wind conditions and different wave conditions. The simulation calculation time for each working condition is 3600 s. To observe the curve changes more clearly and intuitively, this paper intercepts the data from 200 to 1000 s under the steady state operation of the wind turbine to create its dynamic characteristics time history curve.
Waves using the JONSWAP spectrum, the angle of incidence is along the positive direction of the X-axis, waves with significant wave heights of 2.5, 3, 3.6, 4.2, and 5.9 m and spectral peak periods of 9.8, 10, 10.2, 10.5, and 11.3 s were simulated, respectively, and recorded as wave conditions A to E. The wave curves under different wave conditions are shown in Fig. 3.
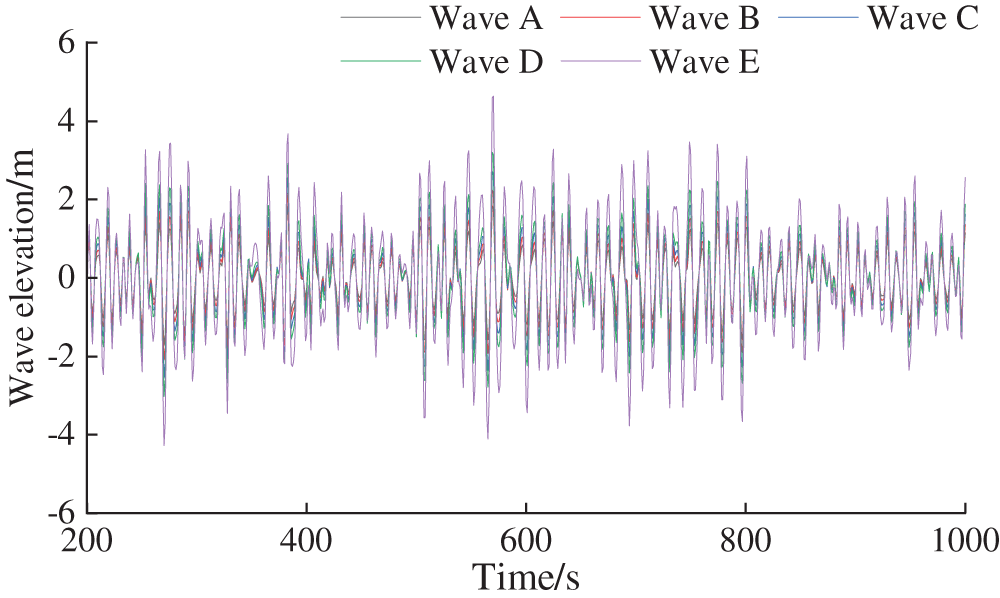
Figure 3: Time series of wave height
Turbulent winds were generated using Turbsim software, and the Kaimal model from IEC 61400-3 specification [22] was selected to generate wind speed time series by Inverse Fast Fourier Transforms (IFFTs) as the input of wind load. The wind direction along the positive direction of the X-axis was obtained from the simulation, and the turbulent wind with a rated wind speed of 11.4 m/s was selected for the model simulation, and the wind speed time series curve is shown in Fig. 4.
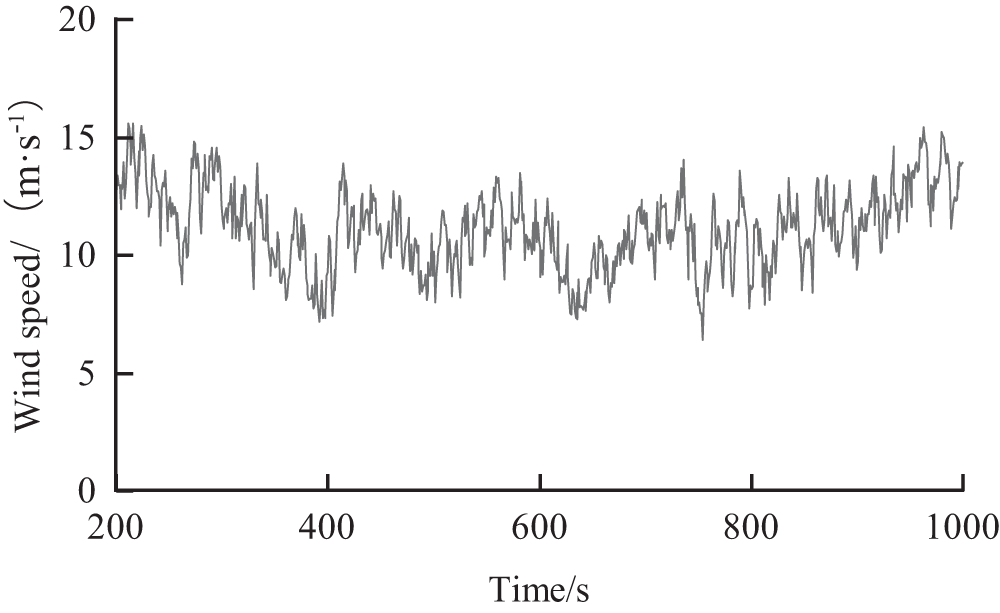
Figure 4: Time series of wind speed
4.2 Dynamic Response of New Floating Wind Turbine under Different Wave Conditions
The time curves and statistical results of the surge, heave, pitch, and yaw motions of the new semi-submersible floating wind turbine under different wave conditions are shown in Figs. 5 and 6.
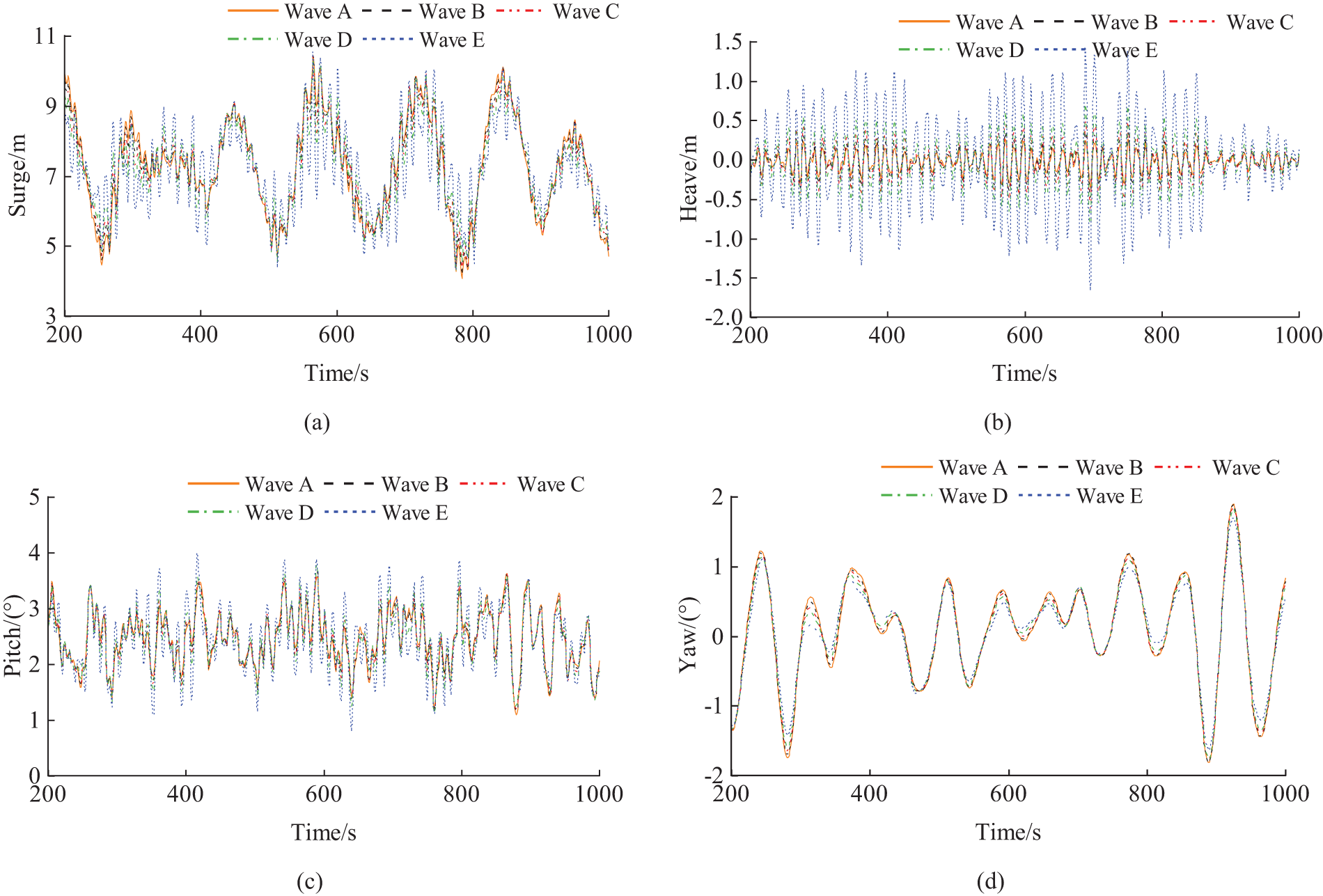
Figure 5: Motion response of floating wind turbine under different wave conditions. (a) Surge. (b) Heave. (c) Pitch. (d) Yaw
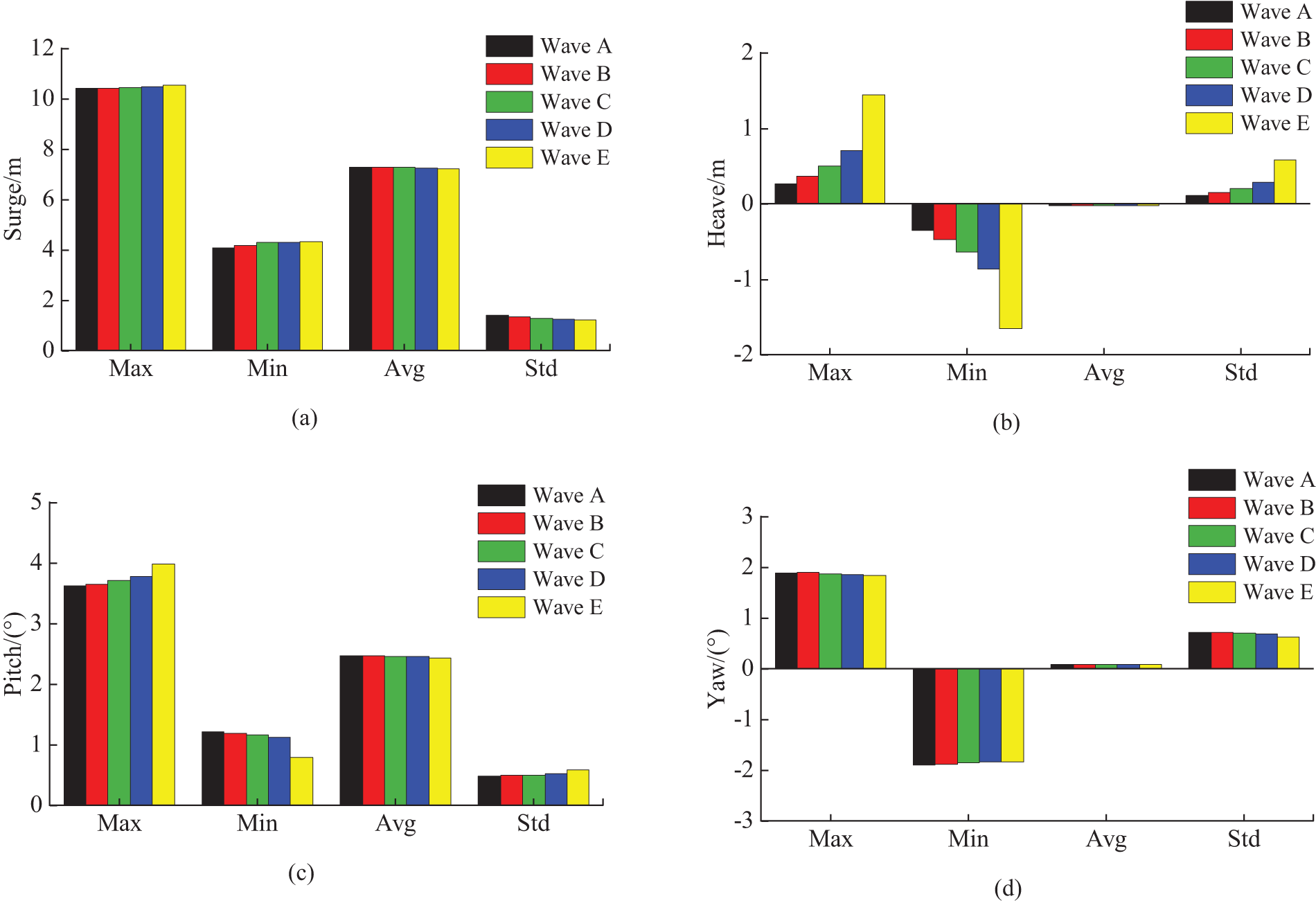
Figure 6: Motion statistics of floating wind turbine under different wave conditions. (a) Surge. (b) Heave. (c) Pitch. (d) Yaw
As seen in Figs. 5a and 6a, the maximum, minimum, mean, and standard deviation of the surge motion of the new semi-submersible floating wind turbine do not change significantly with the increase of the significant wave height and spectral peak period, and their maximum values are all around10.5 m under the conditions of wave conditions A to E, the minimum value is about 4.3 m, the standard deviation changes in a smaller range of about 1.5 m, and the mean value is the same, about 7.2 m; as seen in Figs. 5b and 6b, the maximum value, minimum value and standard deviation of the heave motion response of the new semi-submersible floating wind turbine increase with the increase of wave height, and the maximum values are 0.27 and 1.44 m when the wave height is 2.5 and 5.9 m, respectively, and the latter increases by 81.25% compared with the former. Meanwhile, the maximum heave response under wave condition E, the maximum droop amplitude reaches 1.44 m, and the heave response under wave conditions A to D are smaller, the maximum values are 0.27, 0.36, 0.50 and 0.71 m, respectively, and the average value is around 0 m. It can be seen that the heave motion response of the floating wind turbine increases with the increase of wave load.
As seen in Figs. 5c and 6c, the maximum value and standard deviation of the pitch motion response of the new semi-submersible floating wind turbine increase with the increase of the wave height and the period of the spectral peak, and the average value reaches 2.3°, and the increase is almost zero; from Figs. 5d and 6d, it can be seen that similar to the change law of the surge displacement in different wave conditions, under the conditions of the same wind condition and different wave conditions, the yaw motion response of the new semi-submersible floating wind turbine is closer. The angular variation ranges from −1.8° to 1.8°, with the mean value close to 0° and the standard deviation around 0.7°. This is because the wave load on the floating wind turbine is symmetrical, and the wave injection angle is axisymmetric distributed, which causes almost zero yaw motion response. It can be concluded that the yaw motion response of the floating wind turbine is less affected by different wave conditions.
4.3 Mooring Line Tension Response Analysis under Different Wave Conditions
The mooring line tension time curves of the new semi-submersible floating wind turbine under rated wind conditions and wave conditions A to E are shown in Fig. 7. Fig. 7 shows the tension time curves of mooring lines 1# and 2# in two orientations, respectively, on the back-wave side and front-wave side, and the corresponding mooring line tension comparison statistics are shown in Fig. 8.
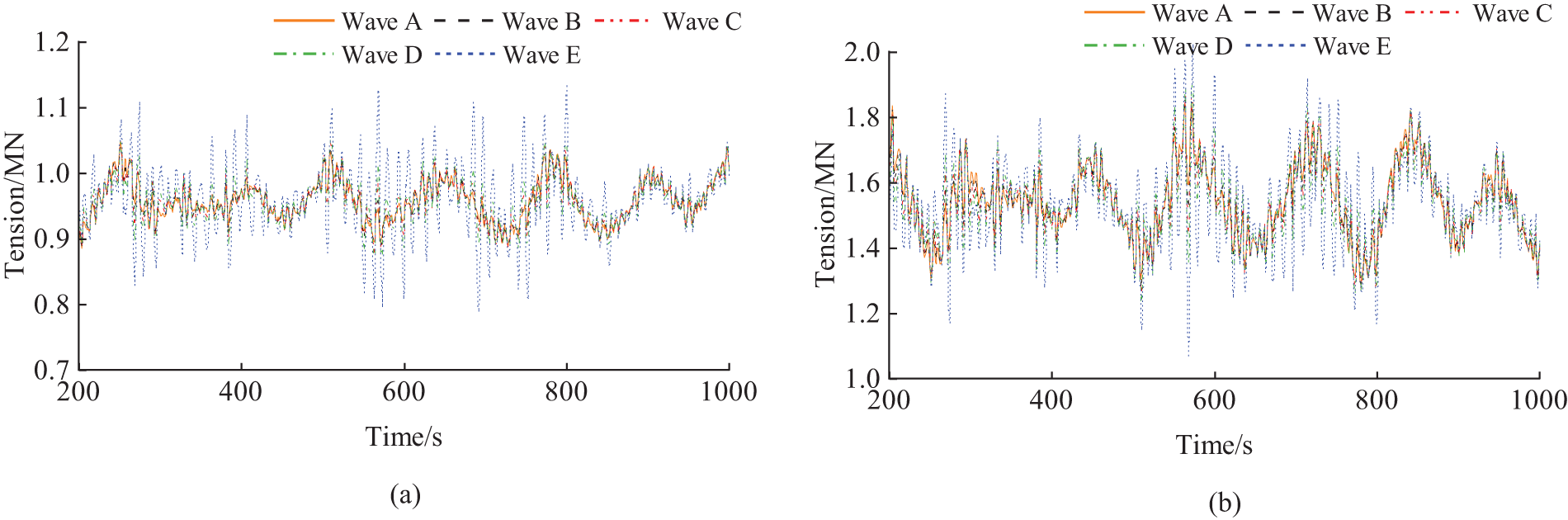
Figure 7: Time history curve of mooring line tension under different wave conditions, (a) 1#mooring line. (b) 2#mooring line
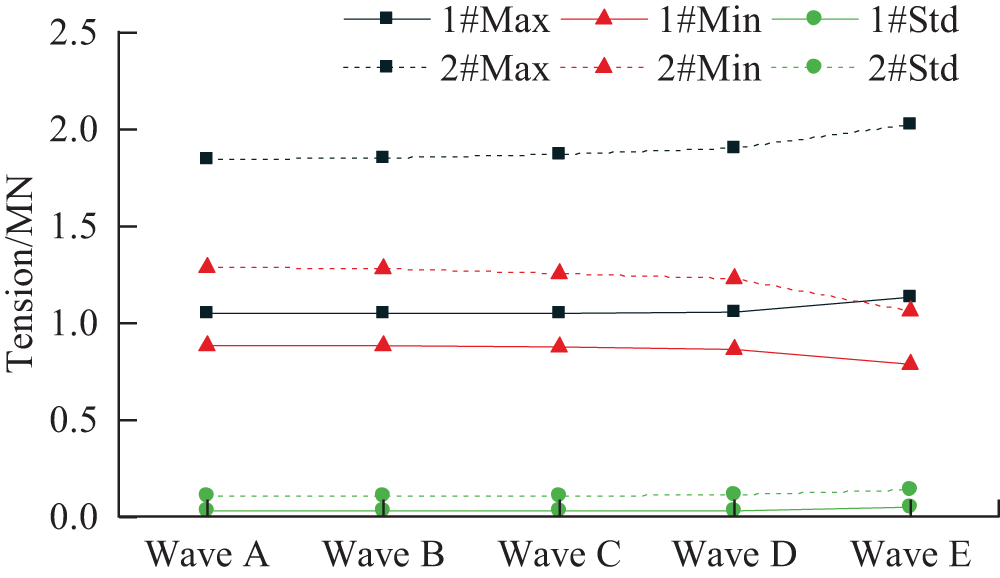
Figure 8: Tension comparison of mooring line 1# and 2#
According to Figs. 7 and 8, it can be found that the maximum value and standard deviation of the mooring line tension increase with the increase of the significant wave height and spectral peak period, while the minimum value decreases with the increase of the significant wave height and spectral peak period under different wave conditions. When the wave height increases from 2.5 to 5.9 m, the maximum values increase from 1.045 and 1.848 MN to 1.137 and 2.025 MN in the back wave side and front wave side conditions, respectively, with an increase of 8.8% and 9.6%; the standard deviations increase from 0.030 and 0.112 MN to 0.052 and 0.139 MN, respectively; the minimum values were reached at a significant wave height of 5.9 m and a spectral peak period of 11.3 s, with 0.786 and 1.065 MN, and a decrease of 11.2% and 17.1%, respectively. From the above values, the mooring line always maintains the tension state under different wave conditions and will not be relaxed. And because floating wind turbines are influenced by the response of the heave motion under different wave conditions, the difference between the elastic deformation of the mooring line and the tensioning force increases with the increase of the amplitude of the heave motion, respectively. Therefore, as the wave height and period increase, the value of the difference between the mooring line elastic deformation and the tension force increases, and the response to the mooring line tension motion increases.
4.4 Comparative Analysis of Six Degrees of Freedom Motion Response of Floating Wind Turbine Platform
The rated wind speed of 11.4 m/s, the meaningful wave height of 4 m, and the spectral peak period of 10 s were selected to compare the six degrees of freedom dynamic response of the new semi-submersible floating wind turbine with that of the OC4-DeepCwind turbine. The time curves of the motion response of the two types of floating wind turbines are shown in Fig. 9, and the corresponding statistical results are detailed in Table 5.
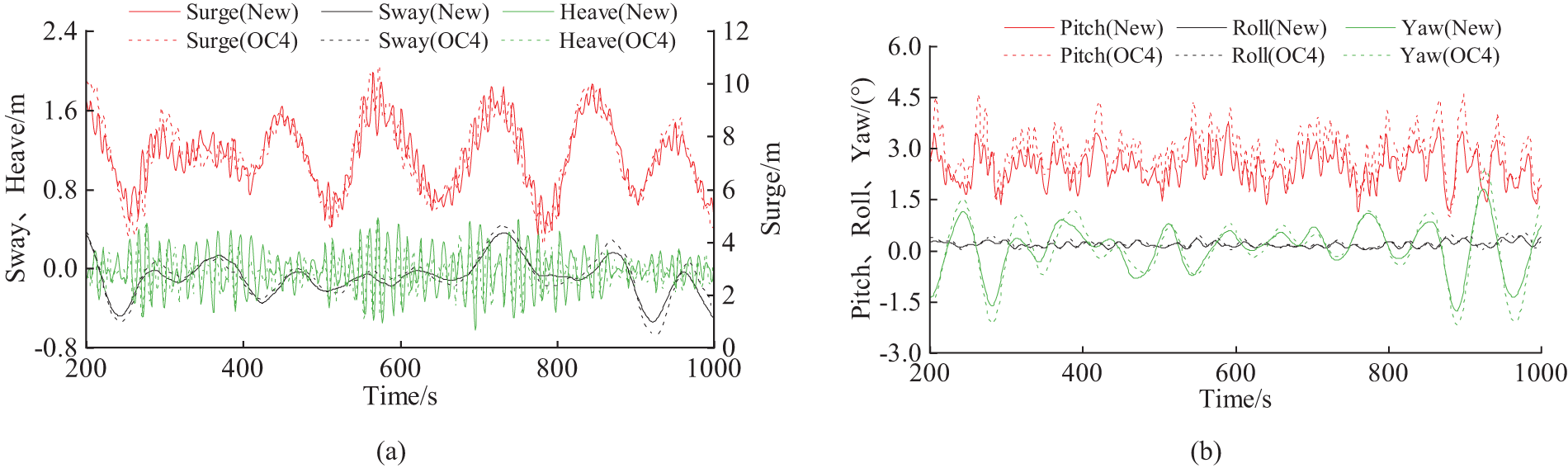
Figure 9: Motion response time curves of different floating wind turbines. (a) Surge, sway, and heave. (b) Pitch, roll, and yaw
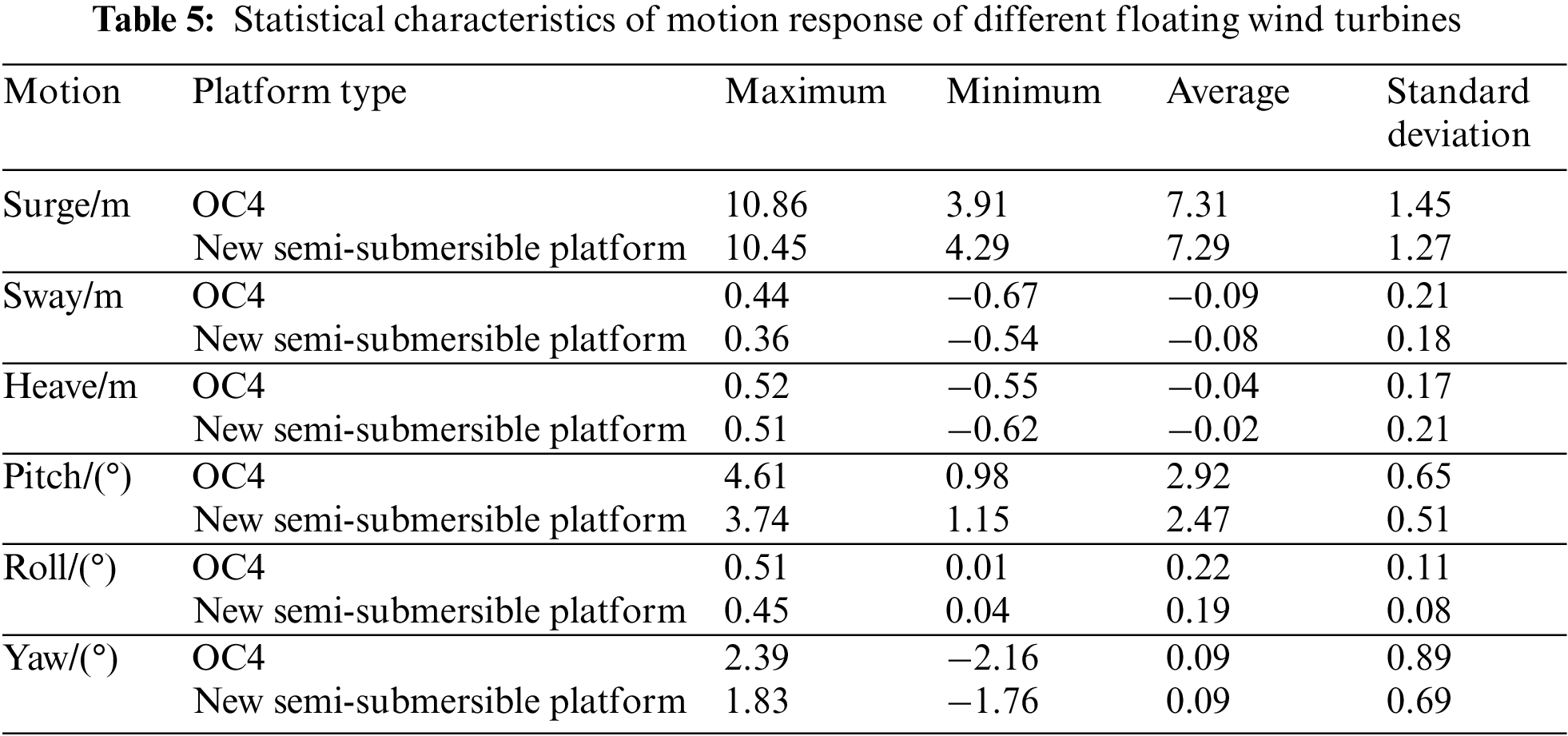
According to Fig. 9a and Table 5, it can be found that the surge response of the two floating wind turbine platforms is significantly larger and the sway response is smaller because the wind wave incidence direction is along the positive direction of the X-axis. The average values of surge and sway responses of the OC4 platform are 7.31 and −0.09 m, respectively. The average values of surge and sway responses of the truncated-cone-type pontoon platform are 7.29 and −0.08 m, respectively, and its average values are slightly smaller than those of the OC4 platform. Compared with the OC4 platform, the standard deviation of surge and sway responses of the new platform decreased by 12.0% and 15.4%, respectively, and the platform fluctuation was reduced. This is because the upper pontoon of the new platform adopts the truncated-cone-type structure, and its volume is smaller below the waterline surface, thus reducing the wave load on the platform. The maximum heave response values of the OC4 platform and the truncated-cone-type pontoon platform are not significantly different, with 0.52 and 0.51 m, respectively, and the average values are around 0 m. Both platforms have good heave performance.
As shown in Fig. 9b and Table 5, similar to surge and sway, the wind and waves mainly follow the positive X-axis direction, while the Y-axis direction has a smaller component. Therefore, the pitch response of the two types of floating wind turbines is significantly larger, while the roll and yaw responses are smaller. Compared with the OC4 platform, the maximum values, average, and standard deviations of pitch and roll motion responses of the new platform decrease, while the minimum values increase. Among them, the maximum values of pitch and roll motion responses of the OC4 platform are 4.61° and 0.51°, respectively, while the maximum values corresponding to the motion response of the new platform are 3.74° and 0.45°, respectively. The motion response of the truncated-cone-type pontoon platform was reduced by 18.9% and 11.8%, respectively. This is due to the larger volume of the part of the new platform above the waterline surface, which can effectively increase the buoyancy to counteract the tilting moment when the wind and wave loads occur, preventing the wind turbine platform from further tilting, and thus reduce the platform’s roll and pitch motion. Compared with the OC4 platform, the maximum values, minimum values, and standard deviations of the yaw motion response of the truncated-cone-type pontoon platform decreased, and the average is not significantly different. It can be seen that the amplitude of the yaw motion and the fluctuation amplitude of the new platform are reduced.
This paper proposes a new type of offshore wind turbine semi-submersible platform, based on the coupled hydrodynamic, aerodynamic, and mooring force physical fields of FAST, analyzes its dynamic response at rated wind speed, different wave conditions, and mooring line tension response, and compares the dynamic responses of the new semi-submersible platform with the OC4-DeepCwind platform at six degrees of freedom, with the following main findings:
1) The new floating wind turbine integrates the characteristics of the floating foundation of the semi-submersible offshore wind turbine and designs the upper pontoons as truncated-cone-type, with higher stability and improved restoring torque, which effectively reduces the platform pitch and yaw motions; the lower end reduces the contact surface with the seawater and reduces the wave load borne.
2) The new floating wind turbine has the most obvious heave and pitch motions under different wave conditions, mainly caused by wave load, controlled by the significant wave height and spectral peak period, and the response amplitude of heave and pitch motions increases with the increase of wave height; the surge and yaw motions are less affected by the wave condition, and the truncated-cone-type upper pontoon can effectively improve the restoring torque, thus reducing the surge and yaw motions of the wind turbine.
3) The tensegrity time response of the new floating wind turbine mooring system in both the back-wave side and front-wave side conditions is strongly influenced by different wave conditions. The value of the difference between the elastic deformation of the mooring line and the tensioning force increases with the increase of the amplitude of the heave and pitch motions, respectively.
4) Comparing the six degrees of freedom dynamic response of the new semi-submersible platform with the OC4-DeepCwind platform, it was found that the pitch, roll, surge, and sway characteristics of the new semi-submersible platform were better than those of the OC4 platform, in which pitch and roll advantages of the new platform were the most obvious, and the motion responses decreased by 18.9% and 11.8% respectively compared with that of the OC4 platform, thus verifying that the new semi-submersible floating wind turbine platform has good stability.
Acknowledgement: The authors would like to acknowledge the Institute of Wind Power Blade New Technology Industrialization of Shandong University of Technology for providing technical guidance for this project.
Funding Statement: This research was funded by the National Key R&D Program of China (Grant Number 2018YFB1501203). Meanwhile, this research was funded by the National Natural Science Foundation of China (Grant Number 52075305).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Xuemei Huang, Mingzhen Jiang; data collection: Guanghui Qiao, Jiwen Chen; analysis and interpretation of results: Leian Zhang, Yongshuang Wen and Yuhuan Zhang; draft manuscript preparation: Mingzhen Jiang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data used in this research are available upon the request from the corresponding author. Some data is not available because of the confidentiality of the industry.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Zhao, Y. S., She, X. H., He, Y. P., Yang, J. M., Kou, Y. F. (2018). Experimental study on new multi-column tension-leg-type floating wind turbine. China Ocean Engineering, 32(2), 123–131. [Google Scholar]
2. Meng, L., He, Y. P., Zhao, Y. S., Yang, J., Yang, H. et al. (2020). Dynamic response of 6 MW spar type floating offshore wind turbine by experiment and numerical analyses. China Ocean Engineering, 34(5), 608–620. [Google Scholar]
3. Zhang, M., Tan, B., Xu, J. (2016). Smart fatigue load control on the large-scale wind turbine blades using different sensing signals. Renewable Energy, 87, 111–119. [Google Scholar]
4. Skaare, B., Nielsen, F. G., Hanson, T. D., Yttervik, R., Havmoller, O. et al. (2015). Analysis of measurements and simulations from the hywind demo floating wind turbine. Wind Energy, 18(6), 1105–1122. [Google Scholar]
5. Bachynski, E. E., Moan, T. (2012). Design considerations for tension leg platform wind turbines. Marine Structures, 29(1), 89–114. [Google Scholar]
6. Zhao, Y. S., Yang, J. M., He, Y. P., Gu, M. T. (2016). Dynamic response analysis of a multi-column tension-leg-type floating wind turbine under combined wind and wave loading. Journal of Shanghai Jiaotong University (Science), 21(1), 103–111. [Google Scholar]
7. Robertson, A. N., Jonkman, J. M. (2011). Loads analysis of several offshore floating wind turbine concepts. Office of Entific & Technical Information Technical Reports. [Google Scholar]
8. Wang, B., Bi, T., Xiao, Z. Y. (2018). Summary of foundation design for offshore floating wind turbine. Electric Power Survey & Design, 116(9), 56–61. [Google Scholar]
9. Li, Q. C., Chen, B., Liu, Y. N. (2019). Optimization analysis on the mooring system of a new type of semi-spar wind turbine platform. Journal of Ocean Technology, 38(4), 85–90. [Google Scholar]
10. Zhou, X. H., Wang, Y. H., Deng, R. (2020). Review on floating foundation structures for offshore wind turbines. Electric Power, 53(7), 100–105+112. [Google Scholar]
11. Wu, Z. X., Wang, Y. X., Li, H. B., Yu, R. G. (2019). Conceptual design and performance analysis of new floating foundation for the wind turbines. Modern Manufacturing Engineering, 11(7), 136–141+148. [Google Scholar]
12. Chen, J. H., Pei, A. G., Ma, Z. R., Pang, C. Y. (2020). A review of the key technologies for floating offshore wind turbines. Southern Energy Construction, 7(1), 8–20. [Google Scholar]
13. Guzmán, S. D., Marón, D., Bueno, P., Taboada, M., Moreu, M. (2018). A reduced draft spar concept for large offshore wind turbines. ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, pp. 1–10. Madrid, Spain. [Google Scholar]
14. Huang, Y., Zhuang, Y., Wan, D. C. (2020). Hydro-dynamic study and performance analysis of the OC4-deepcwind platform by CFD method. International Journal of Computational Methods, 18(4), 2050020. https://doi.org/10.1142/s0219876220500206 [Google Scholar] [CrossRef]
15. Roddier, D., Cermelli, C., Aubault, A., Weinstein, A. (2010). WindFloat: A floating foundation for offshore wind turbines. Journal of Renewable & Sustainable Energy, 2(3), 033104. [Google Scholar]
16. Zhang, H., Wang, Y. H., Yan, B. W., Zhou, X. H. (2021). Coupled dynamic response analysis of offshore floating fan on steel lattice foundation under combined wind wave action. Progress of Building Steel Structure, 23(3), 85–96. [Google Scholar]
17. Zhang, H. J., Cai, X., Xu, B. F. (2021). Study on dynamic response of floating fan semi-submersible platform. Renewable Energy, 39(9), 1210–1216. [Google Scholar]
18. Jonkman, J. M., Buhl, M. L. (2005). FAST user’s guide. Golden, Colorado: National Renewable Energy Laboratory. [Google Scholar]
19. Wu, H. T., Zhang, L., Ma, Y., Zhao, J. (2014). Random response analysis of semi-submersible offshore floating wind turbine platform. Journal of Huazhong University of science and Technology, 42(5), 111–115+121. [Google Scholar]
20. Yang, Y. P., Zhu, F., Chen, L. Z., Qian, Y. M. (2021). Application of Morison formula in wave load calculation of suspension tunnel. Waterway Port, 42(4), 471–478. [Google Scholar]
21. Jonkman, J. M., Butterfield, S., Musial, W., Scott, G. (2009). Definition of a 5 MW reference wind turbine for offshore system development. Golden, Colorado: National Renewable Energy Laboratory. [Google Scholar]
22. Wang, Y. (2021). Study on wave load and motion response of semi-submersible platform. Journal of Jiangsu Shipping Vocational and Technical College, 20(4), 70–75. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools