Energy Engineering

---

DOI: 10.32604/ee.2022.020472

ARTICLE

Effects of Hydrogen Storage System and Renewable Energy Sources for Optimal Bidding Strategy in Electricity Market

Can Li* and Xiaode Zuo

School of Management, Jinan University, Guangzhou, 510632, China
*Corresponding Author: Can Li. Email: canlee1992@stu2016.jnu.edu.cn
Received: 25 November 2021; Accepted: 30 December 2021

Nomenclature

Abbreviations
WT	Wind turbine
PV	Photovoltaic
IGDT	Information gap decision theory
ESS	Electric storage systems
BC	Bilateral contracts
MT	Micro turbine
MILP	Mixed-integer linear program
RMILP	Robust mixed-integer linear program
PM	Power market
MPPT	Maximum power point tracking

Indices

h	cost function of micro-turbines index
i	minimum ON and OFF-time limits running modelling
j	micro-turbines index
l	bilateral contracts
s	scenario index
t	time (hour) index

Parameters

B	bilateral contracts no
c(s,s′):	function to calculate the scenarios s and s/ of a random variable distance.
CtB	battery storage operation cost at time t [$/MWh]
Ctwind	wind-turbine operation cost at time t [$/MWh]
CtPV	PV system operation cost at time t [$/MWh]
Gt,sa	time t in scenario s insulation
Ga0	the standard condition Insulation (W/m2)
MUTj,MDTj:	jth micro-turbine Minimum up/down time of [hour]
Nh	Generation blocks of micro-turbines no
NMT	micro-turbines no
Ns	scenarios no
NOCT	PV system normal operating cell temperature
ρs	sth scenario probability after the scenario reduction
Pj,hMAX	hth block Output size of jth micro-turbines unit [MWh]
Pl,tmax	lth contract maximum capacity at time t [MW]
Pl,tmin	lth contract minimum capacity at time t [MW]
pr	wind-turbine rated power [MW]
Pt,swind,max	wind turbine maximum power at time t in scenario s
Pt,sM,max	PV system maximum available power at time t in scenario s
Pchargemax,Pdiscmax	charging/discharging maximum power at time t in scenario s
PMax,0M	standard condition maximum power
Rjup,Rjdown	rate limit of ramp up/down of jth micro-turbine [MW/hour]
Sj,hMT	hth block cost of jth unit of micro-turbines [$/MWh]
T	times number
Tt,sa	time t in scenario s temperature
TM,0	standard condition of module temperature
Upi,j,Dni,j	MUT/ MDT constraints variables
Vt,sw	wind speed
Vr,Vci,Vc0	cut-in and cut-out wind speed rated values [m/s]
Xbmax,Xbmin	energy of battery storage maximum/minimum value
χ,η	battery storage charge/discharge efficiency
λt,s	energy price at time t in scenario s [$/MWh]
λl,t	price of contracts l at time t [$/MWh]

Variables

loadt,s	Load demand (time t, scenario s)
Pl,tBC	Purchased power of bilateral contract l (time t)
PtBC	Total purchased power of bilateral contracts (time t)
Pt,sp	Power market Purchased power (time t, scenario s)
Pt,sSale	Power market sold power (time t, scenario s)
Pj,t,sMT	jth unit of the micro-turbine produced power (time t, scenario s)
Pj,h,t,sMT	Retad power of block h of jth micro-turbines unit (time t, scenario s)
Pt,scharge,Pt,sdisc	Charge and discharge power of storage (time t, scenario s)
Pt,swind	Wind-turbine production (time t, scenario s)
Pt,sPV	PV system production (time t, scenario s)
Pt,swind	Wind-turbine purchased power (time t, scenario s)
Pt,sPV	PV system purchased power (time t, scenario s)
sl	Binary variable for lth bilateral agreement
Uj,tMT	Binary variable for jth start of micro-turbine
Ut,scharge,Ut,sdisc	Binary variables of charge/discharge of battery storage
Xt,sb	Energy of storage [J]

1  Introduction

Providing energy with min expenditure is a significant problem in restricted power market, chiefly for large consumers [1]. In order to deal with tariff variation of market, various power sources can be used. Accordingly, mutual treaties, electricity market and self-owned production units are most significant units [2]. Wind turbines [3] and PV systems [4] can be regarded as production systems for cooling load of users. Besides, coalition of synthetic WT and photovoltaic unit with power storage unit can be regarded for handling of uncertainty effects of green sources [5].

1.1 Literature Review

Unlike to small users that must purchase their needed power just from retail sellers or retail market, main users can utilize various methods for providing of their required power [6]. These methods are parted to three general classes including: pool market, mutual treaties and internal production [7]. In [8], a model of pool tariffs variation to benefit of large users is proposed. Also, in [9] an improved model for large consumers in order to obtain optimal reserve bids in a security limited power market is presented. Authors in [10], are discussed around electrical energy supplement of large consumer in a power market covering of pool market as well as mutual contracts. Moreover, Fang et al. [11] modeled an auction for a contract among competitive production units and large consumers, aiming to determine power price among them. In [12], in order to deal with requirement of large consumers by various generators including: photovoltaic units, fuel cell (FC) and upper grid, a multi objective (MO) method is suggested. Heating and energy hub (EH) models are suggested for providing of energy for an industrial user in [13].

Various stochastic models of power supplement problem based on meta heuristic [14], multi objective HBMO [15], imperialist competitive algorithm [16] and firefly technique [17] are proposed in pervious works. Authors in [18] proposed a new stochastic model-based power supplement method for large consumers with containing of distributed generations (DGs), mutual treaties and pool market purchase in presence of demand response program (DRP). Also, Hartmann et al. [19] utilized a power storage system in an industrial/commercial user and evaluated its impacts. Equal work is made in [20] for large consumer by information gap decision theory (IGDT) method where 2 standards are utilized covering decision robustness vs. facing high supplement expenditures, and opportunity of taking benefit of low supplement expenditures. In addition, a test system is offered in [21], for depicting of IGDT approach. As well, equal approach is suggested in [22], to cope bidding method in day-ahead yield of a large consumer. In [23], an optimization is made for long-term power supplement of large consumer with regarding of long-term transactions and uncertain parameters. Also, the risk-limited bidding method is formulized in [24] for large consumers with considering of DRP. Authors in [25] studied a mid-term programing for big industrial power utilities with second-order stochastic dominance. Moreover, MO demand optimization method is presented in [26] for industrial utilizes with DR through blending of stochastic, quadratic, and evolutionary scheduling with MO optimization and continuous simulations. Furthermore, a decision-making method based on fuzzy system for power supplement is suggested in [27] by green sources. The authors in [28], has considered the influence of demand, price, and wind uncertainties on total costs with reliability in the structure of energy hub. In [29], the wind power and coal chemical based on the hydrogen storage system is combined, as a result the penetration ability of wind energy is improved and total cost is minimized.

In [30], an integrated model of offering strategy for microgrid management considering day-ahead, intra and unbalanced market is proposed. The model is applied for microgrid with demand and various generation to achieve optimal management of microgrid components. A novel combined dynamic and emission dispatch model for electric vehicles, wind turbines using multi objective function is proposed in [31]. A multi stage model based optimal dispatch for wind turbine, thermal and energy storage is modeled in [32], which the offering strategy is done in energy and reserve markets. In [33], an optimal bidding strategy in daily market and real-time market for microgrid based on two-stage framework is proposed. Ac power follow, hourly reconfiguration of microgrid, hydrogen energy modelling, using multiple shiftable loads are the suggested model’s primary benefits. An optimal participation of HPP with considering risk-averse strategies [34] is considered to achieve best benefits using three-stage decision making model. Also, some improved uncertainties model such as robust-stochastic approach [35] and uncertainties in deregulated electricity market [36] are proposed to achieve the best benefits in bidding problem modellings.

This work studied bidding/offering optimization methods for electricity supplement problem of big electricity utilities with including photovoltaic systems, wind turbines and hydrogen storage system with considering uncertainty on demand, reliability index, electricity market tariff and outlet power of wind turbine and photovoltaic units. Synthetic robust-stochastic method is suggested. In this method, robust method is regarded for modeling of demand uncertainty whereas remain uncertain parameters are modeled by stochastic optimization.

1.2 Novelty and Contributions of This Paper

According to the literature review, there is no work that combined stochastic and robust methods for achieving to optimum offering/bidding methods in case of large consumer’s power supplement in presence of alternative power resources and power storage units. Respect to this description, novelties of this work can be represented by:

a) Bidding/offering optimization approaches for large consumer energy supplement are proposed.

b) Stochastic and robust power supplement expenditure functions are combined.

c) Some uncertain parameters, i.e., demand, market tariff and outlet energy of WT and PV systems are considered.

d) The hydrogen storage system with fuel cell has been exploited in hub energy.

e) Evaluation criteria for optimal scheduling, reliability matrices are considered.

1.3 Construction of Article

Rest of this work is structured as: Section 2 provides power supplement problem for large consumers by considering green generators and storage devices. Following that, Section 3 introduces artificial uncertain-robust method and used it to suggested model. Section 4 describes the results of proposed method in test system. Eventually, conclusion of paper is presented in Section 5.

2  Problem Formulation

Cost effective energy supplement of large consumer is studied in this work. Deterministic models of generators are linearized and also the cost function is suggested in this part of paper. Also, the assumptions of this paper are considered as:

•   This problem is formulated as an integer linear model.

•   In order to prediction, the market price, wind speed, sun irradiation and temperature are available and applied to system as input data.

•   Several electrical energy resources including: micro turbines, wind turbine, photovoltaic system, hydrogen storage and fuel cell offering model are formulated together.

•   The problem is formulated as uncertain problem and based on the nature of parameters, the suitable model is applied for them

2.1 Objective Function

Considered large consumer of this work is procured by means of various resources and using bilateral contracts (BC), electricity market, MT, photovoltaic units, wind turbines and batteries. This work suggested following objective that must be minimized:

Minimize∑l=1B∑t=1Tλl,tPl,tBC+∑t=1T{λt(Ptp−PtSale)+∑j=1Nj∑h=1NhSj,hMTPj,h,tMT+CtB×(χ×Ptcharg⁡e+Ptdiscη)+Ctwind×Ptwind+CtPV×PtPV}(1)

where, first part of formula is the power supplement expense by bilateral contracts. Second part represents the provided power by PM, MT as well as operational expense of storage devices, wind turbines and photovoltaic systems. Also, 3-block piece-wise linear function is considered in order to model the operational expenditure of MT.

2.2 Energy Balance Limitation

The provided energy by various sources must cope total demand power. Aiming this regard, provided energy by PM, MT, bilateral contract, solar power, wind turbine and batteries must be equal to power demand in every time t. this constraint is represented by following equation:

∑l=1BPl,tBC+Ptp−PtSale+∑j=1Nj∑h=1NhPj,h,tMT+Ptwind+PtPV+Ptdisc−Ptcharg⁡e=loadt;∀t(2)

2.3 BC Constrains

Modeling of provided electrical energy by bilateral contracts is made using Eq. (3). This equation shows that the total of the bilateral contracts at any time is equal sum of all contracts in that time. It is remarkable, supplied electrical energy is bounded by relation (4). Also, this equation shows each contract should be limited to maximum and minimum amount.

PtBC=∑l=1NlPl,tBC;∀t(3)

Pl,tminsl<Pl,tBC<Pl,tmaxsl;∀l,t(4)

2.4 Modeling of Micro Turbine

As illustrated in Fig. 1, objective function of MT is presented by 3-block piece-wise linear curve. Mathematically expressing of this figure is provided by Eq. (5). As well, the related limitations are presented with Eqs. (6)–(11), in which, provided power by MT is bounded to max potential of blocks that is denoted in (6) and (7). Moreover, ramp up/down proportions constraint is expressed by (8) and (9). At last, Eqs. (10) and (11) are respectively provided the min up and min down time limitations. For modeling of min up and min down time for micro turbines, ancillary parameters of and are introduced in relation (12) [37].

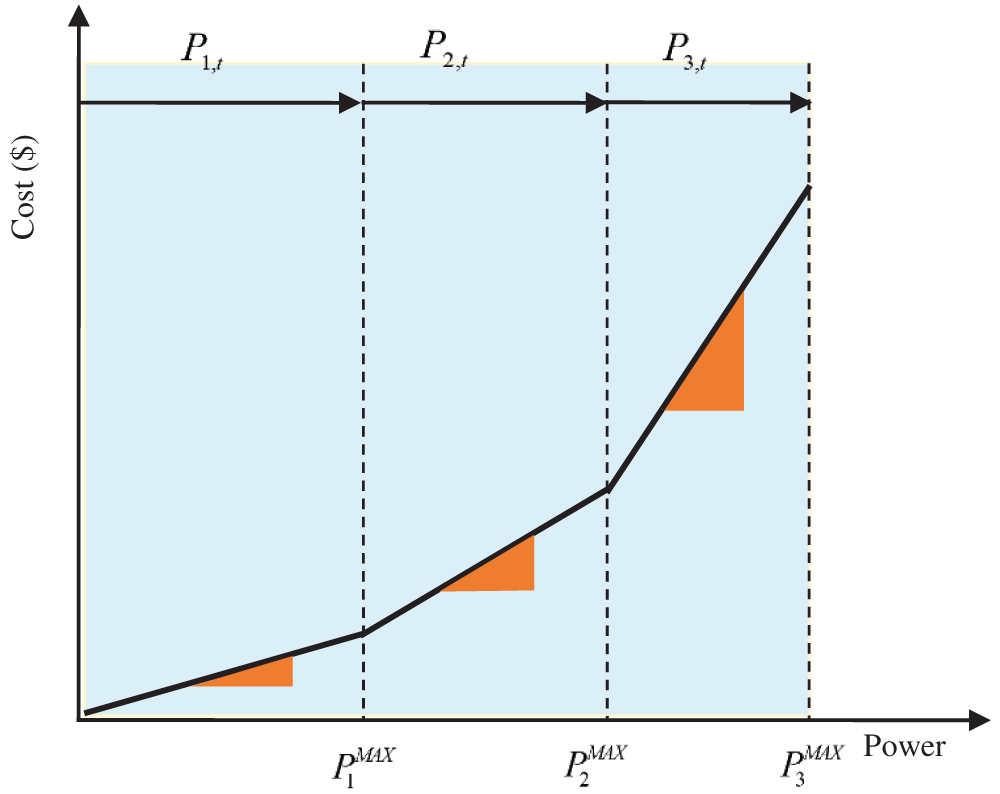
Figure 1: Operation cost model of MT

CostMT=∑t=1T∑j=1Nj∑h=1NhSj,hMTPj,h,tMT(5)

0≤Pj,h,tMT≤(Pj,hMAX−Pj,h−1MAX)×Uj,tMT;∀j,h,t(6)

0≤Pj,1,tMT≤Pj,1MAX×Uj,tMT;∀j,t(7)

∑h=1NhPj,h,tMT−∑h=1NhPj,h,t−1MT≤Rjup×Uj,tMT;∀j,t(8)

∑h=1NhPj,h,t−1MT−∑h=1NhPj,h,tMT≤Rjdown×Uj,t−1MT;∀j,t(9)

Uj,tMT−Uj,t−1MT≤Uj,t+Upj,iMT;∀j,∀t,∀i(10)

Uj,t−1MT−Uj,tMT≤1−Uj,t+Dnj,iMT;∀j,∀t,∀i(11)

Upj,i={ii≤MUTj0,i≻MUTj}Dnj,i={ii≤MDTj0i≻MDTj}(12)

2.5 Modelling WT

Respect to [38], Eq. (13) provides the max outlet electrical energy of WT at each time t.

Ptwind,max={0Vtw<Vcipr×(Vtw−VciVr−Vci)3Vci<Vtw<VcrprVr<Vtw<Vc00Vtw>Vc0(13)

Provided power for a big power user in time t is bounded by following relation:

Ptwind≤Ptwind,max;∀t,(14)

2.6 Photovoltaic System Model

In present work, regarding to maximum power point tracking (MPPT), photovoltaic modules are utilized at their max energy for big power utilities. MPPT guarantees that photovoltaic system generates most possible electrical energy in case of whole every temperatures and irradiations. The max accessible energy of photovoltaic unit at each time t is expressed in following equation [39]:

PtM,max=GtaGa0×{PMax,0M+μPmax×(Tta+Gta×NOCT−20800−TM,0)}(15)

Provided power for big power utilities by photovoltaic unit is bounded by Eq. (16).

PtPV≤PtM,max;∀t(16)

2.7 Power Storage Device Model

Following relations express the ESS limitations [39]. Starting power of battery is expressed in (17). Also, Eqs. (18) and (19) are respectively bounded the charging and discharging energy at time t. Moreover, saved power level of battery is presented in Eq. (20). Furthermore, Eq. (21) ensures that charging and discharging of battery are not in a same time. Finally, relation (22) represents the dynamical model of storage device.

Xt0b=X0b(17)

Ptcharg⁡e≤Pcharg⁡emax×Utcharg⁡e;∀t(18)

Ptdisc≤Pdiscmax×Utdisc;∀t(19)

Xbmin≤Xtb≤Xbmax;∀t(20)

Utcharg⁡e+Utdisc≤1;∀t(21)

Xtb=Xt−1b+χ×Ptcharg⁡e−Ptdiscη;∀t(22)

2.8 Hydrogen Storage System Model

Since hydrogen can be stored as a gas, liquid and solid material, it is a suitable carrier for energy. One of the most suitable storage sources is hydrogen storage system. The hydrogen storage system consists of three parts:

•   an electrolyzer

•   a fuel cell

•   a hydrogen storage tank

The structure of a hydrogen storage is shown in Fig. 2. Also, in Fig. 3, the amount of hydrogen injected to storage in comparison of achieved electricity from wind form is shown. In Fig. 4, the amount of hydrogen obtained from storage which is converted to electricity in fuel cell is shown.

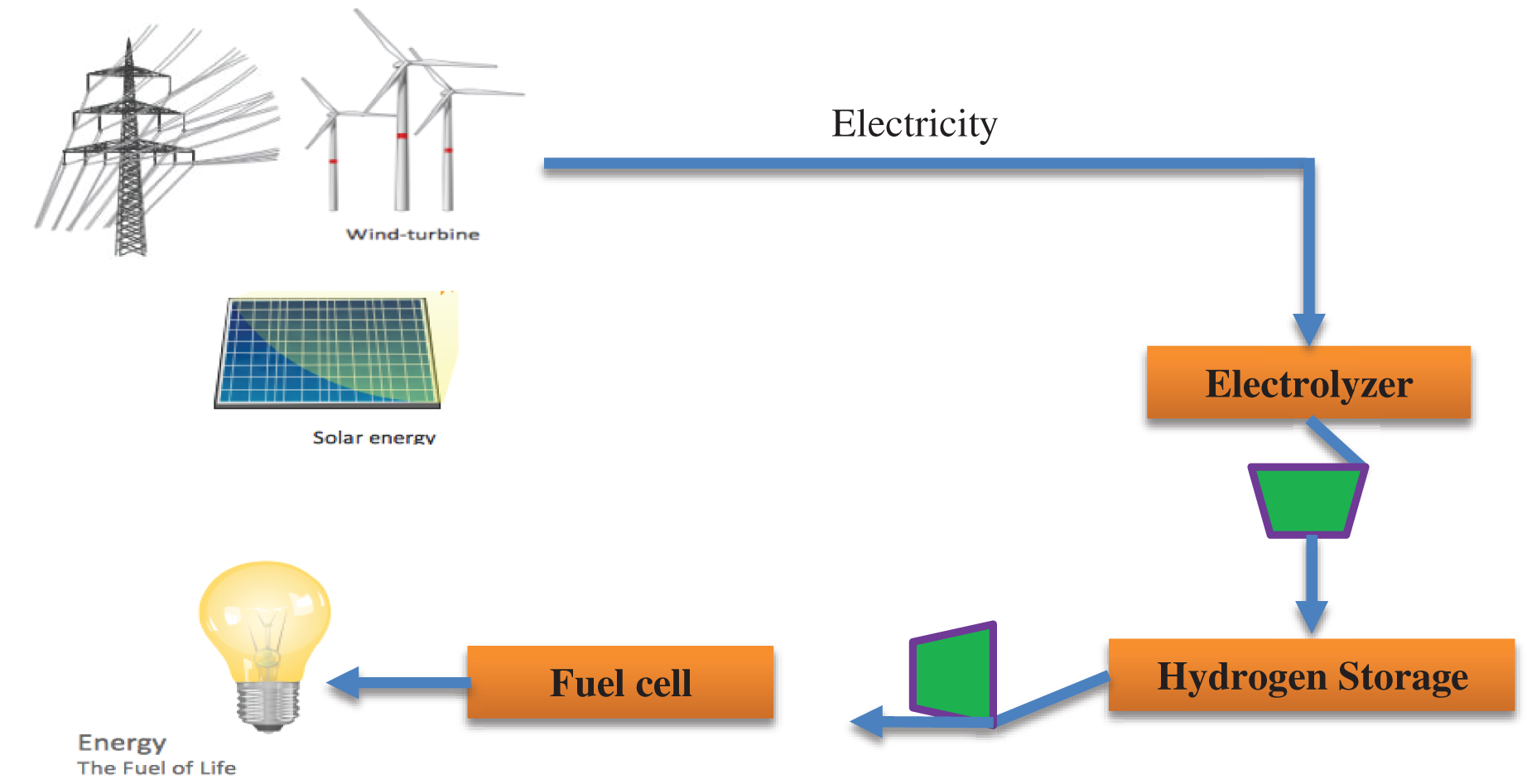
Figure 2: The structure of hydrogen storage in network

Figure 3: Wind farm and hydrogen storage for storage-hydrogen to storage

Figure 4: Wind farm and hydrogen storage for storage constrained case-hydrogen from storage

2.8.1 Electrolyzer

In this part, the process of decomposition of water molecules is carried out to H2 and O2. Using Eq. (23), electrolyzer input power concentrate is defined [40].

PELminIEL(t)≤PEL(t)≤PELmaxIEL(t)(23)

In this equation, the upper and lower amount of electrolyzer input power are represented through PELmax and PELmin, respectively. Also, IEL (t) defines the on or off state of the electrolyzer unit, which is equal to 0 or 1.

2.8.2 Hydrogen Storage Tank

In this part, the produced hydrogen is saved in the hydrogen tank. Input and output hydrogen molar injected to the tank and their upper values are formulated via Eqs. (14)–(17), respectively.

NH2CH=PH2CH(t)ηH2CHLHVH2(24)

NH2DIS=PH2DIS(t)ηH2DISLHVH2(25)

NH2ch≤NH2chmaxIH2ch(26)

NH2DIS≤NH2DISmaxIH2DIS(27)

Input and output molar of hydrogen storage are represented by NH2ch and NH2DIS. On the other hand, IH2ch and IH2DIS are the charge or discharge state of hydrogen tank which is equal to 0 or 1.

Pressure of hydrogen tank and primary pressure of hydrogen tank are show by Eqs. (28) and (29). Also, pressure level of hydrogen tank is defined via Eq. (30), in order to avoid the charge and discharge of hydrogen storage tank at the same time, Eq. (31) is formulated.

prH2minIEL(t)≤prH2(t)≤prH2mAX(28)

prH2(t0)=prH2(initial)(29)

prH2(t)=prH2(t−1)+RTV(NH2ch−NH2dis)(30)

IH2CH+IH2DIS≤1(31)

In this equation, hydrogen pressure tank is defined by prH2(t), as well as, R is gas constant. Mean temperature inside the vessel is shown by T. V and LHV are total tank volume and lower heating value of hydrogen, respectively.

2.8.3 Fuel Cell

In this part the stored hydrogen in hydrogen tank is converted to electricity via fuel cell. Eq. (32) indicates the output energy concentrate.

PFCminIFC(t)≤PFC(t)≤PFCmaxIFC(t)(32)

In this equation, the upper and lower amount of electrolyzer input power are represented through Pfcmax and Pfcmin, respectively. Also, IFC (t) defines the on or off state of the fuel cell unit, which is equal to 0 or 1.

3  Combined Stochastic-Robust Model

In achieved system model in Eqs. (1)–(22), there exists some uncertain parameters including: energy price, required power, radiation, temperature and wind speed. According to these uncertain parameters, the optimal intelligence strategy is suggested in this paper.

In the proposed strategy, demand takes value inside of a robust method, while modeling of uncertainties of market tariffs, radiation, temperature as well as wind speed are made via a collection of scenarios. Uncertainty of demand power is expressed considering sum of limited uncertain parameters to achieve a RMILP and in order to be solved for a collection of price cases (stochastic programing).

The suggested strategy is defined in next section.

3.1 Evaluating Hub Energy in the Presence of Reliability Limitation

In this section, some reliability indicates, such as expected energy not supplied (EENS), Expected load not supplied (ELNS), and loss of load expectation (LOLE), have been used to evaluate the reliability and stability of the energy hub, which is defined as follows:

ELNStβ=∑sρs,tLs,tβ^(33)

EENStβ=∑sρs,tLs,tβ^(34)

LOLEtβ=∑sρs,tts,tβ^(35)

LOLPtβ=∑sρs,tts,tβ^T×100(36)

It should be noted that operating calculations are hour-based, and calculating ELNS in a time period will result in achieving EENS in this block. Finally, ELNS is computed using Eq. (37) (Refer to [41,42] for more detail).

ELNSβ=∑γ∑tργ,tβϕγ,tβ×(ϕγ,tβ+Rγ,tβ−RHUB,tβ)(37)

The limitation of ELNS is determined using Eq. (38).

ELNSβ≤ELNSmaxβ(38)

where

ELNSmaxβ=∑γ∑tIγβRγβϕγ,tβ×(ϕγ,tβ+Rγ,tβ−Rhub,tβ)(39)

Then, in order to verify the reliability of the energy hub, PCβ is defined as a penalty coefficient which is formulated by Eq. (5) that the hub operator should pay because not being able to supply some β loads.

PCβ=EENSUBβ×VLβ(40)

where VLβ represents the value of lost load.

Another reliability parameter (LOLB¯β) is defined as constraint which is defined by Eq. (41).

LOLPmaxβ≤LOLPβ¯(41)

In this equation, LOLPmaxβ is the upper allowable value of LOLPβ, and it is defined through the hub operator or by users.

3.2 Robust Formulation

The optimal robust method is a venture management technique that is less computationally intensive than other techniques. The criteria MILP formulation of the proposed representational model in (1)–(22) may be written as follows:

Min∑t=1nct.xt+∑βPCβIR(1+IR)γ(1+IR)γ−1(42)

s.t.:

∑t=1nait.xt≤bi∀i=1,….m(43)

xt≥0∀t=1,…,n(44)

xt∈{0,1}forsomet=1,…,n(45)

In these equations, the variables of problem are denoted by xt; limitation matric coefficients are determined by ait; also the right side array coefficients are shown with bi. Modeling of uncertain entries ait is done as a random limitation, independent, equal and limited that has indefinite distribution, ait that its amount is in range of [ait−a~it,ait+a~it] in which a~it the equivalent deviation from average amount of coefficients ait. Also, reliability index is determined by a penalty coefficient.

In this paper, a control variable Γi is defined for all limitations for formulization of a robust mixed-integer linear program with uncertainty. The control variable is used to assess the situational robustness of the proposed technique vs. the level of conservatism selected. This parameter’s value is between [0,|Ji|], while Ji={j|a~ij≥0}. In the presented problem by (1)–(22) the uncertainty is in right side parameters bi, especially loadt in Eq. (2), also reliability index is considered as a penalty coefficient. Therefore, a minor different xn+1 is proposed. Also, mixed-integer linear program is represented by:

Min∑t=1nct.xt+∑βPCβIR(1+IR)γ(1+IR)γ−1(46)

s.t.:

∑t=1nait.xt−bi.xn+1≤0,∀i=1,…,m(47)

xt≥0∀t=1,…,n(48)

xn+1=0(49)

xt∈{0,1}forsomet=1,…,n(50)

In which, bi provides a random parameter b^i that has amount in range of [bi−b^i,bi+b^i].

It is remarkable, in Eqs. (27)–(31), parameters of bi are inserted in matric of parameters [ait].

Equivalent robust combined-integer linear model to represented problem in (46)–(50) in presence of uncertain parameters and reliability index in right side terms can be expressed by:

Min∑t=1nct.xt+∑βPCβIR(1+IR)γ(1+IR)γ−1(51)

s.t.:

∑t=1nait.xt≤bi+zi.Γi+qi,n+1,∀i=1,….,m(52)

zi.Γi+qi,n+1≥b^i.yn+1i=1,…,m(53)

qi,n+1≥0i=1,…,m(54)

yn+1≥0(55)

zi≥0i=1,…,m(56)

1≤yn+1(57)

xj≥0j=1,…,n(58)

xj∈{0,1}forsomej=1,…,n(59)

where xj, qi,n+1, yn+1, and zi identify the variables of the problem, which, zi and double variations of the fundamental basic problem used for considering of variation break of constraints bi whereas yn+1 signifies a secondary variant that is used to create linear representation. Due to the presence of just 1 unknown variable in one constraint, the value of the control factors is between of 0--1 once b^i>0 and Γi=0 once b^i=0.

The required power in each time (loadt) that is the uncertain variable of presented problem of (1)–(22), seen in the cross-limitation array on the right. The power demand is modeling using a random version loa^dt that its value is in range of [loadt−loa^dt,loadt+loa^dt], in which loa^dt>0, equivalence of departure from the mean for the value of parameters loadt. In order to create a robust model of (51)–(59), it is worthy to note, the uncertainty is in Eq. (2). Thus, limitations (3)–(22) stay unchanged due to lack of uncertain variable in these equations. Respect to Eqs. (51)–(59), the robust model with considering of uncertain parameters ab penalty factor from reliability index can be expressed in following form:

Minimize∑l=1B∑t=1Tλl,tPl,tBC+∑t=1T{λt(Ptp−PtSale)+∑j=1Nj∑h=1NhSj,hMTPj,h,tMT+CtB×(χ×Ptcharg⁡e+Ptdiscη)+Ctwind×Ptwind+CtPV×PtPV}+∑βPCβIR(1+IR)γ(1+IR)γ−1(60)

Subject to:

∑l=1BPl,tBC+Ptp−PtSale+∑j=1Nj∑h=1NhPj,h,tMT+Ptwind+PtPV+Ptdisc−Ptcharg⁡e=loadt.1+Zt.Γt+qt;∀t(61)

Zt+qt≥loa^dt.yt∀t|loa^dt>0(62)

qt≥0∀t|loa^dt>0(63)

yt≥0(64)

Zt≥0(65)

1≤yt(66)

Constraints (3)--(21)(67)

Where, robustness variable amount is in range of 0–1 once the power demand has uncertainty (loa^dt≥0), whereas gamma is zero once loa^dt=0. Limitation (61) expresses the equilibrium among total produced energy by various generators, and power requirement by regarding uncertainty of power demand based on presented robust problem in (51)–(59). Limitations (62)–(66) are forced by robust formulation.

3.3 Synthetic Stochastic-Robust Formulization

This part of paper suggests some cases by stochastic programing frame for modeling of uncertain parameters including: yield prices, solar radiation, temperature and wind speed in robust Eqs. (60)–(67). Also, Weibull distribution is utilized for modeling wind speed uncertainty in electricity yield works. In this way, a set of scenarios for wind speed are created respect to Weibull distribution profile of wind speed. As well, ordinary distribution is employed for modeling some unknown variables, such as temperature, market tariffs, solar radiation, and reliability index which is defined in second part of the Eq. (68). Combined stochastic-robust model can be formulized by:

Minimize∑l=1B∑t=1Tλl,tPl,tBC+∑t=1T∑s=1Nsρs×{λt,s(Pt,sp−Pt,sSale)+∑j=1Nj∑h=1NhSj,hMTPj,h,t,sMT+CtB×(χ×Pt,scharg⁡e+Pt,sdiscη)+Ctwind×Pt,swind+CtPV×Pt,sPV}+∑βPCβIR(1+IR)γ(1+IR)γ−1(68)

Subject to:

∑l=1BPl,tBC+Pt,sp−Pt,sSale+∑j=1Nj∑h=1NhPj,h,t,sMT+Pt,swind+Pt,sPV+Pt,sdisc−Pt,scharg⁡e=loadt.1+Zt,s.Γt+qt,s;∀t,s(69)

Zt,s+qt,s≥loa^dt.yt,s;∀t|loa^dt>0,∀s(70)

qt,s≥0∀t|loa^dt>0;∀s(71)

yt,s≥0∀t,s(72)

Zt,s≥0(73)

1≤yt,s∀t,s(74)

Pl,tminsl<Pl,tBC<Pl,tmaxsl;∀l,t(75)

PtBC=∑l=1NlPl,tBC;∀t(76)

CostMT=∑t=1T∑j=1Nj∑h=1Nh∑s=1Nsρs×Sj,hMTPj,h,t,sMT(77)

0≤Pj,h,t,sMT≤(Pj,hMAX−Pj,h−1MAX)×Uj,tMT;∀j,h,t,s(78)

0≤Pj,1,t,sMT≤Pj,1MAX×Uj,tMT;∀j,t,s(79)

∑h=1NhPj,h,tMT−∑h=1NhPj,h,t−1MT≤Rjup×Uj,tMT;∀j,t(80)

Uj,tMT−Uj,t−1MT≤Uj,t+Upj,iMT;∀j,∀t,∀i(81)

Uj,t−1MT−Uj,tMT≤1−Uj,t+Dnj,iMT;∀j,∀t,∀i(82)

Upj,i={ii≤MUTj0i≻MUTj}Dnj,i={ii≤MDTj0i≻MDTj}(83)

Pt,swind,max={0Vt,sw<Vcipr×(Vt,sw−VciVr−Vci)3Vci<Vt,sw<VcrprVr<Vt,sw<Vc00Vt,sw>Vc0(84)

Pt,swind≤Pt,swind,max;∀t,s(85)

Pt,sM,max=Gt,saGa0×{PMax,0M+μPmax×(Tt,sa+Gt,sa×NOCT−20800−TM,0)}(86)

Pt,sPV≤Pt,sM,max;∀t,s(87)

Xt0b=X0b(88)

Pt,scharg⁡e≤Pcharg⁡emax×Ut,scharg⁡e;∀t,s(89)

Pt,sdisc≤Pdiscmax×Ut,sdisc;∀t,s(90)

Xbmin≤Xt,sb≤Xbmax;∀t,s(91)

Ut,scharg⁡e+Ut,sdisc≤1;∀t,s(92)

Xt,sb=Xt−1,sb+χ×Pt,scharg⁡e−Pt,sdiscη;∀t,s(93)

Pt,sSale−Pt,s~Sale≥0ifλt,s≥λt,s~(94)

Pt,s^p−Pt,sp≥0ifλt,s≥λt,s^(95)

Eq. (68) represents the cost function of this optimization, and limitations (69)–(74) express the equivalent constraints to (51)–(59) of robust model in each price case. Also, Eqs. (75)–(93) denote the corresponding constraints to (3)–(22) in deterministic linear problem, except that, replicated for each case.

The expressed limitations in (94) and (95) guarantee, offering and offering profiles are continually growing and dipping that is a normal necessity in power markets. Eq. (94) illustrates, that given an equal-time offering profile, the energy outlet equivalent to a case with high price related to another one must be greater than or equal to the second case’s channel energy. This is also true in reverse for Eq. (95), which is used to create bidding profiles. The flowchart of the proposed model based on the problem formulation is shown in Fig. 5.

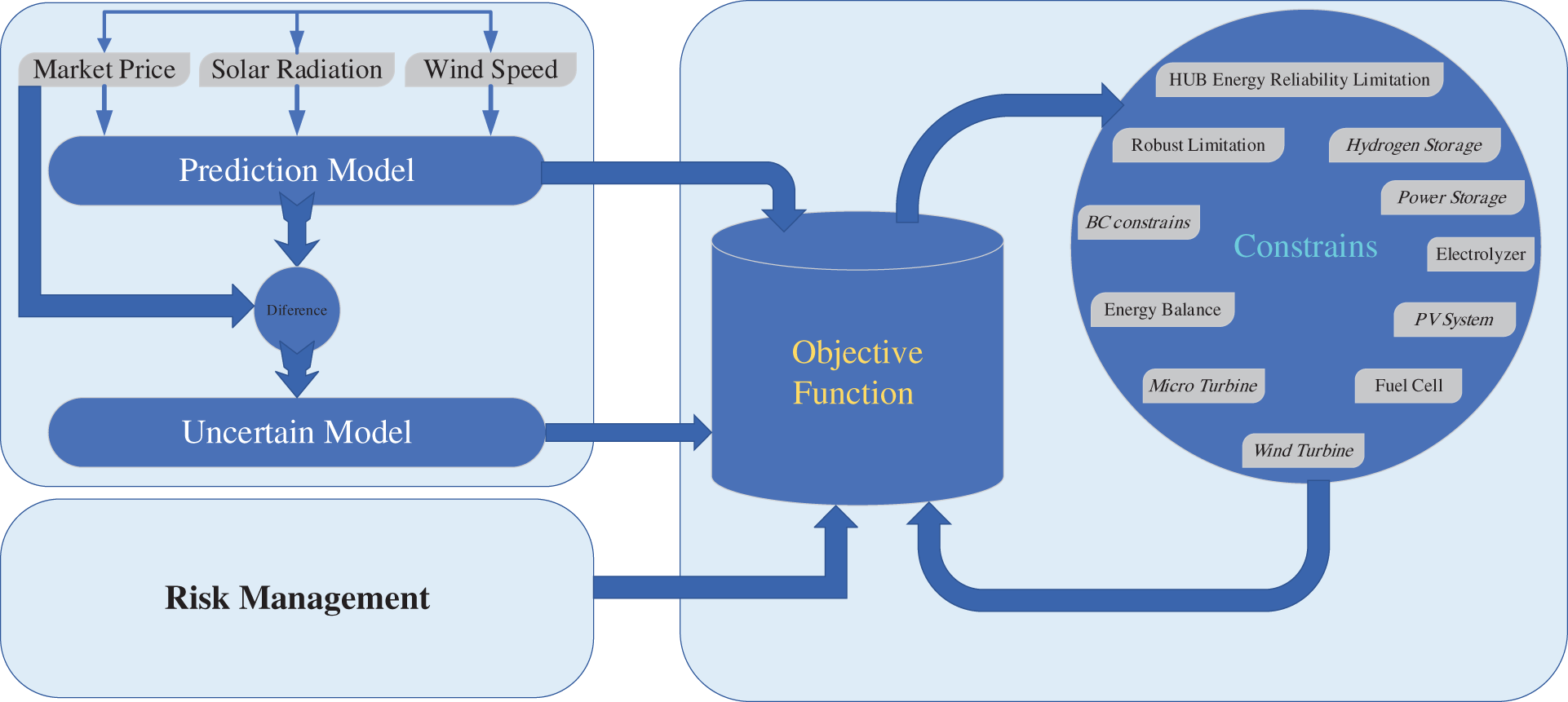
Figure 5: The flowchart of the proposed model

4  Simulations Numerical

This section proposes a synthetic stochastic-robust approach, applies it to a test system, and discusses the findings obtained.

4.1 Data

Whole needed data for original load amount, BCs, wind turbine, photovoltaic system as well as daily wind speed are quoted that [1] whereas predicted load and market tariff data are considered as [6].

4.2 Results

For the purpose of attaining optimal bidding and offering profiles of presented model by (68)–(95), the presented optimization is resolved by means of CPLEX solver [43] in GAMS [44] software. The electrical energy supplement expenditure by robust method for big utilities vs. gamma (control variable) is illustrated by Fig. 6. It is remarkable, there is 11 repetition respect to gamma amounts from 0 to 1 with 0.1 step size. Growth of amount of this parameter leads to increasing of conservatism. Robust expense for Γ=0, is obtained $39.63. Also, this expenditure for worst situation that is achieved by considering Γ=1 is equal to $49.47. Respect to these results depict over 25% growth of energy supplement expenditure that is because of robust vs. demand uncertainty.

The optimum offering profiles at 1–2 and 24 h are depicted in Figs. 7–9 which gained for various control parameter amounts. Respect to this figure, with greatest amount of gamma, large power utility has not shared in offering profile due to that be conservative vs. demand uncertainty. As shown in Fig. 7, for first time intervals of curve, big power utility has not taken part until the energy tariff augmented more than $70/MW. Also, Fig. 8 shows offering profile at time 4 where the large power utility has not suggested once control variable value is in greatest level whereas once it is 0.5, with achieving the marker tariff to $64.59, large power utility has begun to bid energy to market. Moreover, Fig. 9 shows the offering profile at 24 h. As shown in this figure, growth of gamma amount results in decrement in suggested energy to market.

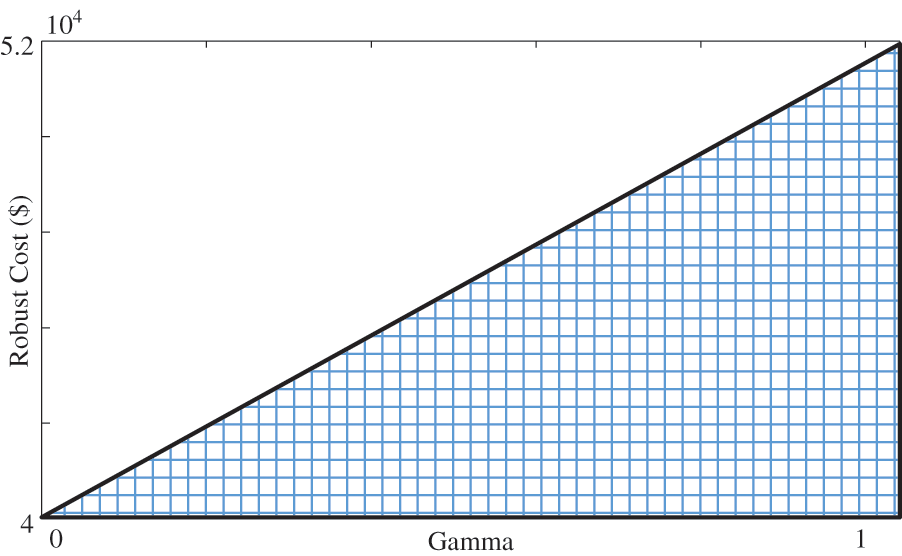
Figure 6: Robust cost against gamma value

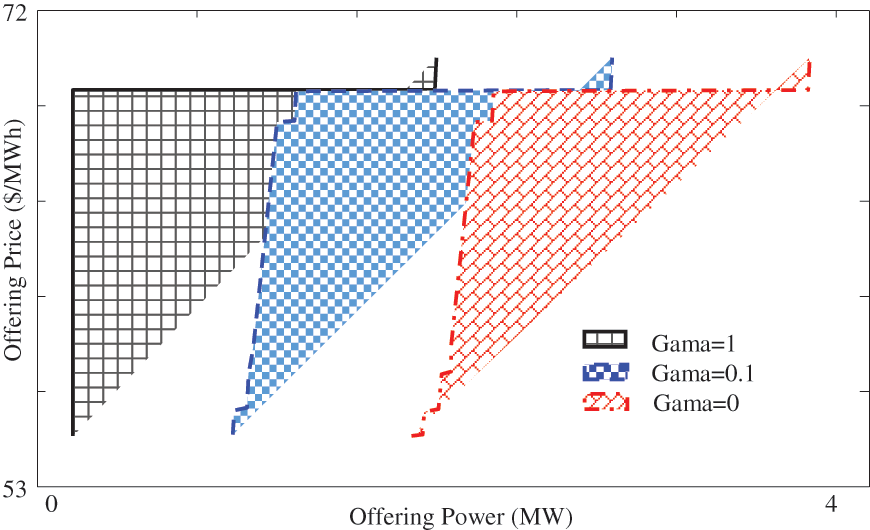
Figure 7: Persuade curve in first h in various gamma amount

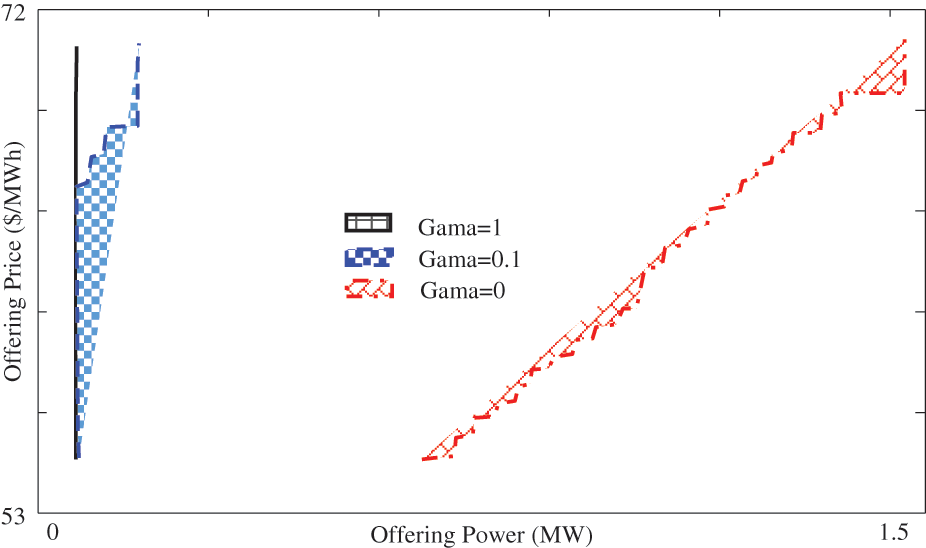
Figure 8: Offering of 2nd h for various gamma amount

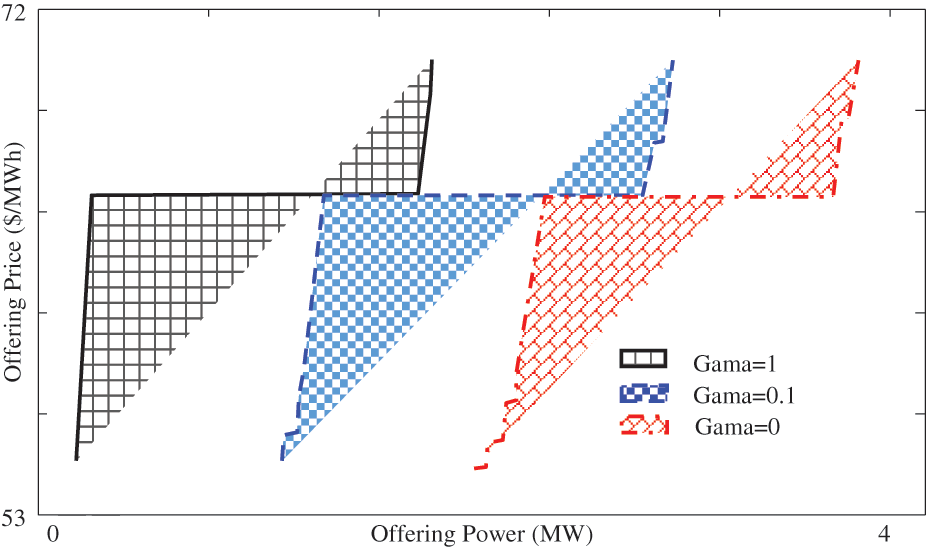
Figure 9: Offering of a day for various gamma amount

Figs. 10–12 illustrate achieved optimum bidding results for 16, 20 and 24 time steps for various control parameter amounts. As expected, increasing this parameter results in a growth in the quantity of bidding energy for increasing of robustness vs. demand uncertainty. In this scenario and according to Fig. 10 which shows the bidding profile of 16th h, bidding electrical energy is augmented with growth of uncertain control variable, for equal price. It is true also about Fig. 9, which depicts the profile of bidding for 7th h. In case of Fig. 12, by assuming zero value for gamma, bidding energy is 0 once electrical energy tariff is greater than $80, whereas in case of Γ=1 this amount is 0.29 MW and by using hydrogen storage the amount of bidding price is reduced. It is clear that taking into account the reliability index leads to cost optimization.

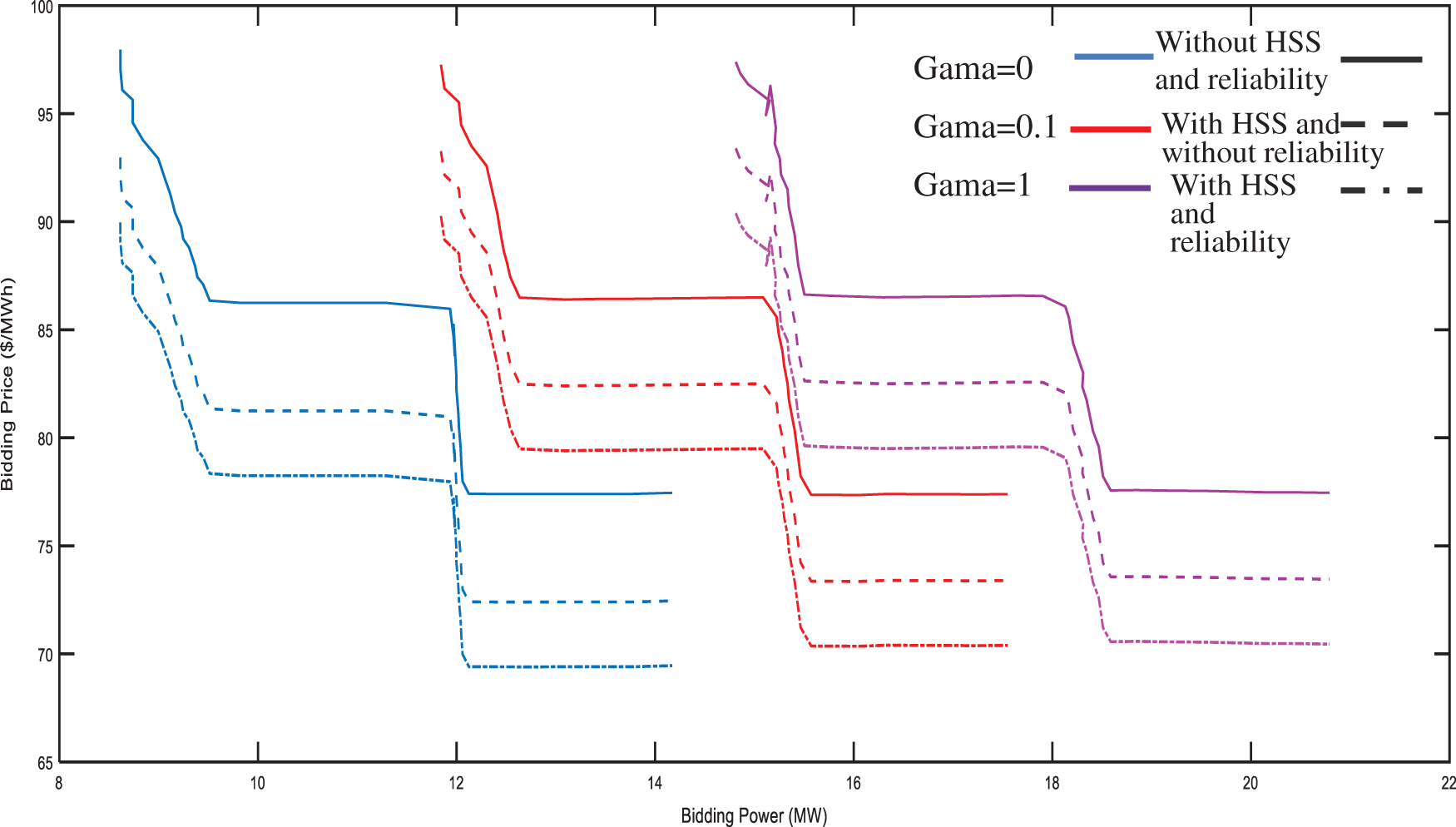
Figure 10: Bidding curve of 16th h for various gamma amount (presence of HSS and reliability)

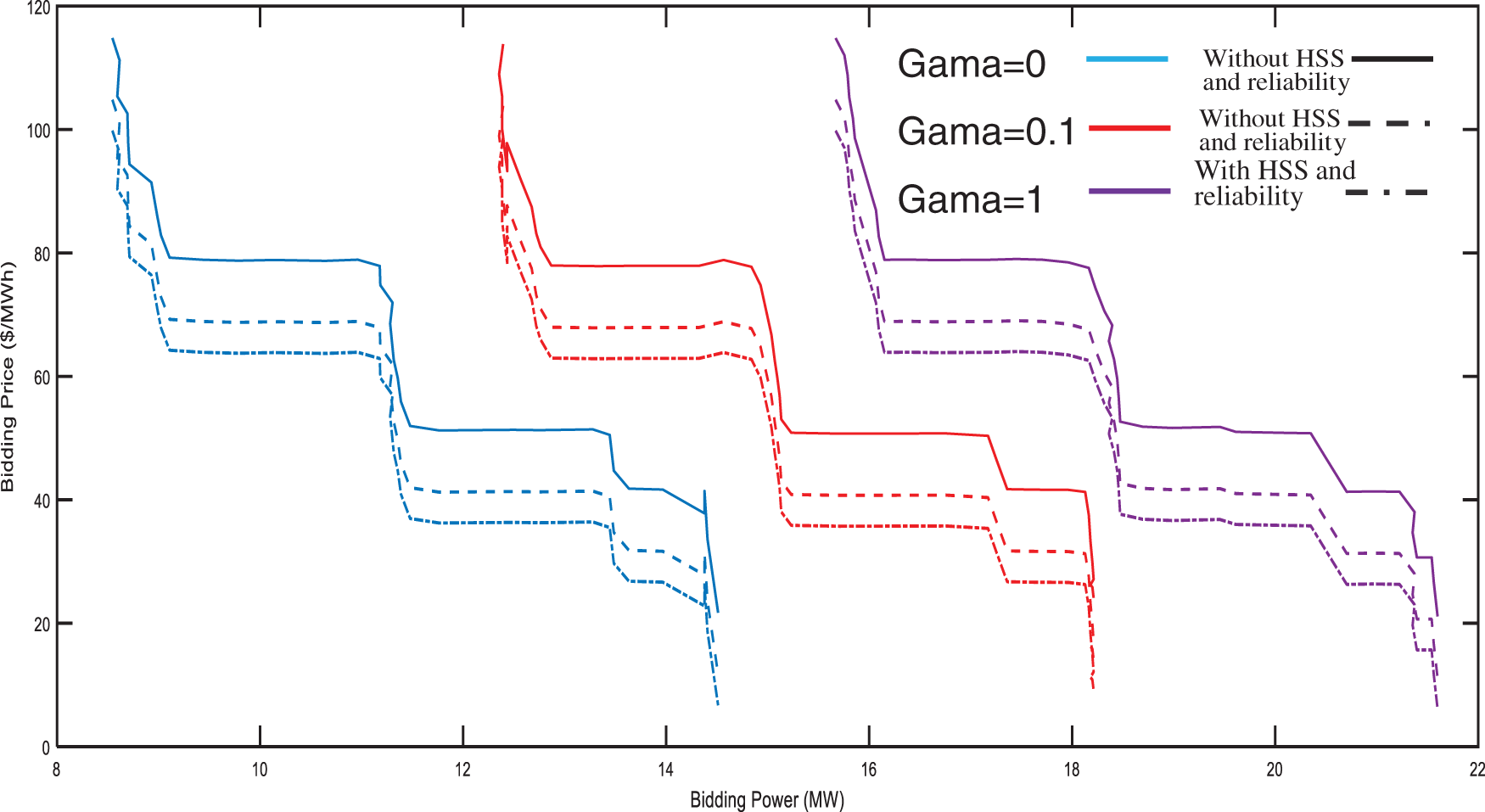
Figure 11: Bidding curve of 20th h in various gamma amount in presence of HSS and reliability

Figure 12: Bidding of a day for various gamma amount

The interchanged electricity among big power utility and upper grid is depicted in Fig. 13 for case 47, where positive numbers express provided energy than upper grid whereas minor ones are sold electrical energy to upstream grid. As could be anticipated, provided energy is augmented once the control parameter reaches to its max amount (Γ=1). However, the sold energy is reduced when gamma is equal to one in robust programing of big power utility.

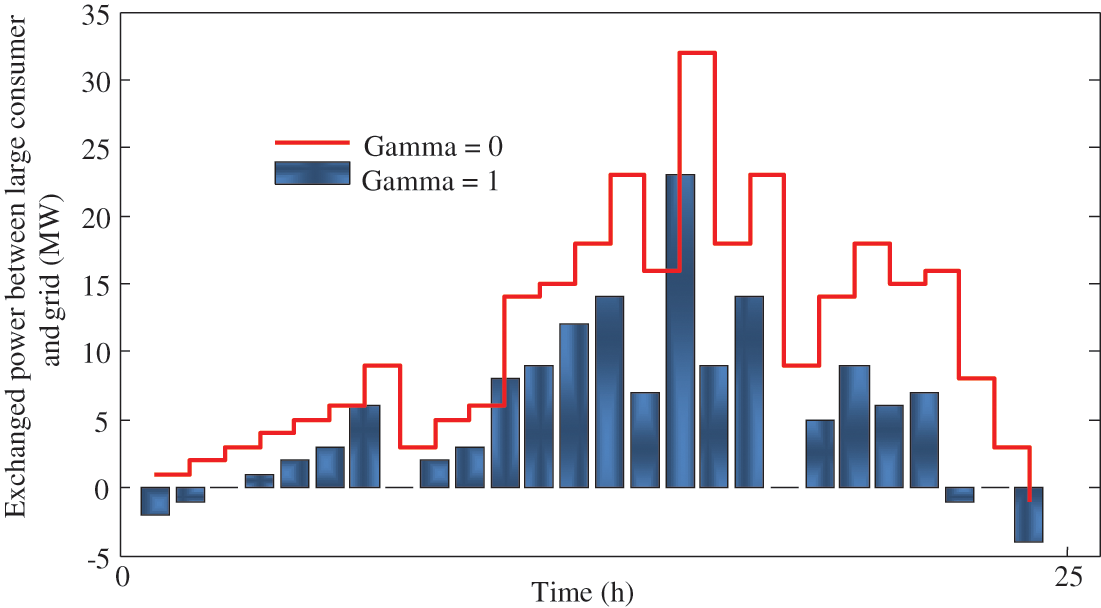
Figure 13: Power swapped between high demand and grid

This work presented 40 case for modeling of uncertainty on market tariff, solar radiation, temperature and wind speed. Association of provided energy from 12 BCs for case 35 is shown in Fig. 14. As seen in Fig. 10, this amount is nearly equal for both the bottom and upper values of gamma.

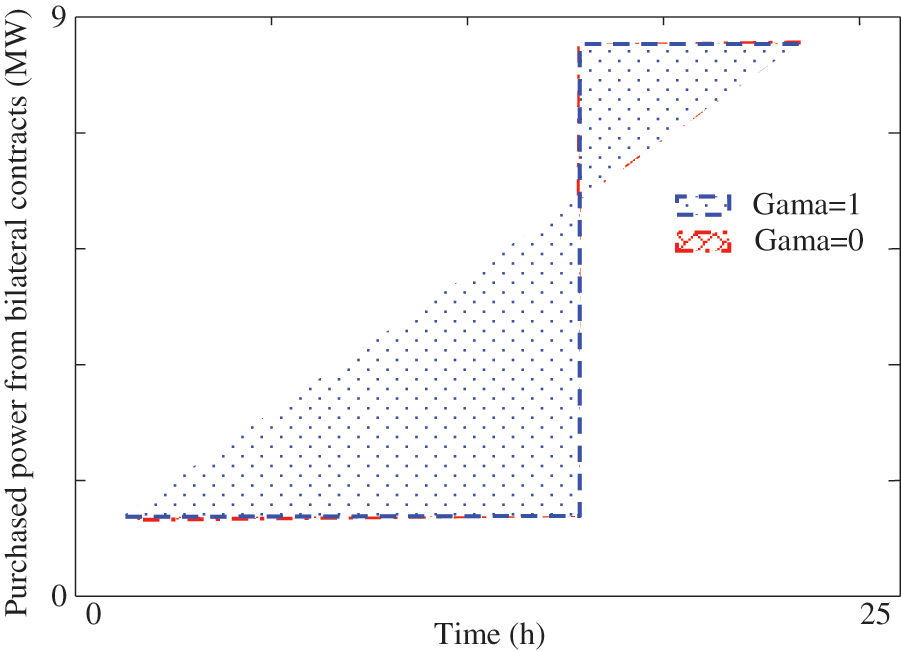
Figure 14: 35th scenario procured power for bilateral contracts

Also, Fig. 15 shows charging/discharging of battery, in which positive ones are charged energy whereas negative ones are utilized to present discharged electricity. Respect to this figure, once Γ=1, discharged energy is greater compared to remain scenarios to meet demand uncertainty.

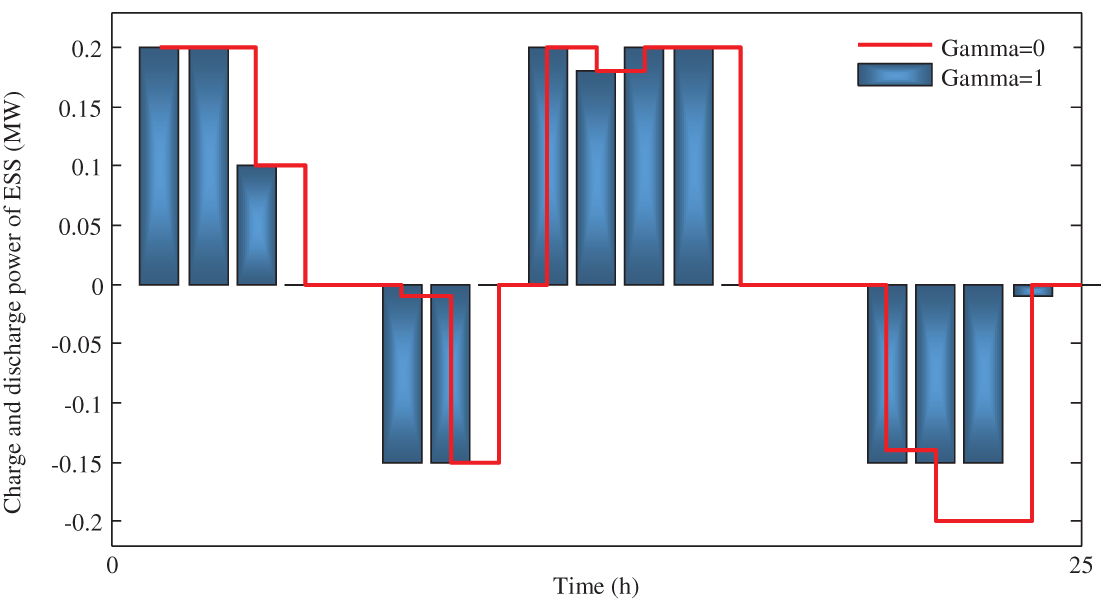
Figure 15: 46th scenarios charge and discharge power results

4.3 Supplementary Analysis: Time-of-Use Pricing Determination

In this model, the energy seller controls the selling cost as low, medium and peak demands. This approach ban be close to real price and market. In this approach, the system is analyzed including and excluding HSS. Obtained results are presented in Table 1, for two model of including and excluding the HSS.

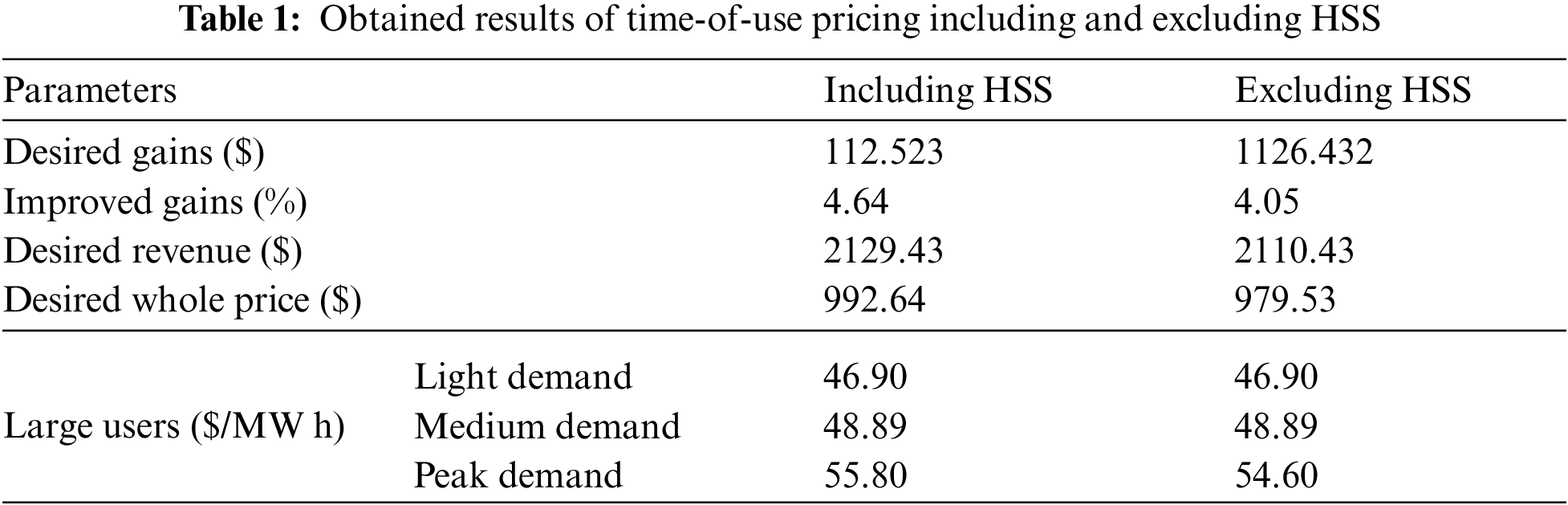
By considering to this table, it can be said that more profits are provided in utilizing the HSS which can be suitable for retailers as well as end-user consumers. The retailer’s provided demand is presented in Figs. 16 and 17 in two models of including and excluding HSS. In Figs. 18 and 19 the charge and discharge energy and stored pressure level of hydrogen storage system is presented as well.

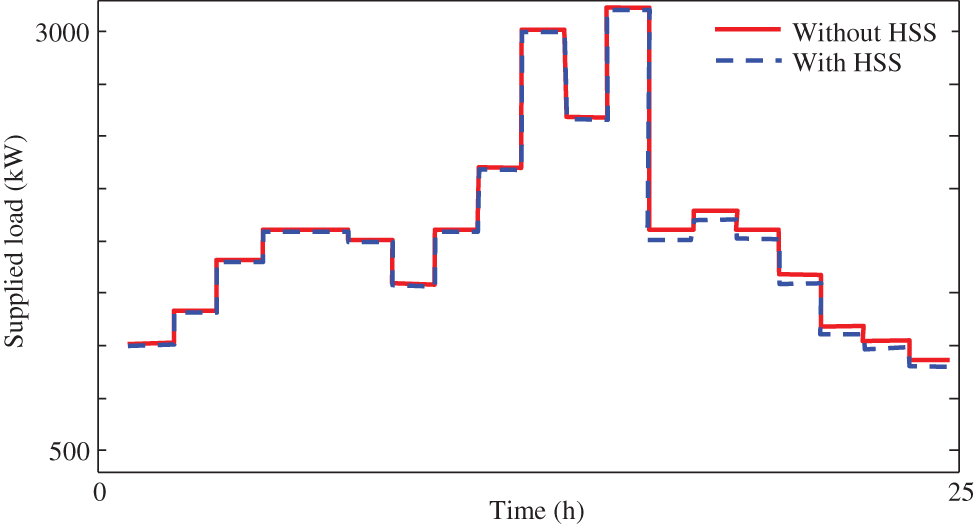
Figure 16: Demand power of results of retailer in time-of-use pricing

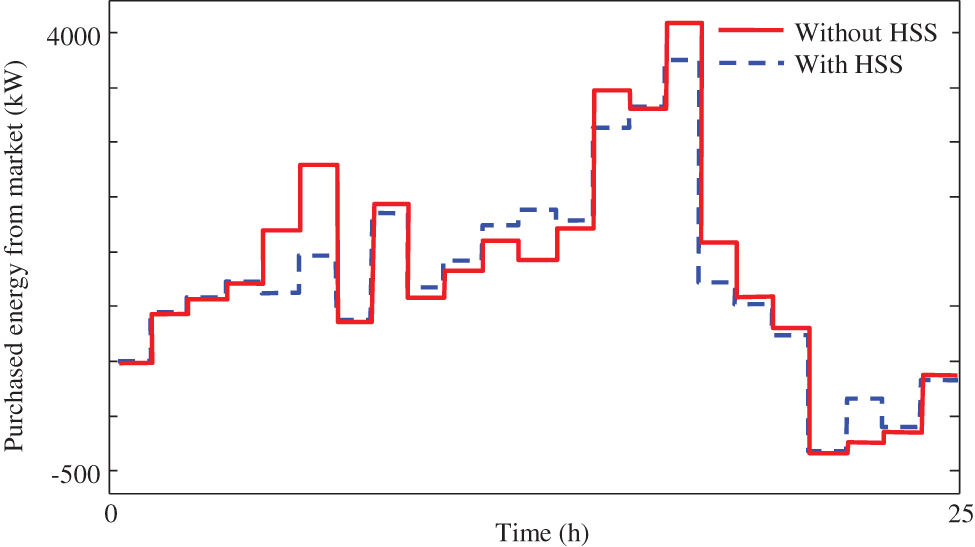
Figure 17: Energy procurement from market in time-of-use pricing

Figure 18: Charge of HSS in time-of-use pricing

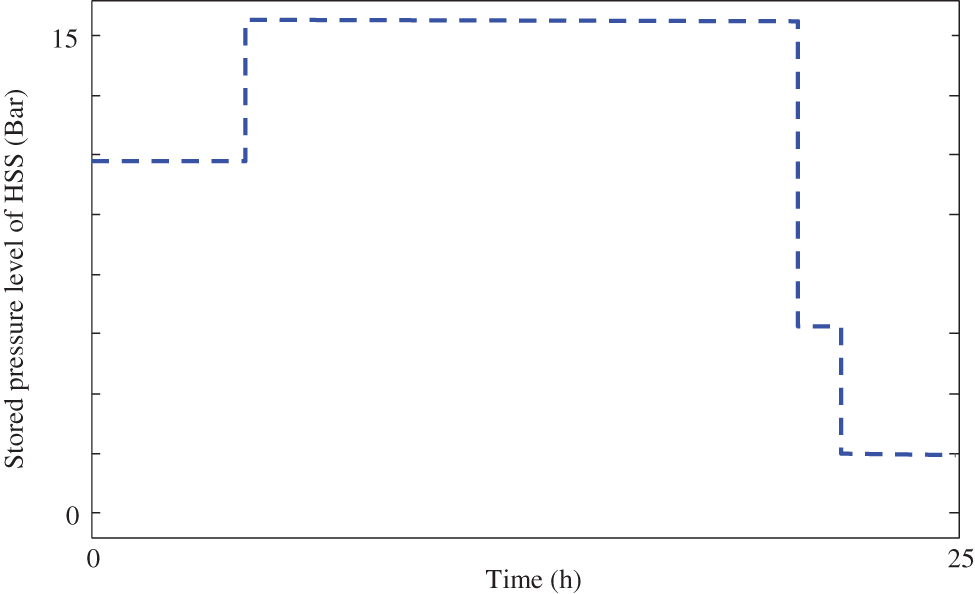
Figure 19: The level of HSS pressure storage in time-of-use pricing

5  Conclusion

This article suggested a novel model of bidding strategy in power markets for various generation contains; Micro turbines, wind turbine, PV, energy storage and, etc., in big power utilities. It is worthy to note, market tariff, solar radiation, temperature, and wind speed are regarded as unknown factors and their modeling is made by means of stochastic method whereas modeling of demand uncertainty is done by robust method. In this work, the uncertainty of power demand is modeled by robust optimal method whereas remain uncertain parameters are incorporated in model by stochastic method. The unbalanced amount of power between generation and bidding value of green energies are compensated by storage devices and the loss of unbalanced loss become minimum. Also, a control variable Γ was introduced for determining of conservatism level for demand uncertainty. It is remarkable, that the value of this control parameter is between 0 and 1. On the other point, a hydrogen storage system is utilized and for mage the power demand in hub energy, the reliability index is considered. The achieved results present, greater values of this variable leaded to greater supplement cost for big power utility. However, greater price causes to greater robustness vs. demand uncertainty. The entire energy supplement cost, in case of Γ=0, is gained $39,63 whereas its amount is $49,47, once gamma takes its max amount which is equal to one. It translates, higher robustness vs. demand uncertainty cost 25 percent for big utility. With growth of conservative level, provided electrical energy than upper grid is augmented whereas sold energy to upstream grid has mitigated. In case of Γ=1, more electricity is provided from power storage device to cope demand uncertainty whereas provided energy from BCs stayed almost unchanged. As a result, exploitation of hydrogen storage system by considering the reliability index has reduced the cost of the system. Additionally, based on obtained numerical analysis, more profits are provided in utilizing the HSS which can be suitable for retailers as well as end-user consumers.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Vallés, M., Bello, A., Reneses, J., Frías, P. (2018). Probabilistic characterization of electricity consumer responsiveness to economic incentives. Applied Energy, 216, 296–310. DOI 10.1016/j.apenergy.2018.02.058. [Google Scholar] [CrossRef]

 2.  Kim, H. J., Kim, M. K. (2021). Risk-based hybrid energy management with developing bidding strategy and advanced demand response of grid-connected microgrid based on stochastic/information gap decision theory. International Journal of Electrical Power and Energy Systems, 131, 107046. DOI 10.1016/j.ijepes.2021.107046. [Google Scholar] [CrossRef]

 3.  Khalilzadeh, S., Nezhad, A. H. (2020). Using waste heat of high capacity wind turbines in a novel combined heating, cooling, and power system. Journal of Cleaner Production, 276, 123221. DOI 10.1016/j.jclepro.2020.123221. [Google Scholar] [CrossRef]

 4.  Luerssen, C., Gandhi, O., Reindl, T., Sekhar, C., Cheong, D. (2020). Life cycle cost analysis (LCCA) of PV-powered cooling systems with thermal energy and battery storage for off-grid applications. Applied Energy, 273, 115145. DOI 10.1016/j.apenergy.2020.115145. [Google Scholar] [CrossRef]

 5.  Cao, Y., Wang, Q., Fan, Q., Nojavan, S., Jermsittiparsert, K. (2020). Risk-constrained stochastic power procurement of storage-based large electricity consumer. Journal of Energy Storage, 28, 101183. DOI 10.1016/j.est.2019.101183. [Google Scholar] [CrossRef]

 6.  Aalami, H. A., Nojavan, S. (2016). Energy storage system and demand response program effects on stochastic energy procurement of large consumers considering renewable generation. IET Generation, Transmission and Distribution, 10(1), 107–114. DOI 10.1049/iet-gtd.2015.0473. [Google Scholar] [CrossRef]

 7.  Soroudi, A., Ehsan, M. (2012). IGDT based robust decision making tool for DNOs in load procurement under severe uncertainty. IEEE Transactions on Smart Grid, 4(2), 886–895. DOI 10.1109/TSG.2012.2214071. [Google Scholar] [CrossRef]

 8.  Kazempour, S. J., Conejo, A. J., Ruiz, C. (2014). Strategic bidding for a large consumer. IEEE Transactions on Power Systems, 30(2), 848–856. DOI 10.1109/TPWRS.2014.2332540. [Google Scholar] [CrossRef]

 9.  Cleland, N., Zakeri, G., Pritchard, G., Young, B. (2016). Integrating consumption and reserve strategies for large consumers in electricity markets. In: Computational management science, pp. 23–30. Cham: Springer [Google Scholar]

10. Conejo, A. J., Fernandez-Gonzalez, J. J., Alguacil, N. (2005). Energy procurement for large consumers in electricity markets. IEE Proceedings-Generation, Transmission and Distribution, 152(3), 357–364. DOI 10.1049/ip-gtd:20041252. [Google Scholar] [CrossRef]

11. Fang, D., Wu, J., Tang, D. (2012). A double auction model for competitive generators and large consumers considering power transmission cost. International Journal of Electrical Power and Energy Systems, 43(1), 880–888. DOI 10.1016/j.ijepes.2012.05.041. [Google Scholar] [CrossRef]

12. Rezaeipour, R., Zahedi, A. (2017). Multi-objective based economic operation and environmental performance of PV-based large industrial consumer. Solar Energy, 157, 227–235. DOI 10.1016/j.solener.2017.08.022. [Google Scholar] [CrossRef]

13. Soudmand, B. M., Esfetanaj, N. N., Mehdipour, S., Rezaeipour, R. (2017). Heating hub and power hub models for optimal performance of an industrial consumer. Energy Conversion and Management, 150, 425–432. DOI 10.1016/j.enconman.2017.08.037. [Google Scholar] [CrossRef]

14. Bekravi, M., Abedinia, O. (2013). A new multi-objective meta heuristic algorithm based on environmental/economic load dispatch with wind effect. Technical and Physical Problems of Engineering, 5(2), 15. [Google Scholar]

15. Abedinia, O., Amjady, N., Izadfar, H. R., Shayanfar, H. A. (2012). Multi-machine power system oscillation damping: Placement and tuning PSS VIA multi-objective HBMO. International Journal of Technical and Physical Problems of Engineering, 4(3), 12. [Google Scholar]

16. Kaveh, A., Talatahari, S. (2010). Optimum design of skeletal structures using imperialist competitive algorithm. Computers & Structures, 88(21–22), pp. 1220–1229. [Google Scholar]

17. Abedinia, O., Amjady, N., Naderi, M. S. (2012). Multi-objective environmental/economic dispatch using firefly technique. 2012 11th International Conference on Environment and Electrical Engineering, pp. 461–466. DOI 10.1109/EEEIC.2012.6221422. [Google Scholar] [CrossRef]

18. Shayanfar, H. A., Ghasemi, A., Amjady, N., Abedinia, O. (2012). Optimal sizing and placement of distribution generation using imperialist competitive algorithm. Proceedings on the International Conference on Artificial Intelligence (ICAI). http://worldcomp-proceedings.com/proc/p2012/ICA2728.pdf. [Google Scholar]

19. Hartmann, B., Divényi, D., Vokony, I. (2018). Evaluation of business possibilities of energy storage at commercial and industrial consumers--A case study. Applied Energy, 222, 59–66. DOI 10.1016/j.apenergy.2018.04.005. [Google Scholar] [CrossRef]

20. Zare, K., Moghaddam, M. P., Sheikh-El-Eslami, M. K. (2011). Risk-based electricity procurement for large consumers. IEEE Transactions on Power Systems, 26(4), 1826–1835. DOI 10.1109/TPWRS.2011.2112675. [Google Scholar] [CrossRef]

21. Zare, K., Moghaddam, M. P., El Eslami, M. K. S. (2010). Electricity procurement for large consumers based on information gap decision theory. Energy Policy, 38(1), 234–242, DOI 10.1016/j.enpol.2009.09.010. [Google Scholar] [CrossRef]

22. Zare, K., Conejo, A. J., Carrión, M., Moghaddam, M. P. (2010). Multi-market energy procurement for a large consumer using a risk-aversion procedure. Electric Power Systems Research, 80(1), 63–70. DOI 10.1016/j.epsr.2009.08.006. [Google Scholar] [CrossRef]

23. Zhang, Q., Bremen, A. M., Grossmann, I. E., Pinto, J. M. (2018). Long-term electricity procurement for large industrial consumers under uncertainty. Industrial & Engineering Chemistry Research, 57(9), 3333–3347. DOI 10.1021/acs.iecr.7b04589. [Google Scholar] [CrossRef]

24. Kazemi, M., Mohammadi-Ivatloo, B., Ehsan, M. (2014). Risk-based bidding of large electric utilities using information gap decision theory considering demand response. Electric Power Systems Research, 114, 86–92. DOI 10.1016/j.epsr.2014.04.016. [Google Scholar] [CrossRef]

25. Zarif, M., Javidi, M. H., Ghazizadeh, M. S. (2012). Self-scheduling of large consumers with second-order stochastic dominance constraints. IEEE Transactions on Power Systems, 28(1), 289–299. DOI 10.1109/TPWRS.2012.2197831. [Google Scholar] [CrossRef]

26. Abdulaal, A., Moghaddass, R., Asfour, S. (2017). Two-stage discrete-continuous multi-objective load optimization: An industrial consumer utility approach to demand response. Applied Energy, 206, 206–221. DOI 10.1016/j.apenergy.2017.08.053. [Google Scholar] [CrossRef]

27. Zarif, M., Javidi, M. H., Ghazizadeh, M. S. (2012). Self-scheduling approach for large consumers in competitive electricity markets based on a probabilistic fuzzy system. IET Generation, Transmission and Distribution, 6(1), 50–58. DOI 10.1049/iet-gtd.2011.0308. [Google Scholar] [CrossRef]

28. Levitin, G., Lisnianski, A. (2000). Optimization of imperfect preventive maintenance for multi-state systems. Reliability Engineering & System Safety, 67(2), 193–203. DOI 10.1016/S0951-8320(99)00067-8. [Google Scholar] [CrossRef]

29. Panahandeh, B., Bard, J., Outzourhit, A., Zejli, D. (2011). Simulation of PV-Wind-hybrid systems combined with hydrogen storage for rural electrification. International Journal of Hydrogen Energy, 36(6), 4185–4197. DOI 10.1016/j.ijhydene.2010.07.151. [Google Scholar] [CrossRef]

30. Shayeghi, H., Sobhani, B. (2014). Integrated offering strategy for profit enhancement of distributed resources and demand response in microgrids considering system uncertainties. Energy Conversion and Management, 87, 765–777. DOI 10.1016/j.enconman.2014.07.068. [Google Scholar] [CrossRef]

31. Zou, Y., Zhao, J., Ding, D., Miao, F., Sobhani, B. (2021). Solving dynamic economic and emission dispatch in power system integrated electric vehicle and wind turbine using multi-objective virus colony search algorithm. Sustainable Cities and Society, 67, 102722. DOI 10.1016/j.scs.2021.102722. [Google Scholar] [CrossRef]

32. Khaloie, H., Abdollahi, A., Shafie-Khah, M., Anvari-Moghaddam, A., Nojavan, S. et al. (2020). Coordinated wind-thermal-energy storage offering strategy in energy and spinning reserve markets using a multi-stage model. Applied Energy, 259, 114168. DOI 10.1016/j.apenergy.2019.114168. [Google Scholar] [CrossRef]

33. Mirzaei, M. A., Hemmati, M., Zare, K., Abapour, M., Mohammadi-Ivatloo, B. et al. (2020). A novel hybrid two-stage framework for flexible bidding strategy of reconfigurable micro-grid in day-ahead and real-time markets. International Journal of Electrical Power and Energy Systems, 123, 106293. DOI 10.1016/j.ijepes.2020.106293. [Google Scholar] [CrossRef]

34. Khaloie, H., Mollahassani-Pour, M., Anvari-Moghaddam, A. (2020). Optimal behavior of a hybrid power producer in day-ahead and intraday markets: A bi-objective CVaR-based approach. IEEE Transactions on Sustainable Energy, 12(2), 931–943. DOI 10.1109/TSTE.2020.3026066. [Google Scholar] [CrossRef]

35. Oskouei, M. Z., Mirzaei, M. A., Mohammadi-Ivatloo, B., Shafiee, M., Marzband, M. et al. (2021). A hybrid robust-stochastic approach to evaluate the profit of a multi-energy retailer in tri-layer energy markets. Energy, 214, 118948. DOI 10.1016/j.energy.2020.118948. [Google Scholar] [CrossRef]

36. Khaloie, H., Abdollahi, A., Shafie-Khah, M., Siano, P., Nojavan, S. et al. (2020). Co-optimized bidding strategy of an integrated wind-thermal-photovoltaic system in deregulated electricity market under uncertainties. Journal of Cleaner Production, 242, 118434. DOI 10.1016/j.jclepro.2019.118434. [Google Scholar] [CrossRef]

37. Conejo, A. J., Carrión, M., Morales, J. M. (2010). Decision making under uncertainty in electricity markets, vol. 1, pp. 376--384. New York: Springer. [Google Scholar]

38. Karami, M., Shayanfar, H. A., Aghaei, J., Ahmadi, A. (2013). Scenario-based security-constrained hydrothermal coordination with volatile wind power generation. Renewable and Sustainable Energy Reviews, 28, 726–737. DOI 10.1016/j.rser.2013.07.052. [Google Scholar] [CrossRef]

39. Nguyen, D. T., Le, L. B. (2014). Optimal bidding strategy for microgrids considering renewable energy and building thermal dynamics. IEEE Transactions on Smart Grid, 5(4), 1608–1620. DOI 10.1109/TSG.2014.2313612. [Google Scholar] [CrossRef]

40. Kholardi, F., Assili, M., Lasemi, M. A., Hajizadeh, A. (2018). Optimal management of energy hub with considering hydrogen network. 2018 International Conference on Smart Energy Systems and Technologies (SEST), pp. 1–6. IEEE. DOI 10.1109/SEST.2018.8495664. [Google Scholar] [CrossRef]

41. Shahmohammadi, A., Moradi-Dalvand, M., Ghasemi, H., Ghazizadeh, M. S. (2014). Optimal design of multicarrier energy systems considering reliability constraints. IEEE Transactions on Power Delivery, 30(2), 878–886. DOI 10.1109/TPWRD.2014.2365491. [Google Scholar] [CrossRef]

42. Nojavan, S., Mohammadi-Ivatloo, B., Zare, K. (2015). RETRACTED: Robust optimization based price-taker retailer bidding strategy under pool market price uncertainty. International Journal of Electrical Power & Energy Systems, 73, 955--963. DOI 10.1016/j.ijepes.2020.106482. [Google Scholar] [CrossRef]

43. Brooke, A., Kendrick, D., Meeraus, A. (1990). GAMS user’s guide. Redwood City (CAThe Scientific Press. [Google Scholar]

44. The GAMS Software Website (2018). http://www.gams.com/dd/docs/solvers/cplex.pdf. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.