Energy Engineering

DOI: 10.32604/ee.2022.020082

ARTICLE

Multi-Agent Consensus Control Scheme for the Load Control Problem

Te Xu1, Zhixian Lin1, Xinwei Lin1, Changsheng Lin1, Feng Gao1, Zixuan Li2 and Peiwen Liu2,*

1Shenzhen Power Supply Bureau Co., Ltd., Shenzhen, 518000, China
2School of Electrical Engineering, Southeast University, Nanjing, 210096, China
*Corresponding Author: Peiwen Liu. Email: 220192756@seu.edu.cn
Received: 03 November 2021; Accepted: 07 December 2021

1  Introduction

With the rapid development of smart grid technology, more and more user equipment can participate in demand response by providing support for load balancing in the grid [1]. Traditional centralized control (Fig. 1, upper) requires the control center to collect and transmit information to ensure that the best system performance is obtained under strictly defined conditions. On the contrary, through distributed control (Fig. 1, lower), the system does not need to centrally manage each user control center. This control method defines one or more controlled units in the system that receive and control response information as the dominant node, so that the system completes the information exchange between the units [2–4]. This distributed control method not only realizes the functions of signal exchange, but also reduces the communication burden of the control center and simplifies the system network topology, so that the reliability of the system is better guaranteed [5–7].

Multi-agent consensus control is to make each agent in the system provide the same response to a certain command. At present, there are various researches on the multi-agent consensus control problems of load side resources. In [8], a multi-agent control method and an online optimization method is proposed to managing the power consumption of large amount of thermostatically controlled loads (TCLs). In [9], multi-agent technology is combined with load control. It fully considers the functions and characteristics of power load control, and establishes a power load control system based on multi-agent, which makes full use of intelligent technology. In [10], a novel approach for a distributed real-time coordination of power flow control is presented. A multi-agent system located decentrally at the substation level has been developed only relying on local measurements and integrant communication in contrast to global system models and centralized computations. In [11], a distributed control law using only local information is proposed to solve the load tracking control problem of an interrelated leader-follower multi-agent system, in which the dynamics of the leader and the follower states are interrelated. In [12], a distributed optimal tie-line power flow control strategy based on multi-agent is proposed. By covering the regional communication network of each MG and the distributed sensor monitoring the power flow of the tie line, the microgrid can be coordinated to achieve the best dispatch in real time under constant load fluctuations. In [13], a multi-agent-based multi-layer hierarchical control system is proposed for residential load management under real-time pricing environment. In this way, the purpose of reducing peak load demand, power cost and user discomfort is achieved. In [14], a multi-agent consensus control algorithm is proposed to meet the requirements of accurate load control of residential air conditioning resources.

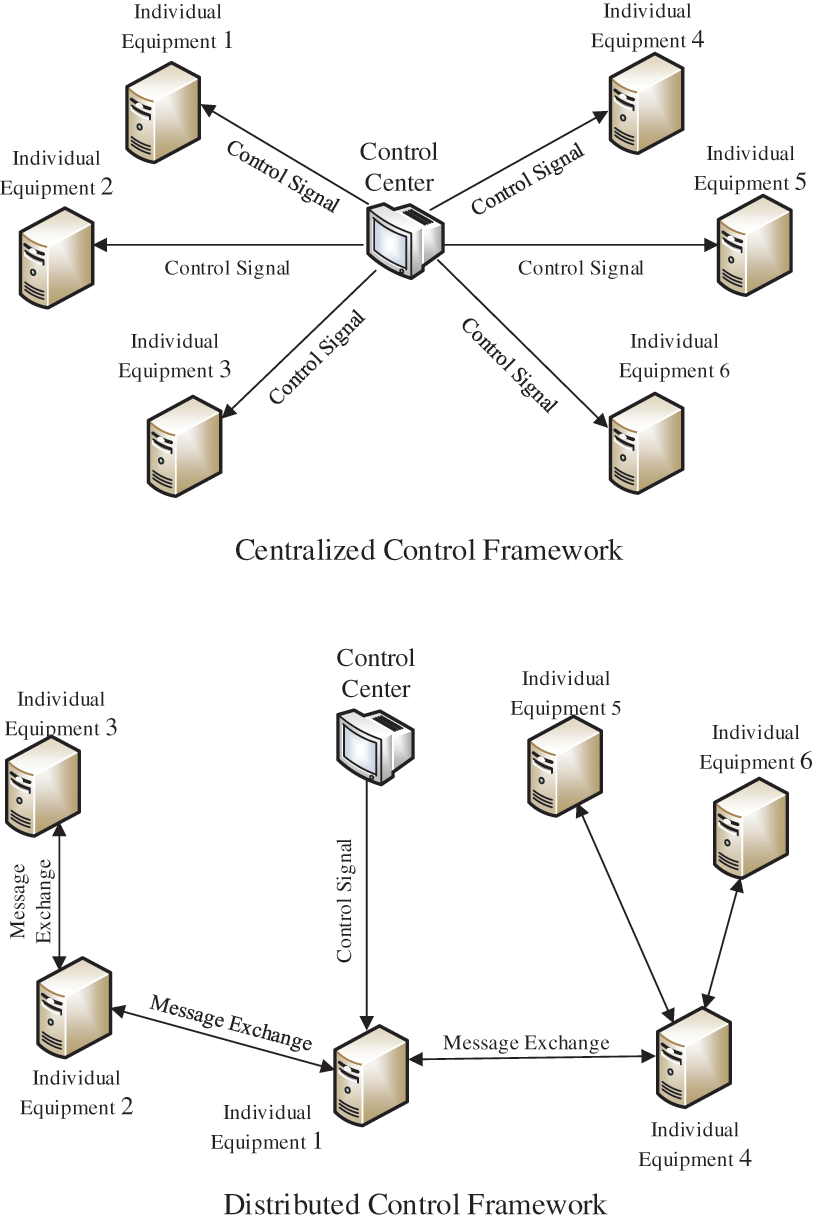
Figure 1: Centralized and distributed control framework

Notwithstanding the feasibility of the above methods, these methods belong to first-order multi-agent method which only considers position as the state to communicate with neighbor nodes. Other information, such as velocity information is neglected, and the performance is therefore limited.

Focusing on improving the load control performance, this paper applies second-order multi-agent consensus control method to the load control problem. By using the second-order multi-agent consensus control method, the velocity information is introduced as the additional state in the control model, the system can be converged faster than first-order multi-agent method.

The remaining of this paper is organized as following. In Section 2, the second-order multi-agent consensus control method is presented. The simulation results are provided in Section 3. And the conclusions are summarized in Section 4.

2  Second-Order Multi-Agent Consensus Algorithm

The multi-agent consensus control method is a kind of distributed control method that can deliver the control command to the distributed nodes through communication with neighbor nodes. In this section, the traditional first-order consensus algorithm is briefly introduced and then the load control method based on discrete second-order consensus algorithm is presented.

2.1 First-Order Multi-Agent Consensus System

Considering the dynamic state equation as Eq. (1):

x˙i(t)=ui(t),i=1,⋯,n(1)

where xi(t) is the state of agent i at time t, ui(t)∈R is the control input of i at time t. For a control input ui(t), and indexes i, j satisfy i,j=1,⋯,n, and for any initial condition, when t→∞ the following Eq. (2) satisfies:

limt→∞⁡(xi(t)−xj(t))=0,i,j=1,⋯,n(2)

The control input ui(t) can successfully lead to the convergence of the multi-agent system.

By analyzing the convergence condition of the multi-agent system, reference [15] derives the expression of ui(t) as Eq. (3):

ui(t)=∑j∈N(ξ,i)⁡aij(xj(t)−xi(t)),i=1,⋯,n(3)

By introducing Eq. (3) in the state Eq. (1), the following expression can be obtained in Eq. (4):

x˙(t)=−Lx(t)(4)

where L is the Laplacian Matrix of connected graph ξ, and x(t)=[x1(t)x2(t)⋯xn(t)]∈Rn.

2.2 Second-Order Multi-Agent Consensus System

By introducing the velocity of the state, the state equation of second-order multi-agent consensus system can be written by Eq. (5):

{x˙i(t)=vi(t)v˙i(t)=ui(t),i=1,⋯,n(5)

where xi(t) represents the position of the ith node, vi(t) represents the velocity, and ui(t) represents the control input.

Different with first-order multi-agent system, the second-order multi-agent system contains velocity state in addition to the position state in Eq. (5).

Similarly, to realize the convergence of the second-order multi-agent system, the input ui(t) should be carefully designed so that when t→∞, the following equation satisfies condition of Eq. (6):

{limt→∞⁡(xi(t)−xj(t))=0limt→∞⁡(vi(t)−vj(t))=0,∀i≠j,i,j=1,⋯,n(6)

For the multi-agent system Eq. (5), the control strategy can be modified as Eq. (7):

ui(t)=∑j∈N(ξ,i)⁡aij(xj(t)−xi(t))+γaij(vj(t)−vi(t))(7)

where γ is the parameter which influence the convergence speed of the system.

With the control strategy (7), the multi-agent system is converged under the condition of Eq. (8):

Re[γλi(L)±γ2λi2(L)+4λi(L)2]<0(8)

where λi(L) denotes characteristic root of Laplacian Matrices L, i = 1, 2, … n.

2.3 Proof of Second-Order Multi-Agent Consensus System

In this subsection, proof of the stability of the multi-agent consensus system is provided. By introducing Eq. (7) in Eqs. (5) and (9) can be obtained:

[x˙i(t)v˙i(t)]=[0n×nIn−L−γL][x(t)v(t)](9)

{x(t)=[x1(t)x2(t)⋯xn(t)]v(t)=[v1(t)v2(t)⋯vn(t)]

where L is the Laplacian Matrices of connected graph, and the characteristic equation of system Eq. (9) can be defined as Eq. (10):

det(λ2In+(1+γλ)L)=∏i=1n⁡(λ2−(1+γλ)λi(L))(10)

The characteristic root of Eq. (10) can be obtained as Eq. (11):

γλi(L)±γ2λi2(L)+4λi(L)2,i=1,⋯,n(11)

The convergence of the system can be realized on the condition that the characteristic root of the system has negative real part. If condition (8) is satisfied, the characteristic root (Eq. (11)) has negative real part, and the system stability can be guaranteed.

2.4 Discrete Second-Order Multi-Agent System

Based on the continuous second-order multi-agent system Eq. (5), the discrete second-order multi-agent system can be obtained by Eq. (12):

{xi(k+1)=xi(k)+δvi(k)vi(k+1)=vi(k)+δui(k),i=1,⋯,n(12)

where δ>0 denote the sampling time.

For system Eq. (12), the control algorithm can be finally obtained as Eq. (13):

ui(k)=∑j∈N(ξ,i)⁡aij[p1(xj(k)−xi(k))+p2(vj(k)−vi(k))](13)

where p1,p2 are two parameters, N(ξ,i) is the neighbor set of node i.

2.5 Load Control by the Multi-Agent System

For the load control problem, the task is to deliver the load control command to individual consumers, so that the consumers can provide load curtailment services. To apply the multi-agent consensus algorithm to the load control problem, the position xi(t) represent the load response amount for individual consumers. After the leader node receive the load control command, the command can be distributed to individual consumers by information exchange based on the consensus algorithm. The flow chart of the load control process is shown in Fig. 2.

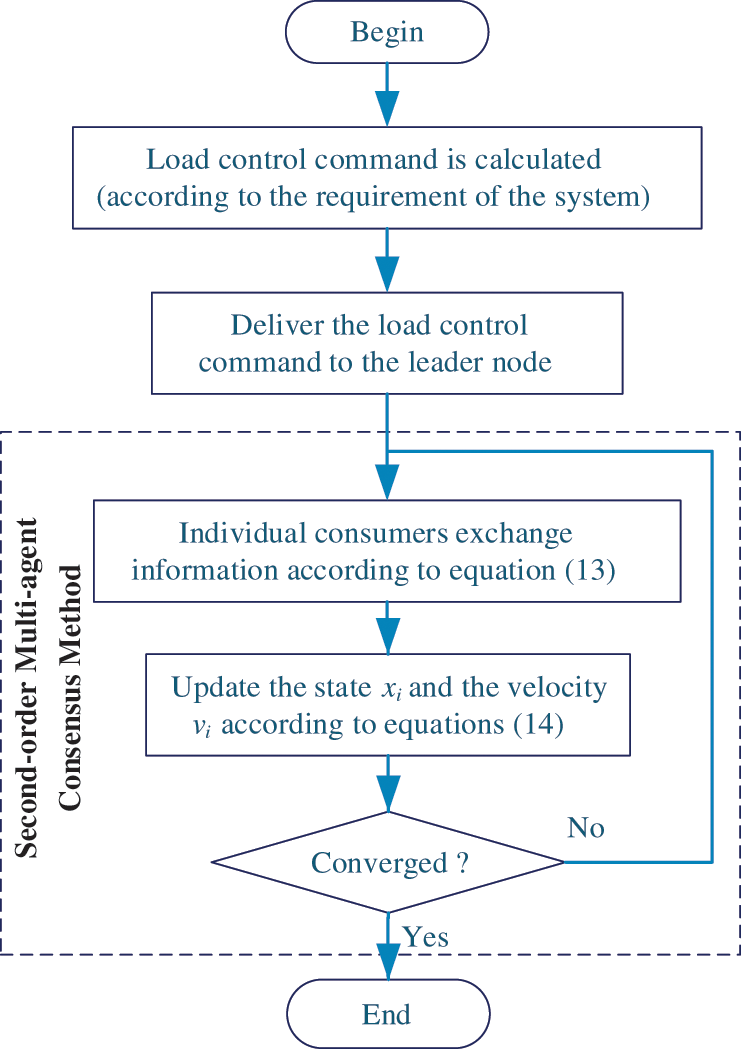
Figure 2: Flow chart of the load control process

3  Testing Examples

The testing examples consider load control problems under different scenarios. Different consensus control methods and different topologies of communication network are compared in order to show the effectiveness of the proposed method.

3.1 Comparison of the Convergence Speed of Different Consensus Algorithms

This subsection compares the convergence speed between the traditional and the proposed consensus algorithm, which are defined as following:

   Traditional method

The traditional method adopts first-order consensus algorithm. By the analysis of the previous section, the first-order consensus algorithm can be formulated by Eq. (14):

ui(k)=∑j∈N(ξ,i)⁡aij(xj(k)−xi(k))(14)

   Proposed method

The proposed method adopts second-order consensus algorithm. The second-order consensus algorithm can be formulated by Eq. (15):

ui(k)=∑j∈N(ξ,i)⁡aij[p1(xj(k)−xi(k))+p2(vj(k)−vi(k))](15)

where p1, p2 are parameters, N(ξ,i) is the neighbor set of node i.

The multi-agent system is defined in Fig. 3. It can be seen that each node can not only communicate with its neighborhood nodes, but also communicate with neighbor's neighbor. The Laplacian Matrices of the connected graph can be written as following:

L~1=[4−1−1000−1−1−14−1−1000−1−1−14−1−10000−1−14−1−10000−1−14−1−10000−1−14−1−1−1000−1−14−1−1−1000−1−14]

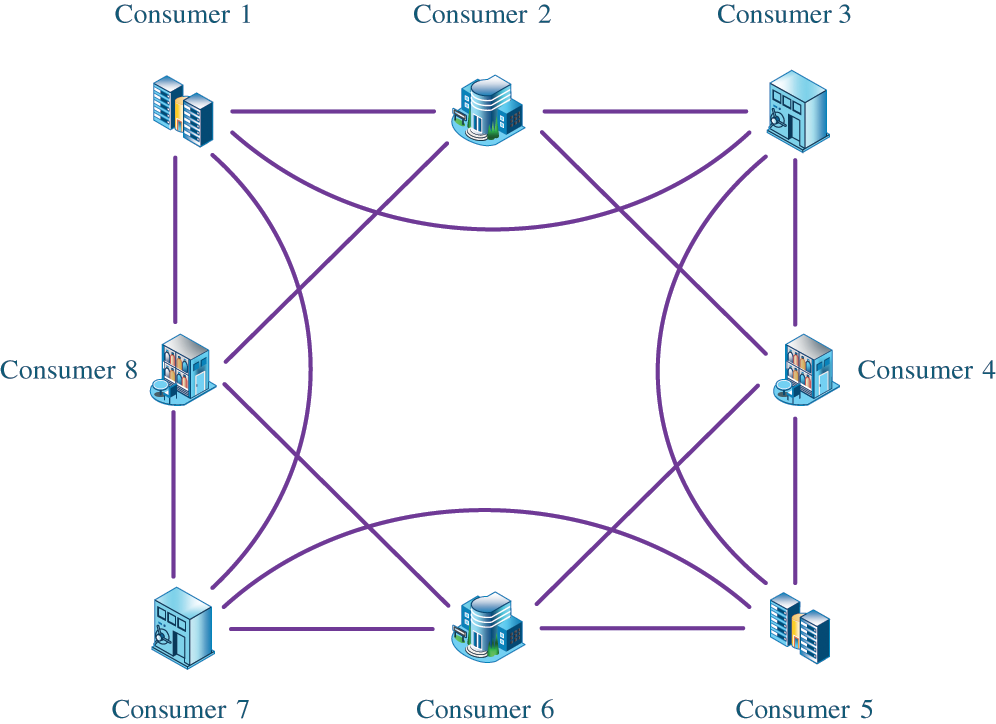
Figure 3: The structure of multi-agent consensus system

The parameters are selected as following:

p1=0.1,p2=0.15

Consumer 1 is selected as the leader node. To deliver 8 MW load control command to the distributed consumers, the initial states are defined as:

{x(0)=[80000000]Tv(0)=[00000000]T

The simulation results of position (amount of load response), velocity and input under the traditional method and the proposed method are shown in Figs. 4 and 5, respectively.

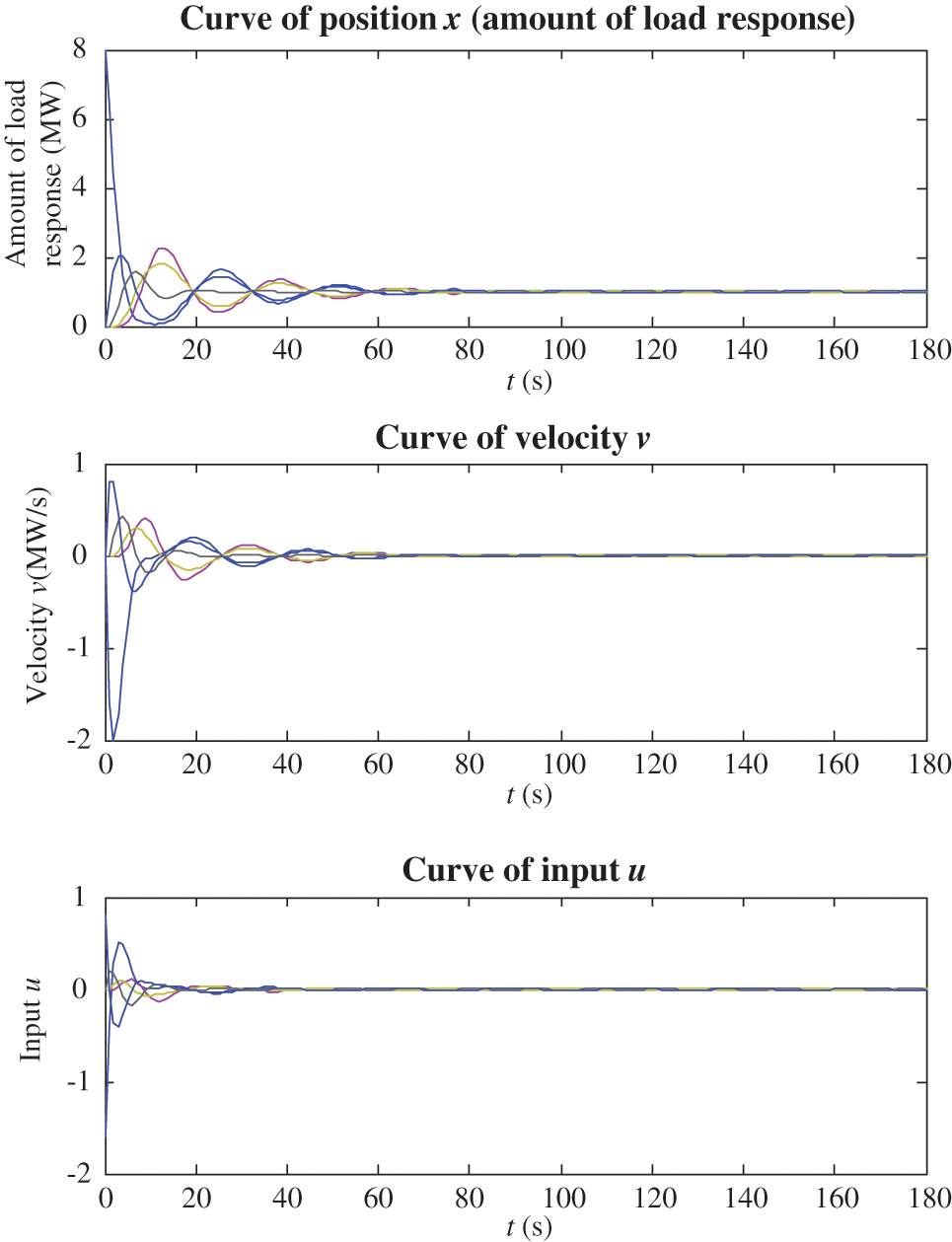
Figure 4: Simulation results of the traditional method

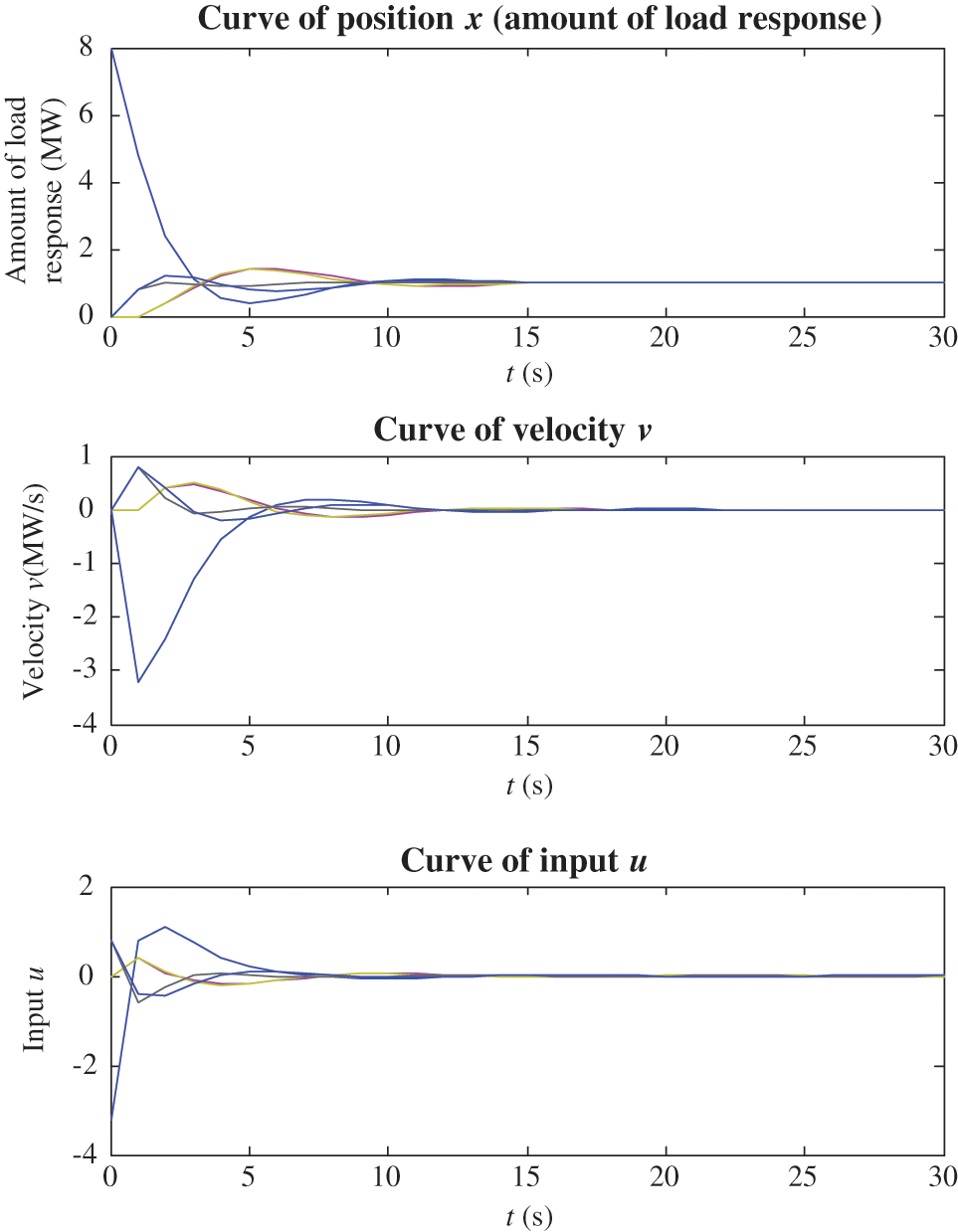
Figure 5: Simulation results of the proposed method

By comparing Figs. 4 and 5, it can be seen that the position (amount of load response), velocity and input of traditional method result in convergence at the 120 s, the 140 and 50 s, whereas the proposed method converge at the 20 s, the 25 and 13 s. Though the parameters are the same, the proposed method result in much faster convergence than the traditional method, showing superiority over the traditional method.

3.2 Comparison of Convergence under Different Topology of the Communication Network

From the analysis of the previous subsection, it can be found that the proposed method has much faster convergence than the traditional method. In the following analysis, second-order consensus algorithm is adopted and different topologies of the communication network are compared.

   Linear-topology

The linear-topology multi-agent system can be structured as Fig. 6. It can be seen that every two consumers are connected with each other except the first and the last one. The structure is similar to a line.

Figure 6: The structure of linear-topology multi-agent system

For such system, the Laplacian Matrices of the connected graph can be derived by:

L~2=[1−1000000−12−1000000−12−1000000−12−1000000−12−1000000−12−1000000−12−1000000−11]

Considering totally 8 MW load response, the simulation results of position (amount of load response), velocity and input is shown in Fig. 7. It can be seen that the position and the velocity are converged after 400 and 200 s, respectively.

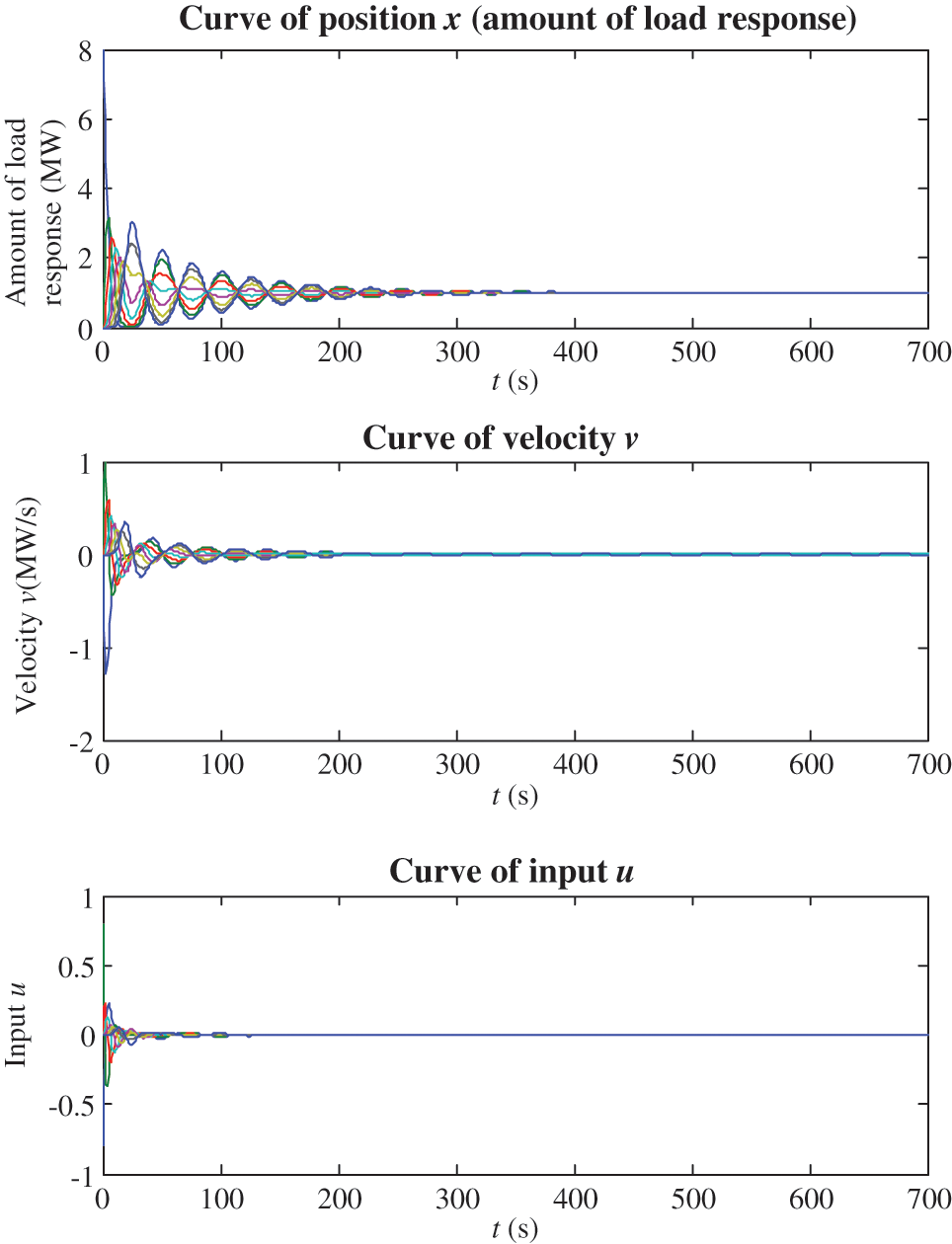
Figure 7: Simulation results of the linear-topology multi-agent system

   Star-topology multi-agent system

Similarly, the star-topology multi-agent system can be designed as Fig. 8. It can be seen that two consumers are selected as center node, and other consumers are connected to the center node. The structure is similar to a star.

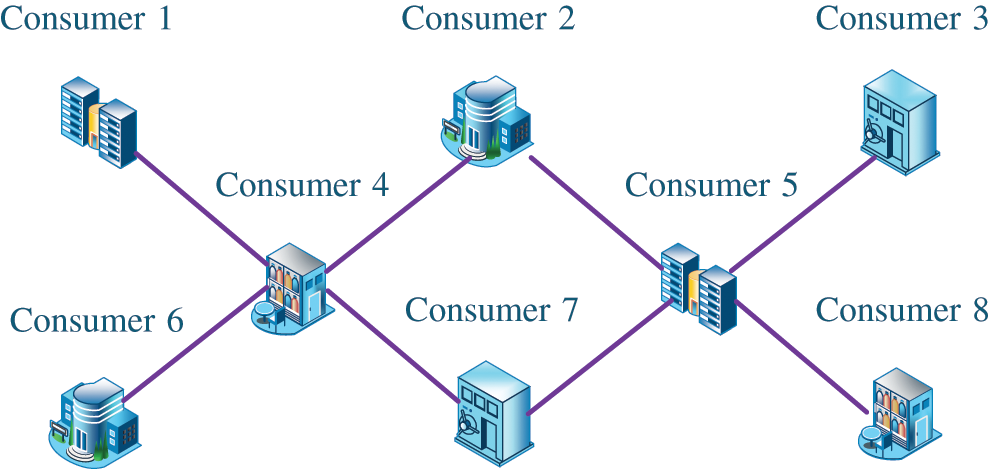
Figure 8: The structure of star-topology multi-agent system

The Laplacian Matrices can be derived by:

L~3=[100−10000020−1−10000010−1000−1−1040−1−100−1−1040−1−1000−10100000−1−10200000−1001]

Then consumer 1 is selected as the leader node to deliver 8 MW load response command to the distributed consumers. By implementing the simulation of 200 s, the position (amount of load response), velocity and input are shown in Fig. 9. It can be seen that the position and the velocity are finally converged at 110 and 100 s, respectively.

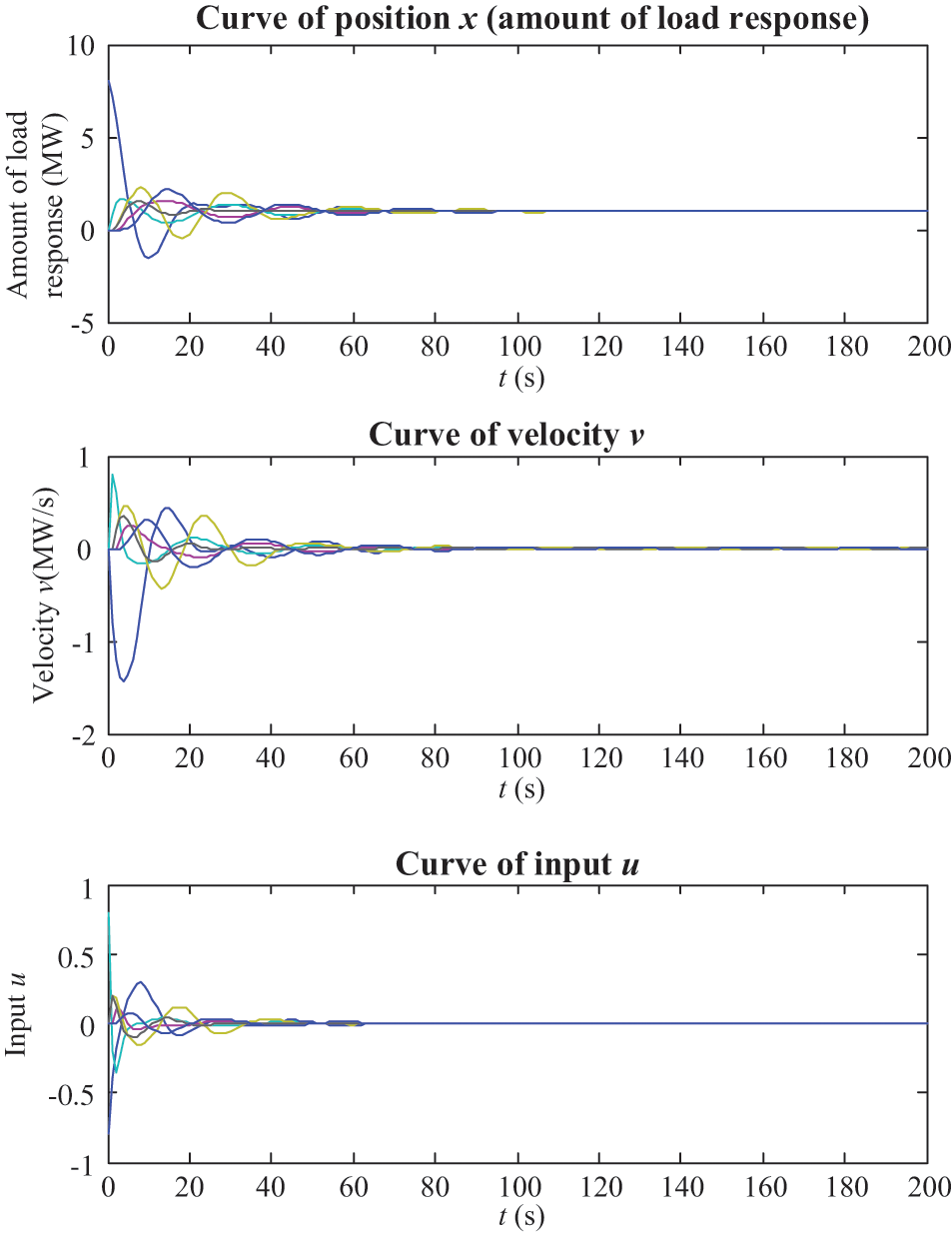
Figure 9: Simulation results of the star-topology multi-agent system

   Net-topology multi-agent system

The net-topology multi-agent system is considered. The topology of the system is shown in Fig. 10. It can be seen that each node is connected to at least 3 neighbor nodes. The structure is similar to a net.

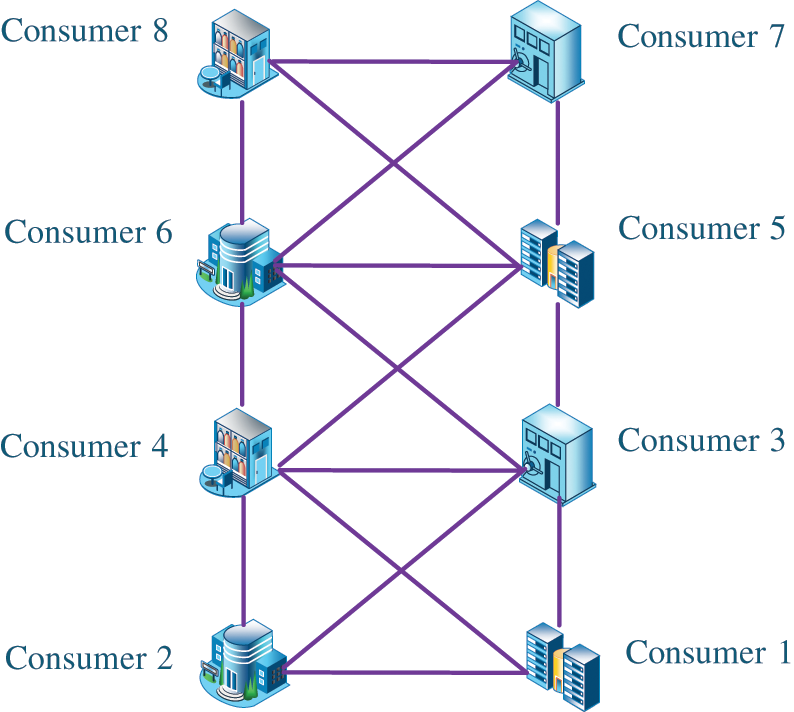
Figure 10: The structure of net-topology multi-agent system

The Laplacian Matrices is defined as following:

L~4=[3−1−1−10000−13−1−10000−1−15−1−1−100−1−1−15−1−10000−1−15−1−1−100−1−1−15−1−10000−1−13−10000−1−1−13]

Consumer 1 is selected as the leader node to deliver 8 MW load control command to the distributed consumers. By implementing the simulation of 100 s, the position (amount of load response), velocity and input are shown in Fig. 11. It can be seen that the position and the velocity are finally converged at 50 and 40 s, respectively.

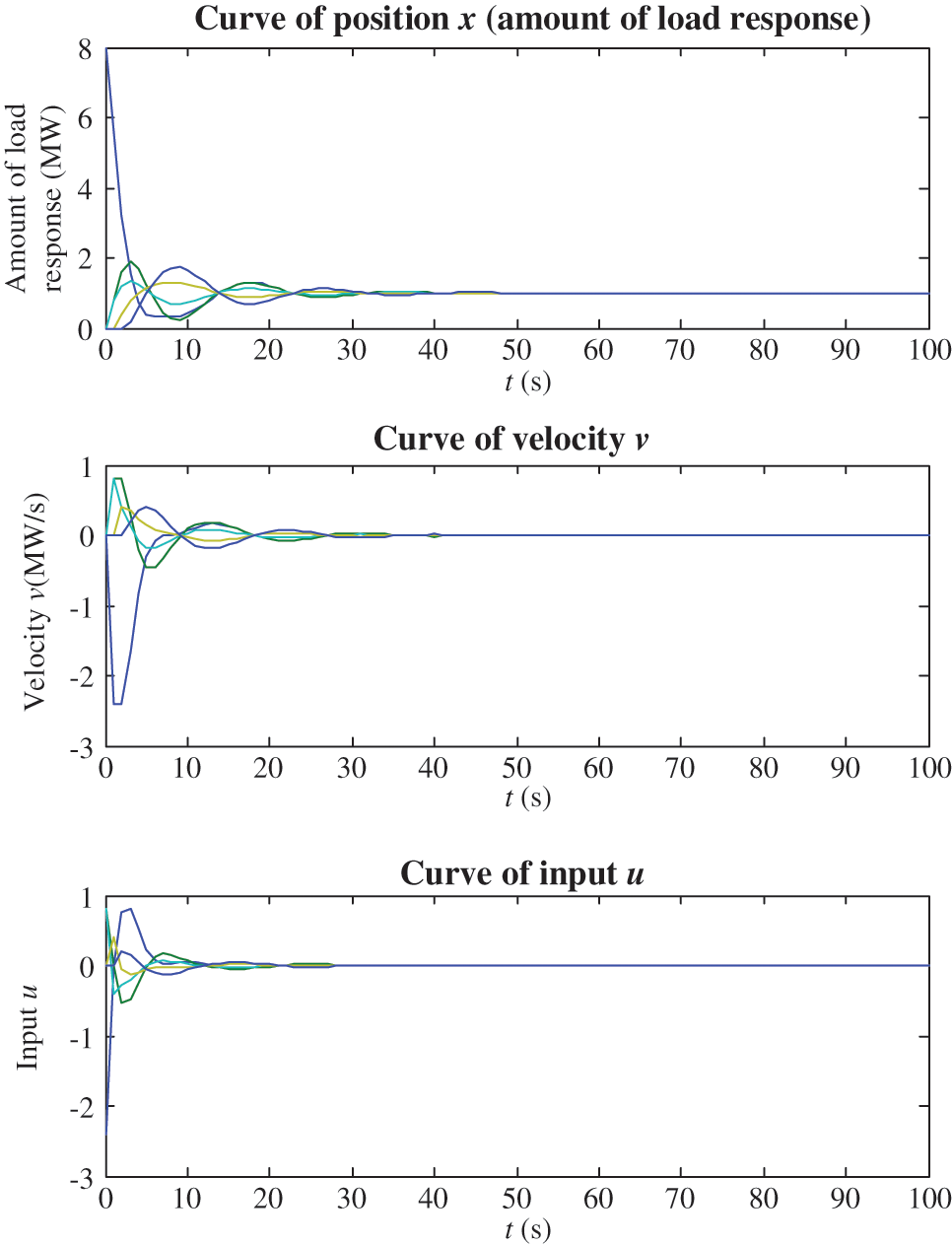
Figure 11: Simulation results of the net-topology multi-agent system

Table 1 summarizes the convergence speed of different topologies. From Table 1, it can be seen that the net-topology multi-agent result in quickest convergence, which is good selection for the load control command to send to the consumers.

3.3 Comparison of Control Performance under Different Communication Delay

In a real control system, the communication delay always exists due to the hardware implementation. Therefore, it is of significant importance to analyze the influence of the communication delay on the control performance. Fig. 12 shows the position (amount of load response), velocity and input of the net-topology multi-agent system under different communication delay.

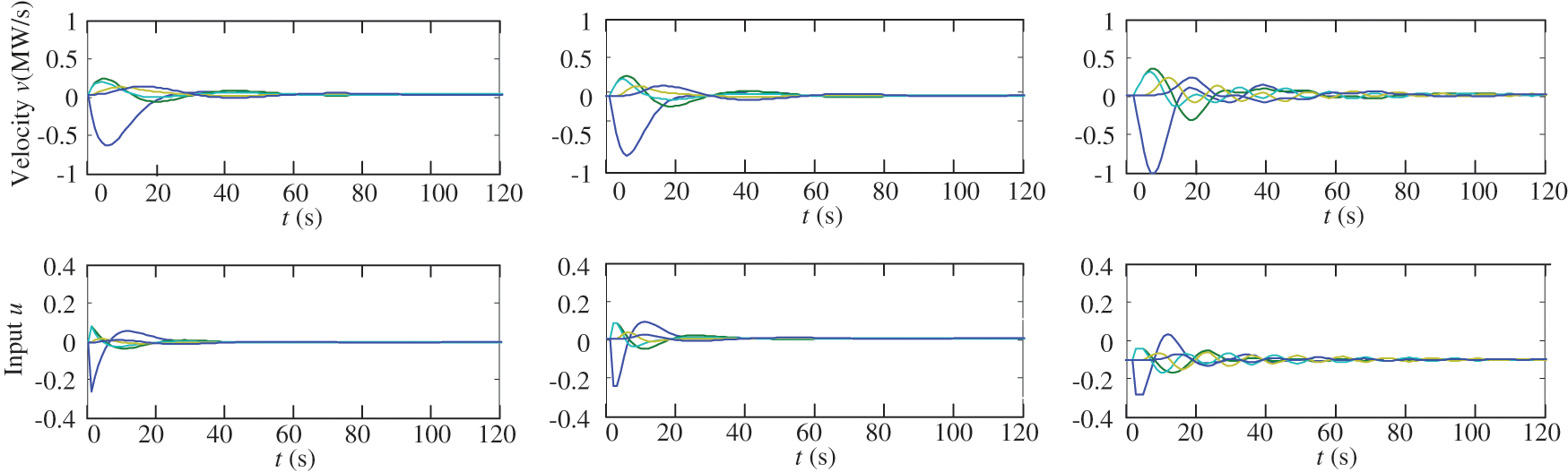
Figure 12: Simulation results of n multi-agent system with different communication delay

Fig. 13 summarizes the convergence speed of the net-topology multi-agent system under different communication delays. It can be seen from Fig. 13 that the communication delay influences the control performance and larger communication delay slows down the convergence speed. Under 1 s communication delay, the responsive load is converged in about 74 s, whereas under 3 s communication delay, the converging time increases to about 133 s. Larger converging time leads to higher oscillations of the responsive power, which would have negative influence on the control performance. To guarantee good control performance, small response delay should be kept.

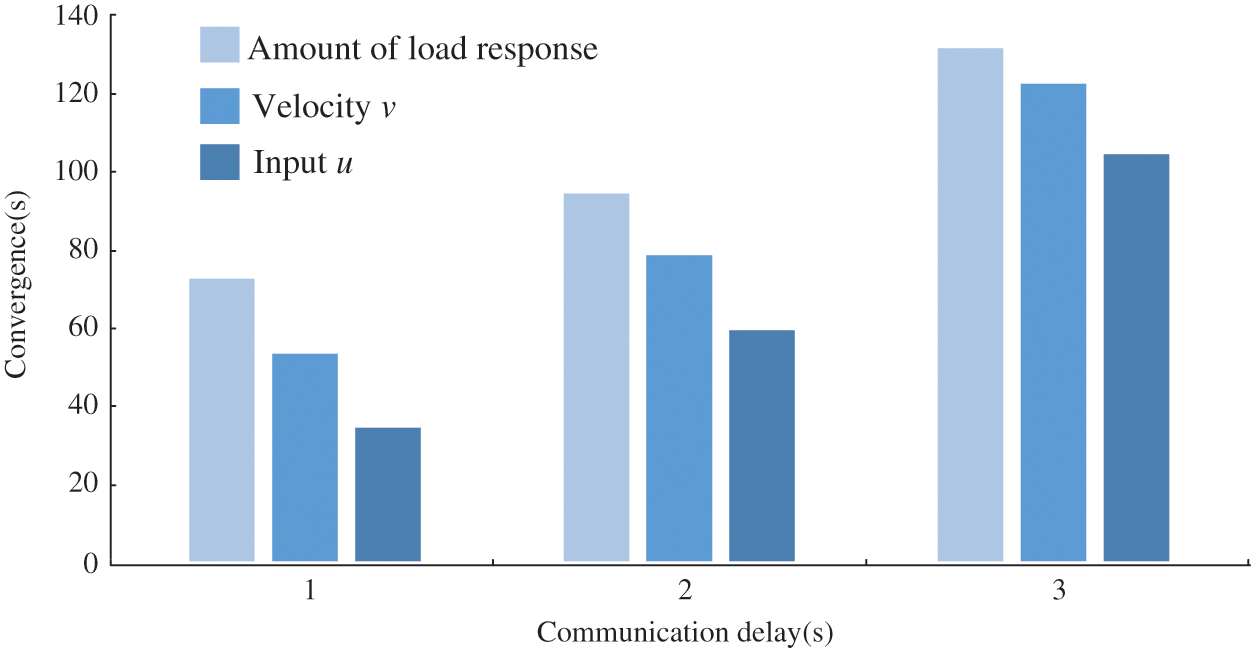
Figure 13: Convergence speed of multi-agent system with different communication delay

4  Conclusion

This paper proposes a second-order-multi-agent-consensus-based load control scheme. By introducing velocity state into the communication network and the correspondence modified control algorithm, the proposed method results in better performance than traditional control scheme. The contribution of this paper can be summarized as following:

1)   Proposing a novel second-order consensus control scheme for the load control of multi-agent system. By introducing the velocity state into the model, the proposed method achieves better performance than traditional first-order consensus control scheme.

2)   Analyzing different topologies that affect the performance of the second-order multi-agent system, and concluding that net-topology multi-agent has quickest convergence.

3)   Analyzing the influences of the response delay on the convergence of the control system, and showing the importance of minimizing the response delay.

Notwithstanding the contributions listed above, there are still limitations that needs to be completed in the future research. For example, external interference may affect the control signal, and therefore influence the final control performance. Therefore, the future work may be focusing on designing methods for coping with external interferences.

Funding Statement: This paper is supported by Science and Technology Project of China Southern Power Grid Corporation (090000KK52190230).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Azeroual, M., Lamhamdi, T., El Moussaoui, H., El Markhi, H. (2020). Intelligent energy management system of a smart microgrid using multiagent systems. Archives of Electrical Engineering, 69(1), 23–38. DOI 10.24425/aee.2020.131756. [Google Scholar] [CrossRef]

 2.  Adbabaie, A., Lin, J., Morse, A. S. (2003). Coordination of groups of mobile autonomous agents using nearest neighor rules. IEEE Transactions on Automatic Control, 48(9), 988–1001. DOI 10.1109/TAC.2003.812781. [Google Scholar] [CrossRef]

 3.  Liu, H. W., Sun, T., Zhong, C. Q. (2021). New results on consensus of multi-agent systems with time-varying delays: A cyclic switching technique. IEEE Access, 9, 91402–91409. DOI 10.1109/ACCESS.2021.3090782. [Google Scholar] [CrossRef]

 4.  Tan, C., Yue, L., Li, Y. (2021). Group leader-following consensus control for heterogeneous multi-agent systems with time delays. IEEE Access, 9, 72743–72758. DOI 10.1109/ACCESS.2021.3079814. [Google Scholar] [CrossRef]

 5.  Ren, W., Atkins, E. (2005). Second-order consensus protocols in multiple vehicle systems with local interactions. Proceeding of AIAA Guidance, Navigation, and Control Conference and Exhibit, pp. 3689–3701. San Francisco, USA. [Google Scholar]

 6.  Chu, H., Yue, D., Dou, C., Chu, L. (2021). Adaptive pi control for consensus of multiagent systems with relative state saturation constraints. IEEE Transactions on Cybernetics, 51(4), 2296–2302. DOI 10.1109/TCYB.2019.2954955. [Google Scholar] [CrossRef]

 7.  Xie, D. M., Wang, S. K. (2011). Consensus of second-order discrete-time multi-agent systems with fixed topology. Journal of Mathematical Analysis and Applications, 387(1), 8–16. DOI 10.1016/j.jmaa.2011.08.052. [Google Scholar] [CrossRef]

 8.  Franceschelli, M., Pilloni, A., Gasparri, A. (2021). Multi-agent coordination of thermostatically controlled loads by smart power sockets for electric demand side management. IEEE Transactions on Control Systems Technology, 29(2), 731–743. DOI 10.1109/TCST.87. [Google Scholar] [CrossRef]

 9.  Zhao, T., Man, Z., Bi, G. (2008). The research of electric load control system based on multi-agent. International Conference on Advanced Computer Theory and Engineering, pp. 482–486. Phuket. [Google Scholar]

10. Müller, S. C., Häger, U., Rehtanz, C. (2014). A multiagent system for adaptive power flow control in electrical transmission systems. IEEE Transactions on Industrial Informatics, 10(4), 2290–2299. DOI 10.1109/TII.2014.2315499. [Google Scholar] [CrossRef]

11. Cai, H., Hu, G. (2017). Distributed tracking control of an interconnected leader–Follower multiagent system. IEEE Transactions on Automatic Control, 62(7), 3494–3501. DOI 10.1109/TAC.2017.2660298. [Google Scholar] [CrossRef]

12. Liu, Y., Li, Y., Xin, H., Gooi, H. B., Pan, J. (2019). Distributed optimal Tie-line power flow control for multiple interconnected AC microgrids. IEEE Transactions on Power Systems, 34(3), 1869–1880. DOI 10.1109/TPWRS.59. [Google Scholar] [CrossRef]

13. Rasheed, M. B., Javaid, N., Arshad Malik, M. S., Asif, M., Hanif, M. K. et al. (2019). Intelligent multi-agent based multilayered control system for opportunistic load scheduling in smart buildings. IEEE Access, 7, 23990–24006. DOI 10.1109/ACCESS.2019.2900049. [Google Scholar] [CrossRef]

14. Liu, P., Chen, L., Ma, T., Bai, X., Xu, H. (2020). Multi-agent consensus control of distributed inverter Air conditioning load based on the demand response. 2020 39th Chinese Control Conference (CCC), pp. 6105–6110. Shenyang, China. [Google Scholar]

15. Olfati-Saber, R., Murry, M. (2004). Consensus problems in networks of agents with switching topology and time-delays. IEEE Transactions on Automatic Control, 49(9), 1520–1533. DOI 10.1109/TAC.2004.834113. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.