

 | Energy Engineering |  |
DOI: 10.32604/ee.2022.018033
ARTICLE
How Load Aggregators Avoid Risks in Spot Electricity Market: In the Framework of Power Consumption Right Option Contracts
1School of Economic and Management, North China Electric Power University, Beijing, 102206, China
2School of Economic and Management, Yan'an University, Yan'an, 716000, China
*Corresponding Author: Zhongfu Tan. Email: tanzhongfu@sina.com
Received: 05 July 2021; Accepted: 30 September 2021
Abstract: There is uncertainty in the electricity price of spot electricity market, which makes load aggregators undertake price risks for their agent users. In order to allow load aggregators to reduce the spot market price risk, scholars have proposed many solutions, such as improving the declaration decision-making model, signing power mutual insurance contracts, and adding energy storage and mobilizing demand-side resources to respond. In terms of demand side, calling flexible demand-side resources can be considered as a key solution. The user's power consumption rights (PCRs) are core contents of the demand-side resources. However, there have been few studies on the pricing of PCR contracts and transaction decisions to solve the problem of price forecast deviation and to manage the uncertainty of spot market prices. In addition, in traditional PCR contracts, PCRs are mostly priced using a single price mechanism, that is, the power user is compensated for part of the electricity that was interrupted or reduced in power supply. However, some power users might engage in speculative behaviours under this mechanism. Further, for load aggregators, their price risk avoidance ability has not substantially improved. As a financial derivative, options can solve the above problems. In this article, firstly, the option method is used to build an option pricing optimization model for power consumption right contracts that can calculate the optimal option premium and strike price of option contracts of power consumption rights. Secondly, from the perspective of power users and load aggregators, a simulation model of power consumption right transaction decision-making is constructed. The results of calculation examples show that (1) Under the model in this article, the pricing of option contracts for power consumption rights with better risk aversion capabilities than traditional compensation contracts can be obtained. (2) The decision to sell or purchase the power consumption rights will converge at respective high-value periods, and option contracts will expedite the process. (3) Option contracts can significantly reduce the loss caused by the uncertainty of spot electricity prices for load aggregators without reducing users’ willingness to sell power consumption rights.
Keywords: Load aggregator; demand response; power consumption right; option pricing; decision-making
The spot electricity market has the function of discovering the price of electricity commodities [1]. With the increase renewable energy generation, the proportion and position of the spot electricity market are also improving continuously [2,3]. Moreover, the power system has to maintain real-time balance between power supply and demand, which will inevitably lead to great uncertainty in the electricity prices of spot electricity market. For the participants of spot electricity market, how to make reasonable decisions has always been a controversial issue under the conditions of great price uncertainty and enormous instability of earnings.
Electricity retailers purchase electricity in the wholesale electricity market and sell it to power users in the retail electricity market [4]. The price uncertainty will cause electricity retailers to undertake price risks for their agent users [5–8]. In China, with the liberalization of retail electricity markets, the enthusiasm for the establishment of electricity-selling companies by social capital has risen unprecedentedly [7]. Until now, the number of electricity-selling companies registered through industrial and commercial operations has reached about 10,000. However, among such a large number of electricity retailers, very few are profitable. The main reason is that the electricity retailers have limited ability to foresee and avoid the risks brought by the uncertainty of spot market prices [6,7].
Electricity retailers represent power users to participate in market bidding. In essence, they are a type of load aggregator [4]. In order to allow load aggregators to reduce the spot market price risk, scholars have proposed many solutions, such as improving the declaration decision-making model[8–10], signing power mutual insurance contracts [11,12], adding energy storage [13–15] and mobilizing demand-side resources to respond [16–18]. In terms of demand response, the user's power consumption rights (PCRs) are core contents of the demand-side resources [19]. As a typical PCR contract [18,19], the purpose of interruptible load contracts is to alleviate power shortage or provide peak-regulating ancillary services [20,21], that is, to solve the forecast deviation quantity problem. However, there have been few studies on the pricing of PCR contracts and transaction decisions to solve the problem of price forecast deviation and to manage the uncertainty of spot market prices. In addition, in traditional PCR contracts, PCRs are mostly priced using a single price mechanism, that is, the power user is compensated for part of the electricity that was interrupted or reduced in power supply [22]. However, some power users might engage in speculative behaviours under this mechanism [23]. Further, for load aggregators, their price risk avoidance ability has not substantially improved [24]. As a financial derivative, options can solve the above problems [25,26]. Load aggregators can purchase PCRs by users to form option contracts, thereby achieving hedging in the face of the uncertainty in electricity spot prices.
Against the above background, this paper compares the price settlement and transaction mechanisms of PCR compensation contracts and PCR options contracts, and builds an option pricing model for PCR contracts to optimize option premium and strike price on the premise of increasing the power users’ willingness to sign option contracts and increasing the profitability of load aggregators. In addition, based on the PCRs transaction process, from the perspective of power users and load aggregators, the simulation model of PCRs transaction decision-making is constructed.
2 Option Pricing Mechanism for PCR Contracts
2.1 Pricing Mechanism of PCR Compensation Contracts
Under the principal-agent model, most of the retail electricity prices provided by load aggregators to users are pre-negotiated and at a relatively fixed price [22], and when the cost of purchasing electricity is higher than the price of selling electricity, load aggregators will bear the losses. To avoid the loss risk, load aggregators can sign PCR contracts with power users. In a traditional PCR contract (such as an interruptible load contract), the load aggregator submits an application for the purchase of PCRs to power users. Meanwhile, the users respond to the compensation price signal, provide the PCRs to the load aggregator, and receive compensation for the sale of PCRs. After the load aggregator obtains PCRs, the load aggregator can interrupt or reduce power supply of power users during the stipulated period of the contract. The load aggregator's unit retail electricity price is set to W, and the compensation for unit PCR is set to A, the transaction mechanism of compensation contracts of PCR is as shown in Fig. 1:
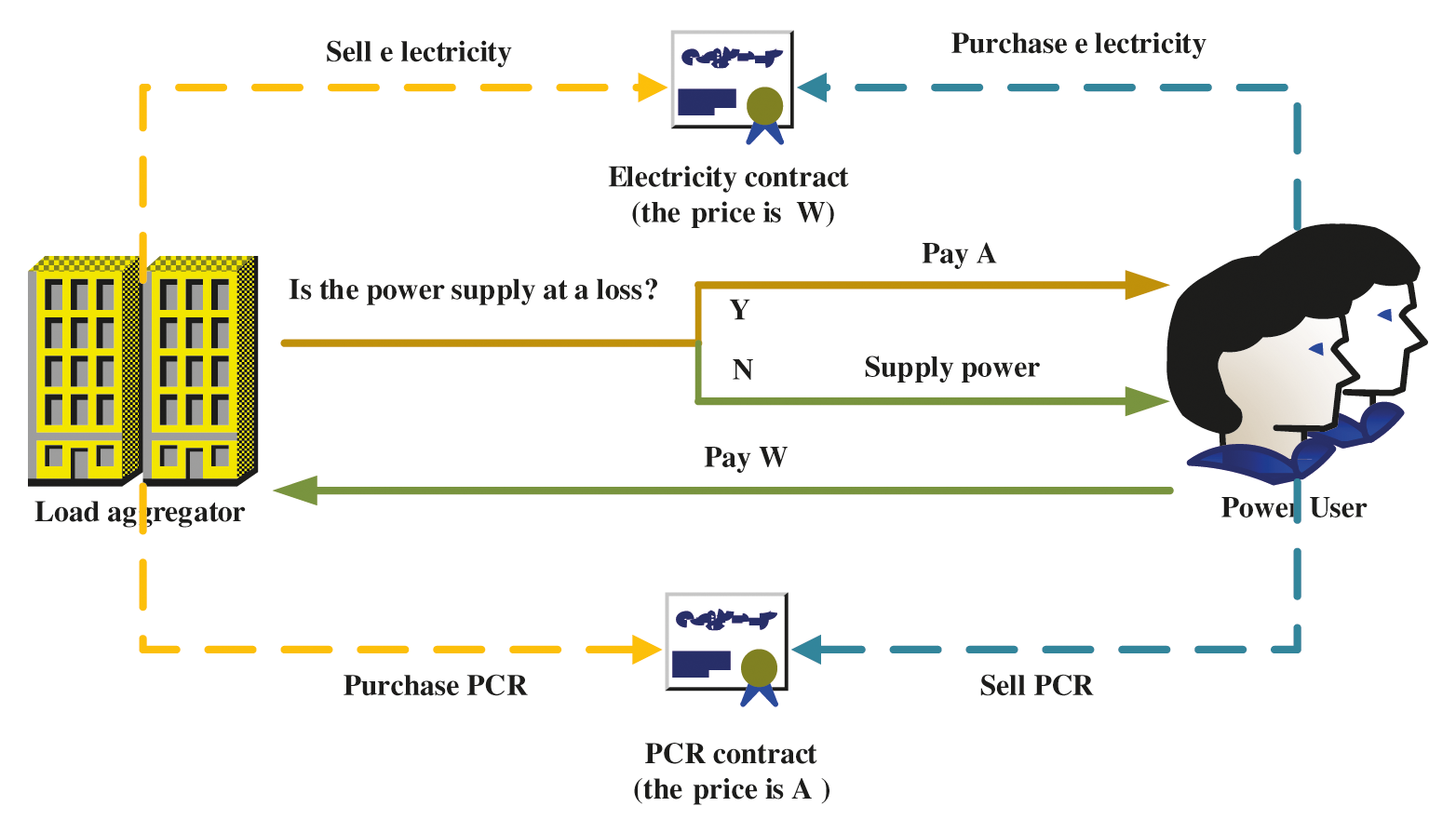
Figure 1: Transaction mechanism of compensation contracts of PCR
The compensation price of PCR is a very important part, which can determine the response degree of power users and further determine the level of risk avoidance of the load aggregator. Reasonable compensation prices will enhance the willingness of users to sign compensation contracts, further, the load aggregator will receive intended load cuts.
2.2 Pricing Optimization of PCR Contracts Based on Option Theory
Due to the real-time balance and non-transferability of electricity, the power users’ profits and losses of signing electricity option contracts are different from signing conventional option contracts. In conventional options, the maximum profit of the seller of the option is the premium of the option, and the minimum profit has no lower limit, which is based on the assumption that the value of the subject matter is the market price and it can vary flexibly. In fact, for users, the value of electricity is not its market price but the production benefit brought by using it, that is, users cannot sell electricity again at market prices, and they can only use electricity for production and operation activities. In the PCR option contracts, the unit electricity consumption benefit of user is set to V €, the unit option premium of PCR option contract is set to L €, and the unit strike price is set to K €, which represents the payment price of the user's unit load cut when the option is executed. The profits and losses of transaction of PCR option contracts are as shown in Fig. 2.
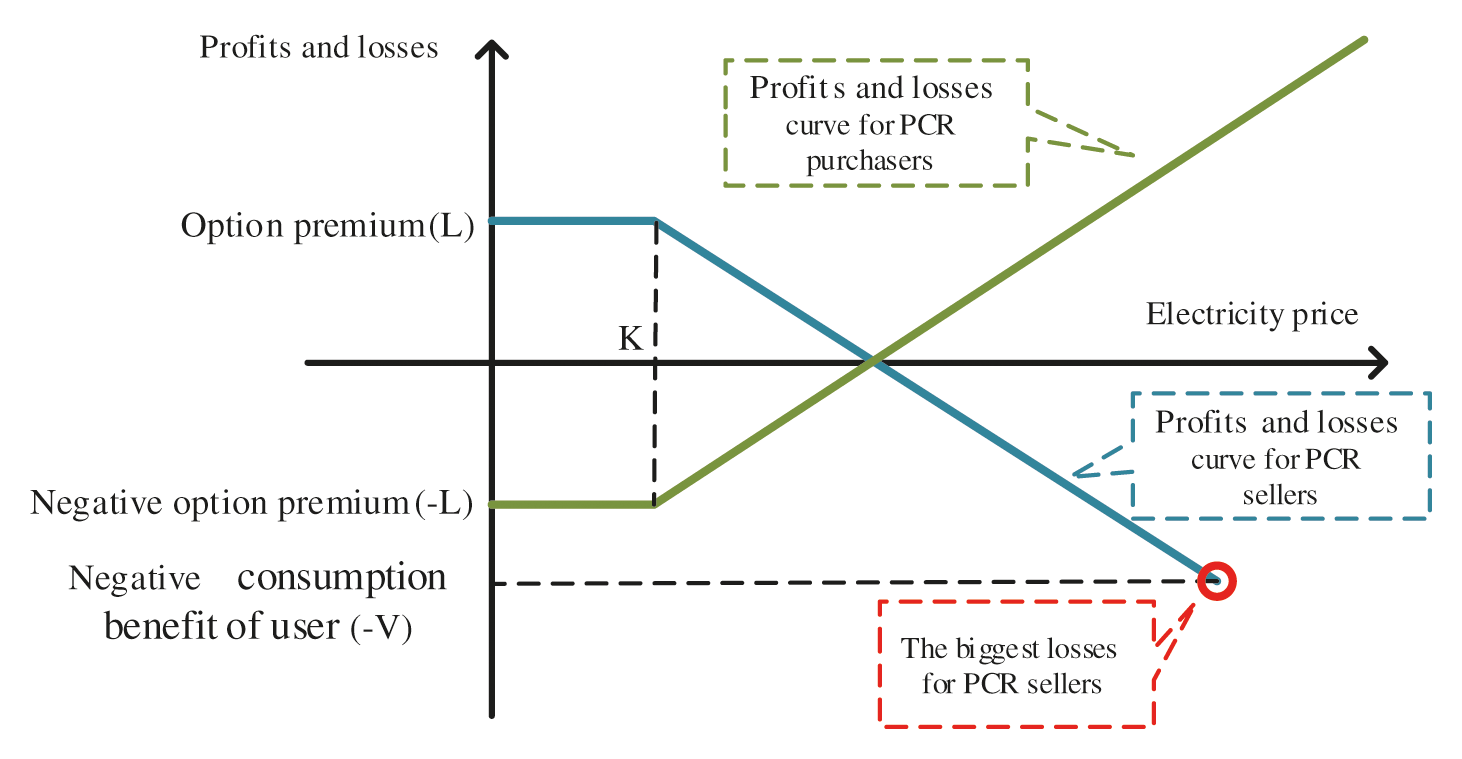
Figure 2: Profits and losses of transaction of PCR option contracts
After signing of an PCR option contract, load aggregator will pay the option premium to power user, which is used to pay the expenses needed for exercising the right to purchase PCRs, and the exercise of this right will reduce or interrupt the power supply of the user for a certain time. The load aggregator will pay for the cost of reducing or interrupting part of the power supply, and the cost is the strike price of the option. It can be seen that the PCR option is a call option essentially. So, the option is a real value option when the load aggregator's purchase and sale spread is greater than the option cost, the option is a binary option when the spread is equal to the option cost, and others are out-of-money options. The transaction mechanism of PCR option contracts is as shown in Fig. 3.
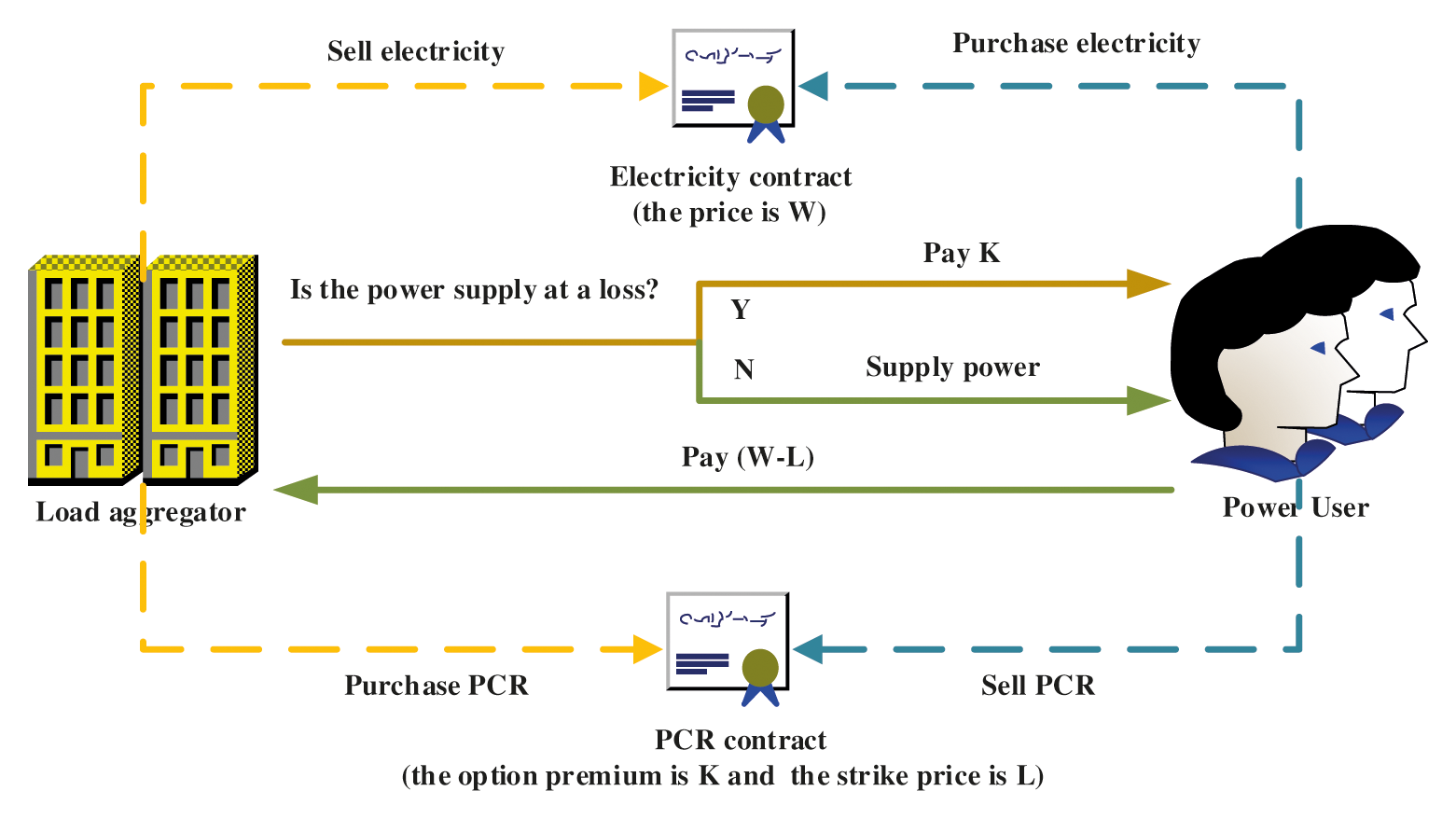
Figure 3: Transaction mechanism of PCR option contracts
For option pricing, in 1973, Black et al. proposed the famous Black-Scholes option pricing model [27], which is still very significant today. Subsequent scholars have proposed many improved option pricing models. As a whole, the existing option pricing method belongs to the category of statistics and measurement methods. However, the option pricing method from the perspective of statistics and measurement is not completely applicable to PCR contracts, for the following reasons:
1) The characteristics of the electricity price cannot be completely described by the geometric Brownian motion [28].
2) In the early stage of the development of the electricity market, the electricity market data are incomplete and random.
3) The load aggregator must consider the possibility of misreporting information from the perspective of power users.
Under the constraints of the above problems, this paper attempts to solve the problem of PCR option pricing through optimization ideas: determine the optimal PCR option pricing based on the compensation price, and ensure that load aggregators have better risk aversion capabilities without reducing power users’ willingness to sell PCRs.
3 Pricing Optimization Model for PCR Option Contracts
3.1 Selection of Optimization Methods and Generation of Price Data
The optimization method used in this paper is stochastic optimization method. The stochastic optimization method converts uncertainty optimization into deterministic optimization under a certain probability distribution through methods such as probability statistics and stochastic process analysis. The generation of random samples is the basis of stochastic optimization, which will generate specific sample data and probability distributions of uncertain variables [29]. The K-means method is a typical classification method for clustering, which can effectively process large-scale and high-dimensional datasets and perform efficient classification. The implementation steps of the K-means method are as shown in Fig. 4.
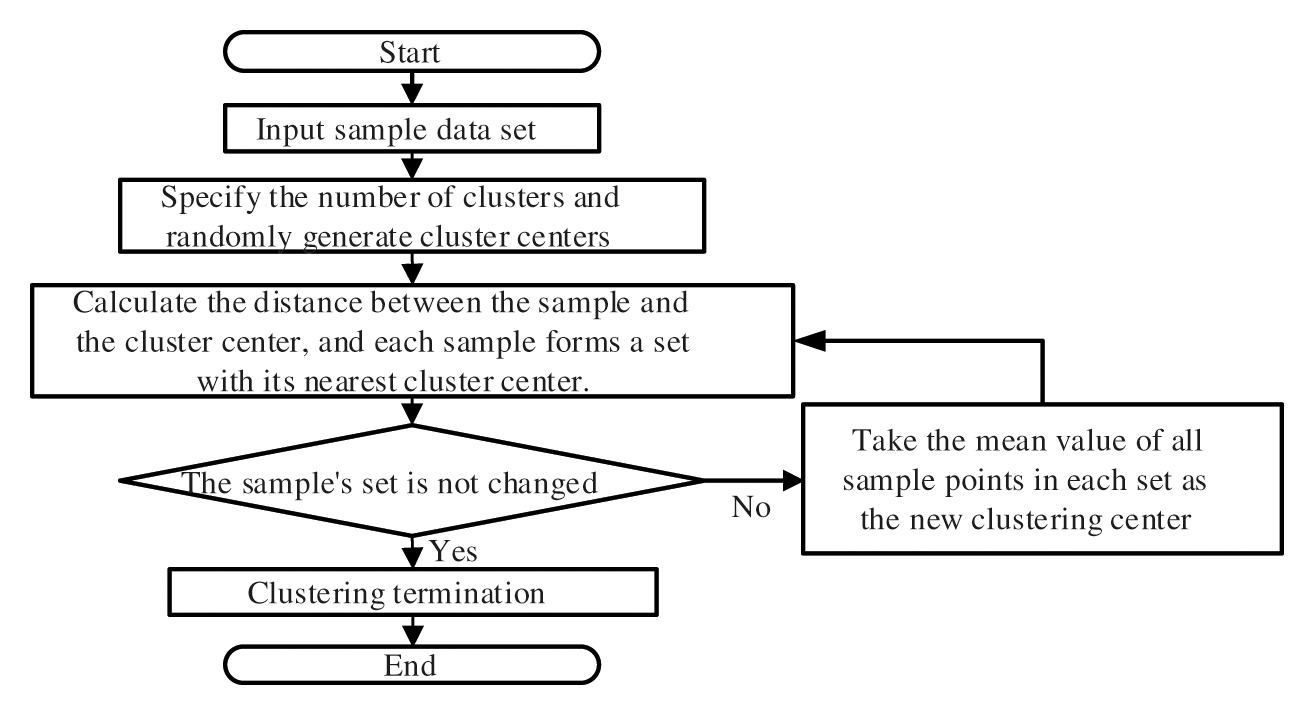
Figure 4: The process of K-means algorithm clustering
In this paper, the K-means method is used to iteratively find I clusters of electricity price sample data in spot electricity market, thus, the load aggregator can determine if the power supply of each time will lose. The final cluster centre of each cluster is used to represent the eigenvalues of random samples, and each characteristic value includes the spot electricity market price for 24 periods, thereby generating random probability samples.
3.2 Principles of Pricing Optimization Model for PCR Option Contracts
For the pricing optimization model, the following principles must be observed:
(1) Firstly, after the load aggregator and power users sign an PCR option contract, the contract can minimize losses caused by the price uncertainty of the spot electricity market. The unit electricity price in spot electricity market is set to R, and the unit power loss (positive value represents loss) brought to the load aggregator by the PCR option contracts is:
Based on the above, the goal is to minimize the sum of losses in all periods after the option contracts are signed between the load aggregator and power users, that is:
(2) Secondly, compared with compensation contracts, it is necessary to ensure that the power users’ willingness to sell PCRs after signing option contracts is unchanged or increased. The subjective psychological probability that the user believes the PCR will be exercised is set to
Under the option contracts, the profit that power users believe they may obtain by signing a PCR contract is:
Assuming that power users are rational, users are more willing to choose an option contract than a compensation contract when
(3) Finally, it should be ensured that option contracts of PCRs can enhance the risk aversion capability of load aggregator compared with compensation contracts. Therefore, the principle must be followed that the performance of option contract is better than compensation contract in terms of the expected value of the unit loss of load aggregator under the uncertainty of spot electricity price, and the specific constraints are as follows:
where,
3.3 Pricing Optimization Model for PCR Option Contracts
The optimization goal for load aggregator is to determine the optimal option premium and strike price of PCR option contracts to minimize expected loss. Therefore, the objective function is set to:
where, I represents the number of random samples, and
Constraints mainly include power users’ incentive constraints, risk loss constraints, upper and lower limit constraints on option premiums and strike prices. Among them, users’ incentive constraints are discussed above, and the constraints can be expressed as:
where,
Since
Since
where, D represents the measurement period, and
For
where,
The PCR contracts are designed from the perspective of maximizing the profit of the load aggregator. When PCRs are exercised, they can be considered to be beneficial to load aggregator and relatively unprofitable to power user. If the power user fully responds, that is, when the aforementioned ideal state of the load aggregator (
To ensure that the PCR option contracts can improve the risk avoidance ability of load aggregator, also to meet the risk loss constraints of the above principle (3), it is necessary to meet the minimum expected value of losses after the option contracts are signed, and the constraints can be expressed as:
In addition, the upper limit of the option premium and strike price should not exceed the compensation price, and the lower limit can be set to a constant greater than 0, and the constraint conditions can be expressed as:
So far, the objective function of the constructed pricing optimization model for option contracts of PCR is Eq. (8), and the constraint conditions include Eqs. (9)–(10) and (16)–(18).
4 Simulation Model of Transaction Decision-Making for PCR Option Contracts
4.1 Transaction Process and Characteristics for PCR Option Contracts
To meet the transaction characteristics of traditional compensation PCR contracts and avoid the inefficiencies caused by repeated signing of contracts, the load aggregator sign 24-h PCR option contracts for the next day with the power users in one day ahead. The transaction steps are as shown in Fig. 5.
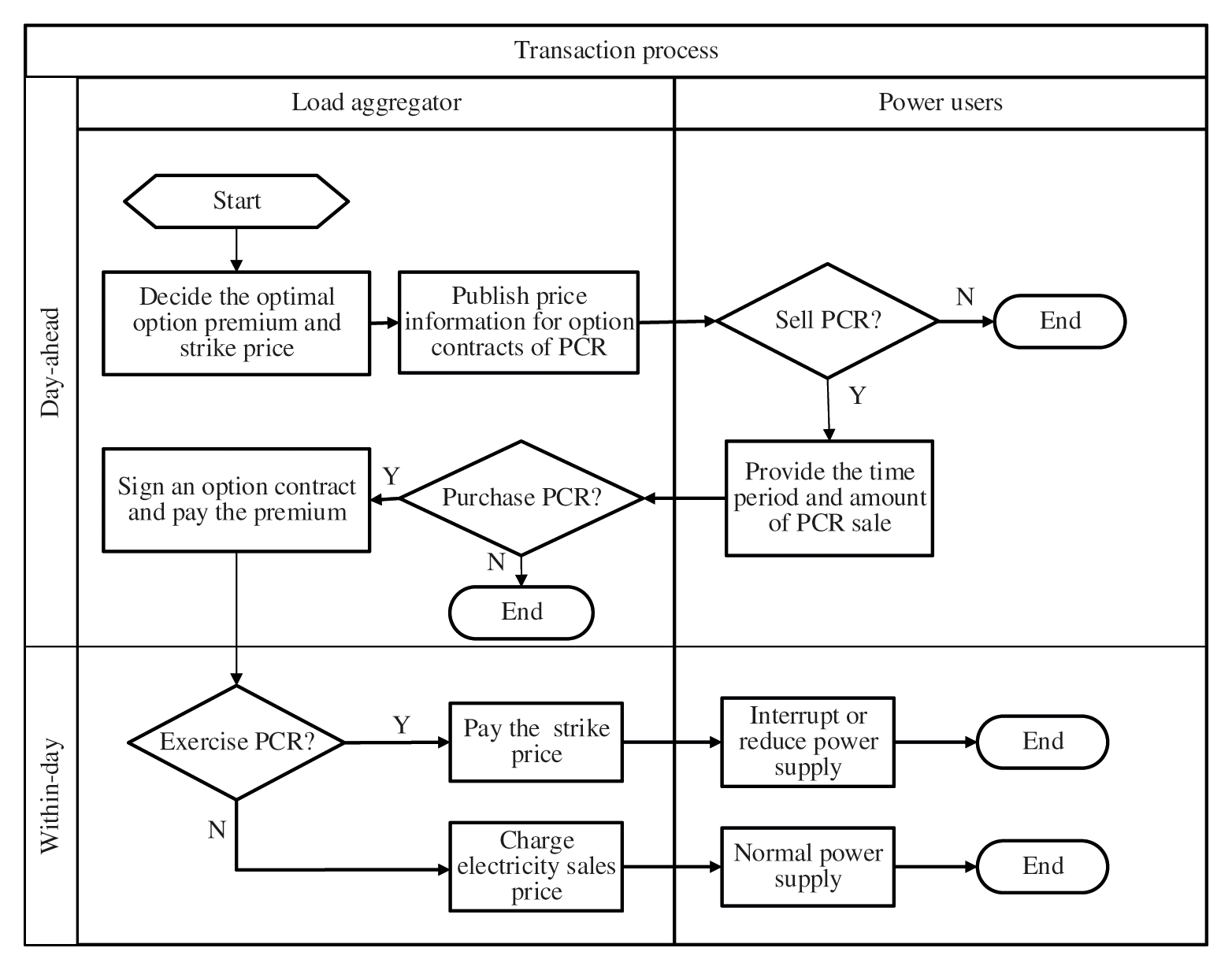
Figure 5: The specific transaction steps of option contracts for PCR
4.2 Simulation Model for Power Users’ Transaction Decision-Making of PCR Contracts
Power users do not care about the price of the wholesale electricity market, and they only care about the retail electricity price set by the load aggregator. Therefore, after the load aggregator sets the option premium and strike price of the option contracts, users only need to consider the profits and losses from the sale of PCRs to determine whether to sell them.
In the traditional PCR compensation contracts, when the contract is signed, the profit (positive value) or loss of the unit electricity of the power users is:
where, PL represent the profit (positive value) or loss of the unit electricity of the power users in the traditional PCR compensation contracts.
In the traditional PCR compensation contracts, since each power user makes decisions independently and does not interfere with the others, the objective function for power users’ transaction decision-making can be set to the maximum sum of the profits of all users participating in the transaction of compensation contracts, as:
In the transaction of PCR option contracts, the unit electricity profit (positive value) or loss of the power users is:
where, PC represent the unit electricity profit (positive value) or loss of the power users when signing the option contracts.
In the transaction of PCR option contracts, the objective function of the simulation model for power users’ transaction decision-making is to maximize the profit of the PCRs sold by power users, as:
where,
The constraint conditions include total users’ power loss constraints, PCR sales duration constraints, and total PCR sales duration constraints. The last two items should be stipulated in the PCR contracts. Power users must make decisions in conjunction with the contract content. The total users’ power loss constraints indicate that, after a user sells PCRs in one day, the total amount of interrupted or reduced electricity should be less than the maximum amount that the user can bear:
where
The constraints on the duration of PCRs sales means that the sum of the periods during which the power users continue to sell the PCRs cannot exceed the maximum limit:
where
Constraints on the total duration of the sale of PCRs represent the sum of the allowed sale durations in a day. This constraint is used to prevent some power users with low power efficiency from using the PCR contracts to speculate:
where
4.3 Simulation Model for Load Aggregator's Transaction Decision-Making of PCR Contracts
After obtaining the relevant information (including time periods and capacity) of the power users’ PCRs that can be sold, the load aggregator will combine the predicted electricity price in the intraday electricity market to determine the purchase period and purchase amount of each power user's PCR. Under the compensation PCR contract, the objective function is as follows:
where
In the PCR option contracts, the goal of the load aggregator is to maximize the total value of the PCR option contracts. The decision objective is as follows:
Constraints include constraints on the purchase of the amount of PCRs in each time period, constraints on the total amount of power reduction, and constraints on the power users’ PCRs selling decisions.
Constraints on the purchase of the amount of PCRs in each time period mean that the amount of PCRs purchased by the load aggregator in each time period cannot exceed the saleable amount of PCRs declared by the power users:
The constraints on the total amount of power reduction mean that the total power reduction caused by the load aggregator's purchase of PCRs cannot exceed the maximum limit. The total power reduction should not exceed the electricity purchase amount in the intraday market. Otherwise, it will have an impact on the load aggregator's electricity purchase plans in the medium and long-term markets and the day-ahead market, resulting in deviation penalty costs [30]. Therefore, this constraint can be expressed as:
where
Constraints on the power users’ PCRs selling decisions mean that the load aggregator can only purchase PCRs for the periods when power user has agreed to sell:
Because the objective function of the above model is a non-convex function, and constraints (30)–(31) are non-linear constraints, it is difficult to solve. Further, regarding practical problems, the load aggregator represents a large number of power users conducting electricity transactions. The decision-making dimension is high, and it is easy to fall into a curse of dimensionality. The option model is converted to achieve a simple solution. The transformed model is as follows:
The transformed models (32)–(35) are equivalent to (28)–(31). The objective function and constraints are linearized by transferring nonlinear items in the objective function to constraints, and they can be solved by Matlab Yalmip Toolbox. The decision-making model of compensation contracts can be transformed in the same way.
This paper uses the hourly clearing price in the Nord Pool market from 01 January 2017 to 31 December 2017 as the original data and uses IBM SPSS Statistics software to perform K-means clustering in the intraday period of the above 8,760 time periods. As shown in Fig. 6, 10 groups of samples are generated through clustering. Meanwhile, the corresponding probability values of different samples are calculated, as shown in Fig. 7.
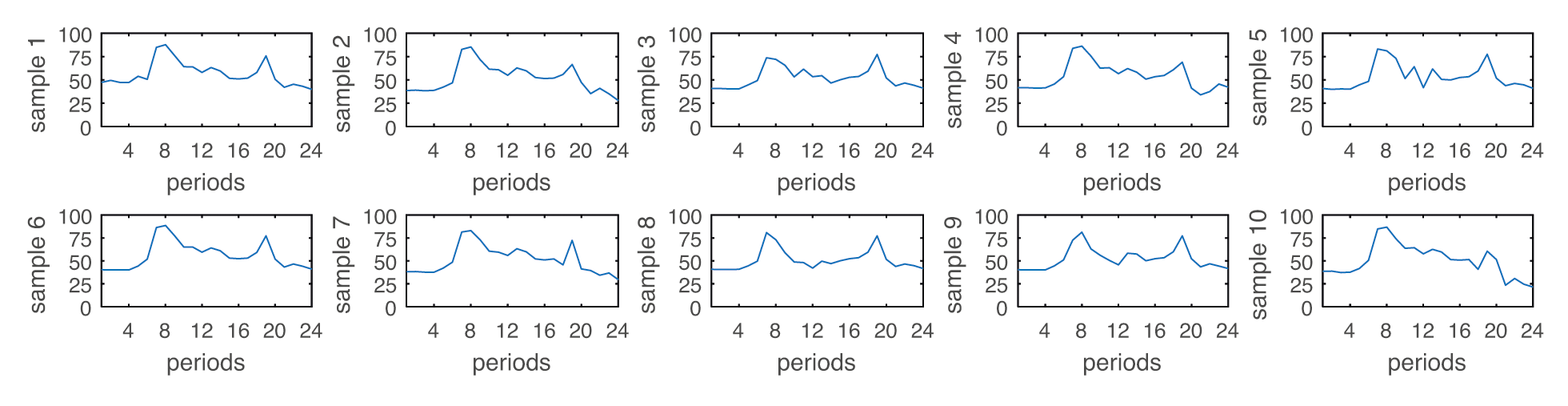
Figure 6: Price clustering results of spot electricity market (MW)
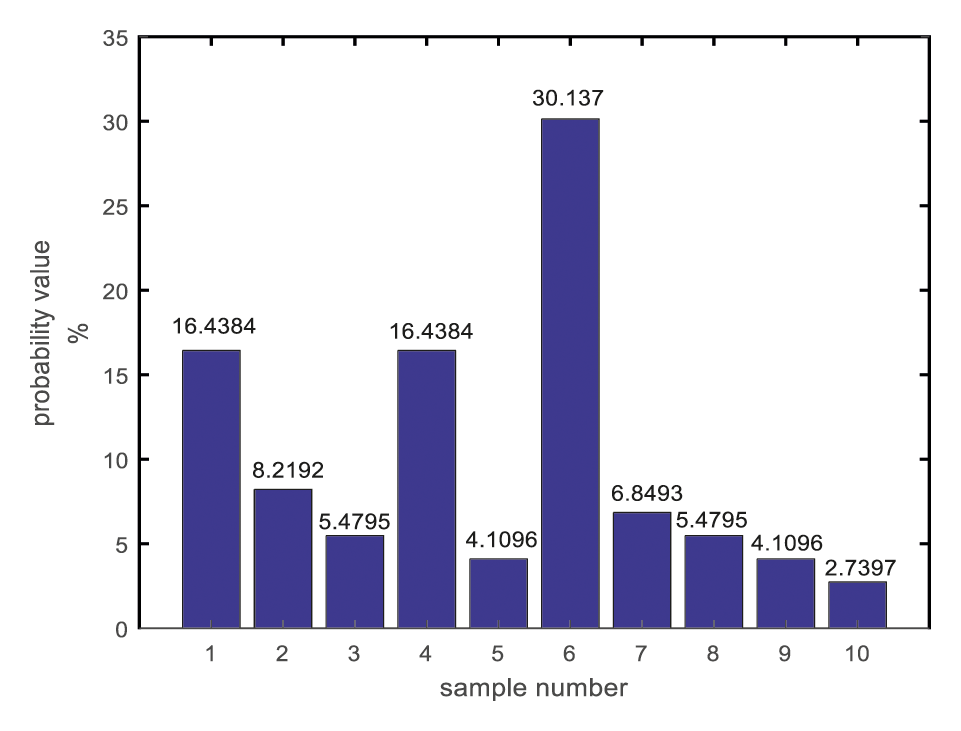
Figure 7: The probability of occurrence of each sample
From the clustering results (Fig. 6), it can be seen that the peak time of the hourly clearing prices in the intraday electricity market is around periods 7–9 and 19, the flat time is around periods 10–18, and the off-peak time is around periods 1–6 and 20–24. Sample 1, Sample 4 and Sample 9 have the highest appearance probability. The retail electricity price data is known to input data, as shown in Table 1.
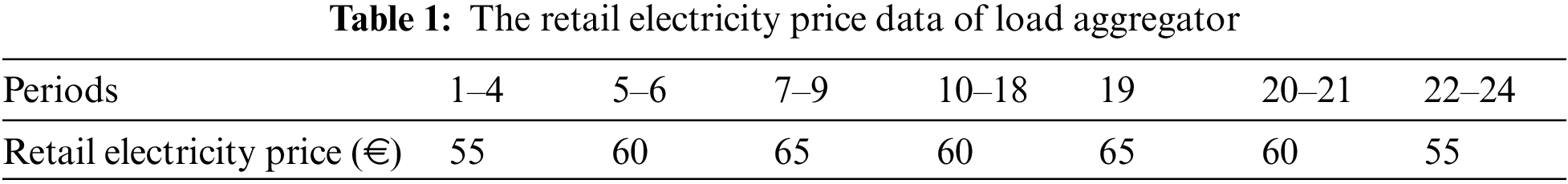
5.2 The Optimization Result of Option Prices of PCR Contracts
In order to more in line with the actual situation, the subjective psychological probability of the most conservative power user regarding the exercise of PCR is set to 0.6, the minimum option premium and strike price are set to one-fifth of the compensation price. Through the calculation of the pricing optimization model for PCR option contracts, the optimal option premium and strike price can be obtained, as shown in Fig. 8.
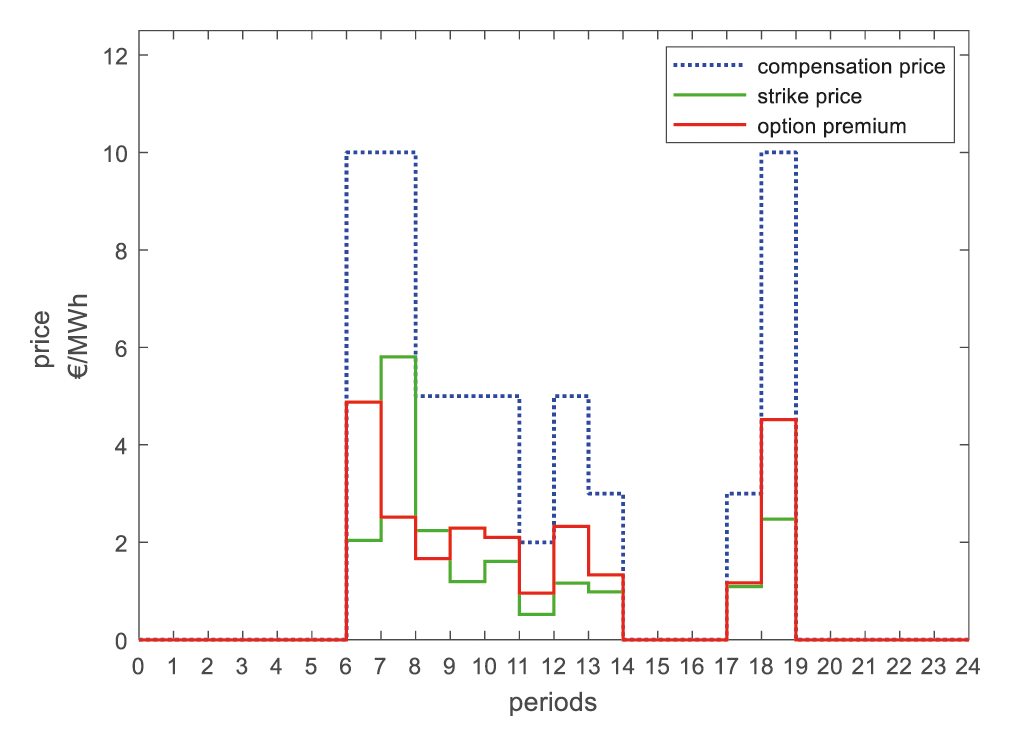
Figure 8: Optimization results of the option premium and strike prices
The sum of the option premium and strike price is generally cheaper than the compensation price because the option premium is a risk-free profit to power users, which is valuable for users. In the compensation mode, the loss reduction of the unit power supply of the load aggregator in a certain period is
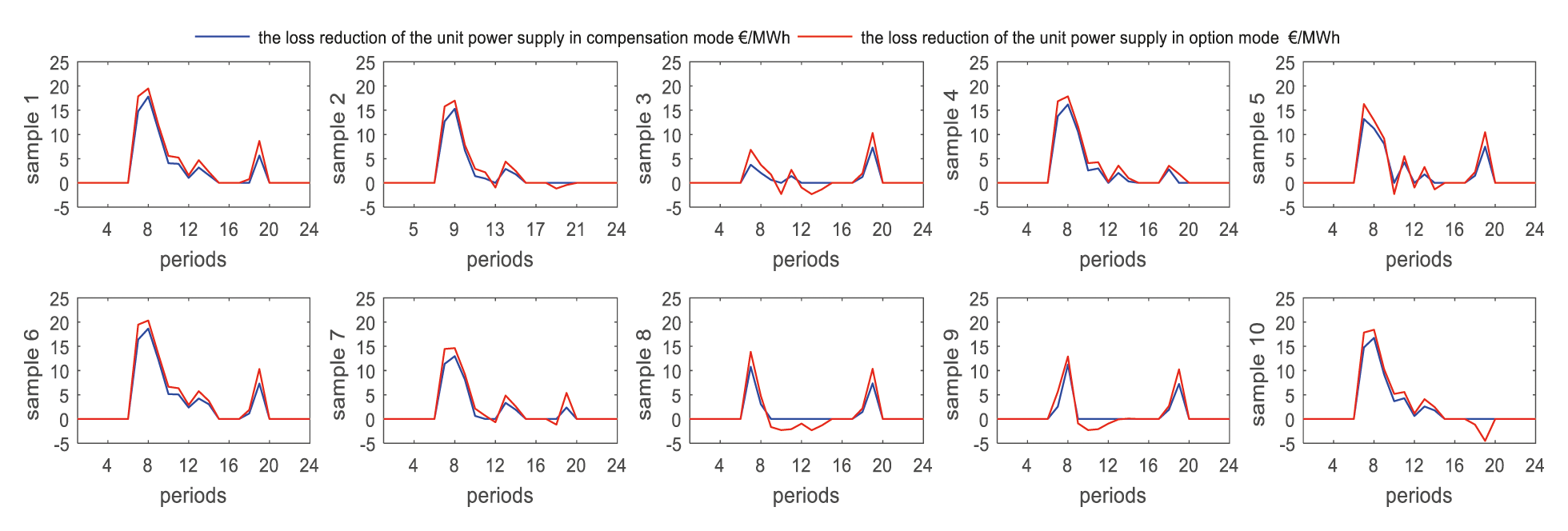
Figure 9: The loss reduction of the unit power supply of load aggregator in each sample
As seen from the figure, in each period of Sample 1, Sample 4 and Sample 6, the loss reduction of the unit power supply caused by the option contracts is greater than (or equal to) the loss reduction of the unit power supply caused by the compensation contracts. That means under the option PCR contracts, the load aggregator can decrease its losses caused by the uncertainty of the electricity price in the spot electricity market. The total probability of occurrence of these three samples is 63%. That is to say, the probability that the value of the option contracts is greater than (or equal to) the value of the compensation contracts at all times of the day is 63%.
As shown in Fig. 10, the value of the PCR contracts is the largest in periods 7–9. The expected values of loss reduction caused by option contracts is greater than (or equal to) compensation contracts. Under the assumption that the probability distribution of future is consistent with that of past in stochastic optimization, option contracts can improve the ability for the load aggregator to avoid the spot price risk compared to the compensation contracts, which is also consistent with the third pricing principle (The load aggregator must consider the possibility of misreporting information from the perspective of power users). Therefore, it is recommended that load aggregators use option contracts to improve risk aversion capabilities and obtain better utilization than to give power users compensation for selling PCRs.
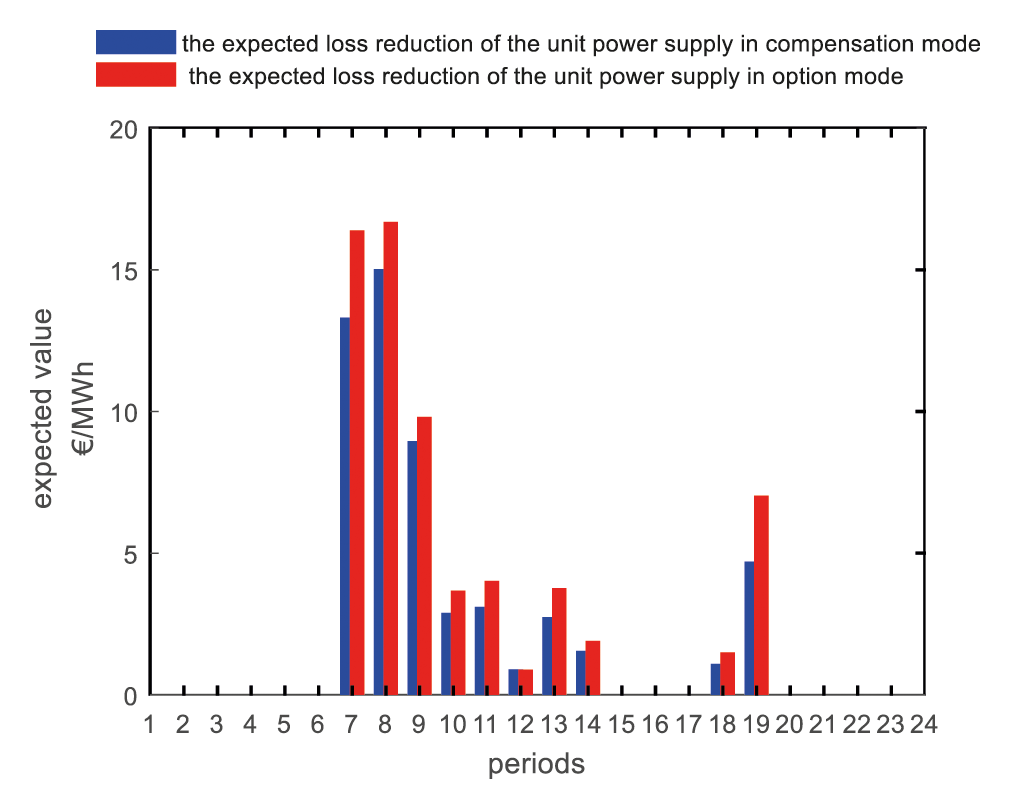
Figure 10: The expected loss reduction of the unit power supply of load aggregator
5.3 The Simulation Result of Transaction Decision-Making of PCR
It is assumed that there are four power users. To simplify the calculation and form a better control experiment scenario, it is assumed that the capacity of the four power users’ PCRs that can be sold in each period is 6 MW, the maximum duration of the PCRs that can be sold by the users is 5 h, the maximum total duration of the PCRs that can be sold by the load aggregator for each user is 8 h, the total load of the PCRs purchased for each power user is not more than 18 MW, and the maximum total amount of the PCRs purchased shall not exceed 72 MWh. Under the above data settings, four groups of scenarios are established as follows:
Compensation contracts scenario 1: The subjective psychological probabilities that the four power users believe that the PCRs will be exercised are 0.6, 0.55, 0.45, and 0.4, respectively, and the unit electricity consumption benefit of all four power users is 350 €/MWh. The power users and the load aggregator sign compensation contracts to trade PCRs.
Option contracts scenario 2: The subjective psychological probabilities of four power users are 0.6, 0.55, 0.45, and 0.4, respectively, and the unit electricity consumption benefit of all four power users is 350 €/MWh. The power users and load aggregator sign option contracts to trade PCRs.
Compensation contracts scenario 3: The subjective psychological probability of all four users is 0.4, and the unit electricity consumption benefit for the four power users are 350 €/MWh, 300 €/MWh, 250 €/MWh, and 200 €/MWh. The power users and load aggregator sign compensation contracts to trade PCRs.
Option contracts scenario 4: The subjective psychological probability of all four users is 0.4, and the unit electricity consumption benefit for the four power users are 350 €/MWh, 300 €/MWh, 250 €/MWh, and 200 €/MWh. The power users and load aggregator sign option contracts to trade PCRs.
As shown in Fig. 11, the results being presented are the solutions of the optimization problem (20) under the constraints (24)–(26). In scenario 1, power user 1 and power user 2 choose not to sell the PCRs, it was found that the subjective psychological probabilities of power user 1 and power user 2 are both greater than 0.5, and they are more inclined to believe that the PCRs will be exercised after the sale. Through calculation, power user's expected profit of compensation contract for each period (expressed as

Figure 11: The strategy for power users to sell PCRs in scenario 1
Based on the application results of power users in scenario 1, the load aggregator chooses to sign compensation PCR contracts with power user 3 in periods 7–8 and 18 and signed compensation contracts with power user 4 in periods 7–9 as shown in Fig. 12, the results being presented are the solutions of the optimization problem (32) under the constraints (33)–(35). Compared with Fig. 10, he expectations of the value of compensation contracts at each time period (expressed as
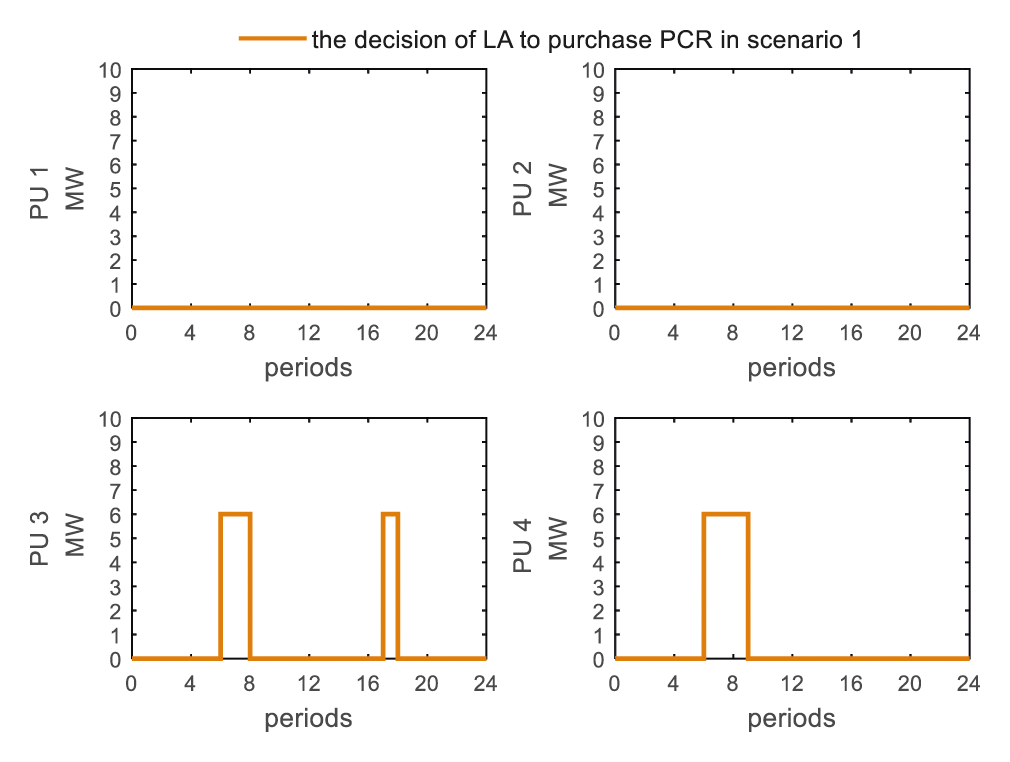
Figure 12: The strategy for load aggregator to purchase PCRs in scenario 1
As shown in Fig. 13, the results being presented are the solutions of the optimization problem (23) under the constraints (24)–(26). In scenario 2, power user 1 and power user 2 chose not to sell the PCRs, and their expected profit of the option contract for each period (expressed as
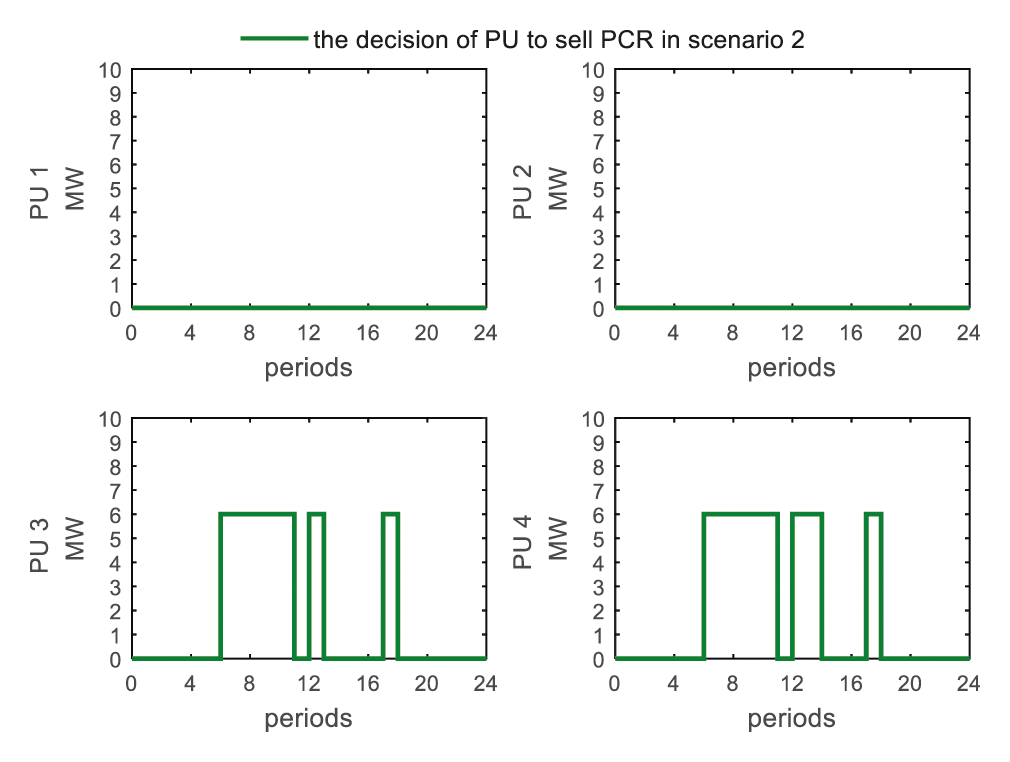
Figure 13: The strategy for power users to sell PCRs in scenario 2
Based on the application results of power users in scenario 2, the load aggregator chooses to sign option PCR contracts with power user 3 and power user 4 in periods 7–9 as shown in Fig. 14, the results being presented are the solutions of the optimization problem (32) under the constraints (33)–(35). Compared with scenario 1, under the option mode, the time periods for the load aggregator and power user 3 to sign the PCR contracts are changed from 7–8 and 18 to 7–9, and it has been calculated that PU's perception of profit under the options contracts for each period (expressed as
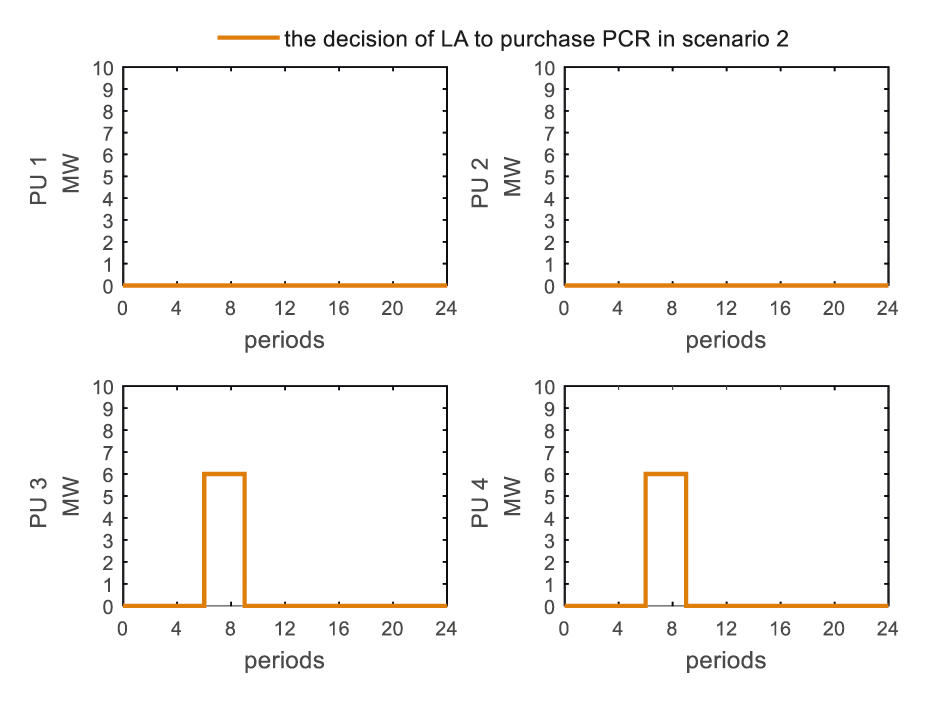
Figure 14: The strategy for load aggregator to purchase PCRs in scenario 2
As shown in Fig. 15, the results being presented are the solutions of the optimization problem (20) under the constraints (24)–(26). Power user 1 chooses to sell PCRs in periods 7–8 and 18. Power user 2 chooses to sell PCRs in periods 7–11, 13, and 18. Power user 3 and power user 4 choose to sell PCRs in periods 7–11, 13–14, and 18. With other conditions unchanged, as the power user's unit electricity consumption profit decreases, the power user's willingness to sell PCRs increases, that is because the user with lower unit electricity consumption benefits will have larger expected profit of the compensation contract for each period (expressed as
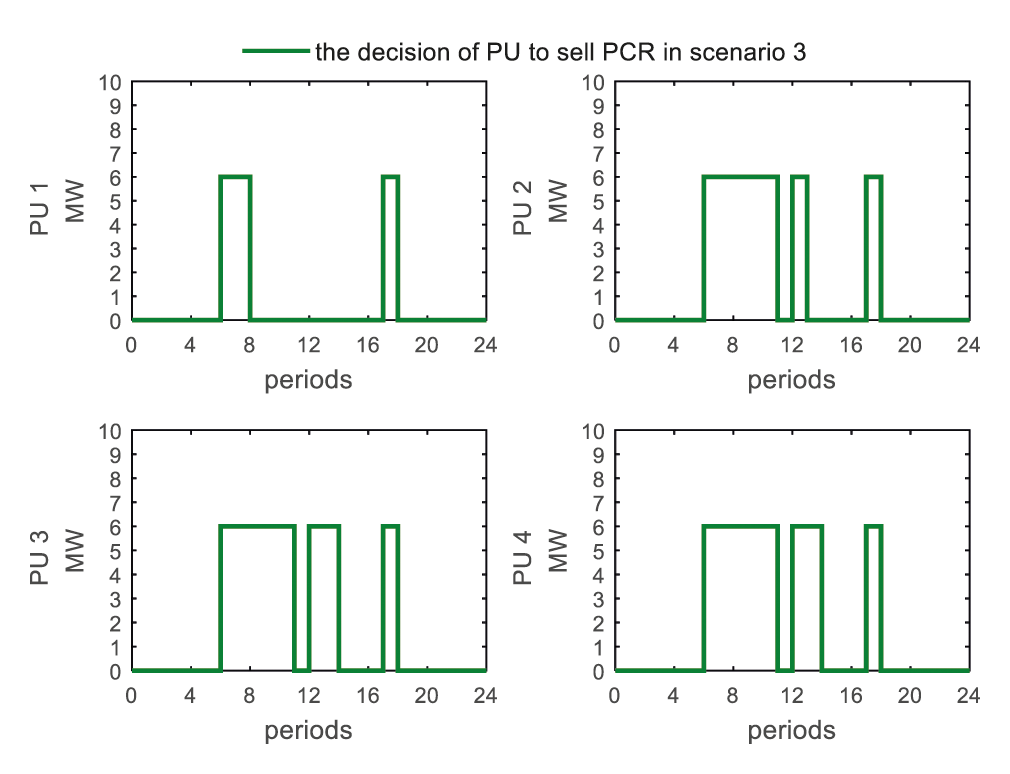
Figure 15: The strategy for power users to sell PCRs in scenario 3
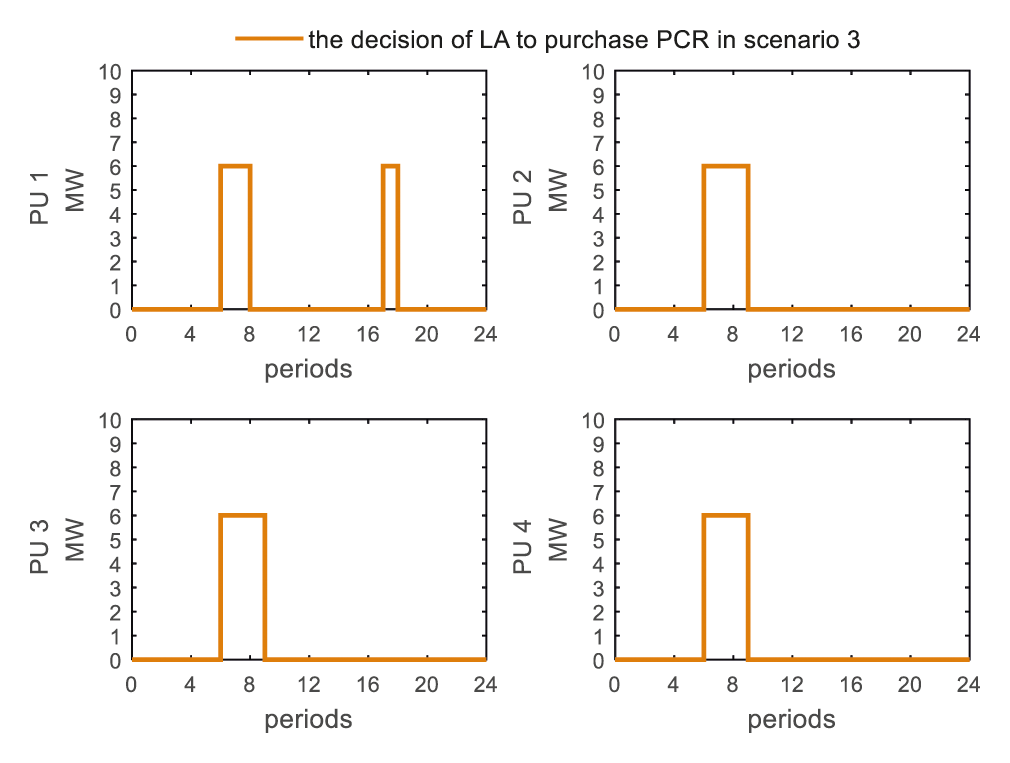
Figure 16: The strategy for load aggregator to purchase PCRs in scenario 3
As shown in Fig. 17, the results being presented are the solutions of the optimization problem (23) under the constraints (24)–(26). In scenario 4, power user 1 chooses to sell PCRs in periods 7–11, 13, and 18. Power user 2, power user 3 and power user 4 choose to sell PCRs in periods 7–11, 13–14, and 18. Compared with scenario 3, the power user is more willing to sign option contracts to sell PCRs with other conditions unchanged. As the power user's unit electricity consumption benefit decreases, the power user's willingness to sell PCR increases, that is because the power user with lower unit electricity consumption benefit will have larger expected benefit of the option contract for each period (expressed as
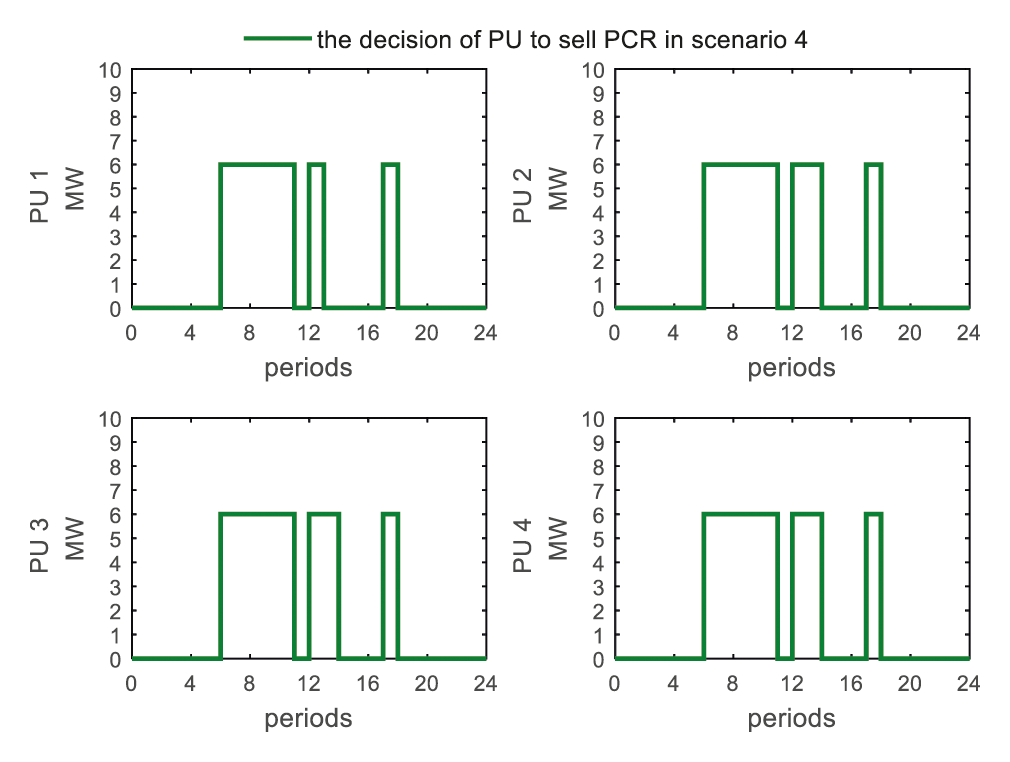
Figure 17: The strategy for power users to sell PCRs scenario
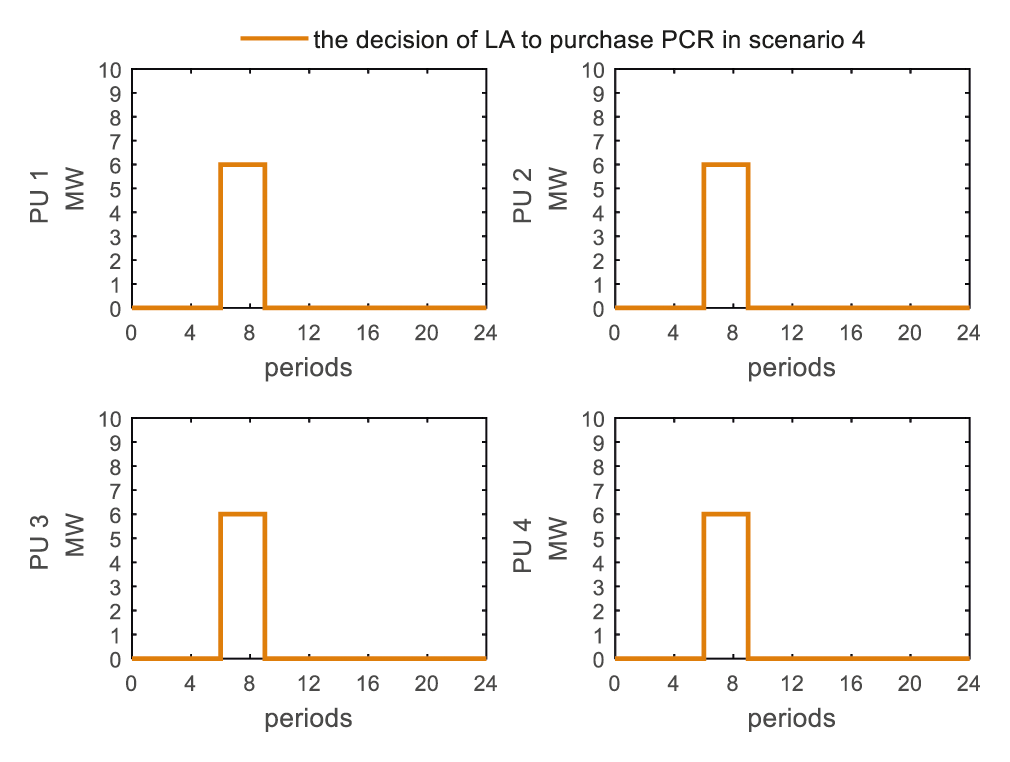
Figure 18: The strategy for load aggregator to purchase PCRs in scenario 4
In summary, the decision to sell PCRs of power users and the decision to purchase PCRs of load aggregator will converge to their respective high-value periods, and PCR option contracts will speed up the process. Compared with the compensation contracts, the PCR option contracts can significantly increase the power users’ willingness to sell PCRs, thereby providing higher value purchase options for load aggregators.
5.4 Sensitivity Analysis of Power Users’ Decision-Making
Further, in the option mode and the compensation mode, the power user's decision-making behaviour in PCR sales is analyzed. The power user's unit electricity consumption benefit V and subjective psychological probability
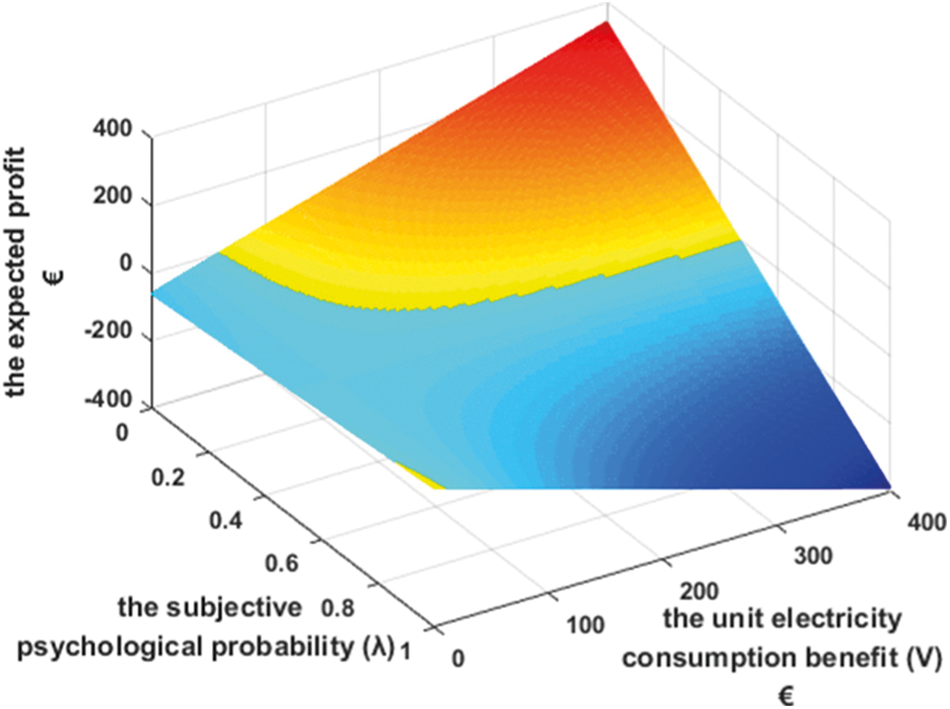
Figure 19: The expected profit of power user signing compensation contracts
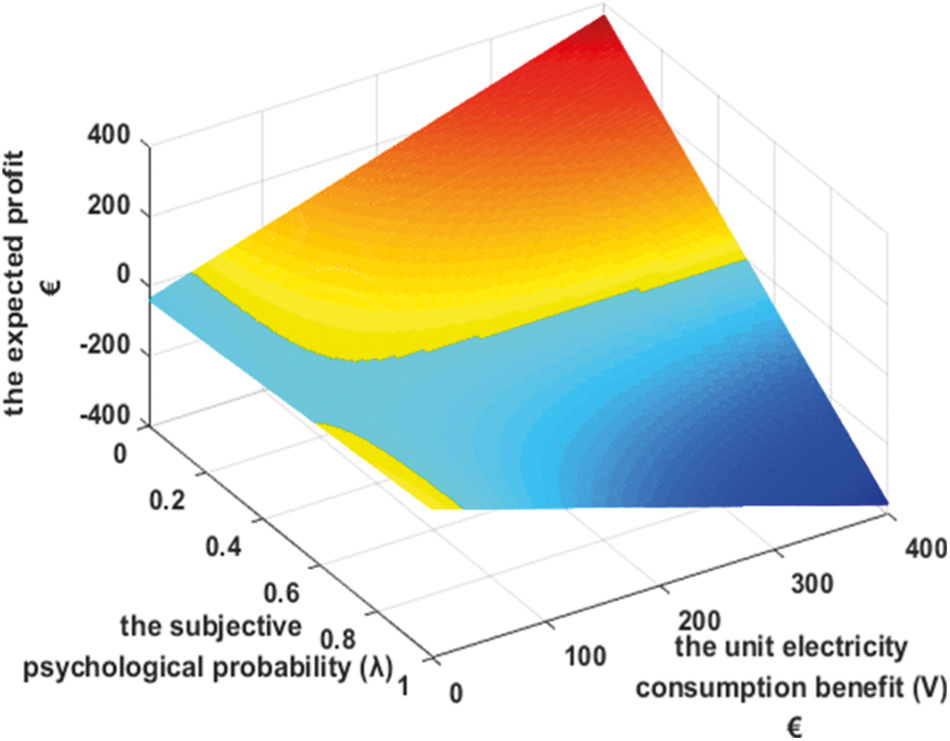
Figure 20: The expected profit of power user signing option contracts
Users with high unit electricity consumption benefit are more inclined to sell PCRs in the subjective psychological probability interval of [0, 0.5]. In addition, the willingness of users with high unit electricity consumption benefit to sell PCRs is negatively correlated with the subjective psychological probability within the probability interval of [0, 0.5]. Users with low unit electricity consumption benefit are more inclined to sell PCRs in the subjective psychological probability interval of [0.5, 1], and the willingness of users with low unit electricity consumption benefit to sell PCRs is positive correlated with the subjective psychological probability within the probability interval of [0.5, 1].
Compared with the compensation contract, more power users will choose to sign option contracts to sell PCRs, and the expected profit of signing an option contract with the same user is greater than the expected profit of signing a compensation contract. Considering the subjective psychological probability of 0.4 as an example, when the users’ unit electricity consumption benefit is 75 €/MWh, the users choose not to sell PCRs under the compensation contract mode in the seventh period, but they choose to sign option contracts for selling PCRs, the reason of the differences in users’ decision-making.
5.5 The Profits and Losses of Power Users and Load Aggregator
This section takes the 7–9 periods as the analysis object to analyse the exercising of PCR and the actual returns of the load aggregator based on the transaction results with power user 4 (the unit electricity consumption profit is 200 €/MWh).
Table 2 shows the exercise of PCRs in periods 7–9 after load aggregator signed the compensation contracts with power user 4. In this Table 1 indicates that PCRs are exercised, and 0 indicates that PCRs are not exercised, and the criterion is that they will be exercised when the value of compensation contracts (expressed as

Table 3 shows the exercise of PCRs in periods of 7–9 after the load aggregator and power user 4 signed the option contracts. The criterion is similar to compensation contract (

We further analyze the actual profit of load aggregator in the three cases of no PCR transaction, signing of PCR compensation contracts, and signing of PCR options contracts. As shown in Fig. 21, in the case of signing option contracts, the actual profits obtained by load aggregator in periods 7–9 are −12.15 €, −31.11 €, and −14.54 €. The option contracts can significantly reduce the loss caused by the uncertainty of electricity prices in spot electricity market to load aggregator without reducing the power users’ willingness to sell PCRs, which will increase the profitability of the load aggregator. That is because load aggregators can obtain accurate electricity price information in spot electricity market so that they can make fully rational decisions about the exercise of PCR. The inequality of information causes the load aggregator to be at an advantage in the transaction of PCRs. Therefore, the PCR option contracts designed by the load aggregator can obtain a higher profit than the compensation contracts on the premise of protecting the power users’ purchase intentions.
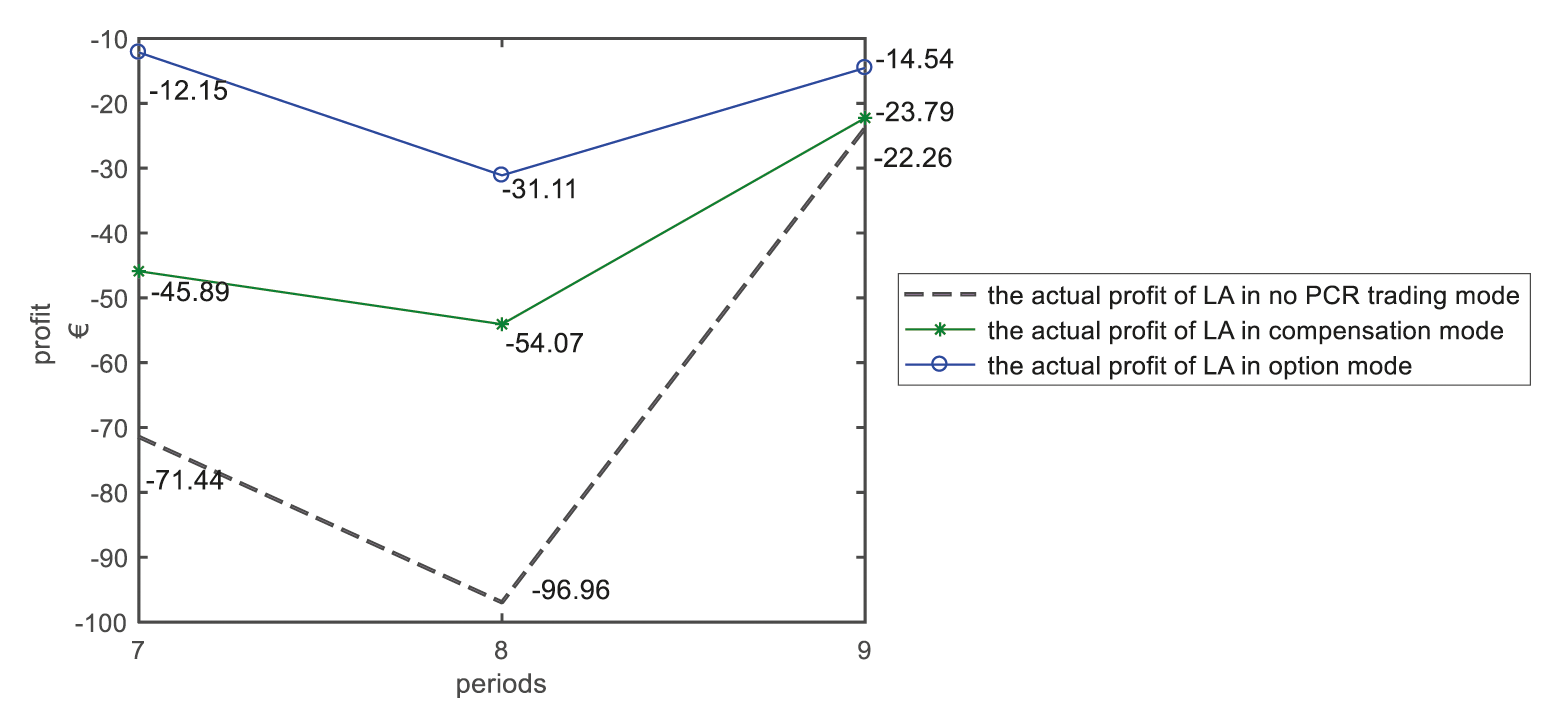
Figure 21: The actual profit of load aggregator's transaction with power user 4 in 7–9 periods
In the case of spot electricity price with large uncertainty, to address the issue of effective risk aversion for load aggregators, this paper considers what the load aggregator calls flexible demand-side resources, and constructs an option pricing model for PCR contracts on the premise of increasing the power users’ willingness to sign option contracts and increasing the profitability of load aggregators. Then, the simulation model of PCRs transaction decision-making is constructed. The results of the research indicate the following:
(1) Since the option contracts perform better in terms of the expected value of loss reduction of the unit power supply, compared to the compensation contracts, option contracts can further improve the ability of load aggregators to avoid the risk of electricity prices’ uncertainty in spot electricity market.
(2) The option contracts designed in this paper can significantly increase the power users’ willingness to sell PCRs. The decision to trade the PCRs will converge at respective high-value periods, and option contracts will expedite the process.
(3) On the profits and losses of PCR contracts, optimized option contracts can significantly reduce the loss caused by the uncertainty of electricity prices in spot electricity markets to load aggregators without reducing the users’ willingness to sell power consumption rights.
In the case where the option contract is advantageous, for load aggregators, it is recommended to modify the PCR compensation contracts by using the optimization method, and build the PCR option contract mechanism. However, the research in this paper still has some limitations. For example, in reality, users are not completely rational, and there might be deviations between actual and expected decisions. In the future, further research could be combined with behavioural economics knowledge, such as prospect theory.
Funding Statement: This research was funded by the National Natural Science Foundation of China, China (Grant No. 72174062), and the 2018 Key Projects of Philosophy and Social Sciences Research, Ministry of Education, China (Grant No. 18JZD032). The completion of this article was accomplished with the help of many teachers and classmates. We sincerely thank them for their help and guidance.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Moery, M. J. (2001). Power market auction design: Rules and lessons in market-based control for the new electricity industry. Edison Electric Institute, Washington D.C, USA. [Google Scholar]
2. Shu, Y. B., Zhang, Z. G., Guo, J. B., Zhang, Z. L. (2017). Study on key factors and solution of renewable energy accommodation. Proceedings of the CSEE, 37(1), 1–8. DOI 10.13334/j.0258-8013.pcsee.162555. [Google Scholar] [CrossRef]
3. Levin, T., Botterud, A. (2015). Capacity adequacy and revenue sufficiency in electricity markets with wind power. IEEE Transactions on Power Systems, 30(3), 1644–1653. DOI 10.1109/TPWRS.2015.2403714. [Google Scholar] [CrossRef]
4. Yang, J. J., Zhao, J. H., Wen, F. S., Meng, K., Dong, Z. Y. (2017). Key business framework and purchase/sale decision-making for electricity retailer. Automation of Electric Power Systems, 41(14), 10–18. DOI 10.7500/AEPS20170220014. [Google Scholar] [CrossRef]
5. Kettunen, J., Salo, A., Bunn, D. W. (2010). Optimization of electricity retailer's contract portfolio subject to risk preferences. IEEE Transactions on Power Systems, 25(1), 117–128. DOI 10.1109/TPWRS.2009.2032233. [Google Scholar] [CrossRef]
6. Yang, M., AI, X., Tang, L., Guo, S., Luo, G. Y. (2016). Optimal trading strategy in balancing market for electricity retailer considering risk aversion. Power System Technology, 40(11), 3300–3309. DOI 10.13335/j.1000-3673.pst.2016.11.004. [Google Scholar] [CrossRef]
7. Karandikar, R. G., Khaparde, S. A., Kulkarni, S. V. (2010). Strategic evaluation of bilateral contract for electricity retailer in restructured power market. International Journal of Electrical Power & Energy Systems, 32(5), 457–463. DOI 10.1016/j.ijepes.2009.09.018. [Google Scholar] [CrossRef]
8. Gan, Y. X., Jiang, C. W., Bai, H. K., Wang, J. B., Yang, M. (2018). Optimal bidding strategy and operation of industrial park electricity retailer in electricity market. Power System Technology, 42(3), 707–714. DOI 10.13335/j.1000-3673.pst.2017.2827. [Google Scholar] [CrossRef]
9. Janne, K., Ahti, S., Derek, W. B. (2010). Optimization of electricity retailer's contract portfolio subject to risk preferences. IEEE Transactions on Power Systems, 25(1), 117–128. DOI 10.1109/TPWRS.2009.2032233. [Google Scholar] [CrossRef]
10. Alireza, H., Hossein, S., Sheikh-El-slami, M. K. (2011). A Stochastic-based decision-making framework for an electricity retailer: Time-of-use pricing and electricity portfolio optimization. IEEE Transactions on Power Systems, 26(4), 1808–1816. DOI 10.1109/TPWRS.2010.2095431. [Google Scholar] [CrossRef]
11. Yang, Y., Liu, J. (2017). Two-stage decision-making method of retailers considering power transfer strategy. Automation of Electric Power Systems, 41(24), 120–128. DOI 10.7500/AEPS20170612008. [Google Scholar] [CrossRef]
12. Yang, Z., Peng, S. C., Liao, Q. F., Liu, D. C., Xu, Y. Y. et al. (2018). Noncooperative trading method for three market entities in integrated community energy system. Automation of Electric Power Systems, 42(14), 32–39. DOI 10.7500/AEPS20170915007. [Google Scholar] [CrossRef]
13. Pavan, B., Le, A. T., Lina, B. T. (2013). Stochastic programming based model of an electricity retailer considering uncertainty associated with electric vehicle charging. IEEE International Conference on European Energy Market, Stockholm, Sweden. DOI 10.1109/EEM.2013.6607404. [Google Scholar] [CrossRef]
14. Wang, Z., Gu, C., Li, F., Bale, P., Sun, H. (2013). Active demand response using shared energy storage for household energy management. IEEE Transactions on Smart Grid, 4(4), 1888–1897. DOI 10.1109/TSG.2013.2258046. [Google Scholar] [CrossRef]
15. Nojavan, S., Zare, K., Mohammadhvatloo, B. (2017). Application of fuel cell and electrolyzer as hydrogen energy storage system in energy management of electricity energy retailer in the presence of the renewable energy sources and plug-in electric vehicles. Energy Conversion and Management, 136, 404–417. DOI 10.1016/j.enconman.2017.01.017. [Google Scholar] [CrossRef]
16. Gu, W., Ren, J. Y., Gao, J., Gao, F., Song, X. H. et al. (2017). Optimal dispatching model of electricity retailers considering distributed generator and adjusted load. Automation of Electric Power Systems, 41(14), 37–44. DOI 10.7500/AEPS20170217005. [Google Scholar] [CrossRef]
17. Daniel, S. K. (2003). Demand-side view of electricity markets. IEEE Transactions on Power Systems, 18(2), 520–527. DOI 10.1109/TPWRS.2003.810692. [Google Scholar] [CrossRef]
18. Huang, K. Y., Chin, H. C., Huang, Y. C. (2004). A model reference adaptive control strategy for interruptible load management. IEEE Transactions on Power Systems, 19(1), 683–689. DOI 10.1109/TPWRS.2003.821444. [Google Scholar] [CrossRef]
19. Doudna, J. H. (2001). Overview of California ISO summer 2000 demand response programs. IEEE Proceedings of Power Engineering Society Winter Meeting, Piscataway, NJ, USA. DOI 10.1109/PESW.2001.917039. [Google Scholar] [CrossRef]
20. Wang, B. B., Li, Y. R., Li, Y., Dou, X. (2015). Optimal coordination between system reserve and interruptible loads with response uncertainty. Electric Power Automation Equipment, 35(11), 82–89. DOI 10.16081/j.issn.1006-6047.2015.11.013. [Google Scholar] [CrossRef]
21. Tuan, L. A., Bhattacharya, K. (2001). Interruptible load management within secondary reserve ancillary service market. IEEE Porto Power Tech Conference, Porto, Portugal. DOI 10.1109/PTC.2001.964571. [Google Scholar] [CrossRef]
22. Zhang, Y., Han, X., Zhang, L., Xu, B., Wang, M. et al. (2018). Integrated generation-consumption dispatch based on compensation mechanism considering demand response behaviour. Journal of Modern Power Systems and Clean Energy, 6(5), 1025–1041. DOI 10.1007/s40565-018-0382-8. [Google Scholar] [CrossRef]
23. Strbac, G. (2008). Demand side management: Benefits and challenges. Energy Policy, 36(12), 4419–4426. DOI 10.1016/j.enpol.2008.09.030. [Google Scholar] [CrossRef]
24. Daniel, S., Kirschen, G. S. (2006). Fundamentals of power system economics. John Wiley & Sons, New York, USA. [Google Scholar]
25. Wang, L., Zhang, L., Zhang, F., Jin, D. (2018). Decision-making and risk assessment of purchasing and selling business for electricity retailers. Automation of Electric PowerSystems Press, 42(1), 47–54+ 143. DOI 10.7500/AEPS20170522001. [Google Scholar] [CrossRef]
26. Deng, S. J., Oren, S. S. (2006). Electricity derivatives and risk management. Energy, 31(6), 940–953. DOI 10.1016/j.energy.2005.02.015. [Google Scholar] [CrossRef]
27. Black, F., Schole, M. (1973). The pricing of options and corporate liabilities. Journal of Political Economy, 81(3), 637–654. DOI 10.1086/260062. [Google Scholar] [CrossRef]
28. Gonzalez, A. M., Roque, A. M. S., Garciagonzalez, J. (2005). Modeling and forecasting electricity prices with input/output hidden Markov models. IEEE Transactions on Power Systems, 20(1), 13–24. DOI 10.1109/TPWRS.2004.840412. [Google Scholar] [CrossRef]
29. Omisch, J. A. (2003). Scenario reduction in stochastic programming: An approach using probability metrics. Mathematical Programming, 95(3), 493–511. DOI 10.1007/s10107-002-0331-0. [Google Scholar] [CrossRef]
30. Song, M., Amelin, M. (2017). Purchase transaction strategy for a retailer with flexible demands in day-ahead electricity market. IEEE Transactions on Power Systems, 32(3), 1839–1850. DOI 10.1109/TPWRS.2016.2608762. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |