Energy Engineering

DOI: 10.32604/ee.2022.018025

ARTICLE

Kalman Filter Estimation of Lithium Battery SOC Based on Model Capacity Updating

Min Deng1, Quan Min1, Ge Yang1 and Man Yu2,3,*

1CCCC Second Highway Consultants Co., Ltd., Wuhan, 430056, China
2Xi'an Aeronautical University, Xi'an, 710077, China
3Key Laboratory of Automobile Transportation Safety Guarantee Technology and Transportation Industry, Xi'an, 710064, China
*Corresponding Author: Man Yu. Email: 201902004@xaau.edu.cn
Received: 24 June 2021; Accepted: 09 August 2021

1  Introduction

State of charge (SOC) estimation of power battery is one of the core functions of battery management system. It is directly displayed as residual capacity and indirectly as driving range. SOC of power battery is an important basis for formulating optimal energy management strategy of vehicle electronic control system, which is of great significance for improving stability, safety, service life and energy utilization rate of power battery. In the actual design and production process, the power battery is composed of series and parallel cells. Due to the influence of factors such as the inconsistency between the cells, the difference of using environment, the increase of battery cycle times, and further the SOC cannot be measured directly, only by estimated indirectly, SOC estimation is one of the research hotspots of new energy vehicles. How to accurately estimate SOC based on the voltage, current, temperature and other simple physical information of power battery is a technical bottleneck in the design and production of new energy vehicle battery management system (BMS) [1–5].

Most of the research on battery SOC estimation algorithms are limited to the laboratory environment, such as specific temperature and current conditions, without considering factors which will affect the battery performance when the vehicle is operating. At the same time, there are many factors affecting battery SOC estimation, such as cell inconsistency, battery aging, temperature, dynamic hysteresis characteristics, self-discharge and charge-discharge rate, etc., which will affect the performance of the battery, resulting in the change of battery capacity. In reference [6], the battery terminal voltage curve is obtained by discharging the battery at different rates, and the battery SOC is accurately predicted by using statistical method to predict the battery open circuit voltage. The method is more suitable for obtaining the open circuit voltage (OCV) curve of the cell under laboratory conditions, and then the curve is applied to other SOC estimation algorithms. In reference [7], an intelligent SOC estimation algorithm is proposed based on Ah counting method. The algorithm is modified by referring to the charging and discharging efficiency of the battery to improve the SOC estimation accuracy. In reference [8], an equivalent circuit model including capacitors and inductors under high and low frequency operating conditions is established. The impedance value of the model is calculated by nonlinear least square fitting method under different charging conditions. However, if the system is not in steady state, the result of EIS estimation is not ideal. In reference [9], the battery state space model is obtained through mathematical derivation, and different Qw and Rv settings are adopted based on Kalman filter to improve the estimation performance and effectively reduce the root mean square error. However, Kalman filter only have good estimation effect for linear system state, it cannot be used for nonlinear state estimation of power battery. In reference [10], the SOC of LiFePO4 battery is estimated by extended Kalman filter (EKF) and double EKF based on two battery models of zero hysteretic state and hysteretic state. The results show that the method can accurately estimate SOC in dynamic environment with maximum error less than 4%. In reference [11], a zero-state hysteresis model for lithium-ion battery is proposed based on AUKF. The advantage of the model is that it can adaptively correct the noise covariance in the process and observation state. At the same time, due to the simple structure of the zero-state hysteresis model, it can quickly and accurately estimate the battery state, and the calculation cost is low. SOC estimation algorithm also needs to consider such issues as accuracy, computation amount, real-time performance and computational cost, etc. In reference [12], an improved iterate calculation method is proposed to improve the charged state prediction accuracy of the lithium-ion battery packs by introducing a novel splice Kalman filtering algorithm with adaptive robust performance. Because each model and estimation algorithm have defects, finding a model and algorithm with the best comprehensive performance is a problem that the majority of researchers have been committed to solve. Thus, in this paper, the Singular Value Decomposition-Unscented Kalman Filter (SVD-UKF) combined lithium battery SOC estimation algorithm with model capacity update is proposed to further improve the SOC estimation accuracy of lithium battery, which is based on the forgetting factor recursive least square method (FFRLS) and Thevenin equivalent circuit model.

In this paper, the Thevenin equivalent circuit model is used in Section 2 to emulate the dynamic behavior of battery. The forgetting factor recursive least square method and singular value decomposition unscented Kalman filter are combined in Section 3 to estimate the parameters and states of the model. At the same time, the capacity updating algorithm is also used to consider the influence of lithium battery available capacity attenuation on SOC estimation, so as to improve the accuracy and robustness of SOC estimation. The test results and errors are shown in Section 4 and the conclusion are drawn in Section 5.

2  Model Parameter Identification

Thevenin model [13] is a first-order RC model, which adds an RC loop to simulate the polarization reaction inside the battery based on the Rint model. R1 is the polarization impedance and C1 is the polarization capacitance. Based on this, the influences of temperature and charge-discharge rate on the internal impedance dynamics of the battery can be simulated. Even the model cannot reflect the influences of self-discharge and cycle life on the dynamic characteristics of the battery, the model has the advantages of less computation, low computational cost, and the accuracy can meet the requirements of engineering application, so it is a widely used equivalent circuit model [14–17]. The Thevenin equivalent circuit model is shown in Fig. 1, and Eqs. (1) and (2) is the mathematical state equation of Thevenin model.

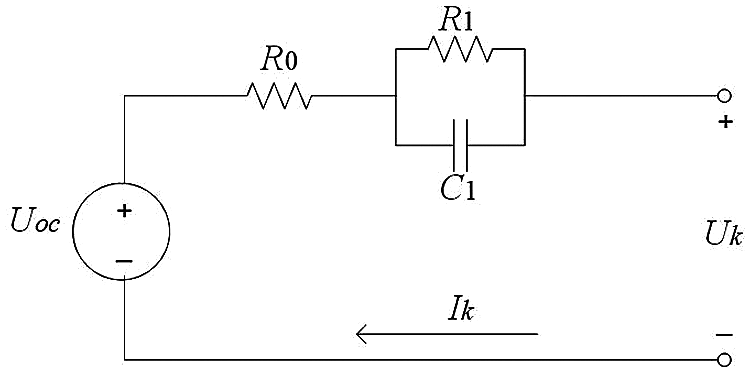
Figure 1: Equivalent circuit model

U1,k∙=−U1,kR1C1+IkC1(1)

Uk=Uoc,k−IkR0−U1,k(2)

where, Uoc,k represents the OCV, which can obtained by measuring the battery terminal voltage. Uk is the terminal voltage, U1,k is the polarization voltage across C1. In this paper, set E(k)=Uk − Uoc,k. Based on Laplace transform and bilinear transformation, linear discretization process from frequency domain to time domain of Eqs. (1) and (2) is carried out, and further simplified to obtain Eqs. (3) and (4):

E(k)=aE(k−1)+bI(k)+cI(k−1)(3)

{a=T−2R1C1T+2R1C1b=R0T+R1T+2R0R1C1T+2R1C1c=R0T+R1T−2R0R1C1T+2R1C1(4)

where, T represents the data sampling interval, then the values of a, b and c can be estimated by the system, so as to obtain the internal impedance parameters of the battery, as shown in Eq. (5):

{R0=b−c1+aR1=2(b+c)a2−1C1=(a+1)24(b+c)(5)

Let φ(k)=[E(k−1) I(k) I(k−1)], θ(k)=[a b c]T, φ(k) be the input of the system, θ(k) be the state variables of the system to be measured, y(k) be the output of the system. If the system error at k time is e(k), then Eq. (3) can be transformed into Eq. (6):

y(k)=φ(k)θ(k)+e(k)(6)

Therefore, the parameters of Thevenin equivalent battery model can be estimated online by using the forgetting factor recursive least square method (FFRLS) based on the real-time terminal voltage and current of lithium battery. The FFRLS online identification of lithium battery equivalent circuit model parameter equations are shown in Eqs. (7)–(10):

Step 1: calculate the gain K(k):

K(k)=P(k−1)φT(k)λ+φ(k)P(k−1)φT(k)(7)

Step 2: calculate the covariance P(k):

P(k)=P(k−1)−K(k)φ(k)P(k−1)λ(8)

Step 3: calculate the estimation error e(k):

e(k)=E(k)−φ(k)θ∧⁡(k−1)(9)

Step 4: update system state θ∧⁡(k):

θ∧⁡(k)=θ∧⁡(k−1)+K(k)e(k)(10)

3  SOC Estimation Algorithm

The physical meaning of SOC of the battery is the ratio of the real-time capacity to the total capacity of the battery under charge and discharge, so it is often used to estimate the remaining capacity of the battery. When extended Kalman filter [18–20] is used to estimate battery SOC, linearization is needed to deal with the nonlinear battery state space model, which can cause the unavoidable linearization error, and the computationally costly Jacobian matrix calculation. For the highly nonlinear system, if the linearization is not established, the filtering performance will be reduced and the filtering results will be divergent, which will not only make the calculation complex, but also reduce the accuracy, resulting in the long running time of the program and poor effect. However, for nonlinear systems, unscented Kalman filter (UKF) [21–24] does not linearize the nonlinear function, but adopts statistical linearization method (UT-unscented transform), which does not need to derive Jacobian matrix. So, it does not ignore the high-order term, and can achieve the third-order Taylor expansion approximation effect, has a good estimation effect for highly nonlinear systems. At the same time, because UKF takes into account the system observation and process noise, it has strong robustness to noise. When the estimated value deviates from the real value of the system, it has the ability of self-updating according to the filter gain. It can adapt to all kinds of current changes in SOC estimation of ternary lithium battery, which is in line with the development demand of new energy vehicles for power battery system. However, in practical application, it is found that UKF is prone to produce non-positive definite covariance matrix because of processor calculation errors, uncertain system noise and model disturbances. The singular value decomposition algorithm can solve this problem by restraining the non-positivity of covariance matrix of the system [25,26]. Accordingly, SVD-UKF (Singular Value Decomposition-Unscented Kalman Filter) algorithm can be proposed to estimate the SOC of lithium battery.

3.1 Singular Value Decomposition

Singular value decomposition is a matrix decomposition method with good stability and accuracy. Suppose, A∈Rm×n(m≥n), then the singular value decomposition of the matrix A is:

A=UΛVT=U(S000)VT(11)

where, U∈Rm×m, Λ∈Rm×n, V∈Rn×n, the column vectors of U and V are the left and right singular vectors of the matrix A respectively, S=diag(s1,s2,⋯,sr) are the singular values of the matrix A, and s1≥s1≥⋯≥s1≥0.

3.2 SVD-Unscented Transform

Suppose that the state vector of nonlinear system X is n-dimensional random vector, the mean and variance are X¯ and P. The covariance matrix P is easy to become non positive definite, singular value decomposition is applied to P, then 2n + 1 Sigma point sets [Xi] are obtained by distributed sampling, as shown in Eqs. (12) and (13):

P=USVT(12)

[X¯X¯+ρUS,i=1,⋯,nX¯−ρUS,i=n+1,⋯,2n](13)

where, ρ is the scaling factor, and the value is generally 1≤ρ≤2.

Then the mean weight wim and covariance weight wic of Sigma points are calculated by Eq. (14):

{w0m=λn+λw0c=λn+λ+(1−α2+β)wim=wic=λ2(n+λ),i=1,2,⋯,2n(14)

where, the superscript m represents the mean value, c represents the covariance, and the subscript represents the i-th sampling point, parameter λ=a2(n+κ)−n is a scale parameter used to reduce the total prediction error, the value range of a is (e−4≤a≤1), determining the distribution state of Sigma point set. The κ is an unbounded value, β is a non-negative state distribution parameter used to refer to the influencing factors of higher-order terms in the Eq. (14).

3.3 SVD-Unscented Kalman Filter Algorithm

When SVD-UKF is used to estimate the SOC of ternary lithium battery, the nonlinear system equation is shown in Eqs. (15) and (16):

Xk+1=f(Xk,uk)+Wk=(SOCk+1Uk+11)⇒(100exp⁡(−Tτ))(SOCkUk1)+(TCnR1(1−exp⁡(−Tτ)))(Ik)+(Wk1Wk2)(15)

Zk=g(Xk,uk)+Vk=OCV(SOCk)+IkR0+Uk1+Vk(16)

The system state vector is Xk=[SOCk,Uk1]T, the system control input is Ik, corresponding to the lithium battery current, the charging direction is positive, and the discharge direction is negative; The system observation vector Zk corresponds to the terminal voltage Uk of lithium battery. The basic steps of using UKF to estimate the SOC of lithium battery are as follows:

1)   Initialization of lithium battery SOC estimation by SVD-UKF:

{X¯0/0=E[X0]P0/0=E[(X0−X¯0)(X0−X¯0)T](17)

2)   The first SVD-UT transform, the Sigma point set is obtained by Eqs. (13) and (14):

The predicted residual error ek=g(Xk,uk)−Zk, then the discriminant statistics of state model error are as follows:

Δek=((ek)Tek/tr(∑ek))1/2(18)

The adaptive factor is:

αk={1|Δek|≤dd|Δek||Δek|>d(19)

S^k/k=Sk/k/α(20)

Xk/ki=(X^k/kX^k/k+ρUk/kS^k/kX^k/k−ρUk/kS^k/k)(21)

where, ∑ekis the covariance matrix of ek, tr(∙) is the matrix trace operator, and d is the empirical value, 1<d<2.5.

3)   One step state prediction of sigma point set:

Xk+1/ki=f[Xk/ki,uki](22)

4)   One step prediction of sigma point set, covariance matrix and its singular value decomposition are solved:

{ X^k+1/k=∑i2nwiXk+1/kiPk+1/k=∑i2nwi[ X^k+1/k−Xk+1/ki ][ X^k+1/k−Xk+1/ki ]T+QSk+1/k=svd{ [ wic(Xk+1/k−X^k+1/k) ] }S^k+1/k=Sk+1/k/α(23)

where, svd{} is SVD decomposition operator.

5)   According to the one step prediction value in 4), a new Sigma point set is obtained by SVD-UT transform:

Xk+1/ki=(X^k+1/kX^k+1/k+ρUk+1/kS^k+1/kX^k+1/k−ρUk+1/kSk+1/k∧)(24)

6)   Through the new sigma point set, the predicted observations are obtained from the system observation equation:

Zk+1/ki=g(Xk+1/ki,uki)(25)

7)   The mean and covariance of the predicted values of the system are obtained from the predicted observations of the new Sigma point set:

{Z¯k+1/k=∑i=02nwiZk+1/kiPzkzk=∑i=02nwi[Zk+1/ki−Z−k+1/k][Zk+1/ki−Z−k+1/k]T+RPxkzk=∑i=02nwi[Zk+1/ki−Z−k+1/k][Zk+1/ki−Z−k+1/k]T(26)

8)   System state estimation and covariance updating:

{Kk+1=PxkzkPzkzk−1X^k+1/k+1=X^k+1/k+Kk+1(Zk+1−Z∧k+1/k)Pk+1/k+1=Pk+1/k−Kk+1PzkzkKk+1T(27)

From the above process of using SVD-UKF to estimate the SOC of lithium battery, it can be seen that SVD-UKF does not linearize the nonlinear system at the estimated point using Taylor expansion as EKF does. Instead, the SVD-UT transform is used to obtain the sigma point set which is symmetrically distributed near the estimation point and consistent with the original system state mean and covariance, and avoid the non-positive definite problem of covariance matrix. Then, the Sigma point set is used for nonlinear mapping based on the state space model of the system, which is a statistical approximate linearization method. The accuracy of SVD-UKF can reach the third-order Taylor accuracy, and it does not neglect the influence of higher-order terms, and does not need to calculate the complex Jacobian matrix. Compared with EKF, the amount of computation is not much. So SVD-UKF is widely used in highly nonlinear systems [27].

The current maximum capacity Cn given by the state space model in Eq. (15) is the initial capacity of lithium battery. In the actual using process, the current maximum capacity of lithium battery is decreasing. It can be seen that the smaller the current maximum capacity of lithium battery, the smaller the actual SOC value. When the new energy vehicle is actually used, especially when the number of cycles increases, it is necessary to re-estimate the current maximum capacity of the lithium battery to update the capacity of the model, and then correct the SOC estimation error. SOC of lithium battery is the ratio of current remaining capacity to current maximum capacity of lithium battery. At the same time, SOC can be estimated not only by SVD-UKF, but also by OCV-SOC curve. The relationship between SOC and OCV is fitted with experimental data, and the functional relationship between SOC and OCV is obtained as Eq. (28):

Uoc=25.33z6−79.42z5+93.67z4−50.31z3+11.88z2−0.4486z+3.454(28)

According to the “parallelogram rule” of lithium battery voltage and SOC, the same voltage difference corresponding to the same SOC difference can be obtained under different life span and the same temperature and current environment. This means that in the charging curve of the battery, take two SOC points, SOC1, SOC2, the “dAH/dSOC” in this interval equal to the current available capacity.

As shown in Fig. 2, two SOC points, SOCa and SOCb, are obtained in the SOC estimation process, and the lithium battery capacity difference ΔAh between the two target points can be obtained by Ah integration, then the current maximum capacity of lithium battery can be calculated by Eq. (29) [28–30]:

C^n=ΔAhΔSOC=∫abIkdtSOCb−SOCa(29)

where, setting SOCa = 30%, SOCb = 80%.

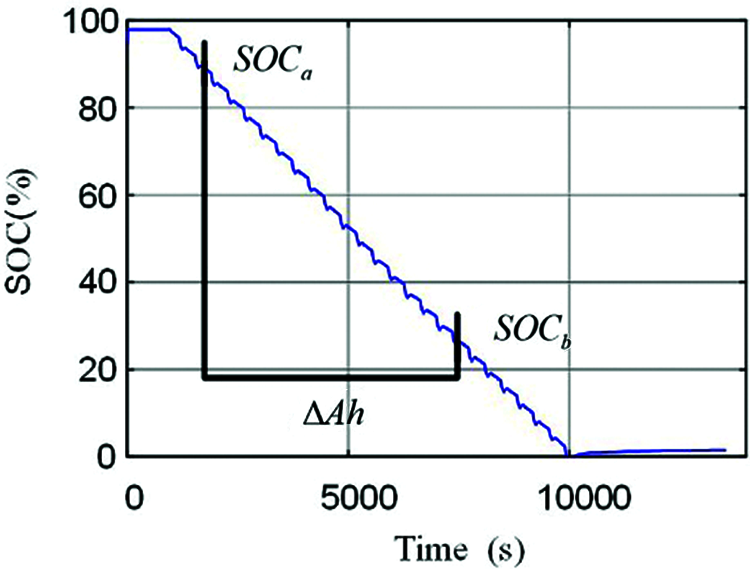
Figure 2: Capacity difference of battery

In order to ensure the reliability and stability of the estimated current maximum capacity of lithium battery, the convergence coefficient δ is used to determine whether the current estimated maximum capacity is reliable. The convergence coefficient δ is shown in Eq. (30):

δ=max|C^n,k+1−C^n,kC^n,k|(30)

where, C^n,k represents the maximum capacity of lithium battery estimated at time k; δ≤ 2%, Cn = C^n,k+1; δ > 2%, Cn = C^n,k.

4  Test Result

In order to verify the reliability of the model parameter identification, the test data of dynamic stress test (DST) condition and federal urban driving schedule (FUDS) condition are used to verify the Thevenin model and FFRLS parameter identification method under Simulink environment. The initial SOC is 100%, the test temperature is set to 25°C the charging current is positive and the discharge current is negative.

Figs. 3 and 4 show the verification results of online parameter identification of Thevenin model under DST condition and FUDS condition respectively. The results show that the FFRLS on-line parameter identification method-has a good overall effect, which can be applied to different conditions. The analysis in the figure shows: (1) At the start and the end stages of the working condition, that is, when the current is 0, the FFRLS on-line identification parameter results have the 2–3 times larger jitter error than the average value; (2) In the middle stage of the working condition, as the current changes drastically, FFRLS on-line parameter identification method can estimate the model parameters well in real time, and there is no huge jitter error.

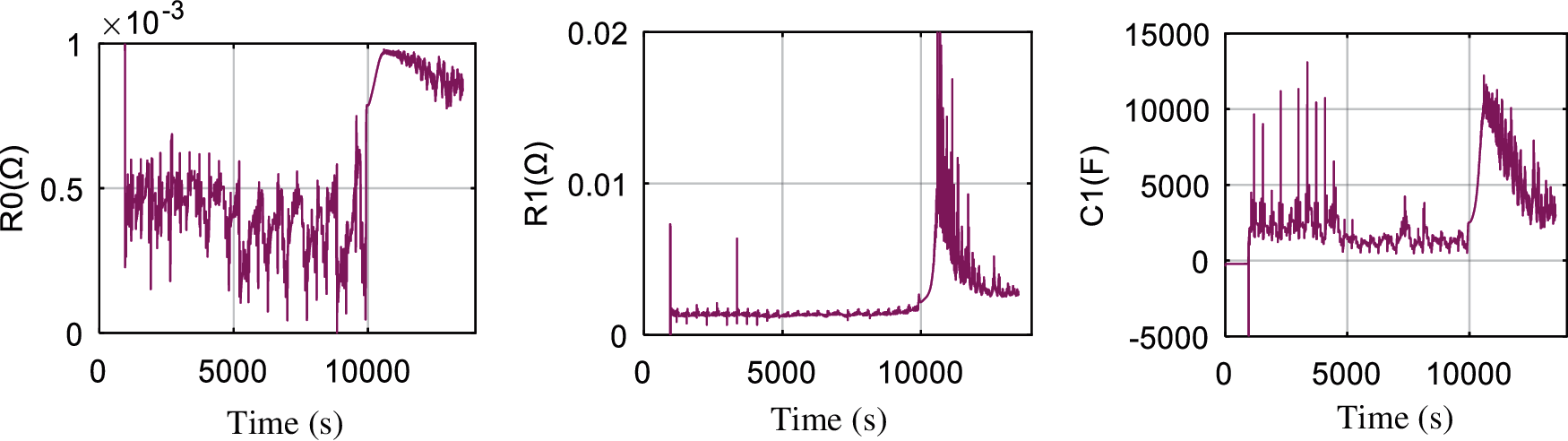
Figure 3: On-line parameter identification results of Thevenin model under DST

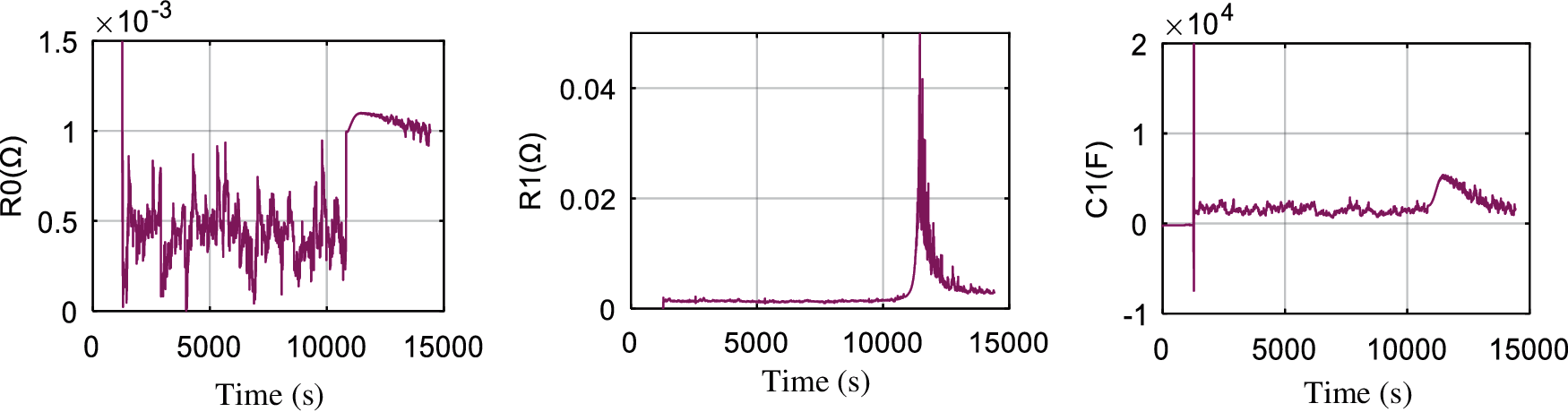
Figure 4: On-line parameter identification results of Thevenin model under FUDS

Figs. 5a and 6a show the verification results of online parameter identification under 25°C DST condition and FUDS condition respectively, and absolute error of Thevenin model are shown in Figs. 5b and 6b, respectively. The verification results show that the estimated voltage of the model can always follow the actual voltage very well, no matter how drastic the current changes under the two conditions. It can be seen that the accuracy of FFRLS online identification results in the first half of the working condition is very good, and the error is within 0.02 V. In the latter half, the error of FFRLS online identification results is doubled. This is because as the number of charging and discharging increases, the activity of the chemical substances inside the battery decreases, the polarization phenomenon is obvious, and the parameters of the battery model also fluctuate, which leads to an increase in the error of the online parameter identification results. But the accuracy is still within the allowable range. Therefore, the FFRLS online parameter identification method can accurately estimate the internal impedance parameters of the battery under the current working conditions when it is used for the parameter identification of Thevenin model.

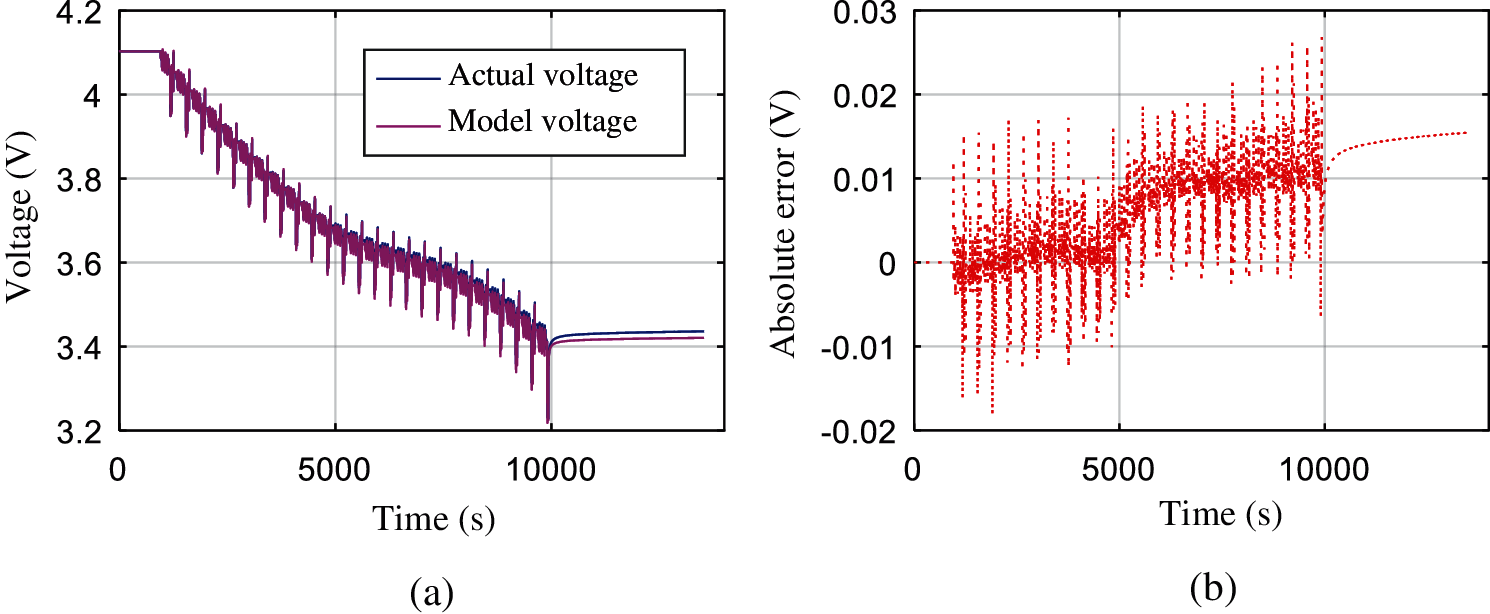
Figure 5: On-line identification result and absolute error of Thevenin model under DST (a) On-line identification result under DST (b) Absolute error under DST

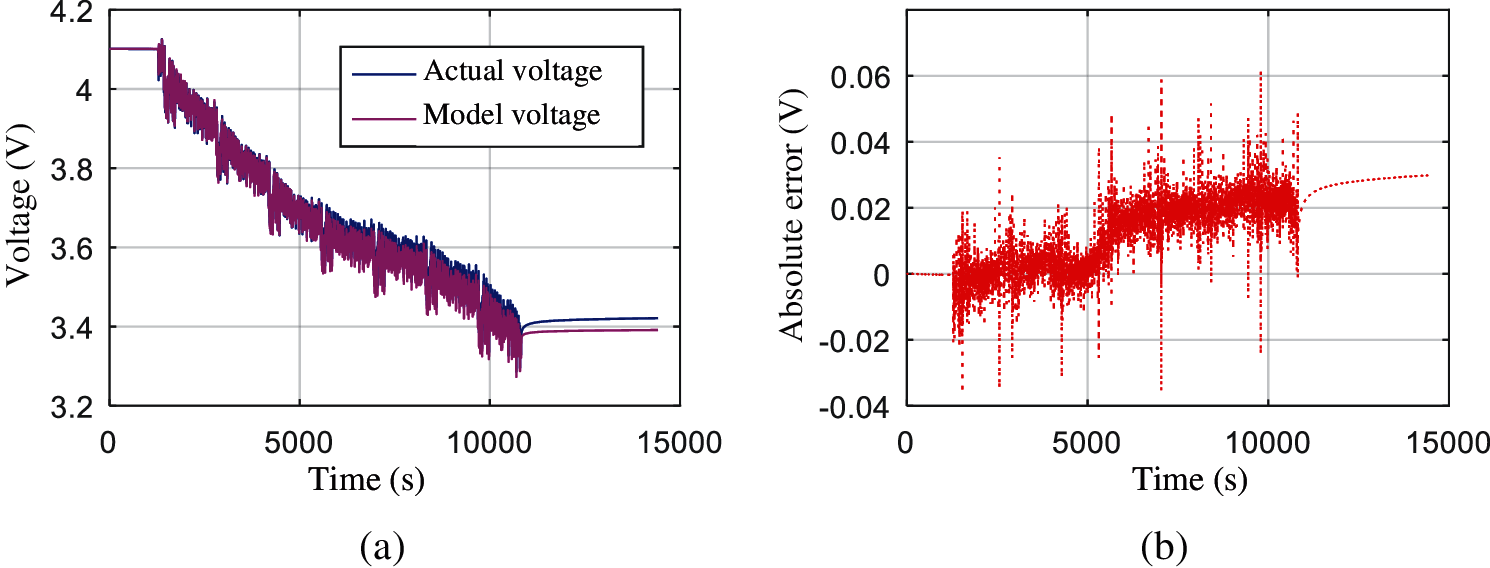
Figure 6: On-line identification result and absolute error of Thevenin model under FUDS (a) On-line identification result under FUDS (b) Absolute error under FUDS

In order to verify the SOC estimation accuracy of the proposed SVD-UKF based on model capacity updating under the condition of continuous declining of the lithium battery maximum capacity, the endurance cycle condition test data of voltage as shown in Fig. 7a and current in Fig. 7b are used for verification. The total time of the endurance cycle condition is 1,076,400 s, which consists of a complete charge and 72 times NEDC discharge cycle. The variation of voltage and current of lithium battery during the discharge of endurance cycle condition voltage and current are shown in Figs. 8a and 8b, respectively.

Fig. 9 shows the variation of the maximum available capacity of the ternary lithium battery in the endurance cycle. The initial value of the maximum available capacity is 37.2 Ah, which decreases sharply in the initial 55 h, and then tends to stabilize to 35.8 Ah. It is consistent with the change of lithium battery capacity during actual use.

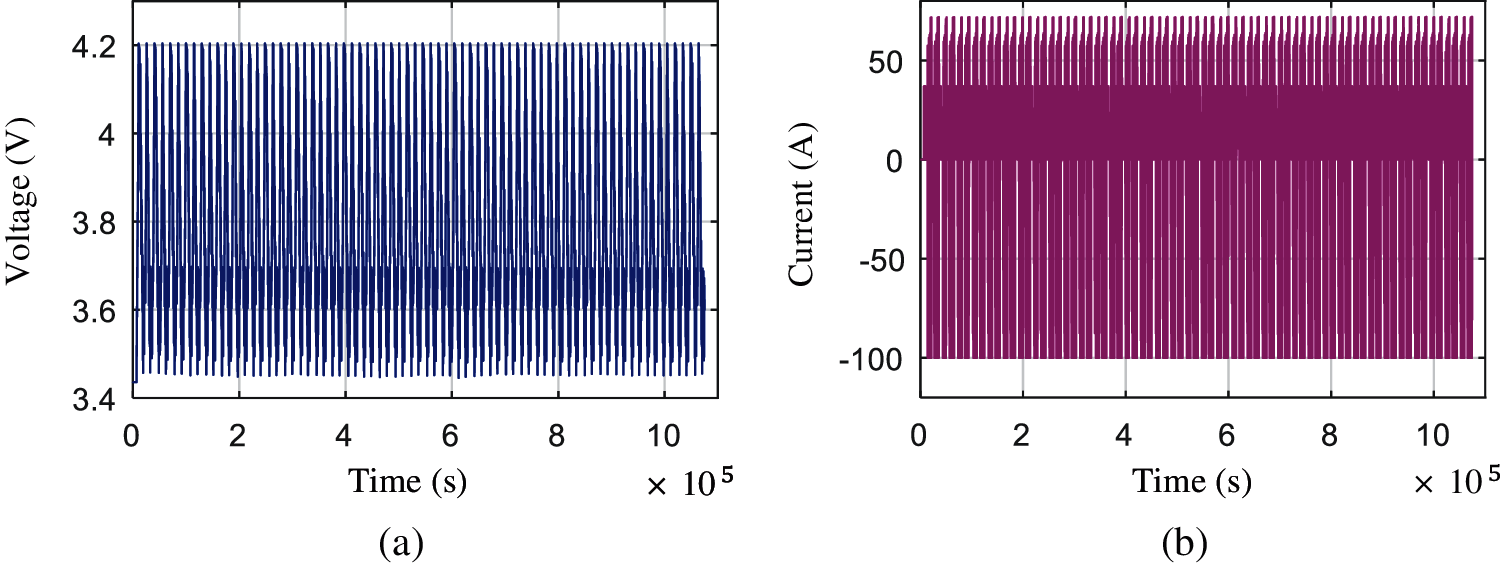
Figure 7: Three-dimensional lithium battery durable cycle conditions (a) Voltage under durable cycle condition (b) Current under durable cycle condition

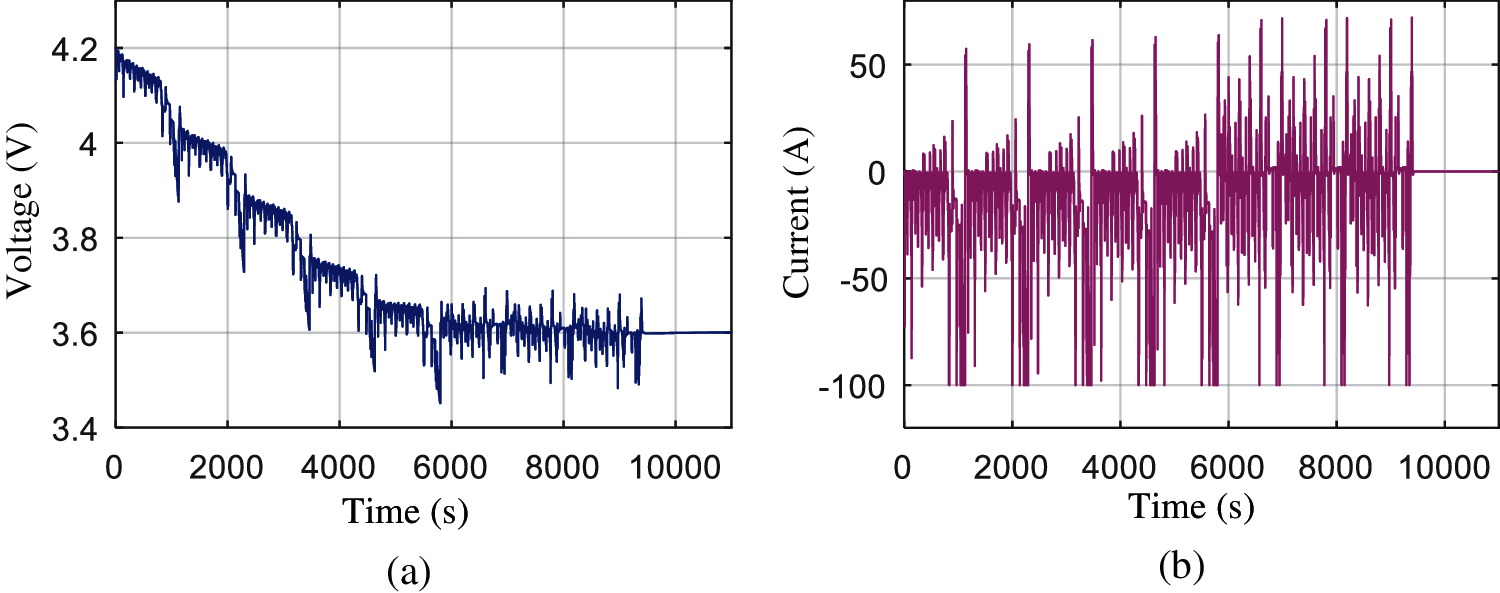
Figure 8: Discharge process of durable cycle (a) Voltage during the discharge process (b) Current during the discharge process

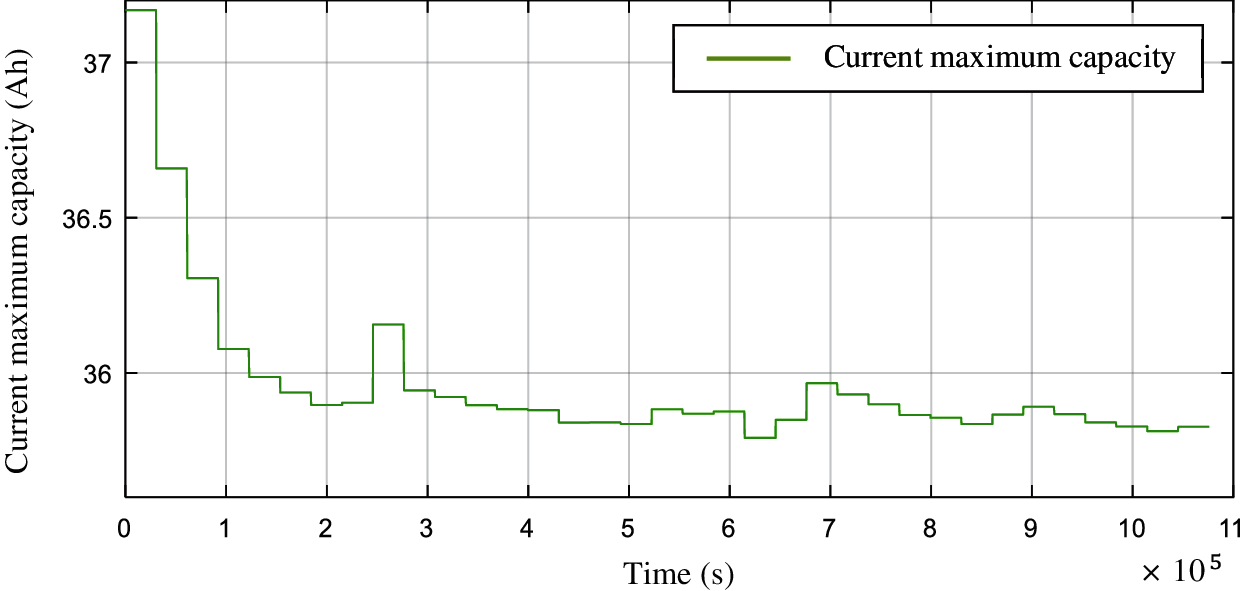
Figure 9: Decline of capacity under durable cycle condition

In order to verify that the SVD-UKF algorithm based on model capacity updating can estimate the SOC with high accuracy under the condition of continuous decline of cell capacity, the 1st, 6th and 72nd discharge processes are selected for analysis and comparison. The SOC estimation comparison diagram of the 1st, 6th and 72nd discharge process is shown in Figs. 10--12, and the SOC estimation error results of the three discharge processes are shown in Table 1, where AE is absolute error and RMSE is root mean square error.

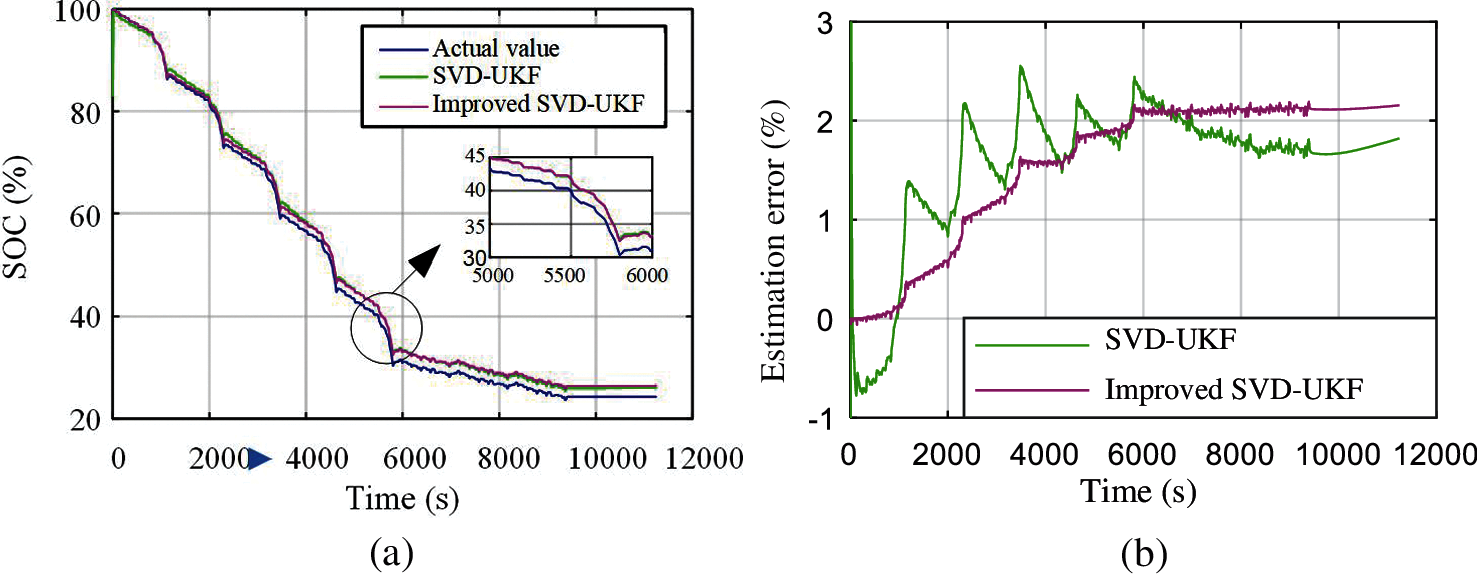
Figure 10: Estimation and error in the 1st discharge process of durable condition (a) Estimation result in the 1st discharge process (b) Estimation error in the 1st discharge process

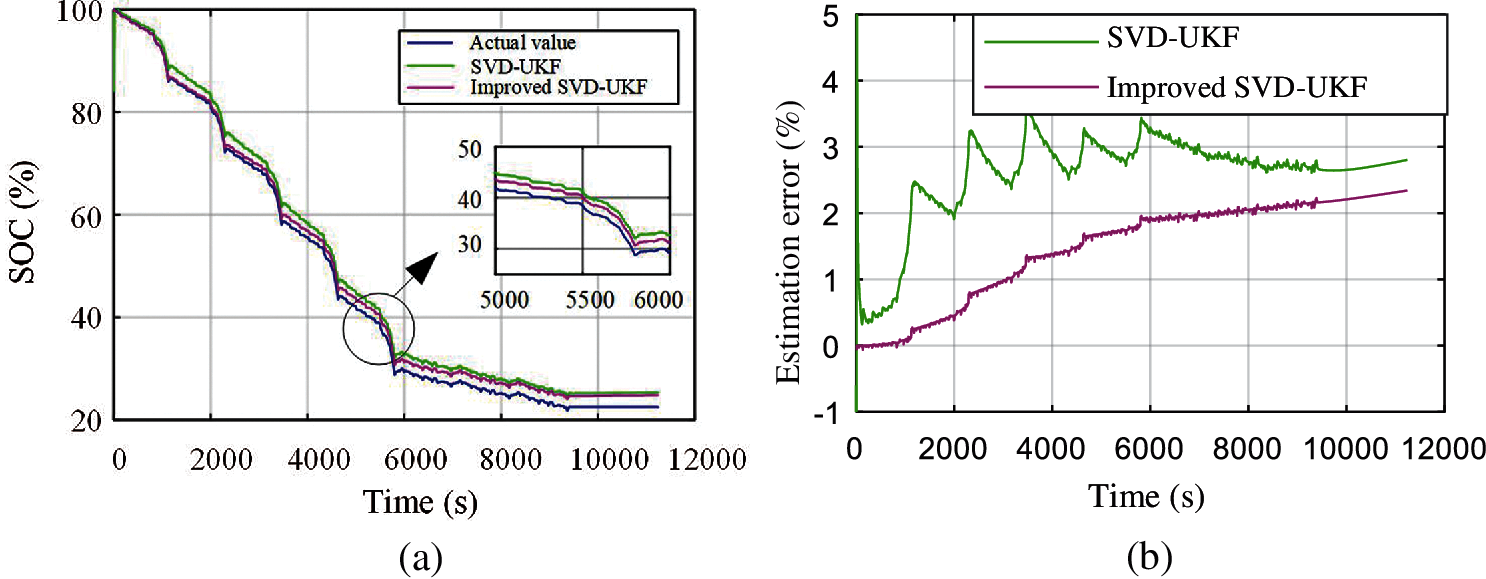
Figure 11: Estimation and error in the 6th discharge process of durable condition (a) Estimation result in the 6th discharge process (b) Estimation error in the 6th discharge process

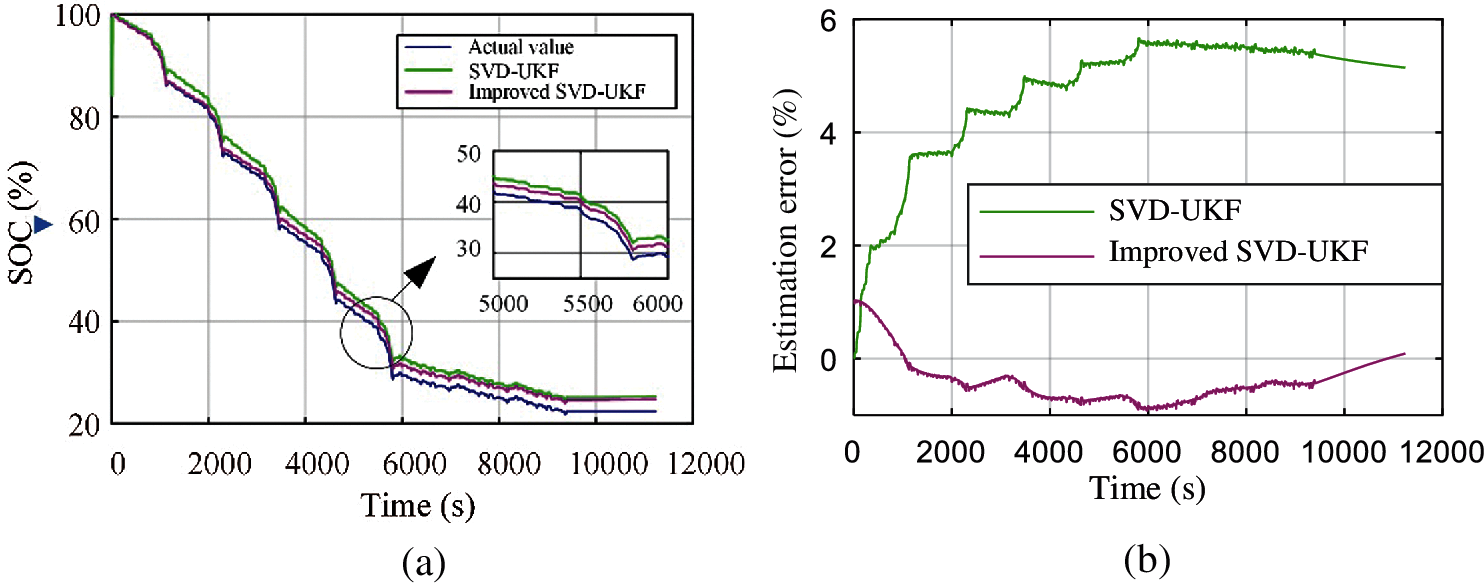
Figure 12: Estimation and error in the 72th discharge process of durable condition (a) Estimation result in the 72th discharge process (b) Estimation error in the 72th discharge process

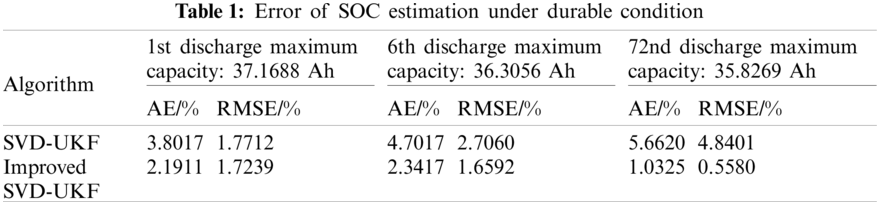
As it can be seen, as the discharge reaction progresses, the internal material activity of the battery decreases, and the polarization phenomenon is obvious. The estimation error of the SVD-UKF algorithm gradually increases, and finally reaches 5.7%. However, the estimation error of the SVD-UKF algorithm based on capacity updating has always been maintained at about 2%, whose error has not changed much. The results show that the SVD-UKF based on capacity updating can estimate the SOC of lithium battery in real time. The SVD-UKF algorithm based on capacity updating has convergence and can meet the accuracy requirements of the battery under dynamic working conditions.

5  Conclusion

In this paper, the Thevenin equivalent circuit model is adopted to simulate the dynamic behavior of battery. The parameters of battery model are identified by combining the forgetting factor recursive least square method with singular value decomposition unscented Kalman filter. What's more, in order to improve the accuracy and robustness of SOC estimation, the capacity updating algorithm is also used, which consider the influence of lithium battery available capacity attenuation on SOC estimation.

The comparative analysis shows that when the initial capacity is 37.2 Ah, the estimation error of the two SOC estimation algorithms is less than 4%, and the SVD-UKF algorithm based on capacity update has higher accuracy, reaching 2.2% estimation error. As the capacity of lithium battery decreases from 37 Ah to 35 Ah, the estimation error of SVD-UKF algorithm increases gradually, and finally reaches 5.7%. The SVD-UKF algorithm based on capacity updating can control the estimation error at about 2%.

Therefore, when the maximum available capacity of lithium battery is continuously declining, the SVD-UKF based on capacity update can estimate the SOC of lithium battery in real time excellently, and the absolute error is less than 3%, and the algorithm does not show divergence phenomenon.

It is verified that the SOC estimation algorithm based on capacity update proposed in this paper can estimate the SOC of ternary lithium battery with real-time and high accuracy under the condition of lithium battery capacity attenuation, which realizes the research purpose of improving the SOC estimation accuracy in this paper.

Funding Statement: This research was funded by Natural Science Basic Research Program of Shaanxi (2020JQ-913), Key Research and Development Program of Shaanxi (2020ZDLGY16-01, 2020ZDLGY16-02, 2019ZDLGY15-01, 2019ZDLGY15-02, 2018ZDCXL-GY-05-03-01), Key Laboratory Open Fund of Ministry of Communications (300102220503).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.