Energy Engineering

DOI: 10.32604/EE.2021.017657

ARTICLE

A Study on Heat Transfer Enhancement through Various Nanofluids in a Square Cavity with Localized Heating

Sheikh Hassan1, Didarul Ahasan Redwan1, Md. Mamun Molla1,2,*, Sharaban Thohura3, M. Abu Taher4 and Sadia Siddiqa5

1Department of Mathematics and Physics, North South University, Dhaka, Bangladesh
2Center for Applied and Scientific Computing (CASC), North South University, Dhaka, Bangladesh
3Department of Mathematics, Jagannath University, Dhaka, Bangladesh
4Department of Mathematics, Dhaka University of Engineering and Technology, Gazipur, Bangladesh
5Department of Mathematics, COMSAT University Islamabad, Attock Campus, Attock, Pakistan
*Corresponding Author: Md. Mamun Molla. Email: mamun.molla@northsouth.edu
Received: 28 May 2021; Accepted: 02 August 2021

Nomenclature

Greek symbols

Subscripts

1  Introduction

Nanofluids are immersions of nanosized particles in a base fluid. The base fluid could be water, ethylene glycol, etc., whereas there are varieties of nanoparticles to choose from, for example, copper (Cu), aluminum oxide ( Al2O3 ), titanium ( TiO2 ), etc. Compared to pure fluids, nanofluids exhibit a few superior properties, including their enhanced thermal conductivity and heat transfer coefficient. Massive research has been conducted by several researchers explaining the flow and thermal behavior of nanofluids. An experimental study by He et al. [1] investigates the heat and flow behavior of TiO2 nanofluids flowing through a vertical pipe. Results show that nanoparticles enhanced the convective heat transfer coefficient for both laminar and turbulent flow regimes, enhancing laminar flow being much smaller than for turbulent flow. A two-dimensional experimental analysis by Shafahi et al. [2] using aluminum oxide ( Al2O3 ), titanium oxide ( TiO2 ) and copper oxide (CuO) in water base fluid, showed that temperature distribution depends on effective thermal conductivity. In another study by Pang et al. [3], thermal enhancement in Al2O3 was found to be less than that in silicon dioxide ( SiO2 ). This anomaly was attributed to the larger cluster size of SiO2 and it was concluded that clustering increases thermal conductivity. A similar study on thermal conductivity by Lee et al. [4] showed that thermal conductivity and viscosity increase with increasing the nanoparticle volume fraction.

In a study by Truong et al. [5] to investigate if nanoparticles increase Critical Heat Flux (CHF) on a passively engineered heating surface, bares and blasted plates were used to establish a baseline for the CHF measurement and the nanofluids used included diamond, alumina and zinc oxide with volume fractions of 1%, 10%, and 20%, respectively. The CHF value for diamond showed an 11% enhancement, and that for both zinc oxide and alumina showed 35% enhancement. Extended research was carried by Wen [6] in further increasing the already enhanced CHF value for nanofluids reviews experiments performed on enhanced CHF and investigated possible mechanisms that increase CHF enhancement. A simplified dry patch model was developed, and the structural disjoining pressure was investigated by calculating interfacial shapes for pure fluid and various concentrations of nanofluids. An experiment by Chun et al. [7] elucidates the effect of nanofluids on boiling heat transfer of silicon, silicon carbide, and water using platinum (Pt) wire as a heat source. The experiment shows that nanoparticle-coated Pt wires are cooled down at a much higher rate compared to the bare Pt wires cooled by water and Si nanofluids.

Among works done on natural convective heat transfer, Wen et al. [8] formulated the transient and steady heat transfer coefficient for different concentrations of nanofluids under natural convective conditions in a range of Rayleigh numbers (Ra) from 106 to 109 . Lin et al. [9] studied the heat and fluid flow of natural convection in a cavity filled with Al2O3 /water nanofluid operating under differentially heated walls. The results show that heat transfer characteristics of the nanofluid can be increased when the ratio of minimum to maximum nanoparticle diameter is increased from 0.001 to 0.007 nm or the mean nanoparticle diameter is decreased from 250 to 5 nm. Corcione [10] conducted a theoretical study on the natural convection heat transfer of nanofluids using three different nanoparticles-Cu, Al2O3 , and TiO2 in two different base fluids-water and ethylene glycol. Ashorynejad et al. [11] showed that the Nusselt number drops off as the Hartmann number increases; however, it rises with the rise of the Rayleigh number and nanoparticle volume fraction. The magnetic field increases or decreases with the influence produced by the existence of nanoparticles concerning the Rayleigh number. Yu et al. [12] illustrated that nanofluid has a comparatively higher heat transfer coefficient for the same Reynolds number, and this coefficient increases with the increasing value of the mass fraction of CuO nanoparticles. They also reported that nanofluid does not have major influence on heat transfer factors at very small volume concentrations and increasing mass fraction causes the pressure of nanofluid to increase. Mutuku [13] clearly showed that CuO-EG nanofluids lead to a swift decline of heat at the boundary layer. Alsoy-Akgün [14] observed that the behaviours of all the variables are subjective to the varying values of parameters (Rayleigh number, Hartmann number, and particle fraction). Zahan et al. [15] found that increasing the value of the Rayleigh number and divider position causes an increase in the heat transfer, but an increase in Hartmann number reduces the heat transfer. Also, they figured that increasing solid volume fraction improves the heat transfer performance. Alsabery et al. [16] showed that the porous layer increment considerably influences the heat transfer. Xiong et al. [17] considered a square cavity with a square thermal column to study the natural convection of the SiO2 -water nanofuid.

Among works done with nanofluids in various geometries, the numerical study by Vajjha et al. [18] investigates heat transfer of nanofluids placed in the flat tubes of an automobile radiator. The results show a considerable increase in average heat transfer coefficient with increasing concentration and Reynolds number. In another numerical study by Maiga et al. [19] to investigate thermal characteristics of the forced convective flow of nanofluids, Al2O3 /Ethylene glycol and Al2O3 Al/water nanofluids flowing in tube and radial geometric configurations were considered. Results show that nanofluids enhanced the heat transfer coefficient, and this enhancement is higher at higher particle concentrations. Abu-Nada et al. [20] studied the effect of inclination angles on a 2D enclosure filled with Cu/water nanofluid. Khanafer et al. [21] numerically investigated the heat transfer characteristics of nanofluids within two-dimensional side heated enclosures for various pertinent parameters. Results show that the presence of nanoparticles enhances the heat transfer characteristics of a fluid and the heat transfer characteristics of nanofluids increase significantly with an increase in volume fraction. Saleem et al. [22] demonstrated that platelet shape geometry has maximum convective flow and a more random pattern of isotherms due to Darcy’s number. Javaherdeh et al. [23] carried out a computational investigation to analyze laminar natural convection heat characteristics in a wavy cavity filled with CuO /water nanofluid. The magnetic field caused the local Nusselt number to decrease in value, at the hot wall, in their work. Moreover, increasing nanoparticle concentration resulted in enhancing the heat transfer performance. Nevertheless, the presence of nanoparticles leads to a noteworthy improvement in heat transfer for all values of the Rayleigh number. Rahimi et al. [24] considered a hollow L-shaped cavity filled with SiO2--TiO2 /water-EG mixture of nanofluid to examine the natural convective heat transfer and fluid flow by lattice Boltzmann method.

Jung et al. [25] conducted an experimental study to investigate the heat transfer coefficient and friction factor of nanofluids in a rectangular-shaped microchannel. Kondaraju et al. [26] conducted a numerical simulation to investigate the effects of coagulation of particles on thermal conductivity and found that heat transfer increases with an increase in volume fraction. Oztop et al. [27] conducted another numerical study to examine the heat and fluid flow due to the natural convection of nanofluids inside a partially heated rectangular-shaped enclosure. Results indicate that the heat transfer enhances with an increase in Rayleigh number as well as with an increase in particle concentration. The numerical investigation on mixed convection heat transfer by Kherbeet et al. [28] shows that the Nusselt number increases with increasing the solid volume fraction and Reynolds number and also reveals that the nanofluid containing SiO2 nanoparticles have the highest Nusselt number. To investigate the forced convection flow behavior of Al2O3 nanofluid in a radial cooling system, Yang et al. [29] conducted a numerical simulation and found that heat transfer enhances with a rise in Reynolds number and particle concentration. A comprehensive review that presents an all-inclusive study on forced convective heat transfer enhancement was presented by Kakac et al. [30].

Yang et al. [31] conducted an experimental study on nanofluids that exhibit both viscosity and elastic properties and found that thermal conductivity increases with increasing particle volume concentration and temperature. Viscosity was found to be higher when using visco-elastic nanofluid rather than the base fluid, and it increases with increasing particle volume concentration but decreases when the temperature was increased. A study performed by Khanafer et al. [32] analyses the synthesis of thermo-physical properties of nanofluids and their contribution in heat transfer enhancement. It was concluded that the types of models that give appropriate values at different temperatures were not clearly defined, suggesting further investigations in the measurement of nanofluid properties.

An interesting numerical study on nanoparticles of various shapes, performed by Fan et al. [33], investigates the effects of thermal conductivity ratio, particle volume fraction, and particle morphology on multiple aspects of nanoparticles such as temperature gradient, phase lags of heat flux, and thermal conductivity. Results reveal that two aspects of nanoparticle geometry affect thermal conductivity, i.e., particle’s radius of gyration and/or non-dimensional interfacial area. In a study performed on transient buoyancy-driven convective heat transfer of bottom-heated water-based nanofluids by Yu et al. [34], results with and without considering Brownian motion were recorded for each volume fraction value. Here a phenomenon called Pitchfork bifurcation was observed for Gr>5.60×104 , the critical Grashof number. Ghalambaz et al. [35] showed that adding a mixture of nanoparticles for a conductive-dominant system (low Rayleigh number) causes an enhancement in the heat transfer. They showed that the Rayleigh number and the thermal conductivity ratio are the escalating factors of the heat transfer rate. Their results showed that the local Nusselt number at the surface of the conjugate wall shrinks significantly for a convective-dominant flow (high Rayleigh number) and an excellent thermally conductive wall.

Comparative analyses on the effects of different nanoparticles on the heat transfer characteristic are available. However, research on the impact of varying base fluid on the nanofluid heat transfer characteristics is rare in the literature. Based on the literature review and to the best of the authors’ knowledge, there is no scholarly work comparing water and ethylene-glycol as the base fluids used for heat transfer medium as nanofluid. To remove the bulk heat or to cool a device in an industry or laboratory is a significant event for enhancing the efficiency of a machine or electrical system, and choosing an appropriate base fluid while using nanofluid plays an important role. The present research is a comparative investigation of the flow and thermal performance between nanofluids and pure-fluids flowing in such a square cavity whose bottom wall is partially heated by a heat source of variable length. The governing non-dimensional Navier Stokes and energy equations are solved numerically using the finite volume method with the staggered grid.

2  Formulation of the Problem

A square cavity has been considered with a heat source placed at its bottom wall, as shown in Fig. 1. The top border is entirely adiabatic, and a part of the bottom wall is kept heated while the rest is adiabatic. The sidewalls are cool. Considering this cavity contains nanofluid, the flow and thermal behavior are investigated when the bottom wall is heated at different lengths and different base fluids and solid particles. There are some predefined underlined assumptions for the simplicity of the problem, and these are: fluid flow is laminar, steady-state, Newtonian, and incompressible. Viscous dissipation, as well as radiation effects, are neglected here. For buoyancy force density variation, Boussinesq approximations have been considered. The flow is governed by the following Navier Stokes and energy equations:

∂u∂x+∂v∂y=0 (1)

∂u∂t+u∂u∂x+v∂u∂y=−1ρnf∂p∂x+μnfρnf(∂2u∂x2+∂2u∂y2) (2)

∂v∂t+v∂v∂y+u∂v∂x=−1ρnf∂p∂y+μnfρnf(∂2v∂y2+∂2v∂x2)+g(ρβ)nf(T−Tc)ρnf (3)

∂T∂t+u∂T∂x+v∂T∂y=αnf(∂2T∂x2+∂2T∂y2) (4)

where ρnf is the density, μnf is the viscosity, βnf is the thermal expansion coefficient, αnf is the thermal diffusivity of nanofluid, and g is the acceleration due to gravity.

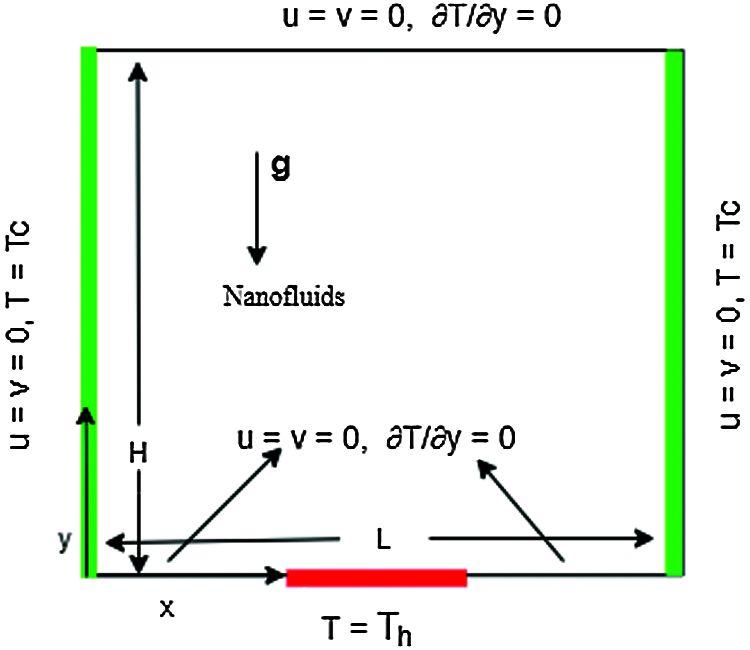
Figure 1: Schematic model and coordinate systems

To non-dimensionalizing the above mentioned governing equations, the appropriate non-dimensional variables are defined as follows:

P=pL2ρfαf2,Pr=νfαf,Ra=gβ(Th−Tc)L3Prνf2,τ=αftL2, (5)

where xh is the dimensional heat source length of the bottom wall, Pr is the Prandtl number and Ra is the Rayleigh number.

The effective viscosity for a suspension containing small spherical solid nanoparticles is given by Brinkman [36]:

μnf=μf(1−ϕ)1.5 (6)

The effective density and thermal expansion coefficient of a fluid containing solid nanoparticles can be given as [37]:

ρnf=(1−ϕ)ρf+ϕρs (7)

(ρβ)nf=(1−ϕ)(ρβ)f+ϕ(ρβ)s (8)

The heat capacitance of nanofluid is given as:

(ρcp)nf=(1−ϕ)(ρcp)f+ϕ(ρcp)s (9)

The Maxwell–Garnetts model [38] for effective thermal conductivity of a mixture of base fluid along with the particular concentration of nanoparticles states:

knf=ks+2kf−2(kf−ks)ϕks+2kf+(kf−ks)ϕkf (10)

Applying the above non-dimensional variables into Eqs. (1)–(4) yield the following non-dimensional equations:

∂U∂X+∂V∂Y=0 (11)

∂U∂τ+U∂U∂X+V∂U∂Y=−1(1−ϕ)+ϕρsρf∂P∂X+Pr(1−ϕ)2.5[(1−ϕ)+ϕρsρf](∂2U∂X2+∂2U∂Y2) (12)

∂V∂τ+U∂V∂X+V∂V∂Y=−1(1−ϕ)+ϕρsρf∂P∂Y+Pr(1−ϕ)2.5[(1−ϕ)+ϕρsρf](∂2V∂X2+∂2V∂Y2)+RaPrΘ[11+(1−ϕ)ρfϕρsβsβf+11+(1−ϕ)ρfϕρs](13)

∂Θ∂τ+U∂Θ∂X+V∂Θ∂Y=knfkf[(1−ϕ)+ϕ(ρcp)s(ρcp)f](∂2Θ∂X2+∂2Θ∂Y2) (14)

The physical properties of the particles and fluid taken into consideration are tabulated in Tab. 1.

To solve the non-dimensional governing Eqs. (11)–(14) the following boundary conditions are used:

Θ=0,U=V=0,atX=0,1,0<Y<1 (15)

where ϵ is the non-dimensional heat source length which can vary.

The rate of heat transfer is measured in terms of the Nusselt number. The local Nusselt number is defined by

and the average Nusselt number on the heated bottom wall is defined by

3  Numerical Procedure and Code Validation

A SIMPLE (Semi-Implicit Method for Pressure-Linked Equations) algorithm, also known as a pressure-corrector method, is used to integrate the problem (11)–(14) numerically in the given cavity. The SIMPLE algorithm involves the nodal momentum contributions and cell-face dissipation coefficients in the pressure-correction equation on a collocated or staggered grid arrangement. For the pressure and temperature, computational results are computed and stored at the center of the node. A three-point backward difference formula is used for the time derivative of the velocity and temperature, whereas the central difference quotient is used for the convective and diffusion terms. After discretizing the governing Eqs. (11)–(14), the resulting quasi-linear algebraic equations are solved using the line Gauss–Siedel method. In this study, the local mesh refinement is performed with a tangential hyperbolic stretching function. Further, a constant time step Δτ=104 is used to ensure the CFL number lies between 0 and 1.

In order to validate our code, the present results have been compared to the benchmark solution of Davis [42], in which side heated cavity flow was considered (Tab. 2). In this comparison, the results are presented in terms of the average Nusselt number and maximum U and V velocities for three different Rayleigh numbers. From this table, it is seen that results are in good agreement with the benchmark solutions of Davis [42]. Khanafer et al. [21] conducted a numerical study on the natural convection of nanofluid in a side heated square cavity. A comparison has been made with these numerical results for Gr 105 and 0.1(10) . The results are shown in Fig. 2a, which clearly illustrate a good agreement of our solutions with Khanafer et al. [21]. In addition, one comparison is also performed with the experimental study conducted by Calcagni et al. [43] in which the present geometric configuration is utilized, that is, localized heating from the bottom and symmetrically cooling from the sides. For comparison, solutions are obtained for pure fluid with Pr = 0.71 Ra = 1.205 × 105 and heat source length ɛ = 4/5, and the agreement is good indeed, as depicted in Fig. 2b.

For the present problem, a grid independence test has been conducted for Pr = 16.6, Ra=105 , ϵ=3/5 and ϕ=0.1 . Three grid arrangements are taken into consideration as 100 × 100, 140 × 140, and 180 × 180, and the results are shown in Fig. 2c. For these three different grid arrangements, the results are almost independent for temperature distribution Θ . Therefore, it is reasonable to select the 140 × 140 control volumes, and the rest of the simulations are performed with this grid size.

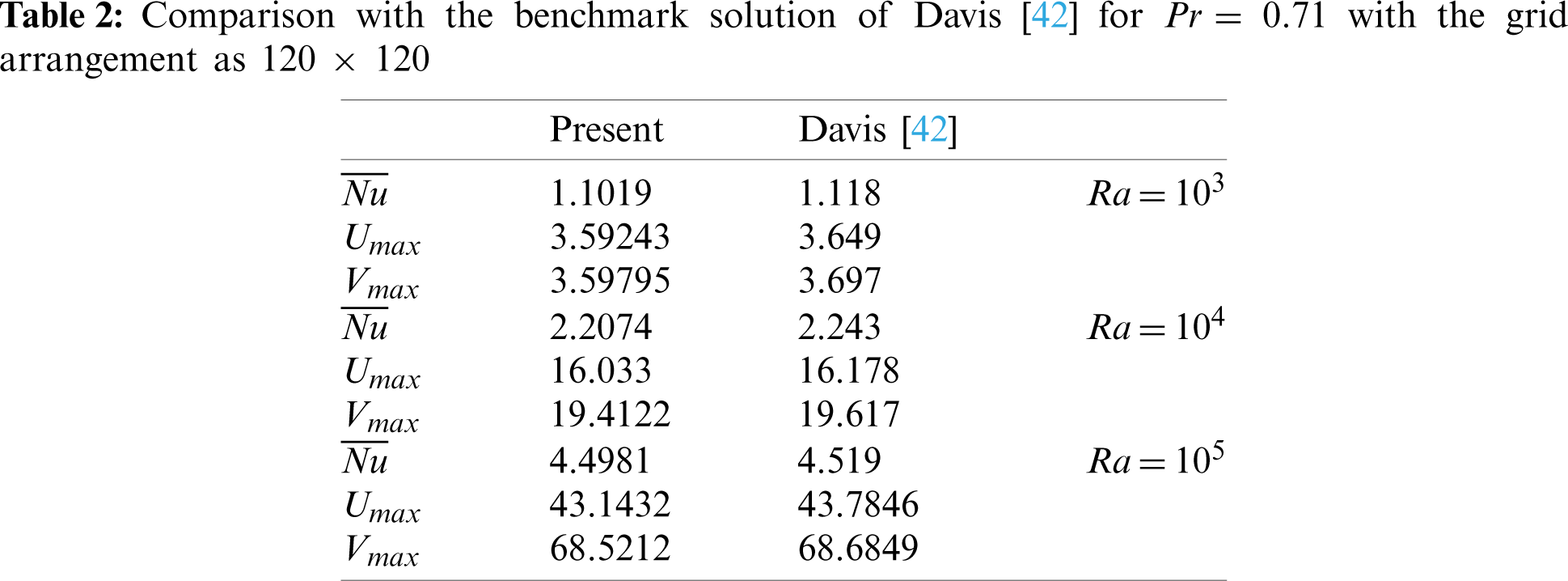
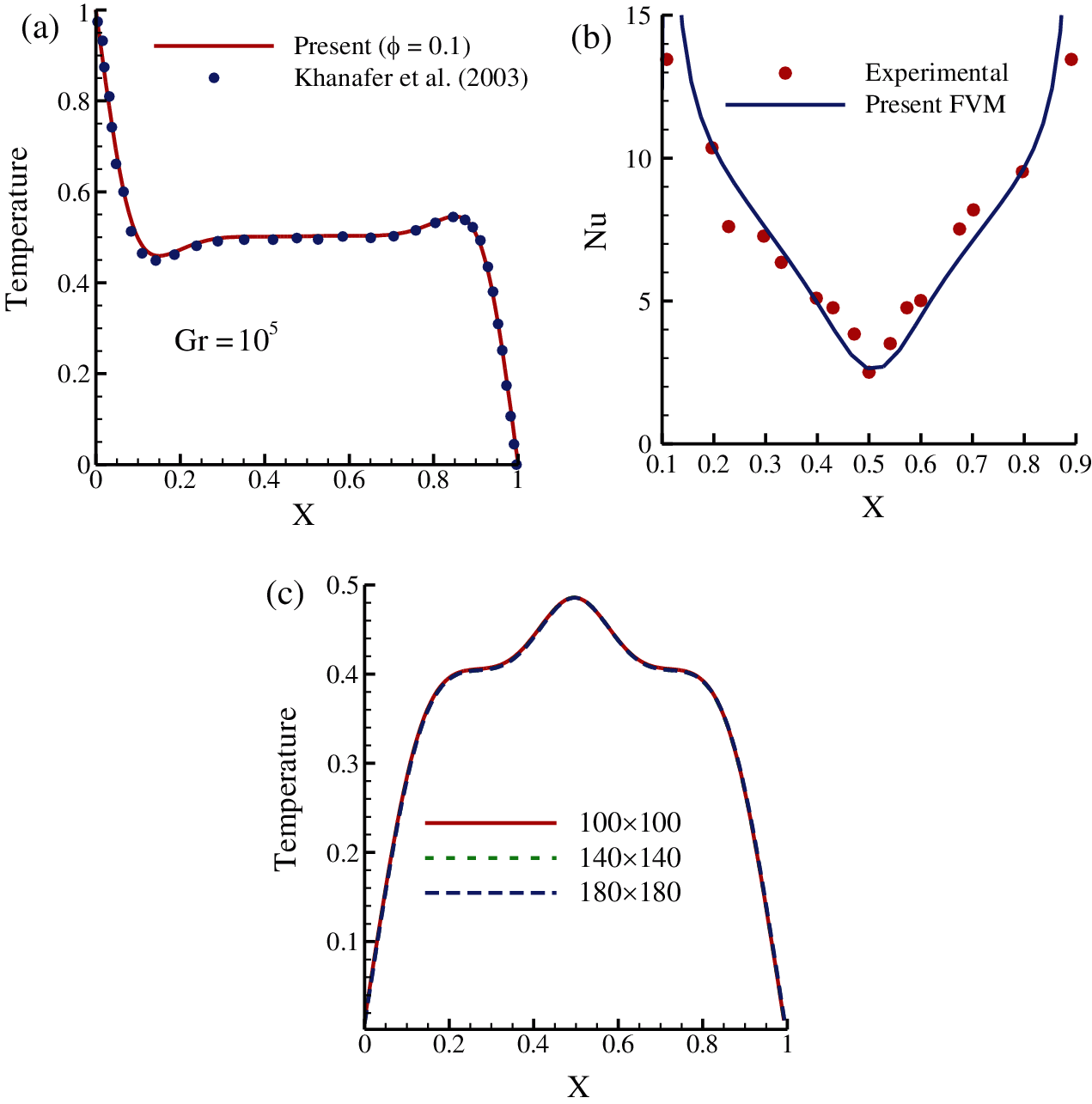
Figure 2: (a) Comparison of the temperature distribution with the numerical results of Khanafer et al. [21] while Pr = 6.2, Gr = 105, and ϕ=0.1(10%) (Cu/water nanofluid) (b) Comparison of the local Nusselt number Nu with the experimental results of Calcagni et al. [43] while Pr = 0.71, Ra = 1.205 × 105, ɛ = 4/5 and ϕ=0.0 (purefluid) (c) Grid independence test for temperature Θ at mid plane of y while Pr=16.6 , Ra=105 , ϵ=3/5 , and ϕ=0.1 (Cu/ethylene glycol nanofluid)

4  Results and Discussion

Simulations have been carried out for several Rayleigh numbers, Ra, from 103 to 105 and nanoparticle volume fraction between 0 . Five separate cases are considered here as follows.

4.1 Case 1: ϵ = 3/5 for Cu/Ethylene Glycol Nanofluid

The isotherms and streamlines at ϕ=10 (solid line) and at ϕ=0 (dashed line) are plotted for a range of Rayleigh numbers and are shown in Fig. 3. From these figures, it is evident that at a low Ra of 103 there is no break in the symmetry between the right and left cells but at high Ra of 105 the right core vortex is smaller than the left one. The maximum magnitudes of the stream function, ψmax while Ra = 103,104,105 are 0.21, 3.23 and 15.6 for pure-fluid and 0.17, 2.85 and 16.18 for nanofluid, respectively. With an increase in Ra, the flow rate of the fluid increases. At Ra=103 and 104 nanofluids exhibit a lower flow rate than pure-fluid but at 105 the flow rate becomes higher for nanofluid in comparison to pure-fluid. From Fig. 3, it is also seen that at Ra numbers 103 and 104 , the isotherms appear as smooth curves over most parts of the cavity with a few vertical lines on the edges. At a high Rayleigh number of 105 the flow becomes slightly transitional, and more vertical isotherms appear, and the curves have sharper turning points. Also, the deviation in temperature distribution between pure and nanofluid increases with an increase in the Rayleigh number. This kind of characteristic is observed because, at a low Rayleigh number, the mode of heat transfer is dominated by conduction, while with an increase in the Rayleigh numbers, the mode of heat transfer shifted from conduction to convection. That is, at a higher Rayleigh number, convection heat transfer becomes more dominant than conduction, which distorts the isotherm symmetry and higher flow rate of the fluid.

The velocity and temperature distribution at mid X and mid Y planes of the cavity for both pure and nanofluid are illustrated in Figs. 4a--4b, respectively. Fig. 4a shows that there is a higher difference in the profiles between high Ra and low Ra. This occurs because, at low Rayleigh number, the heat transfer is heavily influenced by conduction, but at higher Rayleigh number, the heat transfer occurs prominently by convection which causes the velocities of the fluids to rise. From Fig. 4b, it can be seen that at Ra (= 103 and 104 ) the temperature value at any point in the cavity is higher for pure fluid than for nanofluid, which indicates that the presence of nanofluid enhances heat transfer rate, and therefore the heated part of the cavity becomes cooler. At Ra=105 the flow is slightly transitional, for which at some points nanofluid exhibits higher temperature than pure-fluids.

Fig. 5 represents how the local Nusselt number varies along the heated bottom wall for Ra (= 103,104,105 ) at ϕ=10 and ϵ=3/5 . It can be seen from this figure that for any particular Ra the Nusselt number is minimum at the mid-length of the heat source. The variation of average Nusselt number at three different Ra with varying ϕ are tabulated in Tab. 3. From this table, it is clearly seen that increasing the Ra and the nanoparticle volume fraction ϕ lead to an increase in the average rate of heat transfer.

The velocity and temperature behavior of the nanofluid within the cavity is observed as well for various concentrations, ϕ (= 0, 0.05, 0.1) with Ra = 105. These results are illustrated in Figs. 6a--6b. Here it is interesting to note that when pure fluid is used, the velocity is lower, and the temperature is higher than that for nanofluids. As we keep increasing the concentration, the difference between nano and pure fluid keeps rising. This reveals that the use of nanofluid is adequate for cooling since the cavity exhibits lower temperature than it did when it contained pure fluid. Moreover, it also shows that with an increase in the concentration of nanoparticles, the cavity cools down and its temperature rises further, and consequently, heat transfer rate is enhanced.

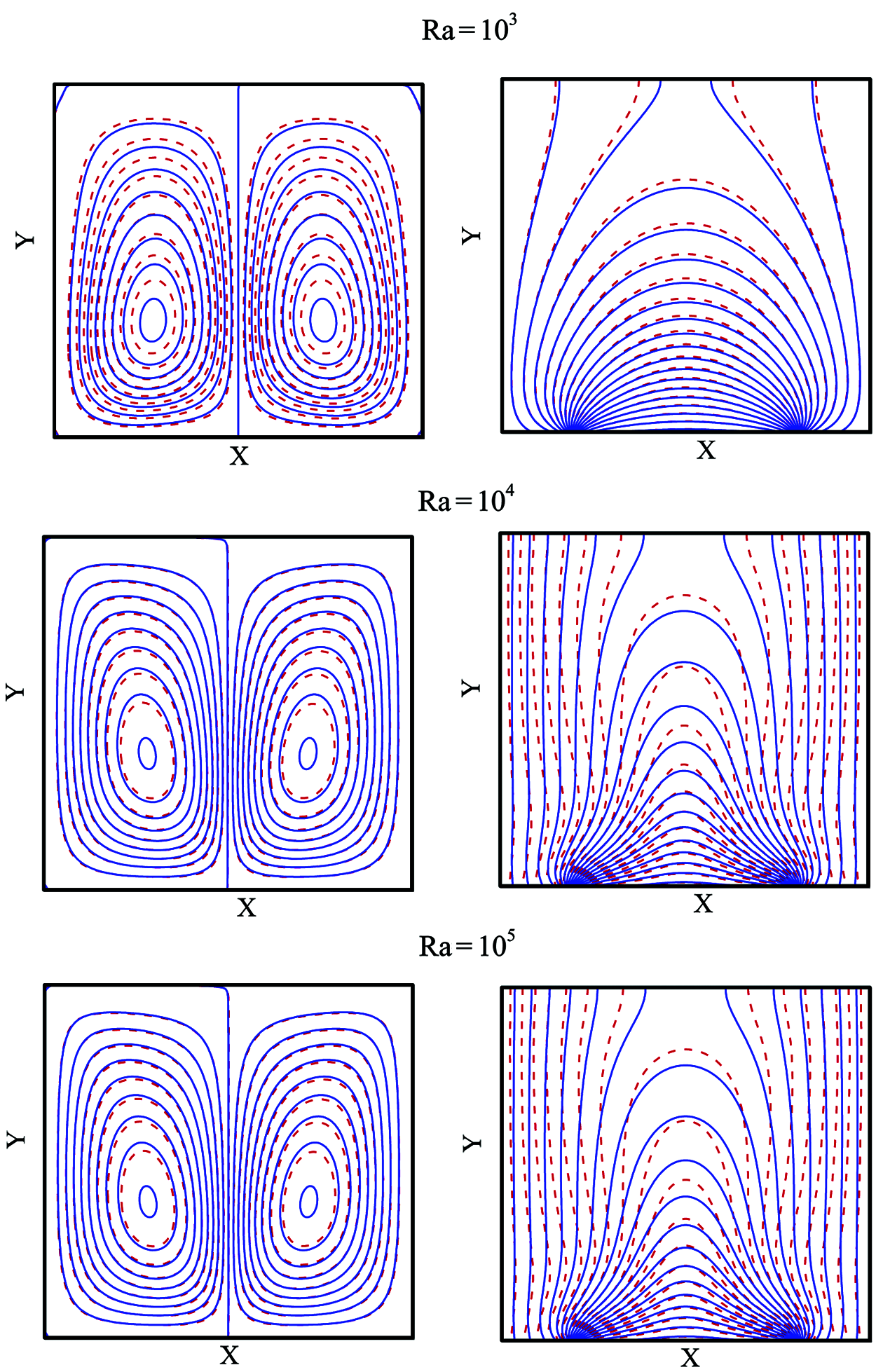
Figure 3: Comparison of streamlines (left) and isotherms (right) between nanofluid (solid line) and pure fluid (dashed line) at various Ra while

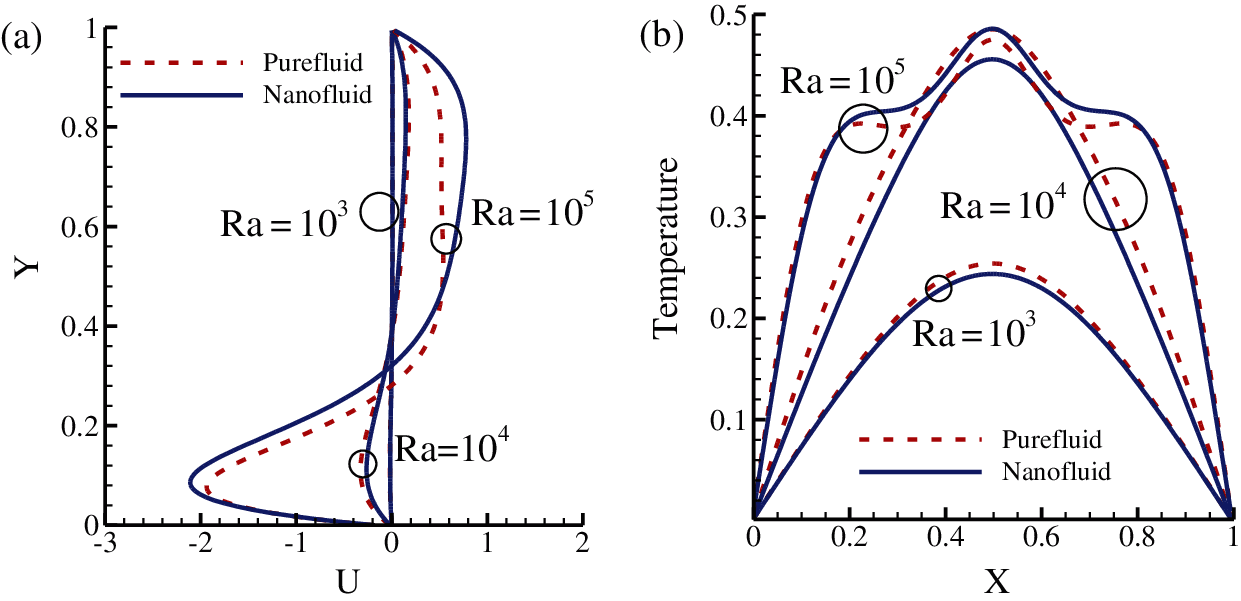
Figure 4: (a) U velocity at x midplane (b) Temperature distribution Θ at Y midplane for different Ra while ϵ=3/5 , ϕ=10%, Pr=16.6

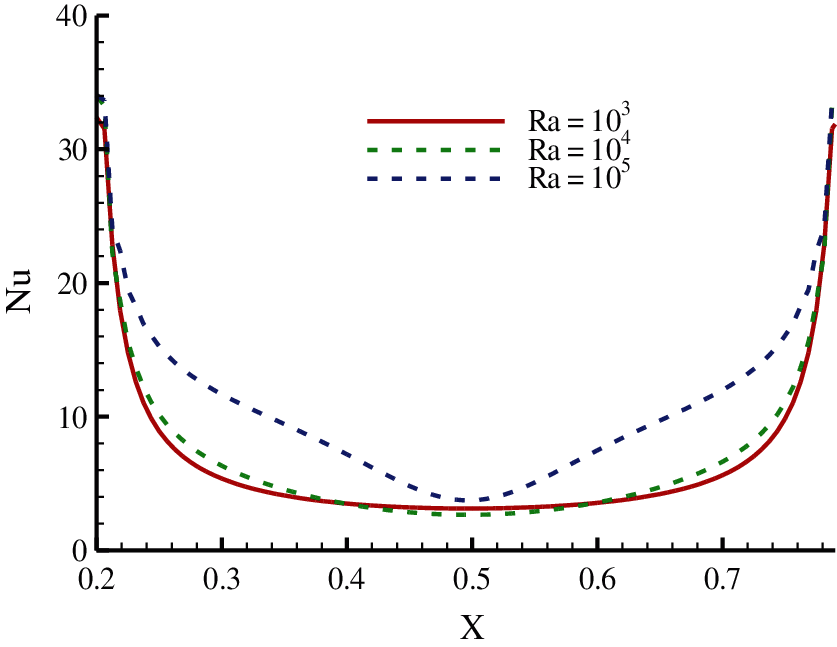
Figure 5: Variation of local Nusselt number, Nu with Rayleigh number while ϵ=3/5 , ϕ=10% and Pr=16.6

4.2 Case 2: ϵ=2/5 for Cu/Ethylene Glycol Nanofluid

In this case, the length of the heat source on the bottom wall was reduced to 2/5. The isotherms and streamlines at ϕ=10 and ϕ=0 are plotted in Fig. 7 for Rayleigh numbers 103,104, and 105 . The isotherms reveal a smaller deviation between nanofluid and pure fluid as far as temperature distribution is concerned than in Case 1. As Rayleigh’s number increases, the isotherms’ turning points get sharper, just as we observed in Case 1. The streamline plot shows that the two vortices are almost similar, with minor differences in nano and pure fluids. The maximum stream function values, in this case, are 0.191, 2.793, and 13.30 for pure-fluid and 0.163, 2.435, and 14.04 for nanofluid, while Ra is 103,104 and 105 , respectively. The maximum stream function values for nanofluid is lesser than pure fluid for the first two Rayleigh numbers. For Ra=105 the maximum value is higher for nanofluid. Comparing Case 1 and Case 2, for any choice of fluid and Rayleigh number, the quantity ψmax always has a higher value in Case 1 than in this case, meaning that the flow rate is higher when heat source length is larger.

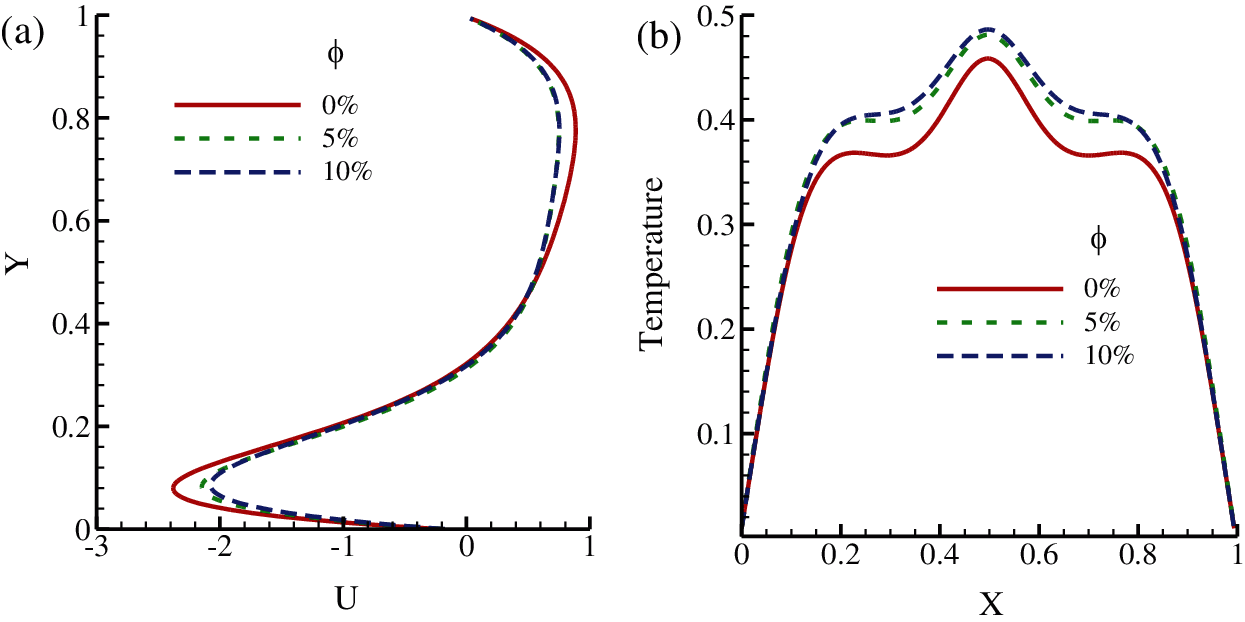
Figure 6: (a) U-velocity at X = 0.5 (b) temperature at Y = 0.5 for varying concentrations of nanofluid while Ra=105 , ϵ=3/5 and Pr=16.6

In Fig. 8, the graphs follow the same trend as that in Fig. 4. However, the maximum values of U velocity for each set of Rayleigh numbers are much lesser in this case than in Case 1. Comparing Figs. 4a and 8a, it is also evident that there is a remarkable similarity in the U velocity profiles in Case 1. In the temperature profile in Fig. 8b, the maximum temperature was reached at the midplane of the cavity at Ra=105 which also occurred in Case 1. For Ra = 103 and Ra = 104, a linear increase up to the midplane is observed, and a decrease is observed after the midplane. But the temperature profile did not rise linearly for Ra = 105. A plateau is seen during both increment and decrement of temperature profile before and after the midplane as the natural convection mode of heat transfer becomes dominant for high Ra number compared to conduction heat transfer. The linear augmentation in the temperature profile is decelerated before the midplane as two opposing vortexes tend to hamper the natural circulation of fluid flow, which decreases the temperature rise just before the midplane. The linear decrease after the midplane is also observed for the same reason.

4.3 Case 3: ϵ=1/5 for Cu/Ethylene Glycol Nanofluid

In this case, the length of the heat source was further reduced to 1/5 to investigate its impact on the flow and thermal behavior of nanofluids. The streamlines and isotherms are illustrated in Fig. 9 and the temperature and velocity profiles in Fig. 10. By comparing Figs. 9 and 10, it can be seen that changing ϵ does not have any profound effect on the shape of the flow field as it still stays in a similar shape. The maximum stream function values, in this case, are 0.149, 2.0295, and 10.685 for pure fluid and 0.128, 1.736, and 10.1607 for nanofluid, while Ra is 103,104 and 105 , respectively. Comparing among three cases, for any choice of fluid and Rayleigh number, the ψmax always has a higher value in Case 1 than Case 2 and Case 3, which means the flow rate is higher when the heat source length ϵ is larger.

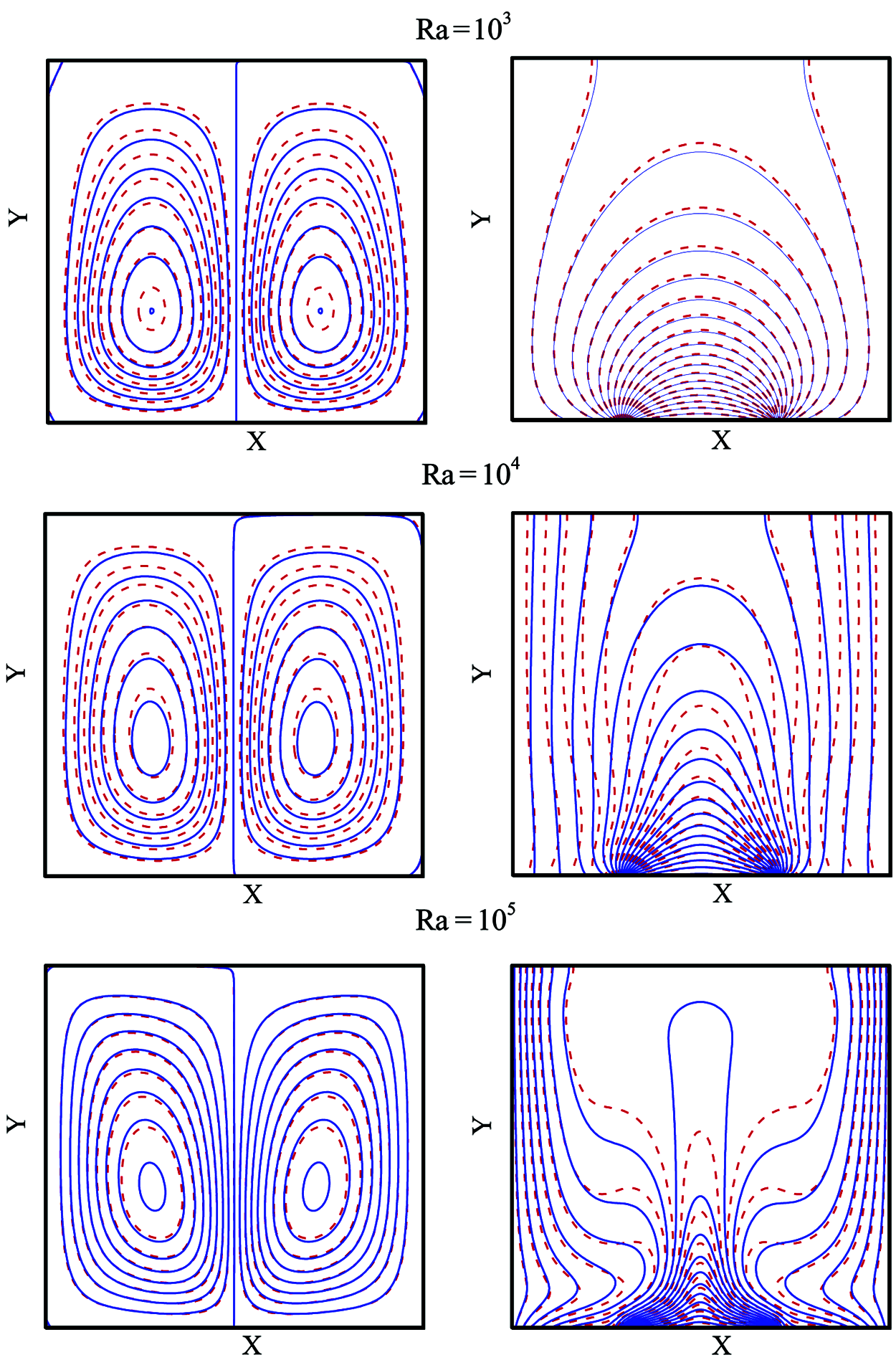
Figure 7: Streamlines (left) and isotherms (right) contours between nanofluid (solid line) and pure-fluid (dashed line) at various Rayleigh numbers while ϵ=2/5 , ϕ=10% and Pr=16.6

Considering Figs. 4 and 10, it is revealed that maximum velocity is reached in both cases at Ra=105 . However, in Case 1, the maximum velocity found was way higher than in this case, showing that if heat source length is increased, then flow velocity at the midplane of the cavity also gets higher. Comparison between Figs. 4 and 10 reveals that the profile shapes look very similar, but there are differences in the magnitudes. In both Figs. 4b and 10b at Ra=104 , the maximum temperature was obtained at the midplane of the cavity. The difference is that in Fig. 10b of Case 3, the maximum temperature was lower than in Fig. 4b of Case 1, showing that if the length of the heat source is reduced, then the cavity temperature by default becomes cooler as a result of smaller heating length.

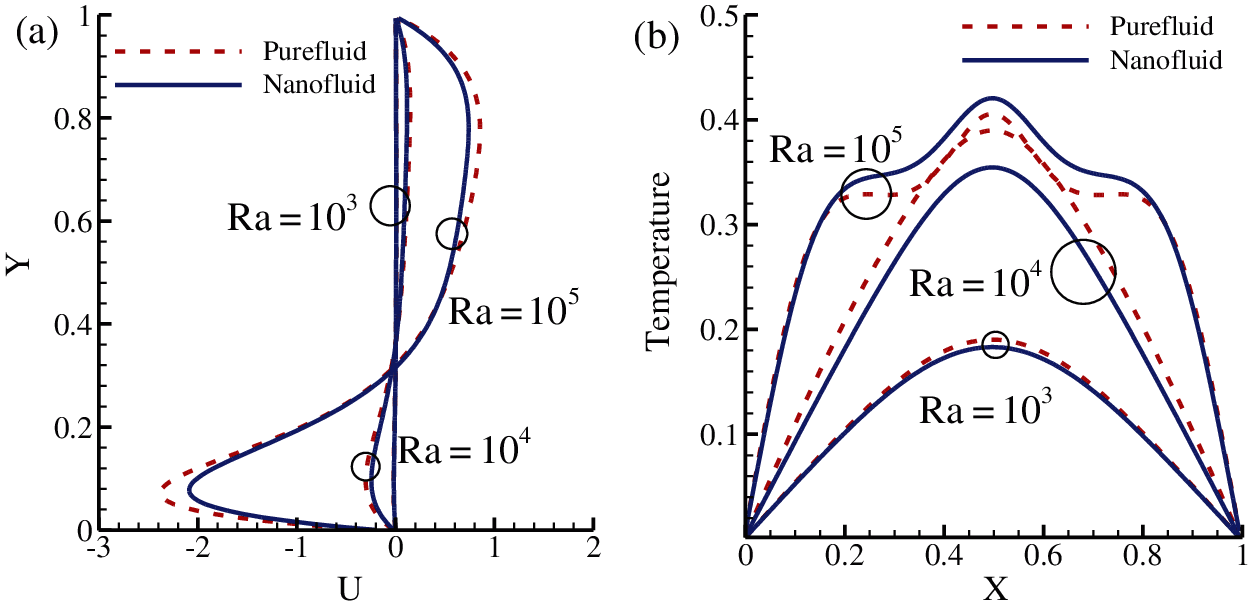
Figure 8: (a) U-velocity at X = 0.5 (b) temperature at Y = 0.5 of nanofluid (solid line) and pure-fluid (dashed line) at various Rayleigh numbers while ϵ=2/5 , ϕ=10% , and Pr=16.6

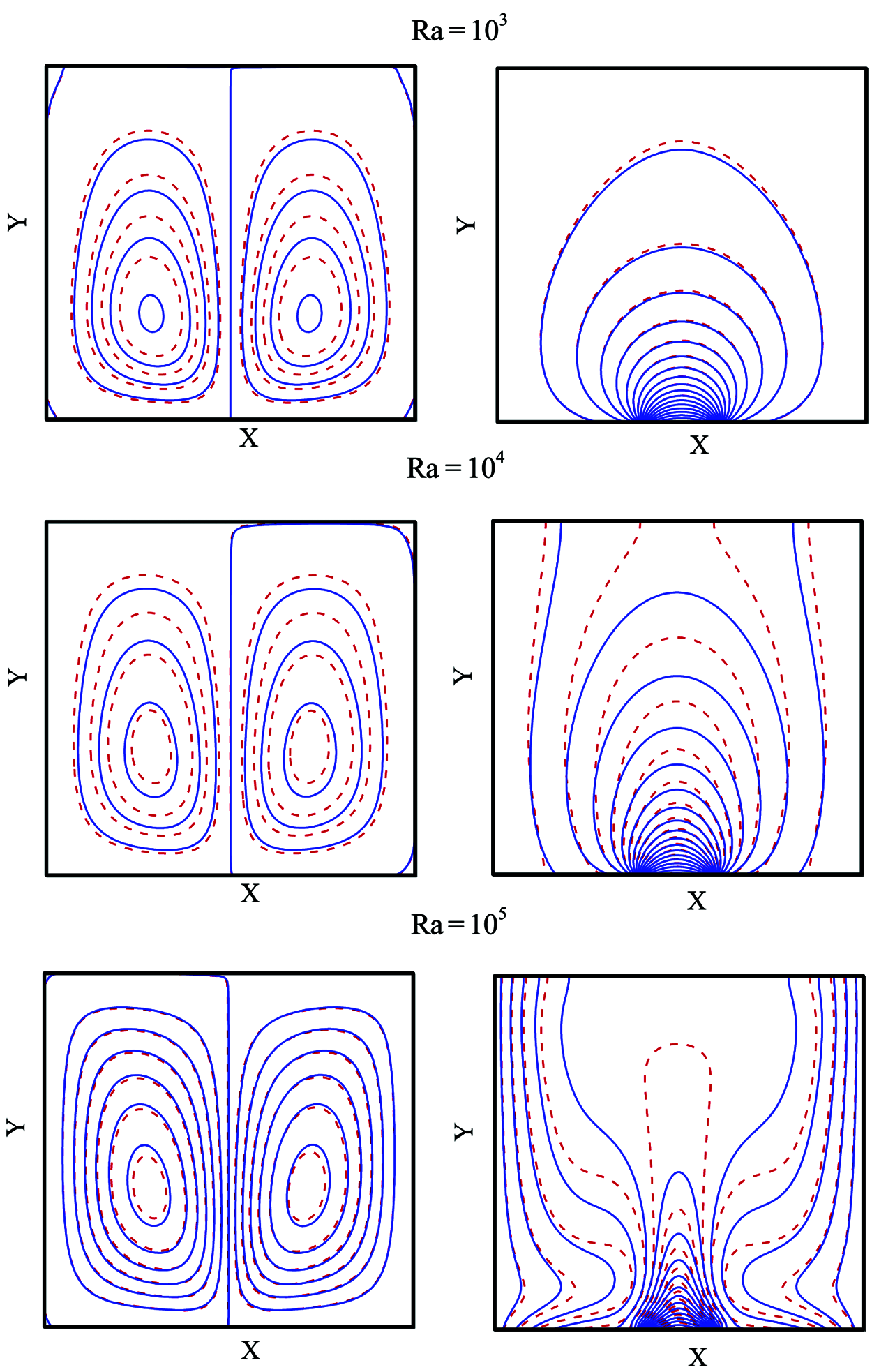
Figure 9: Comparison of streamlines and isotherms contours between nanofluid (solid line) and pure fluid (dashed line) at various Rayleigh numbers while ϵ=1/5 , ϕ=10% , Pr=16.6

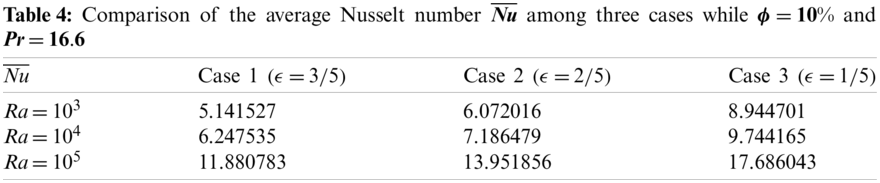
The comparison of the average Nusselt numbers, Nu¯ , at three different lengths of heat source is tabulated in Tab. 4. This table reveals that for any specific Rayleigh number, the average Nusselt number is always higher for ϵ=1/5 than for ϵ=2/5 and ϵ=3/5 meaning that the heat transfer rate is increased when the heat source length is reduced.

4.4 Case 4: Effect of Changing Base Fluid on Average Nusselt Number

The Prandtl number characterizes the choice of the type of base fluid. Initially, ethylene glycol is chosen as the base fluid, which has a Prandtl number of 16.6. Keeping ϕ=10 the changes, if any, due to a different type of base fluid on average Nusselt number was observed. Then the base fluid was changed to water which has a Prandtl number of 6.2. The resulting average Nusselt numbers, Nu¯ , along with the Nu¯ of Case 1 are inserted in Tab. 5. It can be inferred from Tab. 5 that the average Nusselt number is always lower in this case than in Case 1, meaning heat transfer is less with water as base fluid rather than with ethylene glycol. Hence for a better heat transfer rate, the choice of base fluid should be ethylene glycol instead of water.

The effect of nanoparticles in the ethylene glycol-based nanofluid is more predominant compared to water-based nanofluid. This phenomenon is observed as the value of Pr is higher for ethylene glycol (ethylene glycol has a Pr of 16.6). According to the definition of Prandtl number, it is the ratio of momentum diffusivity and thermal diffusivity. When Pr < 1, it signifies that heat transfer in the fluid medium would be in conduction mode as thermal diffusivity would be more dominant in the fluid. On the other hand, when the Pr number is greater than one, transferring energy is more effective in convection mode as the momentum diffusivity of fluid is dominant. This also contributes to augment the impact of nanoparticles in the ethylene glycol on the heat transfer rate. As momentum diffusivity is more prevalent, the convection flow of fluid gets more robust, and more heat is carried away from the bottom heat source. As a result, the effect of nanoparticles in ethylene is more significant than the water as a base fluid.

4.5 Case 5: Effect of Changing the Nanoparticle

The choice of the type of nanoparticle is characterized by (cp)s,ρs,κs and βs . These parameters are changed for aluminum oxide Al2O3 nanoparticles to check whether this type of nanoparticles would cause any significant change in behavior of the nanofluid in comparison to Cu nanoparticles or not. A comparison of the average Nusselt number achieved in this case and in Case 1 is illustrated in Tab. 6. The table reveals that as far as the rate of heat transfer is concerned, the choice of particle should be Copper (Cu) since its average Nusselt number at any Rayleigh number is slightly higher than the one achieved when Al2O3 nanoparticles are used.

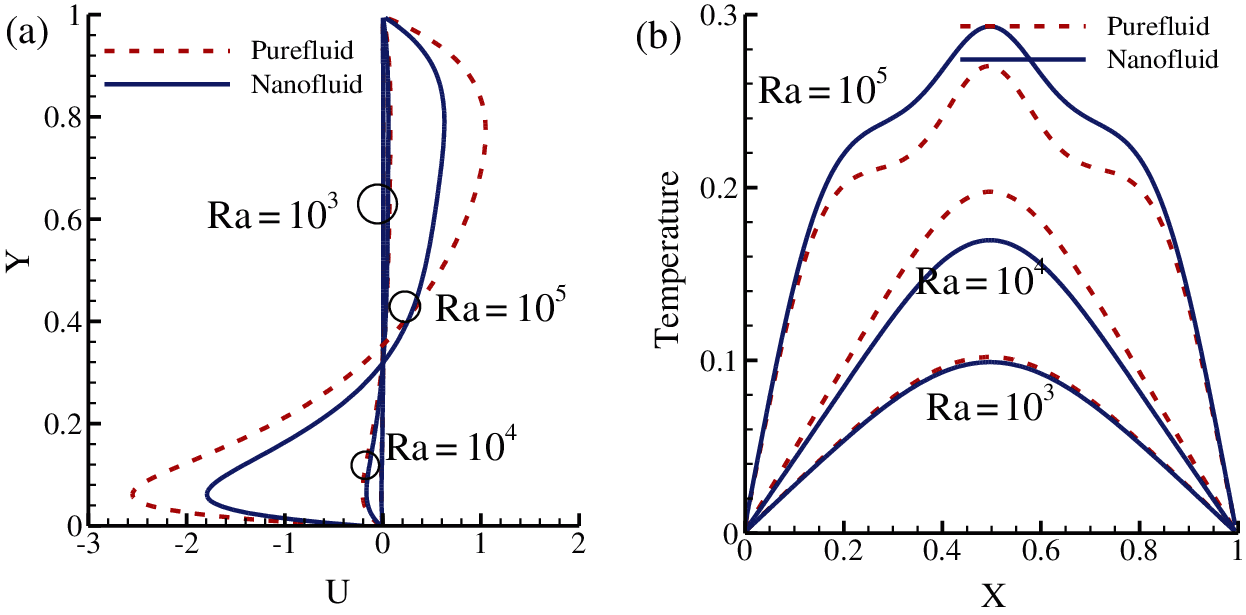
Figure 10: (a) U-velocity at x = 0.5 (b) temperature at y = 0.5 of nanofluid (solid line) and pure fluid (dashed line) at various Rayleigh numbers while ϵ=1/5 , ϕ=10% , Pr=16.6

5  Conclusion

The objective of the work is to investigate the flow and thermal behavior of nanofluid in a square cavity compared to ordinary pure fluid with localized heating at the bottom wall. At the end of the research, it is found that nanofluids are superior to pure fluid in transferring heat away from a cavity where the bottom border is heated. The length of heat source ϵ has a significant impact on flow behavior and the rate of heat transfer from the heat source. Lower the ϵ higher is the heating effect taking place, and hence the temperature distribution is almost the same at high ϵ values whereas it is very much different for low ϵ values. It is also found that the Rayleigh number affects the flow and thermal behavior of nanofluids. As far as the average Nusselt number is concerned, it decreased with an increase in ϵ . Changing base fluid to water instead of ethylene glycol reduces the average Nusselt number for any particular Ra indicating that ethylene glycol is a better transporter of heat energy away from a system rather than water. Choosing the appropriate nanoparticle in the nanofluid has also been found to be a key factor since it is observed that when the solid particle was Cu, the value of the average Nusselt number was higher than it was when the solid particle was Al2O3 . In a nutshell, it can be said that if there is a large laboratory or a system where there are plenty of devices generating a huge amount of bulk heat, then cooling with the help of nanofluids, instead of cooling via fans or pure fluids, will be a very effective and wise method since it will drive heat away faster and will increase the overall efficiency of the heat-generating components involved.

The results obtained from this research can be of good use to manage the bulk heat in telecom field data centers. Since nanofluids are proven to have a faster heat transfer rate than pure fluids, their use as a coolant will more likely reduce the load on chillers and air conditioners, bringing down the electricity cost. A comparative analysis between two different base fluids (water and ethylene glycol) has been carried out. The study would help engineers utilize an optimum nanofluid to maximize the heat transfer rate. Moreover, the impact of different nanoparticles (Al2O3 and Cu) on the flow circulation and heat transfer rate was also analyzed. As a consequence, this article could be a guideline for thermal engineers to design more efficient heat transfer equipment.

Funding Statement: The third author acknowledges the Ministry of Science and Technology (MOST), the People's Republic of Bangladesh (https://most.gov.bd/), for providing the financial support for this research gratefully (Grant No. 441-EAS). The third author also acknowledges gratefully to the North South University for the financial support as a Faculty Research Grant (CTRG-20-SEPS-15) (http://www.northsouth.edu/research-office/).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  He, Y., Jin, Y., Chen, H., Ding, Y., Cang, D. et al. (2007). Heat transfer and flow behaviour of aqueous suspensions of TiO2 nanoparticles (nanofluids) flowing upward through a vertical pipe. International Journal of Heat and Mass Transfer, 50(11–12), 2272–2281. DOI 10.1016/j.ijheatmasstransfer.2006.10.024. [Google Scholar] [CrossRef]

 2.  Shafahi, M., Bianco, V., Vafai, K., Manca, O. (2010). An investigation of the thermal performance of cylindrical heat pipes. International Journal of Heat and Mass Transfer, 53(1--3), 376–383. DOI 10.1016/j.ijheatmasstransfer.2009.09.019. [Google Scholar] [CrossRef]

 3.  Pang, C., Jung, J., Lee, J., Kang, Y. (2012). Thermal conductivity measurement of methanol-based nanofluids with Al2O3 and SiO2 nanoparticles. International Journal of Heat and Mass Transfer, 55(21–22), 5597–5602. DOI 10.1016/j.ijheatmasstransfer.2012.05.048. [Google Scholar] [CrossRef]

 4.  Lee, S., Park, S., Kang, S., Bang, I., Kim, J. (2011). Investigation of viscosity and thermal conductivity of SiC nanofluids for heat transfer applications. International Journal of Heat and Mass Transfer, 54(1–3), 433–438. DOI 10.1016/j.ijheatmasstransfer.2010.09.026. [Google Scholar] [CrossRef]

 5.  Truong, B., Hu, L., Buongiorno, J., McKrell, T. (2010). Modification of sandblasted plate heaters using nanofluids to enhance pool boiling critical heat flux. International Journal of Heat and Mass Transfer, 53(1–3), 85–94. DOI 10.1016/j.ijheatmasstransfer.2009.10.002. [Google Scholar] [CrossRef]

 6.  Wen, D. (2008). Mechanisms of thermal nanofluids on enhanced critical heat flux (CHF). International Journal of Heat and Mass Transfer, 51(19–20), 4958–4965. DOI 10.1016/j.ijheatmasstransfer.2008.01.034. [Google Scholar] [CrossRef]

 7.  Chun, S., Bang, I., Choo, Y., Song, C. (2011). Heat transfer characteristics of Si and SiC nanofluids during a rapid quenching and nanoparticles deposition effects. International Journal of Heat and Mass Transfer, 54(5–6), 1217–1223. DOI 10.1016/j.ijheatmasstransfer.2010.10.029. [Google Scholar] [CrossRef]

 8.  Wen, D., Ding, Y. (2005). Formulation of nanofluids for natural convective heat transfer applications. International Journal of Heat and Fluid Flow, 26(6), 855–864. DOI 10.1016/j.ijheatfluidflow.2005.10.005. [Google Scholar] [CrossRef]

 9.  Lin, K., Violi, A. (2010). Natural convection heat transfer of nanofluids in a vertical cavity: Effects of non-uniform particle diameter and temperature on thermal conductivity. International Journal of Heat and Fluid Flow, 31(2), 236–245. DOI 10.1016/j.ijheatfluidflow.2009.11.003. [Google Scholar] [CrossRef]

10. Corcione, M. (2011). Rayleigh–Bénard convection heat transfer in nanoparticle suspensions. International Journal of Heat and Fluid Flow, 32(1), 65–77. DOI 10.1016/j.ijheatfluidflow.2010.08.004. [Google Scholar] [CrossRef]

11. Ashorynejad, H., Shahriari, A. (2018). MHD natural convection of hybrid nanofluid in an open wavy cavity. Results in Physics, 9(27), 440–455. DOI 10.1016/j.rinp.2018.02.045. [Google Scholar] [CrossRef]

12. Yu, G. B., Gao, D. J., Chen, J. H., Dai, B., Liu, D. et al. (2016). Experimental research on heat transfer characteristics of CuO nanofluid in adiabatic condition. Journal of Nanomaterials, 2016(7), 1–7. DOI 10.1155/2016/3693249. [Google Scholar] [CrossRef]

13. Mutuku, W. (2016). Ethylene glycol (EG)-based nanofluids as a coolant for automotive radiator. Asia Pacific Journal on Computational Engineering, 3(1), 1. DOI 10.1186/s40540-016-0017-3. [Google Scholar] [CrossRef]

14. Alsoy-Akgün, N. (2019). Effect of an uniform magnetic field on unsteady natural convection of nanofluid. Journal of Taibah University for Science, 13(1), 1073–1086. DOI 10.1080/16583655.2019.1682342. [Google Scholar] [CrossRef]

15. Zahan, I., Nasrin, R., Alim, M. (2018). MHD effect on conjugate heat transfer in a nanofluid filled rectangular enclosure. International Journal of Petrochemical Science & Engineering, 3(3), 114–123. DOI 10.15406/ipcse.2018.03.00085. [Google Scholar] [CrossRef]

16. Alsabery, A., Chamkha, A., Saleh, H., Hashim, I. (2017). Natural convection flow of a nanofluid in an inclined square enclosure partially filled with a porous medium. Scientific Reports, 7(1), 1–18. DOI 10.1038/s41598-017-02241-x. [Google Scholar] [CrossRef]

17. Xiong, X., Chen, S., Yang, B. (2017). Natural convection of SiO2-water nanofluid in square cavity with thermal square column. Applied Mathematics and Mechanics, 38(4), 585–602. DOI 10.1007/s10483-017-2183-6. [Google Scholar] [CrossRef]

18. Vajjha, R. S., Das, D. K., Namburu, P. K. (2010). Numerical study of fluid dynamic and heat transfer performance of Al2O3 and CuO nanofluids in the flat tubes of a radiator. International Journal of Heat and Fluid Flow, 31(4), 613–621. DOI 10.1016/j.ijheatfluidflow.2010.02.016. [Google Scholar] [CrossRef]

19. Maiga, S., Palm, S., Nguyen, C., Roy, G., Galanis, N. (2005). Heat transfer enhancement by using nanofluids in forced convection flows. International Journal of Heat and Fluid Flow, 26(4), 530–546. DOI 10.1016/j.ijheatfluidflow.2005.02.004. [Google Scholar] [CrossRef]

20. Abu-Nada, E., Oztop, H. (2009). Effects of inclination angle on natural convection in enclosures filled with Cu-water nanofluid. International Journal of Heat and Fluid Flow, 30(4), 669–678. DOI 10.1016/j.ijheatfluidflow.2009.02.001. [Google Scholar] [CrossRef]

21. Khanafer, K., Vafai, K., Lightstone, M. (2003). Buoyancy-driven heat transfer enhancement in a two dimensional enclosure utilizing nanofluids. International Journal of Heat and Mass Transfer, 46(19), 3639–3653. DOI 10.1016/S0017-9310(03)00156-X. [Google Scholar] [CrossRef]

22. Saleem, S., Nguyen-Thoi, T., Shafee, A., Li, Z., Bonyah, E. et al. (2019). Steady laminar natural convection of nanofluid under the impact of magnetic field on two-dimensional cavity with radiation. AIP Advances, 9(6), 65008. DOI 10.1063/1.5109192. [Google Scholar] [CrossRef]

23. Javaherdeh, K., Moslemi, M., Shahbazi, M. (2017). Natural convection of nanofluid in a wavy cavity in the presence of magnetic field on variable heat surface temperature. Journal of Mechanical Science and Technology, 31(4), 1937–1945. DOI 10.1007/s12206-017-0342-7. [Google Scholar] [CrossRef]

24. Rahimi, A., Kasaeipoor, A., Malekshah, E., Amiri, A. (2018). Natural convection analysis employing entropy generation and heatline visualization in a hollow L-shaped cavity filled with nanofluid using lattice Boltzmann method-experimental thermo-physical properties. Physica E: Low-Dimensional Systems and Nanostructures, 97(5), 82–97. DOI 10.1016/j.physe.2017.10.004. [Google Scholar] [CrossRef]

25. Jung, J., Oh, H., Kwak, H. (2009). Forced convective heat transfer of nanofluids in microchannels. International Journal of Heat and Mass Transfer, 52(1–2), 466–472. DOI 10.1016/j.ijheatmasstransfer.2008.03.033. [Google Scholar] [CrossRef]

26. Kondaraju, S., Jin, E., Lee, J. (2010). Direct numerical simulation of thermal conductivity of nanofluids: The effect of temperature two-way coupling and coagulation of particles. International Journal of Heat and Mass Transfer, 53(5–6), 862–869. DOI 10.1016/j.ijheatmasstransfer.2009.11.038. [Google Scholar] [CrossRef]

27. Oztop, H., Abu-Nada, E. (2008). Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. International Journal of Heat and Fluid Flow, 29(5), 1326–1336. DOI 10.1016/j.ijheatfluidflow.2008.04.009. [Google Scholar] [CrossRef]

28. Kherbeet, A., Mohammed, H., Salman, B. (2012). The effect of nanofluids flow on mixed convection heat transfer over microscale backward-facing step. International Journal of Heat and Mass Transfer, 55(21–22), 5870–5881. DOI 10.1016/j.ijheatmasstransfer.2012.05.084. [Google Scholar] [CrossRef]

29. Yang, Y., Lai, F. (2010). Numerical study of heat transfer enhancement with the use of nanofluids in radial flow cooling system. International Journal of Heat and Mass Transfer, 53(25–26), 5895–5904. DOI 10.1016/j.ijheatmasstransfer.2010.07.045. [Google Scholar] [CrossRef]

30. Kakac, S., Pramuanjaroenkij, A. (2009). Review of convective heat transfer enhancement with nanofluids. International Journal of Heat and Mass Transfer, 52(13–14), 3187–3196. DOI 10.1016/j.ijheatmasstransfer.2009.02.006. [Google Scholar] [CrossRef]

31. Yang, J., Li, F., Zhou, W., He, Y., Jiang, B. (2012). Experimental investigation on the thermal conductivity and shear viscosity of viscoelastic-fluid-based nanofluids. International Journal of Heat and Mass Transfer, 55(11–12), 3160–3166. DOI 10.1016/j.ijheatmasstransfer.2012.02.052. [Google Scholar] [CrossRef]

32. Khanafer, K., Vafai, K. (2011). A critical synthesis of thermophysical characteristics of nanofluids. International Journal of Heat and Mass Transfer, 54(19–20), 4410–4428. DOI 10.1016/j.ijheatmasstransfer.2011.04.048. [Google Scholar] [CrossRef]

33. Fan, J., Wang, L. (2011). Heat conduction in nanofluids: Structure-property correlation. International Journal of Heat and Mass Transfer, 54(19–20), 4349–4359. DOI 10.1016/j.ijheatmasstransfer.2011.05.009. [Google Scholar] [CrossRef]

34. Yu, Z., Xu, X., Hu, Y., Fan, L., Cen, K. (2011). Numerical study of transient buoyancy-driven convective heat transfer of water-based nanofluids in a bottom-heated isosceles triangular enclosure. International Journal of Heat and Mass Transfer, 54(1–3), 526–532. DOI 10.1016/j.ijheatmasstransfer.2010.09.017. [Google Scholar] [CrossRef]

35. Ghalambaz, M., Doostani, A., Izadpanahi, E., Chamkha, A. (2020). Conjugate natural convection flow of Ag-MgO/water hybrid nanofluid in a square cavity. Journal of Thermal Analysis and Calorimetry, 139(3), 2321–2336. DOI 10.1007/s10973-019-08617-7. [Google Scholar] [CrossRef]

36. Brinkman, H. (1952). The viscosity of concentrated suspensions and solutions. Journal of Chemical Physics, 20, 571–581. DOI 10.1063/1.1700493. [Google Scholar] [CrossRef]

37. Xuan, Y., Roetzel, W. (2000). Conceptions for heat transfer correlation of nanofluids. International Journal of Heat and Mass Transfer, 43(19), 3701–3707. DOI 10.1016/S0017-9310(99)00369-5. [Google Scholar] [CrossRef]

38. Maxwell, J. (1892Electricity and magnetism, vol. 1. Clarendon, Oxford: CP. [Google Scholar]

39. Gholinia, M., Gholinia, S., Hosseinzadeh, K. H., Ganji, D. D. (2018). Investigation on ethylene glycol nano fluid over a vertical permeable circular cylinder under effect of magnatic field. Results in Physics, 9, 1525–1533. DOI 10.1016/j.rinp.2018.04.070. [Google Scholar] [CrossRef]

40. Prince, H. A., Rozin, E. H., Chowdhury, E. H., Redwan, D. A., Mamun, M. A. H. (2021). A numerical comparison among different water-based hybrid nanofluids on their influences on natural convection heat transfer in a triangular solar collector for different tilt angles. Heat Transfer, 50(5), 4264–4288. DOI 10.1002/htj.22074. [Google Scholar] [CrossRef]

41. Redwan, D. A., Rahman, M. H., Prince, H. A., Chowdhury, E. H., Amin, M. R. (2020). Influence of Cu-water and CNT-water nanofluid on natural convection heat transfer in a triangular solar collector. ASME 2020 International Mechanical Engineering Congress and Exposition, vol. 11. American Society ofMechanical Engineers (ASME). DOI 10.1115/IMECE2020-23191. [Google Scholar] [CrossRef]

42. Davis, D. V. (1983). Natural convection of air in a square cavity: A benchmark numerical solution. International Journal of Numerical Methods in Fluids, 3, 249–264. DOI 10.1002/fld.1650030305. [Google Scholar] [CrossRef]

43. Calcagni, B., Marsili, F., Paroncini, M. (2005). Natural convective heat transfer in square enclosures heated from below. Applied Thermal Engineering, 25(16), 2522–2531. DOI 10.1016/j.applthermaleng.2004.11.032. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.