

 | Energy Engineering |  |
DOI: 10.32604/EE.2021.014467
REVIEW
Progress on Heat Transfer in Fractures of Hot Dry Rock Enhanced Geothermal System
1School of Petroleum Engineering, Changzhou University, Changzhou, China
*Corresponding Author: Hailong Yu. Email: yhl.doctor@163.com
Received: 29 September 2020; Accepted: 19 December 2020
Abstract: Hot Dry Rock (HDR) is the most potential renewable geothermal energy in the future. Enhanced Geothermal System (EGS) is the most effective method for the development and utilization of HDR resources, and fractures are the main flow channels and one of the most important conditions for studying heat transfer process of EGS. Therefore, the heat transfer process and the heat transfer mechanism in fractures of EGS have been the hot spots of research. Due to the particularity of the mathematical models of heat transfer, research in this field has been at an exploratory stage, and its methods are mainly experimental tests and numerical simulations. This paper introduces the progress on heat transfer in fractures of Hot Dry Rock EGS in detail, provides a comparative analysis of the research results and prospects for future research directions: It is suggested that relevant scholars should further study the mathematical equations which are applicable to engineering construction of seepage heat transfer in irregular fractures of the rock mass, the unsteady heat transfer process between multiple fractures of the rock mass and the heat transfer mechanism of the complex three-dimensional models of EGS.
Keywords: Hot Dry Rock; seepage heat transfer; mathematical equations; numerical simulation; fractures
In recent years, primary energy demand is largely provided by non-renewable energy, which has led to global warming. Therefore, energy shortage has always been the focus of sustainable development. Many countries have gradually improved their research on renewable energy to reduce dependence on non-renewable energy sources such as, fossil fuels, coal, etc. [1–4]. The European Parliament passed the “Renewable Energy Directive” on December 17, 2008. The National Development and Reform Commission of China passed the “13th Five-Year Plan for Renewable Energy Development” in December 2016 [5] International Energy Outlook 2017, published by the USA Energy Information Administration, expects the renewable energy industry to grow 66% over the next two decades to meet energy demand in 2040 [6]. These provide an effective way to diversify and balance the development of renewable energy [7,8]. Geothermal energy, as a renewable energy stored in the deep layer of the earth, is very rich in thermal energy and can help increase the global share of renewable resources to meet the higher demand for energy in the future [9–13]. Geothermal energy capacity is projected to reach 7.92 GW in the U.S. by 2050 and 18.3 GW globally by 2021 [6,14]. Archaeologists have discovered that the first use of geothermal resources by humans occurred more than 10,000 years ago. In the 14th century, the first geothermal heating system was installed in the French town of Chaudes-Aigues. Today, geothermal energy is being given more uses in homes, businesses, and industry, but these often utilize shallow geothermal heat, which is extracted by a ground source heat pump (GSHP) [15,16]. The development and utilization of deep geothermal resources (HDR), however, are still in the exploratory stage. In 2018, according to the statistics of the “China Geothermal Energy Development Report” [17], in China, the annual recoverable amount of shallow geothermal energy is equivalent to 700 million tons of standard coal, the annual recoverable amount of hydro-thermal geothermal energy is equivalent to 1,865 million tons of standard coal, and the storage amount of HDR geothermal resources is equivalent to 856 trillion tons of standard coal. Therefore, the development of HDR geothermal resources has a broad space for development.
The thermal energy of HDR which is a potential geothermal energy source is stored in a variety of metamorphic or crystalline rock bodies. Hydraulic pumps, therefore, are often required to stimulate the rock formations, causing fractures in the rock, which create a network of fractures as flow paths in the geothermal reservoir between the injection and production wells, resulting in the formation of EGS for heat extraction [18–20]. EGS was originally conceived in the 1970s in the Fenton Hill Project at Los Alamos National Laboratory in the United States [21]. The purpose of EGS is to use underground rock resources where there is insufficient water or low permeability. The process involves increasing the permeability of existing fractures or creating new ones by hydraulic fracturing, circulating water or other fluids into the fractures and pumping the fluids to the surface to extract heat [22–24]. Although there is enough heat available in the rocks several kilometers underground for mining, and the emissions of pollutants from EGS energy supply are small and more stable and continuous than other renewable energy sources such as solar and wind [25,26], the permeability of rocks at this depth is usually very low [27], and there are particularities in the heat transfer mechanism when fluids flow in EGS after fracturing, so the heat transfer mechanism and influencing factors need to be explored further. Also, fractures are the main flow channels and one of the most important conditions for studying heat transfer process of EGS [28,29], so understanding the heat transfer mechanism of fractures of EGS is important for the efficient exploitation of heat energy in HDR. In addition, studying the geometric distribution of underground fractures and their flow and heat transfer processes is not easy. Experimental testing is difficult due to the depth of HDR and the limited amount of accurate data that can be obtained from fractures [30]. The numerical simulation method, however, can provide more convenient conditions for the research of the heat transfer in fractures of Hot Dry Rock EGS and improve the accuracy of the results of the research. Therefore, the numerical simulation method is the main method of this research. The development of numerical simulation method firstly needs to establish a complete set of Hot Dry Rock EGS heat transfer mathematical model.
It is predicted that if only 2% of the EGS resource is recovered, underground thermal reservoirs have the potential to provide enough energy for more than 5,000 years in China [31]. However, at present, the reason for less development in Hot Dry Rock EGS in China may be that the initial investment is large and construction is difficult. The fundamental reason is that the research on the mechanics of heat transfer in fractures and the contributing factors of heat transfer process on Hot Dry Rock EGS are not deep enough. Especially so far, there is no mathematical equation for calculating the heat transfer amount of Hot Dry Rock EGS to meet the engineering application, which makes it impossible to calculate construction data accurately and it is difficult to accurately estimate construction costs. This phenomenon is not only found in China; the SpaUrach project in Germany, started in 1977, was abandoned in 1981 due to financial problems [32]. The Basel project in Switzerland [33] and the Geysers power plant in the United States [34] were abandoned due to technical difficulties. Based on these, this paper summarizes the research progress of the influence of the fracture structure and fluid flow in the fractures on the heat transfer of Hot Dry Rock EGS, as well as the progress on the heat transfer coefficient of the heat transfer process of the fractured rock mass, and prospects for future research directions.
2 The Mechanism of Heat Transfer in Fractures of Hot Dry Rock EGS
After reading a lot of literature and theoretical analysis, the author believes that the mechanism of heat transfer in fractures of Hot Dry Rock EGS is mainly divided into two directions, one is convective heat transfer mechanism, and the other is seepage heat transfer mechanism. The convective heat transfer mechanism mostly refers to the theories and mathematical equations that are continuously optimized based on Newton’s law of cooling, and the seepage heat transfer mechanism mostly refers to the theories and mathematical equations that are continuously optimized based on Darcy’s Law.
2.1 The Mechanism of Convective Heat Transfer
At present, the vast majority of scholars at home and abroad think that the heat transfer process between fluids and rocks in Hot Dry Rock EGS is mainly convective heat transfer supplemented by heat conduction. Therefore, the research work is mainly based on the mechanism of “convection & heat conduction”.
2.1.1 Convective Heat Transfer in Hot Dry Rock EGS
Convective heat exchange in Hot Dry Rock EGS refers to the heat exchange between the fluid and the rock mass when the fluid flows over the surface of the rock mass or the fractured surface of the rock mass [35], and its heat transfer mechanism basically follows Newton’s Cooling Formula [36]. But the convective heat transfer coefficient is no longer a constant and changes with the change of some factors which are the fluid temperature, the center temperature of the rock mass, the confining pressure and the roughness of the fractured surface of the rock mass. For the convective heat transfer coefficient in Hot Dry Rock EGS, the following four calculation equations are derived by domestic and foreign scholars [37–40]:
where
2.1.2 Heat Conduction in Hot Dry Rock EGS
Heat conduction in Hot Dry Rock EGS refers to the spontaneous heat transfer process from high temperature to low temperature caused by the temperature gradient in the hot dry rock mass. When the heat transfer medium is injected into Hot Dry Rock EGS, there is a temperature gradient between the fractured surface of the rock mass and the rock interior, which will inevitably cause heat conduction, because the temperature of the heat transfer medium is always lower than that of the rock mass. The heat conduction in Hot Dry Rock EGS is the main heat supplement way in which the heat transfer medium can continuously extract heat, and the amount of heat conduction depends on the internal energy of the rock mass at that position [36], which is directly related to the rock initial temperature, the thermal conductivity, the heat transfer area and the temperature gradient. For the determined Hot Dry Rock EGS, the rock initial temperature is related to the local geothermal geological conditions, such as the geothermal gradient, and the depth of drilling and fracturing [41,42]. Generally speaking, the more the geothermal gradient and drilling depth, the higher the rock initial temperature. The thermal conductivity is approximately considered to be a constant. The size of the heat transfer area mainly depends on the amount and degree of elongation of fractures of Hot Dry Rock EGS. In other words, the more fractures, the lager the fracturing range, which cause the larger the heat exchange area and the higher the amount of heat conduction. The degree of the temperature gradient mainly depends on the heat extraction rate which is directly related to the character of the heat transfer medium, the inlet temperature and velocity. This means that the lower the inlet temperature of the medium and/or the greater velocity, the more the temperature gradient and heat conduction [43–45].
In fact, for a certain large-scale Hot Dry Rock EGS, its heat conduction is an unsteady state process. When the heat extraction rate is greater than the heat recovery rate, the temperature of the rock mass will gradually decrease with time going by. When the temperature of the fractured surface of the rock mass is reduced to a certain extent, HDR geothermal well will lose the ability to extract heat, or the outlet temperature of the heat transfer medium will not reach the design value. At this time, HDR wells need to be sealed until the geothermal temperature meets the requirements to open the well to get heat [46]. The heat extraction rate, therefore, directly affects the heat extraction efficiency, the heat extraction cycle and life of HDR wells. So it is very important to study the unsteady heat conduction in Hot Dry Rock EGS for studying the performance of Hot Dry Rock EGS.
2.2 The Mechanism of Seepage Heat Transfer in Fractures of Hot Dry Rock EGS
The rock is in pressure equilibrium prior to hydraulic fracturing, and a pressure difference is formed after hydraulic fracturing between the upper and lower thermal reservoirs and the fracturing fluid, which leads to deformation of the rock, resulting in the formation of small fractures similar to porous media [47]. The flow state of the heat exchange medium injected by external pressure in these fractures is closer to seepage flow, so there should be seepage heat transfer in the Hot Dry Rock EGS. Seepage heat transfer refers to the heat transfer between the fluid and the rock mass in the process of seeping through the small fractures. The shape and distribution of those small fractures are extremely complex [48], so the trajectory of water during seepage heat transfer is irregular and random. However, author thinks that the seepage heat transfer characteristics of the fractures which are inhomogeneous and anisotropic of Hot Dry Rock EGS, which may require assumptions based on local thermal non-equilibrium, are not identical to those of the standard single porous medium, which is based on the assumption that the fracture medium achieves local thermal equilibrium [49]. The process of seepage heat transfer in fractures of Hot Dry Rock EGS is an unsteady process, because the temperature of the rock is constantly changing during the operation of EGS [50–52]. Also, the shape and distribution of the small particles used for support may have a certain impact on the seepage heat transfer in fractures of Hot Dry Rock EGS [53,54].In addition, the author thinks that the seepage heat transfer mechanism and convective heat transfer mechanism may be quite different. The thermal material parameters such as the viscosity and surface tension of the heat transfer medium may play a leading role during the seepage heat transfer process, which may profoundly affects the seepage heat transfer process, but the relationship with the macroscopic flow state of the convective heat transfer process is weak. However, so far, scholars have less relative research on the mechanism of seepage heat transfer in fractures of Hot Dry Rock EGS.
3 Research Progress of the Effect of Fracture Structure of Hot Dry Rock EGS on Heat Transfer
The research models of fracture structure of Hot Dry Rock EGS, so far, are divided into two main types, two-dimensional model and three-dimensional model respectively. Since two-dimensional models are easier to model, scholars have studied fracture structures that are closer to the real situation, with the main directions being single fracture and complex fracture, where the research on the effect of a single fracture structure on heat transfer has focused on the effect of fracture surface roughness on heat transfer. However, scholars usually build 3D single-fracture models, 3D parallel-fracture models or 3D simple cross-fracture models for numerical simulation calculations due to the complexity of three-dimensional modeling.
3.1 Research Progress on Two-Dimensional Model Simulating the Effect of Fracture Structure on Heat Transfer
3.1.1 Research Progress on the Effect of Single Fracture on Heat Transfer
Tsang [55] and Brown [56] both suggested that if real fractures were simulated using parallel plate theory, it may lead to 1–2 orders of magnitude errors in flow estimates. Zhao et al. [57] studied water flowing though the rock mass with a single fracture. The results showed that the fracture surface roughness significantly affected the heat transfer characteristics of water flowing through the fracture, and the distribution of water temperature did not show the linear increase along the flow direction. Xie et al. [58] and Zhao [59] all conducted experiments of water flowing through the single fracture and compared the experimental results with the results calculated by traditional equations. The comparison results showed that the heat transfer amount of traditional convection equation calculations was higher than that of experiments. Barton et al. [60] recommended the joint roughness coefficient (JRC) and obtained 10 typical fracture roughness profiles from many measurements, where the JRC ranged from 0–2, 2–4, etc., up to 16–18, 18–20. Ranjith [61] found that fracture surface roughness was one of the main determinants of Reynolds number which was a parameter describing the flow state based on experimental data. These findings all indicated that the fracture surface roughness played a major role in heat transfer in rock fractures. To measure the fractal dimension (D), Babadagli et al. [62] used a fully computer-controlled surface scanning device to map the rough surface of the fracture and calculated the fractal dimension for each surface by ANOVA using a two-dimensional dataset, proving that the fractal dimension was a measure of the roughness coefficient.
In recent years, more detailed studies on the influence of the fracture surface roughness on the heat transfer process have been carried out.
Neuville et al. [63] investigated the effect of fracture roughness on hydraulic permeability and heat flux on both sides of the fracture when cold fluids flowed through a single fracture by simulating the heat exchange process during laminar flow in a single fracture (The schematic diagram of the two-dimensional model of the rough fracture are shown in Fig. 1). Also, Neuville et al. proposed a numerical model which suggested that the fracture roughness may be responsible for the flow of fluids within the fractures to estimate the effect of fracture roughness on the heat exchange between the cold fluid and the surrounding rock. However, the model used in this study was a self-affine model for fracture roughness, and the results were not verified by comparison with simulation results of other types of geometric models.
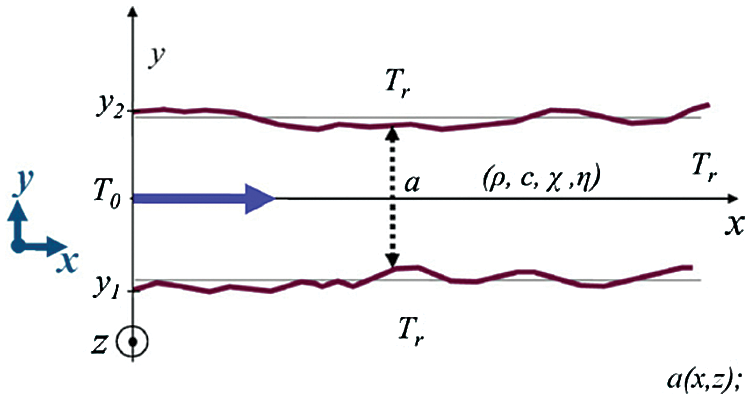
Figure 1: The schematic diagram of the two-dimensional model of the rough fracture of Neuville et al. [63]
Li et al. [64] carried out experiments on the seepage heat transfer characteristics in single-fractured rock mass under different temperatures (60°C to 100°C) and different water flow conditions. The granite rock samples of smooth fracture and rough fracture were used, and the distilled water was selected as the fluid. The results showed that influences of two fractured surfaces of rack mass with different roughness on the overall convective heat transfer intensity were not much different, but influences on the local convective heat transfer intensity were quite different. Also, the local convective heat transfer intensity of the two fractured surfaces showed multiple peaks and nonlinear trend and this trend was more obvious in the rough surface. In addition, the increase of the convective heat transfer coefficient in the two fractured surfaces was greater than the increase of flow and the two measures were positively correlated. Although high-pressure plunger double-cylinder pump, ring-pressure pump and real-time monitoring temperature system were used in the experiment to ensure the constant pressure and the constant current and the continuity of the experiment and obtain more accurate test data, this experiment assumed that the single fracture core was a core with a constant temperature on both the outer surface and the inner surface of the fracture, which not only caused errors in the calculation of Newton’s cooling formula in the later data processing, but also ignored the error from the mass change caused by the temperature change of the rock.
Luo et al. [65] conducted the experiment on the heat transfer characteristics of distilled water flowing through smooth and rough granite rock mass. A high-pressure plunger pump, an electric control plunger pump, a temperature control system, a data acquisition system and a sample clamping system were used in the experiment. The heat transfer characteristics of rock mass at 4 initial temperatures (60°C, 70°C, 80°C, 90°C) were studied in this experiment. The experimental results showed that the total heat of the rock mass was linearly positively correlated with the increase of the initial temperature for a given volumetric flow rate of water, and the total heat transfer amount was positively correlated with the volume flow for a given temperature. Compared with the experiment of Li and others [64], although the calculation method of the convective heat transfer coefficient proposed by Bai et al. [39,40] was used in the experiment, which means that the error caused by solving the internal surface temperature of the center of the rock mass will not occur during the calculation, the team did not conduct a comparison experiment on the heat transfer characteristics of the fractured surfaces with different roughness and the conclusions were relatively vague.
He et al. [66] performed a numerical simulation of the heat transfer process in a single-fractured rock mass with different surface roughness with a two-dimensional model (The schematic diagram of the two-dimensional model of the heat transfer process in fractured rock mass is shown in Fig. 2, and the different roughness curves are shown in Fig. 3). They proposed morphological condition factor (MCF) and calculated with 468 sets of examples to study MCF. MCF denoted the effect of the fracture morphology of the fractured surface of the rock mass on the heat transfer process. The reference equation about MCF is as follows [66]:
where
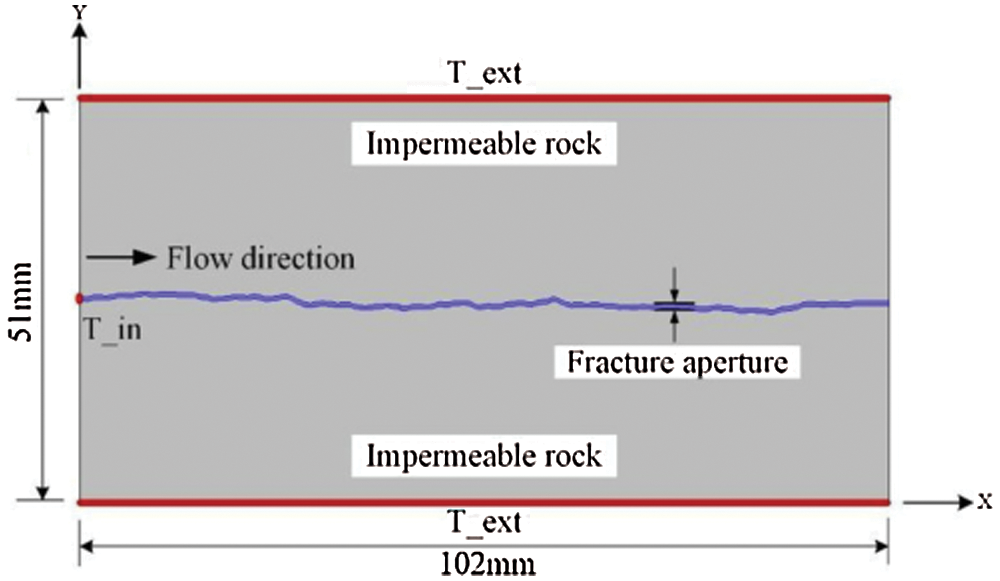
Figure 2: The schematic diagram of the two-dimensional model of the heat transfer process in fractured rock mass of He et al. [66] (Tin in the figure represents the temperature of inlet fluid, and Text in the figure represents the surface temperature outside the rock mass)
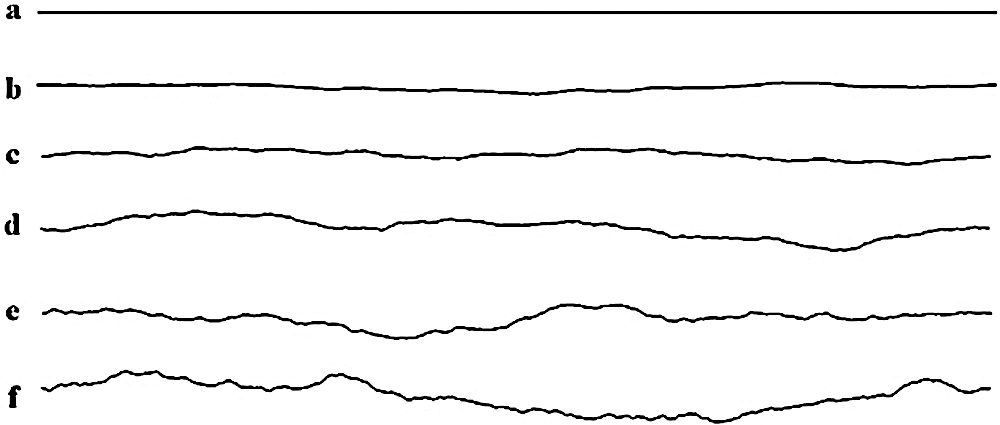
Figure 3: The different roughness curves of He et al. [66]
The numerical simulation results of He and Rong et al showed that the roughness of the fracture morphology of the fractured surface of the rock mass not only promoted the increase of heat transfer intensity but also promoted the effect with the increase of the roughness under the same flow rate and this promotion was weakened when the flow rate increased. Similarly, under the certain flow rate, the temperature of the fluid at the outlet in the rough fracture was higher than that in the smooth fracture and the temperature of the fluid at the outlet increased with the increase of the roughness of the fractured surface. Also, the pressure difference between inlet and outlet increased with the increase of roughness of the fractured surface of the rock mass. The two-dimensional model used in this numerical simulation cannot represent the anisotropy of rock mass between the rough fractures, and the author did not make numerical simulation on the relationship between parameter B and the fracture width, so the effect of MCF on heat transfer process should be further studied.
He et al. [67] used fractal dimensions (D) and profile curves (Y) to characterize surface roughness, and combined experimental and numerical simulation methods to study the effect of fracture surface roughness on the characteristics of heat transfer in a single fracture of granite (The schematic diagram of the two-dimensional model of structure of the single fracture is shown in Fig. 4, and profile curves and fractal dimensions of the five slices are shown in Fig. 5). The results showed that the fracture surface roughness played a major role in the distribution of the local heat transfer coefficient, which mainly depended on roughness, followed by aperture and flow velocity, and had little influence on water temperature and the distribution of internal surface temperature. Although the method for characterizing fracture surface roughness of He and Bai et al. [67] was different from that of He and Rong et al. [67], the research results were similar.
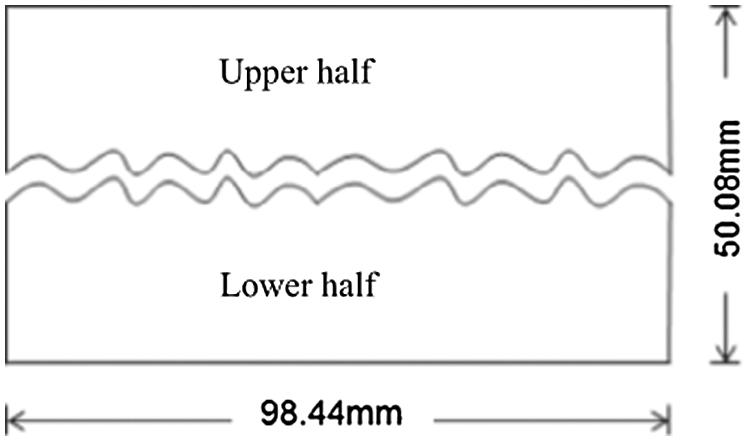
Figure 4: The schematic diagram of the two-dimensional model of structure of the single fracture of He et al. [67]
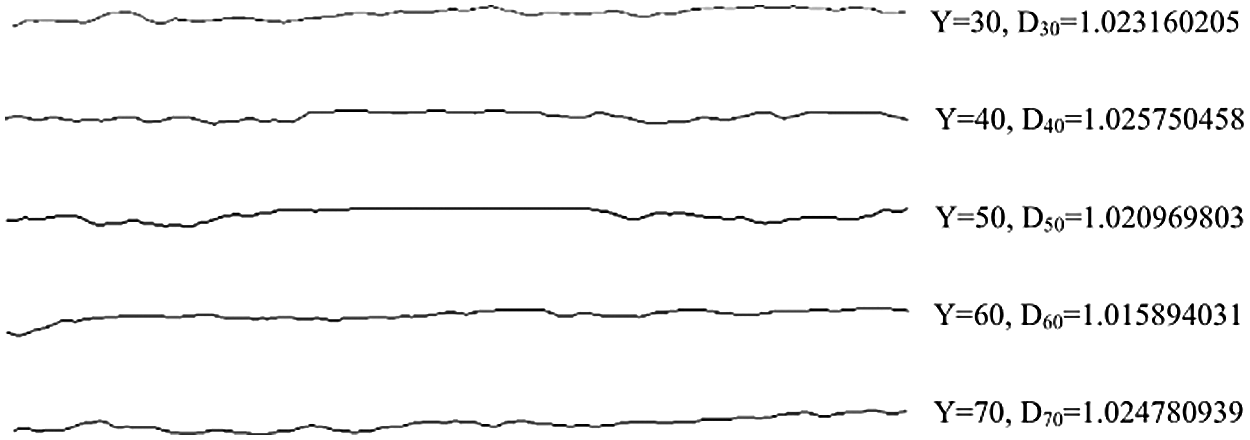
Figure 5: Profile curves and fractal dimensions of the five slices of He et al. [67]
Wu et al. [68] simulated the heat transfer process under water flow in a rock mass with a single smooth fracture and a single rough fracture respectively (The schematic diagram of the two-dimensional model of structure of the single rough fracture is shown in Fig. 6), and analyzed the effects of fracture opening, seepage velocity and roughness on the heat transfer process. The results showed that the greater the fracture opening, the smaller the rate of growth of the rock wall temperature and the greater the extent of the slow increase in water temperature. Similarly, the seepage velocity affected the temperature of the rock wall to some extent, and the greater the seepage velocity, the smaller the temperature of the water at the same location. Also, as the roughness of the fracture surface increased, the water temperature at the same location decreased, and the wall temperature suddenly dropped when the roughness was between 0% and 20%. And last but not least, changing the fracture surface roughness can improve the cooling efficiency of the rock wall compared to the percolation rate. Although the numerical simulation results of Wu et al. were in agreement with the relevant literature, the roughness of the simulated cracks was more regular and may differ from the actual roughness.
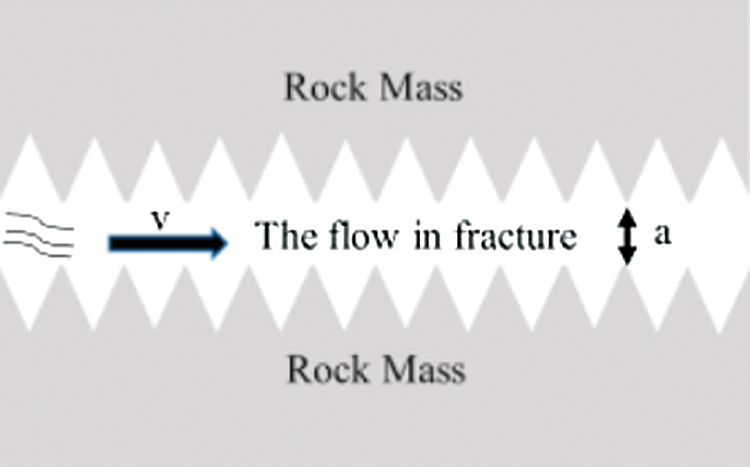
Figure 6: The schematic diagram of the two-dimensional model of structure of the single roughness fracture of Wu et al. [68]
3.1.2 Research Progress on the Effect of Complex Fracture on Heat Transfer
Zhou et al. [69] analyzed the influence of various factors on the performance of thermal reservoirs of granite through numerical simulation and artificial neural network (ANN). 32 representative time points were selected to build 32 neural network models, which was to predict the 30-year production temperature of 32 time nodes in the system (The network architecture of the artificial neural network model is shown in Fig. 7). The results showed that injection rate had the greatest effect on total heat extraction, followed by injection temperature and well spacing, while fracture permeability had the least effect. Also, increasing the injection flow rate, lowering the injection temperature, increasing the distance between the injection and the producing well, and decreasing the fracture permeability can all increase the heat extraction within certain limits. Although using the artificial neural networks to predict production temperature had high prediction accuracy, it was too complicated to use for engineering.
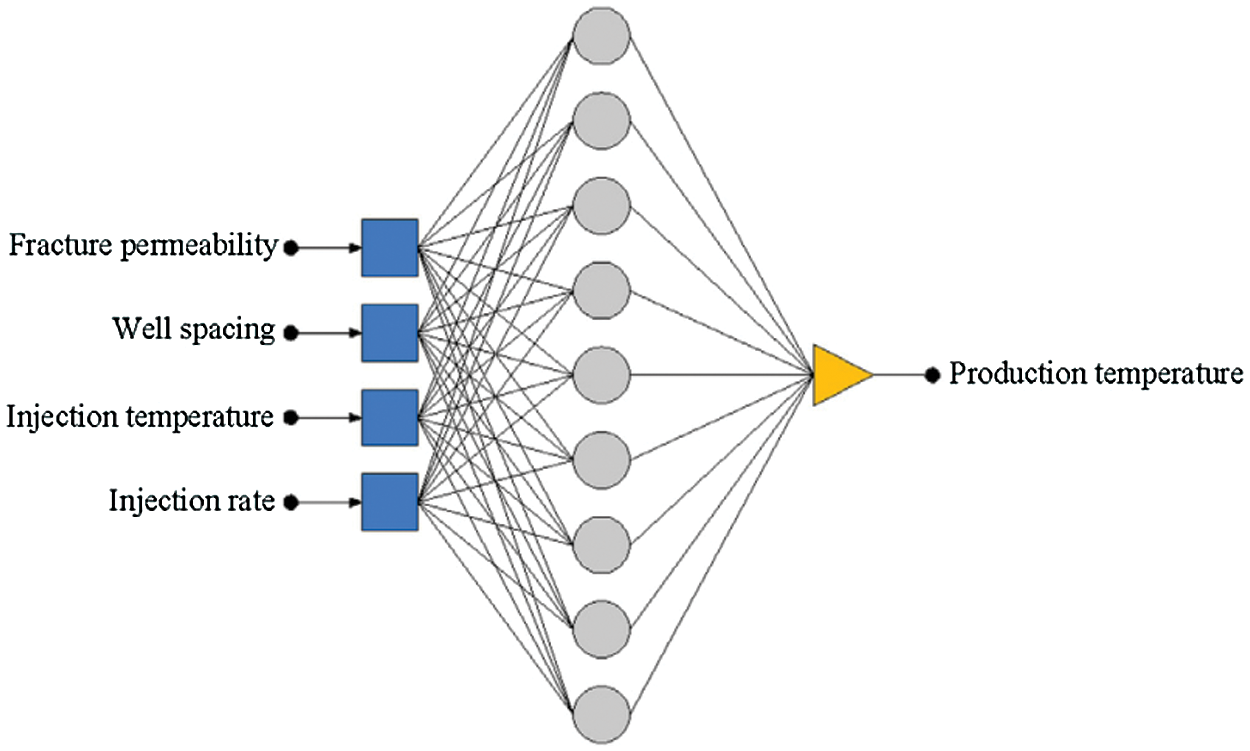
Figure 7: The network architecture of the artificial neural network model of Zhou et al. [69]
Gao et al. [70] conducted numerical simulation on the model of cross-fracture rock mass, where the fracture distribution was two vertical fractures and two oblique fractures (The dimension diagram of the fractures is shown in Fig. 8). Using 3DEC software to establish size and boundary conditions (except for the local heat source boundary, the rest of the outer sides were the external heat conduction boundaries of
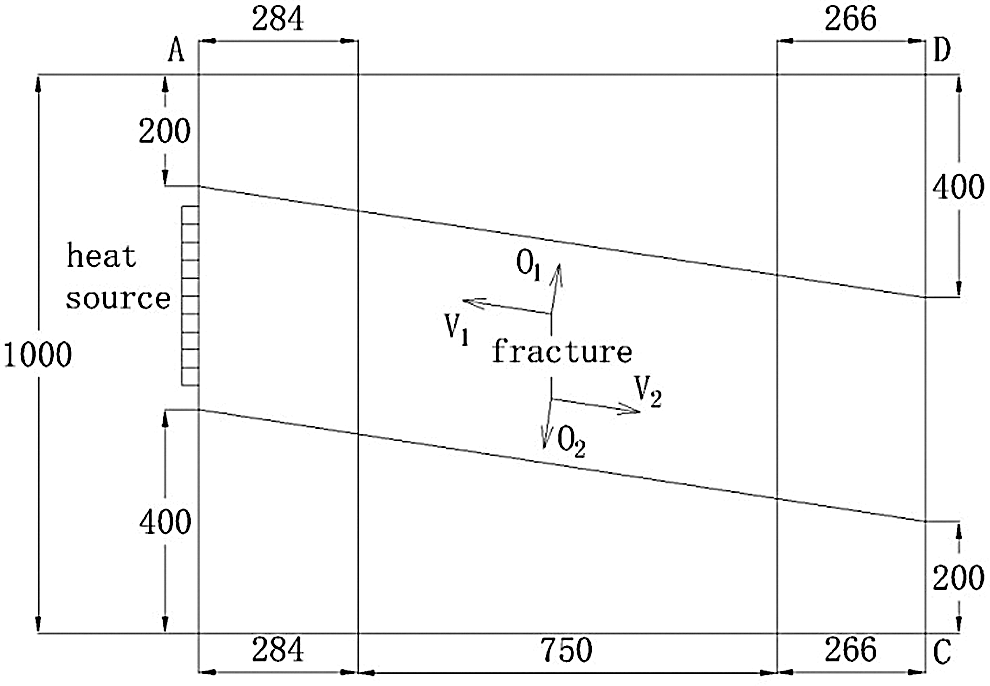
Figure 8: Dimension diagram of the fracture of Gao et al. [70]
Ma et al. [71] introduced a leaf-like bifurcation fracture network in a multi-well enhanced geothermal system (EGS) (The diagram of the leaf-like bifurcation fracture network is shown in Fig. 9) and investigated the effect of the leaf-like bifurcation fracture network on the characteristics of heat extraction performance. Numerical simulation results showed that the higher fracture bifurcation level is beneficial to improve the heat absorption rate. Moreover, a higher fracture length ratio made the fracture distribution more uniform so as to avoid the local thermal cooling phenomenon and to obtain better heat extraction performance. In addition, the positive effect of the fracture bifurcation angle was weaker than that of the bifurcation level and the length ratio, and the fracture aperture ratio also had little effect on the heat extraction performance. Although the leaf-like bifurcation fracture network established by Ma et al. [71] can describe fracture heterogeneity, the network was only applicable to multi-well EGS.
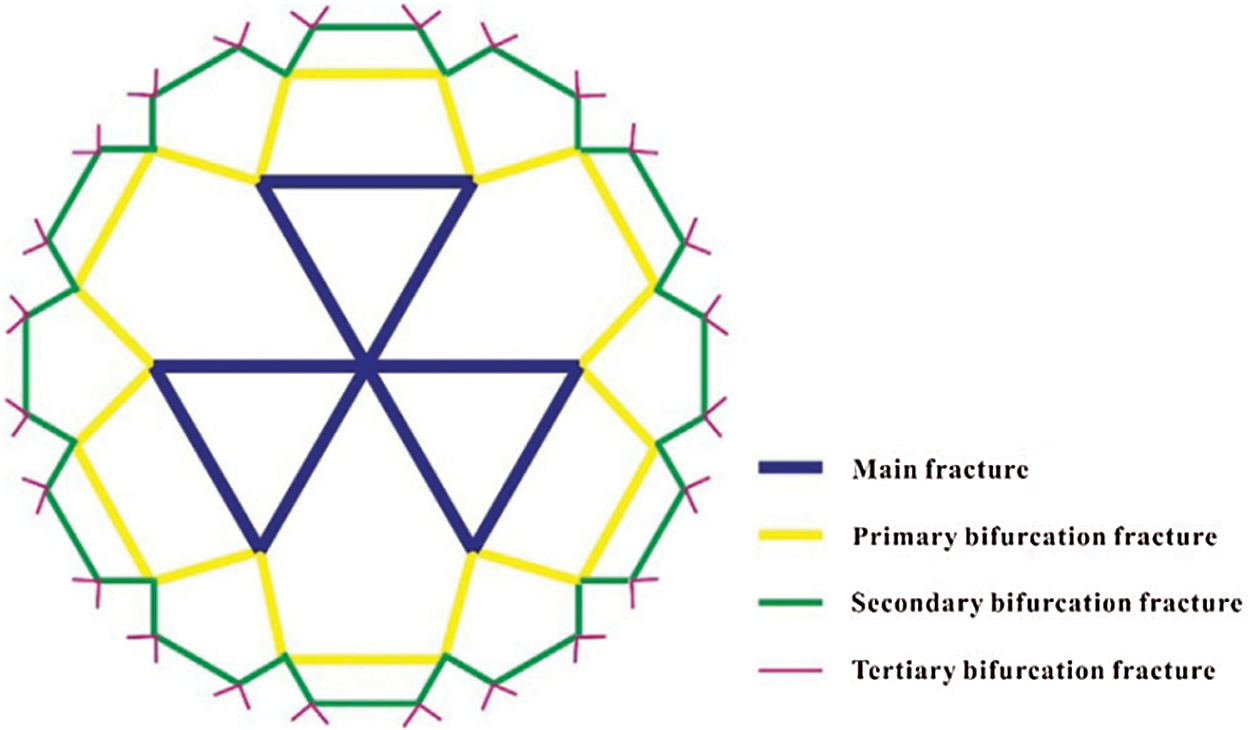
Figure 9: The diagram of the leaf-like bifurcation fracture network of Ma et al. [71]
Vasilyeva et al. [72] studied heat and mass transfer in EGS with complex fracture networks (The schematic diagram of complex fracture networks is shown in Fig. 10) and successfully developed a general multi-scale finite element method for calculating fluid temperature and pressure in fractured porous media. Although the proposed multi-scale method can more accurately solve the heat and mass transfer problems in the cracked medium related to EGS operation, the calculating process was complicated for engineering.

Figure 10: The schematic diagram of complex fracture networks of Vasilyeva et al. [72]
Similar to the complex network studied by Vasilyeva et al. [72], Shi et al. [73] compared the heat extraction performance of 11 types of complex fracture networks with natural fractures and hydraulic fractures in the multi-well EGS (The diagrams of 11 types of complex fracture networks are shown in Fig. 11). The results showed that under the same total fracture length, when the natural fracture was shorter and the hydraulic fracture was longer, the production temperature and thermal power were higher. However, when the longer hydraulic fracturing fractures were concentrated around the side well, thermal penetration would occur. Moreover, more hydraulic fractures were connected with natural fractures, which can better disperse the working fluid and reduce thermal penetration.
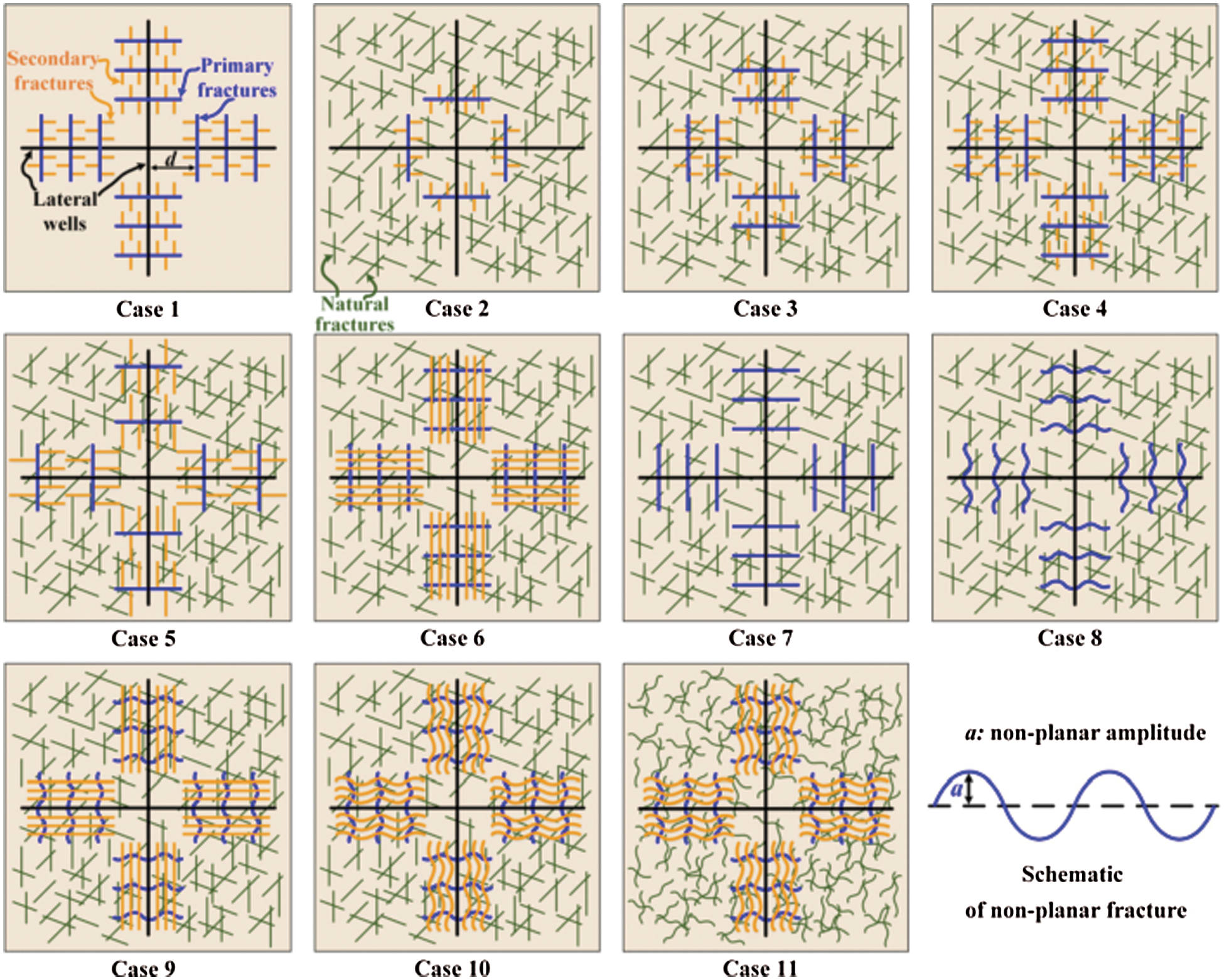
Figure 11: The diagrams of 11 types of complex fracture networks of Shi et al. [73]
3.2 Research Progress on Three-Dimensional Model Simulating the Effect of Fracture Structure on Heat Transfer
Huang et al. [74] based on the results of Barton and Choubey and 3D printing techniques to study the seepage heat transfer process of fluids in the rough fracture and analyzed the effect of fracture roughness on the characteristics of seepage heat transfer in the fracture of rock masses (Typical roughness profiles for JRC = 10–12, 18–20 are shown in Fig. 12). The results showed that fracture roughness had a significant effect on rock wall temperature which may vary at the projections and grooves of rough fracture surfaces. Moreover, with high roughness perpendicular to the flow direction, turbulence was generated and the heat transfer coefficient was increased. Conversely, with high roughness parallel to the flow direction, seepage was generated and the heat transfer performance was decreased. It said that the directionality of roughness had a significant effect on heat transfer and seepage.

Figure 12: Typical roughness profiles for JRC = 10–12, 18–20 used by Huang et al. [74]
Xin et al. [75] used three-dimensional model which was the model with a single ideal fracture to simulate the heat transfer process of fractured rock mass (The three-dimensional model is shown in Fig. 13) and established the THM coupling control equations based on the local thermal non-equilibrium theory. The numerical simulation results showed that the temperature of rock mass away from the fractures decreased and the low temperature zone of the reservoir expanded with the mining time going by, which were due to heat conduction. Moreover, the factors that affect the average outlet temperature of the fluid were the fracture width and the inlet temperature and the viscosity and mass flow had limited effect on the average outlet temperature of the fluid. Compared with the numerical simulation of the two-dimensional model of He et al., although the three-dimensional model used in this simulation took the dynamic changes of the fractures aperture into account, the anisotropy of the rock mass was neglected and the ideal single fracture was not representative.
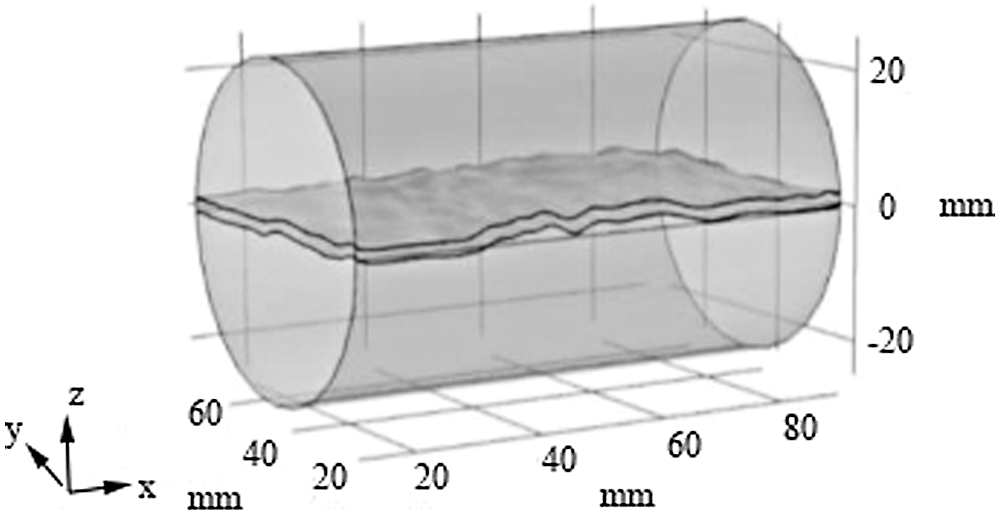
Figure 13: The schematic diagram of the three-dimensional model of Xin et al. [75]
Jiang et al. [76] and Ghassemi et al. [77] established a three-dimensional transient numerical model to simulate the flow and heat transfer processes in underground fractures of cold fluids injected from the surface to the subsurface and developed a new three-dimensional model which simplified the EGS underground multi-domain to a single domain with multiple sub-areas for modeling and analyzing the underground heat exchange process in EGS (The schematic diagram of the three-dimensional model and its grid system is shown in Fig. 14). Although the model avoided the typical difficulties of setting boundary conditions of matching subdomains in the traditional method of multi-domain and simplified the complete underground heat exchange process during numerical simulations, the model did not consider the influence of mechanical fields.
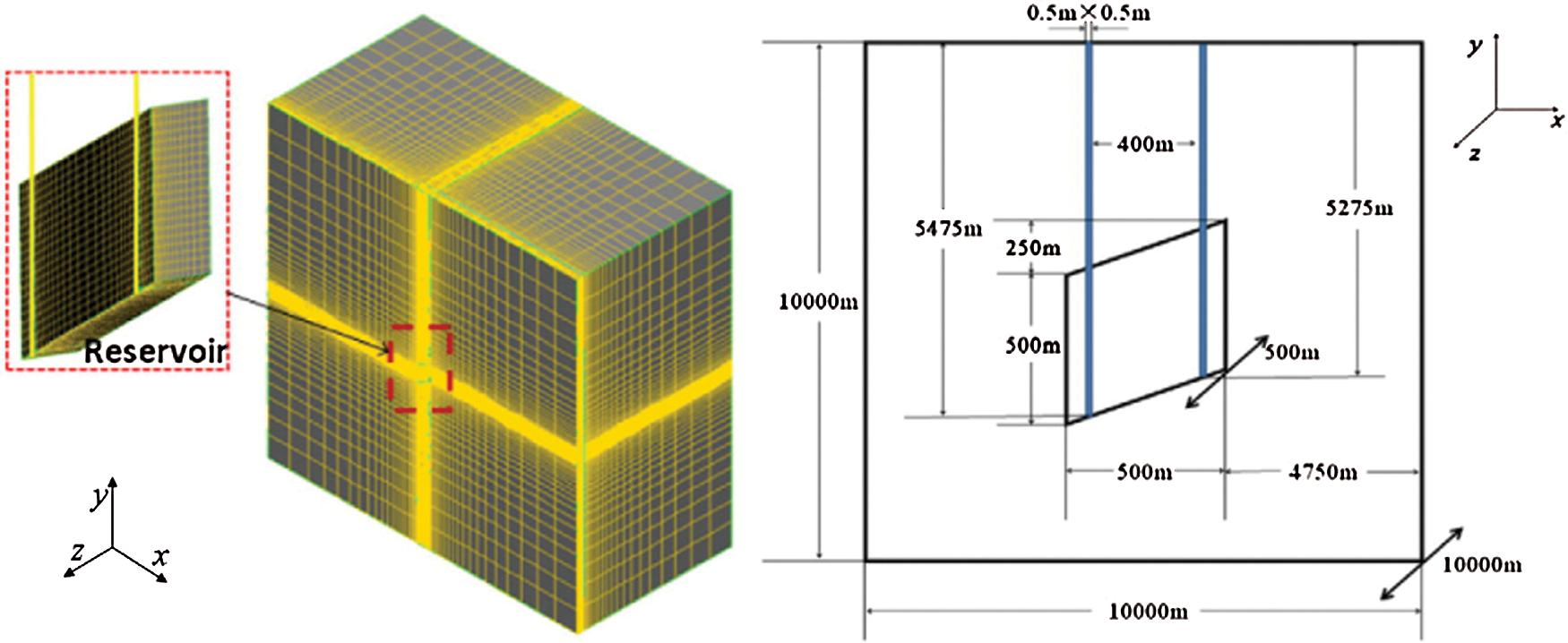
Figure 14: The schematic diagram of the three-dimensional model and its grid system of Jiang et al. [76]
Similar to the geometric model studied by Jiang et al. [76] Cao et al. [78] also established a three-dimensional transient numerical model to analyze the heat extraction process of EGS and the factors influencing the volumetric heat transfer coefficient (ha) related to EGS heat extraction(The schematic diagram of the three-dimensional model and its grid system is shown in Fig. 15). The results showed that lower ha reduced the heat exchange between rock and fluid and the effective stress, and expanded the porosity and permeability of the rock thermal reservoir to a limited extent. Moreover, the model developed by Cao et al. [78] provided a good prediction of the combined effect of effective stress and fluid properties on EGS heat recovery by varying the injection pressure and temperature. Although the three-dimensional model of Cao et al. [78] can predict the influencing factors of the EGS heat extraction rate, it is necessary to establish a benchmark test program that is closer to the actual EGS heat extraction process if the model becomes a viable tool for engineering applications.
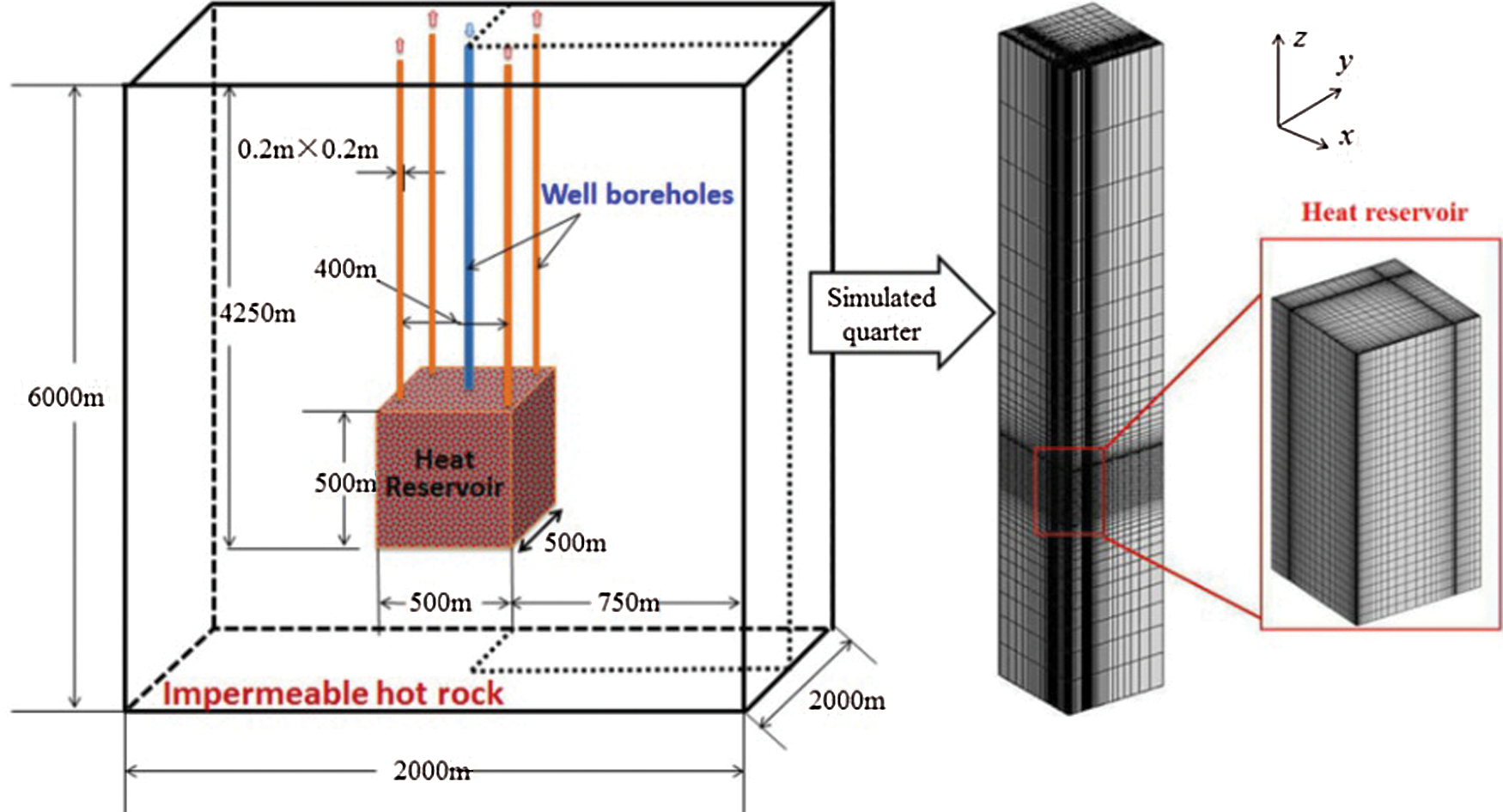
Figure 15: The schematic diagram of the three-dimensional model and its grid system of Cao et al. [78]
Sun et al. [79] used the commercial software COMSOL to create an ideal three-dimensional numerical model of EGS with double horizontal wells (The schematic diagram of the three-dimensional model is shown in Fig. 16), and applied the model to solve problems of predicting EGS performance, such as operational performance, utilization and service life.
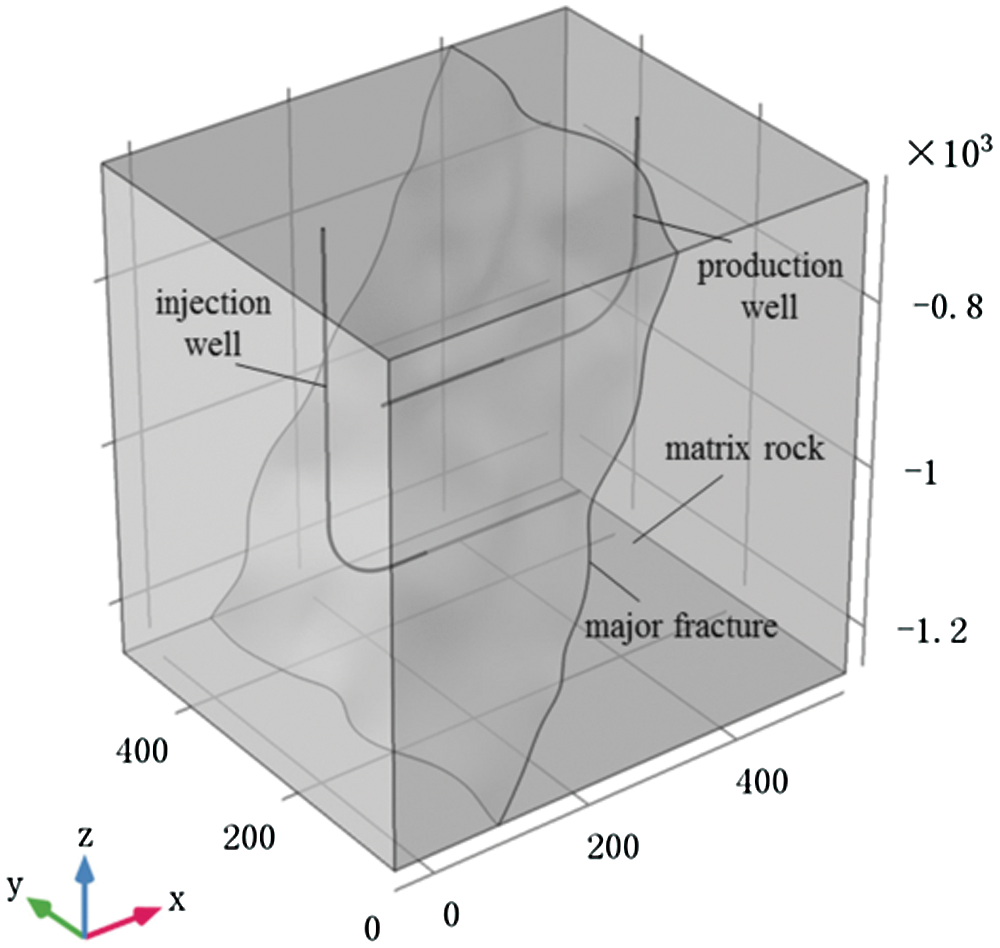
Figure 16: The schematic diagram of the three-dimensional model of Sun et al. [79]
Similar to the geometric model established by Sun et al., Pandey et al. [80] used Finite Element for Heat and Mass Transfer(FEHM) to perform coupled thermal-hydraulic-mechanical (THM) simulations of a three-dimensional model of a single fracture connecting the injection and production well, where the fracture was considered to be an equivalent porous medium (The schematic diagram of the three-dimensional model is shown in Fig. 17). The results showed that due to the greater flux of cold water in the fracture, the thermal contraction of the rock was greater when the permeability was greater.
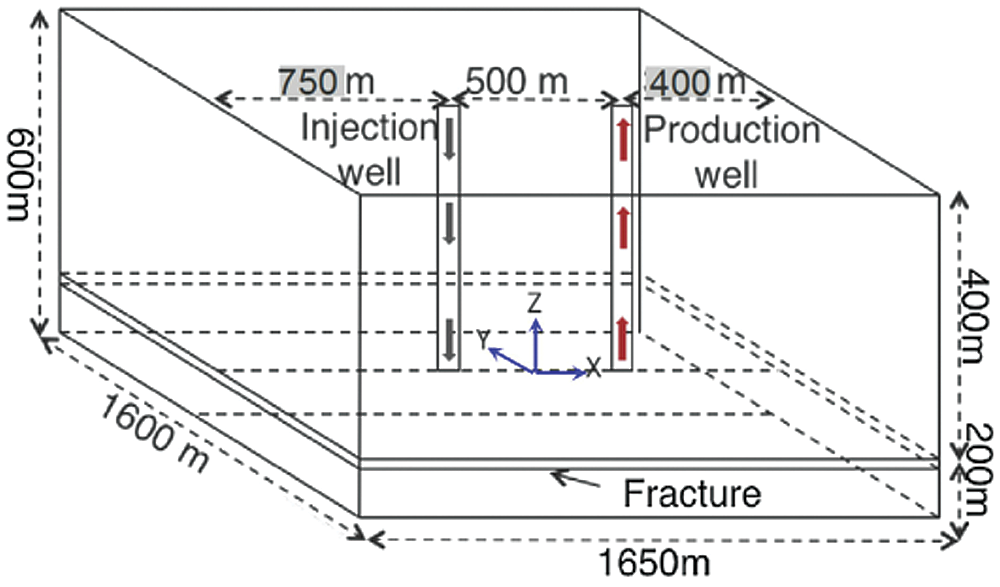
Figure 17: The schematic diagram of the three-dimensional model of Pandey et al. [80]
Li et al. [81] established a three-dimensional model of specific EGS which was combined horizontal wells and multiple parallel fractures (The schematic diagrams of the three-dimensional model of the injection and production well and multiple parallel fractures are shown in Fig. 18) to analyze the effect of fracture geometry and the spacing of two adjacent fractures on EGS heat extraction performance, and compared the specific EGS with the classic EGS with double or three wells and a single fracture. The results showed that larger injection rates, smaller well aperture and larger fracture widths caused short-circuiting effects and reduced the performance of this specific EGS. In addition, this specific EGS offered higher performance and longer economical production times than the classic EGS.
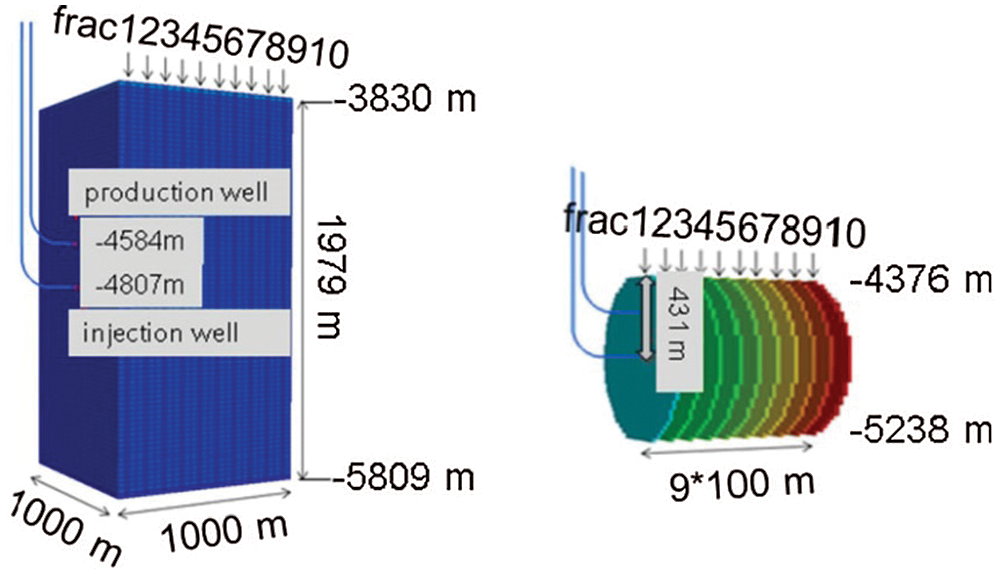
Figure 18: The schematic diagrams of the three-dimensional model of the injection and production well and multiple parallel fractures of Li et al. [81]
Ma et al. [82] designed a three-dimensional model of a granite thermal reservoir with two intersecting fractures and performed numerical simulation calculations to evaluate its heat production performance (The schematic diagrams of the three-dimensional model of the reservoir is shown in Fig. 19), and compared four models of intersecting fractures at different angles. The results showed that the water temperature at different locations along the direction of seepage followed different patterns with time going by. In addition, the larger the angle between the two fractures, the faster the temperature of the outlet water dropped. Also, when the fractures were more evenly distributed in the reservoir, the flowing water extracted heat from the surrounding reservoir faster.
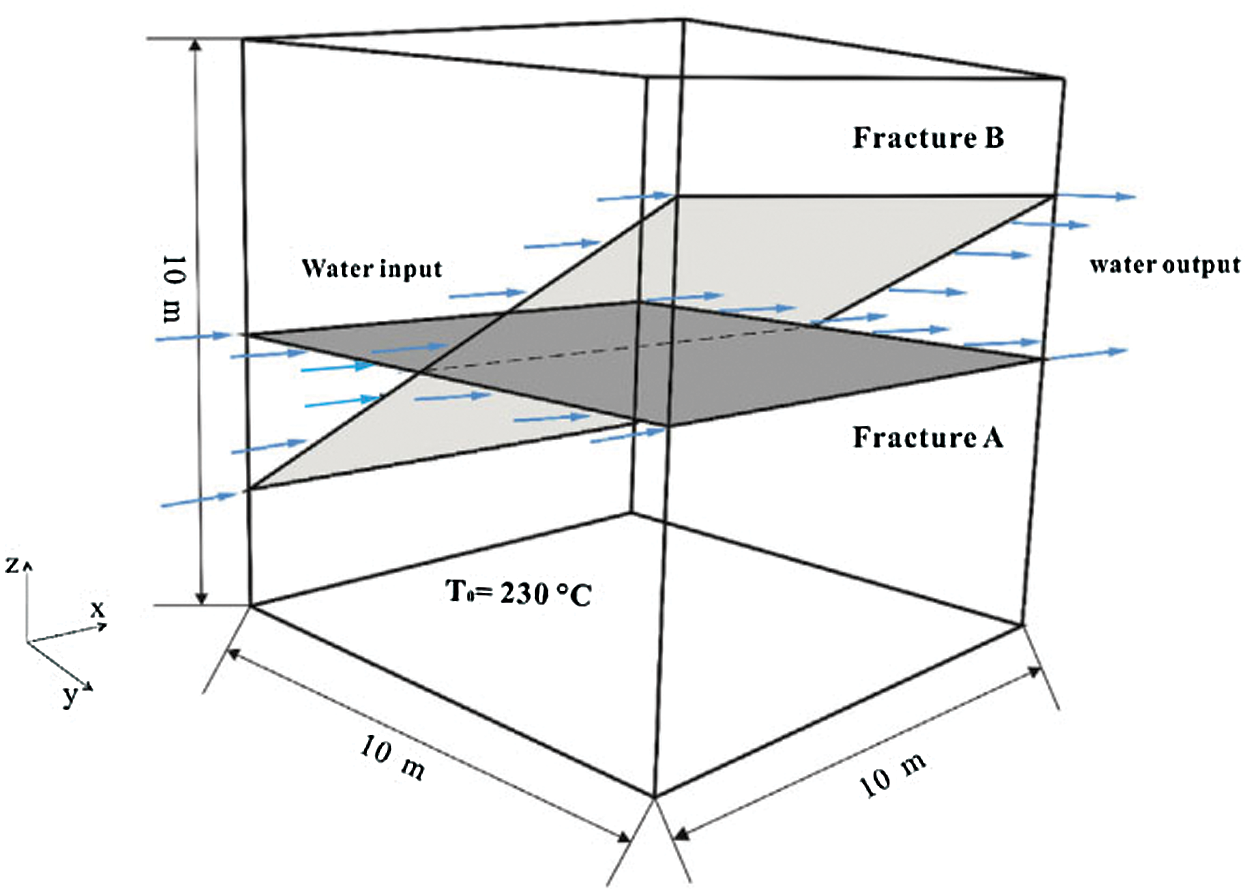
Figure 19: The schematic diagrams of the three-dimensional model of the granite thermal reservoir with two intersecting fractures of Ma et al. [82]
4 Research Progress of the Effect of Fluid Flow in the Fractures of Hot Dry Rock EGS on Heat Transfer
In the 1950s, the former Soviet Union and some Western scholars studied the water flow characteristics of single-fractured rock and summarized the mathematical expression:
Eq. (7) is called the Cubic Law. It shows that the flow rate of the working flow flowing through the single-fractured rock mass is proportional to the cubic of the fracture width. However, the Cubic Law applies only to the calculation of water flow in smooth parallel plate fractures. Since the assumptions in the Cubic Law are quite different from the actual situation, some scholars have carried out further experiments and put forward different methods of calculating correction coefficients for the existence of certain deviations in this equation.
Lomize proposed the equations [83]:
Laminar flow:
Turbulent flow:
Reynolds number:
among them,
Louis proposed the equations [84]:
Laminar flow:
Turbulent flow:
The Reynolds number curve is shown in Fig. 20, where
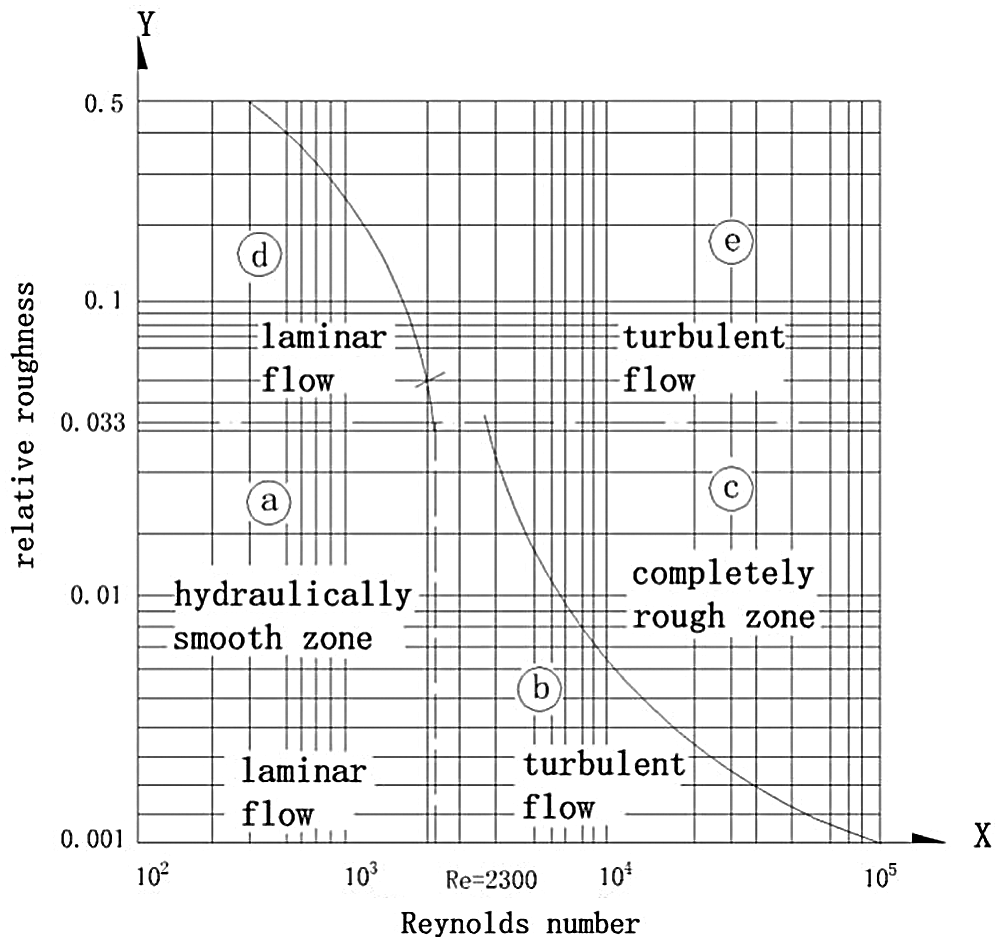
Figure 20: Relationship between Reynolds number and relative roughness proposed by Louis [84]
Both scholars strictly divided the water flow state of the single-fractured rock mass, but this may not be consistent with the water flow state in the actual fractured rock mass. So Su et al. [85] put forward the mathematical expression:
where
Instead of dividing the states of water flow, Eq. (13) combined laminar flow and turbulence flow, which greatly reduced the calculation amount.
Asai et al. [86] simulated and derived mathematical equations based on Kirchhoff’s law (which describes current distribution in closed-loop multi-circuit circuits) for planning and designing the fracture spacing to control the flow distribution in any EGS of dual-structure system drilled along the same direction, thus ensuring that fluids were uniformly distributed across all fractures to extract heat from the entire reservoir. The equations are as Eqs. (14) and (15). Although these mathematical equations are helpful for evaluating the effectiveness of EGS and optimizing parameters, it is necessary to calculate the relationship between injection pressure and fracture width, the relationship between friction loss in fractures and other parameters when calculating the mathematical equation and to iterate the system of equations until a convergent solution is obtained (because the flow resistance is a function of volume flow). Thus, the mathematical equations are too complicated for the calculation of engineering construction operations [86].
where
Kluge et al. [87] studied the relationship between the permeability of a single fracture and fracture average aperture size and distribution based on the Cubic Law. The results showed that the average aperture size and distribution of a single fracture depended on the offset of the fracture and that the permeability also depended on the offset of the fracture, but this relationship cannot be explained simply by the Cubic Law. In addition, the permeability of a natural fracture with a rough surface was always less than that estimated by the Cubic Law, and the rougher the fracture surface, the greater the deviation of the permeability estimated by the Cubic Law.
Huang et al. [88] studied fluid friction and heat transfer in the process of fluid flowing through a single rough fracture. The results showed that the process of fluid flowing through a single granite fracture was very different from that of fluid flowing through a rectangular channel. Also, the flow friction increased and the heat transfer decreased due to the relatively roughness of the granite fracture. Lu et al. [89] conducted water flow and heat transfer experiments on regularly fractured granite and developed a finite difference scheme and computer code for calculating water flow and heat transfer in regular fractured rocks. The results showed that rock temperature distribution was strongly influenced by water flow in fractures. Wu et al. [90] simplified two-dimensional equations of fluid flow in fractures into one-dimensional equations by using velocity potential and streamline functions instead of actual coordinates, and established a semi-analytical model to predict the heat extraction from the fractures. Ren et al. [91,92]developed an effective unified pipe network method (UPM) in order to overcome the difficulty of simulating fluid flow in a highly discontinuous dual-permeability medium, which discretized the dual-permeability rock mass into virtual pipes network system including crack pipe network and matrix pipe network. After verification, this method had strong robust for analysis of seepage in fractured rock mass and porous rock mass.
5 Research Progress on the Heat Transfer Coefficient of the Heat Transfer Process of the Fractured Rock Mass
Chapman [93] found an earlier proposed equation for estimating the heat transfer coefficient in the book. Zhao [37,94], Zhao et al. [95], and Zhao et al. [96] successively proposed equations for estimating the heat transfer coefficient of heat transfer in fractures in order to study the heat exchange process of fluid flowing through rock fractures. Ogino et al. [97] conducted forced convection experiments on circular fractures and verified the experimental results using numerical simulations, and then proposed the heat transfer coefficient of water flowing through circular fractures in a two-dimensional model.
In recent years, more and more scholars successively studied in depth the heat transfer coefficient of heat transfer process of fractured rock mass.
Zhao [38] established two sets of fractured rock mass models and simulated heat transfer process with water as the medium. The experimental results showed that the heat transfer coefficient in the fracture was smaller than the theoretical value of the flat-panel thermal boundary layer but larger than the estimated value, and the two sets of data showed that the water temperature increased non-linearly along the fracture direction. However, the water temperature distribution at the fracture was not obtained in the experiment, so it was not possible to accurately obtain the heat transfer coefficient value during the heat transfer process of the fractured rock mass.
Heninze et al. [98] carried out further experiments on Zhao’s theory. Based on the dynamic changes of thermal properties of rock mass and the local heterogeneity of rock mass, the calculation of the heat transfer coefficient between fluid and fractured rock mass during fluid flow through the fractured rock mass was derived.
When
where
However, this method was biased when calculating the rock temperature of 140°C and almost all calculations were still greater than the estimated value. And the authors believed that the possible cause was that experiment under the condition of unknown pressure affected the fluid flow. The simulation experiment had inconsistency in the data set and the model was too simple, so the reliability of the conclusion should be further studied.
Bai et al. [39,40] conducted further research based on the research theories of Zhao. They carried out the experiment with the a cylindrical granite (The size is
For OHTC, they believed that the reason for the abnormal values of OHTC may be that the denominator contained subtraction or more variables, and for this reason, a new mathematical expression of OHTC (h) was proposed (The mathematical expression is as Eq. (4)). It applies not only to water, but also to other fluids. The breakthrough of this equation was that there was no need to solve the thermal conduction equation to obtain the inner surface temperature (Ti0) at the center of the rock mass and no abnormal values were generated.
For LHTC, a numerical model based on COMSOL model was developed by Bai et al. The results showed that [12]:
1. LHTC had relationship with the roughness of the fractured surface of the rock mass, and in a certain range of fracture width, the narrower the fracture and the stronger the local heat transfer capacity.
2. The increase of water flow rate can significantly improve the local heat transfer ability of the rough fractured surface of the rock mass within the fixed fracture width of the rock mass.
3. The polynomial established by the experimental data showed that LHTC had a negative correlation with the fractured surface of the rock mass, and LHTC had a larger value at the groove of the rough crack surface.
Not only that, but the team compared LHTC with OHTC, and the comparison showed that:
1. The OHTC was always larger than LHTC at fixed fracture width and same flow.
2. As the water flow increased, the OHTC value increased, but the arithmetic mean of LHTC increased firstly and then decreased.
Although the results of the experiment were more accurate and the results of the experiment were more reliable, there were also shortcomings. First of all, the experiment only studied the single-fractured rock mass, and did not consider whether unsteady heat conduction process among fractures in multiple fractures would affect the heat transfer coefficient.
Ma et al. [99] used a combination of numerical simulation and experimentation and produced specimens with different rough surfaces by 3D printing, in order to investigate the heat transfer characteristics and local heat transfer coefficients of water flowing through rough fractures along the flow direction. The results showed that:
1. When joint roughness coefficient (JRC) of the fracture was kept constant, the total heat transfer coefficient was positively correlated with the volume flow rate. When the volume flow rate is kept constant, the total heat transfer coefficient increased with the increase of JRC.
2. The results of the distribution of the local heat transfer coefficient showed that the local heat transfer coefficient increased to a maximum value at the inlet and then decreased to a relatively constant value along the flow direction.
3. The volume flow rate did not affect the distribution of the local heat transfer coefficient. When the curvature of the fracture surface was kept constant, the local heat transfer coefficient increased with the increase in volume flow rate.
Although the distribution of local heat transfer coefficients was analyzed by Ma et al., the results can be better verified if they are compared and analyzed with the local heat transfer coefficient equations derived by other authors.
After the analysis and summary of the research status of the mathematical models of heat transfer of Hot Dry Rock EGS at home and abroad, the following conclusions and suggestions can be drawn:
1. At present, the experimental tests and numerical simulations of the mathematical models of heat transfer of Hot Dry Rock EGS in the domestic and foreign countries are mostly studied for the horizontal or vertical single fracture or intersecting fracture of the rock mass. This single-fractured rock model provides more convenient conditions for experimental tests and numerical simulations. However, there is a great deviation from the actual heat transfer process of Hot Dry Rock EGS, and the results of these numerical simulations are difficult to guide the actual situation. Although there are many researches on irregular fractures, most of them are only at the level of academic research and the methods used are too complicated for engineering construction. Therefore, it is suggested that the relevant scholars should further study the mathematical equations, which are applicable to engineering construction, of seepage heat transfer in irregular fractures of the rock mass to improve the efficiency of construction.
2. At present, the experimental tests and numerical simulations of the mathematical models of heat transfer of Hot Dry Rock EGS in the domestic and foreign countries are mostly studied for steady heat transfer process. The steady heat transfer process cannot test or simulate the temperature change trend of the rocks around the HDR geothermal wells over time, so it is difficult to estimate the service life of Hot Dry Rock EGS. Whether the heating by themselves and the heating from surrounding HDR during the non-heating period can maintain the continuous and stable operation of EGS during the heating period is a worth problem for further study. Therefore, it is suggested that the unsteady heat transfer process and the mathematical models of heat transfer among the multiple fractures of HDR should be studied in depth by scholars, which has great practical significance to guide the practical application of the project.
3. At present, limited by the experimental test conditions, domestic and foreign scholars have a wide range of research on computer programming of heat transfer numerical simulation of Hot Dry Rock EGS, and many numerical simulation methods and procedures provide convenient conditions for scholars to study HDR in the future. However, the current numerical simulation is only fits the two-dimensional model deeply, which usually ignores the problem of anisotropy of the rock mass. Although some domestic and foreign scholars have also found this defect and carried out some numerical simulation studies for the three-dimensional model, these three-dimensional models are usually ideal simple single-fractured rock models which still have some bias compared with the actual situation. Therefore, considering the anisotropy of rock masses, the heat transfer process and mathematical models of heat transfer on Hot Dry Rock EGS in the model of complex three-dimensional fractures should be studied deeply with a view to getting closer to the real situation.
Funding Statement: Support for this work was provided by the Postgraduate Research & Practice Innovation Program of Jiangsu Province, China (Project No. SJCX20_0984).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Aikins, K. A., Choi, J. M. (2012). Current status of the performance of GSHP (ground source heat pump) units in the Republic of Korea. Energy, 47(1), 77–82. DOI 10.1016/j.energy.2012.05.048. [Google Scholar] [CrossRef]
2. Hepbasli, A. (2004). Development of geothermal energy utilization in Turkey: A review. Renewable and Sustainable Energy Reviews, 8(5), 433–460. DOI 10.1016/j.rser.2003.12.004. [Google Scholar] [CrossRef]
3. Kumari, W. G. P., Ranjith, P. G. (2019). Sustainable development of enhanced geothermal systems based on geotechnical research–A review. Earth-Science Reviews, 199, 102955. [Google Scholar]
4. Zhu, J., Hu, K., Lu, X., Huang, X., Liu, K. et al. (2015). A review of geothermal energy resources, development, and applications in China: Current status and prospects. Energy, 93, 466–483. DOI 10.1016/j.energy.2015.08.098. [Google Scholar] [CrossRef]
5. National Development and Reform Commission (2016). The 13th five-year plan for renewable energy development. http://en.rccn.com.cn/content_article_2192.html. [Google Scholar]
6. International Energy Outlook (2017). Energy Information Administration of USA. [Google Scholar]
7. Feng, Z., Zhao, Y., Zhou, A., Zhang, N. (2012). Development program of hot dry rock geothermal resource in the Yangbajing Basin of China. Renewable Energy, 39(1), 490–495. DOI 10.1016/j.renene.2011.09.005. [Google Scholar] [CrossRef]
8. Sarbu, I., Sebarchievici, C. (2014). General review of ground-source heat pump systems for heating and cooling of buildings. Energy and Buildings, 70, 441–454. DOI 10.1016/j.enbuild.2013.11.068. [Google Scholar] [CrossRef]
9. Kamali-Asl, A., Ghazanfari, E., Perdrial, N., Bredice, N. (2018). Experimental study of fracture response in granite specimens subjected to hydrothermal conditions relevant for enhanced geothermal systems. Geothermics, 72, 205–224. [Google Scholar]
10. Jacobson, M. Z., Delucchi, M. A., Cameron, M. A., Mathiesen, B. V. (2018). Matching demand with supply at low cost in 139 countries among 20 world regions with 100% intermittent wind, water, and sunlight (WWS) for all purposes. Renewable Energy, 123, 236–248. DOI 10.1016/j.renene.2018.02.009. [Google Scholar] [CrossRef]
11. Kamali-Asl, A., Ghazanfari, E., Perdrial, N., Bredice, N. (2018). Experimental study of fracture response in granite specimens subjected to hydrothermal conditions relevant for enhanced geothermal systems. Geothermics, 72, 205–224. DOI 10.1016/j.geothermics.2017.11.014. [Google Scholar] [CrossRef]
12. Li, L., Si, D. H., Li, J. S., Yu, Y. J. (2011). Three-dimensional modeling of heat flow field for Hot Dry Rock Crannies. Procedia Engineering, 15, 4504–4510. DOI 10.1016/j.proeng.2011.08.846. [Google Scholar] [CrossRef]
13. Lu, S. M. (2018). A global review of enhanced geothermal system (EGS). Renewable and Sustainable Energy Reviews, 81, 2902–2921. DOI 10.1016/j.rser.2017.06.097. [Google Scholar] [CrossRef]
14. Annual USA & Global Geothermal Power Production Report (2016). Geothermal Energy Association. [Google Scholar]
15. Olasolo, P., Juárez, M. C., Morales, M. P., D’Amico, S., Liarte, I. A. (2016). Enhanced geothermal systems (EGSA review. Renewable and Sustainable Energy Reviews, 56, 133–144. DOI 10.1016/j.rser.2015.11.031. [Google Scholar] [CrossRef]
16. Zhu, N., Hu, P., Xu, L., Jiang, Z., Lei, F. (2014). Recent research and applications of ground source heat pump integrated with thermal energy storage systems: A review. Applied Thermal Engineering, 71(1), 142–151. DOI 10.1016/j.applthermaleng.2014.06.040. [Google Scholar] [CrossRef]
17. Geological Survey Bureau of the Ministry of Nature Energy of China (2018). Geothermal energy development report of China. [Google Scholar]
18. Fox, D. B., Sutter, D., Beckers, K. F., Lukawski, M. Z., Koch, D. L. et al. (2013). Sustainable heat farming: Modeling extraction and recovery in discretely fractured geothermal reservoirs. Geothermics, 46, 42–54. DOI 10.1016/j.geothermics.2012.09.001. [Google Scholar] [CrossRef]
19. Salimzadeh, S., Grandahl, M., Medetbekova, M., Nick, H. M. (2019). A novel radial jet drilling stimulation technique for enhancing heat recovery from fractured geothermal reservoirs. Renewable Energy, 139, 395–409. DOI 10.1016/j.renene.2019.02.073. [Google Scholar] [CrossRef]
20. Yu, L., Wu, X., Wang, Y., Ma, W., Liu, G. (2020). Stratified rock hydraulic fracturing for enhanced geothermal system and fracture geometry evaluation via effective length. Renewable Energy, 152, 713–723. DOI 10.1016/j.renene.2020.01.097. [Google Scholar] [CrossRef]
21. McClure, M. W., Horne, R. N. (2014). An investigation of stimulation mechanisms in Enhanced Geothermal Systems. International Journal of Rock Mechanics and Mining Sciences, 72, 242–260. DOI 10.1016/j.ijrmms.2014.07.011. [Google Scholar] [CrossRef]
22. Chamorro, C. R., García-Cuesta, J. L., Mondéjar, M. E., Pérez-Madrazo, A. (2014). Enhanced geothermal systems in Europe: An estimation and comparison of the technical and sustainable potentials. Energy, 65, 250–263. [Google Scholar]
23. AbuAisha, M., Loret, B. (2016). Stabilization of forced heat convection: Applications to enhanced geothermal systems (EGS). Transport in Porous Media, 112(1), 229–252. DOI 10.1007/s11242-016-0642-x. [Google Scholar] [CrossRef]
24. Gong, F., Guo, T., Sun, W., Li, Z., Yang, B. et al. (2020). Evaluation of geothermal energy extraction in Enhanced Geothermal System (EGS) with multiple fracturing horizontal wells (MFHW). Renewable Energy, 151, 1339–1351. DOI 10.1016/j.renene.2019.11.134. [Google Scholar] [CrossRef]
25. Guo, T., Tang, S., Sun, J., Gong, F., Liu, X. et al. (2020). A coupled thermal-hydraulic-mechanical modeling and evaluation of geothermal extraction in the enhanced geothermal system based on analytic hierarchy process and fuzzy comprehensive evaluation. Applied Energy, 258, 113981. DOI 10.1016/j.apenergy.2019.113981. [Google Scholar] [CrossRef]
26. Huang, W., Cao, W., Jiang, F. (2018). A novel single-well geothermal system for hot dry rock geothermal energy exploitation. Energy, 162, 630–644. DOI 10.1016/j.energy.2018.08.055. [Google Scholar] [CrossRef]
27. Cao, W., Huang, W., Jiang, F. (2016). Numerical study on variable thermophysical properties of heat transfer fluid affecting EGS heat extraction. International Journal of Heat and Mass Transfer, 92, 1205–1217. DOI 10.1016/j.ijheatmasstransfer.2015.09.081. [Google Scholar] [CrossRef]
28. Ghassemi, A. (2012). A review of some rock mechanics issues in geothermal reservoir development. Geotechnical and Geological Engineering, 30(3), 647–664. DOI 10.1007/s10706-012-9508-3. [Google Scholar] [CrossRef]
29. Ren, F., Ma, G., Fan, L., Wang, Y., Zhu, H. (2017). Equivalent discrete fracture networks for modelling fluid flow in highly fractured rock mass. Engineering Geology, 229, 21–30. DOI 10.1016/j.enggeo.2017.09.013. [Google Scholar] [CrossRef]
30. Bisdom, K., Bertotti, G., Nick, H. M. (2016). A geometrically based method for predicting stress-induced fracture aperture and flow in discrete fracture networks. AAPG Bulletin, 100(7), 1075–1097. DOI 10.1306/02111615127. [Google Scholar] [CrossRef]
31. Samin, M. Y., Faramarzi, A., Jefferson, I., Harireche, O. (2019). A hybrid optimisation approach to improve long-term performance of enhanced geothermal system (EGS) reservoirs. Renewable Energy, 134, 379–389. DOI 10.1016/j.renene.2018.11.045. [Google Scholar] [CrossRef]
32. DiPippo, R. (2012). Geothermal power plants: Principles, applications, case studies and environmental impact. Butterworth-Heinemann. [Google Scholar]
33. Breede, K., Dzebisashvili, K., Liu, X. L., Falcone, G. (2013). A systematic review of enhanced (or engineered) geothermal systems: Past, present and future. Geothermal Energy, 1(1), 163. DOI 10.1186/2195-9706-1-4. [Google Scholar] [CrossRef]
34. Macmillan (2009). Geothermal quake risks must be faced. Nature, 462, 848–849. [Google Scholar]
35. AbuAisha, M., Loret, B., Eaton, D. (2016). Enhanced Geothermal Systems (EGSHydraulic fracturing in a thermo-poroelastic framework. Journal of Petroleum Science and Engineering, 146, 1179–1191. DOI 10.1016/j.petrol.2016.07.027. [Google Scholar] [CrossRef]
36. Yang, S., Tao, W. (2008). Heat transfer. Beijing: Higher Education Press. [Google Scholar]
37. Zhao, J. (1992). Analytical and experimental studies of heat convection by water flow in rock fractures. Balkema Rotterdam. [Google Scholar]
38. Zhao, Z. (2014). On the heat transfer coefficient between rock fracture walls and flowing fluid. Computers and Geotechnics, 59, 105–111. DOI 10.1016/j.compgeo.2014.03.002. [Google Scholar] [CrossRef]
39. Bai, B., He, Y., Li, X., Hu, S., Huang, X. et al. (2016). Local heat transfer characteristics of water flowing through a single fracture within a cylindrical granite specimen. Environmental Earth Sciences, 75(22), 877. DOI 10.1007/s12665-016-6249-2. [Google Scholar] [CrossRef]
40. Bai, B., He, Y., Li, X., Li, J., Huang, X. et al. (2017). Experimental and analytical study of the overall heat transfer coefficient of water flowing through a single fracture in a granite core. Applied Thermal Engineering, 116, 79–90. DOI 10.1016/j.applthermaleng.2017.01.020. [Google Scholar] [CrossRef]
41. Hadgu, T., Kalinina, E., Lowry, T. S. (2016). Modeling of heat extraction from variably fractured porous media in Enhanced Geothermal Systems. Geothermics, 61, 75–85. DOI 10.1016/j.geothermics.2016.01.009. [Google Scholar] [CrossRef]
42. Zeng, Y. C., Wu, N. Y., Su, Z., Wang, X. X., Hu, J. (2013). Numerical simulation of heat production potential from hot dry rock by water circulating through a novel single vertical fracture at Desert Peak geothermal field. Energy, 63, 268–282. DOI 10.1016/j.energy.2013.10.036. [Google Scholar] [CrossRef]
43. Aliyu, M. D., Chen, H. P. (2017). Sensitivity analysis of deep geothermal reservoir: Effect of reservoir parameters on production temperature. Energy, 129, 101–113. DOI 10.1016/j.energy.2017.04.091. [Google Scholar] [CrossRef]
44. Asai, P., Panja, P., McLennan, J., Moore, J. (2018). Performance evaluation of enhanced geothermal system (EGSSurrogate models, sensitivity study and ranking key parameters. Renewable Energy, 122, 184–195. DOI 10.1016/j.renene.2018.01.098. [Google Scholar] [CrossRef]
45. Chen, J., Luo, L., Jiang, F. (2013). Thermal compensation of rocks encircling heat reservoir in heat extraction of enhanced geothermal system. Chinese Journal of Computation Physics, 30(6), 862–870. [Google Scholar]
46. Chen, J., Jiang, F. (2013). A numerical study to heat mining process of enhanced geothermal systems. Chinese Journal of Advances in New and Renewable Energy, 1(2), 187–195. [Google Scholar]
47. Shi, Y., Song, X., Li, J., Wang, G., Zheng, R. et al. (2019). Numerical investigation on heat extraction performance of a multilateral-well enhanced geothermal system with a discrete fracture network. Fuel, 244, 207–226. [Google Scholar]
48. Chen, L., Li, J., Zhang, Y., Han, F., Ji, C. et al. (2019). Study on coupled heat transfer and seepage in large sparsely fractured surrounding rocks in deep underground spaces. Applied Thermal Engineering, 162, 1–13. [Google Scholar]
49. Shaik, A. R., Rahman, S. S., Tran, N. H., Tran, T. (2011). Numerical simulation of Fluid-Rock coupling heat transfer in naturally fractured geothermal system. Applied Thermal Engineering, 31(10), 1600–1606. DOI 10.1016/j.applthermaleng.2011.01.038. [Google Scholar] [CrossRef]
50. Huang, W., Cao, W., Guo, J., Jiang, F. (2017). An analytical method to determine the fluid-rock heat transfer rate in two-equation thermal model for EGS heat reservoir. International Journal of Heat and Mass Transfer, 113, 1281–1290. DOI 10.1016/j.ijheatmasstransfer.2017.06.045. [Google Scholar] [CrossRef]
51. Ma, Y., Zhang, Y., Huang, Y., Zhang, Y., Hu, Z. (2019). Experimental study on flow and heat transfer characteristics of water flowing through a rock fracture induced by hydraulic fracturing for an enhanced geothermal system. Applied Thermal Engineering, 154, 433–441. DOI 10.1016/j.applthermaleng.2019.03.114. [Google Scholar] [CrossRef]
52. Hu, G., Xu, W., Cheng, H. (2002). Gas flow and heat transfer in a moving packed bed of particle. Chinese Journal of Cumbustion Science and Technology, 1, 9–12. [Google Scholar]
53. Wanniarachchi, W. A. M., Ranjith, P. G., Perera, M. S. A., Rathnaweera, T. D., Zhang, D. C. et al. (2018). Investigation of effects of fracturing fluid on hydraulic fracturing and fracture permeability of reservoir rocks: An experimental study using water and foam fracturing. Engineering Fracture Mechanics, 194, 117–135. DOI 10.1016/j.engfracmech.2018.03.009. [Google Scholar] [CrossRef]
54. Guo, P. Y., Liu, D. (2016). Numerical model of convention heat transfer in coarse sandstone. http://www.doc88.com/p-2456927085576.html. [Google Scholar]
55. Tsang, Y. W. (1984). The effect of tortuosity on fluid flow through a single fracture. Water Resources Research, 20(9), 1209–1215. [Google Scholar]
56. Brown, S. R. (1987). Fluid-flow through rock joints: The effect of surface-roughness. Journal of Geophysical Research, 92(B2), 1337–1347. DOI 10.1029/JB092iB02p01337. [Google Scholar] [CrossRef]
57. Zhao, J., Tso, C. P. (1993). Heat transfer by water flow in rock fractures and the application to hot dry rock geothermal systems. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 30(6), 633–641. DOI 10.1016/0148-9062(93)91223-6. [Google Scholar] [CrossRef]
58. Xie, H., Pariseau, W. G. (1994). Fractal estimation of joint roughness coefficients. Chinese Science Abstracts Series B, 24(5), 524–530. [Google Scholar]
59. Zhao, J. (1999). Experimental study of flow-rock heat transfer in rock fractures. Chinese Journal of Rock Mechanics and Engineering, 2, 1–5. [Google Scholar]
60. Barton, N., Choubey, V. (1977). The shear strength of rock joints in theory and practice. Rock Mechanics, 10, 1–54. [Google Scholar]
61. Ranjith, P. G. (2010). An experimental study of single and two-phase fluid flow through fractured granite specimens. Environmental Earth Sciences, 59(7), 1389–1395. DOI 10.1007/s12665-009-0124-3. [Google Scholar] [CrossRef]
62. Babadagli, T., Ren, X., Develi, K. (2015). Effects of fractal surface roughness and lithology on single and multiphase flow in a single fracture: An experimental investigation. International Journal of Multiphase Flow, 68, 40–58. DOI 10.1016/j.ijmultiphaseflow.2014.10.004. [Google Scholar] [CrossRef]
63. Neuville, A., Toussaint, R., Schmittbuhl, J. (2010). Fracture roughness and thermal exchange: A case study at Soultz-sous-Forêts. Comptes Rendus Geoscience, 342(7–8), 616–625. DOI 10.1016/j.crte.2009.03.006. [Google Scholar] [CrossRef]
64. Li, Z., Zhang, Y., Zhang, C., Xu, T. (2018). Experiment on convection heat transfer characteristics of single granite fractured. Rock and Soil Mechanics, 39(9), 3261–3269. [Google Scholar]
65. Luo, Y., Xu, W., Lei, Y., Wu, P., Qin, G. et al. (2019). Experimental study of heat transfer by water flowing through smooth and rough rock fractures. Energy Reports, 5, 1025–1029. DOI 10.1016/j.egyr.2019.07.018. [Google Scholar] [CrossRef]
66. He, R., Rong, G., Tan, J., Cheng, L. (2019). Numerical investigation of fracture morphology effect on heat transfer characteristics of water flow through a single fracture. Geothermics, 82, 51–62. DOI 10.1016/j.geothermics.2019.05.014. [Google Scholar] [CrossRef]
67. He, Y., Bai, B., Hu, S., Li, X. (2016). Effects of surface roughness on the heat transfer characteristics of water flow through a single granite fracture. Computers and Geotechnics, 80, 312–321. DOI 10.1016/j.compgeo.2016.09.002. [Google Scholar] [CrossRef]
68. Wu, X., Guo, Q., Cai, M., Zhu, Y., Zhang, J. et al. (2020). Study on the influence of fracture flow on the temperature field of rock mass with high temperature. Case Studies in Thermal Engineering, 22, 100755. DOI 10.1016/j.csite.2020.100755. [Google Scholar] [CrossRef]
69. Zhou, L., Zhang, Y., Hu, Z., Yu, Z., Luo, Y. et al. (2019). Analysis of influencing factors of the production performance of an enhanced geothermal system (EGS) with numerical simulation and artificial neural network (ANN). Energy and Buildings, 200, 31–46. DOI 10.1016/j.enbuild.2019.07.045. [Google Scholar] [CrossRef]
70. Gao, J., Xiang, Y. (2017). Numerical analysis on crossed water flow and heat transfer on the temperature of fractured rocks. Chinese Journal of Underground Space and Engineering, 13(S2), 598–604. [Google Scholar]
71. Ma, Y., Li, S., Zhang, L., Liu, S., Liu, Z. et al. (2020). Analysis on the heat extraction performance of multi-well injection enhanced geothermal system based on leaf-like bifurcated fracture networks. Energy, 213, 118990. DOI 10.1016/j.energy.2020.118990. [Google Scholar] [CrossRef]
72. Vasilyeva, M., Babaei, M., Chung, E. T., Spiridonov, D. (2019). Multiscale modeling of heat and mass transfer in fractured media for enhanced geothermal systems applications. Applied Mathematical Modelling, 67, 159–178. DOI 10.1016/j.apm.2018.10.025. [Google Scholar] [CrossRef]
73. Shi, Y., Song, X., Wang, G., Li, J., Geng, L. et al. (2019). Numerical study on heat extraction performance of a multilateral-well enhanced geothermal system considering complex hydraulic and natural fractures. Renewable Energy, 141, 950–963. DOI 10.1016/j.renene.2019.03.142. [Google Scholar] [CrossRef]
74. Huang, Y., Zhang, Y., Yu, Z., Ma, Y., Zhang, C. (2019). Experimental investigation of seepage and heat transfer in rough fractures for enhanced geothermal systems. Renewable Energy, 135, 846–855. DOI 10.1016/j.renene.2018.12.063. [Google Scholar] [CrossRef]
75. Xin, Y., Sun, Z., Zhuang, L., Yao, J., Zhang, K. et al. (2019). Numerical simulation of fluid flow and heat transfer in EGS with thermal-hydraulic-mechanical coupling method based on a rough fracture model. Energy Procedia, 158, 6038–6045. DOI 10.1016/j.egypro.2019.01.514. [Google Scholar] [CrossRef]
76. Jiang, F., Luo, L., Chen, J. (2013). A novel three-dimensional transient model for subsurface heat exchange in enhanced geothermal systems. International Communications in Heat and Mass Transfer, 41, 57–62. DOI 10.1016/j.icheatmasstransfer.2012.11.003. [Google Scholar] [CrossRef]
77. Ghassemi, A., Zhou, X. (2011). A three-dimensional thermo-poroelastic model for fracture response to injection/extraction in enhanced geothermal systems. Geothermics, 40(1), 39–49. DOI 10.1016/j.geothermics.2010.12.001. [Google Scholar] [CrossRef]
78. Cao, W., Huang, W., Jiang, F. (2016). A novel thermal-hydraulic–mechanical model for the enhanced geothermal system heat extraction. International Journal of Heat and Mass Transfer, 100, 661–671. DOI 10.1016/j.ijheatmasstransfer.2016.04.078. [Google Scholar] [CrossRef]
79. Sun, Z., Xin, Y., Yao, J., Zhang, K., Zhuang, L. et al. (2018). Numerical investigation on the heat extraction capacity of dual horizontal wells in enhanced geothermal systems based on the 3-D THM model. Energies, 11(2), 280. DOI 10.3390/en11020280. [Google Scholar] [CrossRef]
80. Pandey, S. N., Chaudhuri, A., Kelkar, S. (2017). A coupled thermo-hydro-mechanical modeling of fracture aperture alteration and reservoir deformation during heat extraction from a geothermal reservoir. Geothermics, 65, 17–31. DOI 10.1016/j.geothermics.2016.08.006. [Google Scholar] [CrossRef]
81. Li, M., Gou, Y., Hou, Z., Were, P. (2015). Investigation of a new HDR system with horizontal wells and multiple fractures using the coupled wellbore-reservoir simulator TOUGH2MP-WELL/EOS3. Environmental Earth Sciences, 73(10), 6047–6058. DOI 10.1007/s12665-015-4242-9. [Google Scholar] [CrossRef]
82. Ma, Y., Zhang, Y., Hu, Z., Yu, Z., Zhou, L. et al. (2020). Numerical investigation of heat transfer performance of water flowing through a reservoir with two intersecting fractures. Renewable Energy, 153, 93–107. DOI 10.1016/j.renene.2020.01.141. [Google Scholar] [CrossRef]
83. Lomize, G. M. (1951). Flow in fractured rocks. Moscow: Gesenergoizdat. [Google Scholar]
84. Louis, C. (1969). A study of groundwater floe in jointed rock and its influence on the stability of rock masses. London: Imperial College. [Google Scholar]
85. Su, B., Zhan, M., Zhao, J. (1995). Experimental research on seepage in natural rock mass. Chinese Journal of Geotechnical Engineering, 17(5), 19–24. [Google Scholar]
86. Asai, P., Panja, P., Velasco, R., McLennan, J., Moore, J. (2018). Fluid flow distribution in fractures for a doublet system in Enhanced Geothermal Systems (EGS). Geothermics, 75, 171–179. DOI 10.1016/j.geothermics.2018.05.005. [Google Scholar] [CrossRef]
87. Klugea, C., Milscha, H., Blöcher, G. (2017). Permeability of displaced fractures. Energy Procedia, 125, 88–97. DOI 10.1016/j.egypro.2017.08.077. [Google Scholar] [CrossRef]
88. Huang, X., Zhu, J., Li, J., Bai, B., Zhang, G. (2016). Fluid friction and heat transfer through a single rough fracture in granitic rock under confining pressure. International Communications in Heat and Mass Transfer, 75, 78–85. DOI 10.1016/j.icheatmasstransfer.2016.03.027. [Google Scholar] [CrossRef]
89. Lu, W., Xiang, Y. Y. (2012). Experiments and sensitivity analyses for heat transfer in a meter-scale regularly fractured granite model with water flow. Journal of Zhejiang University Science A, 13(12), 958–968. DOI 10.1631/jzus.A1200153. [Google Scholar] [CrossRef]
90. Wu, B., Zhang, X., Jeffrey, R. G., Bunger, A. P., Jia, S. (2016). A simplified model for heat extraction by circulating fluid through a closed-loop multiple-fracture enhanced geothermal system. Applied Energy, 183, 1664–1681. DOI 10.1016/j.apenergy.2016.09.113. [Google Scholar] [CrossRef]
91. Ren, F., Ma, G. W., Wang, Y., Fan, L. F. (2016). Pipe network model for unconfined seepage analysis in fractured rock masses. International Journal of Rock Mechanics and Mining Sciences, 88, 183–196. DOI 10.1016/j.ijrmms.2016.07.023. [Google Scholar] [CrossRef]
92. Ren, F., Ma, G., Wang, Y., Li, T., Zhu, H. (2017). Unified pipe network method for simulation of water flow in fractured porous rock. Journal of Hydrology, 547, 80–96. DOI 10.1016/j.jhydrol.2017.01.044. [Google Scholar] [CrossRef]
93. Chapman, A. J. (1989). Heat transfer. New York: Macmilan Publishing Company. [Google Scholar]
94. Zhao, J. (1987). Experimental studies of the hydro-thermo-mechanical behavior of joints in granite. London: Imperial College. [Google Scholar]
95. Zhao, J., Brown, E. T. (1992). Hydro-thermo-mechanical properties of joints in the Carnmenellis granite. Quarterly Journal of Engineering Geology and Hydrogeology, 25(4), 279–290. DOI 10.1144/GSL.QJEG.1992.025.04.03. [Google Scholar] [CrossRef]
96. Zhao, J., Tso, C. P. (1993). Heat-transfer by water-flow in rock fractures and the application to hot dry rock geothermal systems. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 30(6), 633–641. DOI 10.1016/0148-9062(93)91223-6. [Google Scholar] [CrossRef]
97. Ogino, F., Yamamura, M., Fukuda, T. (1999). Heat transfer from hot dry rock to water flowing through a circular fracture. Geothermics, 28, 21–44. [Google Scholar]
98. Heinze, T., Hamidi, S., Galvan, B. (2017). A dynamic heat transfer coefficient between fractured rock and flowing fluid. Geothermics, 65, 10–16. DOI 10.1016/j.geothermics.2016.08.007. [Google Scholar] [CrossRef]
99. Ma, Y., Zhang, Y., Yu, Z., Huang, Y., Zhang, C. (2018). Heat transfer by water flowing through rough fractures and distribution of local heat transfer coefficient along the flow direction. International Journal of Heat and Mass Transfer, 119, 139–147. DOI 10.1016/j.ijheatmasstransfer.2017.11.102. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |