An Adaptive Parallel Feedback-Accelerated Picard Iteration Method for Simulating Orbit Propagation

Nomenclature

1  Introduction

In recent years, the complexity of aerospace missions has grown, leading to an urgent need for precise and real-time orbit computing. For instance, it is crucial to obtain accurate long-term orbit propagation results in spacecraft on-orbit service operations [1]; meanwhile, the real-time computation of spacecraft position is vital in guidance navigation [2,3] and formation flying tasks [4,5]. These missions all require fast and accurate methods for solving orbit propagation problems.

Unfortunately, the traditional numerical methods based on finite difference method fail to meet the demand for high accuracy and high efficiency simultaneously because they rely on small integration steps to ensure accuracy [6]. To overcome this challenge, scholars have proposed a family of iterative collocation methods without the limitation of small integration steps, such as the Modified Chebyshev-Picard Iteration method and the Feedback-Accelerated Picard Iteration method [7–10]. These methods approach the real solution by correcting the approximated solution iteratively and simplify integration operations using the idea of discretization, which has been applied extensively in aerospace missions such as orbit propagation, Lambert’s problem and so on [11–14]. Some excellent latest research for iterative collocation methods have been developed, such as the new balanced space-time Sinc-collocation method [15] and the error analysis of the Orthogonal Spline Collocation (OSC) method [16], which contributes effective method and improves the theoretical foundation. Moreover, these methods exhibit scalability to be parallel accelerated [17,18]. The Parallel Feedback-Accelerated Picard Iteration (P-FAPI) method is a representative parallel iterative collocation method that can quickly obtain highly accurate solutions to orbit propagation problems. However, improper method parameters will reduce the efficiency and accuracy of the P-FAPI method. While some adaptive methods exist for iterative collocation methods [19,20], there is a lack of adaptive methods utilizing parallel technology for parallel iterative collocation methods.

In this paper, we propose a new Adaptive Parallel Feedback-Accelerated Picard Iteration (AP-FAPI) method, which refines the method parameters of the P-FAPI method to maximize efficiency while ensuring accuracy. To achieve the highest possible efficiency, we define the method’s computation speed and optimize it according to the relationship between the step size and the convergence speed represented by the iteration count. More importantly, we can efficiently obtain a series of iteration counts with parallel technology. To ensure the desired accuracy, we terminate prematurely in case of an excessive iteration count or significant computational error and consider the current iteration non-convergent.

This paper is organized as follows. In Section 2, we introduce the theory of the P-FAPI. In Section 3, we propose the Adaptive Parallel Feedback-Accelerated Picard Iteration method. In Section 4, we illustrate three orbit propagation cases to verify the high performance of the AP-FAPI method. Finally, we present our conclusions in Section 5.

2  Parallel Feedback-Accelerated Picard Iteration Method

The orbit propagation problems are often described as the nonlinear ordinary differential equation. The Parallel Feedback-Accelerated Picard Iteration (P-FAPI) method is an advanced iterative collocation method for solving these problems, which combines the variational iteration method [21] with the collocation method. The P-FAPI method can approach the real solution in large steps with parallel acceleration. This section introduces the P-FAPI method by solving the general first-order nonlinear differential equation as follows:

{dxdt=g(x(t),t),t∈[t0,tf]x(t0)=x0(1)

where x(t)=[x1(t),x2(t),…,xd(t),…,xD(t)]T is a D-dimensional vector and xd(t) denotes the d-th component of x(t). Here, we set t0=−1,tf=1.

In the variational iterative method, the solution will converge iteratively to the real solution with an initial guess x0(t) and the following corrective iterative formula:

xn+1(t)=xn(t)+∫−1tλ(τ){x˙n(τ)−g[xn(τ),τ]}dτ(2)

where λ(τ) is a generalized Lagrange multiplier to be determined. Based on the variational principle, we obtain the first-order Taylor series expansion of λ(τ) at the point of τ=t:

λ(τ)≈λ(t)+λ˙(t)(τ−t)=−I+J(t)(τ−t)(3)

xn+1(t)=xn(t)−{I+J(t)t}∫−1tG(τ)dτ+J(t)∫−1tτG(τ)dτ(4)

Then the linear combination of N+1 Chebyshev orthogonal basis functions is used to approximate each element of x(t), x˙(t), G(t) and ∫−1tG(τ)dτ:

{xd(t)≈∑n=0Nαd,nϕn(t)=Φ(t)Adx˙d(t)≈∑n=0Nαd,nϕ˙n(t)=Φ˙(t)AdGd(t)≈∑n=0Nβd,nϕn(t)=Φ(t)Bd∫−1tGd(τ)dτ≈∑n=0Nβd,n∫−1tϕn(τ)dτ=∫−1tΦ(τ)dτBd(5)

where Ad=[αd,0,αd,1,…,αd,N]T and Bd=[βd,0,βd,1,…,βd,N]T are the coefficient vectors of the basis function, Φ(t)=[ϕ0(t),ϕ1(t),…,ϕN(t)] is the vector of the Chebyshev basis function.

Next, Eq. (5) is discretized by the collocation method. Here Chebyshev-Gauss-Lobatto (CGL) nodes are chosen as the collocation points, which are defined as

tj=−cos⁡((j−1)πM−1),j=1,2,…,M(6)

where the number of collocation points M is usually selected as N+1, the same as the number of Chebyshev orthogonal basis functions. After discretizing, we have

[x˙d(t1)x˙d(t2)⋮x˙d(tM)]=[Φ˙(t1)Φ˙(t2)⋮Φ˙(tM)][Φ(t1)Φ(t2)⋮Φ(tM)]−1[xd(t1)xd(t2)⋮xd(tM)]=Qχd(7)

[∫−1t1Gd(τ)dτ∫−1t2Gd(τ)dτ⋮∫−1tMGd(τ)dτ]=[∫−1t1Φ(τ)dτ∫−1t2Φ(τ)dτ⋮∫−1tMΦ(τ)dτ][Φ(t1)Φ(t2)⋮Φ(tM)]−1[Gd(t1)Gd(t2)⋮Gd(tM)]=PGd(8)

By substituting Eqs. (7) and (8) into Eq. (4), an iterative formula in matrix form is derived as follows:

[G1G2⋮Gd⋮GD]n=([Q⋱Q][χ1χ2⋮χd⋮χD]n−[g~1g~2⋮g~d⋮g~D]n)(9)

x~n+1=[χ1χ2⋮χd⋮χD]n+1=[χ1χ2⋮χd⋮χD]n+[J11H−PJ12H…J1dH…J1DHJ21HJ22H−P…J2dH…J2DH⋮⋮⋱⋮⋱⋮Jd1HJd2H…JddH−P…JdDH⋮⋮⋱⋮⋱⋮JD1HJD2H…JDdH…JDDH−P]n[G1G2⋮Gd⋮GD]n=x~n+Jn∗Gn(10)

The details of P, Q, g~d, Ji,j and H are provided in Appendix A. Then the flowchart of the P-FAPI method is obtained as Fig. 1.

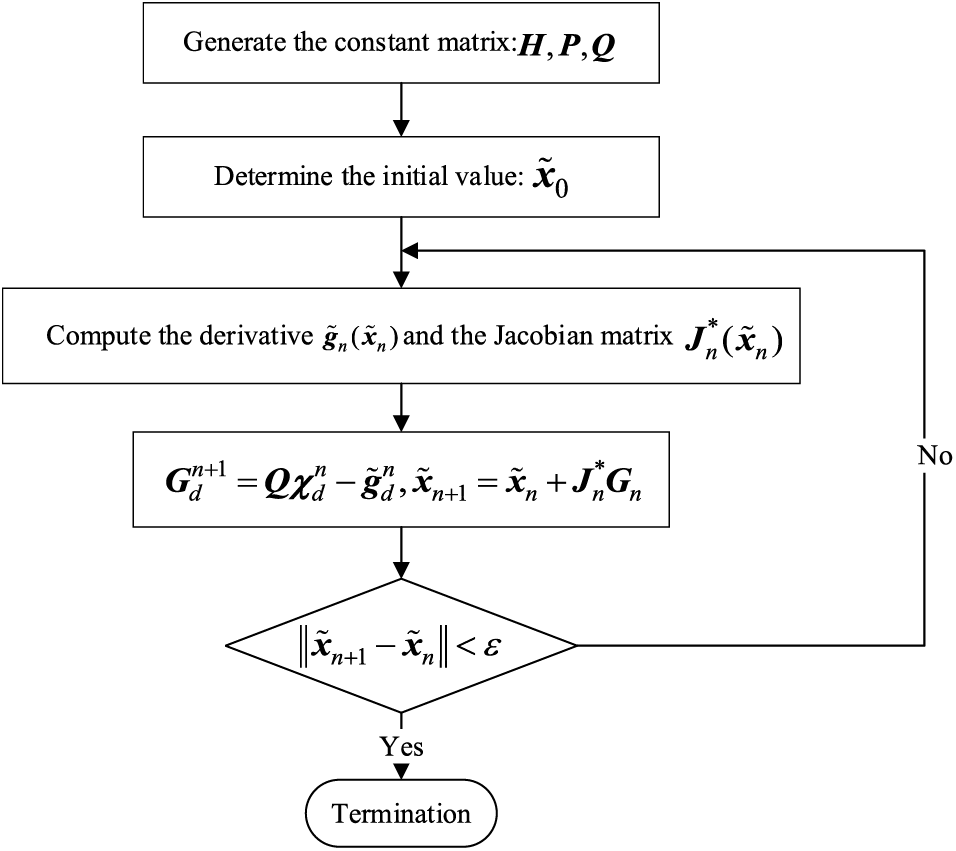
Figure 1: Flowchart of the P-FAPI method

3  Adaptive Parallel Feedback-Accelerated Picard Iteration Method

The performance of the P-FAPI method is heavily affected by the parameters, such as the number of collocations and step size. Excessive collocation points and small steps decrease the method’s efficiency, whereas few collocation points and large steps compromise accuracy. In other words, the mismatch between the number of collocation points and step size will reduce performance. To achieve the highest possible efficiency while meeting accuracy requirements, we propose the Adaptive Parallel Feedback-Accelerated Picard Iteration (AP-FAPI) method by adjusting the step size to match the number of collocation points with inspiration from the finite volume scheme [22,23]. The adjustment principle of step size is presented as follows.

To characterize the efficiency of the P-FAPI method, we define the computation speed as follows:

vm=dtIc⋅1tc(11)

where Ic, tc, and dt denote the iteration count, the computational time of one iteration, and the step size, respectively. tc is determined by the number of collocation points M, and Ic is associated with dt and M.

In the P-FAPI method, the number of collocation points is usually determined according to the compute architecture, meaning tc is considered a constant. Under this premise, we maximize the equivalent step size for unit iteration dt/Ic in Eq. (11) by adjusting the step size to improve the computation speed as much as possible, where the iteration count Ic is recorded during the computation process. With CUDA stream technology [24], one computing process can obtain a group of iteration counts, dramatically increasing the method’s efficiency. The process of the AP-FAPI method is illustrated as follows and shown in Fig. 2.

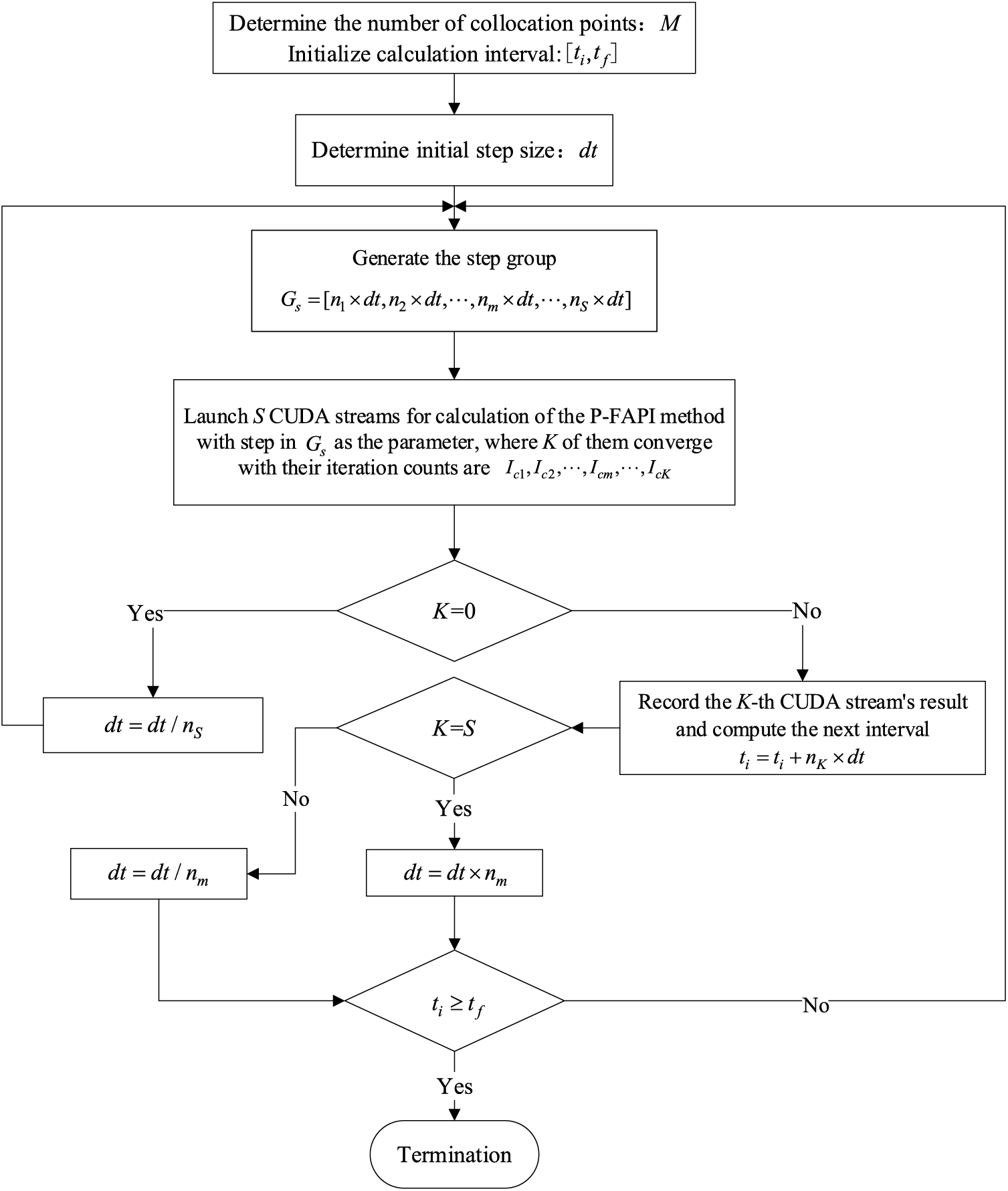
Figure 2: Flowchart of the AP-FAPI method

1.   Generate a group containing S steps by the initial step size dt as follows:

Gs=[n1×dt,n2×dt,…,nm×dt,…,nS×dt],0<n1<n2<…<nm<…<nS(12)

2.   Launch S CUDA streams for calculation of the P-FAPI method with step in Gs as the parameter.

3.   Without loss of generality, we can assume that there are K converged calculations in the above CUDA streams and their iteration counts are Ic1,Ic2,…,Icm,…,IcK, respectively, where 0≤K≤S.

4.   When K=0, set step size as dt=dt/nS and recalculate within this interval. Otherwise, record the K-th CUDA stream’s result, compute the next interval, and determine its step size based on the following formula:

dt={ dt×nmK=Sdt/nmK<S,   nm=argmaxm∈[ 1,2,…,K ]nm×dtIcm(13)

To further ensure the accuracy of the P-FAPI method, we defined the maximum iteration count Im and the maximum iteration error Em. During the iterative process, if the iteration count exceeds the maximum iteration count or the iteration error exceeds the maximum iteration error, the iteration is considered non-convergent.

4  Numerical Simulation

In this section, the high performance of the AP-FAPI method is validated in three typical orbit propagation problems based on the 40th-order EGM: a Low Earth Orbit (LEO) propagation problem, a Highly Elliptical Orbit (HEO) problem, and a Geostationary Earth Orbit (GEO) propagation problem. Their initial parameters and intervals are shown in Table 1, and the schematic diagram is shown in Fig. 3.

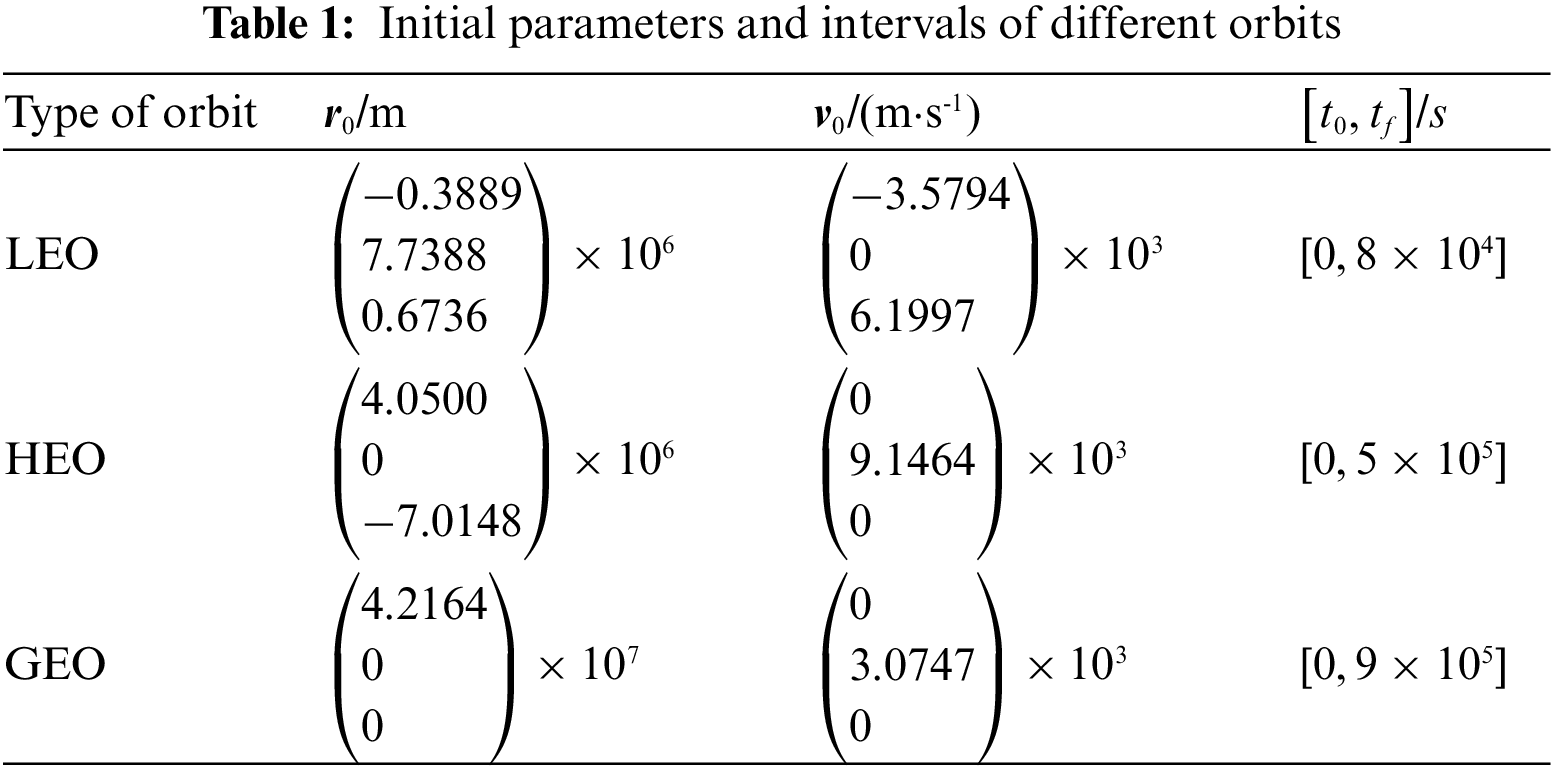
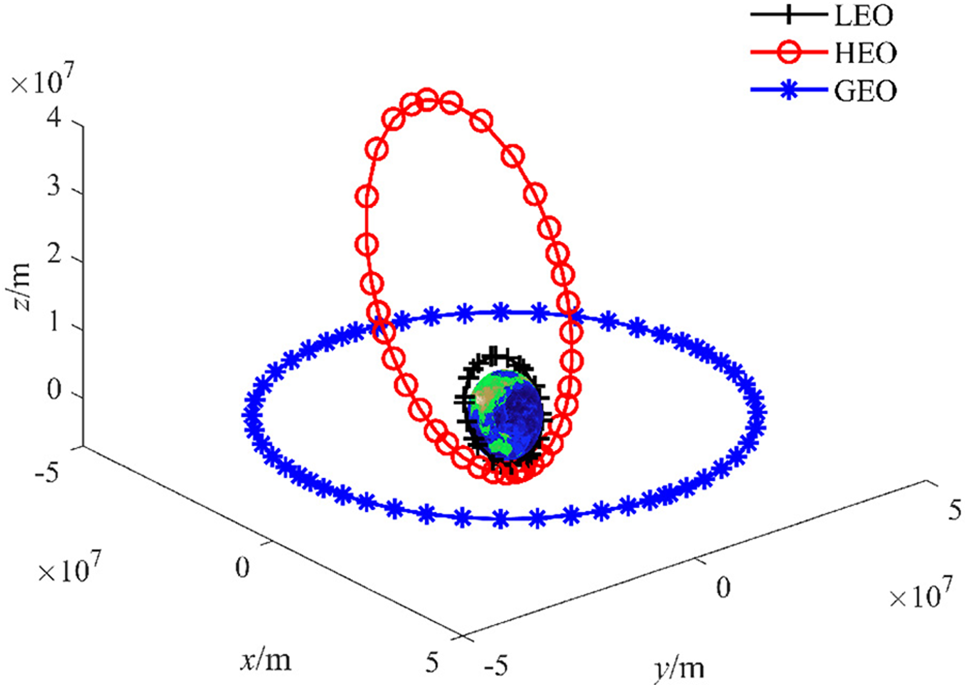
Figure 3: Illustration of LEO, HEO and GEO

The numerical simulation is carried out in Microsoft Visual Studio 2019, using a computer with the Intel 9 12900K CPU and NVIDIA Quadro P1000 GPU. The performance of the AP-FAPI method is compared with that of the P-FAPI method and ODE45, the implementation of DP5(4) in MATLAB. Their parameters are shown in Tables 2 and 3.

The positional errors of different methods are shown in Fig. 4 (The reference solutions are obtained by ODE45 with the highest accuracy). The computational times and iteration counts of different methods are shown in Table 4. The iteration counts and generated step sizes in the AP-FAPI method are shown in Fig. 5.

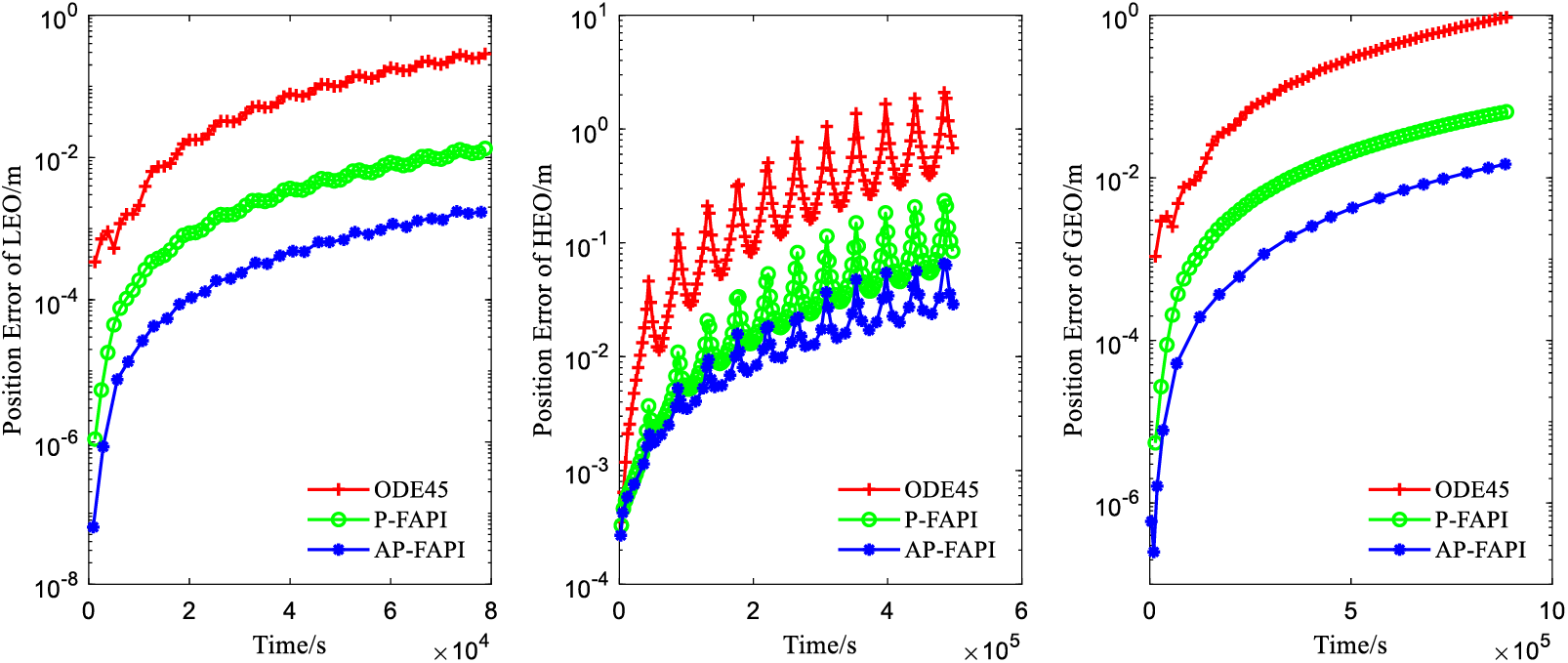
Figure 4: Positional errors of different methods

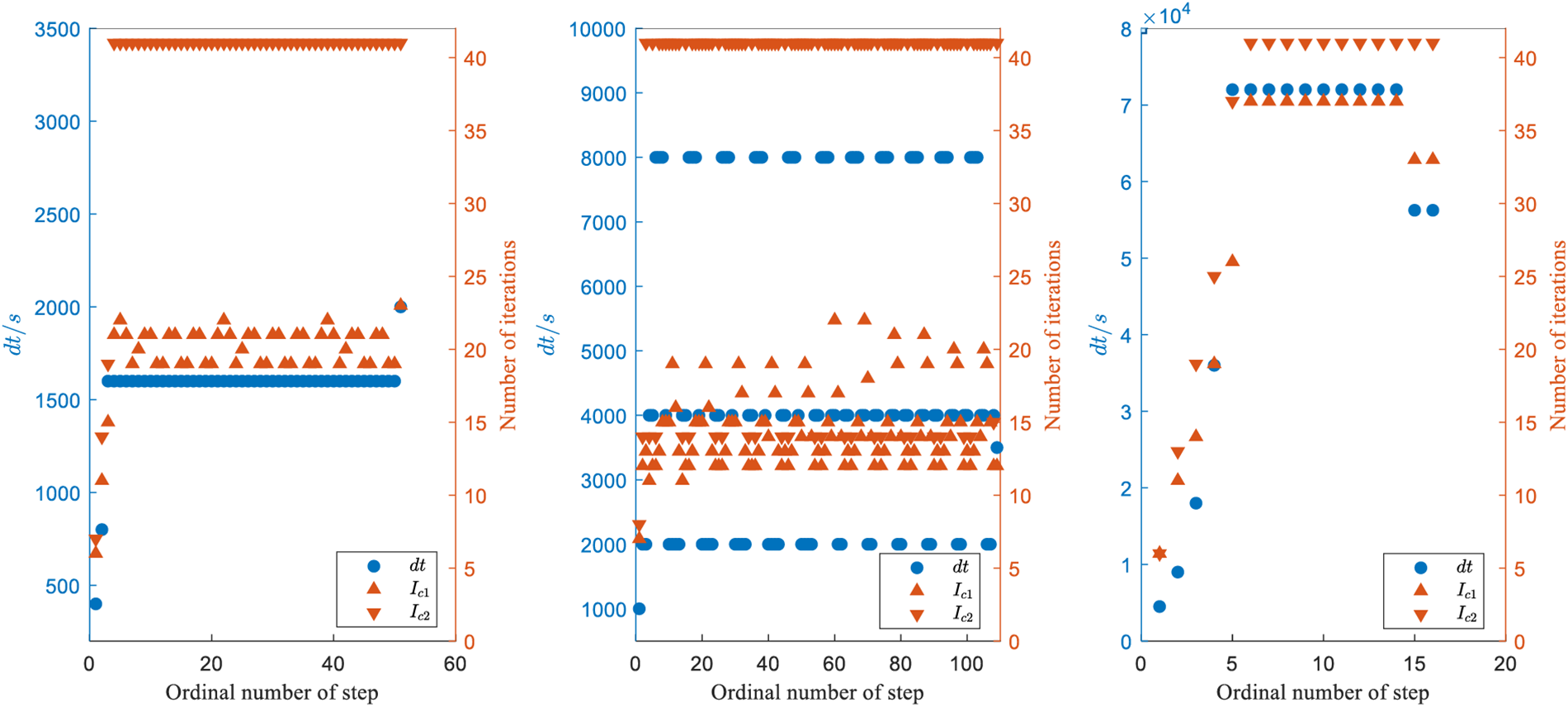
Figure 5: Iteration counts and generated step sizes in the AP-FAPI method

In Fig. 4, the results in three illustrative examples demonstrate that the P-FAPI method attains approximately one order of magnitude higher accuracy compared to ODE45, while the AP-FAPI method achieves approximately two orders of magnitude higher accuracy. The results in Table 4 indicate that the P-FAPI method is at least twice as fast as ODE45, and the AP-FAPI method is at least four times faster than ODE45. Fig. 5 demonstrates that in LEO and GEO propagation problems, the step size rapidly adjusts to an optimal value after a few iterations and remains consistent throughout the subsequent computations. In contrast, in HEO propagation problems, the step size varies frequently throughout the calculation process. This aligns with the fact that the LEO and GEO curves are flat, whereas the HEO curves exhibit a steep.

Overall, the results from the three simulations confirm that the AP-FAPI method with optimized parameters achieves greater accuracy and efficiency when compared to ODE45 and the P-FAPI method.

5  Conclusion

We proposed a novel adaptive parallel feedback accelerated Picard iteration method by refining the parameter during calculation. A mismatch between the parameters of the P-FAPI method, namely the number of collocation points and step size, will result in reduced performance. The proposed method could optimize efficiency while meeting the expected accuracy. It dynamically adjusts the step size to align with the number of collocation points based on the relationship between the step size and convergence represented by the iteration count. The high performance of the proposed method is verified in solving three typical orbit propagation problems. Numerical simulations show that the AP-FAPI method is at least four times faster than ODE45 and twice as fast as the P-FAPI method. It is also the most accurate method, yielding two orders of magnitude higher accuracy than ODE45 and one order higher than the P-FAPI method. The proposed method can be applied to solve various nonlinear dynamic problems efficiently and accurately. Future research can focus on the application of the AP-FAPI method in more complicated systems to explore its efficiency [25].

Acknowledgement: We would like to express our sincere appreciation for the exceptional contributions made by Professor Satya Atluri in the field of computational mechanics and engineering. On the occasion of Professor Satya Atluri’s 80th birthday, we extend our warmest wishes for good health and continued success in his academic endeavors. Additionally, we gratefully acknowledge Professor Dai for his invaluable guidance and meticulous support throughout the preparation of this paper.

Funding Statement: This study was co-supported by the National Key Research and Development Program of China (No. 2021YFA0717100) and the National Natural Science Foundation of China (Nos. 12072270, U2013206).

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and adaptive method design: C. Wang, H. Dai; test case design: C. Wang, W. Yang; analysis and interpretation of results: C. Wang, W. Yang; draft manuscript preparation: C. Wang, W. Yang; All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used in this study are available upon request from the GitHub: https://github.com/CT-Wang/TSP-DEDT-data.git.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Zhang, Z., Deng, L., Feng, J., Chang, L., Li, D. et al. (2022). A survey of precision formation relative state measurement technology for distributed spacecraft. Aerospace, 9(7), 362. [Google Scholar]

2. Zhang, H., Li, J., Wang, Z., Guan, Y. (2021). Guidance navigation and control for chang’E-5 powered descent. Space: Science & Technology. [Google Scholar]

3. Huang, X., Li, M., Wang, X., Hu, J., Zhao, Y. et al. (2021). The Tianwen-1 guidance, navigation, and control for mars entry, descent, and landing. Space: Science & Technology, 2021, 9846185. [Google Scholar]

4. Gao, C., Zhao, Y. (2023). Model predictive control-based coupled orbit-attitude control for solar sail formation flying in the Earth-Moon system. Astrophysics and Space Science, 368(6), 47. [Google Scholar]

5. Bandyopadhyay, S., Foust, R., Subramanian, G. P., Chung, S. J., Hadaegh, F. Y. (2016). Review of formation flying and constellation missions using nanosatellites. Journal of Spacecraft and Rockets, 53(3), 567–578. [Google Scholar]

6. Chen, W., Cheng, J., Wu, X. (2014). Numerical solutions of differential equations. Shanghai, China: Fudan University Press. [Google Scholar]

7. Wang, X., Yue, X., Dai, H., Atluri, S. N. (2017). Feedback-accelerated picard iteration for orbit propagation and lambert’s problem. Journal of Guidance Control and Dynamics, 40(10), 2442–2451. [Google Scholar]

8. Wang, Y., Ni, G., Liu, Y. (2020). Multistep newton-picard method for nonlinear differential equations. Journal of Guidance, Control, and Dynamics, 43(11), 2148–2155. [Google Scholar]

9. Bai, X., Junkins, J. L. (2011). Modified chebyshev-picard iteration methods for orbit propagation. The Journal of the Astronautical Sciences, 58(4), 583–613. [Google Scholar]

10. Woollands, R., Junkins, J. L. (2019). Nonlinear differential equation solvers via adaptive picard-chebyshev iteration: Applications in astrodynamics. Journal of Guidance, Control, and Dynamics, 42(5), 1007–1022. [Google Scholar]

11. Bai, X., Junkins, J. L. (2011). Modified chebyshev-picard iteration methods for solution of boundary value problems. The Journal of the Astronautical Sciences, 58(4), 615–642. [Google Scholar]

12. Feng, H., Yue, X., Wang, X. (2021). A quasi-linear local variational iteration method for orbit transfer problems. Aerospace Science and Technology, 119, 107222. [Google Scholar]

13. Wang, X., Xu, Q., Atluri, S. N. (2020). Combination of the variational iteration method and numerical algorithms for nonlinear problems. Applied Mathematical Modelling, 79, 243–259. [Google Scholar]

14. Feng, H., Yue, X., Wang, X., Zhang, Z. (2023). Decoupling and quasi-linearization methods for boundary value problems in relative orbital mechanics. Nonlinear Dynamics, 111(1), 199–215. [Google Scholar]

15. Yang, X., Wu, L., Zhang, H. (2023). A space-time spectral order sinc-collocation method for the fourth-order nonlocal heat model arising in viscoelasticity. Applied Mathematics and Computation, 457, 128192. [Google Scholar]

16. Zhang, H., Yang, X., Tang, Q., Xu, D. (2023). A robust error analysis of the OSC method for a multi-term fourth-order sub-diffusion equation. Computers & Mathematics with Applications, 109(1), 180–190. [Google Scholar]

17. Bai, X. (2010). Modified Chebyshev-Picard iteration methods for solution of initial value and boundary value problems (Ph.D. Thesis). Texas A&M University, USA. [Google Scholar]

18. Wang, C., Dai, H., Zhang, Z., Wang, X., Yue, X. (2023). Parallel accelerated local variational iteration method and its application in orbit computation. Chinese Journal of Theoretical and Applied Mechanics, 55(4), 991–1003. [Google Scholar]

19. Dai, H., Zhang, Z., Wang, X., Feng, H., Wang, C. et al. (2023). Fast and accurate adaptive collocation iteration method for orbit dynamic problems. Chinese Journal of Aeronautics, 36(9), 231–242. [Google Scholar]

20. Wang, X., Elgohary, T. A., Zhang, Z., Tasif, T. H., Feng, H. et al. (2023). An adaptive local variational iteration method for orbit propagation in astrodynamics problems. The Journal of the Astronautical Sciences, 70(1), 2. [Google Scholar]

21. He, J. (1999). Variational iteration method—A kind of non-linear analytical technique: Some examples. International Journal of Non-Linear Mechanics, 34(4), 699–708. [Google Scholar]

22. Yang, X., Zhang, H., Zhang, Q., Yuan, G. (2022). Simple positivity-preserving nonlinear finite volume scheme for subdiffusion equations on general non-conforming distorted meshes. Nonlinear Dynamics, 108(4), 3859–3886. [Google Scholar]

23. Yang, X., Zhang, H., Zhang, Q., Yuan, G., Sheng, Z. (2019). The finite volume scheme preserving maximum principle for two-dimensional time-fractional Fokker-Planck equations on distorted meshe. Applied Mathematics Letters, 97, 99–106. [Google Scholar]

24. Cheng, J., Grossman, M., McKercher, T. (2014). Professional CUDA C programming. USA: John Wiley & Sons. [Google Scholar]

25. Zhang, H., Liu, Y., Yang, X. (2014). An efficient ADI difference scheme for the nonlocal evolution problem in three-dimensional space. Journal of Applied Mathematics and Computing, 69(1), 651–674. [Google Scholar]

Appendix A

In Eq. (10), the matrixes Q, P, Ji,j, H and the vector g~d are as follows:

Q=[Φ˙(t1)Φ˙(t2)⋮Φ˙(tM)][Φ(t1)Φ(t2)⋮Φ(tM)]−1,P=[∫−1t1Φ(τ)dτ∫−1t2Φ(τ)dτ⋮∫−1tMΦ(τ)dτ][Φ(t1)Φ(t2)⋮Φ(tM)]−1(A.1)

Ji,j=dig(∂gi(x(t1),t1)xj(t1),…,∂gi(x(tM),tM)xj(tM))(A.2)

T=dig(t1,t2,…,tM),H=PT−TP(A.3)

g~d=[gd(x(t1),t1)gd(x(t2),t2)⋮gd(x(tM),tM)](A.4)