Improved Resilience of Image Encryption Based on Hybrid TEA and RSA Techniques

1  Introduction

General data security incorporates concepts like confidentiality, authentication, non-repudiation, access control, and availability, which are relevant in image protection. Unauthorized modification, access, or distribution of sensitive or copyrighted materials contained in images needs to be prevented at all costs. This need is met through observance of confidentiality which ensures that only authorized people can view the image, more so when it comes to private images such as medical or personal information [1]. In addition, authentication verifies that the person entity developing the image is the same that owns it, this prevents fraudsters from using images that do not belong to them [2].

Cryptography has provided solutions to overcome these issues [3]. It converts information in such a way that the recipient can decode it. Cryptographers consider several aspects while designing algorithms including their security strength, among others. The contemporary world is characterized by numerous security concerns grounded on information leakage. Cryptography in the modern day has become an effective tool for ensuring confidentiality. Thus, the focus here is on examining crucial factors in the development of cryptographic algorithms in terms of how they deal with confidentiality. Building cryptographic algorithms involves looking into your security, algorithm features, and computational complexity issues among others while creating them. Encryption involves converting original data into cipher text or unreadable format to keep it away from unauthorized people. To secure information such as images transmitted over networks stored on devices/servers or shared among users, encryption becomes a basic technique. There are two main types of encryptions, which include symmetric key encryption and asymmetric key encryption. However, it is important to note that these methods are only effective if used correctly. To solve these problems, designers should work with an encryption method that consumes less processing power, makes the protected image less visible, encrypts quickly, and can maintain the image information when decryption. One major category of such lightweight algorithms is based on classical cryptography. A symmetric lightweight algorithm with stream and block ciphers is one where the text is encrypted bit by bit thus making it more rapid than the same block one. Symmetric and asymmetric encryption are two distinct methods for encrypting data [3].

Cryptanalysis is the investigation and training of evaluating and cracking cryptographic techniques. It encompasses detecting weaknesses or vulnerabilities in encryption methods and interpreting encrypted images without the key or original encryption method. It shows a necessary role in cybersecurity, both for strengthening cryptographic systems and assessing their security [4]. There are many kinds of cryptanalysis attacks that can be applied to the encrypted image such as cropping, Differential attacks.

Symmetric encryption solution refers to shared secret encryption in which only one secret key is utilized in both encryption and decryption of a message [4]. This stipulates that both the sender and receiver must have a common secret key to encode and decode (See Fig. 1). The sender uses a secret key to hash the plain text into cipher text, which can be read only by someone with access to that key. DES (Data Encryption Standard) [5], and AES (Advanced Encryption Standard) [6] are some examples of symmetric encryption algorithms. According to [7], the Tiny Encryption Algorithm (TEA) encryption and decryption routines are designed to provide secure cryptographic operations; The TEA routines perform encryption or decryption on a given data block using the provided key. The resulting cipher text or plaintext is returned separately, enabling the easier implementation of advanced cipher modes beyond the basic Electronic Code Book (ECB) mode. The separate return of the result in TEA is advantageous when implementing modes such as Cipher Block Chaining (CBC) or Counter (CTR) mode, which require more complex operations involving feedback from previous blocks or counters. This design choice offers increased flexibility and versatility in constructing secure cryptographic systems. An experiment conducted by [8] revealed several weaknesses within the algorithm. Finding hash collisions through brute force is relatively straightforward. For a given key, one can systematically try different input data, storing each resulting hash value (along with the corresponding input) in a data structure for efficient lookup. If two distinct inputs produce the same hash value, a collision has occurred. Brute-force key searches within the key space are also easily implemented. By iterating through potential keys sequentially, one can attempt to decrypt known plaintext-cipher text pairs until a match is found.

Figure 1: Symmetric encryption/decryption process [2]

Asymmetric encryption, often termed public key encryption, is a form of cryptographic technique that requires two separate keys, a public key and a private key for coding and decoding messages [9]. The public keys can be shared by any person who wishes to send his or her messages to the receiver while the private key is only known to him or her. The mainframe for the asymmetric encryption approach is presented in Fig. 2 [2]. The message is encrypted with the public key and only decrypted through the corresponding private key. The RSA algorithm is a typical algorithm used in public key encryption. It was invented by Ron Rivest, Adi Shamir and Leonard Adleman in 1977 and is named after their initials. RSA is a widely used and trusted encryption algorithm that relies on the difficulty of factoring large integers to ensure the security of the encrypted data [10,11]. RSA works as follows: the key pair’s owner generates a large composite number by multiplying two prime numbers. This composite number is the modulus for the encryption and decryption process. The owner then generates public and private keys based on the modulus. RSA encryption, while a foundational algorithm in modern cryptography, faces several inherent limitations. Firstly, RSA imposes a constraint on the message size, requiring it to be smaller than the key’s bit length to ensure successful encryption. Secondly, compared to symmetric encryption algorithms, RSA operations are computationally more intensive, resulting in slower encryption and decryption speeds. This performance overhead is a direct consequence of the public-key nature of RSA, which necessitates more complex mathematical operations [12]. Table 1 provides a comparison between symmetric and asymmetric image techniques.

Figure 2: Asymmetric encryption/decryption process [2]

A good image encryption algorithm ought to generate an encrypted image that has a minimal correlation to the original image for better imperceptibility. Unfortunately, designing such is not that easy as there are some impediments including constructing a lightweight cryptographic algorithm without necessarily increasing computational burden, high imperceptibility for the images after they have been encrypted, facilitating prompt response times during encryption and lastly maintaining a high level of information embodied within these images when decrypting them. The categorization of lightweight cryptographic algorithms is like that of conventional cryptography algorithms, stream and block ciphers are the main symmetric algorithms for lightweight cryptography whereas the categories include symmetric and asymmetric algorithms [13].

The following is the classification of this research paper: Section 2 reviews past studies to contextualize this study, picking up where those studies would leave off, thus necessitating further investigation into these matters in future research. The methodology behind this present work can be found in part three which lays bare the structure of a novel hybrid image encryption algorithm (TEA-RSA) combining TEA and RSA. Consequently, Section 4 presents experimental results proving the effectiveness of our encryption method through various statistical analyses (performance metrics). Lastly, Section 5 sums up key findings from different episodes within the manuscript itself and discusses some routes that may be followed in future research.

TEA and RSA are two encryption algorithms used in many cases to increase security in image encryption. The proposed hybrid encryption method provides solutions to issues of confidentiality, authentication, and integrity while at the same time ensuring that images remain accessible and maintain their quality during the encryption process. Through symmetric key encryption methods and asymmetric key encryption methods, we establish a strong platform that can resist any kind of security attack like brute force attack and statistical analysis. The hybrid technique offers high-security levels while at the same time allowing quick encryptions and decryptions in real-time systems. Also, the proposed approach can stand against different kinds of attacks such as cropping and differential attacks. This is evidenced by experiments conducted to verify efficiency in preventing unauthorized access and use of digital images.

2  Literature Review

In this section, we will discuss extensively different approaches in image encryption techniques in the symmetric and asymmetric domains. This part aims to provide an inclusive understanding of the subject. Investigating different methods, techniques, and algorithms developed in the image encryption field. Moreover, the strengths and limitations of each method are judgmentally analyzed. We separated this section into symmetric, asymmetric, and Hybrid encryption approaches.

2.1 Symmetric Image Encryption

Symmetric encryption techniques apply only one key (public key) for both the encryption and decryption processes. These kinds of techniques are less complex but face security as the key issue. The work in [14] proposed an original cryptosystem arranged around plaintext, where the permutation-diffusion process appears concurrently. The synchronized performance of this process, labeled PDSO (permutation-diffusion simultaneous operation), fosters a reciprocal interaction between confusion and diffusion. Accordingly, this synchronized technique improved both the security and efficiency of the encryption process. To enhance the dynamic characteristics of 1D chaotic maps, a novel approach known as the linear-delay-modulation method (LDM) is proposed in [15]. The LDM is utilized to establish a Delayed Sine Map (DSM) obtained from the Sine map. The DSM is applied to modify the conventional Sine map in the Structural Intensity Mean Measure (SIMM) system, leading to the creation of a controlled technique referred to as the Delayed SIMM (DSIMM). The chaotic performance of the DSIMM technique is then examined through the analysis of phase diagrams using Lyapunoy exponent spectra.

The authors in [16] proposed an encryption approach that used the leverage of chaotic sequences and cross-diffusion of bits to improve the security concept. It commences by producing two chaotic sequences through two-dimensional logic-sine coupling mapping, which is used to scramble an original image. The scrambled image experiences a transformation into a one-dimensional sequence, where low-order bits between neighboring pixels are fused to bolster resistance against differential attacks. In the final step, chaotic sequences generated by iterative logical mapping facilitate pixel replacement and cipher text diffusion, completing the encryption process. In work [17], the authors developed a medical image encryption system that relies on a chaotic system, it is involving the two- dimensional Sine Logistic Modulation Map (2D-SLMM) and the two-dimensional Henon-Sine Map (2D-HSM). The elementary encryption process encompasses zigzag scrambling, pixel gray value transformation, and dynamic diffusion. To enhance the security aspect, authors in [18] proposed an improved Advanced Encryption Standard (AES) and they introduced a keystream generator (A5/1, W7) to enhance encryption performance. The study indicated that the keystream producer extensively impacts the overall encryption performance, and the new approach demonstrated high security.

2.2 Asymmetric Image Encryption

Asymmetric techniques are more secure regarding the security of the key, but these methods are complex, and they are not suitable for real-time applications. An innovative asymmetric image encryption method has been presented in [19], it is based on utilizing elliptic curve El-Gamal (EC-ElGamal) cryptography and chaotic theory. The method involved initializing a chaotic technique with values generated through SHA-512 hash. To improve the security issue, a crossover permutation, guided by a chaotic index sequence, is applied to effectively scramble the plain image for enhanced security. In [20], an asymmetric image encryption algorithm is introduced, utilizing a three-dimensional improved logistic chaotic map (3D-ILM) alongside the public-key Rivest, Shamir, Adleman (RSA) cryptography. The design of 3D-ILM is informed by analyses of existing chaotic image encryption frameworks. The authors in [21] introduced a visually secure asymmetric image encryption scheme, integrating the Rivest, Shamir, Adleman (RSA) algorithm with a hyperchaotic map. The technique aimed to leverage the strengths of both RSA and chaos-based image encryption algorithms. A novel one-dimensional chaotic map amplifier (1-DCMA) is introduced by [22]. The assessment of the proposed chaotic system reveals that the 1-DCMA enhances the chaotic behavior, structural control parameters, and sensitivity of the one-dimensional chaotic maps employed as input. The authors in [23] proposed a novel randomized chaotic asymmetric-key algorithm for color image encryption. The proposed method utilized a multiplicative coupled Chebyshev-based encryption algorithm and introduced a novel chaotic key establishment algorithm using Chebyshev polynomials. An image encryption algorithm with a high level of security is proposed in [24], a chaotic system is introduced, and its state variables are employed to generate a new substitution matrix. The research [25] proposed a novel image encryption scheme based on the Lorenz hyper-chaotic system and RSA algorithm. The original values of the Lorenz hyper-chaotic technique are generated by the RSA algorithm, and the key stream is generated iteratively. The diffusion image values are redesigned into a one- one-dimensional image array, which is chaotic, and lacks repeating to cover the image data. Then, the restricted field diffusion algorithm is implemented to recognize the third hiding of the image information. The work in [26] introduced an innovative image encryption scheme that relies on a generalized Arnold map in combination with the Rivest-Shamir-Adleman (RSA) algorithm. The work in [27] introduced an innovative image encryption scheme that relies on a generalized Arnold map in combination with the Rivest-Shamir-Adleman (RSA) algorithm. In [28], the RSA algorithm is employed to encrypt image files, thereby reinforcing security in the communication domain for data transmission. In [28], a quantum logistic image encryption algorithm is introduced, incorporating the Rivest–Shamir–Adleman (RSA) and secure hash (SHA-3) algorithms.

2.3 Hybrid Image Encryption

In this section, we will present the most relevant and recent hybrid image encryption works. The main goal of these approaches is to enhance the security concept, reduce the complexity, and improve the efficiency of the techniques. The work in [29] introduced a novel image encryption method using an improved Henon map in a hybrid domain. The algorithm exercised a three-stage process, incorporating a Two-Dimensional Information Content Histogram Metric (2D-ICHM) map, a double sandwich structure, and SHA-512 hash values for enhanced sensitivity to plaintext. While it demonstrates robust security features, it includes a large key space and resistance to cryptanalysis, but it is not suitable for real-time communication and cannot directly encrypt color images. To address these limitations and explore broader applications in data security, the study [30] proposed a novel hybrid system introduced for secure image transfer, combining TEA and Key-Based Random Permutation (KBRP) encryption techniques. The system enhances security by scrambling images using randomly generated pixel passwords and client-side passwords. This method guarantees robust and comprehensive image security during transfer. A new image encryption method is proposed by [31], the work is combining a chaos sequence with a modified AES algorithm. The encryption key is generated using the Arnold chaos sequence, the approach encrypts the original image through the modified AES algorithm. The algorithm claimed a large key space and prevented brute-force attacks. However, its extreme sensitivity to primary estimates and input images might cause significant changes in the encrypted output with slight alterations. Notably, the research requires explicit discussions on resistance against known-plaintext attacks, chosen-plaintext attacks, and noise assaults.

In [32], a novel image encryption algorithm utilizing SHA-256 and a hyper-chaotic system was presented. The approach integrated permutation, diffusion, and surrounding pixel processes, enhancing security against attacks. However, the work failed to present the values of the Peak Signal-to-Noise Ratio (PSNR) for image quality evaluation, requiring further clarity on the algorithm’s quality and security. In [33], DES encryption combined with random image overlapping was used for heightened image security and reduced information loss. The method showcased increased RGB variation and minimal information loss during decryption. However, the evaluation was limited to histograms, indicating a need for comprehensive testing. Study [34] presented MECCHC (Modified Elliptic Curve Cryptography and Hill Cipher), a data protection method that combines Modified Elliptic Curve Cryptography (MECC) with Hill Cipher (HC). MECCHC enhances the asymmetric key encryption of Elliptic Curve Cryptography by integrating the symmetric encryption of Hill Cipher. This integration achieves a balance between security and computational efficiency, resulting in simpler and faster computations compared to more complex encryption methods associated with Elliptic Curve Cryptography (ECC).

The authors in [35] introduced a hybrid image encryption method, involving the encryption of a digital image using a combination of Vigenere and RSA algorithms. Study [36] presented a robust hybrid image encryption scheme that integrates a cyclic elliptic curve and a chaotic system, effectively mitigating challenges identified in comparable approaches. Study [37] specifically addresses the security concerns about an image encryption technique that combines ECC with Hill cipher (EC- CHC). To improve the security of the image encryption system, an optical image compression and encryption scheme based on compressive sensing and RSA public-key cryptographic algorithm is proposed in [38]. The optical compressive imaging system is employed to model the original image. Walsh-Hadamard transformed into deployed in the encryption phase. Deoxyribonucleic acid (DNA) sequence operations are manipulated to modify the pixel values. The keys managed in the approach are generated based on the original image and are protected by the RSA algorithm. Authors in [39] proposed a new RSA technique applicable to wireless communication devices such as IoT. The study presented a technique that notably decreases the encryption key by employing a true prime random number generator (TPRNG), which creates a prime number whereas it will not be predicted through bio-signals and a disposable RSA encryption key. The authors in [40] proposed novel encryption and watermarking. The watermark is embedded into the Singular Value Decomposition (SVD) of the original image while the One Time Pad (OTP) technique is applied to encrypt the watermarked image. This approach aimed to increase the security level while compromising the complexity and robustness of features. The work focused on the key management complexity for data owners and users.

3  Methodology

Image encryption is an essential area of research as it protects the confidentiality of images during transmission and storage. This study used a hybrid system of the Tiny Encryption Algorithm (TEA) and the Rivest-Shamir-Adleman (RSA) algorithm for image encryption and we called the approach (TEA-RSA).

3.1 Encryption Using TEA-RSA Algorithm

The enhanced Tiny Encryption Algorithm (TEA) will encrypt the collected images. TEA-RSA is a symmetric block cipher, an enhanced version of the TEA that operates on 64-bit blocks and uses a 128-bit key. The encryption process involved dividing the image into 8 × 8 blocks and applying the TEA algorithm to each block (Fig. 3). The key used for encryption was randomly generated and stored securely.

Figure 3: TEA-RSA encryption process

The RSA encryption process involved generating a public and private key pair and encrypting the TEA-RSA encryption key. The RSA key size was 2048 bits, considered secure for modern applications.

Fig. 3 illustrates the following process to perform image encryption using the hybrid system combining the extended tiny encryption algorithm with RSA. In real-time applications, encryption and decryption must be done rapidly without compromising security since the speed of operation is a critical factor. The aim here is to develop an encryption scheme that is highly optimized and integrates the speed advantages of TEA with the strong security provided by RSA (TEA-RSA).

This section also provides details relating to our implementation including how TEA and RSA algorithms were integrated, the optimization techniques adopted to improve encryption speed, as well as measures taken for secure key handling. A thorough analysis of the algorithm will be done using step-by-step demonstrations of its encryption and decryption processes to prove its effectiveness and reliability with image encryption systems. The tests will focus on validating the performance and capabilities of our image encryption system.

A sequence of steps is always followed during image encryption to convert original image data into cipher form and subsequent decryption is demonstrated in Algorithm 1.

This type of hybrid is recommendable for protecting highly sensitive images because it uses both TEA and RSA algorithms. At the outset, raw data from an image is divided into blocks each comprising 64 bits. In cases where contents within an image do not perfectly tally with these dimensions, it must be padded with zeros until everything becomes uniform after breaking apart at 64 bits per block in succession without exception since it helps maintain system activity during each application stage concerning this kind of encryption leading to increased manageability as well as heightened security measures being observed throughout its entire length.

The image is one single element that cannot be separated, and it forms one entity code or instructions identifying that image all over the internet among other things. So, the TEA encryption round divides a 64-bit block into two halves of 32 bits each represented by v and v1. Such a 128-bit encryption key is further split up into four 32-bit sub-keys (k; k1; k2; k3)—these are the sub-keys used during the various encryption rounds performed on v and v1 within the TEA-RSA algorithm. Here we talk about 64 rounds of these procedures following the originally developed extended TEA-RSA iteration procedure, where each round makes certain changes in V and V1 according to special rules to concerning sub-keys involved in it as well for this algorithm. After all these encryption series are over, v + v1 forms one block that has been encrypted, and all blocks are concatenated to yield the complete encrypted image data.

RSA encryption is used to protect the TEA-RSA encryption key itself. This involves generating an RSA key pair using large prime numbers to find the public modules and private keys that have a bit length of 2048 to ensure a high level of security and is considered fast since the TEA-RSA key will be only encrypted. The TEA-RSA key is then encrypted using the public RSA key to obtain the Encrypted TEA-RSA Key which can only be decrypted with the corresponding private key used during creation. The double encryption process not only protects the image content but ensures the safety of your keys. The process depicts the TEA-RSA encryption Process displayed in Fig. 4. Algorithm 1 presents the main steps of the Hybrid Image Encryption using TEA and RSA.

Figure 4: TEA-RSA algorithm process

3.2 Decryption Using TEA-RSA Algorithm

The decryption process involved dividing the encrypted image into 8 × 8 blocks and then applying the TEA algorithm to each block. The RSA decryption process uses the private key (Fig. 5).

Figure 5: TEA-RSA decryption process

4  Cryptoanalysis

The recent cryptology technique has been divided into the cryptography process and cryptoanalysis technique. The objective of cryptography is to recommend systems that can be resistant to various attacks. Even if it is revealed, the difficulty of its encoding approach becomes problematic for numerous attackers to recover and retrieve the original data. The theory of cryptanalysis is contrasting, and generally applied to explore and decode encrypted information. Thus, in cryptanalysis, an attacker can be studied to have a temporary approach to the encryption and decryption machine with the extreme endeavor of achieving the corresponding key [41]. Based on Kerckhoff’s principle, there are four common attack methods. These attacks are Ciphertext-only attacks, Known-plaintext attacks, Chosen-plaintext attacks, and Chosen-ciphertext attacks. In a Ciphertext-only attack, the attacker interrupts one or several ciphertexts encrypted with the same key, examining them to discover the plaintext or the key. In a Known-plaintext attack, the attacker has part of the plaintext and its equivalent ciphertext, investigating them to discover the key or the used encryption technique. Chosen-plaintext attack, the attacker can randomly choose the plaintext and get its corresponding ciphertext, examining them to discover the key. But in a Chosen-ciphertext attack, the attacker may randomly choose the ciphertext and find its corresponding plaintext, investigating them to find the key. However, a well-performing cryptosystem is mandatory to be able to resist at least these four attack approaches to provide secure cryptography systems. TEA is a symmetric-key algorithm that is fast and efficient for encrypting large amounts of data but has known vulnerabilities are a weak key management and small block size. RSA is an asymmetric key algorithm that is secure for key exchange and encrypting small amounts of data but is slow and inefficient for encrypting large data. By merging them, RSA is used to securely exchange or encrypt a symmetric key. While TEA approaches encrypt the real data efficiently using the symmetric key. Below, we examine our approach against these attacks.

4.1 Cyphertext-Only Attack

Merging TEA (Tiny Encryption Algorithm) and RSA can make a hybrid encryption scheme that controls the strengths of both symmetric and asymmetric cryptography. This approach can recover security against ciphertext-only attacks, where the attacker only has access to encrypted data.

A ciphertext-only attack is one of the weakest attack models, where the attacker only has access to encrypted data. The hybrid scheme described above provides strong security against such attacks because RSA Offers Secure Key Exchange. The symmetric key is encrypted using RSA with Optimal Asymmetric Encryption Padding (OAEP) padding, which is secure against chosen-plaintext attacks and other known attacks. Without the RSA private key, the attacker cannot recuperate the symmetric key. Also, without the symmetric key of RSA, the attacker cannot decrypt the TEA-encrypted data.

We use the random symmetric key which provides a randomization encryption process. Making it difficult for the attacker to recover and guess the patterns or relationships between plaintext and ciphertext. The length of the RSA is large size (2048 bits) making it computationally unworkable to brute-force the symmetric key. So, our approach is secure against this attack.

4.2 Known-Plaintext Attack

In known-plaintext attacks (KPA), the attacker has access to together plaintext and corresponding ciphertext pairs. The objective is to deduce the encryption key or decrypt other ciphertexts. To defend against such attacks, the encryption scheme must ensure that the same plaintext does not always produce the same ciphertext (encryption must be randomized). Also, the key material is secured, and it is not easily detectable from the known plaintext.

In our approach, the symmetric key is encrypted using RSA with OAEP padding, which presents randomness and confirms that the same symmetric key encrypts dissimilar ciphertexts each time. Exclusive of the RSA private key, the attacker cannot recuperate the symmetric key, even if they recognize some plaintext-ciphertext pairs. Also, the practice of a unique IV for each TEA encryption warrants that the same plaintext encrypts to dissimilar ciphertexts, even with the same symmetric key. This randomization prevents the attacker from inferring the key or plaintext from known pairs.

The symmetric key is used in our approach only for encrypting the data, and it is itself encrypted using RSA. This separation guarantees that compromising one part of the system does not compromise the other. Even if the attacker recognizes some plaintext-ciphertext pairs for TEA, they cannot easily recover the symmetric key because the key is protected by RSA.

4.3 Chosen-Plaintext Attack

In a chosen plaintext attack, the attacker can choose random plaintexts and investigate their corresponding ciphertexts. Use this information to deduce the encryption key or decrypt other ciphertexts. To defend against such attacks, the encryption scheme must ensure that the encryption procedure is randomized, whereas the same plaintext encrypts to various ciphertexts each time. The key material is protected and cannot be deduced from the chosen plaintext-ciphertext pairs.

The hybrid scheme presents robust security against chosen-plaintext attacks because RSA shields the symmetric key. The symmetric key is encrypted using RSA with OAEP padding, which proposes randomness and guarantees that the same symmetric key encrypts to various ciphertexts each time. Without the RSA private key, the attacker cannot recover the symmetric key, even if they can choose plaintexts and obtain ciphertexts. The application of a unique IV for each TEA encryption guarantees that the same plaintext encrypts to various ciphertexts, even with the same symmetric key. This randomization prevents the attacker from deducing the key or plaintext from chosen plaintext-ciphertext pairs. The symmetric key is applied only for encrypting the data, and it is encrypted using RSA. This separation ensures that compromising one part of the system does not compromise the other. Even if the attacker can select plaintexts and find ciphertexts for TEA, they cannot simply retrieve the symmetric key because the key is protected by RSA. Moreover, the application of a secure mode of operation with a unique IV makes it complicated to deduce the key.

4.4 Chosen-Ciphertext Attack

To expand the security of a hybrid encryption scheme combining TEA (Tiny Encryption Algorithm) and RSA against chosen-ciphertext attacks (CCA), we necessary to confirm that the structure is resistant to attackers who can not only choose plaintexts and obtain their corresponding ciphertexts but also choose ciphertexts and obtain their corresponding plaintexts. In a chosen-ciphertext attack, the attacker can choose randomly ciphertexts and recover their corresponding plaintexts (decryption). To defend against such attacks, the encryption scheme essentially confirms that the encryption process is randomized, so the same plaintext encrypts to different ciphertexts each time. the decryption process is authenticated, so tampered ciphertexts are rejected. the key material is protected and cannot be deduced from chosen ciphertext-plaintext pairs.

The proposed scheme offers robust security against chosen-ciphertext attacks because RSA protects the symmetric key and RSA is applied with OAEP padding, which introduces randomness and ensures that the same symmetric key encrypts to different ciphertexts each time. TEA Encrypts the Data with randomization. The use of a unique IV for each TEA encryption ensures that the same plaintext encrypts to different ciphertexts, even with the same symmetric key. This process prevents the attacker from deducing the key or plaintext from chosen ciphertext-plaintext pairs. The symmetric key is applied only for encrypting the data, and it is itself encrypted using RSA. This separation ensures that compromising one part of the system does not compromise the other. Even if the attacker can choose ciphertexts and obtain plaintexts, they cannot easily recover the symmetric key because the key is protected by RSA. Also, the use of a secure mode of operation with a unique IV makes it difficult to deduce the key.

5  Security Analysis and Comparisons

To prove our efficiency and the performance of the proposed TEA-RSA encryption approach, we are analyzing correlation coefficients, NPCR, and UACI, we evaluate the algorithm’s effectiveness in securing images. Comparisons with the most relevant and recent encryption techniques highlight the strengths of the proposed method. Moreover, we evaluate the algorithm’s computational efficiency through encryption and decryption phases. This comprehensive analysis demonstrates the robustness of the TEA-RSA approach and efficiency in image encryption. To develop the code of the TEA-RSA image encryption algorithm we had to employ certain libraries to ensure that our implementation will work as expected. Those libraries played a significant role in developing this algorithm and ensuring its capabilities to perform as designed libraries the project utilized several Python libraries for various purposes.

The “time” library was employed to measure execution time, providing valuable insights for benchmarking and debugging processes. The “os” library facilitated interactions with the operating system, enabling file operations and program launching. The “struct” library played a crucial role in converting data between different formats, offering functions for serialization and ensuring compatibility across systems.

“PIL” (Python Imaging Library) allows image manipulation tasks such as loading, saving, and modifying images, including resizing and applying filters. The “Crypto.PublicKey” library provided functionalities for generating and utilizing public keys, essential for secure data encryption. Encryption and decryption processes were implemented using the functions from the “Crypto.Cipher” library, ensuring data security and protection against unauthorized access. The “pytea” library enabled the implementation of the XExtended Tiny Encryption Algorithm, which provided a balance between fast and secure encryption. The “sys” library granted access to system-level information, useful for optimization purposes and environmental analysis.

5.1 Statistical Analysis (Histogram)

Statistical analysis is mandatory to measure the security factors proposed. Histogram and correlation are efficiently used to evaluate the statistical characteristics.

5.1.1 Histogram Deviation (HD)

Histogram deviation measures the alteration between the histograms of the normal image and the encoded image by estimating their absolute differences [42]. Figs. 6 and 7 show a remarkable transformation in image properties because of the encryption image output. The histograms of the original images (Fig. 6) present evident single-peak distributions, reflecting the non-uniform organization of pixel values that exemplifies significant visual information. Contrariwise, the histograms of the encrypted images (Fig. 7) show a remarkable transformation: their probability distributions closely approximate a regularized, uniform pattern, effectively resembling noise. This whole contrast implies an essential accomplishment of the encryption process, the confusion of visual patterns, and the concealment of significant information within a random tapestry of pixels.

Figure 6: Histogram of image 256 pixel; (a) histogram of the original test image, (b) encrypted image, (c) encrypted image histogram by TEA-RSA

Figure 7: Histogram of image 512 pixels; (a) histogram of the original test image, (b) encrypted image, (c) encrypted image histogram by TEA-RSA

5.2 Correlation Coefficient Analysis

To evaluate the effectiveness of the proposed approach, we will analyze the values of the Correlation coefficients of the plain and encrypted images. Correlation exhibits a linear association involving two contiguous pixels for an image. The correlation of the plain images is normally excessive, and it could drip information. An excellent encryption technique must eliminate the correlation between adjacent pixels as much as possible. The smaller the correlation, the more efficiently the method performs. The correlation coefficients R(x, y) of a couple of adjacent pixels can be computed according to the below equation [43]:

(1)

where are the expectation and deviation of the variable x, respectively.

In our technique, we measured the value of the correlation coefficients for plain and encrypted images. Table 2 illustrates the obtained correlation coefficients values.

Fig. 8 presents the correlation coefficients of the plain images among horizontal, vertical, and diagonal orientations. The values are extremely elevated (close to 1), demonstrating strong correlations between adjacent pixels. Given that natural images usually feature smooth transitions and rarely abrupt alterations in pixel values, this pointed correlation is to be estimated. The horizontal correlation coefficient, for example, is 0.9476 for the “Cameraman Gray 256” image. Moreover, Fig. 9 explains the correlation coefficients for encrypted images. The values are precise to zero, demonstrating a significant reduction in correlation among adjacent pixels after the encryption. For example, the horizontal correlation coefficient for the encrypted “Cameraman Gray 256” image beads to −0.0574. This near-zero correlation proposes that the encryption process effectively breaks the predictability of pixel relationships.

Figure 8: Correlation coefficients (horizontal, vertical, diagonal) for plain images

Figure 9: Correlation coefficients (horizontal, vertical, diagonal) for encrypted images

We measured the correlation coefficient value among different images (Fig. 8), and the plain and encrypted images have been involved in our assessment. Also, the images have been evaluated horizontally, vertically, and diagonally. Based on the results obtained in Table 3, Figs. 8–10, it is notable that in the plain image, there are high correlations that imply the fundamental consistency and redundancy of plain images, which are objects of encryption methods. In the encrypted case, the obtained values are close to zero and in some cases, it was minus, which improves the security factor by making geometric attacks much more challenging.

Figure 10: Correlation coefficients (horizontal, vertical, diagonal) for encrypted images

We compared the results obtained with the works in [12,25,33,39]. Table 3 presents the comparison results. In Table 3, we compare the correlation coefficients for both plain and encrypted images with the most relevant and recent studies. The marked difference between the high correlations in plain images and the near-zero correlations in encrypted images underscores the effectiveness of the encryption algorithm in disrupting the inherent redundancies in the images. Also, we obtained better results from the other studies in the plain image phase comparison whereas the average is around 0.972. In the encrypted image phase comparison, we obtained less value than the others.

5.3 Complexity and Speed of TEA-RSA Algorithm

Regardless of the security concerns, encryption speed is also essential, especially in real-time internet applications [44]. In the proposed algorithm, we use chaotic sequences for the confusion and diffusion across iterating the hyper-chaotic approach once. Furthermore, when we alter the pixel values of the plain images, the arrangements of the pixels are also altered, which indicates that confusion and diffusion are shared as a union, consequently saving much time. The efficiency of an encryption algorithm is not only determined by its security but also by its computational complexity and speed.

Fig. 11 describes the encryption times (E-Time) for various images using the proposed algorithm TEA-RSA. The encryption times are comparatively small, implying the efficiency of the algorithm. For example, the E-Time for “Camera-man Gray 256” is 0.0064 s, these results propose that the algorithm can encrypt images swiftly, making it appropriate for real-time applications.

Figure 11: Encryption time for TEA-RSA algorithm

While Fig. 12 illustrates the decryption times (D-Time) for the same set of images. The decryption times are also low, additionally proving the algorithm’s efficiency. For instance, the D-Time for “Plain Black 256” is 0.0032 s, and for “Cameraman Gray 512” it is 0.0024 s. The low decryption times imply that the algorithm is not only swift in encryption but also in decryption, which is vital for practical use.

Figure 12: Decryption time for TEA-RSA algorithm

As a result, the proposed encryption algorithm shows robust performance across various metrics. The expressive reduction in correlation coefficients post-encryption, high NPCR, and UACI values, and superior performance compared to other algorithms underscore its effectiveness in securing images. Additionally, the algorithm consumes very little time in the encryption and decryption phases. It highlights its efficiency, making it suitable for real-time applications. Generally, the proposed algorithm offers a compelling solution for secure and efficient image encryption.

5.4 Resistance to Cropping Attack

Cropping attacks are a playing field model of cryptographic attack that proposes randomness into precise zones of an image, thus flexible the reliability of the ciphertext and reducing it inaudible to the expected addressee. The competence of an encryption approach to withstand such attacks is a vital value of its characteristics. The TEA or RSA alone is sensitive to cropping attacks, while the hybrid TEA-RSA proposed algorithm establishes improved resistance to these attacks. Fig. 13 illustrates the brilliant anti-cropping capability of the proposed algorithm.

Figure 13: Resistance to cropping attacks, (a) cropping area of 64 × 64 of the cameraman, (b) cropping area of 128 × 128 of the cameraman, (c) cropping area of 128 × 256 of the cameraman, (d)–(f) decrypted images of cameraman

Based on the results obtained in Fig. 13, the proposed technique can retrieve the original image from the decrypted image after crop attacks at an acceptable level.

5.5 Resistance to Differential Attacks

Cryptographic systems are assessed for their ability to withstand differential attacks using the number of changing pixel rates (NPCR) [45] and unified averaged changed intensity (UACI). Figs. 14 and 15 show the results of NPCR and UACI tests. The NPCR and UACI of the cipher text are greater than 99.6% and 33.46%, respectively [46].

(2)

(3)

(4)

Figure 14: NPCR values for various images using the TEA-RSA algorithm

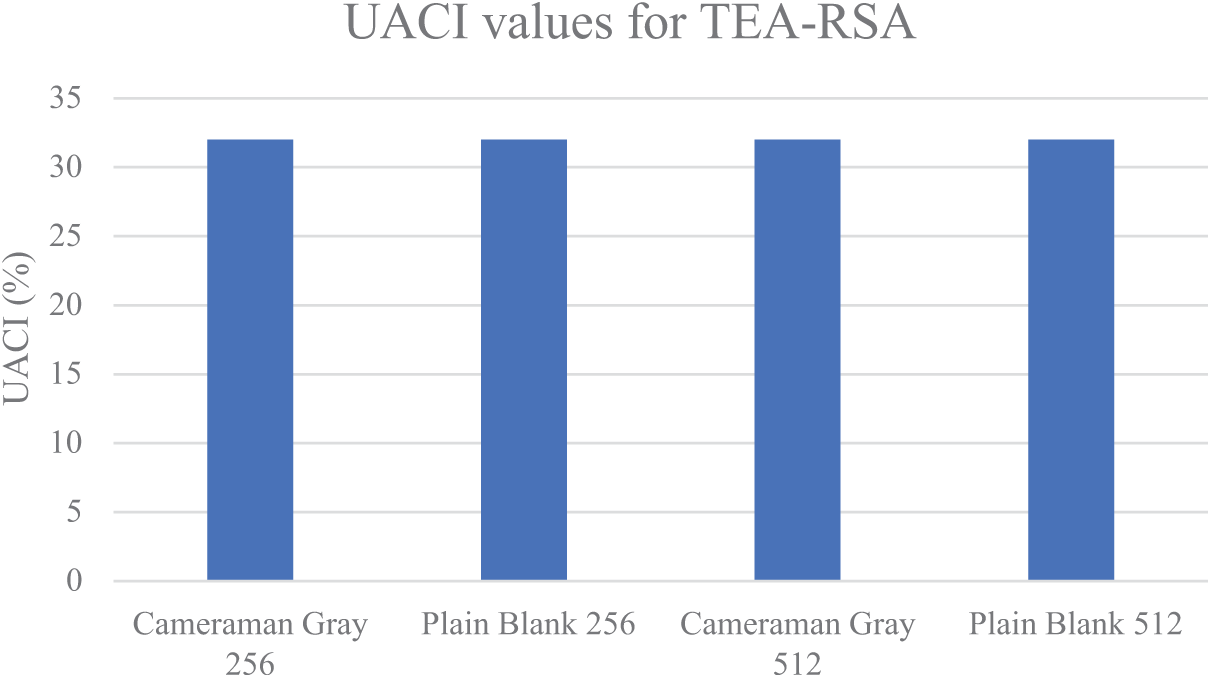
Figure 15: UACI values various images using the TEA-RSA algorithm

C1 and C2 are the encrypted images before and after the plain pixel image is changed, W and H are the width and the height of the image, respectively.

In the chart below, NPCR and UACI values are visually represented for various images encrypted using the TEA-RSA encryption algorithm. For assessing the effectiveness of cryptographic systems against differential attacks, NPCR and UACI are crucial metrics. Fig. 14 illustrates the decimal values of NPCR and UACI for a variety of images, including, “Cameraman Gray 256”, and “Cameraman Gray 512”. The precise observations at each data point provide an accurate statistical value, highlighting the consistency of the proposed technique and robustness in preserving great security among various test scenarios. This comprehensive visualization results utilities in the importance of the algorithm’s capability to provide extreme performance in image encryption by confirming substantial deviations in pixel intensity and distribution with negligible deviation among different images.

Fig. 14 illustrates the NPCR values for various images using the proposed approach TEA-RSA algorithm. The NPCR values are constantly high, all above 99%, representing that the encryption algorithm reasons considerable adjustments in the pixel values of the images. For instance, the NPCR value for “Cameraman Gray 256” is 99.215%. These extreme NPCR values indicate that the encryption algorithm effectively changes a significant portion of the image pixels, and construction obscures attackers from deciphering any significant information from the encrypted image.

In Fig. 15, we display the UACI values for the matching set of images. The UACI values, all above 33%, imply meaningful alterations in the intensity of the pixels. For example, the UACI value for “Plain Black 256” is 33.93%, and for “Cameraman 512” it is 33.63%. These extreme UACI values verify that the encryption approach not only alters the locations of the pixels but also their intensity values, in this manner, it is improving the encryption’s robustness.

To extend the performance evaluation of the proposed encryption algorithm, we compare its NPCR and UACI results with those of other established algorithms in the works [25,34,39,40,44].

Table 4 compares the NPCR scores of the proposed algorithm with five other algorithms [25,34,39,40,44]. Based on the results obtained, we note that the proposed algorithm consistently indicates higher NPCR values across different images.

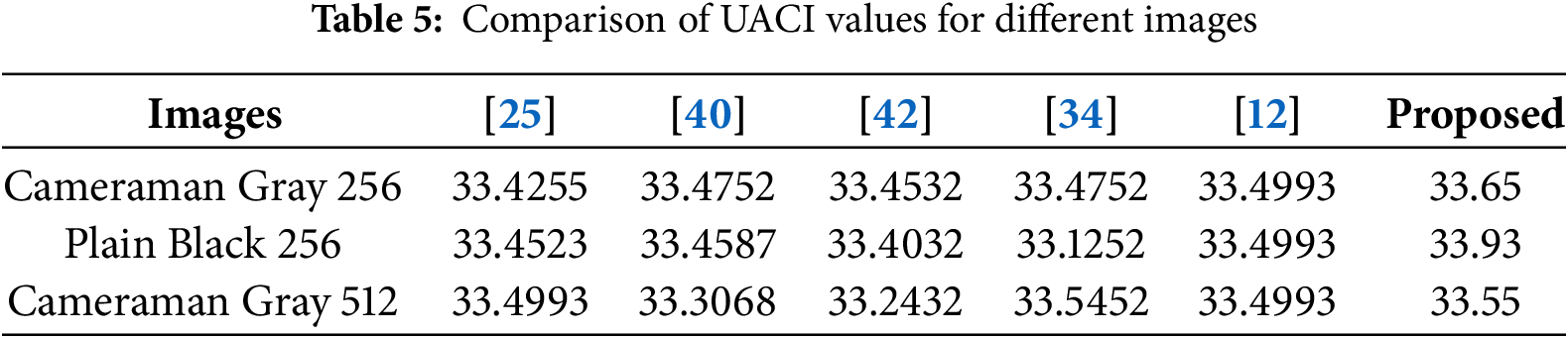
In Table 5, we illustrate the UACI scores for the same set of algorithms and images. The proposed algorithm demonstrates superior performance, with consistently high UACI values. For example, for “Cameraman Gray 256,” the proposed algorithm has a UACI of 33.65%, while algorithm [25] has 33.4255% and algorithm [40] has 33.4752%. These results imply that the proposed algorithm encourages more important intensity modifications in the pixels, further improving the security of the encrypted images.

6  Conclusion

In this paper, we proposed a hybrid image encryption algorithm TEA-RSA approach for improving the confidentiality, integrity, and authenticity of the image content. The performance of this algorithm is promising in terms of cost and complexity, with an encryption time that is below 10 ms recorded. It is implied by correlation coefficient analysis that after encryption there is a notable decrease in pixel correlation, therefore making it effective at disguising pixel relationships via obfuscation. Moreover, our technique achieved the highest NPCC, NPCR value over 99% consistent, and a UACI value which stands at around 33.86 thereby making it insensitive to statistical attacks hence leading to massive alteration of pixel values and intensities. These make clear the resistance of this process to any hacking attempt whatsoever that might want unauthorized access into its domain. It is important to note that the integrity of images is well preserved throughout the encryption and decryption stages, which are clear indications of these low decryption times. These results collectively indicate that the algorithm is effective in ensuring secure and efficient image encryption while maintaining the overall integrity and quality of the encrypted images. Moreover, cropping and differential attacks have been addressed for cryptanalysis approval, the approach provided an acceptable level of the decrypted image after applying these attacks.

For the future development of the algorithm, there could be an inclusion of AI alongside chaotic systems which would bring new dimensions to how this algorithm operates in confusion and diffusion parameters. Also, because such a change would improve the general security and solidity of this algorithm, it is prudent that the use of IPsec be considered as a substitute for the encryption key.

Acknowledgement: None.

Funding Statement: The authors received no specific funding for this work.

Author Contributions: Muath AlShaikh contributed to conceptualization, data collection, and analysis of the results. Ahmad Manea Alkhalifah was responsible for methodology development and data interpretation. Sultan Alamri assisted in writing and reviewing the manuscript. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Lin Y, Yang Y, Li P. Development and future of compression-combined digital image encryption: a literature review. Digital Signal Process. 2025;158(2):104908. doi:10.1016/j.dsp.2024.104908. [Google Scholar] [CrossRef]

2. SaberiKamarposhti M, Ghorbani A, Yadollahi M. A comprehensive survey on image encryption: taxonomy, challenges, and future directions. Chaos Solit Fract. 2024;178(9):114361. doi:10.1016/j.chaos.2023.114361. [Google Scholar] [CrossRef]

3. Pankaj S, Dua M. Chaos based medical image encryption techniques: a comprehensive review and analysis. Inform Secur J: A Global Perspect. 2024;33(3):332–58. doi:10.1080/19393555.2024.2312975. [Google Scholar] [CrossRef]

4. Zhao C, Du R, He K, Chen J, Li J, Liu X, et al. Efficient verifiable dynamic searchable symmetric encryption with forward and backward security. IEEE Internet Things J. 2025;12(3):2633–45. doi:10.1109/JIOT.2024.3470772. [Google Scholar] [CrossRef]

5. Smid ME, Branstad DK. Data encryption standard: past and future. Proc IEEE. 1988;76(5):550–9. doi:10.1109/5.4441. [Google Scholar] [CrossRef]

6. Mohammed ZA, Gheni HQ, Hussein ZJ, Al-Qurabat AKM. Advancing cloud image security via AES algorithm enhancement techniques. Eng Technol Appl Sci Res. 2024;14(1):12694–701. doi:10.48084/etasr.6601. [Google Scholar] [CrossRef]

7. Shepherd SJ. The tiny encryption algorithm. Cryptologia. 2007;31(3):233–45. doi:10.1080/01611190601090606. [Google Scholar] [CrossRef]

8. Wheeler DJ, Needham RM. TEA, a tiny encryption algorithm. In: Fast software encryption. Berlin/Heidelberg: Springer Berlin Heidelberg; 1995. p. 363–6. doi:10.1007/3-540-60590-8_29. [Google Scholar] [CrossRef]

9. Usmonov M. Asymmetric cryptosystems. INDEXING. 2024;1(1):76–80. [Google Scholar]

10. Liu Y, Tang S, Liu R, Zhang L, Ma Z. Secure and robust digital image watermarking scheme using logistic and RSA encryption. Expert Syst Appl. 2018;97(C):95–105. doi:10.1016/j.eswa.2017.12.003. [Google Scholar] [CrossRef]

11. Al-Kaabi SS, Belhaouari SB. Methods toward enhancing rsa algorithm: a survey. Int J Netw Secur Its Applicat. 2019;11(3):53–70. doi:10.5121/ijnsa.2019.11305. [Google Scholar] [CrossRef]

12. Karolin M, Meyyappan T. Image encryption and decryption using RSA algorithm with share creation techniques. Inte J Comput Sci Eng Technol. 2019;9(2):2797–800. doi:10.35940/ijeat.B4021.129219. [Google Scholar] [CrossRef]

13. Kara M, Laouid A, Hammoudeh M, AlShaikh M, Bounceur A. Proof of chance: a lightweight consensus algorithm for the internet of things. IEEE Trans Ind Inform. 2022;18(11):8336–45. doi:10.1109/TII.2022.3168747. [Google Scholar] [CrossRef]

14. He P, Sun K, Zhu C. A novel image encryption algorithm based on the delayed maps and permutation-confusion-diffusion architecture. Secur Commun Netw. 2021;2021(1):6679288. doi:10.1155/2021/6679288. [Google Scholar] [CrossRef]

15. Zhang S, Liu L. Generation of ideal chaotic sequences by reducing the dynamical degradation of digital chaotic maps. Soft Comput. 2024;28(5):4471–87. doi:10.1007/s00500-023-08836-z. [Google Scholar] [CrossRef]

16. Geng S, Wu T, Wang S, Zhang X, Niu Y. A novel image encryption algorithm based on chaotic sequences and cross-diffusion of bits. IEEE Photonics J. 2021;13(1):1–15. doi:10.1109/jphot.2020.3044222. [Google Scholar] [CrossRef]

17. Li S, Zhao L, Yang N. Medical image encryption based on 2D zigzag confusion and dynamic diffusion. Secur Commun Netw. 2021;2021(7):6624809. doi:10.1155/2021/6624809. [Google Scholar] [CrossRef]

18. Zeghid M, Machhout M, Khriji L, Baganne A, Tourki R. A modified AES based algorithm for image encryption. Int J Comput Sci Eng. 2017;1(3):70–5. [Google Scholar]

19. Luo Y, Ouyang X, Liu J, Cao L. An image encryption method based on elliptic curve elgamal encryption and chaotic systems. IEEE Access. 2019;7:38507–22. doi:10.1109/ACCESS.2019.2906052. [Google Scholar] [CrossRef]

20. Ye GD, Wu HS, Huang XL, Tan SY. Asymmetric image encryption algorithm based on a new three-dimensional improved logistic chaotic map. Chin Phys B. 2023;32(3):030504. doi:10.1088/1674-1056/ac7dbb. [Google Scholar] [CrossRef]

21. Xu Q, Sun K, Zhu C. A visually secure asymmetric image encryption scheme based on RSA algorithm and hyperchaotic map. Phys Scr. 2020;95(3):035223. doi:10.1088/1402-4896/ab52bc. [Google Scholar] [CrossRef]

22. Mansouri A, Wang X. A novel one-dimensional chaotic map generator and its application in a new index representation-based image encryption scheme. Inf Sci. 2021;563(8):91–110. doi:10.1016/j.ins.2021.02.022. [Google Scholar] [CrossRef]

23. Shakiba A. A randomized CPA-secure asymmetric-key chaotic color image encryption scheme based on the Chebyshev mappings and one-time pad. J King Saud Univ-Comput Inf Sci. 2021;33(5):562–71. doi:10.1016/j.jksuci.2019.03.003. [Google Scholar] [CrossRef]

24. Maazouz M, Toubal A, Bengherbia B, Houhou O, Batel N. FPGA implementation of a chaos-based image encryption algorithm. J King Saud Univ-Comput Inf Sci. 2022;34(10):9926–41. doi:10.1016/j.jksuci.2021.12.022. [Google Scholar] [CrossRef]

25. Lin R, Li S. An image encryption scheme based on Lorenz hyperchaotic system and RSA algorithm. Secur Commun Netw. 2021;2021(1):5586959. doi:10.1155/2021/5586959. [Google Scholar] [CrossRef]

26. Jiao K, Ye G, Dong Y, Huang X, He J. Image encryption scheme based on a generalized Arnold map and RSA algorithm. Secur Commun Netw. 2020;2020(1):9721675. doi:10.1155/2020/9721675. [Google Scholar] [CrossRef]

27. Anandakumar S. Image cryptography using RSA algorithm in network security. Int J Comput Sci Eng Technol. 2015;5(9):326–30. [Google Scholar]

28. Ye G, Jiao K, Huang X. Quantum logistic image encryption algorithm based on SHA-3 and RSA. Nonlinear Dyn. 2021;104(3):2807–27. doi:10.1007/s11071-021-06422-2. [Google Scholar] [CrossRef]

29. Chen Y, Xie S, Zhang J. A hybrid domain image encryption algorithm based on improved henon map. Entropy. 2022;24(2):287. doi:10.3390/e24020287. [Google Scholar] [PubMed] [CrossRef]

30. George AA, Riyadh M, Prajitha MV. Secure image transferring using KBRP and TEA algorithms. In: 2015 International Conference on Innovations in Information, Embedded and Communication Systems (ICIIECS); 2015 Mar 19–20; Coimbatore, India: IEEE; 2015. p. 1–5. doi:10.1109/ICIIECS.2015.7193117. [Google Scholar] [CrossRef]

31. Arab A, Rostami MJ, Ghavami B. An image encryption method based on chaos system and AES algorithm. J Supercomput. 2019;75(10):6663–82. doi:10.1007/s11227-019-02878-7. [Google Scholar] [CrossRef]

32. Zhu S, Zhu C, Wang W. A new image encryption algorithm based on chaos and secure hash SHA-256. Entropy. 2018;20(9):716. doi:10.3390/e20090716. [Google Scholar] [PubMed] [CrossRef]

33. Shivhare R, Shrivastava R, Gupta C. An enhanced image encryption technique using DES algorithm with random image overlapping and random key generation. In: 2018 International Conference on Advanced Computation and Telecommunication (ICACAT); 2018 Dec 28–29; Bhopal, India: IEEE; 2018. p. 1–9. doi:10.1109/ICACAT.2018.8933591. [Google Scholar] [CrossRef]

34. Rajvir C, Satapathy S, Rajkumar S, Ramanathan L. Image encryption utilizing modified elliptic curve cryptography and hill cipher. In: Proceedings of the Third International Conference on Smart Computing and Informatics, Volume 1, Smart Intelligent Computing and Applications; 2020; Singapore: Springer. p. 675–83. [Google Scholar]

35. Darari R, Winarko E, Damayanti A. Encryption and decryption application on images with hybrid algorithm vigenere and RSA. Contemp Math App. 2020;2(2):109. doi:10.20473/conmatha.v2i2.23855. [Google Scholar] [CrossRef]

36. Abd El-Latif AA, Niu X. A hybrid chaotic system and cyclic elliptic curve for image encryption. AEU Int J Electron Commun. 2013;67(2):136–43. doi:10.1016/j.aeue.2012.07.004. [Google Scholar] [CrossRef]

37. Benssalah M, Rhaskali Y, Drouiche K. An efficient image encryption scheme for TMIS based on elliptic curve integrated encryption and linear cryptography. Multimed Tools Appl. 2021;80(2):2081–107. doi:10.1007/s11042-020-09775-9. [Google Scholar] [CrossRef]

38. Gong L, Qiu K, Deng C, Zhou N. An optical image compression and encryption scheme based on compressive sensing and RSA algorithm. Opt Lasers Eng. 2019;121:169–80. doi:10.1016/j.optlaseng.2019.03.006. [Google Scholar] [CrossRef]

39. Yu H, Kim Y. New RSA encryption mechanism using one-time encryption keys and unpredictable bio-signal for wireless communication devices. Electronics. 2020;9(2):246. doi:10.3390/electronics9020246. [Google Scholar] [CrossRef]

40. AlShaikh M. Robust and recovery watermarking approach based on SVD and OTP encryption. J Signal Process Syst. 2024;96(6):385–99. doi:10.1007/s11265-024-01919-6. [Google Scholar] [CrossRef]

41. Wen H, Lin Y, Yang L, Chen R. Cryptanalysis of an image encryption scheme using variant Hill cipher and chaos. Expert Syst Appl. 2024;250(1):123748. doi:10.1016/j.eswa.2024.123748. [Google Scholar] [CrossRef]

42. Roy S, Bhalla K, Patel R. Mathematical analysis of histogram equalization techniques for medical image enhancement: a tutorial from the perspective of data loss. Multimed Tools Appl. 2024;83(5):14363–92. doi:10.1007/s11042-023-15799-8. [Google Scholar] [CrossRef]

43. AlShaikh M. A novel reduced reference image quality assessment based on formal concept analysis. Comput J. 2023;66(7):1749–60. doi:10.1093/comjnl/bxac038. [Google Scholar] [PubMed] [CrossRef]

44. AlShaikh M, Alzaqebah M, Gmati N, Alrefai N, Alsmadi MK, Almarashdeh I, et al. Image encryption algorithm based on factorial decomposition. Multimed Tools Appl. 2024;83(40):88447–67. doi:10.1007/s11042-023-17663-1. [Google Scholar] [CrossRef]

45. El Habib Kahla M, Beggas M, Laouid A, AlShaikh M, Hammoudeh M. An IoMT image crypto-system based on spatial watermarking and asymmetric encryption. Multimed Tools Appl. 2024;83(39):86681–706. doi:10.1007/s11042-024-19632-8. [Google Scholar] [CrossRef]

46. Kara M, Karampidis K, Papadourakis G, Hammoudeh M, AlShaikh M. An enhanced learning with error-based cryptosystem: a lightweight quantum-secure cryptography method. J. 2024;7(4):406–20. doi:10.3390/j7040024. [Google Scholar] [CrossRef]