Software Reliability Prediction Using Ensemble Learning on Selected Features in Imbalanced and Balanced Datasets: A Review

1  Introduction

Various methodologies have been explored in software engineering to anticipate critical aspects crucial for project success. One study conducts a comprehensive literature review, focusing on utilizing machine learning techniques to predict software effort, and evaluating their effectiveness empirically [1]. Another study examines the precision of models predicting effort for software maintenance tasks, drawing insights from practical implementations [2]. Additional research delves into predicting software maintainability and associated metrics, amalgamating existing studies to identify common metrics and their predictive utility [3]. Another focus lies in forecasting the maintainability of object-oriented software using multivariate adaptive regression splines, proposing potential approaches for evaluating and predicting software system maintenance ease [4]. Transfer learning techniques are explored for cross-company software defect prediction, suggesting strategies to enhance prediction accuracy across diverse organizational settings [5]. Furthermore, practical considerations in implementing statistical methods for reliability prediction are examined, leveraging a case study within the Turkish telecommunications industry to offer insights into real-world challenges and best practices [6]. Additionally, fuzzy clustering techniques are discussed for software quality prediction, aiming to categorize projects and forecast their quality levels based on specific attributes [7]. Lastly, a critical evaluation of software defect prediction models is presented, analyzing their strengths, weaknesses, and potential avenues for improvement within the research domain [8]. Defective software parts have severe effects on the amount spent on development and maintenance as well as on customer satisfaction [9]. In their respective research endeavors, Wu et al. [10] propose an innovative strategy for software defect prediction by employing weighted classification via association rule mining. This method boosts prediction accuracy by assigning weights to pertinent features identified through association rules. Meanwhile, Zhao et al. [11] undertakes a systematic examination of just-in-time software defect prediction, offering a comprehensive overview of the various techniques and methodologies utilized in this domain. Han et al. [12] introduce a Bayesian approach aimed at integrating low-cost, high-frequency sensor data into watershed water quality modeling, presenting a valuable technique for the seamless integration of sensor data into water quality assessment procedures. Hernández-Molinos et al. [13] delve into software defect prediction using Bayesian methodologies, exploring the application of Bayesian techniques and providing insights into probabilistic modeling approaches for this purpose. Lastly, Elsagheer et al. [14] introduce a hybrid model for automatic modulation classification, which amalgamates residual neural networks and long short-term memory architectures to achieve precise automatic modulation classification. However, when confronted with redundant and skewed defect datasets, these approaches demonstrate inadequate performance [15]. The accuracy of their predictions tends to decline in the presence of missing or irrelevant information within the defect datasets [16]. Classifiers biased towards the dominant class, such as Artificial Neural Network-Multi-Layer Perceptron’s [17] ANN-MLPs and Support Vector Machines (SVMs) [18], emerge with large false negative rates [19]. Notably, ensemble learning techniques are ideally adapted to address the aforementioned data issues. Random forests [20], outperform the aforementioned approaches in locating damaged or defective modules, even though they are not specifically designed to resolve imbalanced data [21]. In addition, any residual influence brought on by irrelevant and redundant features is reduced via ensemble learning’s voting technique. To achieve this, classifiers with strong performance on the testing datasets are given heavier weights. Prediction performance is certainly improved by tolerating irrelevant and redundant features. Voting does, in fact, ensure that noise effects are reduced, which enhances the accuracy of predictions in general. The proposed system includes eight classifiers: Bernoulli Naive Bayes, Gradient Boosting, Weighted SVMs, Random Forests Stochastic Gradient Descent, Extreme Learning Machine, Logistic Regression and Multinomial Naive Bayes. According to the paper’s conclusion, the basis classifiers were selected following thorough simulation validation. The literature recognizes several classifiers, such as Weighted-SVMs and Random Forest models, as “de-facto” classifiers [22]. Moreover, due to the varying classification abilities of the individual fundamental classifiers, their combination proves valuable in the presented ensemble learning approach. Through the integration of these techniques, they can incorporate a diverse array of statistical features that are inherent in the underlying data.

This study has two primary objectives. Firstly, it aims to demonstrate the efficacy of feature selection in enhancing the accuracy of reliability prediction. Secondly, it aims to propose a twofold ensemble learning approach that maintains robustness even when faced with challenges such as data imbalance and feature redundancy. A key contribution credited to this study is the recommended two-variant ensemble approach’s improved robustness to duplicate and irrelevant attributes. The paper is structured as follows: Section 2 presents a comprehensive overview of related research in the field. Section 3 comprehensively describes the experimental setup, methodology, and datasets employed for software defect prediction. The design of the experiment and its results are presented in Section 4, in Section 5, a detailed analysis and discussion of the data are provided, along with an exploration of validity concerns. In conclusion, Section 6 of the paper summarizes the key findings of the study and provides conclusions. It also offers recommendations for future research directions in the field.

2  Literature Review

The following is a comprehensive summary of the current related work in the field: A breakdown of the sampling procedures necessary to properly manage data imbalance is given after a discussion of general prediction approaches. After that, a summary of popular cost-effective classification methods is given. Next, there will be an explanation of how ensemble learning models can be employed to tackle data imbalance. Subsequently, the section will wrap up with a discourse on different fault classification techniques; feature selection procedures are finally covered. The basis for machine learning-driven approaches in fault classification was laid by Bayesian approaches, Decision trees, and ANNs, these techniques use software metrics to categorize malfunctioning software components accurately. To be clear, typically, these methods tend to overlook the skewness and other statistical attributes present in the fault datasets. It is highly detrimental to classification performance not to include these features [19]. Traditional methods like Bayesian networks [12] and SVMs [17] often neglect the minority class, which in this context refers to defective modules. To address the issue of imbalanced datasets, two widely used techniques are oversampling and undersampling [21]. Oversampling is the process of duplicating instances from the minority class, whereas undersampling involves reducing instances from the majority class. Both approaches aim to improve the class balance in the dataset. While undersampling removes data samples from the majority class, oversampling involves introducing duplicate or artificial samples to the minority class. In software failure detection applications, the accuracy of classification is enhanced through the implementation of data sampling techniques, as stated by Seiffert et al. [23]. The investigation conducted in [24] examined the utilization of undersampling and oversampling techniques for data stratification in software failure prediction. To oversample data from the minority class, the Synthetic minority oversampling technique method was utilized, generating artificial samples [25]. Misclassifying various software problem classes may result in higher costs, even when sampling algorithms often balance data distribution adequately. Khoshgoftaar et al. [26] introduced an ensemble learning method that combines a cost-sensitive boosting technique with a feature incorporating cost sensitivity in their research. This means that when defective software components are misclassified, the penalty costs associated with such errors are considerably higher. Quinlan improved classification performance through the utilization of the C4.5 decision tree as an initial classifier in comparison to the original boosting technique [27]. Three different cost-sensitive prediction model types were looked at in a different study by Zheng [28]. Boosted ANN methods, consisting of 10 essential back-propagation ANN blocks, each containing 11 hidden neurons, were used in all three models. The threshold shifting strategy for weight updates produced the smallest estimated expense of misclassification (ECM) when compared to fixed weighted update techniques the findings revealed that the threshold moving method demonstrated greater resilience concerning cost estimation.

Although not specifically designed to handle data imbalance, ensemble learning algorithms have demonstrated high effectiveness in managing small and imbalanced datasets [29]. A variety of tasks have effectively used ensemble learning [30], such as concept recognition, live tumor detection [31], and functional role prediction in bioinformatics [32]. Similarly, text classification [33], bioinformatics, and biological networks [34] are just a few of the disciplines where feature selection, an essential preliminary processing step in Machine Learning (ML), has been extensively used. A variety of metrics could be correlated with software systems’ defect propensity, which is a widely acknowledged fact. As a result, reducing uncorrelated indicators could improve classification performance. Khoshgoftaar et al. [16] conducted a study where they performed a comparative analysis on 16 software datasets using seven filter-based feature ranking algorithms. In their approach, they focused on the signal-to-noise ratio, a software statistic that is rarely utilized. The ensemble learning architecture they proposed incorporated several essential classifiers, such as Naive Bayes (NB), K-nearest neighbour, ANN, Logistic Regression (LR), and SVM models. The evaluation experiments were assessed using the Area under Receiver Operating Curve (ROC) measure as the performance criterion. The sampling-based online bagging method of ensemble learning was introduced by Wang et al. [35]. The empirical study conducted by the researchers demonstrated that based on sampling in online bagging exhibited in a well-balanced performance in effectively handling both positive and negative samples. However, its results were inconsistent when there were changes in class distributions over time. On the other hand, Wang and Minku presented an online bagging method based on undersampling that can handle samples with varying class distributions. The classification of software defects is a problem that has received numerous ensemble learning-based solutions. Using the Roughly balanced bagging method, Seliya et al. [36] introduced an early modification to the bagged ensemble learning technique. The simulation results demonstrated that the Roughly balanced bagging method outperformed individual classifiers. The roughly balanced bagging technique demonstrated excellent performance of classification, as assessed by the geometric mean, primarily because of its capacity to handle data imbalance in the test datasets. Another study by Sun et al. [37] focused on addressing data skewness in software fault classification. They divided the non-defective parts into bins of similar size, where the bin sizes were determined based on the number of defective modules. A multi-classification issue results from assigning a new class label to each bin after that. The three ensemble learning algorithms of bagging, random forests, and boosting were integrated into each of the preceding coding techniques. When evaluating the performance indicator of Area under ROC, the one-against-one coding scheme outperformed its competitors. Assigning samples of data to bins throughout the data balancing phase is a problem that is not addressed by the suggested solutions. Wang et al. extensively studied the application of ensemble learning in software defect classification by employing multiple machine learning classifiers [38]. The classification results of a single classifier using Naive Bayes were supplied to compare the greater accuracy of various models. By utilizing various public-domain software fault datasets, Wang et al. convincingly showcased the superior performance of the analyzed ensemble models compared to their single classifier counterparts. An intriguing conclusion from the research reported in [38,39] is that ensemble learning approaches based on RF consistently outperform other classification methods, irrespective of the specific software fault dataset employed, and the random forests-based ensemble model consistently demonstrated superior performance in classification accuracy. For defect prediction, Bishnu et al. [40] proposed a more effective unsupervised learning method. Unsupervised learning relies on the quad tree-based K-means clustering algorithm, a variation of the conventional K-means clustering method. Quad-trees show great promise in tackling the classification issue related to software defects because their classification performance is on par with supervised learning methods. There is still room for improvement, though, because these tactics weren’t created expressly to address the irregularity of software fault datasets. The aforementioned classification approaches often produce excellent classification accuracy when the data is evenly distributed. The algorithmic technique involves assigning weights to base classifiers to adjust them and address the imbalance ratio in the dataset. In the domain of software engineering research, obtaining software metric data that accurately represents faulty software in terms of both quantity and quality is challenging, leading to the prevalence of imbalanced datasets [41]. The use of the geometric mean technique proves beneficial for generating more reliable classification measures when dealing with imbalanced data [42]. In this study, the effectiveness of the proposed classifications is evaluated using the G-mean measure.

3  Experimental Design and Setup

This section provides the total details regarding the entire experimental setup and design, performed in this work.

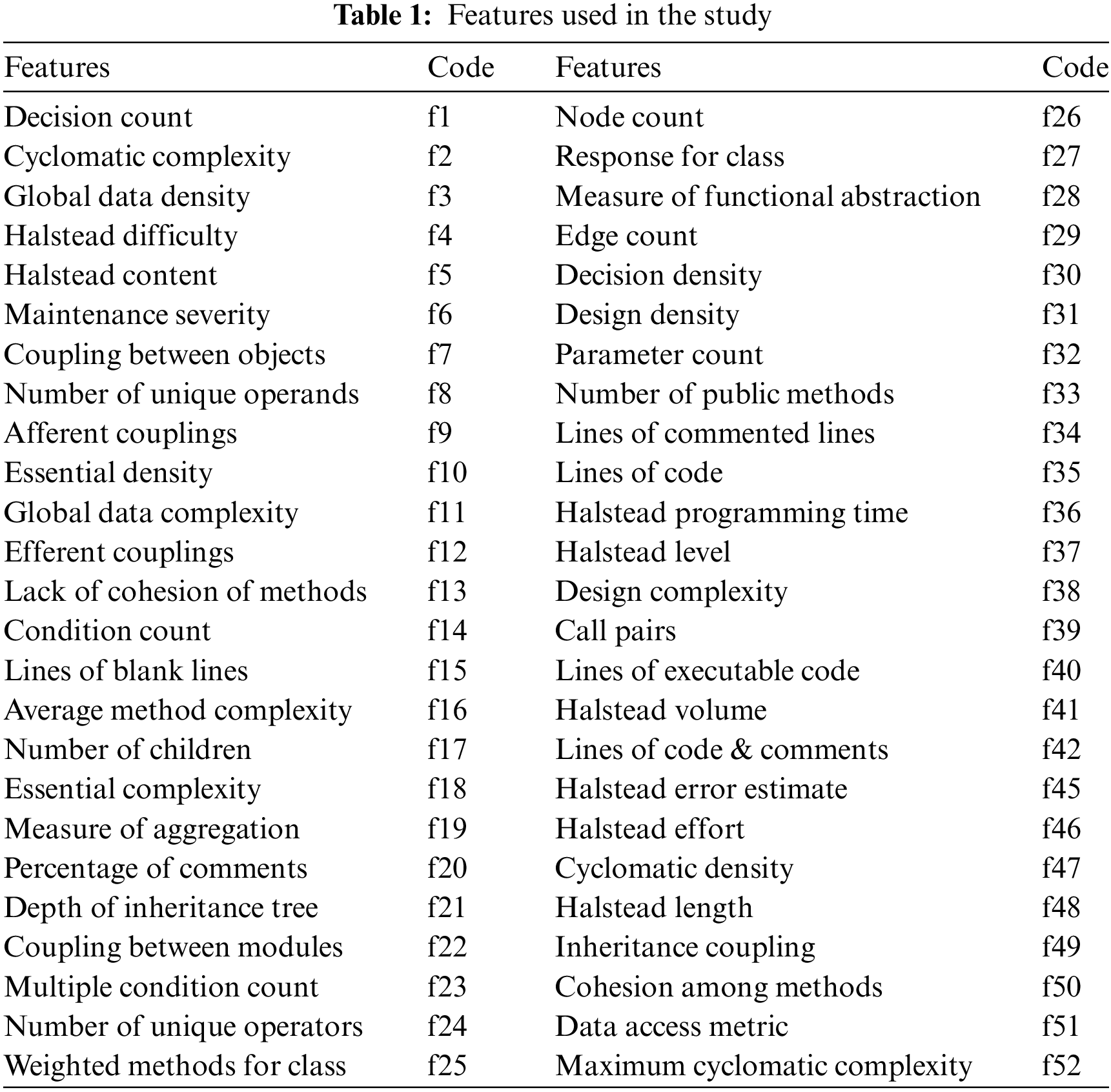
All computational evaluations for this research were carried out on a Windows 10 PC equipped with 32 GB of RAM and an octa-core CPU running at 3.6 GHz. The assessment process involved the implementation of a 10-fold cross-validation technique. The effectiveness of all classifiers was evaluated by analyzing individual datasets containing software faults. The Python programming language was utilized to implement all the evaluated algorithms. The performance of classification was assessed using the Area under the ROC metric. Additionally, Area under the ROC was employed as a metric to evaluate classification systems in the context of unbalanced datasets [37]. Basic classifiers such as Weighted-SVMs, Extreme Learning Machine, and Random Forests were used as benchmarks for the proposed Average Probability Ensemble Learning approach. Furthermore, various feature selection methods were evaluated to address our primary objective. Pearson’s correlation, Greedy forward selection, and Fisher’s Criterion were among the techniques included in the selection criteria considered in the performance evaluation. Finally, six publicly accessible datasets for software defects were utilized to assess the classification performance of the proposed Average Probability Ensemble model. Authors utilized Ant-1.7 in our research, including datasets Camel-1.6 from the Java Repository, and KC3, MC1, PC2, and PC4 datasets from the NASA Repository. The attributes of the datasets used in our analysis are described in Table 1 along with their abbreviated codes.

4  Research Approach

This section describes the research goals, the proposed hypothesis, and the methodology employed. The main objective of this study is to illustrate the effectiveness of feature selection in improving defect classification performance. Additionally, the researchers aim to propose a robust ensemble learning method that can handle duplicated features and imbalanced data. To tackle the challenges associated with software defect categorization, the study introduces a unique and distinctive ensemble learning approach. In addition to being sensitive to imbalanced data, the suggested method also effectively manages redundant features that are typical in datasets for software quality. The following assumptions are defined to achieve the aforementioned objectives: Initially, when it comes to defect classification problems, using different feature subsets leads to very unequal performance. This performance variance is mostly caused by the presence of redundant and useless features. The suggested technique outperforms both single and ensemble classifiers currently in use when dealing with datasets of software defects that have imbalances in data and feature redundancy.

4.1 Experiment Setup

To evaluate the classification performance of suggested frameworks and verify the results of the study, simulations were conducted. These simulations employed a balanced 10-fold cross-validation technique, ensuring that the data was appropriately divided into training and testing sets. When dealing with software fault datasets, which can be time-consuming and expensive to acquire, using 10-fold cross-validation helps to mitigate biases when testing hypotheses based on the data. In contrast, the use of balanced sampling aims to achieve an equitable distribution of fault-free and faulty classes within each fold, ensuring that they comprise similar proportions. This method effectively preserves the class imbalance ratio, ensuring a more accurate evaluation of the models’ performance.

To support the first hypothesis, the following steps are taken:

Step 1. Split the dataset into both testing and training halves (70% and 30%, respectively).

Step 2. Make a feature list named li that is empty.

Step 3. Based on the chosen feature selection criterion, identify the most optimal feature from the training set and add it to the list, ranging from it to li.

Step 4. Utilize the selected training set’s feature to train the ensemble classifiers.

Step 5. Determine which parts of the collection of tests are defective using the previously learned classifier.

Step 6. The performance result should be saved.

Step 7. Repeat Steps 2 and 3 for the other features, then provide performance data.

The stated outcomes for performance would also draw attention to any inconsistent effects that emerged during the feature selection procedure. The article will therefore achieve its first objective.

The steps listed below are used to examine the second hypothesis:

Step 1. Split the dataset into training and testing sets, allocating 70% of the data for training and 30% for testing purposes.

Step 2. To train the proposed model, use the training set.

Step 3. Use the testing set to assess the trained model.

Step 4. Save the classification performance as F1.

Step 5. Using the Greedy forward selection approach select the best features from the training set.

Step 6. Add the different features you’ve chosen to the list of li.

Step 7. The list “li” can be utilized to retrain the Average probability ensemble model. By repeating Steps 5–7 using the testing set, the resulting classification performance is saved as F2.

4.2 Selection of Feature Subsets

Software metrics gathered from source code make up features in software failure datasets. Certain aspects, though, should be deleted since they are superfluous or worthless. Pretreatment of this kind is likely to improve classification performance greatly. Forward selection is a frequent strategy for selecting good characteristics. Let’s examine forward selection with Cyclomatic complexity, Weighted methods per class, and Line of code software parameters as our feature set. The forward selection technique chooses the first feature from an empty feature set. In the first iteration, the feature subgroup comprises simply the line of code parameters. Then, defect categorization is conducted, and the performance of the model is evaluated. Following that, a second feature is picked, and the subset now includes both Line of code and Cyclomatic complexity parameters. This process continues with additional features being added to the subset, and each time the model’s performance is assessed. The classification performance is also assessed using this enhanced subset. Once each trait has been evaluated, the process is gradually repeated. The greatest accuracy feature subset is kept, and that is the last step. Effective feature selection is highly desired. An efficient yet straightforward feature selection method is Greedy forward selection. The Greedy forward selection (GFS) only selects features that favorably influence better classification performance, in contrast to earlier time-consuming techniques like forward and backward selection [22]. The feature with the best classification performance, for instance, is given priority by Greedy forward selection. The most desirable feature is then added to the sustained feature subset under the features that were previously chosen. Instead, a list of traits that are rated according to how closely they relate to the module class is produced using the correlation-based selection technique. The first characteristic picked out is the one that is most biased against different social classes. Specifically, Fisher’s criterion and Pearson’s correlation are utilized to compute the correlation measure.

4.3 Ensemble Learning

This study constructs a group of classifiers aimed at facilitating the challenging task of classifying resilient software defects, with the average probability ensemble (APE) approach serving as the foundational model. Through ensemble learning [43], a series of base classifiers are amalgamated to create robust learning models, addressing prevalent issues in software defect datasets such as data imbalances and feature redundancy. The amalgamation of classification accuracy from diverse classifiers ensures resilience in the model. Unlike voting techniques, classifiers yielding probability outcomes utilize Area under ROC values to gauge the certainty associated with the projected class, thereby assessing the model’s probabilistic predictions’ performance. Furthermore, the employment of voting systems necessitates a stringent cutoff point for classification decisions, which may lead to erroneous outcomes. Hence, the mean of the probability ensemble is chosen for its adherence to the Area under ROC parameters and its avoidance of threshold selection. Each classifier within the recommended APE model estimates the probability of software elements belonging to the problematic class, contributing to the final probability estimate after averaging the output probabilities. The proposed model (Fig. 1) integrates eight base classifiers, including Gradient Boosting, Extreme Learning Machine, Stochastic Gradient Descent, Random Forests, Logistic Regression, Weighted-SVMs, and Bernoulli Naive Bayes, selected based on their broad acceptance within the artificial intelligence domain and among software developers. Various categorization techniques, such as statistical, neural, clustering, decision tree models, and SVM, are employed. Empirical results from the study substantiate the effectiveness of the seven fundamental classifiers selected for the ensemble learning method.

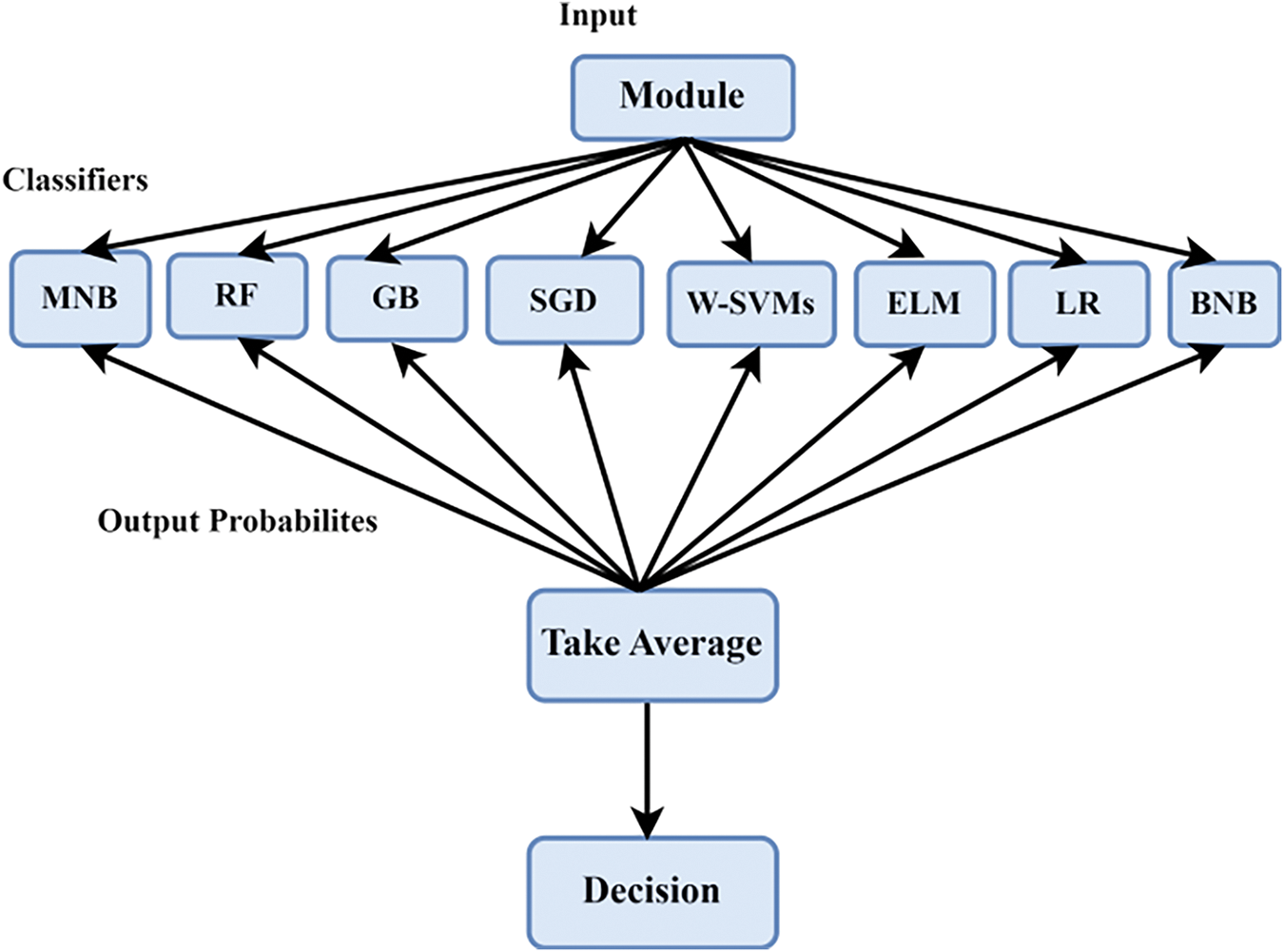
Figure 1: The suggested structure for the ensemble of average probabilities

4.3.1 Random Forests

Random forests are made up of a collection of unpruned regression trees. These trees are built using bootstrap specimens of the initial training data and a random choice of features [20]. The random forest’s trees are fed one data sample from a classification problem at a time. The latter then chooses the class that obtained the most votes from the individual trees as the chosen class. Breiman [20] has demonstrated that the durability of every single tree itself as well as the relationship between two or more trees in the forest have an impact on the number of errors in random forests. On the other hand, it is challenging to understand the findings of random forests. In these circumstances, each tree only manages a small subset of randomly chosen features.

4.3.2 Gradient Boosting and Stochastic Gradient Descent

Friedman introduced gradient boosting as a strategy for dealing with regression difficulties by building a prediction system comprised of a collection of weak predictors [44]. Typically, decision trees are used as the weak predictors within this gradient-boosting framework. Concerning a set of decision trees, {D1, D2,..., Di,..., Dn), Following are the steps used by the gradient boosting methodology to create a weighted average of each tree’s output choices:

f(x)=w0+w1t1(x)+w2t2(x)+…+wntn(x)

where the ith individual tree’s output choice is ti(x). To determine the optimal weights, wi, for each judgment, a differentiable loss function is minimized within the gradient boosting process [44]. Moreover, the gradient boosting technique can be adapted to handle classification problems by transforming them into regressions through the use of suitable loss functions. This enables gradient boosting to effectively address both regression and classification tasks. x represents the ith individual tree’s output selection. Second-order probabilistic gradients and averaged stochastic gradient approaches are used in massive data sets classification as well as regression problems are efficiently solved [45]. Stochastic gradient descent is a method for minimizing cost functions.

wk+1=wk−µ∇wP(xk,wk)

where µ denotes the Stochastic Gradient Descent SGD algorithm’s learning rate

P(xk,wk)–The loss functions approximate instantaneous value

P(x,w)–With the instant k input vector xk.

The features or model parameters, wk, are gradually modified using each input vector.

4.3.3 Logistic Regression

Logistic regression provides a pretty powerful bias using logistic sigmoid function [22]:

g(z)=11+e−z

Logistic regression has been used effectively for categorization challenges. Logistic regression generates a learning model that learns p(Y|x)through the implementation of using the Bayes rule of given two classes and N n-dimensional characteristics {x1,x2,…,xi,…,xn}, labeled Y = 0 and Y = 1, respectively.

4.3.4 Bernoulli Naive Bayes and Multinomial Naive Bayes

Reduced generative models are produced using the fundamental Naive Bayes classifier under the condition of statistical dependence among the model’s inputs and outputs. Based on this assumption

p(y|x)=p(y)∏i=1Np(xi|Y)∑y∏i=1Np(xi|Y)

Using maximum likelihood [22], it is possible to estimate the quantities defined in the aforementioned equation. Multinomial distributions are present in data samples used in multinomial Naive Bayes classifiers. This methodology is regularly applied to text categorization issues. It is preferred to use Bernoulli Naive Bayes classifiers whenever the data being analyzed has a multidimensional Bernoulli distribution. The feature samples in this example are expected to be binary-valued variables. The Bernoulli Naive Bayes classifier has the following definition of the decision rule for a sample, xi:

p(xi|Y)=p(i|Y)xi∗(1−p(i|Y))(1−xi)

Bernoulli-based classifiers, like multinomial Naive Bayes algorithm, reward the absence of a feature “i” that serves as a signal for class Y.

4.3.5 Regular and Weighted Support Vector Machines

Support Vector Machines, which Foster et al. devised based on statistical learning theory [46], have developed successful uses in a variety of disciplines, including text mining, bioinformatics, picture recognition, and system identification [47,48]. SVMs are a type of discriminative classifier that identifies an optimal hyper plane for separating data with two separate categories. Samples of data on the hyperplanes serve as support vector representations. By resolving a Lagrangian optimization issue, SVMs create ideal hyperplanes. The optimization process in SVMs frequently involves utilizing the dual space and incorporating kernels. However, concerns about SVMs include their application to multiple class problems and regression tasks. Furthermore, when compared to other models such as neural networks, determining the optimal parameters for SVMs can be time-consuming. Numerous methods are provided, including the use of kernels, grid search optimization, and derivative-free cost functions, to overcome these issues. Complex kernels are used to enhance SVM discrimination. Finally, other subjects have garnered significant interest in the literature, such as the development of novel kernels customized for specific applications, enhancing the generalization capability of models, and reducing training time for large datasets [22,49].

minE(w,b,ξ)=12||w||2+C.Φ(ξ)

where z(i)=φ(xi) indicates a non-linear mapping that is being applied to the ith feature vector x(i). ξ(i) known as slack variables enable the training samples are deliberately placed within the margin. They are expressed as the w and b of the SVM hyperplane. The term (.) in the equation above penalizes the solutions that are affected by numerous training errors. Weighted SVMS (W-SVMs), which give samples used for training from the minority class greater weight, is built based on the following equation. This work investigates classification methods based on W-SVMs for benchmarking due to the unbalanced composition of the software defect datasets.

4.3.6 Extreme Learning Machine

The concept of Extreme Learning Machines was initially proposed in 2006 as a single hidden layer in a feed-forward network [50,51]. The regularization word from [52] was not utilized in this sentence. The idea to apply separate random nonlinear feature transformations F is the extreme learning machine’s (ELM) most significant contribution. An M-dimensional vector with one of the following definitions for its jth component is created from an input vector, x:

(ΦA(x))j=σ(ωjTx+βj)

(ΦM(x))j=σ(||ωj−x||2/βj)

In ELM, where σ(.) known as nonlinear function, and ωj denotes random weights drawn from uniform distribution, and j is a bias factor that was randomly picked, and Random additive nodes are a common term used to describe transformations defined by, whereas multiplicative nodes are used to describe transformations defined by βj.

The ELM bears similarities to a neural network comprising neurons, as the biases and weights of the first layer are initialized dynamically and fixed, while those of the subsequent layer are determined through the minimization of the least-squares error. There are two notable properties shared with feed forward neural networks [53]: Both universal approximation and interpolation abilities are present. The paper provides an extensive survey of various machine learning techniques designed to improve the accuracy of software reliability prediction, evaluating different methods and their effectiveness in enhancing predictive performance. Theoretical limits on the number of hidden neurons required in feedforward neural networks with bounded nonlinear activation functions are examined in [54], offering important insights into network architecture and design. A detailed framework for analyzing the mean-field limit of multilayer neural networks is presented in [55], which aids in understanding their behavior as they scale. The effects of hidden layers on the efficiency of neural networks are explored [56], providing practical implications for designing and optimizing these networks. Two-hidden-layer feed-forward networks are shown to be universal approximates through a constructive approach in [57], highlighting their capability to approximate any continuous function. The degree of multivariate approximation achievable by the superposition of sigmoidal functions is investigated in [58], offering insights into the approximation capabilities of such functions. New activation functions for single-layer feedforward neural networks are introduced [59], aiming to enhance performance and versatility in various applications. The use of feedforward neural networks and compositional functions in the context of dynamical systems is analyzed in [60], offering a detailed study of their applications for control and optimization. Finally, an integrated computational intelligence paradigm combining neural networks, genetic algorithms, and sequential quadratic programming for modeling nonlinear electric circuits is presented in [61], showcasing an advanced approach to circuit modeling. The effectiveness of ELM as an interpolator is thoroughly proven in [62], The paper discusses an enhanced random search-based incremental extreme learning machine [63], which improves the performance of extreme learning machines through advanced search techniques. The study presents a fully complex extreme learning machine [64], contributing to the development of more robust models for handling complex data. An online sequential fuzzy extreme learning machine for function approximation and classification problems is introduced [65], addressing real-time learning challenges with fuzzy logic enhancements. The paper details a fast and accurate online sequential learning algorithm for feedforward networks [66], enhancing learning efficiency and accuracy in sequential data processing. The concept of an ensemble of online sequential extreme learning machines is explored [67], demonstrating the benefits of combining multiple models for improved performance. Adaptive ensemble models of extreme learning machines for time series prediction are presented [68], showing advancements in predicting temporal data through adaptive methods. An improved software reliability prediction model utilizing feature selection and extreme learning machines is discussed [69], focusing on enhancing prediction accuracy in software engineering. A regularized extreme learning machine is introduced [70], incorporating regularization techniques to prevent overfitting and improve generalization. It is possible to reliably acquire any N randomly distinct samples using a maximum of N hidden nodes if the activation properties of the layer that is hidden are indefinitely distinguishable in every interval. Both universal approximation and interpolation abilities are present. The effectiveness of ELM as an interpolator is thoroughly proven and ensemble ELM [68–70] has both been thoroughly investigated in terms of training efficacy and the previously indicated theoretical assurance. Reference [71] showed the comparison of SVM, ELM, and Least Squares Support Vector Machine (LSSVM), as well as a thorough survey for interested readers. The structure-based risk-minimizing principle and weighted least squares are the foundations of the Regularized Extreme Learning Machine (RELM). Regarding generalization performance, the RELM algorithm surpassed the original ELM method.

5  Analysis and Discussion

This part includes the experiment analysis and commentary.

5.1 Methods for Evaluating the Performance of Feature Selection

For benchmarking purposes, the study also includes the results of two fundamental classifiers: Random forests and Weighted-SVMs, as mentioned earlier. In the case of Weighted-SVMs, the classifier algorithm allows weights that are inversely proportionate to the frequency of every category in the set of data [57], and also higher no of weight is assigned to the most minority classes, which can potentially improve the relevant framework, particularly during the presence of Imbalanced datasets. Indeed, across all the datasets analyzed, Greedy forward selection not only outperforms for these methods, i.e., Fisher’s and Pearson’s correlation techniques but also achieves the maximum Area under ROC curve values. Additionally, the Greedy forward selection method mostly requires the less features or attributes to achieve the best accuracy in classification. The fact that using every feature that was accessible reduced classification performance is another noteworthy finding from the results. Weighted-SVMs achieved Area under ROC values of 0.78 and 0.04, respectively, when using all feature elements on PC2 and ant-1.7 datasets. However, by employing a smaller but more relevant feature set, the Weighted-SVMs model achieved improved Area under ROC values of 0.85 and 0.90 for the respective datasets. On the contrary, Pearson’s correlation technique tends to select numerous undesirable features, negatively impacting the classification performance. After adding the f21, f24, f36, and f39 features to the feature set, the obtained Area under the ROC curve dropped to less than 0.1. However, Pearson’s correlation strategy produced similar results on the other datasets Fisher’s criterion method was also able to select the best features, as shown by the higher Area under ROC Curve values. However, the Greedy forward selection technique outperformed this performance. An examination of the feature list generated by the Greedy forward selection method reveals that f32, f2, f34, f35, f14, and f4 were the most important features that contributed to the improved classification performance. In conclusion, the summary of performance data confirms the supposition of hypothesis 1. As expected, intelligent feature selection, specifically employing the Greedy forward selection method, resulted in performance of enhanced classification while also reducing the required total number of features for achieving that performance. Therefore, the first hypothesis is accepted.

5.2 Evaluation of the Proposed Average Probability Ensemble Model’s Performance

The suggested Average probability ensemble learning approach, as previously stated, incorporates seven fundamental classifiers, and their probabilities that are output by the model are averaged, and also to determine the best classification choice. Using the above datasets, the performance of the Weighted-SVMs and Random forests classifiers is compared to that of the Average probability ensemble model, with emphasis on preprocessing and feature determination. Table 1 compares the Area under ROC values of the four classifiers. According to our second hypothesis, the Average probability ensemble model has the greatest Area under the ROC curve of 0.83, followed by Random forests and Weighted-SVMs, which have an Area under ROC of 0.78 and 0.80, respectively. Surprisingly, the proposed Average probability ensemble model outperformed Weighted-SVMs in terms of performance. The Area under ROC curve values of the four classifiers are shown in Table 1 for comparison. According to the study’s second hypothesis, the Average probability ensemble model had the greatest Area under ROC curve score of 0.83, followed by Weighted-SVMs and Random forests, which had Area under ROC curve ratings of 0.78 and 0.80, respectively. Surprisingly, the proposed Average probability ensemble model beat Weighted-SVMs, which are intended for unbalanced data, implying that such ensembles are well-suited for classifying software flaws. The suggested Average probability ensemble model scored a remarkable Area under the ROC curve of 0.92 for the PC2 dataset, efficiently differentiating across classes. In the identical circumstance, Weighted-SVMs and Random forests achieved an Area under the ROC curve of just 0.54 and 0.74, respectively.

Another key worry is raised by the performance of the suggested Average probability ensemble model, which utilizes Weighted-SVMs as some of its fundamental classifiers. While the Average probability ensemble model scored an amazing Area under ROC of 0.92 for the PC2 dataset, the Weighted-SVMs model only achieved a mediocre Area under ROC curve of 0.54. Individual performance of one of the Average probability ensemble model’s fundamental classifiers does not affect the model’s overall performance. Finally, the performance outcomes shown in Table 2 corroborate the notion expressed in the second hypothesis of this work. In terms of classification accuracy, it has been claimed that ensemble learning outperforms individual classifiers, particularly when the selection of individual classifiers is based on their established performance. Furthermore, low-performing base classifiers in ensemble learning have no negative impact on the method’s overall performance. As a result, the second hypothesis is considered valid and acceptable. Fig. 2 shows the pictorial representation of the result comparison between W-SVMs, RF, ELM, and APE models.

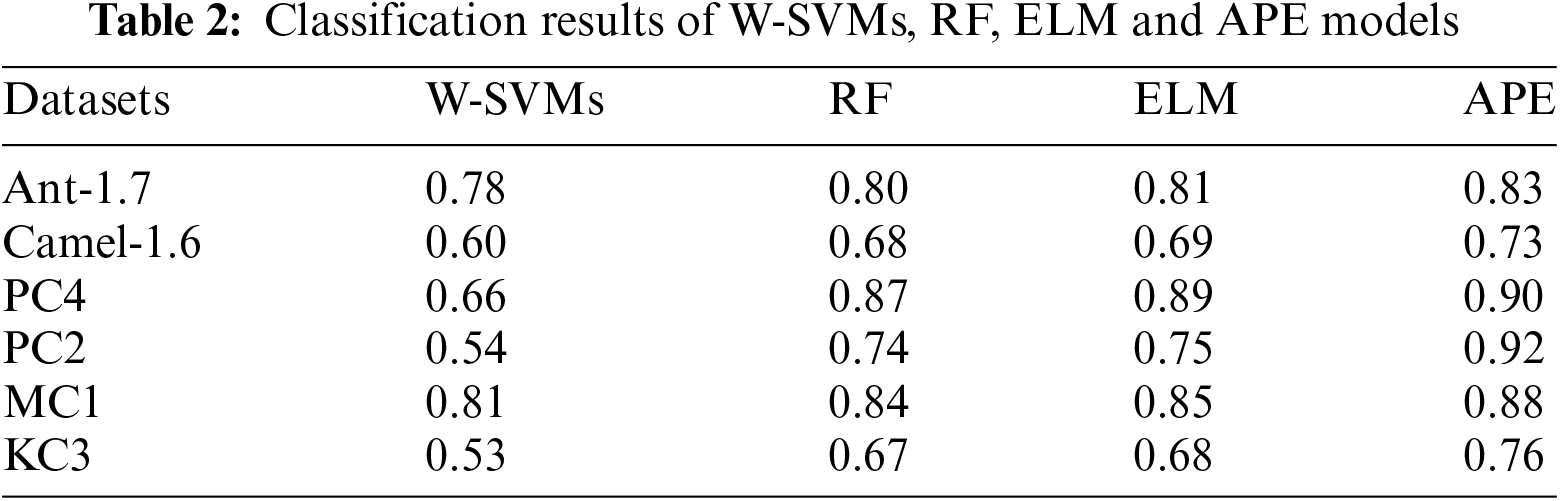
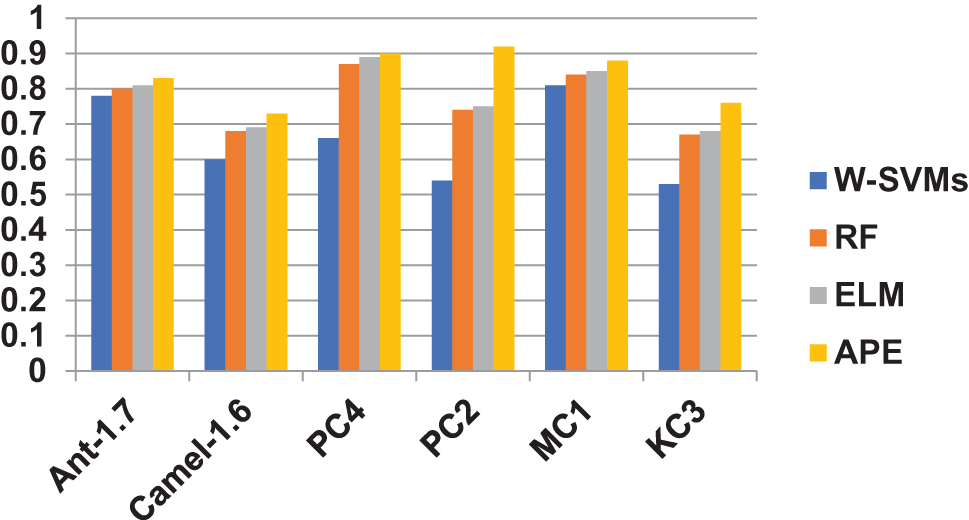
Figure 2: Result comparison between W-SVMs, RF, ELM and APE models

5.3 The Effects of the Number and Kind of Basic Classifiers on APE Classification Performance

The performance of the Average probability ensemble model remains consistent when applied to the Camel and KC3 datasets, even with the inclusion of more than seven classifiers. The employment of nine classifiers even results in a slight performance degradation. Another similar pattern can be seen in the remaining datasets. Seven basis classifiers make up the final model, which is based on an SVM model that has been improved. The Average probability ensemble model performs poorly for each dataset after seven classifiers. Whenever nine classifiers are used, even a small performance hit occurs. Similar trends can be seen in the remaining datasets. The final model is built on an optimized SVM model and consists of seven base classifiers. The heterogeneous Average probability ensemble model model’s ‘‘optimal’’ base classifier count is calculated using a similar methodology. It is clear from comparing the PC2 and PC4 datasets that, after 10 classifiers, the PC4 dataset’s classification performance declines rather than improves. A clear indication of overfitting is evident in the decrease in performance. Nonetheless, for the PC2 dataset, the classification system shows limited improvement beyond a certain point that incorporation of 10 classifiers. The usage of eight fundamental classifiers is advised based on this performance trend. It’s worth noting that the extra datasets behave similarly.

5.4 The Influence of Feature Selection on APE Classification Performance

It is worthwhile to think about including a feature being chosen module in the suggested Average probability ensemble model due to the positive classification results linked to feature selection. The modified Average probability ensemble model, which has been updated, only contains fault signs that are expected to enhance the performance of classification. The Forward Greedy selection approach is also utilized for the selection of features, which performs better than other feature selection techniques. Table 3 summarizes the classification performance of the Average probability ensemble model and it upgraded the different versions, emphasizing the performance improvement produced by the Forward Greedy selection technique. After involving the all-defect datasets, the augmented model outperformed the basic model. This categorization increase is attributable to the Forward Greedy selection method, which limits its analysis to useful and pertinent software metrics. Software metrics that are redundant and useless are so removed. Table 3 shows an unusual depiction of the software parameters connected with each dataset under consideration. There is a higher improvement in classification performance when a dataset contains more redundant and/or irrelevant software metrics. Fig. 3 shows the pictorial representation of the result comparison between APE and Enhanced APE models.

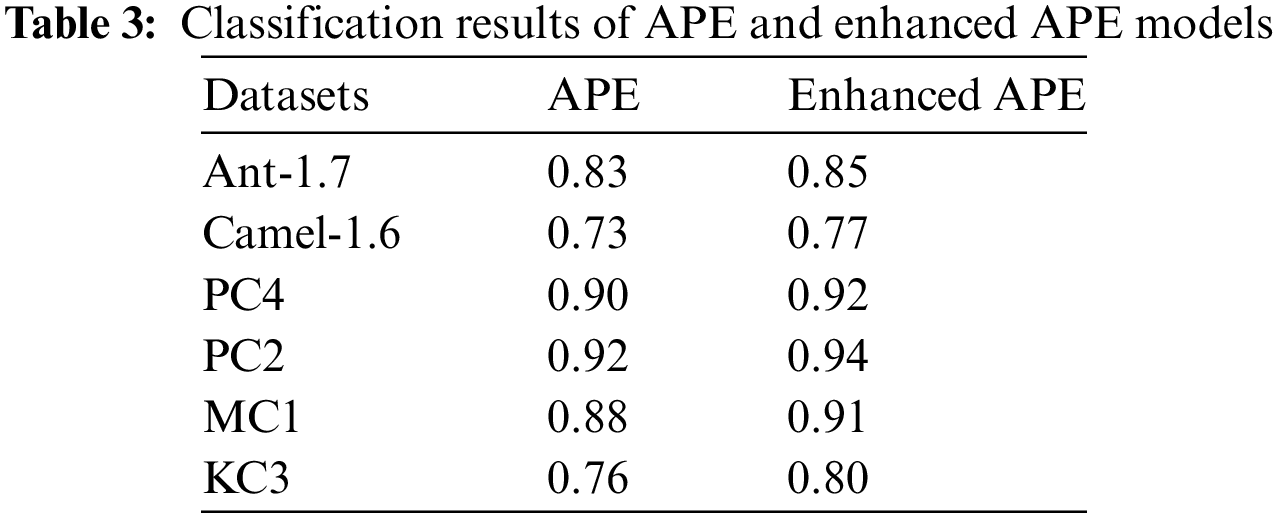
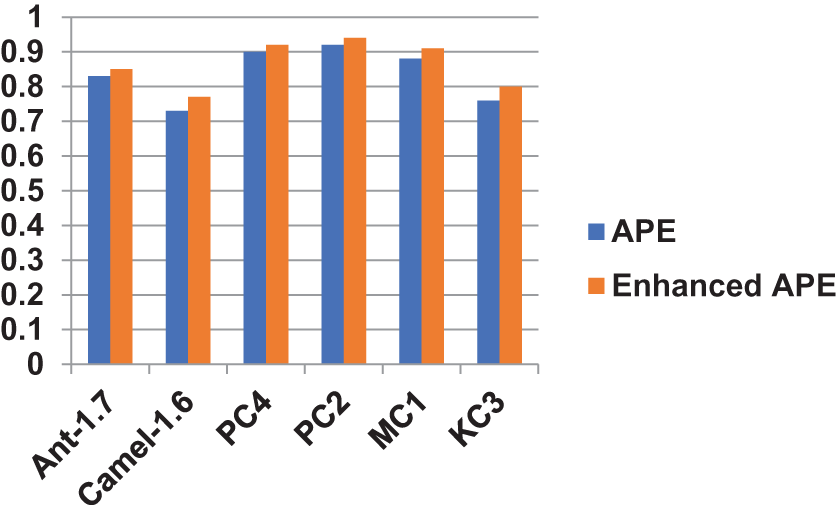
Figure 3: Result comparison between APE and Enhanced APE models

The effectiveness of current algorithms like Weighted-SVMs and Random Forests is analyzed below about the impact of feature selection. The performance of the suggested upgraded algorithm, along with that of the improved Random Forests, Weighted-SVM, and ELM classifiers, is summarized in Table 4, while Fig. 4 shows the pictorial representation of the result comparison between APE, W-SVMs, RF, and ELM models. Feature selection helps both proposed and existing classifiers perform better in terms of classification according to the first hypothesis. The enhanced Weighted-SVM and Random forests classifiers did indeed behave as predicted. Additionally, the improved Average probability ensemble, a variant of the suggested model, outperforms enhanced iterations of the other two classifiers. In classification problems involving unbalanced datasets, the geometric mean is a frequently used performance measure [46]. This metric demonstrates the classifier’s ability to effectively classify both the minority and majority classes. It combines the parameters of specificity and sensitivity, which encompass the following aspects:

Specificity =1−FPTN+FN

Sensitivity =TPTP+FN

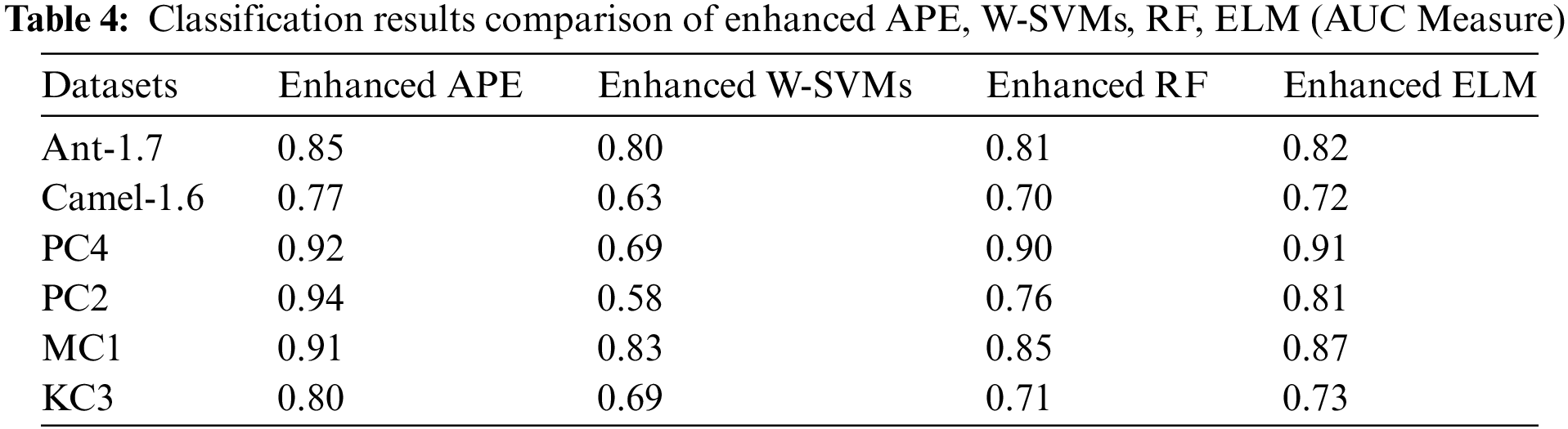
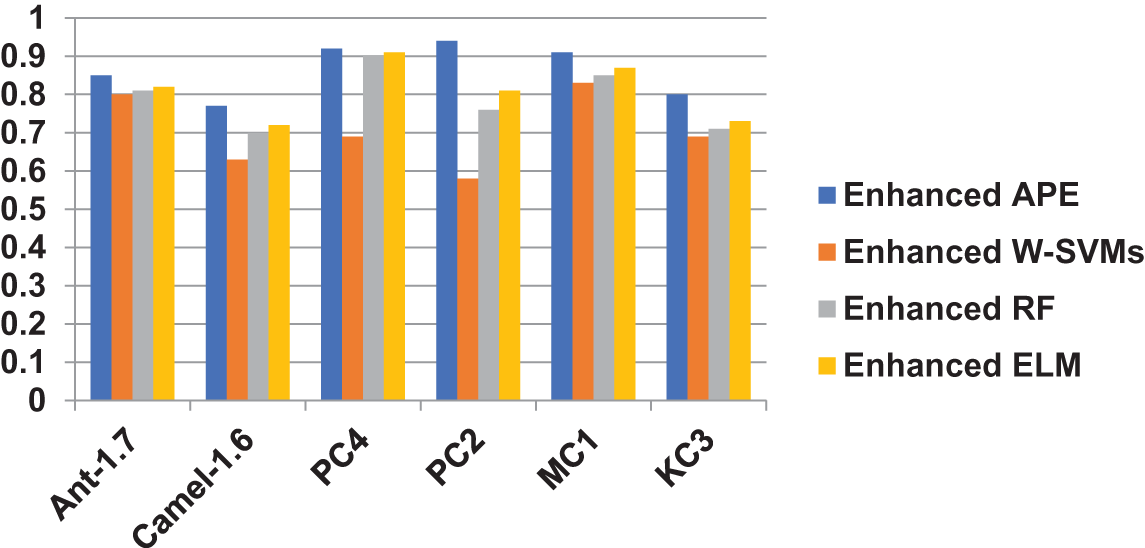
Figure 4: Result comparison between APE, W-SVMs, RF, and ELM models

In this equation, TP represents true positives, TN represents true negatives, FP represents false positives, and FN represents false negatives. The G-mean is a measure that assesses the accuracy of both positive and negative samples by considering sensitivity and specificity [46]:

G-mean =Specificity∗Sensitivity

Table 5 provides a comprehensive representation of the classification outcomes for the suggested ensemble learning technique, employing a multi variant approach. It also includes a comparison to the original and simplified versions of existing algorithms based on the G-mean measure. As shown in Table 4, the G-mean effectively analyses the impact of data imbalance on classification effectiveness. A low G-mean score can be indicative of the classifier’s poor performance in handling minority-related information. This behavior was observed in the Weighted-SVMs classifier, specifically with the PC2, KC3, and ant-1.7 datasets. Similarly, the random forest-based classifier showed similar behavior, particularly with the PC2 dataset. The enhanced model outperformed previous classifiers in performance and achieved the highest classification accuracy with a perfect G-mean measure of one. This represents the highest reported accuracy in the literature for software defect datasets using the G-mean metric.

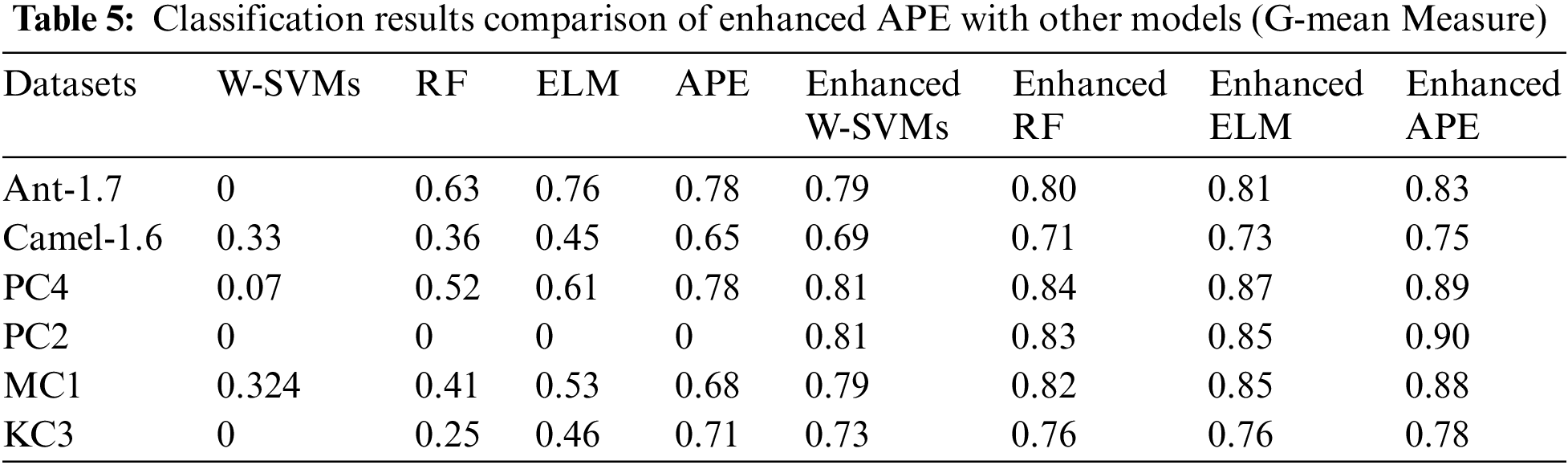
5.5 GFS-Based Selected Features

The results in Table 6 justify the use of the GFS technique to assess the reliability of the chosen features. Table 7 summarizes the preserved characteristics derived by the Greedy forward selection approach using the Area under ROC and G-mean measurements, respectively. Tables 7 and 8 reveal numerous details about the performance of the chosen features. The utility of G-mean measurements in selecting only a small portion of the original metrics becomes evident when evaluating the total number of parameters retained, as compared to the Area under ROC curve measurements. Furthermore, each technique selects a different number of measures, with the improved Average probability ensemble algorithm keeping a somewhat higher number of metrics than the others. As far as the authors are aware, there appears to be little literature investigating the properties of preserved software metrics. Tables 6 and 7 not only establish the correlation between the number of defect instances and software parameters, also they narrow down this type of relationship to a small subset of software parameters. The G-mean measure demonstrates the limited link. The method provided in this review study also makes a substantial contribution by preventing the defect classifier from eliminating observations from the failure class. Table 6 clearly demonstrates this tendency by giving he classifier that tends to neglect minority class data a G-mean score of zero.

5.6 Result Comparison

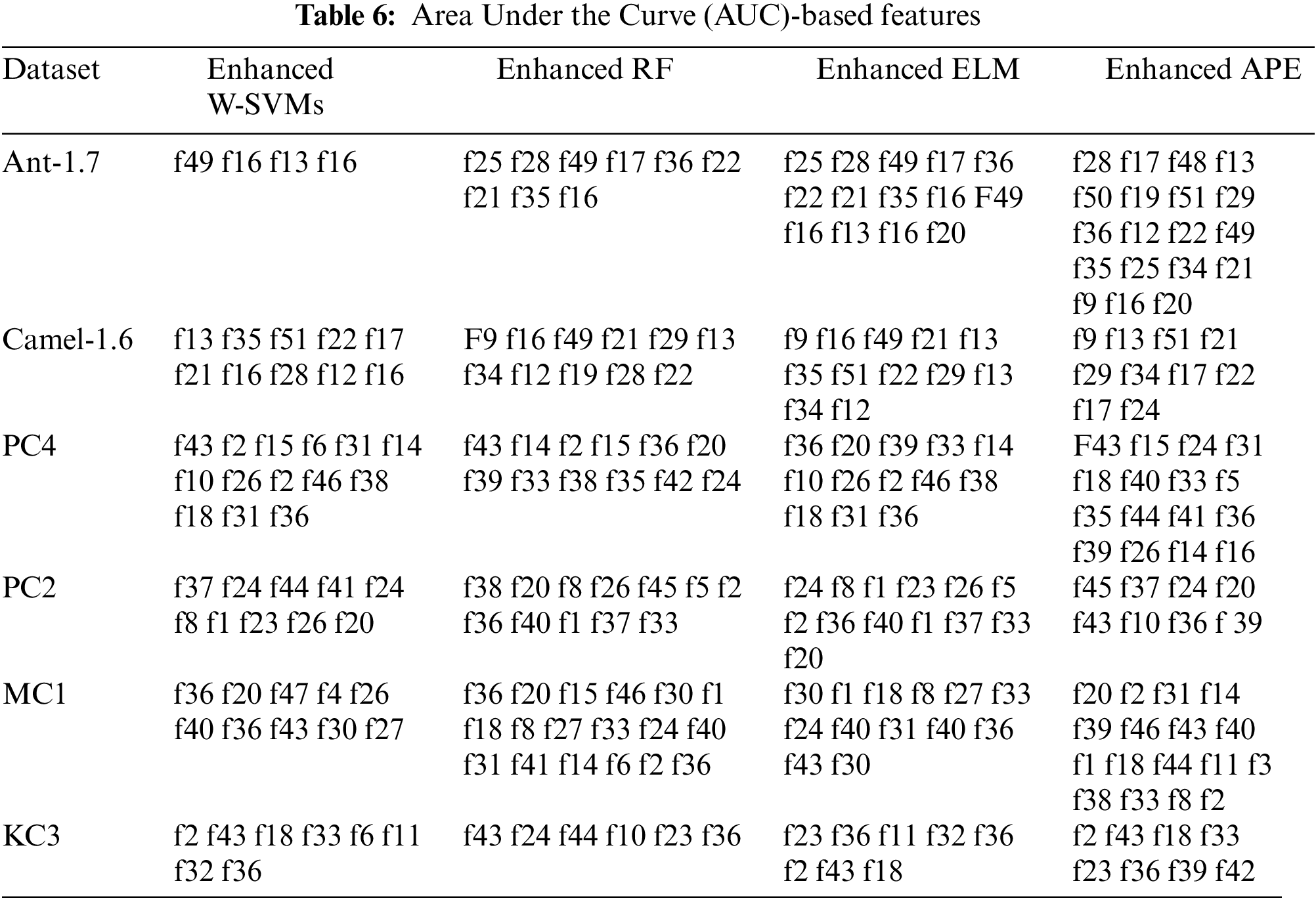
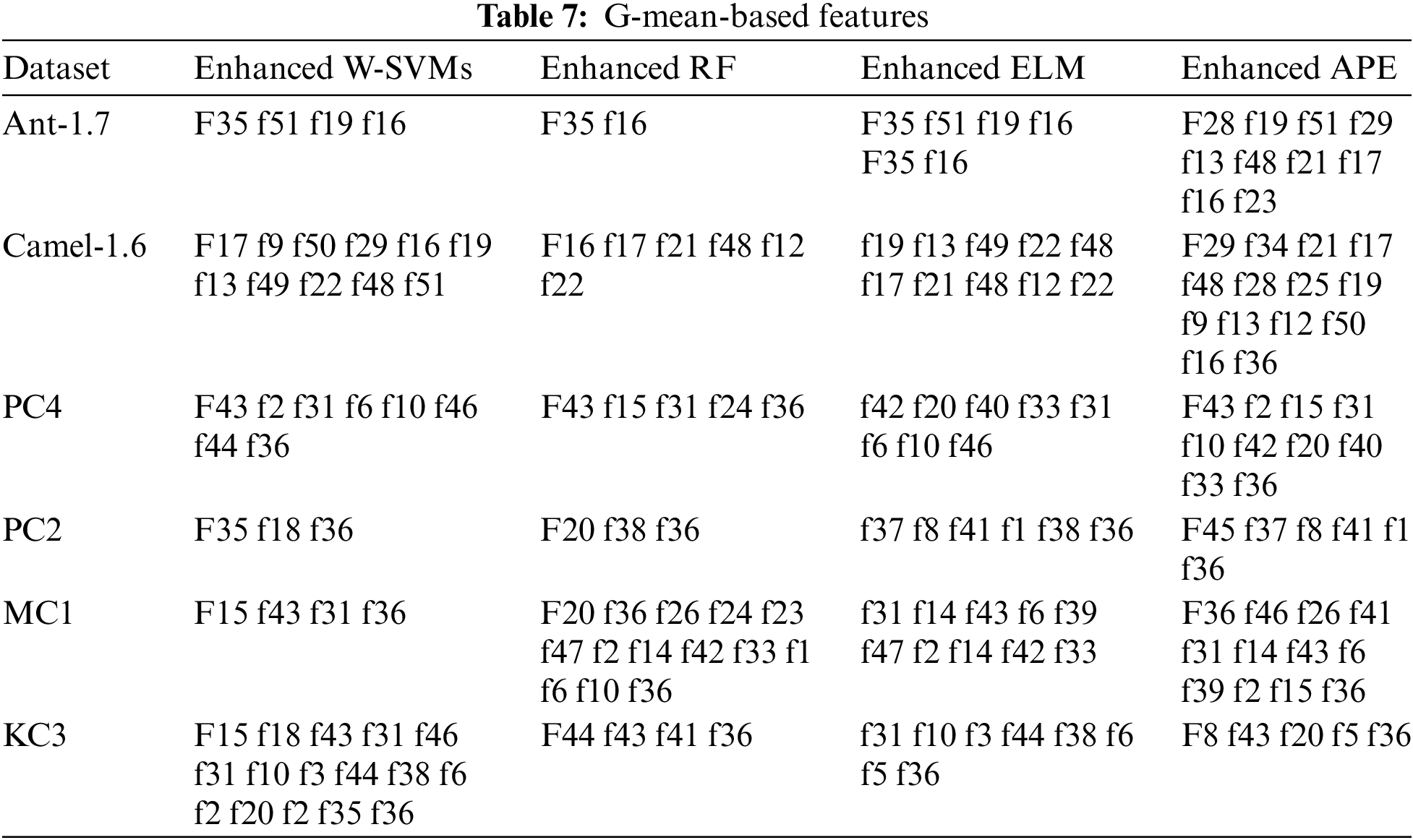
In this section, authors are attempting to compare results with existing work. After reviewing numerous papers, authors have found that there is very little research done in this area, and only a limited number of ML techniques have been utilized. Currently, there are only 2 to 3 papers available wherein researchers have attempted to ascertain accuracy results in this area using methods similar to ours but on different datasets. In Table 8, authors have included their results alongside ours, with the intention that other researchers may further extend this work.

5.7 Threats to Validity

Many risks could affect the study’s findings. The predictors’ chosen indicators affect an internal threat. Academic sources describe many measurements. Although authors used the metrics offered by the datasets authors chose, additional measures may provide a more precise indication of faults. The conclusions reported in this review article are based on the systems chosen. It’s possible that some industrial fields do not use these systems. Furthermore, it was asserted that there is uncertainty regarding the quality of the NASA and Java datasets [41]. In terms of the quantity and size of classes, these frameworks may not be great examples. Although there is a possibility of an external threat that could challenge the accuracy of the frameworks and consequently affect the reliability of the outcomes, this methodology is extensively employed by researchers in the field of software engineering. An additional vulnerability arising from the data analysis process is connected to our utilization of custom code, which might be susceptible to implementation issues that could compromise its effectiveness. To reduce the possibility of coding errors, the authors used benchmark datasets from the Scikit-learn hosting site, a Python machine learning software, to validate the key code blocks.

6  Conclusion

In this review study, authors investigated different methods for selecting features in software defect prediction. The authors found that using a limited number of top-quality features significantly enhances the area under the ROC curve compared to alternative approaches. Additionally, the authors demonstrated ensemble learning’s effectiveness when applied to duplicated, unbalanced datasets. The suggestion is an ensemble learning classifier with two variables. Based on experimental results from six datasets, greedy forward selection demonstrated significantly better performance compared to correlation-based forward selection. Additionally, authors showed that APE outperforms more conventional methods like Weighted-SVMs, ELM, and RF. APE is composed of eight well-constructed learners. Moreover, when the Average probability ensemble algorithm was combined with the Greedy forward selection technique, the resulting model achieved a remarkably high area under ROC values for all datasets examined, with PC2, MC1, and PC4 datasets approaching a value of 1.0. In future research, authors plan to delve into alternative feature selection strategies to expand our understanding of their efficacy in software defect prediction. Specifically, the authors aim to scrutinize the redundancy or ineffectiveness of numerous features prevalent in publicly available software defect datasets, potentially uncovering insights into the essential characteristics for accurate prediction. Furthermore, the authors intend to juxtapose our approach with small-scale Linear Discriminant Analysis and Principal Component Analysis to assess the effectiveness of different feature reduction techniques. Additionally, the authors aim to explore the integration of additional ensemble learners to further enhance predictive performance and provide a comprehensive comparison of various ensemble methods in this context.

Acknowledgement: The authors acknowledge the support of their respective institutions.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Suneel Kumar Rath, Madhusmita Sahu, Shom Prasad Das, Junali Jasmine Jena, Chitralekha Jena, Baseem Khan, Ahmed Ali, Pitshou Bokoro; data collection: Suneel Kumar Rath, Madhusmita Sahu, Shom Prasad Das, Junali Jasmine Jena, Chitralekha Jena, Baseem Khan, Ahmed Ali, Pitshou Bokoro; analysis and interpretation of results: Suneel Kumar Rath, Madhusmita Sahu, Shom Prasad Das, Junali Jasmine Jena, Chitralekha Jena, Baseem Khan, Ahmed Ali, Pitshou Bokoro; draft manuscript preparation: Suneel Kumar Rath, Madhusmita Sahu, Shom Prasad Das, Junali Jasmine Jena, Chitralekha Jena, Baseem Khan, Ahmed Ali, Pitshou Bokoro. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. Ali and C. Gravino, “A systematic literature review of software effort prediction using machine learning methods,” J. Softw.: Evol. Process, vol. 31, no. 10, 2019, Art. no. e2211. [Google Scholar]

2. M. Jorgensen, “Experience with the accuracy of software maintenance task effort prediction models,” IEEE Trans. Softw. Eng., vol. 21, no. 7, pp. 674–681, 1995. doi: 10.1109/32.403791. [Google Scholar] [CrossRef]

3. M. Riaz, E. Mendes, and E. Tempero, “A systematic review of software maintainability prediction and metrics,” in Proc. 2009 3rd Int. Symp. Empir. Softw. Eng. Meas., 2009, pp. 367–377. [Google Scholar]

4. Y. Zhou and H. Leung, “Predicting object-oriented software maintainability using multivariate adaptive regression splines,” J. Syst. Softw., vol. 80, no. 8, pp. 1349–1361, 2007. doi: 10.1016/j.jss.2006.10.049. [Google Scholar] [CrossRef]

5. Y. Ma, G. Luo, X. Zeng, and A. Chen, “Transfer learning for cross-company software defect prediction,” Inf. Softw. Tech., vol. 54, no. 3, pp. 248–256, 2012. doi: 10.1016/j.infsof.2011.09.007. [Google Scholar] [CrossRef]

6. A. Tosun, A. Bener, B. Turhan, and T. Menzies, “Practical considerations in deploying statistical methods for defect prediction: A case study within the Turkish telecommunications industry,” Inf. Softw. Tech., vol. 52, no. 11, pp. 1242–1257, 2010. doi: 10.1016/j.infsof.2010.06.006. [Google Scholar] [CrossRef]

7. X. Yuan, T. M. Khoshgoftaar, E. B. Allen, and K. Ganesan, “An application of fuzzy clustering to software quality prediction,” in 3rd IEEE Symp. Appl.-Specific Syst. Softw. Eng. Technol., 2000, pp. 85–90. [Google Scholar]

8. N. E. Fenton and M. Neil, “A critique of software defect prediction models,” IEEE Trans. Softw. Eng., vol. 25, no. 5, pp. 675–689, 1999. doi: 10.1109/32.815326. [Google Scholar] [CrossRef]

9. A. Koru and H. Liu, “Building effective defect-prediction models in practice,” IEEE Softw., vol. 22, no. 6, pp. 23–29, 2005. doi: 10.1109/MS.2005.149. [Google Scholar] [CrossRef]

10. W. Wu, S. Wang, B. Liu, Y. Shao, and W. Xie, “A novel software defect prediction approach via weighted classification based on association rule mining,” Eng. Appl. Artif. Intell., vol. 129, no. 2, 2024, Art. no. 107622. doi: 10.1016/j.engappai.2023.107622. [Google Scholar] [CrossRef]

11. Y. Zhao, K. Damevski, and H. Chen, “A systematic survey of just-in-time software defect prediction,” ACM Comput. Surv., vol. 55, no. 10, pp. 1–35, 2023. doi: 10.1145/3567550. [Google Scholar] [CrossRef]

12. F. Han, Z. Hu, N. Chen, Y. Wang, J. Jiang and Y. Zheng, “Assimilating low-cost high-frequency sensor data in watershed water quality modeling: A Bayesian approach,” Water Resour. Res., vol. 59, no. 4, 2023. doi: 10.1029/2022WR033673. [Google Scholar] [CrossRef]

13. M. J. Hernández-Molinos, A. J. Sánchez-García, R. E. Barrientos-Martínez, J. C. Pérez-Arriaga, and J. O. Ocharán-Hernández, “Software defect prediction with Bayesian approaches,” Mathematics, vol. 11, no. 11, 2023, Art. no. 2524. doi: 10.3390/math11112524. [Google Scholar] [CrossRef]

14. M. M. Elsagheer and S. M. Ramzy, “A hybrid model for automatic modulation classification based on residual neural networks and long short term memory,” Alex. Eng. J., vol. 67, no. 4, pp. 117–128, 2023. doi: 10.1016/j.aej.2022.08.019. [Google Scholar] [CrossRef]

15. C. Andersson, “A replicated empirical study of a selection method for software reliability growth models,” Empir. Softw. Eng., vol. 12, no. 2, pp. 161–182, 2007. doi: 10.1007/s10664-006-9018-0. [Google Scholar] [CrossRef]

16. T. M. Khoshgoftaar, K. Gao, and A. Napolitano, “An empirical study of feature ranking techniques for software quality prediction,” Int. J. Softw. Eng. Knowl. Eng., vol. 22, no. 2, pp. 161–183, 2012. doi: 10.1142/S0218194012400013. [Google Scholar] [CrossRef]

17. H. Moosaei, M. A. Ganaie, M. Hladík, and M. Tanveer, “Inverse free reduced universum twin support vector machine for imbalanced data classification,” Neural Netw., vol. 157, no. 6, pp. 125–137, 2023. doi: 10.1016/j.neunet.2022.10.003. [Google Scholar] [PubMed] [CrossRef]

18. N. Japkowicz and S. Stephen, “The class imbalance problem: A systematic study,” Intell. Data Anal., vol. 6, no. 5, pp. 429–449, 2002. doi: 10.3233/IDA-2002-6504. [Google Scholar] [CrossRef]

19. Y. Sun, M. S. Kamel, A. K. Wong, and Y. Wang, “Cost-sensitive boosting for classification of imbalanced data,” Pattern Recognit., vol. 40, no. 12, pp. 3358–3378, 2007. doi: 10.1016/j.patcog.2007.04.009. [Google Scholar] [CrossRef]

20. S. K. Rath, M. Sahu, S. P. Das, and S. K. Bisoy, “A comparative analysis of SVM and ELM classification on software reliability prediction model,” Electronics, vol. 11, no. 17, 2022, Art. no. 2707. doi: 10.3390/electronics11172707. [Google Scholar] [CrossRef]

21. G. Aguiar, B. Krawczyk, and A. Cano, “A survey on learning from imbalanced data streams: Taxonomy, challenges, empirical study, and reproducible experimental framework,” in Machine Learning, Dordrecht, Netherlands: Springer, 2024, vol. 113, no. 7, pp. 4165–4243. [Google Scholar]

22. S. K. Rath, M. K. Sahu, and S. P. Das, “Applications of machine learning in industrial reliability model,” in Handbook of Research on Applications of AI, Digital Twin, and Internet of Things for Sustainable Development. Hershey, PA, USA: IGI Global, 2023, pp. 30–46. [Google Scholar]

23. C. Seiffert, T. M. Khoshgoftaar, and J. Van Hulse, “Improving software-quality predictions with data sampling and boosting,” IEEE Trans. Syst., Man, Cybern.: Syst. Humans, vol. 39, no. 5, pp. 1283–1294, 2009. doi: 10.1109/TSMCA.2009.2027131. [Google Scholar] [CrossRef]

24. Z. Xu et al., “A comprehensive comparative study of clustering-based unsupervised defect prediction models,” J. Syst. Softw., vol. 172, no. 3, 2021, Art. no. 110862. doi: 10.1016/j.jss.2020.110862. [Google Scholar] [CrossRef]

25. P. Soltanzadeh and M. Hashemzadeh, “RCSMOTE: Range-Controlled Synthetic Minority Over-Sampling Technique for handling the class imbalance problem,” Inf. Sci., vol. 542, pp. 92–111, 2021. [Google Scholar]

26. T. M. Khoshgoftaar, E. Geleyn, L. Nguyen, and L. Bullard, “Cost-sensitive boosting in software quality modeling,” in 7th IEEE Int. Symp. High Assur. Syst. Eng., 2002, pp. 51–60. [Google Scholar]

27. S. K. Rath, M. Sahu, S. P. Das, and J. Pradhan, “Survey on machine learning techniques for software reliability accuracy prediction,” in Int. Conf. Metaheuristics Softw. Eng. Appl., Springer, 2022, pp. 43–55. [Google Scholar]

28. J. Zheng, “Cost-sensitive boosting neural networks for software defect prediction,” Expert. Syst. Appl., vol. 37, no. 6, pp. 4537–4543, 2010. [Google Scholar]

29. M. Galar, A. Fernández, E. Barrenechea, H. Bustince, and F. Herrera, “A review on ensembles for the class imbalance problem: Bagging-, boosting-, and hybrid-based approaches,” IEEE Trans. Syst., Man, Cybern.: Appl. Rev., vol. 42, no. 4, pp. 463–484, 2012. [Google Scholar]

30. M. Hassam, J. A. Shamsi, A. Khan, A. Al-Harrasi, and R. Uddin, “Prediction of inhibitory activities of small molecules against Pantothenate synthetase from Mycobacterium tuberculosis using machine learning models,” Comput. Biol. Med., vol. 145, 2022, Art. no. 105453. doi: 10.1016/j.compbiomed.2022.105453. [Google Scholar] [PubMed] [CrossRef]

31. C. Rudin, C. Chen, Z. Chen, H. Huang, L. Semenova and C. Zhong, “Interpretable machine learning: Fundamental principles and 10 grand challenges,” Stat. Surv., vol. 16, pp. 1–85, 2022. [Google Scholar]

32. A. Miyamoto, J. Miyakoshi, K. Matsuzaki, and T. Irie, “False-positive reduction of liver tumor detection using ensemble learning method,” in SPIE Med. Imaging, 2013. doi: 10.1117/12.2006329. [Google Scholar] [CrossRef]

33. G. Forman, “An extensive empirical study of feature selection metrics for text classification,” J. Mach. Learn. Res., vol. 3, pp. 1289–1305, 2003. [Google Scholar]

34. Y. Saeys, I. Inza, and P. Larrañaga, “A review of feature selection techniques in bioinformatics,” Bioinformatics, vol. 23, no. 19, pp. 2507–2517, 2007. doi: 10.1093/bioinformatics/btm344. [Google Scholar] [PubMed] [CrossRef]

35. S. Wang, L. L. Minku, and X. Yao, “Online class imbalance learning and its applications in fault detection,” Int. J. Comput. Intell. Appl., vol. 12, no. 1, 2013. doi: 10.1142/S1469026813400014. [Google Scholar] [CrossRef]

36. N. Seliya, T. M. Khoshgoftaar, and J. Van Hulse, “Predicting faults in high assurance software,” in IEEE 12th Int. Symp. High-Assur. Syst. Eng. (HASE), 2010, pp. 26–34. [Google Scholar]

37. Z. Sun, Q. Song, and X. Zhu, “Using coding-based ensemble learning to improve software defect prediction,” IEEE Trans. Syst., Man, Cybern.: Appl. Rev., vol. 42, no. 7, pp. 1806–1817, 2012. doi: 10.1109/TSMCC.2012.2226152. [Google Scholar] [CrossRef]

38. T. Wang, W. Li, H. Shi, and Z. Liu, “Software defect prediction based on classifiers ensemble,” J. Inf. Comput. Sci., vol. 8, no. 12, pp. 4241–4254, 2011. [Google Scholar]

39. S. Lessmann, B. Baesens, C. Mues, and S. Pietsch, “Benchmarking classification models for software defect prediction: A proposed framework and novel findings,” IEEE Trans. Softw. Eng., vol. 34, no. 4, pp. 485–496, 2008. doi: 10.1109/TSE.2008.35. [Google Scholar] [CrossRef]

40. P. S. Bishnu and V. Bhattacherjee, “Software fault prediction using quad tree-based K-means clustering algorithm,” IEEE Trans. Knowl. Data Eng., vol. 24, no. 6, pp. 1146–1150, 2012. doi: 10.1109/TKDE.2011.163. [Google Scholar] [CrossRef]

41. D. Gray, D. Bowes, N. Davey, Y. Sun, and B. Christianson, “The misuse of the NASA metrics data program data sets for automated software defect prediction,” in 15th Ann. Conf. Eval. Assess. Softw. Eng. (EASE 25), Durham, 2011, pp. 12–25. doi: 10.1049/ic.2011.0012. [Google Scholar] [CrossRef]

42. P. Vuttipittayamongkol, E. Elyan, and A. Petrovski, “On the class overlap problem in imbalanced data classification,” Knowl. Based Syst., vol. 212, no. 3, 2021, Art. no. 106631. doi: 10.1016/j.knosys.2020.106631. [Google Scholar] [CrossRef]

43. T. G. Dietterich, “Ensemble learning,” in The Handbook of Brain Theory and Neural Networks, Cambridge, MA, USA: MIT Press, 2002, pp. 405–408. [Google Scholar]

44. U. Schroeders, C. Schmidt, and T. Gnambs, “Detecting careless responding in survey data using stochastic gradient boosting,” Educ. Psychol. Meas., vol. 82, no. 1, pp. 29–56, 2022. doi: 10.1177/00131644211004708. [Google Scholar] [PubMed] [CrossRef]

45. L. Bottou, “Large-scale machine learning with stochastic gradient descent,” in Proc. COMPSTAT’2010, 2010, pp. 177–186. [Google Scholar]

46. D. J. Foster and V. Syrgkanis, “Orthogonal statistical learning,” Ann. Stat., vol. 51, no. 3, pp. 879–908, 2023. doi: 10.1214/23-AOS2258. [Google Scholar] [CrossRef]

47. F. Markowetz, “Support vector machines in bioinformatics,” Master’s thesis, Univ. of Heidelberg, 2001. [Google Scholar]

48. H. Chen, H. Ye, L. Chen, and H. Su, “Application of support vector machine learning to leak detection and location in pipelines,” in Proc. 21st IEEE Instrum. Meas. Technol. Conf. (IMTC '04), 2004, vol. 3, pp. 2273–2277. [Google Scholar]

49. S. K. Rath, M. Sahu, S. P. Das, and S. K. Mohapatra, “Hybrid software reliability prediction model using feature selection and support vector classifier,” in 2022 Int. Conf. Emerg. Smart Comput. Inform. (ESCI), IEEE, 2022, pp. 1–4. doi: 10.1109/ESCI53509.2022.9758339. [Google Scholar] [CrossRef]

50. G. Huang, Q. Zhu, and C. Siew, “Extreme learning machine: Theory and applications,” Neurocomputing, vol. 70, no. 1, pp. 489–501, 2006. doi: 10.1016/j.neucom.2005.12.126. [Google Scholar] [CrossRef]

51. G. Huang, L. Chen, and C. Siew, “Universal approximation using incremental constructive feedforward networks with random hidden nodes,” IEEE Trans. Neural Netw., vol. 17, no. 4, pp. 879–892, 2006. doi: 10.1109/TNN.2006.875977. [Google Scholar] [PubMed] [CrossRef]

52. G. Wahba et al., “Support vector machines, reproducing kernel Hilbert spaces and the randomized GACV,” in Advances in Kernel Methods: Support Vector Learning, Cambridge, MA, USA: MIT Press, 1999, pp. 69–87. [Google Scholar]

53. P. R. Bal and S. Kumar, “WR-ELM: Weighted regularization extreme learning machine for imbalance learning in software fault prediction,” IEEE Trans. Reliab., vol. 69, no. 4, pp. 1355–1375, 2020. doi: 10.1109/TR.2020.2996261. [Google Scholar] [CrossRef]

54. G. Huang and H. Babri, “Upper bounds on the number of hidden neurons in feedforward networks with arbitrary bounded nonlinear activation functions,” IEEE Trans. Neural Netw., vol. 9, no. 1, pp. 224–229, 1998. doi: 10.1109/72.655045. [Google Scholar] [PubMed] [CrossRef]

55. P. -M. Nguyen and H. T. Pham, “A rigorous framework for the mean field limit of multilayer neural networks,” Math. Stat. Learn., vol. 6, no. 3, pp. 201–357, 2023. doi: 10.4171/msl/42. [Google Scholar] [CrossRef]

56. M. Uzair and N. Jamil, “Effects of hidden layers on the efficiency of neural networks,” in 2020 IEEE 23rd Int. Multitopic Conf. (INMIC), IEEE, 2020, pp. 1–6. [Google Scholar]

57. E. Paluzo-Hidalgo, R. Gonzalez-Diaz, and M. A. Gutiérrez-Naranjo, “Two-hidden-layer feed-forward networks are universal approximators: A constructive approach,” Neural Netw., vol. 131, no. 4, pp. 29–36, 2020. doi: 10.1016/j.neunet.2020.07.021. [Google Scholar] [PubMed] [CrossRef]

58. N. W. Hahm, “Degree of multivariate approximation by superposition of a sigmoidal function,” J. Anal. Appl., vol. 20, no. 2, pp. 123–134, 2022. [Google Scholar]

59. Y. Koçak and G. Üstündağ Şiray, “New activation functions for single layer feedforward neural network,” Expert. Syst. Appl., vol. 164, no. 9, 2021, Art. no. 113977. doi: 10.1016/j.eswa.2020.113977. [Google Scholar] [CrossRef]

60. W. Kang and Q. Gong, “Feedforward neural networks and compositional functions with applications to dynamical systems,” SIAM J. Control Optim., vol. 60, no. 2, pp. 786–813, 2022. doi: 10.1137/21M1391596. [Google Scholar] [CrossRef]

61. A. Mehmood, A. Zameer, S. H. Ling, A. U. Rehman, and M. A. Zahoor Raja, “Integrated computational intelligent paradigm for nonlinear electric circuit models using neural networks, genetic algorithms, and sequential quadratic programming,” Neural Comput. Appl., vol. 32, no. 23, pp. 10337–10357, 2020. doi: 10.1007/s00521-019-04573-3. [Google Scholar] [CrossRef]

62. G. Huang and L. Chen, “Convex incremental extreme learning machine,” Neurocomputing, vol. 70, no. 16–18, pp. 3056–3062, 2007. doi: 10.1016/j.neucom.2007.02.009. [Google Scholar] [CrossRef]

63. G. Huang and L. Chen, “Enhanced random search based incremental extreme learning machine,” Neurocomputing, vol. 71, no. 16, pp. 3460–3468, 2008. doi: 10.1016/j.neucom.2007.10.008. [Google Scholar] [CrossRef]

64. M. Li, G. Huang, P. Saratchandran, and N. Sundararajan, “Fully complex extreme learning machine,” Neurocomputing, vol. 68, no. 1–4, pp. 306–314, 2005. doi: 10.1016/j.neucom.2005.03.002. [Google Scholar] [CrossRef]

65. H. Rong, G. Huang, N. Sundararajan, and P. Saratchandran, “Online sequential fuzzy extreme learning machine for function approximation and classification problems,” IEEE Trans. Syst., Man, Cybern.: Part B: Cybern., vol. 39, no. 4, pp. 1067–1072, 2009. doi: 10.1109/TSMCB.2008.2010506. [Google Scholar] [PubMed] [CrossRef]

66. N. Liang, G. Huang, P. Saratchandran, and N. Sundararajan, “A fast and accurate online sequential learning algorithm for feedforward networks,” IEEE Trans. Neural Netw., vol. 17, no. 6, pp. 1411–1423, 2006. doi: 10.1109/TNN.2006.880583. [Google Scholar] [PubMed] [CrossRef]

67. Y. Lan, Y. Soh, and G. Huang, “Ensemble of online sequential extreme learning machine,” Neurocomputing, vol. 72, no. 13–15, pp. 3391–3395, 2009. doi: 10.1016/j.neucom.2009.02.013. [Google Scholar] [CrossRef]

68. M. Van Heeswijk et al., “Adaptive ensemble models of extreme learning machines for time series prediction,” in Lecture Notes in Computer Science, Springer, Berlin, Heidelberg, 2009, vol. 5769, pp. 305–314. doi: 10.1007/978-3-642-04277-5. [Google Scholar] [CrossRef]

69. S. K. Rath, M. Sahu, S. P. Das, and J. Pradhan, “An improved software reliability prediction model by using feature selection and extreme learning machine,” in Int. Conf. Metaheuristics Softw. Eng. Appl., Cham, Springer International Publishing, 2022, pp. 219–231. [Google Scholar]

70. W. Deng, Q. Zheng, and L. Chen, “Regularized extreme learning machine,” in IEEE Symp. Computat. Intell. Data Mining (CIDM’09), IEEE, 2009, pp. 389–395. [Google Scholar]

71. W. Deng and L. Chen, “Color image watermarking using regularized extreme learning machine,” Neural Netw. World, vol. 20, no. 3, pp. 317–330, 2010. [Google Scholar]

72. M. K. Pachariya, M. Agrawal, and C. P. Agrawal, “Artificial neural network-based approach for forecasting software reliability: An empirical study,” 2023. doi: 10.2139/ssrn.4581146. [Google Scholar] [CrossRef]

73. P. William, M. Gupta, N. Chinthamu, A. Shrivastava, I. Kumar and A. K. Rao, “Novel approach for software reliability analysis controlled with multifunctional machine learning approach,” in 2023 4th Int. Conf. Electron. Sustain. Commun. Syst. (ICESC), IEEE, 2023, pp. 1445–1450. [Google Scholar]