Software Cost Estimation Using Social Group Optimization

1  Introduction

The ability to accurately estimate the cost of developing software has become a paramount concern for project managers, stakeholders, and organizations [1–3]. Software cost estimation serves as the foundation for project planning, resource allocation, and decision-making, and its accuracy can significantly impact project success and profitability. Accurate estimation significantly enhances the efficiency and precision of software projects, encompassing aspects like resource allocation, minimizing project failures, determining the required level of reliability, tool selection, programmer proficiency, and more [4,5]. There are two types of software cost estimation techniques: algorithmic and non-algorithmic. It is standard practice to use non-algorithmic techniques like analogy-based estimating, top-down and bottom-up estimation, Parkinson’s Law, and price-to-win. Additionally, algorithmic methods include Software Engineering Laboratory (SEL), Constructive Cost Model-II (COCOMO-II), Halstead, Doty, Putnam, Baily Basil, Walston Filex Model, COCOMO, and Halstead, Doty, Putnam. One of the most used algorithms for algorithmic estimate is COCOMO-II. However, its accuracy remains an ongoing concern. To enhance the precision of this model, various algorithms have undergone rigorous investigation. The field of computational intelligence has made substantial contributions to improving software cost estimation. Particle Swarm Optimization [6], Genetic algorithm [7], Firefly algorithm [8], Differential Evolution [9] and many others have shown their capability while to estimate software cost.

One such technique that has gained prominence in recent years is the Social Group Optimization (SGO) algorithm [10]. SGO is a nature-inspired optimization algorithm inspired by the social behavior of human for solving complex problems. It leverages the collective intelligence of a group of persons to solve complex optimization problems.

Table 1 presents a summary of research contributions and published papers that have employed the SGO method, based on information gathered from the literature.

The remainder of the paper is structured as follows: Introduction is presented in Section 1, related research about the estimation of software projects is covered in Section 2. In Section 3 the proposed approach is covered. Finally, the Sections 4 and 5 describe the results analysis, conclusion, and future directions, respectively.

2  Related Work

Several estimation techniques have been applied to enhance the optimization of coefficients in the COCOMO model [40,41]. These techniques encompass PSO, GA, Tabu Search, Intelligent Water Drop (IWD) algorithms, and more. In a separate investigation [42], the cuckoo search algorithm was employed to fine-tune COCOMO-II coefficients. Experiments were conducted on 18 datasets extracted from NASA-93 software projects to validate these approaches. The results unequivocally demonstrated that the cuckoo search algorithm outperformed Baily-basil, Doty, Hallstead, and the original COCOMO-II models. Building on this research, Kumari et al. [43] proposed an innovative hybrid approach that combined cuckoo search with artificial neural networks to optimize existing COCOMO-II parameters. Additionally, a hybrid technique was introduced in the paper [44], incorporating Tabu Search and GA to optimize COCOMO-II parameters. To improve the performance of the differential evolution technique, Urbanek et al. [45] combined analytical programming and differential evolution techniques for software cost estimation. In order to improve the existing coefficients of COCOMO-II, Dalal et al. [46] presented a generalized reduced gradient nonlinear optimization approach along with best-fit analysis, reporting better results than the original COCOMO-II model.

In a different context, Santos et al. [47] introduced COCOMO-II for effort estimation, employing an organizational case study within the aeronautical industry. Their research indicated that COCOMO-II provided a more accurate estimation technique for real software projects compared to alternative approaches. Additionally, Hughes [48] reviewed expert judgment as an estimating method to calculate software project costs. Effendi et al. [49] introduced bat algorithm to optimize COCOMO-II, while Ahmad et al. [50] devised a hybrid whale-crow optimized-based optimal regression method for estimating software project costs, relying on data from four software industries. Their results indicated that the proposed model outperformed other estimation models. Sheta et al. [51] introduced a soft-computing method for software project cost estimation, utilizing PSO to optimize COCOMO coefficients and incorporating fuzzy logic to create a set of linear methods over the domain of possible software lines of code (LOC). Their algorithms were compared to baseline methods such as HS, WF, BB, and Doty models, although COCOMO-II still exhibited limitations in terms of accuracy.

Despite various works done in the past to estimate the cost using varied algorithms, methods and hybrid approach, still there remains a continuing challenge to achieve better accuracy by tuning the co-efficient of COCOMO model. In this study, we present a novel Stochastic Global Optimization (SGO) approach for optimizing COCOMO-II coefficients. To validate its effectiveness, we compare the proposed algorithm with the conventional COCOMO-II model and several other baseline methods. The simulation results underscore the superior performance of the proposed algorithm in terms of both Mean Magnitude of Relative Error (MMRE) and Mean Deviation (MD) when compared to the original COCOMO-II, PSO, GA, and other baseline models. This highlights the potentials of SGO as a promising avenue for further improving software cost estimation accuracy.

2.1 COCOMO Model

The COCOMO model, initially developed by Boehm in 1981 [52], serves as an algorithmic approach employed for estimating project costs and effort. This model comprises three layers: basic, intermediate, and detail. In 1995, Boehm et al. introduced COCOMO-II [53], a refined version of COCOMO that offers superior software project cost estimation capabilities when compared to its predecessor. Below Fig. 1 illustrates the comprehensive process of COCOMO-II.

Figure 1: COCOMO-II model

COCOMO is an algorithmic approach employed for the estimation of project costs and effort. It calculates the development effort by considering the software’s size, measured in KDSI (Thousands of Delivered Source Instructions), and software cost factors. This model’s calibration was based on data gathered from approximately 63 projects undertaken by NASA. The estimated development effort is determined according to the project’s development mode, categorized as Organic, Semi-detached, or Embedded. COCOMO Model establishes a nonlinear relationship between the project size and the estimated effort.

The formula for estimating effort (in Man Months, MM) is expressed as:

Estimated effort (MM)=a∗(KDSI)b(1)

In the Eq. (1), “a” and “b” represent constants, the values of which depend on the project’s development mode. KDSI denotes the size of the project in thousands of delivered source instructions. Table 2 provides the specific values of “a” and “b” for Organic, Semi-detached, and Embedded projects.

The COCOMO Model recognized 15 cost drivers that have the potential to influence the estimated effort required for a software project. Each of these cost drivers was allocated specific weights that could be applied to the estimated effort, determined by the rating assigned to the cost driver (ranging from very low to extra high).

2.2 COCOMO-II

COCOMO-II, introduced by Barry Boehm in 2000, represents a model that incorporates more precise enhancements in certain cost drivers. It encompasses various software attributes, including 17 Effort Multipliers (EM), 5 Scale Factors (SF), Software Size (measured in Kilo Source Lines of Code, KSLOC), and the estimated effort, all of which are utilized in the COCOMO-II Architecture Post Model. The Effort Multipliers are organized into four categories, and there are 5 Factor Scales (SF).

The formula for estimating effort (in Person-Months, PM) within the COCOMO-II model is represented by Eq. (2):

Estimated effort (PM)=a∗(SIZE)E∗∏I=117EMi(2)

Here, ‘a’ is a constant multiplier with a value of 2.94, which adjusts effort based on specific project conditions. ‘SIZE’ denotes the estimated software size in Kilo Source Lines of Code (KSLOC), and ‘E’ represents the effort’s scale expansion factor. E accounts for the exponential factor that considers the relative economies or diseconomies of scale when dealing with adjustments for the increasing size of software projects. ‘EMi’ signifies the Effort Multiplier, where i can take values from 1 to 17.

To calculate the Scale Factor, the coefficient ‘E’ is determined using Eq. (3):

E=b+0.01∗∑j=15SFj(3)

In this equation, ‘b’ is a constant exponential factor with a value of 0.91, and SFj denotes a Scale Factor, where j can take values from 1 to 5.

3  Proposed Methodology

Software project cost estimation using both COCOMO-I and COCOMO-II is involved with numerous uncertainties. In both the COCOMO models, the multiplicative constants ‘a’ and ‘b’ require optimization to enhance estimation accuracy. This study aims to optimize these constants to elevate the performance of both COCOMO-I and COCOMO-II, employing the SGO method. To assess the effectiveness of SGO-COCOMO, a comprehensive evaluation is conducted by comparing it with other optimization methods such as PSO, GA, DE, BBO, FPA, Hybrid, and various variants of DE algorithms, as well as various cost estimation models including IVR, SEL, Bailey-Basil, Doty, and Halstead [54–58]. The experiments utilize datasets from COCOMO81 and Turkish Industry software projects as input, including project size in terms of KLOC, measured effort, 17 effort multipliers, and 5 scale factors. The output of this optimization process yields new, refined values for ‘a’ and ‘b’ for the COCOMO-I and COCOMO-II models, enhancing the accuracy of cost estimation.

3.1 Fitness Function

When it comes to estimating the costs of various projects, successful completion is indicated when the predicted effort closely aligns with the actual effort. Achieving higher accuracy entails aiming for lower values of MMRE (Mean Magnitude of Relative Error) and MD (Mean Deviation). As a result, our objective is to minimize MD and MMRE, thereby reducing the disparities between the actual and predicted efforts. The fitness functions employed in our experiments are defined in Eqs. (5) and (6).

The primary objective of this estimation method is to validate the precision of predictions. It is essential to minimize the gap between the predicted effort, denoted as Estimate_efforti, and the actual effort observed in real-world conditions, represented as Actual_efforti. A significant difference between Actual_efforti and Estimate_efforti can diminish prediction accuracy and have adverse implications for software system development efforts.

To evaluate the accuracy of estimated effort, this study employs the Magnitude of Relative Error (MRE) [59], a commonly used criterion in software cost estimation. MRE is calculated for each data point according to the formula defined in Eq. (4):

MREi=|Actual_efforti−Estimate_efforti|Actual_efforti×100(4)

Eq. (5) illustrates how MMRE [59] is utilized to calculate the average value of the outcomes from each unique accuracy prediction value that was measured in the MRE criteria:

MMRE=1N∑i=1NMREi(5)

•   Reason for Selection: MMRE is widely recognized in the software engineering community due to its simplicity and effectiveness in providing a straightforward measure of estimation accuracy. It directly reflects the percentage of deviation from actual values, making it intuitive and easy to interpret.

•   Effectiveness: MMRE is particularly effective in comparing the overall accuracy of different cost estimation models, as it aggregates the relative error across all projects, giving a clear picture of the model’s general performance. However, it does have limitations, such as being sensitive to outliers and providing equal weight to overestimation and underestimation.

The Manhattan distance in Eq. (6) is used to determine the absolute gap between actual effort and estimated effort.

MD=∑i=1N|Actual_efforti−Estimate_efforti|(6)

•   Reason for Selection: MD is chosen because it provides a measure of the total error across all projects without normalizing by the actual cost. This metric is particularly useful in understanding the cumulative error, which can be important when the scale of the projects varies significantly.

•   Effectiveness: MD is effective in scenarios where the absolute error is critical, such as when budgeting for large-scale projects. It highlights the overall deviation, making it easier to assess how far off the estimates are from the actual costs in absolute terms.

3.2 SGO Algorithm

Satapathy et al. [10,55] proposed SGO in 2016. It is a stochastic-based computational algorithm known. The following is the explanation of this optimization algorithm. The SGO algorithm draws inspiration from human social dynamics to tackle complex problems. In this approach, a social group’s members represent candidate solutions, each equipped with unique attributes related to their problem-solving abilities. These individual traits correspond to the various dimensions of the problem’s design variables. The optimization process comprises two key phases: the Improving Phase and the Acquiring Phase.

Let’s denote the individuals in the social group as Pi, with i ranging from 1 to pop_size. Here, pop_size represents the number of individuals in the group, and each person, Pi, is characterized by a set of traits (pi1, pi2, pi3,…,piD) that define their dimensions. Additionally, they each have a fitness value, fi, where i ranges from 1 to pop_size.

3.2.1 Phase 1: Improving Phase

In the Improving Phase, the best-performing individual within the social group, referred to as ‘gbest,’ which actively shares knowledge with all other members, aiding in their knowledge enhancement. During this phase, each individual acquires knowledge from ‘gbest.’ The update for each individual is calculated as follows:

Pnewi=c∗Pi+r∗(gbest−Pi)(7)

Accept the new solution, Pnewi, if it leads to an improvement in fitness compared to the current solution. Here, ‘r’ is a random number sampled from a uniform distribution U (0, 1), and ‘c’ is the self-introspection parameter, constrained within the range (0, 1), with a specified value of c = 0.2.

3.2.2 Phase 2: Acquiring Phase

In the Acquiring Phase, an individual within the social group interacts with the best individual (bestP) in the group and engages in random interactions with other group members to acquire knowledge. The Acquiring Phase is expressed as follows:

   For i = 1: pop_size

        Randomly select one person Pr, where i≠r

                If f (Pi) < f (Pr)

Pnewi=Pi+r1∗(Pi−Pr)+r2∗(bestP−Pi)

               Else

Pnewi=Pi+r1∗(Pr−Pi)+r2∗(bestP−Pi)(8)

               End If

     End for

Accept Pnewi if it results in improved fitness compared to the current solution.

Here, r1, r2 are two independently sampled random values from U (0, 1). These random sequences introduce stochasticity into the algorithm.

Pseudo code for SGO-COCOMO-II algorithm is given is given below:

4  Simulation and Experimental Results

4.1 Experiment 1

In this study, we employed the SGO algorithm for software cost estimation to predict the parameters of the COCOMO model. These estimated parameters will greatly enhance the accuracy of effort estimation for a wide range of projects, including organic, semidetached, and embedded ones. We applied Algorithm 1 to compute the COCOMO model parameters as outlined in Eq. (1), and for guiding the evolutionary process of the SGO algorithm, we utilized the parameter set provided in Table 3. To evaluate the effectiveness of our model, we conducted performance tests using a dataset comprising 63 projects (organic (25) projects, semidetached (11) projects, and embedded (27) projects) from the COCOMO81 software project dataset. You can find specific dataset details in Tables A1–A3.

4.1.1 Evaluation Criteria

The evaluation criteria used to assess the accuracy of the software cost estimates generated by the proposed model are designed to align with the actual costs incurred during project development in real-world environments. Detailed information regarding the actual effort and KDSI (Thousands of Delivered Source Instructions) for all types of projects (organic, semidetached, and embedded) can be found in the A, B, C, D. Our evaluation process relies on the dataset from previously executed software projects. Specifically, we focus on the evaluation metric known as MMRE, which is defined in Eq. (5).

4.1.2 Experimental Results and Analysis

To assess the enhanced capabilities of the SGO-based model we developed, experiments were conducted using the COCOMO81 dataset. These experiments yielded parametric values of a = 2.0764 and b = 1.0706. We then compared this proposed model with existing COCOMO algorithms, including GA [6], PSO [7], Hybrid Algorithm (Hybrid Algo) [56], Differential Evolution-Based Model (DEBM) [57], DE [9], and Homeostasis Adaption Based Differential Evolution (HABDE) [58]. The discussion of results for the COCOMO81 software projects (including organic, semidetached, and embedded types) is presented below.

4.1.3 Comparison Effort for COCOMO Based Algorithms

Initially, we calculated the effort estimates obtained from Eq. (1) with the actual COCOMO81 dataset. The comparative analysis of effort levels, as presented in Tables 4–6, clearly demonstrates that our proposed model outperforms other soft computing models. In conclusion, we provide the following remarks:

•   In Table 4, we can find the results of effort estimates produced by seven algorithms for organic projects. SGO consistently outperforms other algorithms such as GA, PSO, DE, DEBM, Hybrid Algo, and HABDE in the majority of organic projects, yielding superior effort values. Likewise, as illustrated in Table 5, SGO delivers superior effort estimates for a significant portion of semi-detached projects. Additionally, Table 6 reveals that SGO excels in generating effort estimates for most embedded projects. This indicates that the effort values (expressed in person-months) derived from SGO exhibit greater diversity and convergence rates in accordance with the proposed model.

4.1.4 Comparison MMRE for COCOMO Based Algorithms

For the project under consideration, another popular error computation technique called MMRE has been utilized, and the results are shown in Table 7. The MMRE value for other compared algorithms is imported from the paper [58]. From the table it is cleared with decreased MMRE for SGO algorithm as compared with other COCOMO based algorithms and it is clearly visible through Figs. 2–4.

Figure 2: MMRE of proposed SGO, GA, PSO, DE, DEBM, HYBRID, HABDE using organic datasets

Figure 3: MMRE of proposed SGO, GA, PSO, DE, DEBM, HYBRID, HABDE using semi-detached datasets

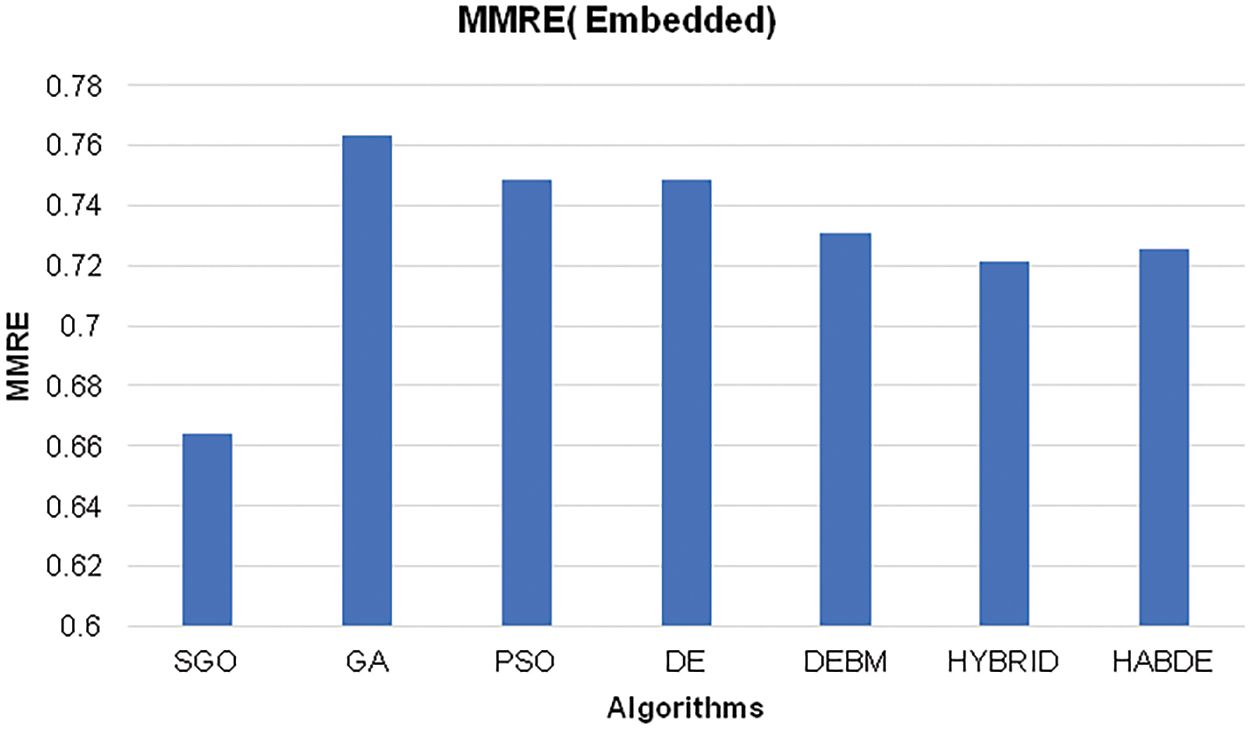
Figure 4: MMRE of proposed SGO, GA, PSO, DE, DEBM, HYBRID, HABDE using embedded datasets

4.1.5 Parameter of COCOMO Based SGO Algorithm

According to Eq. (1), the rate of convergence parameters (a and b) shows how quickly an estimating model approaches the intended value. The findings shown in Fig. 5 demonstrate that the proposed COCOMO-based SGO model has a higher rate of convergence since the SGO algorithm is capable of identifying the ideal value for parameters “a” and “b” after only 25 iterations.

Figure 5: Convergence graph for parameter ‘a’ and ‘b’

4.1.6 Discussion

We can see that the SGO algorithm improves performance more than GA, PSO, DE, Hybrid Algorithm, DEBM, and HABDE. Once more, we can observe that the SGO method can calculate a parameter’s value with less iterations. The proposed technique decreases the number of iterations and error rate. In general, existing methods’ complexity rises since they generate less diversity.

4.2 Experiment 2

In this experiment, we employed the SGO algorithm for software cost estimation to fine-tune the parameters of the COCOMO-II model. Algorithm 1 was executed to estimate the COCOMO-II model parameters, as detailed in Eq. (2). We maintained consistency by utilizing the same set of parameters as in Experiment 1 to guide the evolutionary process of the SGO algorithm. To evaluate the performance of our developed model, we conducted tests using a latest dataset from the Turkish Software Industry. This dataset comprises information from five distinct software companies across various domains, encompassing data from a total of 12 projects. Each project is characterized by 25 attributes, including Project ID, 5 Scale Factors, 17 Effort Multipliers ranging from Very Low to Extra High, Measured Effort as the actual effort, and Project Size measured in KLOC. You can find specific dataset details in Table A4. All project data points were employed for calibration, and the results obtained from this calibration can serve as valuable insights for future projects within a similar category.

4.2.1 Evaluation Criteria

The evaluation criteria employed for assessing the accuracy of software cost estimates in the proposed model are designed to align with the actual costs incurred during real-world project development under live environmental conditions. For Experiment 2, two key evaluation criteria are used: MMRE (Mean Magnitude of Relative Error) and MD (Absolute Difference).

4.2.2 Experimental Results and Analysis

This section describes the experiment and the outcomes that were attained after applying the suggested method to the dataset. The primary goal of the optimization is to use the SGO approach to minimize uncertain parameters from a COCOMO-II model’s coefficients (‘a’ and ‘b’), and then compare the new findings to those from the general Tabu Search [60] and PSO Method [2] coefficients.

The Fig. 6 illustrates the convergence process of SGO over multiple iterations with varying population sizes. Populations of 10, 20, 30, 40, and 50 were examined to evaluate the process’s performance. Remarkably, each experiment involving SGO exhibited the same minimum error during convergence. After several iterations, we successfully obtained newly optimized coefficient values: a = 4.3950 and b = −0.1834, which differ from the original COCOMO-II values of a = 2.94 and b = 0.91. The results, calculated using these newly optimized coefficient values for effort, are presented in Table 8. Additionally, we imported results for COCOMO-II, Tabu Search, and PSO from paper [2] for comparison. The Fig. 7 displays the effort graph, demonstrating that SGO yields smoother and more accurate effort estimates when compared to efforts estimated using the basic COCOMO-II coefficients, Tabu Search, and the PSO Method.

Figure 6: Best cost of MMRE with various population sizes, population size 10, 20, 30, 40, and 50

Figure 7: Effort graph for actual effort, COCOMO-II, Tabu, PSO and SGO

The results plotted in Fig. 8 which show that the proposed COCOMO based SGO model has better convergence rate as within 20 iteration SGO algorithm able to determine the best value for parameter ‘a’ and ‘b’.

Figure 8: Convergence graph for parameters ‘a’ and ‘b’ in case of COCOMO-II based SGO model

The accuracy of the experiment is evaluated using fitness functions outlined in Eqs. (5) and (6). The experimental results are presented in Table 9, providing estimated effort values for all the compared algorithms. Notably, for Project Nos. 2, 8, and 11 with actual efforts of 2, 5, and 1, respectively, the proposed SGO method yielded highly accurate estimates of 2, 5, and 0.9789. This indicates a substantial reduction in error, with improvements of 0.00%, 0.00%, and 2.11%, respectively.

MMRE for each methodology signifies its overall accuracy. The MMRE values for the COCOMO-II model, Tabu Search, PSO, and SGO stand at 733.1400, 139.0699, 34.1939, and 34.1922, respectively. These values signify that SGO reduces errors significantly, by 698.9494% compared to the COCOMO-II model, 104.8793% compared to Tabu Search, and 0.0033% compared to PSO. Similarly, when examining MD (Absolute Difference), COCOMO-II exhibits an MD of 585.9266%, Tabu Search has an MD of 90.5797%, PSO has an MD of 43.2477%, and SGO has an MD of 43.2508%. These figures demonstrate that SGO can reduce errors by the value 542.68% compared to COCOMO-II, 47.3310% compared to Tabu Search, and 0.0011% compared to PSO, as presented in Table 7 and Fig. 6. In summary, the results for MMRE and MD indicate that the effort estimation provided by the proposed SGO method offers a significantly improved solution when compared to the COCOMO-II model, Tabu Search, and the PSO method, as illustrated in Fig. 9.

Figure 9: Comparison of MMRE and MD (in %) for COCOMO-II, Tabu Search, PSO, and SGO

4.2.3 Discussion

In this experiment, we investigated the effectiveness of employing the SGO method to optimize the parameters of the COCOMO-II model, aiming to enhance its accuracy. The SGO method was applied using the Turkish Software Industry dataset, and its performance was rigorously evaluated. The evaluation results clearly demonstrate the superiority of SGO, with a remarkable 698.9494% reduction in MMRE and a substantial 542.68% decrease in MD compared to the standard COCOMO-II model coefficient parameters. Furthermore, SGO outperforms Tabu Search with a 104.8793% lower MMRE and a 47.3310% lower MD, while it achieves an almost negligible 0.0033% MMRE and 0.0011% MD reduction compared to the PSO model. Overall, optimizing the parameters of the COCOMO-II model with the SGO method significantly enhances estimation accuracy when compared to the basic COCOMO-II model.

4.3 Experiment 3

This experiment is identical to Experiment 2, with the sole distinction being the comparison of the SGO algorithm’s performance against BBO-COCOMO-II, PSO, GA, IVR, SEL, Bailey-Basil, Doty, Halstead and PPF (Past Present Future) algorithm [61,62].

4.3.1 Experimental Results and Analysis

The value of parameters ‘a’ and ‘b’ for our proposed SGO algorithm and some other methods is given in Table 10. The Table 11 presents the Magnitude of Relative Errors for estimates obtained using SGO, COCOMO-II, and other models applied to Turkish Industry software projects. Meanwhile, Table 12 provides a comparative analysis of MMRE (mean MMRE) and MD (Manhattan distance) for the proposed SGO, BBO, PSO, GA, PPF and several other models using datasets from the Turkish Industry. For our proposed SGO, experiment is carried out by using MATLAB, while for other models are reported from the paper [48].

Above Figs. 10 and 11 depict the comparisons of MMRE and MD between the proposed SGO method, PPF, BBO, and various other cost estimation techniques applied to Turkish Industry software projects, respectively.

Figure 10: MMRE for proposed SGO, PPF, BBO, PSO, GA, COCOMO-II and others models using Turkish industry datasets

Figure 11: MD for proposed SGO, PPF, BBO, PSO, GA, COCOMO-II and others models using Turkish industry datasets

4.3.2 Discussion

In this experiment, the SGO-based algorithm was employed to optimize the existing parameters of COCOMO-II. The proposed SGO method was rigorously assessed using datasets from the Turkish Industry’s software projects. The simulation results clearly demonstrate the superior performance of the proposed SGO-based approach compared to conventional COCOMO-II, as well as other methods such as BBO, PSO, GA, PPF, and FPA, along with various other cost estimation techniques.

4.4 Scalability, Applicability, Limitations and Challenges of SGO-Based Approach

4.4.1 Scalability and Applicability

While the SGO-based approach has demonstrated significant improvements in software cost estimation accuracy, it is essential to consider its scalability across different types and sizes of software projects. Our experiments primarily focused on datasets like COCOMO81 and Turkish industry projects, which provided a strong foundation for validating the method. However, further investigation is needed to assess how well the SGO algorithm adapts to larger, more complex projects or those in diverse industry domains.

The adaptability of SGO to various project sizes is promising, but it may require adjustments or fine-tuning when applied to very large-scale or small-scale projects. The computational overhead associated with SGO could be a concern in scenarios where projects involve massive datasets or require real-time estimation. This is an area where balancing accuracy and computational efficiency will be crucial.

4.4.2 Limitations and Challenges

Generalizing the SGO-based approach presents several challenges. One potential limitation is the dependency on the quality and quantity of historical data used for training. In environments where historical data is scarce or of poor quality, the effectiveness of the SGO algorithm might be compromised. Additionally, while SGO has shown superiority over other optimization techniques, its performance may vary depending on the specific characteristics of the software project, such as the development methodology, team structure, and project complexity.

Furthermore, the need for fine-tuning the SGO parameters for different types of projects could limit its immediate applicability, requiring domain expertise and iterative experimentation to achieve optimal results. These challenges highlight the importance of ongoing research to refine and adapt the SGO-based method for broader use cases.

5  Conclusion

In this study, we introduced the Social Group Optimization (SGO) algorithm to optimize the parameters of the COCOMO and COCOMO-II models. Testing on COCOMO81 and Turkish Industry software projects showed that SGO outperformed conventional approaches, including COCOMO-II and other optimization algorithms like PSO, GA, BBO, and PPF. The results highlight SGO’s effectiveness in improving software cost estimation accuracy.

Looking ahead, we plan to apply evolutionary algorithms to optimize not only COCOMO coefficients but also those of the Constructive Quality Estimation Model (CQEM). This will lead to a more comprehensive framework for both cost and quality estimation, enhancing project planning and resource allocation. Further, we explore the integration of SGO with other optimization techniques, such as hybrid algorithms or machine learning models, to further enhance its performance and adaptability in complex environments.

In conclusion, the success of SGO in this study underscores its potential as a valuable tool for software cost estimation, paving the way for more accurate and cost-effective software development.

Acknowledgement: The authors thank all the faculty and co-scholars of KIIT Deemed to be University, Bhubaneswar, India. Their goal is to provide a comfortable place to work. They have given us permission to utilize any and all resources at our service to fulfill our contribution’s objective.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Sagiraju Srinadhraju: Study conception and design, Data collection, Analysis and interpretation of results, Draft manuscript preparation; Samaresh Mishra, Sagiraju Srinadhraju: Data collection, Analysis and interpretation of results; Suresh Chandra Satapathy: Analysis and interpretation of results, Draft manuscript preparation. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors. The data that support the findings of this study are available from the corresponding author, Sagiraju Srinadhraju, upon reasonable request. Datasets used in this research are taken from the below URLs:

• http://promise.site.uottawa.ca/SERepository/datasets-page.html (accessed on 01 May 2024)

• https://openscience.us/repo/effort/cocomo/cocomosdr.html (accessed on 01 May 2024)

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. D. Nandal and O. Sangwan, “Software cost estimation by optimizing COCOMO model using hybrid BATGSA algorithm,” Int. J. Intell. Eng. Syst., vol. 11, no. 4, pp. 250–263, Aug. 2018. doi: 10.22266/ijies2018.0831.25. [Google Scholar] [CrossRef]

2. K. Langsari, R. Sarno, and S. Sholiq, “Optimizing effort parameter of COCOMO-II using particle swarm optimization method,” Telkomnika (Telecommun. Comput. Electron. Control), vol. 16, no. 5, pp. 2208–2216, Oct. 2018. doi: 10.12928/telkomnika.v16i5.9703. [Google Scholar] [CrossRef]

3. A. Ullah, B. Wang, J. Sheng, J. Long, M. Asim and F. Riaz, “A novel technique of software cost estimation using flower pollination algorithm,” in 2019 Int. Conf. Intell. Comput. Automat. Syst. (ICICAS), Chongqing, China, 2019, pp. 654–658. doi: 10.1109/icicas48597.2019.00142. [Google Scholar] [CrossRef]

4. A. Trendowicz and R. Jeffery, “Constructive cost model–COCOMO,” in Software Project Effort Estimation: Foundations and Best Practice Guidelines for Success. India: Springer Nature, 2014, pp. 277–293. [Google Scholar]

5. A. Salam, A. Khan, and S. Baseer, “A comparative study for software cost estimation using COCOMO-II & Walston-Felix models,” in 1st Int. Conf. Innov. Comput. Sci. Softw. Eng. (ICONICS 2016), 2016, pp. 15–16. [Google Scholar]

6. F. S. Gharehchopogh and A. Pourali, “A new approach based on continuous genetic algorithm in software cost estimation,” J. Sci. Res. Dev., vol. 2, no. 4, pp. 87–94, 2015. [Google Scholar]

7. F. S. Gharehchopogh, I. Maleki, and S. R. Khaze, “A novel particle swarm optimization approach for software effort estimation,” Int. J. Acad. Res., vol. 6, no. 2, pp. 69–76, Mar. 2014. doi: 10.7813/2075-4124.2014/6-2/a.12 [Google Scholar] [CrossRef]

8. N. Ghatasheh, H. Faris, I. Aljarah, and R. M. H. Al-Sayyed, “Optimizing software effort estimation models using firefly algorithm,” J. Softw. Eng. Appl., vol. 8, no. 3, pp. 133–142, Mar. 2015. doi: 10.4236/jsea.2015.83014. [Google Scholar] [CrossRef]

9. P. Singal, A. C. Kumari, and P. Sharma, “Estimation of software development effort: A differential evolution approach,” Procedia Comput. Sci., vol. 167, pp. 2643–2652, Jan. 2020. doi: 10.1016/j.procs.2020.03.343. [Google Scholar] [CrossRef]

10. S. Satapathy and A. Naik, “Social Group Optimization (SGOA new population evolutionary optimization technique,” Complex Intell. Syst., vol. 2, pp. 173–203, 2016. doi: 10.1007/s40747-016-0022-8. [Google Scholar] [CrossRef]

11. S. Das, P. Saha, S. C. Satapathy, and J. J. Jena, “Social group optimization algorithm for civil engineering structural health monitoring,” Eng. Optim., vol. 53, no. 10, pp. 1651–1670, 2021. doi: 10.1080/0305215X.2020.1808974. [Google Scholar] [CrossRef]

12. A. Naik, S. C. Satapathy, A. S. Ashour, and N. Dey, “Social group optimization for global optimization of multimodal functions & data clustering problems,” Neural Comput. Appl., vol. 30, no. 1, pp. 271–287, 2018. doi: 10.1007/s00521-016-2686-9. [Google Scholar] [CrossRef]

13. S. Rani and B. Suri, “Adopting social group optimization algorithm using mutation testing for test suite generation: SGO-MT,” in Computat. Sci. Apps.– ICCSA 2019, Springer, Cham, 2019, pp. 520–528. [Google Scholar]

14. S. Verma, J. J. Jena, S. C. Satapathy, and M. Rout, “Solving travelling salesman problem using discreet social group optimization,” J. Sci. Ind. Res., vol. 79, no. 10, pp. 928–930, 2020. [Google Scholar]

15. A. Naik and P. K. Chokkalingam, “Binary social group optimization algorithm for solving 0–1 Knapsack problem,” Decis. Sci. Lett., vol. 11, no. 1, pp. 55–72, 2022. doi: 10.5267/j.dsl.2021.8.004. [Google Scholar] [CrossRef]

16. A. Naik, S. C. Satapathy, and A. Abraham, “Modified social group optimization: A meta-heuristic algorithm to solve short-term hydrothermal scheduling,” Appl. Soft Comput., vol. 95, 2020, Art. no. 106524. doi: 10.1016/j.asoc.2020.106524. [Google Scholar] [CrossRef]

17. R. Monisha, R. Mrinalini, M. N. Britto, R. Ramakrishnan, and V. Rajinikanth, “Social group optimization & Shannon’s function-based RGB image multi-level thresholding,” Smart Intell. Comput. Appl., vol. 105, pp. 123–132, 2019. doi: 10.1007/978-981-13-1927-3. [Google Scholar] [CrossRef]

18. A. Reddy and K. V. L. Narayana, “Investigation of a multi-strategy ensemble social group optimization algorithm for the optimization of energy management in electric vehicles,” IEEE Access, vol. 10, pp. 12084–12124, 2022. doi: 10.1109/ACCESS.2022.3144065. [Google Scholar] [CrossRef]

19. K. S. Manic, N. Al Shibli, and R. Al Sulaimi, “SGO & Tsallis entropy assisted segmentation of abnormal regions from brain MRI,” J. Eng. Sci. Tech., vol. 13, pp. 52–62, 2018. [Google Scholar]

20. P. Parwekar, “SGO: A new approach for energy efficient clustering in WSN,” Int. J. Nat. Comput. Res., vol. 7, no. 3, pp. 54–72, 2018. doi: 10.4018/IJNCR. [Google Scholar] [CrossRef]

21. N. Dey, V. Rajinikanth, S. J. Fong, M. S. Kaiser, and M. Mahmud, “Social group optimization-assisted Kapur’s entropy & morphological segmentation for automated detection of COVID-19 infection from computed tomography images,” Cogn. Comput., vol. 12, pp. 1011–1023, 2020. doi: 10.1007/s12559-020-09751-3. [Google Scholar] [PubMed] [CrossRef]

22. A. K. Singh, A. Kumar, M. Mahmud, M. S. Kaiser, and A. Kishore, “COVID-19 infection detection from chest X-ray images using hybrid social group optimization & support vector classifier,” Cogn. Comput., vol. 16, pp. 1765–1777, 2024. doi: 10.1007/s12559-021-09848-3. [Google Scholar] [PubMed] [CrossRef]

23. N. Dey, V. Rajinikanth, A. Ashour, and J. M. Tavares, “Social group optimization supported segmentation & evaluation of skin melanoma images,” Symmetry, vol. 10, no. 2, 2018, Art. no. 51. doi: 10.3390/sym10020051. [Google Scholar] [CrossRef]

24. M. A. M. Akhtar, A. K. Manna, and A. K. Bhunia, “Optimization of a non-instantaneous deteriorating inventory problem with time & price dependent demand over finite time horizon via hybrid DESGO algorithm,” Exp. Sys. Apps., vol. 211, 2023, Art. no. 118676. doi: 10.1016/j.eswa.2022.118676. [Google Scholar] [CrossRef]

25. V. K. R. A. Kalananda and V. L. N. Komanapalli, “A combinatorial social group whale optimization algorithm for numerical & engineering optimization problems,” Appl. Soft Comput., vol. 99, 2021, Art. no. 106903. doi: 10.1016/j.asoc.2020.106903. [Google Scholar] [CrossRef]

26. V. K. R. A. Kalananda and V. L. N. Komanapalli, “Investigation of a social group assisted differential evolution for the optimal PV parameter extraction of standard & modified diode models,” Energy Conv. Manage., vol. 268, 2022, Art. no. 115955. doi: 10.1016/j.enconman.2022.115955. [Google Scholar] [CrossRef]

27. S. P. Praveen, K. T. Rao, and B. Janakiramaiah, “Effective allocation of resources & task scheduling in cloud environment using social group optimization,” Arab. J. Sci. Eng., vol. 43, pp. 4265–4272, 2018. doi: 10.1007/s13369-017-2926-z. [Google Scholar] [CrossRef]

28. H. Kraiem et al., “Parameters identification of photovoltaic cell & module models using modified social group optimization algorithm,” Sustainability, vol. 15, no. 13, 2023, Art. no. 10510. doi: 10.3390/su151310510. [Google Scholar] [CrossRef]

29. D. C. Secui, C. Hora, C. Bendea, M. L. Secui, G. Bendea and F. C. Dan, “Modified social group optimization to solve the problem of economic emission dispatch with the incorporation of wind power,” Sustainability, vol. 16, no. 1, 2024, Art. no. 397. doi: 10.3390/su16010397. [Google Scholar] [CrossRef]

30. D. H. Tran, “Optimizing time-cost in generalized construction projects using multiple-objective social group optimization & multi-criteria decision-making methods,” Eng. Const. Arch. Manage., vol. 27, no. 9, pp. 2287–2313, 2020. doi: 10.1108/ECAM-08-2019-0412. [Google Scholar] [CrossRef]

31. K. Ullah, A. Basit, Z. Ullah, F. R. Albogamy, and G. Hafeez, “A transformer fault diagnosis method based on a hybrid improved social group optimization algorithm & elman neural network,” Energies, vol. 15, no. 5, 2022, Art. no. 1771. doi: 10.3390/en15051771. [Google Scholar] [CrossRef]

32. V. -H. Huynh, T. -H. Nguyen, H. C. Pham, T. -M. -D. Huynh, T. -C. Nguyen and D. -H. Tran, “Multiple objective social group optimization for time-cost–quality-carbon dioxide in generalized construction projects,” Int. J. Civil Eng., vol. 19, pp. 805–822, 2021. doi: 10.1007/s40999-020-00581-w. [Google Scholar] [CrossRef]

33. A. Naik, “Marine predators social group optimization: A hybrid approach,” Evol. Intell., vol. 17, pp. 2355–2386, 2024. doi: 10.1007/s12065-023-00891-7. [Google Scholar] [CrossRef]

34. S. Vadivel, B. C. Sengodan, S. Ramasamy, M. Ahsan, J. Haider and E. M. G. Rodrigues, “Social grouping algorithm aided maximum power point tracking scheme for partial shaded photovoltaic array,” Energies, vol. 15, no. 6, 2022, Art. no. 2105. doi: 10.3390/en15062105. [Google Scholar] [CrossRef]

35. C. Wang et al., “Dual-population social group optimization algorithm based on human social group behavior law,” IEEE Trans. Comput. Soc. Syst., vol. 10, no. 1, pp. 166–177, Feb. 2023. doi: 10.1109/TCSS.2022.3141114. [Google Scholar] [CrossRef]

36. A. Naik, “Multi-objective social group optimization for machining process,” Evol. Intell., vol. 17, pp. 1655–1676, 2024. doi: 10.1007/s12065-023-00856-w. [Google Scholar] [CrossRef]

37. M. T. Tran, H. A. Pham, V. L. Nguyen, and A. T. Trinh, “Optimisation of stiffeners for maximum fundamental frequency of cross-ply laminated cylindrical panels using social group optimisation & smeared stiffener method,” Thin-Walled Struct., vol. 120, pp. 172–179, 2017. doi: 10.1016/j.tws.2017.08.033. [Google Scholar] [CrossRef]

38. P. Garg and R. K. Rama Kishore, “A robust & secured adaptive image watermarking using social group optimization,” Vis. Comput., vol. 39, pp. 4839–4854, 2023. doi: 10.1007/s00371-022-02631-x. [Google Scholar] [CrossRef]

39. S. M. A. Rahaman, M. Azharuddin, and P. Kuila, “Efficient scheduling of charger-UAV in wireless rechargeable sensor networks: Social group optimization based approach,” J. Netw. Syst. Manage., vol. 32, 2024, Art. no. 55. doi: 10.1007/s10922-024-09833-9. [Google Scholar] [CrossRef]

40. W. Zhang, Y. Yang, and Q. Wang, “A study on software effort prediction using machine learning techniques,” Comm. Comp. Info. Sci., vol. 275, pp. 1–15, 2013. doi: 10.1007/978-3-642-32341-6. [Google Scholar] [CrossRef]

41. M. Grover, P. K. Bhatia, and H. Mittal, “Estimating software test effort based on revised UCP model using fuzzy technique,” Smart. Innov. Syst. Tech., vol. 83, pp. 490–498, 2017. doi: 10.1007/978-3-319-63673-3_59. [Google Scholar] [CrossRef]

42. S. Kumari and S. Pushkar, “Software cost estimation using cuckoo search,” Adv. Intell. Syst. Comput., pp. 167–175, Nov. 2016. doi: 10.1007/978-981-10-2525-9_17. [Google Scholar] [CrossRef]

43. S. Kumari and S. Pushkar, “Cuckoo search based hybrid models for improving the accuracy of software effort estimation,” Microsys. Tech., vol. 24, no. 12, pp. 4767–4774, Apr. 2018. doi: 10.1007/s00542-018-3871-9. [Google Scholar] [CrossRef]

44. F. S. Gharehchopogh, R. Rezaii, and B. Arasteh, “A new approach by using Tabu search and genetic algorithms in software cost estimation,” in 9th Int. Conf. App. Inf. Commun. Tech., 2015, pp. 113–117. doi: 10.1109/ICAict.2015.7338528. [Google Scholar] [CrossRef]

45. T. Urbanek, Z. Prokopova, R. Silhavy, and A. Kuncar, “Using analytical programming for software effort estimation,” Adv. Intell. Syst. Comput., pp. 261–272, 2016. doi: 10.1007/978-3-319-33622-0_24. [Google Scholar] [CrossRef]

46. S. Dalal, N. Dahiya, and V. Jaglan, “Efficient tuning of COCOMO model cost drivers through Generalized Reduced Gradient (GRG) nonlinear optimization with best-fit analysis,” in Adv. Comput. Intell. Eng., Springer, 2018, pp. 347–354. [Google Scholar]

47. L. P. D. Santos and M. G. V. Ferreira, “Safety critical software effort estimation using COCOMO II: A case study in aeronautical industry,” Revista IEEE Am. Lat., vol. 16, no. 7, pp. 2069–2078, Jul. 2018. doi: 10.1109/tla.2018.8447378. [Google Scholar] [CrossRef]

48. R. T. Hughes, “Expert judgement as an estimating method,” Inf. Softw. Tech., vol. 38, no. 2, pp. 67–75, Jan. 1996. doi: 10.1016/0950-5849(95)01045-9. [Google Scholar] [CrossRef]

49. Y. A. Effendi, R. Sarno, and J. Prasetyo, “Implementation of bat algorithm for COCOMO II optimization,” Int. Sem. App. Tech. Inf. Commun., pp. 441–446, 2018. doi: 10.1109/isemantic.2018.8549699. [Google Scholar] [CrossRef]

50. S. W. Ahmad and G. R. Bamnote, “Whale-Crow Optimization (WCO)-based optimal regression model for software cost estimation,” Sadhana, vol. 44, no. 4, Mar. 2019, Art. no. 94. doi: 10.1007/s12046-019-1085-1. [Google Scholar] [CrossRef]

51. A. Sheta, D. Rine, and A. Ayesh, “Development of software effort and schedule estimation models using soft computing techniques,” in 2008 IEEE Cong. Evolutiona. Computati. (IEEE World Cong. Computation. Intelligen.), 2008, vol. 43, pp. 1283–1289. doi: 10.1109/cec.2008.4630961. [Google Scholar] [CrossRef]

52. B. W. Boehm, Software Engineering Economics. Englewood Cliffs, NJ: Prentice-Hall, 1981. [Google Scholar]

53. B. Boehm, B. Clark, E. Horowitz, C. Westland, R. Madachy and R. Selby, “Cost models for future software life cycle processes: COCOMO 2.0,” Ann. SE, vol. 1, no. 1, pp. 57–94, Dec. 1995. doi: 10.1007/bf02249046. [Google Scholar] [CrossRef]

54. Srivastava and D. Devesh, “VRS model: A model for estimation of efforts and time duration in development of IVR software system,” Int. J. SE, vol. 5, no. 1, pp. 27–46, 2012. [Google Scholar]

55. A. Naik, “Chaotic social group optimization for structural engineering design problems,” J. Bionic. Eng., vol. 20, no. 4, pp. 1852–1877, Feb. 2023. doi: 10.1007/s42235-023-00340-2. [Google Scholar] [CrossRef]

56. M. Hasanluo and F. S. Gharehchopogh, “Software cost estimation by a new hybrid model of particle swarm optimization and K-nearest neighbor algorithms,” J. Electr. Comput. Eng. Innov., vol. 4, no. 1, pp. 49–55, Jan. 2016. doi: 10.22061/jecei.2016.556. [Google Scholar] [CrossRef]

57. A. K. Bardsiri and S. M. Hashemi, “A differential evolution-based model to estimate the software services development effort,” J. Softw., vol. 28, no. 1, pp. 57–77, Dec. 2015. doi: 10.1002/smr.1765. [Google Scholar] [CrossRef]

58. S. P. Singh, V. P. Singh, and A. K. Mehta, “Differential evolution using homeostasis adaption based mutation operator & its application for software cost estimation,” J. King Saudi Univ.-Com. Info. Sci., vol. 33, no. 6, pp. 740–752, Jul. 2021. doi: 10.1016/j.jksuci.2018.05.009. [Google Scholar] [CrossRef]

59. K. Dejaeger, W. Verbeke, D. Martens, and B. Baesens, “Data mining techniques for software effort estimation: A comparative study,” IEEE Trans. SE, vol. 38, no. 2, pp. 375–397, Mar. 2012. doi: 10.1109/TSE.2011.55. [Google Scholar] [CrossRef]

60. R. Chadha and S. Nagpal, “Optimization of COCOMOII model coefficients using Tabu search,” Int. J. CS IT, vol. 3, no. 8, pp. 4463–4465, 2014. [Google Scholar]

61. A. Ullah, B. Wang, J. Sheng, J. Long, M. Asim and Z. Sun, “Optimization of software cost estimation model based on biogeography-based optimization algorithm,” Int. Decis. Tech., vol. 14, no. 4, pp. 441–448, Jan. 2021. doi: 10.3233/IDT-200103. [Google Scholar] [CrossRef]

62. S. Srinadhraju, S. Mishra, and S. C. Satapathy, “Optimization of software cost estimation model based on present past future algorithm,” in 8th Int. Conf. Inf. Syst. Dgn. Int. App., Dec. 2024, vol. 3. [Google Scholar]

Appendix A