Performance-Oriented Layout Synthesis for Quantum Computing

1  Introduction

Quantum algorithms use the power of quantum superposition states to process multiple qubit states simultaneously, making them more advantageous and efficient compared to traditional algorithms [1,2]. Consequently, quantum computing is poised to become a major trend in the future. However, realizing the full potential of quantum computing requires robust electronic design automation (EDA) systems tailored for quantum circuits.

Fig. 1 shows the architecture diagram of quantum computing Electronic Design Automation (EDA). Before implementing a quantum algorithm, quantum gates used in the algorithm must be represented in a gate library—a process known as logic synthesis. The output of logic synthesis is a series of quantum gates ready for implementation. Subsequently, these gates need to be mapped onto qubits within the quantum computer architecture, and their execution schedule must be determined—a task known as layout synthesis. For typical quantum circuits, the number of possible initial mappings can grow exponentially with the number of logic gates [3], highlighting the necessity of advanced EDA systems.

Figure 1: The architecture diagram of quantum computing Electronic Design Automation (EDA)

Layout synthesis aims to generate mappings that adhere to device constraints while realizing the circuit’s functionality. Typically, commutation optimizations are considered part of logic synthesis. To refine layout synthesis, it is assumed that exchange-based optimizations have been pre-implemented, focusing on basic exchange rules with less emphasis on dependencies that dictate gate order. This approach often involves rearranging phase gates to accommodate two-qubit gates acting on the same qubit, albeit such gates are infrequent in existing quantum circuits.

Existing research in layout synthesis evaluates solutions based on cost, which correlates with the degree of optimization applied and additional gate count [4–6]. Current practices often involve running circuits multiple times and analyzing statistical data to refine layouts [7–9]. From a solution perspective, approaches can be categorized into two main groups: references [10,11] focus on exact solutions using solvers for medium-sized instances, while references [12,13] employ pseudo-Boolean optimization for legalizing two-qubit gates without explicit gate scheduling. Others leverage mixed integer programming (MIP) and satisfiability modulo theories (SMT) solvers [14], time planners for quantum approximate optimization algorithms [15], and fidelity maximization using SMT solvers [16]. Approaches in quantum circuit layout synthesis vary in their methods and effectiveness. For instance, reference [17] divides circuits into levels and inserts gates within these levels to facilitate mappings between them, though these models may not always achieve optimal solutions. Conversely, references [18–20] adopt a strategy of breaking circuits into smaller sub-circuits (or levels), optimizing layout synthesis by transforming mappings between these components. In specific methods, such as those detailed by [21], swap gates are strategically inserted to move required qubits for subsequent two-qubit gates along the shortest path. Similarly, references [22,23] consider distances between qubits involved in other two-qubit gates, while reference [24] emphasizes fidelity in qubit movement. Some approaches, like [25], employ a cost function combining distances and swap gate counts in an A* search, whereas reference [26] utilizes bidirectional search.

The complexity inherent in evaluating these solutions poses significant challenges. Current benchmark tests typically employ quantum circuit libraries [27], containing real-world functionalities. However, researchers can currently only compare methodologies with each other, lacking a definitive measure of how close these solutions are to optimal. Layout synthesis is crucial in quantum computing as it addresses the challenge of designing quantum circuits that adhere to device-specific layout constraints. In our paper, we have developed a benchmark for quantum computing layout synthesis aimed at evaluating optimal circuit depth and gate count. Our goal is to propose a quantum computing layout synthesis algorithm focused on optimizing circuit depth while ensuring fidelity is maintained.

The remainder of this paper is organized as follows: Section 2 describes the terminology and problem formulation related to quantum computing layout synthesis. Section 3 presents the detailed methodology of our proposed algorithm for quantum computing layout synthesis. Section 4 discusses the experimental results obtained from applying our algorithm, providing insights into its performance. Finally, Section 5 presents the conclusions drawn from this study, summarizing the findings and outlining potential future research directions.

2  Terminology and Problem Formulation

We use Quantum Assembly Language (QASM) similar to traditional assembly language to input a quantum circuit [21]. In this way, a quantum logic gate (or simply quantum gate), represented as g1, g2,..., gM, is a basic quantum circuit operating on a small number of qubits represented as q1,..., qN. where M indicates the number of gates and N indicates the number of quantum bits. For example, in a quantum circuit diagram shown in Fig. 2, N = 3, M = 15. In this diagram, each line represents a quantum bit. The gates on the same horizontal line are executed from left to right but on vertical lines do not indicate a specific time order of execution. For instance, gates g8 and g9 can be executed simultaneously. Additionally, if g is a single-qubit gate, |g| = 1; if g is a two-qubit gate, |g| = 2. In Fig. 2, g1 ∪ g2 represents a set of quantum bits containing g1 or g2, and g1 ∈ g2 represents a set of quantum bits containing both g1 and g2. In Fig. 2, q1, q2 ∈ g2, |g6| = 2, |g7| = 1, g1 ∈ g2 = {q2}, g8 ∪ g9 = {q0, q1, q2}. The controlled gates CX represented as • with the target quantum bit depicted as ⊕ act on 2 or more qubits for some operation in Fig. 2.

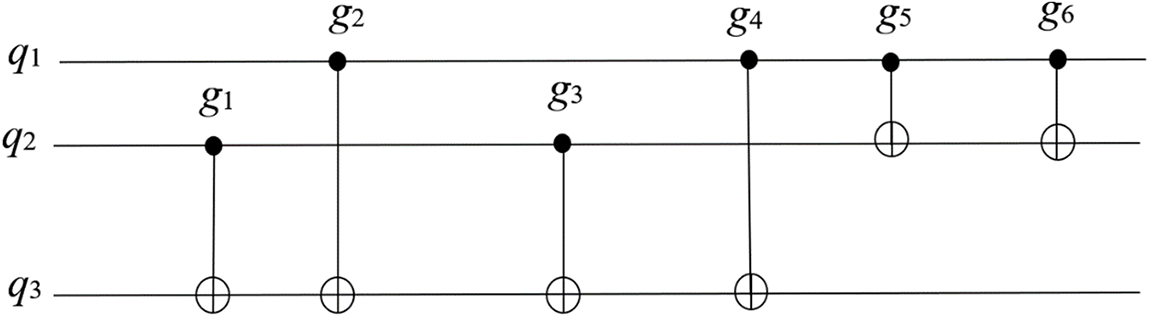
Figure 2: An example of a quantum circuit diagram

We use a graph G = (V, E) to represent the layout of a quantum computing device, where each node v represents a quantum bit and each edge e represents a connection. This graph specifies how physical quantum bits are interconnected. Fig. 3 illustrates an example of such a graph represented the layout of a quantum computing device. Layout synthesis in quantum computing involves two primary tasks: placement and scheduling. A physical qubit is a tangible unit that operates as a two-state quantum system within a computer setup. A logical qubit, whether physical or conceptual, functions according to predefined quantum algorithms or circuits, enduring sufficiently long coherence times to facilitate utilization by quantum logic gates [28]. The placement task focuses on mapping logical qubits to physical qubits, as illustrated in Fig. 4.

Figure 3: An example of a graph represented the layout of a quantum computing device

Figure 4: A placement example of the quantum computing

Each two-qubit gate requires physical qubits that are interconnected in the quantum graph. The designers typically assume all logical qubits have full connectivity but it isn’t always the case in many quantum computing architectures. When logical qubits mapped to a two-qubit gate are placed on physically disconnected qubits, it renders the gate inexecutable. To solve this problem, the two-qubit swap gates are introduced to establish the necessary connectivity between these physical qubits. The swap gate is a gate in quantum computing that swaps the states of two qubits. The swap gate is extremely useful in hardware settings; if two qubits are not physically connected, we can swap one of those qubits with another that is physically connected to the other qubit. However, deploying these swap gates is constrained by the quantum device layout, potentially increasing gate depth and error rates. In quantum computing, circuit depth refers to the maximum time coordinate after layout synthesis, which directly impacts the stability and efficiency of quantum operations. Given the current limitations of quantum computers, where physical qubits can operate reliably only for a limited duration, minimizing circuit depth becomes critical to ensure the stable operation of qubits. In Fig. 5a, the circuit exhibits a non-optimized depth configuration, potentially leading to increased operational time and greater susceptibility to errors. Conversely, Fig. 5b illustrates an optimized depth configuration, where operations are structured to minimize the overall circuit depth. The layout synthesis can yield quantum circuits with various compositions of gates, resulting in different depths. It is advisable to select the optimized depth configuration when multiple compositions achieve the same functionality. This approach maximizes the efficiency of quantum operations, reduces the risk of errors due to qubit instability, and aligns with the practical constraints of current quantum computing technologies. Thus, optimizing circuit depth is crucial for realizing reliable and efficient quantum computations. In the paper, we use fixed discrete time increments assumes a deterministic approach to time evolution. It overlooks the influence of quantum mechanics, including phenomena like superposition and entanglement. The assumptions use classical-like models to reflect the quantum systems effects.

Figure 5: Scheduling examples of quantum computing (a) a non-optimized depth configuration (b) an optimized depth configuration

Based on the definitions, we can formulate the problem of depth-optimal quantum circuit layout synthesis as follows:

Input: A graph G = (V, E) and a set of quantum gates acting on logical qubits, denoted as g1, g2,..., gM. The number of logical qubits, Q, must be less than or equal to the number of physical qubits, P, i.e., |Q| ≤ |P|.

Output: A placement mapping MP : Q → P and a schedule of the quantum circuit, composed of a new gate list 1, 2,..., , where each gate has a time coordinate ti.

Constraints:

1.    All two-qubit gates in the scheduled circuit must be able to connect two qubits in the graph, i = 1 to , if |i| = 2, then xi ∈ E.

2.    All input gates should be executed in form, i.e., there exists an injection mapping f: {1,..., M}→{1,..., } such that gi = f (i) for i = 1 to M. An injection mapping in quantum mechanics refers to a function that maps elements from M to such that each element in M is uniquely mapped to an element in .

3.    Dependencies: for i, i´=1 to M, if i < i´ and gi ∩ gi´ ≠ ∅, then tf(i) < tf(i´).

Objective: Minimize the circuit depth, denoted as d, where d is the maximum time coordinate among all scheduled gates.

3  The Layout Synthesis Algorithm

In quantum computing, the physical arrangement of qubits and their connectivity profoundly influences how quantum circuits are structured and executed. Qubits that interact with each other form the fundamental connections in a quantum circuit, defining the flow of quantum operations. However, long-distance interactions between qubits are susceptible to noise, which can introduce errors and destabilize the system, compromising the accuracy of quantum computations. To mitigate noise and enhance stability, researchers often adopt methods that transform quantum circuits into Nearest Neighbor architectures [29]. In this approach, qubits are constrained to interact solely with their immediate neighbors on a predefined grid. By limiting interaction distances, this strategy minimizes the effects of environmental and operational noise, thereby improving the reliability of quantum computations. However, while effective in noise reduction, adhering to a Nearest Neighbor architecture introduces several trade-offs:

1.    Increased Circuit Depth: Conforming to nearest neighbor constraints often necessitates the introduction of additional quantum gates, such as swap gates, to enable indirect interactions between qubits that are not adjacent. This augmentation typically increases the overall depth of the quantum circuit, as operations may need to be spread over more time steps.

2.    Higher Gate Count: Implementing required swaps or other operations to maintain nearest neighbor interactions can lead to a larger number of quantum gates in the circuit. This increase in gate count complicates the circuit’s complexity and can potentially amplify the risk of errors.

Therefore, while the Nearest Neighbor approach effectively addresses noise-related challenges in quantum computing, it requires careful consideration of the balance between noise reduction and the potential drawbacks of increased circuit complexity and performance degradation. Ongoing research aims to optimize these trade-offs and develop strategies that maximize the overall efficiency and reliability of quantum circuits under real-world conditions.

The quantum circuit synthesis algorithm proposed in this paper begins by mapping a quantum circuit with k qubits onto a graph. However, if k ≥ n, where n is the number of qubits available on the quantum computer, direct implementation becomes impossible. To address this, we introduce an algorithm that extracts non-isomorphic subgraphs from the initial graph. This algorithm identifies a subgraph with k′ qubits that can be implemented on the n-qubit quantum computer, ensuring k′ ≤ n. The detailed steps of this subgraph extraction algorithm are described as follows:

For the extracted subgraph, we use a Linear Nearest Neighbor (LNN) algorithm to design a quantum circuit architecture that adheres to a linear layout while minimizing gate costs. Fig. 6 demonstrates the generation of nearest neighbor compliance. In this paper, we propose an Integer Linear Programming (ILP) approach for synthesizing LNN, aiming to reduce circuit complexity. Specifically, our method focuses on minimizing the number of swap gates needed to transform a given gate-level quantum circuit into an equivalent LNN configuration. Fig. 6a shows an extracted subgraph and a graph represented the layout of a quantum computing device shown in Fig. 6b. Subsequently, by using swap gates to satisfy the nearest neighbor mapping requirements, each qubit in Fig. 6a is mapped to a node in Fig. 6b as shown in Fig. 6c. Given an extracted subgraph, the nearest neighbor algorithm employs swap gates to ensure that all qubits align with their corresponding positions in the graph represented the layout of a quantum computing device.

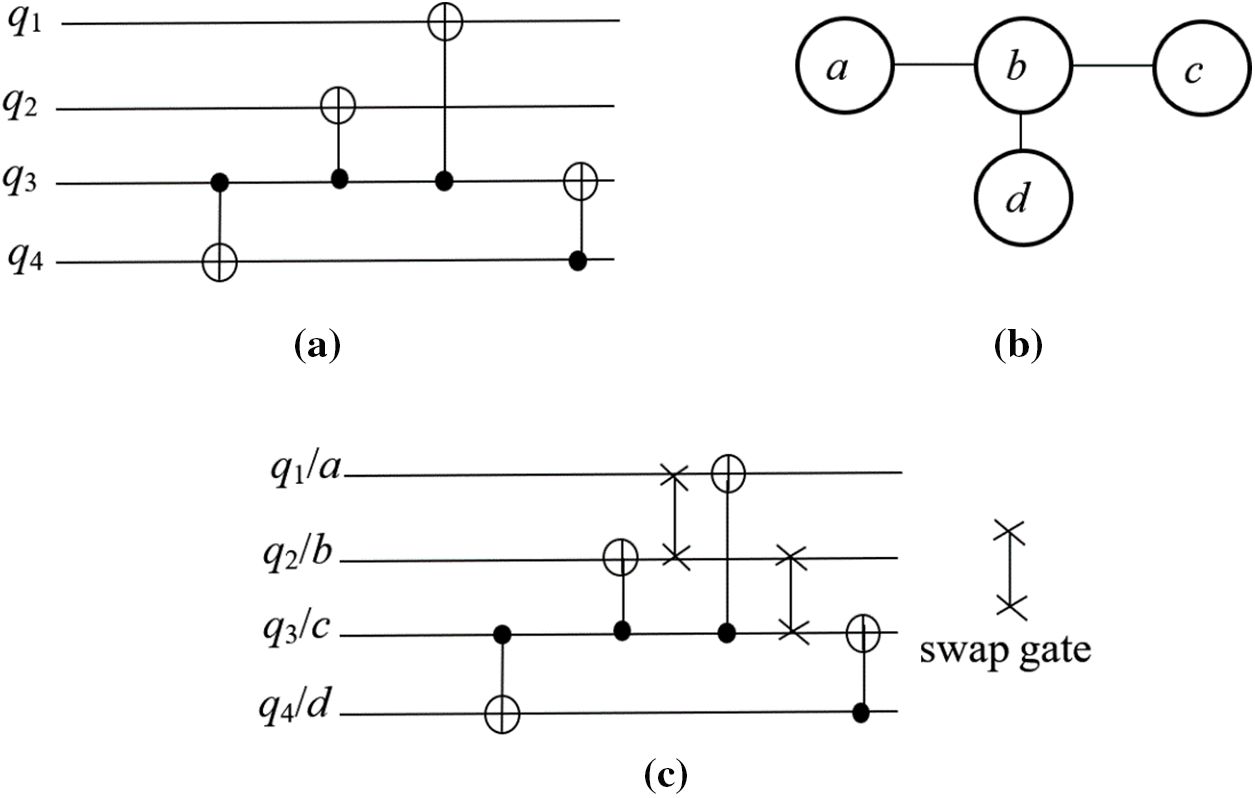
Figure 6: An example the generation of nearest neighbor compliance (a) an extracted subgraph (b) a graph represented the layout of a quantum computing device (c) the nearest neighbor mapping results

The integer linear programming (ILP) involves optimizing a linear objective function subject to linear constraints, where some or all decision variables are restricted to integer values. The objective is to maximize or minimize the linear function, typically representing costs, profits, or resource utilization [30]. By applying ILP techniques, we can systematically optimize the placement and connectivity of qubits in the quantum circuit layout. This optimization ensures that qubits are positioned linearly, which can enhance the circuit’s efficiency and reduce the total gate count required for operations. Overall, our approach contributes to achieving a more cost-effective implementation of quantum circuits by streamlining the use of swap gates in the transition to the LNN architecture. The proposed ILP method is described in detail as follows:

Objective Function:

Minimize∑i=0k∑t=0Ct⋅αi, t(1)

where αi, t is a probability to represents the scheduling of quantum gates in period t for level i.

Constraints:

1.    Layered scheduling constraint: Each layer needs to be scheduled once, and only one layer can be scheduled at a time.

∑i=0kαi, t=1; 0≤i≤k,∑t=0Cαi, t=1; 0≤t≤C(2)

2.    Swap gate blocking constraint: When all quantum gates in level i have been scheduled, no swaps involving qubits in communication in level i can be executed. When i ≤ i′, i′ can only proceed after level i has been completely scheduled.

ebi′, t=ai, t∧(1−mi′, t)(3)

0≤i≤k−1, i+1≤i′≤k, 0≤t≤C(4)

bq, t=∨i(ai, t∨edi, t)∀i∃q∈Ii, 0≤t≤C(5)

bv, q, t=bq, t∧xv, q, t0≤t≤C(6)

sbm, n, t=∨q(bm, q, t∨bn, q, t)∀q∈Q, 0≤t≤C(7)

3.    Chronological communication constraint: Communication i must be satisfied before communication i-1, ensuring a chronological order.

mi,t+1−mi, t≥00≤t≤C−1, 0≤i≤k(8)

mi+1,t−mi, t≥00≤t≤C, 0≤i≤k−1(9)

4.    Nearest neighbor constraint: If two qubits, p and q, are located at positions v and w, or w and v, respectively, then the qubits p and q are considered nearest neighbors. Here, P (p, v), (q, w), t denotes that qubit p is at position v, and qubit v is at position w in the cyclic structure t.

p(p, v), (q, v), t=xv, p, t∧xw, q, t(10)

p(p, w), (q, v), t=xw, p, t∧xv, q, t;(11)

np, q, t=∨(v, w)∈Gε⁡(p(p, v), (q, v), t∨p(p, w), (q, v), t)(12)

5.    Quantum bit position update constraint: If quantum bit q is located at position v in cycle t and no swap operation is performed involving q, or if quantum bit v is at the nearest position w to v and a swap is executed between v and w, then quantum bit v is located at position v in cycle t+1.

uv, q, t+1=(∧(v, w)∈Gε⁡(1−Sv, w, t))∧xv, q, t(13)

cv, q, t=∨(v, w)∈Gε⁡sv, w, t∧xw, q, t(14)

xv, q, t+1=uv, q, t+1∨cv, q, t+1(15)

Quantum bit position and swap constraint: In any given cycle, a quantum bit q can be located exactly at one position. In a given cycle, a position can participate in at most one swap.

∑v∈Gvxv, q, t=1; 0≤t≤T, q∈Q(16)

∑(v, w)∈GεSv, w, t≤1; 0≤t≤T, v∈Gv(17)

The meaning of ILP constraint variables is detailed in Table 1.

By formulating the quantum circuit layout synthesis problem as an Integer Linear Programming (ILP) problem, we can use existing solutions [31,32] to achieve a mapping that meets Nearest Neighbor requirements. The process begins from an initial vertex and iteratively evaluates neighboring vertices. If a neighboring vertex offers a lower objective function value, the algorithm moves to that vertex and continues this process until no neighboring vertex has a lower value. This method ensures the determination of an optimal solution for the mapping.

4  Experimental Results

This study analyzes quantum computing devices from three leading hardware vendors: Google’s Sycamore, IBM’s Tokyo and Rochester, and Rigetti’s Aspen-4. These devices, detailed in Fig. 7, feature 54 qubits for Sycamore, 53 for Rochester, 16 for Aspen-4, and 20 for Tokyo. They are at the forefront of quantum technology, with Sycamore and Tokyo demonstrating enhanced connectivity. The research focuses on two specific gate density vectors: one derived from Google’s pivotal quantum experiment circuit [10] and another from Toffoli gate circuits [33], widely used in quantum logic synthesis algorithms. The paper explores various gate density configurations and benchmarks their impact.

Figure 7: Representative devices from quantum computing hardware vendors

Google, IBM, and Rigetti lead in superconducting quantum computing research, each providing frameworks (Cirq, Qiskit, and pyQuil, respectively) equipped with layout synthesis tools. However, pyQuil lacks complete compilation decomposition into optimization and layout synthesis, precluding its use in this experiment. Qiskit offers precise control over its transpiler, segmented into individual passes, enabling users to configure a pass manager utilizing diverse transpilation modules.

In addressing the layout synthesis challenge, we utilize the tket library [34]. Initially, it employs the Dense Layout module to map logical qubits onto regions of the device graph that exhibit dense connectivity. Subsequently, the Stochastic Swap module introduces perturbations to the distance matrix of physical qubits and conducts heuristic searches to insert swap gates, facilitating the execution of double-qubit gates. These components, dense layout and stochastic swap, constitute the experimental framework depicted in Fig. 8, enabling comprehensive exploration of various configurations.

Figure 8: Experimental framework form by dense layout and stochastic swap

Integer Linear Programming (ILP) problems are indeed known to be NP-hard, indicating that finding optimal solutions can be computationally challenging, especially as problem size grows. This complexity is particularly pertinent in the context of large-scale quantum circuits, which involve numerous qubits and gates, potentially leading to impractically high computational demands. Despite these inherent challenges, ILP algorithms offer significant advantages in terms of improving efficiency, scalability, and the ability to address complex optimization problems.

The outputs of our system include:

1.    Physical Layout Diagram: These diagrams illustrate the physical connections between qubits and gates, taking into consideration specific constraints of quantum computing architectures.

2.    Logical-to-Physical Mapping: This involves mapping logical qubits to physical qubits and identifying the specific paths and connections needed to execute gate operations on the quantum computer.

3.    SWAP Gate and Physical Gate Generation: When logical qubits are not directly connected, our system generates sequences of SWAP gates to achieve logical gates. These sequences optimize paths and distances between physical qubits to minimize time and energy consumption during quantum computer operations.

4.    Delay and Energy Consumption Estimation: These features assist designers in selecting optimal design solutions by simulating and testing the effects of various layouts and gate sequences.

5.    Performance Analysis and Optimization: These capabilities enable designers to assess and refine design solutions by simulating and testing different layouts and gate sequences, aiming for optimal performance.

Table 2 shows the comparison results with previous related studies. One of the methods compared, developed by Wille et al. [21], utilizes a pseudo-Boolean optimizer and SMT solver to minimize additional gate costs. Another comparison is made with the t|ket⟩ method introduced by Seyon et al. [35] for quantum computing layout synthesis. The results indicate that the proposed method achieves notable performance improvements in optimizing circuit depth.

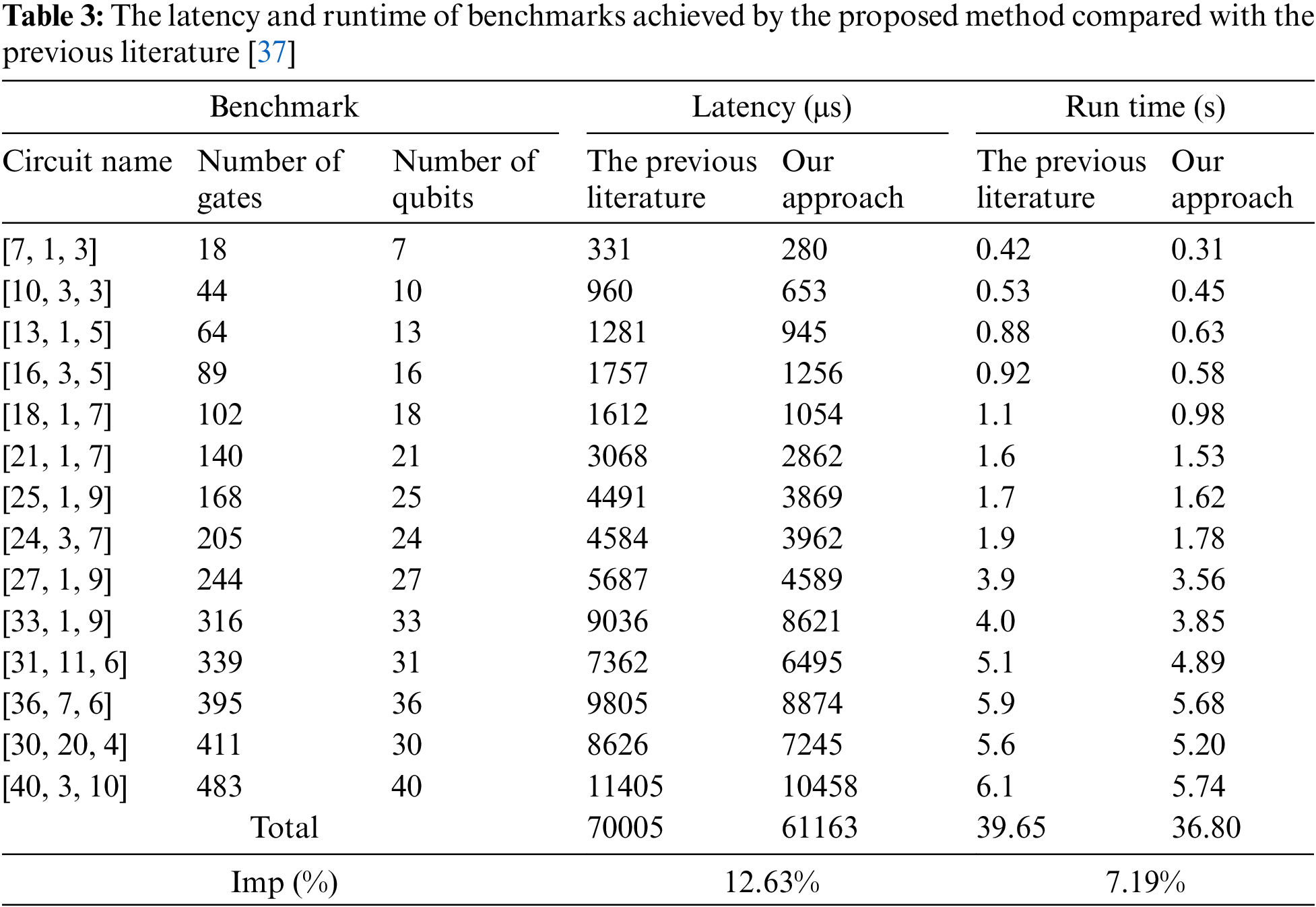
We also evaluated our proposed method using Quantum Error Correction Codes (QECC) benchmark circuits [36]. Table 3 compares the latency and runtime of these benchmark circuits between our method and a method described in the literature [37]. The first three columns list the names of the benchmarks, along with their respective numbers of gates and qubits. The “Latency” column displays results achieved by the previous layout synthesis method in the first entry, and by our proposed method in the second entry. The “Imp” row indicates the improvement achieved by our method compared to the previous approach, showing an enhancement of approximately 12.63%. The runtime overhead is approximately 7.19%. These improvements in latency and runtime highlight the effectiveness of our approach in managing the complexities of the layout generation process.

5  Conclusions

Because quantum computations involve superposition and entanglement, it is crucial to ensure that a quantum gate layout leads to the correct computational result. The proposed methods aim to determine whether a quantum circuit can generate the desired outputs in quantum computing. Coherence issues arise from factors such as noise and errors in controlling quantum systems. These issues can lead to errors in gate operations, resulting in incorrect computations or outcomes. The proposed method ensures that the layout can be verified or simulated to reliably predict outcomes, despite the probabilistic nature of quantum operations. Quantum gates must operate within the coherence time of the quantum system, which dictates how long quantum states can be maintained without significant decoherence. The proposed design minimizes decoherence effects and optimizes gate sequences to reduce errors.

In summary, despite the inherent probabilistic nature and sensitivity to environmental interactions of quantum systems, the approach utilizes integer linear programming to achieve depth-optimized results while satisfying various constraints. Experimental testing demonstrates that compared to existing studies, the proposed method can achieve performance improvements in circuit depth ranging from 3% to 48%.

Acknowledgement: The authors would like to thank all colleagues and students who contributed to this research. We also thank the reviewers and editors for their constructive suggestions on this paper.

Funding Statement: This work was supported by National Science and Technology Council, Taiwan, NSTC 112-2221-E-024-004.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Chi-Chou Kao and Hung-Yi Lin; data collection: Hung-Yi Lin; analysis and interpretation of results: Chi-Chou Kao; draft manuscript preparation: Hung-Yi Lin. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Chi-Chou Kao, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. E. H. Shaik and N. Rangaswamy, “Implementation of quantum gates-based logic circuits using IBM qiskit,” in Proc. 2020 Int. Conf. Comput. Commun. Secur., ICCCS 2020, 2020, pp. 1–6. [Google Scholar]

2. S. M. Saeed, R. Wille, and R. Karri, “Locking the design of building blocks for quantum circuits,” ACM Trans. Embed. Comput. Syst., vol. 18, no. 5s, pp. 15, Oct. 2019. doi: 10.1145/3358184. [Google Scholar] [CrossRef]

3. M. Saeedi and IL. Markov, “Synthesis and optimization of reversible circuits—A survey,” ACM Comput. Surv., vol. 45, no. 2, pp. 21, 2013. [Google Scholar]

4. H. Fu, M. Zhu, J. Wu, W. Xie, Z. Su and X-Y. Li, “Effective and efficient qubit mapper,” in 2023 IEEE/ACM Int. Conf. Comput. Aided Design (ICCAD), 2023, pp. 1–9. [Google Scholar]

5. V. Saravanan and SM. Saeed, “Noise adaptive quantum circuit mapping using reinforcement learning and graph neural network,” IEEE Trans. Comput. Aided Des. Integr. Circuits Syst., vol. 43, no. 5, pp. 1374–1386, 2024. doi: 10.1109/TCAD.2023.3340608. [Google Scholar] [CrossRef]

6. B. Tan and J. Cong, “Optimal layout synthesis for quantum computing,” in 2020 IEEE/ACM Int. Conf. Comput. Aided Design (ICCAD), San Diego, CA, USA, 2020, pp. 1–9. [Google Scholar]

7. J. Chen et al., “A survey of compiler testing,” Comput. Surv., vol. 53, no. 1, pp. 1–36, May 2020. [Google Scholar]

8. L. Moro, M. G. A. Paris, M. Restelli, and E. Prati, “Quantum compiling by deep reinforcement learning,” Commun. Phys., vol. 4, no. 1, pp. 1–8, Aug. 2021. doi: 10.1038/s42005-021-00684-3. [Google Scholar] [CrossRef]

9. M. A. Nielsen, I. Chuang, and L. K. Grover, “Quantum computation and quantum information,” Am. J. Phys., vol. 70, no. 5, pp. 558–559, 2002. doi: 10.1119/1.1463744. [Google Scholar] [CrossRef]

10. F. Arute et al., “Quantum supremacy using a programmable superconducting processor,” Nature, vol. 574, no. 7779, pp. 505–510, Oct. 2019. doi: 10.1038/s41586-019-1666-5. [Google Scholar] [PubMed] [CrossRef]

11. B. Tan and J. Cong, “Optimality study of existing quantum computing layout synthesis tools,” IEEE Trans. Comput., vol. 70, no. 9, pp. 1363–1373, 2020. doi: 10.1109/TC.2020.3009140. [Google Scholar] [CrossRef]

12. N. K. Macha, B. T. Repalle, S. Geedipally, R. Rios, and M. Rahman, “A new paradigm for fault-tolerant computing with interconnect crosstalks,” in 2018 IEEE Int. Conf. Rebooting Comput. (ICRC), 2018, pp. 1–6. [Google Scholar]

13. M. A. Iqbal, N. K. Macha, B. T. Repalle, and M. Rahman, “A logic simplification approach for very large-scale crosstalk circuit designs,” in 2019 IEEE/ACM Int. Symp. Nanoscale Archit. (NANOARCH), Qingdao, China, 2019, pp. 1–6. [Google Scholar]

14. M. Amy, D. Maslov, M. Mosca, and M. Roetteler, “A meet-in-the-middle algorithm for fast synthesis of depth-optimal quantum circuits,” IEEE Trans. Comput.-Aided Design Integr. Circuits Syst., vol. 32, no. 6, pp. 818–830, Jun. 2013. doi: 10.1109/TCAD.2013.2244643. [Google Scholar] [CrossRef]

15. P. Lathrop, B. Boardman, and S. Martínez, “Quantum search approaches to sampling-based motion planning,” IEEE Access, vol. 11, pp. 89506–89519, 2023. [Google Scholar]

16. K. Seino and S. Yamashita, “An SMT-solver-based synthesis of NNA-compliant quantum circuits consisting of CNOT, H and T gates,” in 2023 28th Asia South Pacific Design Autom. Conf. (ASP-DAC), Tokyo, Japan, 2023, pp. 196–201. [Google Scholar]

17. A. Cowtan, S. Dilkes, R. Duncan, A. Krajenbrink, W. Simmons and S. Sivarajah, “On the qubit routing problem,” in 14th Conf. Theory Quantum Comput. Commun. Cryptogr., 2019, pp. 5:1–5:32. [Google Scholar]

18. P. Czarnik, A. Arrasmith, P. J. Coles, and L. Cincio, “Error mitigation with Clifford quantum-circuit data,” Quantum, vol. 5, p. 592, Nov. 2021. doi: 10.22331/q-2021-11-26-592. [Google Scholar] [CrossRef]

19. T. Giurgica-Tiron, Y. Hindy, R. LaRose, A. Mari, and W. J. Zeng, “Digital zero noise extrapolation for quantum error mitigation,” in 2020 IEEE Int. Conf. Quantum Comput. Eng. (QCE), Denver, CO, USA, 2020, pp. 306–316. doi: 10.1109/QCE49297.2020.00045. [Google Scholar] [CrossRef]

20. P. D. Nation, H. Kang, N. Sundaresan, and J. M. Gambetta, “Scalable mitigation of measurement errors on quantum computers,” PRX Quantum, vol. 2, pp. 40326, Nov. 2021, Art. no. 040326. doi: 10.1103/PRXQuantum.2.040326. [Google Scholar] [CrossRef]

21. R. Wille, A. Lye, and R. Drechsler, “Optimal SWAP gate insertion for nearest neighbor quantum circuits,” in Proc. 19th Asia South Pacific Des. Autom. Conf., 2014, pp. 489–494. [Google Scholar]

22. A. M. Childs, E. Schoute, and C. M. Unsal, “Circuit transformations for quantum architectures,” in Proc. 14th Conf. Theory Quantum Comput. Commun. Cryptogr., Dagstuhl, Germany, 2019, vol. 135, pp. 3:1–3:24. [Google Scholar]

23. A. Zulehner and R. Wille, “Compiling SU(4) quantum circuits to IBM QX architectures,” in Proc. 24th Asia South Pacific Des. Autom. Conf., 2019, pp. 185–190. [Google Scholar]

24. A. Kole, S. Hillmich, K. Datta, R. Wille, and I. Sengupta, “Improved mapping of quantum circuits to IBM QX architectures,” IEEE Trans. Comput. Aided Des. Integr. Circuits Syst., vol. 39, no. 10, pp. 2375–2383, Oct. 2020. doi: 10.1109/TCAD.2019.2962753. [Google Scholar] [CrossRef]

25. P. Wang, M. Usman, U. Parampalli, L. C. L. Hollenberg, and C. R. Myers, “Automated quantum circuit design with Nested Monte Carlo Tree Search,” IEEE Trans. Quantum Eng., vol. 4, pp. 1–20, 2023. [Google Scholar]

26. D. Bhattacharjee, A. A. Saki, M. Alam, A. Chattopadhyay, and S. Ghosh, “MUQUT: Multi-constraint quantum circuit mapping on NISQ computers,” in Proc. IEEE/ACM Int. Conf. Comput.-Aided Des., 2019, pp. 1–7. [Google Scholar]

27. P. Murali, N. M. Linke, M. Martonosi, A. J. Abhari, N. H. Nguyen and C. H. Alderete, “Full-stack, real-system quantum computer studies: Architectural comparisons and design insights,” in 2019 ACM/IEEE 46th Annu. Int. Symp. Comput. Archit. (ISCA), Phoenix, AZ, USA, 2019, pp. 527–540. [Google Scholar]

28. V. Lorenza, K. Emanuel, and L. Raymond, “Constructing qubits in physical systems,” J. Phys. A: Math. Gen., vol. 34, pp. 7067–7079, 2001. doi: 10.1088/0305-4470/34/35/331. [Google Scholar] [CrossRef]

29. X. Cheng, Z. Guan, and P. Zhu, “Nearest neighbor transformation of quantum circuits in 2D architecture,” IEEE Access, vol. 8, pp. 222466–222475, 2020. doi: 10.1109/ACCESS.2020.3043497. [Google Scholar] [CrossRef]

30. P. L. Yu and M. Zeleny, “The set of all nondominated solutions in linear cases and in multicriteria simplex method,” J. Math. Anal. Appl., vol. 49, pp. 430–468, 1975. doi: 10.1016/0022-247X(75)90189-4. [Google Scholar] [CrossRef]

31. S. Holm and D. Klein, “Discrete right-hand side parametrization for linear integer programs,” Eur. J. Oper. Res., vol. 2, pp. 50–53, 1978. doi: 10.1016/0377-2217(78)90123-6. [Google Scholar] [CrossRef]

32. D. -S. Chen, R. G. Batson, and Y. Dang, Applied Integer Programming: Modeling and Solution. New York, USA: John Wiley and Sons, 2010. [Google Scholar]

33. V. V. Shende, A. K. Prasad, I. L. Markov, and J. P. Hayes, “Synthesis of reversible logic circuits,” IEEE Trans. Comput.-Aided Design Integr. Circuits Syst., vol. 22, no. 6, pp. 710–722, Jun. 2003. doi: 10.1109/TCAD.2003.811448. [Google Scholar] [CrossRef]

34. T. Carette, E. Jeandel, S. Perdrix, and R. Vilmart, “Completeness of graphical languages for mixed state quantum mechanics,” ACM Trans. Quantum Comput., vol. 2, no. 4, pp. 1–28, 2021. [Google Scholar]

35. S. Seyon, D. Silas, C. Alexander, S. Will, E. Alec and D. Ross, “t|ket⟩: A retargetable compiler for NISQ devices,” Quant. Sci. Technol., vol. 6, 2020, Art. no. 014003. doi: 10.1088/2058-9565/ab8e92. [Google Scholar] [CrossRef]

36. A. Mondal and K. K. Parhi, “Quantum circuits for stabilizer error correcting codes: A tutorial,” IEEE Circuits Syst. Mag., vol. 24, no. 1, pp. 33–51, 2024. doi: 10.1109/MCAS.2024.3349668. [Google Scholar] [CrossRef]

37. M. Whitney, N. Isailovic, Y. Patel, and J. Kubiatowicz, “Automated generation of layout and control for quantum circuits,” in Proc. 4th Int. Conf. Comput. Front., 2007, pp. 83–94. [Google Scholar]