Solving the Generalized Traveling Salesman Problem Using Sequential Constructive Crossover Operator in Genetic Algorithm

1  Introduction

The traditional travelling salesman problem (TSP) is an important combinatorial optimization problem (COP) in Operations Research and Computer Science. It can be represented as a network of n nodes (or cities) with a cost (or distance) matrix expressed by C = [cij]. The problem aims to find a least-cost Hamiltonian tour for the salesperson. Various exact and heuristic methods are present in the literature to solve this problem. However, in some real-life circumstances, additional restrictions have to be enforced on this usual TSP that creates some variant TSPs, for example, generalized TSP, multiple TSP, TSP with backhauls, TSP with time windows, etc. Amongst different variants, the generalized TSP (GTSP) is considered to be studied here.

The GTSP was first presented in [1], an NP-hard problem [2]. In addition to the usual TSP, in this problem, the set of nodes (or cities), denoted by S, is grouped into m sets or clusters, suppose, S1, S2, …, Sm with S1∪S2∪….∪Sm=SandSi∩Sj=∅ifi≠j. The problem aims to find a least-cost Hamiltonian tour that contains exactly one node from every set Si. Fig. 1 shows an example of a GTSP instance with 13 nodes and 7 sets.

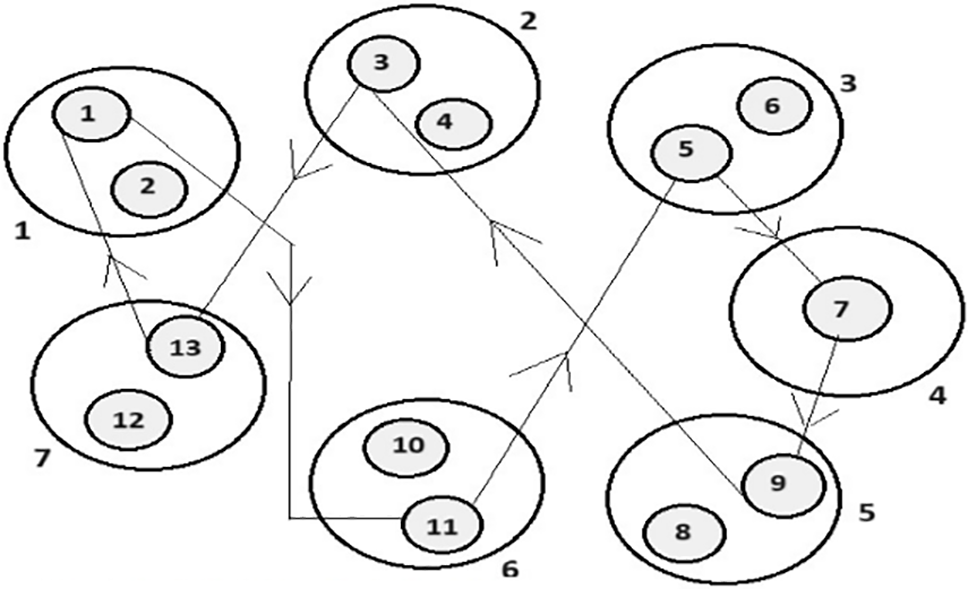
Figure 1: Graphical representation of a GTSP instance with n = 13 and m = 7

The GTSP turns into the usual TSP while the total number of cluster sets and the total number of nodes are same, and every set has only one node. If the associated cost matrix C is symmetric, then the GTSP is symmetric; otherwise, it is asymmetric. The clustered TSP is a variant of GTSP where all nodes in a cluster have to be visited successively before exiting the cluster [3]. The GTSP has many important real-life applications that include airplane routing, mail delivery [4], etc.

Heuristic/metaheuristic and exact procedures can be used to solve the problem. Branch and bound [5], dynamic programming [1], lexisearch algorithm [6], etc., are some well-known exact methods for finding exact solutions. However, finding exact solutions to the problem using these methods becomes impracticable even for moderate-sized problem instances. Therefore, many researchers used heuristic procedures to find heuristic solutions to the problem, and largely modern heuristic approaches to solve such COPs are named metaheuristic procedures. Genetic algorithms [7], ant colony optimization [8], variable neighborhood method [2], particle swarm optimization [9], etc., are some well-known metaheuristic methods for finding heuristic solutions. Generally, heuristic/metaheuristic approaches cannot make sure about exact optimal solutions but can find close to optimal solutions very quickly. Amongst metaheuristic approaches genetic algorithm (GA) is identified as a better metaheuristic technique for solving such COPs.

We are going to develop GA to find heuristic solutions to the problem. In GAs, as the crossover process performs a very crucial role, the crossover methods proposed for the traditional TSP could be adapted for the GTSP. The sequential constructive crossover (SCX) [10] and three other operators are adapted to use in GAs to solve the GTSP. The effectiveness of GA using SCX is verified on some GTSPLIB instances [11] first and then compared against GAs using the other crossover methods. The computational results show the success of the GA using SCX for this problem. Our proposed GA using SCX, and swap mutation could find average solutions whose average percentage of excesses from the best-known solutions is between 0.00 and 14.07 for our investigated instances. Furthermore, we showed a relative rank of the four crossover methods for the GTSP. In this study, we aim to test the effectiveness of four crossover operators, we do not aim to achieve optimal (or best-known) solutions to the GTSP instances.

This paper is arranged as below: Section 2 briefly surveys the literature on the GTSP. Genetic algorithms using four crossover methods are developed in Section 3, while Section 4 reports the computational experiments of different GAs on asymmetric GTSPLIB instances. At the end, Section 5 describes some comments and closing remarks.

2  Literature Survey

The GTSP was introduced, and a dynamic programming technique was developed to solve the problem in [1], where the visited clusters identify a state. An integer linear programming technique was developed to find the solution to the problem and then applied to both non-Euclidean and Euclidean instances [12]. As reported, the technique solved the instance of size up to 50 cities and 10 clusters. A branch-and-bound technique was developed for solving the problem which was based on the minimal rooted tree [5]. As reported, the technique solved the instance of sizes up to 52 cities and 13 clusters. A branch-and-cut technique by combining branch-and-bound and cutting plane techniques was developed to solve the problem [11]. As reported, the technique solved the instance of sizes up to 442 cities and 89 clusters.

A heuristic method, by combining three techniques—initialization, insertion, and improvemen-was developed to solve the problem [13]. A new GA was proposed and improved by using 2-opt and swap techniques to solve the problem [14]. The Lin-Kernighan-Helsgaun technique was developed for finding solutions to the problem [15], and the technique could enhance the solution for some benchmark instances upon the best existing techniques. A memetic algorithm using breakout local search method was proposed to solve the problem [16]. Based bioinspired computing model, some parallel deoxyribonucleic acid (DNA) algorithms were developed to solve the problem [17]. By combining features of GA, a random-permutation based GA was developed to solve the problem [18]. By merging a core GA using a chromosome enhancement procedure and a shortest path algorithm with some local search techniques, a memetic algorithm was proposed to find the solution to the problem [19]. Using an adaptive neighborhood search technique, a heuristic technique was developed to find the solution to the problem [20]. Three new neighborhoods were illustrated and then integrated with an iterated local search technique to solve the problem [21]. Furthermore, cluster optimization was applied. A shortlist of algorithms for solving the problem is reported in Table 1.

3  Proposed Genetic Algorithm

Based on the survival-of-the-fittest theory among different populations in natural science, Goldberg proposed genetic algorithms (GAs) to find solutions to optimization problems. Since GAs are very flexible, and can encode the solutions easily as chromosomes, they are very popular. Several chromosomes are produced initially, termed together as the initial population, and then are processed through three major processes (operators), such as selection, crossover, and mutation, to achieve a suitable solution to the problem. Better chromosomes are picked probabilistically in the selection process. Two-parent chromosomes mate to produce suitable offspring chromosome(s) in the crossover process, while some genetic materials in the chromosomes are randomly altered in the mutation process. Amongst the operators, the crossover operator is the most powerful and important process to design and implement the GAs [22]. Therefore, the probability of using crossover is set very high, whereas the probability of mutation is set very low. The selection and the crossover operators are capable of speeding up the convergence of solutions.

3.1 Genetic Coding and the Initial Population

Using a GA to find the solution to a COP, at first, any chromosome representation method for a solution must be described. The most simple and common representation method is the path representation of the cities in a sequence. The bipartite chromosome is considered for the GTSP. It has two rows, where the first row shows the sequence of clusters, and the second row shows the city chosen from each corresponding cluster. The list of clusters (S1, S2, …, Sm) represents the Hamiltonian cycle {S1−S2−…−Sm−S1}. Given a sequence of clusters (S1, S2, …, Sm), one of the salesman’s tours may be as {v1, v2…, vm), provided that the city vi ∈ Si, for all i ∈ {1, 2 …, m}. For example, suppose that n = 13 and m = 7, with the cluster sets: S1 = {1, 2}, S2 = {3, 4}, S3 = {5, 6}, S4 = {7}, S5 = {8, 9}, S6 = {10, 11} and S7 = {12, 13}. If the sequence of cluster sets is (1, 2, 3, 4, 5, 6, 7, 1), then (1, 3, 5, 7, 9, 10, 12, 1) may be a tour, which is displayed in Table 2 and Fig. 2.

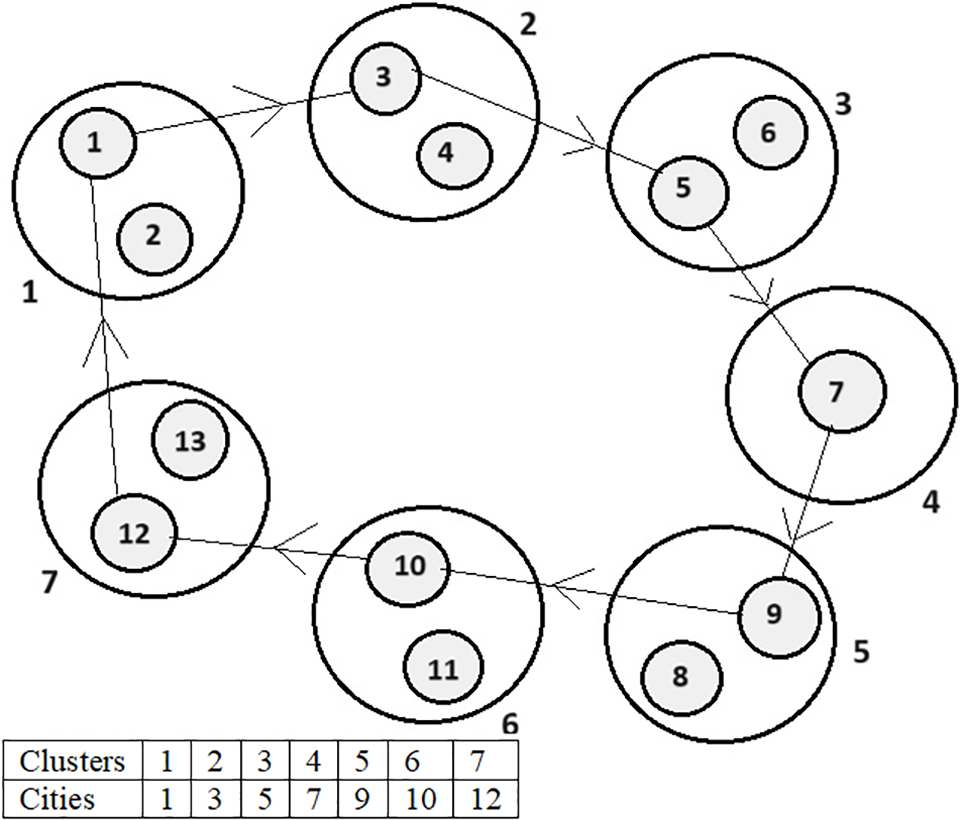
Figure 2: Representation of a tour by a chromosome

In Fig. 2, the second row represents a tour of the salesman whose objective cost is the total cost of the cities that exist in the path. Since the problem is minimization, the fitness cost, suppose fi, of the i-th chromosome, is calculated as the inverse of the objective cost, oi.

fi=11+oi(1)

Thus, at the beginning, a population of pre-fixed size Ps is produced arbitrarily. Once the population is generated, the fitness of each chromosome is evaluated, and the population is passed to the next generation.

3.2 Selection Operator

In the selection process, fitter chromosomes are picked and passed to the following generation, and unproductive chromosomes are removed from the population. This operator upgrades the performance of GAs and can create diverse results all over generations. Furthermore, it assists in reliability between exploitation and exploration of the search space.

Various selection methods exist in literature. We consider the roulette wheel selection (RWS) [22] procedure that uses the fitness proportional law. The RWS is a very popular method that assigns every chromosome a portion of a roulette wheel, and the area of a portion is determined by the fitness of the corresponding chromosome. Next, the wheel is spun, and the chromosome that is ultimately pointed out by the pointer is chosen for the next generation of mating pools. Thus, chromosomes with higher fitness values have a bigger possibility of being chosen, and those with lower fitness values have a bigger possibility of being discarded. However, no one can guarantee that chromosomes with higher fitness values will always be selected. The selection probability pi is calculated for each chromosome in a population of size Ps as follows:

pi=fi∑j=1Psfj;i∈{1,2,…,Ps}(2)

Then, the cumulative probability ki, i ∈ {0, 1, .., Ps} for each chromosome is calculated (k0 = 0). After that, a random number, r ∈ [0,1], is generated. If k(i-1) < r ≤ ki, for i ∈ {1, 2, ⋯, Ps}, then the i-th chromosome is selected. The segment size and probability are kept fixed throughout this selection method. This is a very easy and simple method that assigns balanced distributed probabilities to all chromosomes and assigns the highest probability to the best chromosome.

3.3 Crossover Operators

As the crossover process performs a very crucial role, the crossover methods that were constructed for the traditional TSP could be adapted to apply to the GTSP. Here, partially mapped crossover (PMX) [23], ordered crossover (OX) [24], cycle crossover (CX) [25], and sequential constructive crossover (SCX) [10] operators are modified to apply to the GTSP. We plan to compare the working of these four crossover operators. For that, we plan to develop GAs using these crossover operators and run on asymmetric GTSPLIB instances of different sizes. Furthermore, we plan to show a relative rank of these crossover methods for the GTSP.

3.3.1 Partially Mapped Crossover Operator

The partially mapped crossover (PMX) technique was devised for the TSP that describes an exchange map substrings between two randomly selected points in parent chromosomes [23]. It is modified here and then employed on the GTSP as below. Suppose P1 and P2 are two parent chromosomes with costs 407 and 347, respectively, related to the cost matrix indicated in Table 3 with n = 13 and m = 7.

These same parent chromosomes, as shown in Table 4, will be used to explain all crossover methods.

The PMX operation example is presented in Figs. 3 and 4.

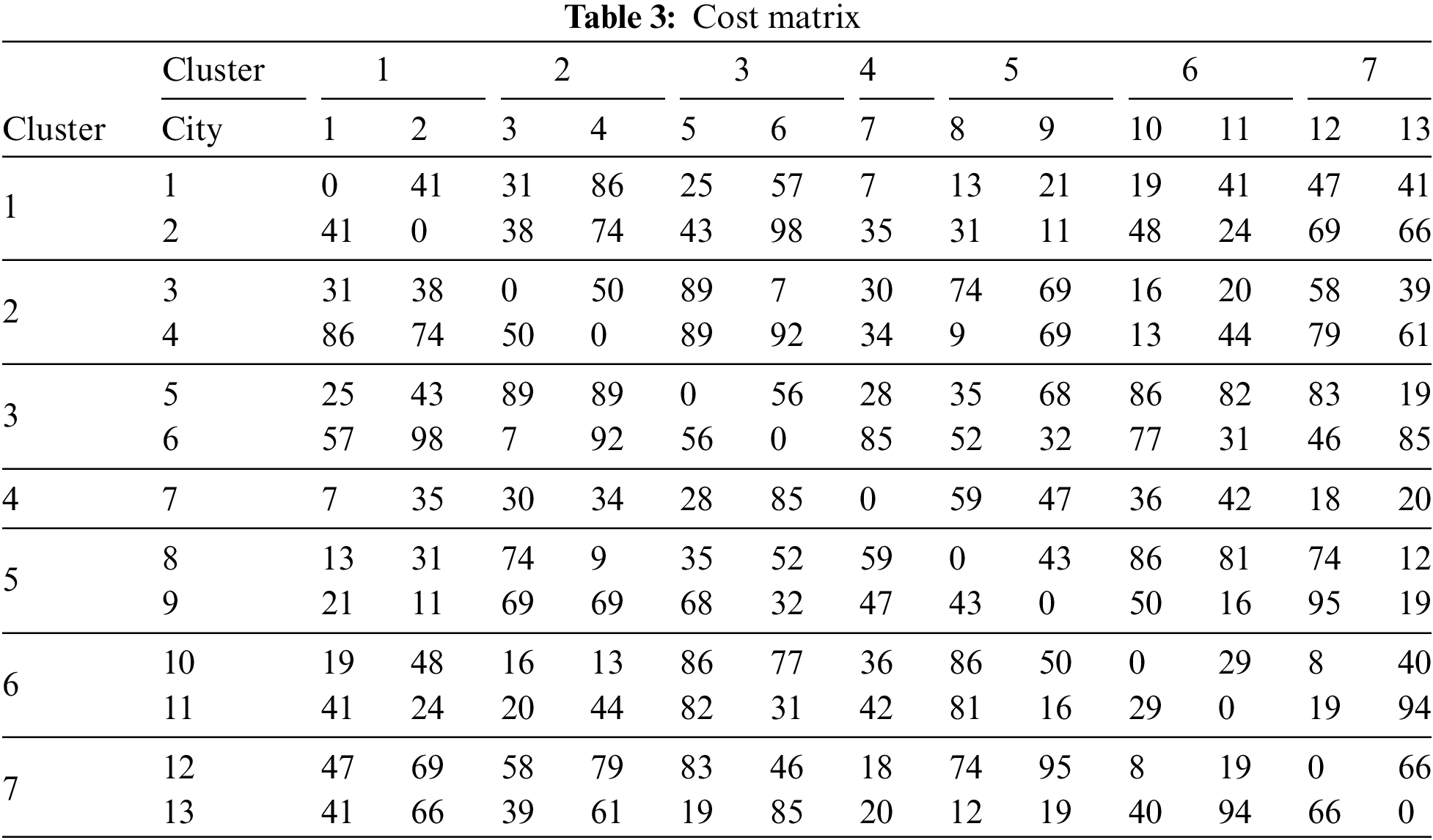
Figure 3: Steps of building the offspring O1 and O2 from parents P1 and P2 using PMX

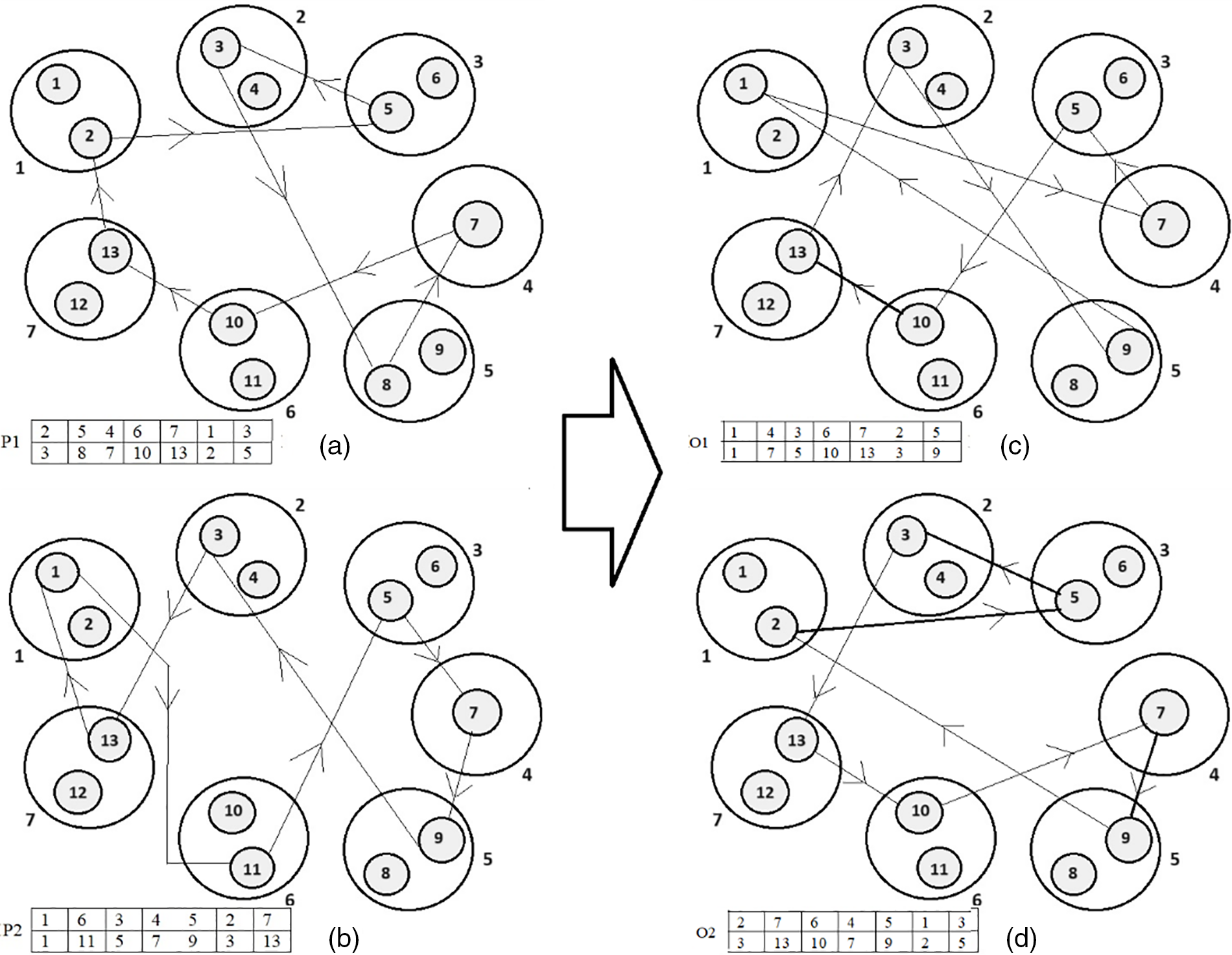
Figure 4: Illustration of the PMX. (a) The first parent chromosome P1. (b) The second parent chromosome P2. (c) The first offspring chromosome O1. (d) The second offspring chromosome O2

In GAs, generally, the crossover inherits the parents’ characteristics. The crossover operator, which can preserve good characteristics of parents as offspring, is supposed to be a better operator. The parent chromosomes are shown in Fig. 4a,d. The bold edges shown in Fig. 4c,d are the edges that exist in either one of the parent chromosomes. In O1 and O2, only one and three edges respectively out of seven edges are chosen from either of the parent chromosomes. This means that 14.29% and 42.86% of the edges of the offspring chromosomes are chosen from the parent chromosomes.

3.3.2 Ordered Crossover Operator

The ordered crossover (OX) technique was devised for the traditional TSP that creates offsprings by picking a subchromosome from a chromosome and saving the relative cluster sequence with subsequent cities from another [24]. It is modified here and then applied to the GTSP as inFigs. 5 and 6.

Figure 5: Steps of building the offspring O1 and O2 from parents P1 and P2 using OX

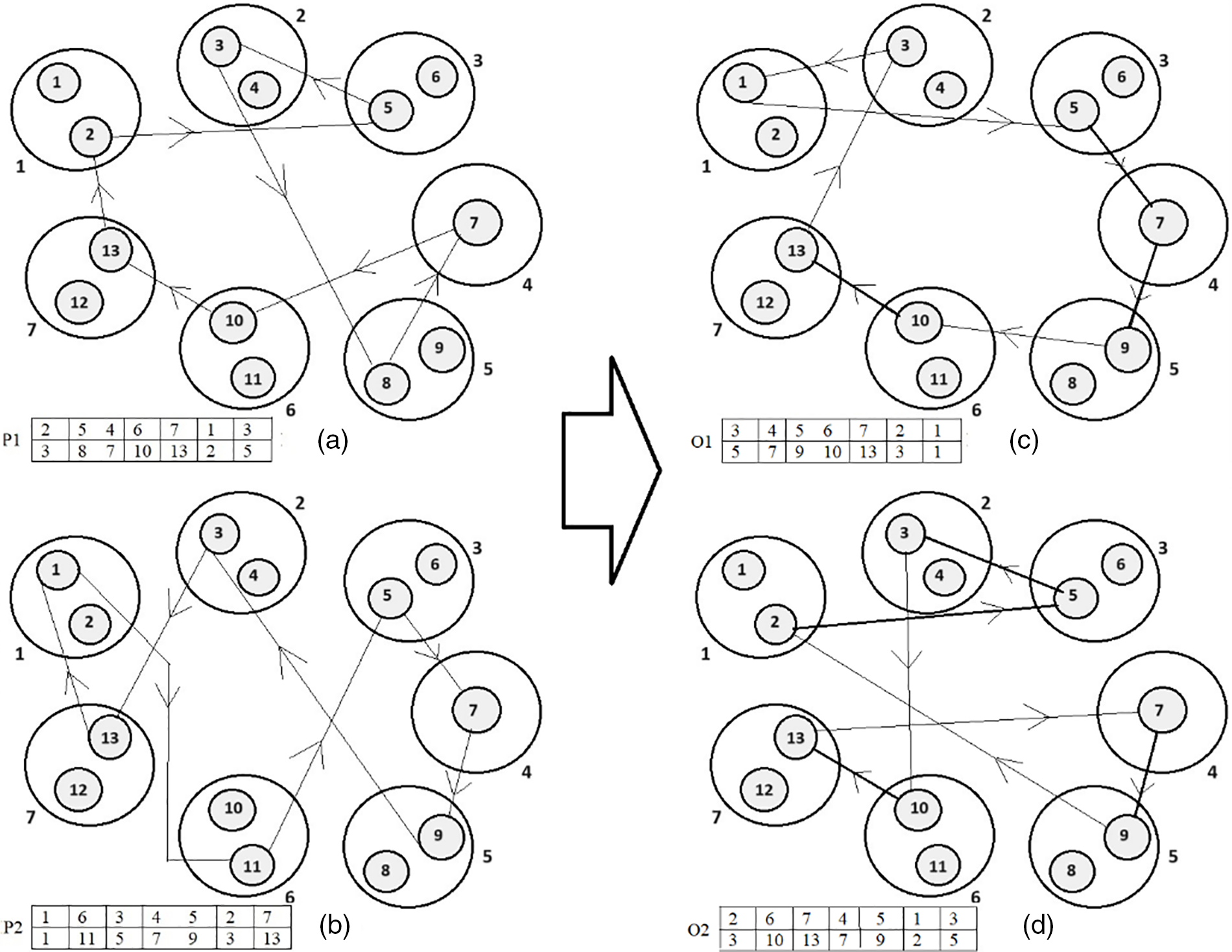
Figure 6: Illustration of the OX. (a) The first parent chromosome P1. (b) The second parent chromosome P2. (c) The first offspring chromosome O1. (d) The second offspring chromosome O2

The parent chromosomes are shown in Fig. 6a,b. The bold edges shown in Fig. 6c,d are the edges that exist in either one of the parent chromosomes. In O1 and O2, only three and four edges respectively out of seven edges are chosen from either of the parent chromosomes. This means that 42.86% and 57.14% of the edges of the offspring chromosomes are chosen from the parent chromosomes.

3.3.3 Cycle Crossover Operator

The cycle crossover (CX) technique was devised for the traditional TSP that creates offspring so that each cluster (and its position) and the subsequent city start from one of the chromosomes [25]. It is modified here and then applied to the GTSP as in Figs. 7 and 8.

Figure 7: Steps of building the offspring O1 and O2 from parents P1 and P2 using CX

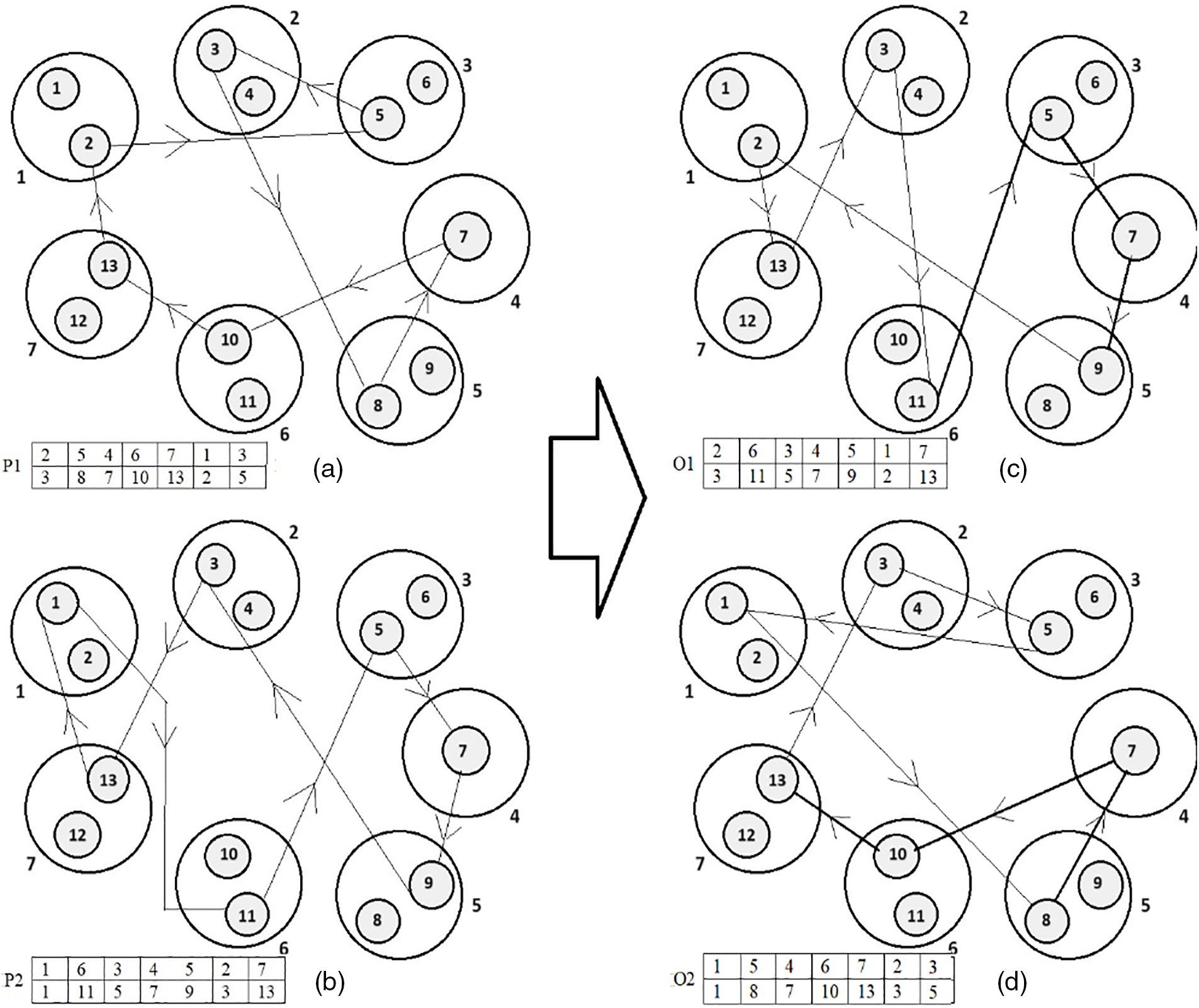
Figure 8: Illustration of the CX. (a) The first parent chromosome P1. (b) The second parent chromosome P2. (c) The first offspring chromosome O1. (d) The second offspring chromosome O2

The parent chromosomes are shown in Fig. 8a,b. The bold edges shown in Fig. 8c,d are the edges that exist in either one of the parent chromosomes. In both O1 and O2, only three edges out of seven edges are chosen from either of the parent chromosomes. This means that 42.86% of the edges of the offspring chromosomes are chosen from the parent chromosomes.

3.3.4 Sequential Constructive Crossover Operator

The sequential constructive crossover (SCX) technique was devised for the traditional TSP which produces one offspring only that checks sequentially both parents and picks the 1st untouched (legitimate) gene from everyone that is seen after the current one. If a legitimate gene is not detected in a parent, it wraps around the parent and chooses the first legitimate gene. Then the cost of each legitimate gene from the current gene is computed, and the cheaper one is augmented to the offspring [10]. This technique was applied successfully to other combinatorial optimization problems ([26–28]). We adapted this technique to the GTSP and reported in Algorithm 1 [7].

The SCX operation example is presented in Fig. 9 and 10. The chromosomes P1 and P2 in Fig. 10a,b, respectively, are the parent chromosomes, while O in Fig. 10c is their offspring. The bold edges shown in Fig. 10c are the edges that exist in either one of the parents. Five edges of seven edges are chosen from either of the parents. This means that 71.44% of the edges of the offspring are chosen from the parents. Out of five edges, there is no common edge selected from either of the parents; only one edge (7, 10) is chosen from P1, while four edges (13, 1), (5, 70), (9, 3) and (3, 13) are chosen from P2. The edges (1, 5) and (10, 9) are new edges that have smaller costs. Thus, SCX can preserve better characteristics of the parents in their offspring. Furthermore, SCX can create various offspring.

Figure 9: Steps of building the offspring O from parents P1 and P2 using SCX

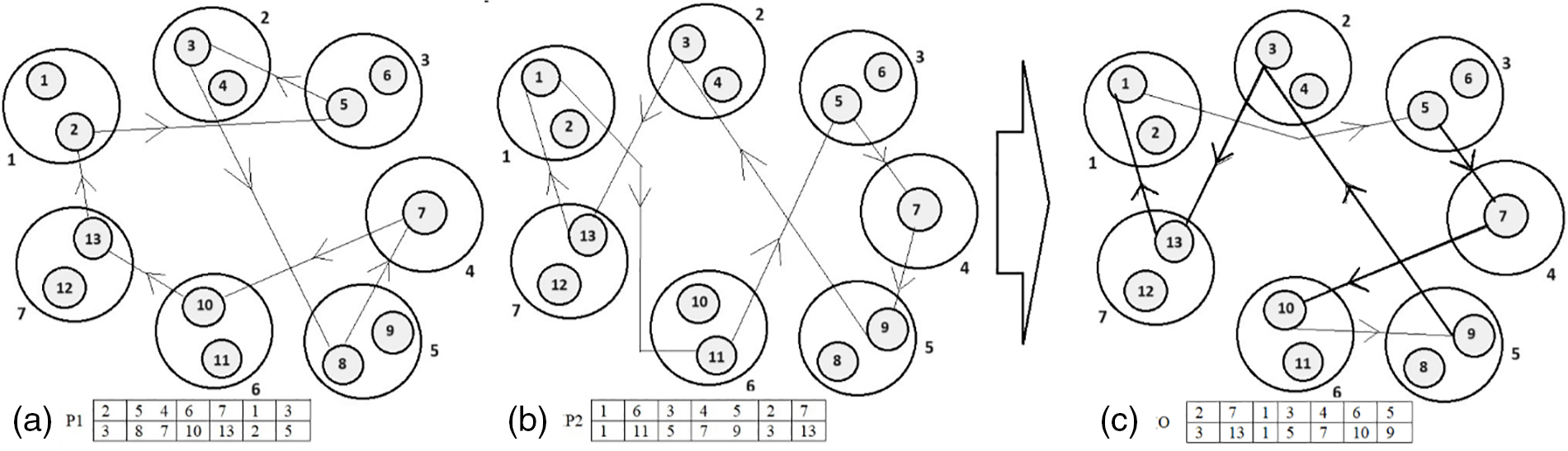
Figure 10: Illustration of the SCX. (a) The first parent chromosome P1. (b) The second parent chromosome P2. (c) The only offspring chromosome O

3.4 Mutation Operator

Mutation operators can increase the variety in the population by initiating random variations in the GA population. It randomly chooses some gene(s) in a parent chromosome and then changes the genes(s); thus, changing the information. We apply the swap mutation (SM) technique with probability, Pmt, that randomly picks two genes from a chromosome and then swaps them [29].

Suppose P is a parent chromosome, and the 3rd and 6th positions are randomly picked. Then cluster 1 with city 1 and cluster 6 with city 10 are exchanged in their positions to create the mutated chromosome E as follows.

3.5 Simple Genetic Algorithms

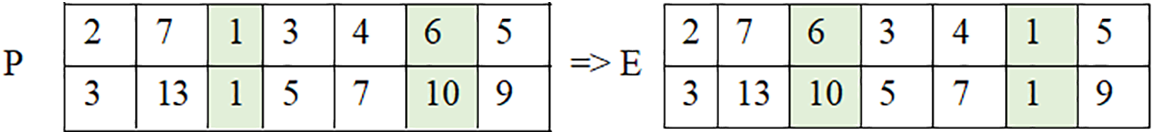
We have developed simple GAs using the traditional GA methods and GA procedures. They start with an arbitrary initial population, choose stronger chromosomes by using the roulette wheel selection technique, apply a selected crossover technique, and swap mutation technique. A simple GA is defined in Algorithm 2.

4  Computational Experiments

Four simple GAs with the crossover methods–PMX, OX, CX, and SC-with swap mutation (SM) are encoded in Visual C++ and tested on asymmetric GTSPLIB problem instances [11] executed on a laptop with the specification as Intel(R) Core(TM) i7-1065G7 CPU@1.30 GHz and 8.00 GB RAM under MS Windows 11. Every GA is run 50 times for every instance. For each instance, we report the best-known solution (BKS) reported in [30], the best-obtained solution (BOS), the average obtained solution (AOS), and the average computational time (ACT) (in seconds) to notice the BOS for the first time within 50 executions, by all algorithms. Since GAs are dominated by the parameters- population size (Ps), crossover probability (Pc), mutation probability (Pmt), and a stopping condition.

First, we check the behavior of the crossover techniques on the asymmetric instances. We set Ps = 100, Pc = 1.0, and at most 10n generations for stopping the GAs. Table 5 shows a comparative study among different GAs using different crossover methods with no mutation technique. We indicated the best results by boldfaces.

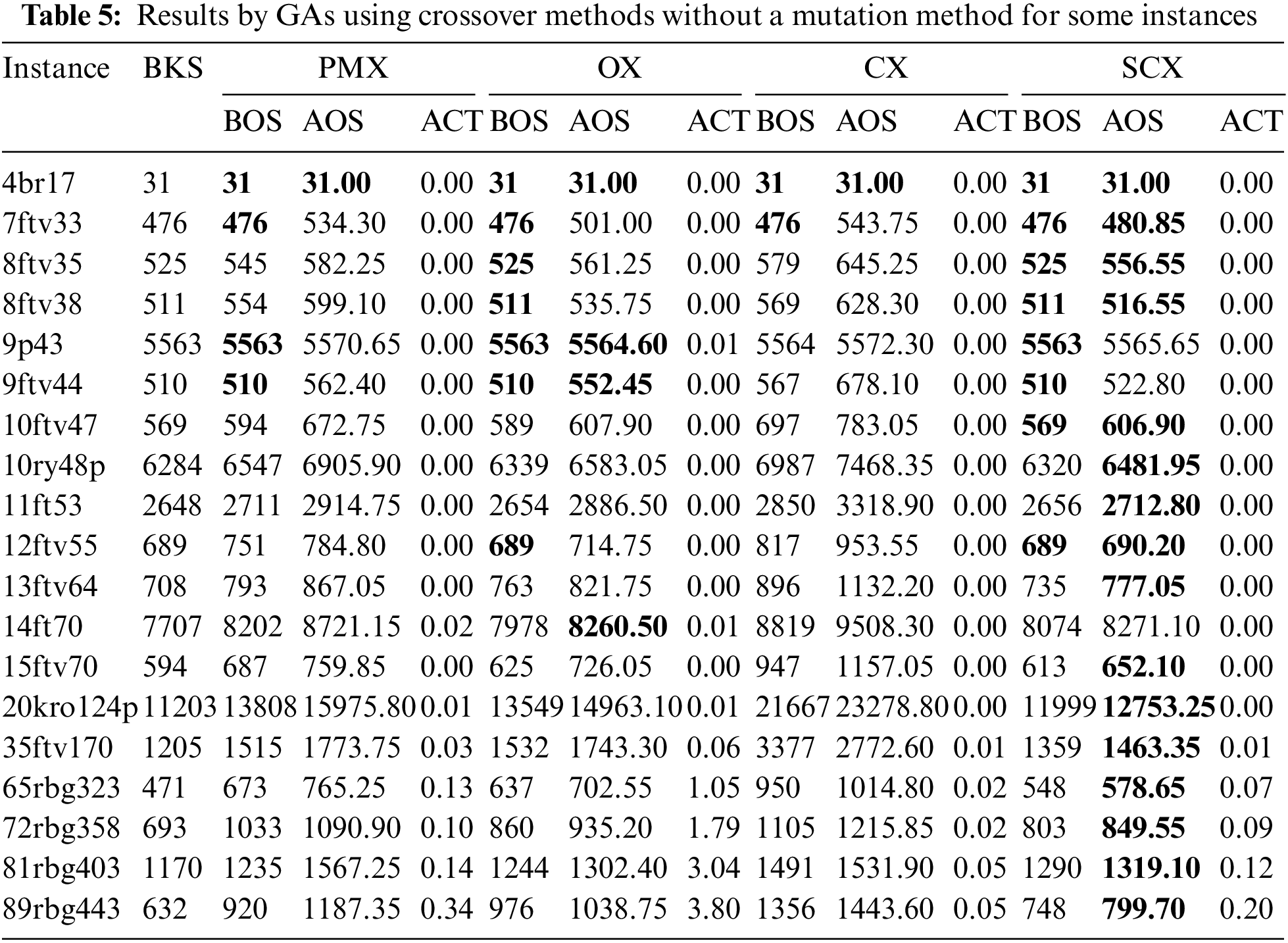
Observing the boldfaces in Table 5, the GA using SCX is shown to be the topmost one. Observing the best-obtained solution, GAs using PMX, OX, CX, and SCX, could obtain the BKS (minimum once in 50 runs) for four, seven, two, and eight instances respectively. So, we can say that SCX, OX and PMX are the topmost, second topmost and third topmost crossover methods, while CX is the most inferior one. Furthermore, observing the average obtained solution in the table, one can draw the same conclusion. Fig. 11 shows the percentage of the excess of the average obtained solution over BKS, which is calculated by the formula: Average Excess (%) = 100 × (AOS/BKS − 1). Looking at the figure, we have the same observation. So, this figure also validates the success of GA using SCX.

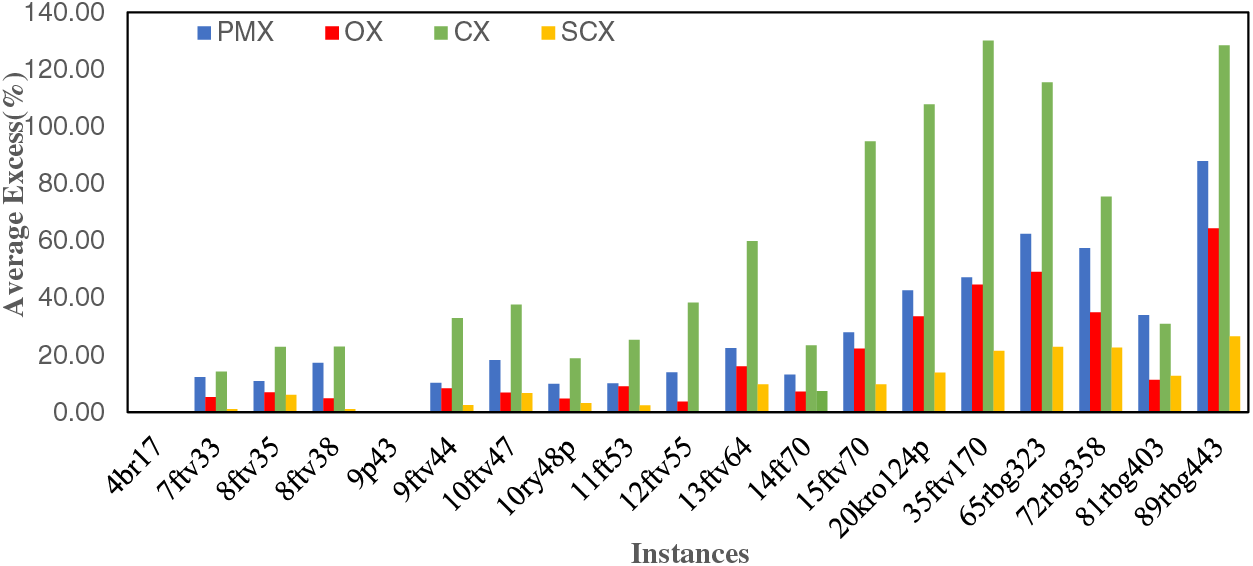
Figure 11: Average Excess (%) by crossover methods without a mutation for some instances

We further conducted a two-tailed Student t-test with a 5% significance level between GA using SCX and GAs using other crossover operators for the above instances to verify our above interpretations. We reported the results in Table 6. As presumed, SCX is the best-ranked crossover, OX is the second-best, PMX is the third-ranked, and CX is the most inferior.

We now run the GAs using crossovers and the swap mutation operator. Naturally, setting the same mutation probability for every instance is a very difficult job. After so many trials, we set Pc = 0.90, Pmt = 0.25, and at most 20n generations for stopping the GAs. We reported a comparative study amongst the GAs using various crossover techniques and SM in Table 7.

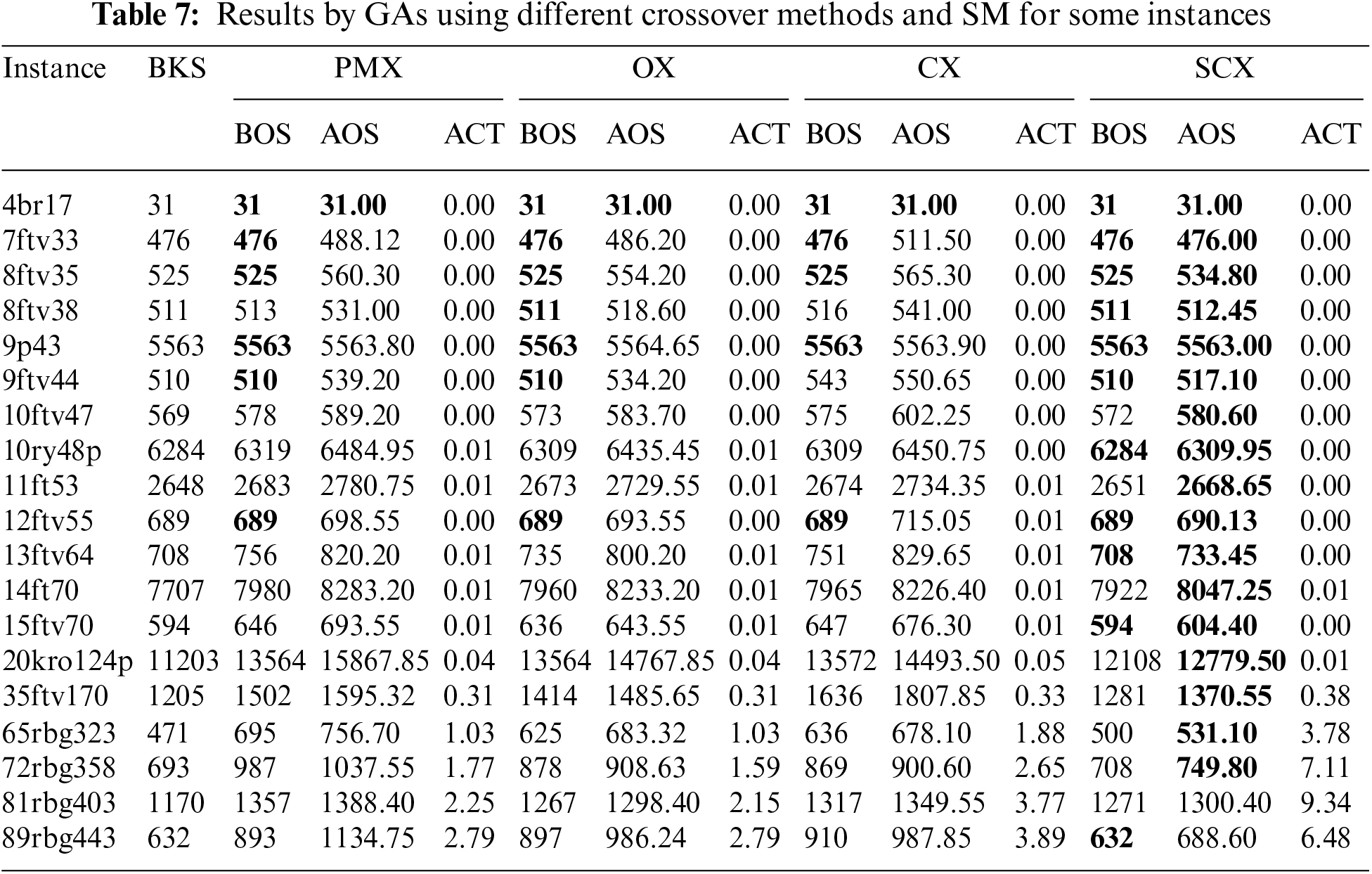
Observing the boldfaces in Table 7, the GA using SCX and SM is proven to be the topmost GA. Observing the best-obtained solution, the GA using PMX and SM, the GA using OX and SM, the GA using CX and SM, and the GA using SCX and SM, could obtain the BKS (minimum once in 50 runs) for six, seven, five, and eleven instances respectively. From this examination, we can confirm that the GA using SCX and SM is the topmost GA, the GA using OX and SM is the second topmost, the GA using PMX and SM is the third topmost, and the GA using CX and SM is the most inferior. Furthermore, observing the average obtained solution in the table, we can draw the same conclusion.

Looking at the average obtained solutions in Table 7, we can have a conclusion. GA using SCX and SM is the best one, GA using OX and SM is the second best, GA using CX and SM is the third best, and GA using PMX and SM is the worst. The results shown in Fig. 12 also prove the success of GA using SCX and SM.

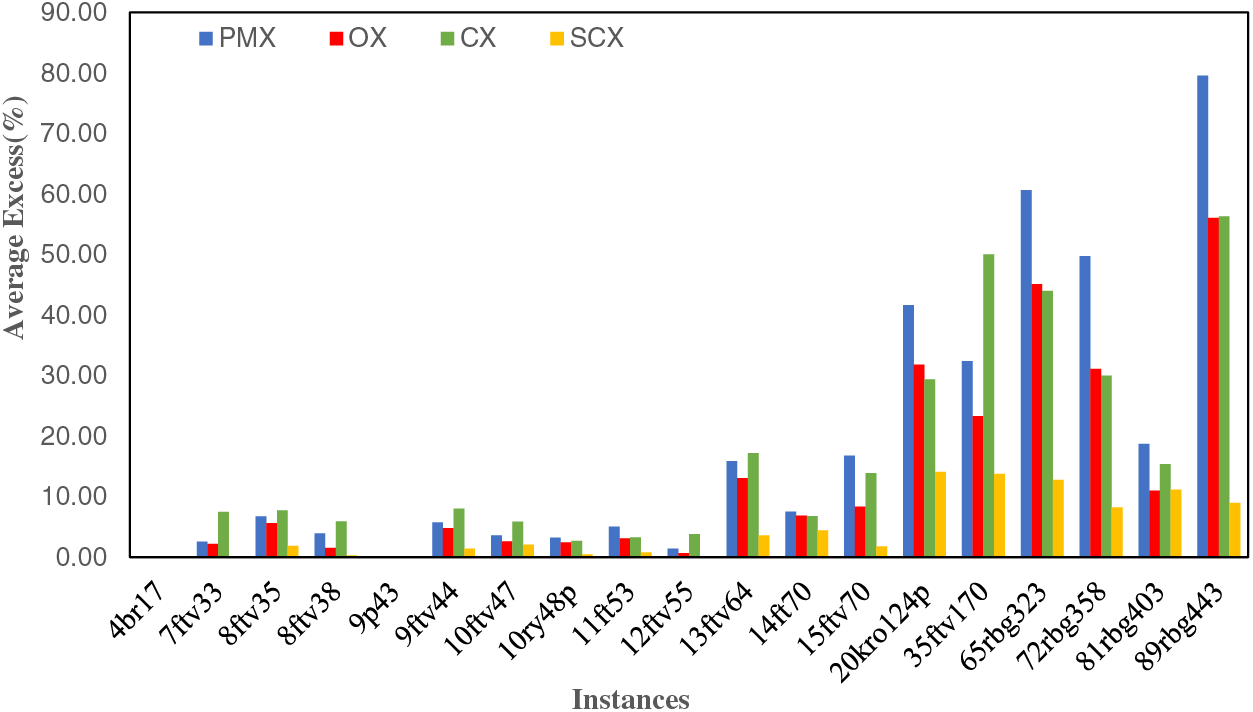
Figure 12: Average Excess (%) by crossover methods with SM operator for some instances

5  Conclusions and Future Work

We have modified ordered crossover (OX), sequential constructive crossover (SCX), partially mapped crossover (PMX), and cycle crossover (CX) for genetic algorithms (GAs) to find solutions to the generalized traveling salesman problem (GTSP). We then illustrated the working of the crossover techniques using an example and encoded the GAs using these crossover methods in Visual C++. Then a comparative study among PMX, OX, CX, and SCX for some asymmetric GTSPLIB instances. On the basis of solution quality, it is followed that crossover PMX is better than crossover CX, crossover OX is better than crossover PMX, and crossover SCX is the topmost. Furthermore, GAs using four crossover techniques and the swap mutation (SM) were compared and found that GA using PMX and SM is the most inferior and GA using SCX and SM is the topmost. Thus, SCX with or without a mutation technique is the topmost crossover technique. Our GA using SCX and SM could find average solutions whose average percentage of excesses from the best-known solutions is between 0.00 and 14.07 for our investigated instances.

In this current study, we aimed to compare the solutions by four crossover techniques to find solutions to the GTSP. Our aim was not to increase the solution quality by a GA using any crossover technique merged with a mutation technique. So, we did not utilize any local search method in GAs to increase the solution quality, and so, we could not find optimal/best-known solutions for many problem instances. However, the integration of a better local search method into the algorithm might solve those instances optimally that is under our future investigation. Furthermore, our SCX can also be modified to apply to other combinatorial optimization problems, which is also under our next investigation.

Acknowledgement: The authors extend their appreciation to the Deanship of Scientific Research, Imam Mohammad Ibn Saud Islamic University (IMSIU), Saudi Arabia, for financial support.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research, Imam Mohammad Ibn Saud Islamic University (IMSIU), Saudi Arabia, for funding this research work through Grant No. (221412020).

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Zakir Hussain Ahmed, Abdul Khader Jilani Saudagar; data collection and implementation: Maha Ata Al-Furhood, Shakir Khan; analysis and interpretation of results: Zakir Hussain Ahmed, Shakir Khan; draft manuscript preparation: Maha Ata Al-Furhood, Abdul Khader Jilani Saudagar; final manuscript preparation and revision: Zakir Hussain Ahmed, Abdul Khader Jilani Saudagar. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets generated and/or analyzed during the current study are available in the GTSPLIB repository, https://www.cs.rhul.ac.uk/home/zvero/GTSPLIB/ (accessed on 25/02/2024).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. L. Henry-Labordere, “The record balancing problem: A dynamic programming solution of a generalized salesman problem,” RIRO, vol. B-2, pp. 43–49, 1969. [Google Scholar]

2. B. Hu and G. R. Raidl, “Effective neighborhood structures for the generalized traveling salesman problem,” Lecture Notes in Comput. Sci., vol. 4972, pp. 36–47, 2008. [Google Scholar]

3. Z. H. Ahmed, “An exact algorithm for the clustered travelling salesman problem,” Opsearch, vol. 50, no. 2, pp. 215–228, 2013. doi: 10.1007/s12597-012-0107-0. [Google Scholar] [CrossRef]

4. P. C. Pop, O. Cosma, C. Sabo, and C. P. Sitar, “A comprehensive survey on the generalized traveling salesman problem,” Eur. J. Oper. Res., vol. 314, no. 3, pp. 819–835, 2024. doi: 10.1016/j.ejor.2023.07.022. [Google Scholar] [CrossRef]

5. V. Dimitrijevic, M. Milosavljevic, and M. Markovic, “A branch and bound algorithm for solving a generalized traveling salesman problem,” in Publikacije Elektrotehnic kog fakulteta. Serija Matematika, University of Belgrade, Serbia. vol. 7, pp. 31–35, 1996. [Google Scholar]

6. A. Prakash, U. Balakrishna, and J. Thenepalle, “An exact algorithm for constrained k-cardinality unbalanced assignment problem,” Int. J. Ind. Eng. Comput., vol. 13, no. 2, pp. 267–276, 2022. doi: 10.5267/j.ijiec.2021.10.002. [Google Scholar] [CrossRef]

7. Z. H. Ahmed, M. T. Choudhary, and I. Al-Dayel, “Effects of crossover operator combined with mutation operator in genetic algorithms for the generalized travelling salesman problem,” Int. J. Ind. Eng. Comput., vol. 15, no. 3, pp. 18, 2024. doi: 10.5267/j.ijiec.2024.5.004. [Google Scholar] [CrossRef]

8. J. Yang, X. Shi, M. Marchese, and Y. Liang, “An ant colony optimization method for generalized TSP problem,” Prog. Natural Sci., vol. 18, no. 11, pp. 1417–1422, 2008. doi: 10.1016/j.pnsc.2008.03.028. [Google Scholar] [CrossRef]

9. M. F. Tasgetiren, P. N. Suganthan, and Q. K. Pan, “A discrete particle swarm optimization algorithm for the generalized traveling salesman problem,” in Proc. GECCO 2007, London, UK, 2007, pp. 158–167. [Google Scholar]

10. Z. H. Ahmed, “Genetic algorithm for the traveling salesman problem using sequential constructive crossover operator,” Int. J. Biometrics & Bioinf., vol. 3, no. 6, pp. 96–105, 2010. [Google Scholar]

11. M. Fischetti, J. J. Salazar-Gonzales, and P. Toth, “A branch-and-cut algorithm for the symmetric generalized traveling salesman problem,” Operat. Res., vol. 45, no. 3, pp. 378–394, 1997. Accessed: Feb. 25, 2024. doi: 10.1287/opre.45.3.378. [Google Scholar] [CrossRef]

12. G. Laporte and Y. Norbert, “Generalized travelling salesman problem through n sets of nodes: An integer programming approach,” INFOR: Inf. Syst. Operat. Res., vol. 21, no. 1, pp. 61–75, 1983. doi: 10.1080/03155986.1983.11731885. [Google Scholar] [CrossRef]

13. J. Renaud, F. F. Boctor, and G. Laporte, “A fast composite heuristic for the symmetric traveling salesman problem,” INFORMS J. Comput., vol. 8, no. 2, pp. 134–143, 1996. doi: 10.1287/ijoc.8.2.134. [Google Scholar] [CrossRef]

14. J. Silberholz and B. Golden, “The generalized traveling salesman problem: A new genetic algorithm approach,” in Extending the Horizons: Advances in Computing, Optimization, and Decision Technologies. In Operations Research/Computer Science Interfaces Series, E. K. Baker, A. Joseph, A. Mehrotra, and M. A. Trick, Eds., Boston, MA, USA: Springer, 2007, vol. 37, pp. 165–181. [Google Scholar]

15. K. Helsgaun, “Solving the equality generalized traveling salesman problem using the Lin-Kernighan-Helsgaun algorithm,” Math. Program. Comput., vol. 7, no. 3, pp. 269–287, 2015. [Google Scholar]

16. M. El Krari, B. Ahiod, and B. El Benani, “A memetic algorithm based on breakout local search for the generalized traveling salesman problem,” Appl. Artif. Intell., vol. 34, no. 7, pp. 537–549, 2020. [Google Scholar]

17. X. Ren, X. Wang, Z. Wang, and T. Wu, “Parallel DNA algorithms of generalized traveling salesman problem-based bioinspired computing model,” Int. J. Comput. Intell. Syst., vol. 14, no. 1, pp. 228–237, 2021. [Google Scholar]

18. I. Khan, M. K. Maiti, and K. Basuli, “A random-permutation based GA for generalized traveling salesman problem in imprecise environments,” Evol. Intell., vol. 16, pp. 229–245, 2023. [Google Scholar]

19. O. Cosma, P. C. Pop, and L. Cosma, “A novel memetic algorithm for solving the generalized traveling salesman problem,” Logic J. IGPL, vol. jzae019, pp. 444, 2024. doi: 10.1093/jigpal/jzae019. [Google Scholar] [CrossRef]

20. S. L. Smith and F. Imeson, “GLNS: An effective large neighborhood search heuristic for the generalized traveling salesman problem,” Comput. & Operat. Res., vol. 87, no. 5, pp. 1–19, 2017. doi: 10.1016/j.cor.2017.05.010. [Google Scholar] [CrossRef]

21. J. Schmidt and S. Irnich, “New neighborhoods and an iterated local search algorithm for the generalized traveling salesman problem,” EURO J. Comput. Optim., vol. 10, pp. 100029, 2022. doi: 10.1016/j.ejco.2022.100029. [Google Scholar] [CrossRef]

22. D. E. Goldberg, Genetic algorithms in search, optimization, and machine learning. New York, USA: Addison-Wesley Longman Publishing Co., 1989. [Google Scholar]

23. D. E. Goldberg and R. Lingle, “Alleles, loci and the travelling salesman problem,” in Proc. ICGA, Pittsburgh, PA, USA, 1985, pp. 154–159. [Google Scholar]

24. L. Davis, “Job-shop scheduling with genetic algorithms,” in Proc. ICGA, Pittsburgh, PA, USA, 1985, pp. 136–140. [Google Scholar]

25. I. M. Oliver, D. J. Smith, and J. R. C. Holland, “A study of permutation crossover operators on the travelling salesman problem,” presented at the 2nd Int. Conf. on Genetic Algorithms, Cambridge, MA, USA, Jul. 28–31, 1987, pp. 224–230. [Google Scholar]

26. Z. H. Ahmed, “A comparative study of eight crossover operators for the maximum scatter travelling salesman problem,” Int. J. Adv. Comput. Sci. Appl. (IJACSA), vol. 11, no. 6, pp. 317–329, 2020. doi: 10.14569/issn.2156-5570. [Google Scholar] [CrossRef]

27. M. A. Al-Furhud and Z. H. Ahmed, “Experimental study of a hybrid genetic algorithm for the multiple travelling salesman problem,” Math. Prob. Eng., vol. 2022, pp. 13, 2020. [Google Scholar]

28. Z. H. Ahmed, N. Al-Otaibi, A. Al-Tameem, and A. K. J. Saudagar, “Genetic crossover operators for the capacitated vehicle routing problem,” Comput. Mater. Contin., vol. 74, no. 1, pp. 1575–1605, 2023. doi: 10.32604/cmc.2023.031325. [Google Scholar] [CrossRef]

29. W. Banzhaf, “The molecular traveling salesman,” Biol. Cybern., vol. 64, no. 1, pp. 7–14, 1990. doi: 10.1007/BF00203625. [Google Scholar] [CrossRef]

30. D. Ben-Arieh, G. Gutin, M. Penn, A. Yeo, and A. Zverovitch, “Transformations of generalized ATSP into ATSP,” Oper. Res. Lett., vol. 31, no. 5, pp. 357–365, 2003. doi: 10.1016/S0167-6377(03)00031-2. [Google Scholar] [CrossRef]