Research on Feature Matching Optimization Algorithm for Automotive Panoramic Surround View System

1  Introduction

The automotive panoramic surround view system combines partial road images from multiple vehicle-mounted cameras to generate real-time 360° panoramic views centered on the current vehicle. This significantly enhances the vehicle’s perception of the surrounding road environment and improves driving safety [1–4]. The key to this technology is efficiently matching high-dimensional feature points across different partial road images. Given the need for real-time road environment perception in intelligent driving, accurately matching these feature points has become a primary focus and challenge in the field.

Currently, researchers have embarked on investigations into feature matching for high-dimensional images, broadly falling into four categories:

(i)   Brute-Force Matching: These algorithms make similarity comparison between the feature points to be matched and the reference feature points one by one, and takes the reference feature points with the highest similarity as the best match. Alaee et al. [5] utilized a brute-force matching method based on Euclidean distance, followed by a ratio test using a dynamic threshold to determine matched point pairs, effectively enhancing matching robustness. Sun et al. [6] proposed a bidirectional brute-force matching strategy. This strategy computes the distance ratio between the nearest and second nearest neighbors for the pair of feature points to be matched. It adjusts the threshold according to the change of the number of feature point pairs, and solves the problem of one-to-many matching effectively. Although these algorithms can quickly and accurately match the features with a small number of features and low dimension, they are less efficient when matching high-dimensional features.

(ii)   Feature Dimensionality Reduction: These algorithms reduce computational complexity and eliminate redundant information by transforming the high-dimensional feature representation of images into a lower-dimensional representation. Zou et al. [7] introduced a circular region descriptor extraction method based on the SURF algorithm, reducing the dimensionality of descriptors. They utilized the minimum Euclidean distance criterion for matching, effectively enhancing matching speed. Wang et al. [8] proposed a feature dimensionality reduction method based on local linear embedding. While reducing dimensionality, they retained the local linear relationships of features, enhancing robustness in deformation and rotation matching. Although these algorithms can optimize the dimension of feature descriptors to a certain extent and improve the matching speed, the dimensionality reduction degree is limited, and they are not suitable for massive high-dimensional feature points between road images.

(iii)   Metaheuristic Feature Matching: These algorithms optimize the feature matching process by using meta-heuristic algorithms, such as genetic algorithm, particle swarm optimization algorithm, ant colony algorithm, etc. Tran et al. [9] proposed a variable-length particle swarm optimization algorithm, enabling particles to have different and shorter lengths, thereby defining a smaller feature matching search space and effectively enhancing matching speed. Ghosh et al. [10] introduced a feature selection technique based on ant colony optimization algorithms, combining them with wrapping and filtering methods, and utilizing filtering methods for feature subset evaluation, thereby reducing computational complexity. Such algorithm optimizes the feature matching process by simulating biologically inspired thinking, which is flexible and efficient. However, its performance is limited by the design of heuristic rules, and it may encounter the problem of local optimal solution in the feature matching process.

(iv)   Deep Learning Matching Algorithms: These algorithms obtain the matching rules between high-dimensional feature points through large-scale data learning, and realizes efficient and accurate feature point matching. Ma et al. [11] used a Convolutional Neural Network (CNN) based on homography transformation to extract feature points. They employed a neural network with a cross-attention mechanism for high-dimensional feature matching, effectively addressing the issue of poor feature matching under large disparities and distortion transformations. Chaudhari et al. [12] combined a neural network with image grayscale information to form a feature descriptor grid. They used same-name point constraints to match regions, effectively addressing the matching problem caused by abrupt feature content changes across different viewpoints. Such algorithms can automatically learn feature representations and process high-dimensional feature relationships, but feature matching based on artificial intelligence requires large computational resources, is poor in real-time, and is more sensitive to abnormal data, which is prone to overfitting.

It can be seen that the current algorithms for matching high-dimensional features suffer from low matching efficiency and poor real-time performance. There is still considerable room for improvement before these algorithms can be practically applied in automotive panoramic surround view systems. To address these issues and meet the real-time and matching accuracy requirements for local road image stitching in automotive panoramic surround view systems, this paper proposes a high-performance dimensionality reduction parallel algorithm, named SUPD (SURF combining PCA and DHF), based on the SURF algorithm.

Addressing the computational complexity caused by high-dimensional descriptors in traditional SURF algorithm [13–15], the SUPD employs Principal Component Analysis (PCA) to project the feature point set onto a lower-dimensional space. It also utilizes the Square Euclidean Distance (SED), which has lower computational cost, for ranking estimation in feature point matching. Additionally, to eliminate mis-matching, the SUPD employs the Double Heap Filter (DHF) for feature point purification. This involves re-projecting the matched point pairs in the PCA space back into the high-dimensional space for verification, effectively eliminating erroneous matched point pairs. Furthermore, the SUPD improves the feature point matching process by transforming the traditional sequential matching process into a grouped matching process, making full use of multi-core computing resources and enhancing the matching speed of image feature points.

The contributions of this algorithm are as follows:

(1)   Dimensionality reduction projection is applied to high-dimensional image feature points, replacing the high-dimensional Euclidean distance with the square Euclidean distance in a lower-dimensional space, thereby reducing computational overhead by reducing the dimensionality of feature points and avoiding square root calculations.

(2)   To eliminate erroneous matches, the Double Heap Filter algorithm is proposed to filter and refine the matched point pairs, enhancing the matching accuracy of the SUPD.

(3)   To enhance the concurrency performance of the SUPD algorithm, a multi-core parallel matching strategy is proposed. This strategy involves parallel matching of reference feature points in a grouped manner, thereby improving the efficiency of feature point matching.

2  System Model

Consider the matching process of the partial road images Git and Gjt captured by the neighboring car-mounted camera positions Li and Lj at time t. Define dit(ki) as the feature point with index ki in Git at time t. The set of feature points in image Git can be represented as Dit = {dit(k1),dit(k2),⋯}. Let Dit be the set of query feature points and Djt be the set of reference feature points. In the matching process, the total number of matched point pairs is obtained by the ratio of nearest neighbor distance to the second nearest neighbor distance, denoted as Ns(Dit,Djt). To achieve the correct fusion of partial road images Git and Gjt, it is necessary to use a transformation matrix to map the feature point coordinates in Git to the corresponding feature point coordinates in Gjt, thereby establishing a geometric correspondence between the two images. Let matrix H represent the transformation matrix between Git and Gjt, and Nh represent the number of matched point pairs satisfying the transformation matrix H.

Define σi(ki) as the time to complete matching of the query feature point dit(ki), i.e., the time taken to find the nearest reference feature point in Djt. Then, the total time t to complete matching of all query feature points is shown in Eq. (1).

t(σi,n)=∑i=1nσi(ki)(1)

where n=|Dit| is the overall number of query feature points.

Define the matching accuracy ξ as the percentage of matched point pairs Nh satisfying the transformation matrix H out of total matched point pairs Ns(Dit,Djt), as shown in Eq. (2).

ξ(Ns,Nh)=NhNs(Dit,Djt)⋅100%(2)

Define the matching efficiency E as the matching accuracy ξ(Ns,Nh) divided by the feature matching time t(σi,n), the matching process of partial road images can be described as a mathematical optimization problem as shown in Eq. (3), based on the above definitions.

maxE(σi,Ns,Nh)=ξ(Ns,Nh)t(σi,n)=Nh(∑i=1nσi(ki))⋅Ns(Dit,Djt)(3)

s. t. φ≥4(4)

where Eq. (3) represents the objective function for completing feature matching in the partial road images matching process. A higher value of E indicates a better matching efficiency of the algorithm. Constraint (4) requires the number of correctly matched feature point pairs φ to satisfy the generation condition of the transformation matrix.

3  Implementation of SUPD

In order to meet the requirements of panoramic surround view systems in terms of matching accuracy and real-time performance, this paper proposes a novel panoramic image feature matching algorithm named SUPD. This algorithm integrates the advantages of PCA and DHF algorithms, aiming to perform dimensionality reduction matching and purification filtering on high-dimensional feature points. Simultaneously, by employing a parallel matching strategy to fully utilize computational resources, the algorithm further accelerates the matching efficiency.

3.1 Distance Ranking Based on PCA Dimensionality Reductions

Principal Component Analysis (PCA) is a commonly used dimensionality reduction technique. Its fundamental concept involves projecting high-dimensional data onto a lower-dimensional space, extracting essential features, and reducing redundant information, thereby offering a more concise and efficient data representation for subsequent data analysis and modeling processes [16–18]. Applied to the domain of feature matching, PCA employs a projection matrix P to project the feature point set from the high-dimensional original space to a lower-dimensional space (PCA space) for distance estimation. This estimation predicts the similarity between query and reference feature points.

In this paper, singular value decomposition is used to obtain the projection matrix P. For the matrix S composed of eigenvectors of feature points in the original space, the singular value decomposition is shown in Eq. (5).

S=UZVT(5)

where U and V are the eigenvectors of SST and STS, respectively. Z=diag(γ1,γ2,⋯,γn) is a diagonal matrix, with its diagonal elements being the square roots of the eigenvalues.

From Eq. (5), the eigenvalues and corresponding eigenvectors of matrix S can be obtained. According to the eigenvalues, cumulative contribution rate μ is computed, and the number of principal components c corresponding to achieving the cumulative contribution rate is determined using Eq. (6).

μ=∑ecλe∑emλe(6)

where m represents the total number of principal components. Reference [19] showed the value of μ is generally taken to be between 85% and 95%. Here, m represents the total number of principal components, λe signifies the eigenvalue of matrix S, and e represents the index of the eigenvalue, with its range spanning from 1 to m.

Once the number of principal components c corresponding to achieving the cumulative contribution rate is determined, the number of retained eigenvectors is obtained, which further yields the projection matrix P.

After obtaining the projection matrix P, the reference feature point set R={r1,r2,⋯,rn} and query feature point qi are projected into the lower-dimensional PCA space, as shown in Eq. (7).

{R′=PR={r1′,⋯,rn′}qi′=Pqi(7)

Upon completing the projection, the distance between each reference feature point ri′ and query feature point qi′ in the PCA space can be calculated. To reduce computational cost, the squared Euclidean distance SED(ri′,qi′) is employed to estimate the distance between ri′ and q′, as shown in Eq. (8).

SED(ri′,qi′)=‖ri′,qi′‖2=∑n=1w(qin′−rin′)2(8)

where w is the dimension of the PCA space.

The nearest reference feature point ri′ to query feature point q′ can be obtained by ranking the SED values, generating matched point pairs. Since the principal components retain the crucial information between points in the original space, the ranking of distances between any two points qi and rj in the high-dimensional space and the corresponding projection points qi′ and rj′ in the low-dimensional space are closely related.

As shown in Fig. 1a, considering a three-dimensional vector where q represents the query feature point and A,B,C,D represent feature points. All feature points are projected into the PCA space for dimensionality reduction, resulting in the projection points q′,A′,B′,C′,D′. The distance ranking is presented in Table 1. In the PCA space, the order of reference feature points based on SED ranking is A′-B′-C′-D′, which is the same as the ranking of Euclidean distances (ED) in the original three-dimensional spaceA-B-C-D. Finally, matched point pairs are determined by the ratio of distances between the nearest neighbor and the second nearest neighbor, as shown in Eq. (9).

dqAdqB<ℛ(9)

where dqA represents the distance between the query point q and its nearest point A, dqB represents the distance between the query point q and its second nearest point B, and ℛ is the distance ratio threshold, typically set as ℛ=0.8.

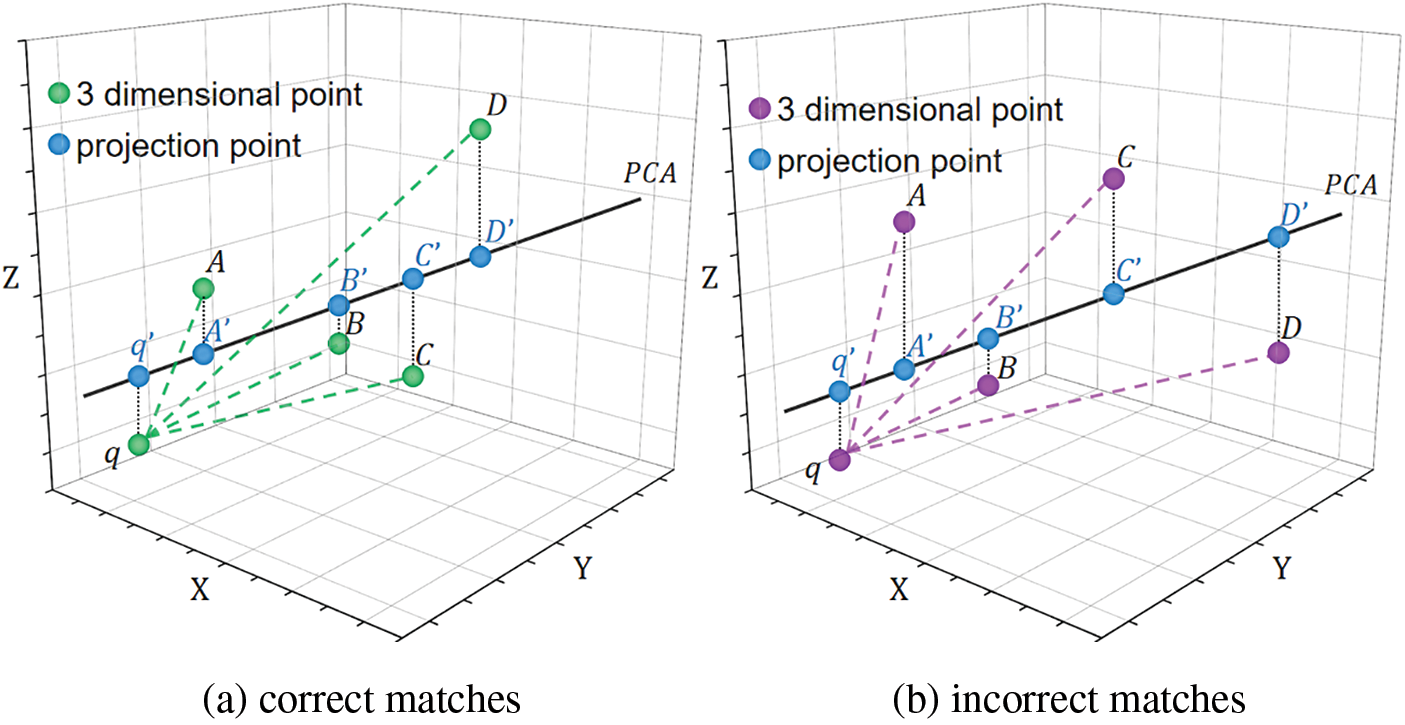
Figure 1: Three-dimensional feature points and their projections in the PCA space. (a) correct matches. (b) incorrect matches

3.2 Dual-Heap Filtering

Although using the squared Euclidean distance ranking in the low-dimensional PCA space can predict the similarity between query points and reference feature points, occasional incorrect matches may occur, as depicted in Fig. 1b and Table 2. In the PCA space, the distance ranking is A′−B′−C′−D′, while in the original three-dimensional space, the distance ranking is B−A−C−D. Relying solely on the distance ranking in the PCA space for matching could lead to erroneous matched point pairs.

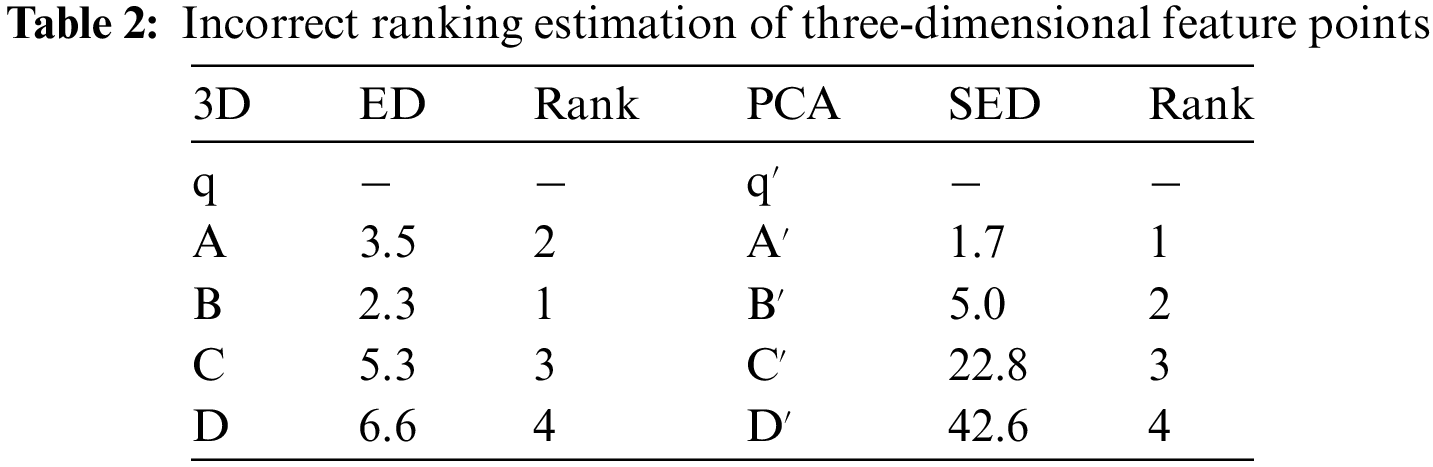
To address the aforementioned issue, this paper proposes a Dual-Heap Filtering (DHF) algorithm based on PCA ranking prediction. DHF maintains two filtering heaps: one in the PCA space called the filtering heap, and the other in the original space called the validation heap. Each heap retains the top k nearest neighbor distance results, providing filtering for the projected feature points. The structure of DHF is illustrated in Fig. 2.

Figure 2: Illustration of the dual-heap filtering

When using the DHF algorithm to filter feature points, the first step is to calculate the squared Euclidean distance (SED) between the projected reference feature point and the query point in the PCA space. If this squared Euclidean distance is greater than the maximum value in the filtering heap, the reference feature point is discarded. If the squared Euclidean distance is less than the maximum value in the filtering heap, the Euclidean distance (ED) between the reference feature point and the query point in the original space is then calculated. If this Euclidean distance is greater than the maximum value in the validation heap, the reference feature point is discarded. If it is less than the maximum value, it is considered a correct judgment. The respective Euclidean distance value and squared Euclidean distance value are then inserted into the validation heap and the filtering heap, respectively, replacing their initial maximum values and reordering them accordingly. The specific code implementation is as follows:

The relationship between the adjustment factor α and the number of the nearest neighbors is k′=αk. The parameter α adjusts the size of the filtering heap, effectively reducing the phenomenon of poor filtering performance caused by using only a portion of the principal component information. The values of α and k will be achieved through experimental analysis.

3.3 Multi-Core Parallel Matching

Traditional matching algorithms typically involve matching according to the index order of reference feature points, with each matching task performed on a per-reference-point basis. For instance, matching algorithms utilizing kd-trees necessitate continuous searching of reference feature points based on tree-like indexing [20–22]. However, due to the large number of reference feature points overall, this matching approach imposes a significant computational burden during the matching process of individual query points, thereby complicating the task of load balancing within the system.

Due to the relatively independent nature of the matching tasks for each reference feature point in the proposed algorithm, it is particularly suitable for parallel processing when dealing with a large number of reference feature points [23–25]. To achieve this, we have designed a multi-core parallel matching strategy, dividing the matching tasks into multiple subsets and concurrently assigning these subsets to multiple processing cores for parallel computation, as illustrated in Fig. 3.

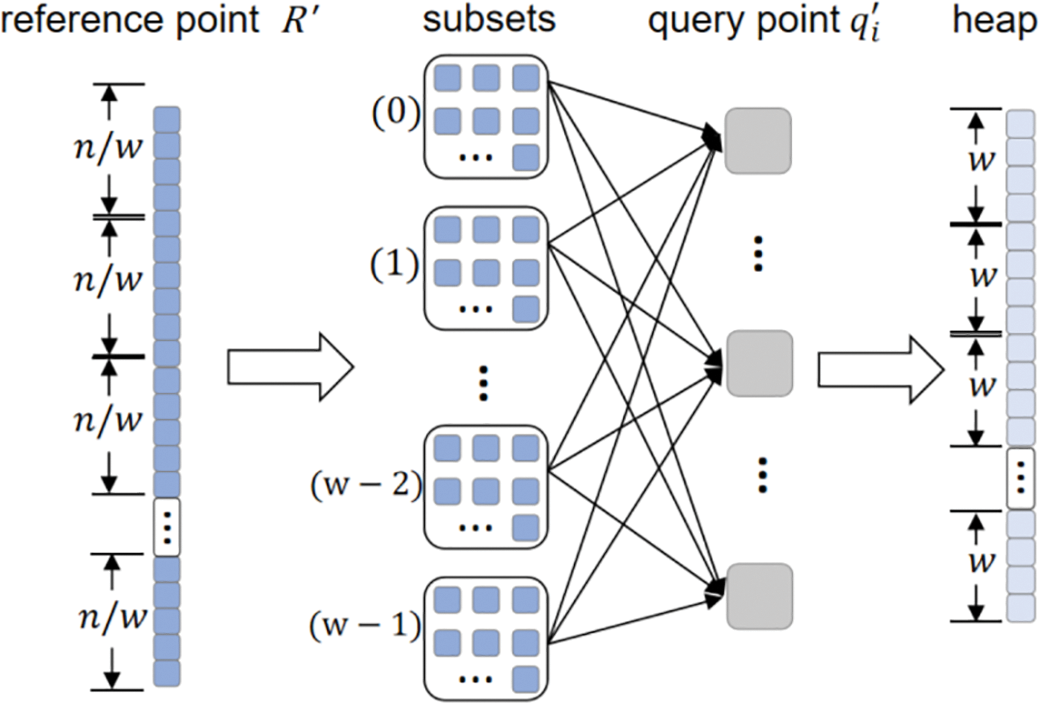
Figure 3: Schematic diagram of multi-core parallel matching

During feature matching, the first step involves partitioning the reference feature point set R′, which has been projected into the PCA space, into w subsets. Subsequently, while sequentially matching each projected query point qi′, these subsets are allocated to different threads for parallel computation within the system. Each subset generates its own k nearest neighbor results. Ultimately, a max-heap of size k is maintained, where the k nearest neighbor results obtained from each subset serve as the initial elements of the max-heap. Continuous adjustment of the max-heap is performed by comparing distance metric values, resulting in the final k nearest neighbor results. This parallel matching strategy breaks down the originally serial computational tasks into multiple smaller tasks, distributing them among multiple processor cores for simultaneous computation. This fully utilizes computational resources and enhances the efficiency of matching feature points. The specific implementation code is presented as follows:

4  Performance Analysis

4.1 Time and Space Complexity

In this section, brute-force search (BF) will be used as a comparative algorithm to analyze the time and space complexity of the SUPD. For the matching of a single query feature point, the BF algorithm calculates and matches the distances of all reference feature points in the original space through exhaustive search [26–28]. Due to the high dimensionality of the original space, the BF algorithm needs to traverse all reference feature points, resulting in a high space complexity of O(ND), where N is the number of reference feature points, and D is the dimensionality of the original high-dimensional space.

However, in the actual matching process, if most unnecessary distance calculations are avoided, the algorithm’s performance can be significantly improved. The SUPD precisely possesses this characteristic. This algorithm first projects feature points into a low-dimensional PCA space and then utilizes the K-nearest neighbors (KNN)-based DHP algorithm for filtering. Although these two steps introduce some computational overhead, they play a crucial role in reducing the computational load in the subsequent matching process.

In the dimensionality reduction process, Principal Component Analysis is used to project feature points from high-dimensional space to low-dimensional space, thereby eliminating redundant information among features. Although PCA involves calculating the covariance matrix and decomposing eigenvectors, which may incur some computational overhead, it can significantly reduce the amount of data to be processed in the subsequent matching steps. Therefore, from an overall performance perspective, this overhead is worthwhile. Next, the DHP utilizes the KNN for filtering. The space complexity of the KNN mainly stems from the construction of the tree, while the tree search process does not require additional storage space [29–30]. Although tree construction may introduce some additional computational overhead, this overhead is negligible compared to the subsequent avoided matching computations. By filtering out most of the unlikely matching feature points, the DHP significantly improves the efficiency of the matching process.

Considering these computational overheads, the space complexity of the SUPD after dimensionality reduction and filtering can be approximated as O(Nd), where d is the dimension of the PCA space. From subsequent experimental results, it can be inferred that d is much smaller than D. Furthermore, to fully utilize computational resources, this paper divides the reference feature point set into w subsets and assigns each subset to a thread for parallel matching. This parallelization strategy further reduces the space complexity to O(Ndw), which is much smaller than the space complexity of the BF algorithm, O(ND).

Suppose the total time required for the BF algorithm to compute all distances for a single query feature point in the original space is denoted as TD. However, the SUPD successfully reduces this time through dimensionality reduction and multi-core parallel matching. By employing principal component analysis to project feature points into a d-dimensional space, the effective reduction in dimensionality enables the computation time for matching distances of the given query feature point to be reduced to dDTD. Furthermore, with the utilization of a multi-core parallel matching strategy, the reference feature point set awaiting matching with the query feature point is divided into w subsets, allowing the query feature point to match simultaneously with the reference feature points in these w subsets. This further shortens the total matching time to dDwTD. This indicates that the efficiency of the SUPD is significantly better than that of the BF algorithm.

4.2 Parameter Range

The principal parameters of the SUPD encompass the number of principal components (c) required to achieve the cumulative contribution rate, the number of nearest neighbors (k) and adjustment factor (α) for DHF, and the number of subset divisions (w) into which the projected reference feature point set is partitioned. In this section, we analyze the specific value ranges for these parameters, thereby laying the groundwork for subsequent parameter setting experiments.

Firstly, when employing Principal Component Analysis for dimensionality reduction, it is essential to determine the number of retained principal components, namely the reduced dimensionality. Having too many principal components (large c values) will result in the data still maintaining a relatively high dimensionality after reduction, increasing computational overhead. Conversely, too few principal components will result in the reduced-dimensional data being unable to fully capture the characteristics of the original data. Therefore, the selection of an appropriate number of principal components is crucial. The retained number of principal components (c) can be determined by calculating the cumulative contribution rate (μ). According to reference, a typical range for the value of c is between 85% to 95%. This paper suggests selecting the lower limit cl corresponding to μ=65%, and the upper limit cu corresponding to μ=95%. Consequently, the range for the selection of c is set as [cl,cu], with the optimal value for c being determined through experimentation, thereby achieving optimal dimensionality reduction.

Subsequently, the DHP is employed to refine and extract matching point pairs. The size of the filtering heap is determined by α×k, where k signifies the count of nearest neighbors within the validation heap. The validation heap serves to confirm the preliminary refined matching point pairs within the filtering heap; therefore, an excessively large k is inadvisable. In most k nearest neighbors-based feature matching algorithms, k is commonly set to 2. Accordingly, this paper also designates k as 2. The adjustment factor α for the filtering heap influences the count of matching point pairs obtained after initial filtering. If α is set too large, the computational complexity will increase due to the use of Euclidean distance in the validation heap calculation in the original high-dimensional space. Conversely, setting α excessively small might lead to erroneous filtering, where a reference feature point in the PCA space has a distance greater than the maximum value in the filtering heap. However, in the original space, the distance between that point and the query point is smaller than the maximum value in the verification heap. This can result in mistakenly filtering out that point during actual matching. Moreover, when α=1, the size of the filtering heap is equal to that of the validation heap, and the role of the filtering heap cannot be demonstrated. Hence, the selection range of α is set as [2,5], and the most appropriate α value is determined through experiments to achieve the best filtering effect.

Finally, the projected reference feature point set is divided into w subsets for parallel matching. The count of subsets w impacts whether computational resources can be utilized to the maximum extent. The quantity of subset divisions determines the granularity of parallel tasks. Smaller task granularity reduces memory access conflicts, and facilitates load balancing [31–32]. However, excessively small divisions may lead to frequent communication and synchronization operations, increasing computational overhead [33–34]. Additionally, while determining the count of subset divisions consideration should be given to the count of cores on the experimental platform. The count of cores reflects the upper limit of tasks that can be executed in parallel. Thus, to maximize the utilization of computational resources, this paper sets the range for the count of subset divisions as [2,C+2], where C represents the maximum count of cores on the experimental platform. The optimal value for w is determined through experimentation, thus achieving the goal of optimizing algorithm performance.

5  Evaluation

5.1 Experimental Setup

5.1.1 Experimental Platform

The hardware platform for this experiment is an AMD Opteron Processor 6376 CPU @ 2.30 GHz with 16 MB L3 cache, 16 cores, 32 logical processors, and 128 GB of memory. The software platform consists of a 64-bit Windows 10 operating system, Visual Studio Code, and OpenCV 4.

5.1.2 Datasets

To meet the research requirements, this paper utilized a self-constructed dataset comprising 100 sets of local road images with a certain degree of overlap. The images are sized at 1000 pixels × 700 pixels and are formatted as JPG. The dataset covers various road scenarios, including urban roads, rural lanes, highways, etc. It exhibits significant diversity in perspectives, lighting conditions, and weather conditions to better reflect the complexity of real road environments.

5.1.3 Evaluation Metrics

Total Matching Time (total_time): The sum of feature extraction Te and feature matching time Tm, where the feature matching time includes the time spent on excluding incorrect matches and performing local optimizations. Its definition is shown in Eq. (10).

tota_time=Te+Tm(10)

Matching Accuracy (matching_accuracy): As an evaluation metric for algorithm precision, matching accuracy is the percentage of correctly matched point pairs Nc out of the total matched point pairs Ns. Its definition is shown in Eq. (11).

matching_accuracy=NcNs⋅100% (11)

Root Mean Square Error of Matches (MERD): The root means square error between the coordinates (xi,yi) of query feature points and the coordinates (xi′,yi′) of reference feature points transformed by the projection transformation model fh(x). MERD can effectively assess the matching quality of the overall point pairs between query images and reference images. A smaller MERD indicates better overall matching quality, while a larger MERD indicates poorer overall matching quality. Its definition is shown in Eq. (12).

MERD=1Ns∑i=1Ns‖(xi,yi)−fh(xi′,yi′)‖2(12)

5.2 Parameter Determination

This section establishes the precise values of each parameter when the algorithm achieved optimal performance through experimentation, based on the parameter ranges analyzed in Section 4.2. Before the experiments were conducted, the evaluation criteria for parameter selection were first defined as follows:

a)   Speedup Ratio: Matching time of brute-force matching divided by the matching time of the algorithm proposed in this paper.

b)   Acceleration Ratio: Serial matching time of the algorithm divided by parallel matching time.

c)   Comprehensive Efficiency Index: This index is obtained by multiplying the speedup ratio with the matching accuracy rate, thereby comprehensively considering the algorithm’s runtime and matching precision.

According to the analysis in Section 4.2, it is calculated that the number of principal components corresponding to the cumulative contribution rates of 55% and 95% for the dataset are 5 and 20, respectively. Therefore, this study analyzes the number of principal components, denoted as c, within the range of [5,20] to evaluate their impact on algorithm performance. Additionally, considering that the number of principal components, c, and the adjustment factor α of the filter heap may mutually influence each other within different ranges of values, while the subset partition number, w, remains relatively independent. Thus, with the assumption of w=10, the experimental analysis is conducted to investigate the effects of the number of principal components, c, and the adjustment factor α on algorithm performance.

The experimental results are shown in Fig. 4, demonstrate a similar trend between the comprehensive efficiency index and the number of principal components under different conditions of the filter heap adjustment factor α. Within the specified range, smaller values of α correspond to larger overall comprehensive efficiency index values. Simultaneously, as the number of principal components, c, increases, the retained feature information also increases correspondingly, leading to a significant increase in matching accuracy and thereby an increase in the comprehensive efficiency index. However, when the value of c exceeds a certain threshold, the improvement in matching accuracy gradually stabilizes, while the matching time increases accordingly, resulting in a decrease in the comprehensive efficiency index. Therefore, based on the experimental results, the optimal (c,α) for the dataset in this paper is determined to be (14,2).

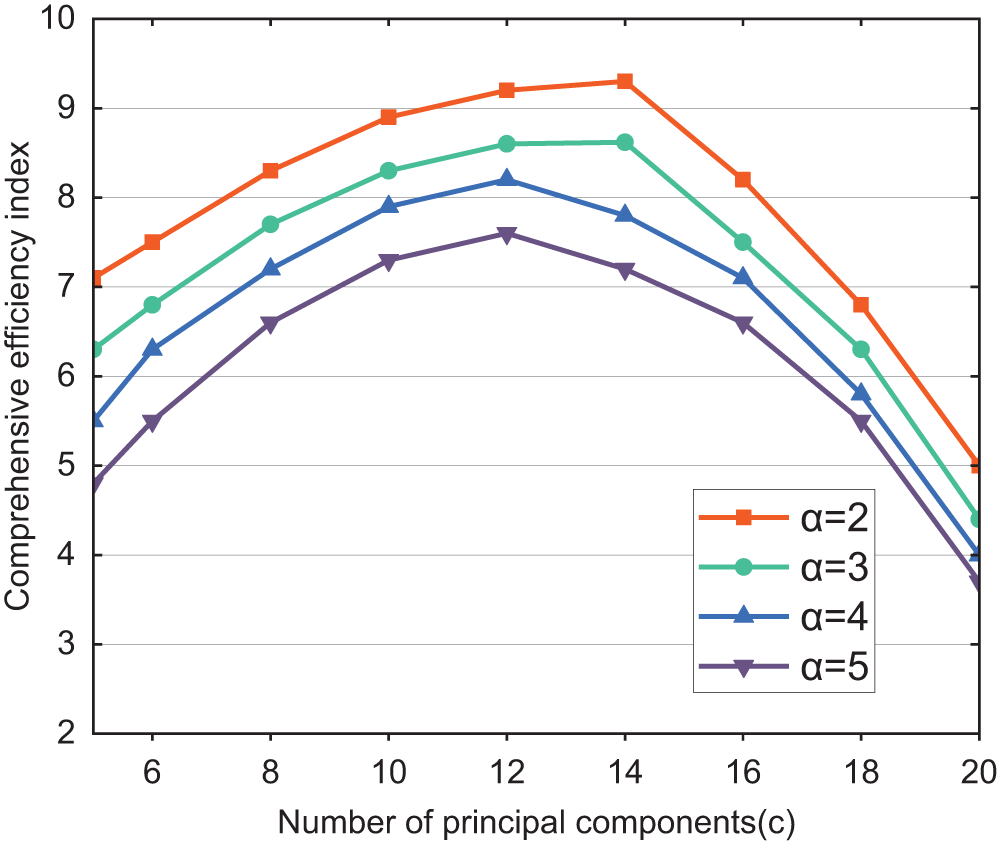
Figure 4: Influence on the performance of the algorithm for the number of principal components (c) and adjustment factor (α)

Considering the relatively high independence of the number of subset divisions (w), which is unaffected by the number of principal components and the adjustment factor of the filtering heap, this study will conduct separate experiments to analyze its influence on algorithm performance.

The experimental results are depicted in Fig. 5. With the increase of w, the acceleration ratio demonstrates a rising trend. When w reaches the maximum number of cores available on the experimental platform, the acceleration ratio reaches its peak. This indicates optimal utilization of computational resources, resulting in minimized matching time. However, it is noteworthy that surpassing the maximum number of cores may lead to parallel computing issues, such as increased scheduling overhead and load imbalance. Consequently, this may cause a gradual decline in the acceleration ratio and a corresponding extension of the matching time. Therefore, based on the experimental findings, the most suitable subset number, w, is determined to be 16.

Figure 5: Influence on the performance of the algorithm for the number of subset divisions

5.3 Experimental Results

To verify the performance of the SUPD, this paper divides the data set into 5 groups according to the complexity of color and texture, and the complexity of the experimental group increases from 1 to 5. For each experimental group, the average values of matching total time, matching accuracy, and MERD were calculated. Additionally, comparative experiments were conducted with traditional SIFT and SURF to obtain more comprehensive performance comparison results. Both SIFT and SURF algorithms were paired with the built-in brute-force matching algorithm in OpenCV for feature matching.

5.3.1 Total Matching Time

Total matching time as a significant metric effectively measures the real-time performance of algorithms. Fig. 6 presents a comparison of the total matching time between the SUPD and two other traditional algorithms. It is evident that the SUPD outperforms the conventional SIFT and SURF in terms of total matching time, reducing the time by 77% to 80%. This improvement in real-time performance stems from the specific design of the SUPD. The algorithm employs Principal Component Analysis to perform dimensionality reduction on feature descriptors, effectively reducing computational complexity. Additionally, the SUPD introduces a multi-core parallel matching strategy, allowing multiple processing cores to simultaneously execute matching operations. This not only accelerates the computation process but also enhances system throughput, significantly boosting the overall algorithm’s running speed.

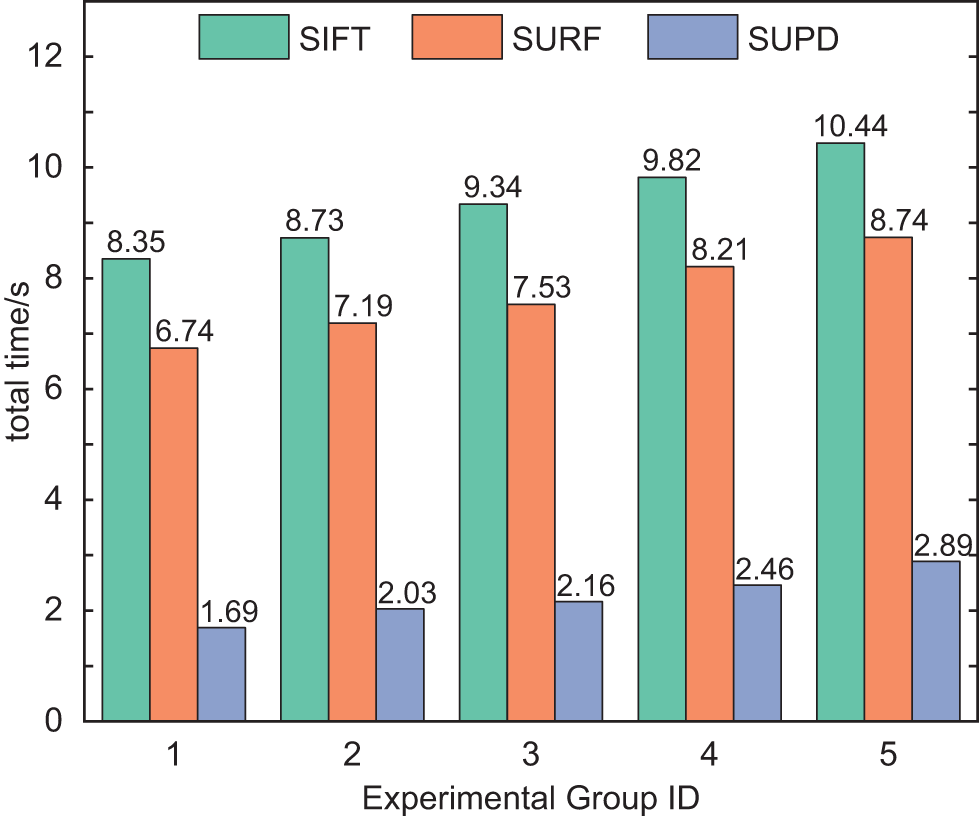
Figure 6: Total matching time of SIFT, SURF and SUPD

5.3.2 Matching Accuracy

Matching accuracy effectively reflects the precision and robustness of feature matching algorithms. Its calculation method is shown in Eq. (11). Fig. 7 illustrates the comparison results of matching accuracy between the SUPD and two other traditional algorithms. The comparison reveals that compared to traditional SIFT and SURF algorithms, the SUPD improves accuracy by 5% to 15%.

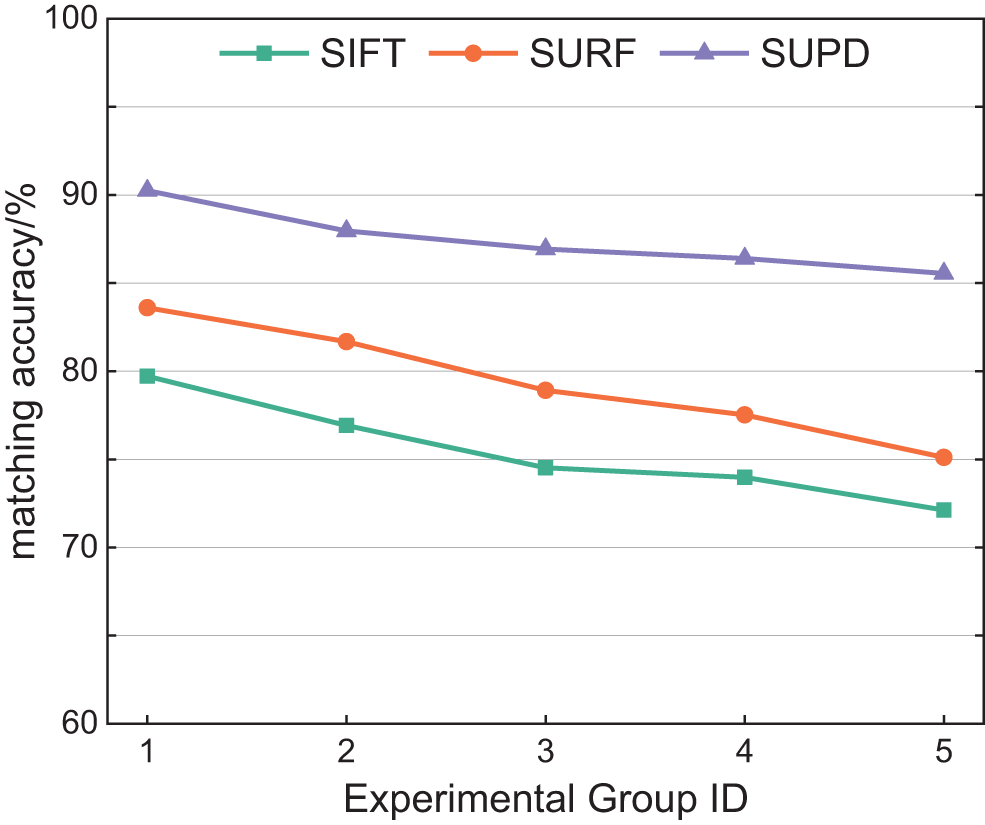
Figure 7: Matching accuracy of SIFT, SURF and SUPD

To provide a more intuitive representation of the contrasting matching accuracy, this paper takes the matching results of the first experiment in the third group as an example to analyze the relative performance of the SUPD against the traditional SIFT and SURF in terms of matching accuracy, as shown in Fig. 8.

Figure 8: Matching results of different algorithms. (a) The query image. (b) The reference image. (c) SIFT algorithm (d) SURF algorithm. (e) SUPD algorithm

From Fig. 8c,d, it can be seen that traditional SIFT and SURF exhibit a significant number of issues like cross-matching and repetitive matching, leading to lower matching accuracy. In contrast, the matching effect of the SUPD is shown in Fig. 8e. The algorithm filters and refines the matched point pairs using the two maintained filtering heaps in the DHF algorithm. This process effectively reduces false matching and ensures a high level of matching accuracy.

5.3.3 Matching Error Root Mean Square

In order to provide a more intuitive representation of the overall matching quality between feature point pairs, this paper introduces the Matching Error Root Mean Square (MERD) as an evaluation metric. A smaller MERD value indicates higher overall matching quality between feature point pairs, whereas a larger MERD value suggests poorer matching quality. The calculation formula for MERD is given in Eq. (12). Fig. 9 illustrates the comparison results of the SUPD and two other traditional algorithms in terms of MERD. It can be observed that the MERD values of the SUPD are consistently lower than those of the SIFT and SURF, with reductions ranging from 12% to 32%. This indicates that the SUPD exhibits superior performance in matching feature point pairs overall, enabling more accurate matching of high-dimensional features between local road images.

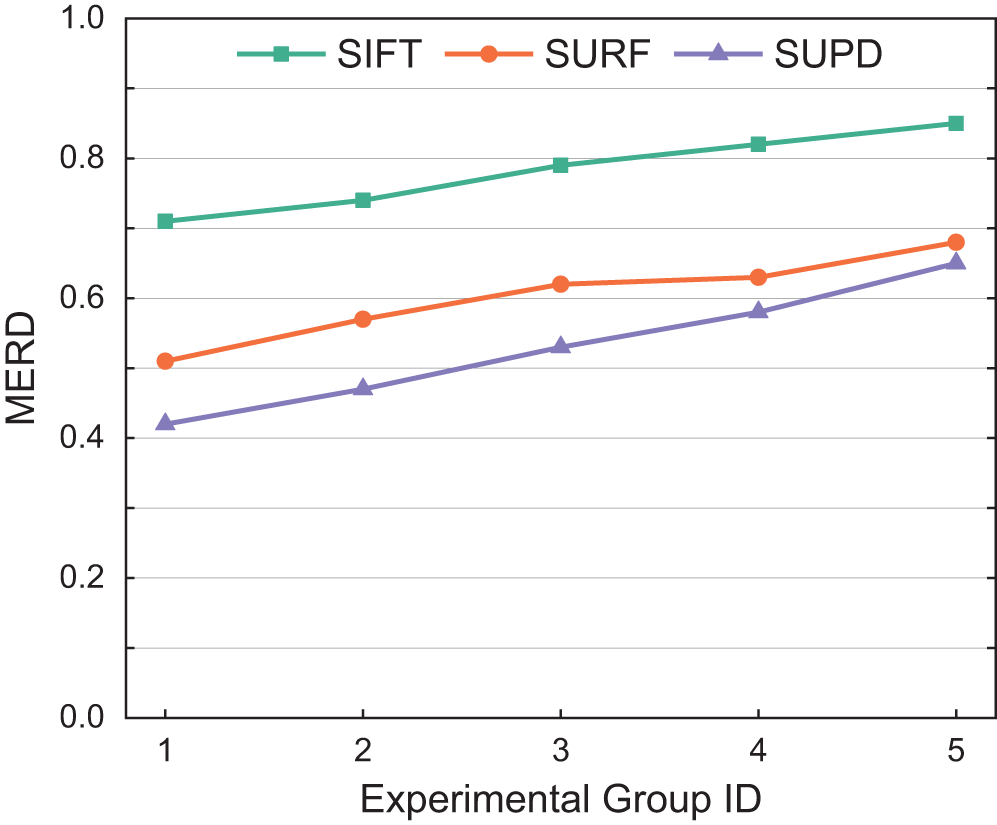
Figure 9: Matching error root mean square of SIFT, SURF and SUPD

6  Conclusions

Addressing the inefficiencies of traditional image feature matching algorithms in handling high-dimensional feature points within partial road images, this paper proposes a high-performance dimensionality reduction and parallel matching algorithm that combines Principal Component Analysis (PCA) and Dual-Heap Filtering. Through PCA, the algorithm projects the feature point set into a lower-dimensional space and employs squared Euclidean distance for rank estimation, effectively reducing the computational complexity during the matching process. Furthermore, to ensure the accuracy of feature matching, the proposed algorithm employs the Dual-Heap Filtering for refining matched point pairs. In addition, the algorithm utilizes a parallel structure to fully leverage computational resources, enhancing the overall matching speed. Experimental results demonstrate that the proposed algorithm holds distinct advantages over traditional image feature matching algorithms in terms of total matching time, matching accuracy, and MERD. Thus, the algorithm strikes a balance between matching accuracy and real-time performance, making it suitable for efficient matching of high-dimensional feature points in partial road images.

Despite the advantages presented by this algorithm, there are challenges that might arise when it is applied to extremely large datasets, especially within environments constrained by limited computational resources. In response to these challenges, future research will be directed towards the development of more effective strategies and optimization techniques. This includes plans to update the experimental equipment and to conduct experiments with a broader range of datasets to enhance the scalability and robustness of the algorithm in complex environments. Furthermore, the integration of machine learning methods for the automatic adjustment and optimization of the algorithm’s parameters is under consideration. Such steps are anticipated to improve the adaptability and performance of the algorithm in various application scenarios.

Acknowledgement: The authors thank their institutions for infrastructure support.

Funding Statement: The authors would like to thank the National Natural Science Foundation of China (61803206), the Key R&D Program of Jiangsu Province (BE2022053-2), and the Nanjing Forestry University Youth Science and Technology Innovation Fund (CX2018004) for partly funding this project.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Guangbing Xiao, Ruijie Gu; data collection: Ning Sun; analysis and interpretation of results: Ruijie Gu, Ning Sun; draft manuscript preparation: Ruijie Gu, Yong Zhang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. X. Guo, Z. Wang, and W. Zhu, “Research on DSO vision positioning technology based on binocular stereo panoramic vision system,” Def. Technol., vol. 18, no. 4, pp. 593–603, 2022. doi: 10.1016/j.dt.2021.12.010. [Google Scholar] [CrossRef]

2. P. Paul and A. Sharma, “A comprehensive review of navigation system, design, and safety issues for autonomous vehicle development,” in Autonomous Driving and Advanced Driver-Assistance Systems (ADAS), 1st, ed., CRC Press, 2021, pp. 87–104. [Google Scholar]

3. D. Li, K. Cao, L. Kong, and H. Yu, “Fully distributed cooperative circumnavigation of networked unmanned aerial vehicles,” IEEE/ASME Trans. Mechatron., vol. 26, no. 2, pp. 709–718, 2021. doi: 10.1109/TMECH.2021.3055654. [Google Scholar] [CrossRef]

4. S. Li, X. Shao, W. Zhang, and Q. Zhang, “Distributed multicircular circumnavigation control for UAVs with desired angular spacing,” Def. Technol., vol. 31, no. 4, pp. 429–446, 2024. doi: 10.1016/j.dt.2023.02.007. [Google Scholar] [CrossRef]

5. S. Alaee, R. Mercer, K. Kamgar, and E. Keogh, “Time series motifs discovery under DTW allows more robust discovery of conserved structure,” Data Min. Knowl. Discov., vol. 35, no. 3, pp. 863–910, 2021. doi: 10.1007/s10618-021-00740-0. [Google Scholar] [CrossRef]

6. C. Sun, X. Wu, J. Sun, C. Sun, and L. Dong, “Robust pose estimation via hybrid point and twin line reprojection for RGB-D vision navigation,” IEEE Trans. Instrum. Meas., vol. 71, pp. 1–19, 2022. doi: 10.1109/TIM.2022.3170980. [Google Scholar] [CrossRef]

7. X. Zou and B. Pan, “Full-automatic seed point selection and initialization for digital image correlation robust to large rotation and deformation,” Opt. Lasers Eng., vol. 138, no. 8, pp. 106432, 2021. doi: 10.1016/j.optlaseng.2020.106432. [Google Scholar] [CrossRef]

8. X. Wang, Q. Xie, T. Ma, and J. Zhu, “Feature extraction based on dimension reduction and clustering for maize leaf spot images,” Int. J. Pattern Recognit. Artif. Intell., vol. 32, no. 12, pp. 1854029, 2018. doi: 10.1142/S0218001418540290. [Google Scholar] [CrossRef]

9. B. Tran, B. Xue, and M. Zhang, “Variable-length particle swarm optimization for feature selection on high-dimensional classification,” IEEE Trans. Evol. Comput., vol. 23, no. 3, pp. 473–487, 2018. doi: 10.1109/TEVC.2018.2869405. [Google Scholar] [CrossRef]

10. M. Ghosh, R. Guha, R. Sarkar, and A. Abraham, “A wrapper-filter feature selection technique based on ant colony optimization,” Neural Comput. Appl., vol. 32, no. 12, pp. 7839–7857, 2020. doi: 10.1007/s00521-019-04171-3. [Google Scholar] [CrossRef]

11. W. Ma, J. Zhang, Y. Wu, L. Jiao, H. Zhu and W. Zhao, “A novel two-step registration method for remote sensing images based on deep and local features,” IEEE Trans. Geosci. Remote Sens., vol. 57, no. 7, pp. 4834–4843, 2019. doi: 10.1109/TGRS.2019.2893310. [Google Scholar] [CrossRef]

12. S. Chaudhari, V. Mithal, G. Polatkan, and R. Ramanath, “An attentive survey of attention models,” ACM Trans. Intell. Syst. Technol., vol. 12, no. 5, pp. 1–32, 2021. doi: 10.1145/3465055. [Google Scholar] [CrossRef]

13. B. Y. Wang, X. H. Zhang, and W. B. Wang, “Feature matching method based on SURF and fast library for approximate nearest neighbor search,” Integr. Ferroelectr., vol. 218, no. 1, pp. 147–154, 2021. doi: 10.1080/10584587.2021.1911336. [Google Scholar] [CrossRef]

14. S. Magdy, Y. Abouelseoud, and M. Mikhail, “Privacy preserving search index for image databases based on SURF and order preserving encryption,” IET Image Process., vol. 14, no. 5, pp. 874–881, 2020. doi: 10.1049/iet-ipr.2019.0575. [Google Scholar] [CrossRef]

15. S. Gupta, K. Thakur, and M. Kumar, “2D-human face recognition using SIFT and SURF descriptors of face’s feature regions,” Vis. Comput., vol. 37, no. 3, pp. 447–456, 2021. doi: 10.1007/s00371-020-01814-8. [Google Scholar] [CrossRef]

16. B. M. S. Hasan and A. M. Abdulazeez, “A review of principal component analysis algorithm for dimensionality reduction,” J. Soft Comput. Data Mining, vol. 2, no. 1, pp. 20–30, 2021. [Google Scholar]

17. D. Huang, F. Jiang, K. Li, G. Tong, and G. Zhou, “Scaled PCA: A new approach to dimension reduction,” Manage. Sci., vol. 68, no. 3, pp. 1678–1695, 2022. doi: 10.1287/mnsc.2021.4020. [Google Scholar] [CrossRef]

18. C. Happ and S. Greven, “Multivariate functional principal component analysis for data observed on different (dimensional) domains,” J. Am. Stat. Assoc., vol. 113, no. 522, pp. 649–659, 2018. doi: 10.1080/01621459.2016.1273115. [Google Scholar] [CrossRef]

19. A. Kunimatsu, N. Kunimatsu, K. Kamiya, T. Watadani, H. Mori and O. Abe, “Comparison between glioblastoma and primary central nervous system lymphoma using MR image-based texture analysis,” Magn. Reson. Med. Sci., vol. 17, no. 1, pp. 50–57, 2018. doi: 10.2463/mrms.mp.2017-0044. [Google Scholar] [PubMed] [CrossRef]

20. W. Xu, Y. Cai, D. He, J. Lin, and F. Zhang, “FAST-LIO2: Fast direct lidar-inertial odometry,” IEEE Trans. Robot., vol. 38, no. 4, pp. 2053–2073, 2022. doi: 10.1109/TRO.2022.3141876. [Google Scholar] [CrossRef]

21. Y. Liu et al., “Robust feature matching via advanced neighborhood topology consensus,” Neurocomputing, vol. 421, no. 1, pp. 273–284, 2021. doi: 10.1016/j.neucom.2020.09.047. [Google Scholar] [CrossRef]

22. Y. Chen et al., “Fast neighbor search by using revised kd tree,” Inf. Sci., vol. 472, no. 1, pp. 145–162, 2019. doi: 10.1016/j.ins.2018.09.012. [Google Scholar] [CrossRef]

23. Q. Wu, Y. Chen, J. P. Wilson, X. Liu, and H. Li, “An effective parallelization algorithm for DEM generalization based on CUDA,” Environ. Model. Softw., vol. 114, no. 2, pp. 64–74, 2019. doi: 10.1016/j.envsoft.2019.01.002. [Google Scholar] [CrossRef]

24. Y. Lu, Y. Li, B. Song, W. Zhang, H. Chen and L. Peng, “Parallelizing image feature extraction algorithms on multi-core platforms,” J. Parallel Distr. Comput., vol. 92, pp. 1–14, 2016. doi: 10.1016/j.jpdc.2016.03.001. [Google Scholar] [CrossRef]

25. M. Denham and K. Laneri, “Using efficient parallelization in graphic processing units to parameterize stochastic fire propagation models,” J. Comput. Sci., vol. 25, no. 6154, pp. 76–88, 2018. doi: 10.1016/j.jocs.2018.02.007. [Google Scholar] [CrossRef]

26. M. S. Reis, G. Estrela, C. E. Ferreira, and J. Barrera, “Optimal Boolean lattice-based algorithms for the U-curve optimization problem,” Inf. Sci., vol. 471, pp. 97–114, 2019. [Google Scholar]

27. K. Zhao, X. Jin, J. Ji, J. Wang, H. Ma and X. Zhu, “Individual identification of Holstein dairy cows based on detecting and matching feature points in body images,” Biosyst. Eng., vol. 181, no. 2, pp. 128–139, 2019. doi: 10.1016/j.biosystemseng.2019.03.004. [Google Scholar] [CrossRef]

28. J. Feng, J. Fu, Z. Lin, C. Shang, and X. Niu, “Layered infill area generation from triply periodic minimal surfaces for additive manufacturing,” Comput-Aided Design, vol. 107, pp. 50–63, 2019. [Google Scholar]

29. Z. Chang, D. Xie, F. Li, J. M. Phillips, and R. Balasubramonian, “Efficient oblivious query processing for range and knn queries,” IEEE Trans. Knowl. Data Eng., vol. 34, no. 12, pp. 5741–5754, 2021. doi: 10.1109/TKDE.2021.3060757. [Google Scholar] [CrossRef]

30. L. Hu and S. Nooshabadi, “High-dimensional image descriptor matching using highly parallel KD-tree construction and approximate nearest neighbor search,” J. Parallel Distr. Comput., vol. 132, no. 3, pp. 127–140, 2019. doi: 10.1016/j.jpdc.2019.06.003. [Google Scholar] [CrossRef]

31. J. Hu et al., “Adjusting switching granularity of load balancing for heterogeneous datacenter traffic,” IEEE/ACM Trans. Netw., vol. 29, no. 5, pp. 2367–2384, 2021. doi: 10.1109/TNET.2021.3088276. [Google Scholar] [CrossRef]

32. S. Bora, B. Walker, and M. Fidler, “The tiny-tasks granularity trade-off: Balancing overhead versus performance in parallel systems,” IEEE Trans. Parallel Distrib. Syst., vol. 34, no. 4, pp. 1128–1144, 2023. doi: 10.1109/TPDS.2022.3233712. [Google Scholar] [CrossRef]

33. C. Pagetti, J. Forget, F. Boniol, M. Cordovilla, and D. Lesens, “Multi-task implementation of multi-periodic synchronous programs,” Discrete Event Dyn. Syst., vol. 21, no. 3, pp. 307–338, 2011. doi: 10.1007/s10626-011-0107-x. [Google Scholar] [CrossRef]

34. F. Glaser, G. Tagliavini, D. Rossi, G. Haugou, Q. Huang and L. Benini, “Energy-efficient hardware-accelerated synchronization for shared-L1-memory multiprocessor clusters,” IEEE Trans. Parallel Distrib. Syst., vol. 32, no. 3, pp. 633–648, 2020. doi: 10.1109/TPDS.2020.3028691. [Google Scholar] [CrossRef]