Reducing the Encrypted Data Size: Healthcare with IoT-Cloud Computing Applications

1  Introduction

Cloud computing is the technology that focuses on transferring, processing, computing, and storing data from a personal or local computer to a virtual space, which is a server device accessed through the Internet (Fig. 1) [1]. This technology offers solutions to some critical issues like maintenance and development for both clients and companies since the client’s efforts are solely devoted to utilizing its services. The cloud’s infrastructure depends on advanced databases and provides significant resources for clients. The Virtual Cloud (VC) guarantees its accessibility (constant connection) to all devices anytime. With the increased development of technology available through the Internet, many private and public companies are seeking to deliver their applications by using cloud technology. After purchasing a certain space, the users can store their data on cloud servers’ space, which can be accessible anytime and anywhere with an Internet connection.

Figure 1: Cloud storage of big data gathered from different sources

Big data comprises digital data that are produced through the utilization of new technology for personal or professional purposes; it is primarily composed of compounded datasets derived from different sources. Big data could be considered a collection of diverse data, which is increasingly generated in greater volumes and at a higher rate. Consequently, traditional data processing software cannot handle or store it locally. These large amounts of data can be provided to find solutions to issues that were previously considered to be unsolved.

The power and capacity of cloud computing lie in providing a tremendous advantage of storing, analyzing, and processing large amounts of data. The data gathered from intelligent hardware will be studied in multiple disciplines, examples include market basket analysis [2], web-analysis [3], healthcare [4], bioinformatics [5], and prediction [6]. Access to the cloud service saves considerable data collection costs; yet, data from multiple sources improves accuracy and efficiency in exploration results [7]. However, when cloud servers collect various data, they also collect sensitive client information; therefore, disclosing such data may harm users’ privacy. Thus, data protection and security become crucial when storing them [8].

Cloud security is paramount to all data types, the majority of which are digital and should be only accessible by the owner [9,10]. Information technology’s advancements and increasing computational power raise many security concerns because of the volume, speed, and variety of data generated [11]. The collective use of cloud data has become increasingly important in the security domain, mainly in the encryption domain [12–14]. When discussing the process of exchanging or storing data, the time complexity and the size of the storage should be considered [15].

Healthcare data security is centered on safeguarding the information, computers, and networks utilized by healthcare providers and organizations. Viewing clinical data as a public asset leads to concerns about the protection and security of individual patient files. Ensuring the confidentiality of these records is crucial. The public’s view of privacy regarding medical records is directly tied to their trust in the healthcare system at large and plays a significant role in debates about sharing health data.

Among the various security threats, false data injection attacks (FDIA) are very important. FDIA is concerned with the case where an attacker alters the data to conceal mistakes in calculating variables and values [16]. However, the influence of the FDIA on healthcare has been almost disregarded in recent years. A study conducted by IBM Security X-Force in 2023 report showed that reconnaissance activities, in which attackers search for security gaps and valuable data, are the major contributors to healthcare-related cyber incidents. Moreover, the recent increase in data security incidents in the healthcare sector has reaffirmed the necessity of preventive measures into account [17]. Hence, this demonstrates the importance of early-stage threat detection in healthcare. Confidential data might be intercepted or read by hackers in a data-sharing system such as a healthcare system in a cloud computing environment. Data cannot be secured by any other centralized control system since it cannot assume any third-party security infrastructure to protect this confidential data [18].

Data cybersecurity requires effective cryptographic systems to ensure data confidentiality, availability, and security. Nowadays, cloud computing is common in information technology, but storage and security issues have raised a challenge for users. Data encryption is an efficient solution, as most current encryption techniques support privacy and security. Unlike most encryption techniques, some [19,20] take the size of encrypted data that will be stored in the cloud seriously into consideration. Thus, as the size of the encrypted data increases, the higher it costs [21].

In this work, an encryption method is presented that reduces the size of ciphertext to approximately 1/10 and 1/20 when compared against other schemes using the same parameters and size of data, which in return reduces the cost of storage while still preserving the confidentiality, privacy, and integrity of data that are stored in the cloud by private or public healthcare organizations. The proposed approach consists of grouping more than one information field into a single ciphertext by using a multiple secret keys technique. Furthermore, the proposal has been analyzed, and an equation that represents a reference to calculate the difference in the ciphertext size has been provided, reaching a rate of reduction equal to 88%. Moreover, to store data in the cloud at reduced costs, a case study of diabetes clinics has been performed. Another study on reducing the size using Modular Multiplicative Inverse was also conducted; this study is valid for almost any encryption technique with a storage space gain of up to 50%. Eventually, this will allow the owners of these clinics to store the data of their patients in the cloud securely and inexpensively.

The rest of this paper is organized as follows. Section 2 provides an overview of encryption schemes. In Section 3, the proposed method is presented, while in Section 4, an analysis of the proposed technique is provided. Section 5 shows the conducted experiments and the overall performance of the proposed method. Section 5.1 discusses the size reduction by the inverse of a ciphertext. Section 6 presents a case study, and finally, in Section 7, a conclusion along with directions for future research work is given.

2  Related Work

In the literature, several cryptographic techniques have been proposed. Playfair encryption [22] replaces each letter pair in the plaintext with another pair; for this, the Playfair scheme uses a square table (matrix) 5 × 5 built from a key, where each pair of letters gives the coordinates of a rectangle in the matrix. This creative method was not used very often since it could be easily deciphered by looking at which pair of letters appear most frequently in the ciphertext, assuming that they represent the most common pair of letters.

Hill’s scheme [23] is used to encrypt the 26 letters using modulo 26. In ADFGVX systems [24], both techniques transposition and substitution have been mixed where the 26 letters of the alphabet, as well as the 10 digits, must be stored in a table of six boxes. Each letter in the plain text is replaced by a pair of letters corresponding to its row and column. The 3-rotor ENIGMA [25] is the most famous machine among rotor machines. This electric machine comprises an alphabetical keyboard, a light display, and three rotors. With each keystroke, the first rotor is rotated by one notch; at the end of a full turn, the second rotor is shifted by one, and so on. To define the encryption key, the rotors were positioned differently every time (FAC, for example). Data Encryption Standard Algorithm [26] (DES) is a block symmetric encryption algorithm that encrypts 64-bit words given a 56-bit key (56-bit encryption + 8-bit parity used to verify the integrity of the key). For that, the plaintext message is split into 64-bit blocks. Each block bit is permuted according to the arrangement of the table. The 64-bit block is split into two 32-bit blocks denoted as G0 and D0, where G0 contains all the even bits of the initial message, and D0 contains all the odd bits. Rijndael also proposed Advanced Encryption Standard (AES) [27]. AES is a multi-turn block cipher similar to DES. However, AES uses larger, variable block and key sizes, such as 128, 196, and 256 bits.

The most essential problem of symmetric cryptography is the distribution of keys. If n people can communicate confidentially, then n(n − 1)/2 keys are needed. The original idea of public-key cryptosystems was proposed by Rivest et al. [28], in which the fundamental principle is to use different encryption and decryption keys, unreconstructed from one another. Therefore, a public key is used for the encryption and a secret key for the decryption, where the public key plays the role of a padlock, and only the one that has the secret key can read the data. A major problem with this approach is that it is slower compared to asymmetric cryptography, which is nearly a thousand times faster. The Rivest-Shamir-Adleman (RSA) encryption algorithm [29], based on the work of public-key cryptography of Diffie and Hellman, is a key exchange protocol, that allows two parties A and B, who are connected by an unsecured channel, to generate a secret cryptographic key. The key is difficult to find by an adversary intruding on the used channel.

In cryptography, there is also, the so-called homomorphic encryption [30] that allows us to perform operations on encrypted data without being decrypted. Encryption is a crucial mechanism to maintain the confidentiality of any sensitive data. However, with the utilization of conventional encryption techniques, calculations on encrypted data are not applicable unless they are decrypted. Thus, the users must sacrifice their privacy to benefit from cloud services such as file storage, sharing, and collaboration. In addition, processes from servers, providers, and untrusted popular cloud operators may continue to physically identify their clients’ data long after the client has terminated the relationship with the services. For that, this is a major privacy issue for customers. It would have been desirable if there was a mechanism that would not restrict the operations to be computed on the encrypted data while it was still encrypted; this can be achieved with homomorphism. The homomorphic properties can be shown in Eq. (1).

Dec(Enc(m1)ΔEnc(m2))=m1Δm2(1)

where m is the plaintext, ∀ m1, m2 ∈ m and Δ denotes addition or multiplication.

In [31], Gentry presented a fully homomorphic encryption technique using bootstrapping. Bootstrapping offers unlimited additive and multiplicative homomorphic operations. In 2019, Elgamal [32] proposed a new homomorphic encryption scheme for integer arithmetic using a variant based on the Chinese Remainder Theorem (CRT) secret sharing. RSA [29] and Boneh [33] are the first feasible public key schemes as multiplicative cryptosystems, this property can be presented by Eq. (2).

Dec(Enc(m1)×Enc(m2))=m1×m2(2)

van Dijk et al. [34] proposed BGN (Boneh, Goh, and Nissim) scheme which supports an arbitrary number of additions and one multiplication represented by Eq. (3).

c=Enc(m)=gm×hrmodn(3)

where m is the plaintext, g, h, and u are the generators with (h=uq), r is a random number and n=p×q, where p and q are two prime numbers. Dasgupta et al. [35] proposed an FHE scheme that can be presented by Eq. (4).

c=Enc(m)=m+2×r+p×q(4)

where m ∈ {0,1} and r is a random (r << p). The decryption operation is m=Dec(c)=(cmodp)mod2. Doröz et al. [36] proposed an asymmetric homomorphic encryption scheme, making it fully homomorphic using a refresh operation. In [37], Doroz et al. proposed a leveled encryption based on a generalization of the open-source public-key cryptosystem NTRU (Number Theory Research Unit). Using blockchain technology and a hash function, the author of [38] encrypted images in an industrial IoT (IIoT) environment, encrypted data of more than 780,000 bits to encrypt a single bit. The puwhich needs solutions deeply optimized in terms of data processing and energy efficiency [39]. Most schemes generate a large amount of data or face network management and monitoring challenges [40] that may require public key size ranging from 70 Megabytes for the small setting and 2.3 Gigabytes for the large setting.

To improve data storage in cloud computing, Ahmad et al. [41] proposed a block-cipher-based anti-codify technique. the cipher text is generated using Deoxyribo Nucleic Acid (DNA) model. To raise the security level, the authors divide the original file into two separate blocks. In the field of securing healthcare data, Wei et al. [42] presented an image protection technique for healthcare applications to save patients’ medical data transmitted in the Internet of Medical Things networks. For more performance, this technique uses an enhanced 2D discrete chaotic map allowing dynamic substitution that is founded on an optimized nonlinear S-box.

While the encryption schemes mentioned earlier produce a substantial amount of encrypted data, this paper seeks to introduce an alternative technique. This method allows users to achieve reduced storage usage and minimized costs for the equivalent data employed in previous encryption schemes, all the while maintaining a high level of confidentiality and security.

3  The Proposed Approach

In this paper, a new concept of embedded encryption (EE) has been introduced. It is known that EE [43,44] means to include an additional level of protection such as providing a physical layer of security or using multiple encryption algorithms. Indeed, these solutions are either financially expensive or not applicable in some environments, such as the Internet of Things. Typically, these solutions will eventually increase the volume of encrypted data and the processing time (the time required for the encryption and decryption processes). Embedding in the proposed technique is to hide a group of fields in a single field using several small-sized keys. Fig. 2 shows the difference between the proposed encryption and other encryption schemes.

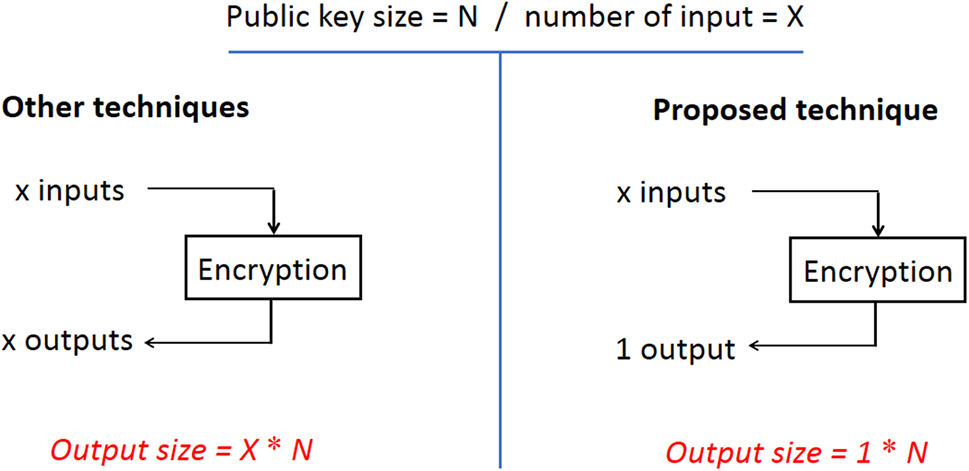
Figure 2: Input and output comparison

3.1 The Core of the Proposed Scheme

To simplify the understanding of our proposed Multi-Key Embedded Encryption (MKEE), it would be better to start by explaining the technique with a simple example shown in Fig. 3.

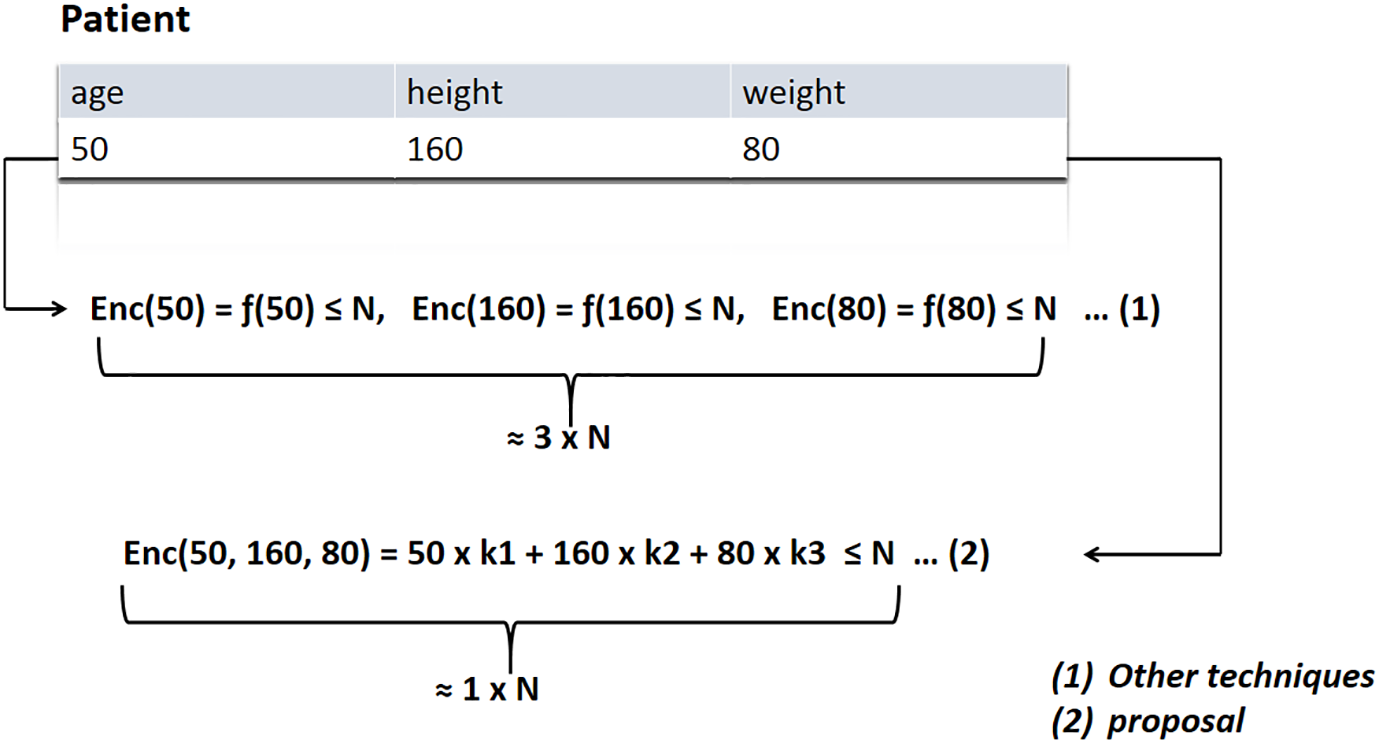
Figure 3: Example of encryption with three fields

In other systems, each entry is individually coded according to Eq. (5).

Enc(m)=function(m,N)(5)

where m is the message to be encrypted and N is the public key. Most of the encryption methods [29,33,34] work with the modulo operation, which means that the size of the encrypted text will be in the range of the public key N. These techniques encrypt each message independently, i.e., if a record contains three fields (Fig. 3), each field will be considered as an independent input. Therefore, if there are three encrypted values, each of them must be in the range of the public key N. Thus, it is not possible to encrypt all fields (or inputs) in one ciphertext because these techniques are not linear; many of them are based on exponential functions (e.g., RSA) or they treat the bit level depending on multi-round process (e.g., AES). The proposed encryption scheme is a linear technique that contains multiplication and addition operations (see Algorithm 1).

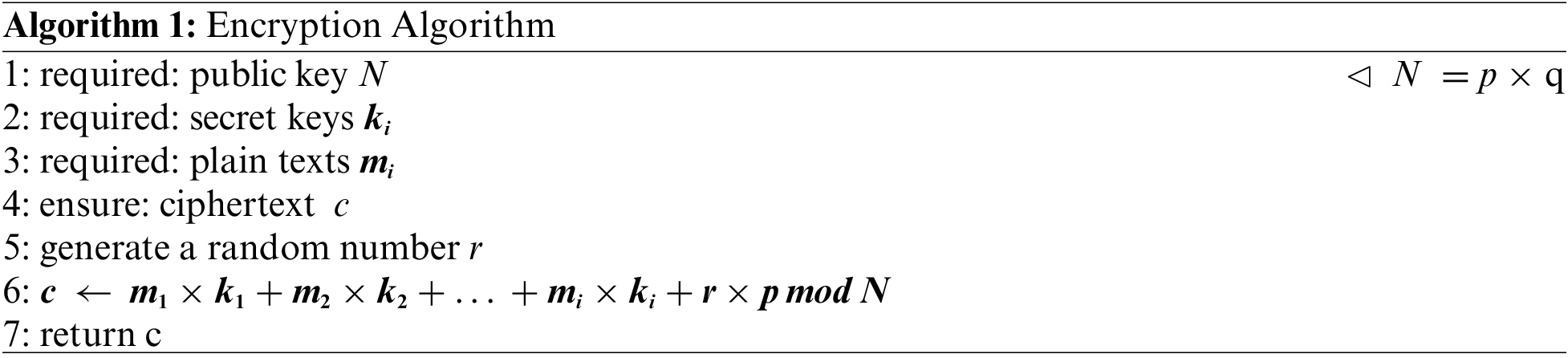
Multiplication helps to mask the message value; the addition operation helps to separate hidden values so that can be retrieved during decryption. Eq. (6) shows the proposed symmetric encryption method:

Enc(sym,ki)(m)=(r×p+∑j=1i(mj×kj))modN(6)

where N = p × q with p and q are two large prime numbers, r is a random number, ∀ j, kj is a secret key, and each mj is a field or information such as First name, Last name, Age, etc. As shown in Eq. (6), the modulo operation is only performed once after hiding the fields and collecting them in a single ciphertext at the range of the public key N. In asymmetric representation, Enc() can be defined as follows:

Enc(asym,pki)(m)=c=(∑j=1i(mj×pkj))modN(7)

where pki=ki+ri×p. In fact, Eq. (6) ↔ Eq. (7) because Enc(asym,pki)(m)=p×∑j=1i(mj×rj)+∑j=1i(mj×kj). Assuming R=∑j=1i(mj×rj), will get Enc(asym,pki)(m)=R×p+∑j=1i(mj×kj).

Eq. (8) shows the decryption process:

mj=(c−(cmodp))kj(8)

The decryption process depends on the succession of the division’s operations. mj is the quotient obtained when we calculate ckj. After obtaining mj, we calculate c′ = c − mj × kj; then, mj−1=c′kj−1 and so on.

Algorithm 2 shows how to go from a complete record which is represented by the ciphertext c to a set of information each represented by a plaintext m.

To ensure a mathematically correct decryption operation, three conditions must be met:

1.    mi<ki∀i

2.    ∑j=0i−1mj×kj<ki,∀i,j

3.    ∑j=0imj×kj<p,∀i,j

Proof. If mi>ki, then (mi×ki)mod(ki−1)=α where α<mi; therefore, mi cannot be retrieved. Suppose that c=m1×k1+m2×k2; when decoding, c mod k2 will be calculated first, then c mod k1. If m1×k1>k2, then c mod k2=β+m2≠m1×k1+m2, where β <mi, the values m1 and m2 cannot be retrieved.

3.2 Homomorphic Addition Property

The proposed method is a homomorphic encryption that verifies the homomorphic addition property as shown in Eq. (9).

Enc(m1)+Enc(m2)=Enc(m1+m2)(9)

This homomorphic addition property is used in the sectors, where privacy preservation is needed, due to its importance in providing statistics on the user’s data while respecting his confidentiality.

For that, it satisfies the homomorphic addition.

Enc(m1,m2,.. mi)=m1×k1+m2×k2+...+mi×ki

Enc(m1′,m2′,.. mi′)=m1′×k1+m2′×k2+...+mi′×ki

Enc(m)+Enc(m′)=m1×k1+m2×k2+...+mi×ki+m1′×k1+m2′×k2+...+mi′×ki

=(m1+m1′)×k1+(m2+m2′)×k2+…+(mi+mi′)×ki=Enc(m+m′)

Thanks to the proposed method, a user will be able to ask the cloud server to perform operations on the patient’s data without access to its real value. For example, a user wants to calculate the average number of epilepsy times, (∑i=1nm1i)/n, where m1i are the number of epilepsy times. The cloud server will calculate s=(∑i=1nm1i×k1)/n. Using the secret key k1, the client will decrypt s as follows:

The average number of epilepsy times =smod(k1−1)=(∑i=1nm1i×k1)/n.

4  Security Analysis

In cloud computing, confidentiality and preserving privacy problems are still challenging [45]. Generally, data stored in the cloud will be processed by servers. Such storage may be practical solely under a trusted cloud. Unfortunately, the data may be accessed, deleted, or manipulated by an untrusted provider. The security increases exponentially by increasing the number of files to be embedded in a single record. In this part, the proposal relies on the polynomial reconstruction problem robustness. In another part, our approach is based on the robustness of the number’s factorization problem. In healthcare settings where data security and privacy are critical, we need to use a suitable number of fields besides utilizing secure prime numbers.

When the proposed method relies on the robustness of the number’s factorization problem, i.e., the enemy has to factorize the public key N = p × q in order to get p or q, and eventually extract the secret key k. Thus, the secret key must be large, the trapdoor p also must be a safe and large prime number of form: 2 × ℎ + 1 where ℎ is a prime number. The original encryption is to multiply m by k (m × k). This technique is vulnerable to several attacks. By a couple (Enc (m), m), the enemy can obtain the secret key k. Deterministic schemes are vulnerable to Chosen Plain text Attack (CPA) and they are not semantically secure. In CPA, the adversary has the cipher text c and he tries to find the plaintext m. The adversary chooses m′ and calculates c′ = Enc (m′). Then, he decrypts c × c′ to get m × m′ and get m.

In the proposed method, Enc(m)=c+c′=m×k1+m′×k2 where k1 < k2; if the enemy has m, he will multiply Enc (m) by m−1, he will get k1+m−1×m′×k2; this does not give the enemy anything and he cannot get either k1 or k2 Even if the enemy has m and m′, this will not help him in anything because the information encrypted by the multiplication operation is protected by the addition operation, and therefore neither of the two keys k1 nor k2 can be extracted. With the proposed method, there are 𝑖 fields to encrypt in one value (𝑖 > 2). To get ki, the enemy must have ii messages with their corresponding encryption, which is not possible because each m × k is hidden inside. Therefore, the proposed technique is robust against chosen plaintext attacks and chosen ciphertext attacks.

We propose to hide a group of fields in a single field using several small-sized keys. Therefore, the factors that affect the proposed method are the size and nature of the data. On the one hand, the greater the size of the data, the greater the effectiveness because it follows the embedded encryption approach. On the other hand, the nature of the data may affect the effectiveness in terms of partitioning, because the input must be divided into fields so that each field is readable first, and second, the field length must be less than the key length.

5  Experimental and Results

In this Section, we will present the numerical results of MKEE and MMI techniques.

5.1 Size Reduction by Multi-Key Embedded Encryption (MKEE)

In the conducted experiments, the RSA cryptosystem was utilized for comparison since it is the most common and widely used encryption algorithm in the world. Two fields were initially encrypted, then three fields, etc., up to ten fields. A field with 8 bits length and a public key with 1024 bits were used. In RSA, each field was encrypted separately. Therefore, to store two encrypted fields, a space equal to 2048 bits was needed; for three encrypted fields 1024 × 3 bits are needed, and eventually the required space is equal to 1024 × n, where n denotes the number of fields to be encrypted.

In the proposed method, the value of the first field is multiplied by the first key (size (k1) = 1024 bits), and the result is 1032 bits. That is, the size of the second key must be at least 1033 bits (3.1), therefore, the ciphertext size for both fields is 1033 bits. To encrypt the second value, it should be multiplied by the second key, which gives a value of 1041 bits, hence the size of the third key must be at least 1042 bits. Namely, encoding three fields gives us a total encrypted text of 1042 bits (compared to 1024 × 3 bits in RSA). To ensure encryption, the field size must be less than the first key size (k1). Eqs. (10) and (11) formulate a general rule by which the total size of the encrypted text (the volume of storage needed) can be calculated.

size=k×h…(others)(10)

size=k+(h−1)×(l+1)…(proposal)(11)

where k is the secret key size, ℎ denotes the number of fields, and l is the size of one field. The experiment in Fig. 4 shows the difference between the proposed encryption and RSA encryption schemes.

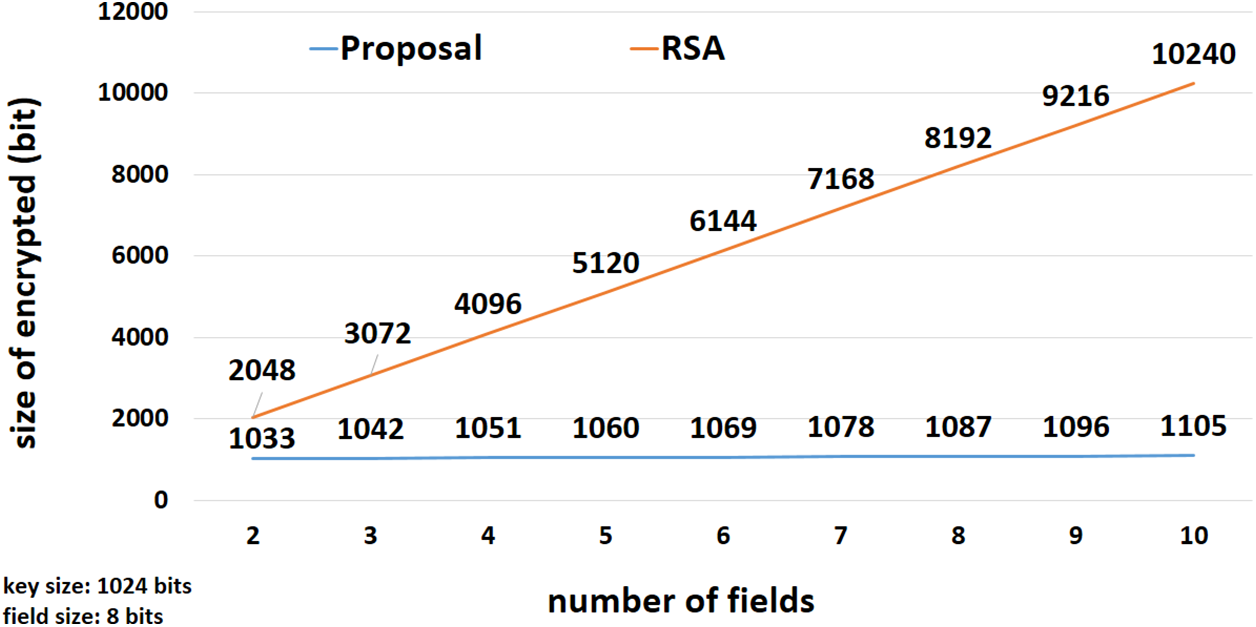
Figure 4: Size of ciphertext(s) in RSA and in the proposed encryption method

Fig. 5 shows how effective the proposed MKEE is in reducing the size of the digit and, therefore, the storage space. When encoding only two fields, the size’s reduction rate is around 50%, because storing two RSA-encoded values requires 1024 + 1024 bits. On the other hand, in the proposed method, the ciphertext size is only 1033 bits (approximate text). The total size of the ciphertext in the proposed technique increases by 9 bits (nine is the field length plus one), unlike other techniques, where the total size increases by the addition of the size of the public key (1024, 2048, 3072, 4096, etc.). When encrypting 5 fields, the size reduction rate becomes 78% until reaching 88% when encrypting 10 fields, which is a very high ratio (0.5 vs. 5 kbits).

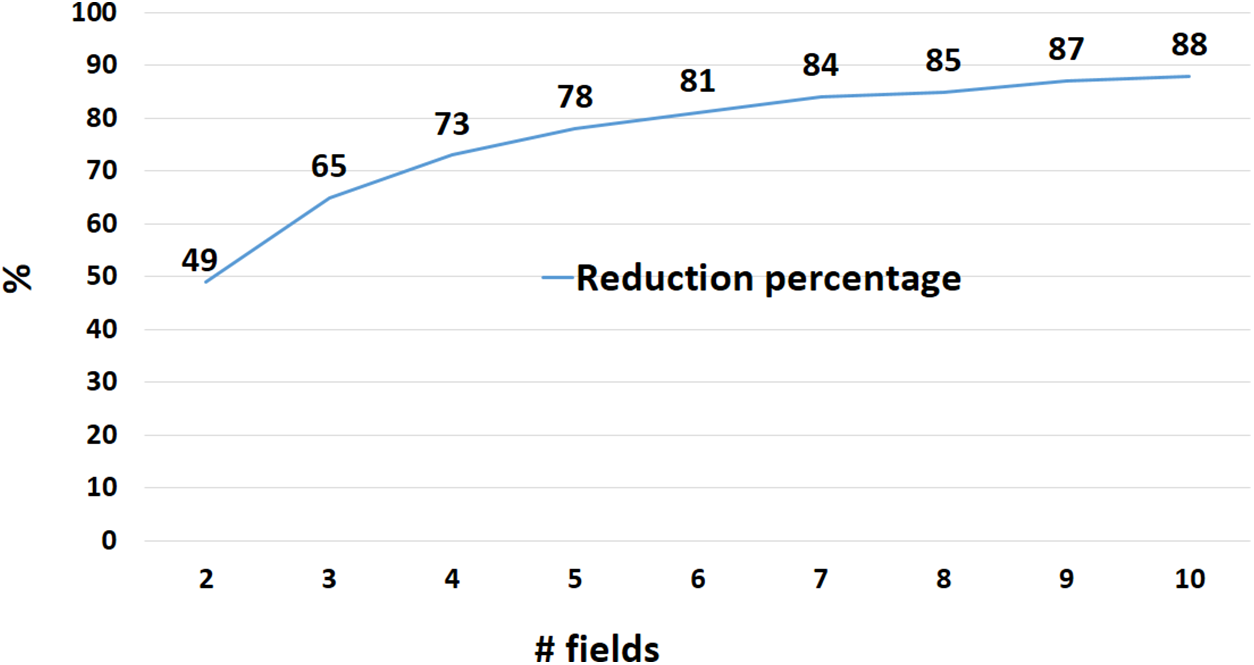
Figure 5: Percentage of size reduction by MKEE

On the other hand, we need ten multiplications and addition operations to encrypt 10 fields in MKEE. in contrast, ten exponential operations are needed in the RSA for the same number of fields. This makes our linear technique much faster in terms of execution time compared with the RSA cryptosystem.

5.2 Size Reduction by Multiplicative Inverse Method (MMI)

In addition to the experiments described in Section 5.1, more experiments that aim to gain storage space were conducted by using the Modular Multiplicative Inverse (MMI). Let x−1 be the MMI of 𝑥 relative to a number p represented by MMIp(x)=x−1, the MMI verifies the following equation:

x×x−1modp=1(12)

The idea was to replace the ciphertext c by its inverse c−1 if the size of c−1 is less than the size of c. A bit (0, 1) at each ciphertext is associated, for which this bit indicates whether this ciphertext is inverted or not (the value 0 means that the ciphertext is not inverted and the value 1 is the opposite). Algorithm 3 presents the utilized pseudocode.

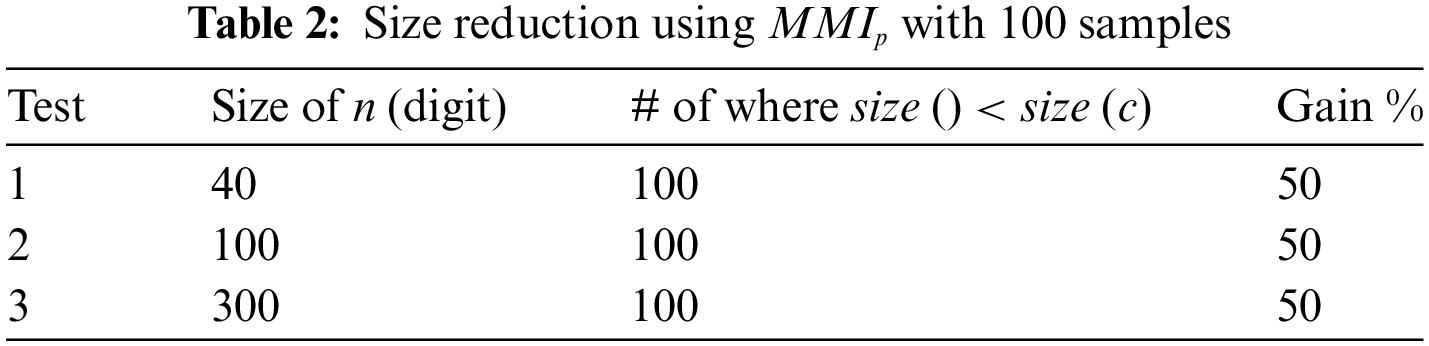
We can summarize this method as follows. The goal of MMI is to replace a ciphertext c by its multiplicative inverse c−1 when the size of c−1 is less than the size of c. It is an easy and lightweight operation to compute the MMI value. To further reduce the size of the ciphertext, this value can be computed according to the public modulo n or according to the private key p where n = p x q. Tables 1 and 2 show these two uses of MMI (MMIn and MMIp), where the gain was 2% with MMIn and 50% with MMIp. Therefore, the trade-off associated with using MMI is the type of employing this technique.

Step 1

Experiments by calculating the MMI of c for the public key n have been performed, where n = p × q. The results are shown in Table 1.

Step 2

Experiments by calculating the MMI of c for the private key p have been performed, where n = p × q. The results are shown in Table 2.

By comparing Tables 1 and 2, it is evident that MMIp achieved a very high result and it gave a space-saving of about 50% the size of the primitives k, p, q, and r (of which pk = k + r × p and n = p × q). The calculation of the Modular Multiplicative Inverse for the private key p poses a risk of vulnerability with deterministic encryption. Storing c−1 (where Encpk(m)=c and c−1=MMIp(c)) in an untrusted cloud, the adversary can extract sensitive information, i.e., he can get the private key p from an even (m, c−1). In other words, if the adversary knows a single plaintext m and its corresponding ciphertext c−1, he will calculate MMIn(c−1) to return to c.

Knowing that MMIn(c−1)=c+α×p where α is a random number, the adversary will calculate Encpk(m)=c. The problem in deterministic encryption is that c in (MMIn(c−1)=c+α×p) is the same in (Encpk(m)=c), so the adversary will get α × p and therefore p.

In probabilistic encryption, Encpk(m)=c′≠c, i.e., c − c′ ≠ 0 where c′ is calculated by the adversary using the public key pk with a random fragmentation of the plaintext m, and c is calculated by the user using his own random fragmentation of the plaintext m; this implies c + α × p − c′ ≠ α × p. Given the encryption example where the user’s ciphertext is c=m1×pk+m2(m=m1+m2 with random fragmentation), the ciphertext generated by the adversary who knows m is Encpk(m)=c′=m1′×pk+m2′. So, c−c′=m1′′×pk+m2′′≠0 (in more general terms, ≠ α × p). Therefore, the adversary will not be able to obtain α × p.

It should be noted here that there are techniques that can be called partially probabilistic. For instance, the technique Enc (m) = c = m + r × p where r is a random number at each message. In the general definition of probabilistic encryption, there are:

Enc1(m)=candEnc2(m)=c′withc≠c′(13)

But this definition does not address a very important aspect in the field of security, which is calculating the difference between c and c′, where (c − c′) mod n can be equal to α × p, with α is a random number. That will give the adversary the possibility to get the private key p. On the other hand, there are encryption techniques that can be called fully probabilistic: c ≠ c′ and (c − c′) mod n ≠ α × p. For example, the encryption scheme where Enc(m)=m1×pk+m2 with m=m1+m2 by random fragmentation is a fully probabilistic technique. Therefore, if there is a need to use the MMIp, a fully probabilistic encryption technique should be utilized. By summarizing:

Partially Probabilistic Encrypt𝑖ion (ppE): c≠c′ and (c−c′) mod n=α×p

Fully Probabilistic Encryption (FpE): c≠c′ and (c−c′) mod n≠α×p

As a result, one can save 50% of the storage space in any FPE scheme if one uses the MMI. Indeed, the proposed MKEE is a deterministic schema with an asymmetric use, because mi×pkimodN does not change. MKEE is a partially probabilistic scheme with its symmetric use because c=r×p+∑j=1i(mj×kj) where r is a random number in each encrypted record. In order to take advantage of the MMI method, there is a need to transform MKEE into a fully probabilistic scheme.

For this, the following new definition of MKEE is proposed:

c=(r+∑j=1i(mj×kj))modN(14)

where r is a small random number generated for each record, and r < ki. Noting that r=(cmodp)modki; so for decryption, c − r should be computed, then the decryption function, that previously defined (Eq. (8)), can be used. By this new formula, MKEE verifies the condition of FPE. Thus, combining MKEE and MMI gives us a reduction ratio for the size of the encrypted data estimated at 94%, i.e., it is approximately equal to 1/20 of the size obtained by using other encryption techniques.

Fig. 6 shows two curves, on the left, it illustrates the relationship between size and security. The security increases exponentially with the number of fields. On the right, the figure illustrates the relationship between size and encryption time. The encryption time does not increase significantly when the size is increased because the adopted technique is linear. We will increase one multiplication and one addition operation with each added field, which gives us 10 units of time per field.

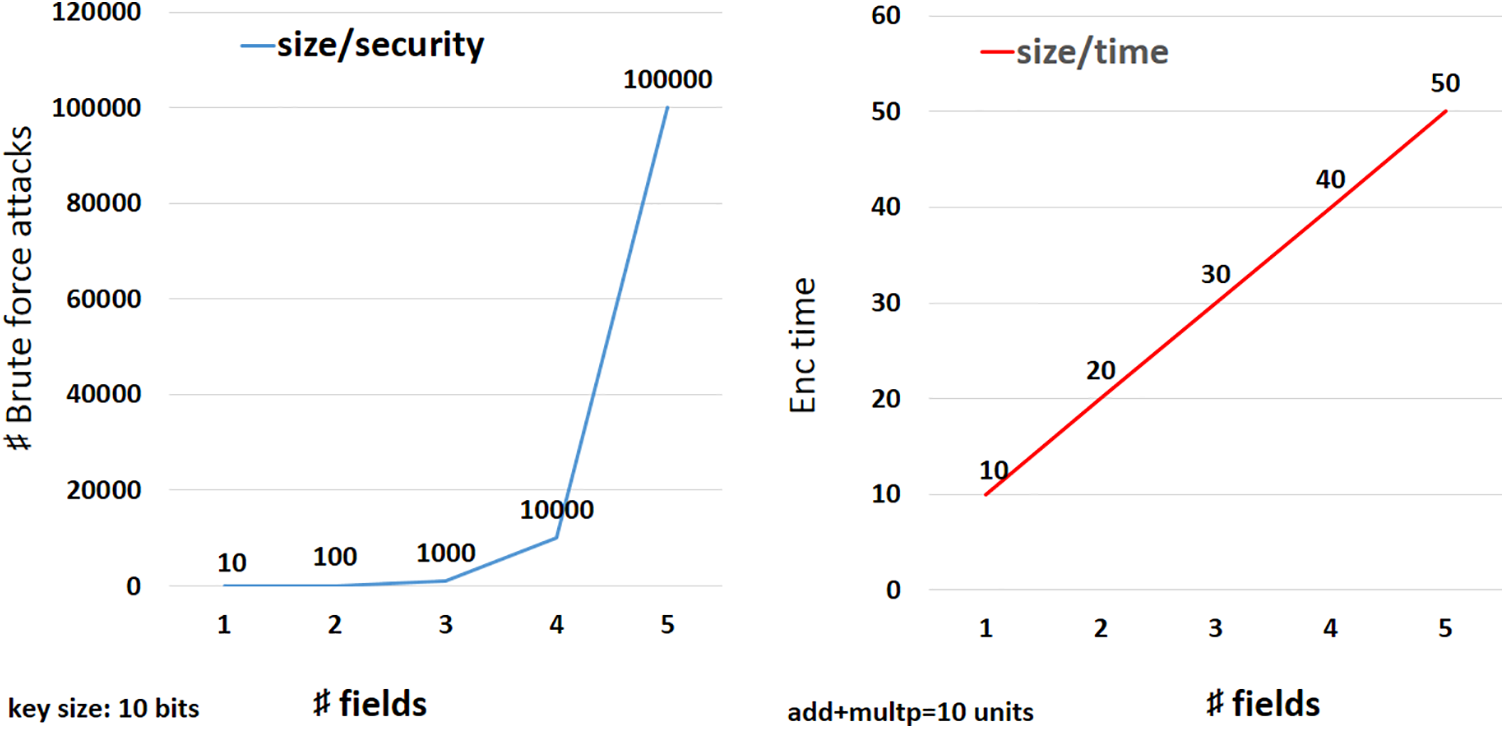
Figure 6: Comparison concerning memory size, security, and time

6  A Case Study: Diabetes Clinics

Nowadays, the importance of data in business and other sectors has increased. Data is the engine of customer relationships and mediation, the foundation of business strategy and any profitable project. Data management issues are a challenge for many organizations; however, the used data quality and the stored data quantity continue to be problems. The value of the data depends first on its quality and then on its size; therefore, these two factors are of great importance in the data world.

Correctly processed data delivers greater added value at all levels of the business. The strength of the encryption of a cryptography algorithm is generally linked to the size of its key: a large key results in more secure encryption. Advances in cryptographic analysis have largely influenced the increase in the key size used with algorithms. For example, in RSA, whenever the key size is doubled, the decryption operation requires six to seven times more processing power. Although it requires more computing power, the performance of computers, today, is sufficiently advanced to meet this demand.

Since January 2011, the Certification Authorities have tried to comply with the recommendations of the NIST (National Institute of Standards and Technology), by deciding that the key must be 2048 bits or more. Hence, some certification authorities have implemented the 2048-bit key length in their encryption systems.

Diabetes clinics offer health services that rely on a multidisciplinary team as well as pioneering research to ensure that the client receives the best care available. Comprehensive health assessments and treatments are coordinated by doctors, working with experienced nurses, social workers, and others. The clinics take care of diabetes problems and also provide psychological counseling to all groups. The clinics receive many patients and people looking for medical consultations every day (Fig. 7). Doctors and researchers benefit from this information by using statistics; therefore, these clinics should store all the data related to their patients and visitors. As a result, a huge amount of data is acquired, and this data is typically stored in the cloud. However, the more data stored in the cloud, the higher the cost the clinic pays.

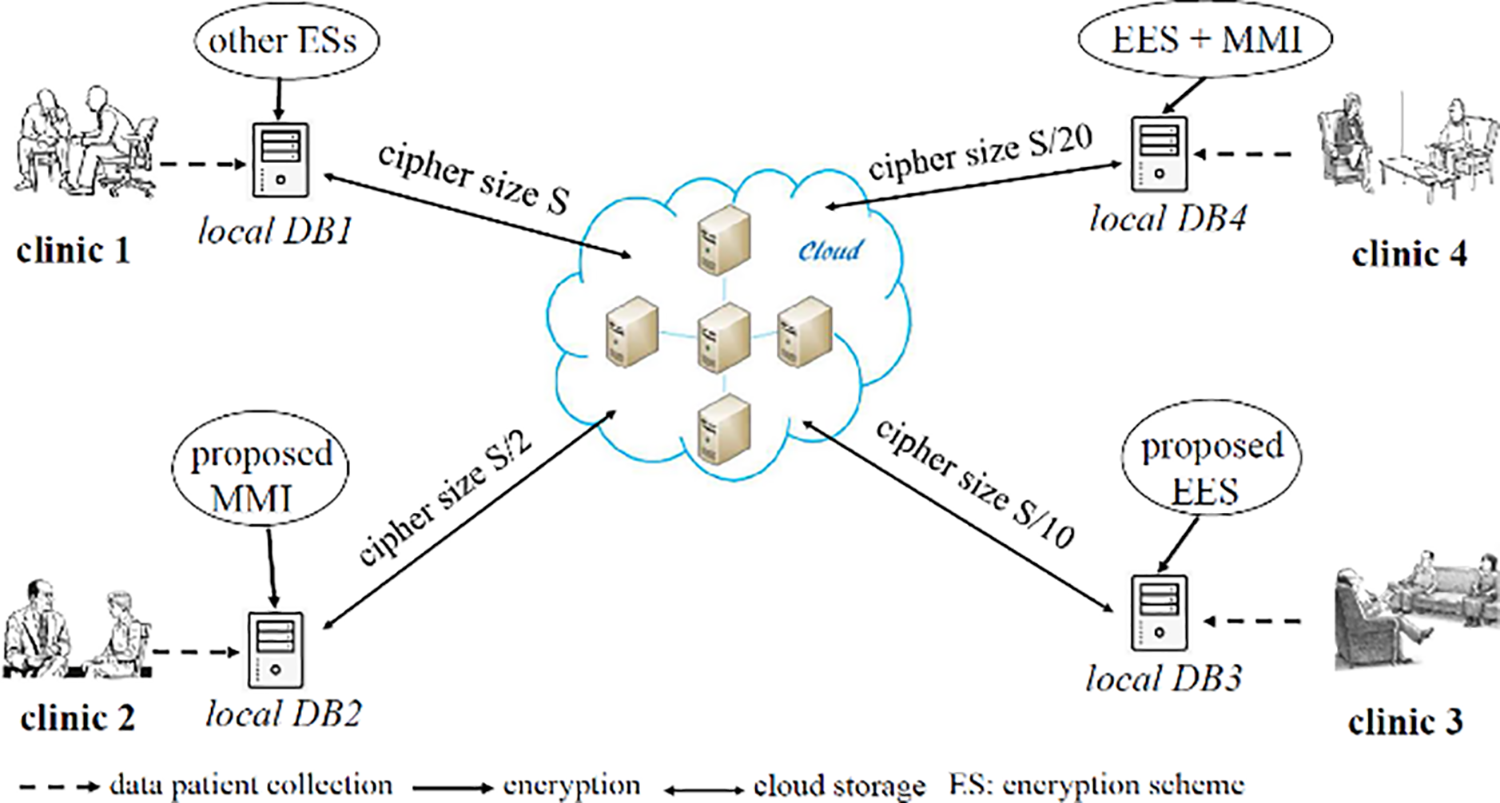
Figure 7: Proposed embedded encryption scheme (EES) and modular multiplicative inverse (MMI) in the use case

One of the clinics’ goals, whether public or private, is to increase profits by reducing the share of expenses and payments. In this paper, the proposed scheme reduces the size of the encrypted data to a rate of about 1/10 compared with other schemes, which is equivalent to 88% by grouping ten fields, that is ten values of information relating to one patient. For instance, this information could be the patient’s name, address, age, weight, height, date of birth, date of examination, type of disease, and medication. Note here that this is just an example (the ten fields), and many clinics may use more information about a single patient. For example, when using twenty fields, according to the study conducted in Section 5, the percentage of size reduction will be equal to 87% (1024 + 19 × 81 vs. 1024 × 20) since the key length is 1 kbits and the size of a field is 80 bits. With an estimation of the storage capacity needed for a clinic that receives 100 visitors per day, and using the current size of the encryption key (2048 bits) in order to provide a high rate of security, an annual volume of data is estimated at:

2 kbits × 20 × 100 × 365 = 1460 Mbits

Using the proposed method, the size will be:

(2048 + 19 × 81) × 100 × 365 = 130 Mbits

There is a big difference here in the capacity needed for storage and, of course, this will result in a big difference in the price needed for cloud-level storage. For example, iCloud, Amazon Cloud, and Google Drive provide an annual cost of between 15 dollars and 140 dollars per year for a capacity of 100 Gbits.

Finally, the research contributes in all fields to reduce the size of data, when we have a set of sensitive data units that can be read individually. Applications in healthcare include remote patient monitoring, individualized treatment strategies, and streamlined healthcare delivery. Also, for other types of sensitive data such as Personal and Private Customer, Employee, Financial, Business, and Operational data.

7  Conclusion

In today’s digital landscape, data security, and efficient storage have become paramount, especially in scenarios where data is stored in paid cloud services. The cost implications of large-scale data storage have prompted innovative approaches to reduce both the size of encrypted data and the associated storage expenses. In this paper, we presented an innovative encryption method designed to significantly reduce the size of the ciphered text. This size reduction is particularly advantageous for data storage in paid cloud services, as it results in substantial cost savings. The key strength of this technique lies in its robustness, achieved through the inherent correlation of the encrypted data, facilitated by the addition operation. The analysis of this approach yielded highly promising results, with an impressive 88% reduction in size when compared to traditional encryption techniques that encrypt each piece of information separately. This substantial reduction translates to a tenfold decrease in storage costs (1/10th of the original cost).

Furthermore, a study was conducted to explore the use of Modular Multiplicative Inverse for size reduction. The experiments conducted in this context showed a significant storage space gain of 50% when compared to certain other encryption techniques. To illustrate the practical application of our approach, we conducted a case study on diabetes clinics, which routinely store data related to tens of thousands of visitors each year for future research and analysis.

Acknowledgement: Not applicable.

Funding Statement: This research received no external funding.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Romaissa Kebache, Mostefa Kara; data collection: Mostefa Kara; validation, analysis and interpretation of results: Abdelkader Laouid, Ahcene Bounceur, Mohammad Hammoudeh; draft manuscript preparation: Romaissa Kebache, Mostefa Kara; Correction: Konstantinos Karampidis, Giorgos Papadourakis. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Due to the sensitive nature of the data, privacy and ethical concerns, neither the data nor its source code can be made available to the public.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. N. Birje, P. S. Challagidad, R. H. Goudar, and M. T. Tapale, “Cloud computing review: Concepts, technology, challenges and security,” Int. J. Cloud Comput., vol. 6, no. 1, pp. 32–57, 2017. doi: 10.1504/IJCC.2017.083905. [Google Scholar] [CrossRef]

2. R. C. Blattberg, B. D. Kim, and S. A. Neslin, “Market basket analysis,” in Database Marketing. International Series in Quantitative Marketing, New York, NY: Springer, 2008, vol. 18, pp. 339–351. doi: 10.1007/978-0-387-72579-6_13. [Google Scholar] [CrossRef]

3. O. Genc, A. Kurt, D. M. Yazan, and E. Edris, “Circular eco-industrial park design inspired by nature: An integrated non-linear optimization, location, and food web analysis,” J. Environ. Manag., vol. 270, pp. 110866, Sep. 2020. doi: 10.1016/j.jenvman.2020.110866. [Google Scholar] [PubMed] [CrossRef]

4. C. Lee et al., “Big healthcare data analytics: Challenges and applications,” in Handbook of Large-Scale Distributed Computing in Smart Healthcare. Scalable Computing and Communications, Cham: Springer, 2017, pp. 11–41. doi: 10.1007/978-3-319-58280-1_2. [Google Scholar] [CrossRef]

5. K. Nagaraj, G. Sharvani, and A. Sridhar, “Emerging trend of big data analytics in bioinformatics: A literature review,” Int. J. Bioinform. Res. Appl., vol. 14, no. 1–2, pp. 144–205, Jan. 2018. doi: 10.1504/IJBRA.2018.089175. [Google Scholar] [CrossRef]

6. L. Oneto et al., “Train delay prediction systems: A big data analytics perspective,” Big Data Res., vol. 11, pp. 54–64, Mar. 2018. doi: 10.1016/j.bdr.2017.05.002. [Google Scholar] [CrossRef]

7. M. Mohammadpoor and F. Torabi, “Big data analytics in oil and gas industry: An emerging trend,” Petroleum, vol. 6, no. 4, pp. 321–328, Dec. 2020. doi: 10.1016/j.petlm.2018.11.001. [Google Scholar] [CrossRef]

8. N. Lakshmi and K. S. Rani, “Privacy preserving association rule mining in vertically partitioned databases,” Int. J. Comput. Appl., vol. 39, no. 13, pp. 29–35, Feb. 2012. doi: 10.5120/4883-7321. [Google Scholar] [CrossRef]

9. M. Kara, K. Karampidis, Z. Sayah, A. Laouid, G. Papadourakis, and M. N. Abid, “A password-based mutual authentication protocol via zero-knowledge proof solution,” in Proc. Int. Conf. Appl. Cybersecurity (ACS) 2023, Dubai, United Arab Emirates, Cham, Springer, Sep. 2023, vol. 760, pp. 31–40. doi: 10.1007/978-3-031-40598-3_4. [Google Scholar] [CrossRef]

10. F. Lalem, A. Laouid, M. Kara, M. Al-Khalidi, and A. Eleyan, “A novel digital signature scheme for advanced asymmetric encryption techniques,” Appl. Sci., vol. 13, no. 8, pp. 5172, Apr. 2023. doi: 10.3390/app13085172. [Google Scholar] [CrossRef]

11. M. I. Bhat and K. J. Giri, “Impact of computational power on cryptography,” in Multimedia Security. Algorithms for Intelligent System, Singapore: Springer, Jan. 2021, pp. 45–88. doi: 10.1007/978-981-15-8711-5_4. [Google Scholar] [CrossRef]

12. S. Medileh et al., “A multi-key with partially homomorphic encryption scheme for low-end devices ensuring data integrity,” Information, vol. 14, no. 5, pp. 263, Apr. 2023. doi: 10.3390/info14050263. [Google Scholar] [CrossRef]

13. M. Kara, K. Karampidis, G. Papadourakis, A. Laouid, and M. AlShaikh, “A probabilistic public-key encryption with ensuring data integrity in cloud computing,” in 2023 Int. Conf. Control, Artificial Intell. Robot. Optimization (ICCAIRO), Crete, Greece, Apr. 11–13, 2023, pp. 59–66. doi: 10.1109/ICCAIRO58903.2023.00017. [Google Scholar] [CrossRef]

14. M. Hammoudeh et al., “A service-oriented approach for sensing in the internet of things: Intelligent transportation systems and privacy use cases,” IEEE Sens. J., vol. 21, no. 14, pp. 15753–15761, 15 Jul. 2021. doi: 10.1109/JSEN.2020.2981558. [Google Scholar] [CrossRef]

15. M. Ahmed and A. S. Barkat Ullah, “False data injection attacks in healthcare,” in Australasian Conf. Data Mining. AusDM 2017. Commun. Comput. Inf. Sci., Singapore, Springer, 2017, vol. 845, pp. 192–202. doi: 10.1007/978-981-13-0292-3_12. [Google Scholar] [CrossRef]

16. A. H. Seh et al., “Healthcare data breaches: Insights and implications,” Healthcare, vol. 8, no. 2, pp. 133, May 2020. doi: 10.3390/healthcare8020133. [Google Scholar] [PubMed] [CrossRef]

17. R. A. Haraty, M. Zbib, and M. Masud, “Data damage assessment and recovery algorithm from malicious attacks in healthcare data sharing systems,” Peer Peer Netw. Appl., vol. 9, no. 5, pp. 812–823, Sep. 2016. doi: 10.1007/s12083-015-0361-z. [Google Scholar] [CrossRef]

18. N. Attrapadung, J. Herranz, F. Laguillaumie, B. E. Libert, E. de Panafieu and C. Ràfols, “Attribute-based encryption schemes with constant-size ciphertexts,” Theor. Comput. Sci., vol. 422, pp. 15–38, Mar. 2012. doi: 10.1016/j.tcs.2011.12.004. [Google Scholar] [CrossRef]

19. M. Usman, I. Ahmed, M. I. Aslam, and U. A. Shah, “SIT: A lightweight encryption algorithm for secure internet of things,” arXiv preprint arXiv:1704.08688, vol. 8, no. 1, 2017. doi: 10.14569/issn.2156-5570. [Google Scholar] [CrossRef]

20. Y. Mansouri, A. N. Toosi, and R. Buyya, “Brokering algorithms for optimizing the availability and cost of cloud storage services,” in 2013 IEEE 5th Int. Conf. Cloud Comput. Technol. Sci., Bristol, UK, Dec. 2–5, 2013, vol. 1, 581–589. doi: 10.1109/CloudCom.2013.83.vol.. [Google Scholar] [CrossRef]

21. R. Rahim and A. Ikhwan, “Cryptography technique with modular multiplication block cipher and playfair cipher,” Int. J. Sci. Res. Sci. Technol., vol. 2, no. 6, pp. 71–78, Nov. 2016. [Google Scholar]

22. Z. E. Dawahdeh, S. N. Yaakob, and R. R. bin Othman, “A new image encryption technique combining elliptic curve cryptosystem with hill cipher,” J. King Saud. Univ. Comput. Inf. Sci., vol. 30, no. 3, pp. 349–355, Jul. 2018. doi: 10.1016/j.jksuci.2017.06.004. [Google Scholar] [CrossRef]

23. F. Patel and M. Farik, “A new substitution cipher-random-X,” Int. J. Sci. Technol. Res., vol. 5, no. 11, pp. 125–128, 2015. [Google Scholar]

24. P. E. Coggins III and T. Glatzer, “An algorithm for a matrix-based enigma encoder from a variation of the hill cipher as an application of 2 × 2 matrices,” Primus, vol. 30, no. 1, pp. 1–18, 2020. doi: 10.1080/10511970.2018.1493010. [Google Scholar] [CrossRef]

25. D. R. Lide, “A century of excellence in measurements, standards, and technology,” Meas. Sci. Technol., vol. 13, no. 10, pp. 1653–1654, 2002. doi: 10.1201/9781351069397. [Google Scholar] [CrossRef]

26. T. Jamil, “The rijndael algorithm,” IEEE Potentials, vol. 23, no. 2, pp. 36–38, 2004. doi: 10.1109/MP.2004.1289996. [Google Scholar] [CrossRef]

27. N. Li, “Research on Diffie-Hellman key exchange protocol,” in 2010 2nd Int. Conf. Comput. Eng. Technol., Chengdu, China, Apr. 2010, vol. 4, pp. V4-634–V4-637. doi: 10.1109/ICCET.2010.5485276. [Google Scholar] [CrossRef]

28. R. L. Rivest, L. Adleman, M. L. Dertouzos, “On data banks and privacy homomorphisms,” Found. Secure Comput., vol. 4, no. 11, pp. 169–180, 1978. [Google Scholar]

29. A. Acar, H. Aksu, A. S. Uluagac, and M. Conti, “A survey on homomorphic encryption schemes: Theory and implementation,” ACM Comput. Surveys, vol. 51, no. 4, pp. 1–35, Jul. 2018. doi: 10.1145/3214303. [Google Scholar] [CrossRef]

30. C. Gentry, “Fully homomorphic encryption using ideal lattices,” in Proc. Forty-first Annu. ACM Symp. Theory Comput., Bethesda, MD, USA, May 2009, pp. 169–178. doi: 10.1145/1536414.1536440. [Google Scholar] [CrossRef]

31. J. Dyer, M. Dyer, and J. Xu, “Practical homomorphic encryption over the integers for secure computation in the cloud,” Int. J. Inf. Secur., vol. 18, no. 5, pp. 549–579, Feb. 2019. doi: 10.1007/s10207-019-00427-0. [Google Scholar] [CrossRef]

32. T. Elgamal, “A public key cryptosystem and a signature scheme based on discrete logarithms,” IEEE Trans. Inf. Theory, vol. 31, no. 4, pp. 469–472, 1985. doi: 10.1109/TIT.1985.1057074. [Google Scholar] [CrossRef]

33. D. Boneh, E. J. Goh, and K. Nissim, “Evaluating 2-DNF formulas on ciphertexts,” in Theory of Cryptography. Lecture Notes in Computer Science, Berlin, Heidelberg: Springer, 2005, vol. 3378, pp. 325–341. doi: 10.1007/978-3-540-30576-7_18 [Google Scholar] [CrossRef]

34. M. van Dijk, C. Gentry, S. Halevi, and V. Vaikuntanathan, “Fully homomorphic encryption over the integers,” in Advances in Cryptology–EUROCRYPT 2010, Berlin, Heidelberg: Springer, 2010, vol. 6110, pp. 24–43, doi: 10.1007/978-3-642-13190-5_2 [Google Scholar] [CrossRef]

35. S. Dasgupta and S. Pal, “Design of a polynomial ring based symmetric homomorphic encryption scheme,” Perspect. Sci., vol. 8, pp. 962–965, Sep. 2016. doi: 10.1016/j.pisc.2016.06.061. [Google Scholar] [CrossRef]

36. Y. Doröz, A. Shahverdi, T. Eisenbarth, and B. Sunar, “Toward practical homomorphic evaluation of block ciphers using prince,” in Int. Conf. Financial Cryptogr. Data Security-Springer, Berlin, Heidelberg, Springer, Oct. 2014, vol. 8438, pp. 208–220. doi: 10.1007/978-3-662-44774-1_17. [Google Scholar] [CrossRef]

37. P. W. Khan and Y. Byun, “A blockchain-based secure image encryption scheme for the industrial internet of things,” Entropy, vol. 22, no. 2, pp. 1–26, Feb. 2020. doi: 10.3390/e22020175. [Google Scholar] [PubMed] [CrossRef]

38. N. Hu, Z. H. Tian, X. J. Du, N. Guizani, and Z.H. Zhu, “Deep-Green: A dispersed energy-efficiency computing paradigm for green industrial IoT,” IEEE Trans. Green Commun. Netw., vol. 5, no. 2, pp. 750–764, Mar. 2021. doi: 10.1109/TGCN.2021.3064683. [Google Scholar] [CrossRef]

39. C. Liu, G. Xiong, G. P. Gou, S. M. Yiu, Z. Li and Z. H. Tian, “Classifying encrypted traffic using adaptive fingerprints with multi-level attributes,” World Wide Web, vol. 24, pp. 2071–2097, Oct. 2021. doi: 10.1007/s11280-021-00940-0. [Google Scholar] [CrossRef]

40. E. Srimathi and P. S. Chokkalingam, “Improved cloud storage encryption using block cipher-based DNA anti-codify model,” Comput. Syst. Sci. Eng., vol. 47, no. 1, pp. 903–918, 2023. doi: 10.32604/csse.2023.029790. [Google Scholar] [CrossRef]

41. M. Ahmad, R. I. Alkanhel, N. F. Soliman, A. D. Algarni, F. E. Abd El-Samie and W. El-Shafai, “Securing healthcare data in IoMT network using enhanced chaos based substitution and diffusion,” Comput. Syst. Sci. Eng., vol. 47, no. 2, pp. 2361–2380, 2023. doi: 10.32604/csse.2023.038439. [Google Scholar] [CrossRef]

42. L. Wei, J. B. Xu, M. D. Tang, and H. Li, “A new embedded encryption algorithm for wireless sensor networks,” in 2009 Int. Forum on Inf. Technol. Appl., Jan. 2009, vol. 1, pp. 119–122. doi: 10.1109/IFITA.2009.165. [Google Scholar] [CrossRef]

43. N. Bruce, W. T. Jang, and H. J. Lee, “An embedded encryption protocol for healthcare networks security,” Int. J. Secur. Appl., vol. 8, no. 2, pp. 139–144, 2014. doi: 10.14257/ijsia.2014.8.2.14. [Google Scholar] [CrossRef]

44. Y. S. Abdulsalam and M. Hedabou, “Security and privacy in cloud computing: Technical review,” Future Internet, vol. 14, no. 1, pp. 11, Dec. 2021. doi: 10.3390/fi14010011. [Google Scholar] [CrossRef]

45. J. K. Dawson, F. Twum, J. B. Hayfron Acquah, and Y. M. Missah, “Ensuring confidentiality and privacy of cloud data using a non-deterministic cryptographic scheme,” PLoS One, vol. 18, no. 2, pp. e0274628, 2023. doi: 10.1371/journal.pone.0274628. [Google Scholar] [PubMed] [CrossRef]