A Multilayer Network Constructed for Herb and Prescription Efficacy Analysis

1  Introduction

Traditional Chinese Medicine (TCM) formula is a common approach in traditional medical treatment and has gained widespread clinical applications [1]. To enhance therapeutic efficacy and reduce adverse effects, practitioners of Chinese medicine prescribe a combination of plant species/minerals in prescriptions based on clinical experience [2]. Ancient classical prescriptions are still with great influence on practitioners nowadays to address various symptoms and pathogenesis based on the theory of syndrome differentiation. However, the role of herbs and their combination rules remain unclear due to the old obscure theory. There are many challenges in exploring the law of herbs in composition to the overall effects and indications: (1) As Chinese medicine theory is of empirical nature with varying descriptive concepts, it is difficult to construct a quantitative model of herb attributes related to the overall effects of prescriptions. (2) Facing large-scale TCM records, it is challenging to uncover the complex relationships between herb attributes, prescriptions and overall effects given various intrinsic relevance. Therefore, outlining the complex relationships of prescriptions, herbs and their efficacy is crucial to show these inherent connections and principles, and is also the key issue needs to be solved in practice.

CM embraces a holistic approach and uses complicated herb prescriptions for treatment targeting complex disease phenomena. Ma et al. mined syndrome differentiating principles from TCM clinical data [3]. Zhou et al. surveyed a range of approaches and applications of the knowledge graph [4], and Zhang et al. applied the knowledge graph for TCM automated diagnosis [5]. In recent years, network pharmacology has been widely used to explain the complex relationships in CM Prescriptions. Network pharmacology [6,7] analyzes disease- gene- target- drug networks to express the synergy of multi-component, multi-pathway and multi-targeting prescriptions, and also reveals the pharmacological mechanism of CM components such as herb pairs [8], classic prescriptions [7] and Chinese patent medicine [9]. Hence, network pharmacology is believed to be a promising drug discovery approach with holistic and systematic ideas in accordance with TCM theory [10]. Sun et al. took the active constituents of Huanglian Jiedu decoction to explore its intervention mechanism in the treatment of Alzheimer’s disease through a pharmacological network [11]. Li et al. focused on mapping disease phenotypes and herbal compounds into biomolecular networks to explore the relationships between herbal prescriptions and diseases or CM syndromes [12,13]. Meanwhile, the research frontier of computer technology is widely integrated with the biomedical field, and has become an important technical means of biomedical research [14].

Former studies on prescription analysis are based on gene or protein databases, unable to uncover the traditional combination theory of CM. Moreover, the dosage and properties of herbs on the effect of prescriptions have been neglected. The simultaneous application of herbs is usually in different dosages traditionally identified in a prescription with different roles. One of the key subjects of prescription research focuses on compatibility regularity while the dosage of herbs has joint action on the overall efficacy of prescriptions. The structure of Monarch, Minister, Assistant and Guide are traditional theories giving compatibility principles of prescriptions. Therefore, herb dosage needs to be integrated with combination rules to investigate the comprehensive mechanism of prescriptions.

We propose a structure of a Prescription-Herb-Function Network (PHFN) with 3 intra networks corresponding to the effects of prescriptions, herb combinations and herbal efficacies with interlayers to illustrate the internal law of compatibility. The research is (1) to build a network model that accurately illustrates the prescriptions, herbs, efficacy and their complex relationships, providing a unified analysis model for an in-depth study of formula compatibility; (2) to introduce a concept of relative dosage to reflect the relative intensity of each herb, and to provide a unified criterion for herb quantity evaluation; (3) to study herbs and their combinations in terms of multivariate tuples and weighted edges in network model to reflect relationships amongst herbs in prescriptions.

2  Methods

Definitions of relative dosage and relative interaction intensity are first introduced, followed by herb-efficacy (HE), prescription-herb (PH), prescription-function (PF) intra networks and PF-PH, PH-HE interlayer networks. The network model comprising various concepts of TCM such as herbs and efficacies are then constructed. Each of the network is explained as follows.

2.1 Definitions in Network Scheme

Definition 1: Relative dosage. Standardized herb dosage that compares the actual dosage with its normal dosage range. Relative dosage is a standardized value ranging (0, 1]. Normally the larger the actual dosage of an herb, the larger the relative dosage prescribed related to patients’ symptoms and clinician’s medication experience. Considering that the negative exponential function features non-linear, continuous, monotone decreasing and asymptotic, the calculation is defined as

Y(x)=1−e−λxβ, (1)

where x and Y(x) are the actual dosage and the standardized dosage, respectively. Y(x) indicates that the efficacy of an herb is enhanced with the increase of herb dosage to 1 as the standardized maximum value. λ is chosen to define a range that Y(x) increases rapidly with x, and the increase becomes less significant when x goes further beyond the particular range. The parameters are chosen as follows, β = 2 and

λ=ln2/[(a+b)/2]2, (2)

where [a, b] is the routine dosage range of an herb [15]. According to the original dosage, the unit Liang is converted to 15.625 g [16], and other units are scaled with literature research and measurements [17].

Definition 2: Relative interaction intensity. The relative dosage of a particular herb to the sum of relative dosage of all herbs in a prescription. Relative interaction intensity describes the relative dosage of an herb in a prescription in proportion to all the other relative dosages, and its range of value is (0, 1]. For a prescription with n number of herbs, and the relative dosage of an herb is denoted as xj, so the relative interaction intensity of ith herb is

xi/∑j=1nxj,i∈(1,n) (3)

Based on the calculation of herb dosage in each formula according to Def. 1, taking Cassia Twig Decoction as an example, according to the original record it is composed of cassia twig 46.875 g, debark peony root 46.875 g, fresh ginger 46.875 g, Chinese date 12 g, and licorice 31.25 g. Based on research of dosage in Treatise on Exogenous Febrile and Miscellaneous Diseases, the routine dosage ranges of cassia twig and debark peony root are [3.9 g, 78.125 g], [3.9 g, 93.75 g], respectively, and their relative dosage in this prescription are 0.5956 and 0.4721, respectively, and their relative action intensities are 0.2541 and 0.2014, respectively. As the relative interaction intensity of an herb depends on the dosage of itself and of other herbs used in combination, the relative interaction intensity varies in different prescriptions even if the herb dosage itself stays the same. For example, although the dosage of cassia twig in Xiaoqinglong decoction is the same as that in cassia twig decoction, its relative action intensity in Xiaoqinglong decoction is 0.1276.

Definition 3: Intra-layer Network. Intra-layer networks include herb-efficacy, prescription-herb, prescription-function networks. PH network demonstrates a set of herbs and their associations based on the composition of prescriptions under analysis. Prescription-herb network is defined as

NPH = <Y,Ry>whereY={y1,y2,…,yn} and Ry={ri,j}∀i,j∈n,i≠j, (4)

where Y is a set of nodes representing herbs appearing in all prescriptions, and Ry for herb-to-herb relationships. ri,j = <n1, φm> is in the form of a tuple representing the relationship between herb yi and herb yj where n1 is the total number of co-existence of yi and yj in all prescriptions under analysis, and φm includes a set of prescriptions where they co-exist and the corresponding original and relative dosage of herb yi and herb yj.

Prescription function network demonstrates associations between functions according to their co-occurrences in prescriptions. It is represented as

NPH = <G,Rg>,where G={g1,g2,…,gn} and Rg={gi,j}∀i,j∈n,i≠j, (5)

where G is a set of functions, and Rg is a set of relationships between them where gi,j includes the number of co-occurrences and a set of prescriptions where they co-exist. Likewise, herbal efficacy network shows associations between efficacies defined as NHE = <E, Rx> where E is a set of efficacies, and Rx represents their relationships between them including co-occurrences from herbs in the scope of the analysis.

Definition 4: Interlayer Network. PH-HE interlayer network represents the relationships between and prescription-herb and herb-efficacy network. PH-HE interlayer network is represented as

NPH−HE =<Y,E,Ry−x>, (6)

where Y and E are a set of herbs and a set of herbal efficacies respectively, and matrix Ry−x represents the relationships between Y and E. If the herb yi from Y has efficacy xi from E, the corresponding element in Ry−x is set as 1 denoting there is a weightless edge between them.

PF-PH interlayer network presents relationships of key herbs in prescriptions and functions of the prescriptions where they are in. It is represented as

NPF−PH =<Y,G,Ry−g>, (7)

where Y and G are a set of herbs and a set of prescription functions, respectively. Herbs in each prescription are sorted according to their relative interaction intensities, and main herbs accounting for more than 60% cumulative relative interaction intensities are linked to establish associations with the functions of corresponding prescription. Ry−g stores these herb-function connections in the matrix, each element in the form of a tuple as Ry−g = <n, φm> where n is the total number of co-occurrences of particular herb y and a particular function g taking account of all prescriptions, and φm is the set of prescriptions where they co-exist.

Prescription-Herb-Function Network (PHFN) is a multidimensional heterogeneous network integrating herb-efficacy, prescription-herb, prescription-function networks and their interlayer networks.

2.2 Solution Design

In order to realize elastic and scalable massive prescription analysis, the prescription data storage and analysis system adopts a distributed database and computing framework, which can be combined with a variety of analysis tools to realize interactive or batch data analysis, machine learning model construction, and graph analysis. As the association between nodes is sparse, in order to optimize the storage efficiency and ensure that the data can be queried interactively, the Cassandra database is adopted as shown in Fig. 1.

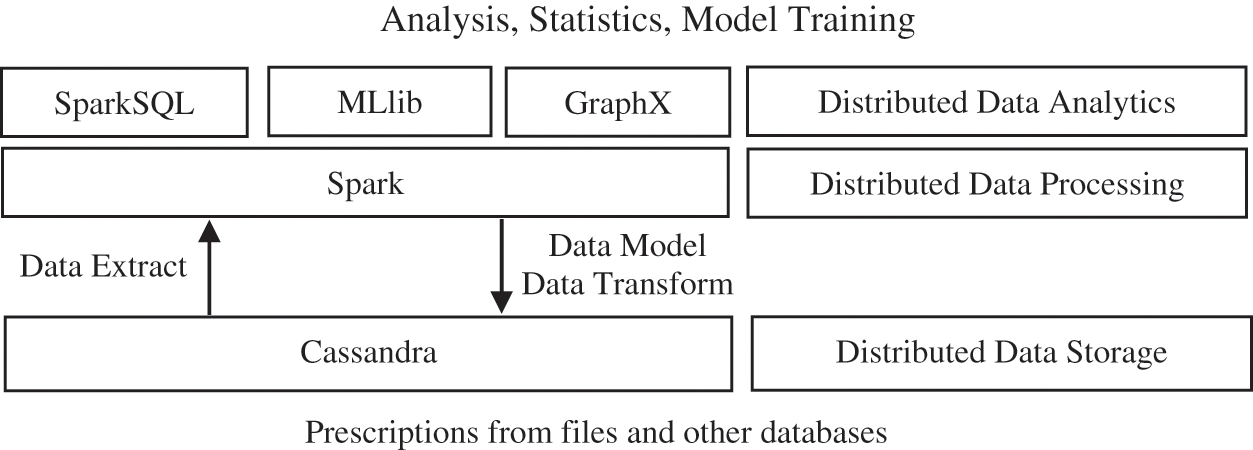
Figure 1: Solution design

2.3 Construction of PHFN

2.3.1 Intra layer Network Construction

PH network is created as an example for intra networks. According to Definition 3, each herb in PH network is a node, and the relationships between herbs are edges whose information is stored in Ry. Each element r in Ry is in the form of <n, φm>. The pseudocode of establishing Ry is shown in Table 1. The original record in Exogenous Febrile and Miscellaneous Diseases is indexed by the name of prescriptions, and synonyms of the same medicinal materials are standardized and unified, such as apricot kernel and bitter apricot kernel. Herbs in all prescriptions and their efficacies are then collected into a dataset.

2.3.2 Interlayer Network Construction

Interlayer networks including PF-PH and PH-HE are based on intra networks previously constructed. The PF-PH interlayer network is created as an example shown in Table 2. Functions of prescriptions in PF network and herbs in PH network are connected based on the composition and functions of each prescription. Herbs selected from each prescription based on the relative interaction intensity in list A are connected to the functions of corresponding prescriptions, so a weighted edge in the value of relative interaction intensity is established between the herb node and the function node represented in Ry−g. The algorithm of PF-PH interlayer network construction is shown in Table 2.

2.4 PHFN Data Querying

2.4.1 Query Based on Specified Herb

As PHFN model stores information of prescription functions, compositions and dosage with internal associations, the constructed network can be seen as a dataset with various relationships. Using the metadata of networks, users could query the stored data by specified herbs or prescriptions to retrieve a sub-network with connected information. As the data of a related network is often in largescale, the data query component facilitates subgraphs to be displayed in the visualization component. The following queries are based on PHFN to extract information of prescriptions or herbal combinations as shown in Table 3.

2.4.2 Query of Herb Pairs

According to Definition 3, the weight of edges in PH network stores the number of the co-existence of all possible two-herb combinations in all prescription data set. The frequency of herb combinations can be obtained by scanning the weight of edges in Ry from PH network. The algorithm of herb pair query is shown in Table 4.

2.4.3 Query of Herbs and Efficacy Based on Prescriptions

For a given formula and PF-PH interlayer networks, main herbs accounting for cumulative relative interaction intensities and the functions of prescriptions can be obtained. Traversing herbs and functions in PH and PF networks respectively will provide further related information. The pseudocode of the algorithm is shown in Table 5.

3  Results

3.1 Construction Results of PHFN

112 prescriptions in Treatise on Exogenous Febrile and Miscellaneous Diseases are collected to illustrate a multidimensional heterogeneous PHFN network, and part of data in networks are shown in Tables 6 to 7. The following clinical terminologies of TCM in this paper are referred to Chinese-English Dictionary of State Standard Clinical Terminologies of Traditional Chinese Medicine [18]. To initialize association-relation in networks, in preprocessing a total of 89 kinds of medicinal materials were obtained, including cinnamon twig, peony, roasted licorice, ginger, jujube, pueraria, magnolia officinalis, almond, processed aconite, etc. 146 functions of prescriptions are obtained after standardization, including relieving muscles, dispelling wind, harmonizing Ying and health, engender fluid, relaxing meridians, relieving exterior, dispersing lung, relieving asthma, supporting yang, etc. Cassia twig and peony root is a common combination, and their relative dosage in different prescriptions is shown in Table 6. They are used in comparable dosage in Guizhi (cassia twig) Decoction to promote sweating and relieve muscles, but varies when used for warming and tonifying deficiency in No. 35 prescription Xiaojianzhong Tang. It can be inferred that the purpose of treatment has a great influence on the usage and dosage of prescriptions.

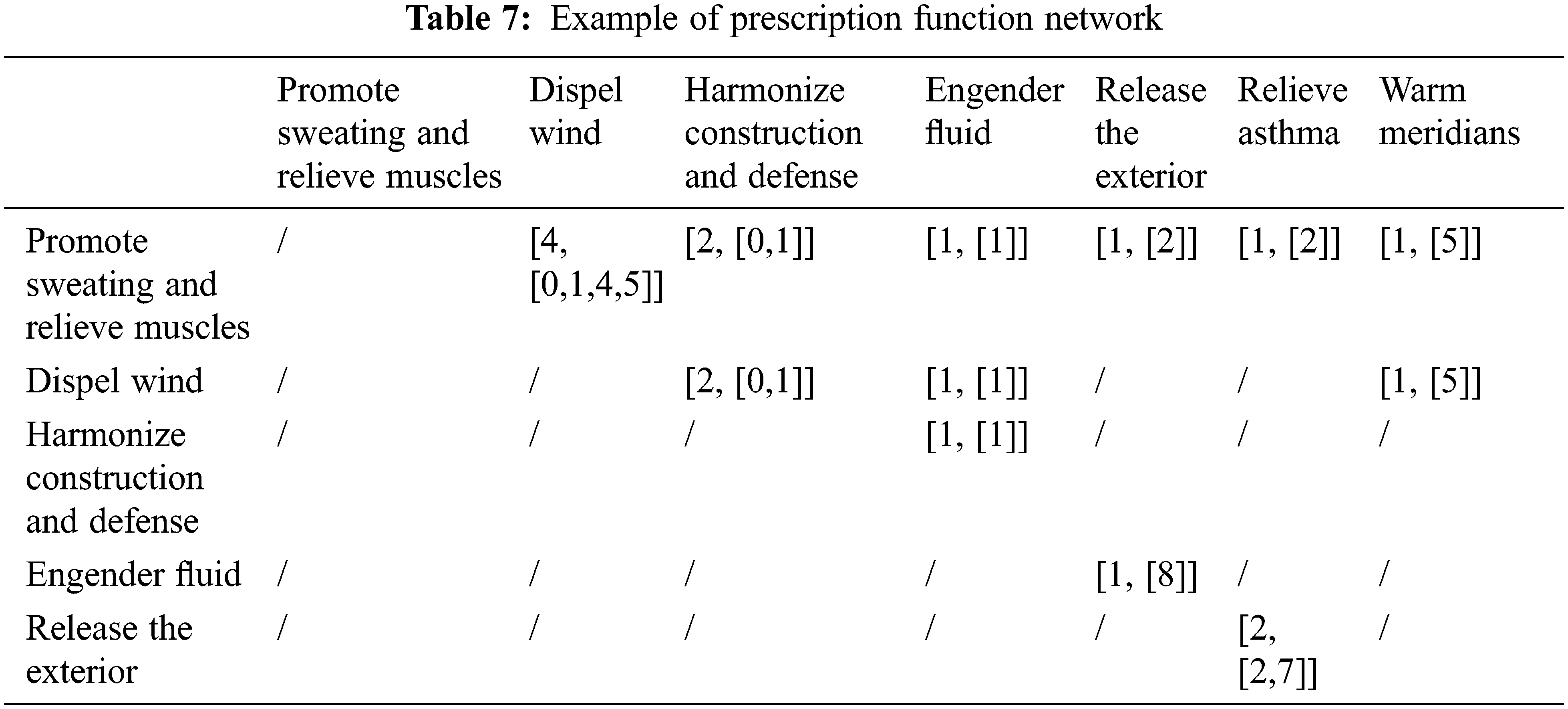
Table 7 shows that the function of promoting sweating to relieve muscles co-occurs with dispelling wind four times in Nos. 0, 1, 4 and 5 prescriptions, in names are Guizhi (cassia twig) Decoction, Guizhi (cassia twig) plus Gegen (pueraria lobata) decoction, Guizhi (cassia twig) decoction without Shaoyao (peony root), Guizhi (cassia twig) and Fuzi (processed aconite root) Decoction without Shaoyao (peony root) respectively. Cassia Twig Decoction (Guizhi Tang) is a classical prescription with functions of harmonizing defensive and nutritive levels of the body, and expelling pathogens from the exterior. It is composed of cassia twig (Guizhi), debark peony root (Baishao), fresh ginger (Shengjiang), Chinese date (Dazao), and licorice (Gancao). Cassia twig is warm and acrid treating the main symptoms, expelling pathogenic wind-cold from muscles and skin. Debark peony root is slightly cold, sour, and sweet, which strengthens the interior, both of them in combination serve to harmonize the body. Licorice harmonizes the actions of the other herbs. Research shows that different proportion of herb pairs produce different material basis [15].

Table 8 shows the associations-relations of main herbs and functions of prescriptions. The main herbs are collected by their cumulative relative interaction intensities of more than a threshold after sorting them in descending order. The threshold is determined by experiment to ensure that the usage of extracted main herbs cover main effects of prescriptions even if they are not matched by herbs with highest value. In the case of Xiaochaihu (Bupleurum) Decoction, the foremost herb bupleurum with relative interaction intensity 0.189 is ranked after pinellia rhizome 0.208 and scutellaria root 0.197. According to the overall analysis of the values of relative interaction intensities, we found that a threshold in the range between 0.6 and 0.8 is appropriate. For example, the relative interaction intensities of cassia twig, licorice and peony in Guizhi (cassia twig) Decoction were 0.263, 0.255 and 0.171, respectively, and that of ephedra and cassia twig in prescription No. 7 Mahuang (Ephedra) Decoction were 0.506 and 0.289, respectively. In order to ensure the accuracy of correlation between herbs and prescription effects without much data noise, the threshold is set at 0.6. In Table 8, the effects of promoting sweating and muscle relieving appear 5 times in Nos. 0, 1, 2, 4, 5 prescriptions. Table 9 lists part of herb efficacy associations on the cases of ephedra, gypsum and rhubarb.

Tables 6 to 8 show that the scale of intra and inter layer networks are related to the number of nodes in different categories, and the number of herbs, efficacies and functions for a particular prescription is limited compared to the total number of nodes in the category. For the PF network, the values of the relative action intensities related to dosage and the number of herbs in prescriptions determine the scale of the herb nodes to be associated with functions. The average number of herbs in all prescriptions is 4.83, and that contributes to prescription functions is 2.6. These herbs are connected to 2 to 4 function nodes, both much smaller than the scale of corresponding intra-layer networks which results in sparse correlations. Similarly, the associations of inter-layer networks are also sparse as the nodes are only connected to limited nodes having similar or medical-related functions.

To compare with other herb dosage standards, we compare our results with a rule that standardizes each herb dosage by di/(dmax+dmin ), where di is the actual dosage of herb di in a prescription, dmax is its maximum usual dosage, and dmin is the minimum usual dosage [19]. The relative interaction intensities are then calculated and sorted based on this standardized herb dosage, and main herbs are then extracted with the same threshold of 0.6. The comparison is that in 20 prescriptions the main herbs by this method have one more herb compared to our methods. The main herbs screened are very similar under the same screening conditions of the cumulative sum of relative action intensity, but the herbs selected by our model are stricter.

3.2 Analysis of PHFN Model

PHFN model demonstrates rich information of prescription dataset. Herb combinations are more various than function or efficacy combinations. As networks are sparse with most of prescription functions or herbal efficacies taken only once or twice, for illustration herb combinations for more than three times in prescriptions are shown in Fig. 2. In a variety of herbs as shown in Fig. 2, most frequent herb combinations are between cassia twig, licorice root, fresh ginger, peony root and jujube. They are also more frequent as main herbs in connection with prescription functions. Licorice is a common herb believed to be used in various kinds of syndromes, often with fresh ginger, Chinese date, and ginseng. The combination of cassia twig and licorice is a famous herb pair with warm nature to enhance the function of warming heart and activating blood circulation [20]. Based on herbs in Fig. 2, their associations in PF-PH Interlayer network are shown in Fig. 3.

Figure 2: Herb combinations in PH network

Figure 3: PF-PH interlayer associations

The significant associations in Fig. 3 are to name a few, the node of releasing the exterior with licorice root, jujube, cassia twig and ephedra, the node of reviving yang with aconite root, the node of harmonizing the stomach with licorice root and pinellia rhizome, the node of sweating and relieving muscles with cassia twig, etc. This provides reference on the selection of herbs according to the efficacy combination for prescriptions. The fact that a prescription is prescribed with a selection of herbs with specific dosage in composition gives more information than the combination itself, so it is important to distinguish the dosage and the effect to understand their overall function and compatibility. However, most dosage prescribed are based on experience. We introduce relative dosage to standardize dosage in uniform range of (0,1], and also based on the value of relative dosage we introduced relative interaction intensity to distinguish the importance of herbs. Further analysis shows that the dosage of herbs is one of the important factors affecting the curative effects of herbs, while other factors including the medicinal properties and efficacies also play major roles for the overall function.

In our network, the TCM information components, such as prescription functions, herbs, and efficacies are represented as nodes, and their co-occurrences or contributions are represented as weighted edges. The associations can be analyzed with graph theory to extract their attribute information. It can be inferred that the sum of weights of all edges in PH network is equal to the sum of the total number of possible combinations of any two herbs appearing in the prescriptions. Furthermore, a function node from a prescription is at least connected with an herb node to form PH interlayer network. Though 112 classical prescriptions in Treatise on Exogenous Febrile and Miscellaneous Diseases are not huge in data volume, it is credible to visualize the associations at different layers. The network if containing more prescriptions data will partly serve as a database of CM classic medication with valuable associations in the metadata. It not only integrates the formula knowledge (e.g., herbs and dosage, herbal efficacy) to visualize the overall functions by networks, but also can help acquire the core herbs, therapeutic effects, and relationships from the large-scale medical data.

Most of the recent network modeling are based on network pharmacology to integrate drug-disease and traditional knowledge of herbal medicines to identify the rationale of herb combinations. Cheng et al. [21] introduced network distance between targets of a drug pair, including closest, separation, shortest, kernel and center to analyze the proximity measure of drug-drug relationships on a network-based modeling of drug combinations. Wang et al. [22] constructed a protein–protein interaction network for a given herb pair by retrieving the associated ingredients and protein targets, and determined ingredient distances with cross-level protein network-based distances based on measurements introduced by Cheng. Jafari et al. [23] constructed a bipartite network based on natural products and chemical ingredients for community detection. Cheng et al. considered only targets and their proximity to drug pairs, but not from the perspective of CM. Wang and Jafari considered the measurements of distances of CM natural products based on targets proximity, but not from the perspective of CM theory and its diagnosis and treatment approaches. Li et al. [24] introduced a distance-based mutual information model to determine herb interactions based on their frequencies and distance, but dosage information not retained. Compared to existing models, our model is in the theory of traditional Chinese medicine with integration of frequencies, combinations and curative effects of all herbs based on a full prescription level combined with dosage information among the herb combinations.

The study on selection of multiple herbs are important for understanding the enhanced and harmonized therapeutic effect. The network is an initial step to integrate herbs, prescriptions, and functions with potential extensions including domain knowledge, such as herb properties (e.g., herb nature and flavor, channel tropism), symptoms and diagnosis to establish a whole treatment framework. Huge volumes of literature and records of the theoretical concepts and practical skills provide data support for analysis of the relationships in prescription composition. Future research will include other network measures, such as correlation and feature analysis, clustering and community detection in weighted networks. We will also focus on the feature extraction and modeling to analyze a treatment network in depth integrating diagnostic information to analyze relationships between treatment and differentiation.

4  Conclusion

PHFN model is proposed to manifest the relationships among prescriptions, herbs, and herbal efficacies to show their internal and mutual associations, and is applied to 112 classical prescriptions in Treatise on Exogenous Febrile and Miscellaneous Diseases.

The network supported by distributed storage and processing is capable of manifesting a range of knowledge of prescriptions in a large scale, and the compatibility rules withdrawn are enriched with a refined summary of CM medication experience. The combinations extracted from the aforementioned research offer insight of the rules and patterns of herbs in CM treatment, also provide a reference for clinical practice and future pharmacological studies. As CM is an experience-based medical system that focuses on clinical observation, summary, and individual differences, these rules and patterns inherited from classics also provide therapeutic evidence of CM in the potential to assist therapy selection and to standardize and clarify the diagnosis and treatment of CM.

Acknowledgement: Authors thank Le Deng for data input.

Funding Statement: This work was supported by grants from National Key Research of Development Projects (2017YFC1703306), Scientific Research Program of Traditional Chinese Medicine in Hunan Province (2020002), Scientific Research Fund of Hunan University of Chinese Medicine (2019XJJJ029), and Scientific Research Projects of Changsha City (No. 468).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: XH, LL; data collection: HL; analysis and interpretation of results: XH, ST, XC; draft manuscript preparation: XH, CD. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, CD, upon reasonable request.

Conflicts of Interest: The authors declare no conflict of interests.

References

1. P. Hao, F. Jiang, J. Cheng, L. Ma, Y. Zhang et al., “Traditional chinese medicine for cardiovascular disease: Evidence and potential mechanisms,” Journal of the American College of Cardiology, vol. 69, no. 24, pp. 2952–2966, 2017 [Google Scholar] [PubMed]

2. G. Arji, R. Safdari, H. Rezaeizadeh, A. Abbassian, M. Mokhtaran et al., “A systematic literature review and classification of knowledge discovery in traditional medicine,” Computer Methods and Programs in Biomedicine, vol. 168, no. 9, pp. 39–57, 2019 [Google Scholar] [PubMed]

3. J. Ma, Z. Wang, H. Guo, Q. Xie, T. Wang et al., “Mining syndrome differentiating principles from traditional chinese medicine clinical data,” Computer Systems Science and Engineering, vol. 40, no. 3, pp. 979–993, 2022. [Google Scholar]

4. H. J. Zhou, T. T. Shen, X. L. Liu, Y. R. Zhang, P. G et al., “Knowledge graph: A survey of approaches and applications knowledge graph,” Journal on Artificial Intelligence, vol. 2, no. 2, pp. 89–101, 2020. [Google Scholar]

5. D. Zhang, Q. Jia, S. Yang, X. Han, C. Xu et al., “Traditional Chinese medicine automated diagnosis based on knowledge graph reasoning,” Computers, Materials & Continua, vol. 71, no. 1, pp. 159–170, 2022. [Google Scholar]

6. M. Zitnik, F. Nguyen, B. Wang, J. Leskovec, A. Goldenberg et al., “Machine learning for integrating data in biology and medicine: Principles, practice, and opportunities,” Information Fusion, vol. 50, no. 7414, pp. 71–91, 2019 [Google Scholar] [PubMed]

7. L. Wang, Z. Li, X. Zhao, W. Liu, Y. Liu et al., “A network study of chinese medicine xuesaitong injection to elucidate a complex mode of action with multicompound, multitarget, and multipathway,” Evidence Based Complement Alternative Medicine, vol. 652373, no. 1, pp. 1–8, 2013. [Google Scholar]

8. J. Zhang, R. Liang, L. Wang and B. Yang, “Effects and mechanisms of Danshen-Shanzha herb-pair for atherosclerosis treatment using network pharmacology and experimental pharmacology,” Journal of Ethnopharmacololgy, vol. 229, pp. 104–114, 2019 [Google Scholar] [PubMed]

9. X. Zhang, Y. Gao, H. Xiang, X. M. Qin and J. S. Tian, “An exploration on mechanism of antidepression of Jiaotai Pills based on network pharmacology,” Chinese Traditional and Herbal Drugs, vol. 48, no. 8, pp. 1584–1590, 2017. [Google Scholar]

10. J. Zhao, D. G. Nagle, Y. Zhou and W. Zhang, “Network Pharmacology in the study of TCM formulae,” in Systems Biology and Its Application in TCM Formulas Research, 1st edition, CA, USA: Academic Press, pp. 69–95, 2018. [Google Scholar]

11. L. M. Sun, B. J. Zhu, H. T. Cao, X. Y. Zhang, Q. C. Zhang et al., “Explore the effects of Huang-Lian-Jie-Du-Tang on Alzheimer’s disease by UPLC-QTOF/MS-based plasma metabolomics study,” Journal of Pharmaceutical and Biomedical Analysis, vol. 151, pp. 75–83, 2018 [Google Scholar] [PubMed]

12. S. Li, “Exploring traditional chinese medicine by a novel therapeutic concept of network target,” Chinese Journal of Integrative Medicine, vol. 22, no. 9, pp. 647–652, 2016 [Google Scholar] [PubMed]

13. S. Li., Q. Ding and X. Wang, “Network target theory and network pharmacology,” in Network Pharmacology, 1st edition, Singapore: Springer, pp. 1–34, 2021. [Google Scholar]

14. X. R. Zhang, X. Sun, W. Sun, T. Xu and P. P. Wang, “Deformation expression of soft tissue based on BP neural network,” Intelligent Automation & Soft Computing, vol. 32, no. 2, pp. 1041–1053, 2022. [Google Scholar]

15. M. Ji, C. Ding, X. Li, H. Liang and X. Cai, “Study on relative dosage and dosage-effect relationship model of TCM,” Chinese Journal of Information on TCM, vol. 27, no. 6, pp. 84–88, 2020 (In Chinese). [Google Scholar]

16. H. Liu and S. Wu, “Dosage conversion of classical prescription,” Chinese Journal of Traditional Chinese Medicine, vol. 29, no. 4, pp. 1007–1009, 2014 (In Chinese). [Google Scholar]

17. M. Z. Guo, “Study on ancient and modern conversion of dosage and compatibility ratio of Zhongjing formula,” Ph.D. dissertation, Beijing University of Chinese Medicine, China, 2009. [Google Scholar]

18. Z. G. Li, Chinese-english dictionary of state standard clinical terminologies of traditional Chinese medicine, 1st ed., Shanghai, China: Shanghai Science and Technical Literature Publishing house, pp. 301–322, 2002. [Google Scholar]

19. L. Wang, Y. Zhang, Y. Zhang, X. Xu and S. Cao, “Prescription function prediction using topic model and multilabel classifiers,” Evidence-Based Complementary and Alternative Medicine, vol. 2017, no. 4, pp. 8279109, 2017 [Google Scholar] [PubMed]

20. X. Wang, H. Zhang, L. Chen, L. Shan., G. Fan et al., “Liquorice, a unique “guide drug” of traditional Chinese medicine: A review of its role in drug interactions,” Journal of Ethnopharmacology, vol. 150, no. 3, pp. 781–790, 2013 [Google Scholar] [PubMed]

21. F. Cheng, I. A. Kovács and A. L. Barabási, “Network-based prediction of drug combinations,” Nature Communications, vol. 10, no. 1, pp. 1–11, 2019. [Google Scholar]

22. Y. Wang, H. Yang, L. Chen, M. Jafari and J. Tang, “Network-based modeling of herb combinations in traditional Chinese medicine,” Briefings in Bioinformatics, vol. 22, no. 5, pp. bbab106, 2021 [Google Scholar] [PubMed]

23. M. Jafari, Y. Wang, A. Amiryousefi and J. Tang, “Unsupervised learning and multipartite network models: A promising approach for understanding traditional medicine,” Frontiers in Pharmacology, vol. 11, pp. 1319, 2020 [Google Scholar] [PubMed]

24. S. Li, B. Zhang, D. Jiang, Y. Wei and N. Zhang, “Herb network construction and co-module analysis for uncovering the combination rule of traditional Chinese herbal formulae,” BMC Bioinformatics, vol. 11, pp. S6, 2010 [Google Scholar] [PubMed]