 Open Access
Open Access
ARTICLE
Movement Function Assessment Based on Human Pose Estimation from Multi-View
1 School of Artificial Intelligence, Hebei University of Technology, Tianjin, 300400, China
2 Intelligent Rehabilitation Device and Detection Technology Engineering Research Centre of the Ministry of Education, Tianjin, 300400, China
* Corresponding Author: Lingling Chen. Email:
Computer Systems Science and Engineering 2024, 48(2), 321-339. https://doi.org/10.32604/csse.2023.037865
Received 18 November 2022; Accepted 17 February 2023; Issue published 19 March 2024
Abstract
Human pose estimation is a basic and critical task in the field of computer vision that involves determining the position (or spatial coordinates) of the joints of the human body in a given image or video. It is widely used in motion analysis, medical evaluation, and behavior monitoring. In this paper, the authors propose a method for multi-view human pose estimation. Two image sensors were placed orthogonally with respect to each other to capture the pose of the subject as they moved, and this yielded accurate and comprehensive results of three-dimensional (3D) motion reconstruction that helped capture their multi-directional poses. Following this, we propose a method based on 3D pose estimation to assess the similarity of the features of motion of patients with motor dysfunction by comparing differences between their range of motion and that of normal subjects. We converted these differences into Fugl–Meyer assessment (FMA) scores in order to quantify them. Finally, we implemented the proposed method in the Unity framework, and built a Virtual Reality platform that provides users with human–computer interaction to make the task more enjoyable for them and ensure their active participation in the assessment process. The goal is to provide a suitable means of assessing movement disorders without requiring the immediate supervision of a physician.Keywords
The number of people suffering from motor dysfunction due to traffic accidents, strokes, and cerebral thrombosis has increased significantly in recent years. The mobility of the human body in general declines with age, and this can lead to a variety of diseases. According to one survey, neurological disorders pose a significant complication and this context, and are a major cause of disabilities among middle-aged and elderly people [1]. Movement disorders are dominant among such disabilities, and affect the patient’s ability to perform daily activities such that they cannot live on their own. In light of this, providing automated methods of assessment for the increasing number of patients with motor dysfunctions and reducing the burden on medical personnel has become an important area of research in modern medicine.
With rapid advances in research on the problems of classification [2,3] and optimization [4] in computer vision in recent years, human pose estimation has been widely used for medical assistance and motion analysis as well as in Virtual Reality technology [5–7]. The main objective is to recover the parameters of pose of the target body and analyze its motion based on the relevant sequences of images. Early work in the area focused on two-dimensional (2D) human pose estimation, and involved recovering 2D poses from images or videos by using either of two general approaches: top-down and bottom-up methods. The top-down method of identifying pose involves first identifying the position of each person in the given image through a target detection network and then estimating their pose. This method is highly accurate because it can leverage the poses of a single subject, but its speed of inference is low because it relies on the target detection network [8,9]. The bottom-up method of pose estimation involves first identifying the joints of all people in the given image through a detection network and then linking the joints belonging to the same person by using a clustering algorithm [10]. The network can directly estimate the joints of all people in the image. Although the accuracy of the bottom-up approach is lower than that of the top-down approach, it can make faster inferences [11]. Networks used to identify 2D poses that are based on deep learning have delivered good performance [12,13]. Subsequent research has focused on 3D pose estimation.
Research on 3D pose estimation can be classified into two types: single-view and multi-view pose estimation. Single-view pose estimation is generally used to locate the 2D joints of the human body in cropped images to convert the detected 2D pose into three dimensions through a learning-based approach [14,15]. While this method is accurate, it is too heavily reliant on the 2D pose detector, and can regress to the 3D pose of the body in the image [16,17]. It is a simple and fast end-to-end approach that can, however, suffer from the problem of ambiguities in the obtained pose. Moreover, the accuracy of single-view 3D pose estimation is far lower than that of multi-view estimation.
Initial research on multi-view pose estimation was based on using 2D features obtained from multi-view image sequences to reconstruct 3D poses [18,19]. Deep learning-based 2D detectors combined with statistical models of human motion have recently been developed, and have delivered impressive results. Joo et al. compared fitted 3D models with the true values of the corresponding images in the Carnegie Mellon University’s (CMU) Panoptic Studio dataset [20] and achieved a model overlap of 87.7% [21]. Dong et al. used the multiplexed matching of 2D poses from multiple views by simply combining the appearance-related and geometric information of the people featured in the images to compare their similarity relationships in 2D [22]. This can significantly reduce the size of the state space and improve the speed of computation, but this method uses an off-the-shelf feature extraction network to simply combine appearance-related information with geometric information in the given image. Its accuracy thus decreases when few cameras are available and it is slow at making inferences, which renders it unsuitable for use. The time taken by the model to make inferences is a key consideration in multi-view human pose estimation. The computational complexity of the model for all views increases exponentially with the number of cameras. Chen et al. used an iterative processing strategy to obtain video frames in chronological order and used them as an iterative frame-by-frame input [23]. This leads to a linear relation between the computational cost and the number of cameras, but the high speed of inference of this method makes it difficult to guarantee its accuracy.
A considerable amount of promising research on the automatic analysis of human behaviors based on deep learning has emerged in recent years. Ullah et al. proposed a long short-term memory (LSTM) network for the automatic recognition of six types of behaviors by using a smartphone that yielded an average improvement of 0.93 in accuracy compared to previous methods. It provides a new idea for the automatic analysis of human behaviors [24]. In this paper, we propose a framework for automated multi-view human pose estimation that can be applied to overcome the drawbacks of the above models. Unlike traditional methods, the proposed method does not require that the subject wear a motor aid or a sensor system [25–27]. This study makes the following contributions to research in the area:
• We propose an architecture for multi-view human pose estimation that delivers a high accuracy and stability at a high frame rate.
• We propose a method to assess the similarity of motion based on the plane of motion-related features. The latter are quantified by being converted into FMA scores.
• We build a Virtual Reality-based evaluation platform, and implement the proposed method on the Unity framework to realistically reflect human motion through the skinned multi-person linear (SMPL) model [28].
2.1 Experimental Hardware Support
The hardware used in the experiments consisted of two Kinect image sensors, a computer, and a large-screen display (integrated into the computer end), as shown in Fig. 1a. The Kinect sensors were placed orthogonally with respect to each other to simultaneously capture images, as shown in Fig. 1b. This setup eliminated the problem of data loss caused by self-occlusion such that more accurate data on human poses could be obtained [29,30]. The large-screen display was used to show the results of reconstruction and the scenarios of virtual assessment.
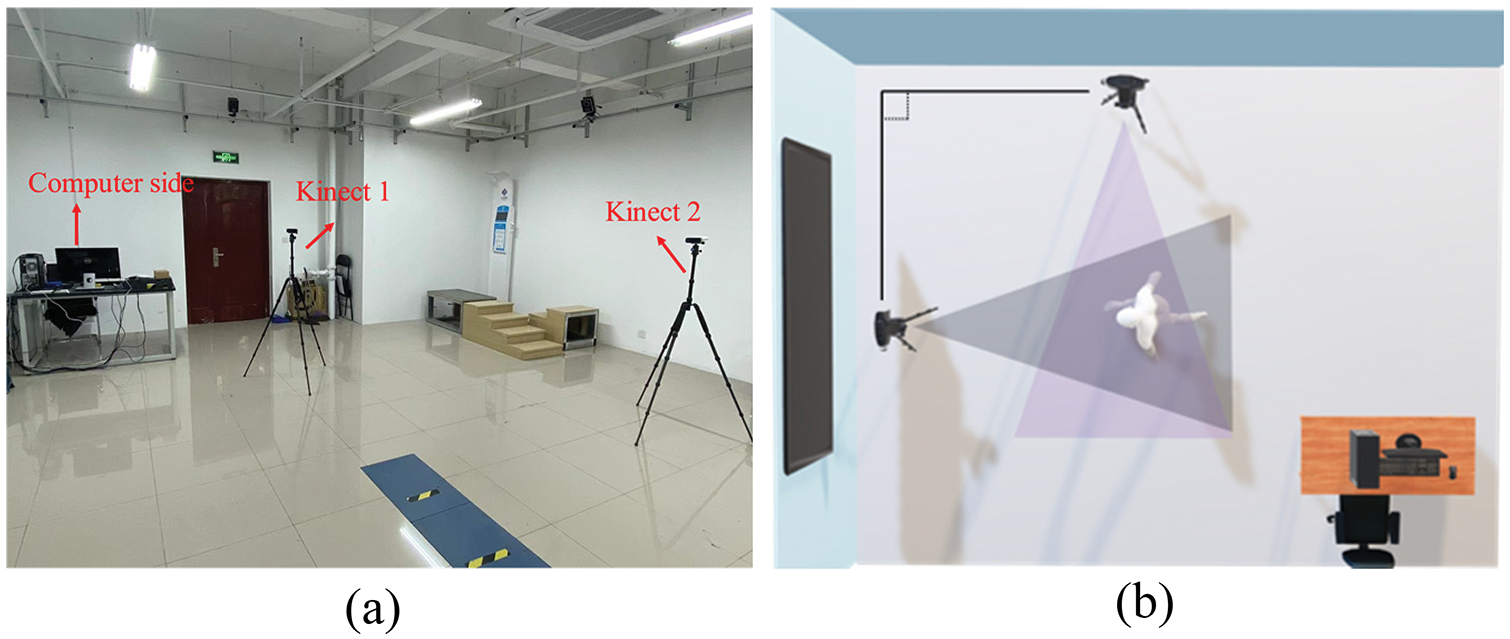
Figure 1: The proposed system. (a) Operational setup. (b) Positions of the cameras
2.2 Human Pose Reconstruction and Motion Data Acquisition
2.2.1 Overall Network Architecture for Multi-View Pose Estimation
The overall architecture of the multi-view pose estimation network is shown in Fig. 2. The You Only Look Once (YOLO) network was used to train the backbone network and design a unique feature loss function to extract the bounding box and appearance-related features from different views. We used a high-resolution network (HRNet), a 2D pose estimation network of the top-down type, to accurately identify the points representing the 2D joints of the human body in the images. Following 2D pose estimation, the 3D pose of the body needed to be reconstructed. Triangulation is the most direct and commonly used method to quickly reconstruct the 3D pose. However, errors in the estimated 2D pose from any given view may seriously degrade the accuracy of 3D pose estimation. We introduced the 3D pictorial structure (3DPS) model and added temporal information to it to compensate for the drawbacks of the above-mentioned methods.
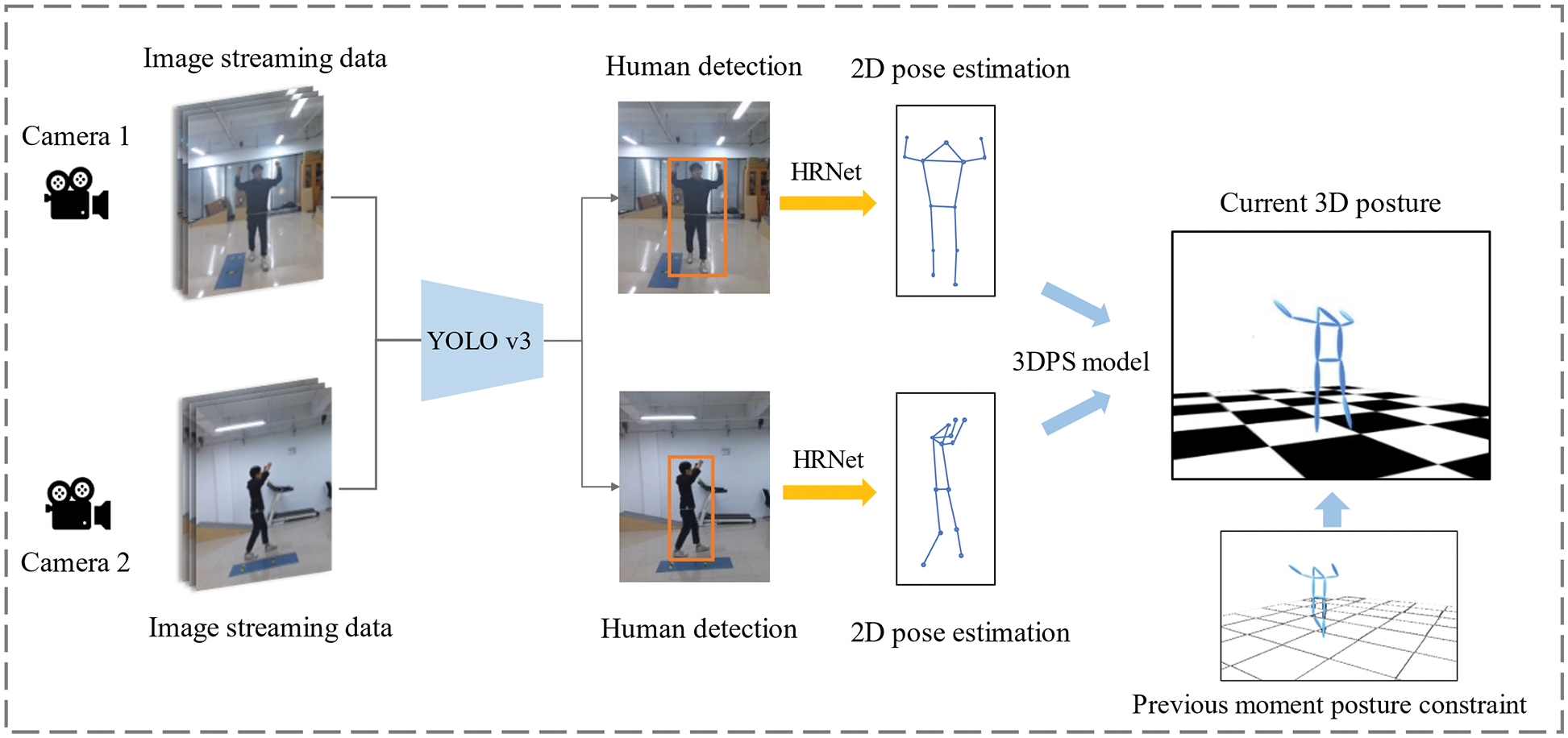
Figure 2: Overall architecture of multi-view pose estimation
The loss function of the YOLO v3 network consists of three components. We removed the loss function for target classification from the network because the task at hand involved the identification of only people in images. To locate the target, the network uses the sum of the squared error (SSE) as the loss function, and constructs it by detecting the error in position between the tensor and the real tensor. The loss function
where
where
The loss function of the IOU is defined by Eqs. (3) and (4):
2.2.3 Human Pose Reconstruction
During 3D human posture reconstruction, the posture in the previous instance can be used to estimate that in the current instance. We add information on the time series to the 3DPS model to constrain the posture and improve the accuracy of 3D pose estimation. We modify the structure of the 3DPS model as follows:
where
where

Figure 3: Results of 3D human pose reconstruction
2.3 Application of Motion Detection: Assessment of Movement Function
2.3.1 Joint Data Filtering Based on Kalman Filter
The reconstructed human pose can be used to obtain the coordinates of points representing the joints. The initial trajectory of these points may be missing or jagged, however, such that they do not match the actual trajectory of the physical motion of the person represented. Given that the points representing the joints are in the form of 3D coordinates with a time series, we use the Kalman filter to correct the initially reconstructed points representing the joints. According to the equation of state of the system, its state at the current moment can be estimated as follows:
where
Following the prediction of the system’s state at the current moment k, its covariance P needs to be updated. The initial value of P is set to a
where
To obtain the predicted value of the system’s state, the observed and the predicted values are combined to obtain the optimal value
where
The corresponding covariance of error is calculated as follows:
where I denotes the unit matrix and
2.3.2 Dynamic Time Warping (DTW)-Based Alignment of a Series of Movements
There is a temporal difference between the test movement, and the standard movement, and direct similarity matching between image frames yields significant errors. We use the DTW algorithm to align two sets of time series of actions. Given two sequences of motion data, X and Y, each frame is a 3D pose. We convert the point coordinates of 3D joints into a 1D sequence of angles to avoid the influence of individual differences, as shown in Fig. 4.
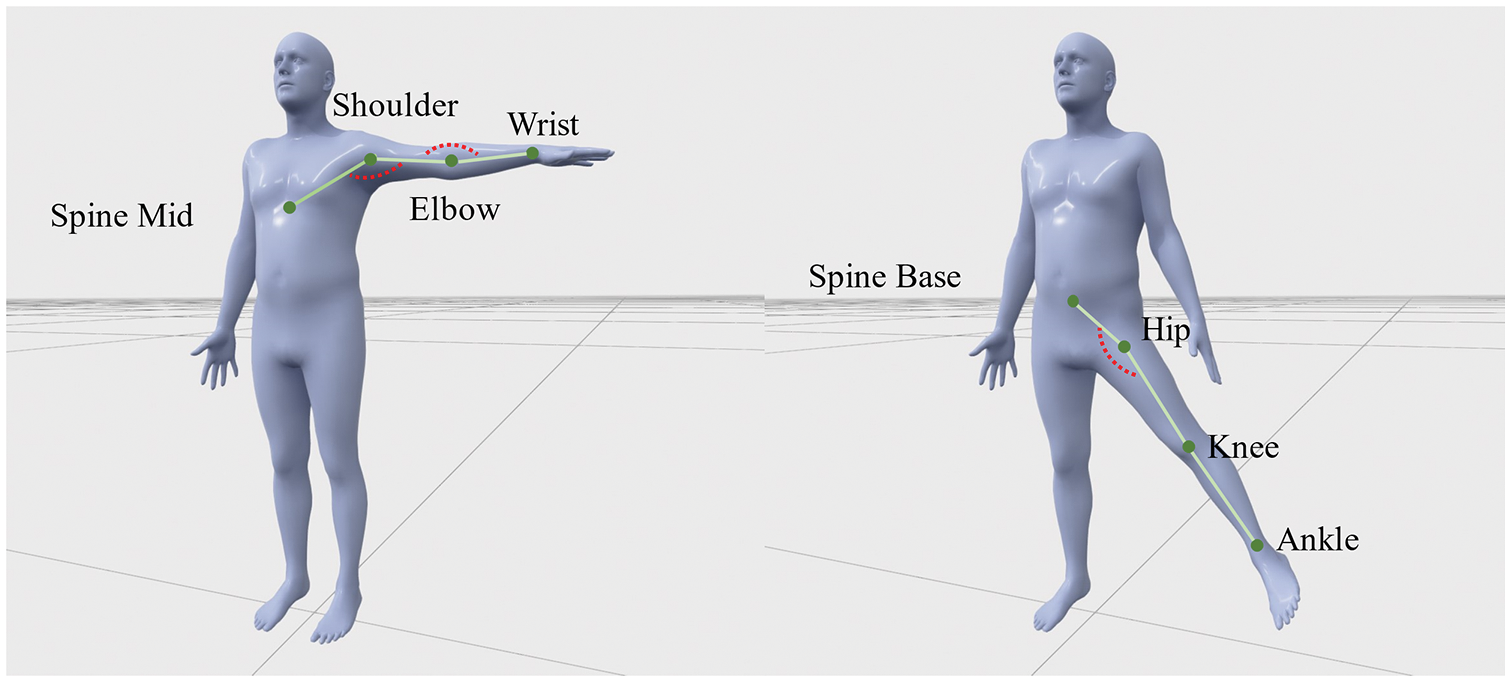
Figure 4: Conversion of the angles of the joints
We thus obtain two sets of angular time series
where
The final output of the DTW is an optimal curve of the twist in
2.3.3 Matching Features on Plane
The method to assess functions of the movements of the limbs was developed by comparing the mobility of the joints of subjects with data on healthy humans. Data on the latter were collected as a reference and analyzed by using a method of similarity assessment. The standard paradigm of movement of the FMA was used. Most researchers have used correlation coefficients or the ED to assess similarity in movements, but this yields inaccurate results due to variations in the shapes of human bodies.
We used the proposed method to extract the image of the human skeleton, and transformed the points representing joints during motion into seven feature planes as the basic planes of calculation, as shown in Fig. 5. Each feature plane represented each part of the human body. Seven normal vectors
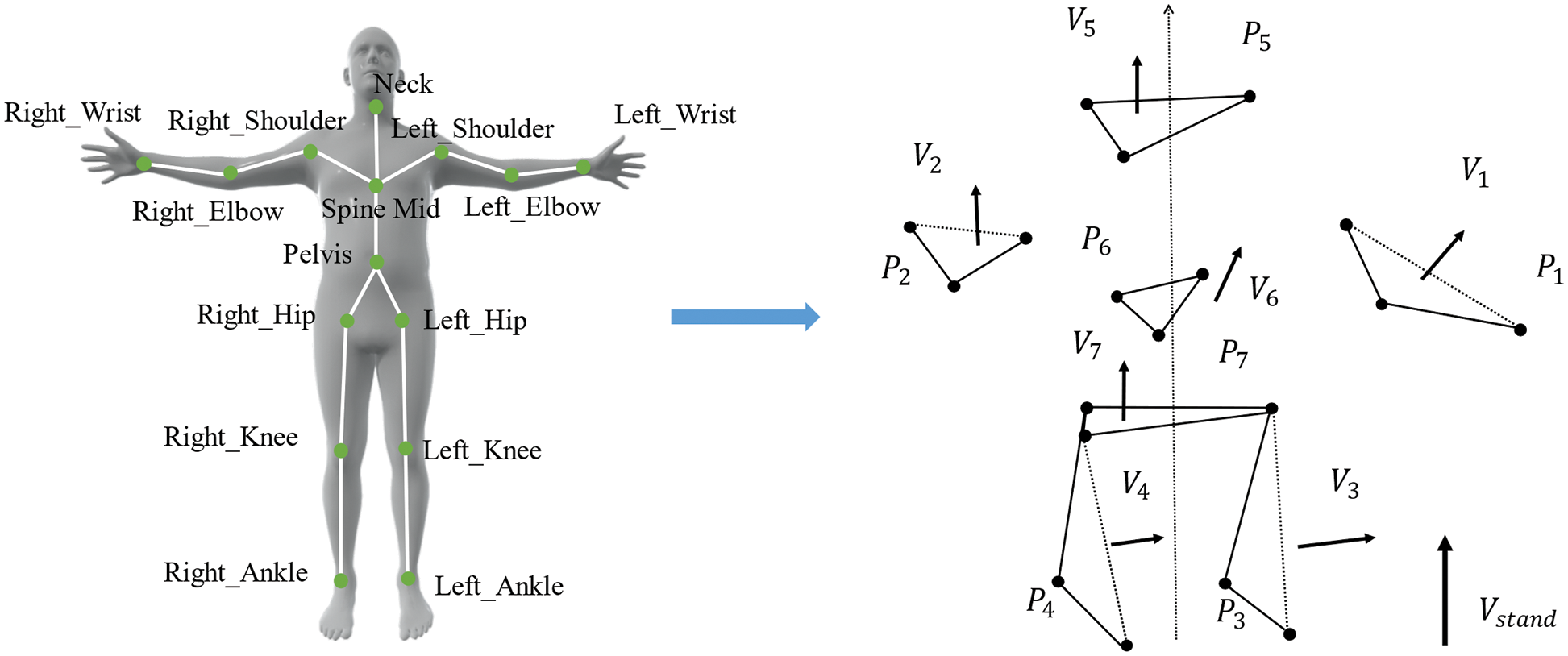
Figure 5: Simplifying the model of the human body
(1) Limb movement
The movement of the limbs can be determined by the inner product of the characteristic plane

(2) Head movement
This can be obtained by comparing the normal vector
(3) Spine movement
This can be obtained by comparing the angle of transformation between the vector in the direction of the spine
(4) Hip movement
When the body is vertical, the plane of the hip

The cosine similarity function is used as the basic metric function. Compared with the ED, it focuses more on the difference in direction between vectors. It is calculated as follows:
where
Cosine similarity can measure the difference in direction between vectors as well as the difference in angles, which is expressed as the magnitude of the ROM:
To train an efficient and robust human detection network, we captured a large number of images from multiple cameras to form a dataset. To quickly obtain a large amount of image-related data, we used four cameras to synchronously take images from different perspectives, and obtained over 70,000 images in total as shown in Fig. 6. We fully considered the light intensity, background, and other factors of the experimental environment in the acquisition process to enrich the image-related data. We considered nine scenes, including corridors, stairs, halls, and laboratories, when capturing images.

Figure 6: Dataset
Subjects in the experiments were asked to simulate actions involved daily activities, including walking, moving objects, talking, and going up and down stairs, while their images were captured to train the recognition network such that it had a strong capability for generalization.
We quantitatively compared the proposed method with prevalent techniques in the area on the publicly available Shelf dataset [19]. This dataset consists of images captured by five cameras at a resolution of
Table 3 shows the accuracies of detection of the proposed method and prevalent methods in the area on all individual frames in the Shelf dataset. Because the proposed method contains a constraint on the temporal information provided to the 3DPS model, and as the accurate detection of static images does not require this feature, it did not exhibit an absolute advantage over the other methods. In fact, its average accuracy was lower by 0.2% compared with that of the method proposed by Zhang et al. However, a practical model needs to reason over a range of dynamic video frames and deliver excellent performance even at high frame rates. We thus designed and conducted a comparative experiment to assess the accuracy of the methods listed in Table 3 on images captured under different frames per second (FPS) to further test the performance of the proposed method. We still used the PCP as the indicator for evaluation, and the results are shown in Table 4.

The proposed method obtained better results than the traditional 3DPS method, and attained results similar to those of the methods developed by Zhang et al. [32] and Dong et al. [22] owing to deep learning-based optimization and because it was trained on a large dataset. However, in terms of speed of reasoning, it was superior to the methods proposed by Zhang et al. [32] and Dong et al. [22] It had an average accuracy of dynamic detection that was higher by 15.6% (30 FPS) than that of Zhang et al.’s method. The latter method did not leverage temporal information, because of which changes in the frame rate of the camera did not have a significant impact on the final results. Temporal information was added to the 3DPS model to optimize the captured pose at any given moment by the pose captured at the previous moment, because of which it yielded more reliable results in scenes captured at a low frame rate or those featuring people moving quickly. Therefore, the proposed method can guarantee a high speed of inference and stable performance while minimizing the loss of accuracy.
We chose two actions from the Clinical Movement Assessment Scale for experiments to illustrate the effectiveness of filtering the points representing the joints in the image. The trajectories of the joints of the shoulder and the elbow were plotted to represent movements of the upper limbs, and those of the joints of the hip and the knee were plotted for movements of the lower limbs. The results are shown in Fig. 7.
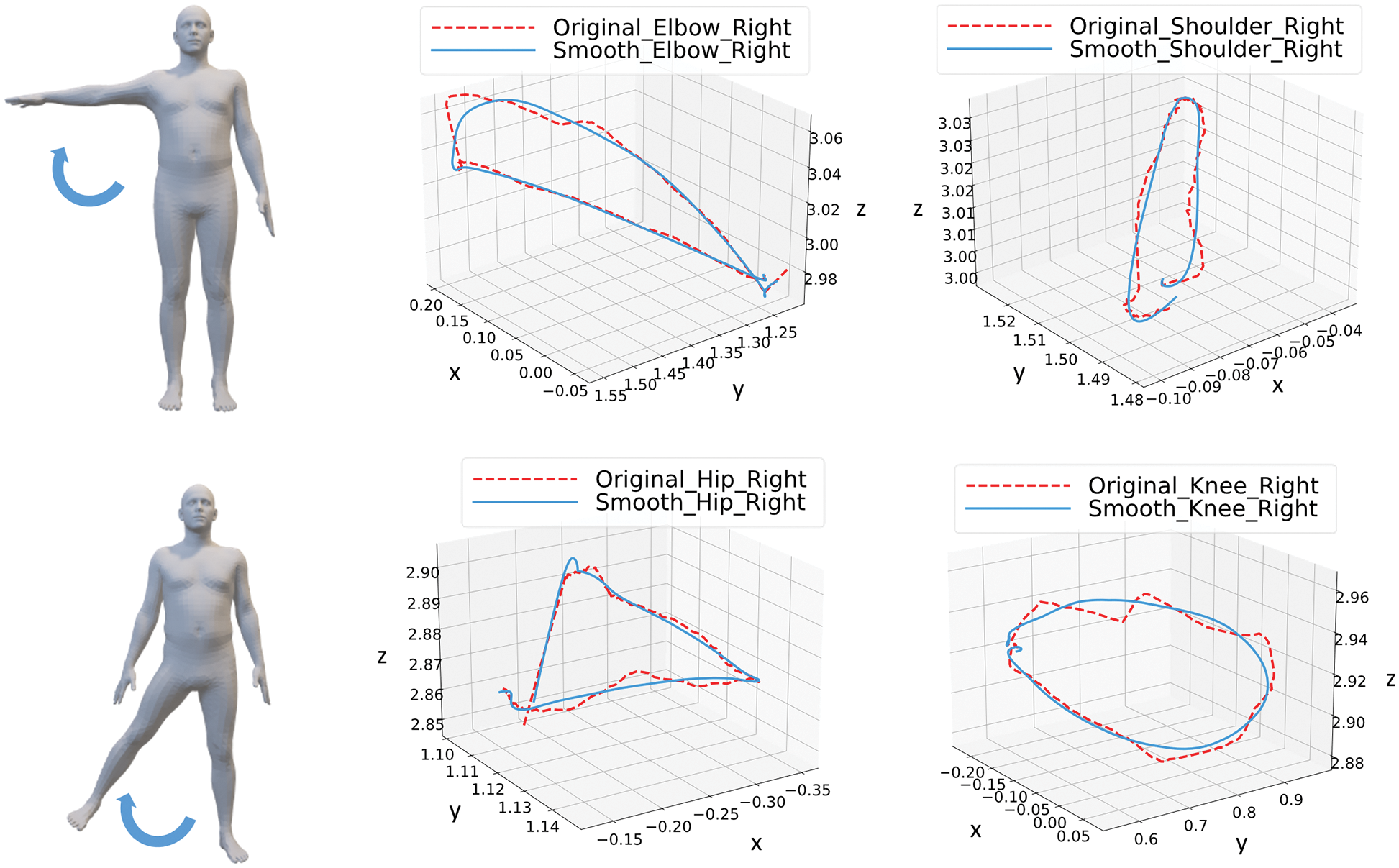
Figure 7: Filtering the points representing the joints by using the Kalman filter
Two sets of angular sequences of abduction of the shoulder (90 degrees) were used as input, one for the group of healthy subjects and the other for the patient’s movement sequence, and the results of alignment are shown in Fig. 8. The DTW algorithm was able to eliminate error in time between the sets of sequential movements.

Figure 8: Results of alignment of the DTW. (a) Path of optimization of the DTW. (b) Original sequence of angles of the joints. (c) Aligned sequence of angles of the joints
3.5 Analysis of Assessment of Movement Functions
In the experiment, the subjects performed shoulder abduction movements. Their feature planes during the movements were plotted and qualitatively analyzed in comparison with those of the normal group. The results are shown in Fig. 9.
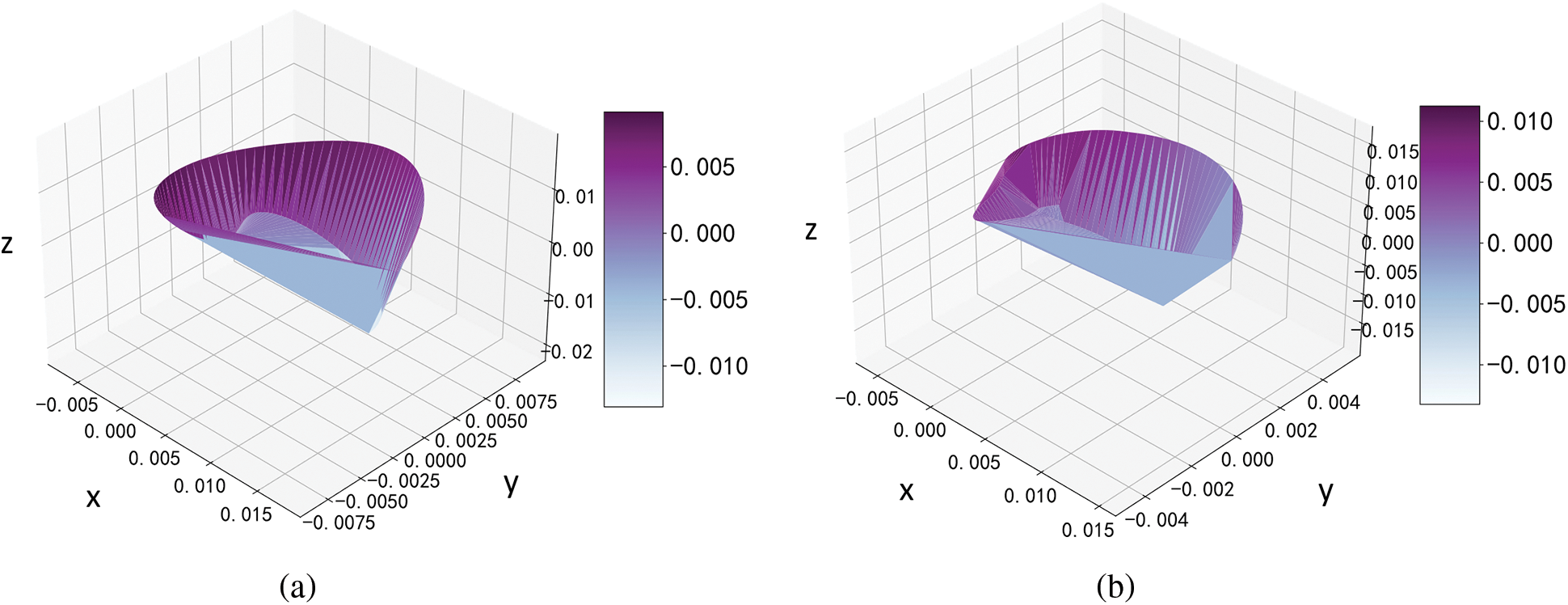
Figure 9: Feature plane during shoulder abduction movement. (a) Standard paradigm of the feature plane of motion. (b) Feature plane of motion of the subject
The results in Fig. 9 show that the area of the feature plane of healthy subjects was larger than that of the subjects with motor dysfunction, where this reflects the poorer accessibility of the movements of limbs of the latter compared with the former.
We performed quantitative calculations to further illustrate the variation between the subjects’ movements and standard movements. The 15 feature indicators listed in Tables 1 and 2 were calculated, and the results are shown in Fig. 10. The quantitative results yielded the similarity scores of each part of the human body. As the experimental movement here was the abduction of the right shoulder, the other parts of the body had lower variation and, thus, higher scores.
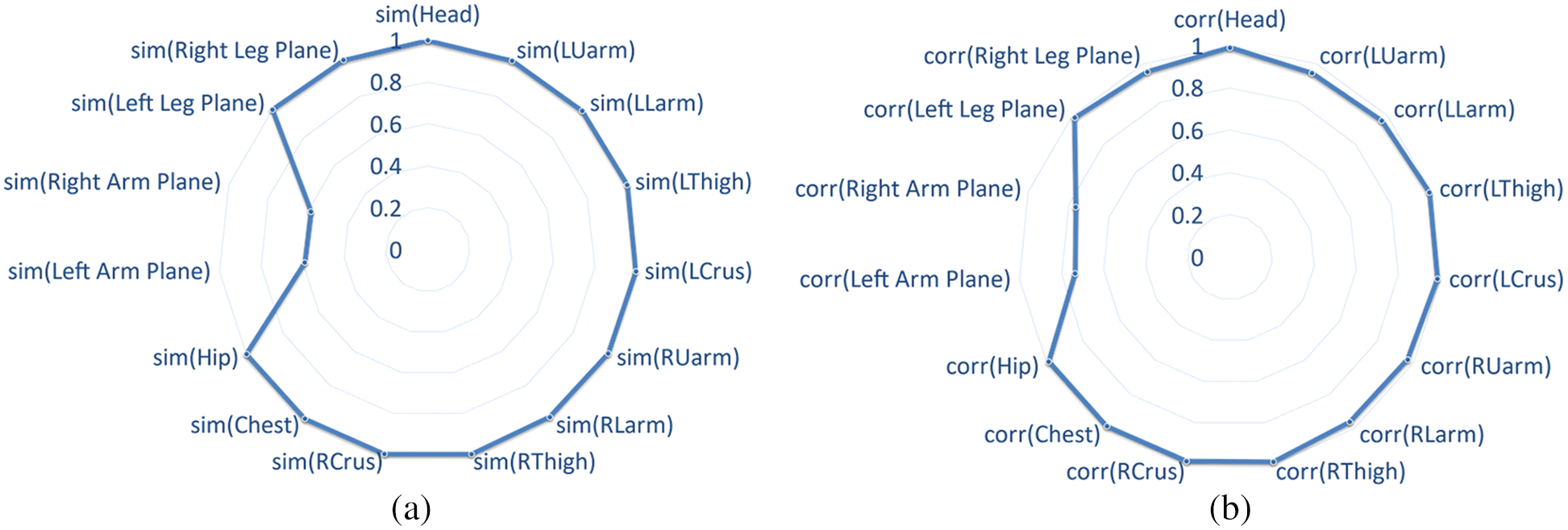
Figure 10: Similarity analysis of the plane of features. (a) Differential scores for the directions of limb movement. (b) Differential scores for the ROM
We set
where
To further illustrate the effectiveness of the proposed method, 18 subjects were invited to participate in the experiments to assess movement functions. All participants were evaluated on the artificial FMA scale as the control group for the experiment and their results were subjected to a correlation analysis. The subjective ratings of experts were regarded as the gold standard to validate the proposed algorithm. All participants were aware of the experimental procedure, and provided their written informed consent for participation before the experiment. It is hereby declared that all the experiments involved in this paper have passed the local ethical review.
Table 5 compares the results of the proposed method of assessment with those of the ED-based method. The correlation coefficient reflected a strong correlation between the proposed method and the artificial scores, with a value of 0.87 (

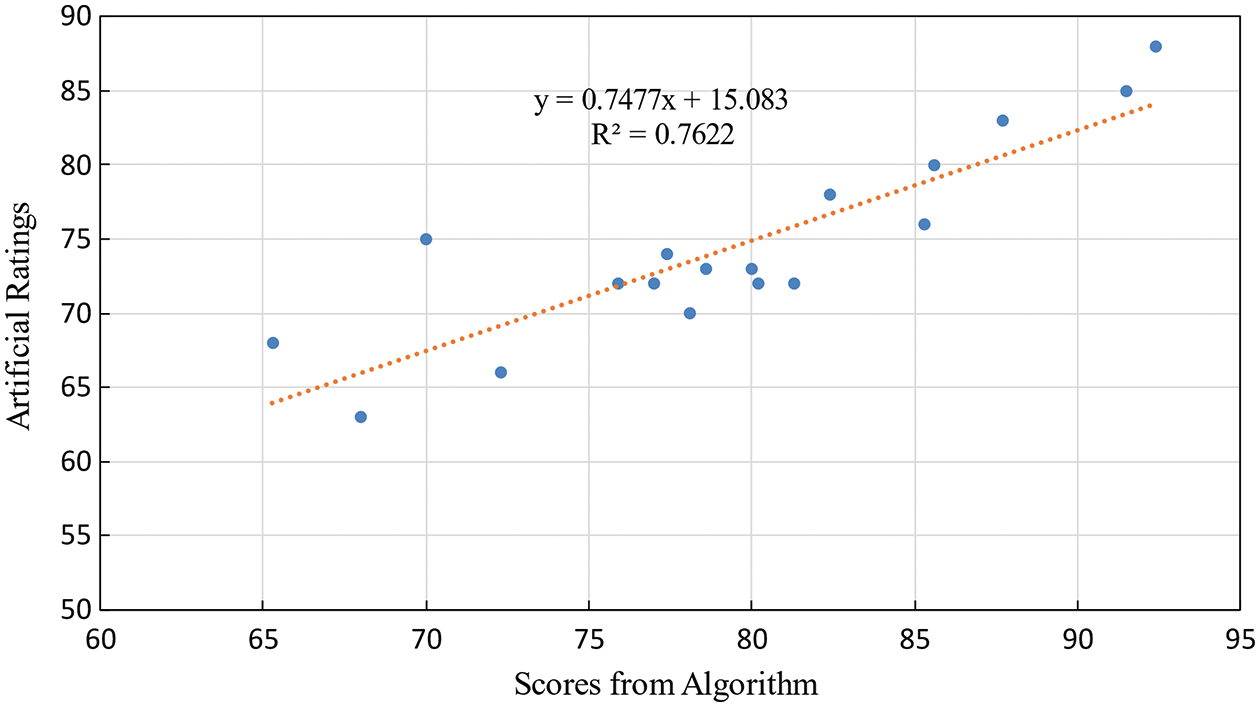
Figure 11: Linear relationship between algorithm scores and artificial ratings
We applied the proposed method to the Unity framework and built a Virtual Reality-based scene for evaluation by using the SMPL as the models of virtual characters and the proposed method of pose estimation as the basic skeleton to drive the models. The use of SMPL models as avatars for exhibiting movement and control allowed for a more realistic reproduction of the movements of the human limbs, as shown in Fig. 12. The virtual coach (left) model was driven by standard movement-related data to guide the subject by mimicking its movements. The user model (right) was driven in real time by the human skeleton as estimated from the subject’s pose to provide immediate feedback to the user on their pose.

Figure 12: Implementation of the proposed method in the unity framework
In this study, we proposed a feasible and lightweight method of pose estimation. A detection network was fully trained by building a large dataset of scenes featuring moving people, and yielded an accuracy of 97.1% while delivering stable performance on images captured at 30 FPS. Following this, we used the proposed method to develop an algorithm to assess the similarity of movements on feature planes. By evaluating the motor functions of 18 subjects and comparing them with their manual scores, we found that the proposed method of evaluation exhibited a strong linear correlation with the manual scores. We used linear regression to fine-tune the model and render its results more realistic. In contrast to past methods that have used performance scores obtained from subjects through serious games to evaluate their motor abilities [33–35], the quantitative scores of movements obtained here are more easily interpretable for use in clinical medicine. Although these scores may be related to the range of motion of certain joints, they are influenced by other factors as well, such as the patient’s level of cognition and the difficulty of the game.
When we used the proposed method of pose estimation in the Unity framework to drive the SMPL models, there were deviations in the local pose of the model, and it even yielded inaccurate poses, because the points representing the joints of the hand and parts of the ankle were not identified. This slightly affected the results of evaluation of the proposed model. In future work, we plan to reconstruct the points representing the joints of the hand and parts of the ankle, and will consider embedding the initial model of the human skeleton into the SMPL model to obtain a more accurate 3D model through forward kinematics. In addition, we plan to exploit multi-person posture estimation to extend the proposed method to simultaneously assess the motor functions of several people to enhance its scope of application.
Acknowledgement: The authors thank their institutions for infrastructure support.
Funding Statement: This work was supported by grants from the Natural Science Foundation of Hebei Province, under Grant No. F2021202021, the S&T Program of Hebei, under Grant No. 22375001D, and the National Key R&D Program of China, under Grant No. 2019YFB1312500.
Author Contributions: Lingling Chen performed the supervision; Tong Liu performed the data analyses and wrote the manuscript; Zhuo Gong performed the experiment and software; Ding Wang performed the methodology and visualization.
Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, L Chen, upon reasonable request.
Ethics Approval: This study was approved by the Biomedical Ethics Committee of Hebei University of Technology (Approval Code: HEBUTHMEC2022018, Approval Date: March 14, 2022). Written informed consent was obtained from all participants.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. A. Schönenberg, U. Teschner and T. Prell, “Expectations and behaviour of older adults with neurological disorders regarding general practitioner consultations: An observational study,” BMC Geriatrics, vol. 21, no. 1, pp. 1–12, 2021. [Google Scholar]
2. W. H. Bangyal, J. Ahmad and H. T. Rauf, “Optimization of neural network using improved bat algorithm for data classification,” Journal of Medical Imaging and Health Informatics, vol. 9, no. 4, pp. 670–681, 2019. [Google Scholar]
3. Y. M. Tang, L. Zhang, G. Q. Bao, F. J. Ren and W. Pedrycz, “Symmetric implicational algorithm derived from intuitionistic fuzzy entropy,” Iranian Journal of Fuzzy Systems, vol. 19, no. 4, pp. 27–44, 2022. [Google Scholar]
4. W. H. Bangyal, K. Nisar, A. A. B. Ag, M. R. Haque, J. J. Rodrigues et al., “Comparative analysis of low discrepancy sequence-based initialization approaches using population-based algorithms for solving the global optimization problems,” Applied Sciences, vol. 11, no. 16, pp. 7591, 2021. [Google Scholar]
5. R. Divya and J. D. Peter, “Smart healthcare system-a brain-like computing approach for analyzing the performance of detectron2 and PoseNet models for anomalous action detection in aged people with movement impairments,” Complex & Intelligent Systems, vol. 8, no. 4, pp. 3021–3040, 2022. [Google Scholar]
6. A. Pardos, A. Menychtas and I. Maglogiannis, “On unifying deep learning and edge computing for human motion analysis in exergames development,” Neural Computing and Applications, vol. 34, no. 2, pp. 951–967, 2022. [Google Scholar]
7. M. H. Li, T. A. Mestre, S. H. Fox and B. Taati, “Vision-based assessment of parkinsonism and levodopa-induced dyskinesia with pose estimation,” Journal of Neuroengineering and Rehabilitation, vol. 15, no. 1, pp. 1–13, 2018. [Google Scholar]
8. Y. Chen, Z. Wang, Y. Peng, Z. Zhang, G. Yu et al., “Cascaded pyramid network for multi-person pose estimation,” in Computer Vision and Pattern Recognition, CVPR 2018, Salt Lake City, UT, USA, pp. 7103–7112, 2018. [Google Scholar]
9. K. Sun, B. Xiao, D. Liu and J. Wang, “Deep high-resolution representation learning for human pose estimation,” in Computer Vision and Pattern Recognition, CVPR 2019, Long Beach, CA, USA, pp. 5693–5703, 2019. [Google Scholar]
10. Y. Tang, Z. Pan, W. Pedrycz, F. Ren and X. Song, “Based kernel fuzzy clustering with weight information granules,” IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 7, no. 2, pp. 342–356, 2022. [Google Scholar]
11. Z. Cao, T. Simon, S. E. Wei and Y. Sheikh, “Realtime multi-person 2D pose estimation using part affinity fields,” in Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, pp. 7291–7299, 2017. [Google Scholar]
12. S. Kreiss, L. Bertoni and A. Alahi, “Pifpaf: Composite fields for human pose estimation,” in Computer Vision and Pattern Recognition, CVPR 2019, Long Beach, CA, USA, pp. 11977–11986, 2019. [Google Scholar]
13. D. C. Luvizon, D. Picard and H. Tabia, “2D/3D pose estimation and action recognition using multitask deep learning,” in Computer Vision and Pattern Recognition, CVPR 2018, Salt Lake City, UT, USA, pp. 5137–5146, 2018. [Google Scholar]
14. F. Moreno-Noguer, “3D human pose estimation from a single image via distance matrix regression,” in Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, pp. 2823–2832, 2017. [Google Scholar]
15. J. Martinez, R. Hossain, J. Romero and J. Little, “A simple yet effective baseline for 3D human pose estimation,” in Int. Conf. on Computer Vision, ICCV 2017, Venice, Italy, pp. 2640–2649, 2017. [Google Scholar]
16. G. Pavlakos, X. Zhou and K. Daniilidis, “Ordinal depth supervision for 3D human pose estimation,” in Computer Vision and Pattern Recognition, CVPR 2018, Salt Lake City, UT, USA, pp. 7307–7316, 2018. [Google Scholar]
17. B. Tekin, P. Márquez-Neila, M. Salzmann and P. Fua, “Learning to fuse 2D and 3D image cues for monocular body pose estimation,” in Int. Conf. on Computer Vision, ICCV 2017, Venice, Italy, pp. 3941–3950, 2017. [Google Scholar]
18. M. Burenius, J. Sullivan and S. Carlsson, “3D pictorial structures for multiple view articulated pose estimation,” in Computer Vision and Pattern Recognition, CVPR 2013, Portland, OR, USA, pp. 3618–3625, 2013. [Google Scholar]
19. V. Belagiannis, S. Amin, M. Andriluka, B. Schiele, N. Navab et al., “3D pictorial structures revisited: Multiple human pose estimation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 38, no. 10, pp. 1929–1942, 2015. [Google Scholar] [PubMed]
20. H. Joo, H. Liu, L. Tan, L. Gui, B. Nabbe et al., “Panoptic studio: A massively multiview system for social motion capture,” in Int. Conf. on Computer Vision, ICCV 2015, Santiago, Chile, pp. 3334–3342, 2015. [Google Scholar]
21. H. Joo, T. Simon and Y. Sheikh, “A 3D deformation model for tracking faces, hands, and bodies,” in Computer Vision and Pattern Recognition, CVPR 2018, Salt Lake City, UT, USA, pp. 8320–8329, 2018. [Google Scholar]
22. J. Dong, W. Jiang, Q. Huang, H. Bao and X. Zhou, “Fast and robust multi-person 3D pose estimation from multiple views,” in Computer Vision and Pattern Recognition, CVPR 2019, Long Beach, CA, USA, pp. 7792–7801, 2019. [Google Scholar]
23. L. Chen, H. Ai, R. Chen, Z. Zhuang and S. Liu, “Cross-view tracking for multi-human 3D pose estimation at over 100 fps,” in Computer Vision and Pattern Recognition, CVPR 2020, Seattle, WA, USA, pp. 3279–3288, 2020. [Google Scholar]
24. M. Ullah, H. Ullah, S. D. Khan and F. A. Cheikh, “Stacked LSTM network for human activity recognition using smartphone data,” in European Workshop on Visual Information Processing, EUVIP 2019, Rome, Italy, pp. 175–180, 2019. [Google Scholar]
25. A. Leardini, G. Lullini, S. Giannini, L. Berti, M. Ortolani et al., “Validation of the angular measurements of a new inertial-measurement-unit based rehabilitation system: Comparison with state-of-the-art gait analysis,” Journal of Neuroengineering and Rehabilitation, vol. 11, no. 1, pp. 1–7, 2014. [Google Scholar]
26. S. V. Prokopenko, E. Y. Mozheiko, M. L. Abroskina, V. S. Ondar, S. B. Ismailova et al., “Personalized rehabilitation assessment of locomotor functions in Parkinson disease using three-dimensional video analysis of motions,” Russian Neurological Journal, vol. 26, no. 1, pp. 23–33, 2021. [Google Scholar]
27. B. Tran, X. Zhang, A. Modan and C. M. Hughes, “Design and evaluation of an IMU sensor-based system for the rehabilitation of upper limb motor dysfunction,” in Biomedical Robotics and Biomechatronics, BioRob 2022, Seoul, Korea, pp. 1–6, 2022. [Google Scholar]
28. M. Loper, N. Mahmood, J. Romero, G. Pons-Moll and M. J. Black, “SMPL: A skinned multi-person linear model,” ACM Transactions on Graphics, vol. 34, no. 6, pp. 1–6, 2015. [Google Scholar]
29. H. Du, Y. Zhao, J. Han, Z. Wang and G. Song, “Data fusion of multiple kinect sensors for a rehabilitation system,” in Engineering in Medicine and Biology Society, EMBC 2016, Orlando, FL, USA, pp. 4869–4872, 2016. [Google Scholar]
30. Y. Jiang, K. Song and J. Wang, “Action recognition based on fusion skeleton of two kinect sensors,” in Int. Conf. on Culture-Oriented Science & Technology, ICCST 2020, Beijing, China, pp. 240–244, 2020. [Google Scholar]
31. S. Ershadi-Nasab, E. Noury, S. Kasaei and E. Sanaei, “Multiple human 3D pose estimation from multiview images,” Multimedia Tools and Applications, vol. 77, no. 12, pp. 15573–15601, 2018. [Google Scholar]
32. Y. Zhang, L. An, T. Yu, X. Li, K. Li et al., “4D association graph for realtime multi-person motion capture using multiple video cameras,” in Computer Vision and Pattern Recognition, CVPR 2020, Seattle, WA, USA, pp. 1324–1333, 2020. [Google Scholar]
33. L. Y. Chen, L. Y. Chang, Y. C. Deng and B. C. Hsieh, “The rehabilitation and assessment in virtual reality game for the patient with cognitive impairment,” in Int. Symp. on Computer, Consumer and Control, IS3C 2020, Taichung, Taiwan, pp. 387–390, 2020. [Google Scholar]
34. D. L. Farias, R. F. Souza, P. A. Nardi and E. F. Damasceno, “A motor rehabilitation’s motion range assessment with low-cost virtual reality serious game,” in Int. Conf. on E-Health Networking, Application & Services, HEALTHCOM 2021, Shenzhen, China, pp. 1–5, 2020. [Google Scholar]
35. M. E. Gabyzon, B. Engel-Yeger, S. Tresser and S. Springer, “Using a virtual reality game to assess goal-directed hand movements in children: A pilot feasibility study,” Technology and Health Care, vol. 24, no. 1, pp. 11–19, 2016. [Google Scholar] [PubMed]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF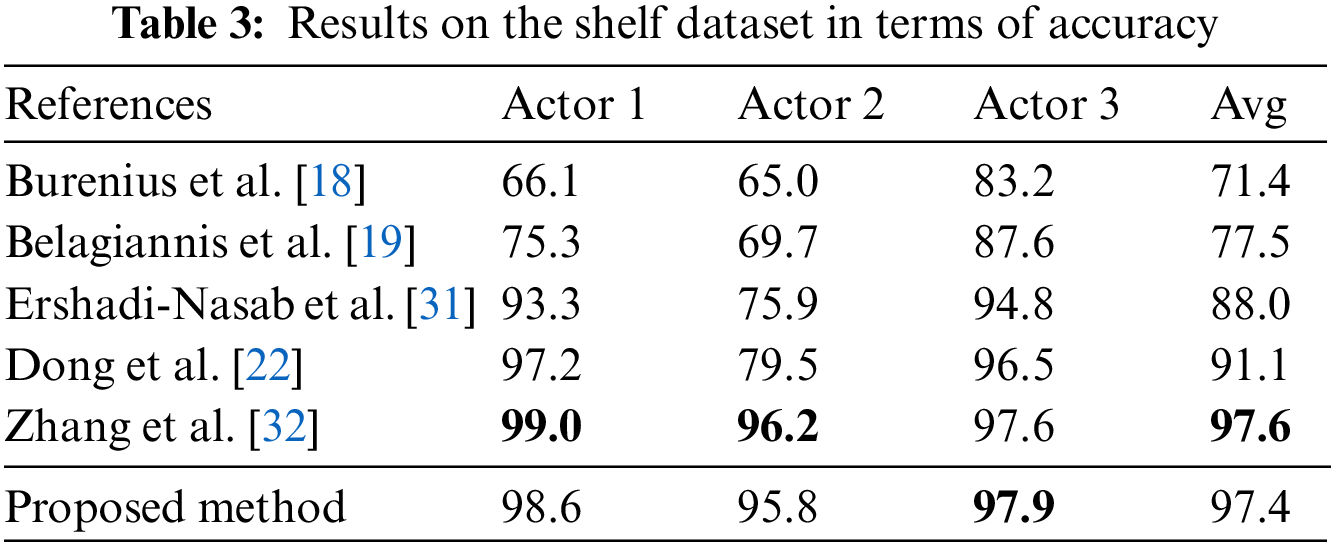
 Downloads
Downloads
 Citation Tools
Citation Tools