Efficient DP-FL: Efficient Differential Privacy Federated Learning Based on Early Stopping Mechanism

1  Introduction

In recent years, with the rapid development of machine learning technology, smart devices have generated massive amounts of data. Machine learning [1–5] techniques are widely used to process these data. However, centralized machine learning requires enormous computing power and attracts centralized attacks. To save computing power and ensure the confidentiality of the client’s local private data, a feasible solution is to put the client’s locally trained model into the federated learning framework for processing. Since federated learning trains data locally and does not upload private data, the privacy overhead of the client is effectively reduced. Therefore, federated learning is widely used in the Industrial Internet of Things [6–10], Blockchain [11–15], and Smart Healthcare [16–18].

Although federated learning can effectively prevent the leakage of users’ local private data, adversaries can still attack the model by analyzing the parameters of the local federated learning model [19–25]. Therefore, ensuring the privacy and security of users’ local data is a challenge.

To address this issue, DP is widely used for privacy protection in deep learning [26–29]. For example, Abadi et al. [30] proposed to use DP for deep learning and developed a new differential privacy stochastic gradient descent (DP-SGD) algorithm. Lee et al. [31] improved upon DP-SGD and allocate a privacy budget in each training session. Recently, DP has also been used in federated learning scenarios [32–35]. For example, Wei et al. [32] proposed to use DP for federated learning and proposed a new framework (NbAFL) based on differential privacy federated learning by adding Gaussian noise before the parameter aggregation of the client model. Xu et al. [33] proposed an Adaptive Fast Convergent Learning Algorithm (ADADP) with a provable privacy budget, when the client participates in model training, the model can show good training performance at a fixed privacy level. Truex et al. [34] proposed a hybrid approach based on DP and Secure Multi-Party Computation (SMC) to prevent inference attacks and generate the better models. However, this also consumes more communication resources. Therefore, it is necessary to design a more efficient differential privacy federated learning algorithm.

To address these challenges, this article proposes an efficient differential privacy federated learning method based on an early stopping mechanism. To summarize, our contributions to this paper focus on three points:

•   An Efficient DP-FL algorithm was proposed. Specifically, the algorithm inherits the advantages of differential privacy and federated learning and protects the actual parameters uploaded by the client during the training process.

•   The Efficient DP-FL algorithm adds an early stopping mechanism to reduces unnecessary noise and improve the availability of the data.

•   The efficiency of the proposed method is shown through theoretical analysis and simulation experiments.

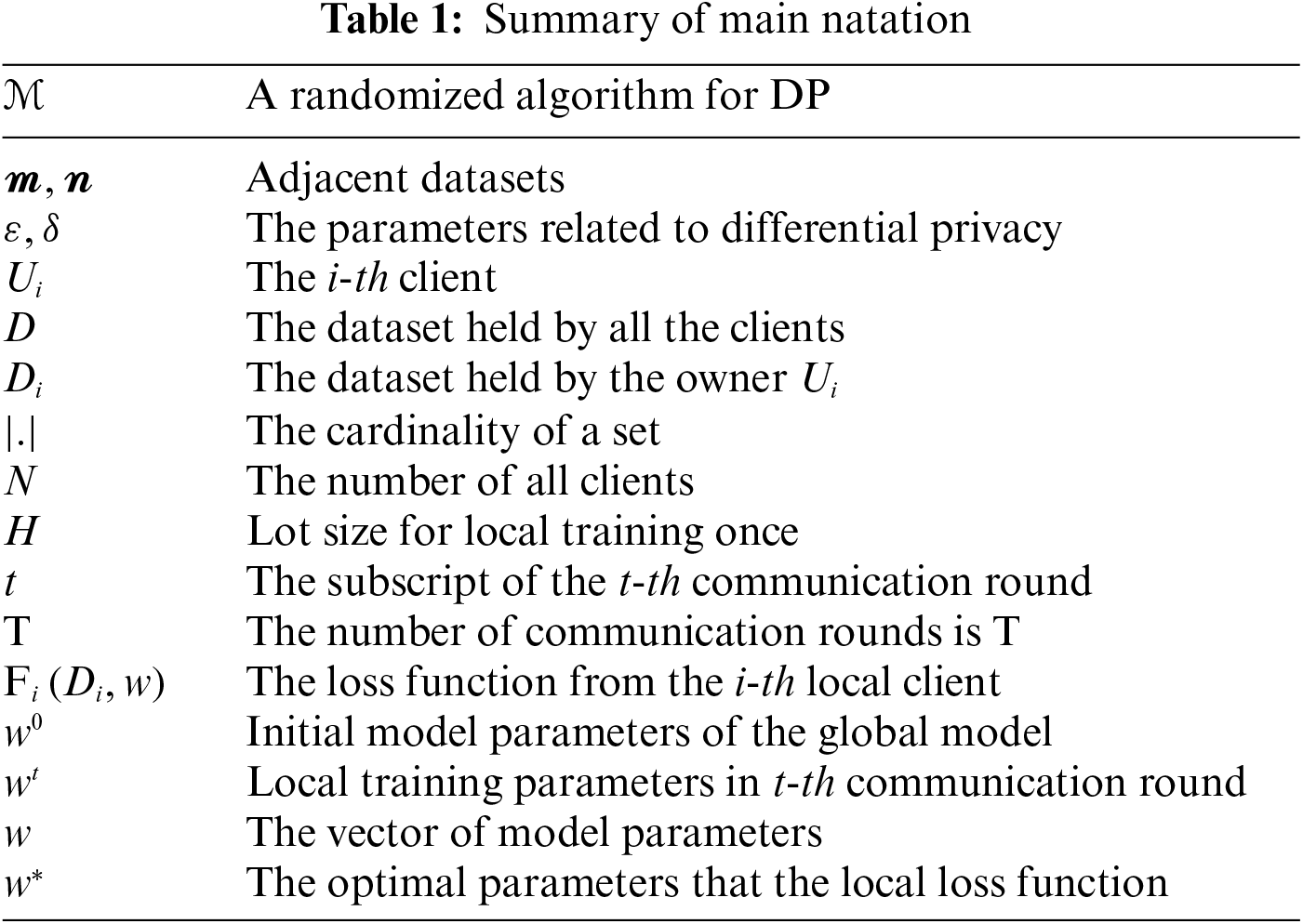
The rest of this paper is organized as follows. In Section 2, some initial preparations for our algorithm are provided. Section 3 proposes an efficient differential privacy federated learning scheme based on an early stopping mechanism, and Section 4 conducts privacy analysis. Experiments is in Section 5. Section 6 gives the conclusion. The basic concepts and meanings of the symbols are summarized in Table 1.

2  Preliminaries

2.1 Federated Learning

Let us observe the system of FL consisting of N clients and an aggregation server, as shown in Fig. 1. Di represents the dataset of the local client Ui, i∈{1,2,⋯,N}. The task of the aggregation server is to train the model from the relevant parameter information of the local clients. The training of the local client aims to find the optimal vector w of the model to minimize some loss function. In general form, the weight that the server aggregate receives from N local clients is as follows:

w=∑i=1Npiwi(1)

where w is the parameter vector aggregated by the server, wi is the parameter vector trained on the i-th client, and N is the number of all clients. pi=|Di||D|≥0, ∑i=1Npi=1, |D|=∑i=1N|Di| is the total number of all datasets, Di is the dataset of the i-th local client. Fi(.) is the loss function of the i-th local client, The optimization task of federated learning can be expressed as:

w∗=argminw⁡∑i=1NpiFi(Di,w)(2)

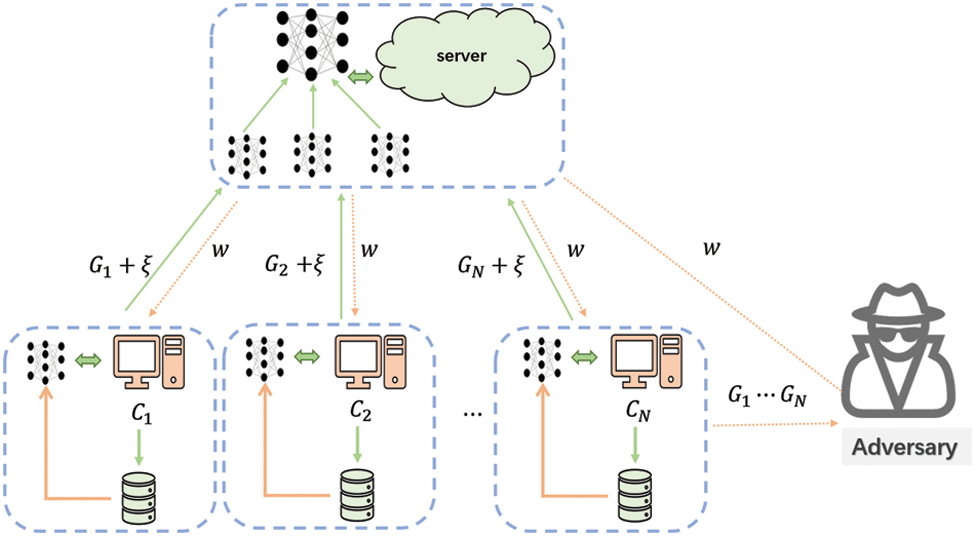
Figure 1: A differential privacy federated learning training model with the hidden adversary

The steps of each round of the training process of the federated learning general system are as follows:

•   Local training: All local clients use local samples to update the model based on the original data, and send the locally trained model parameters to the aggregation server.

•   Model aggregation: The server aggregates and averages the parameters uploaded by each local client and updates the global model.

•   Parameters broadcasting: The aggregation server broadcasts the updated the current parameters to each local client.

•   Model updating: Each local client updates the local model with the latest parameters received and tests the performance of the current model.

2.2 Threat Model

In this paper, the server is assumed to be honest but curious. Although the single dataset of the i-th client is stored locally in FL, the parameter wi needs to be shared with the aggregation server, which may disclose the client’s private. Therefore, semi-honest models are vulnerable to member inference attacks and attribute inference attack. Specifically, an adversary can perform attribute inference attacks by extracting training data during model training or by extracting feature vectors of training data [36–40]. For example, Salem et al. [41] proposed a hybrid generative model, which assumes that the adversary has black-box access to the model and has specific samples as prior knowledge, the adversary can judge whether the training set of the model contains feature samples, and thus initiate Membership inference attack. Lacharité et al. [42] proposed an approximate attribute inference attack, which is a method to enable range queries when the model provides little security. To sum up, the adversary may launch inference attacks based on the parameter information obtained during model training. Therefore, the threat model presented in this article is reasonable.

2.3 Differential Privacy

In recent years, DP has become a standard concept for federated learning privacy protection and has been widely used in federated learning data analysis tasks.

Definition 1: (ε,δ)−DP: A randomized algorithm ℳ:χ→ℛ with domain χ and range ℛ satisfies (ε,δ)−DP if for any two adjacent datasets 𝓶,𝓷∈χ and for all measurable sets 𝒪∈ℛ, it holds that

Pr[ℳ(𝓶)∈𝒪]≤eεPr[ℳ(𝓷)∈𝒪]+δ(3)

A Gaussian mechanism defined in [33] can be used to guarantee (ε,δ)−DP.

3  The Proposed Approach

To reduce privacy costs and improve the model convergence rate, Efficient DP-FL uses an adaptive learning rate for the gradient descent training model. In addition, Efficient DP-FL adds Gaussian noise to the gradient, and the gradient performs adaptive noise processing according to the adaptive learning rate, thereby improving the performance of model training. To further mitigate the impact of noise on model performance, the algorithm introduces an early stopping mechanism. The following will introduce the Efficient DP-FL method and give its differential privacy guarantee.

3.1 Adaptive DP-FL

The gradient descent method is commonly used to train deep learning models. The goal of training the model is to obtain the smallest loss function value. To minimize the local loss function, usually a subset of the data is randomly selected and the parameter wt+1←wt−α∇wtFi (xi,wt). The learning rate determines the step of the gradient descent update. If the learning rate is too large, it will fall into the dilemma of the local optimal solution. If the learning rate is too small, it will take a long time to obtain the optimal solution. Therefore, how to set an appropriate learning rate to avoid falling into a local optimal solution is a challenge we face. Relevant scholars have proposed more advanced optimizers, such as Adadelta, Adagrad, RMSProp, etc., to solve the above problems, and they update parameters by adaptively adjusting the learning rate.

Efficient DP-FL uses an approach similar to adaptive gradient descent with the Adam optimizer. The framework proposed in this paper is not only suitable for other types of gradient descent, but also for adaptive gradient descent with added noise.

Theorem 1: For any ε∈(0,1), c2>2ln⁡(1.25/δ), the Gaussian Mechanism parameter σ≥cΔf/ε is (ε,δ)−DP.

To ensure that the Gaussian noise distribution ξ∼N (0,σ2) satisfies (ε,δ)−DP, Dwork et al. [43] choosed the noise range σ≥cΔf/ε and the c≥2ln⁡(1.25/δ), here N denotes the noise distribution, ε∈(0,1) denotes the additive noise value of a particular data in the dataset, Δf is the sensitivity, Δf=max𝓶,𝓷∈χ‖f(𝓶)−f(𝓷)‖2, and δ is the probability of breaking the strict differential privacy. Theorem 1 is proved as follows:

Proof. There is a dataset D and a query function f, and the mechanism will return f(d)+ξ, where the Gaussian noise is normally distributed. The noise 𝒩(0,σ2) is added. For now, assume f is a real-valued function, so

Δf=Δ1f=Δ2f(4)

To study the different probability of adjacent dataset D and D′, the probability is obtained by the noise generation algorithm. The numerator in the ratio above describes the probability of observing f(d)+x when the dataset is D, and the denominator corresponds to the probability of observing this same value when the dataset is D′. the privacy loss is:

ln⁡e(−1/2σ2)x2e(−1/2σ2)(x+Δf)2(5)

Furthermore, looking at the absolute value.

|ln⁡e(−1/2σ2)x2e(−1/2σ2)(x+Δf)2|=|ln⁡e(−1/2σ2)[x−(x+Δf)2]|=|12σ2(2xΔf+Δf2)|(6)

whenever x<σ2ε/Δf−Δf/2, the quantity is bounded by ε To ensure privacy loss bounded by ε , with a probability of at least 1−δ, it is required that:

Pr[|x|≥σ2ε/Δf−Δf/2]<δ(7)

assume that ε≤1≤Δf, using the tail bound.

Pr[x>t]≤σ2πe(−t2)/2σ2(8)

σ2π1te(−t2)x2<δ/2(9)

⟺ln⁡(tσ)+t22σ2>ln(2/2πδ)(10)

Taking t=σ2ε/Δf−Δf/2,we get

ln⁡((σ2ε/Δf−Δf/2)/σ)+(σ2ε/Δf−Δf/2)2/2σ2>ln⁡(2/2πδ)=ln⁡(2π1δ)(11)

Let us write σ=cΔf/ε, then.

1σ(σ2εΔf−Δf2)=1σ[c2((Δf)2ε2)εΔf−Δf2]=c−ε2c(12)

when ε≤1 and c≥1, we can obtain (c−ε2c)≥c−12. So ln⁡(1σ(σ2εΔf−Δf2))>0 provided c≥32. Therefore focus on the t2σ2 term.

(12σ2σ2εΔf−Δf2)2=12σ2[Δf(c2ε−12)]2=12(c2−ε+ε2/4c2)(13)

Due to ε≤1, the derivative of (c2−ε+ε2/4c2) concerning for to c is positive in the scope we are considering (c≥32), so (c2−ε+ε2/4c2)≥c2−8/9 and it suffices to ensure.

c2−8/9>2ln⁡(2π1δ)(14)

In order words, it needs that

c2>2ln⁡(2π)+2ln⁡(1δ)+ln⁡(e89)=ln⁡(2π)+2ln⁡(1δ)+ln⁡(e89)(15)

which, since (2/π)e8/9<1.55, is satisfied whenever c2>2ln⁡(1.25/δ).

Let R=R1∪R2, where R1={x∈R:|x|≤cΔf/ε} and R2={x∈R:|x|>cΔf/ε}. For any subset S∈R, x∼𝒩(0,σ2), and define

S1={f(x)+x|x∈R1}(16)

S2={f(x)+x|x∈R2}(17)

Pr[f(x)+x∈S]=Pr[f(x)+x∈S1]+Pr[f(x)+x∈S2]≤eε(Pr[f(x)+x∈S1])+δ(18)

yielding (ε,δ)−DP for the Gaussian mechanism in one dimension.

Lemma 1: ℳ(x)≜f(x)+N (0,(2Δfσ)2, Let ε∈(0,1) be arbitrary. For c2>ln⁡(1.25/δ), the Gaussian Mechanism with parameter σ≥cΔf/ϵ is (ε,δ)−DP, where N (0,(2Δfσ)2) is a Gaussian distribution with mean 0 and standard deviation 2Δfσ. When δ>1.25exp(−(σε)2) and ε<1, the Gaussian mechanism is applied to the real-valued function f with sensitivity Δf satisfies (ε,δ)−DP. Lemma 1 is proved as follows:

Based on the proof of Theorem 1. we have the Gaussian noise distribution in this paper is subject to x∼𝒩(0,(2Δfσ)2), when c2>2ln⁡(1.25/δ), we have

(2Δfσ)2≥c2(Δf)2ε2>2ln⁡(1.21/δ)(Δf)2ε2(19)

Namely,

δ>1.25e−σ2ε2(20)

Considering the above differential privacy mechanism, the noise scope affects the privacy cost of the client and the convergence speed of the federated learning training process. Therefore, choosing the appropriate noise level remains a significant research problem. In this paper, the distribution of adding Gaussian noise to the gradient obeys the normal distribution N (0,(2Δfσ)2).

3.2 Early Stopping

The early stopping mechanism its commonly used regularization technique in deep neural networks, and its performance is usually better than general regularization methods. Its popularity is mainly due to its effectiveness and simplicity. The model stores and updates the current best parameters during training. When the error on the validation set does not improve further within a pre-specified number of iterations, the algorithm terminates and uses the last best parameters. This process is more formally described in Algorithm 1.

When training large models with sufficient representational power to the point of overfitting, we often observe that the training error gradually decreases over time but the validation error rises again. The early stopping mechanism is mainly a trade-off between training time and generalization error. It reduces communication overhead while obtaining optimal parameters. And because the algorithm reduces the number of communications, thereby also reducing the noise, the introduction of the early stopping mechanism improves the utility of the data.

3.3 Efficient DP-FL and Main Results

To protect the safety of parameters during federated learning training, it can be considered to add Gaussian noise to each sample gradient. However, adding too much Gaussian noise to the parameters can destroy the performance of the model. Therefore, we need to control the impact of parameter training on model performance during federated learning training. This approach has been extensively studied in previous work [30,33,44], and we make some modifications, especially about the privacy budget. Its training process is shown in Algorithm 2.

4  Privacy Analysis

Many researchers have studied the loss of privacy under specific noise. For example, Beimel et al. [45] proposed a privacy amplification theorem, where q=L/N is the sampling ratio, where each step is satisfying (qε,qδ)−DP. Furthermore, Dwork et al. [43] proposed the strong combination theorem, where each step satisfies (qεTln(1/δ),Tqδ)−DP in the case of sampling. However, the strong combination theorem does not take into account the specific noise distribution. Therefore, we adopt the moment account method of Abadi et al. [30] and show that for a specific range of noise and threshold values, Algorithm 2 satisfies (qεT,δ)−DP. Compared with the strong combination theorem, the moment account method of Abadi et al. [30] and show that for a specific range of noise and threshold values, Algorithm 2 satisfies (qεT,δ)−DP. Compared with the strong combination theorem, the moment account makes both bounds tighter, reducing the ln⁡(1/δ) and Tq parts of δ in the privacy budget ε. Therefore, applying the method of moment account leads to tighter bounds and thus obtains a more accurate estimate of the overall privacy loss.

𝒪 denotes the output result and the random variable Q(𝒪,ℳ,𝓶,𝓷) denotes the privacy loss, defined as:

Definition 2: At s, Q(𝒪,ℳ,𝓶,𝓷)≜log⁡Pr[ℳ(𝓶)]Pr[ℳ(𝓷)]

The moment mother function of the privacy loss random variable is:

Definition 3:αℳ(γ;𝓶,𝓷)≜logE𝒪∼ℳ(d)[exp(γQ(𝒪,ℳ,𝓶,𝓷)].

γ is any positive integer, to satisfy the definition of differential privacy, it is necessary to iterate over all 𝓶,𝓷 prime to obtain αℳ(γ), which we define as:

Definition 4:αℳ(γ)≜maxd,d′⁡αℳ(γ;𝓶,𝓷)

Theorem 2: Let αℳ(γ) be defined as above; ε>0, the random algorithm ℳis(ε,δ)−DP for

δ=minγexp⁡(αℳ(γ)−γε)(21)

According to Definitions 2, 3 and 4, we can prove Theorem 2, the proof is as follows:

Proof. We have Pr[Q(𝒪)≥ε]𝒪∼ℳ(𝓶)≤δ, then

Pr[Q(𝒪)≥ε]𝒪∼ℳ(𝓶)=Pr[exp⁡(γQ(𝒪))≥exp⁡(γε)]𝒪∼ℳ(𝓶)(22)

(Markov’s): P{x≥a}≤E(x)a, we have

Pr[exp⁡(γQ(𝒪))≥exp⁡(γε)]𝒪∼ℳ(𝓶)≤E𝒪∼ℳ(𝓶)[exp⁡(γQ(𝒪))]exp⁡(γε)≤exp⁡(α−γε)≤δ(23)

So, for any ε>0, δ=minγ⁡exp⁡(αℳ(γ)−γε), the mechanism ℳ is (ε,δ)−DP.

In each training iteration, the entire dataset satisfies (qε,qδ)−DP based on random sampling. Assume that the clipping threshold C and noise σ are properly chosen using the method moment account method. In this case, it can be proved that Algorithm 2 satisfies (qεT,δ)−DP, according to Definitions 2, 3, 4, where T denotes the total number of iterations.

5  Experimental Results and Comparison

5.1 Experimental Results

This section conducted extensive comparative experiments on the MNIST and the Fashion-MNIST datasets to evaluate the performance of the proposed Efficient DP-FL scheme. As a baseline for comparison, we choose to compare with the state-of-the-art research scheme [30,33,44]. Finally, the experiment is completed under the NVIDIA GeForce RTX 2080TI GPU (64 GB RAM) and Windows 10 system, and the model training is conducted under the PyTorch framework. Experiments have shown that the Efficient DP-FL method is better than previous research methods.

Experimental settings: The experiment uses the MNIST handwritten digit recognition and the Fashion-MNIST clothing classification dataset. Both datasets consist of 70000 sheets 28 × 28 grayscale image, all of which are divided into 10 categories, with 60000 samples used for training and 10000 samples used for testing. This paper uses a shallow CNN, which consists of two convolutional layers and two fully connected layers. Convolutional Layer Use 5 × 5 convolutions with stride 1. The first convolution outputs 12 for each image 6 × 6 × 64 tensors, second convolution for each image output 6 × 6 × 64 tensors. Then ReLU and 2 × 2 maximum pooling layers flatten the second convolution layer into a vector that is fed to a fully connected layer with 384 units. This article divided the training data from 10 clients into non-IID segments based on digital tags and divided into an average of 400 segments. Each customer is assigned 40 random data segments, so each customer’s sample has two or five tags. Each round of experiments is set at 1000 epochs. We use a fixed value δ=10−5, the initial learning rate using MNIST is 0.001 and Fashion-MNIST is 0.002. ρ1 in Adaptive DP-FL is set to 0.9 and ρ2 is set to 0.999. The clipping threshold C is a popular component of SGD combined with ML and for DP based on FL frameworks, consideration should be given to appropriate clipping threshold C.

5.1.1 Model Performance for Adaptive DP-FL Method on MNIST and Fashion-MNIST Datasets

Fig. 2 investigates the effect of Adaptive DP-FL’s approach on model performance. The accuracy and loss of the Adaptive DP-FL method and the method without ADADP are compared. We set clipping threshold C=4 and privacy budget ε=2 in the MNIST and Fashion-MNIST datasets. Both methods in the MNIST and Fashion-MNIST datasets use constant noise scale σ=2.0 and constant δ=10−5. Set the initial learning rate of the experiment in the MNIST dataset to 0.002and in the Fashion-MNIST dataset to 0.001 and set ρ1 to 0.9, and ρ2 to 0.999. We can see that in the MNIST dataset, the final convergence accuracy of the model using Adaptive DP-FL is 94.58% and the model using ADADP is 92.03%. In the Fashion-MNIST dataset, the final convergence accuracy of the model using Adaptive DP-FL is 88.38% and the model using ADADP is 79.91%. For both datasets, the Adaptive DP-FL method significantly outperforms the ADADP method.

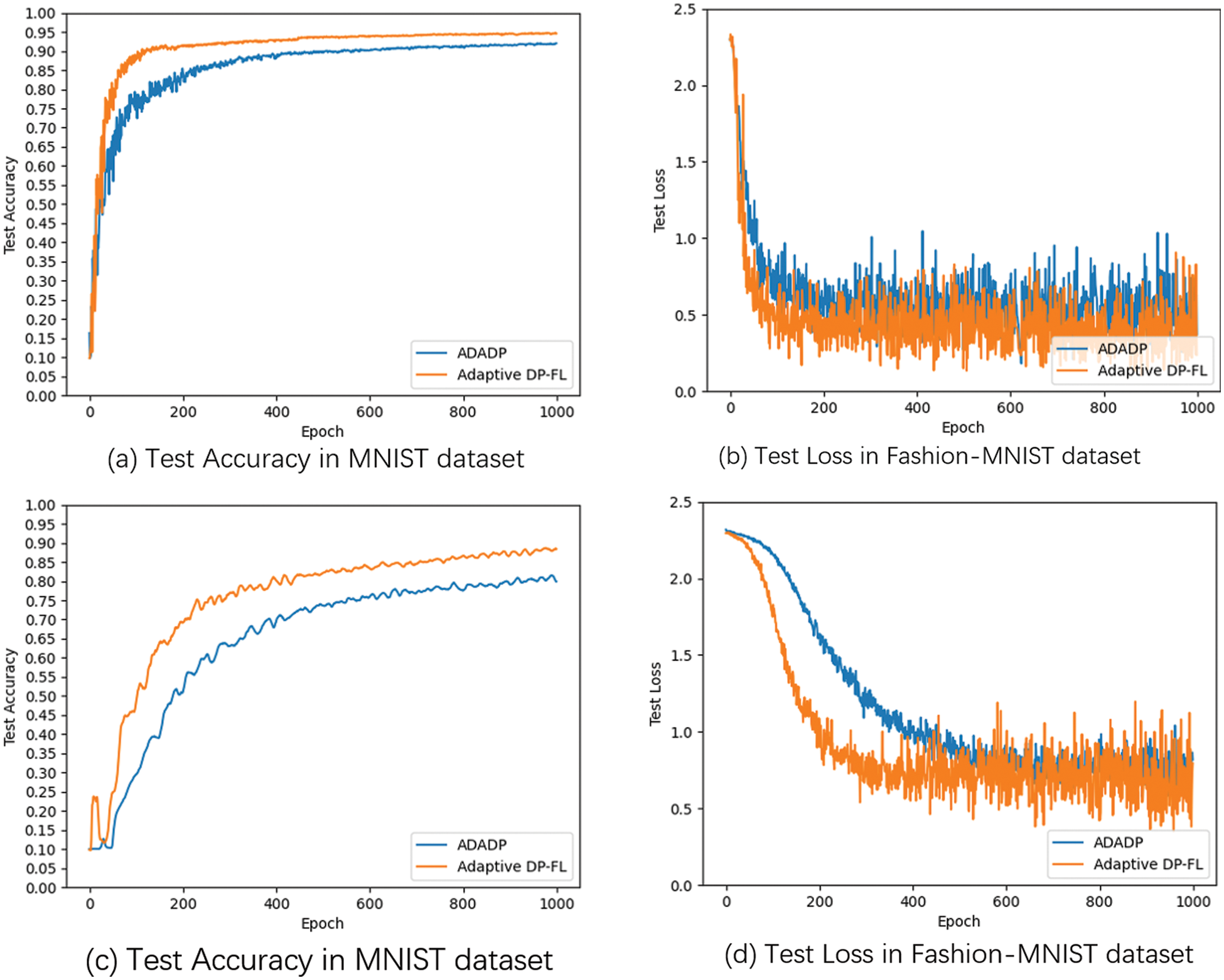
Figure 2: Model performance for adaptive DP-FL method on MNIST and fashion-MNIST datasets

5.1.2 Performance Comparison of Algorithms under Different Noise Scales

As a multi-party collaborative training model method, federated learning its local private data for model training. The data is saved locally on the client and the trained local model is updated to the server, which aggregates the local model. However, federated learning has a natural privacy protection effect. An attacker can still infer local private data through the model parameters of the client or server. Therefore, we introduce a differential privacy technology lighter than the cryptographic method. However, the introduction of differential privacy usually seriously affects the utility of data while protecting data privacy security. To solve this problem, this article proposes a secure and efficient DP-FL scheme. During each update process of the model, add the Gaussian noise to the sample gradient in the differential privacy technology and then iteratively update by an adaptive algorithm. The scheme strengthens the privacy security of the model and improves its performance. To test the robustness of the algorithm under different noise scales, this paper compared the performance of three different algorithms, DPFL-SGD, DPFL-PRMSProp, and the algorithm proposed in this paper under different noise conditions. In general, the larger the noise scale added, the lower the data availability and the worse the model performance.

As seen in Fig. 3, in each plot, δ=10−5, keeping ε fixed, in the same noise scale, we can observe that when adding noise scales σ∈(4,8),ε=0.5, the final accuracy of the three algorithms is 87.81%, 84.19%, and 77.77%. The overall effect of Efficient DP-FL and DPFL-PRMSProp using adaptive algorithm is better than that of DPFL-SGD, which may be due to the DPSGD algorithm being prone to falling into local optima. Specifically, in the early stages of experiments, the accuracy of our model changes faster, followed by DPFL-PRMSProp, and the improvement of DPFL-SGD is slower. In the later stage of the experiment, the convergence speed of the adaptive differential privacy federated learning algorithm tends to stabilize, and the overall performance is better than the DPFL-PRMSProp and DPFL-SGD algorithms. Under different noise scales, we can observe from Fig. 3 that the final accuracy of adding noise scales σ∈(1,2),ε=2, are 92.79%, 93.48%, and 94.69%, respectively. The final accuracies of adding noise scales σ∈(2,4),ε=1, are 88.39%, 91.45%, and 92.58%, and the final accuracies of noise scales σ∈(4,8),ε=0.5 are 77.77%, 84.19%, and 87.81%. That is, the final accuracy of adding noise scales σ∈(1,2),ε=2, are 4.4%, 2.03%, 2.11% higher than adding noise scales σ∈(2,4),ε=1, and 15.02%, 9.29%, 6.88% higher than large noise. Therefore, the greater the noise, the greater the impact on the convergence performance of the model. The impact of moderate noise is next. The smaller the noise, the smaller the impact on algorithm performance.

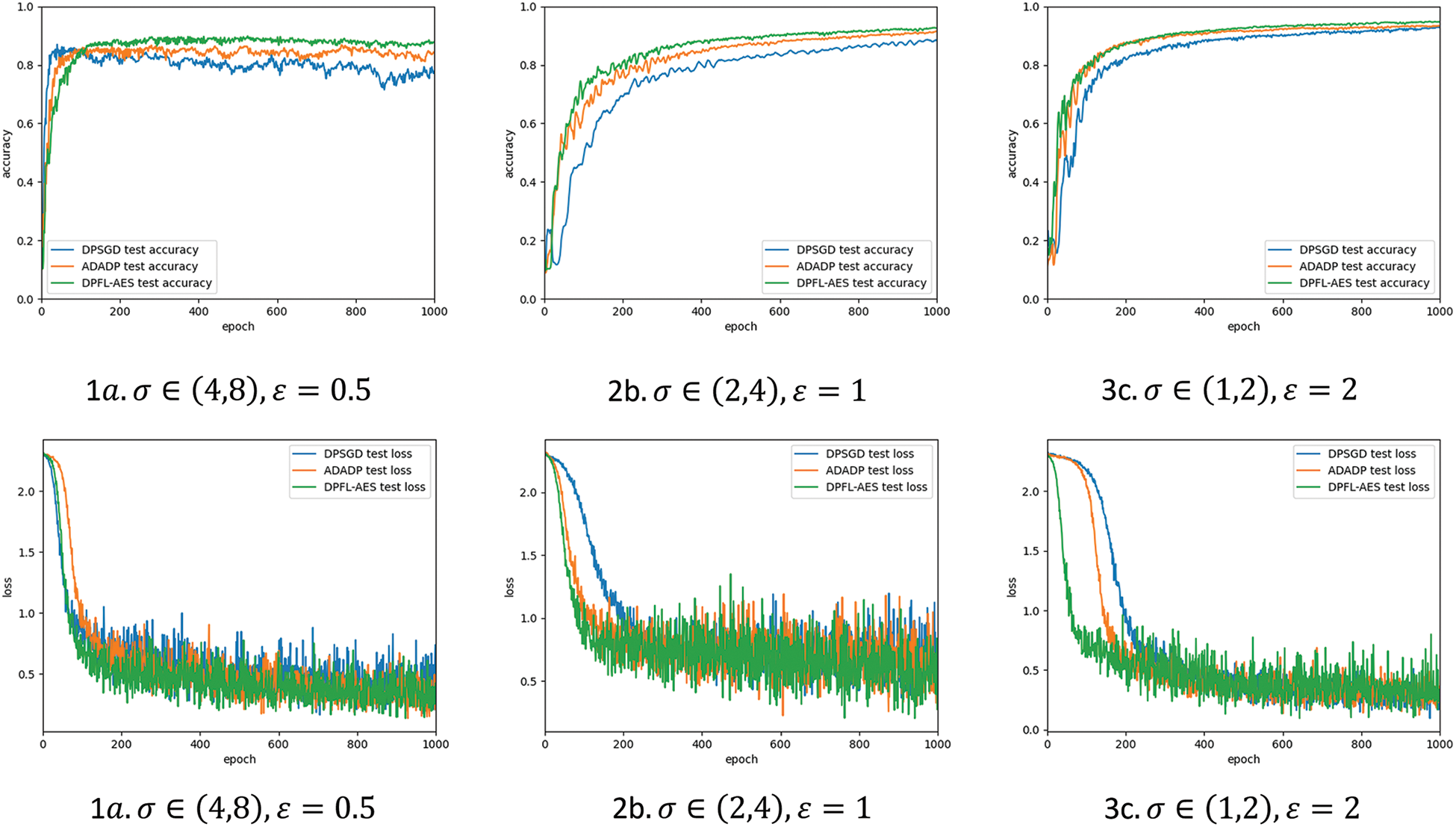
Figure 3: The effect of different noise scales on the convergence performance of the algorithm

The federated learning model with adaptive differential privacy is less sensitive to the size of the noise scale. Experiments show that with a fixed 1000 rounds of communication iterations, our algorithm has faster convergence speed and better final results. Our scheme can achieve better model performance with lower communication costs when applied to actual demand scenarios.

5.1.3 Model Performance for Early Stopping Mechanism on MNIST and Fashion-MNIST Datasets

It can be seen from Fig. 4 that after adding the early stopping mechanism, different algorithms converge in advance. On the MNIST dataset, ADADP converges early with 91.20% accuracy in 762 epochs. Compared with the fixed-setting 1000-round iteration experiment, it saves 238 rounds of communication overhead while achieving similar performance. Our algorithm converges ahead of time with 94.01% accuracy in 639 rounds, which saves 361 rounds of communication overhead while achieving similar performance. On the Fashion-MNIST dataset, ADADP converges early with 91.62% accuracy at 834 rounds. Compared with the fixed-set 1000-round iteration experiment, it saves 166 rounds of communication overhead while achieving similar performance. Our algorithm converges ahead of time with 94.93% accuracy in 785 rounds, which saves 215 rounds of communication overhead while achieving similar performance. At the same time, we can see that our algorithm outperforms previous methods. To sum up, the early stopping mechanism can reduce communication overhead while ensuring the convergence of the model. Therefore, compared to other methods, our algorithm is better able to improve data utility while keeping data safe.

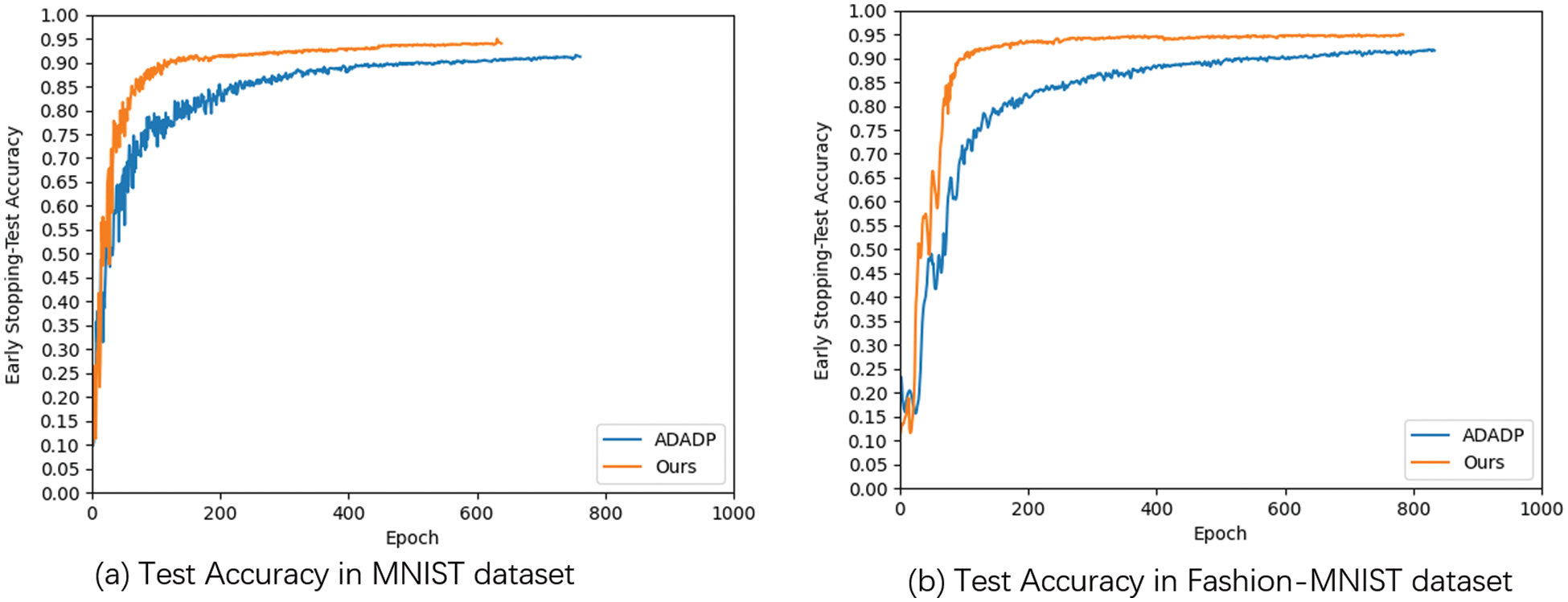
Figure 4: Performance for early stopping mechanism on MNIST and fashion-MNIST datasets

5.1.4 Model Performance for Efficient DP-FL Method on MNIST and Fashion-MNIST Datasets

Fig. 5 investigates the performance of the Efficient DP-FL method on the MNIST and the Fashion-MNIST datasets. The Efficient DP-FL method combines the effects of Adaptive DP-FL and Early Stopping mechanism on model performance. The accuracy and loss of differential privacy federated learning methods with adaptive Gaussian noise and constant noise without adaptation are compared. We set the same clipping threshold C=4 in the MNIST and Fashion-MNIST datasets. The two methods in the MNIST dataset and Fashion-MNIST dataset have constant noise scale σ=2.0 (Because the larger the noise value, the greater the impact on the performance of the model. Setting the noise value too small does not protect data. Through a large number of experiments, it has been found that when the noise value is set to 2, the model performance is the best.) and constant δ=10−5, privacy budget ε=2, set the initial learning rate of the experiment in the MNIST dataset to 0.002 and in the Fashion-MNIST dataset to 0.001, set ρ1 to 0.9, and ρ2 to 0.999. We can see that in the MNIST dataset, the model using Efficient DP-FL converges when the accuracy reaches 94.61% in 578 rounds, and the model using ADADP converges when the accuracy reaches 93.40% in 506 rounds. In the Fashion-MNIST dataset, the model using Efficient DP-FL converges when the accuracy is 94.29% in 636 rounds, and the model using ADADP converges when the accuracy is 92.18% in 751 rounds. For these two data sets, the final accuracy of using Efficient DP-FL is 1.21% and 2.11% higher than that of the method using ADADP, respectively, and the number of communication rounds using Efficient DP-FL is different from that of the method using ADADP. The reduction is 71 rounds, 115 rounds, which shows that the Efficient DP-FL method can save more communication overhead. In addition, we also observed that the Efficient DP-FL method (combining Adaptive DP-FL and Early Stopping mechanism) outperformed the previous Adaptive DP-FL and Early Stopping mechanism method on both datasets. The Efficient DP-FL communication overhead is reduced by 133 rounds and 149 rounds, respectively, compared with the Adaptive DP-FL and Early Stopping mechanism methods alone.

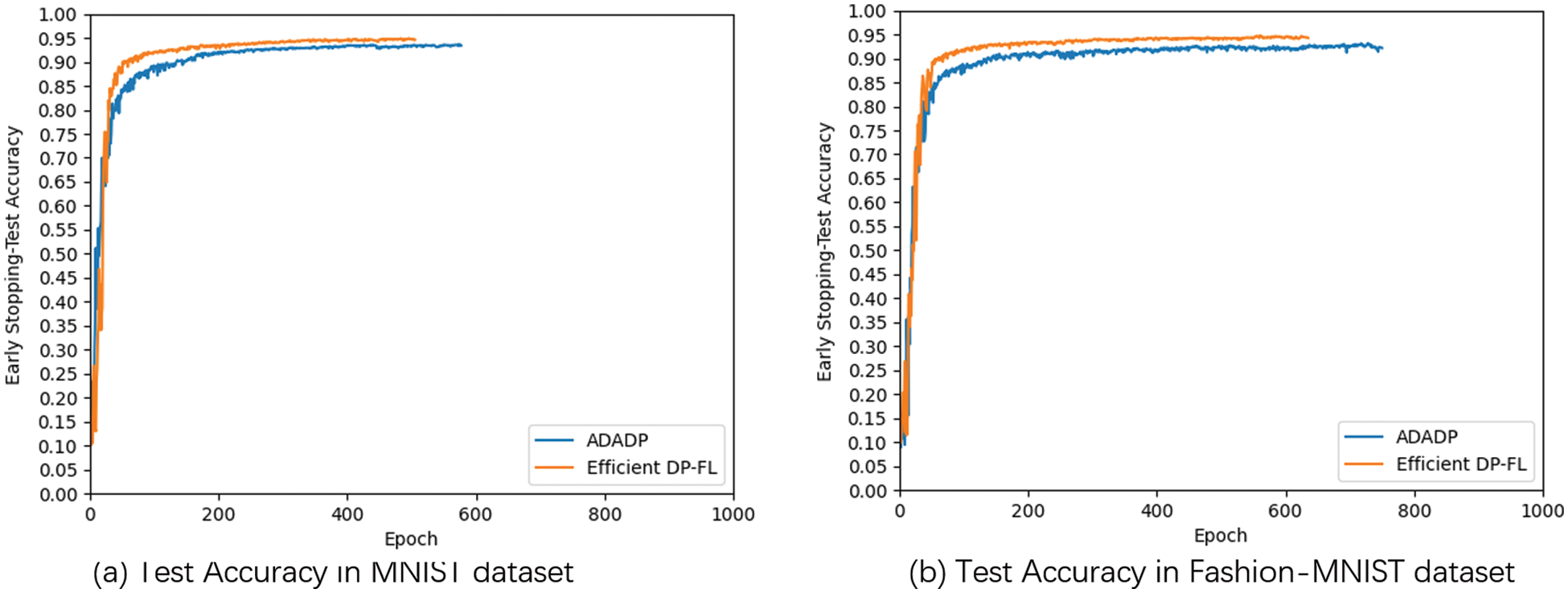
Figure 5: Performance for efficient DP-FL method on MNIST and fashion-MNIST datasets

5.2 Comparison

Table 2 shows a comparison of the studied algorithms, including data security, data utility, adaptation, and communication cost. The above comparison shows that our algorithm can simultaneously satisfy data security, data utility, an adaptability and reduce communication overhead. In contrast, other algorithms do not have this capability. Specifically, reference [30] proposed a DPSGD algorithm for the first time, which uses a Gaussian down-sampling mechanism and uses moment calculation technology to measure privacy loss. Although this algorithm can effectively protect the data security of local clients, adding a large amount of noise to the algorithm will reduce the usefulness of the data, and the algorithm cannot adaptively reduce noise [33]. An ADADP algorithm was proposed, which adaptively adjusts the noise range under a given privacy level, enabling the algorithm to converge quickly [44]. A UDP algorithm with a CRD method are proposed. The UDP algorithm can effectively protect the data security of local users, and a UDP algorithm with a CRD method can effectively reduce the number of communication rounds. However, compared to the scheme proposed in this article, this algorithm cannot effectively improve the utilization rate of data, and the communication cost is not as low as the proposed scheme. However, compared with Efficient DP-FL algorithm, this algorithm cannot effectively improve the utility of data and reduce the communication cost-effectively. In summary, the Efficient DP-FL algorithm fully satisfies the advantages of data security, data utility, adaptability, and low communication overhead. The above is a qualitative analysis of different algorithms. The following will quantitatively analyze the communication costs of different schemes, as shown in Fig. 6. Quantitative comparative analysis has been added.

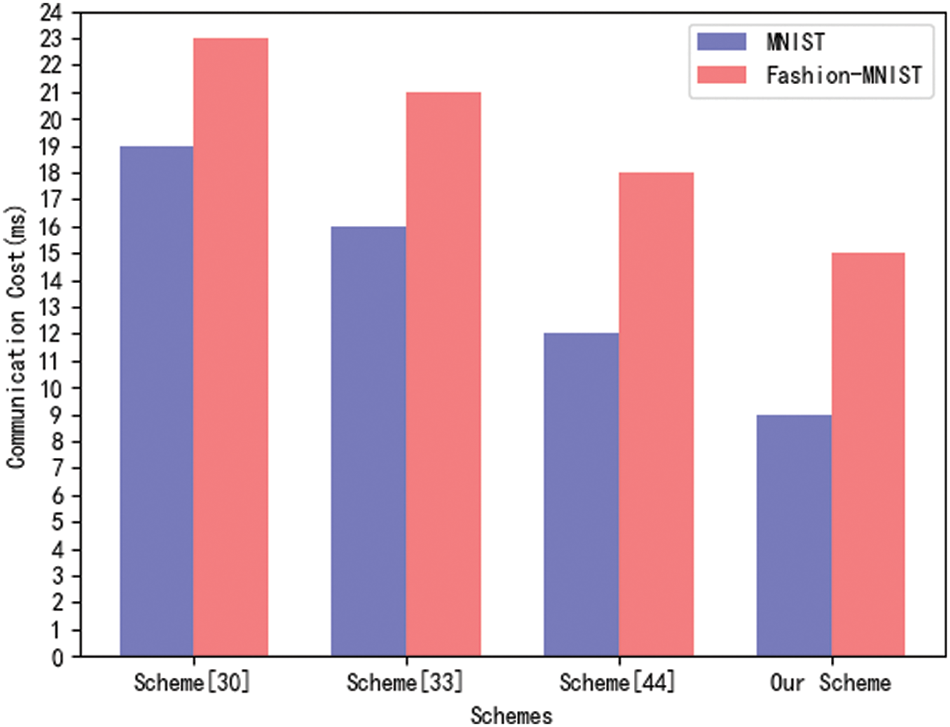
Figure 6: Communication cost comparison of different scheme

Fig. 6 compares the time cost of a round of communication for different schemes. The proposed scheme uses adaptive learning rates to adjust the gradient descent train process to avoid model overfitting and fluctuations, and uses an early shutdown system to reduce noise, ensuring that federated learning schemes train efficiently while protecting data security. The communication cost comparison results are shown in Fig. 6. Looking at Fig. 6, we can draw the following conclusions.

•   The scheme [30] has the longest running time, while the schemes [33] and [44] have the lowest running time. The above comparison shows that the scheme proposed in this article is effective.

•   Because Fashion MNIST is a set of 28 × 28 grayscale clothing images, its image data is more complex than MNIST, the four schemes on MNIST have shorter runtime than those on Fashion-MNIST.

6  Conclusion

The main contributions of this article are reflected in three aspects. Firstly, an Efficient DP-FL algorithm is proposed, which has higher accuracy than previous algorithms. In addition, the Efficient DP-FL algorithm adds an early stopping mechanism to improve the utility of the data. Secondly, it is strictly proved mathematically that the Efficient DP-FL algorithm satisfies differential privacy. Thirdly, the Efficient DP-FL algorithm is applied to train a CNN model on a deep learning network with real datasets, and the better performance of the Efficient DP-FL algorithm compared to previous methods is evaluated through experiments.

Based on the Efficient DP-FL proposed in this article, many further tasks deserve attention. In particular, this article uses a shallow neural network model, and the deeper neural network model is worth further research. In addition, you can apply the techniques in this article to language modeling tasks through experience in the MNIST and Fashion-MNIST.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: This work was supported in part by the Communication Security Laboratory Science and Technology Fund under Grant No. 61421030209012105, in part by the Sichuan Provincial Science and Technology Department Project under Grant 2019YFN0104, in part by the Yibin Science and Technology Plan Project under Grant 2021GY008, and in part by the Sichuan University of Science and Engineering Postgraduate Innovation Fund Project under Grant Y2022154.

Author Contributions: Study conception and design: Sanxiu Jiao; data collection: Jintao Meng; analysis and interpretation of results: Sanxiu Jiao, Yue Zhao, Lecai Cai; draft manuscript preparation: Kui Cheng. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data are derived from public datasets.

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

1. J. G. Greener, S. M. Kandathil, L. Moffat and D. T. Jones, “A guide to machine learning for biologists,” Nature Reviews Molecular Cell Biology, vol. 23, no. 1, pp. 40–55, 2022. [Google Scholar] [PubMed]

2. T. R. Ramesh, U. K. Lilhore, M. Poongodi, S. Simaiya, A. Kaur et al., “Predictive analysis of heart diseases with machine learning approaches,” Malaysian Journal of Computer Science, pp. 132–148, 2022. https://doi.org/10.22452/mjcs.sp2022no1.10 [Google Scholar] [CrossRef]

3. N. Ali, T. M. Ghazal, A. Ahmed, S. Abbas, M. A. Khan et al., “Fusion-based supply chain collaboration using machine learning techniques,” Intelligent Automation & Soft Computing, vol. 31, no. 3, pp. 1671–1687, 2022. [Google Scholar]

4. Y. Zhang, Z. Gao, X. Wang and Q. Liu, “Image representations of numerical simulations for training neural networks,” Computer Modeling in Engineering & Sciences, vol. 134, no. 2, pp. 1–13, 2022. [Google Scholar]

5. Y. Zhang, Z. Gao, X. Wang and Q. Liu, “Predicting the pore-pressure and temperature of fire-loaded concrete by a hybrid neural network,” International Journal of Computational Methods, vol. 19, no. 8, pp. 247, 2022. [Google Scholar]

6. Y. Liu, R. Zhao, J. Kang, A. Yassine and D. Niyato, “Communication-efficient and attack-resistant federated edge learning for Industrial Internet of Things,” ACM Transactions on Internet Technology, vol. 22, no. 3, pp. 1–22, 2021. [Google Scholar]

7. J. Chen, J. Xue, Y. Wang, L. Huang, T. Baker et al., “Privacy-preserving and traceable federated learning for data sharing in industrial IoT applications,” Expert Systems with Applications, vol. 213, pp. 119036, 2023. https://doi.org/10.1016/j.eswa.2022.119036 [Google Scholar] [CrossRef]

8. A. Imteaj, U. Thakker, S. Wang, J. Li and M. H. Amini, “A survey on federated learning for resource-constrained IoT devices,” IEEE Internet of Things Journal, vol. 9, no. 1, pp. 1–24, 2021. [Google Scholar]

9. D. C. Nguyen, M. Ding, P. N. Pathirana, A. Seneviratne, J. Li et al., “Federated learning for Internet of Things: A comprehensive survey,” IEEE Communications Surveys & Tutorials, vol. 23, no. 3, pp. 1622–1658, 2021. [Google Scholar]

10. T. Zhang, L. Gao, C. He, M. Zhang, B. Krishnamachari et al., “Federated learning for the internet of things: Applications, challenges, and opportunities,” IEEE Internet of Things Magazine, vol. 5, no. 1, pp. 24–29, 2022. [Google Scholar]

11. L. Ouyang, F. Y. Wang, Y. Tian, X. Jia, H. Qi et al., “Artificial identification: A novel privacy framework for federated learning based on blockchain,” IEEE Transactions on Computational Social Systems, pp. 1–10, 2023. https://doi.org/10.1109/TCSS.2022.3226861 [Google Scholar] [CrossRef]

12. A. Yazdinejad, A. Dehghantanha, R. M. Parizi, M. Hammoudeh, H. Karimipour et al., “Block hunter: Federated learning for cyber threat hunting in blockchain-based IIoT networks,” IEEE Transactions on Industrial Informatics, vol. 18, no. 11, pp. 8356–8366, 2022. [Google Scholar]

13. A. Islam, A. Al Amin and S. Y. Shin, “FBI: A federated learning-based blockchain-embedded data accumulation scheme using drones for internet of things,” IEEE Wireless Communications Letters, vol. 11, no. 5, pp. 972–976, 2022. [Google Scholar]

14. A. Lakhan, M. A. Mohammed, S. Kadry, S. Al-Qahtani, M. S. Maashi et al., “Federated learning-aware multi-objective modeling and blockchain-enable system for IIoT applications,” Computers and Electrical Engineering, vol. 100, pp. 107839, 2022. https://doi.org/10.1016/j.compeleceng.2022.107839 [Google Scholar] [CrossRef]

15. W. Issa, N. Moustafa, B. Turnbull, N. Sohrabi and Z. Tari, “Blockchain-based federated learning for securing Internet of Things: A comprehensive survey,” ACM Computing Surveys, vol. 55, no. 9, pp. 1–43, 2023. [Google Scholar]

16. M. Ali, F. Naeem, M. Tariq and G. Kaddoum, “Federated learning for privacy preservation in smart healthcare systems: A comprehensive survey,” IEEE Journal of Biomedical and Health Informatics, vol. 27, no. 2, pp. 778–789, 2022. [Google Scholar]

17. K. S. Arikumar, S. B. Prathiba, M. Alazab, T. R. Gadekallu, S. Pandya et al., “FL-PMI: Federated learning-based person movement identification through wearable devices in smart healthcare systems,” Sensors, vol. 22, no. 4, pp. 1377, 2022. [Google Scholar] [PubMed]

18. D. C. Nguyen, Q. V. Pham, P. N. Pathirana, M. Ding, A. Seneviratne et al., “Federated learning for smart healthcare: A survey,” ACM Computing Surveys, vol. 55, no. 3, pp. 1–37, 2022. [Google Scholar]

19. P. Manoharan, R. Walia, C. Iwendi, T. A. Ahanger, S. T. Suganthi et al., “SVM-based generative adverserial networks for federated learning and edge computing attack model and outpoising,” Expert Systems, vol. 40, no. 5, pp. e13072, 2022. https://doi.org/10.1111/exsy.13072 [Google Scholar] [CrossRef]

20. H. Hu, Z. Salcic, L. Sun, G. Dobbie and X. Zhang, “Source inference attacks in federated learning,” in 2021 IEEE Int. Conf. on Data Mining (ICDM), Auckland, New Zealand, pp. 1102–1107, 2021. [Google Scholar]

21. B. Ghimire and D. B. Rawat, “Recent advances on federated learning for cybersecurity and cybersecurity for federated learning for Internet of Things,” IEEE Internet of Things Journal, vol. 9, no. 11, pp. 8229–8249, 2022. [Google Scholar]

22. C. Fu, X. Zhang, S. Ji, J. Chen, J. Wu et al., “Label inference attacks against vertical federated learning,” in 31st USENIX Security Symp. (USENIX Security 22), Boston, MA, pp. 1397–1414, 2022. [Google Scholar]

23. V. Shejwalkar, A. Houmansadr, P. Kairouz and D. Ramage, “Back to the drawing board: A critical evaluation of poisoning attacks on production federated learning,” in 2022 IEEE Symp. on Security and Privacy (SP), Francisco, CA, USA, pp. 1354–1371, 2022. [Google Scholar]

24. C. Chen, L. Lyu, H. Yu and G. Chen, “Practical attribute reconstruction attack against federated learning,” IEEE Transactions on Big Data, pp. 1, 2022. https://doi.org/10.1109/TBDATA.2022.3159236 [Google Scholar] [CrossRef]

25. B. McMahan, E. Moore, D. Ramage, S. Hampson, Y. Arcas et al., “Communication-efficient learning of deep networks from decentralized data, artificial intelligence and statistics,” PMLR, vol. 54, pp. 1273–1282, 2017. [Google Scholar]

26. J. Jin, E. McMurtry, B. I. P. Rubinstein and O. Ohrimenko, “Are we there yet? Timing and floating-point attacks on differential privacy systems,” in 2022 IEEE Symp. on Security and Privacy (SP), Francisco, CA, USA, pp. 473–488, 2022. [Google Scholar]

27. Z. Bu, J. Dong, Q. Long and W. J. Su, “Deep learning with gaussian differential privacy,” Harvard Data Science Review, vol. 2020, no. 23, 2020. [Google Scholar]

28. P. C. M. Arachchige, P. Bertok, I. Khalil, D. Liu and S. Camtepe, “Local differential privacy for deep learning,” IEEE Internet of Things Journal, vol. 7, no. 7, pp. 5827–5842, 2019. [Google Scholar]

29. N. Papernot, A. Thakurta, S. Song, S. Chien and Ú. Erlingsson, “Tempered sigmoid activations for deep learning with differential privacy,” Proceedings of the AAAI Conference on Artificial Intelligence, vol. 35, no. 10, pp. 9312–9321, 2021. https://doi.org/10.1609/aaai.v35i10.17123 [Google Scholar] [CrossRef]

30. M. Abadi, A. Chu, I. Goodfellow, H. B. McMahan, I. Mironov et al., “Deep learning with differential privacy,” in Proc. of the 2016 ACM SIGSAC Conf. on Computer and Communications Security, pp. 308–318, 2016. https://doi.org/10.1145/2976749.2978318 [Google Scholar] [CrossRef]

31. J. Lee and D. Kifer, “Concentrated differentially private gradient descent with adaptive per-iteration privacy budget,” in Proc. of the 24th ACM SIGKDD Int. Conf. on Knowledge Discovery & Data Mining, pp. 1656–1665, 2018. https://doi.org/10.1145/3219819.3220076 [Google Scholar] [CrossRef]

32. K. Wei, J. Li, M. Ding, C. Ma, H. Yang et al., “Federated learning with differential privacy: Algorithms and performance analysis,” IEEE Transactions on Information Forensics and Security, vol. 15, pp. 3454–3469, 2020. [Google Scholar]

33. Z. Xu, S. Shi, A. X. Liu, J. Zhao and L. Chen, “An adaptive and fast convergent approach to differentially private deep learning,” in IEEE INFOCOM 2020-IEEE Conf. on Computer Communications, Toronto, ON, Canada, pp. 1867–1876, 2020. [Google Scholar]

34. S. Truex, N. Baracaldo, A. Anwar, T. Steinke, H. Ludwig et al., “A hybrid approach to privacy-preserving federated learning,” in Proc. of the 12th ACM Workshop on Artificial Intelligence and Security, pp. 1–11, 2019. https://doi.org/10.1145/3338501.3357370 [Google Scholar] [CrossRef]

35. Q. Li, Z. Wen, Z. Wu, S. Hu, N. Wang et al., “A survey on federated learning systems: Vision, hype and reality for data privacy and protection,” IEEE Transactions on Knowledge and Data Engineering, vol. 35, no. 4, pp. 3347–3366, 2021. [Google Scholar]

36. L. Wang, Y. Lin, T. Yao, H. Xiong and K. Liang, “FABRICF: Fast and secure unbounded cross-system encrypted data sharing in cloud computing,” IEEE Transactions on Dependable and Secure Computing, pp. 1–13, 2023. https://doi.org/10.1109/TDSC.2023.3240820 [Google Scholar] [CrossRef]

37. W. Li, P. Wang and K. Liang, “HPAKE: Honey password-authenticated key exchange for fast and safer online authentication,” IEEE Transactions on Information Forensics and Security, vol. 18, pp. 1596–1609, 2022. [Google Scholar]

38. J. Feng, H. Xiong, J. Chen, Y. Xiang and K. H. Yeh, “Scalable and revocable attribute-based data sharing with short revocation list for IIoT,” IEEE Internet of Things Journal, vol. 10, no. 6, pp. 4815–4829, 2022. [Google Scholar]

39. Q. Mei, M. Yang, J. Chen, L. Wang and H. Xiong, “Expressive data sharing and self-controlled fine-grained data deletion in cloud-assisted IoT,” IEEE Transactions on Dependable and Secure Computing, vol. 18, pp. 1–16, 2022. [Google Scholar]

40. X. Huang, H. Xiong, J. Chen and M. Yang, “Efficient revocable storage attribute-based encryption with arithmetic span programs in cloud-assisted internet of things,” IEEE Transactions on Cloud Computing, vol. 11, no. 2, pp. 1273–1285, 2023. [Google Scholar]

41. A. Salem, A. Bhattacharya, M. Backes, M. Fritz and Y. Zhang, “Updates-Leak: Data set inference and reconstruction attacks in online learning,” in 29th USENIX Security Symp. (USENIX Security 20), USENIX Association, pp. 1291–1308, 2020. https://www.usenix.org/conference/usenixsecurity20/presentation/salem [Google Scholar]

42. M. S. Lacharité, B. Minaud and K. G. Paterson, “Improved reconstruction attacks on encrypted data using range query leakage,” in 2018 IEEE Symp. on Security and Privacy (SP), Francisco, CA, USA, pp. 297–314, 2018. [Google Scholar]

43. C. Dwork, K. Kenthapadi, F. McSherry, I. Mironov and M. Naor, “Our data, ourselves: Privacy via distributed noise generation,” in Annual Int. Conf. on the Theory and Applications of Cryptographic Techniques, Berlin, Heidelberg, Springer, vol. 4004, pp. 486–503, 2006. [Google Scholar]

44. K. Wei, J. Li, M. Ding, C. Ma, H. Su et al., “User-level privacy-preserving federated learning: Analysis and performance optimization,” IEEE Transactions on Mobile Computing, vol. 21, no. 9, pp. 3388–3401, 2021. [Google Scholar]

45. A. Beimel, S. P. Kasiviswanathan and K. Nissim, “Bounds on the sample complexity for private learning and private data release,” in Theory of Cryptography Conf., Berlin, Heidelberg, Springer, pp. 437–454, 2010. [Google Scholar]