RLAT: Lightweight Transformer for High-Resolution Range Profile Sequence Recognition

1  Introduction

Radar Automatic Target Recognition (RATR) has been widely applied to military and civilian domains. Currently, radar high-resolution range profiles (HRRP) are commonly used in RATR due to the advantages of easy acquisition, convenient processing, and small storage space [1]. HRRP is the vector sum of target echoes along the radar line of sight direction, containing rich information on target structure characteristics and scattering point distribution, which has significant applications in the target recognition domain. Therefore, HRRP has been widely used in recognizing aircraft [2,3], ships [4], ballistic missiles [5,6], and military vehicles [7,8].

When the radar detects a moving target, it will move relative to the target to obtain the echo information at several azimuth angles, then HRRPs of consecutive azimuth angles constitute the HRRP sequence [9]. The dynamic temporal features of the target can be extracted effectively with the correlation in an HRRP sequence being modeled for efficient target recognition. Since the dimension of the HRRP sequence is large and there is a large number of noisy regions hidden in HRRP, HRRP sequence recognition is a peculiar class of multivariate time series classification problem. However, existing methods for the HRRP recognition method have limited perception ability of global information and weak representation ability of target information [7], which leads to susceptibility to the noise region and poor recognition performance in real scenes. Therefore, feature enhancement and feature extraction of global information are pivotal issues to improve the recognition performance of HRRP sequences further.

Traditional HRRP sequence recognition methods rely on the manual extraction of features with high discriminability. For example, Timothy et al. [10] proposed a recognition method based on Hidden Markov Model (HMM), which extracted six power spectrum features from high-resolution (HRR) radar signal amplitude vs. target distance profiles using HMM. Du et al. [11] proposed a recognition method based on a double-distribution composite statistical model based on the dominant scattering in the range cell of the scattering center model. The range units are divided into three statistical types based on the number of dominant scattering points in the scattering center model’s range units. The echoes of different types of range units are modeled as corresponding distribution forms to accomplish the recognition task. Molchanov et al. [12] proposed a recognition method based on micro-Doppler bicoherence features, which extracts the cepstrum coefficients from the micro-Doppler contributions in radar echoes, then calculates the classification features using bicoherence estimation. However, the manually extracted features are susceptible to the influence of subjective factors and have limited recognition performance because of the weak extraction of representative features.

To overcome the limitations of manual feature extraction, machine learning is introduced into HRRP recognition. Lei et al. [13] proposed a Support Vector Machine (SVM) based recognition method, which defines different classifier confidence levels based on the distance between classifiers given by the confusion matrix, and then integrates the support vector machine values and posterior probabilities into the basic probability assignment to achieve a support vector machine and evidence theory combined with the recognition method. Wang et al. [5] proposed an extreme learning autoencoder (1D ELM-LRF-AE) network based on one-dimensional local perceptual domains for meaningful representation learning of HRRP local structures to achieve efficient representation learning and recognition. The above method overcomes the negative effects of subjective factors of researchers and achieves more effective automatic feature extraction but ignores the correlation and temporal information among HRRPs, which causes significant information loss. Besides, the machine learning method is weak in extracting deep features. Thus, the recognition performance still needs to be improved.

Along with the development of deep learning, Convolutional Neural Networks (CNN) and Recurrent Neural Networks (RNN) are massively applied to HRRP recognition. For example, Xiang et al. [14] proposed a recognition method based on one-dimensional CNN (1D-CNN), which extracts the effective target structure information in HRRP by 1D-CNN and introduces aggregation-perception-recalibration for feature enhancement. Though CNN can effectively extract the local correlation of HRRP sequences, it ignores the temporal information between HRRP sequences. There are limitations to global feature extraction of long sequences since the size of the convolutional kernel limits CNN. In particular, the HRRP sequences in real scenes contain much noisy information, and the local information will harm the generalization of the model due to the influence of noise. Du et al. [15] proposed a recognition method based on a Region-factorized recurrent attentional network with deep clustering, which utilizes the time dependence of recurrent neural network (RNN) in HRRP samples. The clustering mechanism is used to find information regions automatically, weighting the different recognition contributions of the hidden states at each time step. However, RNNs lose important target features when extracting long-range information for long sequences due to the memory loss problem. The essential original information may be lost when the network is stacked deeply. To further enhance the extraction of global information, Pan et al. [16] proposed a recognition method based on CNN-Bi-RNN with Attention Mechanism, which uses convolutional neural networks to obtain a richer embedding representation, and then uses RNN based on Attention Mechanism to extract temporal information, which can use local and global temporal features more effectively, and still maintain high recognition performance for limited samples. With the emergence of the Transformer framework, the long-range information of sequences is modeled by the self-attention mechanism, which adaptively assigns different weights to sequences by calculating the correlation between sequences, paying more attention to the important information of the target region and effectively extracting the global information of sequences. Zhang et al. [17] proposed a recognition method based on a feature-guided Transformer, which effectively enhances the extraction of global information by adding manual features in the attention module and guiding the model to focus on range units with more scattered information, and reduces the dependence on the model on the number of samples. However, the selection of manual features is influenced by human subjective factors and needs further optimization. Diao et al. [18] proposed a recognition method based on Position Embedding-Free Transformer for Radar HRRP Target Recognition, which extracts multiscale information with different weights by combining multiscale convolution with a self-attention mechanism; thus more information and distinguishable features are extracted for recognition. The introduction of multiscale convolution before the self-attention mechanism enables more efficient pre-extraction of multiscale features, but causes a greater computational effort. Although Transformer can achieve better recognition performance, the huge number of model parameters and over-dependence on samples limit its application in edge devices and real scenes.

To achieve a more lightweight and robust recognition method, which facilitates the deployment of real scenes and edge devices. This paper proposes a lightweight HRRP sequence recognition method based on RLAT, which consists of rotary position encoding, local-aggregated attention unit (LAU), and lightweight feedforward neural network (LW-FFN). The method proposed utilizes rotated position encoding to embed relative position information more efficiently. Then, this paper proposes a lightweight local-aggregated attention unit (LAU) to perform local feature aggregation and global perception operations on high-dimensional HRRP sequence data. Feature aggregation can suppress the adverse effects of noise regions, get richer local feature representation, and reduce the number of parameters effectively. Thereby, by putting the aggregated low-dimensional features into the self-attention mechanism, the self-attention mechanism can achieve global information perception and enhancement, which extracts the long-range correlations of HRRP sequences in time and space domains, effectively enhances the extraction ability of important information in the target region and gets highly distinguishable deep temporal features in HRRP sequences. Besides, the information loss problem of deep networks is also solved through residual connection. Moreover, feature extraction is achieved by LW-FFN, which dramatically reduces the number of parameters compared with the traditional FFN. Finally, Label Smoothing is utilized to introduce label noise to avoid over-reliance of the model on limited training data and enhance the generalization of the proposed method in real scenes. Experiments on MSTAR datasets show that the proposed method improves the recognition performance significantly by effectively reducing the number of parameters and achieves better robustness in both variant targets and limited training data experiments.

The main contribution of this paper is as follows:

(1)   Considering the generalization performance and the lightweight of the method, this paper proposes a novel method named RLAT. RLAT consists of Rotary position encoding, LAU, and LW-FFN, which greatly reduces the number of parameters and computational effort by utilizing lightweight modules. In addition, RLAT can represent the relative position information more effectively and deepen the model depth dynamically, which can extract more essential and abstract features.

(2)   To alleviate the reliance on training samples and eliminate the undesirable effect of causing redundant information in HRRP sequences. Label smoothing regularization is adopted to add label noise, which can enhance the tolerance to training loss and the generalization of the method.

(3)   This paper validates the effectiveness and generalization of the proposed method on real-world datasets, including for variant targets and limited sample conditions; the results illustrate that RLAT has remarkable recognition performance and generalization performance for variant samples and limited samples. Besides, the performance of various position encoding methods and significant hyperparameters in the HRRP sequence task are also explored.

This paper is organized as follows. Section 2 introduces the overall framework of the proposed method and describes the critical detail parts of the method. Section 3 first introduces the construction method of the MSTAR sequence dataset, then verifies the proposed method’s effectiveness in real scenes, including variant targets, limited data, and the impact of hyperparameter experiments. Furthermore, comparison experiments verify the proposed method to be more lightweight. Section 4 summarizes the work of this paper and presents the work objectives for the future.

2  Proposed Method

This section presents the overall framework of the proposed method, then introduces and analyzes the principles and details of the essential modules. The overall structure of RLAT is shown in Fig. 1.

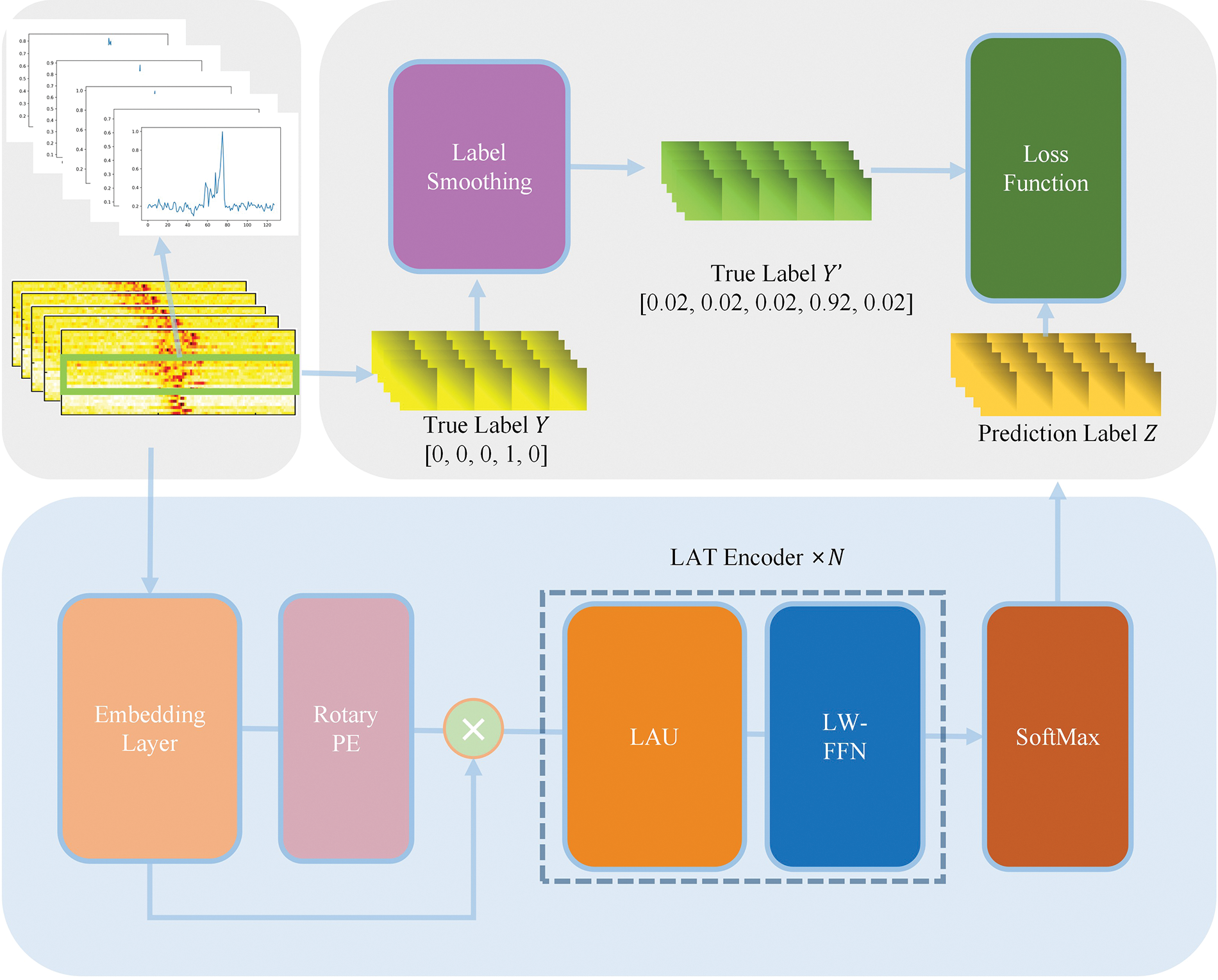
Figure 1: Illustration of the structure of the proposed RLAT

HRRP sequence recognition is a particular class of multivariate time series classification problem with high dimensionality, redundant noise information, and limited data. Therefore, suppressing the adverse effects of redundant information in noisy regions and extracting deep valid information and high separability features are essential to improve the performance of HRRP sequence recognition. In addition, existing methods for HRRP sequence recognition extract deep abstract features by stacking a large number of modules, mostly ignoring the problem of lightweight, which is unfavorable for application to real scenes and deployment to edge devices.

This paper proposes an HRRP sequence recognition method based on RLAT, which consists of rotary position encoding, local-aggregated attention unit (LAU), and lightweight feedforward neural network (LW-FFN). The feature extraction part of RLAT consists of stacked LAT Blocks, which are different from the Encoders of the traditional Transformer. LAT blocks can dynamically adjust the model depth using the adaptive model scaling mechanism. Consequently, the model depth can be dynamically scaled to make the model depth more adaptable to different feature extraction stages, effectively decreasing the number of parameters. Finally, SoftMax is utilized to calculate the probability of each target category achieving recognition.

As shown in Fig. 1, LAT Block is mainly composed of LAU and LW-FFN, where LAU is mainly used for feature enhancement, and LW-FFN is used for feature extraction. LAT Block has significant feature enhancement and feature extraction capabilities and dramatically reduces the number of parameters and computational effort through lightweight methods. To enhance the feature representation of HRRP, traditional deep learning methods introduce richer features by first raising the dimensionality. However, HRRP sequences contain a large amount of redundant noise, and raising the dimensionality often introduces more redundant features, which not only introduces a massive number of parameters but reduces the recognition ability of the model. The traditional group linear transformation uses the channel shuffle mechanism to enhance the global information extraction ability, but this paper discards the channel shuffle mechanism and inputs the aggregated low-dimensional features into the self-attention mechanism, which can complete the global information perception and enhancement. However, this paper discards the channel shuffle mechanism and inputs the aggregated low-dimensional features into the self-attention mechanism, which can perform global information perception and enhancement to obtain the deep temporal features with high distinguishability in HRRP sequences.

The training process of RLAT is shown in Algorithm 1.

2.1 Rotary Position Encoding

Convolutional neural networks and recurrent neural networks get the position information by processing the time series continuously. In contrast, Transformer is a network based on the self-attention mechanism, which is insensitive to position information and needs to add position coding to provide position information for time series. Currently, the commonly used position encoding mainly includes absolute position encoding and relative position encoding. Among them, absolute position encoding is simple to implement, and the number of parameters and computation is smaller. However, the encoded absolute position information is too simplified, which limits the representation of position information, resulting in poor performance in the recognition task. Literature [19] showed that the relevance of sequence data with closer positions is more substantial, thereby adding relative position information is more beneficial to extract the relevance of sequence information. To promote the utilization of relative position information between time series, literature [20] introduced relative position information between sequences in the attention mechanism. Although the performance is improved, the implementation process is complex, and the number of parameters and computations is larger. To achieve a more lightweight relative position encoding, this paper adopts rotary position encoding to add position information to HRRP sequences.

Assuming that the HRRP sequence is X=[x1,x2,…,xN], where N denotes the length of the sequence. The traditional absolute position encoding adds the position information after the embedding layer, which is calculated as

f(xi,i)=W(xi+pi),(1)

where i is the position of xi, and pi∈Rd is a trainable d-dimension position vector that depends on xi. Absolute position encoding adds mutually independent position information to the sequence data at each position, requiring a large amount of data training to perform better. Since HRRP sequences are usually non-cooperative target data with limited data, absolute position encoding will not be appropriate for solving the HRRP sequence recognition problem.

Relative position encoding is to add relative position information to the self-attention mechanism, which is calculated as

{fq(xm)=Wqxmfk(xn,n)=Wk(xn+pck)fv(xn,n)=Wv(xn+pcv),(2)

where fq(⋅),fk(⋅)andfv(⋅) denote the functions that compute the query, key, and value of the self-attention mechanism, respectively, which are used to calculate the correlation between series data, q,k,v represent query, key, and value of the self-attention mechanism, respectively. pck,pcv∈Rd are the relative position vectors, k and v represent key and value of the self-attention mechanism, respectively, the relative position vectors depend on the relative distance of positions, c=clip(m−n,rmin,rmax) represents the relative distance between the positions m and n, as the distance between the relative positions increases, the correlation between the data decreases, and the limit range of c is set as rmax, beyond which the correlation is considered consistent. xm,xn are the HRRPs of position and n, respectively. Wq,Wk,Wv are the learnable parameter matrixes of the self-attention mechanism, respectively.

In pursuit of lightweight relative position encoding, relative position encoding is implemented in the form of absolute position encoding. After adding to the position matrix, the process of the absolute position matrix in the self-attention mechanism is calculated as

qmTkn=xmTWqTWkxn+xmTWqTWkpn+pmTWqTWkxn+pmTWqTWkpn,(3)

The core concept of relative position encoding is to replace the absolute position vector pn embedded in the third and fourth terms with the relative position vector pm−n, and to replace the third and fourth terms with two trainable vectors uT and vT. Moreover, the parameter matrixes are replaced by Wk and Wk′ respectively to distinguish between content and position. So the method of calculating weights by the self-attention mechanism in the relative position encoding becomes

qmTkn=xmTWqTWkxn+xmTWqTWk′pm−n+uTWqTWkxn+vTWqTWk′pm−n.(4)

To fully use the relative position information in the HRRP sequence to extract the deep temporal information. This paper adopts rotary position encoding to improve the relative position encoding, which is a multiplicative encoding to achieve the relative position encoding utilizing absolute position encoding. The position encoding is calculated as

g(xm,m)=RΘ,mdWxm,(5)

where the rotary matrix is

RΘ,md=[cos⁡mθ1−sin⁡mθ100⋯00sin⁡mθ1cos⁡mθ100⋯0000cos⁡mθ2−sin⁡mθ2⋯0000sin⁡mθ2cos⁡mθ2⋯00⋮⋮⋮⋮⋱⋮⋮0000⋯cos⁡mθd/2sin⁡mθd/20000⋯sin⁡mθd/2cos⁡mθd/2],(6)

where Θ={θi=1100002(i−1)d,i∈[1,2,…,d/2]}, the calculation process of rotary position encoding in the self-attention mechanism is

qmTkn=(RΘ,mdWqxm)T(RΘ,ndWkxn)=xTWqRΘ,n−mdWkxn.(7)

The rotary position encoding utilizes a rotary matrix RΘ,n−md to introduce relative position information. The rotary position encoding avoids more learnable parameter matrices, which introduces relative position information in a more lightweight way.

2.2 Local-Aggregated Attention Unit

HRRP sequence is a particular class of multivariate time series containing rich temporal and structural information, which is widely used in RATR. However, operations such as adding windows during target detection make redundant information hidden in HRRP, which will adversely impact feature extraction and confuse effective target features. Augmenting attention to important regions of HRRP by using the attention mechanism can effectively suppress the undesirable effects of noisy regions [16] and improve the effectiveness of feature extraction. To enhance the feature enhancement and extraction of HRRP sequences, the local-aggregated attention unit is proposed. Unlike most methods that perform high-dimensional mapping of the input information, LAU downscales the input HRRP sequences, aggregating the features of local information by local group linear transformations. Then the aggregated low-dimensional features are globally perceived by the self-attention mechanism, which effectively enhances the global information extraction ability. Since the HRRP sequence contains a large amount of redundant noisy information, the shallow high-dimensional mapping will confuse the noisy information and the target information. Instead, this paper adopts multilayer local group linear transformations to perform local feature aggregation by first ascending and then descending the local features. Thus, the low-dimensional aggregated features are more easily processed by the self-attention mechanism, and the local feature aggregation can effectively improve the ability of the self-attention mechanism to focus on global information.

As shown in Fig. 2, LAU consists of local group linear transformations, nonlinear activation, layer normalization, self-attention mechanism, and residual connection. Feature enhancement is effectively performed by local feature aggregation and global perception. The encoded vector I=g(X) is used as the input of LAU, which performs local feature aggregation and global feature enhancement, then outputs the enhanced features F. In the local feature aggregation stage, assuming that there are total L layers of grouped linear transformations. The first layer is up-dimensioned, and the remaining L−⌈L/2⌉ layers are down-dimensioned. The specific procedure to calculate the number of groups in each layer is

nl={min(2l−1,nmax),1≤l≤⌈L/2⌉nL−l,Otherwise,(8)

where nl is the number of groups of the linear transformation of the l th layer, and nmax is the maximum value of the number of groups of the linear transformation of the group. The upper limit of the group value is set to avoid the number of groups being too large. The linear transformation of each layer is calculated as

Hl={G(I,Wl,bl,gl),l=1G(M(I,Hl−1),Wl,bl,gl),Otherwise,(9)

where M(⋅) denotes the operation, including residual connection, nonlinear activation function GELU, and layer normalization. Local feature aggregation can obtain deep local features via first up-dimensioning and then down-dimensioning the local features. Moreover, the residual connection is used to avoid the loss of original information in each layer of the local group linear transformation in the model deepening. Since the low-dimensional aggregated features are facilitated to be processed by the self-attention mechanism, the local feature aggregation can effectively enhance the ability of the self-attention mechanism to focus on global information. Finally, the low-dimensional aggregated features are used as the input of the self-attention mechanism for the global perception operation.

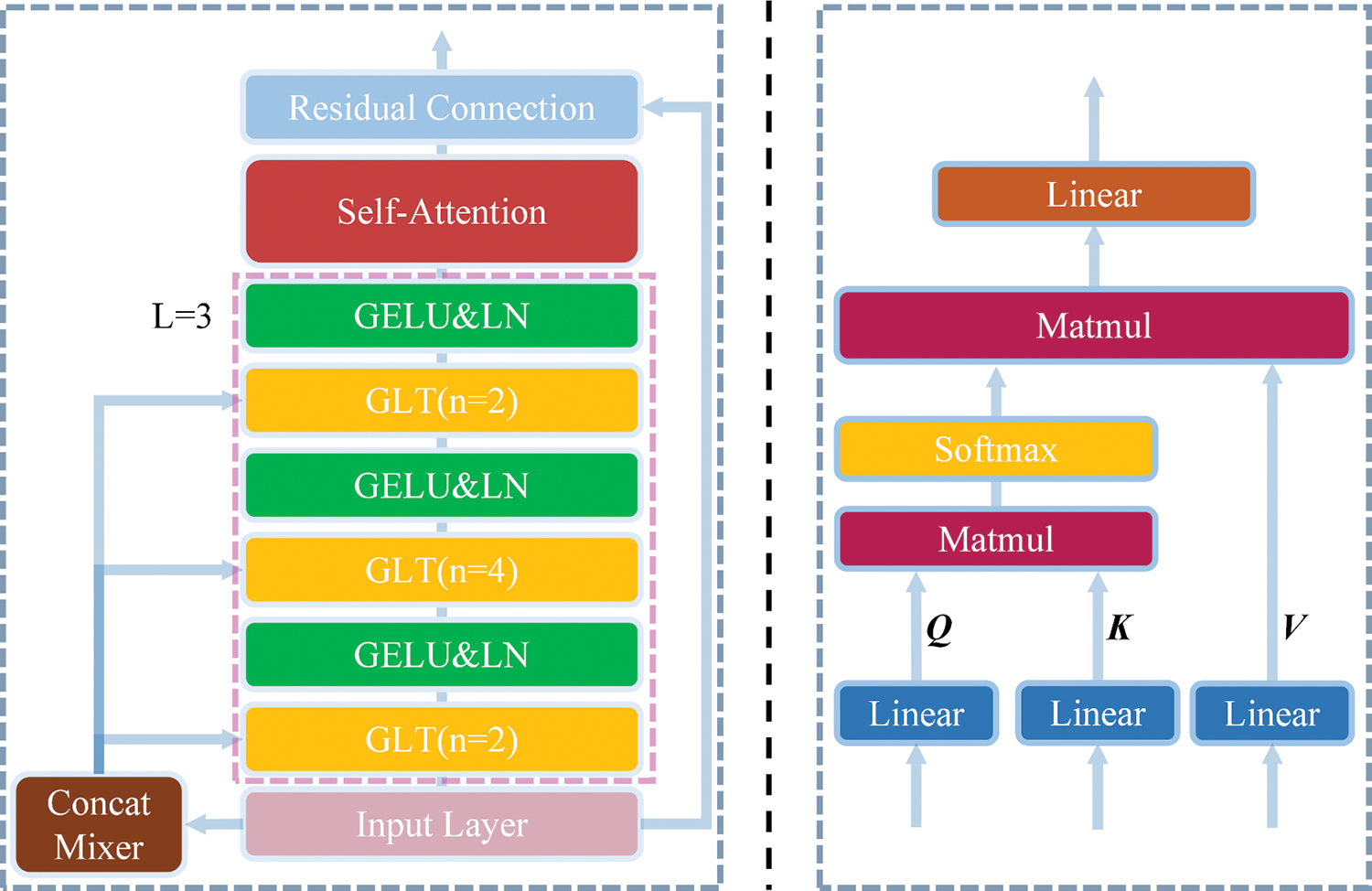
Figure 2: Illustration of the structure of LAU

The self-attention mechanism conducts long-range modeling by calculating correlations between HRRP data, which enhances target features with high discriminability and suppresses the undesirable effects of redundant noisy information, thus effectively performing global enhancement of features after local aggregation. According to the relevant principles of information retrieval, the self-attention mechanism calculates the correlation of sequence data by query vector and key vector to obtain the attention matrix and then calculates the globally enhanced features with the value matrix as

A=SA(HL)=Attention(Q,K,V)=softmax(QKTdk)V,(10)

where Q=YWQ is the query vector, K=YWK is the key vector, and V=YWV is the value vector, WQ,WK,WV are the learnable parameter matrixes Ws, respectively.

Finally, to ensure that the dimensionality of the input and output is consistent, the vector needs to be up-dimensioned first after the self-attention mechanism processing. At the same time, to avoid the loss of important features due to the excessive depth of the model, the residual connection is finally added to retain the vital information in the original features, which can be obtained as

F=I+WsA,(11)

where Ws is the parameter matrix for dimensioning the output of the self-attention mechanism.

2.3 Lightweight Feedforward Neural Network

LAU has a deeper network structure and more significant feature enhancement capability than the traditional multi-head attention mechanism. Therefore, this paper uses a lightweight feedforward neural network instead of the traditional feedforward neural network for feature extraction. Assuming that the dimensionality of the input features F is dm, the traditional FFN (as shown in the left panel of Fig. 3) adopts the way of first up-dimensioning to 4dm and then down-dimensioning to dm for feature extraction, which has a large number of parameters. Since LAU has a significant effect on feature enhancement, this paper adopts lightweight FFN (shown in the right panel of Fig. 3) for feature extraction, which consists of a fully connected layer, a nonlinear activation function, and a residual connection, and is mainly used for feature extraction. The lightweight FFN is first down-dimensioned to dm4, then up-dimensioned to dm. As for lightweight FFN, the total number of parameters is dm24×2=dm22 for both up- and down-dimensional processes, but the traditional FFN first up-dimensionalizing to 4dm and then down-dimensionalizing to dm, the total number of parameters is 4dm2×2=8dm2. Therefore, the lightweight FFN reduces the number of parameters by 16 times compared with the traditional FFN. The computational process of lightweight FFN for feature extraction is

Om=Feedforward(F)=F+((Relu(FW1+b1))W2+b2),(12)

where W1,b1 are the parameter matrix and bias vector at dimensionality reduction, respectively, W2,b2 are the parameter matrix and bias vector at dimensionality reduction, respectively, and Relu(⋅) are the nonlinear activation functions.

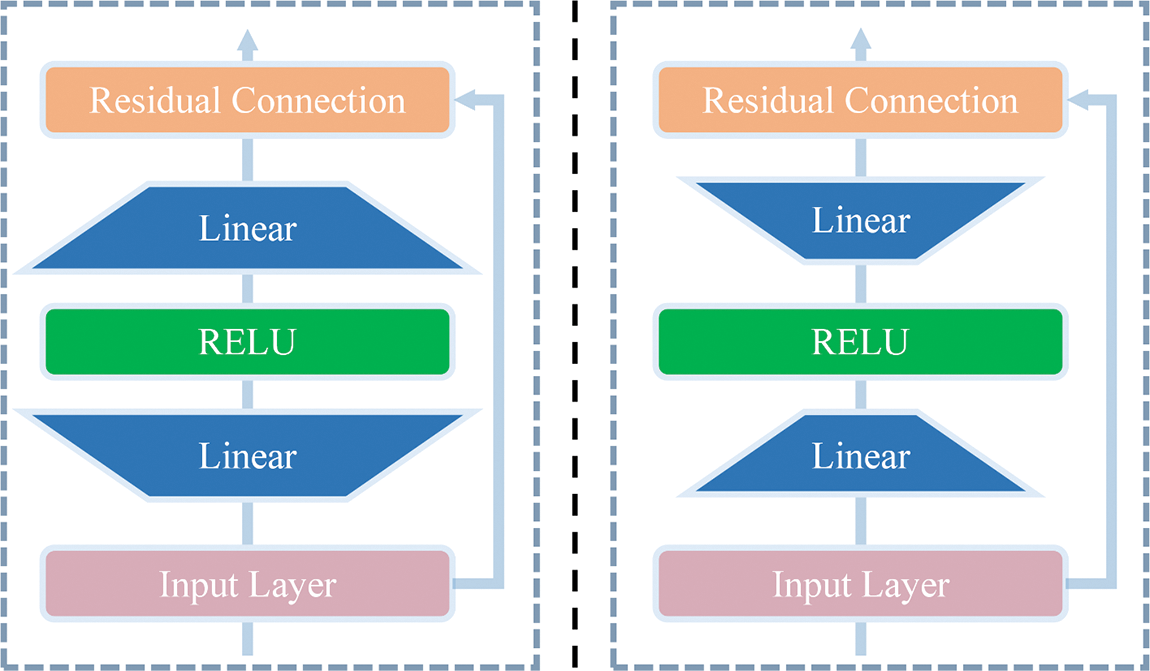
Figure 3: Illustration of the structure of LW-FFN

Following the stacked layer LAT blocks process, finally using SoftMax as the classifier, the output is

Y=SoftMax(OM)=exp⁡(oiM)∑k=1K⁡okM,(13)

where OM is the output of the LAT block at the M th layer, exp⁡(⋅) denotes the exponential function, and K is the total number of categories.

2.4 Label Smoothing Regularization

Against the background of non-cooperative targets, the current HRRP sequence samples are limited in quantities. Furthermore, the HRRPs in real scenes are in a complex noise environment, and there are still some differences in HRRPs of the same targets, which strongly leads to the overfitting problem in HRRP sequence recognition. To solve the overfitting problem, the Label Smoothing regularization strategy is adopted [21]. Label Smoothing adds label noise to avoid the model over-reliance on limited training samples and enhances the generalization performance of the proposed method for application in real scenes.

When coding the labels of the samples, the probability distribution of the traditional one-hot coding is

pi={1i=y0i≠y.(14)

To enhance the generalization performance of the model, one-hot coding is modified to soft one-hot coding to add fuzzy noise to the labels, thus reducing the weight of real sample labels in the computational loss. Consequently, the model will not be overly dependent on a limited number of samples, avoiding falling into local optimal solutions, which finally achieves suppression of the overfitting problem. Once Label Smoothing is added, the probability distribution of soft one-hot labels is

pi={(1−ε)i=yεK−1i≠y,(15)

where K denotes the total number of categories in the task, i denotes the number of categories, and ε is the hyperparameter.

When using the cross-entropy loss function to calculate the loss values between the predicted values and true values, the cross-entropy loss function is calculated as

Loss=−∑i=1Kpilog⁡qi,(16)

where pi is the probability of the true value, and qi is the probability of the predicted value.

The neural network will optimize the model in the direction of low loss value during the training process. However, over-reliance on the training set data will reduce the generalization performance of the recognition task of HRRP sequences in real scenes. The Label Smoothing regularization strategy will avoid overconfidence in the network, slow down the penalty intensity of the loss, and avoid the model falling into the local optimal solution, and its loss function for each category is calculated as

Lossi={(1−ε)⋅Lossi=yε⋅Lossi≠y,(17)

where ε is the hyperparameter. In the neural network training process, the optimal prediction probability distribution is obtained when minimizing the cross-entropy loss values of the predicted and true values, as

Zi={log(K−1)(1−ε)ε+αi=yαi≠y,(18)

where K denotes the total number of categories in the task, ε is a hyperparameter, and α is a real number.

As derived from the prediction probability distribution, Label Smoothing regularization can increase the tolerance to the existence of errors between the true values and predicted values. Consequently, Label Smoothing can prevent the model from over-relying on the training set samples, which can prevent the model from falling into local optimal solutions and enhance the generalization performance of the model.

3  Experiment Results and Analysis

3.1 Datasets

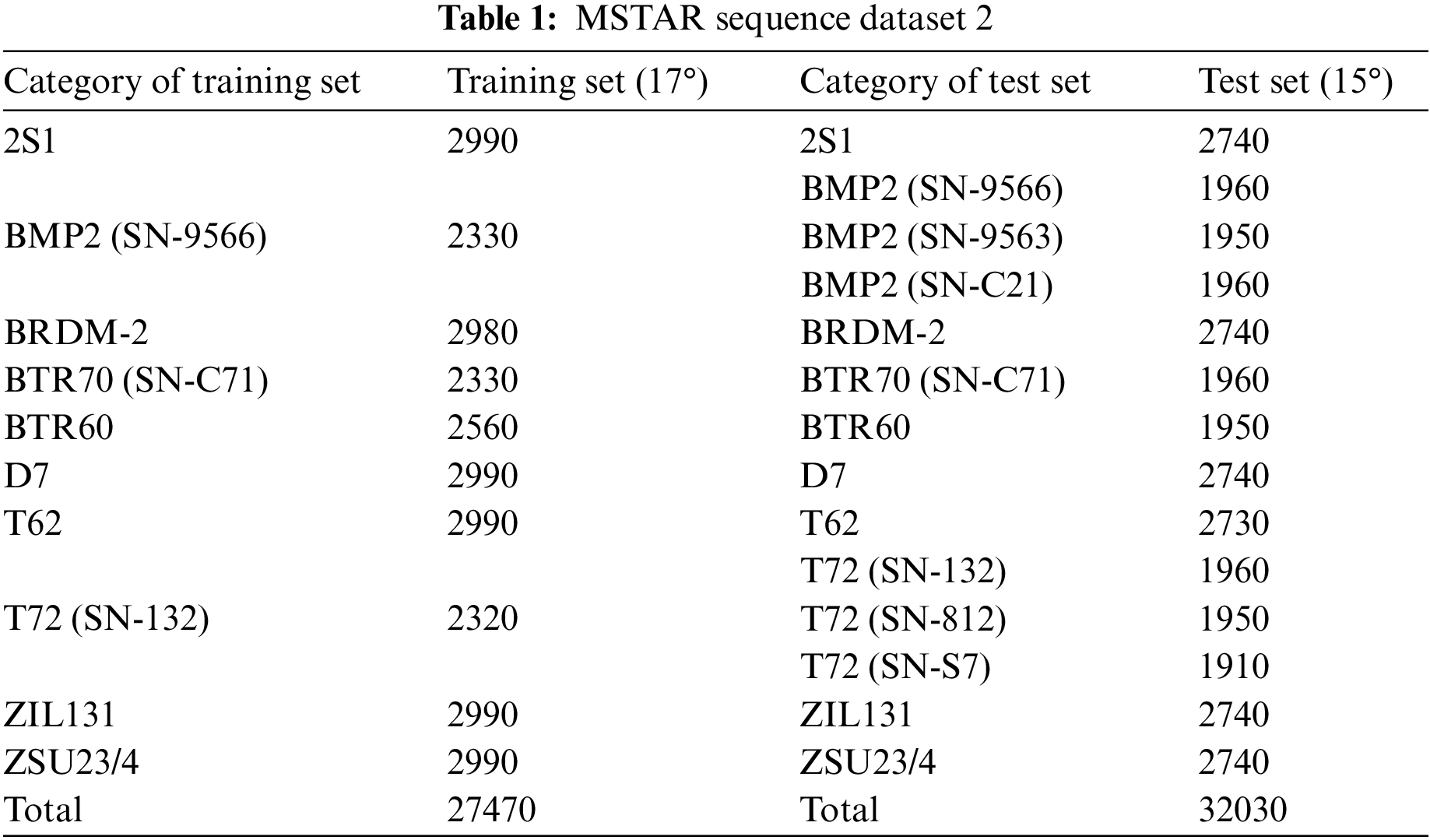
The MSTAR dataset is a standard dataset widely used for SAR target recognition [7,22,23]. Its data source is a high-resolution clustered synthetic aperture radar, which operates in the X-band with a resolution of 0.3 m × 0.3 m and HH polarization. The MSTAR dataset includes ten categories of targets, such as T72, BMP2, and BTR70. The data with a pitch angle of 17° in the dataset is used as the training set, and the data with a pitch angle of 15° are used as the test set. The azimuth angles of all targets cover 0∼360°. Dataset 1 includes the original MSTAR dataset training set of 2747 SAR images, and the test set includes 2348 SAR images. To further test the generalization performance of the model, this paper adds four variant targets of BMP2 (SN-9563), BMP2 (SN-C21), T72 (SN-812), and T72 (SN-S7) to the test set to make up dataset 2. Dataset 2 includes 2747 SAR images in the training set of the original MSTAR dataset and 3203 SAR images in the test set. In this paper, SAR images are converted into HRRP sequences according to the method specified in reference [24], and the MSTAR sequence dataset 2 is composed as shown in Table 1.

The conversion steps are as follows: The dataset is first converted into a complex SAR image, and then an Inverse Fast Fourier Transform (IFFT) is carried out in the orientation dimension of the complex SAR image, and the data obtained along the distance dimension is the HRRP complex sequence. Then the HRRP sequence is obtained after modulo the HRRP complex sequence. 100 HRRP samples could be obtained for each complex SAR image, and the average of every 10 HRRPs can be obtained as 10 average HRRP samples. Consequently, the training set of the original MSTAR dataset includes 24,270 HRRP samples, and the test set includes 32,030 HRRP samples.

Assuming that the length of the generated HRRP sequence is L(L≤50), the sliding window algorithm for generating the HRRP sequence is shown in Algorithm 2.

Use the sliding window algorithm to process HRRP data according to the steps shown in Fig. 4.

Figure 4: Schematic diagram of HRRP sequence generation

As can be seen from Fig. 4, the azimuth angle of 360° is divided into 50 azimuth blocks, and each block contains 7.2°, in which the sampling interval of each SAR image is 1°, and each SAR image can be processed, and ten average HRRP samples are obtained, so the sampling interval of each average HRRP sample is 0.1°. In previous research, denoised and enhanced samples are used as input for the model, which leads to a poor generalization of the model. In this paper, only the HRRP data are energy normalized. In real scenes, data of individual angles are often missing due to aircraft motion. Therefore, the dataset did not interpolate the missing data in the MSTAR dataset, which makes the data more consistent with the real situation.

After processing by the sliding window method, this paper gets 24,270 HRRP sequence samples in the training set and 23,480 HRRP sequence samples in the test set from dataset 1; get 24,270 HRRP sequence samples in the training set and 32,030 HRRP sequence samples in the test set from dataset 2.

The HRRP sequence samples of some targets are shown in Figs. 5a–5h are the corresponding HRRPs, respectively. It can be seen that MSTAR, as a real-world dataset, sample contains a large amount of noisy redundant information, which causes greater difficulties and challenges for effective feature extraction during recognition.

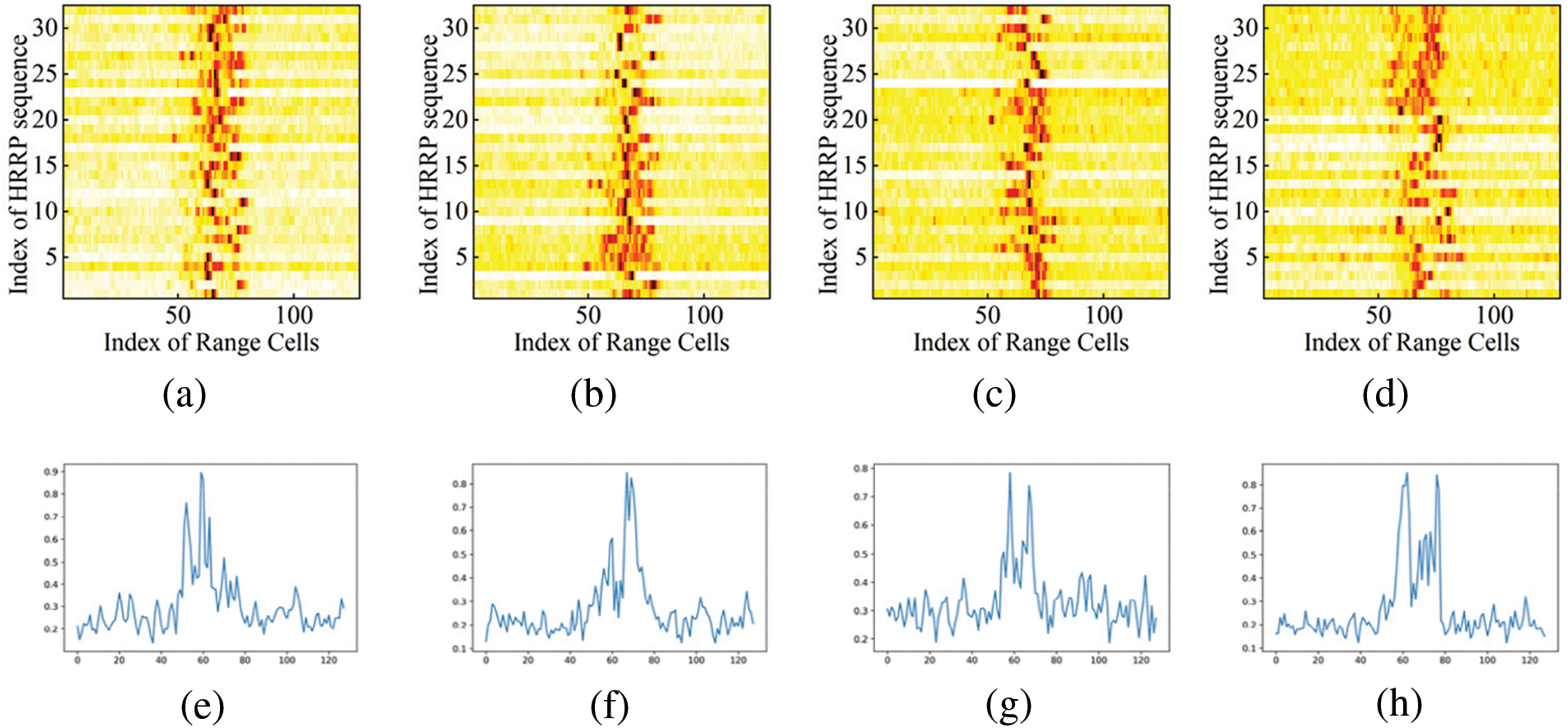
Figure 5: Part of samples of MSTAR datasets

3.2 Recognition Performance Comparison Experiments

To verify the recognition performance of the proposed methods, seven frequently used baseline methods, LSTM [25], GRU [26], 1D-CNN [14], TCN [27], gMLP [28], XCM [29], and Transformer [30], are selected as comparison methods in this paper. Moreover, the model architecture and parameters for the comparison experiments were designed according to the references to achieve optimal model performance. The recognition performance of each method is verified in MSTAR dataset 1, and the recognition results of the comparison experiments on ten categories of targets are shown in Table 2.

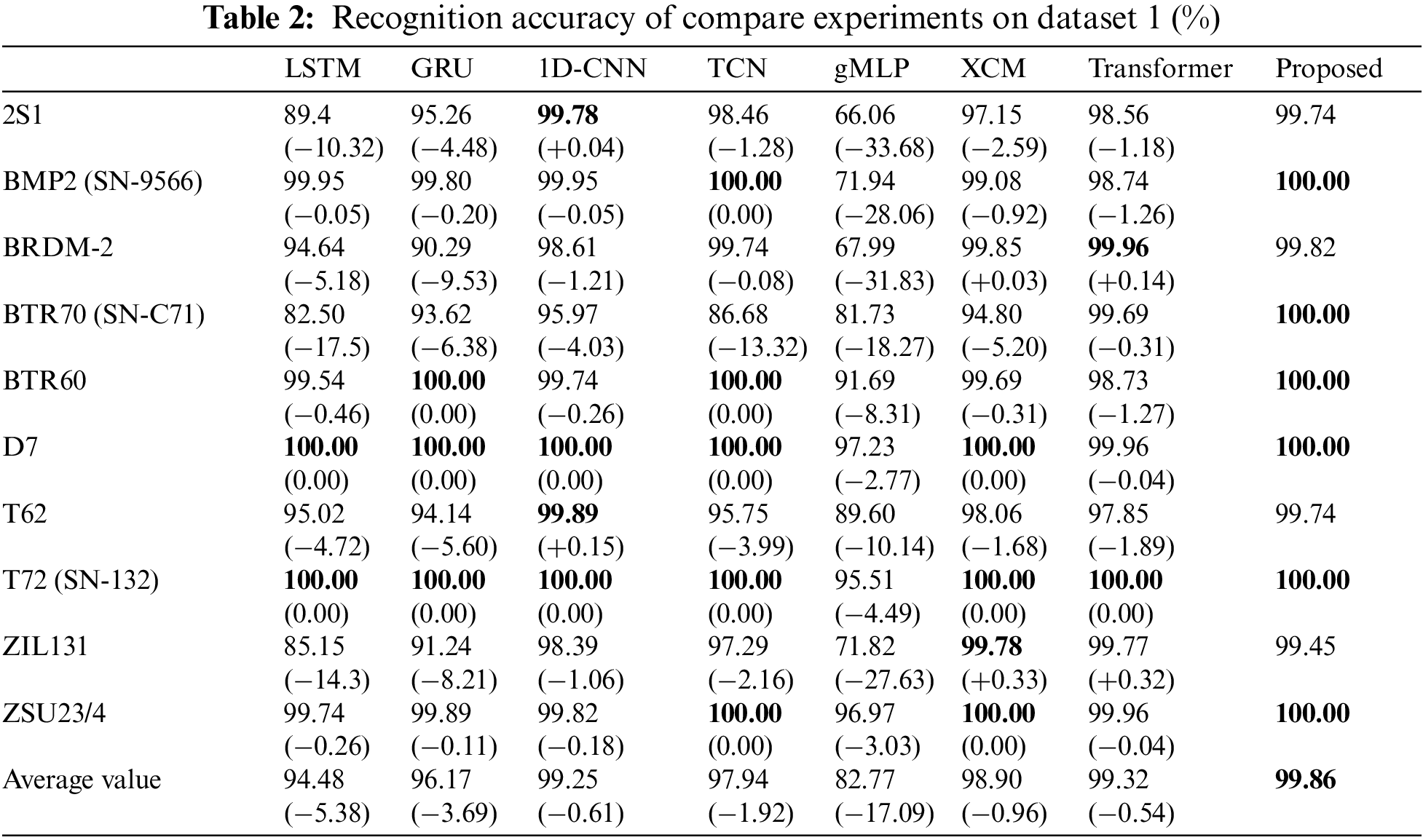
As shown in Table 2, the average accuracy of the RLAT proposed in this paper is the highest for ten categories of target recognition, reaching 99.86%, which is 17.09% better than the gMLP, more than 3.69% better than the commonly used recurrent neural networks LSTM and GRU, 0.61% and 1.92% better than the remarkable performance of convolutional neural networks 1D-CNN and TCN, respectively, 0.96% better than XCM, 0.54% better than Transformer with the same network structure. Besides, the proposed RLAT achieves optimal recognition performance on six targets, TCN achieves optimal performance on five targets, and other methods are less than five, reflecting that the proposed method is more stable than others. The experimental results show that the recognition performance of the Transformer and this work are higher than other methods, which indicates that the long-range modeling information using Transformer can mine the long-range temporal information and represent the features of HRRP sequences more effectively. In addition, RLAT has powerful local feature extraction and global perception capabilities, which can extract the local and global multi-level information between sequences more efficiently than the traditional Transformer, thus achieving the highest recognition performance.

As shown in Fig. 6, the proposed method has a more stable and balanced recognition performance for ten categories of targets, and all other methods have certain recognition shortcomings. In particular, the recognition performance of gMLP and LSTM is very volatile, with a fluctuation range of 31.17% and 17.50%, the fluctuation range of GRU is 9.71%, the fluctuation range of 1D-CNN and TCN is 4.03% and 13.32%, the fluctuation range of XCM is 5.20%, and the fluctuation range of Transformer is 2.15%, respectively. In comparison, the maximum fluctuation range of the proposed method is less than 0.55%. The results illustrate the effectiveness of the RLAT, which can suppress the adverse effects of noisy information and effectively extract highly distinguishable target features.

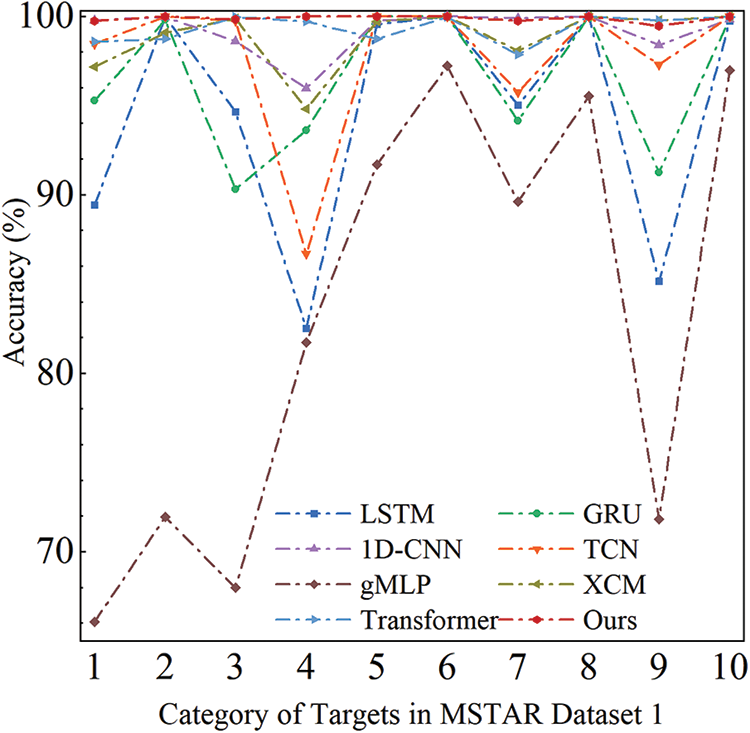
Figure 6: Accuracy of 10 targets in MSTAR dataset 1; the numbers on the x-axis represent ten targets in dataset 1, respectively

3.3 Robustness Comparison Experiments

For real-world application scenes, HRRP data usually come from non-cooperative targets, which usually contain variant versions, resulting in the shape configurations of the variant targets being different from those of the original targets. The recognition performance of the variant targets is an essential factor in measuring the method’s robustness. The robustness of the proposed method on the variant dataset is verified by setting up comparison experiments on the dataset MSTAR dataset 2. Dataset 2 is unchanged compared with the training set of Dataset 1, but about 36% of variant samples are added in the test set, which is mainly distributed on the BMP2 and T72 targets, constituting an unbalanced dataset simultaneously. The experimental results are shown in Table 3.

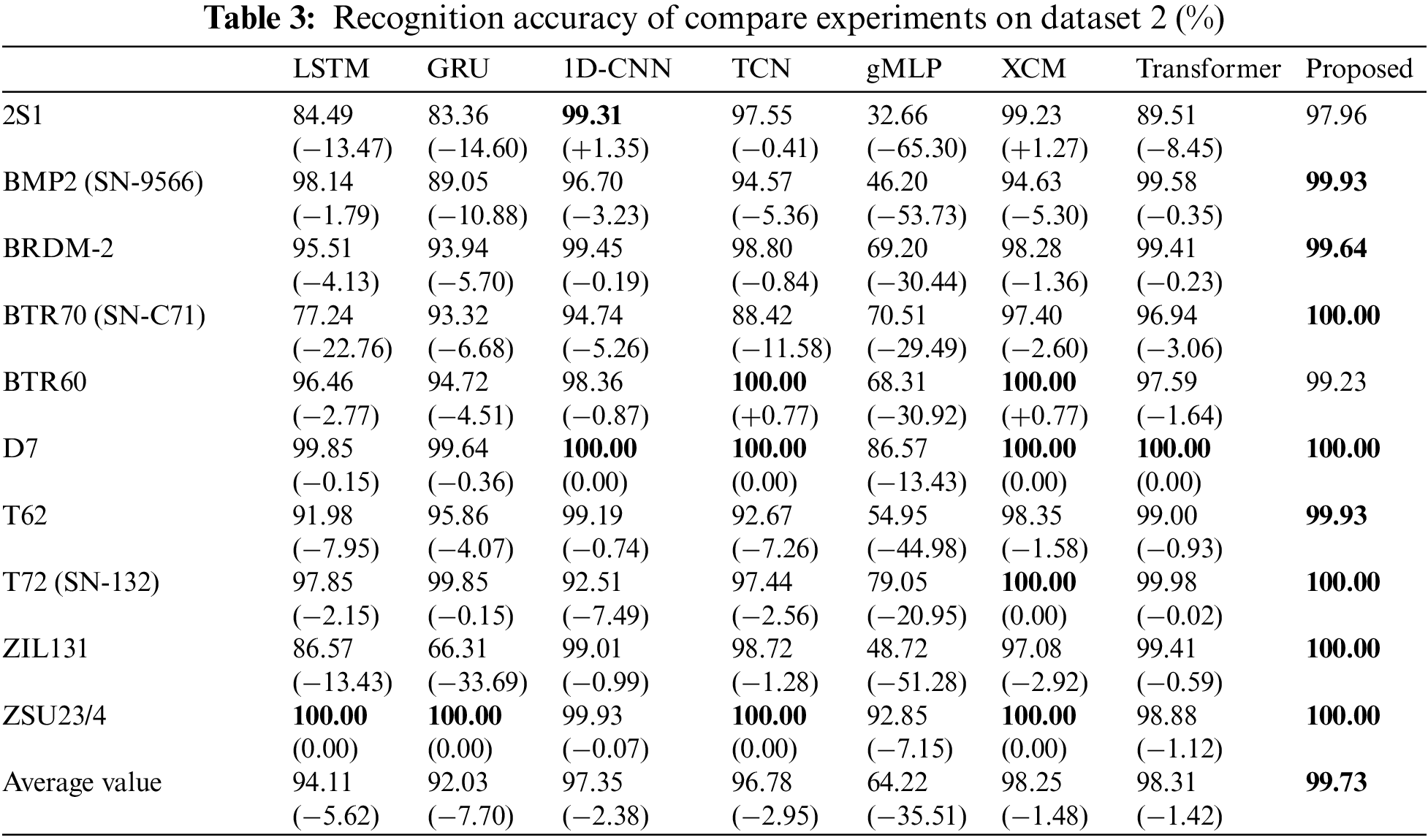
As shown in Table 3, the recognition accuracy of each method decreases due to the increased variant samples and the higher generalization performance required for the model. Nevertheless, the proposed method still achieves the highest average recognition accuracy of 99.73%, which is only 0.13% lower compared to dataset 1. gMLP decreases by 18.55%, LSTM, and GRU by 0.37% and 4.14%, 1D-CNN, and TCN by 1.90% and 1.16%, respectively, and Transformer by 1.01%. At the same time, RLAT is 35.51% better than the gMLP, more than 5.62% better than the commonly used recurrent neural networks LSTM and GRU, 2.38% and 2.95% better than the remarkable performance of convolutional neural networks 1D-CNN and TCN, respectively, 1.48% better than XCM, 1.42% better than Transformer with the same network structure. In addition, the proposed RLAT achieves optimal recognition performance on eight targets, while all other compared methods are less than 4, which is even superior to dataset 1. RLAT has long-range modeling capabilities and dynamically deepens the model depth by LAU, enabling the extraction of more essential and abstract features. Therefore, RLAT shows more remarkable stability on the variant dataset, which has a stronger generalization performance than other methods.

As shown in Fig. 7, the recognition performance of RLAT for the variant dataset is more stable and balanced, with a maximum fluctuation range of only 2.04%. In comparison, the fluctuation ranges of the comparison methods LSTM and GRU are 22.76% and 16.64%, 1D-CNN and TCN are 5.37% and 10.49%, Transformer is 7.49%, XCM is 11.58%, and gMLP is 60.19%, respectively. The results illustrate that the global temporal features extracted by RLAT are more robust, stable, and distinguishable, as well as Label Smoothing can avoid over-reliance on training samples and further improve the generalization performance to variant samples.

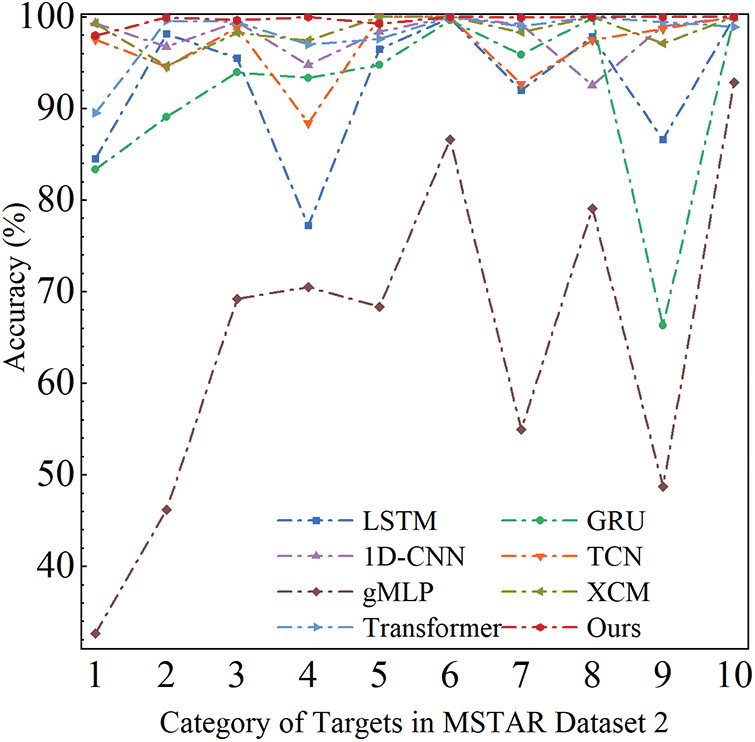
Figure 7: Accuracy of 10 targets in MSTAR dataset 2; the numbers on the x-axis represent 10 targets in dataset 1, respectively

3.4 Lightweight Comparison Experiments

RLAT achieves remarkable recognition performance in both the MSTAR standard dataset D 1 and the variant dataset D 2. To verify the lightweight of the proposed method, the number of parameters and the computational effort for comparing the various methods are shown in Table 4.

As shown in Table 4, the proposed RLAT achieves significant lightweight in terms of the number of parameters and computation, with 90.90% reduction in the number of parameters and 96.70% reduction in the computation compared to the Vanilla Transformer. Since RLAT uses the LAU module, the number of parameters and computations is significantly reduced while ensuring recognition performance. Excluding GRU, the number of parameters of RLAT is smaller than other comparable models, and the computation of the proposed method is smaller than other comparable models. In particular, the results show that the computation of 1D-CNN and XCM is severely increased due to the introduction of convolutional neural networks. As shown in Fig. 8, RLAT achieves better recognition performance under the premise of a more lightweight network structure, which illustrates that RLAT is more favorable for edge devices and real-world application deployment. As shown in Fig. 8, the relationship between accuracy, number of parameters and computation can be more intuitively obtained. The experimental results show that RLAT achieves better recognition performance with a smaller number of parameters and computations.

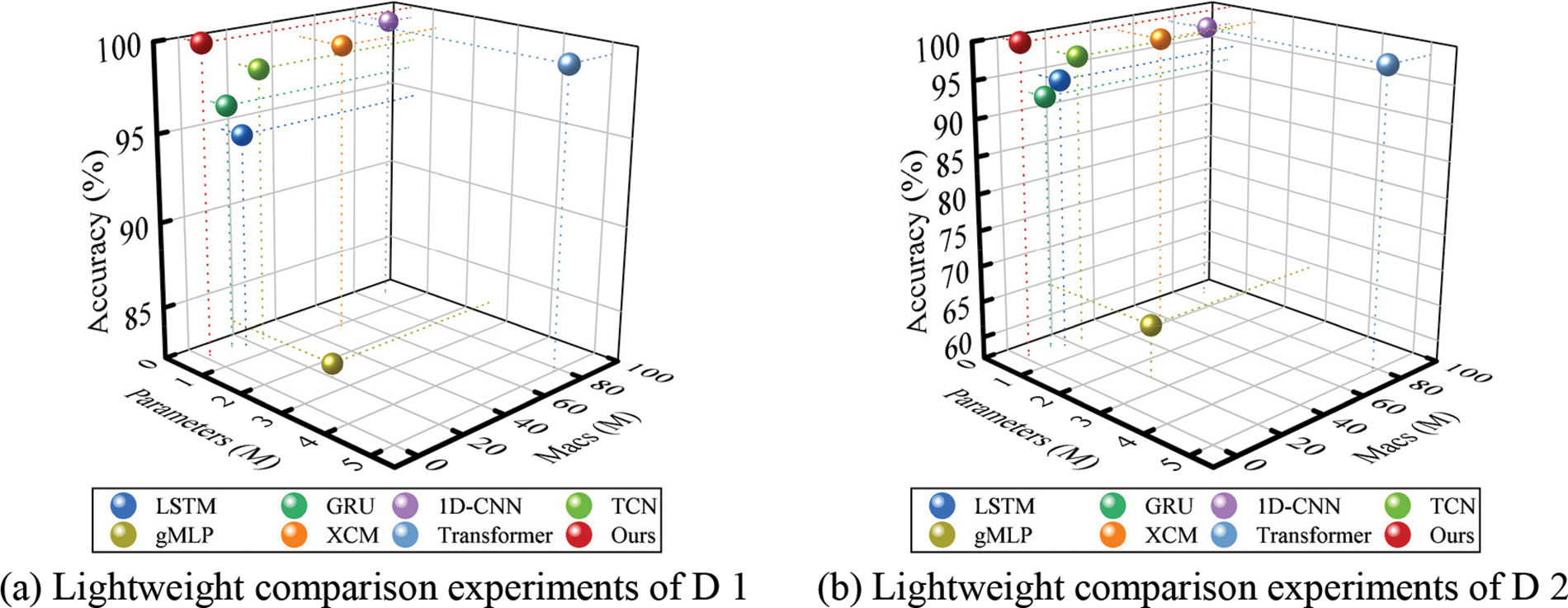
Figure 8: The result of lightweight comparison experiments

3.5 Limited Sample Comparison Experiments

HRRP sequence recognition under limited samples is one of the significant challenges currently. Recognition performance for limited samples is verified for the sequence length of HRRP sequences and the number of training samples. The limited sequence length can improve the real-time performance of the recognition, which achieves the target recognition several times earlier according to the demand. Then, the limited training samples can effectively verify the generalization performance of the model under the non-cooperative target conditions, which can effectively reduce the training time. At the same time, limited samples mean less target information, which has higher expectations on the feature extraction ability of the model. Comparison experiments are set up to verify the recognition performance of the proposed method under the limited sample condition using limited-length HRRP sequence samples and limited training samples. HRRP sequence generation algorithm is used for the generation of datasets, the length of the HRRP sequence is set as {1,2,4,8,16}, and the rate of training samples is set as {1%,2%,5%,10%,50%,90%}, respectively. The following abbreviates MSTAR dataset 1 as D 1 and MSTAR dataset 2 as D 2. The severe experimental conditions are set to verify the recognition performance of the proposed method under the limited sample conditions, and the experimental results are shown in Tables 5 and 6.

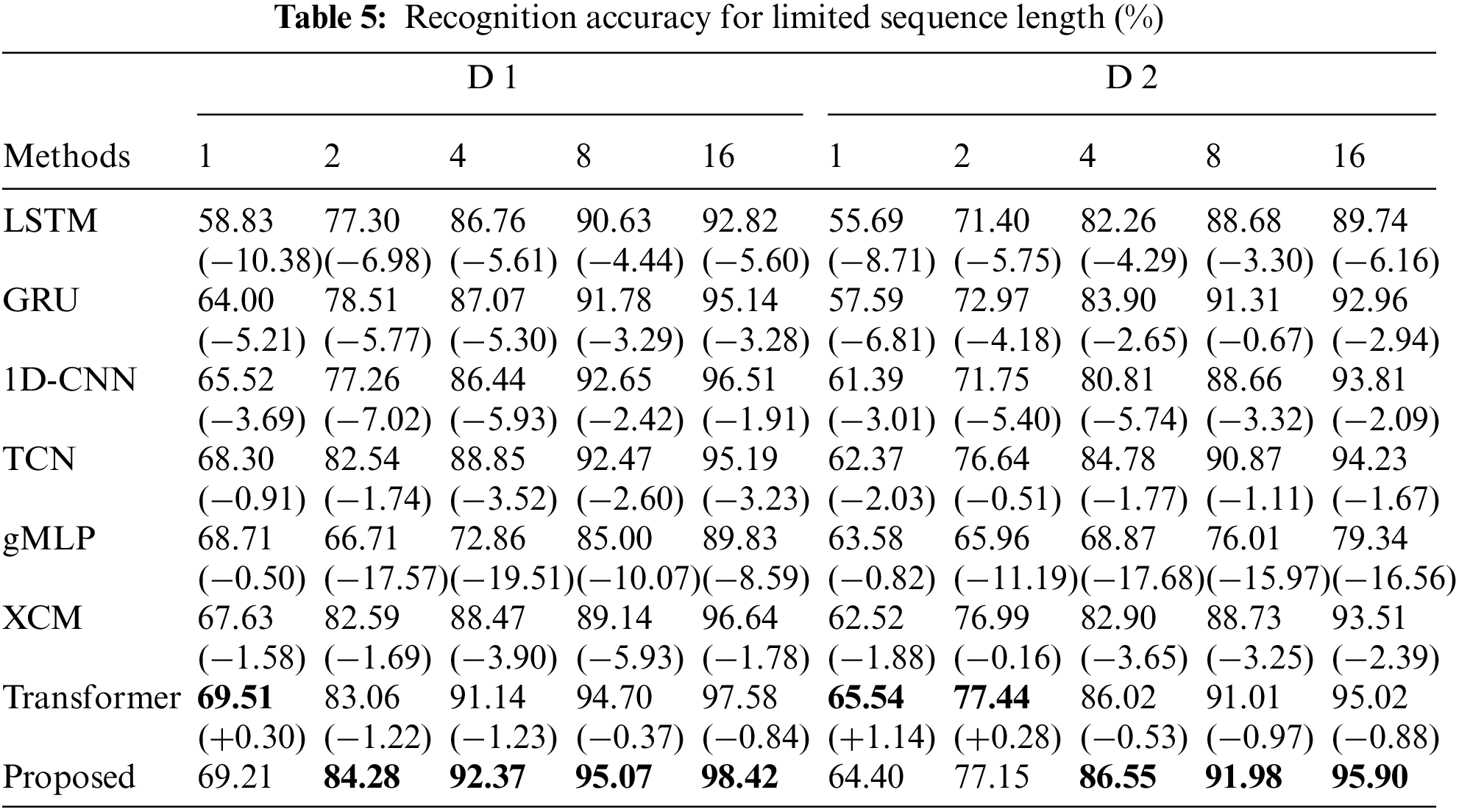
As shown in Table 5 and Fig. 9, the recognition accuracy of HRRP sequences increases with sequence length. The proposed method performs more remarkably than other comparative experiments on most short sequences. The recognition performance of RLAT outperforms the methods except for the Transformer in both the standard dataset D 1 and the variant dataset D 2, which illustrates that the Transformer-based methods utilize the long-range modeling capability to effectively extract valid target information from short HRRP sequences and reduce the adverse effects of noisy redundant information. Since Transformer has a more complex model structure than RLAT and sequences with lengths 1 and 2 contain less information, the recognition performance is slightly higher for D 1 with sequence length 1 and for D 2 dataset with sequence lengths 1 and 2. As the sequence length increases, RLAT can perform feature selection more effectively and discard the adverse effects of redundant information hidden in HRRP sequences, which can achieve more significant recognition performance than Transformer. To present the results of the comparison experiments more visually, the comparison experiments with limited sequence length are shown in Fig. 9.

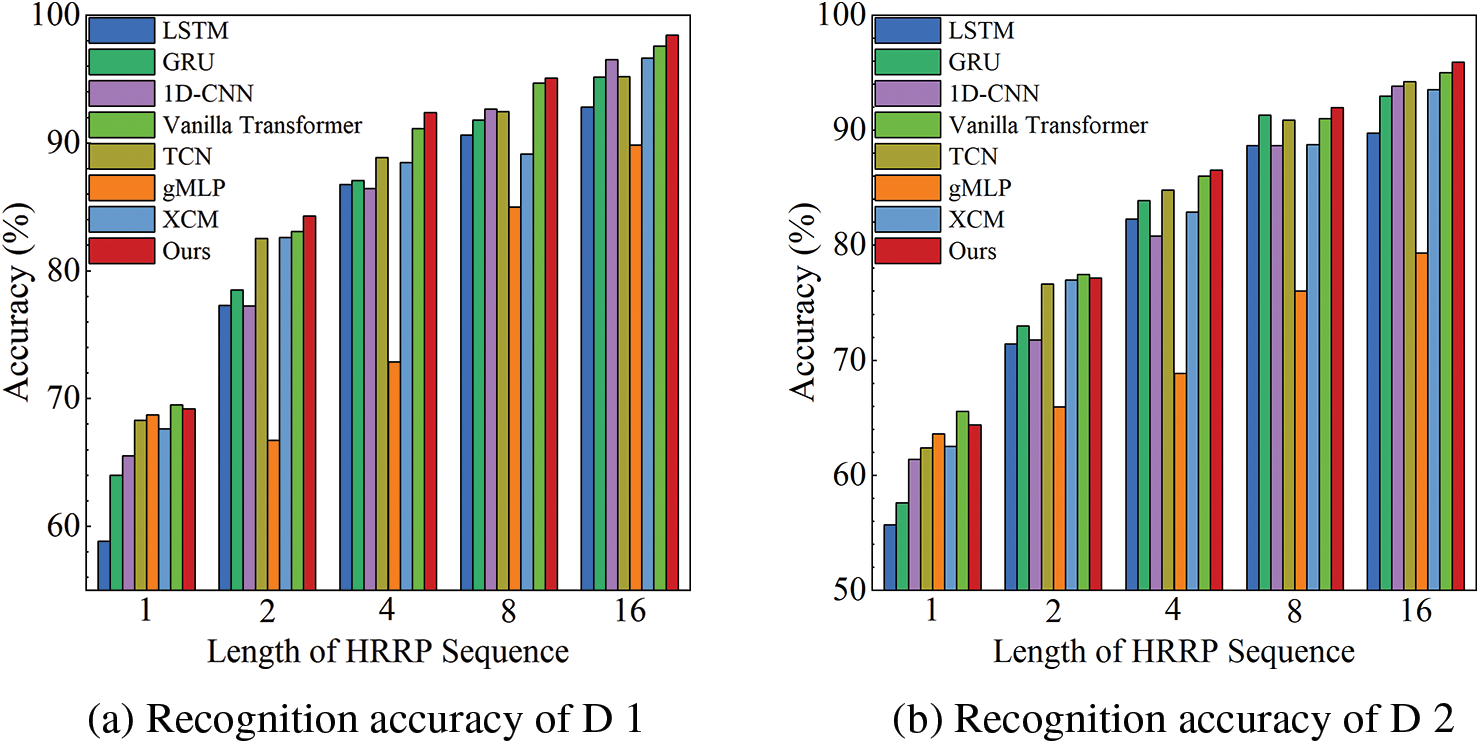
Figure 9: Recognition accuracy for limited sequence length of different methods

The Transformer relies on a large number of training samples to improve the recognition performance, which severely constrains the application of the Transformer in the field of HRRP recognition. In contrast, the feature enhancement and feature extraction capabilities of the RLAT are more remarkable and can effectively improve the recognition performance for limited training samples. To verify the recognition performance of the proposed method under the condition of limited training samples, the sequence length is set as 32, and the number of training samples is kept at {1%,2%,5%,10%,50%,90%}, respectively, where 1% of the original training set contains only 274 training samples, and the recognition performance is shown in Table 6.

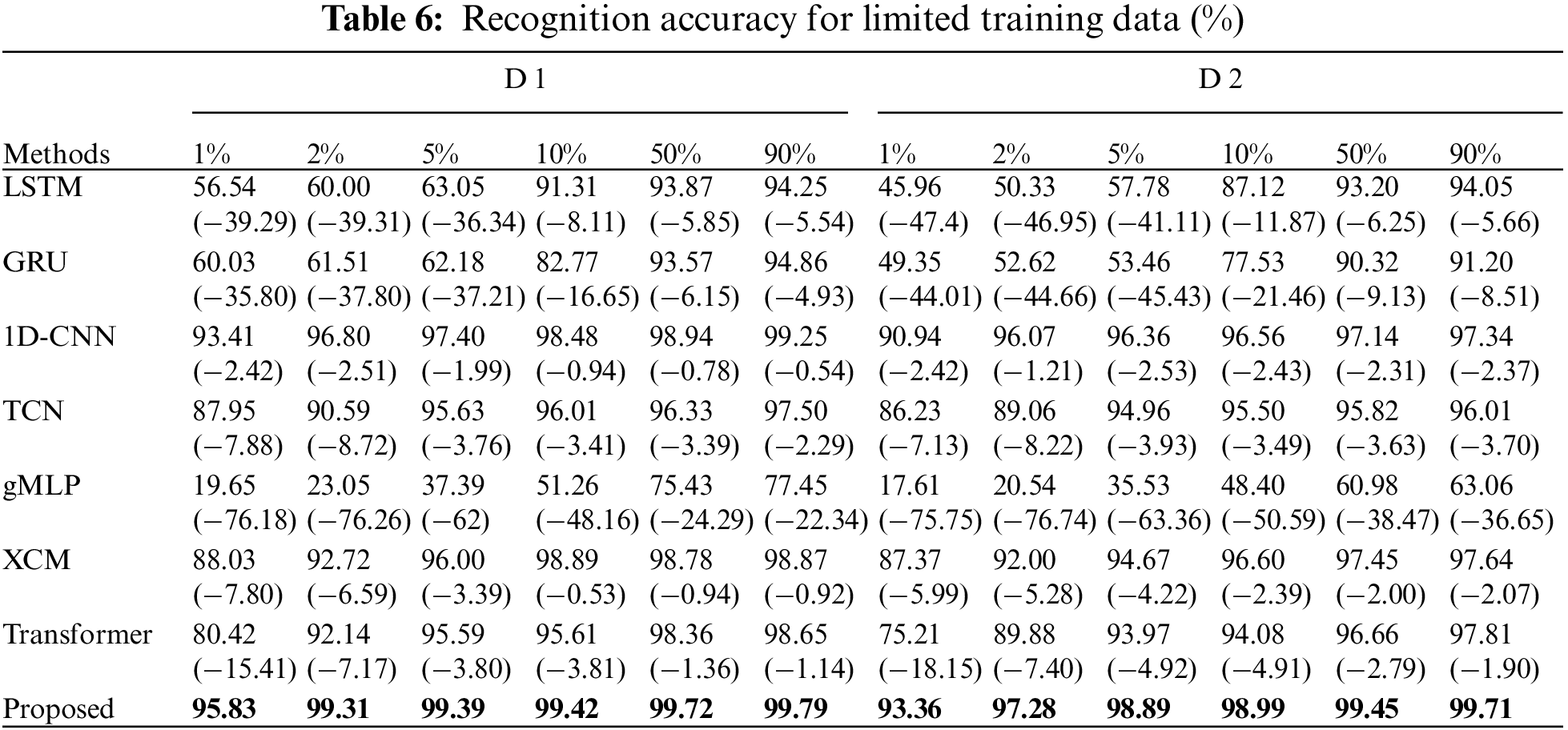
As shown in Table 6 and Fig. 10, the recognition accuracy of HRRP sequences increases with the increase of training samples. RLAT achieves more remarkable recognition performance than other methods on the standard dataset D 1 and the variant dataset D 2 with limited training samples. In particular, RLAT achieves 95.83% accuracy on the MSTAR standard dataset D 1 when the training set is only 1% of the original training set. Compared to Transformer, the accuracy is improved by 15.41%, compared to the gMLP, improved by 76.18%, compared to LSTM and GRU, improved by more than 35.80%, compared to TCN, 1D-CNN, and XCM, improved by more than 2.42%. RLAT achieves 93.36% accuracy in variant dataset D 2 when the training set is only 1% of the original training set. Compared to Transformer, the accuracy is improved by 18.15%, compared to the gMLP, improved by 75.75%, compared to LSTM and GRU, improved by more than 44.01%, compared to TCN, 1D-CNN, and XCM, more than improved by 2.42%. RLAT can extract valid information from limited samples more efficiently, while Transformer exhibits severe sample dependence and performs poorly in limited sample experiments. In addition, the vulnerability of gMLP in limited sample recognition tasks is also reflected by its near failure at low sample amounts.

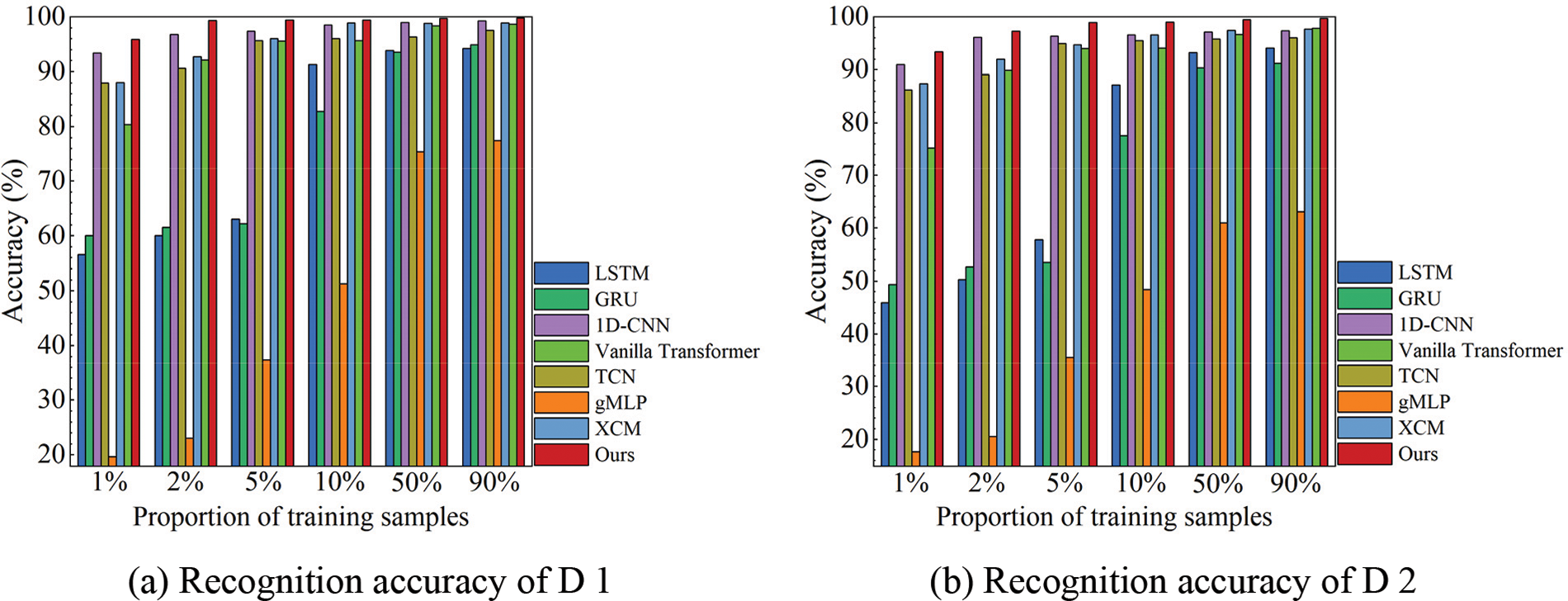
Figure 10: Recognition accuracy for limited training data of different methods

RLAT can achieve remarkable recognition when the training sample is only 274, while other methods are more dependent on the number of samples and seriously affect the training performance when the training sample plummets. The results indicate that RLAT has more outstanding generalization under the limited sample condition and can more effectively recognize HRRP sequences under non-cooperative targets. Since RLAT utilizes LAU for feature enhancement, which can extract local and global multi-level features and dynamically adjust the model depth, making feature extraction more effective. At the same time, Label Smoothing can reduce the dependence of RLAT on training samples and enhance the generalization performance, so that RLAT can still efficiently recognize variant targets under limited sample conditions. To present the results of the comparison experiments more visually, the comparison experiments with limited training data are shown in Fig. 10.

3.6 Position Encoding Comparison Experiments

RLAT is a network based on the self-attention mechanism, which is insensitive to the position information of HRRP sequences. Hence, position encoding is necessary to add position information to HRRP sequences for more efficient time-series feature extraction. Currently, commonly used position encoding mainly includes absolute position encoding and relative position encoding. Absolute position encoding LAPE [31] and relative position encoding T5 [19], XLNET [32] and DEBERTa [20], and Rotary Position Encoding (RoPE) [33] are selected for comparison experiments to verify the different validity for HRRP sequence recognition. The experimental results are shown in Table 7.

As shown in Table 7, for standard dataset D 1, RoPE achieves 99.86% recognition accuracy, which is more than 0.12% better than other relative position encoding methods and 0.45% better than absolute position coding, and the recognition accuracy of relative position encoding is slightly higher than that of absolute position encoding. For variant dataset D 2, RoPE achieves 99.73% recognition accuracy, which is more than 1.34% better than other relative position encoding methods, and 1.23% better than the absolute position encoding method. However, the recognition accuracy of absolute position encoding is slightly higher than relative position encoding.

To analyze the recognition performance of various position encoding methods more visually, Fig. 11 shows the recognition performance of 5 position encoding methods for the standard dataset D 1.

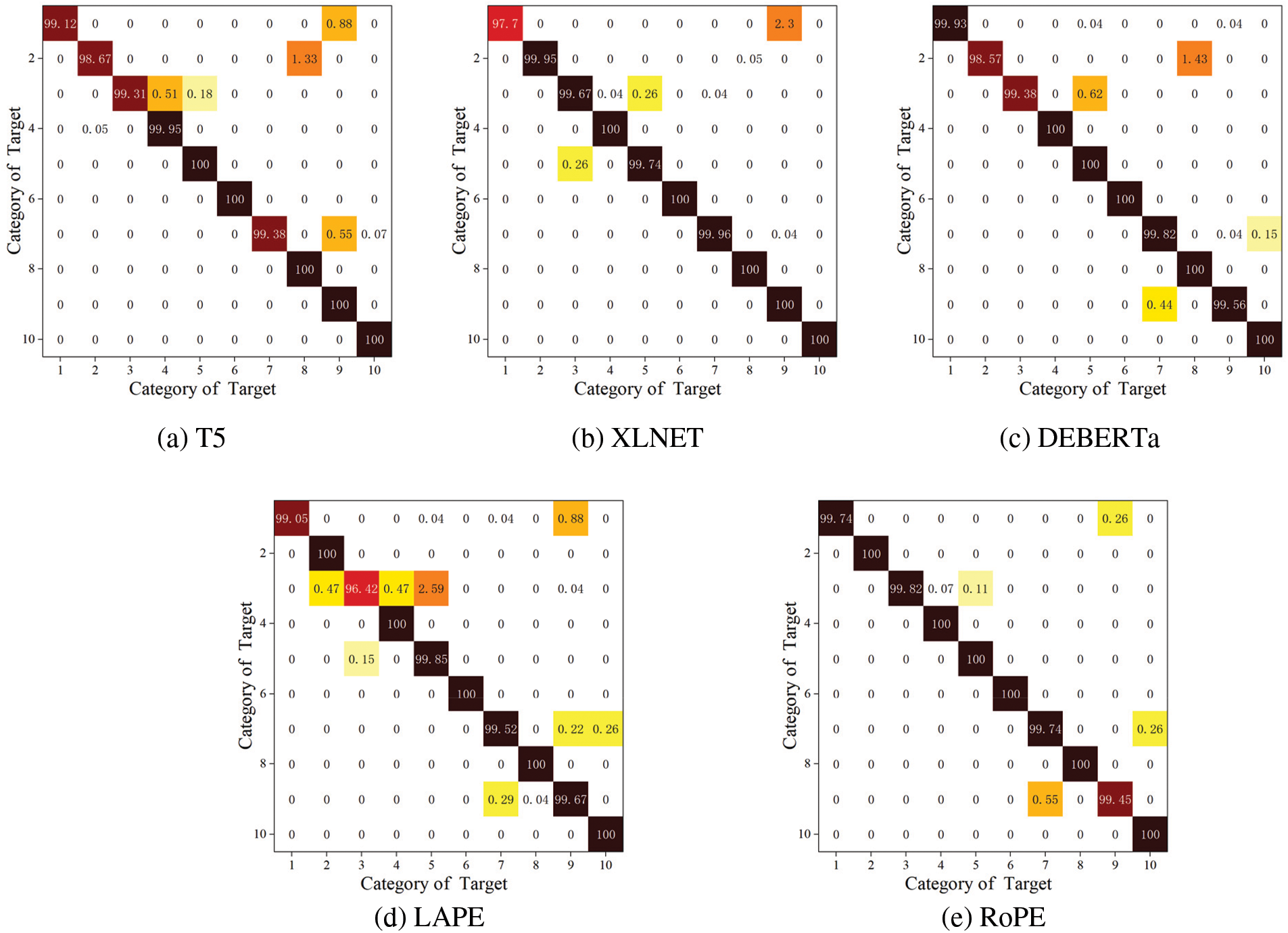
Figure 11: Confusion matrix for different positional encoding methods on D 1

As shown in Fig. 11, for the MSTAR standard dataset D 1, which contains ten categories of military targets, RoPE achieves optimal recognition accuracy for eight categories of targets with a maximum fluctuation in the accuracy of 0.55%, XLNET achieves optimal performance for six categories of targets with a maximum fluctuation of 2.30%, T5 achieves optimal performance for five categories of targets with a maximum fluctuation of 1.33%, DEBERTa achieves optimal performance for five types of targets with a maximum fluctuation of 1.43%, and LAPE achieves optimal performance for five types of targets with a maximum fluctuation of 3.58%. The results show that the recognition performance of RoPE is significantly better than other methods because RoPE has the advantages of both absolute position encoding and relative position encoding, which is more conducive to extracting temporal features. Meanwhile, relative position encoding not only has a higher accuracy than the absolute position encoding method but also has a more balanced recognition performance. Since relative position encoding can extract the relative information between HRRP sequences more effectively, it is beneficial to extract the temporal correlation.

As shown in Fig. 12, for the MSTAR variant dataset D 2, variant targets were added to the test set. RoPE achieved optimal recognition performance for eight categories of targets with a maximum fluctuation in the accuracy of 2.04%, XLNET achieved optimal performance for three categories of targets with a maximum fluctuation of 5.73%, T5 achieved optimal performance for three categories of targets with a maximum fluctuation of 3.58%, DEBERTa achieved optimal performance for three categories of targets with a maximum fluctuation of 6.13%, and LAPE achieves the optimal performance for three categories of targets with a maximum fluctuation of 6.13%. The results show that the recognition performance of RoPE is significantly better than other methods. Furthermore, the average recognition accuracy of absolute position encoding is higher than other relative position encoding methods. Since the variant dataset has 36% more variant samples, which requires a higher generalization of the recognition method, relative position encoding introduces more parameters in the self-attention mechanism, leading to an overfitting problem in the recognition of variant samples. As RoPE has the advantages of both absolute relative position encoding and relative position encoding, which is more conducive to the extraction of temporal features and more robust to variant samples.

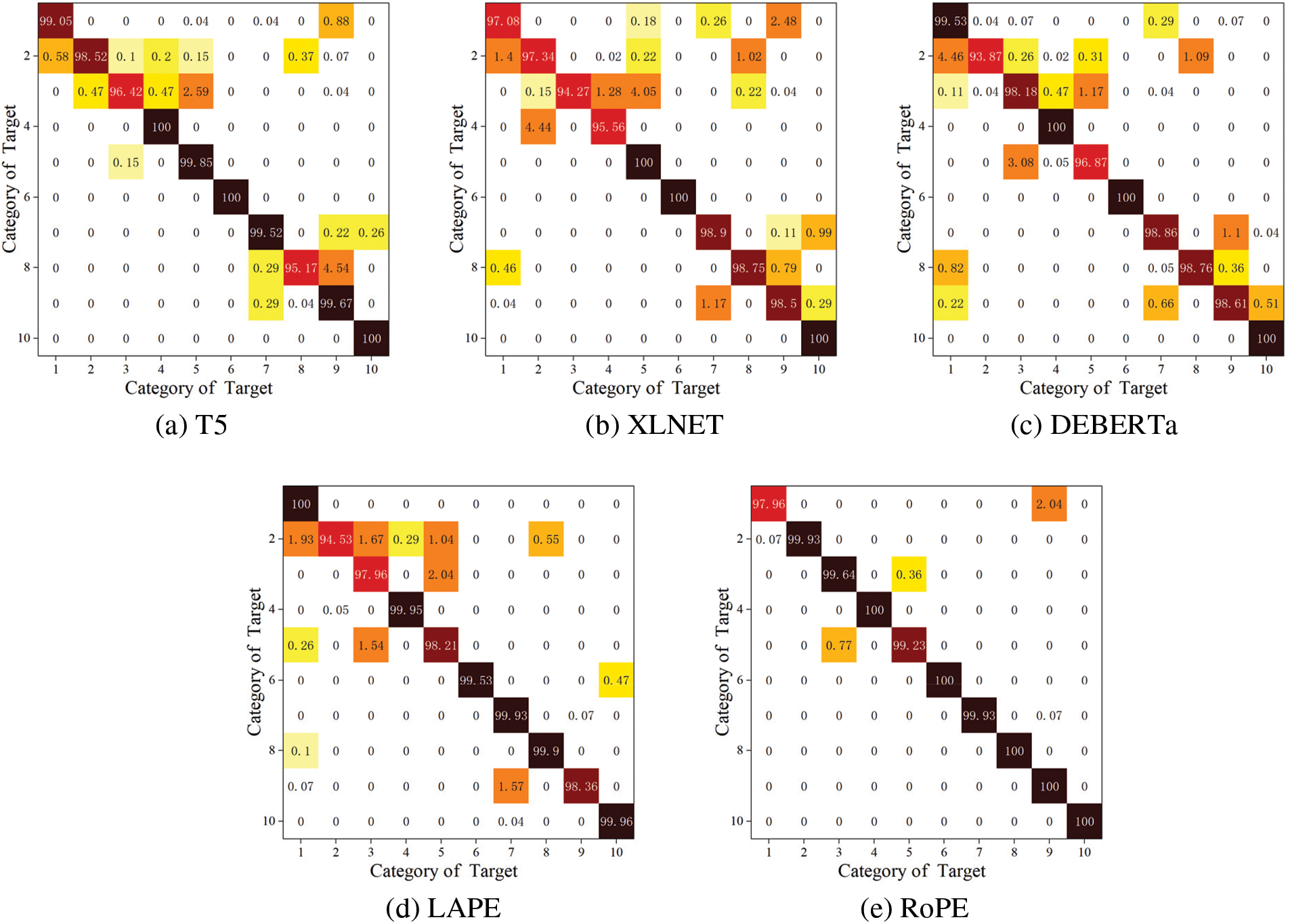
Figure 12: Confusion matrix for different positional encoding methods on D 2

3.7 Effect of Significant Hyperparameters

Hyperparameters play a crucial role in deep learning models. For RLAT, the three hyperparameters of LAU mapping dimension E, the number of stacked layers of LAT M, and the maximum depth of LAU are essential to the model performance, among which the width of a single LAU can be effectively controlled by E, and the number of stacked layers of LAT and the maximum depth of LAU can affect the feature extraction ability of the model in terms of model depth. Meanwhile, three hyperparameters are coupled with each other, so the three hyperparameters are combined to verify their effects on the model. Set the range of mapping dimension Embedding={64,128,256,512}, the range of stacking layers M={1,2,3,4,5,6,7,8}, and the L L AU maximum depth L={2,4,6,8,10}, where Figs. 13a–13c show the experimental results in MSTAR standard dataset D 1 and Figs. 13d–13f show the experimental results in MSTAR variant dataset D 2.

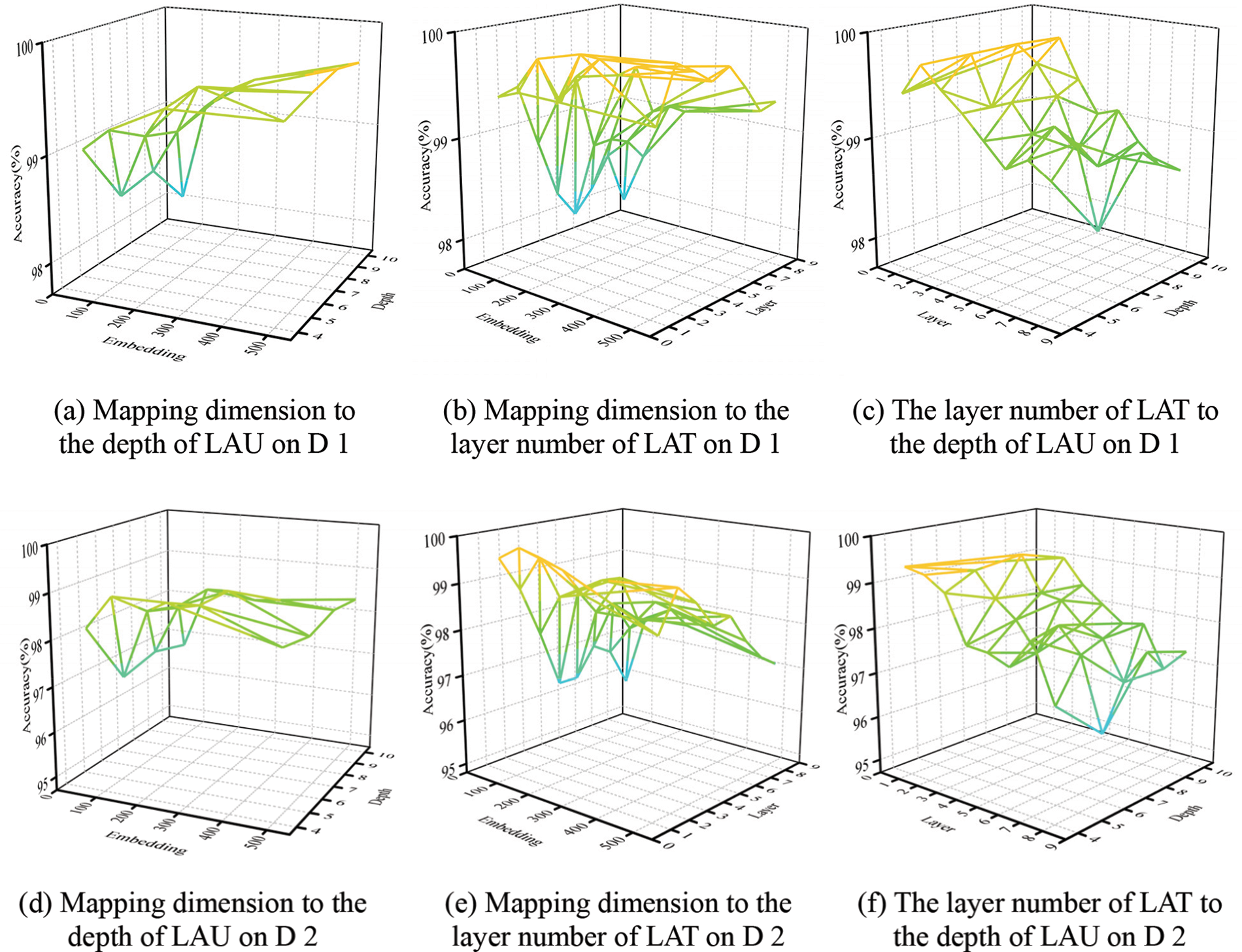
Figure 13: The influence of essential hyperparameters

For the MSTAR standard dataset D 1, as shown in Fig. 13a, the recognition performance of the proposed method increases with the increase of and L. Since the width and depth of LAU increase with the increase of E and L, which can extract richer and more abstract features. As shown in Fig. 13b, the recognition performance of the proposed method shows an increasing trend with the increase of E and shows an increasing and then decreases trend with the increase of M, which shows that too heavy stacking of LATs will harm the recognition performance instead. Too deep models will lead to a sharp increase in the number of parameters, resulting in a severe overfitting problem of the model. As shown in Fig. 13c, the recognition performance of the proposed method tends to increase and then decrease with the increase of M, and shows a slow growth trend with the increase of L. It can be concluded that and L mainly affects the width and depth of LAUs, so they show a positive correlation. While M controls the depth of the whole model, it shows a trend of first increasing and then decreasing. When M=2, the recognition performance is the best. Since the HRRP sequence contains a large number of noisy regions, too deep models can lead to increased overfitting problems.

For the MSTAR variant dataset D 2, the generalization performance of the model is considered to be more challenging due to the addition of a large number of variant samples. As shown in Fig. 13d, the recognition performance of the proposed method tends to increase and then decrease with the increase of E and , because the width of LAU and depth of LAT increase with the increase of E and L, which can extract richer and more abstract features. However, the overfitting problem will be more significant on the variant dataset with increased parameters. As shown in Fig. 13e, the recognition performance of the proposed method shows a trend of increasing and then decreasing with the increase of E and M. The appropriate model width and depth are beneficial to enhance the feature extraction. However, as the width and depth of the model increase, it will lead to a dramatic increase in the number of parameters and aggravate the overfitting problem on the variant dataset. As shown in Fig. 13f, the recognition performance of the proposed method shows a trend of increasing and then decreasing with the increase of M and L. It can be concluded that, unlike the standard dataset, there are certain differences between the training set samples and test set samples in the variant dataset, which are highly susceptible to overfitting problems. Therefore, when the width and depth of the model increase, it shows a trend of first increasing and then decreasing. The recognition performance is best when E=128,M=2,L=6. Models that are too wide and deep will extract a large amount of redundant noise information, which can lead to the aggravation of overfitting problems. The research on the variant dataset is the practical demands. Considering the complex real-world circumstances, researching variant datasets is more relevant and necessary. We will investigate the influence of different scales of variant datasets in future work.

3.8 The Visualization of Feature Extraction

To verify the effectiveness of the proposed method for feature extraction, the features are visualized using the t-Distributed Stochastic Neighbor Embedding (t-SNE) algorithm, which reduces the features to 2 dimensions. Figs. 14a–14b show the original feature distribution and the feature distribution extracted by RLAT for dataset D 1, respectively, and Figs. 14c–14d shows the original feature distribution and the feature distribution extracted by RLAT for dataset D 2, respectively. Fig. 14a shows the distribution of the original features of the ten categories of targets with a high degree of sample overlap and poor discrimination. After feature extraction by RLAT, the feature distribution of Fig. 14b is highly distinguishable, with small intra-class distance and large inter-class distance, which is significantly distinguishable. The distribution distinguishability of the original features of Fig. 14c is poorer compared with Fig. 14a because many variant samples are added, leading to more serious sample confusion and increasing classification difficulty. Fig. 14d has a higher distinction of feature distribution with a significant improvement compared to Fig. 14c, which can effectively achieve the recognition task. Both the feature distributions in Figs. 14b and 14d achieve significant distinguishability compared to the original distribution, illustrating the effectiveness of RLAT feature extraction. Since LAU can deepen the model depth dynamically, it is conducive to extracting the essential abstract features of HRRP sequences and can achieve a more effective temporal feature representation.

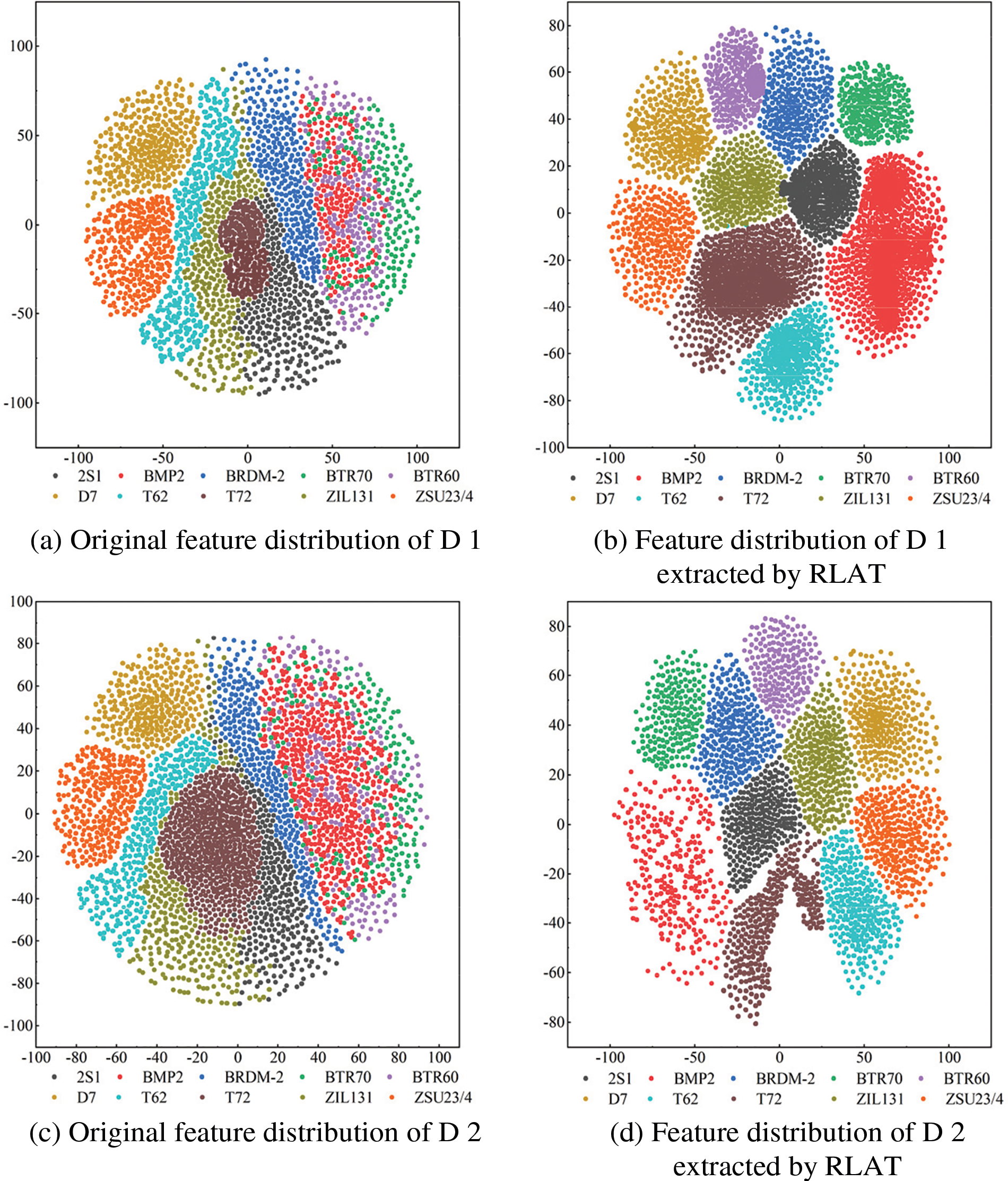
Figure 14: Visualization of RLAT feature extraction

4  Conclusions

This paper explores the application of Transformer in HRRP sequence recognition, and proposes a lightweight Transformer-based HRRP sequence recognition method called RLAT, which utilizes a more lightweight rotary position encoding, local-aggregated attention units, lightweight feedforward neural networks, and Label Smoothing to outperform other baseline methods in real scenes significantly. Besides, RLAT effectively reduces the number of parameters and computation of the model, which helps the application and deployment in edge devices. This paper also explores the recognition performance of the proposed method under variant targets and limited samples, and verifies that the generalization performance of the proposed method is significantly better than other methods. Finally, this paper further investigates the effect of position encoding on recognition performance and the effect of essential hyperparameters of the proposed method, which shows that RoPE can represent the relative position information between temporal features more effectively than other position encoding methods, and the hyperparameters have a significant impact on the recognition performance of RLAT, especially the number of stacked layers of LAT. Future work will further improve the lightweight level of the model, improve the recognition performance of the model under limited samples and variant targets, and extend the proposed method to the research work on open-set recognition of HRRP.

Acknowledgement: The authors would like to thank the editors and reviewers for their review and recommendations.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Grant Numbers 61876189, 61703426, 61273275); the Young Talent Fund of University Association for Science and Technology in Shaanxi, China (Grant Number 20190108); and the Innovation Talent Supporting Project of Shaanxi, China (Grant Number 2020KJXX-065).

Author Contributions: Conceptualization, W. X. and W. P.; methodology, W. X. andW. P.; software, X. Q. and L. J.; validation, W. P., X. Q. and L. J.; formal analysis, W. X. and W. P.; resources, W. P. and L. J.; writing–original draft preparation, W. P.; writing–review and editing, X. Q.; supervision, W. X. and S. Y.; project administration, W. X. and S. Y.; funding acquisition, W. X. and S. Y. All authors have read and agreed to the published version of the manuscript.

Availability of Data and Materials: The MSTAR datasets we used are a publicly available dataset, which can be downloaded in the Air Force Moving and Stationary Target Recognition Database at https://www.sdms.afrl.af.mil.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. Chen, L. Du and L. Y. Liao. “Survey of radar HRRP target recognition based on parametric statistical model,” Journal of Radars, vol. 11, no. 6, pp. 1020–1047, 2022. [Google Scholar]

2. J. Chen, L. Du, G. B. Guo, L. W. Yin and D. Wei, “Target-attentional CNN for radar automatic target recognition with HRRP,” Signal Processing, vol. 196, pp. 108497, 2022. [Google Scholar]

3. X. D. Liu, L. Wang and X. R. Bai, “End-to-end radar HRRP target recognition based on integrated denoising and recognition network,” Remote Sensing, vol. 14, no. 20, pp. 5254, 2022. [Google Scholar]

4. C. L. Lin, T. P. Chen, K. C. Fan, H. Y. Cheng and C. H. Chuang, “Radar high-resolution range profile ship recognition using two-channel convolutional neural networks concatenated with bidirectional long short-term memory,” Remote Sensing, vol. 13, no. 7, pp. 1259, 2021. [Google Scholar]

5. X. D. Wang, R. Li, J. Wang, L. Lei and Y. F. Song, “One-dimension hierarchical local receptive domains based extreme learning machine for radar target HRRP recognition,” Neurocomputing, vol. 418, pp. 314–325, 2020. [Google Scholar]

6. Q. Xiang, X. D. Wang, J. Lai, Y. F. Song, R. Li et al., “Multiscale group-fusion convolutional neural network for high-resolution range profile target recognition,” IET Radar, Sonar & Navigation, vol. 16, no. 12, pp. 1997–2016, 2022. [Google Scholar]

7. X. D. Wang, P. Wang, Y. F. Song and J. T. Li, “Recognition of HRRP sequence based on TCN with attention and elastic net regularization,” in Proc. of 2022 Int. Conf. on Image Processing, Computer Vision and Machine Learning (ICICML), Xi’an, China, pp. 346–351, 2022. [Google Scholar]

8. Y. F. Zhang, F. C. Qian and F. Xiao, “GS-RNN: A novel RNN optimization method based on vanishing gradient mitigation for HRRP sequence estimation and recognition,” in Proc. 2020 IEEE 3rd Int. Conf. on Electronics Technology (ICET), Chengdu, China, pp. 840–844, 2020. [Google Scholar]

9. X. Peng, X. Z. Gao, Y. F. Zhang and X. Li. “An adaptive feature learning model for sequential radar high resolution range profile recognition,” Sensors, vol. 17, no. 7, pp. 1675, 2017. [Google Scholar] [PubMed]

10. W. A. Timothy and C. G. Steven, “Hidden markov models for classifying SAR target images,” in Proc. SPIE Algorithms for Synthetic Aperture Pader Imagery XI, Orlando, Florida, USA, pp. 302–308, 2004. [Google Scholar]

11. L. Du, H. W. Li, Z. Bao and J. Y. Zhang, “A Two-distribution compounded statistical model for radar HRRP target recognition,” IEEE Transactions on Signal Processing, vol. 54, no. 6, pp. 2226–2238, 2006. [Google Scholar]

12. P. Molchanov, K. Egiazarian, J. Astola, A. Totsky, S. Leshchenko et al., “Classification of aircraft using micro-doppler bicoherence-based features,” IEEE Transactions on Aerospace and Electronic Systems, vol. 50, no. 2, pp. 1455–1467, 2014. [Google Scholar]

13. L. Lei, X. D. Wang, Y. Q. Xing and K. Bi, “Multi-polarized HRRP classification by SVM and DS evidence theory,” Control and Decision, vol. 28, no. 6, pp. 861–866, 2013. [Google Scholar]

14. Q. Xiang, X. D. Wang, Y. F. Song, L. Lei, R. Li et al., “One-dimensional convolutional neural networks for high-resolution range profile recognition via adaptively feature recalibrating and automatically channel pruning,” International Journal of Intelligent Systems, vol. 36, no. 1, pp. 332–361, 2021. [Google Scholar]

15. C. Du, L. Tian, B. Chen, L. Zhang, W. Chen et al., “Region-factorized recurrent attentional network with deep clustering for radar HRRP target recognition,” Signal Processing, vol. 183, pp. 108010, 2021. [Google Scholar]

16. M. Pan, A. L. Liu, Y. Z. Yu, P. H. Wang, J. J. Li et al., “Radar HRRP target recognition model based on a stacked CNN–Bi-RNN with attention mechanism,” IEEE Transactions on Geoscience and Remote Sensing, vol. 60, pp. 1–14, 2022. [Google Scholar]

17. L. Zhang, C. Han, Y. H. Wang, Y. Li and T. Long, “Polarimetric HRRP recognition based on feature-guided transformer model,” Electronics Letters, vol. 57, no. 18, pp. 705–707, 2021. [Google Scholar]

18. Y. J. Diao, S. W. Liu, X. Z. Gao and A. F. Liu, “Position embedding-free transformer for radar HRRP target recognition,” in Proc. of 2022 IEEE Int. Geoscience and Remote Sensing Symp. (IGARSS), Kuala Lumpur, Malaysia, pp. 1896–1899, 2022. [Google Scholar]

19. C. Raffel, N. Shazeer, A. Roberts, K. Lee, S. Narang et al., “Exploring the limits of transfer learning with a unified text-to-text transformer,” The Journal of Machine Learning Research, vol. 21, no. 1, pp. 5485–5551, 2020. [Google Scholar]

20. P. C. He, X. D. Liu, J. F. Gao and W. Z. Chen, “DeBERTa: Decoding-enhanced BERT with disentangled attention,” arXiv Preprint arXiv:2006.03654, 2020. [Google Scholar]

21. R. Müller, S. Kornblith and G. Hinton, “When does label smoothing help?” in Proc. of 33rd Conf. on Neural Information Processing Systems (NeurIPS 2019), Vancouver, Canada, 2019. [Google Scholar]

22. B. Erik, M. Uttam, Z. Edmund and V. Vincent, “Review of recent advances in AI/ML using the MSTAR data,” in Proc. of SPIE Algorithms for Synthetic Aperture Radar Imagery XXVII, Orlando, Florida, USA, pp. 113930C, 2020. [Google Scholar]

23. Y. F. Zhang, F. Xiao, F. C. Qian and X. Li, “VGM-RNN: HRRP sequence extrapolation and recognition based on a novel optimized RNN,” IEEE Access, vol. 8, pp. 70071–70081, 2020. [Google Scholar]

24. Y. F. Zhang, X. Z. Gao, X. Peng, J. Q. Ye and X. Li, “Attention-based recurrent temporal restricted boltzmann machine for radar high resolution range profile sequence recognition,” Sensors, vol. 18, no. 5, pp. 1585, 2018. [Google Scholar] [PubMed]

25. F. Karim, S. Majumdar, H. Darabi and S. Harford, “Multivariate LSTM-FCNs for time series classification,” Neural Networks, vol. 116, pp. 237–245, 2019. [Google Scholar] [PubMed]

26. N. Elsayed, A. S. Maida and M. Bayoumi, “Deep gated recurrent and convolutional network hybrid model for univariate time series classification,” International Journal of Advanced Computer Science and Applications, vol. 10, no. 5, pp. 654–664, 2019. [Google Scholar]

27. S. J. Bai, J. Z. Kolter and V. Koltun, “An empirical evaluation of generic convolutional and recurrent networks for sequence modeling,” arXiv preprint arXiv:1803.01271, 2018. [Google Scholar]

28. H. X. Liu, Z. H. Dai, D. R. So and Q. V. Le, “Pay attention to mlps,” Advances in Neural Information Processing Systems, vol. 34, pp. 9204–9215, 2021. [Google Scholar]

29. K. Fauvel, T. Lin, V. Masson, É. Fromont and A. Termier, “XCM: An explainable convolutional neural network for multivariate time series classification,” Mathematics, vol. 9, no. 23, pp. 3137, 2021. [Google Scholar]

30. M. H. Liu, S. Q. Ren, S. Y. Ma, J. H. Jiao, Y. Z. Chen et al., “Gated transformer networks for multivariate time series classification,” arXiv preprint arXiv:2103.14438, 2021. [Google Scholar]

31. J. Gehring, M. Auli, D. Grangier, D. Yarats and Y. N. Dauphin, “Convolutional sequence to sequence learning,” in Proc. of the 34th Int. Conf. on Machine Learning (ICML), Sydney, NSW, Australia, pp. 1243–1252, 2017. [Google Scholar]

32. Z. H. Dai, Z. L. Yang, Y. M. Yang, J. Carbonell, Q. V. Le et al., “Transformer-XL: Attentive language models beyond a fixed-length context,” in Proc. of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, pp. 2978–2988, 2019. [Google Scholar]

33. J. L. Su, Y. Lu, S. F. Pan, A. Murtadha, B. Wen et al., “RoFormer: Enhanced transformer with rotary position embedding,” arXiv preprint arXiv:2104.09864, 2021. [Google Scholar]