A Conditionally Anonymous Linkable Ring Signature for Blockchain Privacy Protection

1  Introduction

Blockchain is a decentralized distributed database that has proliferated in recent times. In 2008, Nakamoto et al. [1] used the blockchain as a crucial part of the cryptocurrency Bitcoin. It enables two users to trade and transfer money using Bitcoin to each other without the limitations of an external third-party trusted center because it is a public transaction platform for international services. Since then, blockchain technology has flourished through the research and development of different cryptocurrencies [2–5]. To improve the performance and flexibility of blockchain, Ethereum [2] as Blockchain 2.0 is proposed, which allows efficient and flexible execution of transactions by deploying smart contracts. Smart contracts, the underlying technology of Ethereum, can be compared to computer programs that autonomously perform all contract-related processes with associated outcomes. In addition to the two typical public blockchains mentioned above, permissioned blockchains are also gaining traction. Hyperledger Fabric [6] is a blockchain technology project initiated by the Linux Foundation to develop a cross-industry commercial blockchain platform technology. In contrast to the well-known public blockchain, Hyperledger Fabric technology also includes a member management service mechanism to make identity management, network privacy, secrecy, and censorship capabilities more economically appropriate. Blockchain technology has numerous applications, including mobile crowdsensing [7], data sharing [8], healthcare [9], and IoT [10]. However, the development of blockchain also faces many challenges [11], such as security issues [12].

Ring signature, invented by Rivest et al. [13], provides a function of anonymity for users. A ring signature is created when a signer signs a message with a set of public keys it chooses and its public-private key combination. A ring is a collection of signers and the public key sets they have selected. The verifier can only ascertain that one of the ring members is the source of the signature value; they cannot identify the valid signer. To safeguard the user’s privacy, the ring signature uses an actual signer whose identity is concealed inside the ring. Ring signature is frequently employed in e-voting [14], e-transactions, and e-money due to their spontaneity and absolute anonymity. Ring signatures can be classified into three categories: identity-based (IBC) ring signatures [15,16], public key infrastructure (PKI) systems [13,17,18], and certificateless (CLC) systems [19–21], depending on the key generation method. Due to the extensive and rapid growth of e-commerce, a significant number of applications have been created that require ring signatures with a wide range of different properties. Ring signature is divided into linkable ring signature [22], deniable ring signature [23], threshold ring signature [24], verifiable ring signature [25], designated-verifier linkable ring signature [26], and so on based on several property attributes. Blockchain systems currently use linkable ring signatures a lot. In 2004, Liu et al. [22] proposed the first linkable ring signature technique and the notion of a linkable ring signature with spontaneity. Based on the ring signature algorithm, the user generates a link to this signature with their private key, which cannot be forged. The ring signature generated by the same signer for different messages has the same link tag, allowing for the link to the signature generated by the same signer. This effectively prevents double-spending attacks on blockchain transactions.

Monero [5] is one of the most successful implementations of blockchain privacy protection mechanisms that use linkable ring signature technology. Its most remarkable feature is the ability to protect the privacy of both parties involved in a transaction. In Monero, a transaction input contains multiple addresses, but only one of them is the actual input. The remaining addresses are combined for obfuscation. Therefore Monero accomplishes the untraceability of transactions and makes it very difficult to tell whether the output of one transaction is the input of another. It leads to the typical blockchain applications for linkable ring signatures, like RingCT1.0 [27], RingCT2.0 [28], and RingCT3.0 [29]. However, in reality, the user of the transaction must be identified in cases of fraud or illegal transactions, hence a conditionally anonymous linkable ring signature should be created to address such issues; Naor [23] first proposes deniable ring signatures for conditional anonymity, but it is an interactive protocol, and the confirmation process is inefficient. While Zheng et al. [30] have constructed a non-interactive protocol for designing conditional anonymous ring signatures, their scheme still requires the signer to send a message to the verifier honestly. As stated earlier, a secure and non-interactive scheme is needed to address the problem of conditional anonymity, where the signer is not required to honestly send a message to the verifier.

This paper constructs a conditionally anonymous linkable ring signature scheme by the idea of the Diffie–Hellman key exchange protocol and Elliptic Curve Discrete Logarithm Assumptions, which can provide a non-interactive and secure protocol compared to the previous schemes. The contributions of this paper are as follows:

•   This paper proposes an efficient conditionally anonymous linkable ring signature scheme, which can directly find the signer of a transaction and thus achieve conditional anonymity when an illegal or malicious transaction occurs in the blockchain. Compared to previous construction methods, the approach outlined in this paper offers a non-interactive, efficient, and secure confirmation process. Additionally, it is linkable to prevent the double-spending attack in the blockchain. This paper also gives detailed security proof of the proposed scheme.

•   This paper provides a complete framework that works with blockchain and uses smart contracts to implement the confirmation procedure. The solution of this paper can effectively run through experimental simulations on a personal computer.

The remainder of this paper is organized as follows. The related work is described in Section 2. Some preliminaries about linkable ring signatures and their security definitions are given in Section 3. The concrete algorithm of the scheme and system framework is given in Section 4. The proof of correctness and security analysis of the scheme is discussed in Section 5. Performance and efficiency analysis of the scheme is described in Section 6. Section 7 is the conclusion of the paper.

2  Related Works

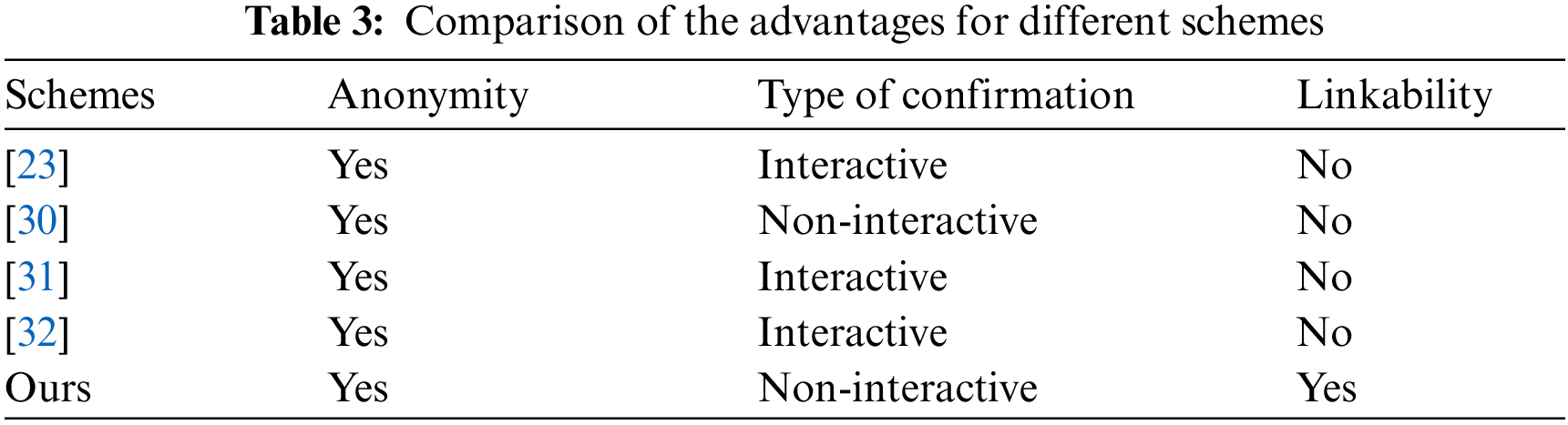
The importance of preserving the security and privacy of blockchain users is growing as blockchain technology develops quickly. In 2013, Saberhagen et al. [5] applied a linkable ring signature to a blockchain-based digital currency protocol. They proposed the CryptoNote protocol for Monero, which effectively protects the identity privacy of both parties to a transaction. However, it cannot achieve conditional anonymity. Naor [23] proposed a deniable ring signature system to address conditional anonymity, which used an interactive protocol to identify the signer of the ring signature. Zheng et al. [30] constructed an efficient conditionally anonymous ring signature in the random oracle model. It simply needed one message to be sent from the signer to the verifier, not multiple interactions. Jiang et al. [31] proposed an anonymous authentication mechanism to achieve conditional anonymity and traceability, but it had a considerable amount of consumption in the signature phase. Zhang et al. [32] designed a novel ring signature scheme with conditional anonymity for permissioned blockchains. Nevertheless, interactive protocols have several security flaws, such as real signers interfering with the interaction maliciously and non-signers not taking part. Although Gao et al. [33] first constructed a non-interactive deniable ring signature scheme, it has unfortunately been proven wrong by Jia et al. [34]. Park et al. [35] proposed a repudiable ring signature approach that can overcome these drawbacks, but it had a large signature length and low efficiency. Although Lin et al. [36] proposed a repudiable ring signature with stronger security and logarithmic-size signature, the confirmation process still needed to be improved. As mentioned above, existing ring signature schemes that achieve conditional anonymity are either interactive protocols or must satisfy the signer to honestly send a message to the verifier. Hence it is significant to build an efficient and secure non-interactive protocol to meet the requirements of conditional anonymity. Based on [23,26,32], this paper constructs a conditionally anonymous linkable ring signature scheme with more efficient and secure.

3  Preliminaries

3.1 Linkable Ring Signature

Definition 1: A linkable ring signature scheme for a message space ℳ and a public key set

L={P0,P1,…,Pn−1}; it has five algorithms: system initialization, key generation, signature generation, signature verification, and linkability. This paper denotes them as LRS.Setup, LRS.KeyGen, LRS.Sign, LRS.Verify and, LRS.Link, respectively, and the details are shown below:

•   LRS.Setup(1λ) →params: After inputting a parameter 1λ, the LRS.Setup can output parameters params.

•   LRS.KeyGen(1λ,params) →(msk,mvk): On inputting the security parameter 1λ and params, the LRS.KeyGen outputs the signing key msk and public key mvk.

•   LRS.Sign(, M,n,L,skπ) →(σ,Qπ): On inputting the message M, n members of the public key set L, and private key skπ of the signer, it can output signature σ and linked tag Qπ.

•   LRS.Verify(params,M,L,σ,Qπ)→{0,1}: On inputting the public key set L, a message M, a signature σ, and a linked tag Qπ, the LRS.Verify outputs 1 or 0, where 1 indicates that the signature is valid.

•   LRS.Link(L, M1, M2, σ1, Q1, σ2, Q2) →{0,1}: On inputting two messages M1 and M2, a public key set L, two signatures σ1 and σ2, and two linked tags Q1 and Q2, if σ1 and σ2 are valid ring signatures and have the same link tag Q1=Q2, it outputs 1, otherwise outputs 0.

3.2 Security Definition

Definition 2: Unforgeability: The unforgeability of the ring signature is defined by the following game between simulator 𝒮 and adversary 𝒜:

•   𝒮 generates parameters params to send to 𝒜.

•   𝒜 will query three random oracles 𝒥𝒪, 𝒞𝒪, and 𝒮𝒪 adaptively, 𝒮 returns some designed values and sent them to 𝒜.

•   𝒜 will output a message M∗, n members of the public key set L∗, and two forged signatures σ1∗ and σ2∗.

This paper can be sure that 𝒜 wins the above game if four of the following conditions are met:

•   Two forged signatures σ1∗ and σ2∗ are valid signatures, and they can pass the verification algorithm: LRS.Verify(params,M,L,σ,Qπ)→1.

•   All public keys of can be queried by random oracle 𝒥𝒪.

•   𝒜 cannot corrupt the public key of L∗ to get the private key.

•   σ1∗ and σ2∗ are not obtained by querying the signature random oracle 𝒮𝒪.

Definition 3: Anonymity: The anonymity of the ring signature scheme is defined by a game between a simulator 𝒮 and an adversary 𝒜 with infinite computational power:

•   𝒮 generates parameters params to send to 𝒜.

•   𝒜 will query a random oracle 𝒥𝒪 and 𝒮 returns some designed values to 𝒜.

•   𝒜 sends a message M∗ and n members of the public key set L∗={P0∗,P1∗,…,Pn−1∗} to 𝒮, where all public keys are obtained by querying 𝒥𝒪. 𝒮 chooses π∈[0,n−1] randomly and generates signature LRS.Sign(M,n,L,skπ) →(σπ,Qπ), where skπ is private key of Pπ. 𝒮 sends σπ∗ to 𝒜.

•   𝒜 guesses a value π′∈[0,n−1].

If the probability that the value π′ guessed by 𝒜 satisfies π′=π is less than or equal to 1n, then the ring signature scheme satisfies anonymity.

Definition 4: Elliptic Curve Discrete Logarithm Problem (ECDLP): Given any two points P and Q on an elliptic curve E(Fp), solve for the value x that satisfies the equation Q=x⋅P is unsolvable in polynomial time.

4  Proposed Scheme Method

4.1 Conditionally Anonymous Linkable Ring Signature Scheme

In this section, this paper designs a conditionally anonymous Linkable ring signature (CA-LRS) scheme to protect the transaction privacy of users. The scheme is divided into six algorithms, the first five of which are similar to the classical linkable ring signature, including Setup, Key Generation (KeyGen), Signature, Verification, and Linking. The final algorithm, Confirmation, can find the signer who generated the ring signature and thus achieve conditional anonymity in exceptional cases, such as illegal transactions. Table 1 explains related symbols, and the concrete steps of the algorithms are as follows:

•   Setup: On inputting parameter ℒ, it outputs parameters param={E,Fp,K,G,q,H1}, where E is an elliptic curve defined over finite field Fp, K is an additive cyclic group about E, G is the generator of K, and q is the order of K. H1:{0,1}∗→Zq∗ is a secure hash function.

•   KeyGen: On inputting public parameters, it generates S={ski=di}(i=0,1,…n−1)∈Zq∗ as private keys for all signers of ring signature. The public key set is L={Pi=di⋅G}(i=0,1,…n−1). In proposed scheme, it defines skπ=dπ(π∈{0,1,…n−1}) as private key of signer. It chooses skD=dD∈Zq∗ and skD∉S, computing PD=dD⋅G as confirmation public key.

•   Signature: After signer inputs his private key, public key set L, and message m, it randomly chooses a,bπ,tπ∈Zq∗ to compute:

P^D=dπ⋅PD.(1)

Q=a⋅G.(2)

R=a⋅P^D.(3)

W=tπ⋅G+bπ⋅PD.(4)

Then it computes cπ+1 by:

cπ+1=H1(L,m,PD,P^D,Q,R,W).(5)

Finally, for i=π+1,…n−1,0,1,…π−1, it picks si,bi,ti∈Zq∗ to compute:

Qi=(si+ci)⋅G+(ti+ci)⋅Pi.(6)

Ri=(si+ci)⋅PD+(ti+ci)⋅P^D.(7)

Wi=ti⋅G+bi⋅PD.(8)

ci+1=H1(L,m,PD,P^D,Qi,Ri,Wi).(9)

It sets sπ=a−cπ−(tπ+cπ)⋅dπ. The generated signature is σ=(c0,{si}i=0n−1,{ti}i=0n−1,{bi}i=0n−1,P^D).

Verification: After receiving the signature σ of message m, it computes:

{Qi′=(si+ci)⋅G+(ti+ci)⋅Pi,Ri′=(si+ci)⋅PD+(ti+ci)⋅P^D,Wi=ti⋅G+bi⋅PD,ci+1=H1(L,m,PD,P^D,Qi′,Ri′,Wi′).(10)

The algorithm outputs 1 (“accept”) if and only if:

c0=cn=H1(L,m,PD,P^D,Qn−1,Rn−1,Wn−1).(11)

Otherwise, it outputs 0 (“reject”).

•   Linking: On inputting the generated two signatures (c0′,{si′}i=0n−1,{ti′}i=0n−1,{bi′}i=0n−1,P^D′) and ∞(c0″,{si″}i=0n−1,{ti″}i=0n−1,{bi″}i=0n−1,P^D″) on two identical rings L, the two signature values are substituted into the verification algorithm, and if both output 1, then verify whether P^D′=P^D″ holds, and if it holds, output 1, otherwise output 0.

•   Confirmation: Once the illegal transaction occurs, the algorithm finds the signer of the ring signature by inputting the private key skD. For any Pi∈L (i from 1 to n), it computes PD′=skD⋅Pi, the algorithm will stop when PD′ equals P^D or i=n.

4.2 Transaction Signature Framework Based on CA-LRS

Based on the framework of CryptoNote [5], this paper introduces the proposed Conditionally Anonymous linkable ring signature (CA-LRS) scheme into the blockchain technology in this section. It records and stores data utilizing ring signature transactions and guarantees the user’s anonymity, and can conditionally find the true signer of the ring signature in case of illegal transactions. Since CryptoNote [5] already contains detailed steps, this paper will simply describe them systematically. As shown in Fig. 1, this paper assumes that Alice wants to transfer her cryptocurrency from her address to Bob. The detailed process of the framework consists of the following five steps:

Figure 1: System model of blockchain transactions

•   Initialization Phase: Alice and Bob run the Setup algorithm and KeyGen algorithm of the CA-LRS scheme to generate their respective public-private key pairs (pkA,skA) and (pkB,skB). Bob randomly chooses a string s and uses a hash function to compute hash(s), and then sends it to Alice. Alice encrypts the hash(s) with Bob’s public key pkB to get Y as the hidden address and inputs the key image X=hash(skA).

•   Execution Phase: Without the involvement of other parties, Alice generates n-1 transactions with the same value as the output of her transaction and mixes the transactions with Bob in all of these external output transactions. Alice stores a public key PD from the blockchain. After the hash computation of this transaction, the signature σ is generated by the Signature algorithm of the CA-LRS scheme. Finally, Alice inputs multiple transaction outputs, Y, X, and σ to generate a new transaction tx.

•   Verification Phase: By running the linking algorithm, miners can verify that the cryptocurrency for the transaction has been spent on preventing the double-spending attack. The miner node then runs the Verification algorithm of the CA-LRS scheme to verify that the signature σ of the transaction tx is valid. The transaction is legitimate and enclosed in a new block if all verification is successful. Otherwise, the transaction will be invalidated.

•   Consensus Phase: Miners broadcast information among themselves and agree to add new blocks containing transactions to the blockchain through a consensus mechanism. Additionally, the system pays miners to construct new blocks.

•   Confirmation Phase: Bob checks the output of multiple transactions and compares them by value Y and then accepts the transactions initiated against him. When there is an illegal transaction already in the blockchain network, the user (Alice) who initiated the transaction needs to be found and this phase will be used. After confirmation by the consensus node, Algorithm 1 can be used to check.

Signer of the ring signature by the integer value returned. Algorithm 1 enables the retrieval of integer i by inputting a public key set of ring signature L and the linkable tag P^D. If the return value is i (i∈[0,n−1]), the owner of the ith public key of the public key set L is the signer of the ring signature.

5  Security Analysis of Our Scheme

5.1 Correctness

Theorem 1. Our CA-LRS scheme meets correctness.

Proof. Assuming that the signature σ=(c0,{si}i=0n−1,{ti}i=0n−1,{bi}i=0n−1,P^D) is generated by algorithm signature and the verifier uses algorithm verification to verify this signature. When i=π, there is the following equation:

Zπ′=(sπ+cπ)⋅G+(tπ+cπ)⋅Pπ=[a−(tπ+cπ)dπ]⋅G+(tπ+cπ)⋅dπG=a⋅G.(12)

Zπ″=(sπ+cπ)⋅PD+(tπ+cπ)⋅P^D=[a−(tπ+cπ)dπ]⋅PD+(tπ+cπ)⋅dπPD=a⋅PD.(13)

Zπ‴=tπ⋅G+bπ⋅PD(14)

From the above equations, it knows that:

cπ+1=H1(L,m,PD,P^D,Zπ′,Zπ″,Zπ‴)=H1(L,m,PD,P^D,Q,R,W).(15)

Therefore the whole verification process will finally satisfy c0=cn−1, so it meets correctness.

5.2 Unforgeability

Theorem 2. If ECDLP is hard, our CA-LRS scheme is unforgeable in the random oracle model.

Proof. Some definitions of security for proof this paper needs to use from [23,29,37]. Assuming ECDLP is hard to be solved, and 𝒜 is a PPT adversary which can forge a valid signature σ of our scheme within a specific time frame, it can construct a simulator 𝒮 that uses 𝒜 as a subroutine to solve the hard problem. 𝒮 first performs the initialization process, generating the required parameters param={E,Fp,G,G,q}, and initial a set L′={Pi}i=0n′−1 to interact with 𝒜 (The elements in the initial L are n′ ECDLP instances). 𝒜 makes at most qH and ql queries for H1 and three random oracles 𝒥𝒪, 𝒞𝒪, and 𝒮𝒪. When 𝒜 queries H1 or one of the three random oracles, 𝒮 will answer by the following:

•   H1: 𝒮 will random choose g∈Zq∗ and output it.

•   𝒥𝒪: 𝒮 will pick g∈Zq∗, compute g⋅G and add it to L.

•   𝒞𝒪: For Pj∉{Pi}i=0n′−1, 𝒮 will output the private key dj of Pj that guarantee Pj=dj⋅G, otherwise this query wille be terminated.

𝒮𝒪: When 𝒮 receives message m, public key set L⊂L′ (The number of elements of L is l), Pπ∈L, and PD∈L′ from 𝒜, different signature values are return to 𝒜 by the value of Pπ. If Pπ∉{Pi}i=0n′−1, 𝒮 has dπ that satisfies dπ⋅G=Pπ. So he can use the algorithm signature of the CA-LRS scheme to generate a signature σ and send it to 𝒜. Otherwise, he computes P^D=x⋅PD by chooosing x∈Zq∗ and chooses {ci}i=0l−1, {ti}i=0l−1, {bi}i=0l−1, and {si}i=0l−1∈Zq∗ randomly. For each i∈[0,l−1], it satisfies the following equation:

ci+1=H1(L,m,PD,P^D,(si+ci)⋅G+(ti+ci)⋅Pi,(si+ci)⋅PD+(ti+ci)⋅P^D,ti⋅G+bi⋅PD).(16)

Then he sends σ=(c0,{si}i=0l−1,{ti}i=0l−1,{bi}i=0l−1,P^D) as the signature of the simulation to 𝒜. After at most ql queries for random oracles, it can assume that 𝒜 can successfully generate the forged signature. Also the forged signature in general has L⊆{Pi}i=0n′−1, Pπ∈L, and PD∈{Pi}i=0n′−1. Since ci+1 in a forged signature is a hash value determined by some value, it can use Forking Lemma of [37] to generate two different signatures with

{x⋅G=(sπ+cπ)⋅G+(tπ+cπ)⋅Pπ=[sπ+cπ+dπ(tπ+cπ)]⋅G,y⋅PD=(sπ+cπ)⋅PD+(tπ+cπ)⋅P^D=[sπ+cπ+dπ(tπ+cπ)]⋅PD,z⋅G=tπ⋅G+bπ⋅PD=(tπ+bπdD)⋅G,(17)

{x⋅G=(sπ′+cπ′)⋅G+(tπ′+cπ′)⋅Pπ=[sπ′+cπ′+dπ(tπ′+cπ′)]⋅G,y⋅PD=(sπ′+cπ′)⋅PD+(tπ′+cπ′)⋅P^D=[sπ′+cπ′+dπ(tπ′+cπ′)]⋅PD,z⋅G=tπ′G+bπ′⋅PD=(tπ′+bπ′dD)⋅G,(18)

If sπ≠sπ′, the above equation about x⋅G gives the value of dπ:

dπ=sπ−sπ′+cπ−cπ′tπ′−tπ+cπ′−cπ.(19)

If tπ≠tπ′ and bπ≠bπ′, the above equation about z⋅G gives the value of dD:

dD=tπ−tπ′bπ′−bπ.(20)

Therefore, the ECDLP instance is solvable which contradicts the assumption, thus the theorem is proved.

5.3 Anonymity

Unlike general linkable ring signatures, our CA-LRS is conditionally anonymous. The signer of the ring signature can be found when the additional condition of the corresponding private key dD of PD is provided; otherwise the generated ring signature is anonymous. The above process of finding a signer is non-interactive, and the proof of conditionally anonymous is given below.

Theorem 3. Our CA-LRS scheme is conditionally anonymous.

Proof. Assume an adversary 𝒜 who does not know dD, the following proof shows that the ring signature generated by any member of the ring is statistically indistinguishable from 𝒜, and thus the scheme is anonymous. Simulator 𝒮 sends parameters param={E,Fp,G,G,q,H1} to 𝒜 firstly, 𝒜 can use up to ql queries on random oracle 𝒥𝒪. 𝒜 chooses message m, public key set L″={Pi}i=0n−1 to send to 𝒮. 𝒮 picks ω∈[0,n−1] randomly, and computes the ring signature value of message m for ring member 𝒜ω. When 𝒜ω constructs all ring signatures as (ci,si,ti,bi)(i∈[0,n−1],i≠ω), it is necessary to randomly select a∈Zq∗ and use the appropriate cω and tω to satisfy the correctness of the ring signature. The correctness of the ring signature is represented by the following equation:

sω=a−cω−(tω+cω)dω.

For generated n-1 signature values (ci,si,ti,bi)(i∈[0,n−1],i≠ω), they also need to satisfy that for i∈[0,n−1], the values of Qi=(si+ci)⋅G+(ti+ci)⋅Pi, Ri=(si+ci)⋅PD+(ti+ci)⋅P^D, and Wi=ti⋅G+bi⋅PD guarantee c0=cn. Therefore, the probability that 𝒜ω constructs n−1 different ring signatures (ci,si,ti,bi)(i∈[0,n−1],i≠ω) is Pr[𝒜ω(σdif)]=1q−11q−2…1q−n+1. The probability that 𝒜ω chooses a particular a such that cω and tω are different from all ci, ti(i≠ω) is 1q−n. This paper can calculate the probability that 𝒜ω constructs a valid ring signature is

Pr[𝒜ω(σ)]=1q−11q−2…1q−n

So the probability of A to distinguish the identity of the real signer of the ring signature is not greater than 1n, and our scheme is anonymous. For verifier 𝒱 who has private key dD of PD, he can compute PD′=dD⋅Pi for any Pi∈L, the user of Pi∈L is real signer if and only if PD′=P^D.

5.4 Linkability

Theorem 4. If ECDLP is hard, our CA-LRS scheme is unforgeable in the random oracle model.

Proof. In the proof of the theorem, this paper continues to follow some of the definitions from the proof of Theorem 2, including a PPT adversary 𝒜 that can generate a linkable signature and three random oracles 𝒥𝒪, 𝒞𝒪, and 𝒮𝒪. 𝒜 at most queries qH hash H1 and ql random oracles, and they return the same values as the proof in Theorem 2. This paper can construct a simulator 𝒮, given nl ECDLP instances {Pi}i=0nl−1, who can output the solution of at least one ECDLP instance by treating 𝒜 as a subroutine. After a successful interaction with 𝒮, 𝒜 will generate some ring signatures denoted as (σ1,σ2…σj). It is worth noting that 𝒜 at most has corrupted j-1 private keys of ring signatures, and cannot get the private key corresponding to PD. For the signatures generated by A, there are two different cases. For the first case, 𝒜 uses less than j private keys in generated j ring signatures, which results in a pair of signatures generated with the same private key dπ, denoted as σi′ and σj′(1≤σi′,σj′≤j). From the proof of Theorem 2 this paper can obtain that:

dπ=sπ−sπ′+cπ−cπ′tπ′−tπ+cπ′−cπmodqordD=tπ−tπ′bπ′−bπmodq.

This means that either the link value of the signature is P^D=dπ⋅PD, or the ECDLP instance pD=dD⋅G is solved. Because ECDLP is hard and it cannot solve it, σi′ and σj′ are linkable is contradictory and the probability that 𝒜 generates a signature linked to signature σj′ is negligible. For the second case, all signatures generated by 𝒜 are created by different private keys, obviously 𝒜 cannot forge a linkable signature in the second case. The above two cases demonstrate that our scheme is linkable.

5.5 Non-Slanderability

Theorem 5. Our scheme is nonslanderable.

Proof. 𝒮 generates parameters param={E,Fp,G,G,q,H1} to send to 𝒜, and 𝒜 will interact with three random oracles 𝒥𝒪, 𝒞𝒪, and 𝒮𝒪 just like in the proof of Theorem 2. 𝒜 selects a message m, public key set L∗={P0,P1,…,Pn−1}, and a chosen signer π∈[0,n−1] to 𝒮, who will generate a corresponding signature σ=(c0,{si}i=0n−1,{ti}i=0n−1,{bi}i=0n−1,P^D) to return to 𝒜. After interacting with three random oracles, 𝒜 corrupts Pπ∗ to get his private key, and finally can forge another signature of the signer π noted as σ=(c0∗,{si∗}i=0n−1,{ti∗}i=0n−1,{bi∗}i=0n−1,P^D∗). P^D∗=dπ∗⋅PD and P^D=dπ⋅PD can successfully pass the verification of algorithm Linkability of our scheme, and we get P^D∗=dπ∗⋅PD=dπ⋅PD=P^D, and it is oblivious that dπ∗PD=dπPD.The final result is dπ∗=dπ, which contradicts the fact that 𝒜 has not queried dπ. Therefore, our scheme meets non-slanderability.

5.6 Security of Our Scheme in the Blockchain

Based on framework Section 4.2, the public-private key pairs of both parties are generated by the Setup algorithm and KeyGen algorithm of our scheme. The Signature algorithm of our scheme generates a signature σ for the final transaction. The security of this part is guaranteed by the security of schemes like [5,7,32]. To finding a real signer of ring signature in the blockchain, it needs to use the consensus algorithm of the blockchain or get the private key corresponding to the PD, so the adversary cannot query the real signer unless it can cheat the consensus nodes of the blockchain or solve the discrete logarithm problem. For the double-spending attack, the nodes within the blockchain system are capable of detecting double-spending attacks by verifying if the links in the ring signatures of two different transactions are identical. As a result, the system can effectively prevent such attacks.

6  Performance Analysis

In this section, this paper analyzes the computation complexity of our scheme and implement it on a personal computer.

6.1 Complexity Analysis

Some of the notation this paper needs to use for complexity analysis are given below:

•   Th:Time costs to run one hash function H1.

•   TGmul:Time costs of running one multiplication operation in additive group G.

•   Tp:Time costs of running one bilinear pair operation.

•   Tm: Time costs of running one multiplication operation in field Zq∗.

•   Te: Time costs of running one exponentiation operation in field Zq∗.

•   n: The size of Public key set.

•   ℒ: Security parameter.

This paper provides a theoretical analysis of the primary algorithms used in some schemes, as given in Table 2. Theoretically, the consumption of algorithm Signature and Verification is nearly equal and their values are 6(n−1)TGmul+nTh and 6nTGmul+nTh, respectively. For algorithm confirmation, this paper takes into account the consumption in the worst case, where all ring signature members need to be checked. According to Table 2, our method has a faster theoretical efficiency than other schemes on algorithm confirmation, where all schemes consider the worst case. Our approach only costs nTGmul, which is significantly cheaper than some of the previous constructions. Incidentally, this paper sacrifices the efficiency of the signature and verification process to improve the efficiency of the validation process, which results in a less efficient signature and verification process for our scheme than other schemes, and it requires internal storage of a private key and ensures that the private key is not compromised. Most importantly, our method is non-interactive and does not request for any ring members to participate, which is a security that interactive protocols do not offer when an illegal transaction takes place and needs to query the signer of the ring signature without being spoofed by a malicious signer. Additionally, our scheme is linkable to prevent the double-spending attack in blockchain transactions. The particular advantages of our scheme are shown in Table 3.

6.2 Implementation

This paper used the VMware Workstation Pro experiment with AMD CPU Ryzen 5 5600H Radeon Graphics @ 3.30 GHz and 16.0 GB RAM. This paper deployed Hyperledger Fabric v1.4.0 on Ubuntu 18.04 to test the smart contract. This paper used Pypbc of Python 3.6.9 to simulate our scheme and compared schemes, running 200 simulations before averaging the results. Notably, this paper uses the BLS12 curve to support bilinear pairings, and the form of the curve is y2=x3+15 defined over a finite field Fq∗, where q is a prime and |q| = 383, and choose SHA-256 as the hash function this paper uses. The time consumption of the signature and verification procedures in our approach, as shown in Figs. 2 and 3, is almost linear with the ring size. When the ring size is 8, the time consumption of the signature and verification algorithms respectively are 116 ms and 170 ms, which is a relatively small time cost. The signature and verification algorithms take 231 ms and 304 ms, respectively, to run when the ring size is 16. When the ring size is 40, the algorithms for signature and verification execute in 560 ms and 791 ms, respectively. The time costs of signature and verification in our method are slightly slower but still within a suitable time range because this paper slightly increases the computation to increase the security and efficiency of the validation process.

Figure 2: Running times of signature for different ring size

Figure 3: Running times of verification for different ring size

As shown in Fig. 4, all schemes simulations were run on the aforementioned personal computer using the same environment. The Confirmation algorithm of our scheme takes far less time than those of other schemes. When the ring size is 4, the time consumption of [30–32], and our scheme are 36, 43, 25, and 2 ms, respectively. The time consumption of [30–32], and our scheme are 215, 300, 141, and 12 ms when the ring size is 24. Time consumption for [30–32], and our scheme when the ring size is 48 are 428, 512, 290, and 26 ms, respectively. The main reason for the larger time consumption of schemes [30,31] is the use of bilinear pair. For scheme [32], its confirmation algorithm is an interactive protocol, and when querying the signer of the ring signature in the worst case, it interacts more often and thus spends more time. From the results in Fig. 4, it can see that the confirmation process of proposed scheme is more efficient.

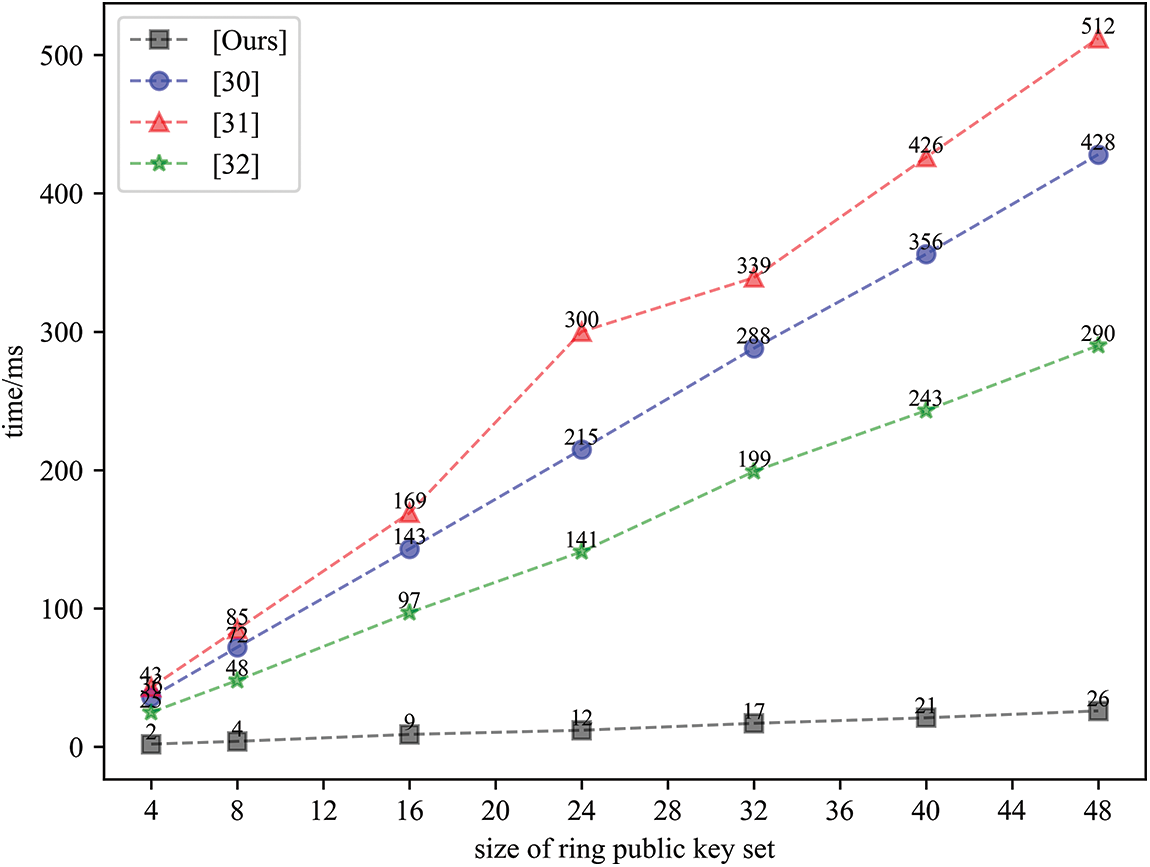
Figure 4: Running times of confirmation for different schemes

This paper created a smart contract in Hyperledger Fabric v1.4.0 and calculated the time costs with various ring sizes. As shown in Fig. 5, the time costs for calling the functions of the smart contract are reasonable.

Figure 5: Time costs of invoking smart contract with different ring size

7  Conclusion

With the rapid development of blockchain applications, the issue of blockchain privacy protection and security in real-life situations becomes increasingly essential. Although a blockchain framework using ring signature technology can safeguard the confidentiality of the identities of both parties to a transaction, this paper still needs to identify the user involved in any illegal transactions. This paper proposes a secure conditionally anonymous linkable ring signature scheme to solve such a problem. The scheme provided in this paper offers a non-interactive and secure confirmation mechanism compared to previous constructions. Proposed scheme is proven to be secure under Elliptic Curve Discrete Logarithm Assumptions. Furthermore, this paper analyzed the performance of proposed scheme. The advantage of proposed scheme over other schemes is that the confirmation algorithm is non-interactive and can provide a link to prevent the double-spending attack in the blockchain. The confirmation algorithm consumes only 2, 16, and 24 ms for ring sizes of 4, 24, and 48, respectively. Designing secure and non-interactive protocols to guarantee conditional anonymity while ensuring that signature and verification algorithms are efficient is the focus of future research.

Acknowledgement: This work is supported in part by the National Key R&D Program of China and National Natural Science Foundation of China.

Funding Statement: This research was funded by the National Key R&D Program of China (Grant Number 2021YFA1000600) and National Natural Science Foundation of China (Grant Number 12171114).

Author Contributions: Study conception and design: Z. Quan, Z. Yulong; data collection: C. Minhui; analysis and interpretation of results: W. Kaijun; draft manuscript preparation: Z. Yulong. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: This article does not involve data availability and this section is not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Nakamoto and A. Bitcoin, A Peer-to-Peer Electronic Cash System, 2008. [Online]. Available: https://bitcoin.org/bitcoin.pdf [Google Scholar]

2. G. Wood, “Ethereum: A secure decentralised generalised transaction ledger,” Yellow Paper, Ethereum Project, Zug, Switzerland, 2014. [Google Scholar]

3. E. Ben-Sasson, “Decentralized anonymous payments from bitcoin,” in 2014 IEEE Symp. on Security and Privacy, San Jose, California, pp. 459–474, 2014. [Google Scholar]

4. D. Hopwood, S. Bowe, T. Hornby and N. Wilcox, Zcash Protocol Specification, 2017. [Online]. Available: https://cryptopapers.info/zcash_protocol/ [Google Scholar]

5. N. van Saberhagen, in Cryptonote v2.0, 2013. [Online]. Available: https://bytecoin.org/old/whitepaper.pdf [Google Scholar]

6. E. Androulaki, A. Barger, V. Bortnikov, C. Cachin, K. Christidis et al., “Hyperledger fabric: A distributed operating system for permissioned blockchains,” in Proc. of the Thirteenth EuroSys Conf., 2018, New York, USA, pp. 1–15, 2018. [Google Scholar]

7. W. Z. Wang, Y. Q. Yang, Z. M. Yin, K. Dev, X. K. Zhou et al., “BSIF: Blockchain-based secure, interactive, and fair mobile crowdsensing,” IEEE Journal on Selected Areas in Communications, vol. 40, no. 12, pp. 3452–3469, 2022. [Google Scholar]

8. L. J. Zhang, Y. F. Zou, M. H. Yousuf, W. Z. Wang, Z. L. Jin et al., “BDSS: Blockchain-based data sharing scheme with fine-grained access control and permission revocation in medical environment,” KSII Transactions on Internet and Information Systems, vol. 16, no. 5, pp. 1634–1652, 2022. [Google Scholar]

9. C. Y. Li, M. X. Dong, J. Li, G. Xu, X. B. Chen et al., “Efficient medical big data management with keyword-searchable encryption in healthchain,” IEEE Systems Journal, vol. 16, no. 4, pp. 5521–5532, 2022. [Google Scholar]

10. W. Z. Wang, H. K. Huang, Z. M. Yin, T. R. Gadekallu, M. Alazab et al., “Smart contract token-based privacy-preserving access control system for industrial internet of things,” Digital Communications and Networks, vol. 9, no. 2, pp. 337–346, 2022. [Google Scholar]

11. Z. B. Zheng, S. A. Xie, H. N. Dai, X. P. Chen and H. M. Wang, “Blockchain challenges and opportunities: A survey,” International Journal of Web and Grid Services, vol. 14, no. 4, pp. 352–375, 2018. [Google Scholar]

12. S. S. Kushwaha, S. Joshi, D. Singh, M. Kaur and H. N. Lee, “Systematic review of security vulnerabilities in ethereum blockchain smart contract,” IEEE Access, vol. 10, pp. 6605–6621, 2022. [Google Scholar]

13. R. L. Rivest, A. Shamir and Y. Tauman, “How to leak a secret,” In: C. Boyd (Ed.Advances in Cryptology–ASIACRYPT 2001, pp. 552–565, Gold Coast, Qld, Australia: Springer, 2001. [Google Scholar]

14. Y. F. Wu, “An e-voting system based on blockchain and ring signature,” Master Dissertation, University of Birmingham, UK, 2017. [Google Scholar]

15. Y. X. Sang, Z. W. Li, L. L. Zhang, H. Jiang and K. C. Li, “Lattice-based identity-based ring signature without trapdoors,” International Journal of Embedded Systems, vol. 11, no. 3, pp. 386–396, 2019. [Google Scholar]

16. M. Nassurdine, H. Zhang and F. G. Zhang, “Identity based linkable ring signature with logarithmic size,” in Information Security and Cryptology: 17th Int. Conf., Inscrypt 2021, Virtual Event, pp. 42–60, 2021. [Google Scholar]

17. E. Fujisaki and K. Suzuki, “Traceable ring signature,” Public Key Cryptography–PKC 2007, pp. 181–200, 2007. [Google Scholar]

18. S. Noether and B. Goodell, “Triptych: Logarithmic-sized linkable ring signatures with applications,” in Data Privacy Management, Cryptocurrencies and Blockchain Technology, Guildford, UK, pp. 337–354, 2020. [Google Scholar]

19. S. Chow and W. Yap, “Certificatelessring signature,” Cryptology ePrint Archive, Report 2007/236, 2007. [Google Scholar]

20. Y. Y. Zhang, J. W. Zeng, W. Li and H. L. Zhu, “A certificateless ring signature scheme with high efficiency in the random oracle model,” Mathematical Problems in Engineering, vol. 2017, 2017. [Google Scholar]

21. L. Z. Deng, H. Y. Shi and Y. Gao, “Certificateless linkable ring signature scheme,” IEEE Access, vol. 2020, no. 8, pp. 54641–54651, 2020. [Google Scholar]

22. J. K. Liu, V. K. Wei and D. S. Wong, “Linkable spontaneous anonymous group signature for ad hoc groups,” Australasian Conference on Information Security and Privacy, vol. 2004, no. 4, pp. 325–335, 2004. [Google Scholar]

23. M. Naor, “Deniable ring authentication,” in CRYPTO 2002: 22nd Annual Int. Cryptology Conf. Santa Barbara, California, USA, pp. 481–498, 2002. [Google Scholar]

24. E. Bresson, J. Stern and M. Szydlo, “Threshold ring signatures and applications to ad-hoc groups,” in CRYPTO 2002: 22nd Annual Int. Cryptology Conf. Santa Barbara, California, USA, vol. 2002, pp. 465–480, 2002. [Google Scholar]

25. J. Lv and X. Wang, “Verifiable ring signature,” in CANS’03–Third Int. Workshop on Cryptology and Network Security, DMS Proc., USA, pp. 663–667, 2003. [Google Scholar]

26. P. Behrouz, P. Grontas, V. Konstantakatos, A. Pagourtzis and M. Spyrakou, “Designated-verifier linkable ring signatures,” Information Security and Cryptology, Seoul, South Korea, vol. 2022, pp. 51–70, 2022. [Google Scholar]

27. S. Noether and A. Mackenzie, “Ring confidential transactions,” Ledger, vol. 2016, no. 1, pp. 1–18, 2016. [Google Scholar]

28. S. F. Sun, M. H. Au, J. K. Liu and T. H. Yuen, “RingCT 2.0: A compact accumulator-based (linkable ring signature) protocol for blockchain cryptocurrency monero,” in Computer Security–ESORICS 2017: 22nd European Symp. on Research in Computer Security, Oslo, Norway, vol. 2017, pp. 456–474, 2017. [Google Scholar]

29. T. H. Yuen, S. F. Sun, J. K. Liu, M. H. Au, M. F. Esgin et al., “Ringct 3.0 for blockchain confidential transaction: Shorter size and stronger security,” in Int. Conf. on Financial Cryptography and Data Security, vol. 2020, pp. 464–483, 2020. [Google Scholar]

30. S. Zheng, S. Jiang and Z. Qin, “An efficient conditionally anonymous ring signature in the random oracle model,” Theoretical Computer Science, vol. 2012, no. 461, pp. 106–114, 2012. [Google Scholar]

31. Y. Z. Jiang, M. X. He, X. H. Zhang and L. Xiong, “Blockchain-based anonymous authentication mechanism with semi-ttp for vanets,” in 2021 IEEE 6th Int. Conf. on Cloud Computing and Big Data Analytics (ICCCBDA), Chengdu, China, vol. 2021, pp. 657–666, 2021. [Google Scholar]

32. X. Zhang and C. Ye, “A novel privacy protection of permissioned blockchains with conditionally anonymous ring signature,” Cluster Computing, vol. 25, no. 2, pp. 1221–1235, 2022. [Google Scholar]

33. W. Gao, L. Chen, Y. P. Hu, C. J. P. Newton, B. C. Wang et al., “Lattice-based deniable ring signatures,” International Journal of Information Security, vol. 18, no. 3, pp. 355–370, 2019. [Google Scholar]

34. H. W. Jia and C. M. Tang, “Cryptanalysis of a non-interactive deniable ring signature scheme,” International Journal of Information Security, vol. 20, no. 1, pp. 103–112, 2021. [Google Scholar]

35. S. Park and A. Sealfon, “It wasn’t me! repudiability and claimability of ring signatures,” in Advances in Cryptology–CRYPTO 2019: 39th Annual Int. Cryptology Conf., Santa Barbara, CA, USA, vol. 2019, pp. 159–190, 2019. [Google Scholar]

36. H. Lin and M. Q. Wang, “Repudiablering signature: Stronger security and logarithmic-size,” Computer Standards & Interfaces, vol. 80, 2022. [Google Scholar]

37. J. Herranz and G. Sáez, “Forking lemmas for ring signature schemes,” in Int. Conf. on Cryptology in India, New Delhi, India, vol. 2003, pp. 266–279. [Google Scholar]