A Novel Incremental Attribute Reduction Algorithm Based on Intuitionistic Fuzzy Partition Distance

1  Introduction

Attribute reduction has long been known as one of the pivotal problems in data preprocessing. The purpose of attribute reduction is to select important attributes and remove redundant or unnecessary ones from decision tables to enhance the efficiency of the classification models, especially for high dimension data. Dubois and Prade applied the fuzzy rough set (FRS) theory to the problem of attribute reduction for addressing directly with the original decision tables consisting of a numerical domain, instead of discretized data. According to this approach, some researches have been published based on fuzzy approximate space. Some typical methods comprise fuzzy membership function [1], fuzzy positive region [2–4], fuzzy information entropy [5–8] and fuzzy distance [9].

In big data trend, the decision tables have often the high dimension and may be updated regularly. The process of adding and removing objects is usually taking place. This problem has brought many difficulties to the traditional attribute reduction approaches. Firstly, the algorithms can meet an obstacle of processing speed and storage space on the high-dimensional decision tables. Secondly, for updated decision tables, the algorithms must also compute the reduct on the entire decision table again which makes to increase the computational time. To deal more effectively with these issues, many researchers proposed some incremental computational techniques for finding the reduct on the dynamic decision table. The incremental methods only update the subset of selected attributes on the altered part of data without re-computing it on the whole decision table. Hence, the processing time can be reduced significantly. Furthermore, with the high-dimensional decision table, it is possible to split data into many parts and apply incremental attribute reduction algorithms. Based on the FRS approach, the incremental algorithms are proposed for solving cases, including addition and removal of the object set [10–14] or the attribute set [15]. Additionally, some researchers extended the incremental algorithms to address incomplete dynamic decision tables. In particular, Giang et al. constructed the tolerance rough set to design hybrid incremental algorithms when supplementing and removing object sets [16]. Afterwards, Thang et al. also developed some formulas for their incremental algorithms for two cases of adding and removing attribute sets [17]. However, Hung et al. showed that the FRS based attribute reduction approach is less efficient in noisy data sets with the low classification accuracy [18].

Recently, some researchers proposed new models using intuitionistic fuzzy sets (IFSs) to solve the attribute selection problem. These models were designed to minimize the noisy information on the decision tables by using a further non-membership function which can adjust noisy objects to give a suitable classification [19]. For such noisy data sets, the IFS based attribute reduction algorithms have often the better processing ability than algorithms using other approaches, such as rough sets or fuzzy rough sets. From the IFSs approach, Tan et al. [20] constructed intuitionistic fuzzy conditional entropy measures and proposed a heuristic algorithm for finding a relative reduct. Then, Thang et al. [21] built a distance measure based on the IFS model. By using the constructed distance measure, they proposed the IFDBAR algorithm in the filter approach to select a subset of important attributes. The experimental results showed that IFDBAR achieved the superior classification ability to the FRS approach on the noisy data sets, especially in case of the low initial classification accuracy.

It can be said that the intuitionistic fuzzy set is a very efficient approach for attribute reduction on the noisy data sets. The subset of features selected from the IFS based algorithms can significantly improve the classification performance of the machine learning models. As mentioned, however, the IFS approach also exists a serious limitation that is the high computational time. Therefore, the attribute reduction algorithms using this approach are often ineffective in dealing with high-dimensional and large datasets. This motivated us to develop a novel incremental method for finding reducts more quickly and efficiently. Specifically, we present an original method to attribute reduction based on intuitionistic fuzzy partition distance. Then we propose an incremental algorithm to extract important attributes from the decision tables in case of the increase of the object number. In our method, an incremental formula is given to fast calculate the intuitionistic fuzzy partition distance on the decision tables when adding an object set. By theoretical and experimental results, we will demonstrate that the proposed method can enhance the performance of the attribute reduction process in comparing with some other state-of-the-art methods in terms of the computational time and classification accuracy.

The paper is organized as follows. The next section will recall several basic concepts of intuitionistic fuzzy sets and related properties. In Section 3, this paper shall define a new reduct based on the intuitionistic fuzzy partition distance and then propose an effective attribute reduction method. This paper will also provide an incremental algorithm for finding reducts on the dynamic decision tables. Section 4 will present experimental results as well as some related analyses. In the last section of this paper, we will draw several conclusions with future works.

2  Preliminary

This section will summarize some basic concepts of intuitionistic fuzzy sets which are an important foundation for proposing an attribute reduction algorithm in the third part of the paper. These basic concepts can be found in [21–23].

First, a decision table is a pair of DT=(U,C∪D), where U is a finite nonempty set of objects, also known as the universe, C and D are finite nonempty sets of attributes such that each a∈C∪D determines a map a:U→Va, where Va is the value set of a. Then, for u∈U and a∈C∪D, the value of a for u is written as a(u). Here, we shall call C as condition attributes and D as decision attributes.

Without losing the comprehensive characteristics, hypothesis D only has one decision attribute d (if D has many attributes, a transformation that can be reduced to an attribute). Accordingly, a decision table can be written as DT=(U,C∪{d}).

Given a decision table DT=(U,C∪{d}), an intuitionistic fuzzy set (IFS) P on U has the form P={⟨u,μP(u),ϑP(u)⟩|u∈U}, in which μP(u):U→[0,1] and ϑP(u):U→[0,1] are respectively the membership and non-membership degrees of u in P such that 0≤μP(u)+ϑP(u)≤1,∀u∈U [22].

The hesitant degree of u in P is determined by πP(u)=1−μP(u)−ϑP(u). When πP(u)=0 ∀u∈U, IFS becomes a traditional FS. The cardinality of P is denoted as |P| determined by the formula [23]:

|P|=∑u∈U1+μP(u)−ϑP(u)2(1)

Consider two IFSs P and Q on U, we will define several set operations to compare them as follows:

1.    P⊆Q iff μP(u)≤μP(u) and ϑP(u)≥ϑQ(u) for any u∈U.

2.    P=Q iff P⊆Q and Q⊆P.

3.    P∩Q={(u,min(μP(u),μQ(u)),max(ϑP(u),ϑQ(u)))}

4.    P∪Q={(u,max(μP(u),μQ(u)),min(ϑP(u),ϑQ(u)))} .

To facilitate the deployment of definitions and calculation formulas later, an IFS P will sometimes be briefly represented by two components, membership and non-membership. Specifically, P={μP(u),ϑP(u)|u∈U}.

Let U be the non-empty finite set of objects. An intuitionistic fuzzy binary relation R on U×U is defined as follows:

R={(u,v),μR(u,v),ϑR(u,v)|(u,v)∈U×U}(2)

where μR(u,v)∈[0,1] and ϑR(u,v)∈[0,1] are the similarity and diversity functions, respectively. The pair (μR(u,v),ϑR(u,v)) is called an intuitionistic fuzzy number between two objects u and v, which satisfies 0≤μR(u,v)+ϑR(u,v)≤1.

Then, R is called an intuitionistic fuzzy equivalence relation (IFER) if R satisfies:

1)   Reflexive: iff μR(u,u)=1 and ϑR(u,u)=0 hold for each u∈U.

2)   Symmetric: iff μR(u,v)=μR(v,u) and ϑR(u,v)=ϑR(v,u) hold for each u,v∈U.

3)   Transitive: iff μR(u,v)≥supt∈U{min(μR(u,t),μR(t,v))};ϑR(u,v)≤inft∈U{max(ϑR(u,t),ϑR(t,v))} hold for each u,v∈U.

Given an IFER R on U, an attribute subset A⊆C and an object u∈U, the intuitionistic fuzzy equivalence class (IFEC) of u according to R on A is denoted RA[u], as follows:

RA[u]={(v,μRA[u](v),ϑRA[u](v))|v∈U}(3)

Consider DT=(U,C∪{d}), each A⊆C determines an IFER RA on U. The IFER RA generates an intuitionistic fuzzy partition (IFP) on U, denoted as ψA, ψA={RA[u]| u∈U} in which RA[u]={(v,μRA[u](v),ϑRA[u](v))|v∈U} is an IFEC of u according to RA. We can see that each IFEC RA[u] is also an IFS on U. To simplify the denotation, for each object v, we denote RA[u](v)=(μA[u](v),ϑA[u](v)).

For A,B⊆C, we have RA[u]=∩a∈AR{a}[u] and RA∪B[u]=RA[u]∩RB[u]. This means that RA∪B[u](v)=(min{μA[u](v),μB[u](v)},max{ϑA[u](v),ϑB[u](v)}) and ψA∪B=ψA∩ψB.

With A⊆C, there are two special cases:

- If RA[u](v)=(0,1),u≠v and RA[u](v)=(1,0) where v∈U then |RA[u]|=1, the IFP ψA is assumed as the smoothest case and it is denoted by ψω.

- If RA[u](v)=(1,0) where v∈U then |RA[u]|=m, the IFP ψA is assumed as the most unsmooth case and it is denoted by ψδ.

Suppose we are given two IFPs ψA and ψB. We say that ψA is finer than ψB, denoted ψA⪯ψB, if for all u∈U, RA[u]⊆RB[u].

3  Attribute Reduction Methods

3.1 Attribute Reduction Based on IFPD

This paper will present in this section a new method for finding a reduct set based on the IFP distance. The cardinal steps of the algorithm are structured as follows. Firstly, we introduce the distance between two IFPs. Then, we define the reduct and the significance of the attribute. Finally, we construct a heuristic algorithm based on the IFP measure.

Given DT=(U,C∪{d}) with U={u1,u2,…,um} and the intuitionistic fuzzy partitions ψA,ψB generated by the intuitionistic fuzzy equivalence classes RA[ui], RB[ui], for all ui∈U and A,B⊆C, then

𝒟(ψA,ψB)=∑i=1m(|RA[ui]∪RB[ui]|−|RA[ui]∩RB[ui]|)m2(4)

is an intuitionistic fuzzy partition distance (IFPD) between ψA and ψB [21].

It is easy to see that the minimum value of 𝒟(ψA,ψB) is equal to 0 when ψA=ψB and the maximum value of 𝒟(ψA,ψB) reaches as m−1m if and only if ψA=ψδ and ψB=ψω (or ψA=ψω and ψB=ψδ). Thus, we have 0≤𝒟(ψA,ψB)≤m−1m.

Based on 𝒟(ψA,ψB), IFPD created by C and C∪{d} on U is computed by:

𝒟(ψC,ψC∪{d})=∑i=1m(|RC[ui]|−|RC[ui]∩R{d}[ui]|)m2(5)

Clearly, if B⊆C, then 𝒟(ψB,ψB∪{d})≥𝒟(ψC,ψC∪{d}). Hence, the intuitionistic fuzzy partition distance satisfies the non-monotonous property with respect to the set of condition attributes. It implies that the size of B is the inverse of the value of 𝒟(ψB,ψB∪{d}). Then, the greater the value of 𝒟(ψB,ψB∪{d}) is, the smaller the size of B is. We can use the intuitionistic fuzzy partition distance as a criterion for choosing attributes in the process of attribute reduction.

Definition 1. Let DT=(U,C∪{d}). A subset M⊆C is called a reduct of C if

1. 𝒟(ψM,ψM∪{d})=𝒟(ψC,ψC∪{d}),

2. ∀M′⊂M,D(ψM′, ψM′∪{d})>D(ψM, ψM∪{d}).

This definition implies that for any b∈M, if 𝒟(ψM\{b},ψM\{b}∪{d})≠𝒟(𝒫C,𝒫C∪{d}), then b is indispensable in M. In contrast, b will be called a redundant attribute in M.

Definition 2. Let DT=(U,C∪{d}), M⊆C and b∈C/M. Then the significance measure of b with respect to M, denoted SIGM(b), is determined by the formula:

SIGM(b)=𝒟(ψM,ψM∪{d})−𝒟(ψM∪{b},ψM∪{b}∪{d})(6)

It can be easily seen that SIGM(b)≥0. Consider any attribute b∈C, its significance for an attribute subset characterizes the classification quality of b. We can see the alteration of the certainty degree. If the value of SIGM(b) is higher, then the attribute b will be more essential. This measure can be considered as a criterion for selecting the necessary attributes. Based on this definition, we design an effective algorithm to extract an optimal attribute subset from a given decision table. The algorithm begins with an empty set and supplements one attribute with the highest significance into the selected feature subset at each iteration until the condition stops happening. In particular, our attribute reduction method, denoted as Algorithm 1, is designed as illustrated below, and its flowchart can be found in Fig. 1.

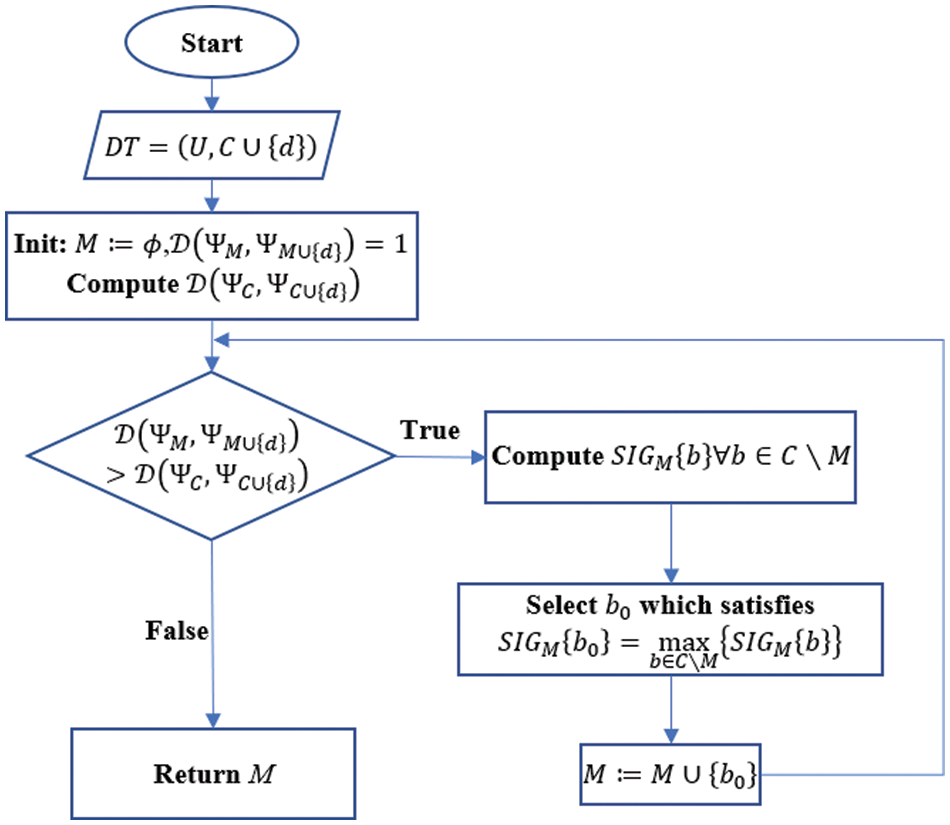
Figure 1: Flowchart of Algorithm 1

We now examine the computational complexity of ARIFPD. Suppose that |C|,|U| are the number of condition attributes and instances on the decision table, respectively. It is clear that IFP ψC can be determined in 𝒪(|C|∗|U|2) time. Hence, the computational complexity of calculating 𝒟(ψC,ψC∪{d}) in line 2 is 𝒪(|C|∗|U|2). Besides, it can be easily seen that the computational cost of 𝒟(ψM∪{b},ψM∪{b}∪{d}) is 𝒪(|U|2), and SIGM(b) in line 7 is calculated in 𝒪(|U|2) time. Thus, the computational time of the For loop from line 4 to line 6 is 𝒪(|C|∗|U|2) and the computational time of the loop While from line 3 to line 9 is 𝒪(|C|2∗|U|2). Summary, ARIFPD has the time complexity to be 𝒪(|C|2∗|U|2).

3.2 Incremental Attribute Reduction Algorithm

We will propose this section an incremental algorithm using IFPD when supplementing a new object set into a given decision table. We now begin with providing a formula to quickly calculate IFPD after supplementing an object set which is extended in [21].

Proposition 1. Given DT=(U,C∪{d}) with U={u1,u2,…,um}, intuitionistic fuzzy equivalence relations RC, R{d} and a new object set ΔU={um+1,um+2,…,um+s}, s≥1, the IFPD between ψC and ψC∪{d} on U∪ΔU is determined by:

𝒟U∪ΔU(ψC,ψC∪{d})=m2∗𝒟U(ψC,ψC∪{d})(m+s)2+2∗∑i=1s(|RC[um+i]|−|RC[um+i]∩R{d}[um+i]|−ζi)(m+s)2(7)

where ζ1=0 and for i≥2, ζi=12∑j=is−1(μC[um+i](um+j+1)−min{μC[um+i](um+j+1),μ{d}[um+i](um+j+1)}−ϑC[um+i](um+j+1)+max{ϑC[um+i](um+j+1),ϑ{d}[um+j](um+j+1)})

Proof:

It is easy to see that if s=1, we have:

𝒟U∪ΔU(ψC,ψC∪{d})=m2∗𝒟U(ψC,ψC∪{d})(m+s)2+2∗∑i=1s(|RC[um+i]|−|RC[um+i]∩R{d}[um+i]|)(m+s)2

To simplify for the proof of this proposition, we will set:

ζij=12(μC[ui](uj)−min{μC[ui](uj),μ{d}[ui](uj)}−ϑC[ui](uj)+max{ϑC[ui](uj),ϑ{d}[ui](uj)})

Since U is added s objects, the formula in (5) becomes:

𝒟U∪ΔU(ψC,ψC∪{d})=∑i=1m+s(|RC[ui]|−|RC[ui]∩R{d}[ui]|)(m+s)2

=1(m+s)2(∑i=1m+s(ζ1i)+…+∑i=1m+s(ζmi)+∑i=1s(|RC[um+i]|−|RC[um+i]∩R{d}[um+i]|))

=1(m+s)2(∑i=1m(ζ1i)+…+∑i=1m(ζmi)+∑i=1s(ζ1m+i)+…+∑i=1s(ζmm+i)+∑i=1s(ζm+1m+i)+…+∑i=1s(ζm+sm+i)−(∑i=1s(ζm+1m+i)+…+∑i=1s(ζm+sm+i))+∑i=1s(|RC[um+i]|−|RC[um+i]∩R{d}[um+i]|))

We have

∑i=1s(ζ1m+i)+…+∑i=1s(ζmm+i)+∑i=1s(ζm+1m+i)+…+∑i=1s(ζm+sm+i)=∑i=1s(|RC[um+i]|−|RC[um+i]∩R{d}[um+i]|),

∑i=1m(ζ1i)+…+∑i=1m(ζmi)=m2∗𝒟U(ψC,ψC∪{d}),(∑i=1s(ζm+1m+i)+…+∑i=1s(ζm+sm+i))=∑i=1s∑j=1s(ζm+im+j),

thus 𝒟U∪ΔU(ψC,ψC∪{d})=1(m+s)2(m2∗𝒟U(ψC,ψC∪{d})+2∗∑i=1s(|RC[um+i]|−|RC[um+i]∩R{d}[um+i]|)−∑i=1s∑j=1s(ζm+im+j))

Furthermore, ζii=0 and ζij=ζji, we get ∑i=1s∑j=1s(ζm+im+j)=2∑i=1s∑j=is−1(ζm+im+j+1)=2∑i=1sζi.

Hence, 𝒟U∪ΔU(ψC,ψC∪{d})=m2∗𝒟U(ψC,ψC∪{d})(m+s)2+2∗∑i=1s(|RC[um+i]|−|RC[um+i]∩R{d}[um+i]|−ζi)(m+s)2.

The formula (6) consists of two main components. The first component computes the distance of two intuitionistic fuzzy partitions without adding the set of new objects. This component is already determined from the previous stages. Therefore, the incremental formula provided in Proposition 1 allows us to only executes on the second component consisting of the intuitionistic fuzzy equivalence classes generated by the additions of the new object set. From this formula, we will replace the formula (5) to conduct on the decision table when supplementing new objects. Accordingly, the algorithm will reduce the computational complexity and obtain a proximate reduct set.

Proposition 2. Let DT=(U,C∪{d}) with U={u1,u2,…,um}. Suppose that M⊆C is a reduct based on IFPD on U and ΔU={um+1,um+2,…,um+s}, s≥1, is an incremental object set. Then

1.    If all objects in ΔU have the same value of decision attribute then

𝒟U∪ΔU(ψC,ψC∪{d})=m2∗𝒟U(ψC,ψC∪{d})(m+s)2+2∗∑i=1s(|RC[um+i]|−|RC[um+i]∩R{d}[um+i]|)(m+s)2

2.    If RM[um+i]⊆R{d}[um+i] for i=1,2,…,s then 𝒟U∪ΔU(ψM,ψM∪{d})=𝒟U∪ΔU(ψC,ψC∪{d})

Proof:

For any i=1,2,…,s and j=1,2,…,(s−1), we consider:

1.    If all objects in ΔU have the same value of decision attribute, then we have μ{d}[um+i](um+j+1)=1 and ϑ{d}[um+j](um+j+1)=0. Thus, min{μC[um+i](um+j+1),μ{d}[um+i](um+j+1)}=μC[um+i](um+j+1) and max{ϑC[um+i](um+j+1),ϑ{d}[um+j](um+j+1)}=ϑC[um+i](um+j+1), from Proposition 1, the formula in the first case is obtained.

2.    If RM[um+i]⊆R{d}[um+i] then RC[um+i]⊆RM[um+i]⊆R{d}[um+i].

Hence |RM[um+i]∩R{d}[um+i]|=|RM[um+i]| and |RC[um+i]∩R{d}[um+i]|=|RC[um+i]|. Thus, we get these equations |RM[um+i]|−|RM[um+i]∩R{d}[um+i]|=0 and |RC[um+i]|−|RC[um+i]∩R{d}[um+i]|=0. More importantly,

min{μM[um+i](um+j+1),μ{d}[um+i](um+j+1)}=μM[um+i](um+j+1),max{ϑM[um+i](um+j+1),ϑ{d}[um+j](um+j+1)}=ϑM[um+i](um+j+1),min{μC[um+i](um+j+1),μ{d}[um+i](um+j+1)}=μC[um+i](um+j+1),max{ϑC[um+i](um+j+1),ϑ{d}[um+j](um+j+1)}=ϑC[um+i](um+j+1).

Based on Proposition 1, we get:

𝒟U∪ΔU(ψC,ψC∪{d})=(mm+s)2𝒟U(ψC,ψC∪{d}) and 𝒟U∪ΔU(ψM,ψM∪{d})=(mm+s)2𝒟U(ψM,ψM∪{d}).

Because M is a reduct of C, from the definition 1, we obtain 𝒟U(ψM,ψM∪{d})=𝒟U(ψC,ψC∪{d}). Thus 𝒟U∪ΔU(ψM,ψM∪{d})=𝒟U∪ΔU(ψC,ψC∪{d}). The proof is complete.

The result of Proposition 2 shown that the incremental algorithm for IFPD based Attribute Reduction when Adding Objects (ARIFPD_AO) comprises four main steps as in Algorithm 2 and its corresponding flowchart is visually represented in Fig. 2.

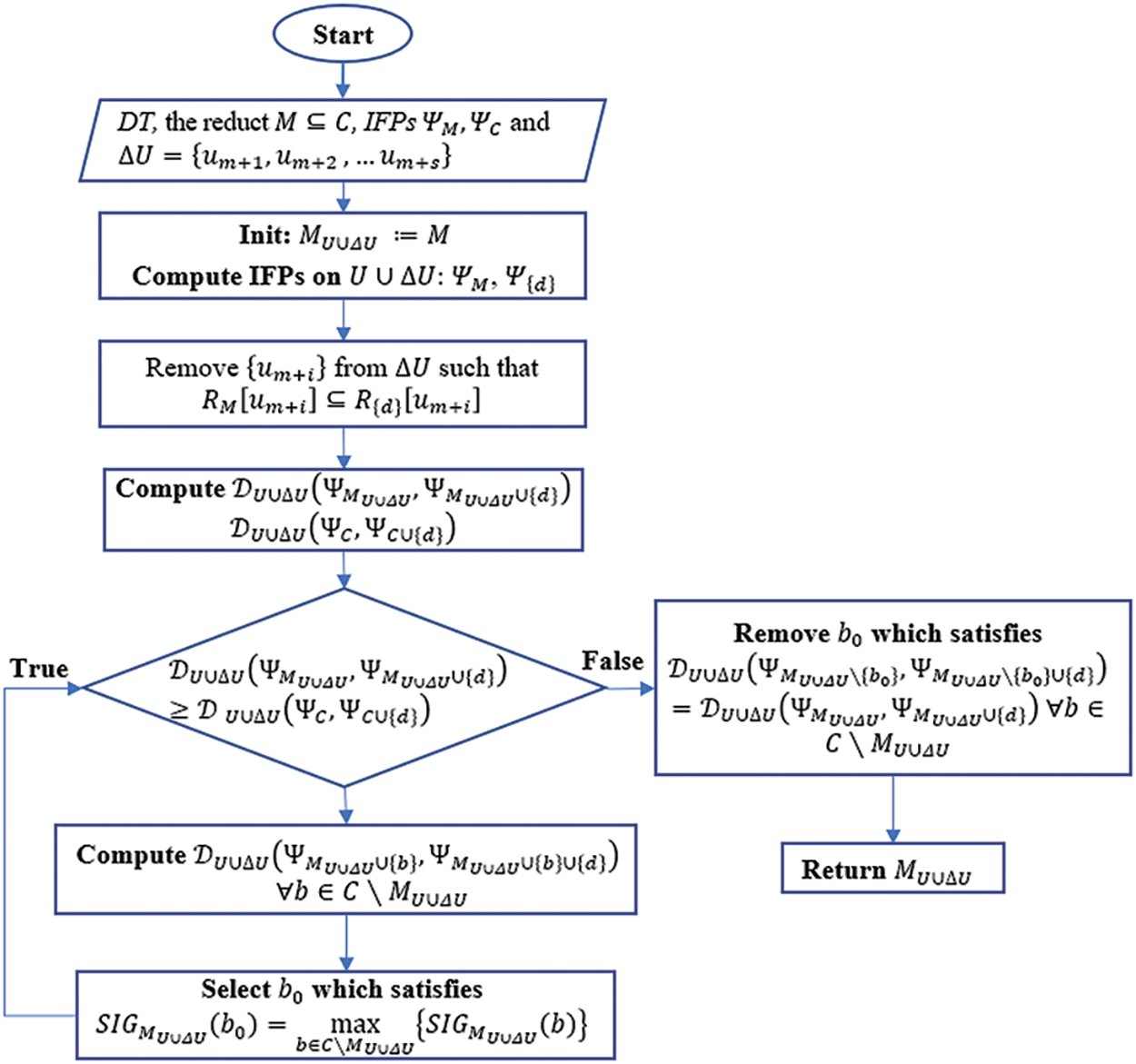
Figure 2: Flowchart of Algorithm 2

We continue to evaluate the computational complexity of the algorithm ARIFPD_AO. We use 3 symbols |C|,|U| and |ΔU| to denote the number of condition attributes, original instances, and instances supplemented to the original set, respectively. The computational complexity of ARIFPD_AO is calculated by the pseudocode above. The computational complexity of computing IFP in line 2 is 𝒪(|MU∪ΔU|∗|ΔU|∗(|U|+|ΔU|)). In the simplest case, the algorithm stops in line 6. Then, the computational time of ARIFPD_AO is 𝒪(|MU∪ΔU|∗|ΔU|∗(|U|+|ΔU|)). For the remaining case the computational time IFPDs in line 9 is 𝒪(|C|∗|ΔU|∗(|U|+|ΔU|)), and the incremental calculation 𝒟U∪ΔU(ψMU∪ΔU∪{b},ψMU∪ΔU∪{b}∪{d}) has a time complexity of 𝒪(|ΔU|∗(|U|+|ΔU|)). Similar to the computational complexity of ARIFPD, the complexity of the loop While in algorithm ARIFPD_AO is 𝒪((|C|−|MU∪ΔU|)2∗|ΔU|∗(|U|+|ΔU|)). From lines 17 to 20, the time complexity of the loop For is 𝒪(|C|2∗|ΔU|∗(|U|+|ΔU|)). Therefore, the complexity of the algorithm in the worst case is 𝒪(|C|2∗|ΔU|∗(|U|+|ΔU|)). The computational complexity of the algorithm is max{𝒪(|MU∪ΔU|∗|ΔU|∗(|U|+|ΔU|)),𝒪(|C|2∗|ΔU|∗(|U|+|ΔU|))}. Thus, the incremental algorithm ARIFPD_AO has the ability to reduce the time complexity.

4  Experiments

In the previous sections, this paper presented an incremental approach based on IFPD to process the dynamic decision table. The paper will demonstrate this part with some experiments to prove the efficiency of our method (ARIFPD_AO). The paper compares the efficiency of the ARIFPD_AO, IFSA in [24] and FDAR_AO in [10] through three criteria: Classification accuracy performance based on classifier KNN (k =10) with tenfold cross-validation, size of reduct and computation time.

4.1 Experiments Setup

Experimental data: To prove the efficiency of the proposed method, we conduct experiments on some benchmark datasets from the UCI Machine learning repository [25]. The experimental data focuses mainly on sets with low initial classification accuracy and with a large number of instances. Data set is split up two subsets with the same number of objects. The first subset is denoted by Uori (Column 5 in Table 1) is used in the algorithm ARIFPD to find the reduct and Uinc (Column 6 in Table 1) is used in the incremental algorithm ARIFPD_AO. Next, the incremental set Uinc is separated into six equal parts U1, U2, U3, U4, U5, U6 respectively.

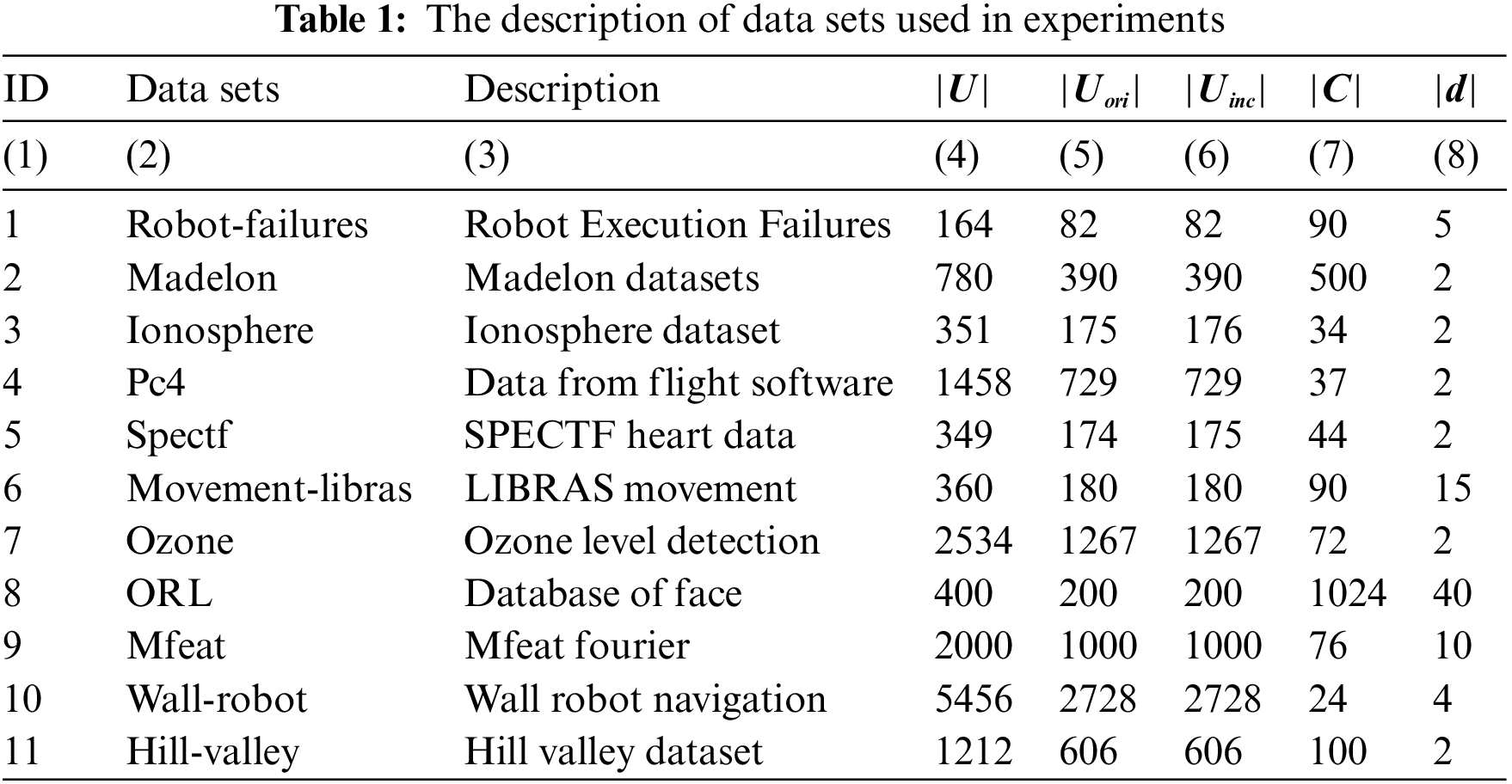
In Table 1, columns |U|, |Uori|, |Uinc|, |C|, |d| are used to denote for the number of objects in each data set, objects in Uori, objects in Uinc, conditional attributes, decision classes, respectively.

Experimental scenario:

First, we use algorithms ARIFPD, GFS [25] and FDAR [10] to find the reduct on Uori. Next, based on the reducts obtained from the three algorithms, we evaluate the incremental algorithms ARIFPD_AO, IFSA and FDAR_AO from U1 to U6 of Uinc.

Now, we construct IFERs including the IF similarity degree and IF diversity degree between two objects u and v with respect to the attribute a.

•   If the value domain of a is a continuous value type, then:

μ{a}[u](v)=1−a(u)−a(v)max(a)−min(a)(8)

The above formula determines the intuitionistic fuzzy similarity degree of the object u with the object v, in which min(a) and max(a) are minimal and maximal values corresponding to a. In essence, the denominator component of the formula above is the process of min-max data normalizing to ensure that the values in the decision table are in the range [0,1]. Finally, we compute the intuitionistic fuzzy diversity degree based on the below formula.

ϑ{a}[u](v)=1−μ{a}[u](v)1+λa∗μ{a}[u](v)withλa>0(9)

Clearly, if λa=0 then υ{a}[u](v)=1−μ{a}[u](v) and the pairs υ{a}[u](v) and υ{a}[u](v) will only present the characteristics of FRS. With λa>0, we can see that the intuitionistic fuzzy similarity and diversity degrees are inversely proportional to each other and satisfy 0≤μ[u](v)+υ[u](v)≤1. We recommend the value λa of the attribute a according to the following formula:

λa={1ifσa=0βaσaifσa>0(10)

in which σa=1|U|−1∑u∈U(a(u)−a¯)2 is the standard deviation of the value domain of the attribute a, βa=|𝒫{a}∪{d}F||𝒫{d}F| is the consistency of the attribute a in the decision table, 𝒫{a}∪{d}F is the fuzzy partition of {a}∪{d} and 𝒫{d}F is the fuzzy partition of d. Clearly, if μ{a}[u](v) has a small value, it will lead to a small consistency of a and ϑ{a}[u](v) has a big value.

•   If the value of a is a categorical value, then:

μA[u](v)={1,a(u)=a(v)0,a(u)≠a(v)(11)

and

ϑA[u](v)=1−μA[u](v)(12)

4.2 Experimental Results

As mentioned above, the paper first compares the efficiency of the FDAR, GFS and ARIFPD algorithms. The size and the classification accuracy of reducts are shown in Table 2. Across all the data sets, it is clear that the reducts obtained from ARIFPD are often the smallest size, while the reducts obtained by FDAR still have large sizes on some datasets. The paper next compares the computational time between the three algorithms. The time of the algorithms is calculated after the step data preprocessing to when the reduct of the algorithms is determined. The results from Table 2 show shorter times when running the GFS algorithm on whole datasets. The reason for this is because the algorithms based on FRSs and IFSs must compute relational matrices with many elements. Besides, the FDAR algorithm only uses the similarity degree to calculate, while the ARIFPD algorithm has to calculate both the similarity and the diversity degree. Thus, the computational time of ARIFPD is the most complex. Next, this paper compares three algorithms through the KNN classifier to evaluate the classification capacity of reducts. Table 2 and Fig. 3 display the comparative results, in which the raw data column is the classification accuracy when we use the whole attributes of each data set to appreciate, and columns according to three methods provide the classification accuracies appreciated through the attribute subset chose by those algorithms. It can be emphasized that our method determines the important attributes very efficiently for different data sets. More especially, the comparison with raw data shows that the classification performance of the reduct from the proposed algorithm is superiority over the raw data in 9 cases. There is only one case where our reducts have lower classification accuracy than the raw data. In addition, the average classification accuracy of the method in this study reached 76.9% and the raw data reached 73.1%. Therefore, it indicated that the classification accuracy of the proposed algorithm is significantly higher than the original data. Even more intriguingly, ARIFPD’s reducts yield superior classification results compared to FDAR and GFS across nearly all datasets, despite ARIFPD selecting a smaller number of attributes, as evidenced in Figs. 3 and 4.

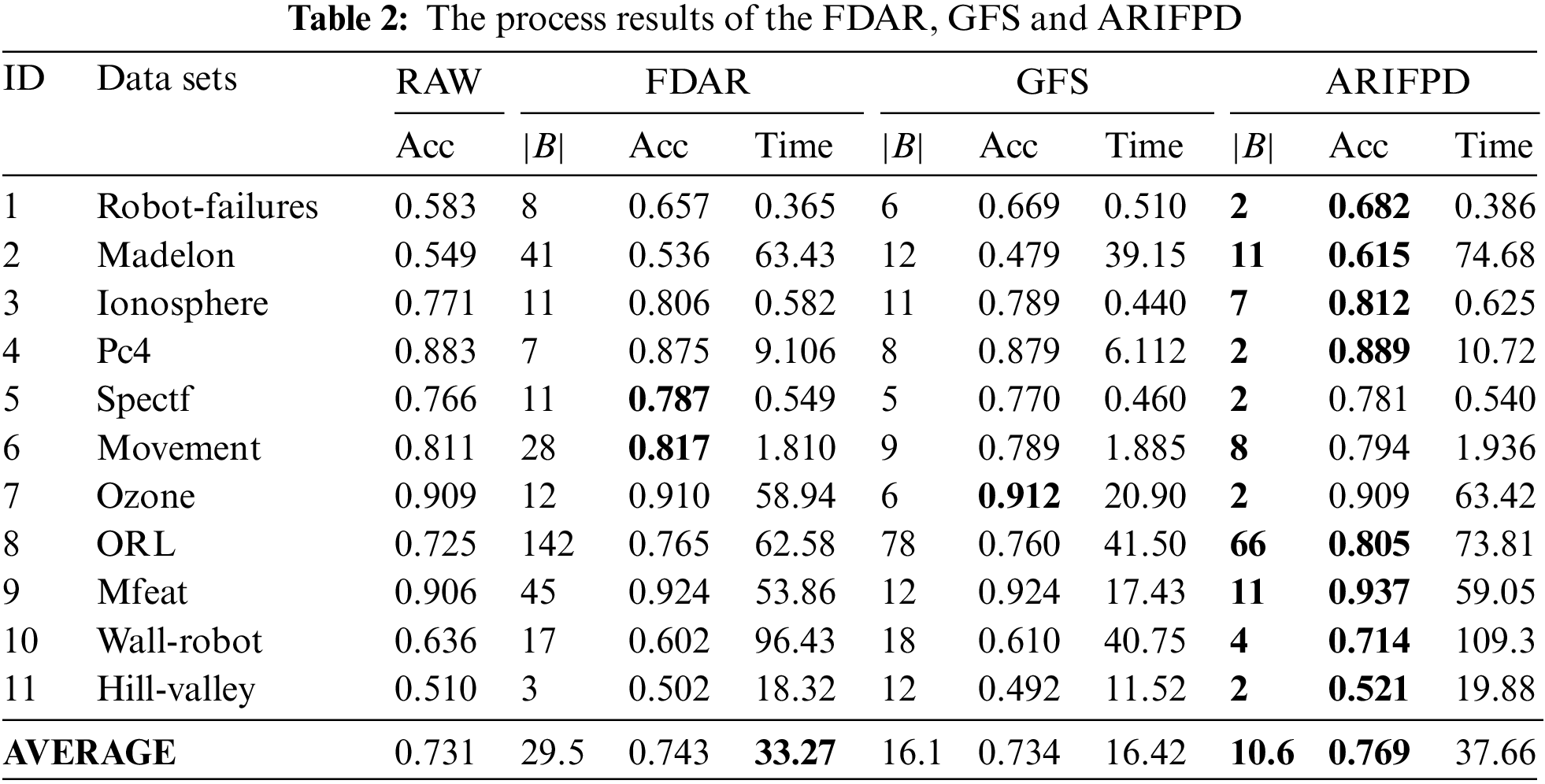
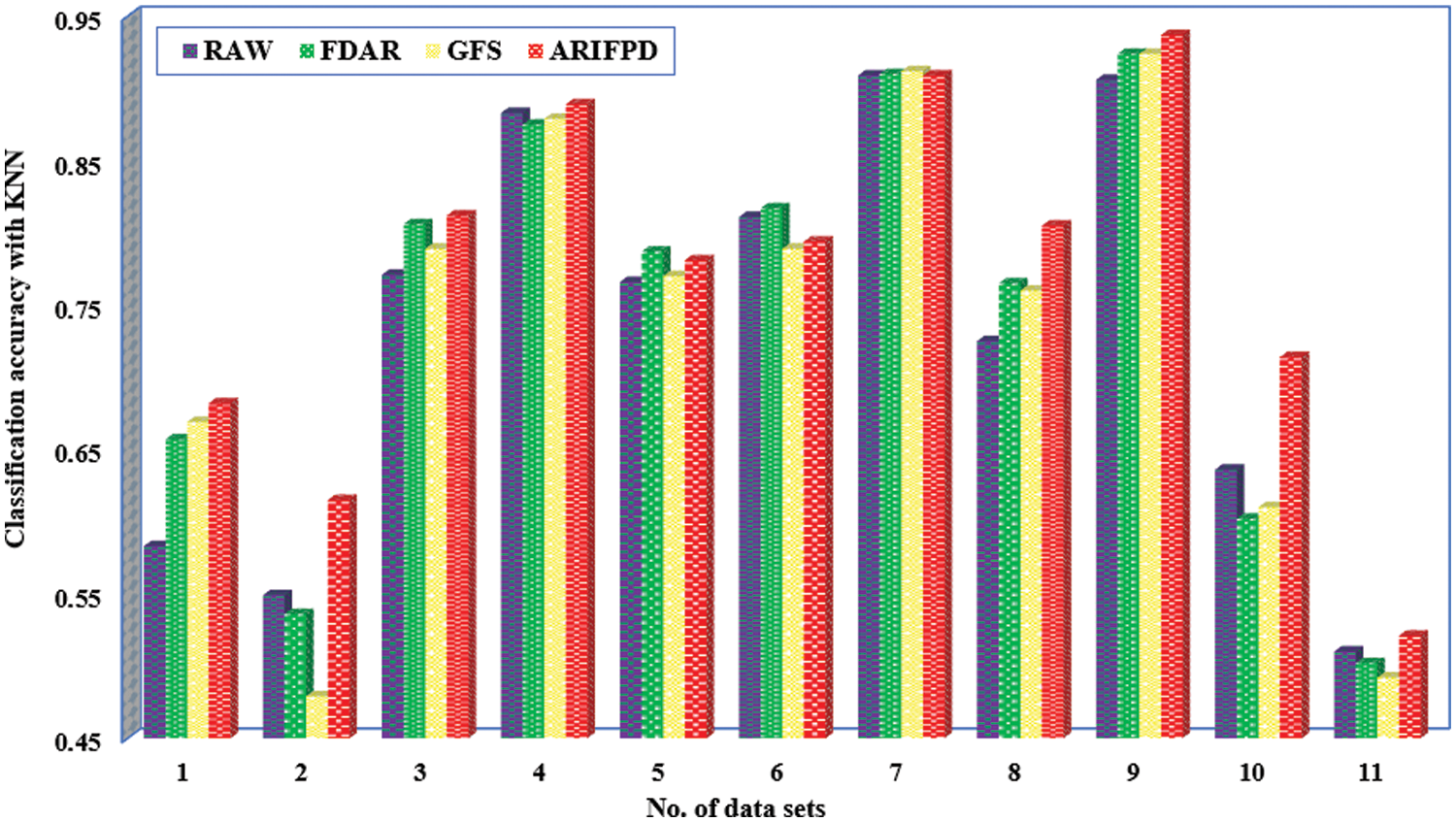
Figure 3: The classification accuracy of the FDAR, GFS and ARIFPD

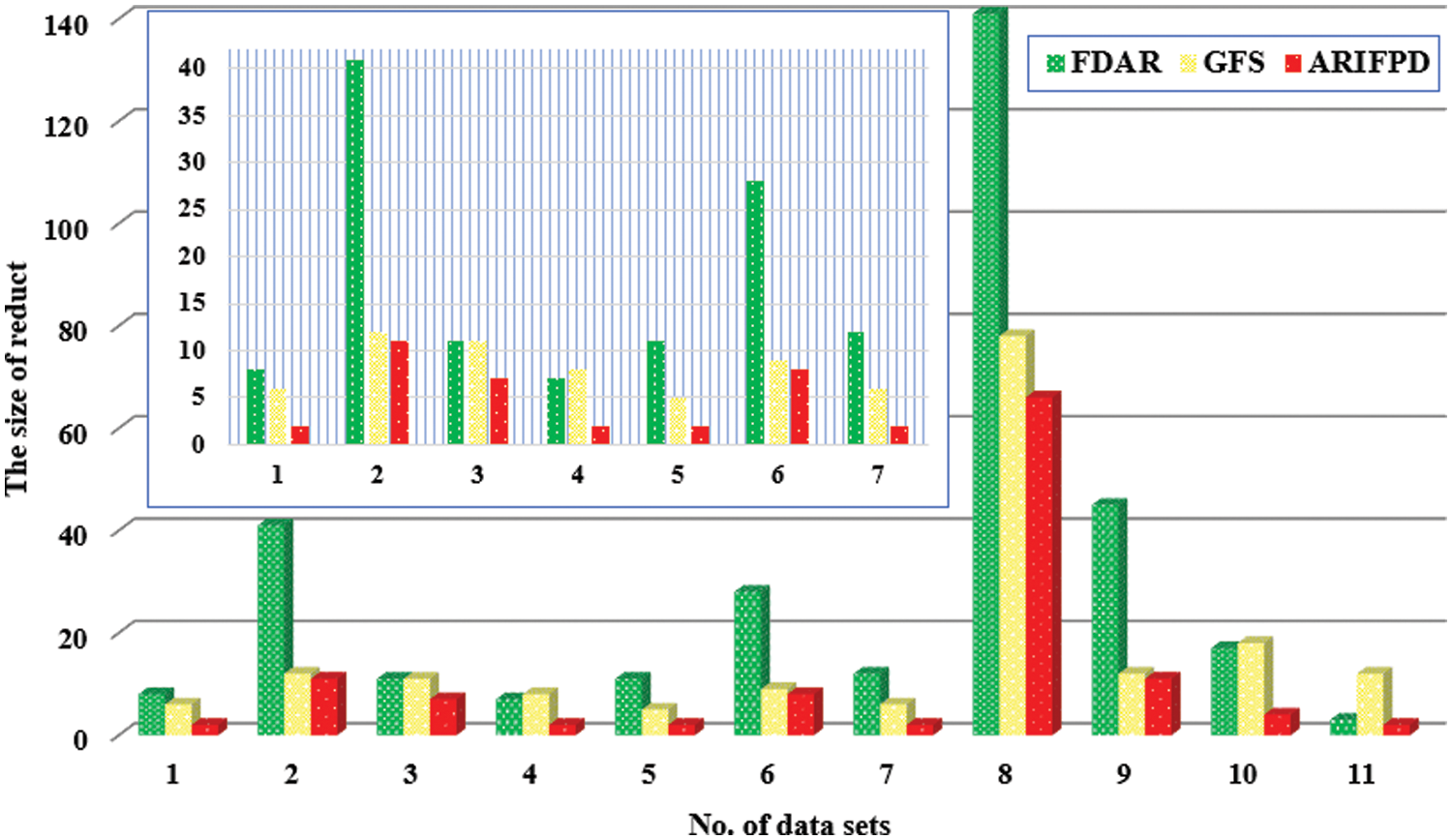
Figure 4: The size of reduct of the FDAR, GFS and ARIFPD

It can be observed more clearly from Table 2 and Fig. 3 that there is one case in the Movement dataset where our reduct has the lower accuracy. However, the average accuracy of our algorithm is also higher than the FDAR and GFS algorithms. It showed that the proposed algorithm has the capacity to select significant attributes for better improvement on the noisy data sets with low classification accuracy.

The performance of the proposed incremental method is appreciated by comparing the FDAR_AO, IFSA and ARIFPD_AO algorithms. First, it is obvious that the incremental algorithms have much faster processing time than the FDAR, IFSA and ARIFPD algorithms because the incremental algorithms compute on the additional parts of the data tables, instead of the whole data table.

Table 3 shows that for most datasets, the execution time of FDAR_AO and IFSA is faster when compared to ARIFPD_AO. It can be also explained similarly with comparing the execution times of the algorithms FDAR and ARIFPD. Furthermore, the proposed algorithm includes a processing step to remove redundant attributes. Hence the processing time of our algorithm will be slower. However, the execution time of ARIFPD_AO is better than FDAR_AO on some data sets, for example Robot-Failure and Ozone. This is because our obtained reduct is smaller than two remaining algorithms. Then the number of loops is conducted less. The accuracy and size of reducts extracted by our method are also investigated in Table 3. For the size of reduct at each incremental phase, ARIFD_AO is much smaller than FDAR_AO and IFSA, especially for several data sets with a large number of attributes, such as Robot-Failure, Libras-Movement.

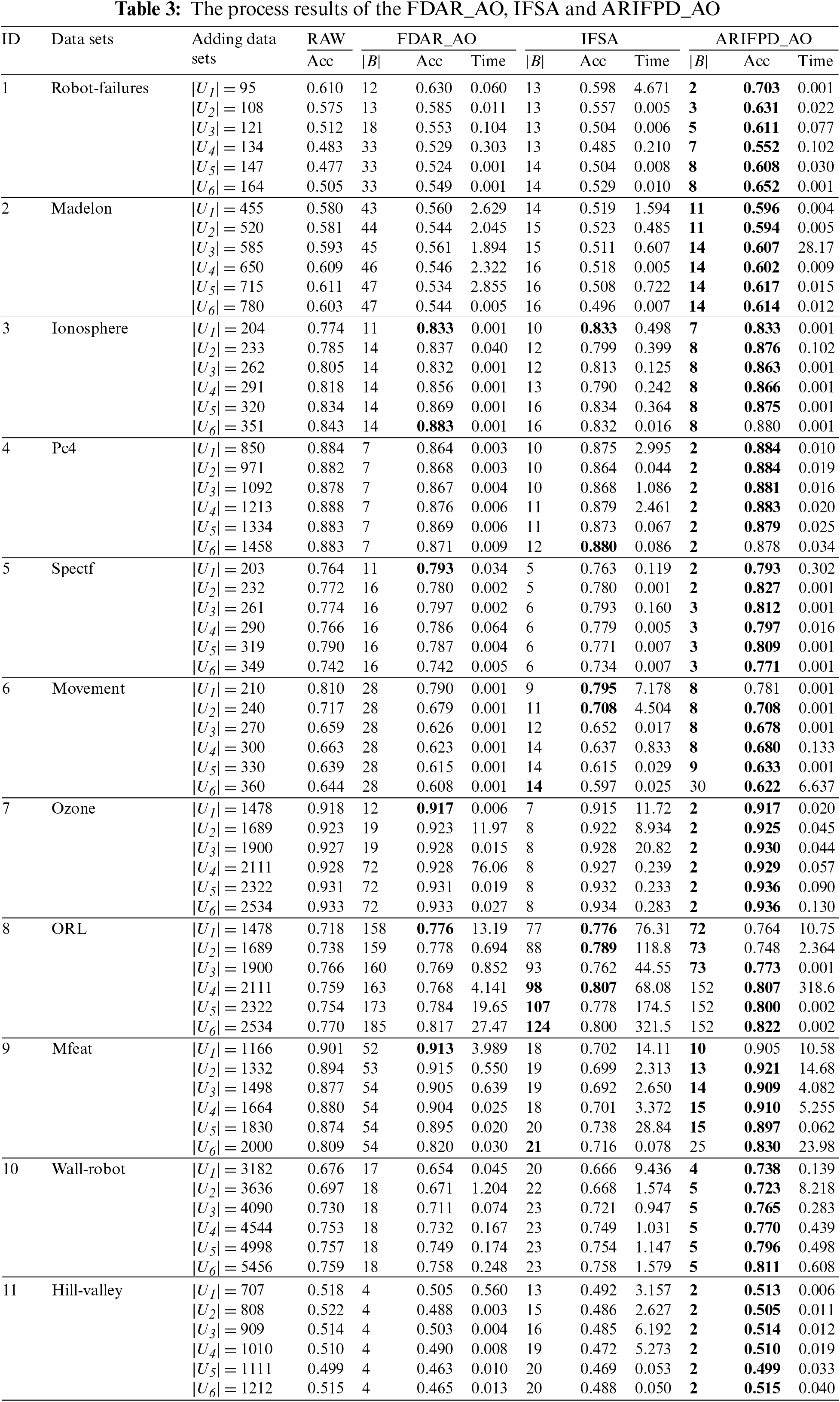
We consider 66 cases when adding the set of objects. There are 7 cases in which our reducts have no higher classification accuracy than the reducts of FDAR_AO. In the remaining 59 cases, the reducts of the proposed method show superiority in accuracy compared to FDBAR_AO and IFSA. Clearly, the proposed incremental method is also very effective on datasets with low initial classification accuracy. In other words, the attribute reduction methods based on the rough set approach and its extensions have many difficulties in improving the classification accuracy for the noisy data.

Based on the accuracy of algorithms in Table 3, paired two-tailed t-tests were also conducted with a confidence level of 0.95 to evaluate the differences between FDAR_AO, IFSA, and ARIFPD_AO. The corresponding p-values (two-tailed) were found at levels 1.17E-10 and 6.85E-10 for KNN. These results provide a sound basis to conclude that our algorithm outperforms the compared algorithms in statistical significance. From the above results, it can be confirmed that the incremental attribute reduction algorithm using the intuitionistic fuzzy set approach has outstanding advantages compared to algorithms based on the fuzzy rough set when processing noisy and inconsistent data.

5  Conclusion

With the primary purpose of reducing the number of features and improving the classification ability, attribute reduction is considered as a critical problem in the data preprocessing step. This paper recommends a measure for intuitionistic fuzzy partition distance and constructs an incremental formula to update the intuitionistic fuzzy partition distance when adding an object set. Thereby, this paper constructs two algorithms based on the intuitionistic fuzzy set approach. The first algorithm proposed to find the reduct on the decision table when there is no additional set of objects. The second algorithm is the incremental algorithm to find the approximate reduct when the decision table is increased in the object set. Compared to methods based on the rough set and fuzzy rough set approaches, the experimental results have shown that our methods can ameliorate the accuracy of inconsistent or low initial classification accuracy data sets.

It can be easily seen that the limitation of intuitionistic fuzzy set-based algorithms is the execution time due to the supplement of the diversity degree in intuitionistic fuzzy equivalence classes. For future researchers, we focus on developing the incremental formula to reduce the computational time and guarantee the classification accuracy. In addition, we also design incremental algorithms based on the intuitionistic fuzzy sets using granular structures. We will continue to study the incremental methods that find reducts from the decision tables in the case of supplementing and removing the set of attributes.

Acknowledgement: The authors thank you for the generous support of the Simulation and High-Performance Computing department (SHPC) of the HaUI Institute of Technology (HIT) for conducting experiments in this paper and sincerely thank you for the assistance of the research team VAST.

Funding Statement: This research is funded by Hanoi University of Industry under Grant Number 27-2022-RD/HĐ-ĐHCN (URL: https://www.haui.edu.vn/).

Author Contributions: Study conception and design: Pham Viet Anh, Nguyen The Thuy; data collection: Pham Dinh Khanh; analysis and interpretation of results: Nguyen Long Giang, Nguyen Ngoc Thuy; draft manuscript preparation: Pham Viet Anh, Nguyen The Thuy, Nguyen Long Giang, Nguyen Ngoc Thuy. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data presented in this study can be made available upon reasonable request from the corresponding author.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. X. Zhang, C. L. Mei, D. G. Chen and Y. Y. Yang, “A fuzzy rough set-based feature selection method using representative instances,” Knowledge Based Systems, vol. 151, pp. 216–229, 2018. https://doi.org/10.1016/j.knosys.2018.03.031 [Google Scholar] [CrossRef]

2. T. K. Sheeja and A. S. Kuriakose, “A novel feature selection method using fuzzy rough sets,” Computers in Industry, vol. 97, no. 3, pp. 111–116, 2018. https://doi.org/10.1016/j.compind.2018.01.014 [Google Scholar] [CrossRef]

3. X. Che, D. Chen and J. Mi, “Label correlation in multi-label classification using local attribute reductions with fuzzy rough sets,” Fuzzy Sets and Systems, vol. 426, pp. 121–144, 2022. https://doi.org/10.1016/j.fss.2021.03.016 [Google Scholar] [CrossRef]

4. Z. Huang and J. Li, “A fitting model for attribute reduction with fuzzy β-covering,” Fuzzy Sets and Systems, vol. 413, pp. 114–137, 2021. https://doi.org/10.1016/j.fss.2020.07.010 [Google Scholar] [CrossRef]

5. Q. H. Hu, D. R. Yu and Z. X. Xie, “Information-preserving hybrid data reduction based on fuzzy-rough techniques,” Pattern Recognition Letters, vol. 27, no. 5, pp. 414–423, 2016. [Google Scholar]

6. A. Meriello and R. Battiti, “Feature selection based on the neighborhood entropy,” IEEE Transactions on Neural Networks and Learning Systems, vol. 29, no. 12, pp. 6313–6322, 2018. [Google Scholar]

7. B. Sang, H. Chen, L. Yang, T. Li and W. Xu, “Incremental feature selection using a conditional entropy based on fuzzy dominance neighborhood rough sets,” IEEE Transactions on Fuzzy Systems, vol. 30, no. 6, pp. 1683–1697, 2021. [Google Scholar]

8. Z. Yuan, H. Chen and T. Li, “Exploring interactive attribute reduction via fuzzy complementary entropy for unlabeled mixed data,” Pattern Recognition, vol. 127, pp. 108651, 2022. https://doi.org/10.1016/j.patcog.2022.108651 [Google Scholar] [CrossRef]

9. C. Z. Wang, Y. Huang, M. W. Shao and X. D. Fan, “Fuzzy rough set based attribute reduction using distance measures,” Knowledge-Based Systems, vol. 164, pp. 205–212, 2019. https://doi.org/10.1016/j.knosys.2018.10.038 [Google Scholar] [CrossRef]

10. N. L. Giang, L. H. Son, T. T. Ngan, T. M. Tuan, H. T. Phuong et al., “Novel incremental algorithms for attribute reduction from dynamic decision systems using hybrid filter-wrapper with fuzzy partition distance,” IEEE Transactions on Fuzzy Systems, vol. 28, no. 5, pp. 858–873, 2020. [Google Scholar]

11. Y. M. Liu, S. Y. Zhao, H. Chen, C. P. Li and Y. M. Lu, “Fuzzy rough incremental attribute reduction applying dependency measures,,” APWeb-WAIM 2017 Web and Big Data, vol. 10366, pp. 484–492, 2017. [Google Scholar]

12. Y. Y. Yang, D. G. Chen, H. Wang, E. C. C. Tsang and D. L. Zhang, “Fuzzy rough set based incremental attribute reduction from dynamic data with sample arriving,” Fuzzy Sets and Systems, vol. 312, pp. 66–86, 2017. https://doi.org/10.1016/j.fss.2016.08.001 [Google Scholar] [CrossRef]

13. Y. Y. Yang, D. G. Chen, H. Wang and X. H. Wang, “Incremental perspective for feature selection based on fuzzy rough sets,” IEEE Transactions on Fuzzy Systems, vol. 26, no. 3, pp. 1257–1273, 2017. [Google Scholar]

14. X. Zhang, C. L. Mei, D. G. Chen, Y. Y. Yang and J. H. Li, “Active incremental feature selection using a fuzzy-rough-set-based information entropy,” IEEE Transactions on Fuzzy Systems, vol. 28, no. 5, pp. 901– 915, 2020. [Google Scholar]

15. P. Ni, S. Y. Zhao, X. H. Wang, H. Chen, C. P. Li et al., “Incremental feature selection based on fuzzy rough sets,” Information Sciences, vol. 536, no. 5, pp. 185–204, 2020. https://doi.org/10.1016/j.ins.2020.04.038 [Google Scholar] [CrossRef]

16. N. L. Giang, L. H. Son, N. A. Tuan, T. T. Ngan, N. N. Son et al., “Filter-wrapper incremental algorithms for finding reduct in incomplete decision systems when adding and deleting an attribute set,” International Journal of Data Warehousing and Mining, vol. 17, no. 2, pp. 39–62, 2021. [Google Scholar]

17. N. T. Thang, N. L. Giang, H. V. Long, N. A. Tuan, T. M. Tuan et al., “Efficient algorithms for dynamic incomplete decision systems,” International Journal of Data Warehousing and Mining, vol. 17, no. 3, pp. 44–67, 2021. [Google Scholar]

18. W. L. Hung and M. S. Yang, “Similarity measures of intuitionistic fuzzy sets based on Lp metric,” International Journal of Approximate Reasoning, vol. 46, no. 1, pp. 120–136, 2007. [Google Scholar]

19. B. Huang, C. X. Guo, Y. L. Zhuang, H. X. Li and X. Z. Zhou, “Intuitionistic fuzzy multigranulation rough sets,” Information Sciences, vol. 277, pp. 299–320, 2014. https://doi.org/10.1016/j.ins.2014.02.064 [Google Scholar] [CrossRef]

20. A. Tan, S. Shi, W. Z. Wu, J. Li, W. Pedrycz et al., “Granularity and entropy of intuitionistic fuzzy information and their applications,” IEEE Transactions on Cybernetics, vol. 52, no. 1, pp. 192–204, 2022. [Google Scholar] [PubMed]

21. N. T. Thang, N. L. Giang, T. T. Dai, T. T. Tuan, N. Q. Huy et al., “A novel filter-wrapper algorithm on intuitionistic fuzzy set for attribute reduction from decision tables,” International Journal of Data Warehousing and Mining, vol. 17, no. 4, pp. 67–100, 2021. https://doi.org/10.4018/IJDWM [Google Scholar] [CrossRef]

22. K. T. Atanassov, “Intuitionistic fuzzy sets,” Fuzzy Sets and Systems, vol. 20, no. 1, pp. 87–96, 1986. [Google Scholar]

23. I. Iancu, “Intuitionistic fuzzy similarity measures based on Frank t-norms family,” Pattern Recognition Letters, vol. 42, pp. 128–136, 2014. https://doi.org/10.1016/j.patrec.2014.02.010 [Google Scholar] [CrossRef]

24. W. Shu, W. Qian and Y. Xie, “Incremental approaches for feature selection from dynamic data with the variation of multiple objects,” Knowledge-Based Systems, vol. 163, pp. 320–331, 2019. https://doi.org/10.1016/j.knosys.2018.08.028 [Google Scholar] [CrossRef]

25. UCI Machine Learning Repository, “Data,” 2021. [Online]. Available: https://archive.ics.uci.edu/ml/index.php [Google Scholar]