 Open Access
Open Access
ARTICLE
CeTrivium: A Stream Cipher Based on Cellular Automata for Securing Real-Time Multimedia Transmission
1 Faculty of Computer and Information Technology, University of Tabuk, Tabuk, 71491, Saudi Arabia
2 Faculty of Computers and Information, Menoufia University, Menoufia, 13829, Egypt
3 School of Computing & Data Science, Wentworth Institute of Technology, Boston, 02115, USA
* Corresponding Author: Osama S. Younes. Email:
Computer Systems Science and Engineering 2023, 47(3), 2895-2920. https://doi.org/10.32604/csse.2023.040162
Received 07 March 2023; Accepted 12 June 2023; Issue published 09 November 2023
Abstract
Due to their significant correlation and redundancy, conventional block cipher cryptosystems are not efficient in encrypting multimedia data. Stream ciphers based on Cellular Automata (CA) can provide a more effective solution. The CA have recently gained recognition as a robust cryptographic primitive, being used as pseudorandom number generators in hash functions, block ciphers and stream ciphers. CA have the ability to perform parallel transformations, resulting in high throughput performance. Additionally, they exhibit a natural tendency to resist fault attacks. Few stream cipher schemes based on CA have been proposed in the literature. Though, their encryption/decryption throughput is relatively low, which makes them unsuitable for multimedia communication. Trivium and Grain are efficient stream ciphers that were selected as finalists in the eSTREAM project, but they have proven to be vulnerable to differential fault attacks. This work introduces a novel and scalable stream cipher named CeTrivium, whose design is based on CA. CeTrivium is a 5-neighborhood CA-based stream cipher inspired by the designs of Trivium and Grain. It is constructed using three building blocks: the Trivium (Tr) block, the Nonlinear-CA (NCA) block, and the Nonlinear Mixing (NM) block. The NCA block is a 64-bit nonlinear hybrid 5-neighborhood CA, while the Tr block has the same structure as the Trivium stream cipher. The NM block is a nonlinear, balanced, and reversible Boolean function that mixes the outputs of the Tr and NCA blocks to produce a keystream. Cryptanalysis of CeTrivium has indicated that it can resist various attacks, including correlation, algebraic, fault, cube, Meier and Staffelbach, and side channel attacks. Moreover, the scheme is evaluated using histogram and spectrogram analysis, as well as several different measurements, including the correlation coefficient, number of samples change rate, signal-to-noise ratio, entropy, and peak signal-to-noise ratio. The performance of CeTrivium is evaluated and compared with other state-of-the-art techniques. CeTrivium outperforms them in terms of encryption throughput while maintaining high security. CeTrivium has high encryption and decryption speeds, is scalable, and resists various attacks, making it suitable for multimedia communication.Keywords
The Real-time Transport Protocol (RTP) [1] is an established standard for the transmission of real-time multimedia streams, including voice and video, over IP networks. The Secure Real-Time Transport Protocol (SRTP) [2] is a security extension to RTP that provides confidentiality, integrity, and replay protection for RTP data. It uses the Advanced Encryption Standard (AES) algorithm for encryption of media streams and the RSA (Rivest–Shamir–Adleman) algorithm for traffic authentication and management of session keys.
The block ciphers require the input data to be divided into specific block sizes. If the data are not the required size, padding is applied before encryption to make the data a multiple of the block size. However, this process can pose several threats when using SRTP [3]. The encrypted padding of the message can be used to perform a brute-force attack to deduce the encryption key. Furthermore, traditional block cipher cryptosystems, including AES, DES (Data Encryption Standard), and 3DES face limitations when encrypting multimedia data, such as speech and video. These limitations arise from factors such as the considerable data size, significant correlation and redundancy, increased power consumption, and degraded encryption performance [4,5]. To overcome these limitations, novel techniques have been introduced that use stream cipher algorithms.
Stream ciphers are a class of symmetric key encryption schemes that use a secret key to generate a sequence of random bits, known as the “keystream”. These keystream bits are then combined with the plaintext using the XOR operation. Stream ciphers encrypt/decrypt data one bit or byte at a time, rather than in fixed-size blocks. This design allows them to be more efficient in encrypting large amounts of multimedia data and can also help to preserve data quality. They are known for their efficiency, speed, and limited error propagation [6]. Additionally, they are easy to implement in both hardware and software and are widely used in multimedia applications such as video conferencing, streaming audio and video, and VoIP calls.
In 2004, the eSTREAM project [7] was initiated as part of ECRYPT [8] with the objective of establishing standard stream ciphers. The project aimed to encourage the development of stream ciphers that are both efficient and compact, facilitating their widespread adoption. Numerous stream ciphers were submitted to the project, undergoing extensive cryptanalysis for a period of four years. Following this thorough evaluation, only a small number of candidate algorithms were chosen, such as Trivium [9], Grain [10], Rabbit [11], and Salsa20/12 [12].
Trivium was designed to be a more secure and efficient replacement for DES and aimed to promote the development of new stream ciphers. After being selected as a finalist in the eSTREAM project, it was further accepted as the ISO standard. It uses a combination of three Linear Feedback Shift Registers (LFSRs) to generate a keystream. Trivium is a highly efficient stream cipher that requires minimal computational resources. It offers high encryption and decryption speeds and can be easily adapted to various block sizes. Additionally, it has low power consumption, making it suitable for portable and embedded devices. Despite its advantages, in both theoretical and practical studies reported in the literature, Trivium was found to be insecure against Differential Fault Analysis (DFA) and fault injection attacks [13,14].
Cellular Automata (CA) [15] consists of regular grids of cells, where each cell has a limited number of states. The cells undergo state updates based on a predetermined rule, which considers the current state of each cell and the states of its neighboring cells. While predicting future states is relatively straightforward using this rule, inferring previous states poses significant challenges. One particularly effective nonlinear rule is Rule 30 for 3-neighborhood CA, which exhibits good statistical properties such as nonlinearity and a higher algebraic degree [16]. Additionally, it has been found that that 5-neighborhood rules outperform 3-neighborhood rules in terms of performance. The reason is that increasing the radius or number of neighbors of CA enhances diffusion and confusion properties [17]. Consequently, CA have evolved as good pseudorandom generators, providing fast evolution and high nonlinearity.
Recent research has highlighted the effectiveness of CA as a robust cryptographic primitive. CA can serve as one-way functions whose inverse is challenging to determine [18]. They boast straightforward hardware implementation, and software-based wordwise implementations can offer high efficiency [6]. Additionally, CA enable parallel transformations, leading to enhanced throughput. Furthermore, CA inherently exhibit resistance against fault attacks [19]. State bits within CA rapidly diffuse, often within a single cycle. The parallel transformation of CA causes injected faults to quickly propagate and dissipate, rendering fault tracking exceedingly challenging.
Several stream cipher schemes based on CA have been proposed in the literature [16,20–24]. However, as explained in Section 6, their encryption throughput is relatively low, which makes them unsuitable for multimedia communication. This work introduces a novel stream cipher called CeTrivium, which is based on cellular automata. CeTrivium is a 5-neighborhood CA-based stream cipher, and it is inspired by the designs of Trivium and Grain. CeTrivium is constructed using three building blocks: the Trivium (Tr) block, the Nonlinear-CA (NCA) block, and the Nonlinear Mixing (NM) block. The NCA block is a 64-bit nonlinear hybrid 5-neighborhood CA. The Tr block has the same structure as the Trivium stream cipher. The NM block is a nonlinear, balanced, and reversible Boolean function that mixes the outputs of the Tr and NCA blocks to produce a keystream that resists various attacks.
The NIST (National Institute of Standards and Technology) [25] statistical test suite has been used for evaluating the quality of the random bitstreams generated by the proposed scheme. In addition, we informally analyzed the security properties of the proposed scheme and showed that it provides security protection against various attacks, including correlation, algebraic, fault, cube, Meier and Staffelbach, and side-channel attacks. Moreover, the proposed scheme was assessed through histogram and spectrogram analysis, along with various measurements including signal-to-noise ratio, correlation coefficient, peak signal-to-noise ratio, entropy, and the number of sample change rates. We also compared the proposed scheme with other state-of-the-art schemes and found that it outperformed them in terms of both performance and security.
The remainder of the paper is organized as follows. Related work is discussed in Section 2. In Section 3, basic concepts about Trivium and Grain stream ciphers and CA are explained. Section 4 explains the proposed stream cipher CeTrivium. The informal security analyses of CeTrivium are discussed in Section 5. Simulation results and a performance comparison are presented in Section 6. Finally, some conclusions are drawn in Section 7.
A Pseudorandom Number Generator (PRNG) is a crucial component of stream ciphers, as it forms the basis of the keystream used to encrypt and decrypt plaintext. Many stream cipher schemes have been proposed in the literature based on different techniques for generating pseudorandom numbers, such as shift registers, DNA encoding, noise sources, tree party machines, and chaotic maps. However, as discussed in [26–28], most of them are vulnerable to attacks. Moreover, most of them are not suitable for real-time multimedia streaming because of their low throughput, as explained in Section 6. The following discusses the most recent and significant schemes.
A speech encryption scheme was proposed in [29] that relies on the Cat map and Zaslavsky map transform. Initially, the plain audio is concealed by incorporating random numbers generated via the Zaslavsky map. Subsequently, the resulting output undergoes processing by the Cat map to bewilder the data samples. Finally, the sampled values are rearranged using the Chen map, which reveals their chaotic behavior.
A speech encryption scheme was proposed in [30] based on chaotic shift keying. In this scheme, the audio signal samples are divided into four levels, and each level undergoes permutation using four distinct chaotic generators: quadratic map, tent map, logistic map, and Bernoulli’s map. A chaotic shift keying technique is used to dynamically assign diverse chaotic maps to diverse levels of sampled values, thereby shuffling the speech samples at each level.
A stream cipher scheme was proposed in [31] for encrypting speech signals. The scheme utilizes a pseudorandom generator that consists of two 256-bit shift registers, one nonlinear and the other linear. Another speech encryption cipher was proposed by Kordov [32], which combines a pseudorandom number generator with a permutation-substitution architecture. The architecture is implemented using a chaotic circle map and modified rotation equations.
In [4], a secure audio transmission scheme was presented that integrates four distinct techniques for audio encryption: dynamic DNA encoding, multichaotic maps, self-adaptive scrambling, and cipher feedback encryption. The scheme encompasses three phases. The initial phase involves self-adaptive bit scrambling, where the SHA512 hash of the input audio is computed to generate a secret key used for cyclically shifting the audio binary stream. The second phase encompasses dynamic DNA encoding, where the scrambled audio is encoded using a secret key derived from a pseudorandom generator employing chaotic maps such as sine, Chebyshev, and logistic maps.
On the basis of the Henon-Tent chaotic pseudorandom number generation technique, an audio encryption scheme was proposed in [5]. The method requires XORing a stream of pseudorandom numbers with the audio file to form a cipher audio. The pseudorandom numbers are produced by the chaotic Henon map and the tent map.
An audio encryption scheme was proposed in [33] that makes use of a dynamical system, incorporating a fractional derivative. This system demonstrates chaotic behavior across a broad spectrum of fractional orders and parameter values. Furthermore, the scheme exhibits multiple coexisting attractors when employing the same parameter values but different initial conditions. Additionally, a nonlinear feedback control technique is employed to regulate the chaos of the system around its stagnation point.
Few CA-based stream cipher schemes have been introduced in the literature. Sandip and Dipanwita developed a stream cipher called NOCAS [20], which is based on hybrid nonlinear 3-neighborhood CA. NOCAS was inspired by the design of Grain. CAvium [21] is a stream cipher inspired by the design of Trivium. Basically, CAvium replaces the shift registers used in the design of Trivium with a hybrid CA with rules 30, 60, 90, 120, 150, 180, 210, and 240. Compared to Trivium, it has better cryptographic characteristics, including nonlinearity, resiliency and algebraic degree.
Das et al. proposed a stream cipher called CASTREAM [22], which is based on CA. CASTREAM uses two nonlinear blocks: one based on an S-box and another based on CA. To generate the keystream, CASTREAM uses a CA-based mixing function that combines the outputs of the two blocks. A CA-based stream cipher called CAR30 was introduced in [18]. The cipher uses a 3-neighborhood CA with rule 30 and is inspired by the design of Grain. CAR30 replaces the LFSR and the Nonlinear Feedback Shift Register (NFSR) in Grain-128 with linear and nonlinear CA with radius one, respectively. The design of CAR30 is easily scalable and can be implemented in both hardware and software. A stream cipher called FResCA was proposed in [23]. The design of FResCA is inspired by Grain’s design and is based on a combination of cellular automata with radii of 1 and 2.
NOCAS, CAvium, and CASTREAM adopt 3-neighborhood CA in their designs. As proven in [34], all nonlinear rules used for 3-neighborhood CA are not immune to first-order correlation. Consequently, any ciphers employing these rules may successfully pass classical statistical tests for checking randomness, but they remain vulnerable to correlation attacks.
In [24], a stream cipher named CARPenter, which is based on a 5-neighborhood cellular automaton, was introduced. The cipher incorporates a linear CA and a nonlinear CA with a mixing function. It demonstrates resilience against various attacks targeting stream ciphers and exhibits various cryptographic properties. The analysis of CARPenter showed that it is resilient against various stream cipher attacks and has good cryptographic properties. The hardware and software resources required to implement CARPenter are similar to those used by other ciphers based on cellular automata, such as CAR30 and NOCAS. John et al. [16] proposed Pentavium, a 5-neighborhood CA-based stream cipher. Pentavium has a similar structure to CAvium [21], but instead of using 3-neighborhood rules such as CAvium, it utilizes 5-neighborhood rules. As explained in Section 6, both CARPenter and Pentavium have low encryption/decryption throughput, making them unsuitable for real-time multimedia streaming.
Cellular automata can be described as a mathematical representation of a discrete system that comprises a grid of cells, where each cell has two possible states (0, 1) [35]. The cells in the system are assigned a state S, which are modified at discrete time steps based on a defined transition function f. This function, also known as a transition rule, takes into account the states of neighboring cells within a symmetric neighborhood of radius r at the previous time steps. By employing a local transition function, the state of each cell is updated simultaneously in discrete time steps as follows:
where
The value of the cell is determined by its current state and the states of adjacent left and right neighbors. Therefore, ECA is called a 3-neighborhood cellular automaton. At time instant t, for the 5-neighborhood cellular automata, the next state of the cell number i is given by:
For ECA, where each cell can store one of two values (0 or 1) and the transition function operates on three cells, the function f can take 23 = 8 various combinations of inputs. As a result, there are 28 = 256 types of outputs. Therefore, there are

Figure 1: The outputs of rule 30
Because rows in CA have a limited number of cells, the boundaries of the rows do not have the complete set of neighbors required by the update function. To address this issue, several approaches exist. A null boundary is used when the values of the extremities’ neighbors are hardcoded as zero. On the other hand, a cyclical or periodic boundary is applied by connecting the extremities’ neighbors to each other. Hybrid CA involve more than one rule in generating the next state [36].
Previous studies have explored the diffusion, confusion and randomness characteristics of cellular automata rules with 3-, 4-, and 5-neighborhood configurations. The results showed that increasing the neighborhood radius of cellular automata improves the effectiveness of CA in various cryptographic properties. 5-neighborhood CA have a high diffusion rate and are therefore appropriate for high-speed applications [24]. However, this enhancement requires increased computation. Figs. 2 and 3 show 3- and 5-neighborhood CA with 128 cells updated with rules 30 and 1452976485, respectively. The CA have a cyclical boundary and were initialized with a random state.
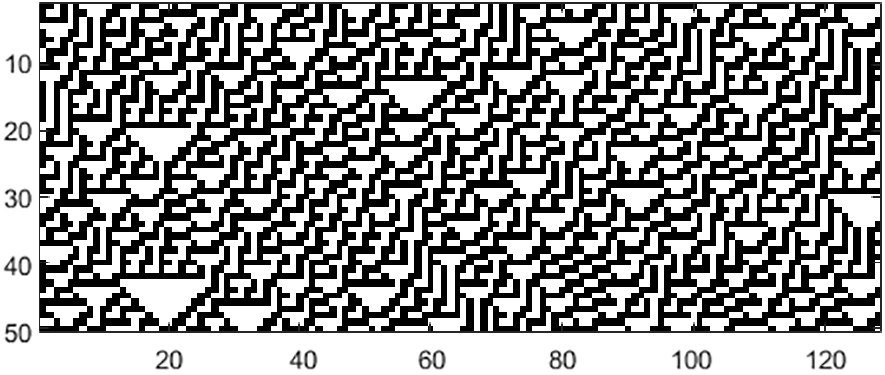
Figure 2: Updating ECA with 128 cells using rule 30 for 50 rows
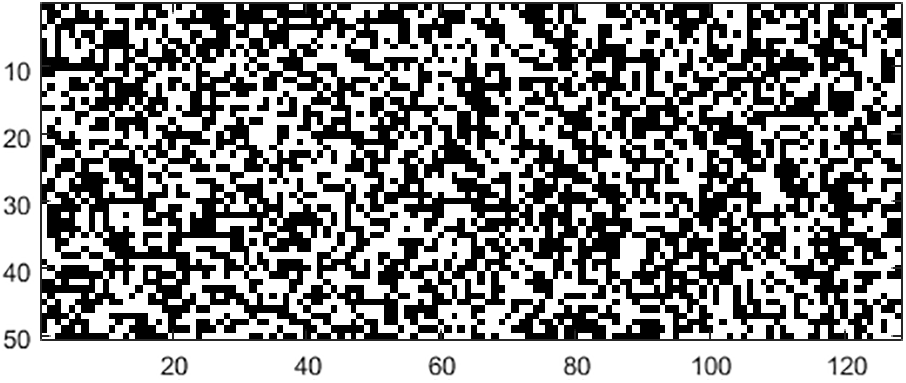
Figure 3: Updating 5-neighborhood CA with 128 cells using rule 1452976485 for 50 rows
In the eSTREAM project, the Trivium stream cipher [9] was selected as a finalist. It has been standardized as part of the standard ISO/IEC 29192-3 for stream ciphers. It is a synchronous and lightweight cipher designed to produce a keystream of fewer than 264 bits. The cipher uses a secret key and an Initialization Vector (IV), each of which is 80 bits in length. The cipher’s structure is dependent on three shift registers, which collectively comprise 288 bits. These shift registers have specific sizes of 93, 84, and 111 bits. The feedback for each shift register is generated by combining AND and XOR operations, as illustrated in Fig. 4.
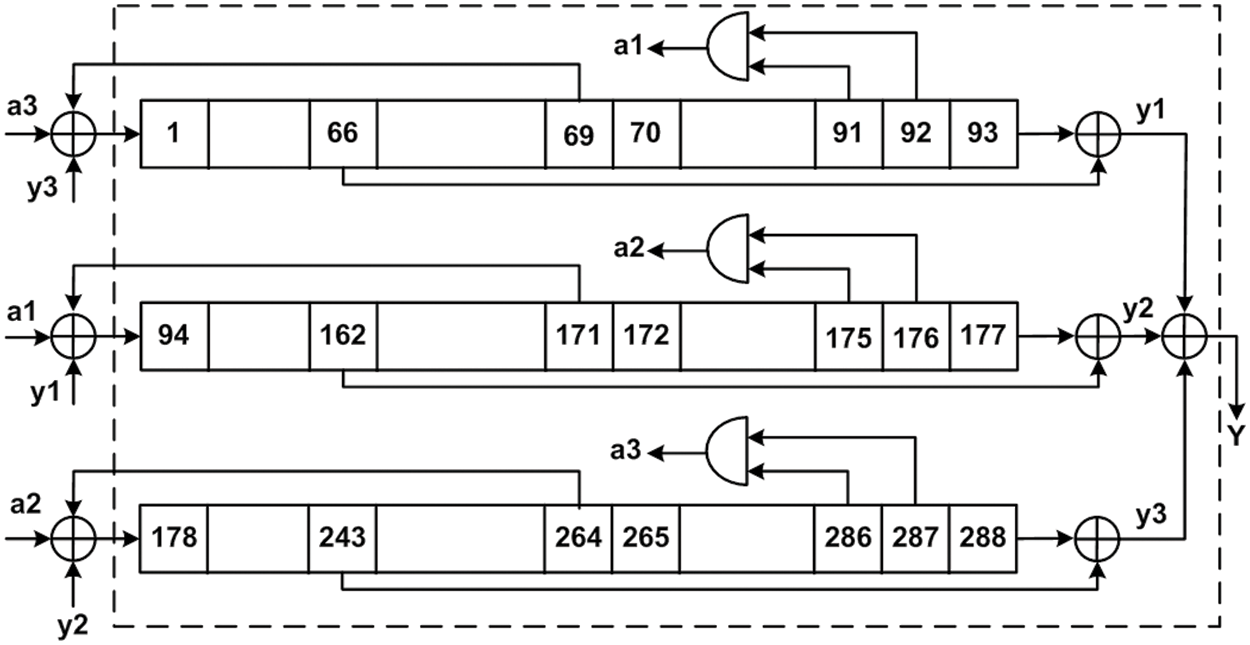
Figure 4: Internal structure of Trivium
The three registers of Trivium are initialized by loading the secret key and the initialization vector, along with a sequence of predetermined zeros and ones. After 1152 iterations, Trivium produces a stream of pseudorandom bits. The keystream is generated by performing XOR operations on specific bits within the three shift registers. Trivium is specifically designed for applications that have limited resources and power. However, as a widely adopted cipher and cryptosystem, it has been the subject of various attacks that undermine its security. These include several differential analysis techniques described in the literature [13,14].
Grain-128 [10] is a stream cipher that falls into the category of lightweight ciphers and was selected as one of the finalists in the eSTREAM project. The cipher comprises three main components: a nonlinear feedback shift register (NFSR), a linear feedback shift register (LFSR), and a nonlinear filter, as illustrated in Fig. 5. The cipher takes a 96-bit IV and a 128-bit secret key as inputs. The LFSR operates using a feedback polynomial denoted as
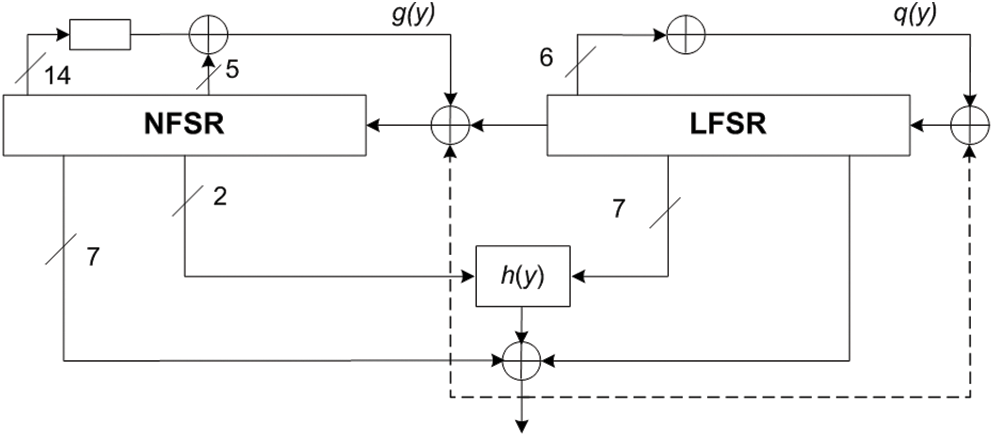
Figure 5: Grain block diagram
The feedback function
The nonlinear filter function is defined as:
where the variables
This section specifies the details of the design of the proposed stream cipher. A high-level block diagram of the construction is shown in Figs. 6 and 7. Fig. 6 shows the initialization phase, and Fig. 7 shows the keystream generation phase.
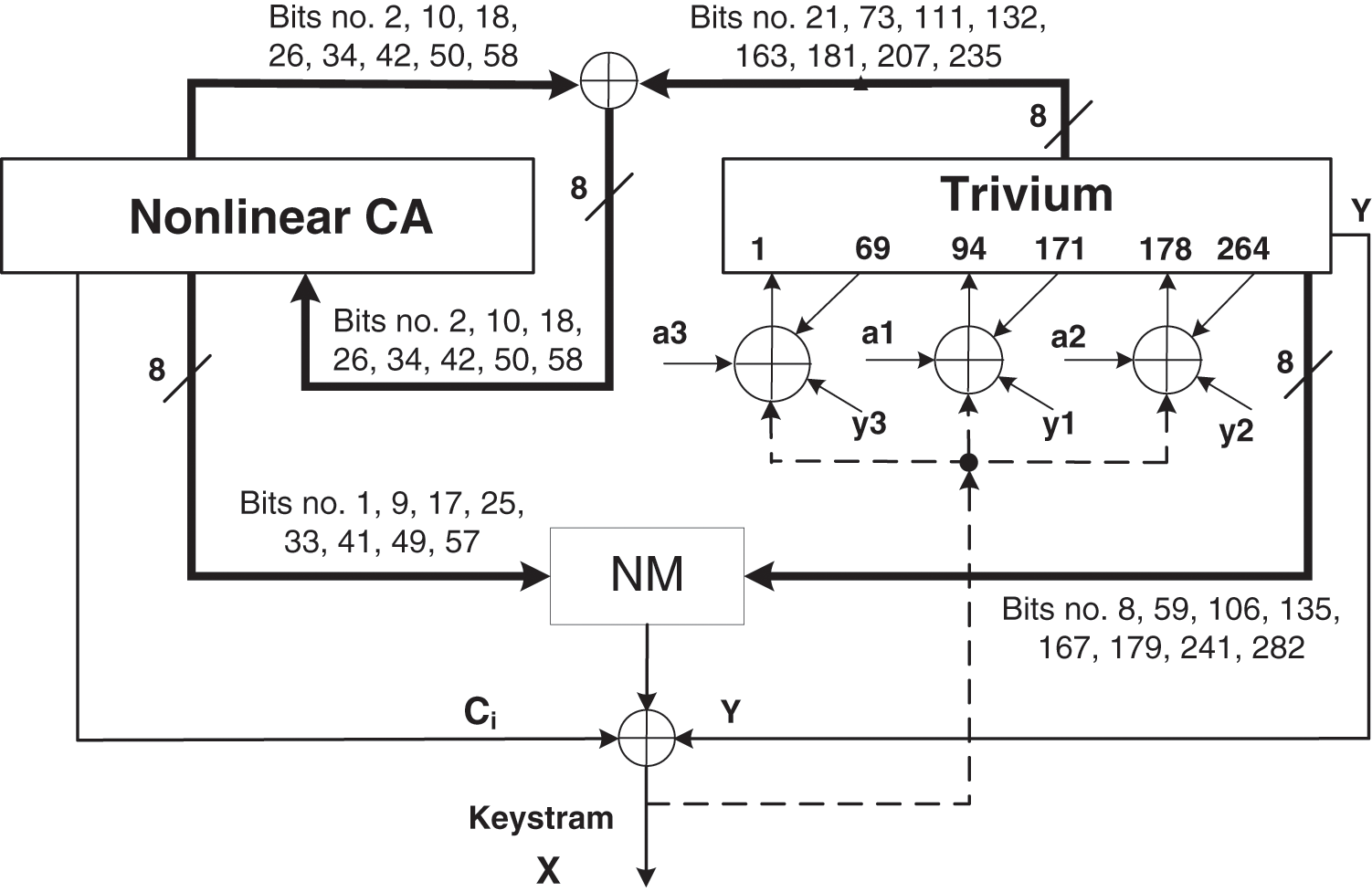
Figure 6: Block diagram for the initialization phase of CeTrivium
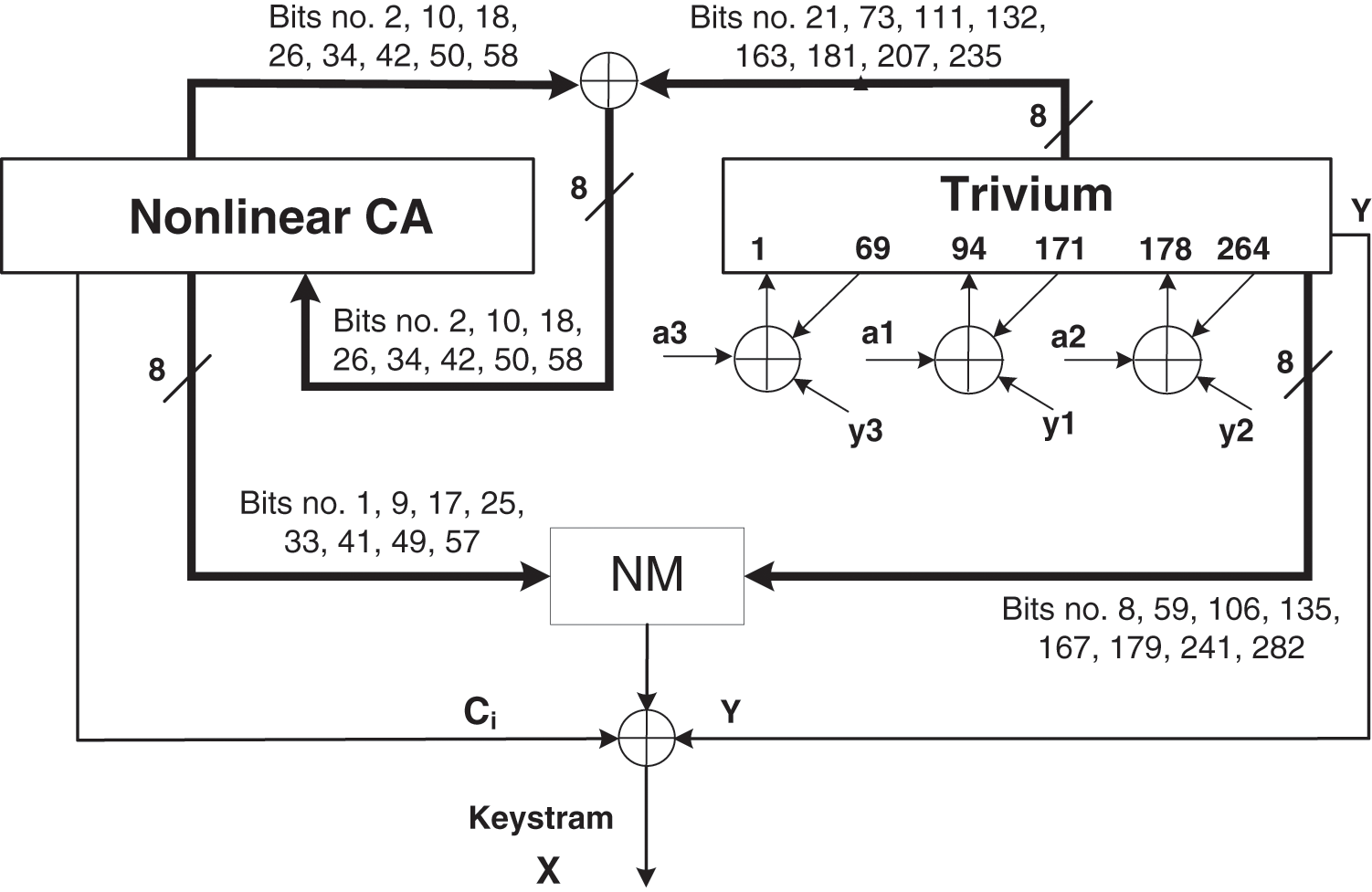
Figure 7: Block diagram for the keystream generation process of CeTrivium
CeTrivium is constructed using three main building blocks, namely, the Tr, NCA, and NM blocks. The Tr block has the same structure as the Trivium stream cipher explained in Section 3 and shown in Fig. 4. However, there is one key difference: bits of the output keystream are returned back and XORed with the inputs of Trivium, as shown in Fig. 6. The NCA block is a nonlinear hybrid 5-neighborhood CA with a length of 64 bits. The cellular automaton follows a periodic boundary configuration, where the extreme bits (rightmost and leftmost cells) are considered to be adjacent to each other. This arrangement enables the CA to produce more complex and varied output than the null boundary CA [37].
The authors in [38] investigated the cryptographic properties of various nonlinear rules for 5-neighborhood cellular automata, where the benchmark is Rule 30. After analyzing the results attained from the NIST tests [25] and ENT (a Pseudorandom Number Sequence Test) [39], the following selected rules performed better than others: R1 = 1520018790, R2 = 2778290790, R3 = 1520018790 and R4 = 1452976485. The cells of the NCA block are modified using one of the four 5-neighborhood nonlinear CA rules: R1, R2, R3 and R4. The cells are updated using these rules in the same order one after another. The rules provide high nonlinearity to the nonlinear CA block, which increases rapidly with each iteration. Additionally, they exhibit good correlation immunity. Therefore, these rules were chosen to generate states of the NCA block. For example, the state transition function
where
The nonlinear mixing block NM is a nonlinear, balanced, and reversible Boolean function [40]. NM receives eight input taps from each block and produces eight bits as output. Only the most significant bit is considered for generating the output keystream. We denote the contents or states of the Tr block by
where
As shown in Fig. 6, the eight taps that are selected from the NCA block correspond to bit positions 1, 9, 17, 25, 33, 41, 49, and 57, where they are equidistant positions. The selected taps from the Tr block correspond to bit positions 8, 59, 106, 135, 167, 179, 241, and 282. These taps are selected from the three shift registers constructing the Tr block: two from the first register and three from each of the other registers. The mixing block NM produces an 8-bit output
The positions of the 16 taps selected from the two blocks are designated to influence the output of the nonlinear mixing function by all the bits in fewer iterations.
The Trivium cipher is vulnerable to fault injection and side channel attacks [13,14] due to several factors: (1) the Trivium initialization algorithm is reversible, (2) the initialization phase is the same as the keystream phase, and (3) the output function of the Trivium is linear in the inner state bits. To address these issues, the inputs of Trivium are XORed with the output keystream bits, as shown in Fig. 6. This approach increases confusion in the Tr block in the initialization phase that prevents fault attacks. Moreover, the outputs of NCA and NM blocks are combined with the Tr block, as shown in Figs. 6 and 7. The NCA block quickly diffuses the state bits, forcing injected faults to propagate rapidly and dissipate. This dynamic behavior poses challenges in tracking and analyzing faults. The mixing function is a resilient and extremely nonlinear Boolean function that filters the cipher state bits, preventing attacks that exploit vulnerabilities in the Trivium cipher.
4.2 Initialization and Keystream Phases
The CeTrivium cipher operates in two phases: the initialization phase and the keystream generation phase. In the initialization phase, the cipher is initialized with secret keys K and IV. The bits of the secret key are denoted as
To initialize the algorithm, the Tr block is loaded with an 80-bit secret key and an 80-bit initialization vector, and the NCA block is loaded with a 64-bit secret key as follows:
Then, the internal state of the cipher is refreshed 1152 times (rotating the Trivium registerers over 4 full cycles). After each clock cycle, the registers in the Tr block are rotated, and the cells of the NCA block are updated according to the 5-neighborhood CA rules. Moreover, the output of NCA block
Before updating the bits of the NCA and Tr blocks, the taps in the Tr block at positions 163, 181, 207, 235, 21, 73, 111, and 132 are XORed with the taps in the NCA block at positions 2, 10, 18, 26, 34, 42, 50 and 58, respectively, to update the corresponding bits in the NCA block. The initialization phase is iterated 1152 times before producing any keystream to ensure that all bits are affected by the IV and the keys. The initialization phase algorithm is shown in Table 1, where the function

For 288 iterations, the generated keystream bits in the initialization phase are suppressed and are not accessible as output. This number of iterations is sufficient to change all 288 and 64 state bits in the Tr and CA blocks, respectively. Furthermore, the generated keystream bit is influenced by all 320 state bits.
The keystream generation process begins on the 289th iteration, immediately following the initialization phase. The processes of the keystream generation are similar to those of the initialization phase, except that the feedback line from the keystream to the Tr block is removed, as shown in Fig. 7. From the beginning of this phase, the output X is considered to be the keystream bits of CeTrivium. The keystream generation algorithm of CeTrivium is shown in Table 2.

In this section, security analysis for the proposed stream cipher is provided to show how it resists different cryptanalytic attacks that can be performed against stream ciphers.
Statistical testing is a widely employed method to evaluate the output quality of stream ciphers or random number generators. The NIST test suite [25] is a standard statistical tool utilized for this purpose, which includes 15 tests designed to assess any behavior that indicates predictability in a random sequence, as shown in Table 3. This suite is commonly used for evaluating the randomness quality of pseudorandom numbers with variable lengths generated by stream ciphers or random number generators.
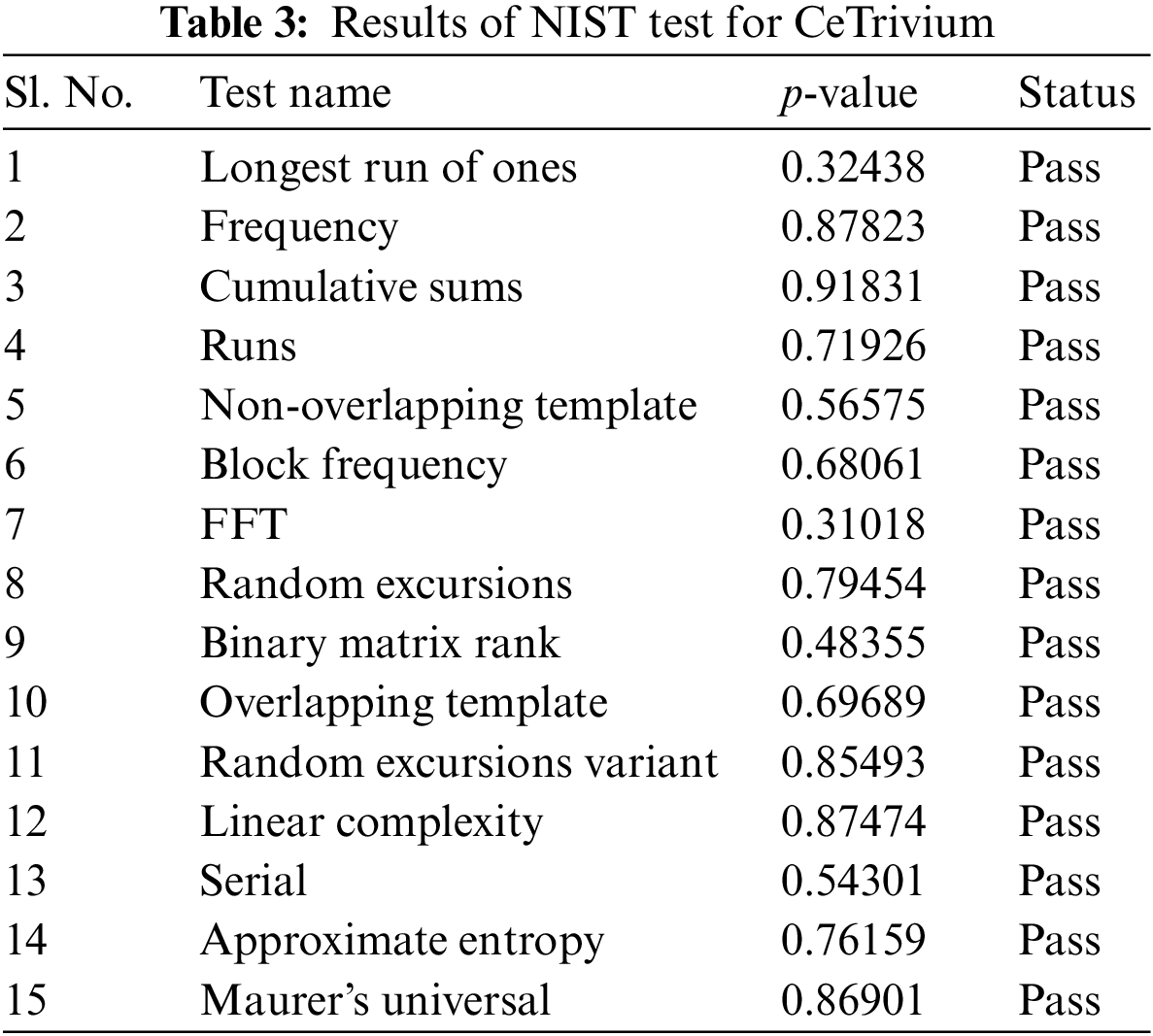
The first four tests, as shown in Table 3, study the frequency of the keystream, while tests 5 and 6 investigate repetitive patterns. Pattern matching characteristics are investigated through tests 7 to 12, while the last three tests evaluate random walk characteristics. For every test, a statistical measure called the Chi-square is computed, and the resulting value is transformed into a random probability value known as p-value. This p-value helps in the analysis of the randomness characteristics of the keystream.
We implemented the CeTrivium cipher using MATLAB and generated different bit streams of length 108 bits. The test suite was then used to divide the input into 100 keystreams of size 106. Table 3 shows the results of the statistical test performed on the bit stream generated by the CeTrivium cipher using the following secret key and IV:
K = 0x5C5C50ED00C48388EA9B0FB7C2047AF6B94E
IV = 0xEBA02E379817D636A144
The results for all tests show that the p-value > 0.01, which implies that the keystream bits generated by CeTrivium passed all tests.
Linear correlations between keystream bits and internal state bits can potentially reveal the cipher state. The characteristic that signifies a cipher’s ability to resist correlation attacks is called as resiliency. A function that is balanced and demonstrates immunity to k-th order correlations is commonly referred to as k-resilient. In [38], the authors investigated a set of bipermutive rules for 5-neighbor CA in terms of the cryptographic characteristic of resiliency. They computed Walsh transforms of the rules to select those that are nonlinear and 2-resilient. Based on the results of various statistical tests, the nonlinear rules (R1, R2, R3, R4) performed better than others [38]. It has been proven that these rules are bipermutive and 2-resilient. According to Tarannikov’s bound [41], the Boolean function with five variables that is 2-resilient gives the best possible trade-off between balancedness and correlation immunity. Therefore, the output of the NCA block is both balanced and 2nd-order correlation immune.
As explained in [9], the Trivium cipher has a correlation coefficient of 10−72. Detecting such a correlation would require at least 2144 bits of keystream that is not feasible in practice. The nonlinear mixing block NM is a resilient Boolean function [40] that was designed as a filter between the cipher state and the generated keystream. By combining the output bits of the NCA, Tr, and NM blocks to generate the keystream of CeTrivium, it becomes much more difficult to search for linear correlations between the keystream and cipher state, effectively preventing correlation attacks.
Algebraic attacks involve identifying a set of equations and then solving them. An algebraic attack depends on the algebraic degree of an encryption algorithm. Increasing the number of nonlinear terms in an encryption algorithm makes it more difficult to attack. As proved in [24], the algebraic degree of the state bits with respect to the previous state bits when the
Trivium stream ciphers are vulnerable to algebraic attacks because of their simple algebraic structure. In [42], the authors developed an algebraic attack against Trivium. The attack can compromise 625 rounds by utilizing just 4096 bits of the keystream, with an overall time complexity equivalent to 242.2 Trivium computations. Therefore, to prevent algebraic attacks, the output of the NCA block is XORed with the outputs of the Tr and NM blocks to generate the keystream. Therefore, CeTrivium can resist algebraic attacks.
A fault attack can be considered an active attack on a cryptosystem [43]. This type of attack assumes that the attacker has the ability to manipulate the encryption algorithm or the used device, enabling them to inject and control faults through methods such as laser beams, voltage peaks, or clock glitches. The cipher behavior can be analyzed by injecting faults into unidentified bit positions within the cipher state and monitoring the effects of these faults. By comparing the faulty output with the anticipated output, it is possible to compromise the cipher’s security keys.
Unfortunately, studies introduced in [13,44,45] have illustrated that the Trivium stream cipher is vulnerable to differential fault analysis attacks and fault injection attacks. These attacks are capable of retrieving the secret information contained in a cryptosystem. Fault attacks depend on using a reversible algorithm. In the event that attackers possess knowledge of the cipher’s state at any clock cycle, they can execute the cipher in reverse until it returns back to the initial state, thereby exposing the secret keys. Stream ciphers implemented using CA are immune to fault attacks due to the rapid diffusion of state bits by CA. This fast diffusion causes any introduced fault to quickly propagate and dissipate, making it difficult to track. In CeTrivium, 5-neighborhood CA are used to prevent fault attacks. As explained above, the algebraic degree of the keystream bits is 73, making fault attacks infeasible.
The cube attack is a form of cryptanalysis attack in which the attacker aims to derive a system of polynomial equations in relation to the unknown bits of the secret key using the output keystream bits of the cipher and a set of IVs [46]. The evaluation of factor polynomials, with linear terms known as superpolys (SP) and factors referred to as cubes, is conducted by treating the cryptosystem as a black box. The attack is performed in 2 stages: preprocessing and online. In the preprocessing stage, the attacker uses chosen keys and IVs to obtain the maxterms and their corresponding SP. In the online stage, SP are evaluated, where the chosen IVs are used to query the black box. This process yields a set of equations that needs to be analyzed and solved in order to get the secret keys.
The effectiveness of cube attacks is contingent upon the algebraic degree of the keystream. As explained above, CeTrivium reaches an algebraic degree of at least 73 after 18 cycles. Additionally, after every cycle, the algebraic degree increases by 4, making it grow rapidly. In addition, the secret key and initialization vector size of 352 further contributes to the complexity of calculating the maxterms. Therefore, CeTrivium can resist cube attacks.
5.6 Meier and Staffelbach Attack
In [47], Wolfram introduced a stream cipher based on Rule 30, where Rule 30 was used as a pseudorandom sequence generator. Meier and Staffelbach subsequently launched an attack on this cipher [48]. They began by generating a random initial state for all bits on the right half of the cellular automaton. Then, starting from the initial state, they generated the adjacent sequence of CA using Rule 30, which is called the temporal sequence. By guessing the initial state for the right half values, they aimed to determine the correct right-adjacent sequence of the temporal sequence. To check this result, they moved backward to determine the left half of the initial state because the left side exhibits a linear relationship with the temporal sequence. Using the computed initial state, the keystream is generated and compared with the actual keystream. By repeating this process, the attackers can guess the correct secret keys.
In CeTrivium, there is feedback from the Tr block to the NCA block that is used to update 8 bits in it. Therefore, moving backward from the right-adjacent sequence to determine the left-hand side of the temporal sequence is not possible. Additionally, because a nonlinear mixing function is used with the NCA block to produce keystream bits, the attacker cannot find a relation between the initial state and the keystream. Hence, CeTrivium is resistant to the Meier-Staffelbach attack.
In Side-Channel Attacks (SCAs), attackers attempt to extract information from devices executing cipher algorithms, such as power consumption and emissions of electromagnetic radiation. In [49], the authors comprehensively evaluated eSTREAM ciphers and demonstrated their vulnerability to SCA. To prevent SCA, certain cryptographic properties are recommended in [50], including algebraic degree, resiliency, and nonlinearity, which prevent information leakage. These properties affect the randomness of the keystream, which has a significant impact on preventing SCA. CeTrivium uses a nonlinear CA block and a nonlinear mixing function that satisfy these cryptographic properties, as explained above. Therefore, CeTrivium is robust against SCA.
As explained in [9], for any key/IV pair, if the AND gates are removed from the Trivium cipher, the cipher becomes a linear scheme, and the period of the generated stream is at least
5.9 Memory/Time/Data Tradeoff Attack
The memory/time/data tradeoff attacks on stream ciphers have a complexity of O (2β/2), where β represents the number the cipher’s internal states [51]. For CeTrivium, with a total of 352 bits defining its internal state, conducting a memory/time/data tradeoff attack becomes challenging.
The authors in [52] developed a tradeoff attack for stream ciphers that have low sampling resistance. They developed different sampling techniques to reduce complexity and make this attack applicable. They showed that the tradeoff attack can be performed on stream ciphers whose states undergo a restricted number of simple operations prior to generating their subsequent output bit. The authors showed that this attack can be performed on Grain-128. CeTrivium was designed using 5-neighborhood nonlinear CA, the Trivium cipher, and the nonlinear mixing function, which makes transformation of its state complex and prevents the tradeoff attack from being performed with a complexity less than that of a brute-force attack.
In this section, the quality of the CeTrivium stream cipher for encrypting audio signals is demonstrated. MATLAB 2022a was used to implement CeTrivium on a personal computer that has an Intel Core i5-10210U CPU running at @ 2.1 GHz, 8 GB of random access memory (RAM) and a 64-bit Windows 11 Professional operating system. The proposed scheme was applied to a variety of uncompressed (.wav) audio files with different sizes and characteristics (speeches, music, songs, etc.). In order to assess the security of CeTrivium, common measurements were adopted, including histogram, spectrogram, correlation coefficient, Signal-to-Noise Ratio (SNR), Number of Samples Change Rate (NSCR), Peak Signal-to-Noise Ratio (PSNR), entropy, and throughput. In all experiments, the secret key and initial vector described in Section 5.1 are utilized.
6.1 Histogram and Spectrogram Analysis
Histogram analysis is employed to calculate the distribution of values and to assess the quality of encrypted audio signals. An encryption scheme that can resist statistical attacks encrypts the audio signal into random noise-like signals with equally probable sample values. Histograms of the plain audio files and the corresponding encrypted audio files are shown in Fig. 8 [b1 to b6] and Fig. 8 [(e1 to e6)], respectively. As shown in Fig. 8, the histograms of the encrypted audio files are relatively flat, indicating that the proposed scheme can resist statistical attacks, such as frequency attacks.
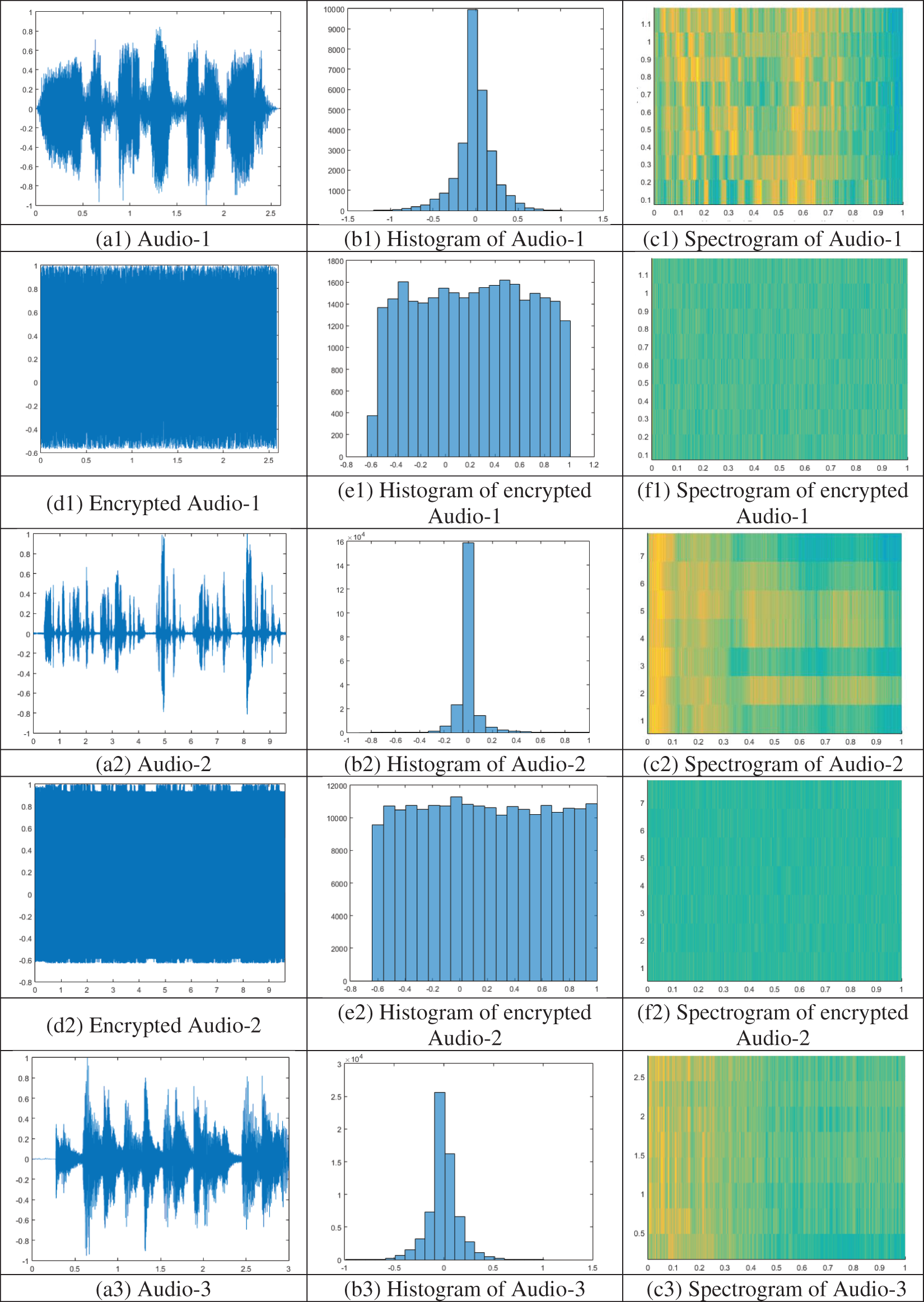
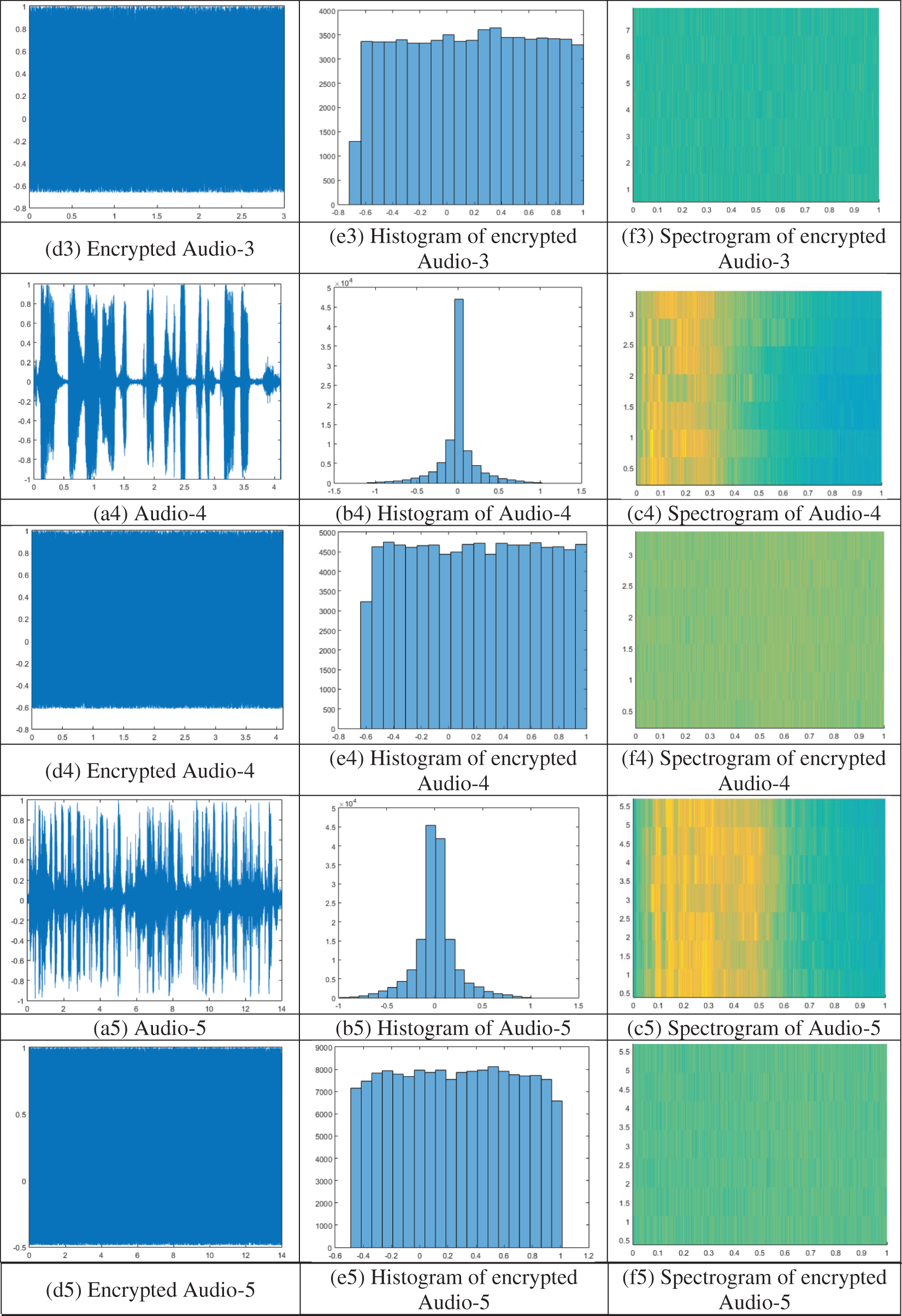
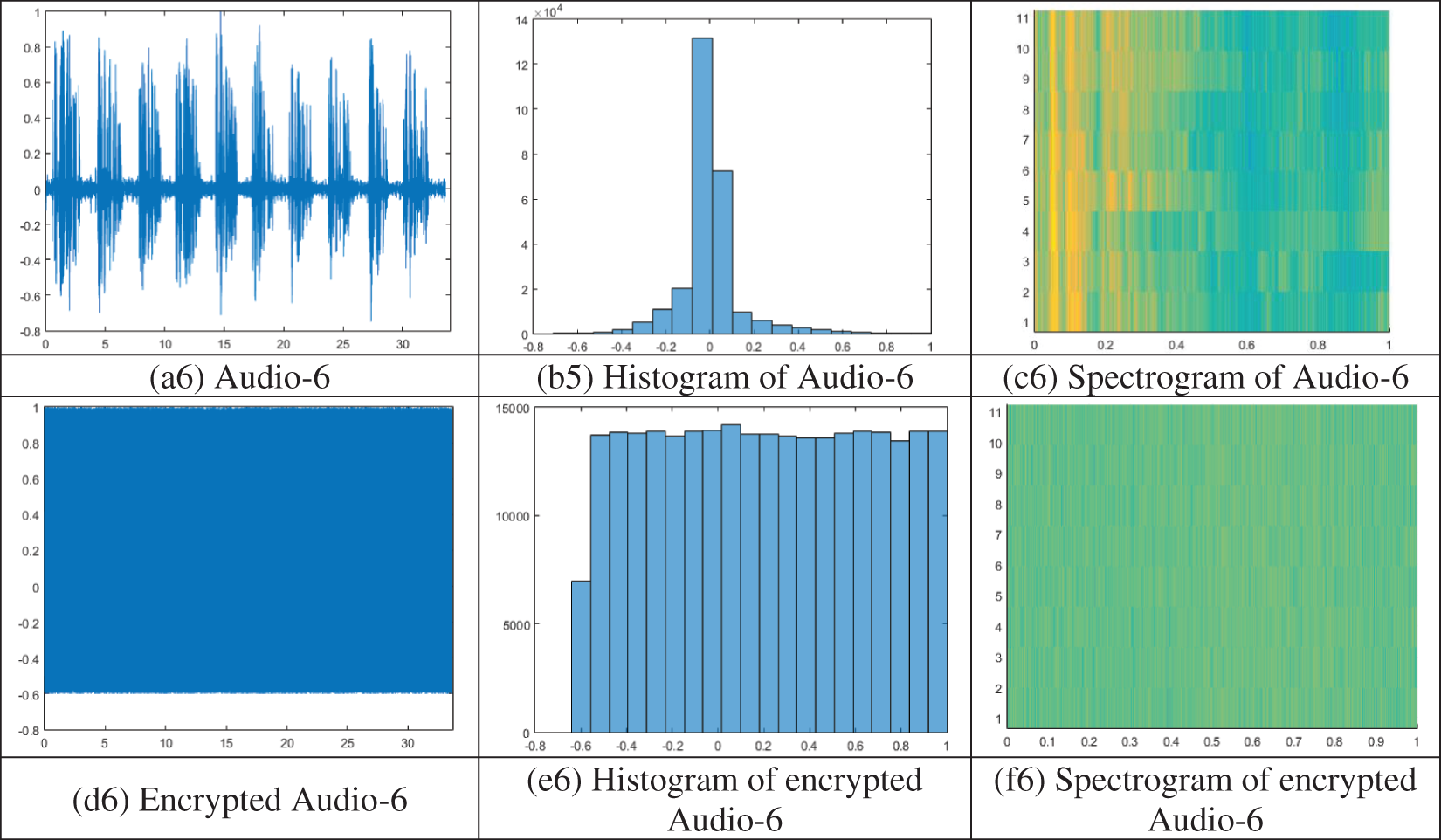
Figure 8: Simulation results: Plain audio files (a1 to a6), histogram of plain audio files (b1 to b6), spectrogram of plain audio files (c1 to c6), encrypted audio files (d1 to d6), histogram of encrypted audio files (e1 to e6), spectrogram of encrypted audio files (f1 to f6)
A spectrogram is a graphical depiction that displays the frequency spectrum of an audio file over time. It can be useful for identifying patterns or features in the signal. It is created by breaking the audio samples into smaller segments and then using the Fourier transform to calculate the magnitude of the frequency spectrum for each segment. Spectrogram analysis is an essential tool for evaluating the quality of the encryption scheme. An encryption scheme of high quality would produce an encrypted signal that appears to be random noise when viewed as a spectrogram.
In Fig. 8, the spectrograms of the tested audio files are presented in subfigures c1 to c6. The spectrograms of the corresponding encrypted audio files can be found in subfigures f1 to f6. As shown in Fig. 8, the encryption scheme scrambled the original frequency content of the signal, making it difficult for an attacker to identify any patterns or features. In addition, the encrypted audio versions are dissimilar to the original audio files.
Correlation analysis is a statistical method used to assess the robustness of an encryption scheme against various types of statistical attacks. It typically examines the correlation between corresponding segments of the original and encrypted audio files, using the correlation coefficient as the metric. A secure encryption algorithm should convert the original data into a signal that resembles random noise with low correlation. A small correlation coefficient signifies that there is little or no similarity between the original and encrypted audio files. The correlation coefficient
where
Table 4 shows the size and duration of plain audio files and the correlation coefficient between the plain audio and the corresponding encrypted audio files. Additionally, a scatter plot diagram comparing samples in plain and encrypted audio files (Audio-1) can be found in Fig. 9. The results demonstrate that the correlation coefficient values are very low, indicating a lack of similarity between plain and encrypted audio files, thus reflecting the randomness of the encrypted audio file. This result shows the superior quality of CeTrivium and demonstrates its effectiveness.
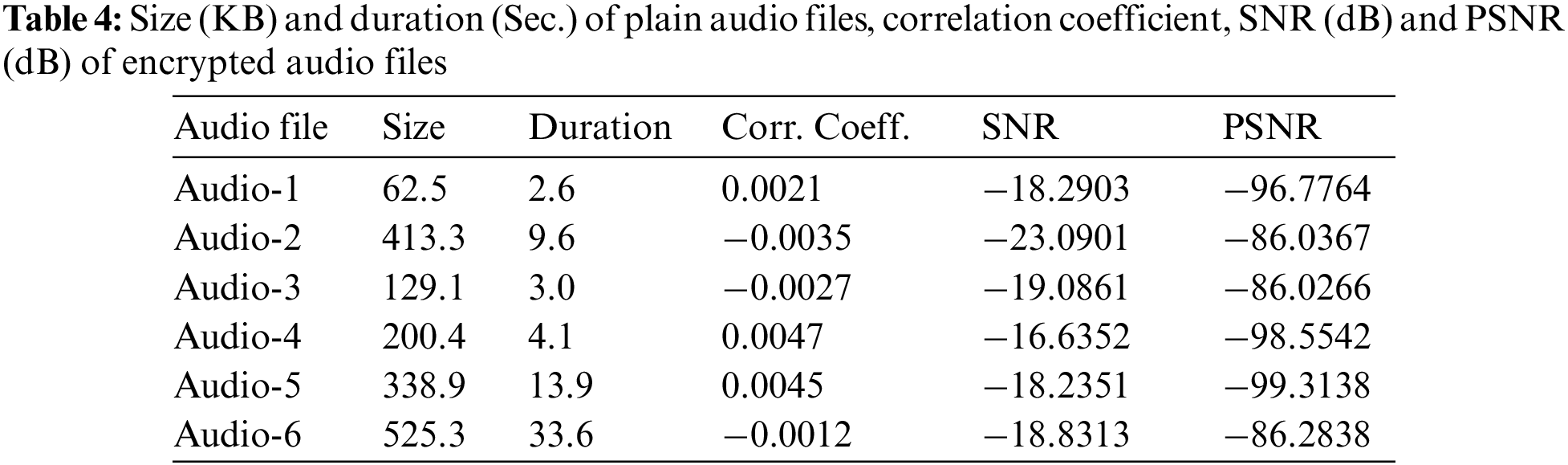
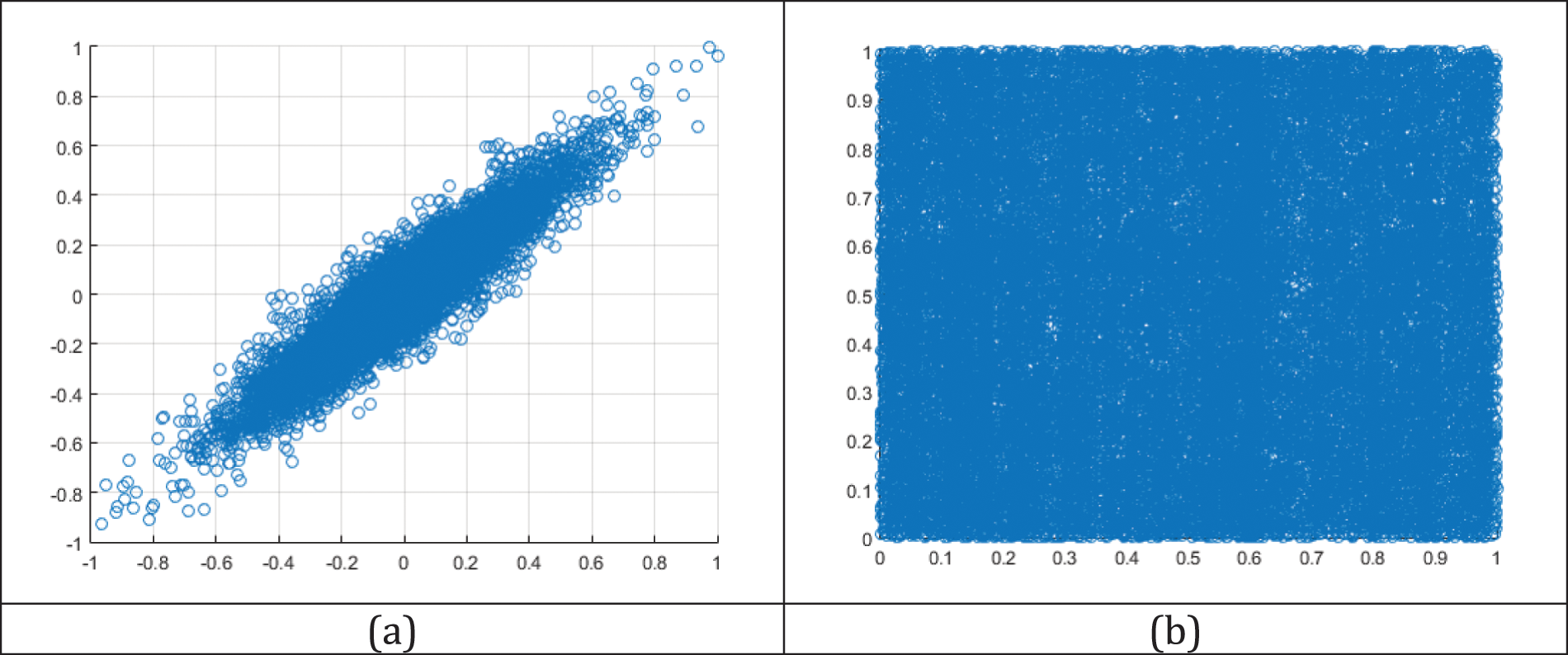
Figure 9: Correlation between samples in (a) plain audio and (b) encrypted audio
SNR is a measure of signal quality and is commonly employed to evaluate the quality of cipher schemes. It determines the level of noise in the encrypted audio signal relative to the original signal. Cryptanalysts often try to add more noise to the encrypted signal to make it harder to extract useful information from it. The signal-to-noise ratio for the plain and encrypted audio signals is computed as follows:
A higher negative SNR value indicates a stronger encryption scheme. The results of the SNR test for CeTrivium are shown in Table 4. The proposed scheme consistently demonstrates a high negative SNR, indicating that it is robust against attacks.
PSNR can be used to evaluate the effectiveness of encryption schemes. It measures the strength of the original, unencrypted signal compared to the strength of the encrypted signal. The calculation of PSNR is performed as follows:
where Peak is the maximum possible value of the audio signal. A higher PSNR value indicates that the integrity of the original signal has not been greatly affected by the encryption, while a lower PSNR value indicates that a significant amount of noise has been introduced into the signal, making it harder to recover the original signal. Therefore, when evaluating encryption schemes using PSNR, a lower value is generally considered more secure, as it indicates a higher level of encryption. Table 4 presents the PSNR values for the encrypted audio files. These values are low, indicating a significant amount of noise in the encrypted audio files, which results in strong resistance to attacks.
6.4 NSCR, Entropy, and Computational Time Analysis
Information entropy analysis is used to determine the level of uncertainty or randomness in a signal. It is used for evaluating encryption algorithms, where a higher entropy value of the encrypted signal indicates greater unpredictability and makes it more difficult to break the encryption using statistical attacks. The entropy of a signal can be calculated as follows:
where
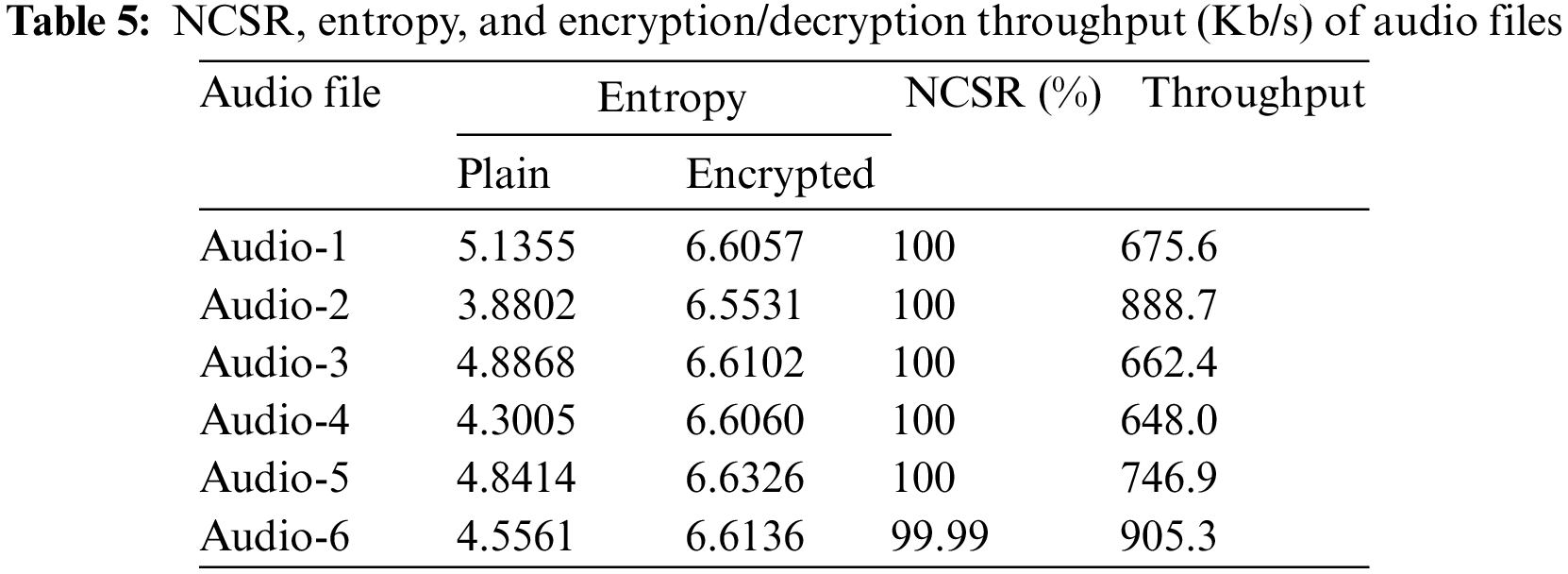
NSCR is a testing method used to evaluate the robustness of ciphering schemes. It measures the percentage of sample values that have changed between the encrypted and original signals. The NSCR test determines how effectively an encryption algorithm has protected the original audio data by comparing the original and encrypted samples.
The ideal NSCR value is 100%, indicating that all sample values have changed during the encryption process. A high NSCR value indicates that the encryption algorithm can efficiently protect the plain audio and is considered highly secure. Conversely, a low NSCR value suggests that the encryption algorithm has not adequately protected the original audio data and is considered less secure. NSCR can be computed as follows:
The NSCR test results for various audio files are shown in Table 5. The table illustrates that the NSCR values are close to the ideal, indicating that the proposed encryption scheme has a high level of security. In addition, Table 5 lists the encryption/decryption throughput of CeTrivium for the tested audio files, which ranges from 648 to 905.3 Kb/s with an average of 754.4 Kb/s.
Table 6 compares the performance of CeTrivium to other state-of-the-art schemes in terms of key space, correlation coefficient, SNR, PSNR, entropy, NSCR, and encryption rate. The comparison includes a standard scheme (AES with a 256-bit key size) adopted by SRTP, two stream cipher schemes based on CA (CARPeter and Pentavium), and seven other encryption schemes that use various concepts, such as DNA coding, chaotic maps, and shift registers.
The size of the key space in an encryption scheme might be sufficiently large to resist brute-force attacks. A key space smaller than 2128 is not considered sufficiently secure [53]. As demonstrated in Table 6, similar to other related schemes, the proposed scheme can withstand brute-force attacks since the key space is larger than 2128.
As shown in Table 5, all cipher schemes have very low correlation coefficients, indicating that the plain audio and encrypted signals are uncorrelated, making it difficult for attackers to gain valuable information through statistical attacks. In addition, the proposed scheme has a low SNR and PSNR, indicating that it adds a significant amount of noise to the original signal, making it robust against various differential attacks. Moreover, the proposed scheme has the highest entropy and NSCR compared to other schemes, which indicates that it is more resistant to attacks. In addition, the encryption throughput of the proposed stream cipher is much higher than that of other schemes, making it more suitable for real-time multimedia transmission. In summary, the proposed stream cipher scheme achieved competitive results compared to the state-of-the-art schemes.
7 Conclusion and Future Directions
This work introduces a new stream cipher called CeTrivium, which is based on a hybrid nonlinear CA. CeTrivium is composed of three building blocks: the Tr block, which is structured similarly to the Trivium cipher; the NCA block, which is a nonlinear hybrid 5-neighborhood CA; and the NM block, which is a nonlinear, balanced, and reversible function that combines the outputs of the Tr and NCA blocks to generate the keystream. The NIST statistical test suite was used to evaluate the quality of keystreams. The p-value for all tests was greater than 0.01, indicating that the keystream generated by CeTrivium passed all tests. Additionally, an analysis of CeTrivium’s security properties revealed that it can resist a variety of attacks. CeTrivium has a correlation coefficient less than 10−72, which requires at least 2144 bits of keystream to detect correlation, which is not feasible. After 18 cycles, the algebraic degree of CeTrivium is 73, which indicates resistance to the algebraic attack and makes performing a fault attack infeasible. The algebraic degree of the keystreams increases by 4 every cycle, making it grow rapidly. This increase in complexity makes it difficult to compute the maxterms and thus helps prevent cube attacks. Because the total number of bits that define the internal state of CeTrivium is 352, it is difficult to perform a data/memory/time/tradeoff attack. Due to using the nonlinear blocks and the nonlinear mixing function, the CeTrivium cipher is robust against side-channel attacks. The scheme is evaluated using histogram and spectrogram analysis, which demonstrates the alterations in encrypted signals compared to orignal signals. In addition, the results for different measurements, such as the correlation coefficient, NSCR, and entropy, confirm the high quality of encryption. The measured SNR and PSNR values show high levels of noise in the encrypted files, which implies resistance to attacks. CeTrivium was compared to other state-of-the-art schemes. We found that it has a higher entropy and NSCR, which indicates that it is more resistant to attacks. Moreover, the encryption throughput of the proposed stream cipher is much higher. We can conclude that CeTrivium has the necessary cryptographic security properties and performance to make it suitable for real-time multimedia transmission. In future work, CeTrivium will be implemented in hardware, and different mixing functions will be adopted to enhance its security performance.
Acknowledgement: The authors are grateful for the reviewer’s valuable comments that improved the manuscript.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Osama Younes, Umar Albalawi; data collection: Abdulmohsen Alharbi, Ali Yasseen, Faisal Alshareef, Faisal Albalawi; carrying out coding and experiments: Osama Younes, Abdulmohsen Alharbi, Ali Yasseen, Faisal Alshareef, Faisal Albalawi; analysis and interpretation of results: Osama Younes, Umar Albalawi, Abdulmohsen Alharbi, Ali Yasseen, Faisal Alshareef, Faisal Albalawi; draft manuscript preparation: Osama Younes, Umar Albalawi, Abdulmohsen Alharbi, Ali Yasseen, Faisal Alshareef, Faisal Albalawi; All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data available on request from the authors.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. H. Schulzrinne, S. Casner, R. Frederick and V. Jacobson, “RFC3550: RTP: A transport protocol for real-time applications,” RFC, 2003. [Online]. Available: https://dl.acm.org/doi/abs/10.17487/rfc3550 [Google Scholar]
2. M. Baugher, D. McGrew, M. Naslund, E. Carrara and K. Norrman, “RFC3711: The secure real-time transport protocol (SRTP),” RFC, 2004. [Online]. Available: https://dl.acm.org/doi/abs/10.17487/RFC3711 [Google Scholar]
3. K. P. Man, K. W. Wong and K. F. Man, “Security enhancement on VoIP using chaotic cryptography,” in Proc. of Annual Conf. on IEEE Industrial Electronics, Paris, France, pp. 3703–3708, 2006. [Google Scholar]
4. R. I. Abdelfatah, “Audio encryption scheme ssing self-adaptive bit scrambling and two multi chaotic-based dynamic DNA computations,” IEEE Access, vol. 8, no. 1, pp. 69894–69907, 2020. [Google Scholar]
5. S. Adhikari and S. Karforma, “A novel audio encryption method using Henon–Tent chaotic pseudo random number sequence,” International Journal of Information Technology, vol. 13, no. 4, pp. 1463–1471, 2021. [Google Scholar]
6. H. Manifavas, G. Hatzivasilis, K. Fysarakis and I. Papaefstathiou, “A survey of lightweight stream ciphers for embedded systems,” Security and Communication Networks, vol. 9, no. 10, pp. 1226–1246, 2015. [Google Scholar]
7. The eSTREAM Project, 2022. [Online]. Available: http://www.ecrypt.eu.org/stream/project.html [Google Scholar]
8. European network of excellence for cryptography, 2022. [Online]. Available: http://www.ecrypt.eu.org/ [Google Scholar]
9. C. de Cannière and B. Preneel, “Trivium,” New Stream Cipher Designs (The eSTREAM FinalistsLecture Notes in Computer Science, vol. 4986, pp. 244–266, 2008. [Google Scholar]
10. M. Hell, T. Johansson, A. Maximov and W. Meier, “A stream cipher proposal: Grain-128,” in Proc. of IEEE Int. Symp. on Information Theory, Seattle, WA, USA, pp. 1614–1618, 2006. [Google Scholar]
11. M. Boesgaard, M. Vesterager and E. Zenner, “The rabbit stream cipher,” Lecture Notes in Computer Science, vol. 4986, pp. 69–83, 2008. [Google Scholar]
12. D. J. Bernstein, “The salsa20 family of stream ciphers,” New Stream Cipher Designs, pp. 84–97, 2008. [Google Scholar]
13. F. E. Potestad-Ordóñez, E. Tena-Sánchez, J. M. Mora-Gutiérrez, M. Valencia-Barrero and C. J. Jiménez-Fernández, “Trivium stream cipher countermeasures against fault injection attacks and DFA,” IEEE Access, vol. 9, no. 1, pp. 168444–168454, 2021. [Google Scholar]
14. C. D. Ye, T. Tian and F. Y. Zeng, “The MILP-aided conditional differential attack and its application to Trivium,” Designs, Codes and Cryptography, vol. 89, no. 2, pp. 317–339, 2021. [Google Scholar]
15. M. Tomassini and M. Perrenoud, “Cryptography with cellular automata,” Applied Soft Computing, vol. 1, no. 2, pp. 151–160, 2001. [Google Scholar]
16. A. John, B. C. Nandu, A. Ajesh and J. Jose, “PENTAVIUM: Potent Trivium-like stream cipher using higher radii cellular automata,” in Proc. of Int. Conf. on Cellular Automata for Research and Industry, Lodz, Poland, pp. 90–100, 2020. [Google Scholar]
17. J. Jose and D. R. Chowdhury, “Investigating four neighbourhood cellular automata as better cryptographic primitives,” Journal of Discrete Mathematical Sciences and Cryptography, vol. 20, no. 8, pp. 1675–1695, 2017. [Google Scholar]
18. S. Das and D. Roy Chowdhury, “CAR30: A new scalable stream cipher with rule 30,” Cryptography and Communications, vol. 5, no. 2, pp. 137–162, 2013. [Google Scholar]
19. J. Jose, S. Das and D. Roy Chowdhury, “Prevention of fault attacks in cellular automata based stream ciphers,” Journal of Cellular Automata, vol. 12, no. 1/2, pp. 141–157, 2016. [Google Scholar]
20. S. Karmakar and D. R. Chowdhury, “NOCAS: A nonlinear cellular automata based stream cipher,” in Proc. of 17th Int. Workshop on Cellular Automata and Discrete Complex Systems, Stockholm, Sweden, pp. 135–146, 2011. [Google Scholar]
21. S. Karmakar, D. Mukhopadhyay and D. Roy Chowdhury, “CAvium - Strengthening Trivium stream cipher using cellular automata,” Journal of Cellular Automata, vol. 7, no. 2, pp. 179–197, 2012. [Google Scholar]
22. S. Das and D. Roy Chowdhury, “CASTREAM: A new stream cipher suitable for both hardware and software,” in Proc. of Int. Conf. on Cellular Automata, Santorini, Greece, pp. 601–610, 2012. [Google Scholar]
23. J. Jose and D. Roy Chowdhury, “FResCA: A fault-resistant cellular automata based stream cipher,” in Proc. of Int. Conf. on Cellular Automata, Fez, Morocco, pp. 24–33, 2016. [Google Scholar]
24. A. John, R. Lakra and J. Jose, “On the design of stream ciphers with cellular automata having radius = 2,” Cryptology ePrint Archive, vol. 327, no. 1, pp. 327–352, 2020. [Google Scholar]
25. NIST Statistical Test Suite, 2022. [Online]. Available: https://csrc.nist.gov/projects/random-bit-generation/documentation-and-software [Google Scholar]
26. R. B. Naik and U. Singh, “A review on applications of chaotic maps in pseudo-random number generators and encryption,” Annals of Data Science, vol. 9, no. 1, pp. 1–26, 2022. [Google Scholar]
27. S. A. Qassir, M. T. Gaata and A. T. Sadiq, “Modern and lightweight component-based symmetric cipher algorithms: A review,” ARO-The Scientific Journal of Koya University, vol. 10, no. 2, pp. 152–168, 2022. [Google Scholar]
28. L. Jiao, Y. Hao and D. Feng, “Stream cipher designs: A review,” Science China Information Sciences, vol. 63, no. 3, pp. 131101, 2020. [Google Scholar]
29. F. J. Farsana and K. Gopakumar, “A novel approach for speech encryption: Zaslavsky map as pseudo random number generator,” Procedia Computer Science, vol. 93, no. 1, pp. 816–823, 2016. [Google Scholar]
30. P. Sathiyamurthi and S. Ramakrishnan, “Speech encryption using chaotic shift keying for secured speech communication,” EURASIP Journal on Audio, Speech, and Music Processing, vol. 2017, no. 1, pp. 20, 2017. [Google Scholar]
31. A. Belmeguenai, Z. Ahmida, S. Ouchtati and R. Djemii, “A novel approach based on stream cipher for selective speech encryption,” International Journal of Speech Technology, vol. 20, no. 3, pp. 685–698, 2017. [Google Scholar]
32. K. Kordov, “A novel audio encryption algorithm with permutation-substitution architecture,” Electronics, vol. 8, no. 5, pp. 1–15, 2019. [Google Scholar]
33. Nasreen and P. Muthukumar, “Secure audio signal encryption based on triple compound-combination synchronization of fractional‐order dynamical systems,” International Journal of Dynamics and Control, vol. 10, no. 6, pp. 2053–2071, 2022. [Google Scholar]
34. A. Leporati and L. Mariot, “1-resiliency of bipermutive cellular automata rules,” Cellular Automata and Discrete Complex Systems, vol. 8155, no. 1, pp. 110–123, 2013. [Google Scholar]
35. K. Cattell and J. C. Muzio, “Synthesis of one-dimensional linear hybrid cellular automata,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 15, no. 3, pp. 325–335, 1996. [Google Scholar]
36. S. Maiti and D. Roy Chowdhury, “Study of five-neighborhood linear hybrid cellular automata and their synthesis,” in Proc. of Int. Conf. on Mathematics and Computing, Singapore, pp. 68–83, 2017. [Google Scholar]
37. S. Nandi and P. P. Chaudhuri, “Analysis of periodic and iIntermediate boundary 90/150 cellular automata,” IEEE Transactions on Computers, vol. 45, no. 1, pp. 1–12, 1996. [Google Scholar]
38. A. Leporati and L. Mariot, “Cryptographic properties of bipermutive cellular automata rules,” Journal of Cellular Automata, vol. 9, no. 1, pp. 437–475, 2014. [Google Scholar]
39. ENT-a pseudorandom number sequence test program, 2022. [Online]. Available: http://www.fourmilab.ch/random/ [Google Scholar]
40. J. Bhaumik and D. R. Chowdhury, “Nmix: An ideal candidate for key mixing,” in Proc. of Int. Conf. on Security and Cryptography, University of Milan, Italy, 2009. [Google Scholar]
41. Y. V. Tarannikov, “On resilient Boolean functions with maximal possible nonlinearity,” in Proc. of Int. Conf. on Cryptology in India, Calcutta, India, pp. 19–30, 2000. [Google Scholar]
42. F. M. Quedenfeld and C. Wolf, “Advanced algebraic attack on Trivium,” Mathematical Aspects of Computer and Information Sciences, vol. 9582, no. 1, pp. 268–282, 2016. [Google Scholar]
43. S. Banik, S. Maitra and S. Sarkar, “A differential fault attack on the grain family of stream ciphers,” in Proc. of Int. Workshop on Cryptographic Hardware and Embedded Systems, Leuven, Belgium, pp. 122–139, 2012. [Google Scholar]
44. P. Dey and A. Adhikari, “Improved multi-bit differential fault analysis of Trivium,” in Proc. of Int. Conf. on Cryptology in India, New Delhi, India, pp. 37–52, 2014. [Google Scholar]
45. F. E. Potestad-Ordóñez, M. Valencia-Barrero, C. Baena-Oliva, P. Parra-Fernández and C. J. Jiménez-Fernández, “Breaking Trivium stream cipher implemented in ASIC using experimental attacks and DFA,” Sensors, vol. 20, no. 23, pp. 6909, 2020. [Google Scholar]
46. I. Dinur and A. Shamir, “Cube attacks on tweakable black box polynomials,” in Proc. of Annual Int. Conf. on the Theory and Applications of Cryptographic Techniques, Cologne, Germany, pp. 278–299, 2009. [Google Scholar]
47. S. Wolfram, “Random sequence generation by cellular automata,” Advances in Applied Mathematics, vol. 7, no. 2, pp. 123–169, 1986. [Google Scholar]
48. W. Meier and O. Staffelbach, “Analysis of pseudo random sequences generated by cellular automata,” Advances in Cryptology—EUROCRYPT ’91, vol. 547, no. 1, pp. 186–199, 1991. [Google Scholar]
49. B. Gierlichs, L. Batina, C. Clavier, T. Eisenbarth, A. Gouget et al., “Susceptibility of eSTREAM candidates towards side channel analysis,” in Proc. of the State of the Art of Stream Ciphers Special Workshop, ECRYPT Network of Excellence, Lausanne, Switzerland, 2008. [Google Scholar]
50. S. Karmakar and D. Roy Chowdhury, “Leakage squeezing using cellular automata,” in Proc. of Int. Workshop on Cellular Automata and Discrete Complex Systems, Gießen, Germany, pp. 98–109, 2013. [Google Scholar]
51. A. Biryukov and A. Shamir, “Cryptanalytic time/memory/data tradeoffs for stream ciphers,” in Proc. of Int. Conf. on the Theory and Application of Cryptology and Information Security, Kyoto, Japan, pp. 1–13, 2000. [Google Scholar]
52. T. E. Bjørstad. “Cryptanalysis of grain using time/memory/data tradeoffs,” ECRYPT Stream Cipher Project Report, 2008/012, 2022. [Online]. Available: http://www.ecrypt.eu.org/stream [Google Scholar]
53. E. Albahrani and T. Alshekly, “A text encryption algorithm based on self-synchronizing stream cipher and chaotic maps,” International Journal of Innovative Research in Science, Engineering and Technology, vol. 3, no. 5, pp. 579–585, 2019. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF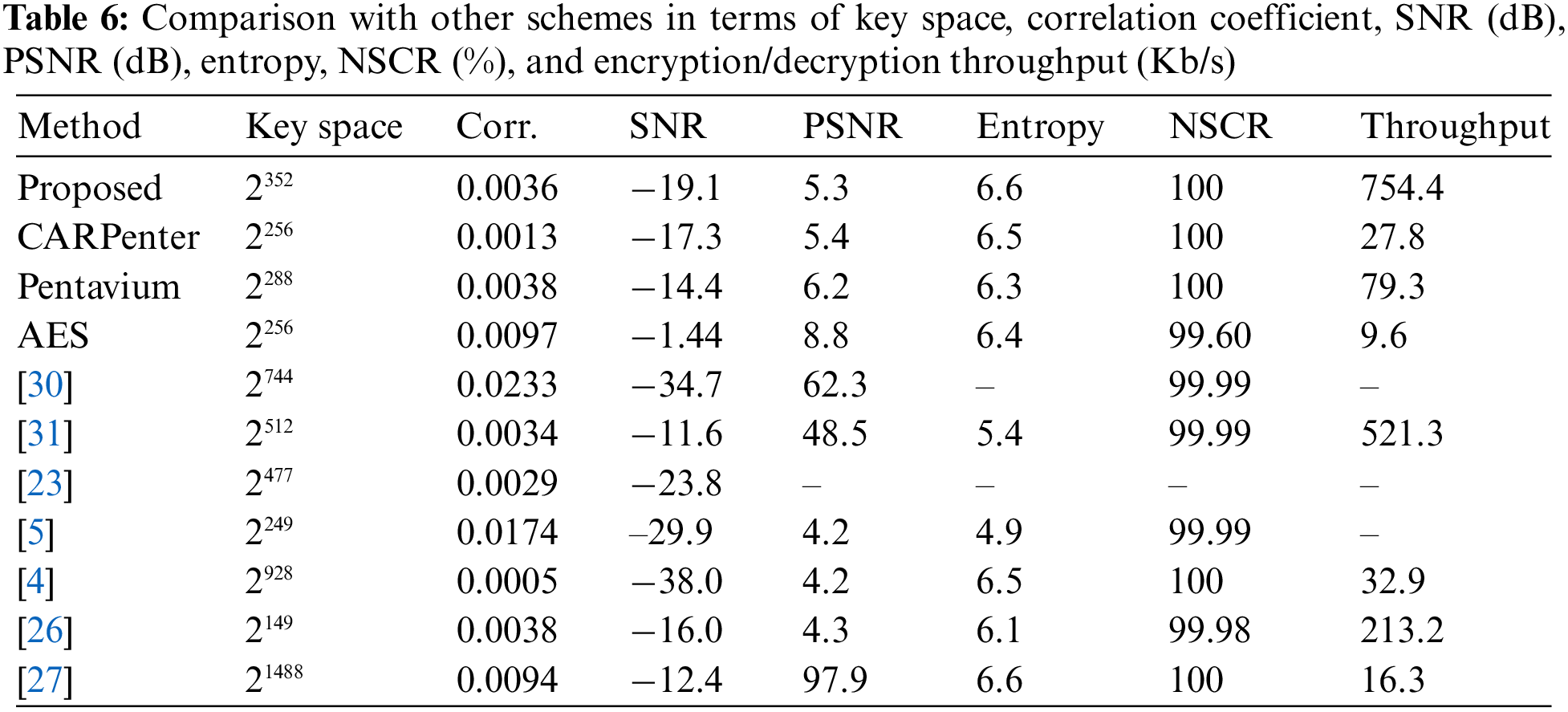
 Downloads
Downloads
 Citation Tools
Citation Tools