An Innovative Technique for Constructing Highly Non-Linear Components of Block Cipher for Data Security against Cyber Attacks

1  Introduction

Modern technical advancements and their successful application in real life have resulted in a massive increase in the volume of data exchanged. Due to the confidential characteristics of information, it is important to develop ways to reduce the risk of improper utilization. A user’s data must be modified before transmission so that it is worthless to an attacker. Cryptography is employed to securely store and transmit data, ensuring that only authorized individuals have access to the original information. By utilizing cryptographic techniques, organizations can protect their sensitive data from unauthorized access. For many decades, basic cryptographic systems have been used in a variety of fields. Various companies and governments have used it in the past to conceal confidential data from adversaries. However, a substantial number of safe and encrypted conversations occur online every day. Cryptographic encryption techniques can be divided into two distinct categories: symmetric and asymmetric encryption. Symmetric encryption involves the use of a single key to both encrypt and decrypt data, while asymmetric encryption requires two separate keys, one for encryption and one for decryption. Both of these encryption techniques are essential for ensuring the security of sensitive data and communications. Modern symmetric encryption systems, which use the same keys for encryption and decryption operations, require fewer processing resources and are more practicable than old encryption algorithms. There are two types of symmetric encryption schemes: stream ciphers and block ciphers [1]. Because of their ease of implementation and ability to offer much-needed cryptographic strength, symmetric block ciphers are among the most extensively utilized algorithms for this purpose [2,3].

The most popular form of block encryption is Advanced Encryption Standard (AES), which employs substitution and permutation operations. To convert plain text into cipher text, the AES block cipher uses a symmetric key and a variable number of rounds. On the input data block, each round is composed of permutation and substitution operations. In substitution processes, input blocks are substituted with output blocks using substitution boxes (S-boxes) [4]. The S-box is a basic characteristic of modern block ciphers that creates confused cipher text from the provided plaintext [5]. As the only nonlinear component of modern block ciphers, an S-box provides a complicated link between the plaintext and the cipher text. This suggests that unsafe cryptosystems are prompted by weak substitution boxes.

As a result, the development of resilient S-boxes is a critical aspect in the evolution of efficient and safe cryptosystems. So, the researchers in this field have concentrated on the development of innovative strategies for creating cryptographically secure S-boxes. Various ideas and methods for building Substitution boxes have emerged in recent years. In [6], the author employed the I-Ching operator to generate the S-box. When tested using several algebraic criteria, the resultant S-box offers good cryptographic features. Authors in [7] gave the innovative technique to construct the strong S-box using quantic fractional transformation, which is further used in image encryption protection. The outcomes of the projected S-box are outstanding and strong against linear and differential attacks. In [8], authors present the novel technique to construct the substitution box by using dynamic polynomial mapping and constructing the large number of S-boxes. The results are good enough to withstand against linear and differential attacks. In [9], the authors describe a revolutionary modular strategy for building a huge number of S-boxes by gently modifying the parameters in a newly constructed transformation.

Razzaq et al. [10] provide a unique approach for generating the 462422016 various numbers of AES-like S-boxes based on the notion of a coset graph and the actions of a symmetric group and a permutation group. Razzaq et al. [11] built the S-box using the concepts of triangle groups (2, 3, 8), symmetric groups, and coset graphs. The resultant S-box has a nonlinearity of 113.75, which is higher than the standard AES S-box. Yousaf et al. [12] build the S-box using the action of a finite Abelian group, and the resulting S-box possesses optimum properties. Shahzad et al. [13] build the S-box using the action A4 on PL(F257). This system is based on a coset diagram and the Fibonacci sequence. To generate S-boxes for the action of PSL(2,Z) on a projective line over a GF(28) which is a finite field, Razzaq et al. [14] employed a unique kind of bijective map and symmetric group. The motivation behind this work is to study the coset graphs and symmetric groups. In literature, construction techniques of S-boxes by action of A4, S4 and triangle group (2, 3, 8) on PL(F257) discussed. This proposed method uses the concept of field extension for the generation of S-box by action of A5 on PL(F269) instead of PL(F257) because the roots of the equation do not exist under mod 257; therefore, the nearest prime field of Galois Field GF(28) in which the roots of the equation exist is used.

The technique of constructing the S-boxes by using the concept of an alternating group and coset diagram is presented in this article. The following is the main contribution in this paper:

1)   A novel group theoretic and graphical construction of S-box based on the orbits of a coset graph, alternating group A5 and field extension is proposed.

2)   Symmetric group S256 utilizes the S-box to generate it with good cryptographic properties.

3)   S-box evaluated through standard S-boxes criteria that show outstanding results against linear and differential attacks.

The remainder of the paper is structured as follows: Section 2 comprises the basic concept and definitions related to the symmetric groups and coset graphs, while the algebraic structure of the generation of suggested S-boxes is discussed in Section 3. Section 4 evaluates and compares the strength of the newly suggested S-boxes to previous well-known S-boxes. Section 5 represents the result and discussion portion. Conclusion and future work are presented in Section 6.

2  Algebraic Preliminaries

This section discusses several fundamental ideas and terms related to coset graphs, alternating groups, and symmetric groups for the generation of S-boxes.

2.1 Modular Group and Coset Diagrams

The modular group M is an infinite, non-cyclic, and non-abelian group composed of two generators, α and β. Basically, the bijective maps are generated by the generators α and β of M defined as follows: α(u)=−1u and β(u)=u−1u. Since the order of α and β is 2 and 3 respectively. Therefore, ⟨α,β : α2=β3=1⟩ is the finite presentation of M [15]. Several fields of science, such as number theory, geometry and topology etc., use this infinite discrete group because it has a wide range of applications. The concept of a coset graph for a modular group was introduced by Graham Higman (FRS) in 1978. Since the modular group M has two generators of orders 2 and 3 respectively. Therefore, the coset graph consists of the lines and triangles that are connected through edges with each other. The vertices of triangle are permuted anti-clockwise by β. If the vertices a,b and c of the triangle T, it means that β(a)=b, β(b)=c and β(c)=a. If the line representing α join the vertices d and e (which may be of same triangle), then β(d)=e. For more on coset graphs, readers refer to [16–19].

Consider a set Zn under multiplication modulo n defined as follows: Zn={0,1,2,…,n−1}. This set forms a field when n is prime number p. The action of modular group M on Zp∪{∞} emerges a finite coset graph. Since α(0)=−10=∞. To make the action of M possible, we adjoin ∞ with Zp. As an illustration, consider the action of M  on Z11∪{∞}={0,1,2,3,…,10,∞}. The permutation representations of α and β, calculated by α(u)=−1u and β(u)=u−1u are given as follows:

α:(0,∞)(1,10)(2,5)(3,7)(4,8)(6,9)

β:(0,∞,1)(2,6,10)(3,8,5)(4,9,7)

The coset graph of Z11∪{∞} has four triangles because the permutation of β contains four cycles. In the permutation of α, cycle (2,6,10) is the triangle with vertex 2,6 and 10 of the coset graph. By doing this, four triangles can be formed. To connect the vertices of a triangle permutations of α are used. For example, by the cycle (1, 10) in α, we mean there is an edge between vertex 1 and 10. The coset graph is obtained by using the above permutation representation of α and β as shown in Fig. 1.

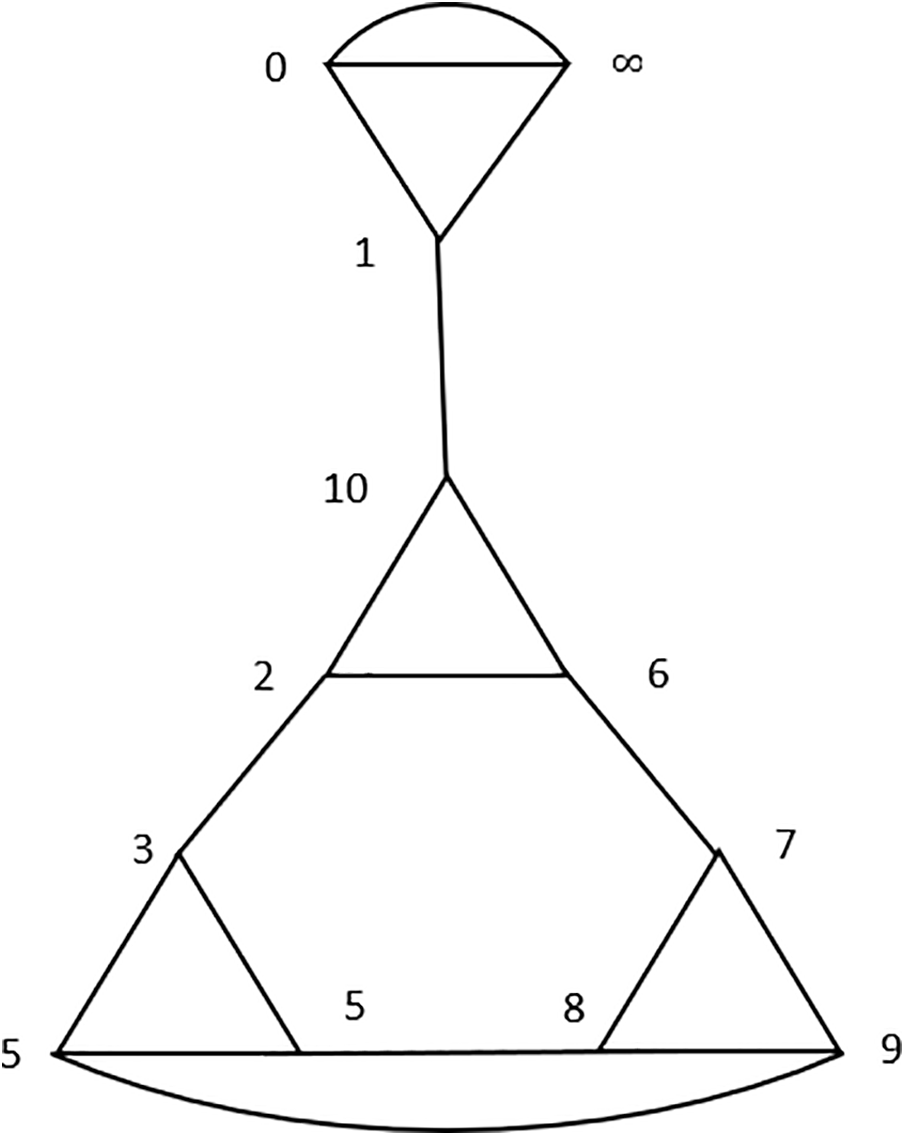
Figure 1: Coset graph for the action of PSL(2,Z) on Z11∪{∞}

The coset graph emerges as a result of natural action of PSL(2,Z) on Z11∪{∞} as shown in Fig. 1. The graphical representation is ⟨α,β : α2=β3=(αβ)11=1⟩ because each vertex of the coset graph is fixed by α2, β3 and (αβ)11. In the case of the natural action of PSL(2,Z) on Zp∪{∞}, only one coset graph can be obtained for each p. Mushtaq in [20] proposed the method to construct the coset graph for each element of ϑ in Zp known as parametrization method. This approach generates coset graphs from which we can extract the order of αβ of our choice. Therefore, we can obtain the coset graphs for various triangular groups (2,3,k).

2.2 Triangle Group and Alternating Group

The triangle group is a group that can be represent in the form: Δ(r,s,t)=⟨α,β : αr=βs=(αβ)t=1⟩ where r,s,t>1. The triangle groups Δ(2,3,t) are particularly significant since they occur as a quotient of PSL(2,Z) in many cases. Therefore, it’s more important to note that the members of the group Δ(2,3,t) are finite when k < 6. The alternating group A4, A5 and symmetric group S3, S4 are finite triangle groups of the form Δ(2,3,t).

2.3 Mushtaq Parametrization Scheme

Let us discuss the Mushtaq technique briefly (for proof and detail, see [20]).

Firstly, set α(u)=au+kccu−a and β(u)=du+kffu−d−1. The values of parameters a,c,d,k,f can be computed for each element of ϑ∈Zp, by solving the equations

 ϑ=r2Δ(2.1)

r2+ks2=3Δ(2.2)

d2+d+kf2+1=0(2.3)

(2d+1)a+2kcf−r=0(2.4)

2fa−(1+2d)c−s=0(2.5)

Table 1 represent the relation between the value of ϑ∈Zp and the order of αβ. By using a parametrization scheme, the value of ϑ for higher value of αβ can be found [20].

3  Algebraic Structure of S-Box

The coset graph for the symmetric group ⟨α,β : α2=β3=(αβ)5=1⟩ emerge as a result of the action of PSL(2, Z) on Z269∪{∞}. For the generation of 8×8 S-box, 256 entries are used, so the nearest prime integer of 256, in which the roots of the equation exist, which is 269. Thus, for the action of M, we opted for Z269∪{∞} is used. The value of ϑ satisfying the polynomial equation ϑ2−3ϑ+1=0 in Z269 is present in Table 1. Since in A5 the order of αβ is 5, therefore, we have θ=73. To find the values of a,c,d,k and f, first solve the Eqs. (2.1) to (2.5). For Eq. (2.1), ϑ=r2Δ, we take Δ=1, then r=197 is obtained. As r2+ks2=3Δ, we assume k=1 to obtain s=71. By substituting d=4 in Eq. (3), f=168 obtained. By putting k=1, d=4,f=168, r=197 and s=71 in the Eqs. (2.4) and (2.5), we find a=65 and c=207. Thus, we have α(x)=65x+207207x−65 and β(x)=4x+168168x−5. Going forward, the permutation representation of each element in Z269∪{∞} by applying these mappings to each individual element is computed. The calculations of α(x) and β(x)∀ x ϵ Z269 are conducted using mod 269 and then represented in the form of permutations as follows:

α: (0, 92)(1, 108)(2,95)(3,112)(4,130)(5,198)(6,203)(7,217)(8,214)(9,16)(10,265)(11,114)

(12,179)(13,34)(14,258)(15,174)(17,251)(18,33)(19,146)(20,152)(21,222)(22,99)(23,121)

(24,223)(25,51)(26,209)(27,249)(28)(29,266)(30,160)(31,139)(32,111)(35,184)(36,257)

(37,207)(38,∞)(39,138)(40,88)(41,161)(42,63)(43,58)(44,234)(45,206)(46,185)(47,79)(48)

(49,96)(50,136)(52,122)(53,224)(54,246)(55,123)(56,193)(57,199)(59,94)(60,67)(61,171)

(62,87)(64,166)(65,231)(66,80)(68,131)(69,128)(70,142)(71,147)(72,215)(73,233)(74,250)

(75,237)(76,253)(77,213)(78,175)(81,228)(82,187)(83,100)(84,239)(85,229)(86,197)(89,156)

(90,102)(91,182)(93,211)(97,140)(98,219)(101,236)(103,143)(104,227)(105,176)(106,261)

(107,172)(109,244)(110,144)(113,129)(115,200)(116,260)(117,264)(118,241)(119,192)

(120,177)(124,133)(125,135)(126,247)(127,157)(132,268)(134,252)(137,164)(141,180)

(145,230)(148,259)(149,194)(150,183)(151,196)(153,226)(154,178)(155,186)(158,263)(159,190)

(162,195)(163,254)(165,204)(167,191)(168,225)(169,240)(170,267)(173,238)(181,208)(188,218)

(189,256)(201,235)(202,242)(205,248)(210,220)(212,221)(216,232)(243,255)(245,262)

β:(0,74,227)(1,242,170)(2,133,148)(3,223,158)(4,260,18)(5,122,220)(6,259,199)(7,104,117)

(8,146,66)(9,71,234)(10,268,125)(11,183,215)(12,153,252)(13,48,114)(14,186,251)(15,94,96)

(16,159,138)(17,217,63)(19,204,175)(20,218,145)(21,258,40)(22,262,178)(23,78,86)

(24,236,151)(25,116,209)(26,73,265)(27,224,196)(28,62,210)(29,162,250)(30,67,254)

(31,202,70)(32,266,228)(33,144,108)(34,98,65)(35,168,216)(36,222,54)(37,58,154)

(38,181,59)(39,243,194)(41,203,136)(42,105,90)(43,139,160)(44,185,214)(45,97,50)

(46,230,173)(47,261,235)(49,64,195)(51,189,131)(52,248,177)(53,164,89)(55,225,253)

(56,57,106)(60,118,240)(61,263,156)(68,77,110)(69,76,255)(72,198,187)(75,192,246)

(79,137,226)(80,93,190)(81,172,257)(82,113,219)(83,149,184)(84,115,247)(85,88,102)

(87,120,129)(91,140,141)(92,155,107)(95,109,112)(99,163,132)(100,152,147)(101,103,182)

(111,119,174)(121,128,211)(123,197,239)(124,171,201)(126,188,232)(127,264,166)

(130,167,212)(134,249,180)(135,169,256)(142,213,241)(143,244,161)(150,231,205)

(157,208,176)(165,238,200)(179,206,193)(191,267,207) (221, 245, 233) (229, ∞,237)

From the above permutation representation, one can see that 0 is mapped onto 92 through α and β send 92 to 155 (i.e., β(0)=155). Proceeding in this manner, 0 is mapped onto itself through (αβ)5. In the same way, (αβ)5 fixes all entries of Z269∪{∞}. This generates the coset graph satisfying the relation α2=β3=(αβ)5=1 of the triangle group (2,3,5), which is isomorphic to the alternating group A5. Fig. 2 depicts a small patch of this coset graph with 54 orbits.

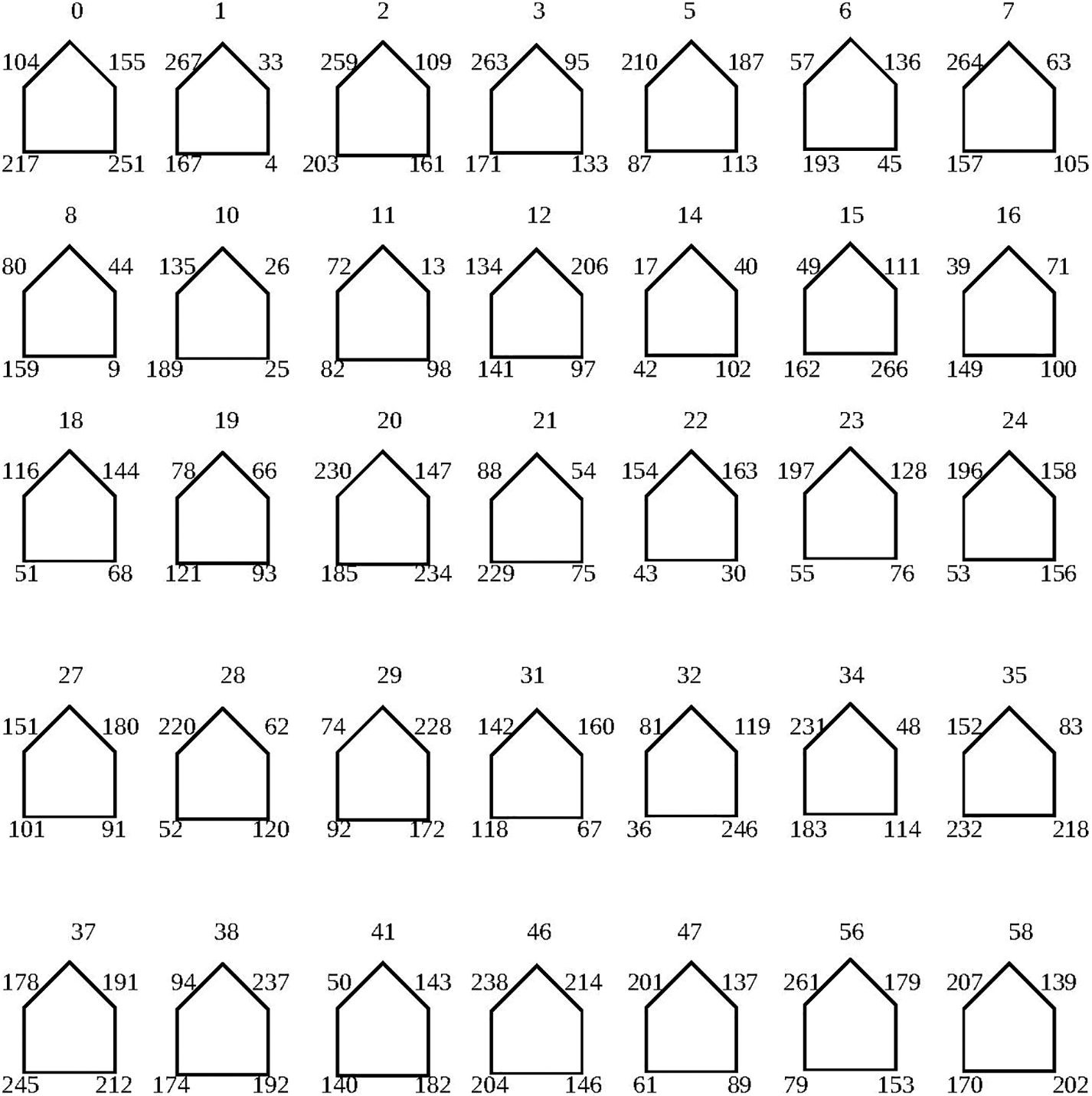
Figure 2: Cyclic graphs of permutation (αβ)5=I

3.1 Proposed S-Box Method

The coset graph of alternating group A5 has 54 cycles of αβ, as shown in Fig. 2:

1)   Find the cycle ω1 in which element 0 is the smallest of all Z269 elements.

2)   Apply (αβ)5 on 0, so that we can move through the cycle 0⇢155⇢251⇢217⇢104⇢0 (see in Fig. 2).

3)   Repeat step 1.2 for the next cycle containing the smallest element of Z269−ω1. Until all the cycles ωi of αβ are eliminated from the coset graphs, this procedure is repeated.

4)   Write all the elements in a tabular form, and then apply a mapping I:Z269→Z257 as follows:

I(x)={xif x≤255 0if x>255(3.1)

After that, omitting the initial 0, disregard all vertices bigger than 255 and ∞ because an S-box consists of 256 entries from 0 to 255. Following this, write the remaining elements in the 16×16 table, which is an elementary S-box, as shown in Table 2.

In the initial S-box, the mean non-linearity value is 101.25; however, this value may be enhanced by using a particular permutation of the symmetric group to construct a robust S-box. In this scenario, the 256 cells of Table 2 are subjected to a specific permutation of the symmetric group S256 given below. As a result, a robust S-box in Table 3 is obtained with a mean non-linearity of 111.75.

3.2 Permutation of Symmetric Group of Order 256

The permutations of S256 are explain as follows,

(1, 179, 164, 242, 33, 34, 123, 73, 53, 77, 28, 243, 38, 192, 233, 108, 125, 91, 224, 107, 193, 5, 47, 212, 190, 55, 180, 177, 75, 69, 27, 114, 35, 196, 162, 102, 74, 170, 134, 141, 221, 195, 148, 173, 81, 40, 166, 14, 119, 106, 110, 67, 3, 236, 160, 60, 248, 101, 11, 225, 138, 208, 235, 137, 83, 117, 42, 189, 30, 109, 4, 87, 57, 120, 46, 113, 56, 23, 19, 231, 252, 147, 59, 95, 45, 16, 122, 43, 150, 214, 103, 7, 171, 37, 78, 249, 44, 93, 201, 176, 229, 21, 17, 163, 85, 68, 241, 65, 142)(2, 187, 24, 63, 172, 254, 105, 140, 18, 240, 198, 204, 184, 144, 89, 100, 70, 218, 54, 124, 12, 20, 52, 6, 175)(8, 145, 94, 222, 13, 191, 217, 128, 188, 232, 155, 251, 215, 98, 197, 255, 203, 230, 206, 158, 61, 131, 50, 10, 143, 49, 130, 127, 194, 58, 199, 167, 174, 228, 92, 223, 133, 22, 72, 80, 71, 213, 121, 48, 165, 115, 245, 186, 99, 112, 64, 149, 154, 104, 116, 181, 129, 51, 161, 39, 88, 227, 209, 66, 153, 237, 86, 146, 76, 211, 62, 152, 168, 29, 111, 247, 26, 207, 136, 159, 200, 183, 135, 79, 97, 126, 157, 185, 15, 205, 234, 219, 250, 139, 118, 151, 256, 216)(9, 84, 96, 32, 25, 246, 244, 36, 169, 31, 156)(41, 132, 178, 226, 90, 182, 82, 253)(220, 238, 239)(202, 210).

4  Algebraic Analysis

In this part, the proposed innovative approach and suggested S-box as shown in Table 3 against widely accepted traditional methods is examined. To examine the cryptographic strength of the S-box, performance standards have been developed. Several key analyses are used to determine the robustness of the S-box, including nonlinearity, differential approximation probability, bit independence criteria, strict avalanche criteria, and linear approximation probability.

4.1 Non-Linearity (NL)

To obtain the original plaintext from an S-box constructed in such a way that the plaintext and cipher text have a linear mapping, it is simple to conduct a linear cryptanalysis attack. An S-box must be constructed with a strong nonlinear mapping among its input and output to withstand this assault. A test based on this criterion was introduced in 1988 by Pieprzyk et al. [21]. Using Eq. (4.1), one can determine the nonlinearity of an n-bit Boolean function.

Nh=(2)n2[1−(2)−nmax|Wh(u)|](4.1)

Wh(u)=∑u∈F2n(−1)h(z)⊕u.z(4.2)

The suggested S-box nonlinearity outcomes for eight balanced Boolean functions are 112, 112, 112, 112, 112, 112, 112, and 110, with a minimum of 110, a maximum of 112, and an average of 111.75. An assessment of the mean nonlinearity of the resultant S-box compared to those of other recent S-boxes is shown in Fig. 3. As can be observed, the final S-box has the necessary capacity to preserve the linearity, making linear cryptanalysis difficult for the attacker.

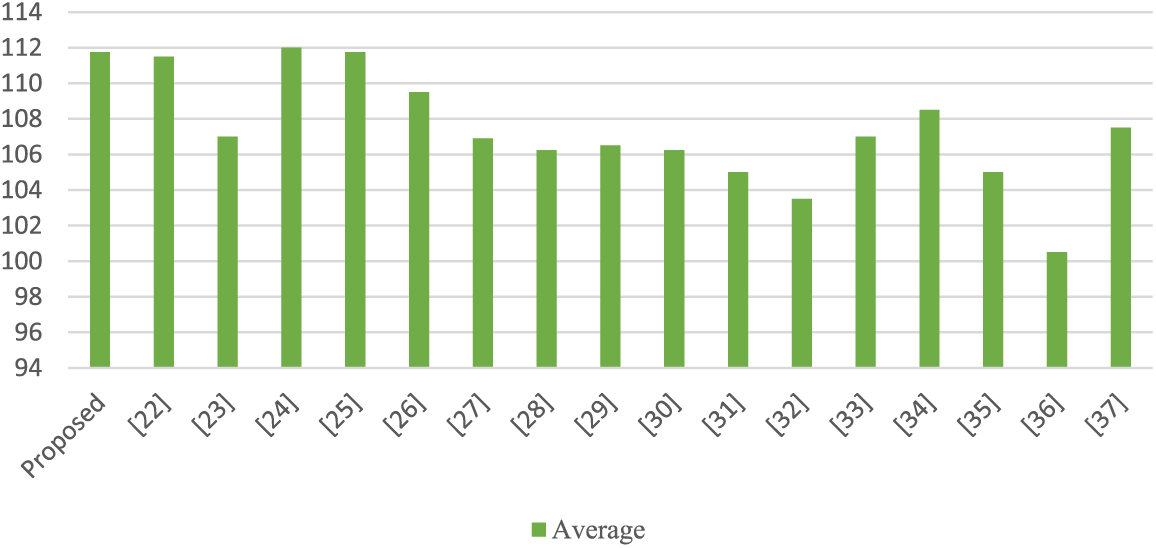
Figure 3: A comparison between average NL value of proposed s-box with various s-boxes

4.2 Strict Avalanche Criterion (SAC)

The strict avalanche criteria [22,23], are fundamental characteristic for every cryptographic S-box, stating that modifications in input and output bit values affect the strict avalanche criteria (SAC). When a single bit alters the input outcomes in a transfer of 1/2 of the output bits, an S-box encounters the SAC. An S-box with a SAC score close to 0.5 has reasonable ambiguity. Table 4 shows the dependency matrix containing the SAC values of the proposed S-box and maximum, minimum values of SAC are displays in the columns of this table. The average SAC value of the S-box is equal to 0.4988. This SAC number demonstrates that the suggested S-box satisfies the SAC property satisfactorily.

4.3 Bit Independent Criterion (BIC)

The bit independence criteria require pairwise comparisons of variables to determine their independence. According to this criterion [22,23], inverting an ith input bit alters output bits jth and kth independently of one another. Secure output bits are generated by an S-box that makes the output bits independent. If an S-box has the BIC quality, all of its constituent Boolean functions are strongly nonlinear and satisfy the SAC requirement. Tables 5 and 6 present the outcomes BIC nonlinearity and BIC-SAC of the resultant S-box, respectively, which identify the relationship between changing ith input and matching changes in jth and kth output bits. Proposed S-box has a mean BIC nonlinearity outcome of 103.64, whereas the average BIC-SAC score is 0.497, which is approximately equal to the ideal score of SAC, which is 0.5. As a result, this S-box meets the BIC’s standards. Comparison of the BIC, SAC, DP and LP outcomes of the resultant S-box to those of other previously suggested S-boxes present in Table 7.

4.4 Linear Probability (LP)

In current block ciphers, the cryptologist aims to provide enough bit diffusion and uncertainty to prevent cryptanalysis. These requirements can be met by strong S-boxes by providing a nonlinear mapping between input and output. A low linear probability (LP) S-box suggests a greater nonlinear mapping and confers resistance to linear cryptanalysis. This criterion determines the greatest value of an event’s imbalance. Matsui [39] developed this analysis, and a mathematical formula for calculating the LP value of the S-box is presented below.

LP=maxa1,a2≠0|#{w∈W|w.a1=g(w).a2}2n−12|(4.3)

where a1 mask denotes the parity of input bits and a2 mask denotes parity of output bits. W is the collection of all input values and 2n is the total number of elements. The highest LP of the suggested S-box is just 0.1328. Table 7 shows a comparison of different S-boxes’ LP scores. The findings of this study show that proposed S-box is robust to linear attacks and that the LP score in the suggested S-box is lower than that of several other S-boxes.

4.5 Differential Probability (DP)

Differential cryptanalysis is thought to be a valuable approach for obtaining the original plaintext. Variations in the plaintext and ciphertext are discovered throughout this attempt. Biham et al. proposed this test [40]. The differential uniformity of a Boolean function is calculated by requiring that the XOR values of each output have the same probability as the XOR values of each input. The formula for calculating DP is provided below.

DPg=maxΔw≠0,Δz(#{w∈W|g(w)⊕g(w⊕Δw)=Δz}2n)(4.4)

Table 7 shows the comparison of differential probability values of the suggested S-box and several other S-boxes. Table 8 explains the differential uniformity values of the suggested S-boxes. Fig. 4 depicts a graphical analysis of the DP score of the suggested S-box and several other S-boxes.

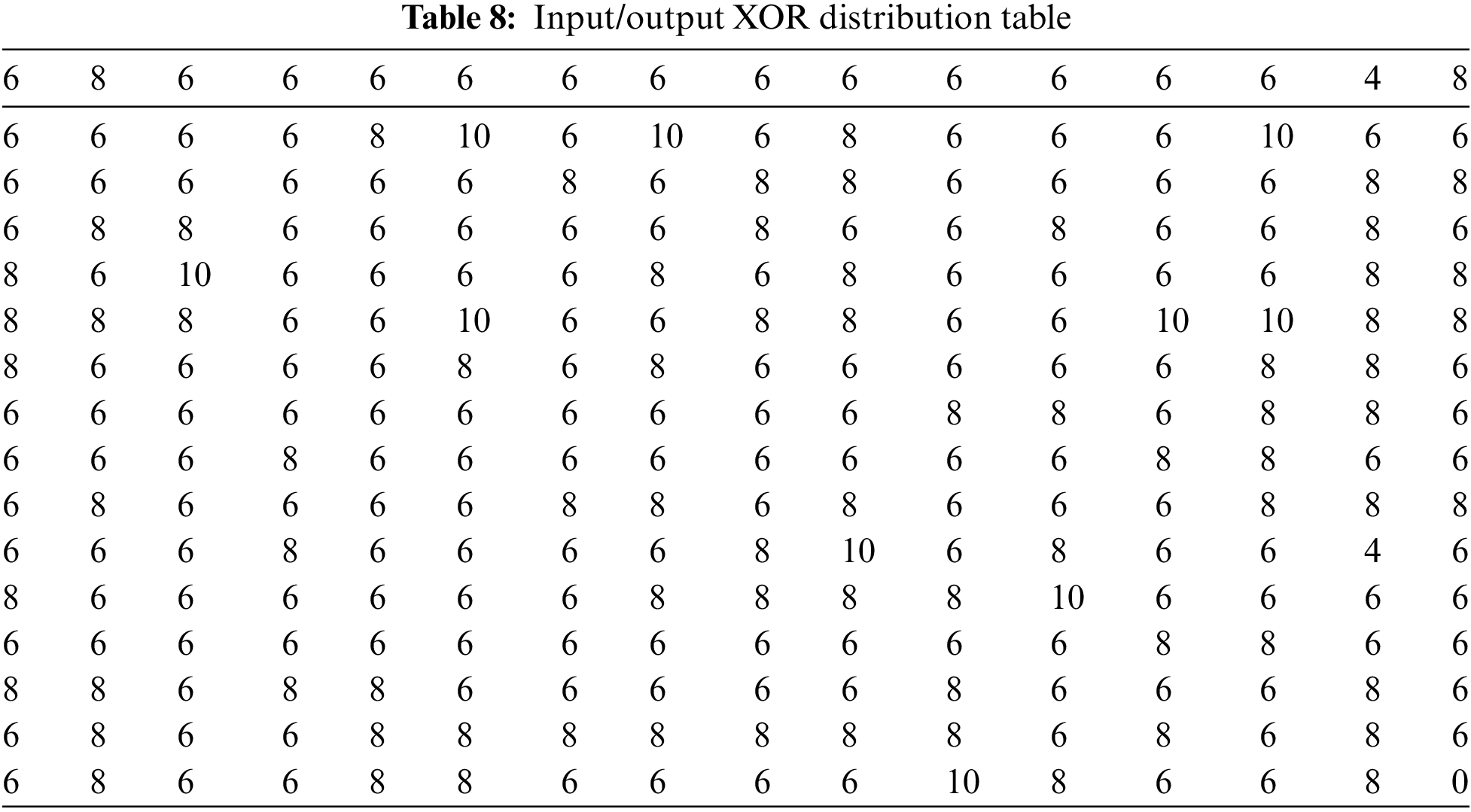
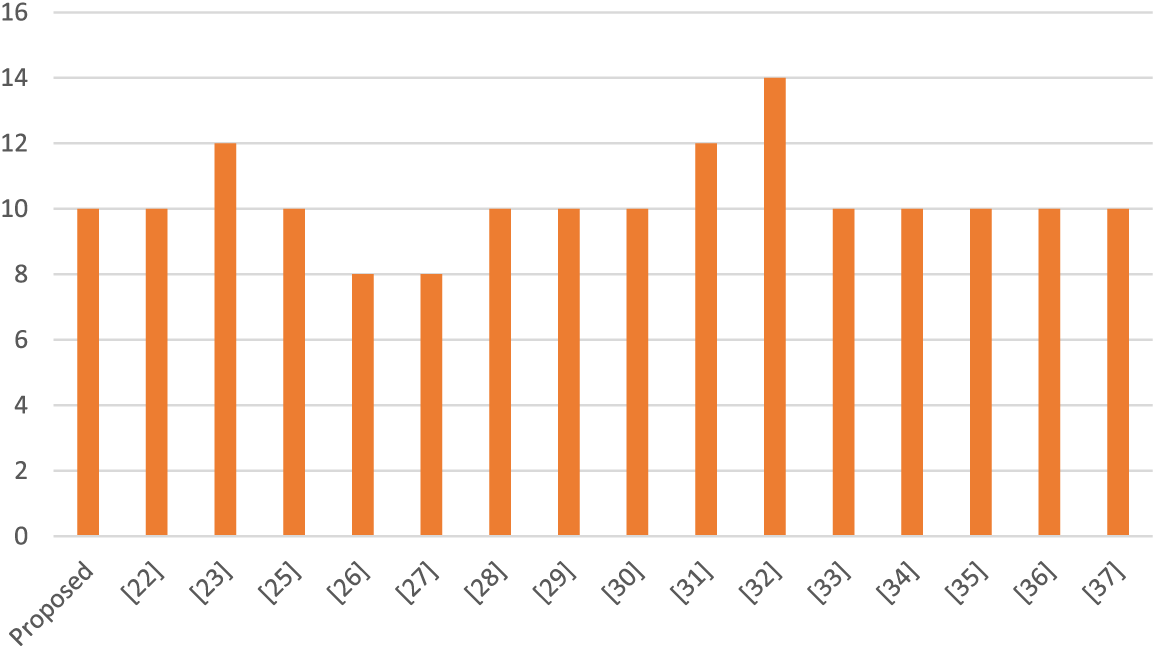
Figure 4: A bar chart showing the DP score of the proposed s-box with different s-boxes

5  Results and Discussion

High nonlinearity is an important criterion for constructing good cryptosystems. In comparison to the other S-boxes shown in Fig. 1, the created S-box’s mean NL score of 111.75 is relatively high. According to this NL score, linear attacks are exceedingly difficult to succeed against the S-box. The SAC score is 0.4988 as shown in Table 4, which is nearly equivalent to the SAC’s ideal score. With regard to nonlinearity, the resultant S-box’s mean BIC score is 103.64 as shown in Table 5, and the resultant S-box has an LP score of 0.1328, which is quite good when compared to existing S-boxes. The complete comparison of DP, BIC-NL, LP, and SAC demonstrate in Table 7. When these outcomes are compared to existing S-boxes, it is clear that the resultant S-box meets the typical S-box security protocols.

6  Conclusion

In this study, a group-theoretical and graphical method for creating the high nonlinear component of the AES block cipher was presented. This approach is simple, innovative, and dynamic in nature. The preliminary 8×8 S-box was generated by the action of PSL(2,Z) on Z269. The construction of the proposed S-box used suitable permutations of the symmetric group S256 to boost the unpredictability of the preliminary S-box. The S-boxes’ algebraic properties, including their high NL value of 111.75, very low LP value of 0.1328, small DP value of 0.039, and ability to fend off attacks from linear and differential operators, make them significantly more effective than more recent S-boxes. In the future, the proposed S-boxes can be used in multimedia security applications such as watermarking, audio and video steganography, and image encryption.

Acknowledgement: Researchers Supporting Project number (RSP2024R167), King Saud University, Riyadh, Saudi Arabia.

Funding Statement: This Project is funded by King Saud University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. B. Rajdeep and R. Hans, “A review and comparative analysis of various encryption algorithms,” International Journal of Security and Its Applications, vol. 9, no. 4, pp. 289–306, 2015. [Google Scholar]

2. P. Christof and J. Pelzl, “Understanding cryptography,” in A Textbook for Students and Practitioners. New York, USA: Springer Science & Business Media, 2009. [Google Scholar]

3. A. Shamir, “Stream ciphers: Dead or alive?,” in Proc. of the 10th Int. Conf. on Theory and Application of Cryptology and Information Security, Jeju Island, Korea, pp. 5–9, 2004. [Google Scholar]

4. L. Dragan and M. Živković, “Comparison of random S-box generation methods,” Publications De L’institut Mathematique, vol. 93, no. 107, pp. 109–115, 2013. [Google Scholar]

5. M. K. Ali and M. Khan, “Application based construction and optimization of substitution boxes over 2D mixed chaotic maps,” International Journal of Theoretical Physics, vol. 58, pp. 3091–3117, 2019. [Google Scholar]

6. T. Zhang, C. P. Chen, L. Chen, X. Xu and B. Hu, “Design of highly nonlinear substitution boxes based on I-ching operators,” IEEE Transactions on Cybernetics, vol. 48, no. 12, pp. 3349–3358, 2018. [Google Scholar] [PubMed]

7. A. Mahboob, M. Asif, M. Nadeem, A. Saleem, S. M. Eldin et al., “A cryptographic scheme for construction of substitution boxes using quantic fractional transformation,” IEEE Access, vol. 10, pp. 132908–132916, 2022. [Google Scholar]

8. A. Mahboob, M. Asif, M. Nadeem, A. Saleem, I. Siddique et al., “A novel construction of substitution box based on polynomial mapped and finite field with image encryption application,” IEEE Access, vol. 10, pp. 119244–119258, 2022. [Google Scholar]

9. A. H. Zahid, E. Al-Solami and M. Ahmad, “A novel modular approach based substitution-box design for image encryption,” IEEE Access, vol. 8, pp. 150326–150340, 2020. [Google Scholar]

10. A. Razaq, H. Alolaiyan, M. Ahmad, M. Yousaf, U. Shuaib et al., “A novel method for generation of strong substitution-boxes based on coset graphs and symmetric groups,” IEEE Access, vol. 8, pp. 75473–75490, 2020. [Google Scholar]

11. A. Razaq, S. Akhter, A. Yousaf, U. Shuaib and M. Ahmad, “A group theoretic construction of highly nonlinear substitution box and its applications in image encryption,” Multimedia Tools and Applications, vol. 81, pp. 4163–4184, 2022. [Google Scholar]

12. M. A. Yousaf, H. Alolaiyan, M. Ahmad, M. Dilbar and A. Razaq, “Comparison of pre and post-action of a finite abelian group over certain nonlinear schemes,” IEEE Access, vol. 8, pp. 39781–39792, 2020. [Google Scholar]

13. I. Shahzad, Q. Mushtaq and A. Razaq, “Construction of new S-box using action of quotient of the modular group for multimedia security,” Security and Communication Networks, vol. 2019, pp. 1–13, 2019. [Google Scholar]

14. A. Razaq, A. Ullah, H. Alolaiyan and A. Yousaf, “A novel group theoretic and graphical approach for designing cryptographically strong nonlinear components of block ciphers,” Wireless Personal Communications, vol. 116, pp. 3165–3190, 2021. [Google Scholar]

15. G. Higman and Q. Mushtaq, “Coset diagrams and relations for PSL(2, Z),” Arab Gulf Journal of Scientific Research, vol. 1, no. 1, pp. 159–164, 1983. [Google Scholar]

16. P. J. Cameron, “Cayley graphs and coset diagrams,” Encyclopedia of Design Theory, vol. 1, pp. 1–9, 2013. [Google Scholar]

17. R. C. Lyndon and P. E. Schupp, Combinatorial Group Theory, vol. 188. Berlin: Springer, 1977. [Google Scholar]

18. Q. Mushtaq, “Coset diagrams for an action of the extended modular group on the projective line over a finite field,” Indian Journal of Pure and Applied Mathematics, vol. 20, no. 8, pp. 747–754, 1989. [Google Scholar]

19. A. Torstensson, “Coset diagrams in the study of finitely presented groups with an application to quotients of the modular group,” Journal of Commutative Algebra, vol. 2, no. 4, pp. 501–514, 2010. [Google Scholar]

20. Q. Mushtaq, “Parametrization of all homomorphisms from PGL(2 Z) into PGL(2, q),” Communications in Algebra, vol. 20, no. 4, pp. 1023–1040, 1989. [Google Scholar]

21. J. Pieprzyk and G. Finkelstein, “Towards effective nonlinear cryptosystem design,” IEE Proceedings E-Computers and Digital Techniques, vol. 135, no. 6, pp. 325–335, 1988. [Google Scholar]

22. A. F. Webster and S. E. Tavares, “On the design of S-boxes,” in Proc. of the Conf. on Theory and Application of Cryptographic Techniques, Santa Barbara, CA, USA, pp. 18–22, August 1986. [Google Scholar]

23. A. H. Zahid, H. Rashid, M. M. U. Shaban, S. Ahmad, E. Ahmed et al., “Dynamic s-box design using a novel square polynomial transformation and permutation,” IEEE Access, vol. 9, pp. 82390–82401, 2021. [Google Scholar]

24. B. M. Alshammari, R. Guesmi, T. Guesmi, H. Alsaif and A. Alzamil, “Implementing a symmetric lightweight cryptosystem in highly constrained IoT devices by using a chaotic S-box,” Symmetry, vol. 13, no. 1, pp. 129, 2021. [Google Scholar]

25. J. Daemen and V. Rijmen, “Aes proposal: Rijndael, aes algorithm submission,” September 3, pp. 37–38, 1999. [Online]. Available: http://www.nist.gov/CryptoToolKit [Google Scholar]

26. A. H. Zahid, A. M. Iliyasu, M. Ahmad, M. M. U. Shaban, M. J. Arshad et al., “A novel construction of dynamic S-box with high nonlinearity using heuristic evolution,” IEEE Access, vol. 9, pp. 67797–67812, 2021. [Google Scholar]

27. M. S. M. Malik, M. A. Ali, M. A. Khan, M. Ehatisham-Ul-Haq, S. N. M. Shah et al., “Generation of highly nonlinear and dynamic AES substitution-boxes (s-boxes) using chaos-based rotational matrices,” IEEE Access, vol. 8, pp. 35682–35695, 2020. [Google Scholar]

28. S. Hussain, S. S. Jamal, T. Shah and I. Hussain, “A power associative loop structure for the construction of non-linear components of block cipher,” IEEE Access, vol. 8, pp. 123492–123506, 2020. [Google Scholar]

29. Q. Lu, C. Zhu and X. Deng, “An efficient image encryption scheme based on the LSS chaotic map and single S-box,” IEEE Access, vol. 8, pp. 25664–25678, 2020. [Google Scholar]

30. W. Gao, B. Idrees, S. Zafar and T. Rashid, “Construction of nonlinear component of block cipher by action of modular group PSL(2, Z) on projective line PL(GF(28)),” IEEE Access, vol. 8, pp. 136736–136749, 2020. [Google Scholar]

31. M. A. B. Farah, A. Farah and T. Farah, “An image encryption scheme based on a new hybrid chaotic map and optimized substitution box,” Nonlinear Dynamics, vol. 99, no. 4, pp. 3041–3064, 2020. [Google Scholar]

32. Y. Q. Zhang, J. L. Hao and X. Y. Wang, “An efficient image encryption scheme based on S-boxes and fractional-order differential logistic map,” IEEE Access, vol. 8, pp. 54175–54188, 2020. [Google Scholar]

33. A. A. A. El-Latif, B. Abd-El-Atty, M. Amin and A. M. Iliyasu, “Quantum inspired cascaded discrete-time quantum walks with induced chaotic dynamics and cryptographic applications,” Scientific Reports, vol. 10, no. 1, pp. 1–16, 2020. [Google Scholar]

34. A. Shafique, “A new algorithm for the construction of substitution box by using chaotic map,” The European Physical Journal Plus, vol. 135, no. 2, pp. 1–13, 2020. [Google Scholar]

35. H. S. Alhadawi, M. A. Majid, D. Lambić and M. Ahmad, “A novel method of S-box design based on discrete chaotic maps and cuckoo search algorithm,” Multimedia Tools Applications, vol. 80, no. 20, pp. 7333–7350, 2021. [Google Scholar]

36. N. Siddiqui, A. Naseer and M. A. Ehatisham-ul-Haq, “Novel scheme of substitution-box design based on modified pascal’s triangle and elliptic curve,” Wireless Personal Communications, vol. 116, no. 20, pp. 3015–3030, 2021. [Google Scholar]

37. A. A. A. El-Latif, B. Abd-El-Atty, W. Mazurczyk, C. Fung and S. E. Venegas-Andraca, “Secure data encryption based on quantum walks for 5G Internet of Things scenario,” IEEE Transactions on Network and Service Management, vol. 17, no. 1, pp. 118–131, 2020. [Google Scholar]

38. C. Adams and S. Tavares, “The structured design of cryptographically good s-boxes,” Journal of Cryptology, vol. 3, pp. 27–31, 1990. [Google Scholar]

39. M. Matsui, “Linear cryptanalysis method for DES cipher,” in Workshop on the Theory and Application of Cryptographic Techniques, Springer, Berlin, Heidelberg, vol. 12, pp. 386–397, 1994. [Google Scholar]

40. E. Biham and A. Shamir, “Differential cryptanalysis of DES-like cryptosystems,” Journal of Cryptology, vol. 4, no. 1, pp. 3–72, 1991. [Google Scholar]