An Efficient Heterogeneous Ring Signcryption Scheme for Wireless Body Area Networks

1  Introduction

WBANs are a collection of different smart medical sensors placed in patients’ bodies [1–3]. These sensors are small, portable, and intercommunicating devices that can be implanted or worn to monitor the critical signs of a patient. WBANs can assist doctors in checking patients’ health states in real-time by the analysis of physiological data, including heart rate and sleep quality, etc. They also can be applied in the fields of health management and sports tracking. The sensors can collect a patient’s movement trail and transmit the physiological information to the servers for analysis and treatment [4–6]. WBANs bring convenient for some patients since they no longer need to go to the hospital often. In addition, they improve the efficacy of healthcare because some diseases and emergency medical responses can be performed remotely. Therefore, WBANs are vital for the creation of a highly trustworthy, ubiquitous healthcare system. Because collected physiological data by the WBANs is sensitive and must be kept secret, unauthorized parties cannot access these data [7–9]. On open channels, users from different network domains are susceptible to various security attacks during the transmission of physiological information, and some of the collected data is scattered. Most body area network connections rely on the star network connection of the central node. If the aggregation node is breached during the communication process, and the data is stolen and tampered with by malicious users, it may cause serious consequences. In addition, resource differences must also be considered, as sensors have resource constraints such as limited computing, storage, bandwidth, and energy capacity, while servers have powerful computing and storage capabilities [10]. Therefore, it isn’t simple to design an efficient heterogeneous security scheme to satisfy these features [11,12]. To further ensure that the patient’s medical data will not be leaked, this article can use ring signcryption technology to optimize the scheme.

1.1 Related Work

Due to the important role of health data stored in WBANs in medical treatment, researchers must address security issues in WBANs before truly developing them. Recently, people have proposed some secure WBANs schemes from different perspectives. It’s worth mentioning that Hu et al. [13] described an approach to preserve the user and WBAN’s communication. Their proposal is attribute-based encryption (ABE) [14]. But ABE couldn’t be the best option due to its expensive cryptographic operations. These expensive activities are a challenge for sensor nodes with limited resources [15,16]. Rehman et al. [17] proposed an efficient lightweight key agreement and authentication scheme for WBAN. Their scheme has shown effectiveness in resisting various known network attacks, such as sensor node simulation attacks, but still has significant computational overhead.

Wu et al. [18] proposed a lightweight dual-factor authentication scheme for WBANs. Their scheme claims to be resistant to internal attacks, offline guessing attacks and session key leakage attacks, but the scheme cannot guarantee forward security. Signing first and then encrypting is a traditional solution. This scheme is inefficient because the calculation time and communication consumption are equal to the sum of signature consumption and encryption consumption. To address the problem of the traditional scheme’s low efficiency, the initial signcryption scheme proposed by Zheng [19] has demonstrated that signcryption consumption is significantly less than the total signature and encryption consumption. At once, the signcryption scheme reduces the computational complexity and communication demands during data transmission by a significant amount.

Tan et al. [20] designed an identity-based signcryption scheme for WBANs. Unlike traditional PKI, which requires a certificate to associate an identity with the public key, IBC eliminates complex certificate management. The user’s public key is generated from identity information, including id numbers, phone numbers, and so on. A trusted third party that generates a user’s private key is referred to as a private key generator (PKG). IBC is perfectly suited for resource-constrained WBANs, and because PKG has the private key of every user, IBC will inevitably encounter key escrow problems [21,22]. Liu et al. [23] designed the authentication scheme for WBANs using CLC. Every user must be authorized to gain access to health data stored on servers. The advantage of Liu’s scheme is the use of CLC, and there is no public key certificate problem or key escrow problem [24,25]. The CLC still requires KGC, which is tasked with creating a partial private key from the master key and an individual’s identification. The user then creates a secret value and mixes it with a partial private key to create the complete private key [26]. Because KGC lacks the secret value, it couldn’t obtain a complete private key. So, the key escrow issue is overcome.

To ensure integrity, non-repudiation, confidentiality, and authentication during the communication process, this article provides an effective CP-HRSC system from the WBANs in CLC to an Internet server in PKI. Compared to current schemes [27], this paper’s solution not just to guarantees a greater level of security and reduces computation and communication costs.

1.2 Motivation and Contribution

This paper aims to design an efficient CP-HRSC scheme for WBANs. This paper’s goal is not only to solve the above-mentioned problems, but also to reduce the computational and communication cost in a way that provides integrity and confidentiality. In addition, this paper’s solution adopts heterogeneous systems and ring signcryption technologies, which are better suited for transmitting data in WBANs. WBANs represent the sender and servers represent the receiver. This paper’s contributions are listed below:

(1)   This article provides a heterogeneous signcryption scheme between the WBANs and server, in which the server is in PKI and the WBANs are in CLC. CLC could solve the limitations of key escrow problems in IBC and public key certificate management in PKI.

(2)   The ring signcryption is a mechanism that allows the controller to anonymously signcrypt physical data on behalf of a set of sensors. This preserves the sensor’s privacy by keeping its identity hidden from the server. Instead, the server just knows that the data was signcrypted by a member of a ring of sensors, it can not determine the exact identity of the sensor who signcrypts the message.

(3)   This paper’s scheme provides anonymity, confidentiality, integrity, non-repudiation, and authentication. It is proven IND-CCA2 and EUF-CMA in ROM.

(4)   The analysis of performance indicates that this paper’s solution is the most effective in terms of computational cost and energy usage. Compared with the other three related schemes [27–29], the computational cost of our scheme is reduced by about 49.5%, 4.1%, and 8.4%, and energy usage of our scheme is reduced by about 49.4%, 3.7%, and 14.2%, respectively.

1.3 Organization

The remainder of the paper is structured as follows: Section 2 describes the network model and security requirements. A CP-HRSC scheme is proposed in Section 3. In Section 4, this article analyzes the security and performance of the scheme. The application of this paper’s scheme is shown in Section 5. Finally, the conclusion is described in Section 6.

2  Preliminaries

In this chapter, this article describes network model and security requirements.

2.1 Network Model

Fig. 1 depicts the conventional WBANs model. Most of the network model is made up of three objects: patients, service providers (SP), and users (e.g., a hospital, a nurse, a doctor, a research institution, etc.). The WBANs consist of a controller and several sensor nodes [30,31]. The sensors and controller can communicate with each other, and the controller can also communicate with the Internet to transmit patients’ medical data to the server. If a user wishes to access patients’ health records, the server must provide permission. When a user wishes to obtain WBAN’s monitoring data, it must first submit a query message to the server. The server then verifies whether or not the user is permitted to access the WBANs. If so, the server transmits the gathered information to the user in a safe manner. If not, it will be rejected.

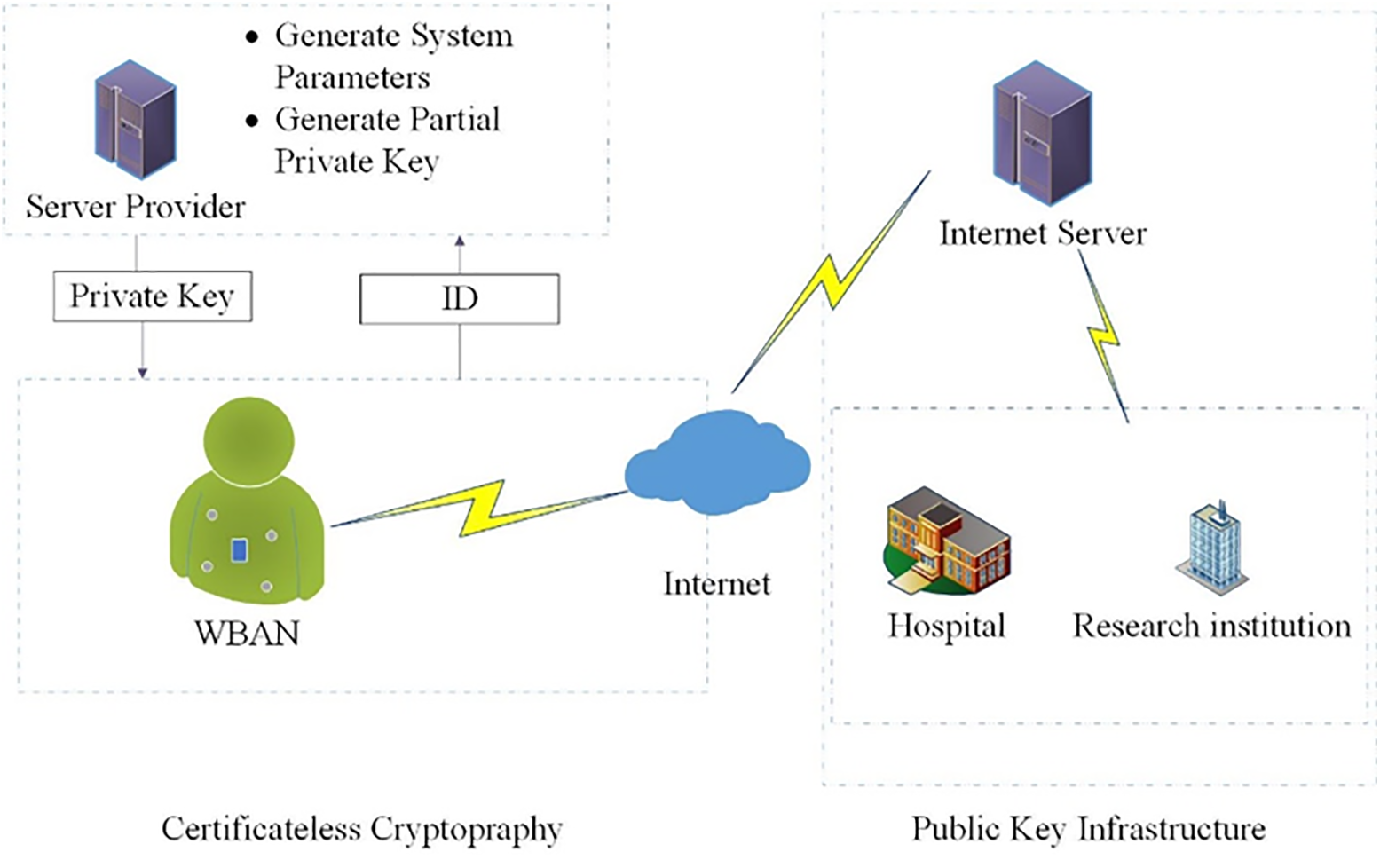
Figure 1: Network model

2.2 Security Requirements

Five security features (anonymity, confidentiality, integrity, non-repudiation, and authentication) must be satisfied by the sensors and server. The confidentiality of query messages keeps them secret from everyone except for the sender and receiver. Authentication guarantees that just those who have been granted permission can view the medical data stored in the WBANs. Integrity ensures that a user’s query message was not modified by unauthorized users. Non-repudiation prevents users from denying their true identity. So, once a user has already sent a request message to WBANs, this activity cannot be denied.

2.3 Bilinear Pairings

Suppose that there are two groups, G1 and G2 in existence. G1 is an additive group, while G2 is multiplicative group that has the same prime order p, P is the generator of G1. This article states that e:G1×G1→G2 has the common attributes:

a.   Bilinearity: ∀r,c∈Zp∗, ∀K,M∈G1, e(rK,cM)=e(K,M)rc.

b.   Non-degeneracy: ∃K,M∈G1 such that e(K,M)≠1.

c.   Computability: There exists a feasible algorithm to find e(K,M), ∀K,M∈G1.

This paper’s scheme’s security is dependent just on the difficulty of the following CDH problem. Offered G1 of order p prime and P, CDH problem in G1 is to calculate mnP offered (P,mP,nP).

Definition 1. If no adversary 𝒜 can solve (ϵ,t)-CDH problem in t-polynomial time with an advantage of at least ϵ, then CDH assumption holds.

3  Proposed Scheme

In this chapter, this article first introduces the basic definition and security concepts of the CP-HRSC scheme, which enables the sender in CLC to transmit the message to the recipient in PKI. Next, this article designs the efficient CP-HRSC scheme and demonstrates its security in ROM. Table 1 contains a listing of this paper’s scheme’s necessary notations.

3.1 Syntax

A basic CP-HRSC system comprises eight algorithms listed below.

(1)   Setup: It is an initialization algorithm run by PKG. The input is the algorithm’s parameter k. The output consists of a master key s and system parameter params with Ppub.

(2)   CLC-PPKE: It is an algorithm for the extraction of partial private keys that is run by PKG. It accepts as input the user’s ID as well as s, and it produces a partial private key DID.

(3)   CLC-SVS: It is an algorithm for setting up a secret value that the users are responsible for running. The algorithm accepts an identity ID as its input and produces a secret value xID.

(4)   CLC-PKS: It is an algorithm for setting up a private key that is run by users, and it generates complete private key SID from DID and xID that are supplied by the users.

(5)   CLC-PKG: It is an algorithm for the generation of public keys that requires the users to supply a secret value xID as an input and produces a public key PKID as its output.

(6)   PKI-KG: It is an algorithm for the production of keys that is used by PKI users. The user will select a secret key x and then generate pk that corresponds to it.

(7)   SC: A sender’s probabilistic signcryption algorithm takes plaintext message m, a set of identities L={ID1,ID2,ID3,…,IDn} that form the ring, sender’s SIDs(1≤s≤n), and then pkr and outputs the ciphertext σ.

(8)   USC: Receiver runs probabilistic unsigncryption algorithm that accepts σ, L={ID1,ID2,…,IDn}, and xr as input and returns m or ⊥ if σ is incorrect ciphertext.

These algorithms should fulfill the CP-HRSC stability condition. If σ=SC(m,SIDs,L,pkr), then m=USC(σ,L,xr).

3.2 Security Notions

CP-HRSC scheme should comply with confidentiality (IND-CCA2) and unforgeability (EUF-CMA). To suit CP-HRSC, this article slightly modifies the [32] concepts.

Definition 2. A CP-HRSC scheme is (ϵ,t,qu)-IND-CCA2 secure if no probabilistic t-polynomial time adversary 𝒜 has advantage at least ϵ after at most qu in the confidentiality game.

Definition 2 grasps the insider security for confidentiality of signcryption since 𝒜 knows all senders’ private keys. The insider security ensures the forward security of the signcryption scheme, i.e., confidentiality is kept in case the sender’s private key is disclosed.

This article takes into consideration the game for both adversary 𝒜 and challenger 𝒞 for confidentiality.

Initial: Assuming a secure parameter k, 𝒞 executes Setup algorithm and passes params along to 𝒜.

Phase 1: 𝒜 executes a limited amount of queries that are polynomially constrained.

(1)   Partial private key extraction queries: 𝒜 selects ID and sends it to 𝒞. 𝒞 executes the CLC-PPKE algorithm and sends DID to 𝒜.

(2)   Private key setup queries: 𝒞 executes the CLC-PKS algorithm when 𝒜 gives it an identity ID and provides 𝒜 the full private key. (If necessary, 𝒞 may first run the CLC-PPKE and CLC-SVS algorithms).

(3)   Public key queries: 𝒜 selects an ID and transmits it to 𝒞. 𝒞 then performs CLC-PKG algorithm and provides resulting public key to 𝒜. (If necessary, 𝒞 might initiate the CLC-SVS algorithm first).

(4)   Public key replacement queries: 𝒜 can change pkID to a value that it chooses.

(5)   Key extraction queries: When 𝒞 gets an ID from 𝒜, it runs the PKI-KE algorithm and sends 𝒜 the private key sID that goes with that identity ID.

(6)   Signcryption queries: 𝒜 selects the message m, an identity for the sender (IDj), and an identity for the receiver (IDj). 𝒞 then executes CLC-PKS and CLC-PKG algorithms in order to obtain the sender’s sIDi and pkIDi. Then 𝒞 sends 𝒜 outcome from SC(m,sIDi,IDi,pkIDi,IDj). If the corresponding public key has been changed, 𝒞 might not know the sender’s secret value. In this instance, 𝒜 is needed to give it to us.

(7)   Unsigncryption queries: 𝒞 executes the PKI-KE and CLC-PKG to obtain private key sIDj and pkIDi, after 𝒜 selects σ and L={ID1,ID2,…,IDn}, sender’s IDi, and receiver’s IDj. 𝒞 sends 𝒜 the outcome of USC(σ,IDi,pkIDi,sIDj,IDj). The output is either m or ⊥.

Challenge: The conclusion of phase 1 is determined by 𝒜.𝒜 creates two plaintexts of identical (m1,m2) and identities L∗={ID1∗,ID2∗,ID3∗,…,IDn−1∗,IDn∗}, the sender’s IDs∗ and the receiver’s IDr∗ that it desires to be challenged on. Keep in mind that during phase 1, IDr∗ should never be sent in response to a key extraction query. 𝒞 picks an unpredictable bit β∈{0,1}, then calculates σ∗=SC(mβ,L∗,sIDs∗,IDs∗,pkIDs∗,IDr∗), that is then passed to 𝒜.

Phase 2: Similar to phase 1, 𝒜 can consider an adaptive amount of polynomially bounded enquires. To gain access to the m, it cannot do key extraction query on IDr or unsigncryption query on (σ∗,L∗,IDs,IDr) until pkIDs has been refreshed during the challenge phase.

Guess: 𝒜 generates β, if β′=β, then 𝒜 wins game.

The benefit for 𝒜 is given by Advantage(𝒜)=|2(Pr[β′=β]−1/2)|, in which Pr[β′=β] stands for such possibility which β′=β.

Definition 3. If no probability t-polynomial time adversary can acquire a minimum of ϵ in confidentiality game by performing at more than private key extraction queries qppk, public key replacement queries qpkr, key extraction queries qk, SC queries qsc, USC queries qusc, the CP-HRSC technique is considered (ϵ,t,qppk,qpkr,qk,qsc,qusc)-Type-I-EUF-CMA secure. Since the adversary knows the private keys of all senders, the above definition covers insider security for SC confidentiality. Confidentiality even though the sender’s private key has been damaged because of the forward security provided by the SC method, which is guaranteed by insider security.

Since the senders are part of the CLC environment, designers must take into account two categories of adversaries to ensure unforgeability. Type-I adversary represents an opponent who does not have access to s of KGC. It can replace users’ pk with other (legal) pk of its choosing. Type-II opponent represents a trusted and inquisitive KGC with knowledge of its master private key. However, it isn’t a solution for the user’s public key.

Take into consideration how the unforgeability game that 𝒞 and 𝒜ℐ play against one another.

Initial: Using the security parameter k, 𝒞 executes Setup procedure and passes results to 𝒜ℐ in the form of params.

Attack: 𝒜ℐ executes a number of inquiries that have a polynomially constrained execution, similar to the confidentiality game.

Forgery: 𝒜ℐ exports σ∗ and L∗={ID1∗,ID2∗,…,IDn∗}, IDs, IDr and is effective if such prerequisites are satisfied:

(1)   USC(σ∗,IDs,pkIDs,sIDr,IDr)=m∗.

(2)   𝒜ℐ just hasn’t submitted a setup request for a private key to be used by any identities in the set L∗.

(3)   𝒜ℐ can’t do each qpkr for any identity in the set L∗ prior to the forgery phase and qppk in a certain phase.

(4)   𝒜ℐ hasn’t requested for qsc on (m∗,L∗).

The possibility that 𝒜ℐ will emerge victorious can be seen to be its advantage.

Definition 4. If no probability t-polynomial time adversary 𝒜ℐℐ can acquire a minimum of ϵ in an unforgeability game by performing at more than qpk, SC queries qsc, then the CP-HRSC technique is considered (ϵ,t,qpk,qsc)-Type-II-EUF-CMA secure.

In the end, let’s think about a unforgeability game that 𝒞 and an adversary of Type-II play against one another.

Initial: 𝒞 executes the Setup procedure with k and provides 𝒜ℐℐ with params and s.

Attack: 𝒜ℐℐ executes a polynomially bounded number of inquiries, public key queries and SC queries similar to the confidentiality game. In addition, the qppk, qpkr, and qusc are unnecessary because 𝒜ℐℐ can perform these tasks on their own.

Forgery: 𝒜ℐℐ exports σ∗ and L∗={ID1∗,ID2∗,…,IDn∗}, IDs, IDr and is effective if such prerequisites are satisfied:

(1)   USC(σ∗,IDs,pkIDs,sIDr,IDr)=m∗.

(2)   𝒜ℐℐ just hasn’t submitted a setup request for a private key to be used by any identities in the set L∗.

(3)   𝒜ℐℐ hasn’t requested for qsc on (m∗,L∗).

The possibility that 𝒜ℐℐ will emerge victorious can be seen to be its advantage.

Definition 5. If an adversary who is not a member of the sender group is unable to identify the real sender with a probability greater than the random chance for any set of n identities, m and σ, then the CP-HRSC scheme is completely anonymous for that set of inputs. In this way, the adversary has a probability of 1/n in identifying the original sender.

3.3 The Proposed Scheme

To build a practical CP-HRSC scheme, this article adopts Chow’s scheme [29] and employs subsequent eight algorithms.

Setup: Given k, the PKG chooses G1 and G2 of prime order p (with G1 additive and G2 multiplicative), P, e:G1×G1→G2, and hash functions H1:{0,1}∗→G1, H2:{0,1}∗→Zp∗ and H3:{0,1}∗→{0,1}α+γ. Here, α indicates the amount of bits in the message that must be delivered, and γ indicates the amount of data required to express a feature of G1. PKG chooses s∈Zp∗ randomly and computes Ppub=sP. PKG publishes params={G1,G2,p,e,α,γ,P,Ppub,Hi(i=1,2,3)} and guarantees s secrets.

CLC-PPKE: User submits ID to the PKG. The PKG computes QID=H1(ID) and sends DID=sQID to user.

CLC-SVS: The user with ID chooses xID∈Zp∗ as secret value.

CLC-PKS: The above algorithm provides the user with the whole private key SID=(xID,DID) only when given it DID and xID.

CLC-PKG: Given xID, the algorithm computes PKID=xIDP.

PKI-KE: Receiver chooses a random xr∈Zp∗ as private key skr and sets pkr=xrP.

SC: Consider the sender group L={ID1,ID2,…,IDn} with n identities. To submit m to a receiver with pkr on behalf of L, the real sender indexed by s (IDs) performs subsequent operations:

(1)   Select r∈Zp∗ at random, calculate F=rP.

(2)   As to j∈{1,2,3,…,n−1,n}∖{s}, select Uj∈G1 and query H2 to obtain hj=H2(m,F,Uj,L).

(3)   Compute Us=rQIDs−∑j=1,j≠sn(Uj+hjQIDj).

(4)   Compute hs=H2(m,F,Us,L).

(5)   Compute V=(hs+r)DIDs.

(6)   Compute w=H3(F,pkr,pks,xspkr), z=(m∥V)⊕w.

(7)   Output σ=(F,U1,U2,…,Un,z).

USC: The receiver with xr executes subsequent actions upon receiving σ=(F,U1,U2,…,Un,z) and L={ID1,ID2,…,IDn}:

(1)   Compute w=H3(F,pkr,pks,xrpks).

(2)   Compute (m∥V)=z⊕w.

(3)   As to j∈{1,2,3,…,n}, compute hj=H2(m,F,Uj,L).

(4)   Check if e(P,V)=e(Ppub,∑j=1n(Uj+hjQIDj)) holds. If pass, output m. Or else, reject σ and output ⊥.

This is where this article demonstrates that the current proposal is correct. As F=rP, rpkr=rxrP=xrF. Because of V=(hs+r)DIDs, so

e(P,V)=e(P,(hs+r)DIDs)=e(P,(hs+r)sQIDs)=e(Ppub,rQIDs+hsQIDs).

Moreover, since Us=rQIDs−∑j=1,j≠sn(Uj+hjQIDj), so

e^(P,V)=e^(Ppub,hsQIDs+Us+∑j=1,j≠sn(Uj+hjQIDj)=e^(Ppub,∑j=1n(Uj+hjQIDj)).

4  Analysis of the Protocol

4.1 Security Analysis

Going to the follow Theorems 1 and 2, this article demonstrates that the suggested CP-HRSC scheme meets the standards for secrecy, anonymity, and unforgeability. This was achieved by adhering to the reasoning process that began with Theorem 1.

Theorem 1. (Confidentiality) In ROM, if 𝒜 has a non-negligible benefit ϵ against by IND-CCA2 security of this paper’s CP-HRSC scheme when trying to run in a time step t and going to perform qu and qHj to hash function Hj(j=1,2,3), then there appears to exist 𝒞 that can solve CDH problem with an additional benefit in time t′<t+O(qH3+qu)tp, where tp represents the expense of pairing computation. The above algorithm could solve the CDH problem with a benefit ϵ′>ϵ(1−qu2k).

Proof. Therefore, in the demonstration, this article would then illustrate what 𝒞 are using 𝒜 as just a subprogram to overcome random instances (P,aP,bP) from both CDH problems.

Initial: 𝒞 provides 𝒜 with master secret key η, params with Ppub=ηP and pkr. Here η is selected at random by 𝒞, it simulates the private key of recipient.

Phase 1: 𝒞 assumes the role of 𝒜’s opponent with in secrecy play described in Section 3. 𝒞 maintains Lj(j=1,2,3) to emulate, correspondingly, the hash function Hj(j=1,2,3). Remember that 𝒞 must keep the same behavior as well as prevent accidents. It is this paper’s belief that 𝒜 will enquire about H1(ID) first before using ID for other queries.

𝒞 checks whether the list L1 appears to include pair (IDj,ej) when 𝒜 tries to apply an H1 query on IDj.

(1)   H1 queries: 𝒞 checks whether the list L1 appears to include pair (IDj,ej) when 𝒜 tries to apply an H1 query on IDj. One if the matching pair has been discovered, 𝒞 comes back ej to 𝒜. If not, 𝒞 selects e∈Zp∗, adds (IDj,e) into L1, and gets back eP to 𝒜.

(2)   H2 queries: When 𝒜 asks H2 query on (m,F,L,Uj), 𝒞 checks L2. If there is a matching entry for this query, then 𝒜 will receive a comparable response as before. If not, 𝒞 gives back t. Both of query and the response are going to be saved in L2.

(3)   H3 queries: When 𝒜 executes H3 on (F,pkr,D), 𝒞 carries out next operations:

a.   If e(aP,bP)=e(D,P), 𝒞 gets back D and stops. 𝒞 has worked out CDH problem that was given.

b.   𝒞 yields w and updates ⋆ with D if the list L2 includes the elements (F,pkr,⋆,w) and as such e(F,pkr)=e(D,P).

c.   If 𝒞 reaches this stage of execution, 𝒞 chooses w from {0,1}α×G1 and gets back it to 𝒜. Both query and response are going to be stored in L3.

(4)   USC queries: 𝒜 selects σ=(T,U1,U2,…,Un,z) and L={ID1,ID2,…,IDn}. Then 𝒞 does the following:

a.   𝒞 checks for different values of D to find one where e(F,pkr)=e(D,P) by cycling through (F,pkr,D,w) iterations in L3. In the event that such a record is located, the correct value for w can be determined. This w is used by 𝒞 to decrypt σ, (m∥V)=z⊕w. If (F,pkr,D) is not present in L3, 𝒞 picks a number w at random from the range {0,1}α×G1, appends (F,pkr,⋆,w) to the end of the list L3, and uses this new random key to decrypt the provided σ.

b.   Obtain hj=H2(m,F,Uj,L) for each j∈{1,2,3,…,n} by querying H2 and test whether e(P,V)=e(Ppub,∑j=1n(Uj+hjQIDj)) holds. If the equation in previous sentence is correct, send the message m back to 𝒜. In that case, this ciphertext should be rejected.

Challenge: 𝒜 produces (m0,m1) as well as identities denoted by L. 𝒞 begins by selecting U and z at random from G1 and G2, respectively. 𝒞 next the transmits 𝒜 the challenge ciphertext after establishing F=aP.

Phase 2: Similar as phase 1, 𝒜 is able to adaptively ask the polynomially bounded amount of qusc to acquire the proper plaintext, but it is unable to ask a query on (σ,L). 𝒞 continues to employ identical methods from phase 1 when responding to 𝒜’s queries.

Guess: 𝒜 generates β′, and 𝒞 will not pay attention to it.

Unless 𝒜 executes H3 query on (F∗,pkr,bF∗), the simulation is flawless. If this tuple is absent from the list L3, 𝒜 will gain no advantage. But even so, whether this situation arises, the first phase of simulating H3 will lead to 𝒞 finding a solution to the CDH issue. During entire phase, its likelihood of failure for qusc seems to be no higher than qu/2k.

Theorem 2. (Unforgeability) This paper’s scheme fulfills the EUF-CMA security requirements in ROM while also satisfying CDH assumptions.

Proof. This theorem’s proof can be found in Lemmas 1 and 2, which are listed in the previous sentence.

Lemma 1. In the ROM, there exists 𝒞 that could resolve CDH problem with an advantage ϵ′⩾ϵ1en(nqk+n)n(1−qs(qs+qH2)2k) in a time O(t) if 𝒜ℐ has ϵ against Type-I-EUF-CMA security of this paper’s CP-HRSC scheme when running in t and performing qk, qs, and qHj.

Proof. Within that demonstration, this article would then illustrate what 𝒞 could use 𝒜ℐ as its own function call to rectify random instance (P,aP,bP) of CDH problems. This will be done by using the example given below.

Initial: 𝒞 provides 𝒜ℐ with params having Ppub=aP, xr of the recipient, and the public key pkr=xrP. Then, xr is selected at random from Zp∗ by 𝒞. It should be noted that 𝒞 doesn’t have access to the value of one that imitates s used by PKG.

Attack: Inside the unforgeability game described in Section 4, 𝒞 acts as an imitation of the challenger 𝒜ℐ faced. 𝒞 retains Lj(j=1,2,3) in order to imitate respective hash functions Hj(j=1,2,3). 𝒞 should keep the same pace and stay away from collisions. This paper is working under the assumption that (1) H1 queries are separate from one another and (2) 𝒜ℐ will first request H1(ID) and then use the ID in those other queries.

(1)   H1 queries: 𝒜ℐ selects an identify IDj and provides it to 𝒞. Then, 𝒞 chooses a bit μ∈{0,1} with probabilities of 0 (ρ) and 1 (1−ρ). (The value of ρ would be defined at a point later.) When μ=0, 𝒞 selects ej at random and returns H1(IDj)=ejP, 𝒞 selects at random ej∈Zp∗ and returns H1(IDj)=ejbP. In both instances, (IDj,ej,μ) must be included to L1.

(2)   H2 queries: 𝒞 examines L2 when 𝒜ℐ executes an H2 query on (m,F,Uj,L). If a record for this query is discovered, 𝒞 will receive the same response. Or else, 𝒞 gets back t generated at random from Zp∗. The query and associated response are going to be saved in L2.

(3)   H3 queries: 𝒞 examines L3 when 𝒜ℐ executes an H3 query on (F,pkr,pks,xrpks). If a record for this query is discovered, 𝒞 will receive the same response. 𝒞 gets back k generated at random from {0,1}α×G1. Both of query and the response are going to be saved in L3.

(4)   Key extraction queries: 𝒞 obtains (IDj,ej,μ) from the list L1 when accepting an identity IDj from 𝒜ℐ. If μ=0, 𝒞 gives back the private key SIDj=ejaP. If not, 𝒞 can’t figure out private key, so it fails and ends.

(5)   SC queries: 𝒜ℐ selects m and L={ID1,ID2,…,IDn}. 𝒞 performs subsequent operations:

a.   Select r∈Zp∗ at random and calculate F=rP.

b.   Select s∈{1,2,…,n} at random.

c.   Each j∈{1,2,…,n}∖{s}, select Uj∈G1 and query H2 to obtain hj=H2(m,L,F,Uj).

d.   Select hs and z from Zp∗, calculate Us=zP−hsQIDs−∑j=1,j≠sn(Uj+hjQIDj) and append (m,F,Us,L,hs) to the list L2. Before that, hs=H2(m,L,F,Us).

e.   Then, compute V=zaP.

f.   Through qH3, w=H3(F,pkr,pks,xspkr).

g.   Compute z=(m∥V)⊕w.

h.   Output σ=(F,U1,U2,…,Un,z).

Forgery: 𝒜ℐ outputs σ=(F∗,U1∗,U2∗,…,Un∗,z∗) and L∗={ID1∗,ID2∗,ID3∗,…,IDn−1∗,IDn∗}.

Similar to [33], this proof is completed using forking derivation for ring signature. If 𝒜ℐ generates valid signature during t with a non-negligible advantage ϵ≥7CnqH2/2k, this paper can create 𝒜ℐ′ that generates (m∗,U1∗,U2∗,…,Un∗,V∗) and (m∗,U1∗,U2∗,…,Un∗,V¯∗) during time 2t with probability ϵ′≥ϵ2/66CnqH2 such that hs=h¯s=H2(m∗,F∗,Us∗,L∗) for s∈{1,2,3,…,n} and hj≠h¯j=H2(m∗,F∗,Uj∗,L∗) for each j∈{1,2,3,…,n}∖{s}. Here CnqH2 represents the number of n-permutations of qH2 factors, CnqH2=qH2×(qH2−1)×…×(qH2−n+1).

Using 𝒜ℐ′ generated from 𝒜ℐ, the CDH issue may be resolved through calculating abP=es−1(hs−h¯s)−1(V∗−V¯∗), in which es has been obtained from L1 besides searching for (IDs,es,μ).

This paper will now calculate ρ’s value. The possibility that 𝒞 will succeed in at least all qk is no greater than ρqk. During the forgery phase, this paper needs to make sure that 𝒜ℐ hasn’t made qk for any identity in L∗. The probability is equal to (1−ρ)n. This simulation has a probability of ρqk(1−ρ)n that 𝒞 would then succeed. This value reaches its maximum at ρ¯=qk/(qk+n). Using this ρ¯, (qkqk+n)qk(1−qkqk+n)n=1(1+nqk)qknn(nqk+n)n.

Moreover, using limλ→0(1+λ)1/λ=e, this paper finds that 1(1+nqk)qkn≥1e for extremely large qk. Therefore, the possibility that 𝒞 wins in virtual competition is at least 1en(nqk+n)n.

And if 𝒞 has a collision on H2, then all qsc could fail for 𝒞, making that possibility H2 is qs(qs+qH2)/2k.

Therefore, ϵ′⩾ϵ1en(nqk+n)n(1−qs(qs+qH2)2k).

Lemma 2. In the ROM, there exists 𝒞 that could resolve the CDH problem with an advantage ϵ′⩾ϵ1en(nqk+n)n(1−qsqH22k) in a time O(t), if 𝒜ℐℐ has ϵ against Type-II-EUF-CMA security of this paper’s CP-HRSC scheme when running in t and performing qk, qs, and qHj.

Proof. Within that demonstration, this paper would then illustrate what 𝒞 could use 𝒜ℐℐ as its own function call to rectify random instance (P,aP,bP) of CDH problem. This will be done by using the example given below.

Initial: 𝒞 provides 𝒜ℐℐ with params by setting Ppub=sP and pkr=bP. 𝒞 chooses s at random. Furthermore, 𝒞 obtains public/private key pair (pkr∗,skr∗) of recipient by executing the PKI-KG algorithm and sending them to 𝒜ℐℐ. 𝒞 then selects challenge identity ID∗∈{0,1}∗ at random and provides it to 𝒜ℐℐ.

Attack: 𝒞 simulates the opponent of 𝒜ℐℐ in Type-II-EUF-CMA game. 𝒞 maintains Lj(j=1,2,3) to imitate relevant hash functions Hj(j=1,2,3). 𝒞 also keeps an initially empty list Lk to store public key information. And this paper presumes H1 queries are distinct and 𝒜ℐℐ would then request H1 prior to using ID in subsequent queries.

(1)   H1 queries: When 𝒜ℐℐ submits an H1 query on IDj, 𝒞 verifies if L1 contains a pair (IDj,ej). When matching pair is discovered, 𝒞 gets back ej to 𝒜ℐℐ. If not, 𝒞 selects e∈Zp∗, adds (IDj,e) into L1, and gets back eP to 𝒜ℐℐ.

(2)   H2 queries: When 𝒜ℐℐ asks H2 query on (m,F,Uj,L), 𝒞 checks L2. If such an entrance matching this query is found, 𝒜ℐℐ will receive same response. If not, 𝒞 gives back t from Zp∗. The query and associated response are going to be saved in L2.

(3)   H3 queries: 𝒞 examines L3 when 𝒜ℐℐ executes an H3 query on (F,pkr,pks,xrpks). If a record for this query is discovered, 𝒞 will receive the same response. 𝒞 gets back k generated at random from {0,1}α×G1. Both of query and the response are going to be saved in L3.

(4)   Public key queries: 𝒜ℐℐ selects IDi as well as transmits it all to 𝒞. 𝒞 comes back pkIDi to 𝒜ℐℐ if Lk includes (IDi,pkIDi,xIDi). If not, 𝒞 selects ri∈Zp∗. At η-th qk, 𝒞 answers by pkη=riaP. For queries pki with i≠η, 𝒞 answers by pki=riP where xi=ri, puts (IDi,pki,xi) into Lk.

(5)   SC queries: 𝒜ℐℐ selects m and L={ID1,ID2,…,IDn}. 𝒞 performs subsequent operations:

a.   Select r∈Zp∗ at random and calculate F=rP.

b.   Select s∈{1,2,3,…,n−1,n} at random.

c.   For each j∈{1,2,…,n}∖{s}, select Uj∈G1 and query H2 to obtain hj=H2(m,L,F,Uj).

d.   Select hs and z from Zp∗, calculate Us=zP−hsQIDs−∑j=1,j≠sn(Uj+hjQIDj) and append (m,F,Us,L,hs) to the list L2. Before that, hs=H2(m,F,Us,L).

e.   Then, compute V=zsP.

f.   Through qH3, w=H3(F,pkr,pks,xspkr).

g.   Compute z=(m∥V)⊕w.

h.   Output σ=(F,U1,U2,U3,…,Un,z).

Forgery: 𝒜ℐℐ outputs σ∗=(F∗,U1∗,U2∗,U3∗,…,Un−1∗,Un∗,z∗) and L∗={ID1∗,ID2∗,…,IDn∗}. It’s indeed simple to demonstrate that 𝒜ℐℐ will be unaware that σ∗ isn’t valid deniable authenticator for ski and receiver unless it asks for H3(F,riaP,bP,riabP). The solution to the CDH problem could be added to L3. Then 𝒞 looks up L3 for tuples of (F,riaP,bP,K). 𝒞 examines both of them to evaluate whether or not e(riP,K)=e(riaP,bP). If the condition is satisfied, 𝒞 will come to a halt and will output the solution K=abP to the CDH problem. 𝒞 will fail and come to a stop if there is no such tuple that satisfies equality.

During the forgery phase, this paper needs to make sure that 𝒜ℐℐ hasn’t made qk for any identity in L∗. The probability is equal to (1−ρ)n. This simulation has a probability of ρqk(1−ρ)n that 𝒞 would then succeed. This value reaches its maximum at ρ¯=qk/(qk+n). Using this ρ¯, (qkqk+n)qk(1−qkqk+n)n=1(1+nqk)qknn(nqk+n)n.

Moreover, using limλ→0(1+λ)1/λ=e, this paper finds that 1(1+nqk)qkn≥1e for extremely large qk. Therefore, the possibility that 𝒞 wins in virtual competition is at least 1en(nqk+n)n.

And if 𝒞 has a collision on H2, then all qsc could fail for 𝒞, making that possibility H2 is qsqH2/2k.

Therefore, ϵ′⩾ϵ1en(nqk+n)n(1−qsqH22k).

4.2 Performance Analysis

This article analyzes the performance and security of this paper’s system in this section. In Table 2, this article tries to compare this paper’s computation and communication costs to that of RG [27], YC [28], and CZ [29].

This article indicates E exponentiation in G2, PM point multiplication in G1, and P pairing computation. In addition, other operations are neglected, because of these operations consume most process time. In which, G1 is the additive group on the elliptic curve, and the multiplication group is denoted by G2. |m| indicates the number of bits of messages. This article provides a quantitative assessment of RG [27], YC [28], CZ [29], and this paper’s scheme. This paper just considers the sensor component because its resources are restricted. This article uses MICA2 as the test platform for communication between sensors and servers in WBANs and refers to the experimental results in [34]. The MICA2 node includes an 8-bit AVR processor and a 128KB programmable flash. It has a 2.4 GHz transmission channel frequency.

According to [34], P requires 1.9 s and an E requires 0.9 s when applying a curve b2+b=a3+a with an embed degree of 4 and using ηT pairing: E(F2271)×E(F2271)→F24⋅271, which is the same as a security level of 80 bits. Moreover, according to [34,35], PM requires 0.81 s. So, the calculation time on the sensor of RG [27], YC [28], and CZ [29] and this paper’s scheme are (2n+2)∗0.81=1.62n+1.62s, (n+4)∗0.81+1.9=0.81n+5.14, (n+1)∗0.81+3∗1.9+3∗0.9=0.81n+9.21s, and (n+2)∗0.81=0.81n+1.62 s. When n=100, the calculation time of RG [27], YC [28], CZ [29] and this paper’s scheme are 163.62, 86.14, 90.21, and 82.62 s, respectively. In terms of calculation time, this paper’s scheme has reduced by 49.5%, 4.1%, and 8.4% respectively.

Throughout [34], this article assumes that the power rating of MICA2 is 3.0 V, sending mode current consumption is 8.0 mA. In terms of energy consumption, pairing uses 3.0∗8.0∗1.9=45.6mJ, exponentiation needs 24.0∗0.9=21.6 and PM uses 24.0∗0.81=19.44 mJ. Therefore, the computational energy cost on the sensor of RG [27], YC [28], CZ [29], and this paper’s scheme are (2n+2)∗19.44=38.88n+38.88 mj, (n+4)∗19.44+45.6=19.44n+123.36 mj, (n+1)∗19.44+3∗21.6+3∗45.6=19.44n+221.04 mj, and (n+2)∗19.44=19.44n+38.88 mJ.

For the expense of communication, this article uses a curve on binary field F2271, G1 is a prime order of 252 bits. The size of an element in group G1 is 542 bits, which can be reduced to 34 bytes. G2 is now 136 bytes long. So in RG [27], YC [28], CZ [29], and this paper’s scheme, the sensor will have to submit out |m| + (2n+1)|G1| + Zp∗ bits = 20+(2n+1)∗34+32 bytes = 68n+86 bytes, |m| + n|G1| + 2Zp∗ bits = 20+n∗34+2∗32 bytes = 34n+84 bytes, |m| + (2n+2)|G1| = 20+(2n+2)∗34 = 68n+88 bytes, |m| + (n+2)|G1| = 20+(n+2)∗34 = 34n+88 bytes. According to [34], the sensor requires 3∗27∗8/12400=0.052 mJ to send a one-byte message. For communication energy consumption, RG [27] is (68n+86)∗0.052=3.536n+4.472 mJ, YC [28] is (34n+84)∗0.052=1.768n+4.368 mJ, CZ [29] is (68n+88)∗0.052=3.536n+4.576 mJ, this paper’s scheme is (34n+88)∗0.052=1.768n+4.576 mJ. The entire energy use of RG [27], YC [28], CZ [29] and this paper’s scheme are 38.88n+38.88+3.536n+4.472=42.416n+43.352 mJ, 19.44n+123.36+1.768n+4.368=21.208n+127.728 mJ, 19.44n+221.04+3.536n+4.576=22.976n+225.616 mJ,21.208n+19.44n+38.88+1.768n+4.576=43.456 mJ. When n=100, the communication energy consumption of RG [27], YC [28], CZ [29] and this paper’s scheme are 4284.952, 2248.528, 2523.216, and 2164.256 mJ, respectively. In terms of communication energy consumption, this paper’s scheme has reduced by 49.4%, 3.7%, and 14.2% respectively.