Enhanced Multi-Objective Grey Wolf Optimizer with Lévy Flight and Mutation Operators for Feature Selection

1  Introduction

Rapid advances in technology nowadays have exponentially increased the dimension size of data. As a result, effective and efficient management of this data becomes more sophisticated. According to [1], manual management of these types of datasets is impractical. There are many difficulties and barriers that researchers and developers face when trying to thoroughly extract meaningful ideas and conclusions from data. In addition to the need for powerful computing resources, the rapid increase in data volume has made data processing and analysis more challenging, which in turn has further amplified the demand for high computing resources. A process must be followed to obtain useful information from data. The knowledge discovery process in the database (KDD) [2] is a general structure that defines the steps needed to acquire useful information from a dataset. The core phase in the KDD process is known as data mining. In information technology research, data mining is recently considered as a fast-growing area due to the massive generation of data that has the potential to be converted into useful information [3]. Data mining is extracting and developing insightful knowledge from raw data. Data mining tasks involve classification, clustering, anomaly detection, association analysis, and regression [4].

The KDD method includes a crucial step called data preprocessing, which is a preparatory phase that plays a significant role in obtaining valuable information from the data. Careful execution of this step is essential because any mistakes can make it difficult to extract useful insights. One aspect of data preprocessing is feature selection, which involves using various strategies to remove irrelevant and redundant attributes from a given dataset [5,6]. In a dataset consisting of instances like emails, patients, communication attempts, user accounts, images, etc., features refer to the attributes associated with each instance. For example, the features for an email might include content, date sent, subject, receiver, sender, etc.

Broadly speaking, data mining utilizes techniques derived from different domains of knowledge, such as statistics and probability, especially machine learning. The three main categories of machine learning are supervised learning, including classification. Unsupervised learning, including clustering and reinforcement learning. Redundant or irrelevant features can degrade a model’s performance [7] and learning from irrelevant features can decrease the exactness of models [8]. Thus, feature selection is an important step that helps to select the most critical features that promise to enhance the system’s performance [9]. Feature selection has numerous advantages, such as increasing the quality of results of a developed model and making the training of a model faster or more cost-effective in terms of computational resource consumption. As well as improve the resulting models by making them smaller and easier to understand [10]. However, selecting a set of optimal features from a dataset with many features is a sophisticated task. The curse of dimensionality is the main problem in such datasets with many features, which decreases the classification performance due to the redundancies or irrelevancies of the features [11]. Therefore, eliminating irrelevant and redundant features by feature selection techniques is becoming necessary to reduce the curse of dimensions [12].

However, feature selection is a sophisticated process because of the complicated interactions between features. When interacting with other features, related features may become redundant/unrelated. Therefore, an ideal subset of features should be a collection of complementary features extending over the groups’ various characteristics to differentiate them better. Moreover, the difficulty can be extended due to the vast search space. The growth of search space is exponential over the number of original features [13]. Some search strategies (e.g., random, breadth, deep searches) are utilized to obtain the best subset of features. However, a complete search is impossible due to the cost of producing candidate solutions. Therefore, an exhaustive search for problems of any size is impractical. To overcome such limitations, researchers intend to use forward and backward sequential selection methods [14,15]. However, the problem of premature convergence arises, as well as such methods suffer from computational time complexity. Solutions to feature selection are therefore proposed in several studies based on metaheuristics or swarm-based search algorithms like a genetic algorithm (GA) [16], ant colony optimization (ACO) [17], particle swarm optimization (PSO) [18,19], differential evolution [20] and Moth-flame optimization algorithm (MFO) [21]. However, most of these techniques trapped in local optima. Thus, an effective global search approach is required to address feature selection problems. Recently, a metaheuristic algorithm named Grey Wolf Optimization (GWO) known as the hunting mechanism was proposed by Mirjalili et al. [22]. GWO has lower computationally cost than other metaheuristic algorithms such as PSO and GA and can converge faster. As a result, GWO has been utilized as an efficient algorithm in several domains, including feature selection [5,23,24].

Generally, feature selection treated as a single objective that optimizes classification accuracy or integrates classification accuracy and the selected number of features into a single-objective problem. In fact, feature selection is a multi-objective problem with two main objectives: maximizing classification accuracy and minimizing the number of features [13]. The aforementioned objectives are often contradictory, so making the best decision between the two goals requires a trade-off. To fulfill the diverse necessities of real-world applications, feature selection should be formulated as a multi-objective problem to produce a non-dominated subset of features [25]. Significant works have been made on feature selection, GWO, and multi-objective optimization; however, they are investigated separately. Moreover, the existing feature selection algorithms consume excessive computational time. Hence, feature selection is an inherently discrete problem by nature because it involves selecting (1) or deselecting (0) features, and this process can be represented as a binary decision problem. Recently, a binary variant of the Multi-objective GWO (BMOGWO-S) for feature selection was proposed in [26]. Compared with other algorithms, this method has proven to be effective in multi-objective optimization feature selection. However, because the lead wolf’s guidance has more effect compared with the random factor, the algorithm can be trapped easily into a local optimum, and this reason can also lead to poor stability. Therefore, enhancing the search ability of this algorithm becomes a necessity.

The main aim of this research is to obtain an accurate estimation of the Pareto optimal solution, which involves an optimal trade-off between classification error rate and feature reduction. An enhanced multi-objective GWO based on Lévy flight and mutation phase (LMuMOGWO) for feature selection is proposed to achieve this aim. The proposed approach is compared with two MOGWO variants and two major benchmark multi-objective methods on 12 commonly used datasets with different classes, instances, and features. The main contributions of this work are summarized as follows:

1.    We proposed an enhanced multi-objective grey wolf optimizer incorporating Lévy flight and mutation phase (LMuMOGWO) for feature selection problems. The proposed algorithm demonstrates excellent search ability in most cases compared to the existing approaches.

2.    The mutation phase was incorporated to reduce the long jump of Lévy flight to obtain a better Pareto optimal solution (classification error rate and the number of features).

3.    An extensive investigation was conducted of the proposed approach’s performance on obtaining Pareto optimal solutions (classification error rate and several features) in comparisons with two MOGWO variants and with two prominent multi-objective algorithms: MOPSO and NSGA-II.

4.    We have tested and evaluated the proposed approach’s classification and computational cost performance on twelve well-known datasets and benchmarked the performance with the existing methods.

The remainder of this paper is organized as follows. The state-of-the-art feature selection methods are presented in Section 2. Section 3 discusses the original MOGWO, and the Binary version BMOGWO-S. The developed enhanced multi-objective algorithm is explained in detail in Section 4. Section 5 provides the experimental setup, results, and discussion. The last section of this work presents the conclusion and provides research directions for future work.

2  State-of-the-Art Feature Selection Methods

Feature selection approaches can be grouped into filter-based and wrapper-based [9,12]. The critical difference is that the subset evaluation in the wrapper-based approach requires a learning algorithm to test the selected features in terms of classification efficiency, while evaluating the subset of features in the filter-based ignores the learning algorithm, which in turn results in less performance in terms of classification [27,28]. Another category of feature selection has been recently added, which is an embedded-based method that combines the learning algorithm and the selected feature into a single process [27,28]. However, this method is conceptually complex, and modifying the classification model to attain better performance is impossible [29]. Therefore, this research emphases on wrapper method. Recently, various feature selection approaches have been proposed [30]. This section reviews the existing feature selection methods.

Researchers used numerous wrapper methods to tackle the problem of feature selection. The first exhaustive/complete search is applied in a few numbers of studies [27,28]. Apart from a small number of features, for instance, 10 or less, the computational complexity of an exhaustive search is costly. To address this limitation, heuristic techniques were applied, and greedy search techniques are an example, both sequential forward and backward selection [14,15]. However, such techniques suffer from nesting consequences; thus, selected/eliminated features cannot be selected/eliminated again. To prevent the nested impact, a technique named plus-take-away-r that compromises the two sequential selection methods was proposed [31]. This technique is applied l time in forward selection and r times in backward.

Nonetheless, identifying suitable values between l and r is difficult. Besides, such techniques possibly converge to a local optimum and are intensive in computation in high-dimensional datasets. To overcome these limitations, two techniques based on consecutive backward and forward floating selection are developed [32]. However, the classical efforts to solve local optima are not enough.

Metaheuristic algorithms have been extensively utilized for feature selection to tackle the limitations of the conventional feature selection schemes. In [33], GA is used to obtain the best features. Results show that GA achieved better accuracy than the conventional SFFS method [32]. The authors in [34] hybridized GA with local search to develop a novel approach that can outperform the GA method. The authors in [35] utilized SA and GA to develop a hybrid filter feature selection scheme. The performance of the hybrid approach is evaluated on 8 UCI datasets where results demonstrated that SA with GA could achieve a good selection performance, particularly in the number of selected features. Another work that has utilized a hybrid GA and SA approach is presented in [36] where its performance is tested on the hand-printed Farsi characters. Benefiting from information correlation, the authors in [37] hybridized PSO with a local search strategy to search for the best subset of features.

Considering microarray data, the work in [38] implemented a hybrid PSO with GA as a wrapper feature selection scheme where the SVM classifier is used to perform classification. The work in [39] proposed a hybrid PSO with GA to select the best features when considering Digital Mammogram datasets. In [40] and [41], GA was hybridized with ACO to solve feature selection problems. Another work on Digital Mammogram datasets is presented in [42] where Cuckoo search (CS) and ACO are hybridized to select the best subset of features. DE and ABC algorithms are combined in [43] to search for the best features. Another hybrid algorithm for feature selection is developed in [44] where a harmony search algorithm was hybridized with a stochastic local search. A recent wrapper feature selection approach was proposed in [45] where SA is hybridized with the Whale Optimization Algorithm (WOA). A hybrid version that consists of antlion optimization (ALO) and GWO is developed in [46] for feature selection. Alwajih et al. [47], suggested a hybrid binary whale with harris hawks for feature selection. In summary, all the aforementioned approaches have shown remarkable performance when solving feature selection problems. Nonetheless, these algorithms suffer from being trapped in local optima and their computational costs are high. In addition, they focus only on single-objective optimization that considers either minimizing classification errors or reducing features. As a result, it is crucial to adapt multi-objective feature selection optimization that can optimize the classification accuracy and the number of selected features simultaneously.

Recently, GWO has been extensively used to solve feature selection problems in diverse areas, including benchmarks problems as in [5,40,48], diagnosis of Parkinson’s disease [49,50], facial emotion recognition facial [51], face recognition [52], EMG signals classification [53], diagnosis of Paraquat disease [54], Coronary Artery disease classification [23], medical diagnosis [55] and intrusion detection [56,57]. A comprehensive review that includes publications from 2015 up to 2019 on feature selection-based GWO is presented in a published book chapter [6], where interested readers on GWO feature selection can find a detailed state-of-the-art.

Several multi-objective optimizations have been utilized for feature selection problems. In [48], an enhanced multi-objective PSO algorithm that utilizes a mutation operator is proposed for feature selection of unreliable data. A non-dominated sorting GA II (NSGAII) algorithm is proposed by Hamdani et al. [58]. Utilizing mutation, non-dominated sorting, and crowding distance. The authors in [59] proposed a multi-objective PSO algorithm (CMDPSO) to jointly optimize classification accuracy and reduce selected features. Based on the results, the CMDPSO algorithms perform better than NSGAII and strength Pareto evolutionary algorithm 2 (SPEA2). Utilizing rough set theory, the work in [60,61] applied a multi-objective PSO algorithm for filter feature selection. A multi-objective feature selection that combines PSO, GWO, and Newton’s law was proposed in [62], which implement two-phase scheme, PSO was applied for the first phase (exploration) while GWO perform the second or exploitation phases. Another study, tested on 14 classical datasets, an enhanced multi-objective multi-verse optimizer is developed in [63] to search for the best features to optimize classification accuracy and eliminate irrelevant features. Also, a multi-objective PSO is proposed in [64], which integrated with adaptive strategies, where its performance is evaluated on 20 diverse datasets. In [65], a novel approach named particle ranking is developed for multi-objective PSO feature selection. This approach treats particles as feature vectors, and particles are ranked based on two bands of non-dominated and dominated particles in an optimization space represented by a mesh structure. The effectiveness of the proposed scheme is evaluated on only seven UCI datasets. The authors in [66] have developed three multi-objective feature selection algorithms based on Harris Hawks Optimization (HHO), Fruit fly Optimization Algorithm (FOA) and a hybrid version of both. Besides, utilizing the ideas of region-based selection, grid and archive, two multi-objective forest optimization feature selection algorithms are developed in [67]. Zhang et al. [68] propose an approach to improve the performance of multi-objective evolutionary algorithms (MOEA/D) for large-scale many-objective optimization problems. The proposed approach combines MOEA/D with an information feedback model that utilizes the Pareto set approximation to provide guidance for the search process. Authors in [69] present an approach to improve the performance of NSGA-III, a popular multi-objective evolutionary algorithm, for large-scale many-objective optimization problems. The proposed approach introduces information feedback models that utilize historical information of individuals in previous generations to guide the search process in the current generation. The performances of the two algorithms are tested on two microarray datasets and nine UCI datasets. Although feature selection has been extensively studied, most state-of-the-art works focus only on single-objective optimization, such as maximizing classification accuracy. Numerous research works have shown the superiority of GWO in tackling feature selection problems; nonetheless, the implementation of multi-objective GWO for feature selection is not well studied. Thus, there is still room to develop novel multi-objective GWO algorithms for feature selection problems.

3  Preliminaries

This section presents an overview the original MOGWO mathematical model and the original Binary version BMOGWO-S.

3.1 Multi-Objective Grey Wolf Optimization (MOGWO)

The GWO mathematical model is developed by using the alpha (α), beta (β), and delta (δ) wolves that represent the best, second best, and third best solutions, respectively, while the remaining wolves are represented by omega (ω).

■   Encircling the Prey

GWO developed a set of equations to mathematically model the encircling Prey behaviors, which are given based on the following:

D→=|C→ .X→ p(t)−X¯ (t) |(1)

X→ (t+1)= X→p(t)+A→ . D→(2)

D→ represents the distance of the wolf X¯ (t)  from the position of the prey X¯ (t), here t denotes the current iteration, C→ and A→ represent 2 coefficient vectors, X→ and Xp→ are position vectors of a grey wolf and a prey, respectively. The mathematical representation of A→ and C→ are given as follows:

A→=2a→.r1→−a→(3)

C→=2.r2→(4)

where a→ starts with a value of 2 and it decreases linearly until it reaches a value of 0 and r1, r2 are two random numbers with values in the range [0, 1].

■   Hunting Prey

A grey wolf can locate the position of prey and encircle it. Generally, alpha is the leader that guides the pack for hunting, and it is occasionally assisted by beta and delta to perform this task. Nevertheless, the optimal location of prey is unknown in a search space. To mathematically model the hunting behavior of grey wolves, it is assumed that alpha, beta, and delta have more knowledge that helps to locate the potential prey. Consequently, the best three solutions are recorded, and the remaining candidate solutions represented by (omegas) are forced to update their positions based on the positions of the best three search agents. This is mathematically modeled as follows:

Dα→=|C1→.X→ α−X→|(5)

Dβ→=|C2→.X→ β−X→|,(6)

Dδ→=|C3→.X→ δ−X→|(7)

X1→=Xα→−A1.(Dα→)(8)

X2→=Xβ→−A2.(Dβ→)(9)

X3→=Xδ→−A3.(Dδ→)(10)

X→(t+1)=X1+X2+X3→3(11)

where Dα→, Dβ→,Dδ→ is the distance of alpha (α), beta (β), and delta (δ) wolves from the prey and X1→,  X2→, X3→ represent the positions of alpha (α), beta (β), and delta (δ) wolves respectively. The X→(t+1) represent the position of the final solution.

■   Attacking Prey

Once prey cannot move, grey wolves begin to attack it. The hunt of grey wolves finishes by attacking the prey now it is unable to move. Approaching the prey is mathematically modeled by decreasing a→. The value of a→ changes during the iterative process as follows:

a→=2−t.2miaxter(12)

where miaxter and t denote the maximum number of iterations and the current iteration, respectively.

GWO was initially proposed for single-objective optimization problems. Expressly, the original GWO approach is not capable of solving multi-objective problems. As a result, Mirjalili et al. developed a multi-objective GWO (MOGWO) [70] that can solve problems with multiple conflicting objectives. The development of MOGWO requires the integration of the two following mechanisms:

■   An archive that can store non-dominated Pareto front solutions.

■   A selection strategy that utilizes the archive to choose the best leader (alpha), the second-best leader (beta), and the third-best leader solutions (delta).

The archive is empowered by a controller who decides which solutions should be saved in the archive. In addition, it has a full awareness in case the archive becomes full. The new non-dominated solutions are compared with the historical ones iteratively. This can lead to numerous situations that can be considered follows:

■   The new solution is not allowed to enter the archive if it is dominated by the previously stored solutions and vice versa.

■   If both the new and previously stored solutions do not dominate each other, then the new solution is added to the archive.

■   In case the archive is full, a grid mechanism could omit one of the cur-rent archive solutions to allow the newly obtained solution to be stored in case it dominates the existing ones.

MOGWO has shown a better convergence speed; nonetheless, it still suffers from being trapped in local optima as well as poor stability behavior. The main reasons for such performance can be summarized as follows:

■   MOGWO shows positive randomness at the initialization stage only where the positions of wolves are randomly initialized. Although MOGWO has a random factor, leader wolves have a more significant influence on updating the positions of wolves at the iterative process compared with the random factor. Therefore, the MOGWO algorithm relies heavily on the initial values and lacks self-regulation ability.

■   MOGWO chooses the best three leaders, i.e., α, β, and δ from the archive even if the archive set has fallen into a local optimum. Thus, it is essential to enhance the exploration ability of MOGWO, particularly at the latter stages of the optimization process.

Since lead wolves strongly attract wolves, they blindly follow them, and they also follow non-dominated solutions that are located around leaders. This causes grey wolves to ignore the non-dominated solutions that are placed beside them. In fact, grey wolves might pass over other non-dominated solutions while they follow the leading wolves. The optimization ability of MOGWO can be significantly enhanced if grey wolves are supported with independent searching. In the Pareto front, it is hard to compare solutions. To tackle this problem, a leader selection technique is proposed. GWO has three leaders known as alpha (the best solution), beta (the second-best solution) and delta (the third-best solution) wolves. These three solutions guide the remaining wolves toward the optimal solution. The leader selection strategy chooses the smallest crowded segment of the space and offers one of its non-dominant solutions.

Utilizing the likelihood of a hypercube, the roulette-wheel method is applied as a selection approach as follows:

Pj=mHj(13)

where m denotes a constant with a value higher than one and H is the overall number of gained Pareto front in the jth segment.

3.2 Binary Multi-Objective Grey Wolf Optimization (BMOGWO-S)

The conventional MOGWO was initially developed to solve optimization problems in continuous search space. MOGWO cannot be directly applied to address binary problems, including multi-objective feature selection optimization problems. As a result, a binary MOGWO version was developed in our pervious study by utilizing the sigmoid function [26]. In the classical MOGWO, search agents have position vectors that contain continuous values that allow them to explore and exploit the search space. To enable binary movements of search agents, the positions update equation in (11) is modified as follows [26]:

xdt+1={1 if sigmoid(x1+x2+x33)≥rand0otherwise(14)

where xdt+1 denotes the newly generated binary position in dimension d at iteration t, a rand is a random number ∈ [1, 0], and sigmoid (a) is given as follows:

sigmoid (a)=11+e−10(x−0.5)(15)

x1,x2 and x3 in (8)–(10) are given based on the following:

x1d={1 if( xαd+bstepαd)≥10                 otherwise(16)

x1d={1 if( xαd+bstepαd)≥10                 otherwise(17)

x3d={1 if( xδd+bstepδd)≥10                 otherwise(18)

where  xα,β,δd  is the vector position of the alpha, beta and delta wolves in dimensions d, and bstepα,β,δd  is a binary stage in dimension d that is given as follows:

bstepα,β,δd={1   if  cstepα,β,δd≥rand0                       otherwise(19)

where cstepα,β,δd  denotes the continuous-valued step size for dimension d, and it is mathematically written as follows:

cstepα,β,δd=11+e−10(A1d Dα,β,δd−0.5) (20)

4  The Proposed Multi-Objective Grey Wolf with Lévy Flight and Mutation Operators (LMuMOGWO)

The previous BMOGWO-S [26] updates its positions to the optimal solutions based on the search leaders, i.e., alpha, beta, and delta, which are the best, second best, and third best search candidates, respectively. However, in some cases, the search candidates of BMOGWO-S tend to have a local optimal stagnation problem. Thus, the issues of immature convergence of BMGWO-S can still be encountered. In certain instances, the previously proposed BMOGWO-S method does not support a seamless exploration-exploitation transition.

A possible solution to the aforementioned problems is to integrate Lévy flight search patterns into the search mechanism of BMOGWO-S, which can enhance the BMOGWO-S in terms of deeper search patterns. This integration can significantly assist BMOGWO-S in achieving more effective global searches. Thus, the issue of stagnation problem will also be remedied. Additionally, Lévy’s integrated BMOGWO-S should enhance the quality of the candidate solutions throughout the simulation process.

For calculating the random walk step length, the Lévy distribution is utilized, which usually begins from one of the best-established positions, then the Lévy flight produces a new generation at a distance dependent on the Lévy distribution that selects the most optimal generation. Two basic steps are included in the Lévy flight: selecting a random direction and generating a new step.

Hence, the power-law is utilized to balance the Lévy distribution step size based on the following equation [71]:

L(s)∼ |s|−1−β   (21)

where 0 < β < 2 denotes Lévy index for stability control, and s is variable. Whereas the Lévy distribution can be mathematically written as follows [71]:

L(s,γ,μ)={γ2πexp [−γ2(s−μ)]1(s−μ)3/2,0<μ<s<inf0,s≤0(22)

where γ > 0 is a scale distribution parameter while μ is a location parameter.

Generally, the Fourier transform is used to define Lévy distribution [72]:

F(k)=exp [−α|k|β],0<β<2(23)

where α is a skewness factor that can have a value in the range [−1, 1], and β ∈ (0, 2) denotes the Lévy index.

Mantegna’s algorithm is utilized to estimate the step length of a random walk based on the following equation [71]:

S=μ|ν|1/β(24)

where μ and ν follow a normal distribution.

μ∼N (O, σμ2),ν∼N (O, σν2),(25)

where

σμ=Γ(1+β)sin⁡(πβ2)Γ(1+β2)βx2β−12,  σν=1(26)

For calculating the step size, the following mathematical formulation is utilized:

Step size=0.01xS(27)

Generally, the main steps of the proposed Lévy integrating BMOGWO-S are like the steps of BMOGWO-S. Here, the Lévy distribution is integrated to generate long steps to the optimal solutions. Therefore, the alpha, best and delta positions of the BMOGWO-S are updated as follows:

xdt+1={1if  sigmoid(x1+x2+x33)+Step size≥rand0otherwise(28)

The Lévy flight helps to address the issue of stagnation in local optimum; however, the motions of Lévy and its tendency to migrate for long repositioning events may cause the possibility to jump across an important/relevant feature without hitting/selecting it so-called (leap-overs). Therefore, to prevent this problem a mutation operator is integrated to provide more informative features that can decrease classification errors. This operator utilizes a nonlinear function, pm, to control the mutation range and the mutation probability of wolves. Iteratively, pm can be updated as follows:

pm=(1−(it−1)/(MaxIt−1))∧(1/mu)(29)

where it is the number of current iterations, MaxIt denotes the maximum number of iterations, and mu is the mutation rate. Algorithm 1 provides the pseudocode of the proposed mutation. Moreover, the representation of a solution is in the form of a one-dimensional binary vector where its length equals the number of features. Each dimension of this vector can have a value of either 0 (feature not selected) or 1 (feature selected).

This work evaluates the selected subsets of features based on the following two main objectives:

■   Minimization of features number.

■   Minimization of classification error rate.

Hence, the multi-objective feature selection minimization problem is mathematically formulated as denoted by Eq. (30):

minimize F(x)={f1(x)=MNM∈ N, N ∈R+f2(x)= FP+FNTP+TN+FP+FN X 100,(P+N) ∈ R+(30)

where M indicates the selected number of features and N represents the overall number. TP, TN, FP, and FN mean true positives, true negatives, false positives, and false negatives, respectively. The first objective function f1 (x) represents the ratio between the selected and total features, while the second objective f2 (x) represents the classification error rate. Artificial Neural Network (ANN) classifier is used evaluate the classification accuracy of the selected feature subsets. The complete pseudocode of the proposed algorithm is presented in Algorithm 2 and its general model is illustrated in Fig. 1.

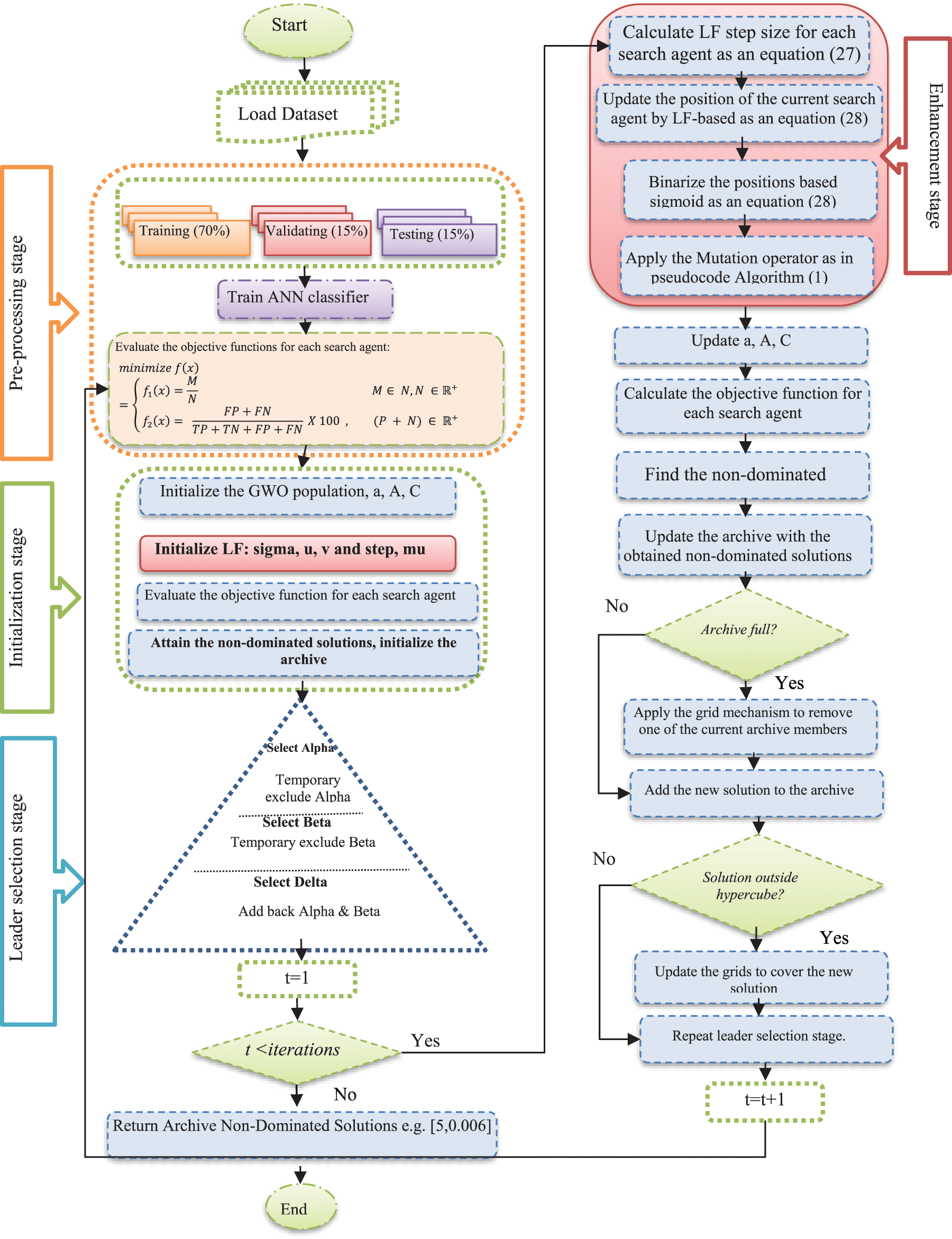
Figure 1: General model of the proposed LMuMOGWO approach

5  Results and Discussion

This section presents the experimental setup followed by the results of the proposed algorithm against the existing methods. First, the results of the proposed LMuMOGWO have clearly described then the comparison between the proposed approach and the existing methods are explained.

5.1 Experimental Setup

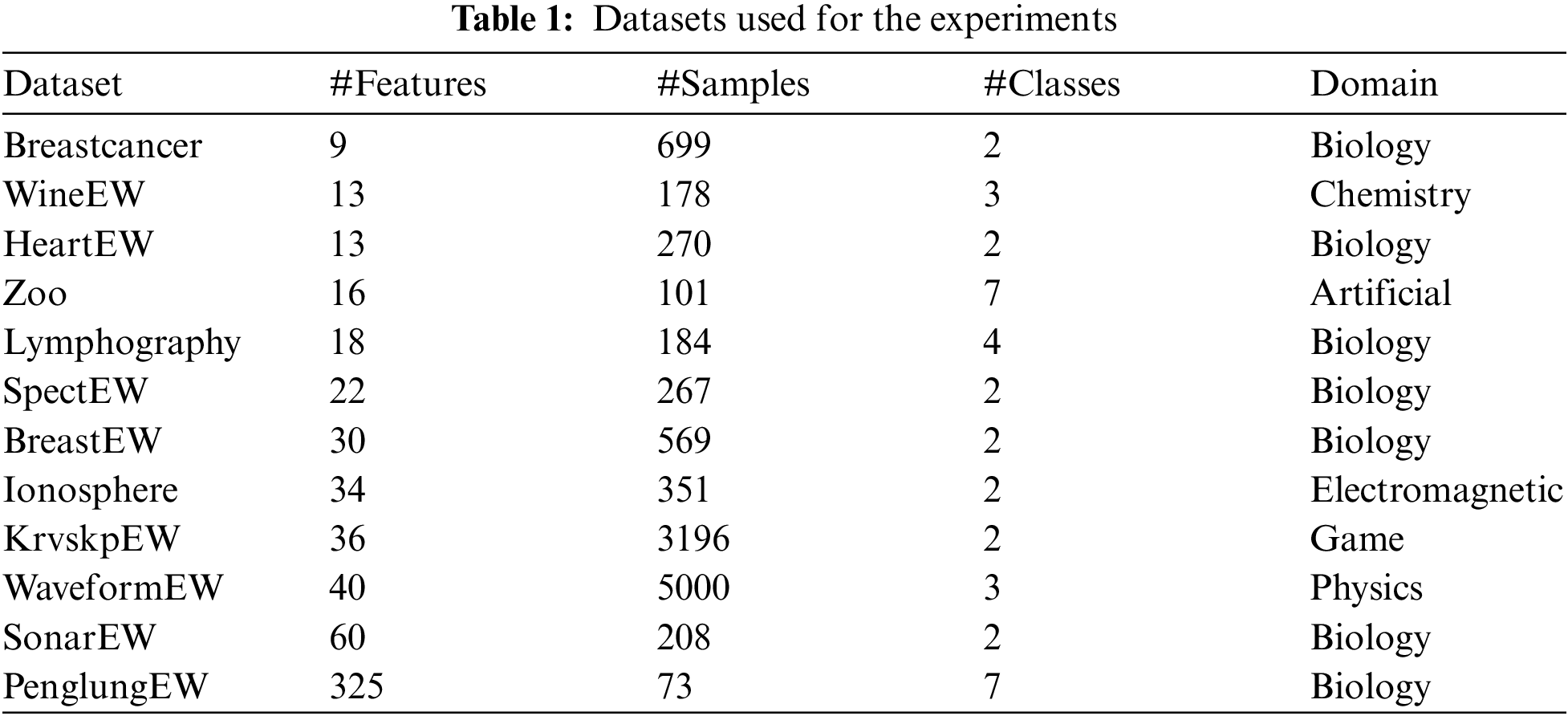
To investigate the performance of the proposed two multi-objective GWO based feature selection algorithms namely: multi-objective grey wolf optimization based sigmoid transfer function BMOGWO-S [26], and BMOGWO-V based tanh transfer function [73]. Two wrapper multi-objective feature selection approaches, i.e., NSGA-II [74] and BMOPSO [59], are used as the benchmark. The performances of the proposed multi-objective algorithms are evaluated on 12 benchmark datasets (shown in Table 1) obtained from the UCI data repository [75]. Table 1 presents the name of each dataset, its number of features, instances, and number of classes. The datasets include different numbers of features starting from 9 (low dimension) to 325 (high dimension). Moreover, the instances and classes of these datasets vary from 73 to 5000 and 2 to 7, respectively.

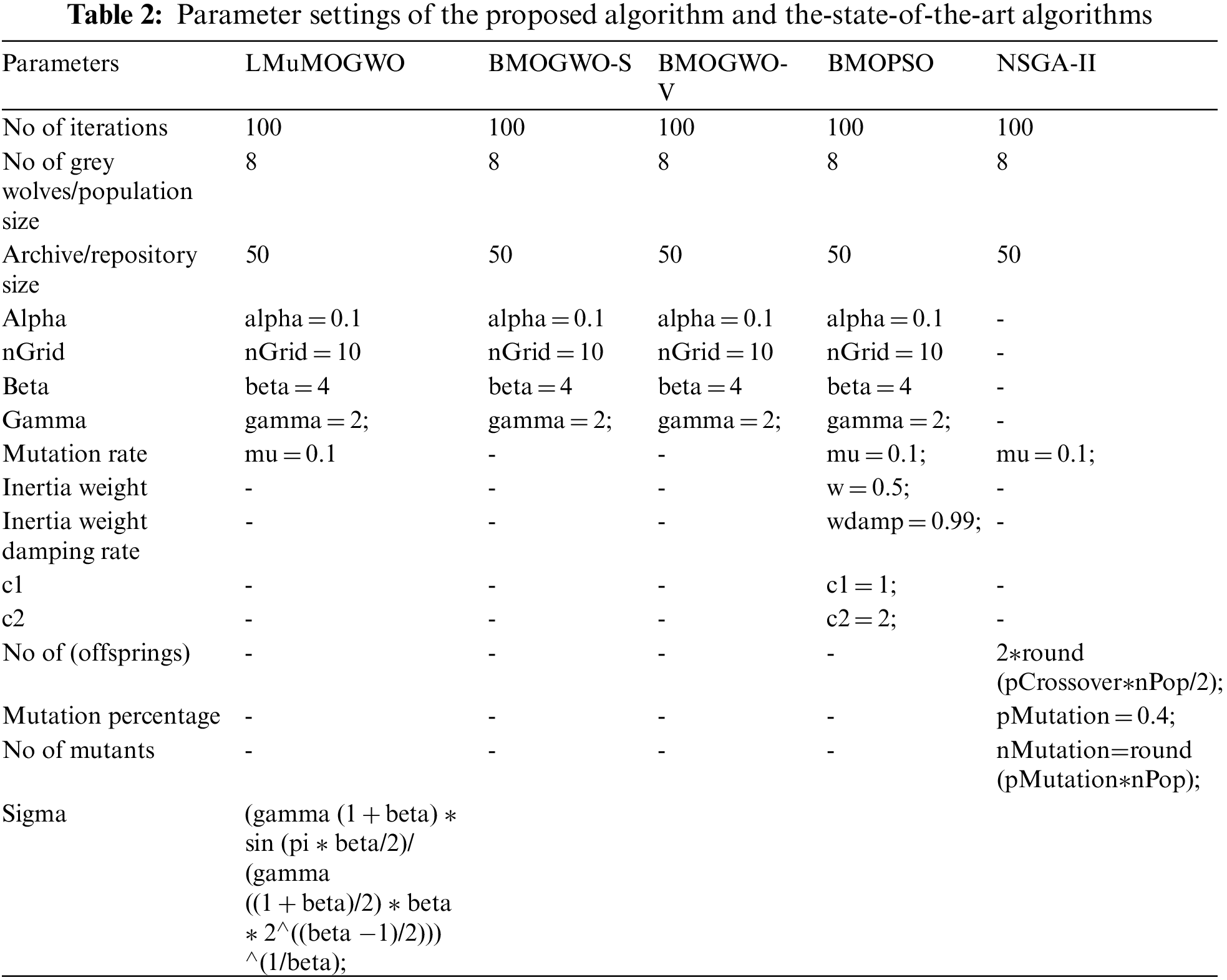
For experiments, instances are split randomly into a training set (70% of the dataset), and the remaining 30% are treated as the validation and test set. In the training phase, a feature subset is represented by one potential solution. Due to the stochastic behavior, all algorithms have been executed 20 times with random seeds. Artificial Neural Network (ANN) is applied in the inner loop of the training process to evaluate the classification accuracy of the selected feature subsets. Once the training process is completed, the test set is utilized to evaluate the selected features by calculating the testing classification accuracy. All algorithms are implemented using MATLAB R2017a on an Intel(R) Core™ i7-6700 machine with 16 GB of RAM and a 3.4 GHz CPU. The parameters of the proposed algorithm and the benchmark approaches are presented in Table 2.

5.2 Results of the Proposed LMuMOGWO

The experimental results of LMuMOGWO for twelve datasets are presented in Fig. 2. Each figure shows the result of one dataset, where the name of the dataset is shown at the top of the figure. Besides the name of the dataset, two values are shown that present the original number of features (first value) and the classification error rate (second value). The X-axis and the Y-axis of the figure present the number of selected features and the classification error rate, respectively. Considering all datasets, it is evident in Fig. 2 that the proposed LMuMOGWO algorithm has a better non-dominated solution that successfully selects a smaller number of features and achieves a lower classification error rate than utilizing all the original features.

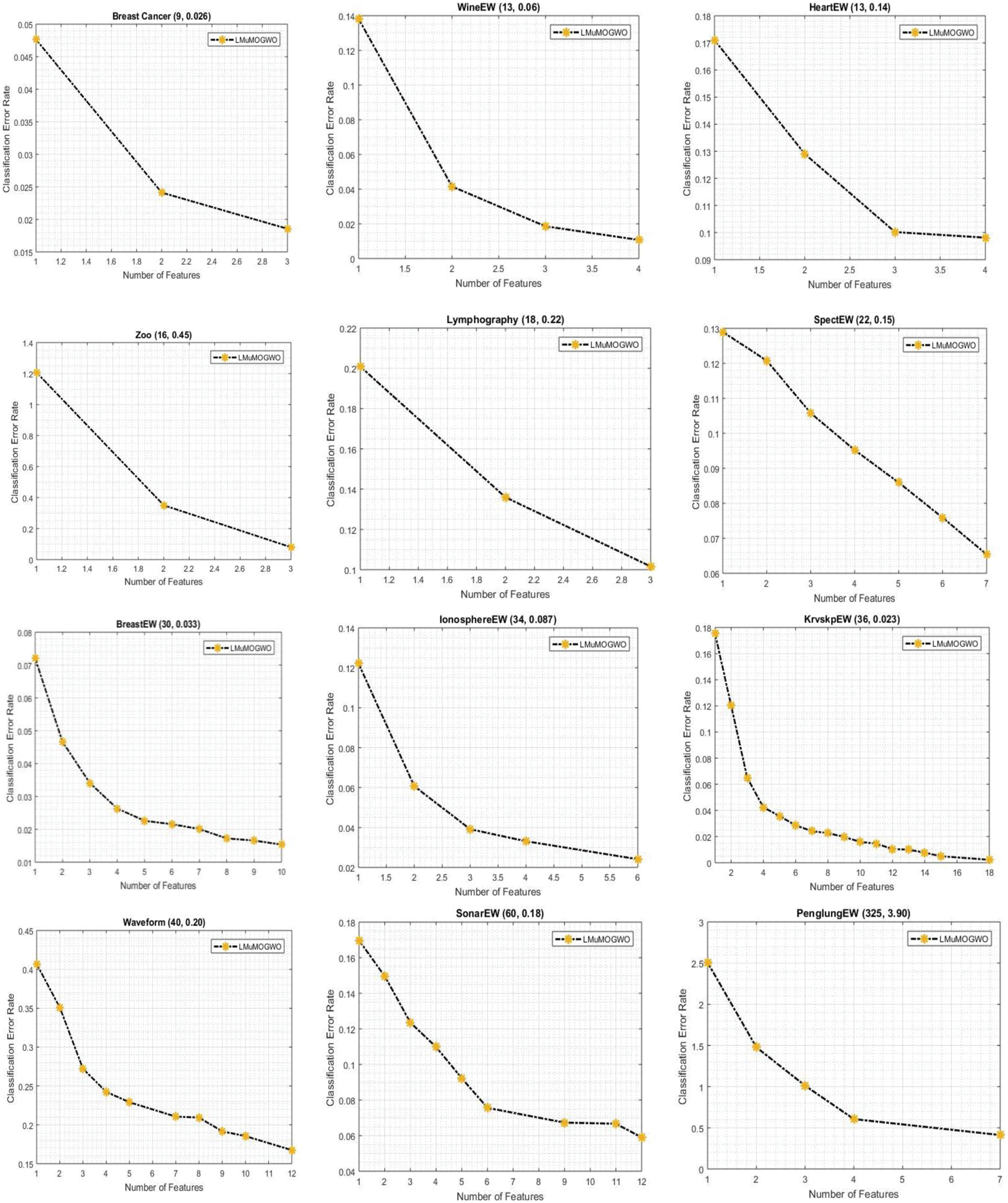
Figure 2: Results of the proposed LMuMOGWO on 12 datasets

Taking the Breast Cancer dataset as an example, LMuMOGWO produces three non-dominated solutions which select approximately 33% from the original features (3 from 9) in which two subsets attain lower classification error rates compared with the usage of all original features. For the HeartEW dataset, LMuMOGWO produces four non-dominated solutions which select approximately 25% of the original features (4 out of 13), and three of the subsets achieve better error rate classification compared with the usage of all original features. Considering the WineEW dataset, four non-dominated solutions are produced (4 from 13) features in which three feature subsets achieved better classification error rates. In the Zoo dataset, only three non-dominated feature subsets are produced from original features (16 features), in which two solutions accomplished better classification error rates compared with the original features. Similarly, in the Lymphography dataset, three non-dominated feature subsets are produced from original features (18 features) in which all solutions attained better classification accuracy compared to utilizing original features. The aforementioned datasets are small-size datasets where in most of these datasets, the number of features is reduced to 30% or less yet attaining higher classification accuracy compared with the usage of the original features.

Fig. 2 shows that the LMuMOGWO produces a better non-dominated solution in all datasets, which successfully selects a smaller number of features and has a lower classification error rate. In the SpectEW dataset, seven out of twenty-two features were selected and obtained a better error rate compared with the usage of all dataset features. In BreastEW, the LMuMOGWO selects 10 from 30 features, in which eight solutions attained a better classification error rate than using original features. In IonosphereEW, only five features are selected from a total of 34 original features, of which four solutions are better in classification performance than original features. In the KrvskpEW dataset, 16 features from 36 features are selected. The 4 datasets mentioned above are medium size datasets where in most of these datasets, the number of features is reduced to 15% or less while still achieving lower classification error rates compared with utilizing the original features. Considering large datasets such as Waveform (10 from 40), SonarEW (9 from 60) features, and PenglungEW (5 from 325), the number of features is decreased to 10% or less in all cases except Waveform dataset (approximately 20%). From these results, it can be revealed that the new integrated mechanisms of Lévy flight and mutation operators can expand the searching abilities of BMOGWO-S. The experiments have demonstrated that LMuMOGWO successfully solves feature selection problems and obtains better non-dominated solutions. LMuMOGWO used several techniques, such as Lévy flight, a random walk where the Lévy distribution is used to determine the jump size. Implementing the Lévy flight has helped to perform effective and extensive global search resulting in feature reduction while simultaneously obtaining low classification error rates.

5.3 Comparison Between the Proposed Lmumogwo and State-of-the-Art Methods

This subsection investigates the performance of the proposed LMuMOGWO on the twelve datasets against four benchmarking methods. Two are based on MOGWO, 1) BMOGWO-S and 2) BMOGWO-V. In addition, two effectives, widely used multi-objective approaches, namely, BMOPSO and NSGA-II, are used for the comparison.

First, the comparison is carried out on twelve datasets, as illustrated in Fig. 3. Each graph presents the result of one dataset where the name of the dataset is shown at the top of the figure. Beside the name of the dataset, the original feature size, as well as the ANN classification error rate, are shown. The X and Y axes present the number of selected features and the classification error rate, respectively. The black, blue, cyan, green, and magenta colors denote the proposed LMuMOGWO, BMOGWO-S, BMOGWO-V, BMOPSO and the NSGA-II algorithms, respectively. As Fig. 3 shows, for the Breast Cancer dataset, in terms of non-dominated solutions, LMuMOGWO attained better results than all benchmarking approaches regarding classification error rate and the number of selected features. The number of selected features in LMuMOGWO is around 3, while BMOGWO-S, BMOGWO-V, BMOPSO, and NSGA-II select 4, 6, 4, and 7, respectively. This indicates the superiority of LMuMOGWO feature reduction.

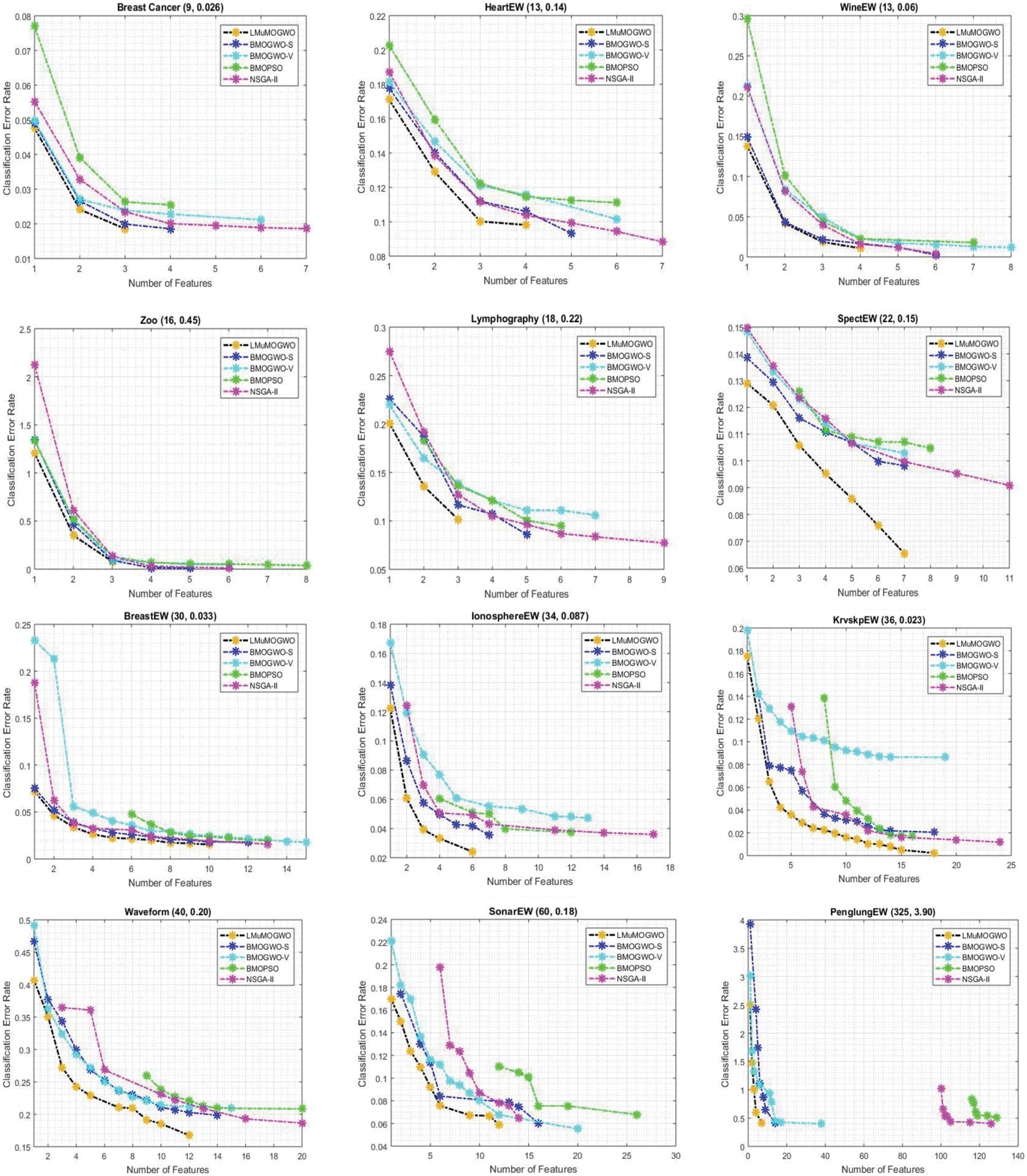
Figure 3: Comparison results between LMuMOGWO and state-of-the-art algorithms on 12 datasets

Similarly, LMuMOGWO achieves less error rate compared with the usage of all features. Besides, the error rate achieved by LMuMOGWO outperforms the ones achieved by the benchmarking methods. The HeartEW dataset clearly demonstrated better performance of LMuMOGWO against its counterparts’ approaches in terms of feature reduction and lower error rate. LMuMOGWO selects four features, whereas BMOGWO-S, BMOGWO-V, BMOPSO, and NSGA-II select 5, 5, 6, and 7, respectively. This means LMuMOGWO can further decrease the number of selected features while preserving or achieving a lower classification error rate compared with using all features, as well as better than the counterparts’ methods. In the WineEW dataset, LMuMOGWO produced non-dominated solutions that dominate all benchmarking approaches in terms of feature reduction and classification accuracy in all cases. Hence four non-dominated solutions are produced, which evolve with less error rate and a small number of features. Four non-dominated solutions are produced by LMuMOGWO while attaining less error rate compared to benchmarking methods.

For the Zoo dataset, LMuMOGWO produced non-dominated solutions that dominate all benchmarking approaches in terms of both feature reduction and minimizing the classification error rate in all cases. Hence, four non-dominated solutions are produced, which evolve less error rate as well a small number of features which demonstrates a better performance of the proposed LMuMOGWO against benchmarking methods. Hence the selected features are (1 or 3, or 2) with error rates (of 1.20 or 0.079 or 0.35) respectively. In the Lymphography dataset, three non-dominated solutions were obtained by LMuMOGWO, which involves higher classification accuracy and lower selected features. The BMOGWO-S, BMOGWO-V, BMOPSO and NSGA-II algorithms produce 5, 7, 5 and 8 non-dominated solutions, which evolve large features and high error rates compared to LMuMOGWO. In the SpectEW dataset, the proposed LMuMOGWO produced non-dominated solutions similar to BMOGWO-S, but more than BMOGWO-V and BMOPSO and better than NSGA-II. However, LMuMOGWO produced a non-dominated solution with a better error rate than all algorithms and fewer features compared to BMOPSO and NSGA-II. LMuMOGWO produced 7 non-dominated solutions, of which the error rates are better than using all features, and the error rates obtained by LMuMOGWO for all non-dominated solutions are better than all benchmarking methods. Similarly, as can be in the BreastEW dataset, the proposed LMuMOGWO produced (10) non-dominated solutions, which is more than the ones achieved by BMOPSO (7) and NSGA-II (8), whereas less than BMOGWO-S (11) and BMOGWO-V (14). How-ever, the non-dominated solution achieved by LMuMOGWO is much better than all benchmarking schemes for both classification accuracy and feature reduction in all cases.

The IonosphereEW dataset also shows that the LMuMOGWO clearly outperforms all benchmarking algorithms in terms of attaining higher classification accuracy and better feature reduction. Five non-dominated solutions are produced by LMuMOGWO, evolving lower classification errors and a smaller number of features compared with the ones produced by the benchmarking approaches. This is because of the new mechanism integrated into the algorithm, which is Lévy flight and the mutation operator, which help select the most informative features with less error rate. Similarly, as can be seen in the KrvskpEW dataset, the proposed LMuMOGWO produced non-dominated solutions that dominate all benchmarking approaches regarding feature reduction and less error rate in all cases. Hence, sixteen non-dominated solutions are produced, evolving to a lower classification error rate and fewer features.

In the Waveform dataset, the proposed LMuMOGWO produced (10) non-dominated solutions that dominate all benchmarking approaches for feature reduction and less error rate in all cases, also reduced the original features from 40 features to a maximum of 12 features where the error rate of classification is much better compared with the usage all features. When the features are reduced to (1 feature), the classification error rate becomes high, which is normal and proves the conflict between the two objectives. Similarly, as seen in the SonarEW dataset, the proposed LMuMOGWO produced non-dominated solutions that dominate all benchmarking approaches in terms of lower error rate and reducing features in all cases, hence nine non-dominated solutions are produced, which evolve less error rate as well small number of features. It is also observed that LMuMOGWO reduces the number of features from 60 feature to a maximum of 12 features in which the classification performance is further improved, also even if the benchmarking methods produced less non-dominated solutions how-ever, these non-dominated solutions involve a larger number of features and higher classification error rate compared to LMuMOGWO. Lastly, in a dataset PengLungEW, the proposed LMuMOGWO clearly outperforms all benchmarking methods in producing non-dominated solutions that involve fewer features and achieve higher classification accuracy. It indicates that the five non-dominated solutions have fewer selected features where the maximum number of selected features is 7 and less classification error rate compared to other algorithms, especially BMOPSO and NSGA-II. Hence their non-dominated solutions involve a relatively large number of features.

From the obtained results, LMuMOGWO dominates all benchmarking approaches on classification accuracy and a number of selected features in most cases. For instance, in the following datasets (Breast Cancer, HeartEw, Zoo, and Lymphography), the proposed LMuMOGWO produces a non-dominated solution better than BMOGWO-S, BMOGWO-V, BMOPSO, and NSGA-II in terms of minimizing the error rate and reducing the number of features. When the non-dominated solutions of LMuMOGWO are compared with BMOGWO-S, BMOGWO-V, BMOPSO, and NSGA-II, mostly all the BreastEW, KrvskpEW, SpectEW, and IonosphereEW datasets, LMuMOGWO achieves superior performance compared with BMOGWO-S and the other compared algorithms in addressing feature selection problems in more than 30 dimensions. In addition, LMuMOGWO achieves better feature reduction performance, and it significantly improves the accuracy of classification. This is due to the effects of the mutation operator as well as Lévy flight embedded mechanism on balancing the exploration and exploitation of the algorithm. Similarly, in Waveform, SonarEW, and PenlungEW datasets, the proposed LMuMOGWO approach achieves better performance, particularly in selecting a lower number of features. For example, in the PenglungEW dataset, the maximum number of selected features in BMOPSO, NSGA-II, BMOGWO-V and BMOGWO-S are 129, 126, 38, and 14, respectively, respectively, whereas the proposed LMuMOGWO selects only 7 effective features with better classification error rate. This proves that LMuMOGWO can reduce about 95% of the original features.

This is because the proposed Lévy flight and mutation embedded strategies efficiently balance the exploration and the exploitation per-formed by the BMOGWO-S algorithm. It is observed that the proposed Lévy flight strategy enriches the explorative behaviors of BMOGWO-S by producing long jumps, and to avoid the drawbacks of such long jumps, which leads to ignoring some more informative features, the mutation operator is integrated in order to add the most applicable features. Those mechanisms can be observed when LMuMOGWO tends to discover unseen areas of the feature selection search space. Accordingly, the new mechanisms have enhanced the BMOGWO-S in obtaining a desired balance between global and local search inclinations and avoiding the local optima problem. We can observe from the obtained results that the proposed LMuMOGWO, which incorporates the Lévy flight and mutation, overcomes the drawback of local optima in the previously proposed BMOGWO-S approach. The results have shown that LMuMOGWO is able to achieve superior classification accuracy and feature reduction performance compared with BMOGWO-S, BMOGWO-V, BMOPSO, and NSGA-II. Overall, we can rank the algorithms according to the results as follows, 1) LMuMOGWO, 2) BMOG-WO-S, 3) BMOGWO-V, 4) BMOPSO, 5) NSGA-II.

5.4 Statistical Results and Computational Time Comparison

For further comparison, statistical results are presented that show how many features are selected by LMuMOGWO, BMOGWO-S, BMOGWO-V, NSGA-II, and BMOPSO. Firstly, as Table 3 shows, datasets like (WineEW, Lymphography, HeartEW, Breast Cancer, and Zoo) show that LMuMOGWO achieves the smallest average number of selected features compared with BMOGWO-S, BMOGWO-V, NSGA-II, and BMOPSO. Likewise, regarding minimum and maximum selected features, the range between the minimum and maximum selected features, and the standard division, the proposed LMuMOGWO achieves better results than the NSGA-II and BMOPSO approaches.

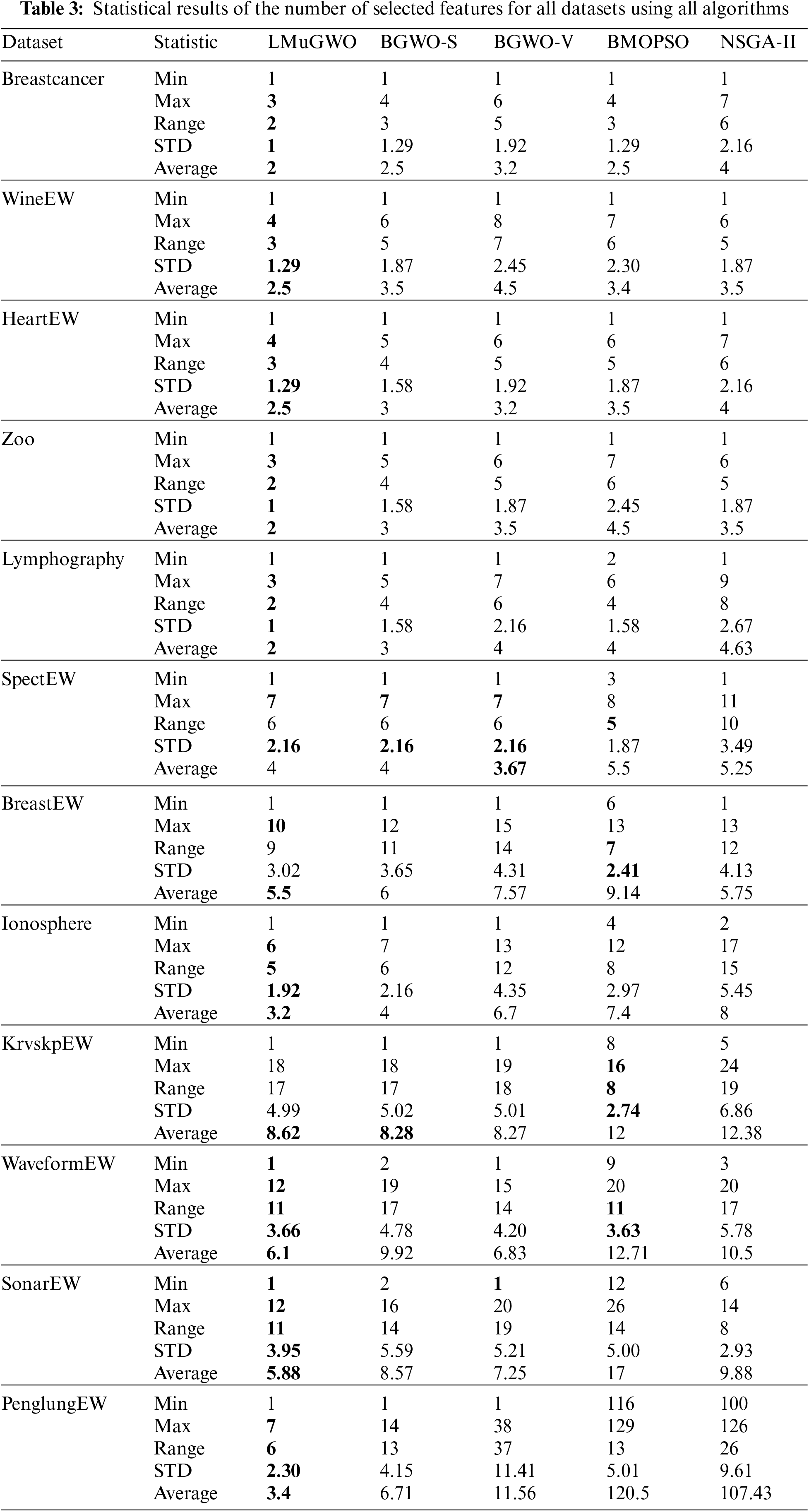
Secondly, considering datasets such as (BreastEW, Ionosphere, SpectEW, and KrvskpEW) LMuMOGWO achieves the smallest average number of features com-pared with benchmarking methods expected in SpectEW and KrvskpEW datasets, BMOGWO-V has the finest average (8.27) in KrvskpEW. However, LMuMOGWO obtains a lower classification error rate. Similarly, considering the SpectEW dataset, BMOGWO-V has the finest average (3.67); however, LMuMOGWO attains a lower classification error rate. Following the ‘No Free Lunch’ theorem, an algorithm commonly best for all problems does not exist [76]. Hence, LMuMOGWO is not an exception. For datasets such as (Waveform, SonarEW, and PenglungEW), the performance of LMuMOGWO is superior as it can achieve the best feature average and produces non-dominated solutions with the minimum features for the rest of the datasets. Considering the PenglungEW dataset, LMuMOGWO achieves a Pareto set with the minimum features (1), and an average of (3.4) on the Pareto sets that is smaller than BMOG-WO-S (6.71), MOGWO-V (11.56), BMOPSO (120.5) and NSGA-II (107.43).

As a result, the proposed LMuMOGWO can outperform the benchmarking methods in many aspects, including minimum classification error rate, the average number of selected features, and non-dominated solutions with minimum and maxi-mum features. The reason is that LMuMOGWO, which embedded Lévy flight and a mutation mechanism, can effectively balance the exploitation and exploration tendencies of the BMOGWO-S. Therefore, these mechanisms improve the tendency of the algorithm to produce more diminutive Lévy jumps based on a preferable subset of features. Moreover, the proposed modifications on LMuMOGWO that include Lévy flight with mutation operator have shown their effectiveness in avoiding the local optima problem, especially when dealing with large-size datasets. If LMuMOGWO escapes some informative features in the search space due to the long jumps of Lévy, the mutation operator helps to add such informative features.

This new mechanism is beneficial to explore new regions close to the newly explored non-dominated solutions. Due to this reason, the new algorithmic modifications have strong abilities to eliminate redundant features, unlike the benchmarking approaches. Table 4 illustrates the average computational time all algorithms need when the number of independent runs is 20. Table 4 illustrates a superior performance of our previously proposed MOGWO-S in most datasets. This is due to the fewer parameters used. Hence, the Lévy flight and mutation operators in the proposed LMuMOGWO take longer in every run than in the basic BMOGWO-S. For the Breastcancer, zoo and Lymphography datasets, LMuMOGWO requires only six minutes which is shorter than other methods. Considering datasets with medium sizes, such as the Ionosphere, and KrvskpEW datasets, LMuMOGWO spends less time than other algorithms. The results of large datasets clearly show that LMuMOGWO takes a significantly shorter time compared to NSGA-II and BMOPSO. Taking WaveformEW, SonarEW, and PenglungEW as examples, MOGWO-S requires only 12.07, 8.57, and 7.78 min, respectively, while BMOPSO requires 19.35, 15.05, and 33.98 min, respectively, whereas the NSGA-II algorithm takes 27.71, 11.07 and 35.93 min, respectively.

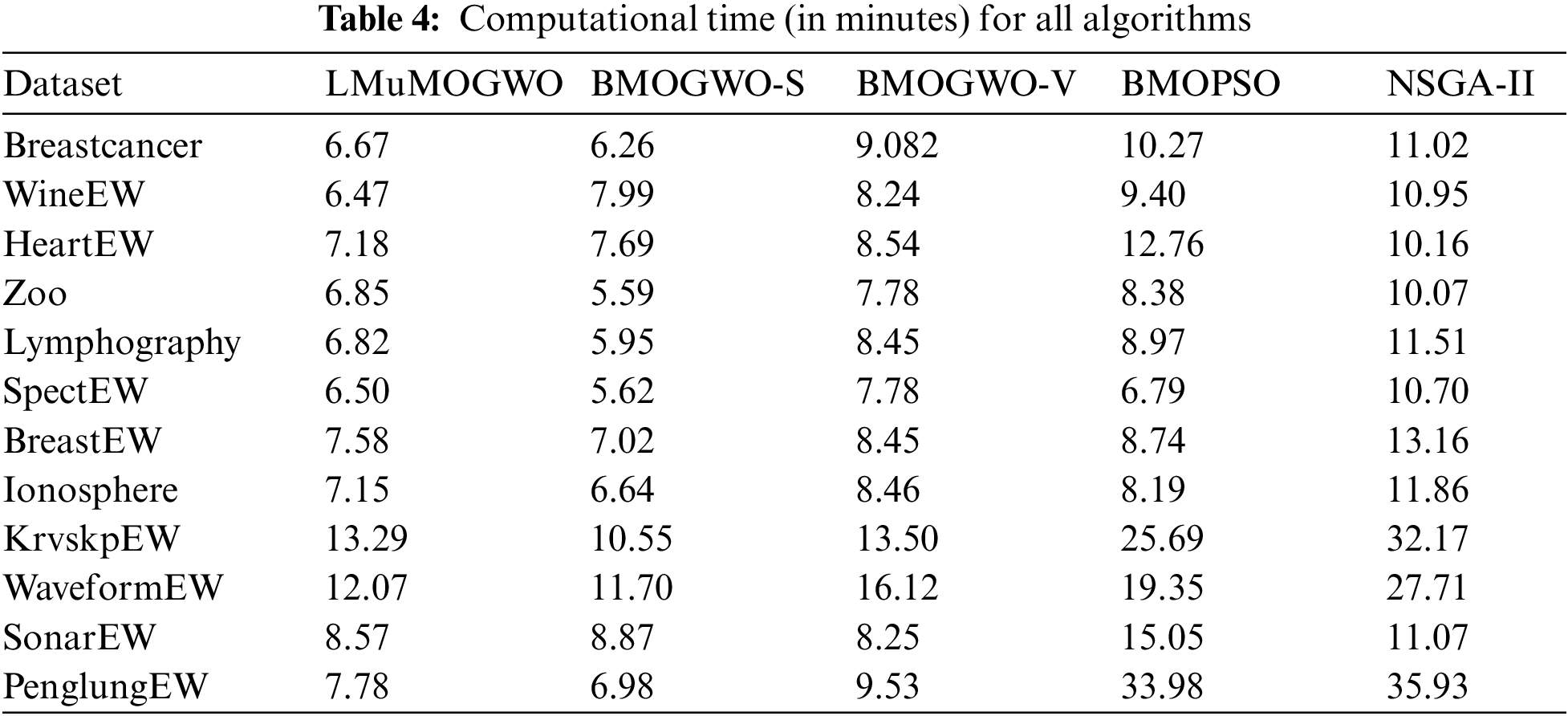
A fair comparison is carried out as population size, the maximum number of iterations and archive/repository size are the same for all compared algorithms. The need to calculate crowding distances and the ranking procedure of non-dominated solutions have generally increased the run time of BMOPSO and NSGA-II. LMuMOGWO only uses a Lévy flight and one-phase mutation mechanism without the need to calculate crowding distances or implement any ranking method, which in turn shortens the execution time of LMuMOGWO.

Furthermore, LMuMOGWO can select fewer features, resulting in less computational time, specifically when large datasets are considered. Based on the overall outcomes, it is evident that LMuMOGWO demonstrates better performance and outperforms the compared algorithms, especially in maximizing the classification accuracy and reducing features. The LMuMOGWO’s exploration capabilities are expanded by integrating the newly proposed mechanisms, the search steps in Lévy, and the mutation operator. Lévy’s long jump action reduces the chance of dropping into a local optimal. In addition, the mutation operator in LMuMOGWO can reduce the risk caused by the long jumps of Lévy in case not select some informative features.

As results have demonstrated, one of the main strengths of LMuMOGWO is its promising exploration abilities compared with our previously proposed BMOG-WO-S. LMuMOGWO achieves this with the help of the Lévy flight walks that can enhance the competency of wolves to discover promising regions of the fitness basins. Results have shown the efficiency and superiority of the LMuMOGWO algorithm in solving feature selection problems. The implemented Lévy flight distribution can adapt to the exploitation and, on occasion, the exploitation. This significantly helps LMuMOGWO to jump out of local optima and find promising regions of the fitness basins. Moreover, the overall performance of LMuMOGWO is better than other algorithms, including BMOGWO-V, BMOPSO, and NSGA-II, as it can explore areas that lead to precise solutions. The two main factors that enable the features mentioned above are adaptive searching behaviors in BMOGWO-S or improved Lévy flight random walks in LMuMOGWO.

Besides, the particular characteristics of the algorithm itself, which has fewer parameters in comparison with other algorithms and its tiny memory size of having a position vector only, while MOPSO has a velocity vector and a position vector. Also, the gird mechanism implemented in the MOGWO removes the stored solution once the archive gets full and there is a superior solution to be added, unlike BMOPSO and NSGA-II, which preserve the stored solutions causing the duplicated of the solutions, which in turn leads to the rapid diversity loss that negatively contributes to the problem of the premature convergence. Nevertheless, the selection of only one solution from the attained non-dominated solution is a crucial matter. For feature selection problems, reducing the selected features and maximizing classification accuracy are two conflicting objectives were optimizing one of them may degrade the performance of the other (a trade-off issue). There are several metrics to assess the performance of multi-objective techniques. However, since our research is a feature selection based on a discrete/binary multi-objective problem, no specific measures for comparing the performance exist since almost all the metrics are intended for continuous multi-objective problems. To summarize, the results of LMuMOGWO are promising for most of the tested datasets in achieving lower classification error rates, reduction of features, and computation time.

5.5 Computational Complexity

The proposed LMuMOGWO algorithm consists of two stages: initialization and the main loop. N agents are generated in the initialization phase resulting in a computational complexity of O(ND) where D is the number of dimensions. The main loop consists of updating the archive, function evaluations, positions update, Lévy flight, and the mutation operator where their computational complexities are O(2N2), O(TC) where C is the cost of evaluation and T is the maximum number of iterations, O(TD), O(DN+CN) and O(ND), respectively. The overall computational complexity of the proposed LMuMOGWO algorithm is:

O(LMuMOGWO)=O(3ND+2N2+T(C+D)+NC)(31)

5.6 Significance Analysis

To evaluate the statistical significance of the variations in the average selected features obtained from the proposed LMuMOGOW algorithm and other optimizers, the Wilcoxon test was utilized. This analysis aims to determine the independence of the results obtained from two tests. The null hypothesis assumes that there is no significant difference between the average selected features obtained from the proposed LMuMOGWO optimizer and other optimizers. A significance level greater than 5% confirms the null hypothesis, while a significance level less than 5% rejects it. The p-values presented in Table 5 indicate that the proposed LMuMOGWO algorithm achieved significant improvement over BMOGWO-S, with a p-value of 0.00219. Moreover, the improvement achieved by LMuMOGWO was considerable in comparison to BMOGWO-V, NSGA-II, and BMOPSO. Therefore, the null hypothesis of similar average selected features at the default 5% significance level is rejected.

6  Conclusion

This work addresses the feature selection problem by proposing an enhanced binary multi-objective grey wolf optimizer. We specifically combined the Lévy flight and mutation operators and the sigmoid transfer function for feature selection search space to improve BMOGWO-S’s global search. Additionally, an Artificial Neural Network (ANN) classifier is utilized to assess non-dominated solutions. On twelve commonly used datasets with varying degrees of complexity, the proposed LMuMOGWO was assessed and compared with four multi-objective approaches, including two that were based on MOGWO and another two high-performance algorithms, BMOPSO and NSGA-II. The results show that, in most cases, LMuMOGWO successfully produced better non-dominated solutions. LMuMOGWO surpasses the existing algorithms in terms of classification accuracy and feature reduction. The study also found that LMuMOGWO can perform deep exploration that allows it to obtain a set of non-dominated solutions instead of considering the problem with only a single solution when feature selection is a problem with multiple objectives. Additionally, users can choose their preferred solutions that satisfy their needs by checking the generated Pareto front by multi-objective optimizations. Although the Pareto front of LMuMOGWO can achieve an ideal set of features, a lot of room still exists for improvement. In section 5, the experimental part analyzes the performance of different algorithms for different-size datasets and verifies the superiority of the LMuMOGWO algorithm in solving multi-objective optimization of feature selection. In future work, we can consider demonstrating the effectiveness of the LMuMOGWO algorithm proposed in this paper on data sets with a more significant number of dimensions or discussing the influence of feature correlation on classification results in data sets. In this paper, ANN is used as the evaluator of the feature subset. In future work, if different packaging schemes are considered, other classifiers can be used to evaluate the proposed LMuMOGWO method, which may have better results.

Funding Statement: This research was supported by Universiti Teknologi PETRONAS, under the Yayasan Universiti Teknologi PETRONAS (YUTP) Fundamental Research Grant Scheme (YUTP-FRG/015LC0-274). The Development of Data Quality Metrics to Assess the Quality of Big Datasets. Also, we would like to acknowledge the support by Researchers Supporting Project Number (RSP-2023/309), King Saud University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. Tang, S. Alelyani and H. Liu, “Feature selection for classification: A review,” in Data Classification: Algorithms and Applications, USA: CRC Press, pp. 37–64, 2014. [Google Scholar]

2. U. Fayyad, G. Piatetsky-Shapiro and P. Smyth, “From data mining to knowledge discovery in databases,” AI Magazine, vol. 17, no. 3, pp. 37, 1996. [Google Scholar]

3. J. Han, J. Pei and M. Kamber, Data Mining: Concepts and Techniques. 3rd ed., Netherlands: Morgan Kaufmann Publishers, Elsevier, pp. 394–441, 2011. [Google Scholar]

4. V. Kotu and B. Deshpande, Predictive Analytics and Data Mining: Concepts and Practice With Rapidminer. 1st ed., USA: Morgan Kaufmann Publishers, pp. 347–370, 2014. https://doi.org/10.1016/C2014-0-00329-2 [Google Scholar] [CrossRef]

5. L. Qu, W. He, J. Li, H. Zhang, C. Yang et al., “Explicit and size-adaptive PSO-based feature selection for classification,” Swarm and Evolutionary Computation, pp. 101249, 2023. [Google Scholar]

6. H. Pan, S. Chen and H. Xiong, “A High-dimensional feature selection method based on modified gray wolf optimization,” Applied Soft Computing, vol. 135, pp. 110031, 2023. [Google Scholar]

7. H. Liu and H. Motoda, “Feature selection for knowledge discovery and data mining,” Springer Science & Business Media, vol. 454, 2012. [Google Scholar]

8. A. L. Blum and P. Langley, “Selection of relevant features and examples in machine learning,” Artificial Intelligence, vol. 97, no. 1–2, pp. 245–271, 1997. [Google Scholar]

9. I. Guyon and A. Elisseeff, “An introduction to variable and feature selection,” Journal of Machine Learning Research, vol. 3, no. Mar, pp. 1157–1182, 2003. [Google Scholar]

10. A. Al-Ragehi, S. Jadid Abdulkadir, A. Muneer, S. Sadeq and Q. Al-Tashi, “Hyper-parameter optimization of semi-supervised gans based-sine cosine algorithm for multimedia datasets,” Computers, Materials & Continua, vol. 73, no. 1, pp. 2169–2186, 2022. [Google Scholar]

11. I. A. Gheyas and L. S. Smith, “Feature subset selection in large dimensionality domains,” Pattern Recognition, vol. 43, no. 1, pp. 5–13, 2010. [Google Scholar]

12. M. Dash and H. Liu, “Feature selection for classification,” Intelligent Data Analysis, vol. 1, no. 3, pp. 131–156, 1997. [Google Scholar]

13. B. Xue, M. Zhang, W. N. Browne and X. Yao, “A survey on evolutionary computation approaches to feature selection,” IEEE Transactions on Evolutionary Computation, vol. 20, no. 4, pp. 606–626, 2015. [Google Scholar]

14. A. W. Whitney, “A direct method of nonparametric measurement selection,” IEEE Transactions on Computers, vol. 100, no. 9, pp. 1100–1103, 1971. [Google Scholar]

15. T. Marill and D. Green, “On the effectiveness of receptors in recognition systems,” IEEE Trans Inf Theory, vol. 9, no. 1, pp. 11–17, 1963. [Google Scholar]

16. M. M. Kabir, M. Shahjahan and K. Murase, “A new local search-based hybrid genetic algorithm for feature selection,” Neurocomputing, vol. 74, no. 17, pp. 2914–2928, 2011. [Google Scholar]

17. S. Kashef and H. Nezamabadi-pour, “An advanced ACO algorithm for feature subset selection,” Neurocomputing, vol. 147, pp. 271–279, 2015. [Google Scholar]

18. R. Bello, Y. Gomez, A. Nowe and M. M. Garcia, “Two-step particle swarm optimization to solve the feature selection problem,” in Seventh Int. Conf. on Intelligent Systems Design and Applications (ISDA 2007), Rio de Janeiro, Brazil, pp. 691–696, 2007. https://doi.org/10.1109/ISDA.2007.101 [Google Scholar] [CrossRef]

19. T. M. Shami, A. A. El-Saleh, M. Alswaitti, Q. Al-Tashi, M. A. Summakieh et al., “Particle swarm optimization: A comprehensive survey,” IEEE Access, vol. 10, pp. 10031–10061, 2022. [Google Scholar]

20. E. Hancer, “Differential evolution for feature selection: A fuzzy wrapper–filter approach,” Soft Computing, vol. 23, pp. 5233–5248, 2019. [Google Scholar]

21. Q. Al-Tashi, S. Mirjalili, J. Wu, S. J. Abdulkadir, T. M. Shami et al. “Moth-flame optimization algorithm for feature selection: A review and future trends,” in Handbook of Moth-Flame Optimization Algorithm, Boca Raton: CRC Press, pp. 11–34, 2022. [Google Scholar]

22. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]

23. S. Ayub, S. M. Ayob, C. W. Tan, S. M. Arif, M. Taimoor et al., “Multi-criteria energy management with preference induced load scheduling using grey wolf optimizer,” Sustainability, vol. 15, no. 2, pp. 957, 2023. [Google Scholar]

24. R. Al-Wajih, S. J. Abdulkadir, N. Aziz, Q. Al-Tashi and N. Talpur, “Hybrid binary grey wolf with harris hawks optimizer for feature selection,” IEEE Access, vol. 9, pp. 31662–31677, 2021. [Google Scholar]

25. Q. Al-Tashi, S. J. Abdulkadir, H. M. Rais, S. Mirjalili and H. Alhussian, “Approaches to multi-objective feature selection: A systematic literature review,” IEEE Access, vol. 8, pp. 125076–125096, 2020. [Google Scholar]

26. Q. Al-Tashi, S. J. Abdulkadir, H. M. Rais, S. Mirjalili, H. Alhussian et al., “Binary multi-objective grey wolf optimizer for feature selection in classification,” IEEE Access, vol. 8, pp. 106247–106263, 2020. [Google Scholar]

27. H. Liu and Z. Zhao, “Manipulating data and dimension reduction methods: Feature selection,” in Computational Complexity: Theory, Techniques, and Applications, New York: Springer, pp. 1790–1800, 2012. [Google Scholar]

28. H. Liu, H. Motoda, R. Setiono and Z. Zhao, “Feature selection: An ever evolving frontier in data mining,” in Feature Selection in Data Mining, Hyderabad, India, PMLR, vol. 10, pp. 4–13, 2010. [Google Scholar]

29. H. Liu and L. Yu “Toward integrating feature selection algorithms for classification and clustering,” IEEE Transactions on Knowledge and Data Engineering, no. 4, pp. 491–502, 2005. [Google Scholar]

30. R. Abu Khurma, I. Aljarah, A. Sharieh, M. Abd Elaziz, R. Damaševičius et al., “A review of the modification strategies of the nature inspired algorithms for feature selection problem,” Mathematics, vol. 10, no. 3, pp. 464, 2022. [Google Scholar]

31. S. Stearns, “On selecting features for pattern recognition,” in Int. Conf. on Pattern Recognition, Coronado, California, pp. 71–75, 1976. [Google Scholar]

32. P. Pudil, J. Novovičová and J. Kittler, “Floating search methods in feature selection,” Pattern Recognition Letters, vol. 15, no. 11, pp. 1119–1125, 1994. [Google Scholar]

33. M. L. Raymer, W. F. Punch, E. D. Goodman, L. A. Kuhn and A. K. Jain, “Dimensionality reduction using genetic algorithms,” IEEE Transactions on Evolutionary Computation, vol. 4, no. 2, pp. 164–171, 2000. [Google Scholar]

34. I. S. Oh, J. S. Lee and B. R. Moon, “Hybrid genetic algorithms for feature selection,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 26, no. 11, pp. 1424–1437, 2004. https://doi.org/10.1109/TPAMI.2004.105 [Google Scholar] [PubMed] [CrossRef]

35. M. Mafarja and S. Abdullah, “Investigating memetic algorithm in solving rough set attribute reduction,” International Journal of Computer Applications in Technology, vol. 48, no. 3, pp. 195–202, 2013. [Google Scholar]

36. R. Azmi, B. Pishgoo, N. Norozi, M. Koohzadi and F. Baesi, “A hybrid GA and SA algorithms for feature selection in recognition of hand-printed Farsi characters,” in 2010 IEEE Int. Conf. on Intelligent Computing and Intelligent Systems, vol. 3, pp. 384–387, 2010. [Google Scholar]

37. P. Moradi and M. Gholampour, “A hybrid particle swarm optimization for feature subset selection by integrating a novel local search strategy,” Applied Soft Computing, vol. 43, pp. 117–130, 2016. [Google Scholar]

38. E. G. Talbi, L. Jourdan, J. Garcia-Nieto and E. Alba, “Comparison of population based metaheuristics for feature selection: Application to microarray data classification,” in 2008 IEEE/ACS Int. Conf. on Computer Systems and Applications, Doha, Qatar, pp. 45–52, 2008. https://doi.org/10.1109/AICCSA.2008.4493515 [Google Scholar] [CrossRef]

39. J. Jona and N. Nagaveni, “A hybrid swarm optimization approach for feature set reduction in digital mammograms,” WSEAS Transactions on Information Science and Applications, vol. 9, pp. 340–349, 2012. [Google Scholar]

40. M. E. Basiri and S. Nemati, “A novel hybrid ACO-GA algorithm for text feature selection,” in 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, pp. 2561–2568, 2009. https://doi.org/10.1109/CEC.2009.4983263 [Google Scholar] [CrossRef]

41. R. S. Babatunde, S. O. Olabiyisi and E. O. Omidiora, “Feature dimensionality reduction using a dual level metaheuristic algorithm,” Optimization, vol. 7, no. 1, pp. 49–52, 2014. [Google Scholar]

42. J. B. Jona and N. Nagaveni, “Ant-cuckoo colony optimization for feature selection in digital mammogram,” Pakistan Journal of Biological Sciences, vol. 17, no. 2, pp. 266, 2014. [Google Scholar] [PubMed]

43. E. Zorarpac and S. A. Özel, “A hybrid approach of differential evolution and artificial bee colony for feature selection,” Expert Systems with Applications, vol. 62, pp. 91–103, 2016. [Google Scholar]

44. M. Nekkaa and D. Boughaci, “Hybrid harmony search combined with stochastic local search for feature selection,” Neural Processing Letters, vol. 44, no. 1, pp. 199–220, 2016. [Google Scholar]

45. M. M. Mafarja and S. Mirjalili, “Hybrid whale optimization algorithm with simulated annealing for feature selection,” Neurocomputing, vol. 260, pp. 302–312, 2017. [Google Scholar]

46. H. M. Zawbaa, E. Emary, C. Grosan and V. Snasel, “Large-dimensionality small-instance set feature selection: A hybrid bio-inspired heuristic approach,” Swarm and Evolutionary Computation, vol. 42, pp. 29–42, 2018. [Google Scholar]

47. R. Alwajih, S. J. Abdulkadir, H. Alhussian, N. Aziz, Q. Al-Tashi et al., “Hybrid binary whale with harris hawks for feature selection,” Neural Computing and Applications, vol. 34, no. 21, pp. 19377–19395, 2022. [Google Scholar]

48. Z. Yong, D. W. Gong and W. Q. Zhang, “Feature selection of unreliable data using an improved multi-objective PSO algorithm,” Neurocomputing, vol. 171, pp. 1281–1290, 2016. [Google Scholar]

49. P. Sharma, S. Sundaram, M. Sharma, A. Sharma and D. Gupta, “Diagnosis of Parkinson’s disease using modified grey wolf optimization,” Cognitive Systems Research, vol. 54, pp. 100–115, 2019. [Google Scholar]

50. R. R. Rajalaxmi and S. Kaavya, “Feature selection for identifying Parkinson’s disease using binary grey wolf optimization,” in Int. Conf. on Intelligent Computing Systems (ICICS), Tamilnadu, India, pp. 11, 2017. [Google Scholar]

51. N. P. N. Sreedharan, B. Ganesan, R. Raveendran, P. Sarala, B. Dennis et al., “Grey wolf optimization-based feature selection and classification for facial emotion recognition,” IET Biometrics, vol. 7, no. 5, pp. 490–499, 2018. [Google Scholar]

52. A. L. Abd, T. El-Hafeez and A. M. Zaki, “Face recognition based on grey wolf optimization for feature selection,” in Int. Conf. on Advanced Intelligent Systems and Informatics, Cairo, Egypt, pp. 273–283, 2018. [Google Scholar]

53. J. Too, A. Abdullah, N. Mohd Saad, N. Mohd Ali and W. Tee, “A new competitive binary grey wolf optimizer to solve the feature selection problem in emg signals classification,” Computers, vol. 7, no. 4, pp. 58, 2018. [Google Scholar]

54. X. Zhao, X. Zhang, Z. Cai, X. Tian, X. Wang et al., “Chaos enhanced grey wolf optimization wrapped ELM for diagnosis of paraquat-poisoned patients,” Computational Biology and Chemistry, vol. 78, pp. 481–490, 2019. [Google Scholar] [PubMed]

55. Q. Li, H. Chen, H. Huang, X. Zhao, Z. Cai et al., “An enhanced grey wolf optimization based feature selection wrapped kernel extreme learning machine for medical diagnosis,” Computational and Mathematical Methods in Medicine, vol. 2017, 2017. [Google Scholar]

56. Q. M. Alzubi, M. Anbar, Z. N. M. Alqattan, M. A. Al-Betar and R. Abdullah, “Intrusion detection system based on a modified binary grey wolf optimisation,” Neural Computing and Applications, vol. 32, pp. 1–13, 2020. [Google Scholar]

57. E. M. Devi and R. C. Suganthe, “Feature selection in intrusion detection grey wolf optimizer,” Asian Journal of Research in Social Sciences and Humanities, vol. 7, no. 3, pp. 671–682, 2017. [Google Scholar]

58. T. M. Hamdani, J. M. Won, A. M. Alimi and F. Karray, “Multi-objective feature selection with NSGA II,” in Adaptive and Natural Computing Algorithms: 8th Int. Conf., Berlin, Heidelberg, Springer, pp. 240–247, 2007. [Google Scholar]

59. B. Xue, M. Zhang and W. N. Browne, “Multi-objective particle swarm optimization (PSO) for feature selection,” in 14th Annual Conf. on Genetic and Evolutionary Computation (GECCO), Philadelphia Pennsylvania, USA, pp. 81–88, 2012. [Google Scholar]

60. B. Xue, L. Cervante, L. Shang, W. N. Browne and M. Zhang, “Binary PSO and rough set theory for feature selection: A multi-objective filter based approach,” International Journal of Computational Intelligence and Applications, vol. 13, no. 2, pp. 1450009, 2014. [Google Scholar]

61. B. Xue, L. Cervante, L. Shang, W. N. Browne and M. Zhang, “Multi-objective evolutionary algorithms for filter based feature selection in classification,” International Journal on Artificial Intelligence Tools, vol. 22, no. 4, pp. 1350024, 2013. [Google Scholar]

62. P. Dhal and C. Azad, “A Multi-objective feature selection method using Newton’s law based PSO with GWO,” Applied Soft Computing, vol. 107, pp. 107394, 2021. [Google Scholar]

63. I. Aljarah, H. Faris, A. A. Heidari, M. M. Mafarja, A. Z. Ala’M et al., “A robust multi-objective feature selection model based on local neighborhood multi-verse optimization,” IEEE Access, vol. 9, pp. 100009–100028, 2021. [Google Scholar]

64. F. Han, W. T. Chen, Q. H. Ling and H. Han, “Multi-objective particle swarm optimization with adaptive strategies for feature selection,” Swarm and Evolutionary Computation, vol. 62, pp. 100847, 2021. [Google Scholar]

65. A. Rashno, M. Shafipour and S. Fadaei, “Particle ranking: An efficient method for multi-objective particle swarm optimization feature selection,” Knowledge-Based Systems, vol. 245, pp. 108640, 2022. [Google Scholar]

66. B. Abdollahzadeh and F. S. Gharehchopogh, “A Multi-objective optimization algorithm for feature selection problems,” Engineering with computers, vol. 38, no. 3, pp. 1845–1863, 2022. [Google Scholar]

67. B. Nouri-Moghaddam, M. Ghazanfari and M. Fathian, “A novel multi-objective forest optimization algorithm for wrapper feature selection,” Expert Systems with Applications, vol. 175, pp. 114737, 2021. [Google Scholar]

68. Y. Zhang, G. G. Wang, K. Li, W. C. Yeh, M. Jian et al., “Enhancing MOEA/D with information feedback models for large-scale many-objective optimization,” Information Sciences, vol. 522, pp. 1–16, 2020. [Google Scholar]

69. Z. M. Gu and G. G. Wang, “Improving NSGA-III algorithms with information feedback models for large-scale many-objective optimization,” Future Generation Computer Systems, vol. 107, pp. 49–69, 2020. [Google Scholar]

70. S. Mirjalili, S. Saremi, S. M. Mirjalili and L. dos S. Coelho, “Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization,” Expert Systems with Applications, vol. 47, pp. 106–119, 2016. [Google Scholar]

71. R. Jensi and G. W. Jiji, “An enhanced particle swarm optimization with Lévy flight for global optimization,” Applied Soft Computing, vol. 43, pp. 248–261, 2016. [Google Scholar]

72. W. A. Hussein, S. Sahran and S. N. H. S. Abdullah, “Patch-lévy-based initialization algorithm for bees algorithm,” Applied Soft Computing, vol. 23, pp. 104–121, 2014. [Google Scholar]

73. A. Sahoo and S. Chandra, “Multi-objective grey wolf optimizer for improved cervix lesion classification,” Applied Soft Computing, vol. 52, pp. 64–80, 2017. [Google Scholar]

74. K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Transactions on Evolutionary Computation, vol. 6, no. 2, pp. 182–197, 2002. [Google Scholar]

75. C. L. Blake, “CJ Merz UCI repository of machine learning databases,” University of California, Irvine, CA. [Online]. Available: http://www.ics.uci.edu/mlearn/MLRepository.html, 1998. [Google Scholar]

76. Y. C. Ho and D. L. Pepyne, “Simple explanation of the no-free-lunch theorem and its implications,” Journal of Optimization Theory and Applications, vol. 115, no. 3, pp. 549–570, 2002. [Google Scholar]