A Multi-Stream Scrambling and DNA Encoding Method Based Image Encryption

1  Introduction

In the past few years, there has been a huge change in how information is shared around the world. Online communication (through a variety of platforms) has slowly become an important way to share information and keeping data safe has become one of the most important issues [1]. Due to how open and shared network transmission is, people are paying more attention to the security of multimedia information communication. This is especially true for digital images from the military, medicine, and other fields that contain sensitive information. Both the field of computer security and the field of communication security rely heavily on the use of encryption and data concealment as their primary methodologies. Methods that make use of encryption and data concealment are investigated with the purpose of enhancing individual privacy [2]. Data hiding is an efficient method for covert communication. The goal of data hiding is to conceal covert data within a cover medium in such a way that the intruder will be unaware of the data’s existence [3]. However, image encryption refers to the process of applying an algorithm to change the information contained inside an image such that it is unintelligible to unauthorized people. Thus, making a secure digital image encryption algorithm is a very important area of research [4]. By turning plaintexts into codes that cannot be recognizable, cryptography is a key part of keeping data communication secure. Conventional cryptography, which relies excessively on mathematical calculations that are hard to do on a computer, is becoming more likely to have its encryption broken as the capability of computers rises. Thus, much research has been done on new ways to encrypt data [5]. However, most text-based cryptography systems, like the Data Encryption Standard (DES) and the Advanced Encryption Standard (AES), are not good for encrypting images. This is because digital images have a huge amount of data, the correlation between adjacent pixels is very strong, and a lot of redundancy [6,7].

Image encryption can be done in different ways, such as by permuting, substituting, shuffling, confusing, and diffusing. Diffusion is a very common operation due to its easy implementation and the good results it produces. The purpose of diffusion is to change the pixel’s value in an image [8,9]. Image encryption method-based confusion and diffusion is the classic structure, which depends on a chaotic system. Thus, image encryption is mostly made up of two phases: confusion and diffusion. During the confusion phase, the pixels’ positions are changed, and during the diffusion phase, the pixel values are changed, and the pixels move around each other. When confusion and diffusion are used together, they can make encryption systems safer. Some cryptosystems can still be broken, though. The reason is that when algorithms are made, the performance of chaos dynamics is not taken into account as much as it should be. For a chaos-based encryption method, how well it works and how safe it is are mostly determined by how the structure of the encryption is built and how well chaotic maps work [10,11]. DNA computing is another technology that has been utilized in the security field due to its significant parallelism, massive storage, and use of very low-power DNA computation. Using DNA sequences and DNA computing to encrypt images has become a popular area of study [12]. The information in a DNA-encrypted code is carried by DNA, and modern biological techniques are used to encrypt it. DNA encoding is not a safe way to encrypt and protect images. DNA encryption technology can be used to encrypt information required in a complicated biological experiment, which increases the cost of information encryption [13]. Therefore, we proposed an image encryption method-based confusion-diffusion phases, and the diffusion phase-based DNA computing method has been proposed. Moreover, we combined DNA encoding with chaotic maps to make image encryption algorithms work better and be more secure. When chaotic maps and DNA computing are used together, the effect of encryption can be improved, and the cost of the experiment can be saved. Currently, DNA coding, DNA (XOR), DNA addition, and DNA subtraction have become more important to image encryption. The main contributions of this work are highlighted:

•   Proposed a confusion method based on multi-stream scrambling, the plain image has been separated into four major blocks during the confusion stage. A 2 × 128 block is extracted from each of the primary blocks to perform the scrambling operation. The confusion method applies a multi-stream scrambling algorithm to the plain image based on several iterations.

•   Proposed a diffusion method based on DNA coding rules. For the diffusion to work, two chaotic sequences are generated by using the Chen’s mapping and Logistic Map on the sequence value received from the confusion image. The image encryption is completed by performing a DNA XOR operation on the DNA molecules between the confused DNA and the obtained key matrix from Chen’s map. Reverse DNA Complementary Rule and XOR operations are presented in this work to perform the diffusion process.

2  Related Work

Previous algorithms can be classified into two groups based on the features of the scrambling algorithm. The first group is to keep unchanged the size of the original image. Some researchers changed the plain image by extending the Arnold map. In particular, the initial values based on the chaotic map are the coordinates of the pixels. The new locations of the pixels are found by repeating the chaotic system. According to [14] used plaintext information to generate the parameters of the extended Arnold map and change the diffusion operation. The main drawback of this algorithm was weak scrambling. Another study by [15] developed a new cryptosystem based on the operation of a circular shift in which the sequence of pseudo-random controls the size of each step. Even though this scheme is very good at encrypting information, it needs to be made more confusing to improve the effect of scrambling. Also, this study by [16] developed a new algorithm based on a chaotic method with confusing pixel values dynamically, pixel bits, as well as a binary bits-based encryption method. Another study by [17] introduced a chaotic double-ring fractional-order erbium-doped fiber laser system. The diffusion phase of this work was utilized to ameliorate a model of universal gravitation, and the Zigzag method was used to scramble the pixels. Fractional-order laser chaotic systems, on the other hand, are used to make order systems and safe and efficient method-based image encryption. In contrast, the other group is that by decomposing the plain image into varying sizes, then it can be scrambled. According to [18] put together a logistic map and a 3D discrete Lorenz map to make a 5D discrete hyperchaotic map. A block-based image encryption algorithm depends on the plain image made from this chaotic system. Scrambling and diffusion are two main parts of the encryption algorithm. A new study by [19] developed a better Josephus ring scrambling method with a variable step size based on the value of each pixel of the original plain image. The robustness of the method was weak against noise attacks and much time was needed to encrypt data. A new method by [20] proposed an algorithm for image encryption depending on the rotation of a bit-plane matrix rotation with two hyperchaotic systems. First, the algorithm breaks the original plain image into eight-bit planes and builds a 3D matrix. Then, a hyper-chaotic system uses PRNS to turn the sub-matrix of the 3D bit-plane matrix in various directions. Furthermore, reference [21] introduced an ameliorated 2D-logistic-adjusted-Sine map. The image scrambling was performed on the bit level, so the scrambling scale can be made larger, and the pixels can be spread out in different ways.

Reference [22] used a modified logistic chaos system with a bit plane to introduce an image encryption method. First, the digital image is scrambled globally. Then, the scrambled image is divided into 4 high-bit planes and 4 low-bit planes. The major drawback of this approach is that the pixel diffusion does not implement on the four lower planes of the image, and there is an assured security risk. The work of [23] introduced a new encryption algorithm that uses a hybrid chaotic shift transform and a modified Henon map. The first operation of this algorithm was to scramble the original plain image. Then, two rounds of diffusion operations were implemented. However, the algorithm’s equivalent key stream is not based on the plain image to be encrypted. This means that a selected-plain image attack can be used to break the equivalent key. A new study by [24] developed a method called Improved Josephus ring-based permutation (IJRBP). This algorithm can offer more good scrambling effects with better efficient permutations compared to many algorithm-based scrambling. In the last few years, it has been found that DNA computing has properties like a huge amount of parallelism, a higher information density, and very low power consumption. Many algorithms for image encryption have been developed based on integrating chaos and DNA computing. Based on this study by [25] introduced a method to encrypt color images based on a hyperchaotic system and a DNA computing concept. The idea of blocking is used as a model for image encryption. Each block picks a DNA coding rule at random. Also, another study by [26] proposed a new way to encrypt images using the chaos system and DNA computing. Both security and encryption effects were ameliorated based on utilizing randomly selected DNA coding rules and low-dimensional chaotic maps. The study in [27] proposed a new algorithm for encrypting color images that are based on how DNA sequences work and a hyperchaotic system. Another study by [28] put forward a way to encrypt images based on chaotic attractors. This algorithm utilizes the integer wavelet transform in the frequency domain and the DNA sequence in the spatial domain to encrypt the image. The study in [29] introduced an image encryption method depending on a matrix of Kronecker products and DNA computing over finite areas. Another study by [11] built a 5D continuous hyperchaotic system. This method used a mechanism based on dynamic DNA coding and a conventional structure scrambling diffusion encryption. The study of [30] came up with an idea for an image encryption method. It was based on a chaotic system with a hidden attractor and a shuffling method.

Examining some of the image encryption techniques described above that are based on scrambling reveals that these algorithms have the following security flaws. The majority of the algorithms that they proposed are conventional scrambling and diffusion-mode techniques. The original plain image is first scrambled, and after that, to change the value of pixels, it is diffused. Because of this, the image needs to be processed in two processes to produce the desired result; also, the level of safety performance is diminished. Moreover, some developed techniques are insufficient to withstand chosen-plain image assaults and are insensitive to tiny variations in the original image. For example, certain encryption approaches have been broken in recent years [14,31,32]. In addition, some research has shown that implementing permutation processes takes a significant amount of time. Particularly the permutation algorithms that involve the generation of large random sequences by sorting and comparing operations. In contrast, using the same previous parameters that have been used in chaotic maps for some image encryption techniques-based DNA. Image encryption is neither secure enough to use simple methods-based confusion and diffusion. It is not secure enough to use an image encryption technique in which the key streams are independent of the original plain images [11,28,29]. In addition to this, a number of limitations have been identified in some of the earlier works. One can acquire the keys by examining a set of images consisting of plain images and encrypted images that correspond to each other. The encryption method is not sensitive enough to any modifications made to the plain images or the keys. As a consequence of this, it has been demonstrated that certain algorithms are not secure because of some drawbacks: employing the same key stream in confusion and diffusion during the encrypting of various original images. This results in a reduced key space, which is considered one of the image encryption drawbacks. Lower sensitivity to the plain image is another issue that encryption techniques suffer from.

3  The Proposed Encryption Algorithm

This work proposed an image encryption approach based on confusion-diffusion techniques. The algorithm uses different key streams based on different chaotic systems, namely, Chen’s map and the logistic map. Based on that, three-dimensional and one-dimensional hyperchaotic systems are used in this study. Then, confusion-diffusion phases are built based on scrambling and DNA computing. In the confusion phase, a multi-stream scrambling method is presented to confuse the original plain image using two different generated chaotic sequences. Then, the confused image is diffused based on the DNA concept and an XOR operation using two different generated chaotic sequences. Finally, based on confusing and diffusing the plain image, the encrypted image is obtained. The encryption approach in this study not only encrypts the plain image securely but also ensures the excellent performance of the proposed encryption algorithm. This section presents the related materials and details of the proposed algorithm.

This section describes the proposed image encryption algorithm. Confusion and diffusion are the two main phases of the proposed algorithm. The encryption algorithm consists of two stages: encryption at the stream pixel scrambling level and encryption at the block scrambling level. The Chen’s chaotic map is employed to conduct stream pixel scrambling and block scrambling. The confusion stage selects an appropriate window size of M × N where several subblocks are generated from the plain image. Then, in each round of the stream pixel scrambling process, every four blocks were handled until the complete blocks were chosen to encrypt the plain image. After this step, the confusion stage continued and was followed by the block scrambling process to destroy the correlations of adjacent pixels. At the phase of diffusion, the diversity of DNA is leveraged for further image encryption. At this stage, the concept of DNA encoding has been used to develop the encryption method based on complementary rules and the exclusive or (XOR) method. A random key-based Chen’s map and another based on a Logistic map are employed to perform this phase of encryption. As a result, this study developed confusion-diffusion phases using different key generations. The configuration of the primary concept of the proposed algorithm is depicted in Fig. 1, which depicts a traditional two-staged cryptosystem.

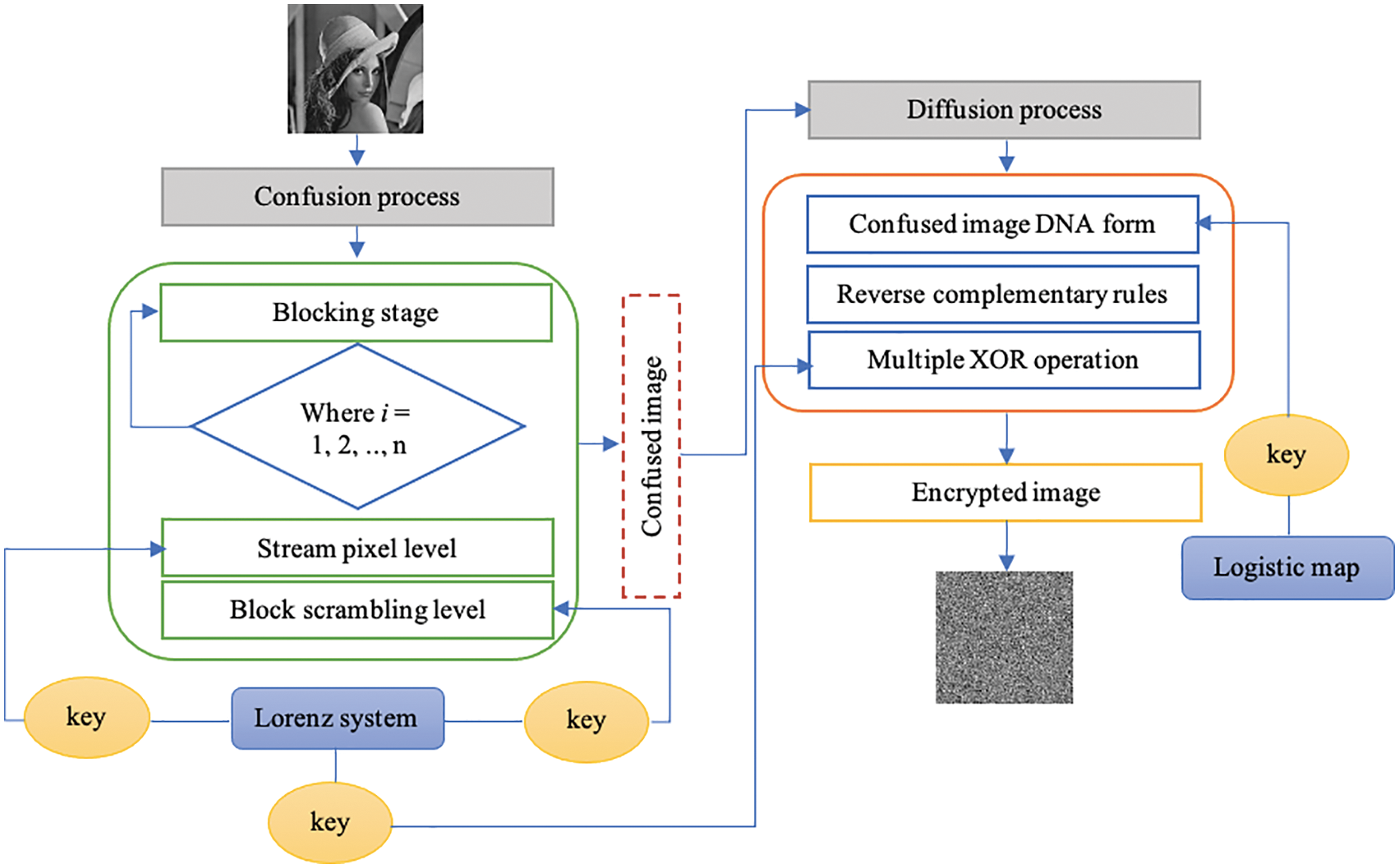
Figure 1: Proposed block diagram-based encryption method

Figure 2: Chen’s chaotic map graph

3.1 Key Generation

While researching chaotic feedback control in 1999, Chen’s chaotic system has been discovered as a system that had dynamic characteristics and was complicated. The equation that represents the mathematical model of Chen’s chaotic system is as follows [33]:

{x˙=a(y−x)y˙=(c−a)x−xz+cy,z˙=xy−bz(1)

where the parameters of Chen’s chaotic system have been denoted as a, b, and c. These parameters are stated as a = 35, b = 3, and c = 28. The 4-order Runge–Kutta is employed to compute Eq. (3). Chen’s chaotic system sets the initial value for parameters (x, y, and z) as (0.1, 0.2, and 0.3), respectively.

A common and reasonably straightforward one-dimensional discrete chaotic map called a logistic map is defined as Eq. (2) [19]. Where the branching parameter is represented by μ, and xn∈ (0, 1).

xn+1=μxn(1−xn)(2)

3.2 Confusion Stage

The significant degree of correlation that exists between neighboring pixels is one of the most crucial aspects of an image. Thus, the main goal of the confusion stage is to break the connection between pixels next to each other by moving them horizontally and vertically. However, if all the connections between pixels in a plain image have to be broken, a large matrix of new positions has to be constructed, and this takes a lot of computing time and resources. During the confusion process, the location of each image pixel will change to break the relationship between the plain image and the encrypted image. By using the confusion process, it seems like the key is not just related to the cipher image. Each pixel in the encrypted image should depend on a different part of the key. The confusion method is made up of two main parts: the generation of dynamic keys and the process of confusing plain images. The first step is called the image stream pixel, and its purpose is to reorder the image’s pixels by shuffling them and severing their connections with their neighbors. Alternatively, this process can dissolve the correlation that exists between neighboring plain image pixels. This process consists of two different subprocesses, which are referred to respectively as initial dynamic key generation and pixel streaming. Utilizing Chen’s map, the dynamic key is constructed. In the first step, the original plain image of size M × N is divided into four main blocks of the same size. Then, an appropriate window size has been selected from each main block for the stream pixel process. Fig. 3 shows the mechanism of plain image blocking and stream pixel scrambling. Then, to perform the stream pixel process and to increase the level of security, one block is taken by size 128 × 2 from each main block in different directions. In the first round, blocks are taken from B1 at position [1, 1], B2 at position [1, 256], B3 at position [129, 127], and B4 at position [129, 129]. Based on this mechanism, the directions of taking blocks are different where the direction of B1 and B4 is from left to right, whereas the direction of B2 and B3 is from right to left. This mechanism will continue until it selects the whole pixels of the plain image. Moreover, in each round, the size of blocks will be larger because taking blocks depends on Eq. (3). Thus, based on this equation, the size of each block is (128 × 2) because i is 1, while when i is 2, the size of each block is considered 128 × 4 until i equal to 7, at which point it is considered 128 × 128 of each block.

BS=(M2)∗2i(3)

where BS denotes block selection and the size of the image is represented by M, which is equal to 256. The range of i starts from 1 to 7. Here, the size of each is represented by 128 × 128 after the blocking process.

Figure 3: Mechanism of blocking process: (a) plain image; (b) blocks of plain image; (c) create sub-blocks from each block; (d) combination of sub-blocks to array 2-d; (e) convert 2-d to the 1-d array

The process of streaming pixels is continued by combining selected blocks to generate a matrix with a size of 128 × 8. Then, the matrix is converted into a one-dimensional array with a size of 1028 when i equals 1. After converting the selected blocks into a one-dimensional array, they have been sorted using a dynamic key generated by Chen’s system. The process of sorting pixel values can help to perform the stream of pixels in a plain image. Then, the one-dimensional array is reshaped to generate four blocks with a size of 128 × 2. At this level, the newly generated blocks are changed to the selected blocks in the plain image. As has been mentioned before, this process will continue until we select the whole plain image-based blocking mechanism. The schematic diagram of the stream pixel-level process-based sorting and reshaping is demonstrated in Fig. 4.

Figure 4: Stream pixel process: (a) array 1-d; (b) confusion key to sort array 1-d; (c) array 1-d after sorting; (d) reshape sub-blocks; (e) replaced the old sub-blocks with new sub-blocks; (f) generate a confused image

Scrambling is the procedure of rearranging the pixels of an image by changing the digital image in a certain way. Based on an analysis of the effects of the scrambling process, the conventional scrambling encryption algorithm is not secure enough. It is more secure when combined with other methods to make hybrid encryption. In this paper, another scrambling process has been performed to make a hybrid scrambling process. The scrambled image from the previous stage was chosen to carry out the block scrambling process based on a dynamic random key that was generated using Chen’s chaotic map. In the previous operation, the plain image, which has a dimension of 256 × 256, is segregated into four main subblocks. The dimension of each subblock is considered 128 × 128. Subsequently, each is defused using the previous process. The defused sub-blocks are obtained after several iterations, where defusing sub-blocks is performed in different iterations. Due to taking further sub-blocks with 128 × 2 in the first iteration, a 128 × 8 matrix is generated and defused. At the second iteration in each sub-block, another sub-block of size 128 × 4 is taken. Thus, in this way, the defused sub-blocks in the first iteration are defused one more time in the second iteration. Furthermore, the number of iterations that have been performed on the defused image for the scrambling process is different, and the obtained scrambled image at each iteration is also different. Because we follow Eq. (1) for taking sub-blocks of the plain image, the selected iteration number in this work is seven times until i equal to 7. The process of scrambling begins after obtaining a defused one-dimensional array and creating a two-dimensional array. The next step is converting the two-dimensional array into four subblocks of the same size as the selected subblocks, which is called the reshaping process. Although the transformation process-based stream pixel scrambling and image reshaping are performed. The correlations between successive elements in the new scrambled image are still not enough. To minimize the correlation, the image pixels are scrambled using the block scrambling process to change the location of pixels in the scrambled image at the previous stage to a new location. Another dynamic random key generated by Chen’s chaotic system is employed to perform this stage of scrambling. The same as the stream pixel scrambling process, the block scrambling process will continue for 7 iterations. In each iteration, a larger image sub-block can be generated and scrambled. Thus, the scrambling process is performed at different times for each sub-block. This process can reduce the correlation between adjacent pixels significantly. To obtain the scrambled image, a confusion process is employed to convert the plain image after hybrid scrambling. However, some performance aspects such as information entropy as well as histogram are still not ensured enough. The encrypted image at this level is still considered intermediate encryption. Fig. 5 shows the process of scrambling image subblocks.

Figure 5: Block scrambling process

When the confusion part is implemented, the pixels next to each other in the image will have less of a link to each other. Because their positions will be changed randomly, which minimizes the correlation between the adjacent pixels. On the other hand, the histogram of the scrambled image will still be the same as the histogram of the original image since the pixel values have not changed. At this level, the only thing that change is the position of the pixel. Thus, the diffusion phase is another process of the proposed algorithm to change the value of pixels.

3.3 Diffusion Stage

To build a robust encryption algorithm with the robust performance of histogram and information entropy, the diffusion encryption method to encrypt the confusing image is performed. The diffusion is applied to the confused image, which is obtained in Sub-Section 3.2. The diffusion process exploits the DNA computing concept to encrypt the image. This process means that the pixel values in an image can be changed in an adequate manner. This helps in diffusing the frequencies of the confused image through many pixel values of the encrypted image (diffused image). To obtain an encrypted image with no statistical features, for example, histogram or information entropy. To produce a meaningful statistical attack, significantly more encrypted images are required. A diffusion process was used to randomly alter pixel values. Chen’s chaotic and logistic maps are used to generate diffuse dynamic random keys. In this study, DNA coding rules are used to convert confusing images into DNA. Then, reverse DNA complementary rules are applied to the confusing image to perform the first level of the diffusion process. An XOR operator between the new form of DNA after reverse complementary rules and the diffusion random key was used to diffuse the image. Fig. 6 illustrates the proposed diffusion process of this work.

Figure 6: The mechanism of the diffusion process

3.3.1 DNA Encoding Rules

DNA computing is a type of parallel computing system that was invented by Leonard Adleman. In DNA computing, four nucleic acids are used to express the information, which is referred to as adenine (A), cytosine (C), guanine (G), and thymine (T) [34]. Adenine and thymine are paired together, while cytosine and guanine are also paired together due to the complementary nature of their properties [12]. The principles for encoding and decoding, as well as algebraic processes for DNA sequences, are the most important aspects of DNA when it comes to encryption. In DNA computing, complementary pairs include 00 (0) and 11 (3), as well as 01 (1) and 10 (2). This is analogous to the way that 0 and 1 are complementary pairs in binary. Adenine and thymine, as defined by the Watson–Crick base pairing, are considered to be complementary pairs. Cytosine and guanine are also considered to be complementary pairs. As a result, this complimentary rule can be satisfied by a total of eight different types of encoding modes; the specifics are presented in Table 1. Each of the nucleic acid bases can store an encoding for every two bits of information. For instance, if we use rule 1, which is presented in Table 1, then the characters ‘00,’ ‘11,’ ‘10,’ and ‘01,’ respectively, can be encoded into the letters ‘C,’ ‘G,’ ‘A,’ and ‘T’. As a result, an M × N grayscale image with 8 bits of resolution can be represented as a nucleotide string with a length of 4MN [35].

Assume that a pixel value in a confusing image is 78 in decimal and that its binary representation is (78)10 = (01001110)2. Then, it is DNA coding was performed according to mode 7, and the sequence “GTAC” was obtained. After that, when we convert the obtained sequence based on another mode, for example, mode 2, (10001101)2 = (141)10 can be obtained. It is clear that by encoding and decoding DNA in its most basic form, a value can be altered dramatically, which results in an improved level of security for digital images.

3.3.2 Reverse DNA Complementary Rule

There are two ways to encrypt an image based on DNA sequence complement, which is the complementary method based on a single base and the method that utilizes the biotechnology principle of matching single bases and double bases to implement the complementary process. This study uses the first complementary rule, which is described in Table 2:

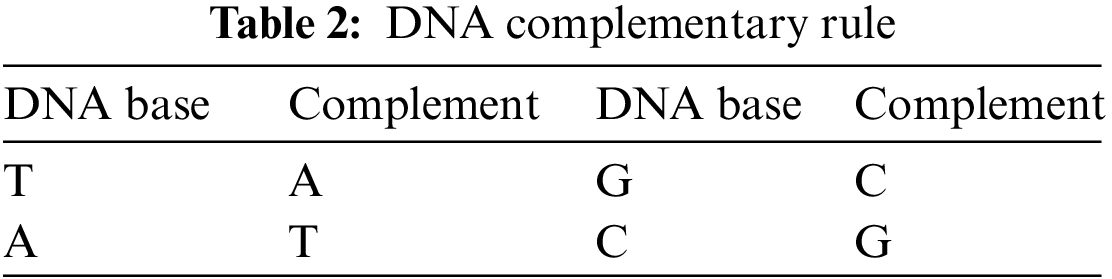
DNA bases (A and T) are complemented pairs whereas (C and G) are other complement pairs. The corresponding binary complement is satisfied when both the complement of 00 is 11 and that of 01 is 10, and vice versa. This study used the idea of single complementary rules after encoding the confusing image to DNA form. Where the T base is converted to A and that G is converted to C, and vice versa. In addition, to increase the security level and to change the pixel values significantly, an inverse complementary method is performed. For example, after obtaining the GTCA sequence from the value of (210)10 using mode 1, this sequence is converted to CAGT and then reversed as TGAC. Thus, instead of obtaining (11010010)2 of binary sequence from (210)10 0r (120)10 = (01111000)2. The value is changed more than one time by obtaining (45)10 = (00101101)2. Thus, this process changes the values from 210 to 120 and then finally to 45.

3.3.3 DNA XOR Operation

The rule that the DNA procedure is premised on is that every two binary values equal one DNA base. There are eight qualified ways to code DNA, and each way has a set of algorithms. This means that each common method is the same as one of eight different DNA algorithms. Table 3 shows how to use the DNA exclusive OR (XOR) operation, which is set by DNA encoding mode 0. The sequence of GTTC can be obtained when the XOR operation is performed between the TTCG and CAGT sequences.

To perform the DNA XOR operation, this study generates a dynamic random key using the Chen’s chaotic system, denoted as K. The size of the generated key should be the same as the size of the image size that is obtained from the reverse complementary rule, denoted as DNArc. Then, the generated key is converted into DNA based on Table 1. After that, another key is constructed from the reverse of K and is denoted as RK. The XOR operation has been performed three times to obtain the final encrypted image. DNArc is XORed with both keys to obtain DNArc1 and DNArc2 as the first and second XOR operations. Finally, both of them are XORed to obtain the final encrypted image.

4  Experimental Results

In this section, the performance and simulation findings were presented, along with presenting comparisons with recently proposed image encryption techniques. MATLAB R2018a software was used to perform manipulations on the experimental to assess the performance of the proposed algorithm. The memory for installation is 8 GB, and the operating system is Windows 10; the CPU is an Intel(R) Core (TM) i7-1065G7 running at 1.50 GHz. Several standard images have been utilized to assess the performance of the proposed algorithm using different tests. Fig. 7 depicts the original Lena with the corresponding encrypted and decrypted Lena. When looking at the encrypted Lena, it can be observed that the encrypted image is an unarranged image that does not reveal any clear information. This is because the clear text information is being hidden by destroying the relationship between adjacent pixels. There is no relation between the Lena that was originally taken and the Lena that was encrypted. The encryption and decryption capabilities of the proposed algorithm are demonstrated to be satisfactory by the findings. This section analyzes the security of the proposed algorithm. In this part of the article, the proposed algorithm will be examined for its level of safety. Several tests and various kinds of security analyses can be used to figure out how robust the proposed encryption algorithm is.

Figure 7: Simulate the result of the proposed method for Lena image: (a) original image; (b) encrypted image; (c) decrypted image

In this study, to validate and ensure the robustness of our proposed algorithm, we used nine standard images that are available publicly. Used images are listed in Table 4. These images are examined through several experiments. Analysis of the key space, analysis of the key sensitivity, analysis of the histogram, analysis of the correlation coefficient between adjacent pixels, analysis of the information entropy, and analysis of differential cryptanalysis are all included in this part of the evaluation.

4.1 Security Key Analysis

A workable image encryption method is necessary to possess a key space that is big enough as well as a key that is sensitive enough to be able to withstand brute force attacks. The analysis of the key space and the security key-based sensitivity has been conducted in this subsection.

4.1.1 Key Space

The key space is a representation of the total number of possible combinations that could be used for the security key. A brute-force assault is one of the most prevalent types of cyberattacks. In this type of attack, an adversary attempts to guess the correct security key by exhaustively scanning the key space of an encryption algorithm. Therefore, to protect the algorithm from an assault using brute force, having a key space that is sufficiently large is one of the primary criteria that can guarantee higher safety [36]. In an image encryption algorithm, the key space is the collection of all of the employed secret keys that can be utilized to decrypt images. It has been observed that a key space with a size of more than 2100 can give an adequate level of security [9]. In this study, the key space is computed as X = Y = Z = X’ = 1015. This contributes to (246.51)4 possible guesses of the value x. This applies to y, z, and X’ as well. Thus, there are 2186 possible values of x, y, z from Chen’s system at the stage of confusion, while (X’ = 1015) from Chen’s system is used in the diffusion process. As a result, the proposed algorithm is capable of withstanding any kind of brute-force assault. Table 5 presents a comparison of the results obtained by using various techniques to analyze key space.

4.1.2 Key Sensitivity

An ideal method for encrypting images ought to be sensitive enough to the security key. This means that even a slight variation in the security keys should provide a completely different result when the image is decrypted. The degree of secrecy that may be maintained by a key is an essential component of any reliable encryption method. This means that even a small shift in the key would result in a very noticeable shift in the output, and this phenomenon can be analyzed using two different aspects. First, during the process of encrypting an image if the same image is encrypted with a key that is even slightly various than the original key, a completely various encrypted image will be produced. Second, during the process of encrypting an image, if ever there is the smallest variance exists between both keys of encryption and decryption, the encrypted image cannot be successfully decrypted. The initial condition and parameter with 1015 are particularly important considerations for double chaotic maps due to their high degree of sensitivity. To begin, a key sensitivity test is performed by encrypting the same images using a key that is only marginally distinct from the initial key which determines how sensitive the key is.

The first row from (1) in Fig. 8 shows the original plain images, the second row from (1) displays the encrypted images, the first row from (2) displays the decrypted images utilizing the incorrect key, and the second row from (2) shows the decrypted images utilizing the correct key. Whenever the error rate of a single key approaches the order of 10−15 or 10−10, it is impossible to achieve the plain image. Moreover, if even a single key from the multiple keys is changed, the plain image will no longer be decryptable. Thus, it is clear that even a relatively minor change can have a significant impact.

Figure 8: The results of key sensitivity-based image encryption

4.2 Statistical Analysis

The development of a cryptosystem requires extensive statistical analysis such as histogram analysis, entropy analysis, and correlation analysis. The perfect algorithm for encrypting images should be able to defend against several types of statistical assaults.

4.2.1 Histogram Analysis

The histogram in grayscale is easier to understand and has good visibility. It is possible to deduce from the figure, the probability of occurrence of the gray value as well as its frequency. The effect of encryption is improved when the histogram is more evenly distributed. The histogram of gray levels displays each possible level of gray as well as the frequency with which that level of gray occurs [43].

Fig. 9 makes it clear that the histograms of the original plain image have both peaks and valleys in their distributions. The histograms of their associated encrypted images, on the other hand, are so flat that they are virtually identical to distributions that are uniform. The histograms of the associated encrypted images are very uniform and very close to one another. It appears as though every grayscale level appears around one thousand times in all of the encrypted images, the original images are very different from one another. The results illustrate that the proposed algorithm is capable of obtaining histograms that are quite uniform over a wide variety of image types, and as a result, it can withstand histogram attacks very successfully. Therefore, the findings demonstrate that the attacker is unable to extract information from the original image from the encrypted image, which suggests that the approach that was developed in this research provides an adequate level of encryption protection.

Figure 9: Histogram analysis: first and second rows are original images and their corresponding histograms; the third and fourth rows are encrypted images and their corresponding histograms

In graphic histograms, the standard deviation and the variance are measurements of dispersion used to support the findings of visual inspection. They gauge the degree to which the components of a collection of data differ from one another around the mean. The mean (average value) of the two datasets may be the same, but the variances may be very different [44,45].

The variance determines the average variance between each value’s deviation from its center x¯. Each difference is squared before its mean is recalculated to create the final average. Squaring is a technique utilized to increase the variance and remove the negative signals in scattered (non-uniform) datasets. In contrast, the following calculation may be used to calculate the histogram variance and shows that it decreases the more uniform the graphic histogram is.

α=1256∑i=1256(xi−x¯)2(4)

x¯=M×N256(5)

The intensity values of the histogram-based frequency for the grayscale image from 0–255 are indicated by x. The histogram variance is represented by α, and x¯ represents the mean of the histogram. The arithmetic average of the fluctuations-based mean of the dataset can be known by standard deviation. Histogram variance-based square root can be calculated using the following equation.

Z=α(6)

Histogram-based standard deviation is represented by Z. Table 6 depicted the results of the plain image and the encrypted image based on the histogram variance as well as the standard deviation. The results show more uniformity of the pixels of the encrypted image by the proposed method, a better encryption effect is produced by this method.

In addition to the graphical examination of the encrypted image’s histogram distribution, we employ the chi-square test to demonstrate that the encrypted image has a uniform histogram distribution. This is done so that we can demonstrate the uniformity of the encrypted image in a manner that is more accurate, less value of this test shows better uniformity. The chi-square test provides the following justification for the equation that was utilized in the process of calculating the proposed encryption method’s effect on the histogram’s uniformity:

Q2=∑i=1256(mj− nj)2nj(7)

The number of gray values is represented by j, and each gray level of occurrence frequency is indicated by mj. Also, nj represents the occurrence frequency of each gray level where nj = M × N/256. The height and width of both original and encrypted images are indicated by M and N. Table 7 presents the result of the Chi-square test for some encrypted images.

4.2.2 Correlation Analysis

As a result of the strong correlation that exists between adjacent pixels in the image, to defend against the statistical attack. The correlation that exists between adjacent pixels should be minimized to the greatest extent possible. The degree of correlation between pixels can be characterized by using a statistic known as the correlation coefficient. There is a significant association between adjacent pixels in the plain image in all directions. The image that has been processed by the encryption technique will only be resistant to statistical attacks if the correlation coefficient of neighboring pixels in the encrypted image is sufficiently low. Calculations are made to determine the correlation coefficients between the original image and the encrypted image using neighboring pixels that have been chosen at random from each direction. Analyses are performed to determine the correlation between neighboring pixels in the plain image and the cipher image. The correlation coefficient rxy can be calculated using the following Eqs. (8)–(11).

rxy=cov(x,y)D(x)D(y)(8)

Cov(x,y)=1N∑i=1N(xi−E(x)) (yi−E(y))(9)

E(x)=1N∑i=1Nxi(10)

D(x)=1N∑i=1N(xi−E(x))2(11)

According to the formula presented above, N indicates all number of pixel points, the gray values of adjacent pixels are indicated by x and y, E(x) indicates the pixel’s average value, and the variance is indicated by D(x), Cov(x, y) indicates the correlation function. The formula also shows that when the absolute value is high, the correlation is stronger.

The correlation between two variables is said to be weaker when the absolute value of the correlation coefficient is smaller. Table 8 presents the correlation coefficient that was found between the original plain image and the encrypted image. It is clear from looking at Table 8 that the image correlation is destroyed after encryption since the absolute value of the original plain image correlation is close to 1, whereas the absolute value of the encrypted image correlation is close to 0. This shows that the image correlation is destroyed after encryption.

To compare the correlation between adjacent location data values of the original plain image and the encrypted same image in a manner that is more easily understood by the human eye. Fig. 10 depicts the correlation between their two neighboring pixels in all directions, including horizontal, vertical, and diagonal. The abscissa represents the value of a data-based random location, and the ordinate represents the data value of the neighboring random point location. The distribution of adjacent pixels in horizontal, vertical, and diagonal directions of a plain image is depicted in Figs. 10a–10c, while the distribution of adjacent pixels in horizontal, vertical, and diagonal directions of an encrypted image is depicted in Figs. 10d–10f. Fig. 10 shows the values of the pixels that are adjacent to one another in the original plain image are constantly distributed. However, the values of the pixels that are adjacent to one another in the encrypted image are randomly distributed. They are dispersed in all directions over two-dimensional space. The encrypted image removes any correlation between neighboring pixels and hides the data features of the plain image.

Figure 10: Distribution maps of adjacent-pixel of the plain images and the encrypted images in all directions: (a), (b), and (c) for the plain image; (d), (e), and (f) for the encrypting-image

The technique that is proposed in this study is contrasted with the algorithms that have been proposed in other similar literature on image encryption. Table 8 presents the results of the proposed algorithm and previously introduced algorithms. Obviously, it can be seen from the table, that the approach that is proposed in this work has the effect of lowering the pixel correlation in all three directions, namely horizontally, vertically, and diagonally, to a value that is relatively close to 0. The effect of the proposed algorithm on reduction is superior to that of other algorithms. The findings of the experiments reveal that the encryption algorithm drastically lowers the pixel correlation of cipher images. This makes it impossible for attackers to extract useful information from cipher images using statistical methods. This research presents a method that has a high level of security, and statistical attacks are unable to break the encryption algorithm.

4.2.3 Information Entropy Analysis

There are different measures that can be used to measure the randomness of pixels whereas the most common and fundamental is information entropy. Mathematically information entropy can be calculated in Eq. (12):

H(x)=− ∑i=02N−1p(xi)logp(xi)(12)

The probability of the grey level value xi, occurring is denoted by p(xi), N is the total number of grey level values, and log indicates that the entropy values are expressed in bits. H(x) is the optimal entropy value. As a result, the more disorder there is in the system, the closer the entropy is to 8, and the more order there is, the more informational entropy diverges from 8. (See Table 9) shows that the entropy value of the encrypted Lena is 7.9975, which is greater than previous techniques. It should be noted that after employing the encryption approach presented in this work, the entropy of the system proposed has significantly improved.

Moreover, for local information entropy, the image has been selected based on the non-overlapping blocks B1, B2, B3, …, Bn. The entropy has been calculated for each subblock using Eq. (12). Then, the information entropy-based average value of image subblocks has been computed using Eq. (13). Table 10 presents the local information entropy results.

H(B)=∑i=1RH(Bk)R(13)

represents the local information entropy for blocks of image, and k is equal to 1, 2, 3, …, R.

4.2.4 Peak Signal-to-Noise Ratio (PSNR)

An objective measure for judging the quality of images is the peak signal-to-noise ratio, and the mathematical equation for determining this value is as follows:

PSNR=10log10⁡(R1/MSE)(14)

MSE=1 N2∑a=1N∑b=1N(P′(i,j)−P(i,j))2(15)

where N × N represents the size of the image, P′(i,j) and P(i,j) respectively indicate the pixel value of the cipher and original images. MSE stands for mean squared error, while R refers to the spectrum of grayscale values that are present in the image. In a general, the PSNR of an image will become lower as the encryption effect will have a greater impact on its quality. When the PSNR of the image is small, this means the effect of encryption is better. The result of the PSNR test may be seen in Table 11.

4.3 Differential Attack Analysis

Image analysis frequently makes use of and benefits from the application of the differential attack analysis method. The differential attack is a very popular and successful analytical method in image analysis. The goal of a differential attack is to investigate how a very small alteration in a plain image can have a significant impact on the corresponding encrypted image. Any slight modifications, even if a bit altered in an original plain image, will result in entirely new encrypted images. This is an essential property that a decent encryption method should have in order to withstand differential assaults. The number of pixels changes rate (NPCR) and the unified average changing intensity (UACI) are two of the most common indices used to quantify the performance of (resisting) withstanding differential attacks in image encryption. In this context, NPCR represents the proportion of various gray values of various encrypted images at the same location. However, UACI represents the average alert density of various encrypted images, NPCR and UACI can be calculated using Eqs. (16) and (17), respectively [43]. In Table 12, the results of differential analysis experiments are shown along with the results of other algorithms found in the literature of similar works.

NPCR=1W×H ∑i=1W∑j=1Hdij×100%(16)

UACI=1255 ×W ×H ∑i=1W∑j=1H|Cij1−Cij2|×100%(17)

dij={0, Cij1=Cij2 1, Cij1≠ Cij2(18)

4.4 Random Test Analysis

To demonstrate that the chaotic system-generated sequence complies with the SP800-22 standard created by the National Institute of Standards fits the characteristics of a random sequence, and fulfills the necessary random standard (NIST). The 3 test items from the NIST Statistical Test Suite are used to determine if the generated sequence is random or not. We shall state that the sequence is not random if the p-value of the items is less than 0.01. Otherwise, the sequence is random and passes the NIST test. The better the p-value, which indicates that the sequence is more random. The outcome is displayed in Table 13 with each value’s average calculation.

4.5 Time Analysis

In real-world applications, the performance of the cryptosystem in terms of both its ability to protect data and how quickly it can process data is a significant metric. In addition to the concern for safety, time is also an essential quality in an image encryption method. The proposed approach is obviously the confusion-diffusion method, and it is made up of a procedure for scrambling the data at the bit level and the block level, as well as a procedure for diffusing the data at the pixel level. Therefore, we demonstrate the speed performance of the system using the confusion time and the diffusion time. In this part of the analysis, the time required for execution is measured in seconds. Table 14 presents the time speed for some image encryption.

5  Discussion

This paper proposes a new method for conducting encryption at the pixel level and block level. The proposed method is based on confusion, which is formed by proposing a stream pixel scrambling algorithm, and diffusion, which is formed by exploiting the DNA concept. The proposed method in this study is based on the use of a double chaos structure. This study exploits the three-dimensional chaos-based Chen’s system and one-dimensional Logistics for ciphering plain images by chaos. The proposed method for image encryption has advantages based on different structures of chaos, being more secure, robust against attackers, and key space. The confusion process in this study has been performed based on Chen’s chaotic system. However, the diffusion process is carried out based on the combination of Chen’s chaotic system and Logistic Map, which utilizes the technology of DNA coding concept to achieve image encryption. By performing the confusion and diffusion process for image encryption based on combining double chaotic systems, the capability against the encryption attackers was developed.

In addition, as is seen in Table 12, the results that have been obtained from the NPCR and UACI based on several standard images, it is difficult to break the proposed encryption algorithm. Since the combined double chaotic system is used in confusion and diffusion encryption, a more significant calculation burden is needed for the proposed encryption algorithm. In the final section of analyzing the performance of the proposed algorithm and experimental results, we were able to determine that this study can expand the key space, have high key sensitivity, and minimize the correlation degree that was present in the original plain image. This ensures that the cipher image has a uniform histogram, maintains an entropy that is close to the full entropy, and withstands the benefits of multiple attacks. Based on that, it has been demonstrated that the technique can successfully defend against statistical attacks. The NPCR scores are adequate for protecting against differential attacks, and the UACI scores are comparable to the ideal outcome. Moreover, the level of the complexity of the algorithm can be evaluated based on the steps that must be completed in order to complete the encryption process. The complexity of the proposed encryption algorithm can be computed based on the confusion and diffusion processes. In the confusion process, the complexity of the proposed encryption algorithm is calculated as O((M × M)+ Bs+(Ps∗RK1)+(Bs∗RK2)). Where M × M is the size of the original image, Bs is block selection which can be computed as (M2)∗2i, Ps∗RK1 is denoted as pixel-level scrambling-based generated random key, and Bs∗RK2is block-level scrambling-based generated random key. According to the diffusion process, the complexity of the proposed algorithm is O((DNAcoding∗8)+(RDNA∗4)+(XOR∗3)). However, a limitation of our proposed algorithm is that it is time-consuming. A grayscale image with a size of 256 × 256 takes 0.43 s to encrypt. These limitations can be considered in further proposed encryption algorithms. Using a low-dimensional chaotic system is considered another limitation of our proposed algorithm. Chaotic systems can be combined to propose a hyperchaotic system to improve algorithms. Moreover, the diffusion process of this algorithm can be improved to be more efficient in operations and make it suitable for color images. Therefore, the field of image encryption is still considered an open research area, and more robust approaches can be improved and proposed.

6  Conclusions

To ensure the security and privacy of digital images, a new image encryption technique-based confusion-diffusion with double chaotic maps namely the Chen’s map and Logistic map is proposed. Confusion is performed based on two stages: scrambling-based stream pixel level and scrambling-based blocking structure. In confusing plain image-related scrambling, the generated sequence of three-dimensional chaotic-based Chen’s maps is controlled. This helps to improve the sensitivity of the plain image as well as its resistance to differential attack. One of the main features of this algorithm is different scrambling operations based on different random chaotic sequences used in confusion. Furthermore, DNA computing is used to build the diffusion stage. It is carried out based on two stages: diffusing-based reverse complementary rule and diffusion-based multi-XOR operation. These operations are carried out using Chen’s chaotic map and the Logistic map, which are based on generated random sequences. This stage can withstand the proposed algorithm from statistical attack strongly. Because the diffusion operation is carried out in two rounds based on randomly generated sequences, it can improve the sensitivity of the proposed algorithm to the plain image. Moreover, to evaluate the proposed algorithm, we have evaluated our algorithm using several standard images including Lena, Baboon, Peppers, Barbara, Cameraman, Boat, Airplane, House, and Pentagon. In addition, to evaluate the performance of our proposed image encryption algorithm, several common analyses are used including Information Entropy, NPCR, and UACI. This algorithm has achieved 7.9975, 99.6189, and 33.4691 as the value of Information Entropy, NPCR, and UACI for image Lena. The results demonstrated that the proposed image encryption algorithm has superb security performance. Image encryption techniques based on DNA computing and chaos systems are still under constant research, also many problems are still required to be further addressed and solved. Multi-image combination encryption, as well as image encoding based on the parallel DNA concept, is considered our next focus to improve the image encryption algorithm.

Funding Statement: The authors extend their appreciation to the Deanship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the Project Number: IFP22UQU4400257DSR031.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. E. Zhu, X. Luo, C. Liu and C. Chen, “An operational DNA strand displacement encryption approach,” Nanomaterials, vol. 12, no. 5, pp. 877, 2022. [Google Scholar] [PubMed]

2. X. Wang, X. Wang, B. Ma, Q. Li and Y. Q. Shi, “High precision error prediction algorithm based on ridge regression predictor for reversible data hiding,” IEEE Signal Processing Letters, vol. 28, pp. 1125–1129, 2021. [Google Scholar]

3. B. Ma and Y. Q. Shi, “A reversible data hiding scheme based on code division multiplexing,” IEEE Transactions on Information Forensics and Security, vol. 11, no. 9, pp. 1914–1927, 2016. [Google Scholar]

4. Y. Kang, L. Huang, Y. He, X. Xiong, S. Cai et al., “On a symmetric image encryption algorithm based on the peculiarity of plaintext DNA coding,” Symmetry, vol. 12, no. 9, pp. 1393, 2020. [Google Scholar]

5. Z. Liang, Q. Qin, C. Zhou, N. Wang, Y. Xu et al., “Medical image encryption algorithm based on a new five-dimensional three-leaf chaotic system and genetic operation,” PLoS One, vol. 16, no. 11, pp. e0260014, 2020. [Google Scholar]

6. Y. Li, C. Wang and H. Chen, “A hyper-chaos-based image encryption algorithm using pixel-level permutation and bit-level permutation,” Optics and Lasers in Engineering, vol. 90, pp. 238–246, 2017. [Google Scholar]

7. X. Wang, X. Zhu and Y. Zhang, “An image encryption algorithm based on Josephus traversing and mixed chaotic map,” IEEE Access, vol. 6, pp. 23733–23746, 2018. [Google Scholar]

8. J. B. Liu, Y. Bao, W. T. Zheng and S. Hayat, “Network coherence analysis on a family of nested weighted n-polygon networks,” FRACTALS (Fractals), vol. 29, no. 8, pp. 1–15, 2021. [Google Scholar]

9. J. B. Liu, X. B. Peng and S. Hayat, “Topological index analysis of a class of networks analogous to alicyclic hydrocarbons and their derivatives,” International Journal of Quantum Chemistry, vol. 122, no. 2, pp. e26827, 2022. [Google Scholar]

10. J. Zheng, Z. Luo and Z. Tang, “An image encryption algorithm based on a multi-chaotic system and DNA coding,” Discrete Dynamics in Nature and Society, vol. 2020, pp. 1–16, 2020. [Google Scholar]

11. S. Zhu and C. Zhu, “Secure image encryption algorithm based on hyperchaos and dynamic DNA coding,” Entropy, vol. 22, no. 7, pp. 772, 2020. [Google Scholar] [PubMed]

12. Z. Azimi and S. Ahadpour, “Color image encryption based on DNA encoding and pair coupled chaotic maps,” Multimedia Tools and Applications, vol. 79, no. 3, pp. 1727–1744, 2020. [Google Scholar]

13. D. A. Zebari, H. Haron, S. R. Zeebaree and D. Q. Zeebaree, “Multi-level of DNA encryption technique based on DNA arithmetic and biological operations,” in 2018 Int. Conf. on Advanced Science and Engineering (ICOASE), Duhok, Iraq, IEEE, pp. 312–317, 2018. [Google Scholar]

14. L. Huang, S. Cai, M. Xiao and X. Xiong, “A simple chaotic map-based image encryption system using both plaintext related permutation and diffusion,” Entropy, vol. 20, no. 7, pp. 1–20, 535, 2018. [Google Scholar]

15. M. Muñoz-Guillermo, “Image encryption using q-deformed logistic map,” Information Sciences, vol. 552, pp. 352–364, 2021. [Google Scholar]

16. X. Wang, S. Chen and Y. Zhang, “A chaotic image encryption algorithm based on random dynamic mixing,” Optics & Laser Technology, vol. 138, pp. 106837, 2021. [Google Scholar]

17. X. Li, J. Mou, L. Xiong, Z. Wang and J. Xu, “Fractional-order double-ring erbium-doped fiber laser chaotic system and its application on image encryption,” Optics & Laser Technology, vol. 140, pp. 107074, 2021. [Google Scholar]

18. S. Zhu and C. Zhu, “Plaintext-related image encryption algorithm based on block structure and five-dimensional chaotic map,” IEEE Access, vol. 7, pp. 147106–147118, 2019. [Google Scholar]

19. Y. Niu and X. Zhang, “A novel plaintext-related image encryption scheme based on chaotic system and pixel permutation,” IEEE Access, vol. 8, pp. 22082–22093, 2020. [Google Scholar]

20. C. Xu, J. Sun and C. Wang, “A novel image encryption algorithm based on bit-plane matrix rotation and hyper chaotic systems,” Multimedia Tools and Applications, vol. 79, no. 9, pp. 5573–5593, 2020. [Google Scholar]

21. C. Zou, X. Wang and H. Li, “Image encryption algorithm with matrix semi-tensor product,” Nonlinear Dynamics, vol. 105, no. 1, pp. 859–876, 2021. [Google Scholar]

22. J. Liu, D. Yang, H. Zhou and S. Chen, “A digital image encryption algorithm based on bit-planes and an improved logistic map,” Multimedia Tools and Applications, vol. 77, no. 8, pp. 10217–10233, 2018. [Google Scholar]

23. K. Zhou, M. Xu, J. Luo, H. Fan and M. Li, “Cryptanalyzing an image encryption based on a modified Henon map using hybrid chaotic shift transform,” Digital Signal Processing, vol. 93, pp. 115–127, 2019. [Google Scholar]

24. Z. Guan, J. Li, L. Huang, X. Xiong, Y. Liu et al., “A novel and fast encryption system based on improved josephus scrambling and chaotic mapping,” Entropy, vol. 24, no. 3, pp. 1–20, 384, 2022. [Google Scholar]

25. A. N. Yaghouti and M. H. Moattar, “Color image encryption based on hybrid chaotic system and DNA sequences,” Multimedia Tools and Applications, vol. 79, no. 1, pp. 1497–1518, 2020. [Google Scholar]

26. J. C. Dagadu, J. P. Li and P. C. Addo, “An image cryptosystem based on pseudorandomly enhanced chaotic DNA and random permutation,” Multimedia Tools and Applications, vol. 78, no. 17, pp. 24979–25000, 2019. [Google Scholar]

27. H. R. Amani and M. Yaghoobi, “A new approach in adaptive encryption algorithm for color images based on DNA sequence operation and hyper-chaotic system,” Multimedia Tools and Applications, vol. 78, no. 15, pp. 21537–21556, 2019. [Google Scholar]

28. S. A. Banu and R. Amirtharajan, “A robust medical image encryption in dual domain: Chaos-DNA-IWT combined approach,” Medical & Biological Engineering & Computing, vol. 58, no. 7, pp. 1445–1458, 2020. [Google Scholar]

29. X. Zhu, H. Liu, Y. Liang and J. Wu, “Image encryption based on kronecker product over finite fields and DNA operation,” Optik, vol. 224, pp. 164725, 2020. [Google Scholar]

30. X. Jin, X. Duan, H. Jin and Y. Ma, “A novel hybrid secure image encryption based on the shuffle algorithm and the hidden attractor chaos system,” Entropy, vol. 22, no. 6, pp. 640, 2020. [Google Scholar] [PubMed]

31. Y. Chen, C. Tang and R. Ye, “Cryptanalysis and improvement of medical image encryption using high-speed scrambling and pixel adaptive diffusion,” Signal Process, vol. 167, pp. 107286, 2020. [Google Scholar]

32. C. Y. Lin and J. L. Wu, “Cryptanalysis and improvement of a chaotic map-based image encryption system using both plaintext related permutation and diffusion,” Entropy, vol. 22, no. 5, pp. 1–23, 589, 2020. [Google Scholar]

33. R. Zhang, L. Yu, D. Jiang, W. Ding, J. Song et al., “A novel plaintext-related color image encryption scheme based on cellular neural network and Chen’s chaotic system,” Symmetry, vol. 13, no. 3, pp. 393, 2021. [Google Scholar]

34. D. A. Zebari, H. Haron and D. Q. Zeebaree, “Security issues in DNA based on data hiding: A review,” International Journal of Applied Engineering Research, vol. 12, no. 24, pp. 0973–4562, 2017. [Google Scholar]

35. Z. Li, C. Peng, W. Tan and L. Li, “A novel chaos-based image encryption scheme by using randomly DNA encode and plaintext related permutation,” Applied Sciences, vol. 10, no. 21, pp. 1–18, 7469, 2020. [Google Scholar]

36. S. Khan, L. Han, G. Mudassir, B. Guehguih and H. Ullah, “3C3R, an image encryption algorithm based on BBI, 2D-CA, and SM-DNA,” Entropy, vol. 21, no. 11, pp. 1–33, 1075, 2019. [Google Scholar]

37. S. Gao, R. Wu, X. Wang, J. Wang, Q. Li et al., “A 3D model encryption scheme based on a cascaded chaotic system,” Signal Processing, vol. 202, pp. 108745, 2023. [Google Scholar]

38. X. Chai, Z. Gan, K. Yuan, Y. Chen and X. Liu, “A novel image encryption scheme based on DNA sequence operations and chaotic systems,” Neural Comput. Appl, vol. 31, pp. 219–237, 2019. [Google Scholar]

39. A. Tutueva, D. Pesterev, A. Karimov, D. Butusov and V. Ostrovskii, “Adaptive Chirikov map for pseudo-random number generation in chaos-based stream encryption,” in 2019 25th Conf. of Open Innovations Association (FRUCT), Helsinki, Finland, IEEE, pp. 333–338, 2019. [Google Scholar]

40. H. Nematzadeh, R. Enayatifar, M. Yadollahi, M. Lee and G. Jeong, “Binary search tree image encryption with DNA,” Optik, vol. 202, pp. 163505, 2020. [Google Scholar]

41. R. Wu, S. Gao, X. Wang, S. Liu, Q. Li et al., “AEA-NCS: An audio encryption algorithm based on a nested chaotic system,” Chaos, Solitons & Fractals, vol. 165, pp. 112770, 2022. [Google Scholar]

42. A. Sambas, S. Vaidyanathan, E. Tlelo-Cuautle, B. Abd-El-Atty, A. A. Abd El-Latif et al., “A 3-D multi-stable system with a peanut-shaped equilibrium curve: Circuit design, FPGA realization, and an application to image encryption,” IEEE Access, vol. 8, pp. 137116–137132, 2020. [Google Scholar]

43. Y. Wan, S. Gu and B. Du, “A new image encryption algorithm based on composite chaos and hyperchaos combined with DNA coding,” Entropy, vol. 22, no. 2, pp. 1–19, 171, 2020. [Google Scholar]

44. T. Wang and M. H. Wang, “Hyperchaotic image encryption algorithm based on bit-level permutation and DNA encoding,” Optics & Laser Technology, vol. 132, pp. 106355, 2020. [Google Scholar]

45. M. A. Murillo-Escobar, M. O. Meranza-Castillón, R. M. López-Gutiérrez and C. Cruz-Hernández, “Suggested integral analysis for chaos-based image cryptosystems,” Entropy, vol. 21, no. 8, pp. 1–24, 815, 2019. [Google Scholar]

46. X. Wang, Y. Wang, X. Zhu and C. Luo, “A novel chaotic algorithm for image encryption utilizing one-time pad based on pixel level and DNA level,” Optics and Lasers in Engineering, vol. 125, pp. 105851, 2020. [Google Scholar]

47. Z. Tang, Z. Yin, R. Wang, X. Wang, J. Yang et al., “A double-layer image encryption scheme based on chaotic maps and DNA strand displacement,” Journal of Chemistry, vol. 2022, pp. 1–10, 2022. [Google Scholar]

48. M. Alawida, A. Samsudin, J. S. Teh and R. S. Alkhawaldeh, “A new hybrid digital chaotic system with applications in image encryption,” Signal Process, vol. 160, pp. 45–58, 2019. [Google Scholar]