Computation of PoA for Selfish Node Detection and Resource Allocation Using Game Theory

1  Introduction

The communication network has been expanding in both quality and quantity over the past few years. High-bandwidth, low-latency connections are becoming increasingly popular as more network-capable devices become available. It is also essential for mission-critical or safety-critical infrastructures to be able to function properly, which makes robust and versatile communication infrastructures even more critical [1–3]. The communication networks, despite their various advantages, have some disadvantages, including the lack of centralized authority, limited power supply, limited bandwidth, routing overhead, limited access to resources, etc. Indeed, a few nodes in a communication network may behave selfishly where every node is supposed to be cooperative and trustworthy [4]. Despite receiving services from other nodes and using the network, these selfish nodes do not help any other node on this network. Each node’s ability to distribute packets determines how multi-hop routes are established in a network. In order to protect its minimal energy supplies, a selfish node might not cooperate. By selecting each network node to be selfish, the network as a whole contracts.

PoA analysis aids in identifying the misbehaving nodes in a network by continuously monitoring and updating the parameter. Since the network behaviour is dynamic, the nodes arriving at the network and the nodes detaching from the network are going to happen frequently, thus the system will have a difficult time observing the node’s activity [5]. Several monitoring algorithms are approachable but it will be difficult for the system to perform when a network’s node count is increasing rapidly or if it is in a dynamic environment. Yet, the cost of a dynamic network is decreased for locating the selfish nodes in a network using the new method of introducing calculation of PoA.

The distribution of resources is another issue that a DCN must handle. The distribution of resources is widely used in research on distributed computing to achieve several objectives including the network’s Quality of Service (QoS) can be enhanced, bandwidth of a node in a network can be used properly, improving resource management effectiveness, enhancing the stability of the system, etc. The key idea is to strategically split up resource-intensive jobs and spread them among several nodes known as service centres and also assessing the tasks and offering services to the nodes at each service centre [6,7–15]. In the mobile-allocated file architecture, for instance, file fragments are transferred to several service centres via resource allocation. Hence, data can be kept with greater reliability. In any case, it is quite challenging to allocate resources among participating nodes in a compact manner when communication networks are dynamic.

Here are the contributions made to the work:

•   Determining self-interested nodes by applying game theory ideas based on NE.

•   Tracking the behaviour of selfish nodes.

•   When the selfish nodes are found, resources are allocated effectively to increase network reliability.

•   Using least-optimal response dynamics to optimize resources and minimize costs.

The remaining sections of the paper are as follows; the detection of selfish nodes and resource allocation in a communication network based on recent works of literature is presented in Section 2. Section 3 explains the proposed methodology of the paper and Section 4 explains the experimental results of the proposed method and Section 5 explains the conclusion of the article.

2  Related Works

Many research have been carried out on selfish node detection and resource allocation in communication networks. This section discusses some of the most recent works; Kumar et al. [16] goal was to effectively identify selfish or non-cooperative nodes in the network. They introduced an intrusion detection scheme based on dynamic trust to do this. Using the specified scheme, they found selfish nodes and isolated them from the network. To give an explanation for the behaviour of selfish nodes, the indirect faith degree, which was estimated based on recommendations from neighbours, and the direct trust degree, which was derived based on interactions of direct communication, were taken into consideration. The authors achieved an improved delivery ratio and throughput after using the suggested strategy. A hybrid chaotic particle dragonfly swarm algorithm was suggested by Prabakeran et al. [17] for the detection and prevention of Distributed Denial of Service (DDoS) threats in Vehicular Ad Hoc Networks (VANET). The suggested algorithm was used at the roadside units to determine each vehicle’s fitness. The fitness value was examined with the statistical information that had been gathered, which comprised the zone of roadside units, packet factors, and vehicle dynamics. Misbehaving and spoofing nodes were identified by this comparison. These detected selfish behaving nodes were not taken into account while interacting with other vehicles. Moreover, chaos theory was applied to refine the parameters used in the algorithm. The communication overhead and latency of the network were decreased by introducing the suggested approach.

Due to the fact that the black hole attack is one of the worst attacks in Mobile Adhoc networks (MANET), A fuzzy logic method for identifying black hole attacks that relies on the trust node, energy auditing, certificate authority, and packet authenticity check was provided by Arulkumaran et al. [18]. The fuzzy logic approach is a type of mathematical logic that makes an effort to resolve issues by taking prediction values for an undefined data range into consideration. Trusted nodes received a certificate of trust once a misbehaving node was found. The proposed approach helped the authors increase their throughput and delivery ratio. A completely decentralised system by Rmayti et al. [19] enables the node to detect and identify rogue nodes around. The suggested technique used the Bernoulli Bayesian model to classify node activity. Moreover, the Markov chain model was used to follow the progression of behaviour. By providing the suggested approaches, the authors were able to attain a high detection accuracy rate.

Chen et al. [20] developed a displayed system for mobile vehicle services to improve the QoS of the vehicle network. In this approach, a learning-based resource allocation method was developed. The computational complexity of resource allocation is not assumed when modeling dynamic switching processes as Markov chains. To effectively and precisely address the problem of dynamic resource allocation, an asynchronous learning algorithm based on merit actor-critic was developed. The study’s conclusions showed that network operators are now receiving larger total rewards. For resource allocation, Gudihatti et al. [21] introduced an unique method based on cooperative game theory. By choosing a cooperative node, the suggested approach secured a maximum payout. The method suggested optimized resource utilization, overhead, and energy consumption. The computational complexity of resource use was lowered by the use of a regression search algorithm, and the suggested strategy outperformed the prior energy efficiency planning scheme in terms of outcomes.

Bhardwaj et al. [22] created a dragonfly search convergence and coverage algorithm for an effective resource allocation method in an industrial wireless network. The approach optimized resource allocation by observing dragonfly behavior. Low latency, low error probability, and high throughput were some of the objective functions used to find the best solution. Convergence rate analysis and statistical analysis were used to assess the effectiveness of the suggested method. From the results, the proposed approach achieved better accuracy, efficiency, and a higher convergence ratio. A model for resource integration was given by Wang et al. [23] utilising an enhanced chaotic firefly algorithm. This approach protected the normal activity of the primary users. A bigger number of clients are covered by the secondary base station, and the efficiency of the secondary structure has also grown. To solve non-linear convex optimization, an improved chaotic firefly algorithm was utilized. According to the findings, the researchers’ recommended system allowed them to reach their maximum throughput.

3  PoA Computation, Detection of Selfish Node and Resource Allocation

3.1 Model Description

A NE-based game theory with PoA analysis is given forth to enhance node-to-node communication in the DCN in order to identify selfish nodes in the network. The flow diagram for detecting selfish nodes is shown in Fig. 1. In the NE for repeated games, PoA is researched in the field of game theory. Based on the PoA value (i.e., larger than one), a selfish node is recognised and eliminated from the network. When the selfish nodes have been eliminated using the CSRA game, resources are allocated to the regular nodes. For resource allocation, the CSRA game is shown. The flow diagram for resource allocation is shown in Fig. 2. To further promote cost reduction, the least good response dynamics-based updating rule for node resources is proposed.

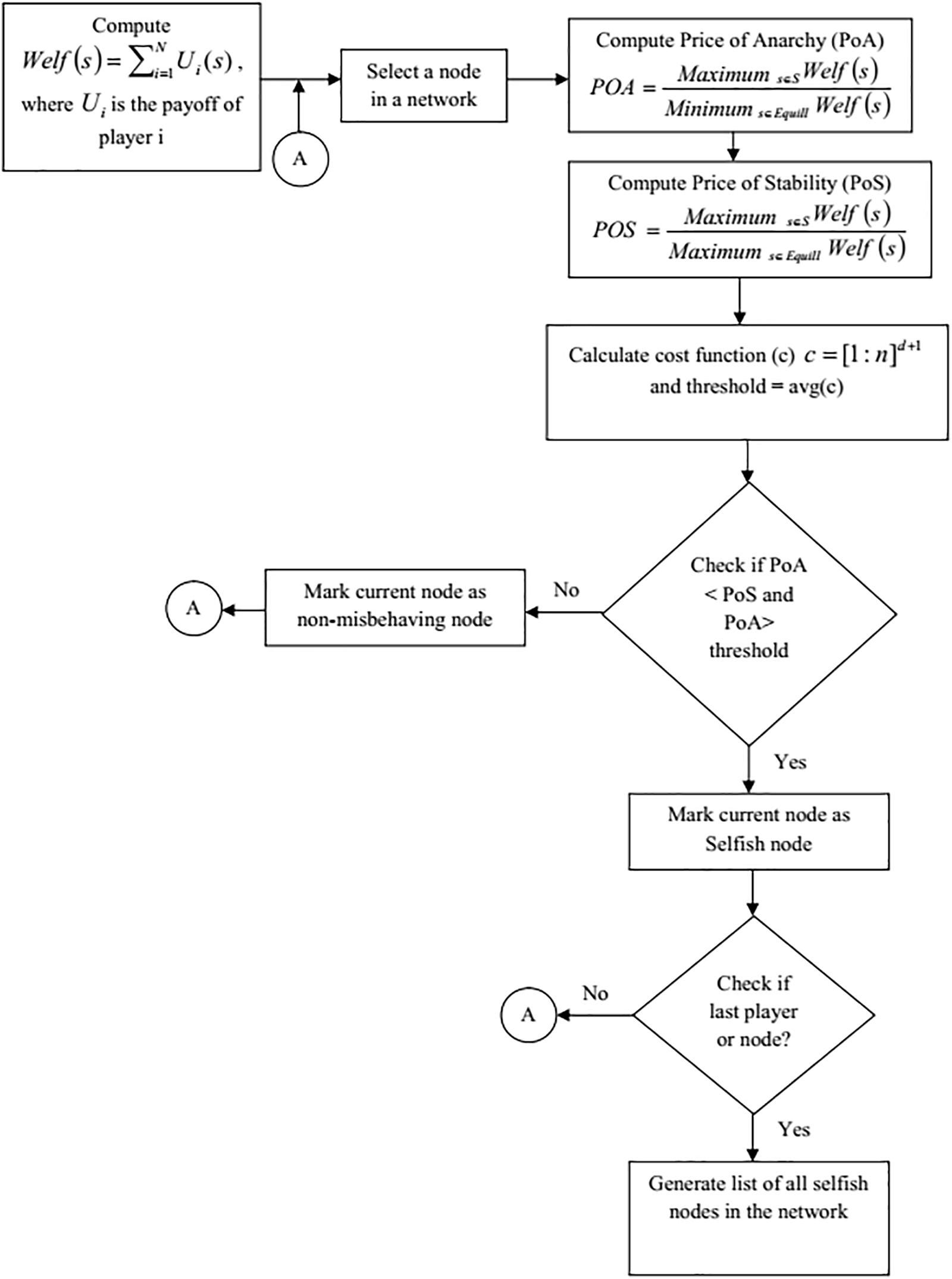
Figure 1: Flow chart to find selfish nodes

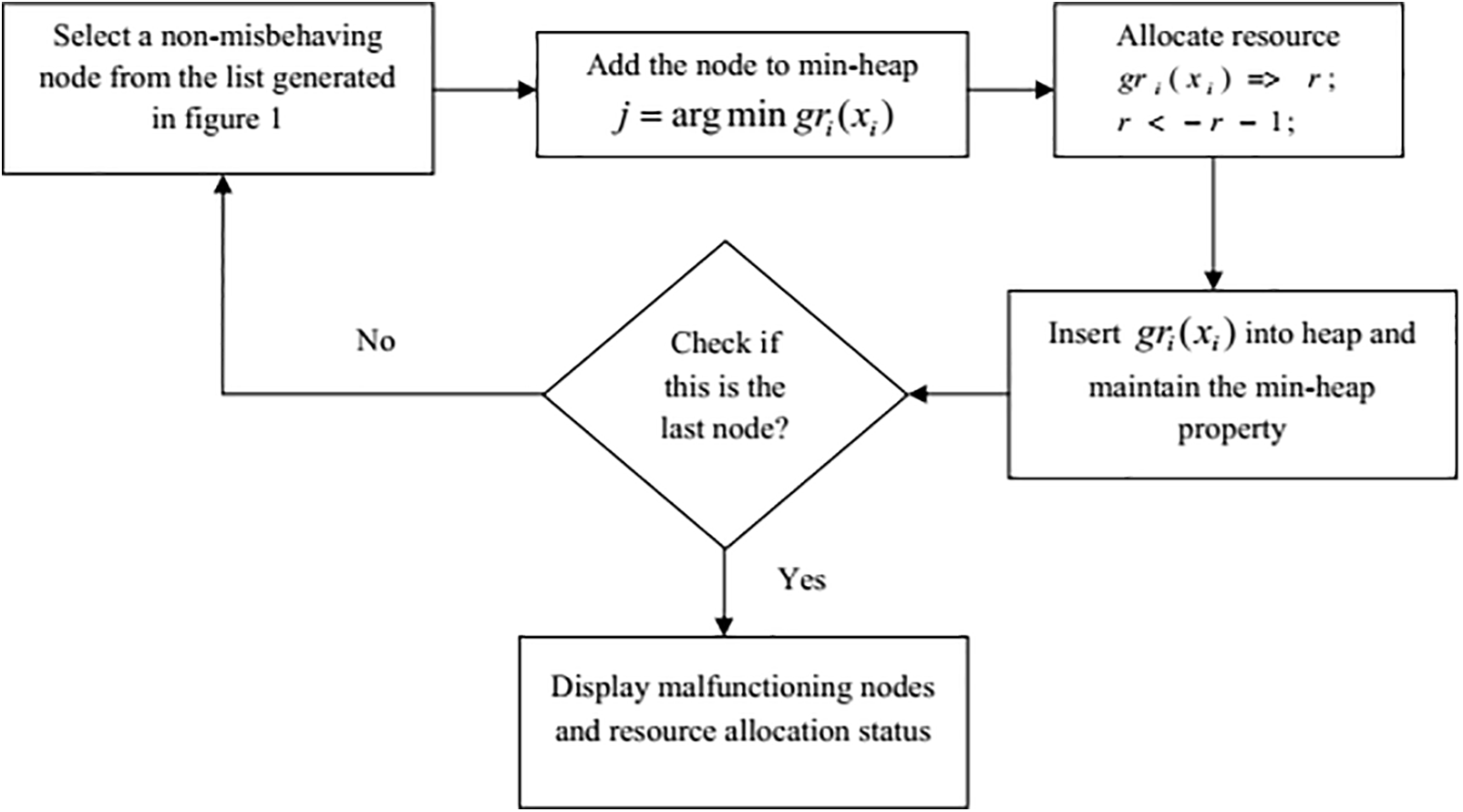
Figure 2: Flow chart of resource allocation for normal nodes

3.2 Identifying Non-Cooperating Nodes or Selfish Nodes

Game theory is introduced as a simulation in which players function as decision-makers and their movements are represented by their actions. A payoff is gained in accordance with the player’s and the other player’s actions. Moreover, a game has a principal and an N-player set [24–28]. Each player is free to select a strategy si∈Si to minimize or maximize the utility U and it is related to the player’s payoff.

Game theory is used in this technique to find selfish nodes in a DCN. The equation below represents the game model;

G={N,A,Si,U}(1)

where, N stands for the number of players, then N={N1,N2………,Nn} and A stands for the set of actions, which is A={A1,A2………,An}. The maximum power available for a data packet can be considered as part of the available resource. The set of strategies for the ith player is representated as Si. Each player considers two strategies: sending or not sending the data packet U denotes the utility function, which is represented using the Eres(residual energy) of the node. Each player in this approach is free to choose their own strategy without interacting with other players.

To increase the player’s payoff, the equilibrium strategy is used. None of these players will succeed if they alter their strategies on their own. The existing strategic options and relative payoffs reach a NE as soon as no player benefits from changing their strategy [29–34] but each player chooses their strategy.

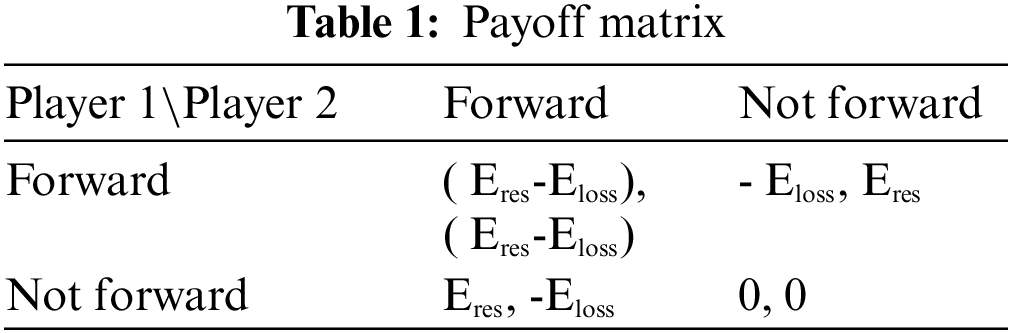
An implementation of the payoff matrix used to identify the selfish node is shown in Table 1. The payoff matrix is formed between two players or two nodes, as illustrated in the table. The payoff or utility of each player is determined based on the residual energy Eres of the nodes. If one node’s packet is forwarded by other nodes, the node’s payoff is represented as residual energy Eres. If a node forwards the data packet of other nodes, the payoff node is denoted as energy loss Eloss. As demonstrated in Table 1, if players 1 and 2 forward packets to each other, the payoff of both nodes is calculated as Eres-Eloss. Moreover, within the set of players, when one player decides to pass the data packet to other players but the second player does not, the payoff of both players is represented as-Eloss and Eres respectively. If neither player decides to transfer the data packets to the other, the payoff for both is zero. As a result, NE is classified as {“Not Forward, Not Forward”}in the single-stage payout matrix. Furthermore, the performance loss of a game owing to selfish actions of players is evaluated using PoS and PoA. The performance metric is the welfare function for each outcome, which is defined as Welf:S→ℜ

The following equation represents the welfare function,

Welf(s)=∑i∈NUi(s)(2)

Here, Ui(s) represents the utility function.

PoA is the ratio of the worst equilibrium to the optimal solution, as provided by the equation below.

POA=Maximums∈SWelf(s)Minimums∈EquillWelf(s)(3)

PoS is the optimal equilibrium to optimal solution ratio, which is provided by the equation below.

POS=Maximums∈SWelf(s)Maximums∈EquillWelf(s)(4)

According to the table, in the single-level game, we are not able to find selfish nodes since all the nodes must cooperate. Selfish nodes can be recognised in a repeated game rather than a single-level game. In a repeated game, a payoff matrix is estimated for every node depending on the activity of the participating nodes. Also, the PoA of NE is estimated for each game as,

POA=Maximums∈SWelf(s)Minimums∈EquillWelf(s)≥1(5)

If step 4 in Algorithm 1 yields ‘False’ when the conditional check returns ‘False,’ NE is considered optimal. If not in the above-mentioned state, the node is called a selfish node. Hence, resources are allocated with lower priority to the identified selfish nodes. To find selfish nodes, researchers have only focused on the PoA calculation parameter in previous research [12,16,17]. The computation of the threshold is not crucial in identifying non-cooperative nodes, which was discovered to be a drawback in those efforts.

Algorithm 1 explains the detection of selfish nodes using the calculation of PoA and PoS. The ‘threshold’ from the cost function is then calculated to indicate a milestone for detecting selfish nodes using the number of players or nodes and the maximum order [35–37]. By comparing PoA with PoS, this algorithm is used to find selfish nodes.

3.3 CSRA Game

The CSRA game model is used to assign resources to normal nodes. Allocation games are often characterised by resource utilisation, with each player (active node) only retaining a specified amount of resources in the cache.

A correspondence diagram identifies the players’ entrance costs, and the goal for each player is to satisfy the needs of his clients while egotistically lowering his costTo avoid excessive expenditures, each participant must give just his or her own resources. Due to a constraint, players cannot retain all of the resources in their caches, thus they may have to obtain a portion of the resources from others that they cannot access in their caches to deliver to their customers, incurring some expenses. The flow chart of resource allocation for typical nodes in the network is shown in Fig. 2.

CSRA model: Players are defined as nodes that are active, but do not include selfish nodes, and are indicated as,

S={1,2,…….,n}(8)

These active nodes are connected using an undirected weightless graph. It is given in the following equation,

G=(S,ε)where,ε=edgeset(9)

In the network, a collection of all resources is stated as,

R={r1,r2,…….r|R|}(10)

Each player has a unit-size cache and each resource is the same size. The ith player’s action is defined as Ai∈S, which indicates the resource assigned by the ith node. In addition, each player’s set of actions is the same and related to S. All active nodes’ action vector or allocation profile o is given below,

A={A1,A2………,An}(11)

The cost of the ith player for a specific allocation A is calculated using the following equation,

Costi(A)=∑r∈R∖AidG(i,Ni(A,r))(12)

Here, the neighbor node of i is indicated as Ni(A,r) and the distance between the ith node and its neighbor node is indicated as dG. For the allocation profile A, ith radius of the player is denoted as ri(A), which possess the same resource as the ith node. The radius ri(A) is given below,

ri(A)=minAi=Aj⁡dG(i,Ni(A,r))(13)

If the neighbor of the ith node does not have a similar resource as ith node, ri(A) is same as network diameter D.

If resource r is not accessible in profile A, then each player’s cost for that resource is specified as

dG(i,Ni(A,r))=D+1,∀i∈S(14)

As a result, it is raised someplace near one of the players to assign the network’s lacking resources. To S≥|R|. For example, S<|R|, the game is simple since each player distributes different resources; Now, it can be considered as S<|R|.

In CSRA, a extended ordinal probability function (Φ) is explained and translated to the variances in each player’s prices of i and Ai,Ai′∈R and A−i.

Ci(Ai,A−i)−Ci(Ai′,A−i)>0⇒Φ(Ai,A−i)−Φ(Ai′,A−i)>0(15)

Here, the allocation profile of each payer apart from i is represented as A−i. Because of the minimizer of Φ, the NE profile of actions is got. In NE, players cannot minimize their costs yet. The generalized ordinal potential function at time step ‘t’ is described as follow,

Φ(A(t))=∑i=1D⁡mi(t)mD−i(16)

Here, the network dimension is indicated as D and the radius of the ith player is represented as mi(t). Besides, if the ith player updates its radius r to r at a time (t), it exceeds r by making its best response. So, Ci(A(t))>Ci(A(t + 1)).

3.4 Least Best Response Dynamics

This part has further update guide for players that discloses NE for all players. In a strictly best response dynamic, Φ(A(t)) decreases with iterations. Because this function is continually non-negative, iterations of the optimal response dynamics will result in a significant NE function reduction. During each iteration of this process, the player with the smallest updating radius is found.

•   Consider that each player possesses a binary flag (fi∈{0,1}) and an integer-valued variable denoted as yi.

•   In this, time intervals ‘t’ and ‘t + 1’, all players’ flags are designated to 1, as the players’ variables at a time ‘t’ is denoted as yi=ri(t), where ri(t) represents the relative radius of the players.

•   Afterward, the variables of each player are exchanged between players and the variables of the neighboring players are also updated. When the D steps are finished, all of the players’ variables are equal to mini=1,….nri(t).

•   The variables and radius of each player are compared once the variables have been updated. Then, when the flag is equal to 0, the former is smaller than the latter and is in the same position.

•   If their flag is considered to be 1, players are assumed to be qualified candidates for an upgrade at ‘t + 1’ after performing D steps.

•   The same protocol may be used to address the attached problematic issue of which candidate to upgrade; now the variables are adjusted to the player’s indices. It resets each of the rest of the flags with the value 1 to 0 exclude the one belonging to the candidate with the least index.

•   This major player will then adjust his resource based on his rigorous best answer at t + 1 in the following step of the algorithm.

4  Results and Discussion

The suggested strategy is implemented in the Python language, with the machine configured as follows: Intel Core i5 processor, 6 GB of memory, and a Windows 10 operating system. It is used in the proposed scheme to be implemented on the Solar Winds platform. The Solar Winds platform allows network monitoring and performance of network nodes. Our network monitoring tool scales and extends in response to the necessities of the network we are functioning on. Multi-vendor network monitoring, intelligent mapping, NetPathand PerfStack for easier troubleshooting, network insights for deeper visibility, sophisticated alerting, and better scalability for big environments are major features of Solar Winds Network Performance Monitor (NPM). In a DCN, monitoring the health of devices is the focus of this proposed approach. It monitors hardware and network devices such as routers, switches, office equipment, mobile devices, and terminals. As discussed in Algorithm 1, The PoA and identification of selfish nodes are provided. The PoA examines how a system’s performance decreases when decision-making is spread rather than centralised. A game design approach focuses on identifying selfish nodes, which does not explicitly design the local decision-making process. Instead, distributed protocol design expresses as utility design and learning design. The interaction of the system’s agents is represented as a complex game, with the set and orders of players forming a utility model. In local decision-making, players are associated with permitted actions or orders, and utility functions are associated with each player. A local learning rule specifies how the player’s behavior will change based on the information available locally.

After computing PoA and PoS, a threshold must be set to isolate selfish nodes. At the required level, the average cost function (f) for all players is determined and set as threshold (t). To find the selfish nodes, first determine if the PoA of a certain player with order (d) is smaller than the associated player’s Price of Stability. Whereas if criteria is satisfied, determine whether PoA is more than the calculated threshold (t). Nodes corresponding to sequence d will be identified as selfish if both conditions are satisfied. Fig. 3 depicts the result of PoA and PoS values, as well as the selfish nodes in the appropriate order. It’s clear from the diagram that, in order 1, player 1 is acting selfishly. Therefore, step 4 of Algorithm 1 enters the picture, indicating that player 1’s PoA value is smaller than his PoS value. Further, the PoA value exceeds the threshold. This means that in order 1, player 1 is acting selfishly. In order 2, player 4 is acting selfishly. In order 3, all of the participants are engaging.

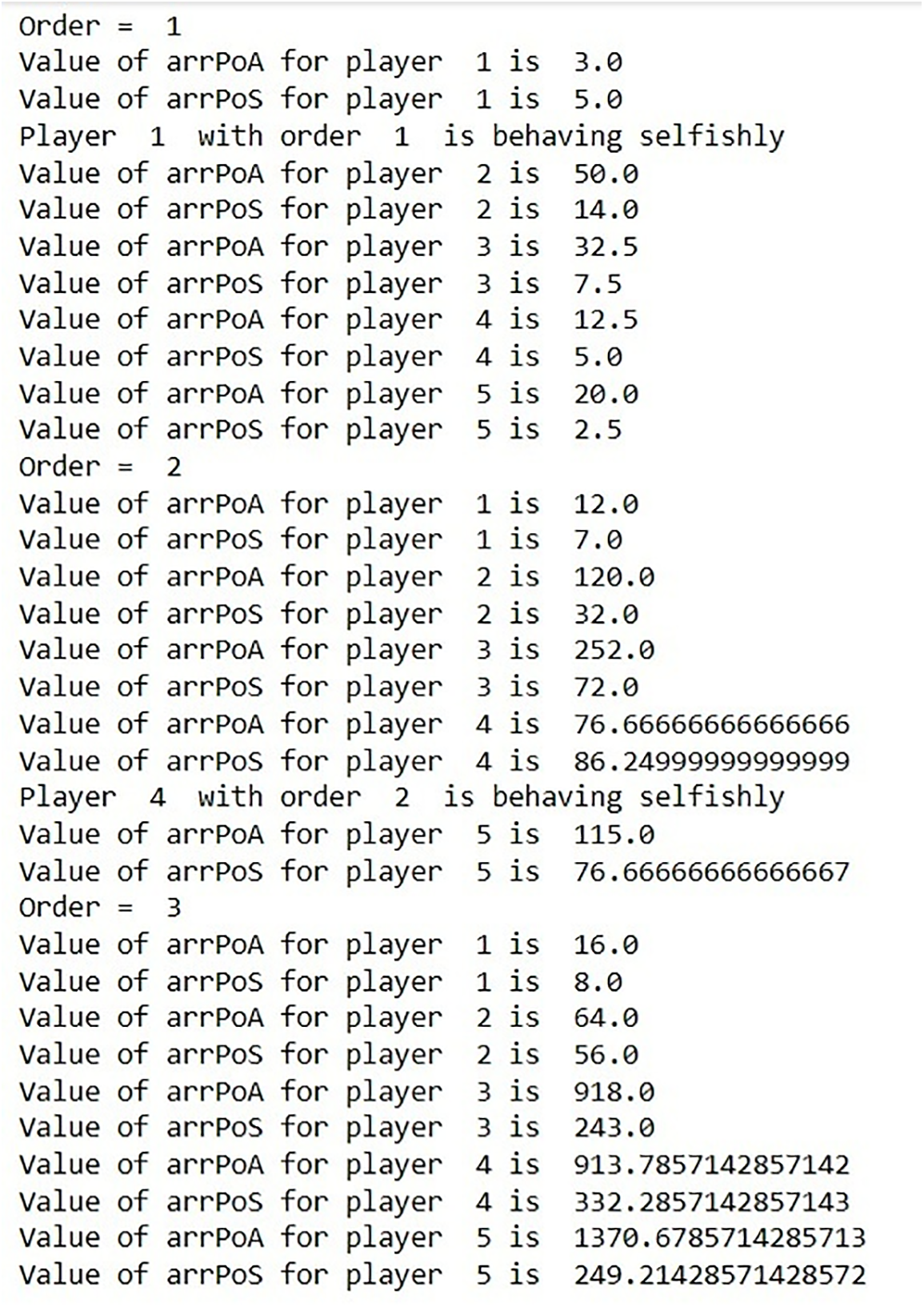
Figure 3: Finding selfish nodes using PoA and PoS computation

The next figures, Figs. 4–6, are depicted by plotting the values stated in Fig. 3. As seen in Fig. 3, player 1 in order 1 is acting selfishly. Fig. 4 PoA/PoS graphing for order 1 for all players.

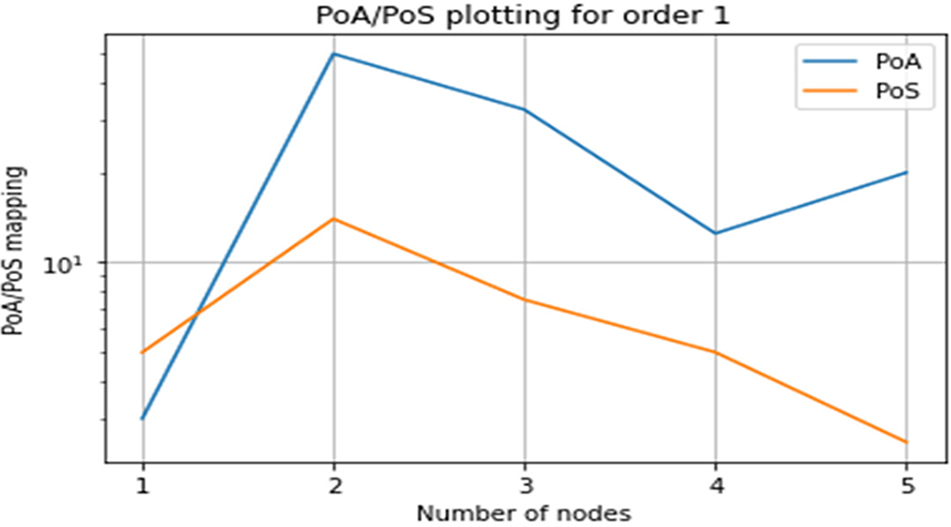
Figure 4: Graphing PoA/PoS for order 1

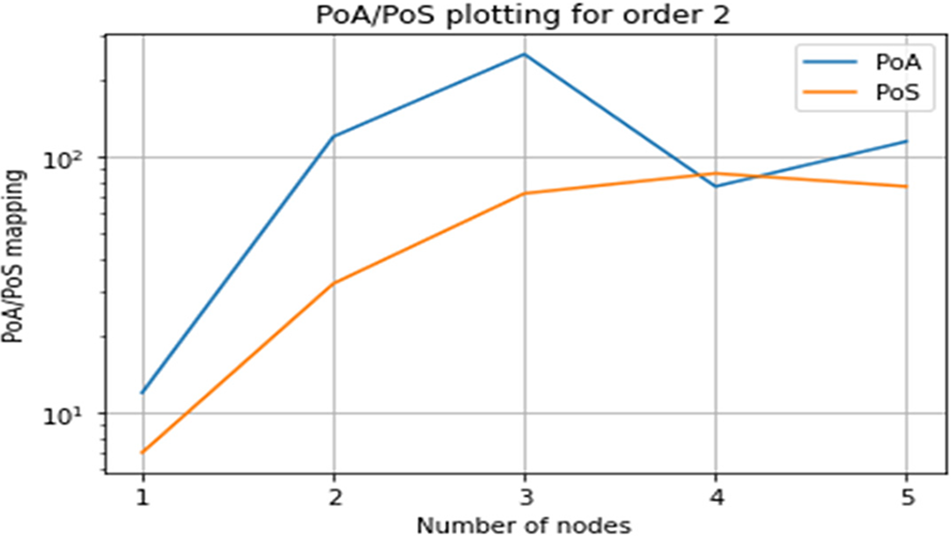
Figure 5: Graphing PoA/PoS for order 2

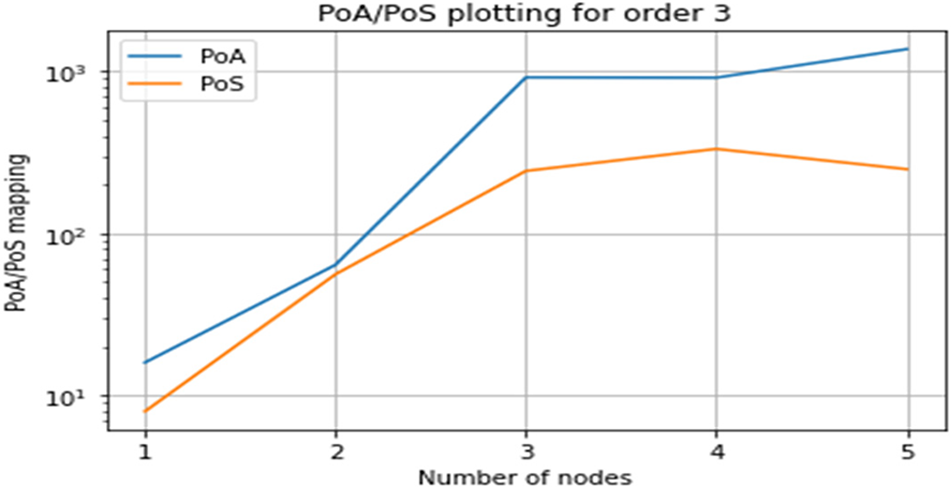
Figure 6: Graphing PoA/PoS for order 3

As seen in Fig. 3, player 4 in order 2 is acting selfishly. Fig. 5 shows the PoA/PoS graphing for order 2 for all players.

As shown in Fig. 3, all participants are working together in order 3. Fig. 6 shows the PoA/PoS charting for order 3 for all players.

4.1 Performance Analysis for Selfish Node Detection

The efficiency of several selfish node identification approaches is evaluated using throughput, delay, and delivery ratio for different numbers of nodes. The planned NE-based game theory (NE-GT) method is compared to the hybrid chaotic particle dragonfly swarm (HCPDS) algorithm and the Fuzzy logic system. Fig. 7 depicts a delay comparison of several techniques. In Fig. 7, the traditional approach has a significant delay when compared to the suggested method. The delay will rise as the number of users rises. The number of nodes 20, 40, and 60 in Fuzzy achieves 2.6, 2.99, and 3.11 s delay, correspondingly. If there are 80 users, the delay time is 3.23 s, and 100 nodes are delayed by 3.34 s. For 100 nodes, the longest delay time is 3.34 s. When compared to GA, HCPDS has a lower delay; the maximum delay for 100 nodes is 3.01 s. The 20 nodes achieve the HCPDS method’s minimal delay of 2.02 s. Nevertheless, our suggested NE-GT strategy yields a maximum delay of 2.01 s for 100 nodes, whereas other existing strategies reach more than 3 s. NE-GT obtained the shortest delay time of 1.08 s.

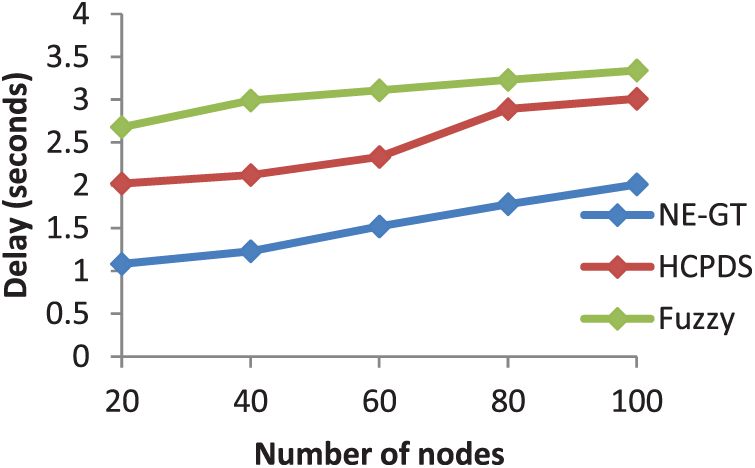
Figure 7: Delay comparisons in selfish node detection methods

Fig. 8 depicts the throughput for various techniques dependent on the number of users. The throughput of our work is measured in kbps. Based on the number of nodes 20 and 40 in NE-GT, 498 and 453 kbps are obtained. Nodes 60, 80, and 100 have throughput of 428, 398, and 365 kbps, respectively. Nonetheless, when compared to other ways, our suggested method achieves the maximum throughput value. The highest throughput of NE-GT is 498 kbps, while the maximum throughput of other techniques is 289 kbps.

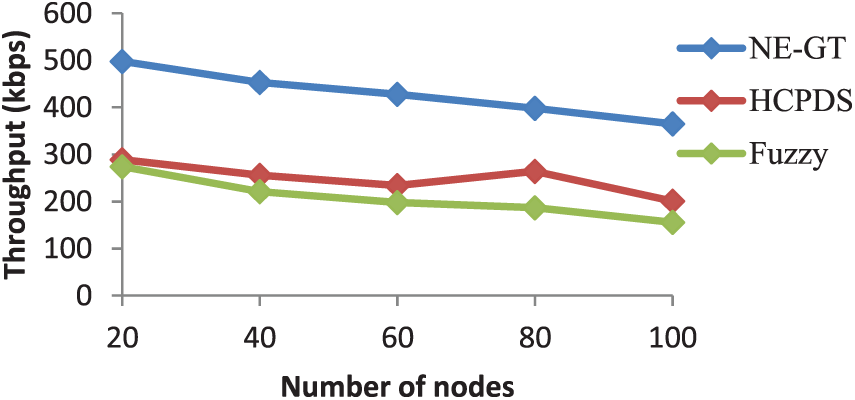
Figure 8: Throughput comparison in selfish node detection algorithms

The delivery ratio dependent on the number of nodes is shown in Fig. 9. Fuzzy achieves 0.654 for 20 nodes, 0.5987 for 40 nodes, and 0.4984 for 60 nodes. For 60 nodes, the highest delivery ratio is attained, which is 0.4984. Nonetheless, for 100 nodes, the NE-GT achieves a minimum delivery ratio of 0.8975 and a maximum delivery ratio of 1. The maximum ratio in HCPDS is 0.8452. As compared to HCPDS and Fuzzy, our suggested approach NE-GT achieves the best delivery ratio.

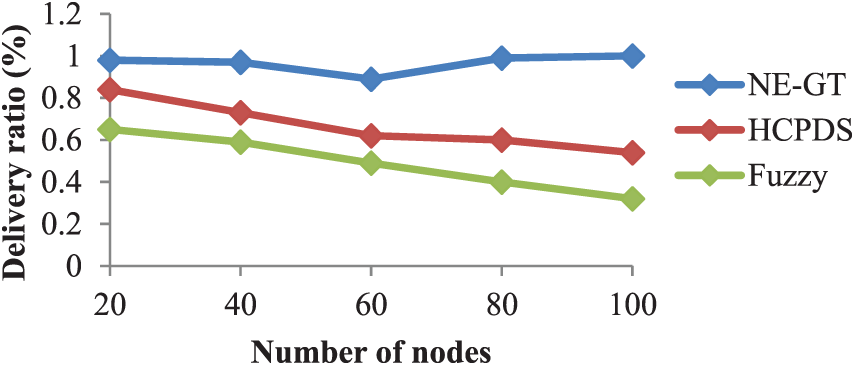
Figure 9: Delivery ratio comparison in selfish node detection algorithms

4.2 Performance Analysis for Resource Allocation

The efficacy of alternative resource allocation methods is evaluated using delivery ratio, latency, and throughput for varied node counts. A line chart illustrating different evaluation metrics of CSRA and Dragonfly approaches is shown in Figs. 10–12. In Fig. 10, the performance of the planned model is compared with various resource allocation models based on delay. From the figure, the Dragonfly approach reached a 1.9 s delay for 100 nodes. In Fig. 10, planned CSRA achieved a minimal delay of 1.08 s when compared to the Dragonfly technique.

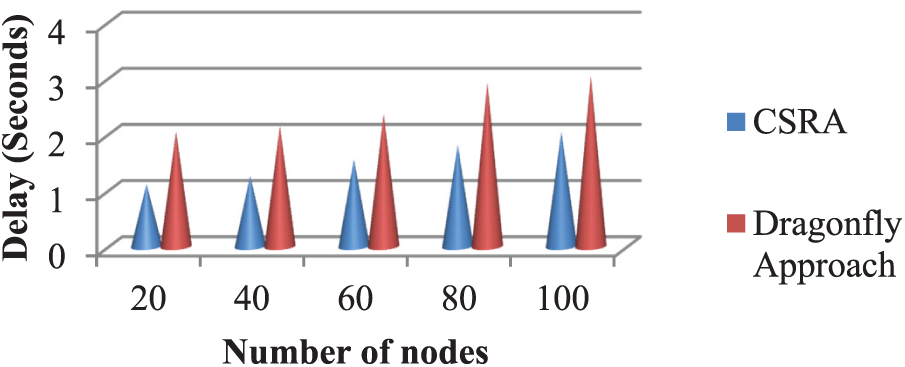
Figure 10: Delay comparison in resource allocation schemes

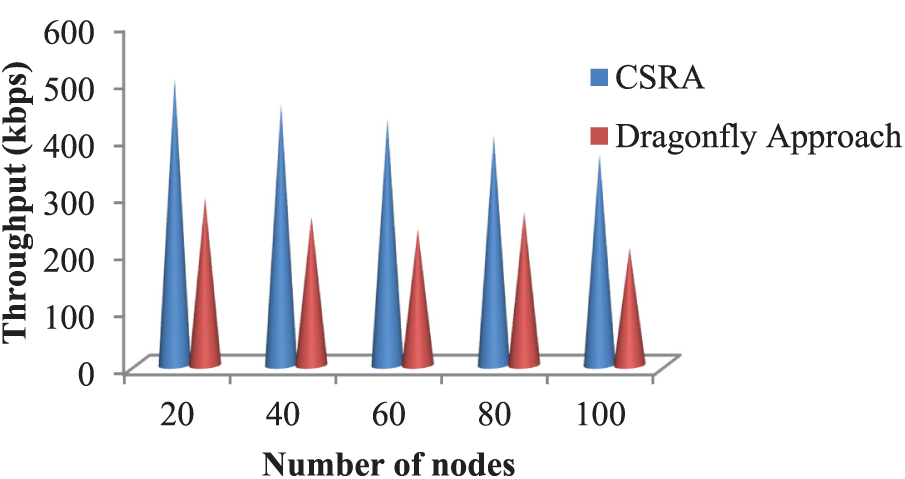
Figure 11: Throughput comparison in resource allocation schemes

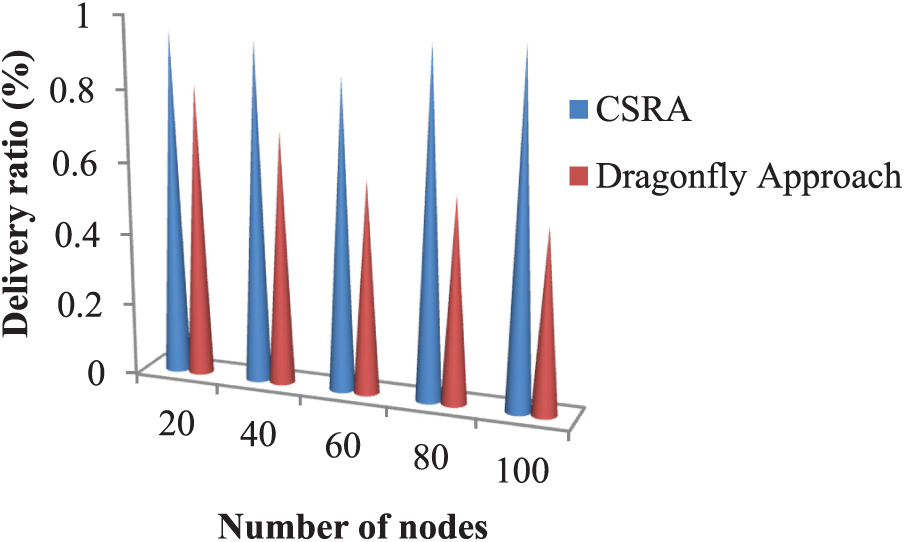
Figure 12: Delivery ratio comparison in resource allocation schemes

In Fig. 11, the performance of the planned model is compared with various resource allocation models based on throughput. From the figure, the Dragonfly approach reached the highest throughput is 289 kbps. When analyzing Fig. 11, the planned CSRA reached maximum throughput compared with the Dragonfly scheme.

In Fig. 12, the effectiveness of the planned model is compared with various resource allocation models based on a delivery ratio After examining Fig. 12, the proposed scheme reached 1 for a total of 100 nodes. Nevertheless, the second technique achieved 0.8452 for a total of 20 nodes.

5  Conclusion

This paper introduced a NE-based game theory method for detecting selfish nodes in DCNs. In order to detect selfish nodes, PoA thresholds are passed in NE. After that, resources are assigned to normal nodes using the CSRA game. The sources were additionally updated using an update mechanism based on least-best response dynamics. The effectiveness of the planned selfish node detection and resource allocation method was evaluated based on delay, delivery rate, and throughput According to simulation findings, the suggested NE-GT excelled the Dragonfly approach-based resource allocation based on HCPDS and Fuzzy logic-based selfish node identification and programmed CSRA game.

Acknowledgement: The author would like to express his gratefulness to the supervisor for his guidance and unconditional support throughout this research.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. D. A. Sivasakthi and R. Gunasekaran. “Dynamic ambient HetNet for hybrid data communication and transmission in IoT networks,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 9, pp. 8899–8911, 2021. [Google Scholar]

2. A. H. Celdrán, M. G. Pérez, F. J. G. Clemente, F. Ippoliti and G. M. Pérez, “Dynamic network slicing management of multimedia scenarios for future remote healthcare,” Multimedia Tools and Applications, vol. 78, no. 17, pp. 24707–24737, 2019. [Google Scholar]

3. A. Fan, J. Li and C. Wei, “Distributed prescribed performance pinning synchronization for complex dynamical networks with event-triggered communication protocols,” Journal of the Franklin Institute, vol. 357, no. 3, pp. 1790–1812, 2020. [Google Scholar]

4. K. R. Abirami and M. G. Sumithra, “Evaluation of neighbor credit value based AODV routing algorithms for selfish node behavior detection,” Cluster Computing, vol. 22, no. 6, pp. 13307–13316, 2019. [Google Scholar]

5. N. Xiao, R. Xinyi, Z. Xiong, F. Xu, X. Zhang et al., “A diversity-based selfish node detection algorithm for socially aware networking,” Journal of Signal Processing Systems, vol. 93, no. 7, pp. 811–825, 2021. [Google Scholar]

6. B. Jedari, F. Xia, H. Chen, S. K. Das, A. Tolba et al., “A social-based watchdog system to detect selfish nodes in opportunistic mobile networks,” Future Generation Computer Systems, vol. 92, pp. 777–788, 2019. [Google Scholar]

7. A. M. Ahmed, X. Kong, L. Liu, F. Xia, S. Abolfazli et al., “BoDMaS: Bio-inspired selfishness detection and mitigation in data management for ad-hoc social networks,” Ad Hoc Networks, vol. 55, pp. 119–131, 2017. [Google Scholar]

8. T. Hu, Z. He, X. Zhang, S. Zhong, K. Shi et al., “Adaptive fuzzy control for quasi-synchronization of uncertain complex dynamical networks with time-varying topology via event-triggered communication strategy,” Information Sciences, vol. 582, pp. 704–724, 2022. [Google Scholar]

9. A. Fan and J. Li, “Prescribed performance synchronization of complex dynamical networks with event-based communication protocols,” Information Sciences, vol. 564, pp. 254–272, 2021. [Google Scholar]

10. X. Meng, S. Wang, Z. Liang, D. Yao, J. Zhou et al., “Semi-supervised anomaly detection in DCNs,” Information Sciences, vol. 571, pp. 527–542, 2021. [Google Scholar]

11. S. Halder, A. Ghosal and M. Conti, “Efficient physical intrusion detection in Internet of Things: A node deployment approach,” Computer Networks, vol. 154, pp. 28–46, 2019. [Google Scholar]

12. L. Yang, Y. Lu, S. X. Yang, Y. Zhong, T. Guo et al., “An evolutionary game-based secure clustering protocol with fuzzy trust evaluation and outlier detection for wireless sensor networks,” IEEE Sensors Journal, vol. 21, no. 12, pp. 13935–13947, 2021. [Google Scholar]

13. Y. Du, J. Xia, J. Ma and W. Zhang, “An optimal decision method for intrusion detection system in wireless sensor networks with enhanced cooperation mechanism,” IEEE Access, vol. 9, pp. 69498–69512, 2021. [Google Scholar]

14. V. Bilò and C. Vinci, “The PoA of affine congestion games with similar strategies,” Theoretical Computer Science, vol. 806, pp. 641–654, 2020. [Google Scholar]

15. G. Dosa, H. Kellerer and Z. Tuza, “Using weight decision for decreasing the PoA in selfish bin packing games,” European Journal of Operational Research, vol. 278, no. 1, pp. 160–169, 2019. [Google Scholar]

16. S. Kumar and K. Dutta, “Trust based intrusion detection technique to detect selfish nodes in mobile ad hoc networks,” Wireless Personal Communications, vol. 101, no. 4, pp. 2029–2052, 2018. [Google Scholar]

17. S. Prabakeran and T. Sethukarasi, “Optimal solution for malicious node detection and prevention using hybrid chaotic particle dragonfly swarm algorithm in VANETs,” Wireless Networks, vol. 26, no. 8, pp. 5897–5917, 2020. [Google Scholar]

18. G. Arulkumaran and R. K. Gnanamurthy, “Fuzzy trust approach for detecting black hole attack in mobile adhoc network,” Mobile Networks and Applications, vol. 24, no. 2, pp. 386–393, 2019. [Google Scholar]

19. M. Rmayti, R. Khatoun, Y. Begriche, L. Khoukhi and D. Gaiti, “A stochastic approach for packet dropping attacks detection in mobile Ad hoc networks,” Computer Networks, vol. 121, pp. 53–64, 2017. [Google Scholar]

20. M. Chen, T. Wang, K. Ota, M. Dong, M. Zhao et al., “Intelligent resource allocation management for vehicles network: An A3C learning approach,” Computer Communications, vol. 151, pp. 485–494, 2020. [Google Scholar]

21. K. N. S. Gudihatti, M. S. Roopa, R. Tanuja, H. S. Manjula and K. R. Venugopal, “Energy aware resource allocation and complexity reduction approach for cognitive radio networks using game theory,” Physical Communication, vol. 42, pp. 101152, 2020. [Google Scholar]

22. S. Bhardwaj and D. Kim, “Dragonfly approach for resource allocation in industrial wireless networks,” Physical Communication, vol. 43, pp. 101198, 2020. [Google Scholar]

23. Z. Wang, D. Liu and A. Jolfaei, “Resource allocation solution for sensor networks using improved chaotic firefly algorithm in IoT environment,” Computer Communications, vol. 156, pp. 91–100, 2020. [Google Scholar]

24. M. Felegyhazi, J. P. Hubaux and L. Buttyan, “Nash equilibria of packet forwarding strategies in wireless ad hoc networks,” IEEE Transactions on Mobile Computing, vol. 5, no. 5, pp. 463–476, 2006. [Google Scholar]

25. S. Durand, F. Garin and B. Gaujal, “Distributed best response dynamics with high playing rates in potential games,” Performance Evaluation, vol. 129, pp. 40–59, 2019. [Google Scholar]

26. C. Ewerhart, “Ordinal potentials in smooth games,” Econ Theory, vol. 70, no. 4, pp. 1069–1100, 2020. [Google Scholar]

27. R. Chandan, D. Paccagnan and J. R. Marden, “Optimal price of anarchy in cost-sharing games,” in 2019 American Control Conf. (ACC), Philadelphia, PA, USA, pp. 2277–2282, 2019. [Google Scholar]

28. Z. Wu, R. H. Mohring, C. Ren and D. Xu, “A convergence analysis of the price of anarchy in atomic congestion games,” Mathematical Programming, vol. 199, pp. 1–57, 2022. [Google Scholar]

29. A. Belov, K. Mattas, M. Makridis, M. Menendez and B. Ciuffo, “A micro simulation based analysis of the price of anarchy in traffic routing: The enhanced Braess network case,” Journal of Intelligent Transportation Systems, vol. 26, no. 4, pp. 448–460, 2021. [Google Scholar]

30. T. Roughgarden, “Intrinsic robustness of the price of anarchy,” JACM, vol. 62, no. 5, pp. 1–42, 2015. [Google Scholar]

31. R. Cominetti, V. Dose and M. Scarsini, “The price of anarchy in routing games as a function of the demand,” Mathematical Programming, pp. 1–28, 2021. [Google Scholar]

32. R. Colini-Baldeschi, R. Cominetti, P. Mertikopoulos and M. Scarsini, “When is selfish routing bad? The price of anarchy in light and heavy traffic,” Operations Research, vol. 68, no. 2, pp. 411–434, 2020. [Google Scholar]

33. R. Colini-Baldeschi, R. Cominetti and M. Scarsini, “Price of anarchy for highly congested routing games in parallel networks,” Theory of Computing System, vol. 63, no. 1, pp. 90–113, 2019. [Google Scholar]

34. M. Takalloo and C. Kwon, “Sensitivity of wardrop equilibria: Revisited,” Optimization Letters, vol. 14, no. 3, pp. 781–796, 2020. [Google Scholar]

35. Z. Wu, R. H. Möhring, Y. Chen and D. Xu, “Selfishness need not be bad,” Operations Research, vol. 69, no. 2, pp. 410–435, 2020. [Google Scholar]

36. D. Paccagnan, R. Chandan, B. L. Ferguson and J. R. Marden, “Optimal taxes in atomic congestion games,” ACM Transactions on Economics and Computation, vol. 9, no. 3, pp. 1–33, 2021. [Google Scholar]

37. S. Shen, L. Huang, H. Zhou, S. Yu, E. Fan et al., “Multistage signaling game-based optimal detection strategies for suppressing malware diffusion in fog-cloud-based IoT networks,” IEEE Internet Things, vol. 5, no. 2, pp. 1043–1054, 2018. [Google Scholar]