Visual Motion Segmentation in Crowd Videos Based on Spatial-Angular Stacked Sparse Autoencoders

1  Introduction

Crowd behavior analysis (CBA) is one of the most significant and critical topics for ensuring that large events in public areas run smoothly, peacefully, and without casualties. Furthermore, CBA is a multidisciplinary topic that concentrates on a variety of domains, including biology, sociology, and computer vision. Among the important applications of CBA is visual motion segmentation (VMS), which provides a significant amount of information about crowd dynamics in both natural and human communities. Generally, one person’s information can only convey a limited amount of local information about the scene. On the other hand, individuals are recognized as union members when crowd motion arises, and they share the same characteristics that are extremely significant for research across many fields. VMS aims to break down a visual image into cohesive subsets corresponding to rigidly and independently moving targets. The pedestrians within each set show collective behaviors and similar motion paths. VMS is an essential preprocessing for a variety of computer vision applications, and it has become a burgeoning study topic in the last few decades. When moving objects are semantically and independently categorized, we obtained motion segments that we can utilize in a variety of video-surveillance tasks, including motion analysis, video indexing, traffic monitoring, activity recognition, crowd counting, crowd tracking, abnormal event detection, disasters recognition, and semantic scene segmentation [1–4].

Even though VMS has progressed considerably [5–10] in the past few years, further improvements are still required to accomplish satisfactory performance. The major challenge in VMS is when the target is too small scaled. Because of the high occlusion in crowd images, state-of-the-art (SOTA) approaches use feature points, which then combined into one group using similar motions to avoid directly detecting pedestrians. Depending on how the objects move in the scene, both structured and unstructured crowd images can be formed. A structured crowd scene has consistent spatiotemporal motion patterns formed by objects that move in concert over the whole scene. Put another way, every spatial location in any structured crowd scene has an identical motion pattern, and the motion’s direction does not change most of the time (Fig. 1a). An unstructured crowd scene, on the other hand, consists of non-uniform spatiotemporal motion patterns formed by irregularly moving objects whose movement direction continually changes and cannot be anticipated (Fig. 1b).

Figure 1: The motion patterns are exhibited as tracklets; every color represents a particular pattern. (a) Structured crowd (b) unstructured crowd

With the evolution of surveillance devices, massive amounts of human trajectory data have been captured, making it vitally difficult and crucial to extract valuable data. A human trajectory is a set of sequenced spatio-temporal data from a single person. Human trajectories provide insight into a variety of real-world applications. An effective way to analyze human trajectories is through trajectory clustering. Trajectory clustering approaches are classified into three groups based on the availability of labeled data: supervised, unsupervised, and semi-supervised. The learning of supervised models occurs before trajectory clustering. Labeled data is typically employed to train a function that creates clusters by mapping data to labels. Then, this function is utilized to predict the clusters of unlabeled data. The objective of unsupervised models is to cluster data without the aid of humans or labeled data. By analyzing unlabeled datasets, an inference function can be built, which can then be used to group data. The former two models are combined through semi-supervised modeling, which is modified using unlabeled data after learning it on labeled data [11]. However, traditional clustering methods would struggle to achieve satisfactory performance if the original data were not evenly distributed owing to high intravariance, as shown on the left side of Fig. 2.

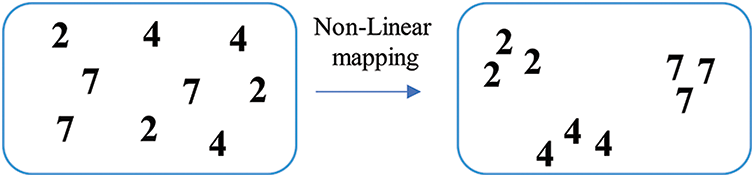
Figure 2: The distribution of the original data is on the left side. Because of the large intravariance, it is hard to separate the data properly. By performing a non-linear transformation function, the points are compacted in a new space with regard to the appropriate cluster centers, as shown on the right side

To address the earlier issue, we aim to map the spatial-angular feature space to a new feature space that is more suited for clustering tasks. The sparse-autoencoder network is a strong contender to solve the above issue. It uses iterative learning to learn both the encoder (EN) and the decoder (DE) to provide a non-linear transformation function. EN is actually the non-linear transformation function, and DE requires reconstructing precise data from the feature representation produced by the EN. Repeating this procedure ensures that the transformation function is reliable and can accurately represent the data. This paper proposes an effective model to cluster human trajectories in different crowd places based on spatial-angular stacked sparse autoencoders (SA-SSAE). When using high-dimensional large-scale datasets, conventional clustering techniques suffer from major performance concerns. For instance, dimensionality reduction techniques must be used prior to using the clustering algorithm to extract features from raw data [12]. Deep learning has always been at the heart of tackling these concerns [13], so we used stacked sparse autoencoders (SSAE) to extract features from the spatio-temporal trajectory data and to group the trajectories together based on their shared characteristics.

The contributions of our work are as follows:

•   An efficient framework called SA-SSAE for VMS has been proposed. The SA-SSAE framework is indispensable for high-level crowd behavior analysis. The proposed framework’s capacity to handle pedestrian flows that are randomly dispersed is one of its main attractions. To our knowledge, this is the first study that leverages stacked sparse autoencoders for visual motion segmentation in crowd videos using trajectory data employing the Chinese University of Hong Kong (CUHK) crowd benchmark.

•   The generalized Kanade-Lucas-Tomasi key point tracker (gKLT) is applied to the input video sequences to extract the trajectories of motion patterns. Individual trajectory formation is a primary concern in the VMS. For studying and analyzing crowded environments, the accurate extraction of individual trajectories over time is crucial. In this study, the generalized KLT tracker is applied to video sequences to construct individual trajectories.

•   Dataset with ground-truth annotations is presented to validate our framework’s performance. The Hajj, a significant pilgrimage to Mecca in Saudi Arabia, is one of Islam’s five pillars. Every year, up to four million pilgrims carry out the Hajj rituals. As a result, it ranks as one of the most significant pedestrian issues worldwide. Therefore, we collected our Hajj dataset from real-world crowd scenes in Mecca. The dataset includes 21 crowd videos with different scenes and scenarios.

•   Our framework is evaluated using two real-world datasets with various crowd densities. On both datasets, we found that our framework can construct high-quality clusters and outperform existing methods quantitatively.

The remainder of the paper is laid out as follows: Section 2 discusses related work. Section 3 presents the proposed spatial-angular stacked sparse autoencoder model for VMS. Comparative results are discussed in Section 4. Concluding remarks are presented in Section 5.

2  Related Work

The various methods for VMS are reviewed in this section. The VMS approaches can be categorized into three main subsets depending on the density of movement flows. Approaches addressing a maximum of five humans are described under the domain of low-level density (LLD). Approaches that address between five and fifteen humans are characterized as mid-level density (MLD). Likewise, approaches that target more than fifteen humans fall under the subset of high-level density (HLD) [14].

LLD Approaches: Nguyen et al. proposed a consensual approach for visual motion segmentation in dynamic views [15]. The model combined unsupervised techniques to address the label correspondence issue. Seyedhosseini et al. put forward a discriminative learning scheme, called CHM, for semantic segmentation. It benefits from contextual data at various resolutions in a hierarchy. The ability of CHM to optimize a posterior probability at various resolutions is its major feature. It effectively and greedily implements this optimization. CHM trains a number of classifiers at various resolutions and uses the gained findings to learn a classifier at the original resolution [16]. An approach for motion segmentation by employing optical flow orientations was proposed by Narayana et al. [17]. The over-segmentation of an image into depth-dependent units was addressed by the utilization of optical flow orientations. Their approach could automatically obtain the quantity of foreground motions. Meunier et al. proposed a CNN-based fully unsupervised approach for VMS from optical flow. Meunier et al. hypothesized that the optical flow input could be expressed as a set of parametric motion models, commonly quadratic or affine. The basic principle of their method is to utilize the Expectation-Maximization to rationally build a loss function and a training procedure for their ground-truth-free neural network for VMS [18]. Choudhury et al. proposed a method for VMS by combining the advantages of appearance-based and motion-based segmentation. They put forward supervising a network of image segmentation with the function of predicting areas that are likely to have simple motion patterns and so are likely to match with targets [19].

MLD Approaches: Mukherjee et al. presented a linear-time video segmentation approach [20] that uses a Gaussian mixture model (GMM) to cluster each video sequence. It also utilizes recursive filtering to re-obtain the parameters of the GMM. In addition to updating the variance iteratively and creating or removing clusters as needed, their hybrid approach can uniquely propagate Gaussian clusters through each subsequent frame. However, a distance threshold parameter is required as its primary input. A cluster similarity criterion, which may be based on a user-defined distance metric, controls how new clusters are included and removed. A unified conditional random field (CRF model) was proposed by [21] for multiple-targets joint-tracking and segmentation in complex video sequences. The model utilizes low-level image features to associate each super pixel with a particular objective or to designate it as a background.

HLD Approaches: A statistical approach established using the Lagrangian-particle-dynamics [22] for flow segmentation and detection of flow instability was presented in [9]. The flow field created by the crowd motion is handled as an aperiodic dynamical system. To determine the Lagrangian coherent structures existent in the underlying flow, a Finite Time Lyapunov exponent field is built using the greatest eigenvalue of the tensor. In a normalized cuts framework, the Lagrangian coherent structures are used to identify the boundaries of the flow segments by dividing the flow into regions with markedly distinct dynamics. Establishing correspondences between flow segments over time allows for the detection of any alteration in the number of flow segments, called instability. From the point of vision, [6] carefully looked at groups’ basic and universal aspects that are present in several crowd environments. These aspects are essential to comprehending congested environments and are driven by sociopsychological investigations. Moreover, a group discovery approach was put forward by learning the collective transition priors.

The VMS problem may alternatively be considered a trajectory clustering (TC) challenge. Determining a proper metric to calculate the similarity of trajectories with different attributes and a proper method to cluster the trajectories on the basis of their commonalities are the two primary issues in TC [23]. Most VMS approaches explored to date either have limited applicability to certain categories of crowd scenes or suffer from major performance concerns. Based on spatial-angular stacked sparse autoencoders, this study provides a model for clustering human trajectories in various crowd environments. The proposed framework is effective and robust for various crowd scene scenarios.

3  Proposed Spatial-Angular Stacked Sparse Autoencoder Model for VMS

The proposed intelligent VMS framework is described in detail in this section. The SSAE network is built based on spatial-angular motion information and is used to find clusters of similar instances in an unlabeled dataset. The framework is illustrated in Fig. 3. Five main steps are involved in constructing the proposed framework: generating trajectories, refining the generated trajectories, obtaining spatial-angular motion information, applying spatial-angular stacked sparse autoencoders, and softmax layer. SA-SSAE is proposed to automatically segment motion patterns, expressed as trajectories. The SA-SSAE framework employs the generalized KLT tracker (gKLT tracker [24]), which is proposed as an improvement to the standard KLT tracker [25]), owing to its computing efficiency and tracking accuracy. Every generated trajectory is made up of a set of 2D spatial coordinates {(x1,y1),(x2,y2),…,(xk,yk)}, where L ∈ [1, k] is the trajectory length. The following sub-section describes each step where trajectories are refined following Shao et al.’s approach. The motion point features that are made from the new trajectories are then used to make both spatial and angular features. This valuable motion information is then fed into the stack sparse autoencoder network to output motion segments.

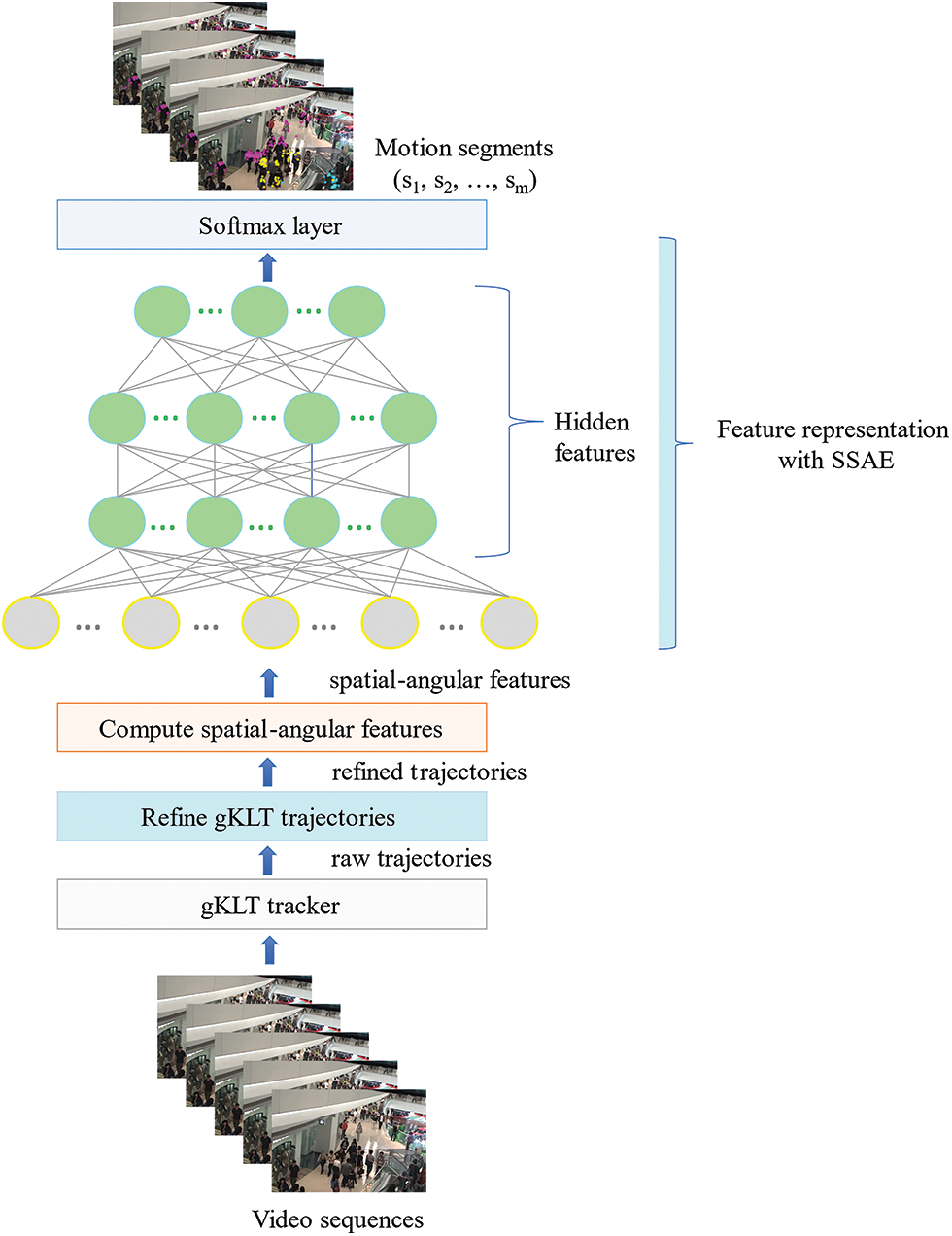
Figure 3: Flowchart of the SA-SSAE framework

3.1 Generating Trajectories

A major challenge in the VMS is the formation of individual trajectories. The precise extraction of individual trajectories over time is critical for investigating and examining crowded scenarios. Following state-of-the-art papers [6,26–28], we utilize the gKLT due to its efficacy in determining trajectories, particularly for small objects in crowd images. The gKLT was first proposed by [25]. First, gKLT obtains the feature points in the moving foreground with enough texture data to detect. The feature points are then tracked, and their velocities are calculated frame by frame based on their displacements. A collection of tracked feature points is thus acquired. The gKLT tracker commences with a group of sparse features in the present frame fi and seeks to locate their positions in the subsequent frame fi + 1 by matching a patch of an image surrounding a feature to its identical image patch in the subsequent frame. The assumption of brightness constancy indicates that the intensities of the patches in the subsequent image will not vary significantly. Utilizing a patch enables differentiation between surrounding points of equivalent intensity. The ω(x) window function, which is commonly a Gaussian function, is employed to highlight nearby pixels more than far-off ones. This explains why points nearer to the feature point are likelier to exhibit comparable motion than those further away. Calculating the error function is the next step in the matching:

ε(d)=∑f(x0)[fi+1(x+d)−fi(x)]2ω(x−x0ηw)(1)

through the window function’s support ω(x0), which is positioned over the feature point x0. The estimated displacement d for the feature point at x0 in picture fi is obtained by decreasing the weighted nonlinear least squares formula. The simulation results (Fig. 4) show that the gKLT algorithm effectively tracks feature points that indicate crowd movement.

Figure 4: gKLT algorithm simulation results

3.2 Refining the Generated Trajectories

Through the former processing, a collection of tracked feature points was obtained. Nevertheless, the points gKLT generated do not accurately describe the pedestrians because, in some cases, there could be numerous points inside the same part of a moving person. Moreover, the points can be located in the background or formed owing to changes in illumination, producing noisy, short, and static tracklets. In our framework, following Shao et al. [6], such tracklets are filtered out, which increase VMS’s overall performance.

3.3 Obtaining Spatial-Angular Motion Information

The spatial locations of motion features are obtained from the newly refined trajectories. The spatial location features of a trajectory are critical because trajectories that are spaced far apart, even if they are identical in shape, often do not belong to the same cluster. The spatial location features for each trajectory ti can be calculated using the following equation:

spti(vi)=1k∑j=1k⁡(vi)(2)

where vi = [xi, yi], and k is the trajectory length. The spti(vi) denotes the spatial location feature vector. Angular features describe the direction of the crowd’s motion [28]. To compute the average feature, the average displacement A¯ti of a trajectory is obtained first using Eq. (3) below:

A¯ti=1(n−1)∑s=2n⁡((xsti−x(s−1)ti),(ysti−y(s−1)ti))(3)

The average displacement vector A¯ contains two components u¯ and v¯. Now, using Eq. (3), the average angular can be calculated based on the following equation [28]:

Θti={cos−1(A¯⋅A^||A¯||∗||A^||)∗180π,v¯>0[2π−cos−1(A¯⋅A^||A¯||∗||A^||)]∗180π,u¯≠0,v¯≤00,u¯,v¯=0(4)

A^ indicates the horizontal direction’s unit vector. The value of Θti∈[0,2π−1] differs based on the values of the vectors u¯ and v¯. Furthermore, a Θti value of zero indicates the absence of motion.

3.4 Spatial-Angular Stacked Sparse Autoencoders

In our sparse-autoencoder with smoothed l2-regularization technique, m numbers of input spatial-angular training features {Xm}m=1M are given such that {(x(1),y(1)),(x(2),y(2)),…,(x(m),y(m))}, where x(i)∈R, and yi∈{1,2,3,…,C} are the labels. These training samples are fed into the proposed stacked sparse-autoencoders network. The encoder and decoder are two main components of the sparse-autoencoder training process. The encoder maps the input data into the hidden representation while the decoder reconstructs data from the hidden representation. The hidden encoder vector calculated from Xm is denoted by the letter hm. X^m indicates the output layer decoder vector. Therefore, the following is the encoding procedure:

hm=fe(WeXm+be)(5)

fe shows the encoding function, We is the encoding weight parameter, and be represents the corresponding bias. The following is a description of the decoder process:

X^m=fd(Wdhm+bd)(6)

fd represents the decoding function. Wd and bd are the decoding weight and bias, respectively.

The sparse-autoencoder model minimizes the reconstruction error to learn a meaningful hidden representation. Thus, to diminish the reconstruction error and resolve the parameters We, Wd, be, and bd, the sparse-autoencoder’s parameter settings are optimized as follows:

ϕ=argmin1m∑k=1m⁡L(Xk,Xk^)(7)

L(Xk,Xk^) represents the loss function, where L(Xk,Xk^)=||X−X^||. Fig. 5 presents the SSAE architecture. SSAE in our framework is built by stacking two sparse-autoencoders into m hidden layers using an unsupervised learning method called “layerwise learning”, which is subsequently fine-tuned utilizing a supervised method. By including a regularizer in the cost-function, it is feasible to promote an autoencoder’s sparsity. This regularizer is based on a neuron’s average output activation value, described as follows:

ρi=1k∑i=1k⁡hn(1)(xj)=1k∑i=1k⁡fe(wn(1)Txi+bn(1))(8)

where k represents the overall quantity of the training patterns. xi is the ith training pattern, wn(1)T is the nth row of the weight matrix W1, and bn(1) is the nth element of the bias vector b(1). The sparse-autoencoder uses back-propagation (bp) to lessen the cost-function, and it can be computed as follows:

Jsparse=[1N∑i=1N⁡12||hW,b(xi−x^i)||2]+λ2∑l=1nl−1⁡∑i=1s1⁡∑j=1sl+1⁡(Wji(l))2+υ∑j=1n⁡S(aj)(9)

where the first expression of Eq. (9) presents the average sum-of-squares error, λ is a variable to control the relative weight of the regularization. Incorporating the l2-weight regularizer makes the solution “smoother” and improves its generalization ability. υ is the sparsity penalty term’s weight. The λ and υ can be specified while training the sparse-autoencoder. S(⋅) denotes the sparsity regularizer that regulates the sparsity of the hidden layer output. S has a low value for every neuron “specializing” in the hidden layer, it produces a high output for a few training samples. On account of this, a lower sparsity fraction promotes a high level of sparsity. aj presents the average output of the jth-hidden-unit and can be obtained using Eq. (10) below:

aj=1k∑i=1k⁡uj(i)(10)

where u is the jth-hidden-unit-output of an ith-training pattern. The parameters l2-weight regularize, and sparsity regularize are utilized to prevent overfitting. The stack sparse-autoencoders are linked to a softmax layer that predicts the probabilistic assignments of clusters. The softmax layer’s mathematical model is as follows [29]:

Oθ(xi)=[p(yi=1|xi;θ)p(yi=2|xi;θ)p(yi=3|xi;θ)⋅⋅⋅p(yi=r|xi;θ)]=1∑i=1r⁡eθjTxi[eθ1Txieθ2Txieθ3Txi⋅⋅⋅eθrTxi](11)

where {θ1,θ2,…,θr} represents the model parameters and the expression 1/∑i=1r⁡eθjTxi normalizes the distribution to guarantee that the sum is equal to one.

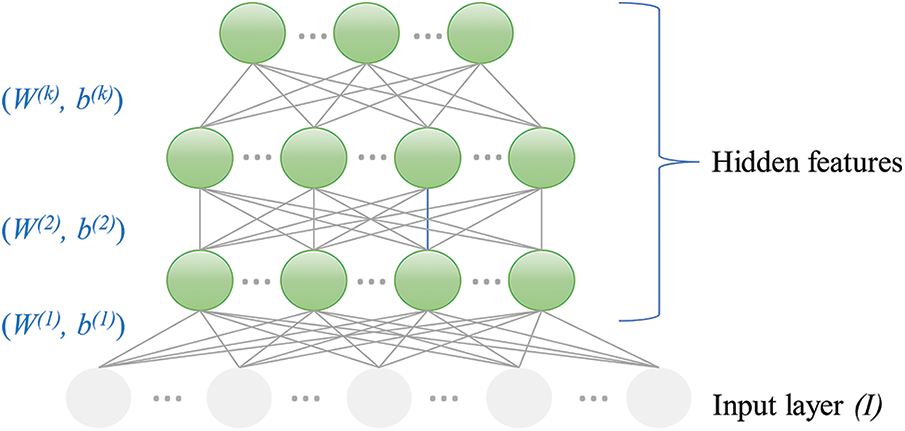
Figure 5: Stacked sparse autoencoder architecture

4  Experiments

In the dense crowd scenes, individuals are a gathering of many groups with similar motion characteristics. Groups are essential components of a crowd. A novel crowd segmentation framework based on spatial-angular stacked sparse autoencoders was presented in this paper to obtain fundamental crowd interactions for subsequent crowd behavior analysis. The proposed framework can be applied to various dense crowd scenes. In this section, we extensively evaluate the performance of the proposed framework for VMS on two crowd video datasets: the Hajj and the CUHK crowd datasets.

4.1 Motion Segmentation Benchmarks

Hajj Benchmark: The Hajj benchmark consists of crowd videos shot in various indoor and outdoor locations in Mecca. Islam’s Hajj, a major pilgrimage to Mecca in Saudi Arabia, is one of the five pillars of Islam. The Hajj rituals are performed annually by up to four million pilgrims. Consequently, it is one of the most significant global pedestrian issues. The benchmark has 21 real-world crowd videos with various scenarios and situations. It has several challenges, including occlusions, lighting, and various object scales. The Hajj benchmark videos contain six scenes, as shown in Fig. 6.

Figure 6: A few examples of Hajj benchmark frames. The original frames of crowded indoor and outdoor scenes are on the right, and the motion patterns are on the left

CUHK Benchmark: The CUHK is a set of crowd videos that includes 55 videos captured by Shao et al. [6], as well as former crowd benchmarks that have already been released from the following SOTA studies [9,24,30,31]. The CUHK collection has 300 annotated crowd clips with different crowd densities, and the benchmark has the groups for each clip’s motion pattern segmentation. These 300 video clips are used to validate the proposed model following the SOTA approaches in [6,14,28]. Based on the crowd dynamics, these clips are grouped into structured and unstructured groups. Additionally, each scene is grouped into indoor and outdoor subcategories based on the location of the recording and the nature of its content. Fig. 7 shows examples of crowd images from the CUHK benchmark.

Figure 7: CUHK benchmark sample frames

4.2 Evaluation Methods and Results

VMS is evaluated as a clustering issue, and the performance evaluation can be achieved by utilizing widely well-known cluster assessment measures: Purity, Rand Index (RI), Normalized Mutual Information (NMI), accuracy, and F-measure [14,32,33]. A larger value denotes better clustering performance; all performance measurements lie within the range [0, 1]. The values of the training parameters for the sparse autoencoders are listed in Table 1. Purelin function and logistic sigmoid function, respectively, serve as the transfer functions for the encoder and decoder. A linear transfer function known as the Purelin function is defined as follows:

f(z)=z(12)

The Logistic sigmoid function is given as:

f(z)=11+e−z(13)

Moreover, scaled conjugate gradient descent (SCGD) was employed for the autoencoder training process to optimize the weights and bias by minimizing Jsparse(W, b) in Eq. (9). The encoder attempts to encode the considerable input features into a smaller hidden representation with only the related information. The decoder turns the process back to reproduce the same set of features as the input. After training, weights will be assigned to every neuron in the hidden layer, enabling them to provide an efficient stimulus against input visual information. The feature set produced from the first sparse AE’s weights is utilized to train the second sparse AE. The first sparse AE’s feature t-Distributed Stochastic Neighbor Embedding (t-SNE) plot is shown in Fig. 8a. The t-SNE demonstrates very clearly that the feature set exhibits good discriminatory behavior. The size of the hidden layers for the first sparse AE is 30, and the size of the hidden layers for the second sparse AE is 10, leading to a smaller representation of the features. A significant difference that may be seen in the t-SNE plots in Figs. 8a and 8b is that the features are compressed about the appropriate cluster centers in the new feature space. Fig. 9 presents some visual motion segmentation results of real-life crowd scenes from the CUHK and Hajj crowd benchmarks. Different colors stand for different motion segments. It is clear that the proposed SA-SSAE framework works very well compared to the ground truth segmentation groups.

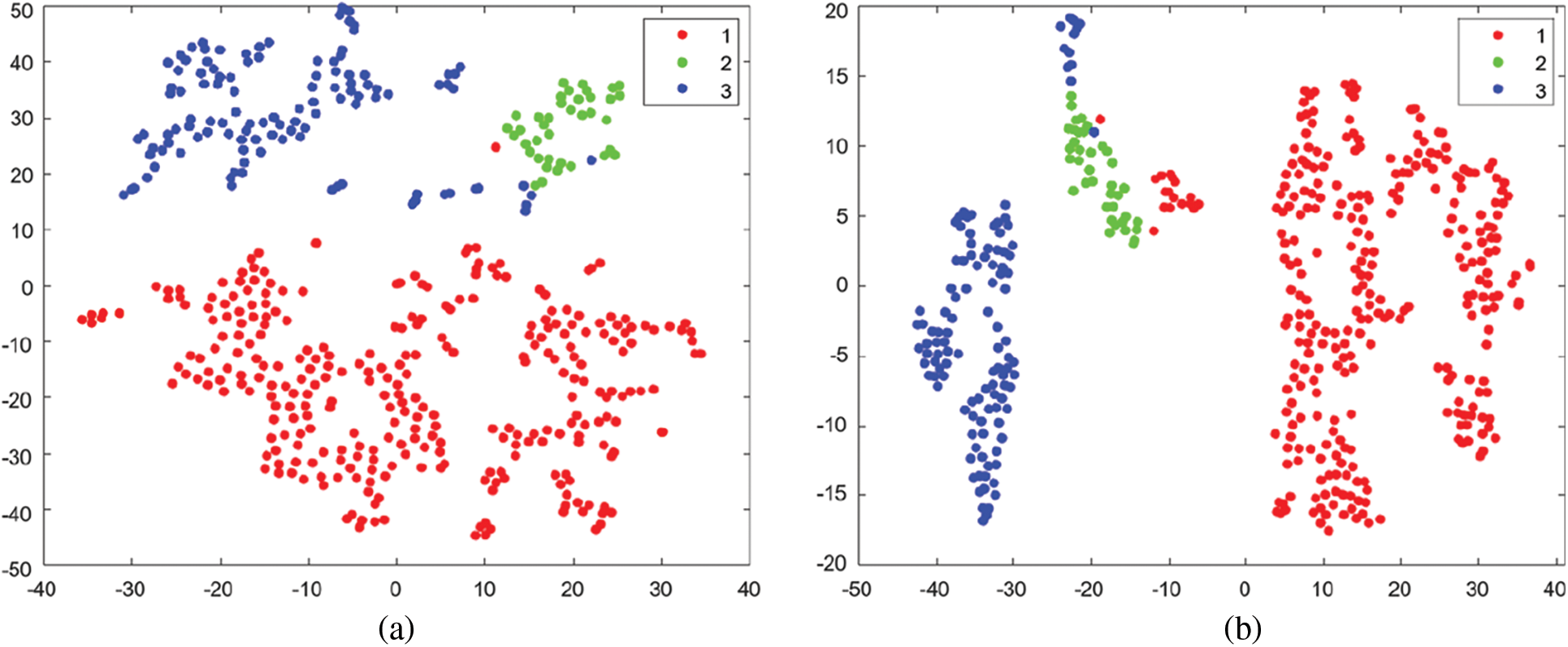
Figure 8: The t-SNE plot of features produced from (a) the first sparse AE, (b) the second sparse AE, using the “exact” method, which maximizes the Kullback-Leibler divergence (KLD) of distributions between the original data space and the embedded data space

Figure 9: Visual motion segmentation results based on the proposed framework

4.2.1 Results on Hajj Crowd Benchmark

Table 2 compares the results and shows the average performance for 21 crowd videos of the Hajj benchmark. It indicates that the proposed model surpasses the recent SADC approach for VMS by a large margin in terms of purity, NMI, and RI. Upon closer examination, we discovered that the NMI-performance-metric always produces a value of zero when one of the two grouping assignments (ground truth or clustering outcome) has only one cluster and the other clustering has multiple clusters. This is not permitted when calculating the NMI. This is because of an underlying mathematical problem with how mutual information is computed. However, such a debate is outside the purview of this study.

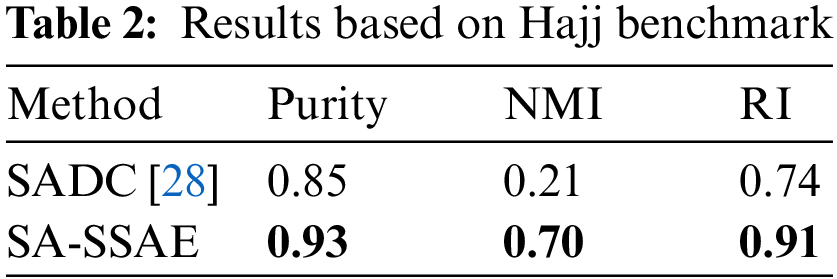
4.2.2 Results on CUHK Crowd Benchmark

To demonstrate the efficacy of the proposed model, its performance results are compared to the following SOTA methods: MCC [24], CT [6], and SADC [28]. As shown in Table 3, the proposed SA-SSAE model outperforms all other approaches. As mentioned previously, the NMI will equal zero if one of the two clustering assignments has only one cluster and the other clustering has more than one. With 25% of the overall videos in the CUHK benchmark having one group ground-truth, this explains why other approaches give smaller values for NMI.

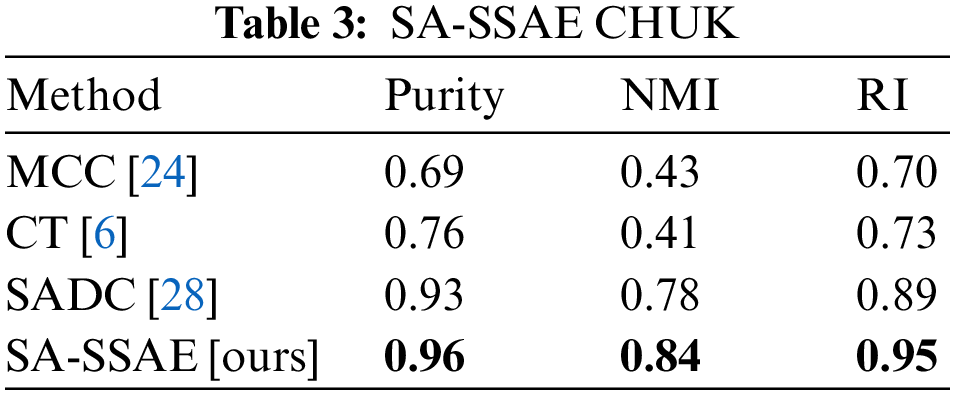
Table 4 presents a comparative assessment in terms of the Acc and F-measure using nine relevant approaches HC [34], CF [35], CT [10], CDC [26], MCC [24], AMR [36], HSIM [14], MPF-l1 [33], and MPF-l2 [33]. Additionally, Fig. 10 illustrates the relative improvement of the SA-SSAE model over the other approaches. The proposed model gets the highest Acc and F-measure values, which shows that it is better at getting motion pattern segments. It is well known that performance decreases when pedestrian distribution varies. All SOTA approaches [10,24,26,33–36] disregard the changes in the distribution of individuals, which only remains true if the motion flow is coherent across time. Such variations generate isolated areas, which in turn, lower overall performance. Furthermore, the SOTA approaches [10,24,26,33–36] cannot group structurally comparable pixels into significative segments. Discovering and segregating isolated pedestrian segments presents a highly complicated issue. Even though the HSIM approach is emphasized for its ability to handle randomly distributed pedestrian flows, our SA-SSAE model achieves better results regarding the F-measure. The relative improvement of the SA-SSAE framework compared to the HSIM approach is 0.36.

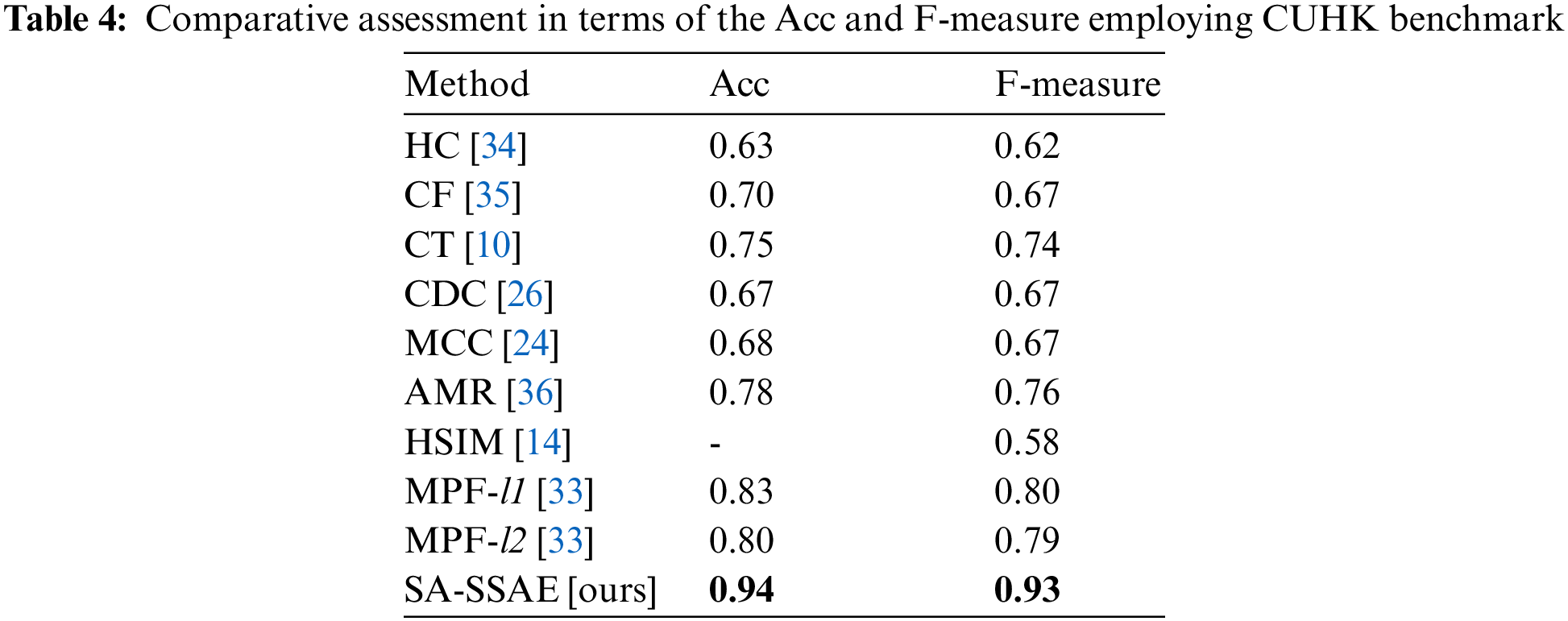
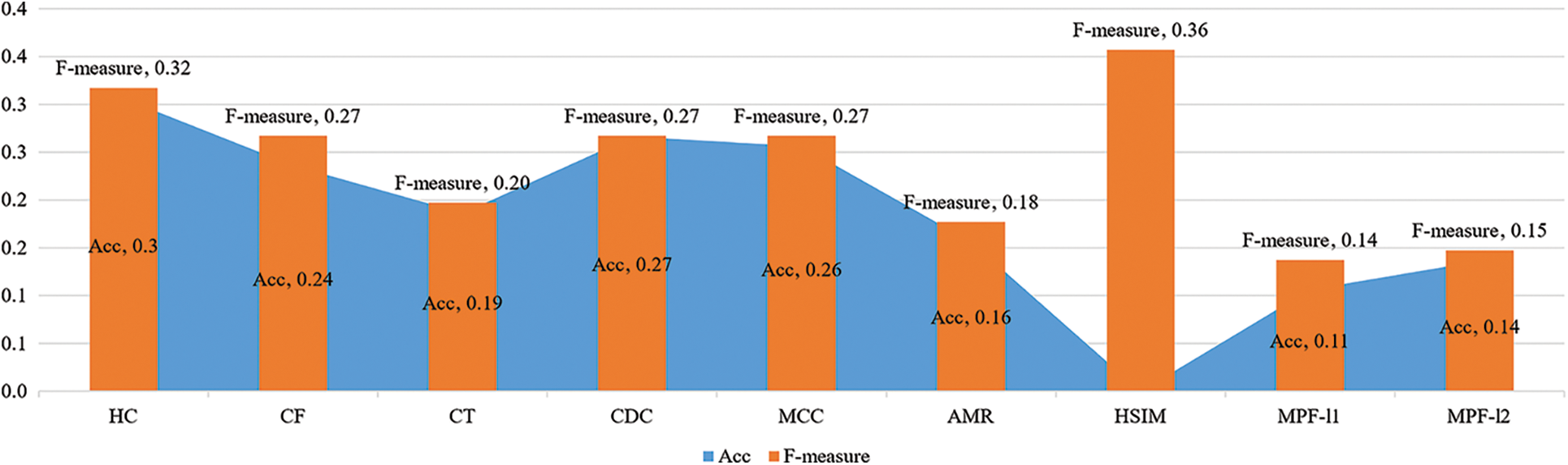
Figure 10: The relative improvements of the SA-SSAE model compared to HC, CF, CT, CDC, MCC, AMR, HSIM, MPF-l1, and MPF-l2

Fig. 11 depicts the comparison findings across several crowd scenario categories (mass movement, street, street-market, station, mall, public pathway, cross-walk, and escalator). The proposed SA-SSAE model performs the best among the other three approaches for all the crowd scenario categories. Moreover, the proposed model provides robust results for all evaluated metrics because it considers the trajectory history for several known frames, which is a significant factor in the model’s training. The NMI results for the mass movement category for MCC and CT approaches are very low (close to zero). The SADC approach succeeds in increasing the results of NMI to 0.59. However, SA-SSAE outperforms SADC by 0.38, which proves our model’s efficiency.

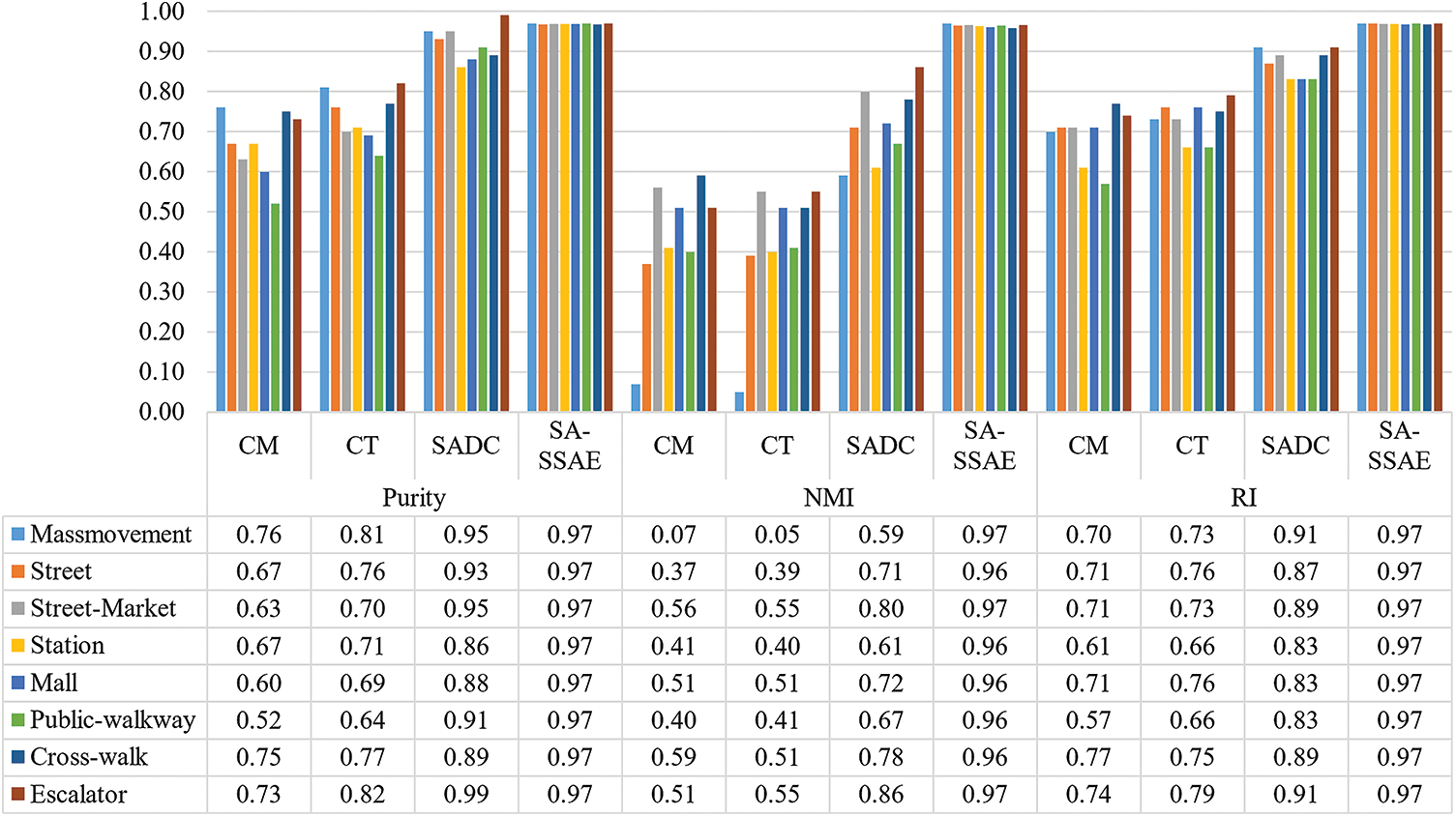
Figure 11: Quantitative comparison according to the scene type (mass movement, street, street-market, station, mall, public-walkway, cross-walk, escalator)

Similarly, Figs. 12 and 13 compare the findings across several crowd scenario categories, structured or unstructured, as well as indoor or outdoor, respectively. SA-SSAE excels in all categories.

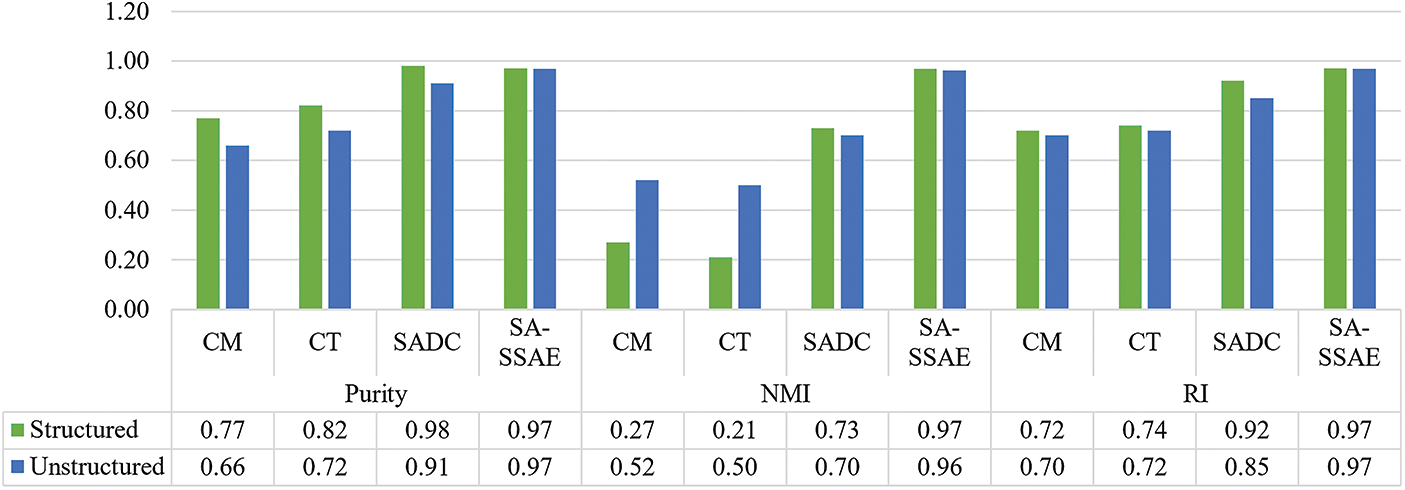
Figure 12: Quantitative comparison according to the crowd movement (structured or unstructured)

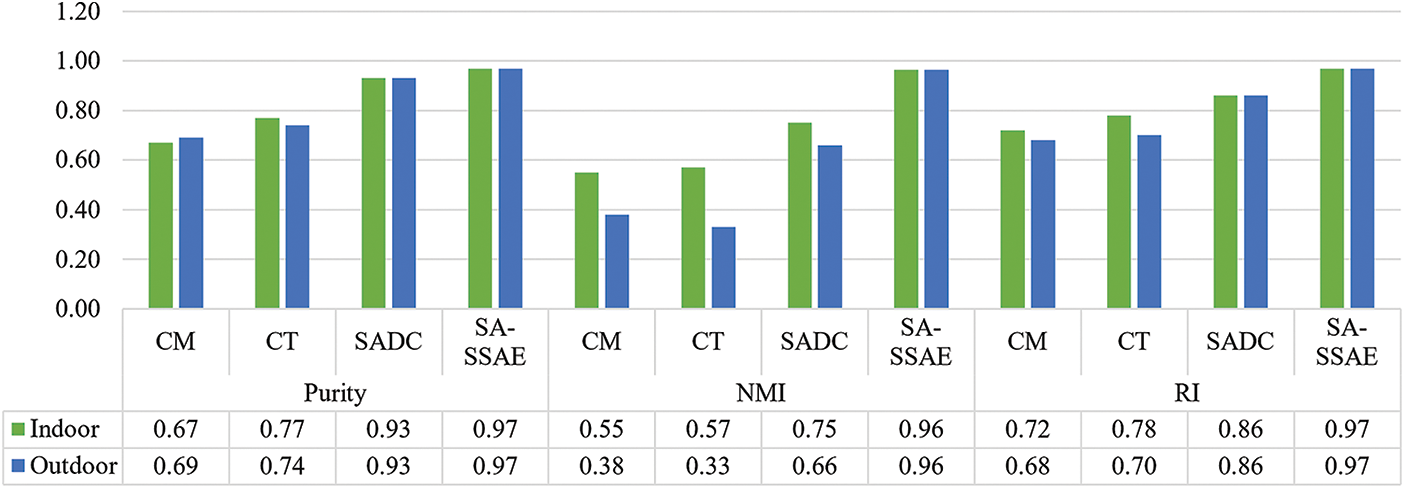
Figure 13: Quantitative comparison according to the crowd location (indoor or outdoor)

4.2.3 Sparsity Parameter Study

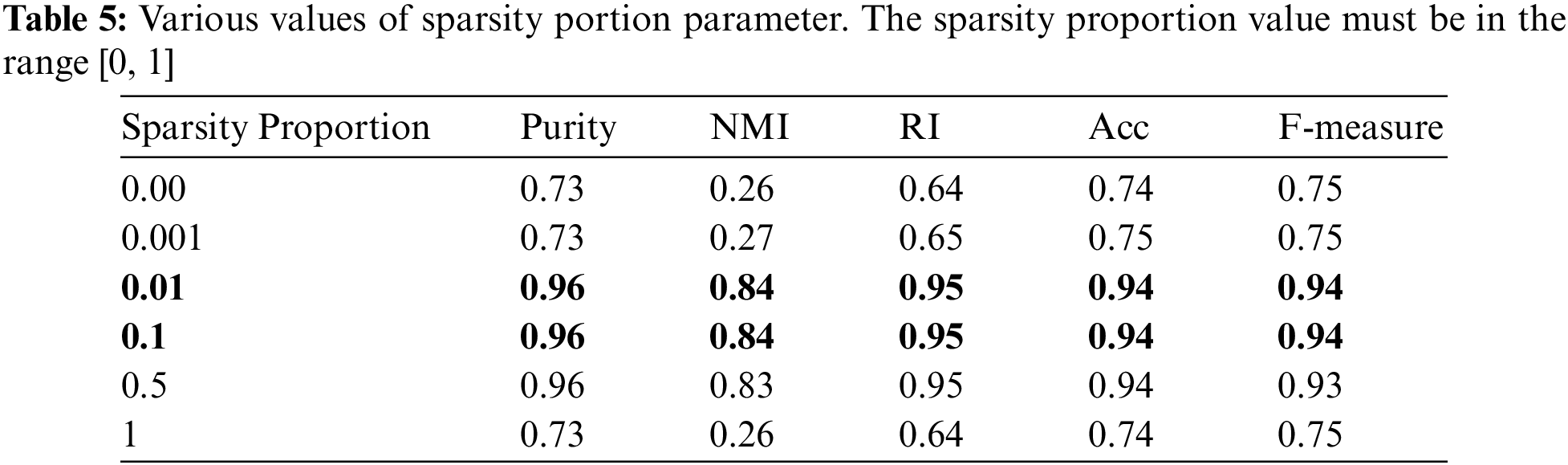
The optimal value of the sparsity proportion parameter for the SA-SSAE model was determined via comparative experiments using the CUHK benchmark. Table 5 illustrates that the sparsity proportion gives the best results for all performance metrics when its value is between 0.01 and 0.1. Thus, 0.01 was determined for the sparsity proportion parameter.

5  Conclusion

This study proposed a deep learning framework for VMS using spatial-angular stacked sparse autoencoders. The framework is meant to aid in proactive stampede avoidance to enhance people’s safety in crowd scenes. In this study, it is suggested to decompose the motion tracks in a given crowd scene into groups. Each group contains trajectories with similar behavioral characteristics. We prove that sparse stack autoencoders can be adopted effectively for VMS and provide better results than traditional clustering methods. According to experimental results, the proposed SA-SSAE model is superior to the comparative methods in terms of purity, NMI, RI, accuracy, and F-measure. Future research will focus on methods for integrating our VSM framework with outlier detection. Another crucial element that we will consider for increasing robustness is camera motion. To further improve the performance of the segmentation results, new features will be researched by utilizing other feature descriptors. Moreover, future research can be implemented by investigating the performance of the Kalman filter and YOLO (You Only Look Once) for VMS.

Acknowledgement: The authors thank the Deputyship of Research & Innovation, Ministry of Education in Saudi Arabia, for funding this research work through Project Number 758. The authors also would like to thank the Research Management Center of Universiti Teknologi Malaysia for managing this fund under Vot. No. 4C396.

Funding Statement: This research work is supported by the Deputyship of Research & Innovation, Ministry of Education in Saudi Arabia (Grant Number 758).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Anthwal and D. Ganotra, “An overview of optical flow-based approaches for motion segmentation,” The Imaging Science Journal, vol. 67, no. 5, pp. 284–294, 2019. [Google Scholar]

2. M. Munsif, H. Afridi, M. Ullah, S. D. Khan, F. A. Cheikh et al., “A lightweight convolution neural network for automatic disasters recognition,” in The 10th European Workshop on Visual Information Processing (EUVIP), Lisbon, Portugal, pp. 1–6, 2022. [Google Scholar]

3. A. Al-Dhamari, R. Sudirman and N. H. Mahmood, “Abnormal behavior detection using sparse representations through sequential generalization of K-means,” Turkish Journal of Electrical Engineering and Computer Sciences, vol. 29, no. 1, pp. 152–168, 2021. [Google Scholar]

4. A. Raza, M. Rafiq, J. Awrejcewicz, N. Ahmed and M. Mohsin, “Dynamical analysis of coronavirus disease with crowding effect, and vaccination: A study of third strain,” Nonlinear Dynamics, vol. 107, no. 4, pp. 3963–3982, 2022. [Google Scholar] [PubMed]

5. S. Wu and H. San Wong, “Crowd motion partitioning in a scattered motion field,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 42, no. 1, pp. 1443–1454, 2012. [Google Scholar]

6. J. Shao, C. C. Loy and X. Wang, “Learning scene-independent group descriptors for crowd understanding,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 27, no. 6, pp. 1290–1303, 2017. [Google Scholar]

7. A. Hafeezallah, A. Al-Dhamari and S. A. R. Abu-Bakar, “Multi-scale network with integrated attention unit for crowd counting,” Computers, Materials & Continua, vol. 73, pp. 3879–3903, 2022. [Google Scholar]

8. A. Hafeezallah, A. Al-Dhamari and S. A. R. Abu-Bakar, “U-ASD net: Supervised crowd counting based on semantic segmentation and adaptive scenario discovery,” IEEE Access, vol. 9, pp. 127444–127459, 2021. [Google Scholar]

9. S. Ali and M. Shah, “A lagrangian particle dynamics approach for crowd flow segmentation and stability analysis,” in IEEE Conf. on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, pp. 1–6, 2007. [Google Scholar]

10. J. Shao, C. Change Loy and X. Wang, “Scene-independent group profiling in crowd,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Columbus, OH, USA, pp. 2219–2226, 2014. [Google Scholar]

11. J. Bian, D. Tian, Y. Tang and D. Tao, “A survey on trajectory clustering analysis,” arXiv Prepr. arXiv1802.06971, 2018. [Google Scholar]

12. H. Li, J. Liu, R. W. Liu, N. Xiong, K. Wu et al., “A dimensionality reduction-based multi-step clustering method for robust vessel trajectory analysis,” Sensors, vol. 17, no. 8, pp. 1792, 2017. [Google Scholar] [PubMed]

13. M. Irfan and M. Munsif, “Deepdive: A learning-based approach for virtual camera in immersive contents,” Virtual Reality & Intelligent Hardware, vol. 4, no. 3, pp. 247–262, 2022. [Google Scholar]

14. H. Ullah, M. Ullah and M. Uzair, “A hybrid social influence model for pedestrian motion segmentation,” Neural Computing and Applications, vol. 31, no. 11, pp. 7317–7333, 2019. [Google Scholar]

15. T. M. Nguyen and Q. J. Wu, “A consensus model for motion segmentation in dynamic scenes,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 26, no. 12, pp. 2240–2249, 2015. [Google Scholar]

16. M. Seyedhosseini and T. Tasdizen, “Semantic image segmentation with contextual hierarchical models,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 38, no. 5, pp. 951–964, 2015. [Google Scholar] [PubMed]

17. M. Narayana, A. Hanson and E. Learned-Miller, “Coherent motion segmentation in moving camera videos using optical flow orientations,” in Proc. of the IEEE Int. Conf. on Computer Vision, Sydney, NSW, Australia, pp. 1577–1584, 2013. [Google Scholar]

18. E. Meunier, A. Badoual and P. Bouthemy, “EM-driven unsupervised learning for efficient motion segmentation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 45, no. 4, pp. 4462–4473, 2022. [Google Scholar]

19. S. Choudhury, L. Karazija, I. Laina, A. Vedaldi and C. Rupprecht, “Guess what moves: Unsupervised video and image segmentation by anticipating motion,” arXiv Prepr. arXiv2205.07844, 2022. [Google Scholar]

20. D. Mukherjee and Q. M. J. Wu, “Streaming spatio-temporal video segmentation using Gaussian mixture model,” in IEEE Int. Conf. on Image Processing (ICIP), Paris, France, pp. 4388–4392, 2014. [Google Scholar]

21. A. Milan, L. Leal-Taixé, K. Schindler and I. Reid, “Joint tracking and segmentation of multiple targets,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Boston, MA, USA, pp. 5397–5406, 2015. [Google Scholar]

22. S. C. Shadden, F. Lekien and J. E. Marsden, “Definition and properties of lagrangian coherent structures from finite-time lyapunov exponents in two-dimensional aperiodic flows,” Physica D: Nonlinear Phenomena, vol. 212, no. 3–4, pp. 271–304, 2005. [Google Scholar]

23. Y. Tang, Z. Pan, W. Pedrycz, F. Ren and X. Song, “Viewpoint-based kernel fuzzy clustering with weight information granules,” IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 7, no. 2, pp. 342–356, 2022. [Google Scholar]

24. B. Zhou, X. Tang, H. Zhang and X. Wang, “Measuring crowd collectiveness,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 36, no. 8, pp. 1586–1599, 2014. [Google Scholar] [PubMed]

25. C. Tomasi and T. Kanade, “Detection and tracking of point,” Int. J. Comput. Vis., vol. 9, pp. 137–154, 1991. [Google Scholar]

26. Y. Wu, Y. Ye and C. Zhao, “Coherent motion detection with collective density clustering,” in Proc. of the 23rd ACM Int. Conf. on Multimedia, Canada, pp. 361–370, 2015. [Google Scholar]

27. W. Lin, Y. Mi, W. Wang, J. Wu, J. Wang et al., “A diffusion and clustering-based approach for finding coherent motions and understanding crowd scenes,” IEEE Transactions on Image Processing, vol. 25, no. 4, pp. 1674–1687, 2016. [Google Scholar]

28. A. K. Pai, A. K. Karunakar and U. Raghavendra, “Scene-independent motion pattern segmentation in crowded video scenes using spatio-angular density-based clustering,” IEEE Access, vol. 8, pp. 145984–145994, 2020. [Google Scholar]

29. S. R. Saufi, Z. A. Bin Ahmad, M. S. Leong and M. H. Lim, “Low-speed bearing fault diagnosis based on ArSSAE model using acoustic emission and vibration signals,” IEEE Access, vol. 7, pp. 46885–46897, 2019. [Google Scholar]

30. M. Rodriguez, J. Sivic, I. Laptev and J. -Y. Audibert, “Data-driven crowd analysis in videos,” in 2011 Int. Conf. on Computer Vision, Barcelona, Spain, pp. 1235–1242, 2011. [Google Scholar]

31. B. Zhou, X. Wang and X. Tang, “Understanding collective crowd behaviors: Learning a mixture model of dynamic pedestrian-agents,” in IEEE Conf. on Computer Vision and Pattern Recognition, Providence, RI, USA, pp. 2871–2878, 2012. [Google Scholar]

32. M. J. Zaki and W. Meira Jr, Data Mining and Machine Learning: Fundamental Concepts and Algorithms. Cambridge, UK: Cambridge University Press, 2020. [Google Scholar]

33. Q. Wang, M. Chen, F. Nie and X. Li, “Detecting coherent groups in crowd scenes by multiview clustering,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 1, pp. 46–58, 2018. [Google Scholar] [PubMed]

34. W. Ge, R. T. Collins and R. B. Ruback, “Vision-based analysis of small groups in pedestrian crowds,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 34, no. 5, pp. 1003–1016, 2012. [Google Scholar] [PubMed]

35. B. Zhou, X. Tang and X. Wang, “Coherent filtering: Detecting coherent motions from crowd clutters,” in European Conf. on Computer Vision, Florence, Italy, pp. 857–871, 2012. [Google Scholar]

36. M. Chen, Q. Wang and X. Li, “Anchor-based group detection in crowd scenes,” in IEEE Int. Conf. on Acoustics, Speech and Signal Processing (ICASSP), USA, pp. 1378–1382, 2017. [Google Scholar]