Intelligent Networked Control of Vasoactive Drug Infusion for Patients with Uncertain Sensitivity

1  Introduction

Hypertension is an important global health challenge because its prevalence and impact on cerebral, cardiovascular and renal damage are still the leading risk factor for death and disability worldwide [1]. About one billion adults globally suffer from hypertension [2]. It is primarily brought on by obesity and raises the risk of heart disease, stroke, and kidney disease. If the systolic blood pressure (SBP) reaches or exceeds 180 mmHg and/or the diastolic blood pressure (DBP) reaches or exceeds 120 mmHg, the hypertension of the patient is deemed severe. Approximately three-quarters of these patients have no symptoms or a severe or imminent change in organ dysfunction or damage; this is known as severe asymptomatic hypertension (SAH).

Mean arterial blood pressure (MAP) is one of the most important hemodynamic parameters in the individual body that should be controlled strictly for the duration of several clinical conditions like anaesthesia management and postoperative healing [3]. An acute type of high blood pressure is post-surgery hypertension which leads to severe complications such as bleeding, cerebrovascular issues, vascular suture lines disruption, and subendocardial ischemia. Therefore, maintaining the MAP of critically ill patients at normal levels is crucial in the medical field. Severe trauma, chronic diseases, and/or side effects of certain medical drugs can cause the human body may fail to regulate blood pressure, and hypertension can lead to heart disease and stroke [4]. So vasoactive drug sodium nitroprusside (SNP) infusion system is well known to be used for hypertensive patients to decrease the mean arterial blood pressure [5]. Despite the infusion of SNP being the most effective technique in lowering the MAP for most patients by reducing the tension in the blood vessel walls, it is a challenge to deal manually with variable patient sensitivities or uncertain clinical situations in different scenarios [6].

1.1 Related Work

Recently, significant works have been presented to design an automated control system of the drug infusion system to handle challenges in drug infusion systems, such as time-varying sensitivity, complexity, and the existence of measurement noise. A classical proportional-integral-derivative PID controller has been applied in [7], where nonlinear PID digital control is presented in [8]. Also, traditional rule-based control strategies have been proposed for drug infusion systems [9]. Robust multiple-model adaptive architecture is investigated in [10], while the fractional order based PID controller is developed in [11]. In addition, a hardware-in-the-loop simulation has been applied for controlling the MAP [12]. A PressorSim software [13] was designed for simulating and monitoring hypotensive patient blood pressure response to intravenous (IV) drugs such as SNP.

Fuzzy systems are one of the adequate soft computing techniques that allow designers and/or researchers to develop a good controller for nonlinear systems based on human experience and knowledge instead of a convenient mathematical approach [14]. In the case of an undermined or ill-defined mathematical model of complex systems, fuzzy logic can be applied to define the relation between input and output. Therefore, due to the uncertainty and inevitably vague of the medical system, the fuzzy rule-based controller is a powerful and victorious technique to be applied in a medical application such as signal processing, medical image processing, diagnosis, therapy, and control as it can handle much of uncertainty exist in biological systems [15–18]. All aforementioned fuzzy controllers can be classified as a type-1 fuzzy control. However, the main issue of type-1 fuzzy controllers is their limitation in the presence of a higher degree of uncertainty in nonlinear systems [19]. They have a deficiency in describing the model because of its partial representation ability. Hence, interval type-2 fuzzy (IT2F) techniques present an extension to a type-1 fuzzy and have the ability to well-defining parameter uncertainties and the nonlinearity of the model [20]. Then, IT2F controllers can be more effective than typer-1 fuzzy counterparts in many real-world applications [21–23]. Additionally, there has been significant research work on IT2F controllers, as they can deal with the uncertainty in a class of nonlinear systems [24–26]. With the use of the lower and upper membership functions, IT2F can effectively capture the parameter uncertainties which result from different sources, such as measurement error, noise, and imprecise models. Also, IT2F systems provide some unique partitions of the input discourse, which type-1 fuzzy systems cannot offer [25]. Based on these advanced capabilities, IT2F systems have been applied in several medical applications [27–29]. Nevertheless, many of the existing systems still suffer from large setting time, instability, inaccurate or incompatibility to a wide range of physiological variations in patient conditions and patient response to IV drugs. Furthermore, medical devices are always placed near the patient to monitor and control his health signals, while the medical staff must interact with the patient directly.

Nowadays, with infectious diseases and COVID-19 outbreaks, there is a necessity to use telemedicine techniques and the remote control of medical devices to avoid the spread of infection among physicians, nursing staff, and patients. Therefore, the use of network-connected systems and telemedicine have recently emerged worldwide in healthcare and clinical procedures [30]. A networked control system (NCS) is a closed-loop system in which the feedback control loops are connected by a communication network such that the control and feedback signals of the system are transmitted among all its components through a common TCP/IP network. The design and analysis of NCSs have gained significant attention in the last decade [31,32]. Moreover, there are many advantages of applying NCS in the medical field, such as reducing the capacity of wired systems near the patient’s bedside, easy troubleshooting and maintenance of medical devices and being more reliable as compared to traditional controllers and minimizing direct contact with critically infected patients.

Metaheuristic optimization algorithms, e.g., swarm intelligence [33], present an efficient technique for auto-tuning parameters of NCS in complex medical procedures, such as the automatic management of SNP infusion rates for hypertensive patients. Teaching-learning-based optimization (TLBO) is a recent metaheuristic optimization algorithm [34]. The TLBO algorithm was proposed to simulate the effect of the influence of a teacher on learners during the learning process. It has been employed to solve many optimization problems, such as tuning PID and fuzzy controllers for different power systems [35,36]. Here, the TLBO algorithm plays an important role in automatically finding the best parameter values of the proposed controller.

The main challenges for a feedback control system are to propose a powerful controller to reduce the complexity of the proposed systems in the existence of several uncertainties, such as various patient sensitivities, outside disturbances, or noise effects. This work aims to propose a networked Interval type2 fuzzy (IT2F) controller. According to the literature studies, the IT2F controller is capable of managing uncertainties in an effective way, and the networked system will reduce the complexity of the proposed scheme. An effective control system requires tuning controller parameters to get optimal values for achieving a good closed-loop response. The TLBO algorithm is used to obtain the optimal controller’s parameters. The proposed controller is conducted to study the robustness performance for noise rejection at the control output and feedback. As a result, the objective of this work is to construct an intelligent networked control system to keep the patient’s MAP at the required level in a closed-loop manner and reduce the effect of noise and perturbation.

1.2 Contributions of This Study

This study aims at developing a new networked IT2F control system for automated vasoactive drug infusion remotely. The proposed IT2F controller achieved the following advancements:

•   Handling hypertensive MAP of patients under different drug sensitivities and noise disturbance.

•   Smooth recovery of blood pressure levels using the proposed vasoactive drug-controlled system with short settling times.

•   Optimizing the parameter values of networked IT2F controller using TLBO algorithm.

•   Conducting a comparative study with traditional PID and Type-I fuzzy controllers in a networked drug infusion system to verify the outperformance of the developed IT2F control.

The remainder of this article is organized as follows. Section 1 presents basic definitions and background of IT2F control, networked control system, and the optimization algorithm of TLBO. Section 2 describes the mathematical patient model linked to the developed drug delivery system. Section 3 demonstrates simulation results and evaluations for all tested cases of anti-hypertensive drug infusion, comparing with the performance of traditional networked controllers under the same circumstances. Sections 4 and 5 give a discussion and conclusions of study findings, respectively, highlighting the future directions of this research work.

2  Preliminaries

2.1 Interval Type-2 Fuzzy Control

Professor J. M. Mendel and his coworkers have proposed the first complete type-2 fuzzy inference process, developed various type-2 fuzzy systems, and established their computational principles and foundations since the mid-1990s. In [37], a designed model is successfully used for modelling imprecision and uncertainties utilizing the IT2F system. With the interval between lower and upper membership functions, IT2F uses the footprint of uncertainty which does not exist in a type-1 fuzzy set. Structurally, IT2F contains an extra component called type-reducer which distinguishes it from type-1 fuzzy, where the form of the rules is the same for both types. Likewise, the secondary membership function of the interval type-2 fuzzy set is constant. A schematic diagram of the basic IT2F control system is shown in Fig. 1.

Figure 1: Basic structure of Interval Type-2 Fuzzy (IT2F) control system

In the IT2F system, the fuzzy set (A~) is bounded by the upper MF (μ¯A~) and lower MF (μ_A~). For K rules, the steps of the singleton fuzzification procedure are summarized next to compute the output control signal of the IT2F logic controller [37]:

1.   Evaluate the membership interval of xi′ on each IT2 fuzzy set A~ik,[μ_A~ik(xi′),μ¯A~ik(xi′)], where (i=1,⋯,N;k=1,⋯,K) and N is a number of input variables.

2.   Compute the firing interval of the kth rule at x=x′ using product t-norm:

[f_k,f¯k]=[μ_A~1k(x1′)×⋯×μ_A~Nk(xN′),μ¯A~1k(x1′)×⋯×μ¯A~Nk(xN′)](1)

3.   Apply type-reducer algorithm to convert the IT2F output set into type-1 reduced fuzzy set:

yll=∑i=1LLf¯ky_k+∑i=LL+1Kf_ky_k∑i=1LLf¯k+∑i=LL+1Kf_k(2)

yrr=∑i=1RRf_ky¯k+∑i=RR+1Kf¯ky¯k∑i=1RRf_k+∑i=RR+1Kf¯k(3)

where y¯k and y_k are the upper and lower value of the interval for the consequence term of IT2F system, yll and yrr are the left and right endpoints for the type-reduced sets. The Kernik-Mendel (KM) algorithm [38,39] is applied to find the switched points (LL, RR) for yll and yrr.

4.   Obtain the defuzzied output:

y=yrr+yll2(4)

where y is a crisp output from the IT2F controller.

2.2 Networked Control Systems

A networked control system (NCS) is a system in which the feedback control system is formed by a communication network, and all signals of the system are transmitted among all components through a common network [31]. The proposed NCS for the drug infusion system is shown in Fig. 2. It has many advantages as compared to traditional controllers, minimizing direct contact with infected patients or dangerous dynamical systems. Therefore, there are numerous potential applications in which the NCS can be applied, such as aerospace systems, power grid systems, smart cities and electric vehicles. With the spread of infectious diseases nowadays, the use of NCS in medical engineering has become an urgent necessity to avoid the spread of infection from patients to the operator. In addition, with the advanced progress of developing internet of medical things (IoMT) devices, the NCS plays an important role in modern healthcare to enable mobility, interoperability, and more flexibility for accomplishing the effectiveness of the medical care.

Figure 2: Networked control system (NCS) for delivering the drug to patients based on a communication link between the measured blood pressure and activating drug infusion pump

2.3 Teaching-Learning-Based Optimization Algorithm

The TLBO algorithm is developed by Rao et al. [34] and it is based on the teacher’s influence on students’ performance. In this optimization method, the population of the optimization problem is described by a set of students, the class subjects offered to students represent the design variables, and the outcome of the student is equivalent to the ‘fitness’ value of the optimization problem. The teacher presents the best solution for the entire population. In addition, the design variables are the parameters involved in the objective function of the given optimization problem, and the best answer is the best value of this objective function. The TLBO algorithm is split into two sections, which are the Teacher phase and the Student phase, as shown in Fig. 3. The TLBO is a simple optimization technique and does need many initialized parameters to be adjusted compared to other metaheuristic optimization techniques. TLBO uses the mean value (Mean) of the population, as given (5), where Xnew and Xold present the new and existing solutions, respectively. Xteacher is the best solution. TF is a teaching factor, and r is a random number between zero and 1.

Figure 3: Main workflow of Teaching-Learning Based Optimization algorithm

Xnew=Xold+r(Xteacher–(TF)Mean)(5)

To achieve a suitable closed-loop response, it is necessary to adjust the controller parameters to obtain optimal values. The TLBO algorithm is utilized for obtaining the optimal parameters of the controller. The study investigates the performance of the proposed controller in terms of noise rejection at the control output and feedback to determine its robustness. Thus, our goal is to create an intelligent networked control system that maintains the patient’s MAP at the required level in a closed-loop fashion while minimizing the impact of noise and disturbance. The TLBO algorithm is used to find the best parameter values of the proposed networked Interval Type 2 fuzzy (IT2F) controller for an anti-hypertensive drug delivery system. An objective function fobj of the optimization problem is defined as the integral time absolute error (ITAE), which is the summation of the absolute error weighted by the elapsed time. The proposed controller scheme is constructed to minimizing the disparity between the target blood pressure value and the actual measurement of the patient’s blood pressure with quick responsiveness under the presence of external disturbances and variation of patient parameters. To fulfill this goal, the gains of the IT2F controller (Ke, Kde, Kp, KI, and KW) have been fine-tuned using the TLBO algorithm to get the best values of the gains that achieve the required response.

3  Methods

3.1 Vasoactive Drug Response Model

In this paper, a continuous third-order single-input-single-output (SISO) transfer function with time delay is addressed to conduct the response of change in patient’s MAP to infusion rates of SNP drug [38], as expressed by

GPR(s)=ΔPMAP(s)USNP(s)=Ksen(1+Td3s)e−sτd(1+Td1s)[(1+Td3s)(1+Td2s)−αp](6)

where ΔPMAP is the change of patient’s MAP due to the effect of SNP drug, USNP the input signal (drug infusion rate); τd pure delay constant; Td1,Td2 and Td3 time constants of a vasoactive drug infusion system; αp is recirculation fraction of drug; Ksen is a sensitivity parameter of the patient to drug.

So, the mean arterial pressure (MAP) for a patient under a vasoactive drug Infusion System is described as

PMAP=ΔPMAP+Pini(7)

where Pini is the patient’s initial MAP in the absence of drug intervention, which is fixed at 150 mmHg [2], Fig. 4 shows the schematic diagram of the patient’s MAP model (open loop).

Figure 4: Block diagram of patient’s drug response model

According to the parameters of the patient model in [2], the system’s time constants are given to be known and time-invariant (Td1 = 50 s, Td2 = 30 s, Td3 = 10 s) and the time-delay parameterτd = 60 s. For simulations purpose, the sensitivity factor Ksen of the patient to SNP drug is assumed to be equal to −0.25 mmHg/ml/h. The main objective of the controller is to regulate the patient’s MAP and attain a value of 100 mmHg from the initial value of 150 mmHg. Nevertheless, the performance criteria for Vasoactive Drug Infusion System, given in Table 1, must be achieved in synthesizing the closed-loop control system. MAP regulation performance has some criteria that must be achieved as follow: MAP for a controlled system must not be below 70 mmHg, settling time must be less than 600 s, the steady-state error must be within ±5 mmHg of the desired level (100 mmHg) and overshoot is not more than 10 mmHg. The adjustment and control of SNP dose by a human operator is imprecise and can lead to possibly fatal results such as an overdose of a drug (more than 180 mlh−1) being toxic to the patient. Also, manual adjustment is tedious, time-consuming, and may cause a poor response. Hence, it is required to design an adequate feedback controller that will overcome the problems of manual control and maintain MAP at the desired level effectively and accurately.

3.2 Proposed Drug Delivery System

In this section, the proposed networked (IT2F) controller for a drug infusion system is developed. The target of the proposed technique is to remotely control the vasoactive drug infusion system to maintain the patient’s MAP at 100 mmHg. The block diagram that describes the operation of the networked control drug system to regulate MAP is given in Fig. 5. The blood pressure sensor and actuator, i.e., a drug infusion pump, are connected to the controller through a communication network that activates the drug infusion pump remotely. The desired value of blood pressure is established in the controller by the operator or physician, which is far away from the patient. Therefore, this technique will reduce direct contact with the patient and prevent the spread of infection from/to patients.

Figure 5: Block diagram of proposed networked Interval Type-2 Fuzzy (IT2F) controller for anti-hypertensive drug infusion system

The controller scheme aims to be robust and get a fast response with a low error between the desired value and the measured blood pressure of the patient. For this purpose, the IT2F controller is proposed and implemented in a networked system, as shown in Fig. 6. The designed gains of the IT2F controller (Ke, Kde, Kp, KI, and KW) have been tuned by the TLBO algorithm, as described above. The proposed controller has two inputs, error (e) and rate of change of error (∆e), with the use of three triangular membership functions, which are given in Fig. 7, for error and change of error, respectively. Table 2 illustrates the FLC rules governing the relationship between the inputs and the infusion rate of the injected drug to the patient. The output of IT2F has five singleton membership functions, and the surface of the IT2F system is shown in Figs. 7 and 8, respectively. This control action, the output of IT2F controller Uaction, is sent via a network to the SNP drug pump to regulate the patient’s MAP.

Figure 6: Block diagram of networked Interval Type-2 Fuzzy (IT2F) controller

Figure 7: Membership Functions of networked Interval Type-2 Fuzzy (IT2F) controller

Figure 8: Control surface for networked Interval Type-2 Fuzzy (IT2F) controller

4  Results and Evaluation

As shown in Fig. 5, the designed networked IT2F controller and TLBO algorithm have been implemented using MATLAB/Simulink environment and toolbox for IT2F Logic Systems [40] and TrueTime simulator for networked control systems [41]. This section presents the simulation results of a networked IT2F control scheme for a vasoactive drug infusion system, compared with classical PID and type-1 fuzzy controllers. The measured values of high blood pressure are sent via the network to the tested controller to compare with the targeted value of MAP is 100 mmHg. Then the controller takes action by activating the infusion pump of the SNP drug to regulate the patient’s blood pressure remotely. For validating the robust performance of the networked IT2F controller, the following results have been divided into three sub-sections to show different sensitivities of the patient to infused SNP drug and the influence of external noise on the performance of the controlled drug delivery system.

4.1 Normal Patient Sensitivity

For the case of fixed or normal patient sensitivity (Ksen = −0.25 mmHg/mlh−1), Fig. 9 shows the response of the proposed IT2F controller for regulating high MAP compared with PID and type-1 fuzzy controllers. Also, the corresponding drug infusion rates produced by three tested controllers are shown in Fig. 9. Table 3 illustrates the characteristics of each tested controller in this study, including optimized control parameters, settling time, maximum overshot or undershot of regulated blood pressure, and steady-state error. Classical PID control caused a relatively long settling time of 515 s with a small hypotension of 7.20 mmHg because a high drug infusion rate is released at about 126.6 mlh−1. In the case of the fuzzy type-1 controller, no hypotension is produced in an intermediate settling time of 319 s, and the drug infusion of 101.25 mlh−1 is achieved. However, this controller could not reach the targeted MAP and has a relatively high value of the steady-state error of 0.63 mmHg. In contrast, the proposed networked IT2F control showed a good performance by achieving a minimal settling time of 221 s and a very small hypotension of 0.85 mmHg is resulted. The steady-state error and maximum drug rate are 0.08 mmHg and 127.2 mlh−1, respectively, within accepted medical ranges.

Figure 9: Blood pressure response and its corresponding drug infusion rates under fixed patient sensitivity

4.2 Presence of External Noise

External noise is added here to the measured MAP to simulate practical scenarios of a clinical environment and to test the stability of all networked controllers. Therefore, a white noise signal with a variance of 1 mmHg is added to the proposed drug delivery system, which results in peak-to-peak 7.0 mmHg. For the case of normal patient sensitivity with the predefined noise signal, the MAP output and drug infusion rate for all tested controllers are shown in Fig. 10. Optimized PID control can regulate MAP successfully within accepted medical ranges, but it takes a long settling time of 370 s and the steady error of approximately 0.8 mmHg. Fuzzy type-1 showed a noisy drug infusion rate with a variance of 20 mlh−1 and the highest value of the steady-state error of 1.4 mmHg among other controllers, as illustrated in Table 4. The proposed IT2F controller is still the best option to handle measured noisy MAP with a minimum settling time of 345 s and the lowest value of the steady-state error of approximately 0.5 mmHg, while it infuses high maximum drug infusion of 146 mlh−1 under the maximum accepted range of 180 mlh−1.

Figure 10: Blood pressure response and its corresponding drug infusion rates of all tested controllers in the presence of external noise

4.3 Variable Patient Sensitivity

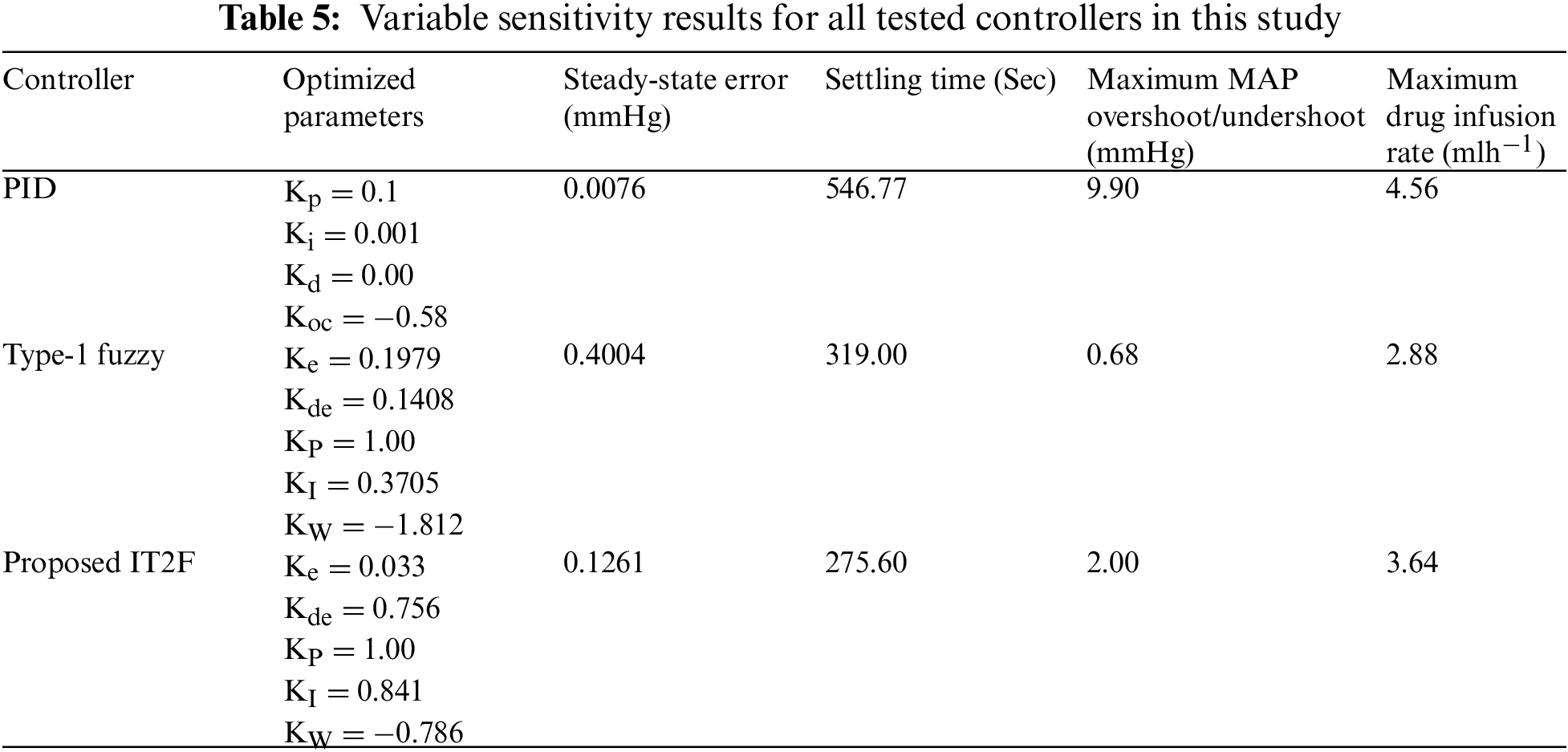
Varying patient sensitivity presents a challenging task for expert physicians to identify the suitable and safe vasoactive drug infusion rates during short-term hypertension treatment. Hence, a customized trajectory of patient sensitivity variations [29] is assumed to test all networked controllers in this study, as depicted in Fig. 11. Classical PID controller caused the highest peak value of hypertension case of 9.9 mmHg because of the high drug infusion rate (4.56 mlh−1), as shown in Fig. 12. The settling time response of PID control is long about 547 s, but approximately no steady-state error is achieved in this case, as illustrated in Table 5. The performance of fuzzy type-1 control can handle varying patient sensitivity smoothly in both profiles of regulated MAP and a minimum drug infusion rate of 2.88 mlh−1. Although the IT2F controller infused a peak drug rate of 3.64 mlh−1, it fits well the clinical requirement to achieve targeted MAP in a short settling time and minimal steady-state error of 276 s and 0.12 mmHg, respectively, as given in Table 5.

Figure 11: Trajectory of variable patient sensitivity to the infused vasoactive drug

Figure 12: Blood pressure response and its corresponding drug infusion rates of all tested controllers under variable patient sensitivity

5  Discussion

The above results demonstrated that the proposed networked control of the vasoactive drug delivery system is stable, and its performance is within accepted ranges for all three techniques. The TLBO algorithm has been applied to ensure estimating optimal values of all networked control parameters under different clinical scenarios of the anti-hypertensive drug delivery system, as defined in (5). The output performance of the networked IT2F controller is the best among classical PID and type-1 fuzzy controllers, as shown in Figs. 9, 10 and 12. The settling time of measured MAP decay is relatively short, with the lowest variations in the blood pressures under all tested three cases, as illustrated in Tables 3 to 5. Additionally, the robustness of the proposed IT2F controller is verified under two cases of adding external noise signal and varying uncertain patient sensitivity. This conducts the advantages of IT2F controller to handle uncertain patient sensitivity in a noisy environment remotely, without a need for direct contact with the medical staff.

The developed networked IT2F controller gives a better and faster performance than other techniques, and it also compensates for the noise in the blood pressure without fluctuating the rate of the SNP drug. In two treatment cases of fixed patient sensitivity and the presence of noise, Type-1 fuzzy controller could not give sufficient drug infusion rate to reach the targeted MAP, especially high fluctuations in drug infusions of traditional fuzzy control may cause a breakdown in the drug pumps, as shown Fig. 10b. On the contrary, the benefits of IT2F control are verified to give a smooth profile of regulated MAP and regular drug infusion rates, as depicted in Figs. 9 and 10.

The aim of this article is to remotely automate an anti-hypertensive drug delivery system via an optimized IT2F controller while keeping all medical constraints, i.e., MAP decay and maximum drug infusion rates, within accepted ranges under all possible clinical situations. That includes normal and variable patient sensitivities with the presence of external noise during blood pressure measurements. Adaptation of the IT2F control structure is still under development to follow any unexpected action in the controlled system, especially for medical applications. Therefore, merging fuzzy sets with deep neural networks in a deep neuro-fuzzy scheme has been recently proposed [42]. Also, converting control gain parameters of IT2F (see Fig. 6) to fractional values can improve its performance to handle the tolerance in the uncertainty [43]. However, the performance of the proposed networked fuzzy controller is still valid and superior to traditional control methods for achieving the targeted treatment of the vasoactive drug delivery system, as illustrated in Tables 3 to 5.

6  Conclusions and Future Work

In this study, a new IT2F controller-based networked system for automated vasoactive drug infusion has been developed to regulate the MAP of hypertensive patients successfully. The developed drug infusion system can remotely control the blood pressure of a patient under different clinical conditions, i.e., uncertain drug sensitivity and the existence of noise signals. The proposed scheme is capable of achieving the main goal, which is stabilizing the MAP to its nominal value of 100 mmHg. In order to achieve an efficient control scheme, the control parameters are tuned using the effective and powerful TLBO algorithm. IT2F controller can manage uncertainties in an effective way, and the networked system will reduce the complexity of the proposed scheme. The IT2F networked control system has the advantages of reduced wiring, ease of maintenance, and more flexibility compared to controlled bedside medical systems that will help physicians treat the patient more quickly. Simulation results showed the outperformance of the IT2F controllers against networked PID and type-1 fuzzy controllers under the same conditions. Also, the designed control system gives better and faster responses than other controllers in case of noise disturbance. For future work, the fractional type-2 fuzzy technique can be applied to enhance the robustness of the drug delivery system. The practical implementation of the developed networked control system is the main prospect of this study to regulate the MAP of hypertensive patients.

Acknowledgement: The authors would like to thank the Deanship of Scientific Research at Shaqra University for supporting this work.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. K. T. Mills, A. Stefanescu and J. He, “The global epidemiology of hypertension,” Nature Reviews Nephrology, vol. 16, no. 4, pp. 223–237, 2020. [Google Scholar] [PubMed]

2. G. D. Rodrigues, L. S. Lima, N. C. S. da Silva, P. G. L. Telles, T. M. da Mota Silva Rocha et al., “Are home-based exercises effective to reduce blood pressure in hypertensive adults? A systematic review,” Clinical Hypertension, vol. 28, no. 1, pp. 28, 2022. [Google Scholar] [PubMed]

3. A. Wiórek and Ł. J. Krzych, “Intraoperative blood pressure variability predicts postoperative mortality in non-cardiac surgery—A prospective observational cohort study,” International Journal of Environmental Research and Public Health, vol. 16, no. 22, pp. 4380, 2019. [Google Scholar]

4. W. S. Aronow, “Treatment of hypertensive emergencies,” Journal Annals of Translational Medicine, vol. 5, no. Supplement 1, pp. S5, 2017. [Google Scholar]

5. D. G. Hottinger, D. S. Beebe, T. Kozhimannil, R. C. Prielipp and K. G. Belani, “Sodium nitroprusside in 2014: A clinical concepts review,” Journal of Anesthesiology Clinical Pharmacology, vol. 30, no. 4, pp. 462–471, 2014. [Google Scholar]

6. M. E. Karar and M. A. El-Brawany, “Automated cardiac drug infusion system using adaptive fuzzy neural networks controller,” Biomedical Engineering and Computational Biology, vol. 3, pp. BECB.S6495, 2011. [Google Scholar]

7. L. C. Sheppard, “Computer control of the infusion of vasoactive drugs,” Annals of Biomedical Engineering, vol. 8, no. 4–6, pp. 431–434, 1980. [Google Scholar] [PubMed]

8. J. B. Slate and L. C. Sheppard, “Automatic control of blood pressure by drug infusion,” IEE Proceedings A (Physical Science, Measurement and Instrumentation, Management and Education, Reviews), vol. 129, no. 9, pp. 639–645, 1982. [Google Scholar]

9. S. Isaka and A. V. Sebald, “Control strategies for arterial blood pressure regulation,” IEEE Transactions on Biomedical Engineering, vol. 40, no. 4, pp. 353–363, 1993. [Google Scholar] [PubMed]

10. N. Malagutti, A. Dehghani and R. A. Kennedy, “Robust control design for automatic regulation of blood pressure,” IET Control Theory and Applications, vol. 7, no. 3, pp. 387–396, 2012. [Google Scholar]

11. S. Urooj and B. Singh, “Fractional-order PID control for postoperative mean arterial blood pressure control scheme,” Procedia Computer Science, vol. 152, pp. 380–389, 2019. [Google Scholar]

12. S. J. da Silva, T. A. Scardovelli, S. R. M. da Silva Boschi, S. C. M. Rodrigues and A. P. da Silva, “Simple adaptive PI controller development and evaluation for mean arterial pressure regulation,” Research on Biomedical Engineering, vol. 35, no. 2, pp. 157–165, 2019. [Google Scholar]

13. G. Cao and K. M. Grigoriadis, “Blood pressure response simulator to vasopressor drug infusion (PressorSim),” International Journal of Control, vol. 94, no. 10, pp. 2919–2933, 2021. [Google Scholar]

14. C. A. Reyes-García and A. A. Torres-García, “Fuzzy logic and fuzzy systems,” in Biosignal Processing and Classification Using Computational Learning and Intelligence, A. A. Torres-García, C. A. Reyes-García, L. Villaseñor-Pineda, O. Mendoza-Montoya (eds.Cambridge, MA, USA: Academic Press, pp. 153–176, 2022, Chapter No. 8. [Google Scholar]

15. M. D. Mohanty and M. N. Mohanty, “Design of fuzzy controller for patients in operation theater,” in Cognitive Informatics and Soft Computing, P. Mallick, V. Balas, A. Bhoi, G. S. Chae (eds.Vol. 1040. Singapore, Singapore: Springer, pp. 547–555, 2020. [Google Scholar]

16. E. Ramirez, P. Melin and G. Prado-Arechiga, “Hybrid model based on neural networks, type-1 and type-2 fuzzy systems for 2-lead cardiac arrhythmia classification,” Expert Systems with Applications, vol. 126, pp. 295–307, 2019. [Google Scholar]

17. B. C. Altay, A. Okumuş and B. Adıgüzel Mercangöz, “An intelligent approach for analyzing the impacts of the COVID-19 pandemic on marketing mix elements (7Ps) of the on-demand grocery delivery service,” Complex & Intelligent Systems, vol. 8, no. 1, pp. 129–140, 2022. [Google Scholar]

18. M. E. Karar, A. H. El-Garawany and M. El-Brawany, “Optimal adaptive intuitionistic fuzzy logic control of anti-cancer drug delivery systems,” Biomedical Signal Processing and Control, vol. 58, pp. 101861, 2020. [Google Scholar]

19. D. Wu, “On the fundamental differences between interval type-2 and type-1 fuzzy logic controllers,” IEEE Transactions on Fuzzy Systems, vol. 20, no. 5, pp. 832–848, 2012. [Google Scholar]

20. O. Castillo, L. Amador-Angulo, J. R. Castro and M. Garcia-Valdez, “A comparative study of type-1 fuzzy logic systems, interval type-2 fuzzy logic systems and generalized type-2 fuzzy logic systems in control problems,” Information Sciences, vol. 354, pp. 257–274, 2016. [Google Scholar]

21. M. Lathamaheswari, D. Nagarajan, J. Kavikumar and S. Broumi, “Interval type-2 fuzzy aggregation operator in decision making and its application,” Complex & Intelligent Systems, vol. 7, no. 3, pp. 1695–1708, 2021. [Google Scholar]

22. N. M. Yahya, N. Elias and M. H. M. Nordin, “A comparison of type 1 and type 2 fuzzy logic controller for dc motor system,” in Enabling Industry 4.0 through Advances in Mechatronics. Singapore: Springer Nature, pp. 125–133, 2022. [Google Scholar]

23. S. Qin, C. Zhang, T. Zhao, W. Tong, Q. Bao et al., “Dynamic high-type interval type-2 fuzzy logic control for photoelectric tracking system,” Process, vol. 10, no. 3, pp. 562, 2022. [Google Scholar]

24. J. Huang, M. Ri, D. Wu and S. Ri, “Interval type-2 fuzzy logic modeling and control of a mobile two-wheeled inverted pendulum,” IEEE Transactions on Fuzzy Systems, vol. 26, no. 4, pp. 2030–2038, 2018. [Google Scholar]

25. D. Wu and J. M. Mendel, “Recommendations on designing practical interval type-2 fuzzy systems,” Engineering Applications of Artificial Intelligence, vol. 85, pp. 182–193, 2019. [Google Scholar]

26. J. Zheng, W. Du, I. Nascu, Y. Zhu and W. Zhong, “An interval type-2 fuzzy controller based on data-driven parameters extraction for cement calciner process,” IEEE Access, vol. 8, pp. 61775–61789, 2020. [Google Scholar]

27. P. A. Herman, G. Prasad and T. M. McGinnity, “Designing an interval type-2 fuzzy logic system for handling uncertainty effects in brain-computer interface classification of motor imagery induced EEG patterns,” IEEE Transactions on Fuzzy Systems, vol. 25, no. 1, pp. 29–42, 2017. [Google Scholar]

28. A. Rubio-Solis, G. Panoutsos, C. Beltran-Perez and U. Martinez-Hernandez, “A multilayer interval type-2 fuzzy extreme learning machine for the recognition of walking activities and gait events using wearable sensors,” Neurocomputing, vol. 389, pp. 42–55, 2020. [Google Scholar]

29. R. Sharma, K. K. Deepak, P. Gaur and D. Joshi, “An optimal interval type-2 fuzzy logic control based closed-loop drug administration to regulate the mean arterial blood pressure,” Computer Methods and Programs in Biomedicine, vol. 185, no. 2, pp. 105167, 2020. [Google Scholar] [PubMed]

30. S. Omboni, R. S. Padwal, T. Alessa, B. Benczur, B. B. Green et al., “The worldwide impact of telemedicine during COVID-19: Current evidence and recommendations for the future,” Connect Health, vol. 1, pp. 7–35, 2022. [Google Scholar] [PubMed]

31. X. M. Zhang, Q. L. Han, X. Ge, D. Ding, L. Ding et al., “Networked control systems: A survey of trends and techniques,” IEEE/CAA Journal of Automatica Sinica, vol. 7, no. 1, pp. 1–17, 2020. [Google Scholar]

32. W. Wang, R. Postoyan, D. Nešić and W. P. M. H. Heemels, “Periodic event-triggered control for nonlinear networked control systems,” IEEE Transactions on Automatic Control, vol. 65, no. 2, pp. 620–635, 2020. [Google Scholar]

33. M. Kiani-Moghaddam, M. Shivaie and P. D. Weinsier, “Introduction to meta-heuristic optimization algorithms,” in Modern Music-Inspired Optimization Algorithms for Electric Power Systems: Modeling, Analysis and Practice, M. Kiani-Moghaddam, M. Shivaie, P. D. Weinsier (eds.Cham, Switzerland: Springer International Publishing, pp. 3–20, 2019. [Google Scholar]

34. R. V. Rao, Teaching learning based optimization algorithm: And its engineering applications, 1st ed., Cham, Switzerland: Springer International Publishing, pp. 9–39, 2015. [Google Scholar]

35. S. Chatterjee and V. Mukherjee, “PID controller for automatic voltage regulator using teaching-learning based optimization technique,” International Journal of Electrical Power & Energy Systems, vol. 77, pp. 418–429, 2016. [Google Scholar]

36. B. K. Sahu, S. Pati, P. K. Mohanty and S. Panda, “Teaching-learning based optimization algorithm based fuzzy-PID controller for automatic generation control of multi-area power system,” Applied Soft Computing, vol. 27, pp. 240–249, 2015. [Google Scholar]

37. J. M. Mendel, Uncertain rule-based fuzzy systems: Introduction and new directions, 2nd ed., Cham, Switzerland: Springer International Publishing, pp. 259–306, 2017. [Google Scholar]

38. P. B. de Moura Oliveira, J. Durães and E. J. S. Pires, “Mean arterial pressure PID control using a PSO-BOIDS algorithm,” in Int. Joint Conf. SOCO’13-CISIS’13-ICEUTE’13, Cham, Switzerland, Springer International Publishing, pp. 91–99, 2014. [Google Scholar]

39. T. -J. Su, S. -M. Wang, H. -Q. Vu, J. -J. Jou and C. -K. Sun, “Mean arterial pressure control system using model predictive control and particle swarm optimization,” Microsystem Technologies, vol. 24, no. 1, pp. 147–153, 2018. [Google Scholar]

40. A. Taskin and T. Kumbasar, “An open-source Matlab/Simulink toolbox for interval type-2 fuzzy logic systems,” in Proc. 2015 IEEE Symp. Series on Computational Intelligence, Cape Town, South Africa, pp. 1561–1568, 2015. [Google Scholar]

41. A. Cervin, D. Henriksson, B. Lincoln, J. Eker and K. E. Arzen, “How does control timing affect performance? Analysis and simulation of timing using Jitterbug and TrueTime,” IEEE Control Systems Magazine, vol. 23, no. 3, pp. 16–30, 2003. [Google Scholar]

42. N. Talpur, S. J. Abdulkadir, H. Alhussian, M. H. Hasan and M. H. A. Abdullah, “Optimizing deep neuro-fuzzy classifier with a novel evolutionary arithmetic optimization algorithm,” Journal of Computational Science, vol. 64, pp. 101867, 2022. [Google Scholar]

43. M. Mazandarani and L. Xiu, “Interval type-2 fractional fuzzy inference systems: Towards an evolution in fuzzy inference systems,” Expert Systems with Applications, vol. 189, pp. 115947, 2022. [Google Scholar]