Modified Dwarf Mongoose Optimization Enabled Energy Aware Clustering Scheme for Cognitive Radio Wireless Sensor Networks

1  Introduction

The growing use of wireless communications increases the challenge of spectrum usage efficiency challenge. Cognitive radio technology has developed as a productive solution for allowing other users, named secondary users (SUs) or cognitive radio users, to share the underused spectrum, offering that there will be no intrusion with primary users (PUs) [1]. When SU is detected, the PU will have appeared; it has to switch to other available channels but not employed by PU. Dynamic spectrum accessibility refers to a spectrum-efficient interaction pattern for Wireless Sensor Networks (WSN) [2]. Such later face an augmented level of intrusions from several wireless mechanisms functioning on the available frequency band like Bluetooth, WiFi, WIMAX, etc. A Cognitive Radio Sensor Network (CRSN) becomes a novel sensor network pattern that accepts the cognitive radio abilities of sensor network systems [3]. CRSNs will be a solution to unscrupulously use the idle parts of the approved spectrum. Presenting to sensor nodes (SNs) temporary use of the accessible licensed networks advances the utility efficacy of the spectrum itself. It offers enhanced quality of service (QoS) regarding prevailing wireless technologies [4]. Cognitive radio users can access any part of the spectrum. Significant interference is made to approved and other users. Schedule-related MAC protocol for cognitive radio networks was devised to solve this complexity. Similarly, there were several difficulties which should be solved [5–7]. Fig. 1 illustrates the infrastructure of WSN.

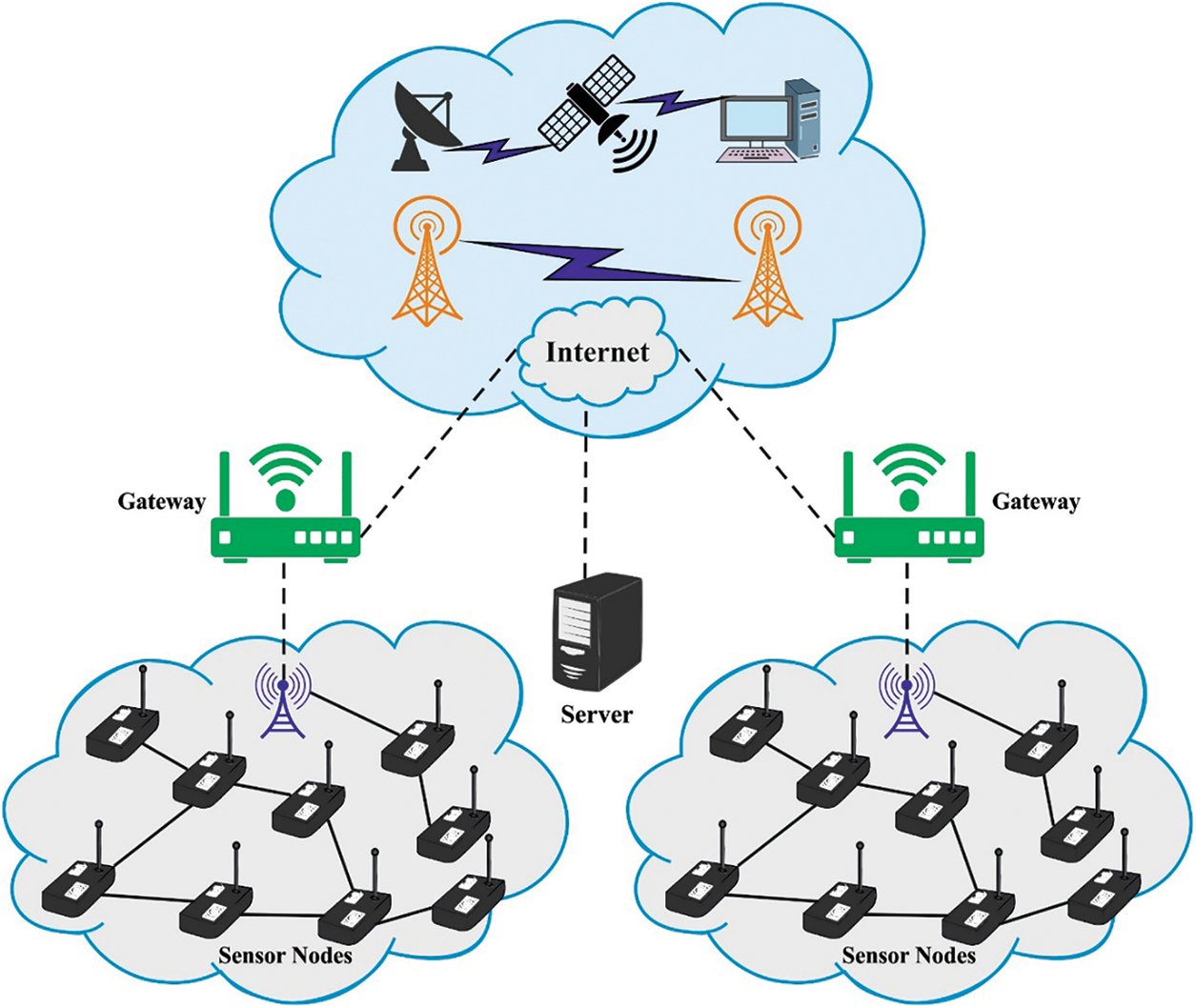
Figure 1: Architecture of WSN

The common control channel issue is mostly unresolved in cognitive radio technology. Then, it was proved that single-user detection methods must execute more effectively to find primary user activity. Lastly, several solutions were devised for only a limited-sized network. A probable solution for such problems was splitting the system into clusters [8]. Unlike earlier studies, that allows different channels to adjacent clusters to avoid collision and income from the whole spectrum remaining by the PUs to raise the correspondence of interactions done by SUs.

Logically consolidating and grouping the same SNs in their closeness with some objects is termed node clustering [9]. A gathered WSN structure becomes beneficial to a non-cluster-related structure in many ways. This non-cluster-related structure is termed a single-tier network structure and depends on flat topologies. Node clustering allows bandwidth reprocessing and effectual resource distribution so that it could enhance system capability [10]. Predominantly, a dense sensor network and, on a large scale, single-tier networks could be overloaded the gateway node, resulting in congestion and communication delay. These single-tier networks were not ascendable for a large set of sensors positioned in a big area. Clustering in CR-WSNs becomes infancy [11]. There was enormous work in clustering for cognitive radio networks (CRNs), mobile ad hoc networks (MANET), and WSNs. Though certain clustering complexities were solved in the study, clustering will remain a vast unexplored field in CR-WSNs [10].

The contribution of the paper is given as follows. This paper focuses on designing the Modified Dwarf Mongoose Optimization Enabled Energy Aware Clustering (MDMO-EAC) Scheme for CRWSN. The MDMO-EAC technique mainly intends to group the nodes into clusters in the CRWSN. Besides, the MDMO-EAC algorithm is based on the dwarf mongoose optimization (DMO) algorithm design with oppositional-based learning (OBL) concept. In addition, the presented MDMO-EAC algorithm computed a multi-objective function for improved network efficiency. The presented model is validated using a comprehensive range of experiments, and the results are inspected under varying measures.

2  Related Works

Prajapat et al. [12] introduce a neighbour discovery technique and 2 greedy k-hop clustering methods (k-SACB-WEC and k-SACB-EC) for CRSN to concentrate on IoT application that needs constant intercluster and intracluster interactions. The researchers concentrate on attaining channel connectivity while optimizing network lifetime. In this clustering, several variables, like nodes’ remaining energy, spectrum awareness, appearance possibility of PUs channel, channel qualities, strength on the arrival of PUs, and the Euclidean distance among nodes were considered for selecting the common channels and hop count for clusters. Bhagyalakshmi et al. [13] provide the optimizing capability of the network lifespan via joint routing and resource allotment with an isolated nodes approach (JR-IN) among isolated nodes and cluster head in a cognitive oriented WSN. In the JR-IN algorithm, the network area can be separated into distinct layers, and cluster size can be developed in every layer so that the cluster size will remain unequal whenever it transfers against the sink. Later the cluster size was large in the outer layer when a comparison was made with the cluster size in the inner layers.

Stephan et al. [14] devise an energy and spectrum-aware unequal clustering (ESAUC) protocol that jointly overwhelms the limits of spectrum and energy for optimizing the CRSN span. This devised protocol enhances equality by attaining remaining energy equilibrium between the SNs and improves the network lifespan by reducing general energy utilization. The deep Belief Networks technique was used for predicting the spectrum holes. ESAUC enhances the cluster constancy through the adjustment of the common channel count optimally. Zheng et al. [15] devise a new stability-aware cluster-related routing (SACR) protocol for CRSNs. The major novelty of SACR is the unified incorporation of opportunistic sending and a stable clustered structure. In cluster creation, the novelists considered energy consumption and spectrum dynamics in the clustering procedure. The resulting clustered structure can be stable, evading large interaction overhead because of high clustering frequency.

In [16], a new technique—energy preservation and network critics-related channel scheduling (EPNCS) approach in CRSNs was devised that regulates the slot time for SNs. Dependent on ecological data traffic, the sleeping period of SNs can be changed, which diminishes energy stylization. A scalable, dynamic slot is calculated for every SN related to the average buffer occupancy, resulting in optimum channel usage. An RF EH-related multi-hop clustering routing protocol (RFMCRP) related to the non-linear EH method was devised in [17]. At First, by using statistical analysis and curve fitting tool, the most reasonable non-linear EH method can be detected and was used by RFMCRP for measuring the harvested energy precisely. Second, the optimum cluster number was hypothetically extracted, and its value was employed as a benchmark for assessing the proposal’s validity. Then, the energy control system was presented for managing node state, which could help enhance cluster building stability. Zheng et al. [18] suggest a short preamble cognitive MAC (SPC-MAC) protocol for CRSNs. The main input of SPC-MAC was the smart grouping of short opportunistic forwarding and preamble sampling. So, SPC-MAC can support fast spectrum access and be reliable whenever minimizing power usage. Additionally, SPC-MAC was a distributed cognitive MAC protocol deprived of any common control channel.

3  The Proposed Model

In this study, a new MDMO-EAC technique has been projected for CRWSN. The MDMO-EAC technique mainly intends to group the nodes into clusters in the CRWSN. Besides, the MDMO-EAC algorithm is based on the design of the DMO algorithm with the OBL concept. In addition, the presented MDMO-EAC algorithm computed a multi-objective function for improved network efficiency. Primarily, the nodes are randomly deployed in the target area, and the initialization phase occurs where the nodes exchange information with their neighbours. Moreover, the BS executes the clustering process and advertises the CHs.

3.1 System Model

In this section, the complete system method adopted in this work was discussed briefly [19].

Network model: The SNs were cognitive radio-assisted. The SNs were distributed haphazardly in the sensor domain. The cognitive radio SNs were resource-limited, and the nodes were mobile, having low speed, 2–4 m or min.

Channel model: It is regarded that there were N channels accessible that should be retrieved through the SUs resourcefully. The PUs approved every N channel. Every channel is devised as Rayleigh fading channel. Based on the proximity of the interactive nodes, there can be meddling amongst the SUs. The words CR and SU node were employed intervariable.

Energy model: In CRWSN, the CR nodes, separately from data transmission and reception, execute supplementary tasks of spectrum switching and sensing. Hereafter, the power utility was higher in CRWSN when compared with the conventional WSN. Therefore, when devising the power utility method, all 4 tasks are under consideration. Assuming that Ess is the power used at the time of spectrum sensing, is the power used at the time of spectrum switching. The power utilized by ith SU at the time of data communication of ℒ bits was articulated as follows.

Etxi(ℒ)={(eRF+eampd2)×L, d<d0(eRF+eamp′d4)×L, d≥d0(1)

whereas eRF denotes the power utilized by the radio frequency circuits for receiving and transmitting the signal, eamp′ and eamp were the amplifier power based on the path loss method utilized, d refers to the distance among receiver and transmitter nodes, and d0 denotes the distance threshold utilized for distinguishing path loss method where d0=eamp/eamp′.

As the ith SU obtains ℒ bits of data, the power used up at the time of the reception mode can be

Erx,i(ℒ)=eRF×ℒ(2)

Mobility model: The purpose of this study was to achieve stable clusters. Thus, the cluster head nodes were predictable, and the nodes had comparatively less mobility. For characterizing the instantaneous nodal mobility Mj, the following expression was employed.

Mi=1T∑t=1T(xt−xt−1)2+(yt−yt−1)2(3)

Whereas (xt,yt) and (xt−1,yt−1) were node coordinates that are ni at time instants t and t−1 correspondingly. Then, T was the period for which this stricture remains as projected. It can be taken into account that the nodes transfer succeeding the random waypoint mobility method.

3.2 Design of MDMO Algorithm

The mathematical process of the DMO technique was established. The nature of the mongoose inspires it in food-finding procedures [20]. In general, it initializes with the assumption of primary values to solutions by Eq. (4):

xi,j=lj+rand×(uj−lj)(4)

Whereas rand refers the arbitrary numbers. uj and LJ suggests the restrictions of the search domain. The swarming of the DMO comprises 3 sets: alpha, babysitter, and scout. Every individual set owns respective outcomes in food determination. The fitness of each solution can be computed once the number of individuals is introduced. Eq. (5) finds the probability value to all the population fitness, and alpha female (α) was selected dependent upon this probability

α=fitiΣi=1nfiti(5)

n relates the count of mongoose from α set. Bs indicate the babysitter count. The mongoose sleeps from the main sleeping mound, which is predefined ∅. It generates candidate food locations using Eq. (6):

Xi+1=Xj+phi×peep(6)

The sleeping mound was offered in Eq. (9), phi denotes the uniform distribution of random value in −1 and 1.

smi=fiti+1−fitimax{|fiti+1,fiti|}(7)

Eq. (8) denotes average sleeping mound values.

φ=Σi=1nsmin(8)

Once the babysitting exchange criteria gets fulfilled, the technique develops into scouting phases, whereas the sleeping mound or next food source is assumed.

As mongooses are recognized to not return to previous sleeping mounds, the scout arrives for the following sleeping mound. Here, scouting as well as foraging were carried out simultaneously. This movement was modeled then an unsuccessful or successful searching sleeping mound. This is because once the family forages far sufficient, it is derived into a novel sleeping mound. The scout mongoose was demonstrated by Eq. (9).

Xi+1={Xi−CF∗phi∗rand∗[Xi−M→]if φi+1>φi  Xi+CF∗phi∗rand∗[Xi−M→](9)

whereas rand represents the arbitrary number from the range between zero and one, CF=(1−iierMaxiter)(2iterMaxiter). M→=Σi=1nXi×smiXi, whereas the mongoose drive to a novel sleeping mound was defined as this vector.

The babysitter fitness weighted is fixed to zero, making sure that the alpha group’s average weight is decreased under the next iteration, obstructing group movement and intensifying development. Fig. 2 represents the flowchart of the DMO technique.

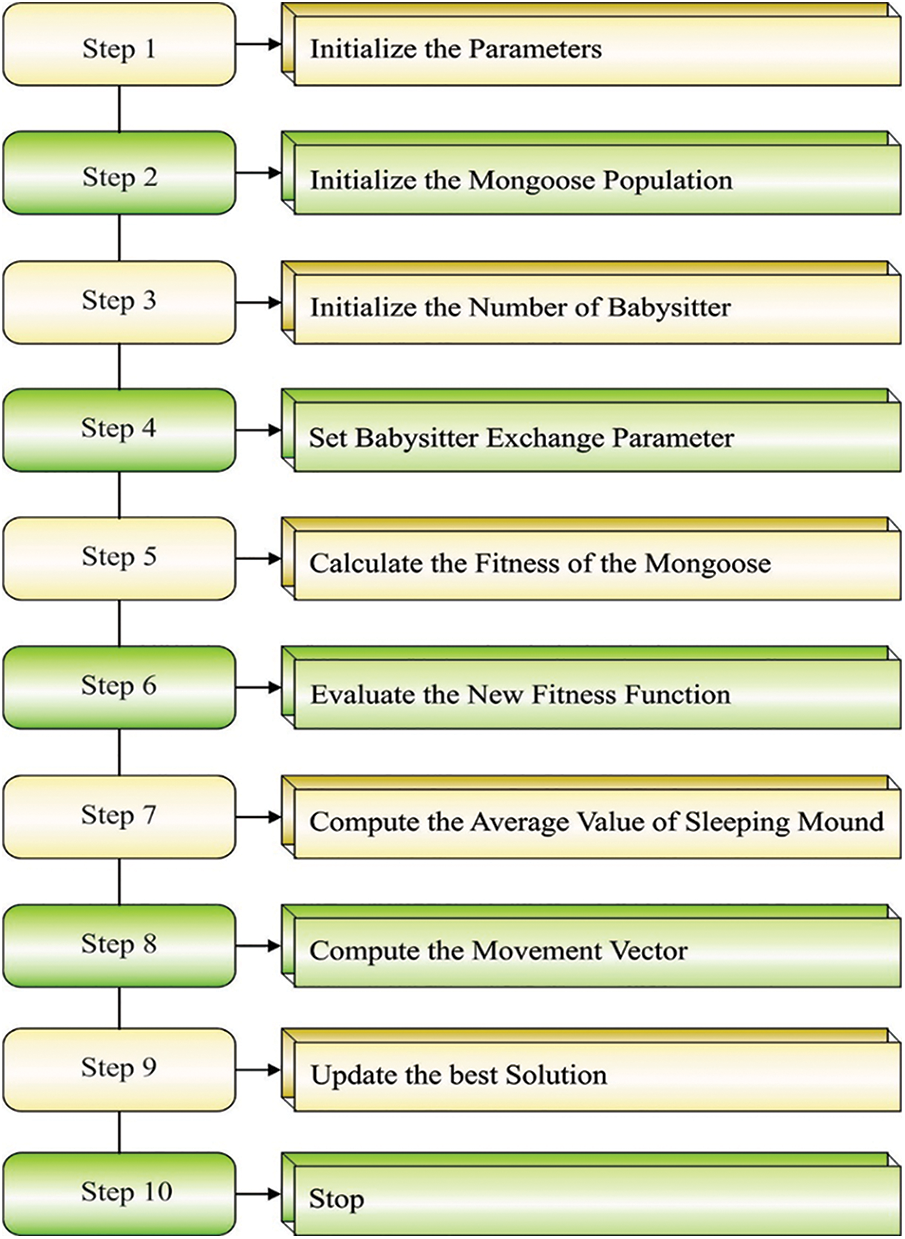
Figure 2: Flowchart of DMO

In the MDMO approach, the OBL can be employed to foster the DMO technique’s presentation. The OBL method was used to create a complete opposition solution to the prevailing solutions [21]. It tries to regulate the optimal solutions that increase the convergence speed rate.

The opposite (X0) of a specified real number (X∈[U, L]) is computed below.

X0=U+L−X(10)

Opposite points: Supposing that X=[X1, X2,…, XDim] becomes a point in a Dim-dimensional search space, and X1, X2,…,XDim∈R and Xj[Uj,Lj]. Therefore, the opposite point (X0) of X can be given b below:

Xj0=UBj+Lj−Xj, where j=1….D.(11)

Furthermore, 2 points ( X and X0) were selected in accordance with the fitness function (FF) values, and the other can be ignored. For minimizing issues, if (X)≤f(X0), X denotes is maintained; oppositely, X0 represents maintained.

Based on the opposite point, the dynamic opposite preference (DXO) of the value X can be given below:

XDo=X+w×r8(r9×X0−X),w>0(12)

where r9 and r8 are random values in the range of [01], w indicates the weighting agent.

3.3 Design of Clustering Process

Here, the presented MDMO-EAC algorithm computed a multi-objective function for improved network efficiency. The optimization problem has two primary objective functions, f1 and f2, that aim at characterizing the optimum part of the load of the CH role that must be allocated to all the nodes in the cluster. Hence, the dimension of particles is equivalent to the node count in a cluster involving the CH nodes. Based on f1, all the nodes must bear a part of the load of the CH role, which is appropriate to its RE (the more RE of a node, the large part of the load of the CH role is allocated to the node). The following equation evaluates the f1 function.

Minimize f1=1m∑i=1m|RiRavgTiTavg|(13)

In Eq. (13), Ri, Ti, Ravi, Tag, and m denotes the similar parameter that has been employed; in other words, once an RW is higher than the energy of another node, the node would be transferring a massive quantity of energy than the energy transferred by the other nodes.

The next objective function is to decrease the energy utilization of the node. Therefore, the node with a higher traffic load must bear a smaller part of the load of the CH role. The following equation evaluates the f2 function:

Maximize f2=1m∑i=1m|LiTi|(14)

In Eq. (14), m shows the number of nodes in the cluster, Li indicates node i, and Ti shows the candidate part of a load of CH role allocated to node i. The optimization problem has constraints in Eq. (4) that guarantees that a load of CH role ECH is distributed accurately through all nodes in the cluster.

Assume that a bio-inspired optimization algorithm was used for unconstraint optimization problems. Therefore, the study used an effective constraint-handling method (a penalty function). The penalty function transforms the constraint optimization problem into un-constraint optimization problems that are resolved using bio-inspired optimization approaches. It can be accomplished by adding the term “quadratic loss function” to the objective function and converting the constraints into objectives in the objective function. It is expressed in the following equation:

F=λ1f1+1+(1−λ)f2−ℬ(∑i=1mTj−ECH)2(15)

The quadratic loss function becomes squared for making the constraints most serious about being employed, ℬ is constant whose value ranges from 10 to 100, and λ shows a weight value.

4  Simulation Results and Analysis

Here, the experimental results of the MDMO-EAC approach are examined under several aspects. The parameter setting is as follows: target region: 200 * 200 m2, number of sensor nodes: 100–500, number of primary users: 5, number of available channels: 5, and data packet size: 50bytes.

Table 1 and Fig. 3 portray the energy level analysis of CH nodes (ELCHN) of the MDMO-EAC model with compared methods on 100 nodes [19]. The experimental values indicated that the MDMO-EAC model had shown improved output with increased ELCHN value. On 20 nodes, the MDMO-EAC approach has obtained increased ELCHN of 97.75%, whereas the NCP-CRWSN, SAC, LEACH, and RATE models have attained reduced ELCHN of 92.92%, 78.05%, 74.33%, and 68.39% respectively. Similarly, with 40 nodes, the MDMO-EAC approach has acquired a higher ELCHN of 97.38%, whereas the NCP-CRWSN, SAC, LEACH, and RATE methodologies have achieved reduced ELCHN of 95.15%, 73.96%, 70.62%, and 66.16% correspondingly. Also, with 60 nodes, the MDMO-EAC method has attained increased ELCHN of 94.40%, whereas the NCP-CRWSN, SAC, LEACH, and RATE algorithms have obtained reduced ELCHN of 89.57%, 68.76%, 67.64%, and 61.32% correspondingly.

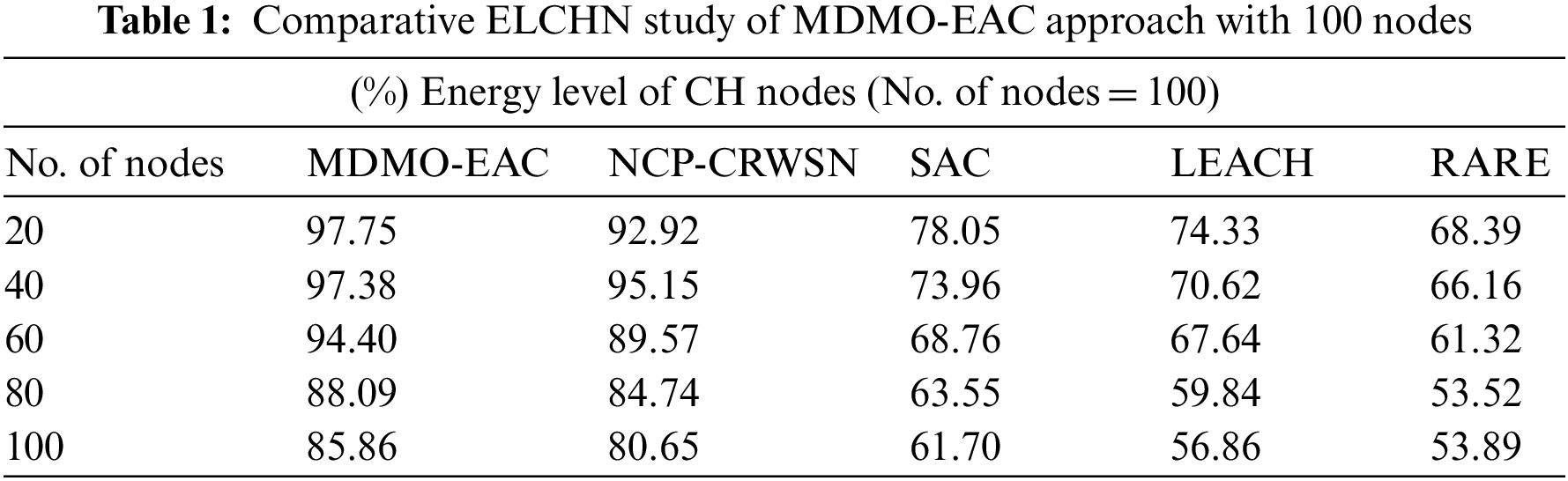
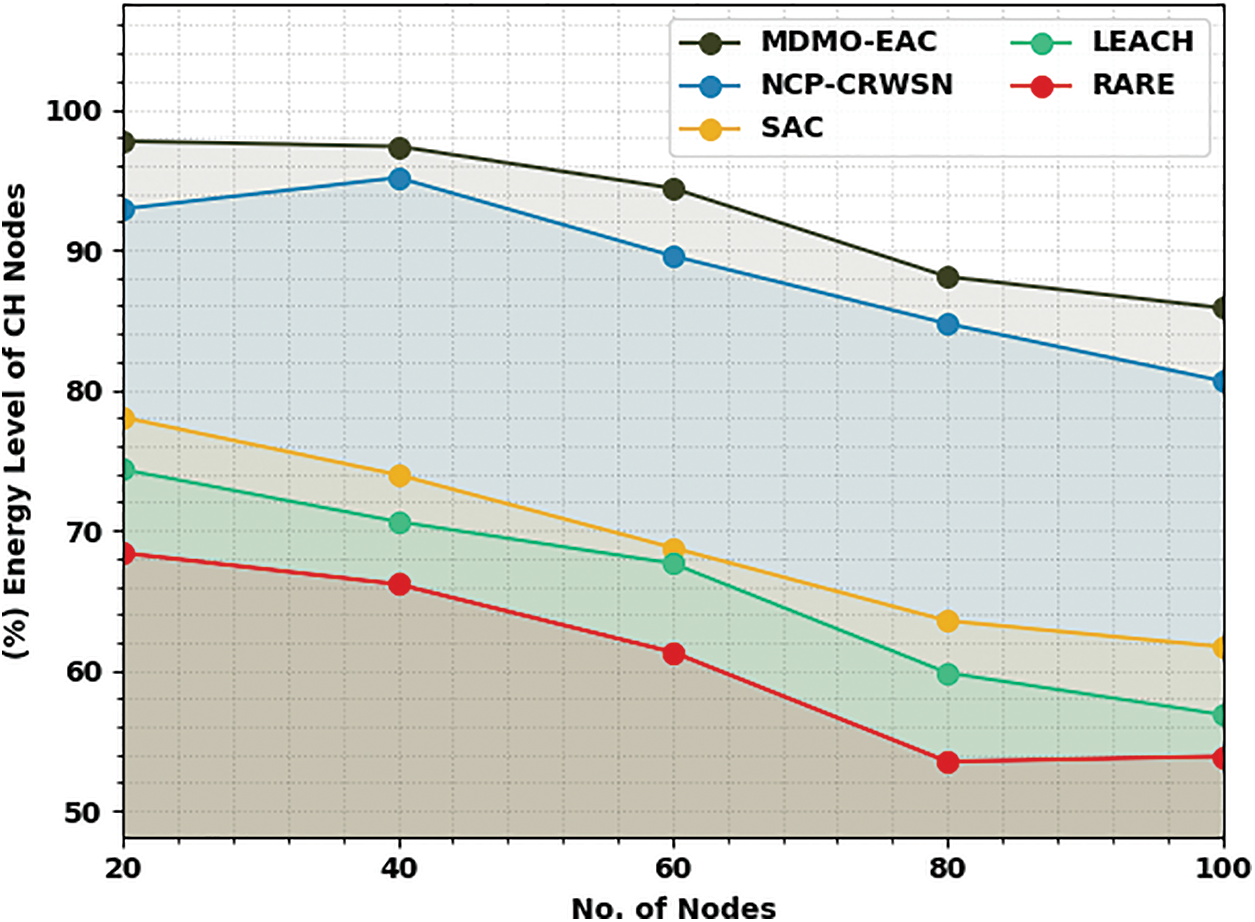
Figure 3: ELCHN analysis of MDMO-EAC approach under 100 nodes

A detailed energy consumption (ECOM) examination of the MDMO-EAC model with recent models is performed under 100 nodes in Table 2 and Fig. 4. The simulation values pointed out the supremacy of the MDMO-EAC model with minimal ECOM values. For instance, with 300 s simulation time, the MDMO-EAC model has resulted in a minimal ECOM of 18 J, whereas the NCP-CRWSN, SAC, LEACH, and RATE models have reached maximum ECOM of 25, 40, 46, and 52 J respectively. Furthermore, with 600 s simulation time, the MDMO-EAC approach has resulted in minimal ECOM of 21 J, whereas the NCP-CRWSN, SAC, LEACH, and RATE techniques have achieved maximum ECOM of 34, 48, 58, and 59 J correspondingly. In the meantime, with 900 s simulation time, the MDMO-EAC method has resulted in a minimal ECOM of 58 J, whereas the NCP-CRWSN, SAC, LEACH, and RATE approaches have attained maximum ECOM of 85, 104, 114, and 125 J correspondingly.

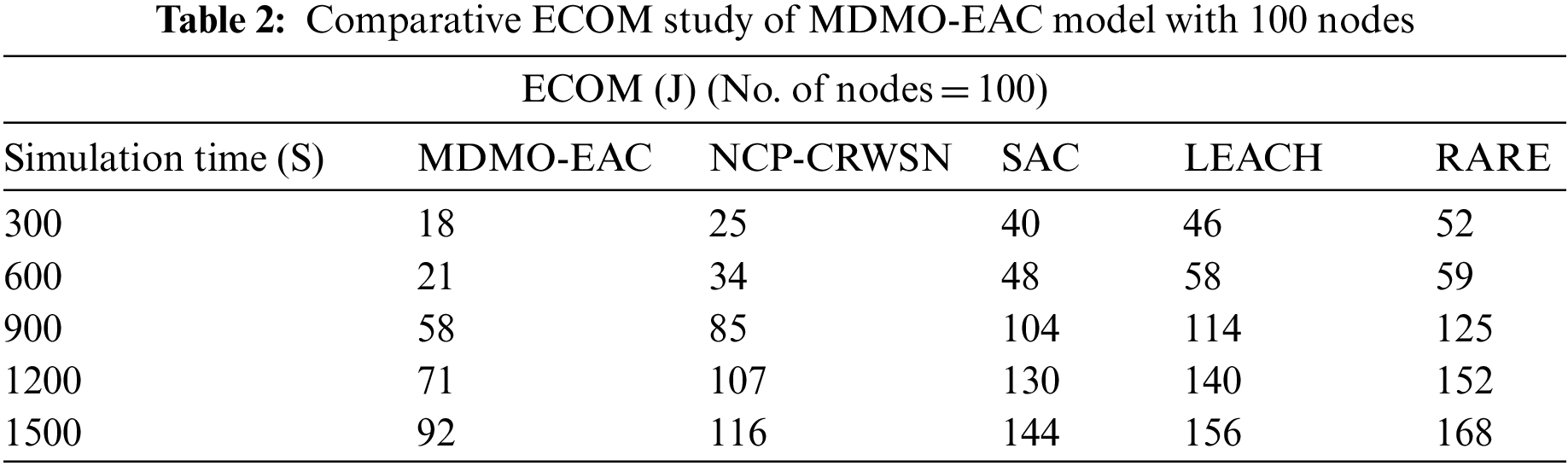
Figure 4: ECOM analysis of MDMO-EAC approach under 100 nodes

Table 3 and Fig. 5 represent the lifetime time (LTT) of the MDMO-EAC algorithm with compared methodologies on 100 nodes. The experimental values highlighted the MDMO-EAC approach had displayed improved output with increased LTT value. On 20 nodes, the MDMO-EAC methodology has attained an increased LTT of 1582 s, whereas the NCP-CRWSN, SAC, LEACH, and RATE methodologies have gained reduced LTT of 1456, 1225, 1046, and 1019 s correspondingly. Further, with 40 nodes, the MDMO-EAC method has reached an increased LTT of 1708 s, whereas the NCP-CRWSN, SAC, LEACH, and RATE approaches have gained reduced LTT of 1522, 1244, 1059, and 960 s correspondingly. Similarly, with 60 nodes, the MDMO-EAC technique has obtained an increased LTT of 1615 s, whereas the NCP-CRWSN, SAC, LEACH, and RATE algorithms have reduced LTT of 1516, 1225, 1053, and 920 s correspondingly.

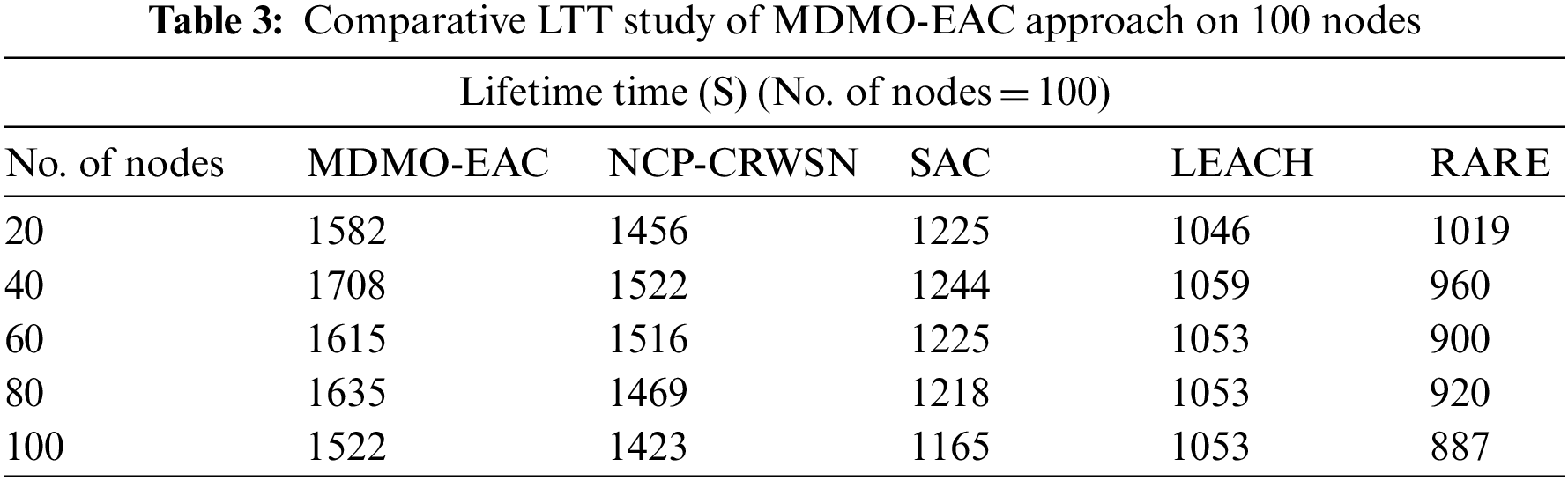
Figure 5: LTT analysis of MDMO-EAC approach under 100 nodes

Table 4 and Fig. 6 portray the ELCHN of the MDMO-EAC technique with compared approaches on 500 nodes. The experimental values indicate the MDMO-EAC approach has exhibited improvised output. On 100 nodes, the MDMO-EAC algorithm has achieved an increased ELCHN of 94.82%, whereas the NCP-CRWSN, SAC, LEACH, and RATE methodologies have achieved reduced ELCHN of 90.76%, 78.58%, 71.94%, and 64.93% correspondingly. Likewise, with 200 nodes, the MDMO-EAC technique has reached an increased ELCHN of 94.08%, whereas the NCP-CRWSN, SAC, LEACH, and RATE methodologies have gained reduced ELCHN of 90.39%, 79.32%, 71.20%, and 64.93% correspondingly. Also, with 300 nodes, the MDMO-EAC approach has reached an ELCHN of 94.08%, whereas the NCP-CRWSN, SAC, LEACH, and RATE algorithms have gained reduced ELCHN of 87.81%, 74.52%, 67.14%, and 62.72% correspondingly.

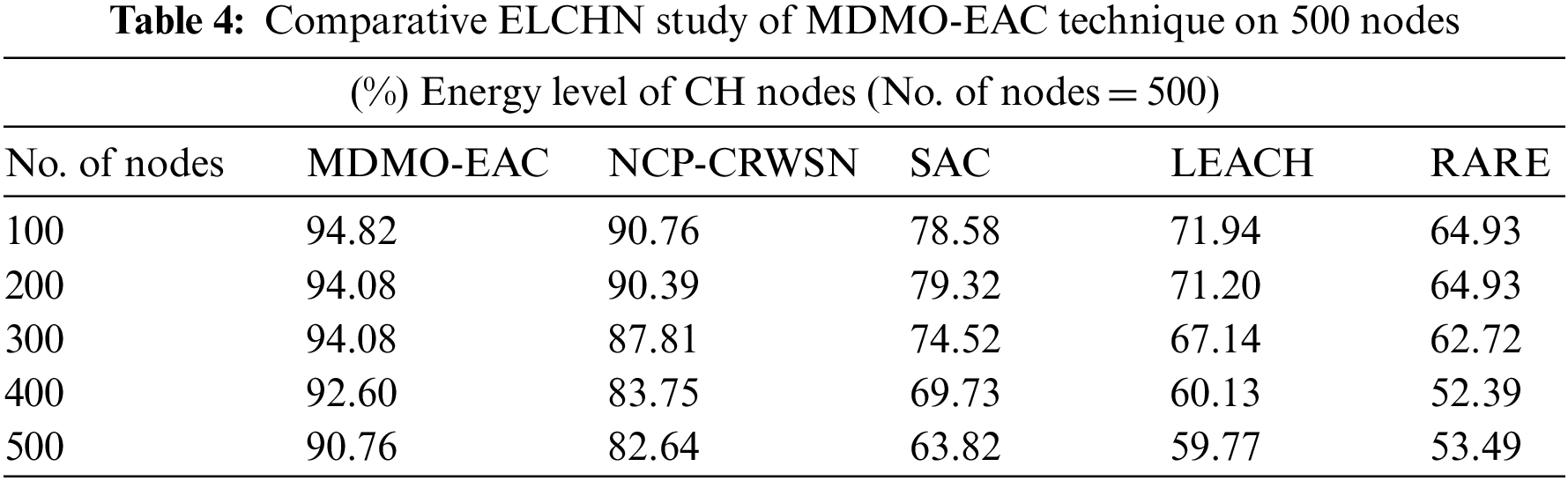
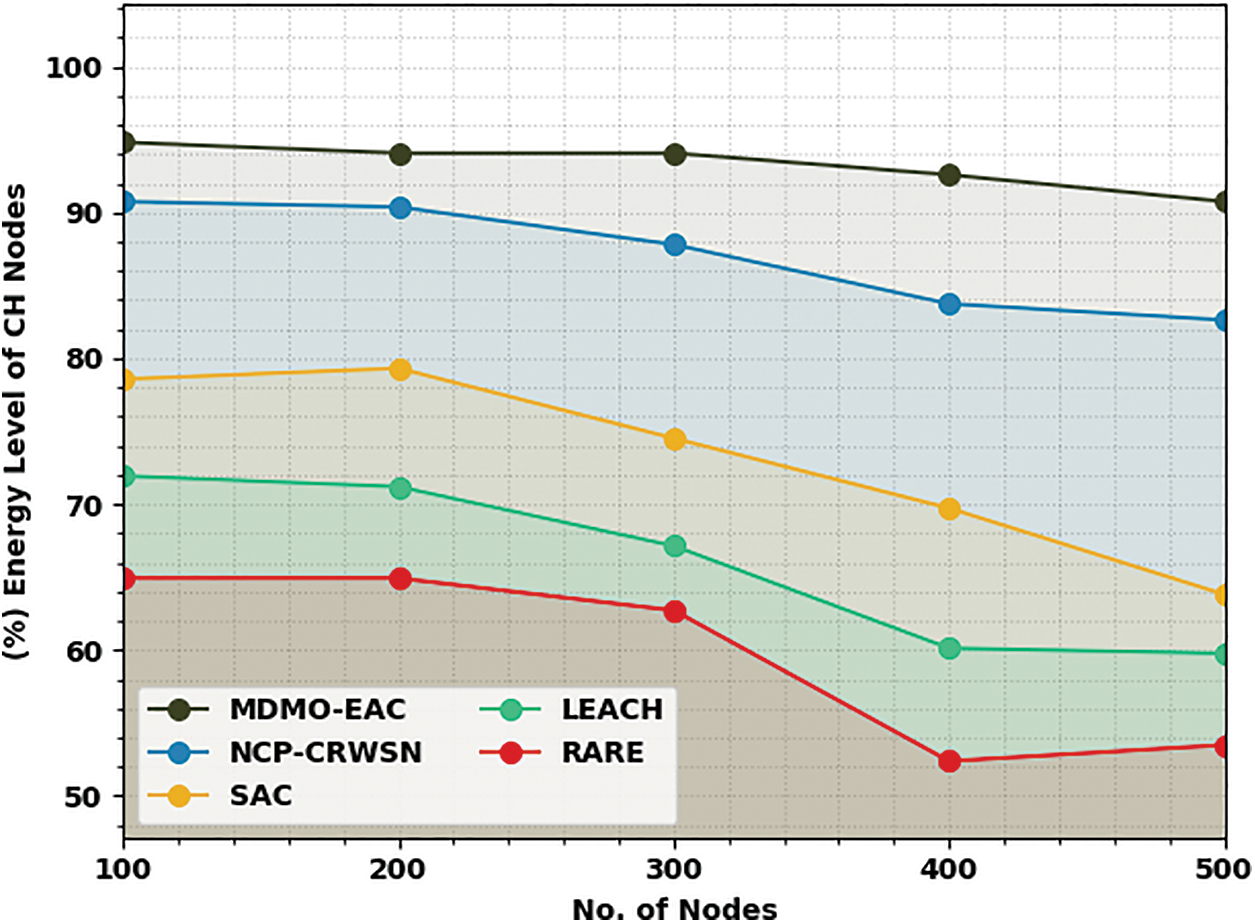
Figure 6: ELCHN analysis of MDMO-EAC approach under 500 nodes

Table 5 and Fig. 7 illustrate the ECOM of the MDMO-EAC method with compared methodologies on 500 nodes. The experimental values denote the MDMO-EAC approach has displayed superior performance with increased ECOM value. On 300 nodes, the MDMO-EAC algorithm has attained an increased ECOM of 16 J, whereas the NCP-CRWSN, SAC, LEACH, and RATE approaches have acquired reduced ECOM of 30, 41, 50, and 67 J correspondingly. Similarly, with 600 nodes, the MDMO-EAC methodology has attained an increased ECOM of 19 J, whereas the NCP-CRWSN, SAC, LEACH, and RATE methods have attained reduced ECOM of 37, 60, 69, and 93 J correspondingly. Moreover, with 900 nodes, the MDMO-EAC method has outperformed the increased ECOM of 44 J, whereas the NCP-CRWSN, SAC, LEACH, and RATE methods have reached reduced ECOM of 72, 104, 117, and 127 J correspondingly.

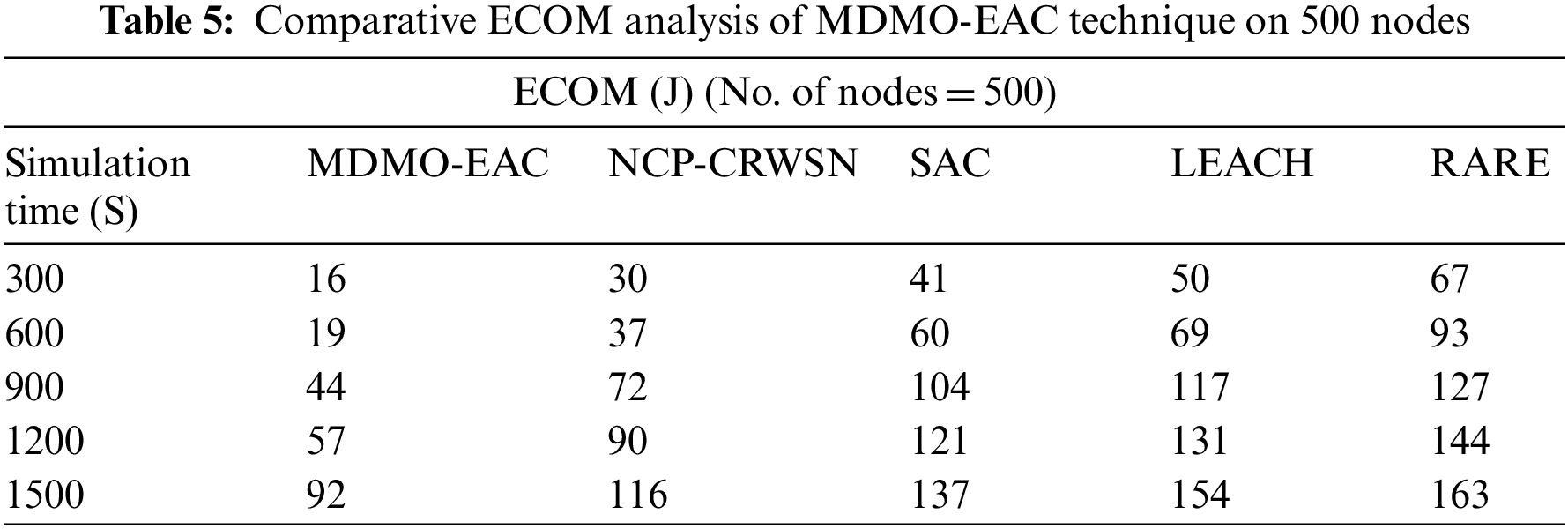
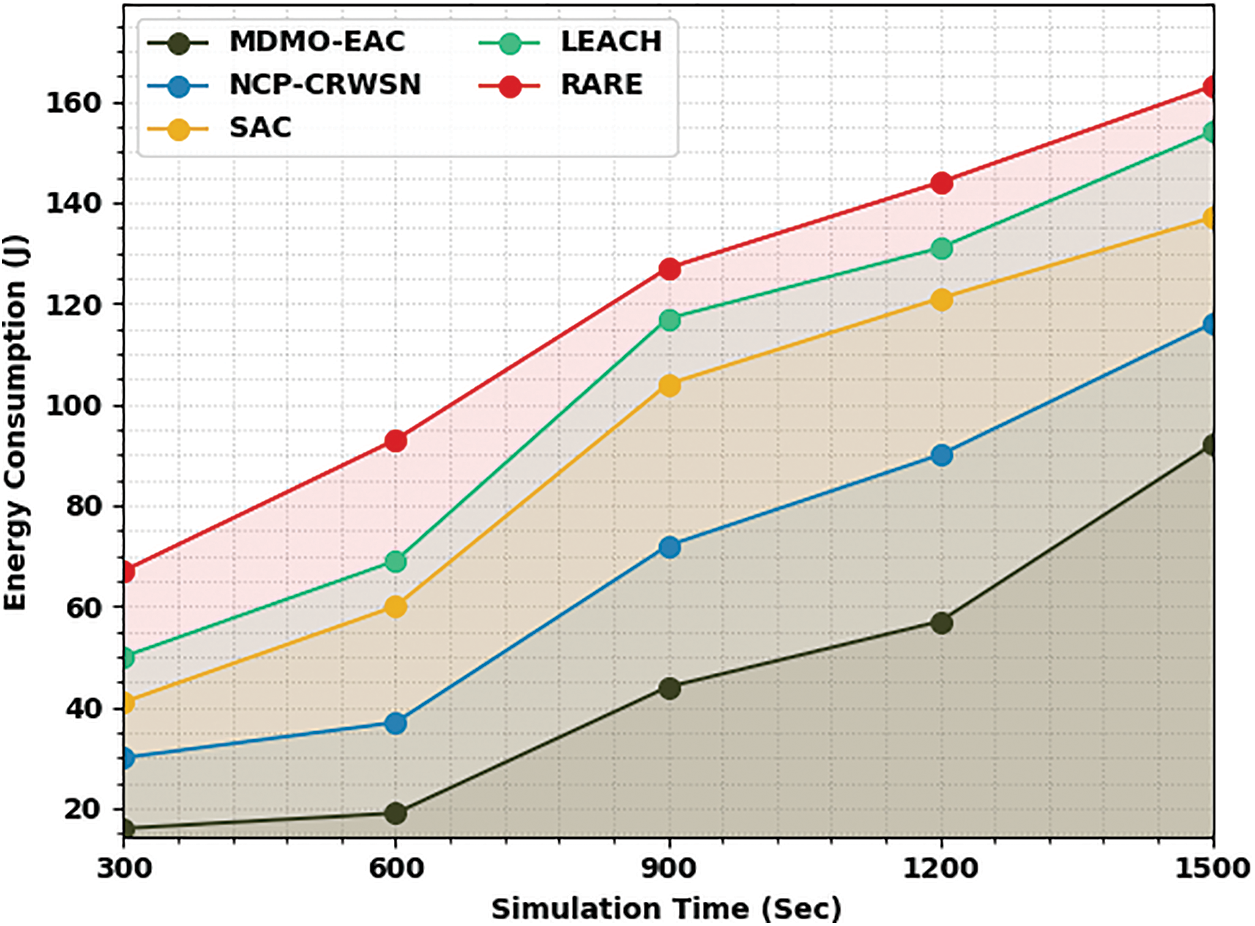
Figure 7: ECOM analysis of MDMO-EAC approach under 500 nodes

Table 6 and Fig. 8 describe the LTT of the MDMO-EAC technique with compared methods on 500 nodes. The experimental values indicate the MDMO-EAC algorithm has exhibited exceeding performance with increased LTT value. Under 100 nodes, the MDMO-EAC technique has attained an increased LTT of 1682 s, whereas the NCP-CRWSN, SAC, LEACH, and RATE methodologies have reached reduced LTT of 1473, 1217, 1132, and 910 s correspondingly. Additionally, with 200 nodes, the MDMO-EAC technique has attained an increased LTT of 1689 s, whereas the NCP-CRWSN, SAC, LEACH, and RATE methods have attained reduced LTT of 1512, 1224, 1073, and 903 s correspondingly. Also, with 300 nodes, the MDMO-EAC technique has gained an increased LTT of 1663 s, whereas the NCP-CRWSN, SAC, LEACH, and RATE approaches have achieved reduced LTT of 1479, 1217, the 1080, and 884 s correspondingly.

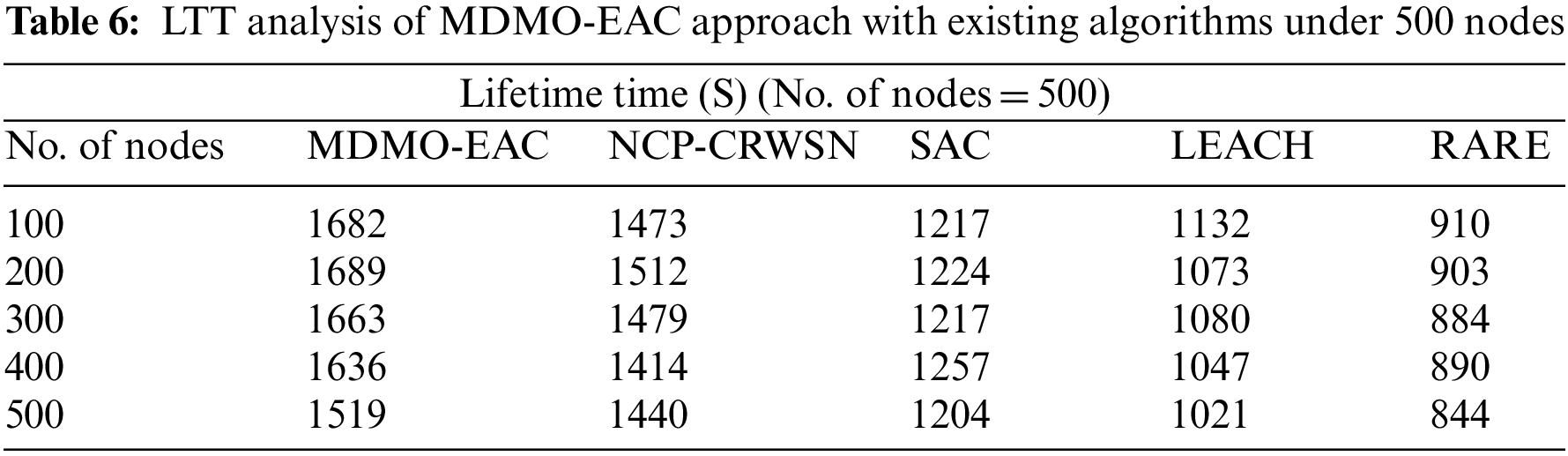
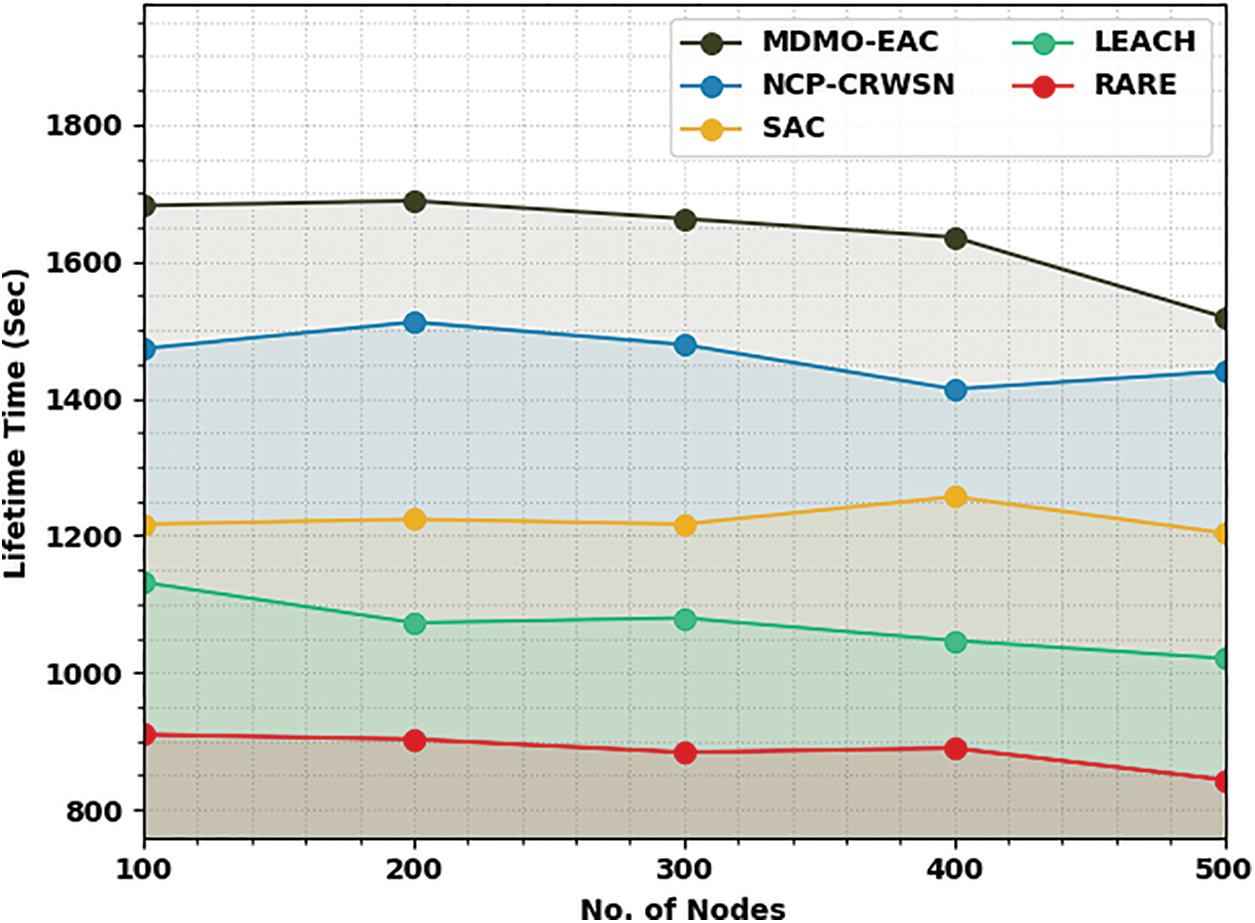
Figure 8: LTT analysis of MDMO-EAC approach under 500 nodes

5  Conclusion

An effective MDMO-EAC technique has been developed for CRWSN. The MDMO-EAC technique focused on clustering sensor nodes into several clusters to accomplish energy efficiency in the CRWSN. The MDMO-EAC algorithm is primarily based on the design of the DMO algorithm with the OBL concept. In addition, the presented MDMO-EAC algorithm computed a multi-objective fitness function for improved network efficiency. The presented model is validated using a comprehensive range of experiments, and the outcomes were reviewed in varying measures. The comparison study stated the improvements of the MDMO-EAC approach over other recent methods. The comparison study stated the improvements of the MDMO-EAC approach over other recent methods. In the future, data aggregation protocols will be designed to enhance the efficacy of the network.

Funding Statement: This research work was funded by Institutional Fund Projects under grant no. (IFPIP: 14-611-1443). Therefore, the authors gratefully acknowledge technical and financial support provided by the Ministry of Education and Deanship of Scientific Research (DSR), King Abdulaziz University (KAU), Jeddah, Saudi Arabia.

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

1. F. Fan, S. C. Chu, J. S. Pan, C. Lin and H. Zhao, “An optimized machine learning technology scheme and its application in fault detection in wireless sensor networks,” Journal of Applied Statistics, pp. 1–18, 2021. https://doi.org/10.1080/02664763.2021.1929089 [Google Scholar] [PubMed] [CrossRef]

2. T. Mahmood, J. Li, Y. Pei, F. Akhtar, S. A. Butt et al., “An intelligent fault detection approach based on reinforcement learning system in wireless sensor network,” The Journal of Supercomputing, vol. 78, no. 3, pp. 3646–3675, 2022. [Google Scholar]

3. U. Saeed, Y. D. Lee, S. U. Jan and I. Koo, “CAFD: Context-aware fault diagnostic scheme towards sensor faults utilizing machine learning,” Sensors, vol. 21, no. 2, pp. 617, 2021. [Google Scholar] [PubMed]

4. A. Singh, J. Amutha, J. Nagar, S. Sharma and C. C. Lee, “Lt-fs-id: Log-transformed feature learning and feature-scaling-based machine learning algorithms to predict the k-barriers for intrusion detection using wireless sensor network,” Sensors, vol. 22, no. 3, pp. 1070, 2022. [Google Scholar] [PubMed]

5. M. Ragab, “Spider monkey optimization with statistical analysis for robust rainfall prediction,” CMC-Computers Materials & Continua, vol. 72, no. 2, pp. 4143–4155, 2022. [Google Scholar]

6. K. Arora, G. P. Joshi, M. Ragab, M. Rawa, A. H. Milyani et al., “Bilateral contract for load frequency and renewable energy sources using advanced controller,”CMC-Computers Materials & Continua, vol. 73, no. 2, pp. 3165–3180, 2022. [Google Scholar]

7. S. Al-Otaibi, A. Al-Rasheed, R. Mansour, E. Yang and G. Joshi et al., “Hybridization of metaheuristic algorithm for dynamic cluster-based routing protocol in wireless sensor Networksx,” IEEE Access, vol. 9, pp. 83751–83761, 2021. [Google Scholar]

8. R. Regin, S. S. Rajest and B. Singh, “Fault detection in wireless sensor network based on deep learning algorithms,” EAI Transactions on Scalable Information Systems, vol. 8, no. 32, pp. 1–7, 2021. [Google Scholar]

9. R. Xia, Y. Chen, and B. Ren, “Improved anti-occlusion object tracking algorithm using Unscented Rauch-Tung-Striebel smoother and kernel correlation filter,” Journal of King Saud University—Computer and Information Sciences, vol. 34, no. 8, pp. 6008–6018, 2022. [Google Scholar]

10. J. Zhang, W. Feng, T. Yuan, J. Wang, and A. K. Sangaiah, “SCSTCF: Spatial-channel selection and temporal regularized correlation filters for visual tracking,” Applied Soft Computing, vol. 118, pp. 108485, 2022. [Google Scholar]

11. S. Gavel, R. Charitha, P. Biswas and A. S. Raghuvanshi, “A data fusion based data aggregation and sensing technique for fault detection in wireless sensor networks,” Computing, vol. 103, no. 11, pp. 2597–2618, 2021. [Google Scholar]

12. R. Prajapat, R. N. Yadav and R. Misra, “Energy-efficient k-hop clustering in cognitive radio sensor network for Internet of Things,” IEEE Internet of Things Journal, vol. 8, no. 17, pp. 13593–13607, 2021. [Google Scholar]

13. L. Bhagyalakshmi, S. K. Suman and T. Sujeethadevi, “Joint routing and resource allocation for cluster-based isolated nodes in cognitive radio wireless sensor networks,” Wireless Personal Communications, vol. 114, no. 4, pp. 3477–3488, 2020. [Google Scholar]

14. T. Stephan, F. Al-Turjman and B. Balusamy, “Energy and spectrum aware unequal clustering with deep learning based primary user classification in cognitive radio sensor networks,” International Journal of Machine Learning and Cybernetics, vol. 12, no. 11, pp. 3261–3294, 2021. [Google Scholar]

15. M. Zheng, C. Wang, M. Song, W. Liang and H. Yu, “SACR: A stability-aware cluster-based routing protocol for cognitive radio sensor networks,” IEEE Sensors Journal, vol. 21, no. 15, pp. 17350–17359, 2021. [Google Scholar]

16. V. Gatate and J. Agarkhed, “Energy preservation and network critic based channel scheduling (EPNCS) in cognitive radio sensor networks,” International Journal of Information Technology, vol. 13, no. 1, pp. 69–81, 2021. [Google Scholar]

17. J. Wang and Y. Ge, “A radio frequency energy harvesting-based multihop clustering routing protocol for cognitive radio sensor networks,” IEEE Sensors Journal, vol. 22, no. 7, pp. 7142–7156, 2022. [Google Scholar]

18. M. Zheng, C. Wang, M. Du, L. Chen, W. Liang et al., “A short preamble cognitive MAC protocol in cognitive radio sensor networks,” IEEE Sensors Journal, vol. 19, no. 15, pp. 6530–6538, 2019. [Google Scholar]

19. P. Rai, M. K. Ghose and H. K. D. Sarma, “Game theory based node clustering for cognitive radio wireless sensor networks,” Egyptian Informatics Journal, vol. 23, no. 2, pp. 315–327, 2022. https://doi.org/10.1016/j.eij.2022.02.003 [Google Scholar] [CrossRef]

20. F. Aldosari, L. Abualigah and K. H. Almotairi, “A normal distributed dwarf mongoose optimization algorithm for global optimization and data clustering applications,” Symmetry, vol. 14, no. 5, pp. 1021, 2022. [Google Scholar]

21. M. F. Ahmad, N. A. M. Isa, W. H. Lim and K. M. Ang, “Differential evolution with modified initialization scheme using chaotic oppositional based learning strategy,” Alexandria Engineering Journal, vol. 61, no. 12, pp. 11835–11858, 2022. [Google Scholar]