Design of Evolutionary Algorithm Based Unequal Clustering for Energy Aware Wireless Sensor Networks

1  Introduction

Wireless Sensor Networks (WSNs) are advanced for monitoring and sensing vital signs of area and environment using linked and distributed sensor nodes (SNs). The SNs were divided into Gateway Nodes (GN), normal, and sink nodes [1]. The SNs were small in size and had insufficient sources concerning processing, storage, and space energy [2]. In many cases, the SNs were deployed in a very harsh and intense ecosystem. The first and foremost goal of this positioning was to sense information distantly and sends it to the system or user for decision-making. To send data, there comes a demand for more effective systems for managing the energy system of nodes and enhancing network lifetime [3]. The SNs perceive and sense the data from nearby environments, make processes, and transmit it to the nearby nodes until data arrives at the base station (BS). In WSN, because of the restricted energy sources of SNs, there comes a crucial need for a well-effective and balanced data aggregation system and energy-efficient routing protocol [4]. The energy feature becomes one factor to consider for devising any solution for WSNs. Numerous routing protocols were devised to conserve the energy of SNs [5]. The clustering approach becomes an effective topological control system that could efficiently enhance the scalability duration and lifetime of WSNs. The WSN applications have achieved popularity, including health monitoring, target tracking, disaster response, environmental monitoring, and security [6].

In a clustering ecosystem, data can be involved from one node to another and occurs energy holes or hotspot difficulties [7]. A hotspot can be made by SNs positioned nearby the BS and rapidly drain energy because traffic arises from other nodes and is sent from it. Such SNs not just transmit their data but also send it from other bases because the initial death of nodes causes hotspot problems. The methods, namely unequal clustering methods and mobile sinks or mobile data mules, were majorly utilized to resolve this problem [8]. But many unequal clustering techniques were devised for the solution of the hotspot leverages cluster, which is smaller in size adjacent to BS and cluster size rose case when we were going far away from BS. The cluster size was inversely proportional to the distance from BS. The clusters adjacent to BS hold a greater quantity of nodes that is helpful in efficient load sharing [9]. The projected method for size allotment and size difference of clusters leads to a reduction of frequency where a specific node turns out to be a cluster head (CH) [10]. This aids in the maintenance of the overall connectivity and thwarts network isolation. In line with this, hot spot issues can be reduced. One of the problems concerning unequal clustering was cluster size decreasing or increasing ratio that was not conferred in prevailing methods.

This article introduces a Jumping Spider Optimization Based Unequal Clustering Protocol for Mitigating Hotspot Problems (JSOUCP-MHP) in WSN. The JSO algorithm is stimulated by the characteristics of spiders in nature and mathematically modelled the hunting mechanism such as search, jumping skills, and persecution to attack prey. The presented JSOUCP-MHP technique mainly resolves the hot spot issue for maximizing the network lifespan. To attain this, the JSOUCP-MHP technique elects a proper set of cluster heads (CHs) using average RE. In addition, the JSOUCP-MHP technique determines the cluster sizes based on two measures i.e., RE and distance to BS (DBS). The proposed JSOUCP-MHP technique is examined under several experiments to ensure its supremacy.

2  Related Works

Arikumar et al. [11] modelled an Energy Efficient LifeTime Maximization (EELTM) technique that uses intelligent techniques of Fuzzy Inference System (FIS) and particle swarm optimization (PSO). In addition, an optimal CH–CR selecting method in this technique exploits fitness values (FV) computed by the PSO approach for determining 2 optimal nodes in every cluster to serve as Cluster Router (CR) and CH. The CH, which is selected, exclusively accumulates the data from its cluster members. However, the CR is accountable for receiving the data collected from its CH and sending it to BS. Mehra [12] formulated an enhanced fuzzy unequal clustering and routing protocol (E-FUCA) in which vital variables were regarded at the time of CH candidate selection, and non-CH nodes considered intellectual decisions utilizing FL at the time of the election of its CH for forming clusters. FL is utilized as the next-hop choice for effective routing to expand the lifespan. And carried out the simulation experimentations for 4 cases, and a comparison was made with the propound performance of protocol with recent similar protocols.

Wang et al. [13] introduced an energy-efficient unequal clustering routing algorithm (UCRA). At first, the monitoring region was separated by concentric circles as rings of various sizes. Then, the CH was selected relating to RE and position. Before clustering, every typical sensor links cluster related to the electability of every CH. Nguyen et al. [14] presented a new optimization technique, like the compact bat algorithm (cBA), for using it for optimisation issues involving gadgets containing inadequate hardware sources. A real-valued prototype vector can be employed for probabilistic functions for generating every candidate solution for optimizing cBA. The projected cBA was widely assessed on numerous continual multi-modal functions and the unequal clustering of WSN (uWSN) issues.

In [15], competitive swarm optimization (CSO) related methods were introduced, together called such methods as CSO-UCRA. Initially, the CH selecting approach relies on CSO related approach after assigning non-CH sensors to CHs. At last, a CSO-related routing method was provided. New fitness functions and efficient particle encoding techniques were advanced for such methods. Guleria et al. [16] devise the new ant colony meta-heuristic related to unequal clustering for novel CH election. The neighbor finding level and link maintenance by Meta-Heuristic Ant Colony Optimization (ACO) technique choose the optimal path among the nodes that raises the packets distributed to the destiny. Though several models are available in the literature review, still much work is needed to resolve the hot spot problem. In addition, unequal clustering should be performed by the use of multiple input parameters.

3  The Proposed Unequal Clustering Protocol

This article presented a novel JSOUCP-MHP algorithm for resolving hot spot issues in WSN. The JSO algorithm is stimulated by the characteristics of spiders in nature and mathematically modelled the hunting mechanism such as search, jumping skills, and persecution to attack prey. The presented JSOUCP-MHP technique mainly resolves the hot spot issue for maximizing network lifespan. Fig. 1 depicts the overall process of the JSOUCP-MHP approach.

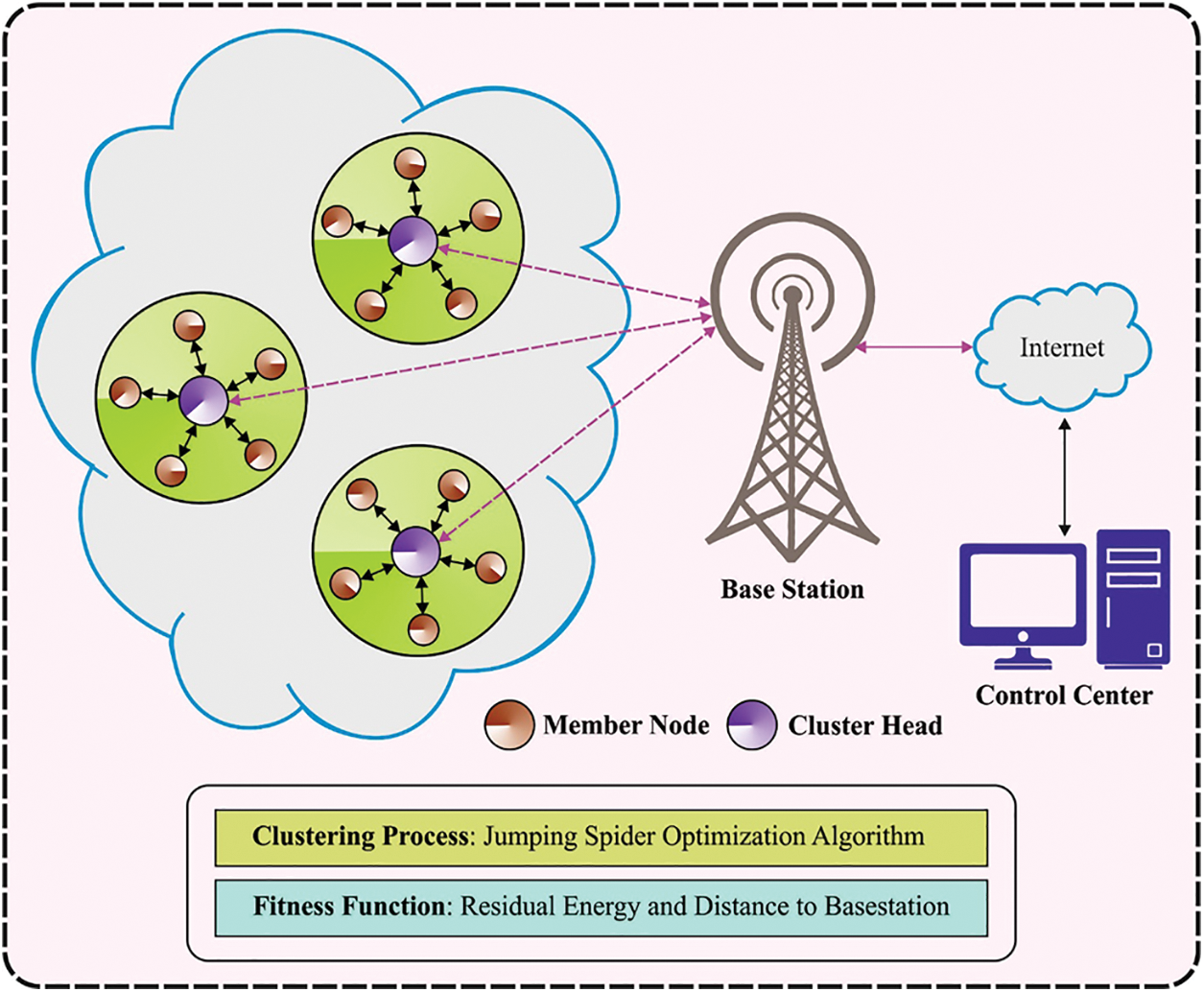
Figure 1: Overall process of JSOUCP-MHP approach

3.1 System Model

A WSN comprises N uniform distribution sensors. There is one BS interconnected with users through the Internet. Let assume S={S1 ,S2, … ,si, sN−1, sN} as the group of nodes, whereby si denotes a nodei and |S|=N . WNS makes use of wireless radio transceivers depending on the different variables, for example, energy utilization and distance. The distance between the receiver and transmitter, followed by attenuated transceiver power, exponentially reduced with increased distance. Now, we represent (xi,⋅yi) and (xj,⋅yj) were the coordinates of nodes i and j . Assume node i sent to destination node j , the energy consumed on communication over d distance can be evaluated as follows:

ETxj(l,d)=ETX−elec(l)+ETx−amp(l, d)={I×Eelec+ϵfs×d2,d < d0I×Eelec+ϵmp×d4,d ≥ d0 (1)

In Eq. (1), E refers to the energy consumption; Tx is to transfer, elect, amp specifies electronic and amplify to modulate, digitalized coding, spreading, and filter signals. It illustrates that multi-hop transmission is highly efficient in WSN. do denotes a threshold of space model,

d0=ϵfsϵmp, (2)

In Eq. (2), the power loss ϵfs/ϵmp are free space and multi-path model, and it is formulated by

ERxij(l)=ERX−elec(l)=l×Eelec.                                  (3)

WSN considered N node in the region of 2D M2 with k cluster. In relation to the hotspot, perplexity in WSN was balancing the load amongst CHs according to the clustering technique. Unequal clustering decreases the cluster size nearer to BS, and the size of the cluster rises as the distance between the BS ad well as CH rises. The cluster member senses the real-time parameter and transfers the sensed value to CH. CH aggregates and receives information to eliminate inessential information and transfer aggregated information to BS directly or through intermediatory CH. In equal clustering, the cluster size remains unchanged all over the network. But, in unequal clustering, the cluster size can be described according to the DBS [17]:

Ec1uster=ECH+(Nk−1)×Emember,                                  (4)

Let N/k−1 be the average of member nodes from the cluster, ECH , Emembers denotes dissipated energy for CH and member correspondingly, and it is evaluated by:

Emember=l×Ee1ec+l×ϵfs×dtoCH2,    (5)

ECH=l×Ee1ec×(Nk−1)+l×EDA×Nk+l×Ee1ec+l×ϵmp×dtoBS4. (6)

As a result, the energy consumed for WSN from the generation formulated from the energy process and transceiver was given by:

Etotal=Ep+Eframe=Ep+k×Ec1uster, (7)

In Eq. (7), Ep is the energy consumed for the microcontroller and source voltage of the node. It doesn’t affect the optimization process. As a result, the consumed energy Eframe optimizes according to the distance for clustering optimization.

3.2 Design of JSO Algorithm

The mathematical modelling of the jumping spider’s hunting strategy is initially proposed. Then, The JSOA approach was introduced. The hunting strategies are searching, jumping on the prey, and attacking by persecution [18]. Also, the algorithm describes the pheromone rate of the spider as follows.

Once the spider is away from a distance, whereas it could catch the prey by jumping, it moves closer by indulging in certain stealthy movements till it is at an attainable distance where it can catch the prey and pounces on it. The persecution approach can be described as the uniform accelerated rectilinear motion.

xi=12at2+v0t     (8)

In Eq. (8), xi demonstrates the location of the ith follower spider, t refers to the time, v0 represents the speed initially. The acceleration can be shown as a=vt , where v=χ−χ0.

In this study, to optimize, every iteration can be regarded as the duration, in which the differences between iterations are equivalent to 1, and initially, the speed is fixed as zero, v0=0 . And it is formulated as follows:

χi(g+1)=12(xi→(g)−xr→(g))    (9)

In Eq. (9), xi→(g+1) represents the novel location of the search agent to generation g+1,xi→(g) indicates the present i - th searching agent in generation g , and xr→(g)→ denotes the r - th searching agent arbitrarily chosen, with i≠r , whereas r represents an arbitrary value ranging from 1 to the size of maximal searching agent.

The jumping spider follows the prey and jumps on them. The hunting strategy of jumping on prey is characterized by a projectile motion.

χi→=v0 cos (α)ti→

dxdt=Vx→=v0 cos (α)i  → (10)

Likewise, the vertical axis and the derivative w.r.t time can be given as.

yi→=(v0sen(α)t21−gt2)j→                (11)

dydt=Vy→=(v0sen(α)−gt)j→

Similarly, time is characterized by strategy 1. Thus we attain the trajectory equation as follows.

y=x tan (α)−gxi2→2V02cos2(α)                    (12)

Lastly, the trajectory is formulated by:

xi→(g+1)=xi→(g)tan (α)−gx2→(g)2V02cos2(α)           (13)

α=φπ180

In Eq. (13), xi→(g+1) refers to the novel location of a searching agent, representing jumping spider movement, xi→(g) denotes the existing i - th searching agent, V0 is fixed as 100 mm/seg, g denotes the gravity ( 9.80665 m/s2) , and the α angle can be measured by an φ angle arbitrarily produced within zero and one.

The Jumping spider implements a random search around the environment to locate prey. Local and global search are the two mathematical functions presented as follows.

The local search can be defined as follows:

xi→(g+1)=xbest(g)+walk→(12−ϵ)    (14)

In Eq. (14), xi→(g+1) refers to the novel location of the searching agent, xbest→(g) denotes the optimal searching agent found from the preceding iteration, the walk was a normally distributed pseudo-random integer within (−2,2) , ϵ denotes a pseudo-random number uniformly distributing from (0,1) .

At the same time, the Global search can be expressed as follows.

xi→(g+1)=xbest→(g)+(xbest→(g)−xworst→(g))λ    (15)

In Eq. (15), xi→(g+1) denotes the novel location of a searching agent, xbest→(g) and xworst→(g) indicates the best and worst searching agent form preceding iteration; correspondingly, and λ refers to a Cauchy random integer with μ fixed as and θ fixed as 1.

Pheromone is released by several animals, amongst which were insects, together with spiders. Nonetheless, they produce pheromones; the modelling of the rate of pheromones was taken and described as follows:

pheromone (i)=Fitnessmax−Fitness(i)Fitnessmax−Fitnessmin     (16)

In Eq. (16), Fitnessmax  and Fitnessmin represent the worst and the best FV in the present generation, correspondingly, while Fitness(i) refers to the present FV of the i - th searching agent. Eq. (16) normalizes the FV within zero and one whereas indicates the worst pheromone rate, while 1 denotes the optimal. The criteria involve for lower pheromone rate value equivalent to or lesser than 0.3 as follows:

xi→(g)=xbest→(g)+12(xr1→(g)−(−1)σXr2→(g)) (17)

In Eq. (17), xi→(g) represent the searching agent (jumping spider) with a lower pheromone rate that is upgraded, r1 and r2 indicate arbitrary number produced from 1 to the maximal size of a searching agent, with r1≠r2 , while xr1→(g) and xr2→(g) are the r1 , r2th searching agent selected, xbest→(g) indicates the best searching agent from preceding iteration and σ indicates a binary number produced, σ∈{0,1} .

3.3 Process Involved in JSOUCP-MHP Technique

In the real-time application of WSN, a massive amount of nodes is positioned generally with a higher node density. Assume a proper threshold T for controlling the proportion of CH , T is fixed at 0.4. Every node Sj evaluates the value of μ . When μ<T , node Sj become a CCH; or else, node Sj becomes a regular node and go to a dormant state until the last CH selection is accomplished as follows.

μ=μ0EavgREi,    (18)

In Eq. (18), μ0 refers to a uniformly distributed arbitrary value within [0,1] , and Eavg indicates the average RE of an alive node. The computation method was given in the following: The data packet transferred by the node includes REi . Afterward, the BS received, the average RE Eavg of each alive node is evaluated; REi characterizes the RE of node Si . Clearly, the large of REi , the small of μ , hence the better possibility that Si becomes a CH.

In the JSOUCP-MHP technique, consider the distance from CH to BS and ignore the energy. This might leads to a lower energy node being the CH, and afterward generating a cluster, the member in the cluster causes an increase in the energy usage of CH. As a result, a competitive radius considering distance and energy is presented, and the competitive radius for CH vi is evaluated as follows.

vi.Rcomp=[1−w1dmax −d(vi,BS)dmax −dmin −w2(1−REviE0)]×Rcomp0, (19)

In Eq. (5), dmax  and dmin  denotes the maximal and minimal distances from the alive node to the BS ; correspondingly, d(vi, BS) represents the distance from vi to the BS, REvi indicates the RE of vi, w1 and w2 are constant within [0,1] , and w1+w2=1 .

4  Performance Validation

A brief set of experimental analyses is carried out to demonstrate the enhanced performance of the JSOUCP-MHP model on WSN. The initial energy is 1 mJ, the node count is 500, and first-order radio energy model is used.

Table 1 and Fig. 2 showcase the network lifetime (NLT) inspection of the JSOUCP-MHP model with existing models under the varying density of sensor nodes (DSN). The experimental outcomes depicted that the JSOUCP-MHP model has shown enhanced performance with higher NLT values. For instance, with 50 DSN, the JSOUCP-MHP model has exhibited an increased NLT of 1757 whereas the enhanced metaheuristic-driven energy-aware cluster-based routing (IMD-EACBR), sunflower optimization (SFO), grey wolf optimization (GWO), and genetic algorithm (GA) models have demonstrated reduced NLT of 1549, 1433, 1422, and 1343 respectively. Moreover, with 250 DSN, the JSOUCP-MHP model has attained a higher NLT of 2556, whereas the IMD-EACBR, SFO, GWO, and GA models have obtained lower NLT of 2374, 2276, 2012, and 1852 respectively. On the other hand, with 500 DSN, the JSOUCP-MHP model has illustrated an improved NLT of 3802, whereas the IMD-EACBR, SFO, GWO, and GA models have depicted reduced NLT of 3789, 3691, 3650, and 3369 respectively.

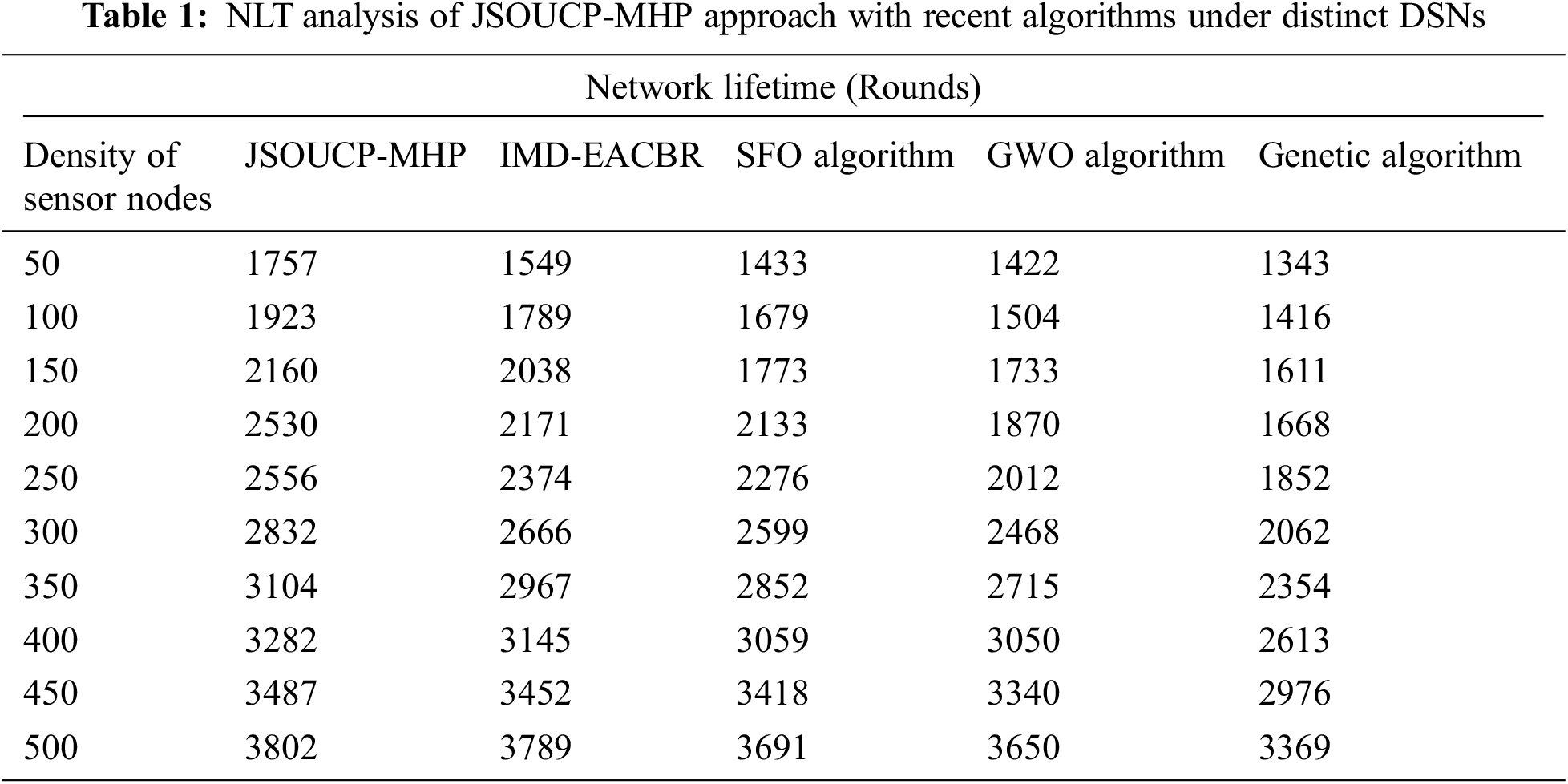
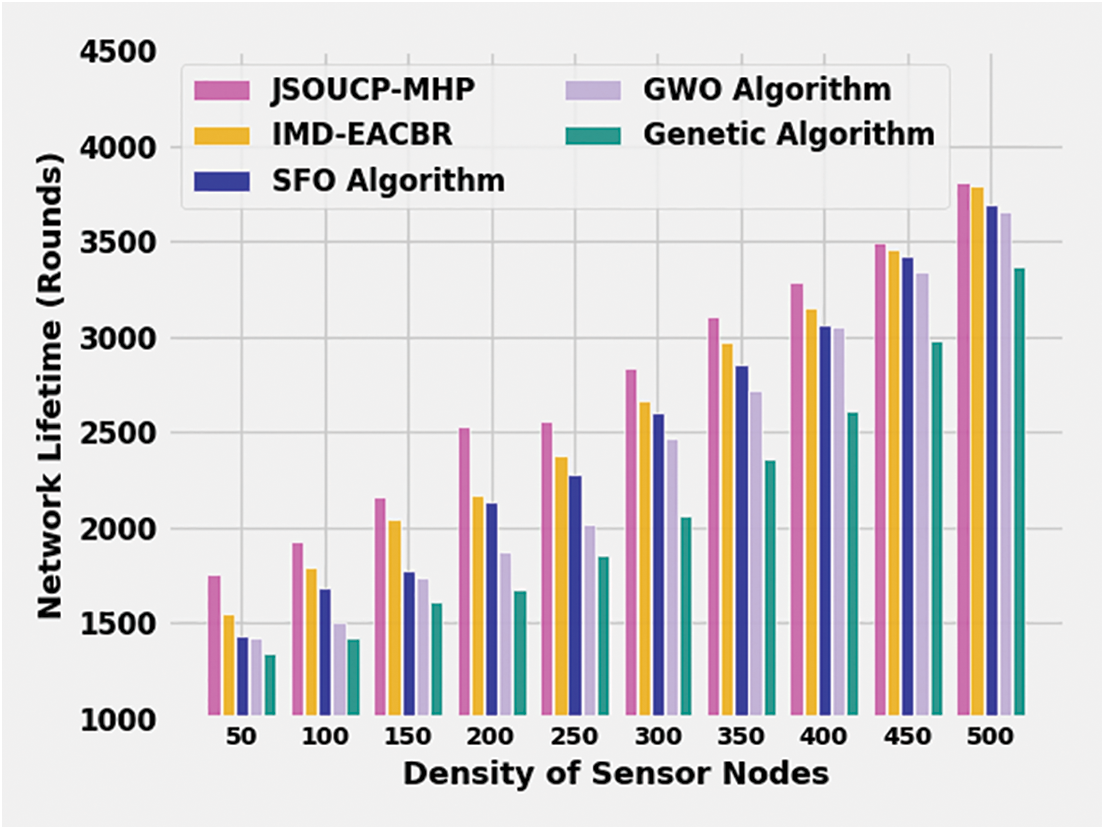
Figure 2: NLT analysis of JSOUCP-MHP approach under distinct DSNs

Table 2 and Fig. 3 exhibits the number of Alive Sensor Nodes (NOASN) analysis of the JSOUCP-MHP algorithm with existing models under varying count of rounds. The experimental outcomes depicted that the JSOUCP-MHP approach has shown enhanced performance with higher NOASN values. For example, with 2000 rounds, the JSOUCP-MHP approach has exhibited improved NOASN of 481 where the IMD-EACBR, SFO, GWO, and GA methods have demonstrated reduced NOASN of 473, 405, 391, and 283 correspondingly. Furthermore, with 3000 rounds, the JSOUCP-MHP method has reached a higher NLT of 367 whereas the IMD-EACBR, SFO, GWO, and GA models have acquired lower NOASN of 264, 112, 80, and 78 correspondingly. In contrast, with 4000 rounds, the JSOUCP-MHP model has demonstrated an improved NOASN of 176 whereas the IMD-EACBR, SFO, GWO, and GA models have shown reduced NOASN of 87, 11, 0, and 0 correspondingly.

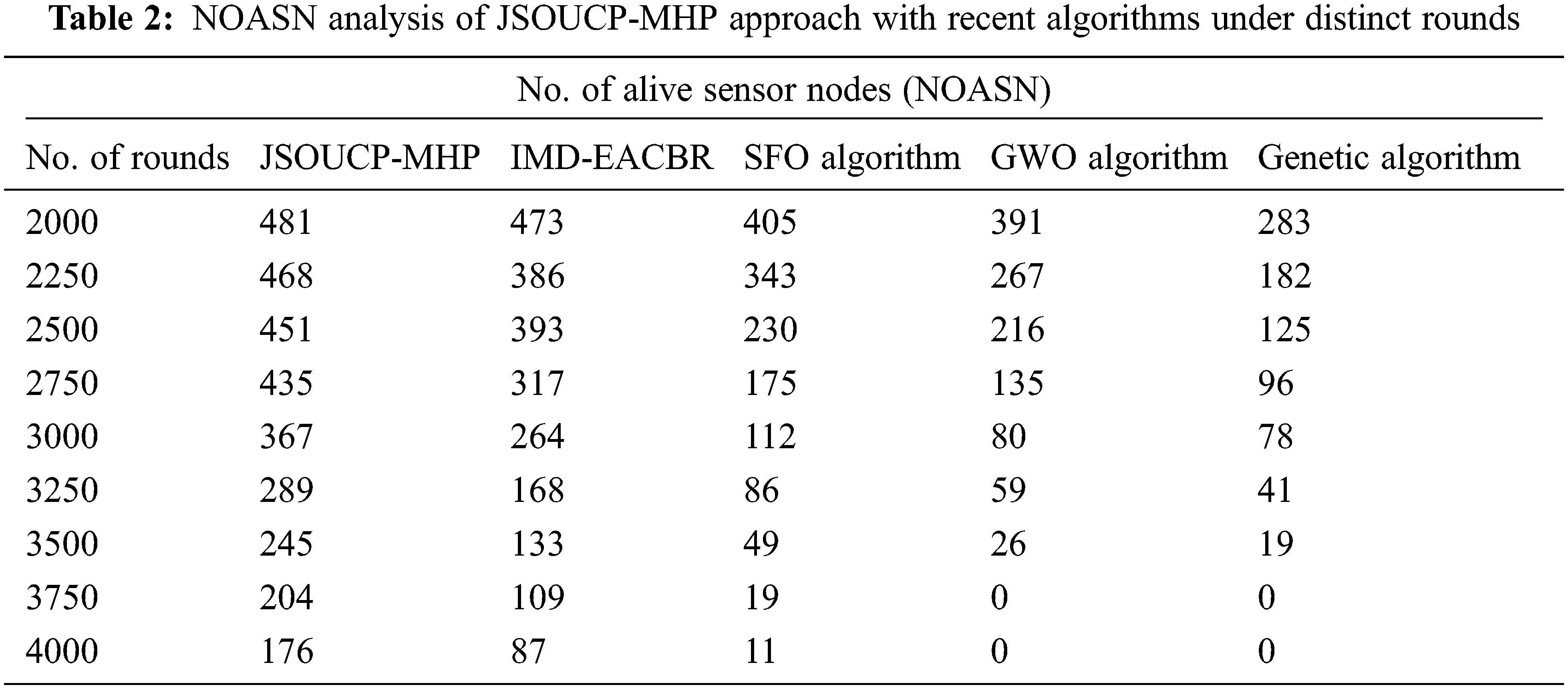
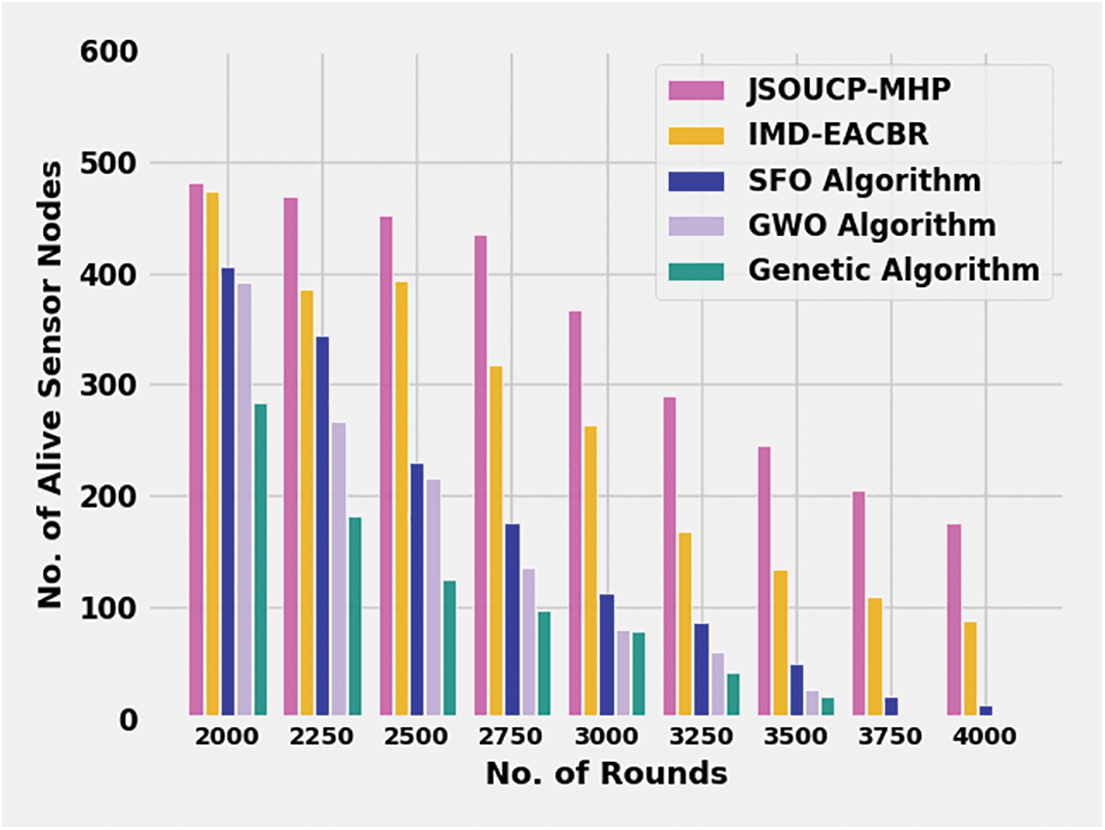
Figure 3: NOASN analysis of JSOUCP-MHP approach under distinct rounds

A detailed number of dead sensor node (NODSN) assessments of the JSOUCP-MHP with recent approaches were performed in Table 3 and Fig. 4. The results inferred the JSOUCP-MHP technique has resulted in enhanced results with minimum values of NODSN. For instance, with 2000 rounds, the JSOUCP-MHP model has achieved the least NODN of 19 whereas the IMD-EACBR, SFO, GWO, and GA models have reached increased NODN of 27, 95, 109, and 217 respectively. Meanwhile, with 3000 rounds, the JSOUCP-MHP model has resulted in decreased NODN of 133 whereas the IMD-EACBR, SFO, GWO, and GA models have exhibited increased NODN of 236, 388, 420, and 422 respectively. Eventually, with 4000 rounds, the JSOUCP-MHP method has rendered a minimal NODN of 324 whereas the IMD-EACBR, SFO, GWO, and GA models have achieved maximum NODN of 413, 489, 500, and 500 correspondingly.

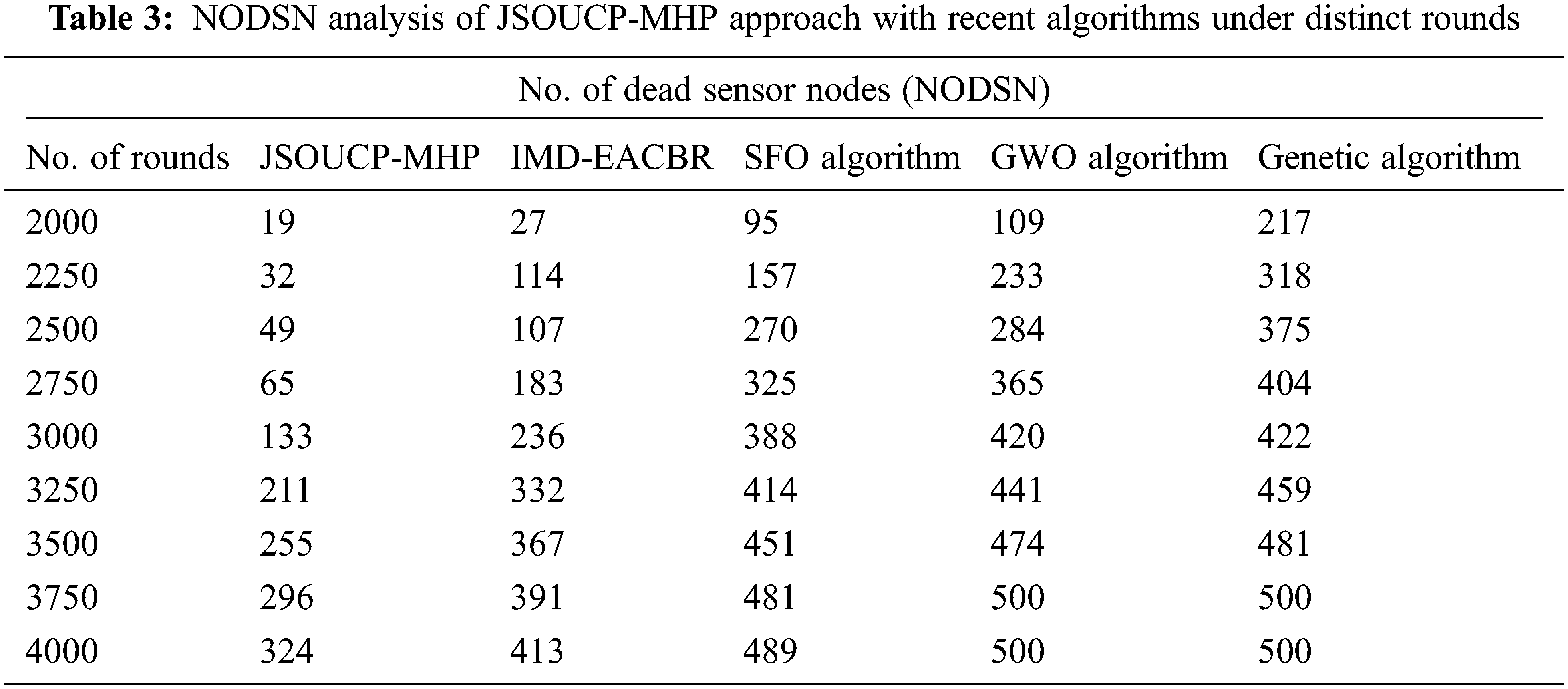
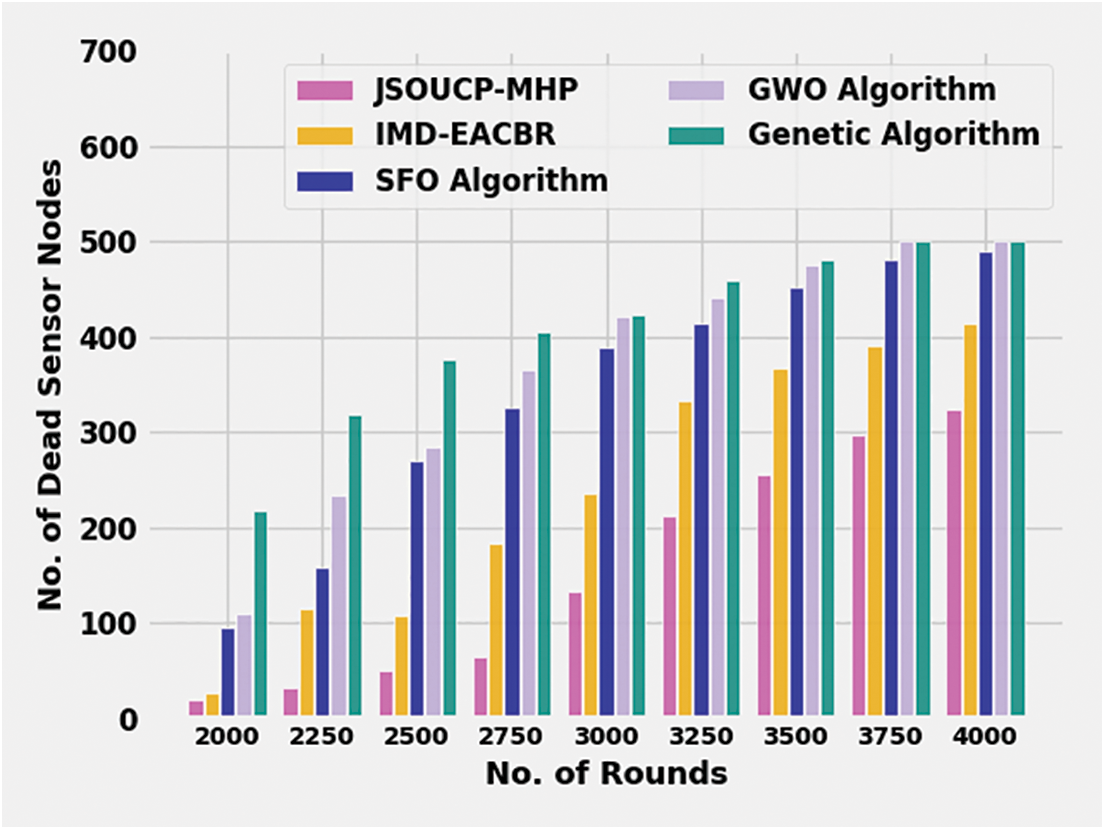
Figure 4: NODSN analysis of JSOUCP-MHP approach under distinct rounds

A detailed energy consumption (ECON) evaluation of the JSOUCP-MHP with recent methods is executed in Table 4 and Fig. 5. The results implicit the JSOUCP-MHP method have resulted in enhanced results with the least values of ECON. For example, with 50 DSN, the JSOUCP-MHP method del has gained the least ECON of 0.0585 mJ whereas the IMD-EACBR, SFO, GWO, and GA models have acquired increased ECON of 0.0936, 0.1117, 0.1373, and 0.2183 mJ correspondingly. In the meantime, with 250 DSN, the JSOUCP-MHP algorithm has resulted in decreased ECON of 0.3004 mJ whereas the IMD-EACBR, SFO, GWO, and GA algorithms have exhibited improved ECON of 0.3201, 0.4321, 0.5201, and 0.5545 mJ respectively. Finally, with 500 DSN, the JSOUCP-MHP model has presented a minimal ECON of 0.5437 mJ whereas the IMD-EACBR, SFO, GWO, and GA models have gained maximum NODN of 0.6608, 0.6678, 0.8210, and 0.8433 mJ correspondingly.

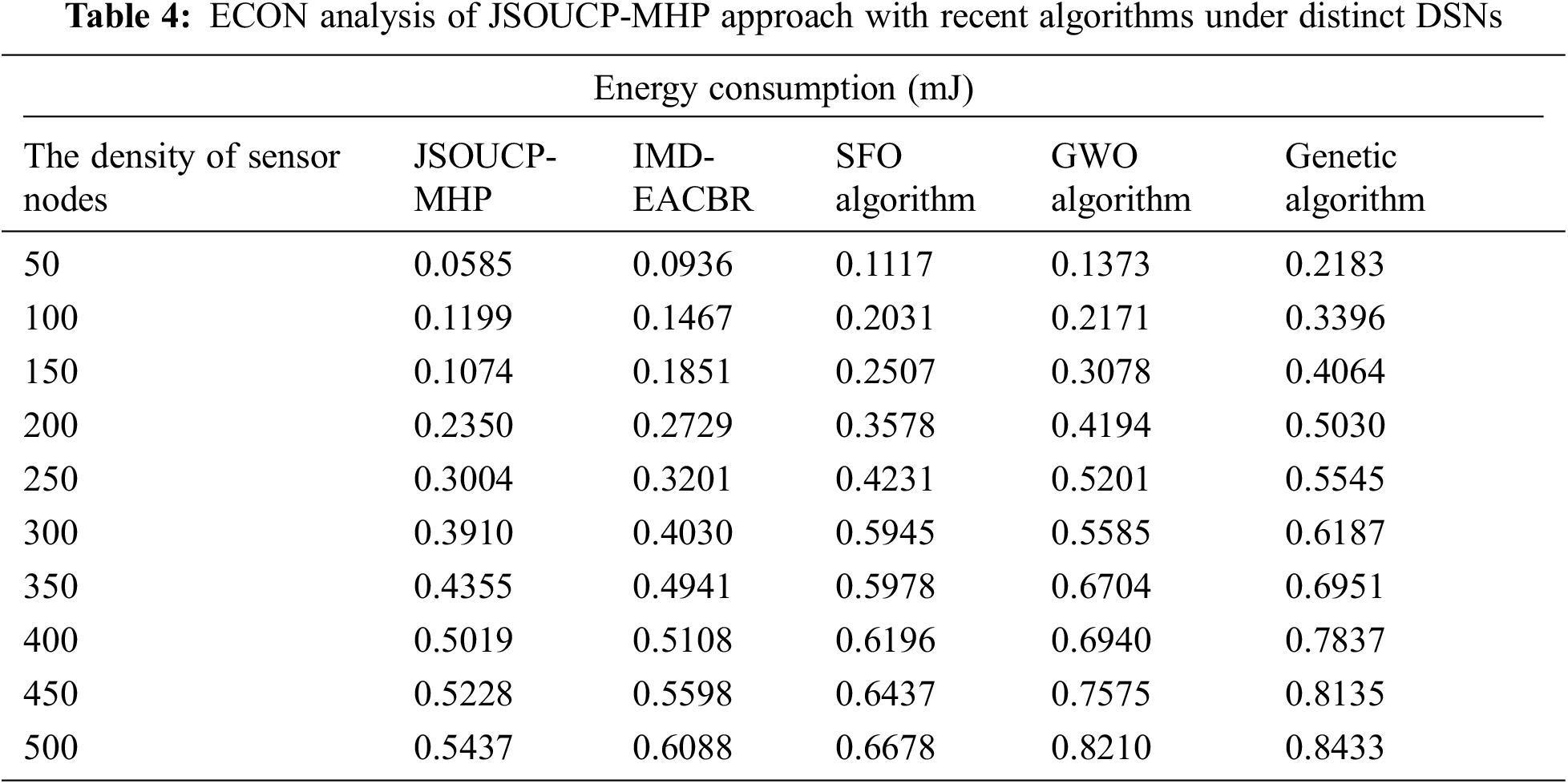
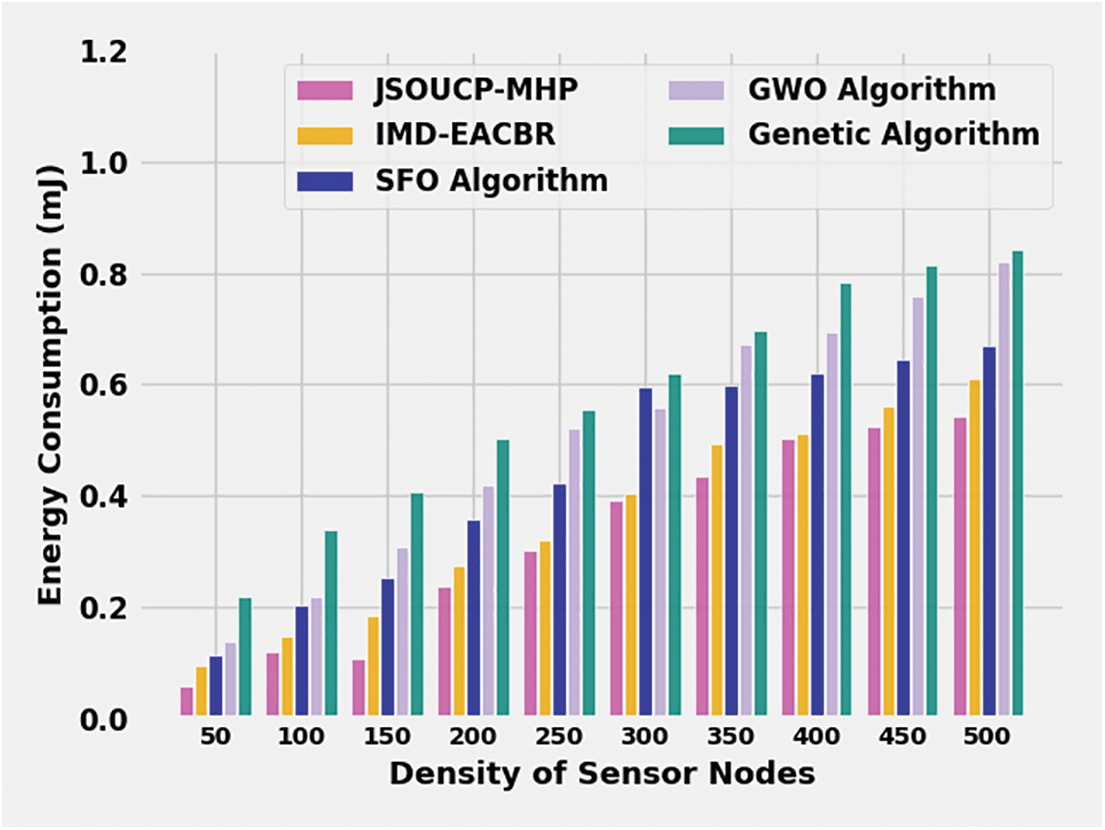
Figure 5: ECON analysis of JSOUCP-MHP approach under distinct DSNs

Table 5 and Fig. 6 display the throughput (THROU) review of the JSOUCP-MHP model with existing models under varying DSN. The experimental outcomes indicated the JSOUCP-MHP model has shown enhanced performance with higher THROU values. For example, with 50 DSN, the JSOUCP-MHP method has exhibited an increased THROU of 0.9875 Mbps whereas the IMD-EACBR, SFO, GWO, and GA models have demonstrated reduced THROU of 0.9323, 0.8915, 0.8640, and 0.8136 Mbps correspondingly. In addition, with 250 DSN, the JSOUCP-MHP model has gained higher THROU of 0.9517 Mbps whereas the IMD-EACBR, SFO, GWO, and GA models have obtained lower THROU of 0.8955, 0.7997, 0.7435, and 0.7031 Mbps correspondingly.

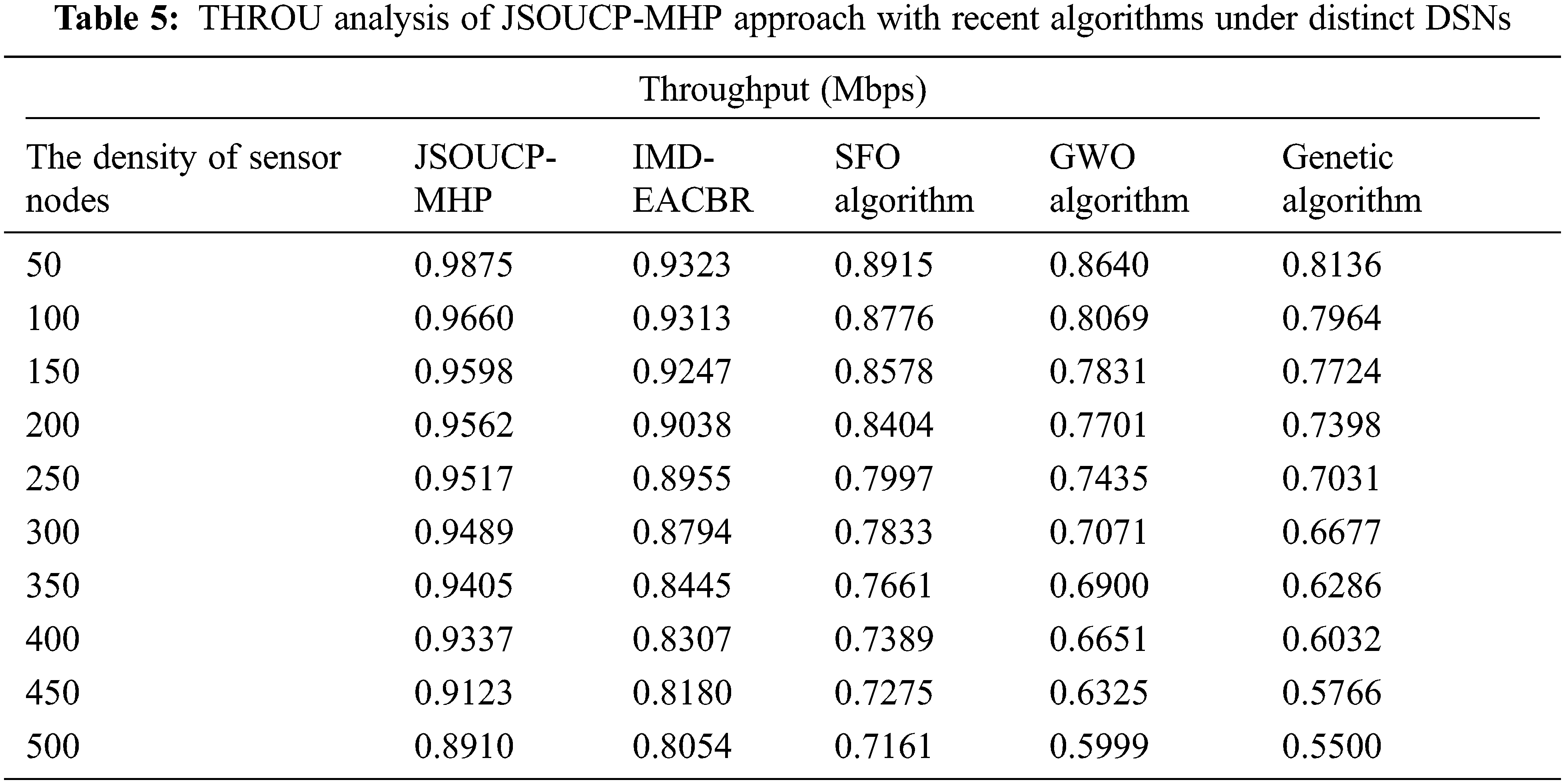
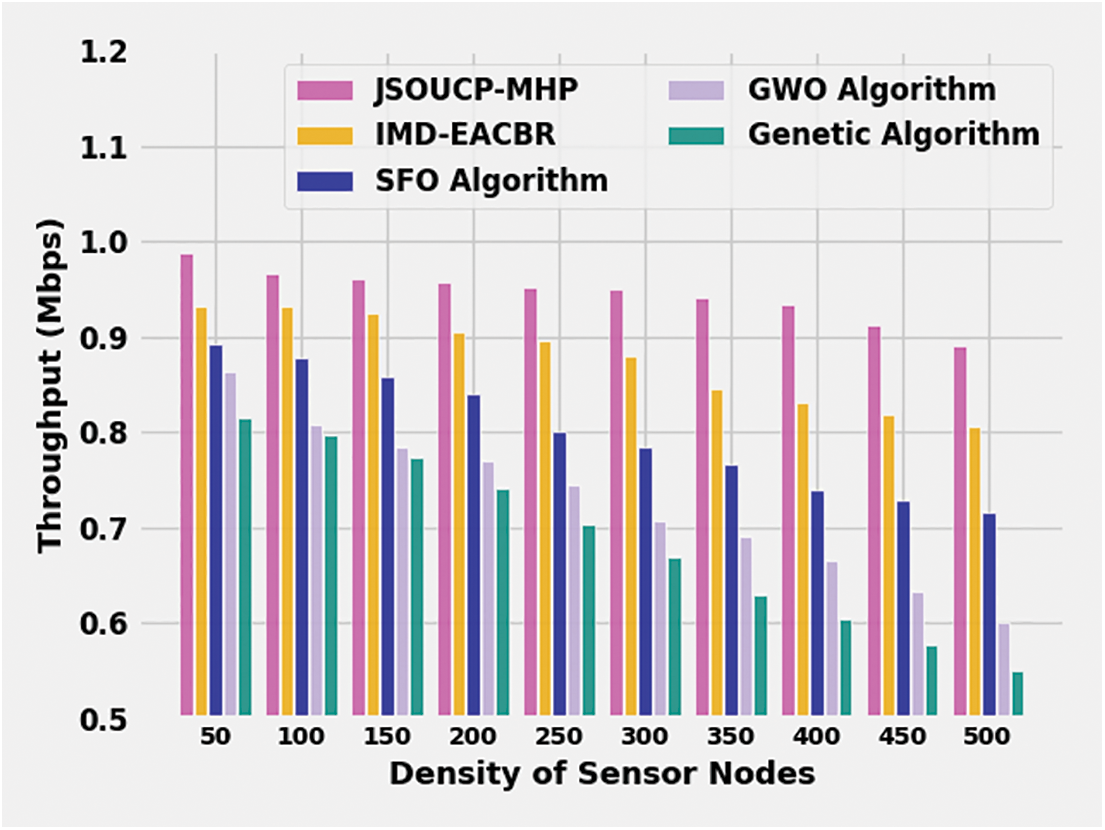
Figure 6: THROU analysis of JSOUCP-MHP approach under distinct DSNs

Conversely, with 500 DSN, the JSOUCP-MHP model has exemplified enhanced THROU of 0.8910 Mbps whereas the IMD-EACBR, SFO, GWO, and GA models have depicted reduced NLT of 0.8054, 0.7161, 0.5999, and 0.5500 Mbps correspondingly.

A detailed Packet Loss Rate (PLR) valuation of the JSOUCP-MHP with recent methods is exhibited in Table 6 and Fig. 7. The results denoted the JSOUCP-MHP approach has resulted in enhanced results with the least values of PLR. For example, with 50 DSN, the JSOUCP-MHP model has attained least PLR of 0.94% whereas the IMD-EACBR, SFO, GWO, and GA models have gained increased PLR of 1.78%, 3.69%, 3.88%, and 4.96% correspondingly.

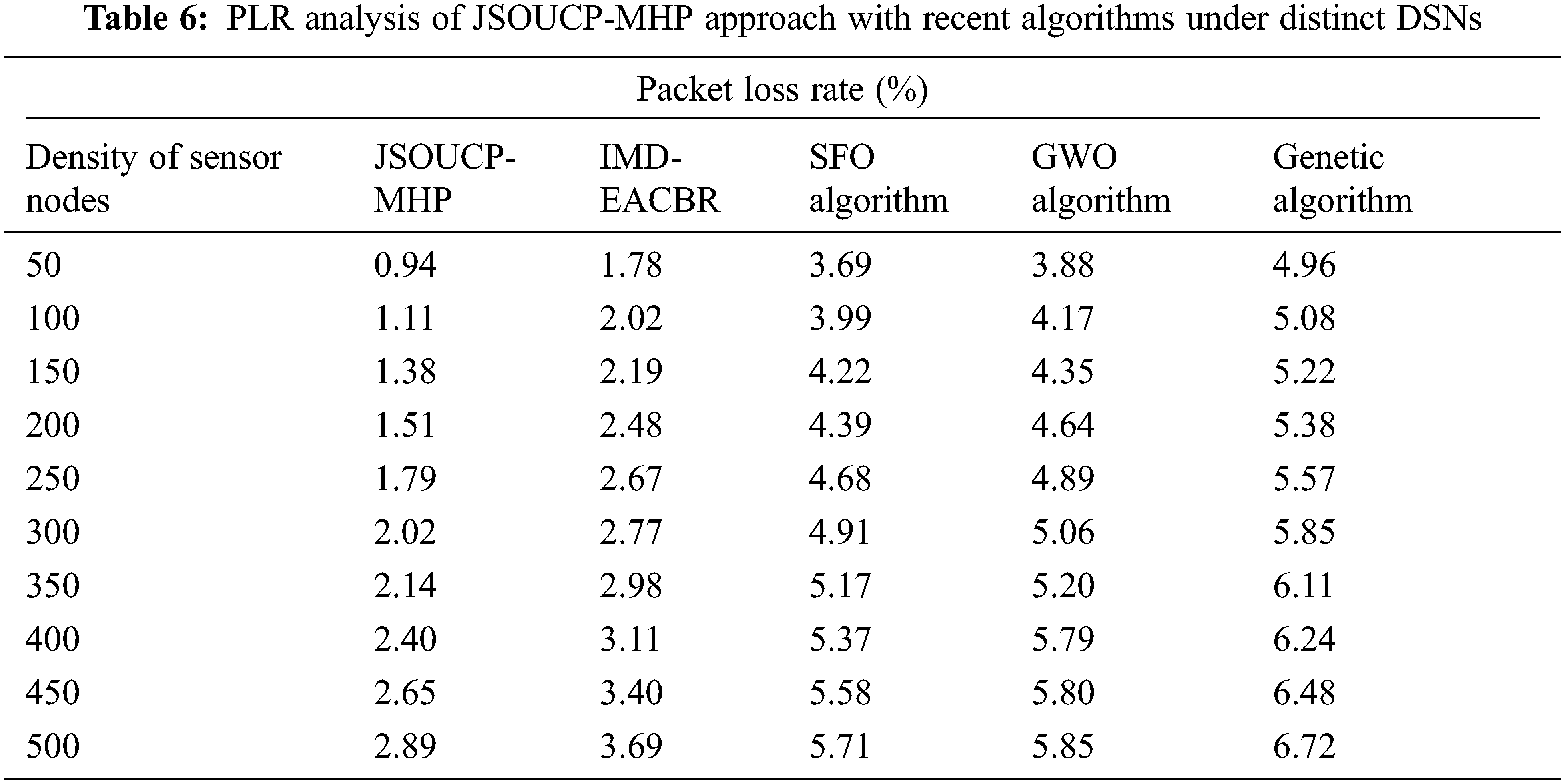
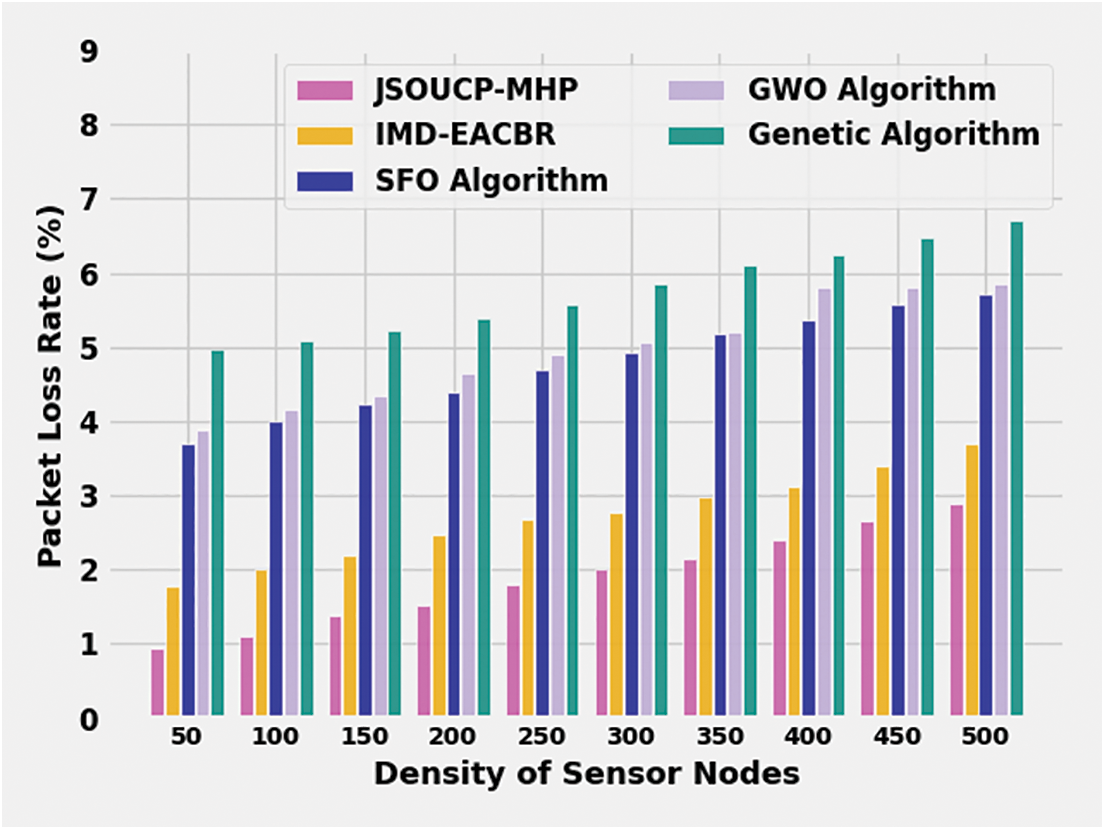
Figure 7: PLR analysis of JSOUCP-MHP approach under distinct DSNs

Meanwhile, with 250 DSN, the JSOUCP-MHP model has resulted in decreased PLR of 1.79% whereas the IMD-EACBR, SFO, GWO, and GA models have exhibited increased PLR of 2.67%, 4.68%, 4.89%, and 5.57% correspondingly. Finally, with 500 DSN, the JSOUCP-MHP model has offered a lesser PLR of 2.89% whereas the IMD-EACBR, SFO, GWO, and GA models have acquired maximum PLR of 3.69%, 5.71%, 5.85%, and 6.72% correspondingly. These results confirmed that the JSOUCP-MHP technique has accomplished enhanced performance over other models.

5  Conclusion

In this article, a novel JSOUCP-MHP system has been presented for resolving hot spot issues in WSN. The JSO algorithm is stimulated by the characteristics of spiders naturally and mathematically modelled the hunting mechanism such as jumping skills, persecution, and search, to attack prey. The presented JSOUCP-MHP technique mainly resolves the hot spot issue for maximizing the network lifetime. To attain this, the JSOUCP-MHP technique elects proper set of CHs using average RE. Also, the JSOUCP-MHP system determines the cluster sizes dependent upon two measures such as RE and DBS. The proposed JSOUCP-MHP technique is examined under several experiments to ensure its supremacy. The comparison study shows the significance of the JSOUCP-MHP technique over other models. In upcoming years, the performance of the JSOUCP-MHP system will be improved by data aggregation approaches.

Funding Statement: This research was supported by the MSIT (Ministry of Science and ICT), Korea, under the ICAN (ICT Challenge and Advanced Network of HRD) program (IITP-2022-2020-0-01832) supervised by the IITP (Institute of Information & Communications Technology Planning & Evaluation) and the Korea Technology and Information Promotion Agency (TIPA) for SMEs grant funded by the Korea government(Ministry of SMEs and Startups) (No. S3271954) and the Soonchunhyang University Research Fund.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. N. Moussa and A. E. B. E. Alaoui, “An energy-efficient cluster-based routing protocol using unequal clustering and improved ACO techniques for WSNs,” Peer to Peer Networking Applications, vol. 14, no. 3, pp. 1334–1347, 2021. [Google Scholar]

2. S. Arjunan and P. Sujatha, “A survey on unequal clustering protocols in wireless sensor networks,” Journal of King Saud University-Computer and Information Sciences, vol. 33, no. 1, pp. 118, 2021. [Google Scholar]

3. A. A. Jasim, M. Y. I. Idris, S. R. B. Azzuhri, N. R. Issa, M. T. Rahman et al., “Energy-efficient wireless sensor network with an unequal clustering protocol based on a balanced energy method (EEUCB),” Sensors, vol. 21, no. 3, pp. 784, 2021 [Google Scholar] [PubMed]

4. K. W. Al-ani, F. B. Abdullah and S. Yossuf, “Unequal clustering in wireless sensor network: A review,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 22, no. 1, pp. 419, 2021. [Google Scholar]

5. D. Agrawal and S. Pandey, “Load balanced fuzzy-based unequal clustering for wireless sensor networks assisted Internet of Things,” Engineering Reports, vol. 2, no. 3, pp. e12130, 2020. [Google Scholar]

6. R. Vinodhini and C. Gomathy, “Fuzzy based unequal clustering and context-aware routing based on glow-worm swarm optimization in wireless sensor networks: Forest fire detection,” Wireless Personal Communications, vol. 118, no. 4, pp. 3501–3522, 2021. [Google Scholar]

7. S. Phoemphon, C. So-In, P. Aimtongkham and T. G. Nguyen, “An energy-efficient fuzzy-based scheme for unequal multi-hop clustering in wireless sensor networks,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 1, pp. 873–2021, 2021. [Google Scholar]

8. F. Zhu and J. Wei, “An energy-efficient unequal clustering routing protocol for wireless sensor networks,” International Journal of Distributed Sensor Networks, vol. 15, no. 9, pp. 155014771987938, 2019. [Google Scholar]

9. N. M. Shagari, M. Y. I. Idris, R. B. Salleh, I. Ahmedy, G. Murtaza et al., “A hybridization strategy using equal and unequal clustering schemes to mitigate idle listening for lifetime maximization of wireless sensor network,” Wireless Networks, vol. 27, no. 4, pp. 2641–2670, 2021. [Google Scholar]

10. B. M. Sahoo and T. Amgoth, “An improved bat algorithm for unequal clustering in heterogeneous wireless sensor networks,” SN Computer Science, vol. 2, no. 4, pp. 290, 2021. [Google Scholar]

11. K. S. Arikumar, V. Natarajan and S. C. Satapathy, “EELTM: An energy efficient lifetime maximization approach for wsn by pso and fuzzy-based unequal clustering,” Arabian Journal for Science and Engineering, vol. 45, no. 12, pp. 10245–10260, 2020. [Google Scholar]

12. P. S. Mehra, “E-FUCA: Enhancement in fuzzy unequal clustering and routing for sustainable wireless sensor network,” Complex & Intelligent Systems, vol. 8, no. 1, pp. 393–412, 2022. [Google Scholar]

13. F. Wang and H. Hu, “An energy-efficient unequal clustering routing algorithm for wireless sensor network,” Revue d’IntelligenceArtificielle, vol. 33, no. 3, pp. 249–254, 2019. [Google Scholar]

14. T. T. Nguyen, J. S. Pan and T. K. Dao, “A compact bat algorithm for unequal clustering in wireless sensor networks,” Applied Sciences, vol. 9, no. 10, pp. 1973, 2019. [Google Scholar]

15. P. C. S. Rao, P. Lalwani, H. Banka and G. S. N. Rao, “Competitive swarm optimization based unequal clustering and routing algorithms (CSO-UCRA) for wireless sensor networks,” Multimedia Tools and Applications, vol. 80, no. 17, pp. 26093–26119, 2021. [Google Scholar]

16. K. Guleria and A. K. Verma, “Meta-heuristic ant colony optimization based unequal clustering for wireless sensor network,” Wireless Personal Communications, vol. 105, no. 3, pp. 891–911, 2019. [Google Scholar]

17. T. T. Nguyen, J. S. Pan, T. K. Dao and S. C. Chu, “Load balancing for mitigating hotspot problem in wireless sensor network based on enhanced diversity pollen,” Journal of Information and Telecommunication, vol. 2, no. 1, pp. 91–106, 2018. [Google Scholar]

18. H. P. Vázquez, A. P. Delgado, P. Ranjan, C. Barde, A. Choubey et al., “A bio-inspired method for mathematical optimization inspired by arachnida salticidade,” Mathematics, vol. 10, no. 1, pp. 102, 2021. [Google Scholar]