Tight Sandstone Image Augmentation for Image Identification Using Deep Learning

1  Introduction

Unconventional oil and gas have become a critical replacement field for the sustainable development of the global oil industry [1,2]. Unlike conventional oil and gas, unconventional oil and gas reservoirs represented by tight sandstones have complex pore structures and special fluid transport and aggregation mechanisms, making their large-scale exploration and development difficult [3,4]. Therefore, the image identification of tight sandstone thin slices is important to analyze the microscopic pore structure and explore the fluid transport and aggregation mechanisms [5,6].

Currently, deep learning-based image analysis methods are widely used for tight sandstone image analysis tasks because they have the advantages of more accurate results and faster speed than traditional methods [7–9]. However, such deep learning algorithms typically fall within the domain of supervised artificial intelligence and often rely too much on high-quality, labeled big data for training. The tight sandstone image dataset is relatively limited due to the difficulty of data acquisition, the high cost of labeling, and privacy protection. This makes it hard to improve the generalization ability of deep learning models. For this reason, researchers usually use data deformation methods or data oversampling methods for data augmentation to generate “new data” by transforming the original data, so that deep learning models can extract more useful information and improve the generalization ability of the models [10].

The data deformation method takes a single image itself as the object of operation. It changes the manifestation of the original image by various transformations (rotation, scale, distortion, etc.) to produce a large number of “new images” different from the original image [11]. Cirillo et al. [12] used data deformation methods to achieve brain tumor image augmentation. By comparing the augmentation effects of different operations, he concluded that augmentation strategies need to be developed based on image properties and task requirements. But the augmentation strategy needs to be manually chosen, making it relatively subjective and inefficient. Inspired by previous works of Automatic Machine Learning (AutoML) on Neural Architecture Search (NAS) [13–15], some researchers propose using reinforcement learning [16] or density matching [17] to search for augmentation strategies, which solved the problem of augmentation strategies requiring manual selection and obtained higher validation accuracy than the manual formulation of augmentation strategies on the target dataset [18–20]. However, such algorithms were designed for natural images, so it is hard to apply directly to the tight sandstone image augmentation.

Generative Adversarial Networks (GANs) are a representative technique of data oversampling methods [21], which synthesize “new images” that do not exist in real scenes but have a probability of occurrence by oversampling the data distribution. But the network requires a large amount of data for training, and it is hard to generate high-resolution images [11]. Karras et al. [22–24] investigated the application of GANs in generating high-resolution images and effectively improved the quality of generated images with small-scale data training by redesigning the generator’s structure and adding adaptive discriminator augmentation. However, the quality of the generated images is unsatisfactory in the case of many foreground targets, complex structures, and relatively smaller training data scales [8].

In summary, it is difficult to solve the tight sandstone image augmentation problem with limited quantity and complex image structure using the data deformation method or the data oversampling method alone. To this end, this paper proposes a hybrid tight sandstone image augmentation method by fusing the respective advantages of the data deformation method and the data oversampling method. Firstly, to improve the data diversity, the style control method and the augmentation intensity adjustment period are modified for the StyleGAN to propose the Self-Attention-Based Style Generative Adversarial Network (SA-StyleGAN) to generate high-resolution tight sandstone images. Secondly, to expand the data scale, the augmentation strategy search space and the search algorithm are redesigned for the AutoAugment to propose the Adaptive Stochastic Natural Gradient-Based Automatic Data Augmentation (ASNG-AA) algorithm to search for the optimal augmentation strategy. Finally, the effectiveness of the method is experimentally demonstrated in real appliance scenarios.

The method proposed in this paper has been applied to real scenarios and has good results. For example, this method was used by the Research Institute of Exploration and Development of Daqing Oilfield to augment the tight sandstone thin slice images in the Putaohua reservoir in the Sanzhao Sag of the Songliao Basin [25] to train the Mask Region-Based Convolutional Neural Network (Mask R-CNN) [26] algorithm to realize the segmentation and recognition of tight oil reservoir sandstone images. In the practical application process, the method effectively improves the recognition performance of the model, saving considerable time and economic costs for research institutions and contributing to unconventional oil and gas reservoir evaluation and exploration research.

The rest of this paper is organized as follows. Section 2 elaborates on the tight sandstone image augmentation research method and condenses the key issues. The improvement schemes of SA-StyleGAN and ASNG-AA are described in Section 3 and Section 4, respectively. Section 5 discusses the experimental results. Section 6 summarizes the work of this paper and provides an outlook for future work.

2  Tight Sandstone Image Augmentation Framework

In order to solve the problems of insufficient diversity and the limited number of tight sandstone images, this study proposes a hybrid tight sandstone image augmentation method based on the idea of “divide and conquer, complementary advantages.” The problems are solved separately by integrating the generative adversarial network and automatic data augmentation. The general framework of the proposed method is shown in Fig. 1.

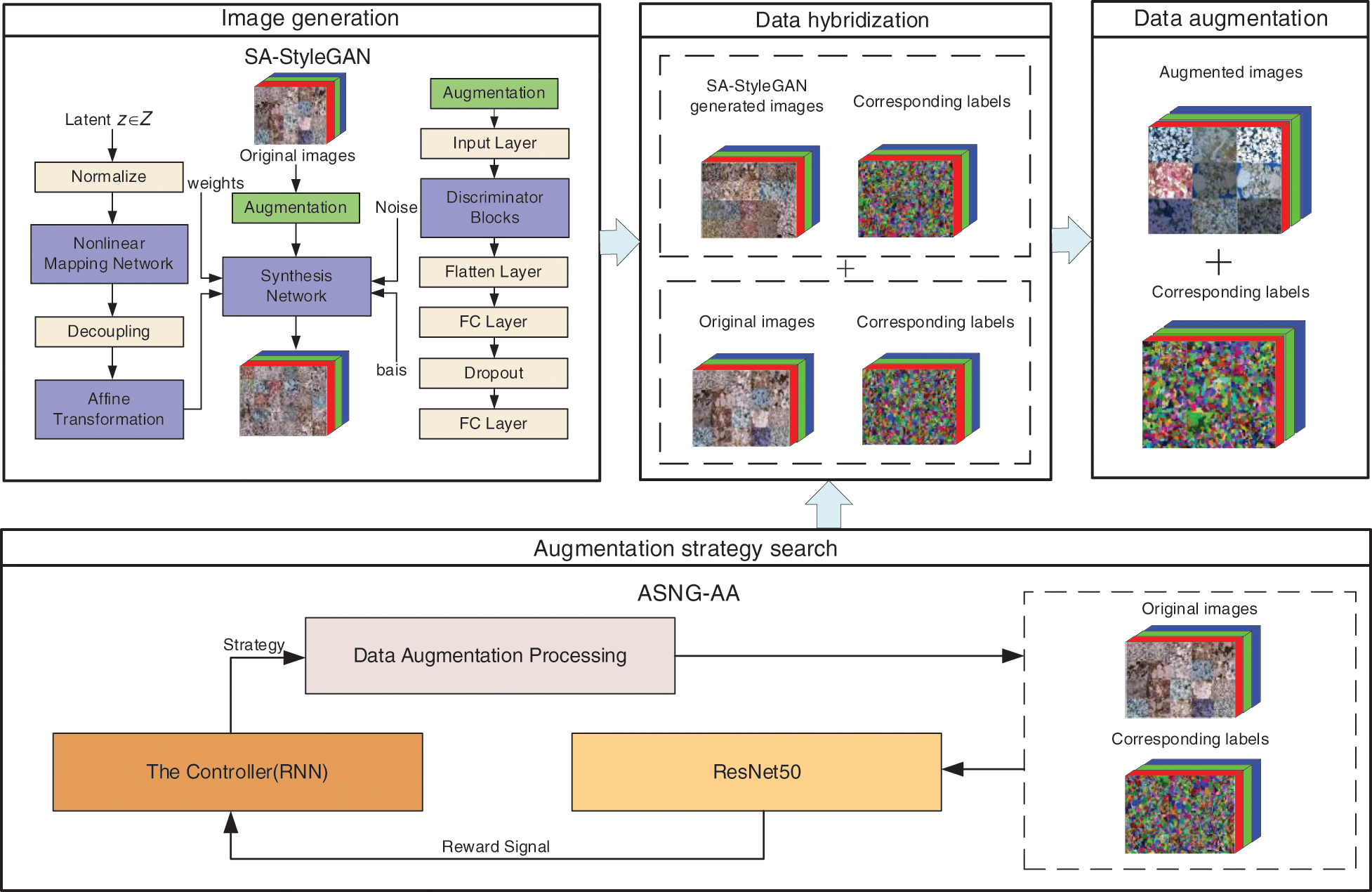
Figure 1: The framework of the hybrid tight sandstone image augmentation method

The framework for augmentation of tight sandstone images proposed in this paper primarily consists of the following four parts. The first two are the critical parts of research.

(1)   Image generation: Based on the basic architecture of StyleGAN, SA-StyleGAN is proposed to use the original tight sandstone image training to generate new images.

(2)   Augmentation strategy search: Based on the basic architecture of AutoAugment and with Residual Network 50 (ResNet50) [27] as the sub-network, ASNG-AA is proposed to train a sub-network using the original tight sandstone images to search for the optimal augmentation strategy.

(3)   Data hybridization: Hybridizing the original image with the generated image improves data diversity and preliminarily expands the data scale.

(4)   Data augmentation: Augmentation of hybrid datasets through search strategies to achieve large-scale dataset augmentation.

2.1 Critical Technologies

2.1.1 StyleGAN

StyleGAN achieves unsupervised and highly controllable natural image generation by mainly relying on three components: latent code, noise, and adaptive discriminator augmentation. The natural image has a single number of foreground targets, continuous information, and significant stylistic variation, making it significantly different from the tight sandstone image. The issues with these three components when generating tight sandstone images are discussed further below.

(1)   Latent code and mixing regularization

StyleGAN controls the key features such as shape, color, and texture of foreground targets in the generated images by latent codes and further achieves a scale-specific level of feature control with the help of mixing regularization operations. However, the number of foreground targets in tight sandstone images is numerous. The mixing regularization operation will lead to feature fusion of different kinds of neighboring foreground targets, making the generated images difficult to distinguish and process.

(2)   Noise

The StyleGAN generation network adds noise to each pixel in the generated image after each convolution to achieve random changes in the image features. This noise affects only the feature details of the generated image. It does not change the image’s key features and overall structure. However, the same class of foreground target features in the tight sandstone image are similar and do not differ significantly. Too much-added noise will cause the generated image to contain unnecessary noise and degrade the quality.

(3)   Adaptive discriminator augmentation

StyleGAN augments the training images during the training process and uses a heuristic Eq. (1) to judge the degree of model overfitting once every 4 minibatch and reduces or increases the augmentation strength according to the degree of model overfitting to alleviate the overfitting problem arising from training with limited data. The heuristic is defined as

r=E[sign(Dtrian)] (1)

E[sign(Dtrian)] indicates the mean value of the discriminator judged results on four consecutive small batches when r=0 indicates no overfitting and r=1 indicates overfitting. Since there are only 1/10 as many training images in this paper as there are in the citation [24], it is hard to effectively alleviate the overfitting problem by using a fixed judgement interval to adjust the strength of the augmentation.

2.1.2 AutoAugment

AutoAugment mainly relies on the augmentation strategy search space and the search algorithm to realize the automatic search of augmentation strategies. Given a search algorithm and a sub-network, the Recurrent Neural Network (RNN) controller [28] trains the sub-network by sampling augmentation strategies from the augmentation strategy search space and returning the validation accuracy of the sub-network to the controller, enabling it to generate better augmentation strategies over time.

Since this is the first time AutoAugment has been applied to tight sandstone image augmentation, the problems of these two parts in the search process of the tight sandstone image augmentation strategy are described in detail below.

(1)   Augmentation strategy search space

There are differences in semantic information and image structure between natural images and tight sandstone images. Therefore, it is hard to transfer the augmentation strategy search space designed for natural images to the domain of tight sandstone images.

(2)   Search algorithm

AutoAugment uses reinforcement learning [15] as the search algorithm, trained using partial data from the target dataset [18], which still takes 5000 GPU hours. Fast AutoAugment uses an augmentation strategy search method based on density matching [29], which requires splitting the training data into K-folds [30]. However, the tight sandstone image dataset is small. Overfitting happens when too little data is used to train sub-networks.

2.2 Question Condensation

We combine the above and the introduction section to know that the tight sandstone image augmentation method proposed in this paper must solve the following two problems to achieve tight sandstone image augmentation:

(1)   How to improve StyleGAN to generate high-quality tight sandstone images to increase the variety of data.

(2)   How to improve AutoAugment to make it applicable to tight sandstone image augmentation and quickly search for the optimal augmentation strategy in the augmentation strategy search space to expand the data scale.

Given the above problems, the critical techniques are improved to be applicable for tight sandstone image augmentation in this paper. Details of the improvements will be elaborated on in chapters 3 and 4.

3  Tight Sandstone Image Generation

To address the differences between tight sandstone images and natural images, we modified the style control method and the augmentation intensity adjustment period based on the original StyleGAN, added the self-attention mechanism [31,32], and named it SA-StyleGAN to generate high-quality tight sandstone images, and the completed modifications are as follows. The network structure of SA-StyleGAN is shown in Fig. 2.

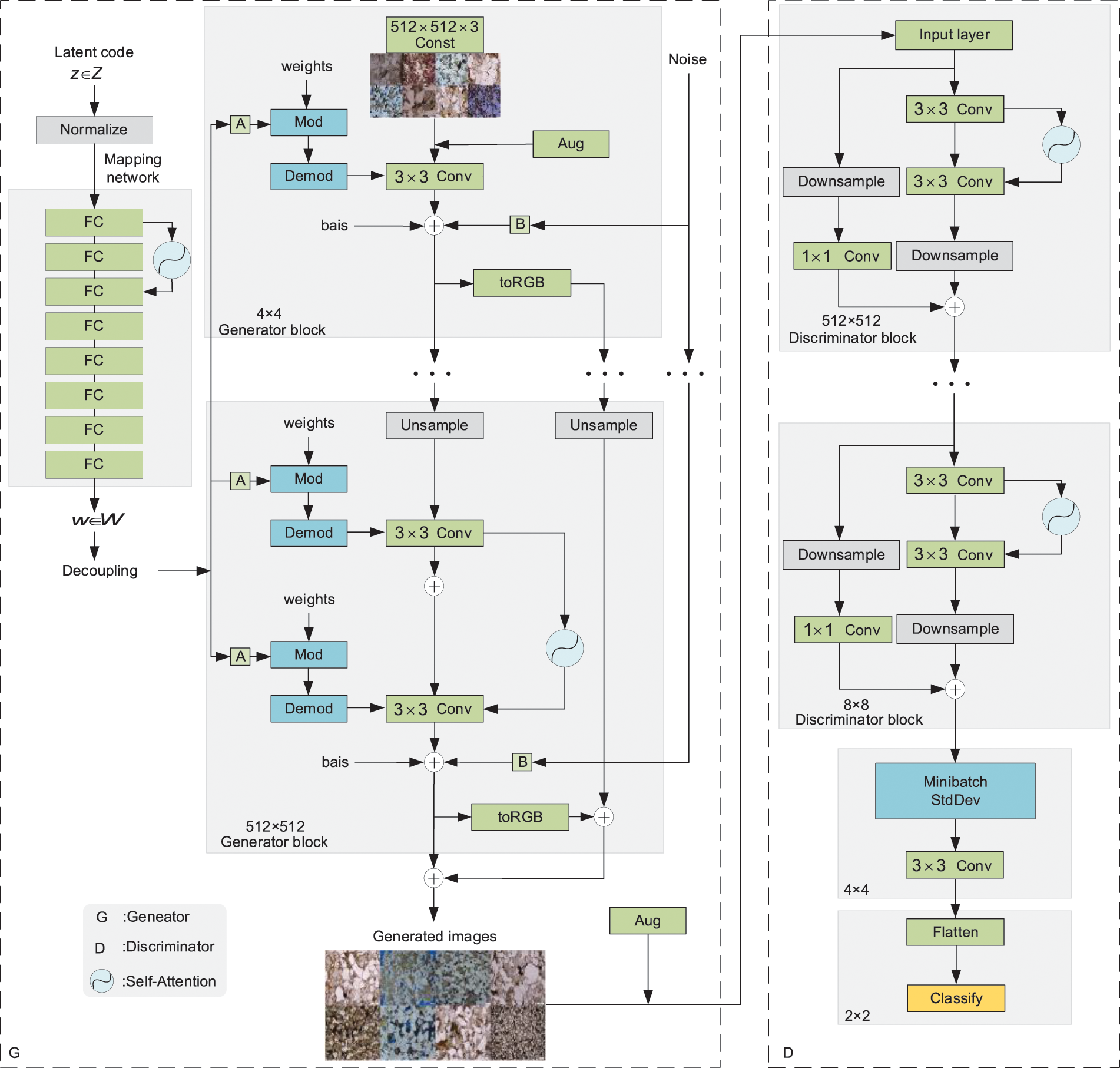
Figure 2: The network structure of the SA-StyleGAN

3.1 Modification of the Style Control Method

(1)   Remove mixed regularization

To address the problem of feature fusion easily occurring between different kinds of neighboring foreground targets in generating tight sandstone images. This paper abandoned mixed regularization and used only one latent code to control the key features of the generated image. That eliminates the problem of foreground target distortion overlap and unclearness in the generated image.

(2)   Improved noise addition mechanism

Since the foreground target features of the same kind in the tight sandstone images are similar, not much random variation is needed. In this paper, we improve the noise addition mechanism by adding noise only once after the second 3×3 convolutional layer in the generator block, except for the first generator block (which adds noise twice), and so on, to reduce the impact of noise on the generated images.

(3)   Self-attention Module

Due to the many foreground targets in tight sandstone images, this paper adds the self-attentive module to the generator (only in the 256×256 and 512×512 pixels generator blocks) and discriminator networks as a complement to the traditional convolution to better extract the foreground target features of tight sandstone images. The specific equation is as follows:

As shown in Eq. (2), we use attention weights αj to indicate the extent to which the model attends to the ith location when synthesizing the jth region. x={xi}Npi=1 is the feature map from the previous convolutional layer, and N is the number of feature locations in the feature map. Wk and Wv are 1×1 convolution modules.

αj=exp⁡(Wkxj)∑i=1Npexp⁡(Wkxi) (2)

As shown in Eq. (3), using the weights αj , the global feature oj of location jth is calculated by weighted average.

oj=Wv∑j=1Npαjxj (3)

Finally, we add the output of the attention layer and the original feature image through the matrix to obtain the output feature map z. As shown in Eq. (4).

zi=xi+oi (4)

Fig. 3 compares the tight sandstone samples generated by the original StyleGAN and the SA-StyleGAN.

Figure 3: Comparison of StyleGAN and SA-StyleGAN generated samples, where (a), (b) represent the images generated by the original StyleGAN, (c), (d) represent the images generated by SA-StyleGAN

As shown in Fig. 3, (a) and (b) are the samples generated by the original StyleGAN, and (c) and (d) are the samples generated by SA-StyleGAN. Compared with the original StyleGAN, SA-StyleGAN generated images have almost no noise, different kinds of sandstone particles have no distortion similar to the style transfer, and the edges of the particles are more apparent, which are high-quality samples.

3.2 Adaptive Augmentation Intensity Adjustment Period

In this paper, we stop using a fixed interval to adjust the intensity of the augmentation and instead use the adaptive augmentation intensity adjustment period. As shown in Eq. (5), this allows the model to change the intensity of the augmentation based on the degree of overfitting while adjusting the position of the next judgment dynamically.

an={an−1+1, if 2≤an−1≤N and r=0an−1−1, if 2≤an−1≤N and r=1N, if an−1= N and r=01, if an−1<2 and r=1 (5)

The initial minibatch interval a0=N is set first, and the training process uses recursive Eq. (5) to dynamically calculate where the adaptive discriminator will next determine the degree of model fit. From Eq. (1), if r=1 , it means that the model is overfitted, reduce the adjustment interval a until a=1 ; if r=0 , it means that the model is overfitted, increase the adjustment interval a until a=N . Fig. 4 shows the changes in the quality of StyleGAN and SA-StyleGAN generated images as the number of iterations increases.

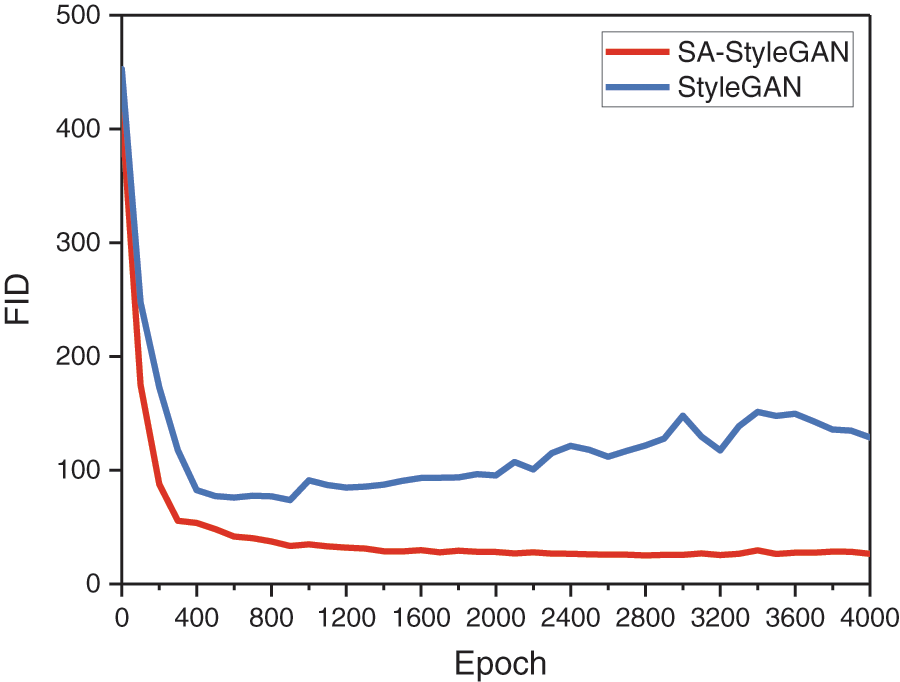
Figure 4: Variation of generated image quality with iterations

Fig. 4 shows that the original StyleGAN gets the best result when Epoch=900 , but the Fréchet Inception Distance (FID) [33] value tends to go up during further training, which means that the model has been overfitted. The SA-StyleGAN achieves the best result at Epoch=2800 , stays stable during further training without overfitting, and always has a lower FID value than the original StyleGAN. That shows that the quality and stability of the best results of the images generated by the SA-StyleGAN proposed in this paper are significantly better than the original StyleGAN.

4  Tight Sandstone Image Augmentation Strategy Search

In order to realize the automatic search of tight sandstone image augmentation strategies, this paper selects and improves AutoAugment to describe the problem of finding the optimal augmentation strategy as a discrete search problem. First, redesign the augmentation strategy search space applicable to tight sandstone images; second, set the augmentation constraint rules to reduce the sampling scale of the augmentation strategy and the search complexity; and finally, use the Adaptive Stochastic Natural Gradient (ASNG) [34] method as the optimization algorithm to improve the search speed. The ASNG-AA algorithm framework is shown in Fig. 5.

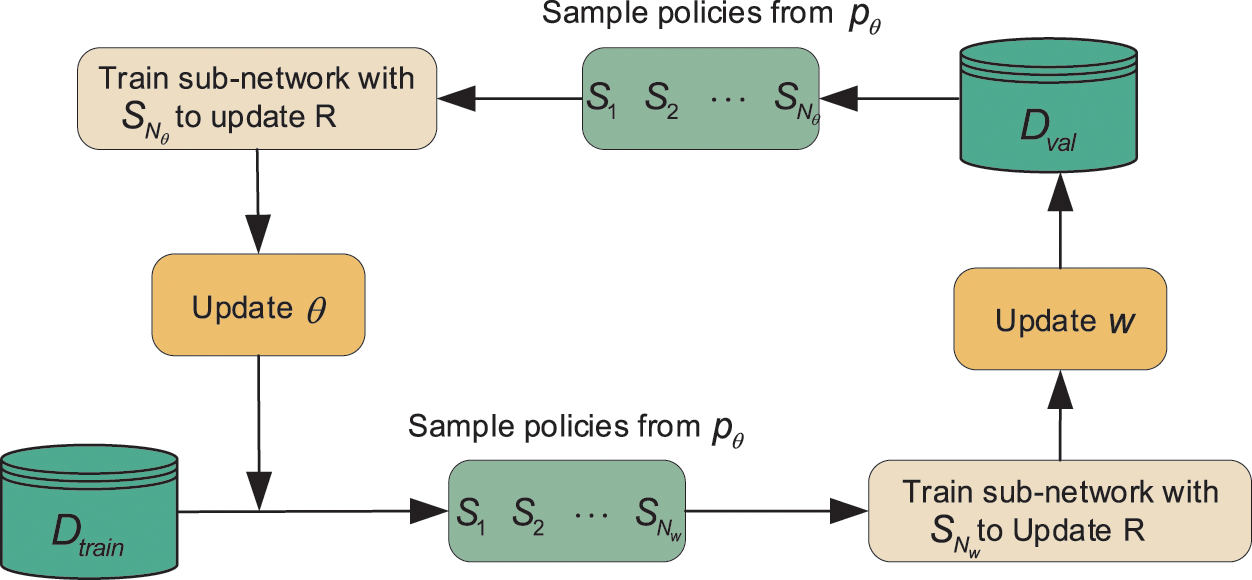
Figure 5: ASNG-AA algorithm framework. Dtrain and Dval represent the training dataset and validation dataset respectively, pθ represents the distribution of the augmentation strategy S

4.1 Augmentation Strategy Search Space for Tight Sandstone Images

Since this is the first time the AutoAugment algorithm has been applied to the tight sandstone image, we must design the augmentation strategy search space for the ASNG-AA algorithm. There are 12 augmentation operations from Augmentor [35] in the search space of this paper. Each of these operations has three basic properties: (1) the kind of operation, (2) the magnitude of the operation, and (3) the probability of applying this operation. The complete list of augmentation operations used in this paper is shown in Table 1.

In this paper, the following expansion constraint rules are set to reduce the search complexity of the augmentation strategy while keeping diversity and ensuring that the category distribution of the augmented images stays within a safe range.

(1)   To reduce the search complexity while maintaining the diversity of the expansion strategies. Set a fixed magnitude interval for each augmentation operation, determine the left boundary (LB) and the right boundary (LR) of the magnitude interval, and discretize the magnitude into 10 values with a uniform interval. Similarly, the application probability of each operation is discretized from 0 to 1 into 11 values with a uniform interval.

(2)   To maintain the augmentation strategy rationality and avoid the situation where the augmented image category deviates from the actual data distribution due to multiple augmentation operations on the same image. It is specified that each augmentation strategy contains only two augmentation operations.

In summary, searching for one augmentation operation has 1011 possibilities, so an efficient augmentation strategy search algorithm is needed, as described below.

4.2 Stochastic Relaxation Optimization of Strategy Search

In this paper, we will describe the augmentation strategy search as a bi-level optimization problem, which can be written as follows:

{w∗(s)=arg⁡minwftrain(w, s)minsfval(w∗(s), s) (6)

In Eq. (6), f(w, s) is the differentiable objective function of the augmentation strategy s∈S and the network parameters w∈W . ftrain and fval are the training loss and the validation loss, respectively. The augmentation strategy search algorithm aims to optimize w and s by using gradients ∇wf and ∇sf , respectively. The optimal network weight w∗ is first found using the minimization of training loss. Then, the optimal network weight is used to find the optimal augmentation strategy s∗ by minimizing the validation loss. However, we cannot get the gradient ∇sf of the objective function with respect to strategy s, so it is hard to use the gradient descent method to optimize strategy s. Although reinforcement learning is utilized to search for s in the paper [16], evaluating each s performance is computationally very costly.

So that gradient descent can be used to optimize strategy s, this paper first uses stochastic relaxation [34] to turn the problem of coupled optimizing both the weight and the strategy into an optimization problem for a differentiable objective function J. Then, the weight and the strategy are optimized using a natural gradient descent method [36] and adaptive learning rates.

The idea of stochastic relaxation is not to directly optimize the gradient ∇sf of the strategy s, instead defines a probability distribution pθ(s) parameterized by θ to minimize the validation loss fval of the objective function f(w, s) for θ , as shown in Eq. (7).

{minθJ(w, θ)=∫s∈Sfval(w∗(s), s)pθ(s)dsw∗(s)=arg⁡minwftrain(w, s) (7)

The stochastic relaxation objective function J not only takes on all of the properties of the objective function f(w, c) , but it also makes differentiable both w and θ , so that the gradient descent method can be used to update w and θ . However, the gradient ∇wJ(w, θ) cannot be processed because the mean performance of s cannot be evaluated in a closed-form way. Therefore, the gradient ∇wJ(wt, si) of w is estimated using Monte-Carlo (MC), as shown in Eq. (8).

Gw(wt, θt)=1Nw∑i=1Nw∇wftrain(wt, si) (8)

si∼pθt(s), i=1, …, Nw in Eq. (8), using adaptive stochastic natural gradient descent [34] to update wt . Since Gw(wt, θt) is used instead of ∇wJ(w, θ) , wt can be expressed as:

wt+1=wt−lwGw(wt, θt) (9)

lθ represents the learning rate, and this paper uses the adaptive learning rate to accelerate the training speed. For θt , the gradient ∇θJ(w, θ) of θ is estimated using MC. Since the distance between the two probability distributions is not Euclidean, we update θt using natural gradient descent [36], as shown in Eq. (10).

θt+1=θt−lθF(θt)−11Nθ∑j=1Nθ∇θfval(wt+1, sj)ln⁡pθ(sj) (10)

F(θt) is the Fisher matrix and is calculated as seen in the paper [34]. The execution process of the algorithm is as follows:

5  Example Verification

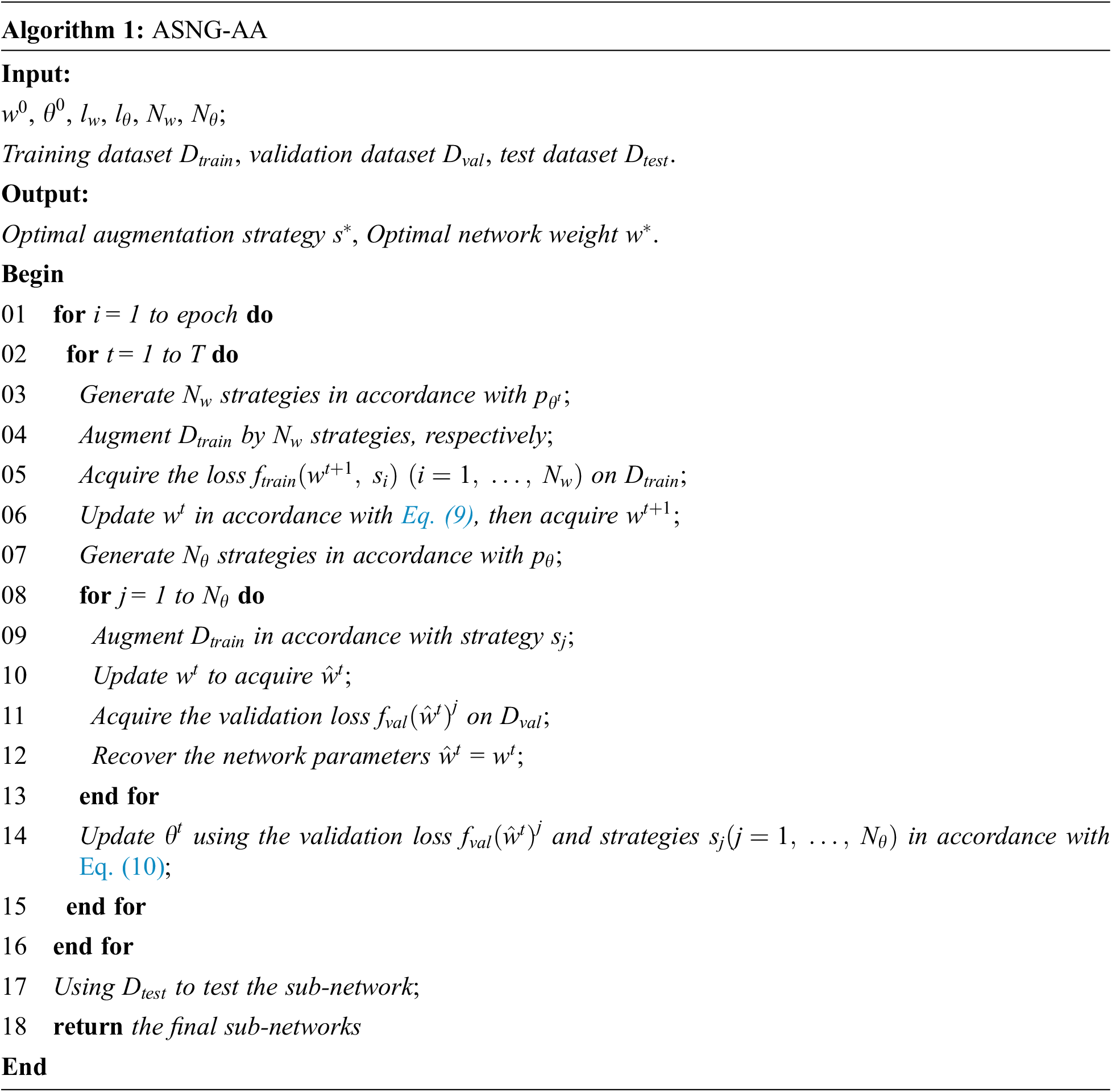
The experiments in this paper include the experiments on generated image quality comparisons and the effects evaluation of the augmentation method. A brief description of the experimental design is shown below.

(1)   Describe how the experiment was prepared, including the experimental environment, experimental dataset, validation algorithm, and evaluation metrics.

(2)   Compare the generated image quality evaluation results of SA-StyleGAN and the comparison algorithm to argue that SA-StyleGAN generated images have obvious advantages in terms of clarity and diversity.

(3)   Analyze the variation of performance metrics of the Mask R-CNN model under various conditions to demonstrate that ASNG-AA, SA-StyleGAN, and hybrid tight sandstone image augmentation methods have significant advantages in enhancing the generalization ability of the model.

5.1 Experiment Preparation

(1)   Experimental environment. The operating system is Ubuntu 20.04.3, the experimental framework is TensorFlow-GPU 1.15.0, the CPU is Intel Xeon Silver 4210R, the memory is 64 G, and the GPU is RTX 6000.

(2)   Experimental dataset. The experimental dataset is the tight sandstone thin slice images in the Putaohua reservoir in the Sanzhao Sag of the Songliao Basin. It has 150 sandstone thin slice images, each with a fixed size of 616×468 pixels and a mode of three-channel RGB images, as shown in Table 2.

In this experiment, we use the Resize image processing method to resize the image to 512×512 pixels and divide it into a training dataset, validation dataset, and test dataset according to the ratio of 7:2:1 under the condition that the distribution is as equal as possible.

(3)   Validation algorithm. The Mask R-CNN instance segmentation algorithm is used as the validation algorithm, and the backbone network is Residual Network 101 (ResNet101) [27]. Using Stochastic Gradient Descent (SGD) [37] as the optimizer, the initial learning rate is set to 0.01, and the learning rate decay factor is also set to 0.01. The momentum factor is set to 0.9 so that the model training does not fall into the local optimum. The transfer learning [38] method speeds up training by using as a pre-trained model the model that was trained with the coco dataset [39].

(4)   Generate image quality evaluation metrics. Three metrics, FID, Inception Score (IS) [40], and Kernel Inception Distance (KID) [41], were used to measure the clarity and diversity of the generated images.

(5)   Augmentation performance evaluation metrics. The training Mask R-CNN model’s recognition accuracy and segmentation precision on the test dataset is used as the augmentation performance evaluation metrics. The IOU value is set to 0.5 during testing.

Recognition accuracy represents the number of correctly recognized targets as a percentage of the total number of correct, incorrect, and missed detections, as shown in Eq. (11).

Accuracy=TPTP+FP+FN (11)

In the above equation, TP denotes the number of correctly recognized targets, FP denotes the number of incorrectly recognized targets, and FN denotes the number of unrecognized targets.

The segmentation precision is expressed in the segmentation error rate r, which represents the error between the correct segmentation of sandstone particle content by the model and the manual labeling of sandstone particle content, as shown in Eq. (12). We use the mask to calculate the sandstone particle pixel size, as shown in Fig. 6.

r=(S1−S2)S1 (12)

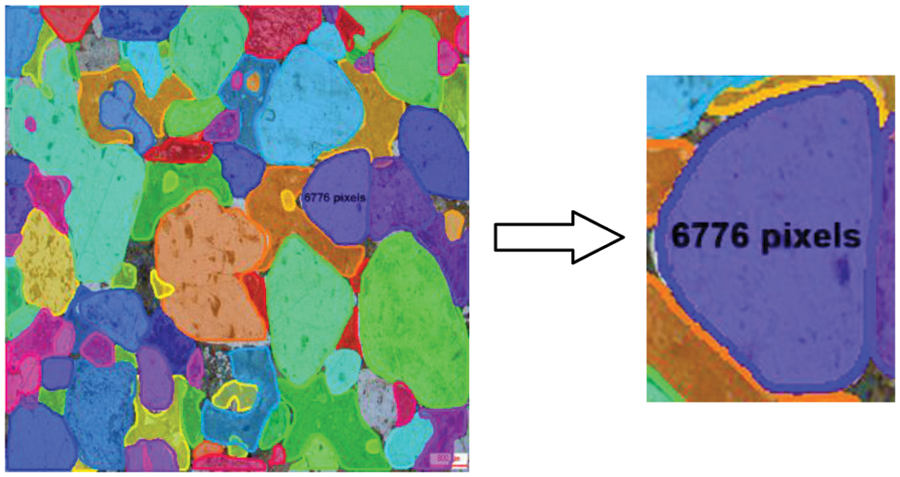
Figure 6: Calculate particle content using the results of Mask R-CNN segmentation

In the above equation, S1 and S2 are the particle content values for manual labeled and Mask R-CNN segmentation, respectively.

5.2 Quality Comparison Experiments of Generated Images

In this paper, SA-StyleGAN and StyleGAN, Deep Convolutional GANs (DC-GAN) [42], Gradient Penalty Based Wasserstein GANs (WGAN-GP) [43], and Least Squares GANs (LS-GAN) [44] were trained using the original image training dataset to generate 1000 images of sandstone thin slice images, respectively. Due to the model performance limitation, DC-GAN, WGAN-GP, and LS-GAN generate images of 256×256 pixels in size. The generated samples are evaluated 20 times, and the average of the 20 evaluations is finally calculated. The experimental results are shown in Table 3 and Fig. 7.

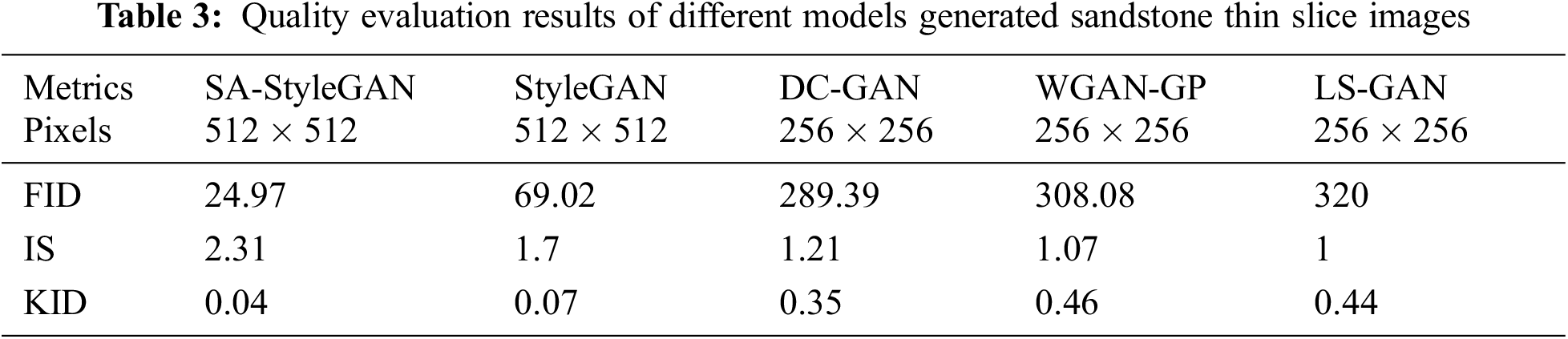
Figure 7: Comparison results of different models generated sandstone thin slice images

In Table 3, the IS value (higher is better) of the sandstone thin slice images generated by SA-StyleGAN is the highest, reaching 2.3, which is 0.61, 1.1, 1.31, 1.24, and 1.31 higher than the other five methods, respectively. The FID value (lower is better) was the lowest, reaching 24.97, which was 44.05, 264.42, 283.11, and 295.03 lower than the other five methods, respectively. The KID value (lower is better) is the lowest, reaching 0.04, which is 0.03, 0.31, 0.42, and 0.4 lower than the other five methods, respectively. This indicates that SA-StyleGAN generates images with higher clarity and better diversity.

5.3 Effect Experiments of Augmentation Methods

Before starting the experiment, set the kind of training dataset, the quantity level, and the number of training iterations of the Mask R-CNN algorithm. Use D, D′ , and D′′ to denote the original image training dataset, the original StyleGAN generated image training dataset, and the SA-StyleGAN generated image training dataset, respectively. It is ensured that the three training datasets have the same number of samples and that the sample distribution is as similar as possible. To see how the performance of a model changes as training data is added, the data groups Daug1⊂Daug2⊂⋅⋅⋅⊂Daug11 are established, where aug stands for the augmentation method and the number stands for the order of quantity level that increases in turn. The first data group Daug1 contains only pre-augmentation training images. We create many augmented images for each original training image using augmentation strategies. Then, we use random sampling to add the same number of augmented images to each data group until all of the augmented images have been added. During model training, the number of iterations is set to 100, and the weight with the lowest validation loss is selected as the training result. To test the actual training effect of the model, Mask R-CNN used 15 images from the original image test dataset for recognition and segmentation, and the average recognition accuracy and segmentation error rate were counted and calculated.

5.3.1 ASNG-AA Method Effect Evaluation Experiment

The optimal augmentation strategy is searched on the original image training dataset D using the ASNG-AA algorithm. For the selection of sub-networks in the search strategy process, we draw on the paper [16] in which Ekin et al. chose to use small networks to implement the search and validation of the strategies and then used the searched strategies on more complex and different types of networks. The model performance was still improved, demonstrating that the selection of sub-networks does not affect the effectiveness of the final strategy. Therefore, for computational cost consideration in this paper, we use ResNet50 as a sub-network and set the training initial learning rate to be set to 0.01 and the learning rate decay factor to be set to 0.01. After the training was completed, the 25 best augmentation strategies were selected as the final strategies, and the training dataset was expanded to 26 times the original scale. Table 4 shows the top five augmentation strategies (some operations do not use magnitudes, such as Rotate90 and Fliplr). Fig. 8 shows the training images and their labels after the final strategy augmentation.

Figure 8: The examples of ASNG-AA search strategy augmentation. The first line is the original image and its corresponding labels, and the second is the augmented image and its corresponding labels

For the choice of comparison algorithms, the search augmentation strategy using AutoAugment in the paper [16] takes a lot of time and computational cost. Fast AutoAugment in the paper [17] is overfitted with a small amount of training data. The existing augmentation strategies of the two methods above are for natural image search. They cannot be transferred to the field of tight sandstone images. So, in this paper, we design a manual augmentation strategy (MA) based on expert knowledge instead of using the first two methods as the comparison algorithm. The operations used are included in the ASNG-AA augmentation strategy search space. We use two strategies to augment the original image training dataset and then train the Mask R-CNN model, respectively. After the training is completed, the original image test dataset is used for instance segmentation, and the model recognition accuracy and the segmentation error rate of the two algorithms are compared. The experimental results are shown in Fig. 9.

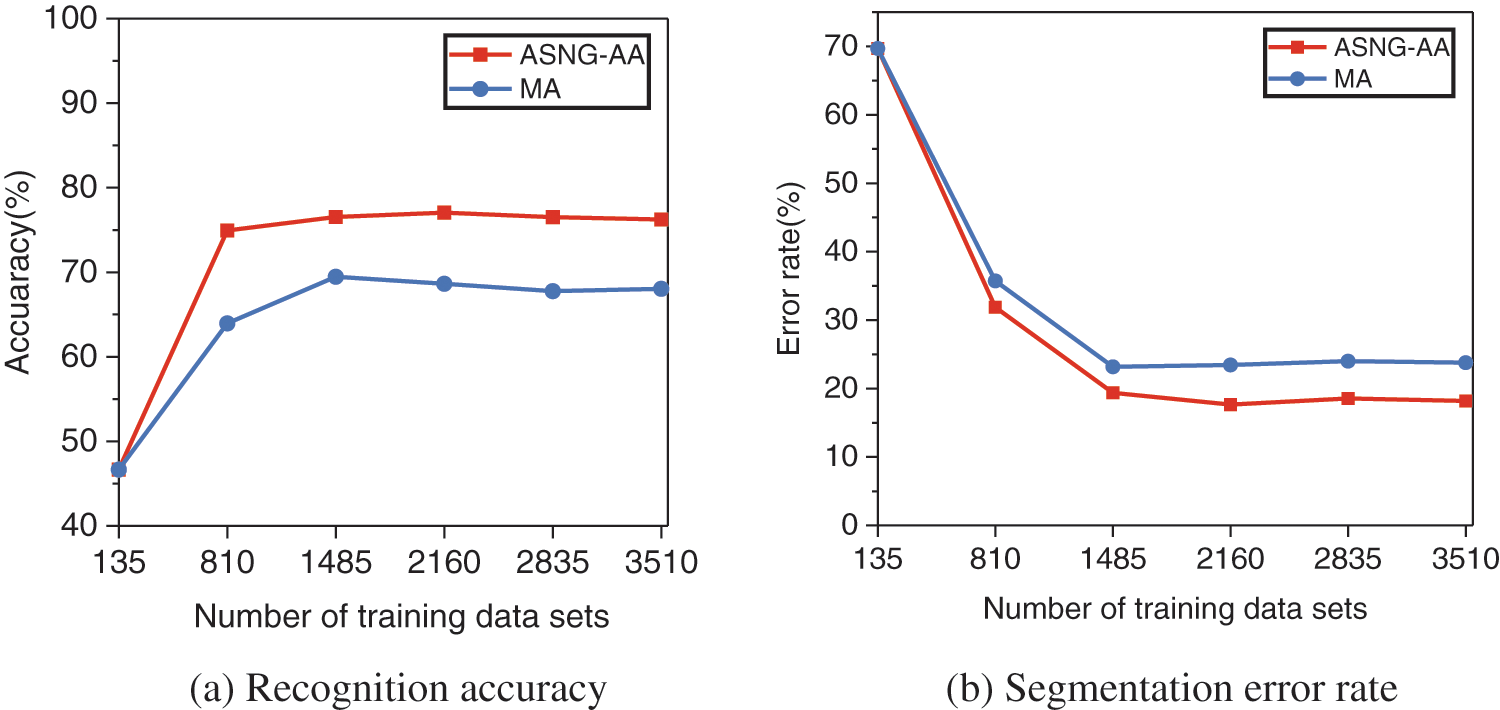
Figure 9: Comparison of the effects of the ASNG-AA search strategies and the MA strategies

By analyzing the experimental results, we obtained the following conclusions.

(1)   As shown in Fig. 9a, the Mask R-CNN recognition accuracy without data augmentation is 46.64%. The recognition accuracy of the model gradually increased with the increase of training images and finally reached saturation (DAA4=2160,DMA3=1485) with the recognition accuracy of 77.03% (ASNG-AA) and 68.02% (MA), respectively. It indicates that ASNG-AA can effectively improve the model’s recognition accuracy relative to MA.

(2)   As shown in Fig. 9b, the segmentation error rate of the Mask R-CNN without data augmentation is 69.69%. The segmentation error rate of the model gradually reduced with the increase of training images and finally reached saturation (DAA4=2160,DMA3=1485) with the segmentation error rate of 17.65% (ASNG-AA) and 23.16% (MA), respectively. It indicates that ASNG-AA can effectively reduce the model’s segmentation error rate relative to MA.

5.3.2 SA-StyleGAN Method Effect Evaluation Experiment

The original image training dataset D and the generated dataset ( D′ , D′′ ) are augmented using the ASNG-AA algorithm search strategy. The Mask-RCNN model is trained using the augmented training dataset. After the training is completed, the original image test dataset is used for instance segmentation and to compare the variation of model recognition accuracy and segmentation error rate with increasing quantity levels for the three datasets. The experimental results are shown in Fig. 10.

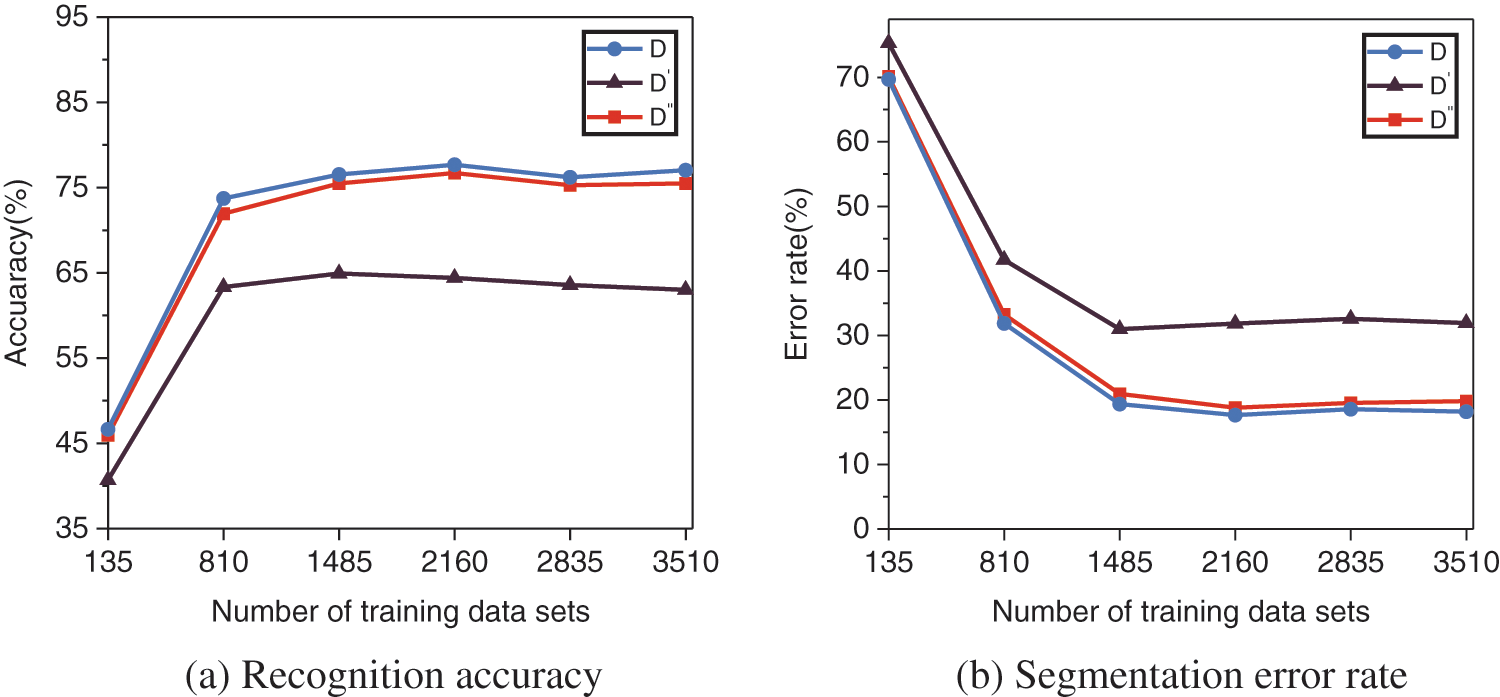
Figure 10: Comparison of the instance segmentation effects of the three datasets

By analyzing the experimental results, we obtained the following conclusions.

(1)   As shown in Fig. 10a, the Mask R-CNN models were trained using the generated datasets D′ and D′′ , respectively, and the recognition accuracy of 40.68% and 45.95% without augmentation. The recognition accuracy gradually increased with the increase of training images and finally reached saturation ( DAA′3=1485 , DAA′′4=2160 ) with the recognition accuracy of 64.91% and 76.7%. It indicates that under the condition of the same training data, the model recognition accuracy of the generated dataset D′′ is higher than that of D′ and is close to the real data.

(2)   As shown in Fig. 10b, the Mask R-CNN models were trained using the generated datasets D′ and D′′ , respectively, and the segmentation error rate of 75.33% and 70.13% without augmentation. The segmentation error rate gradually reduced with the increase of training images and finally reached saturation ( DAA′3=1485 , DAA′′4=2160 ) with the recognition accuracy of 30.97% and 18.78%. It indicates that under the condition of the same training data, the model segmentation error rate of the generated dataset D′′ is lower than that of D′ and is close to the real data.

5.3.3 Hybrid Tight Sandstone Image Augmentation Method Effect Evaluation Experiment

The original dataset D and the generated dataset D′′ are augmented using the ASNG-AA search strategy. Firstly, the Mask-RCNN model is trained using the augmented training dataset D. When the model performance reaches saturation, the location of the saturation point is recorded, and the generated dataset D′′ is added at the initial saturation point to continue the training. The original image test dataset is used to instance segmentation after the training is completed, and the change in recognition accuracy and the segmentation error rate of the model after the generated data is added is observed. The experimental results are shown in Fig. 11.

(1)   As shown in Fig. 11a, the training is performed using the original dataset D. When no augmentation is used, the model recognition accuracy is 46.64%. The model’s recognition accuracy gradually increases with the number of training images until it reaches saturation at DAA4=2160, after which adding more training data cannot improve the model’s recognition effect any further. The saturation recognition accuracy is 77.03%, and Fig. 12a shows the confusion matrix of the saturation point. We call DAA4=2160 the saturation point, and after adding the augmented generated image dataset D′′ at this point, we find that the recognition accuracy of the model continues to improve and reaches saturation at DAA4+DAA′′4=4860 with a recognition accuracy of 87.42%. The best recognition effect confusion matrix is shown in Fig. 12b.

(2)   As shown in Fig. 11b, the training is performed using the original dataset D. When no augmentation is used, the model segmentation error rate is 69.69%. The model’s segmentation error rate gradually reduced with the number of training images until it reaches saturation at DAA4=2160 , after which adding more training data cannot improve the model’s segmentation effect any further. The saturation recognition accuracy is 17.65%. We call DAA4=2160 the saturation point, and after adding the augmented generated image dataset D′′ at this point, we find that the segmentation error rate of the model continues to reduce and reaches saturation at DAA4+DAA′′4=4860 with a recognition accuracy of 7.3%. Table 5 shows the difference between the manual labeled content and saturation point detected content of the test dataset.

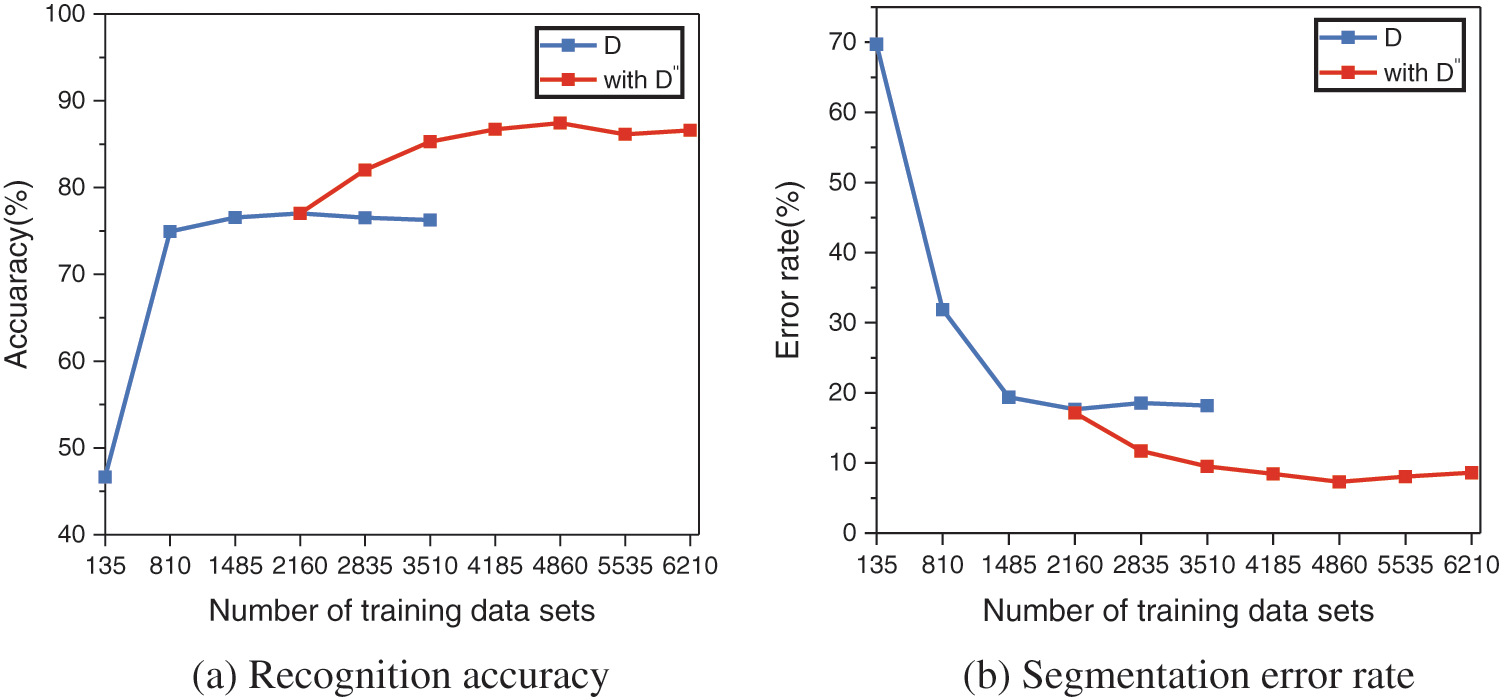
Figure 11: Experimental results for hybrid tight sandstone image augmentation

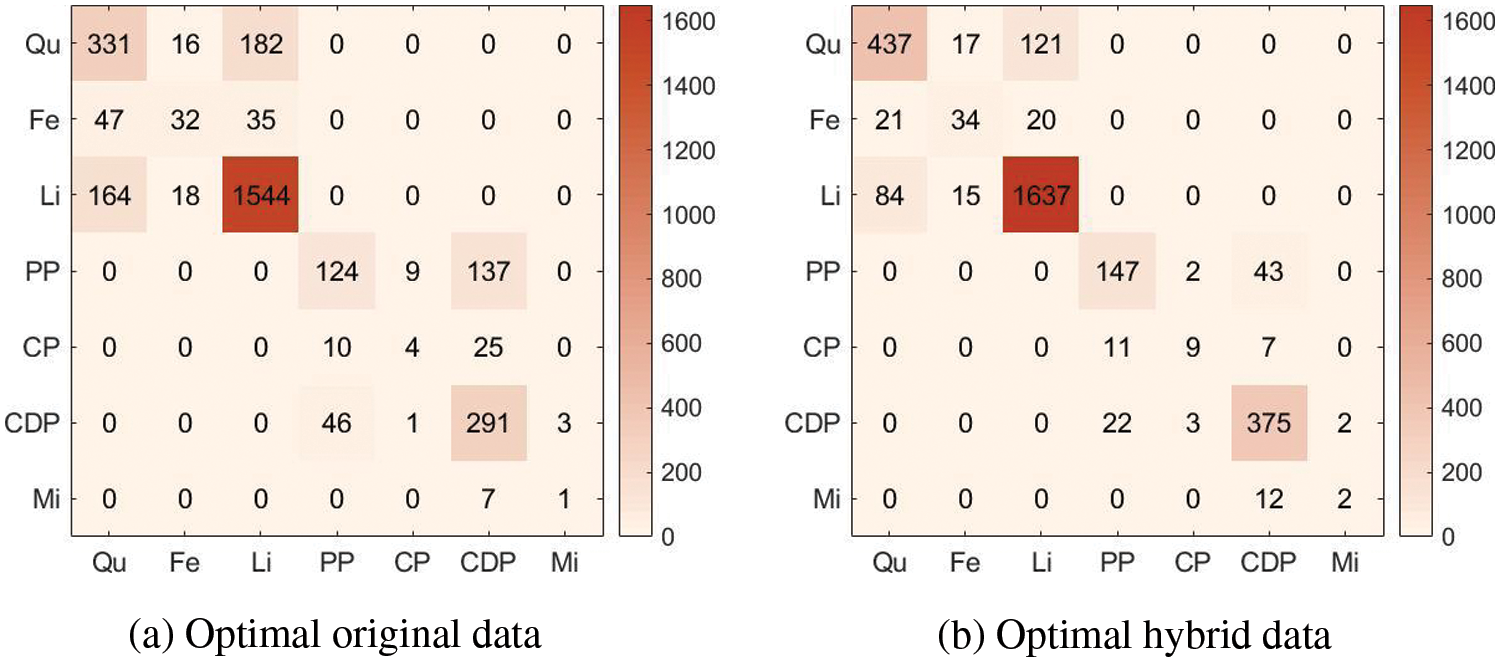
Figure 12: Confusion matrix for target recognition results. The labels Qu, Fe, Li, PP, CP, CDP, and Mi stand for Quartz, Feldspar, Lithic, Primary Pore, Casting Pore, Cemented Dissolution Pore, and Microcrack

As a side note, Figs. 13 and 14 show a comparison of the instance segmentation effects of Mask R-CNN trained with the optimal original data augmentation and the optimal hybrid data augmentation, as well as the training and validation loss curves of the model in the optimal hybrid data augmentation state.

Figure 13: Comparison of instance segmentation effects

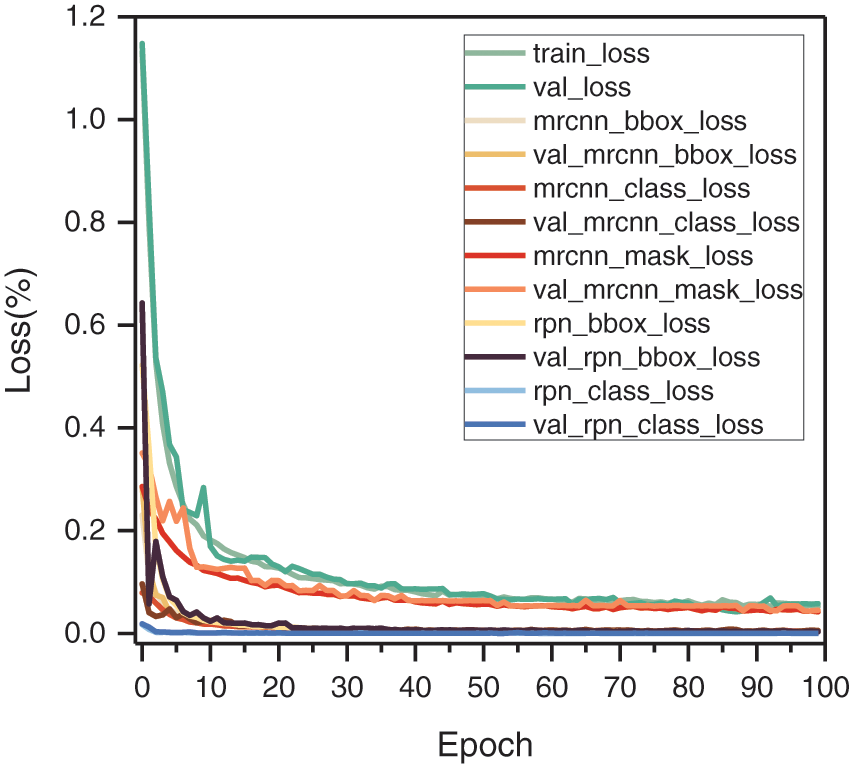
Figure 14: Validation loss curve of Maks R-CNN trained using optimal hybrid data augmentation

6  Conclusion

In this paper, we propose a tight sandstone image augmentation method to solve the problem of poor augmentation effects of traditional augmentation methods caused by the sparse sample, complex image structure, and difficulty of the domain transfer by integrating the respective advantages of the generative adversarial network and automatic data augmentation, which effectively improves the training effect of the Mask R-CNN algorithm. The research conclusions are given as follows through theoretical elaboration and experimental demonstration.

(1)   SA-StyleGAN can generate high-resolution tight sandstone images. The experimental results show that SA-StyleGAN generates images with significantly higher clarity, diversity, and realism than other algorithms, which can effectively improve data diversity;

(2)   ASNG-AA is applicable to search for tight sandstone image augmentation strategies. The experimental results show that the augmentation strategy searched by the ASNG-AA algorithm can produce a better recognition segmentation effect by the Mask R-CNN algorithm compared with the manual formulation augmentation strategy, and the search process only takes less than 300 GPU hours;

(3)   The hybrid tight sandstone image augmentation method proposed in this paper can improve data scale and diversity simultaneously. However, as the training data increases, the model performance eventually reaches saturation. Adding more data not only fails to improve the training performance but also reduces the training speed of the model. Therefore, the scale of the training data needs to be adjusted to strike a balance between the “model performance saturation point” and the “model training speed.”

In future work, we plan to improve the Mask R-CNN instance segmentation algorithm to further enhance the recognition effect by optimizing the network structure design. Furthermore, we are interested in applying the method to multi-foreground target image augmentation and recognition in the medical cell field to evaluate the potential of the method.

Funding Statement: This research was funded by the National Natural Science Foundation of China (Project No. 42172161), Heilongjiang Provincial Natural Science Foundation of China (Project No. LH2020F003), Heilongjiang Provincial Department of Education Project of China (Project No. UNPYSCT-2020144), and Northeast Petroleum University Guided Innovation Fund (2021YDL-12).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Y. Song, Z. Li, Z. Jiang, Q. Luo, D. Li et al., “Progress and development trend of unconventional oil and gas geological research,” Petroleum Exploration and Development, vol. 44, no. 4, pp. 675–685, 2017. [Google Scholar]

2. H. Wang, F. Ma, X. Tong, Z. Liu, X. Zhang et al., “Assessment of global unconventional oil and gas resources,” Petroleum Exploration and Development, vol. 43, no. 6, pp. 925–940, 2016. [Google Scholar]

3. H. Liu, T. Guo, M. Song, H. Wang, Z. Liu et al., “Study on microscopic pore characteristics of tight sandstone,” in Proc. of the IOP Conf. Series: Materials Science and Engineering, Bristol, Britain, pp. 052004–052008, 2019. [Google Scholar]

4. S. Wu, R. Zhu, J. Cui, Z. Mao, K. Liu et al., “Ideas and prospect of porous structure characterization in unconventional reservoirs,” Geological Review, vol. 66, no. 1, pp. 151–154, 2020. [Google Scholar]

5. Y. Cai, Q. Teng and B. Tu, “Automatic extraction of pores in thin slice images of rock castings based on deep learning,” Science Technology and Engineering, vol. 28, no. 2, pp. 296–304, 2021. [Google Scholar]

6. H. Zhou, C. Zhang, X. Zhang, Q. Chen and Y. Zhang, “Edge extraction and particle segmentation based on coherent features of rock slice sequence images,” Journal of Jilin University, vol. 51, no. 6, pp. 1897–1907, 2021. [Google Scholar]

7. Y. Wang, Y. Wang, N. Qin, S. Huang, L. Chang et al., “Quantifying the mechanical properties of white sandstone based on computer fractal theory,” Computer Systems Science and Engineering, vol. 39, no. 1, pp. 121–131, 2021. [Google Scholar]

8. F. Jiang, Q. Gu, H. Hao and N. Li, “Feature extraction and grain segmentation of sandstone images based on convolutional neural networks,” in Proc. of the 24th Int. Conf. on Pattern Recognition, Beijing, China, pp. 2636–2641, 2018. [Google Scholar]

9. N. Saxena, R. J. Day-Stirrat, A. Hows and R. Hofmann, “Application of deep learning for semantic segmentation of sandstone thin sections,” Computers & Geosciences, vol. 152, no. 7, pp. 104778, 2021. [Google Scholar]

10. J. Wang and L. Perez, “The effectiveness of data augmentation in image classification using deep learning,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Hawaii, USA, pp. 1–8, 2017. [Google Scholar]

11. C. Shorten and T. M. Khoshgoftaar, “A survey on image data augmentation for deep learning,” Journal of Big Data, vol. 6, no. 7, pp. 1–48, 2019. [Google Scholar]

12. M. D. Cirillo, D. Abramian and A. Eklund, “What is the best data augmentation for 3D brain tumor segmentation,” in Proc. of the 2021 IEEE Int. Conf. on Image Processing, Anchorage, AK, USA, pp. 36–40, 2021. [Google Scholar]

13. B. Zoph, V. Vasudevan, J. Shlens and Q. V. Le, “Learning transferable architectures for scalable image recognition,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, Utah, USA, pp. 8697–8710, 2018. [Google Scholar]

14. H. Liu, K. Simonyan and Y. Yang, “DARTS: Differentiable architecture search,” in Proc. of the Int. Conf. on Learning Representations, New Orleans, Louisiana, USA, pp. 1–13, 2018. [Google Scholar]

15. I. Bello, B. Zoph, V. Vasudevan and Q. V. Le, “Neural optimizer search with reinforcement learning,” in Proc. of the Int. Conf. on Machine Learning, Sydney, New South Wales, Australia, pp. 459–468, 2017. [Google Scholar]

16. E. D. Cubuk, B. Zoph, D. Mane, V. Vasudevan and Q. V. Le, “Autoaugment: Learning augmentation strategies from data,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Los Angeles, USA, pp. 113–123, 2019. [Google Scholar]

17. S. Lim, I. Kim, T. Kim, C. Kim and S. Kim, “Fast autoaugment,” in Proc. of the 33rd Int. Conf. on Neural Information Processing Systems, Vancouver, Canada, pp. 6665–6675, 2019. [Google Scholar]

18. A. Krizhevsky, “Learning multiple layers of features from tiny images,” M.S. dissertation, University of Tront, Japan, 2009. [Google Scholar]

19. Y. Netzer, T. Wang, A. Coates, A. Bissacco, B. Wu et al., “Reading digits in natural images with unsupervised feature learning,” in Proc. of the NIPS Workshop Conf. on Deep Learning and Un-Supervised Feature Learning, Granada, Spain, pp. 69–78, 2011. [Google Scholar]

20. J. Deng, W. Dong, R. Socher, L. J. Li, K. Li et al., “Imagenet: A large-scale hierarchical image database,” in Proc. of the 2009 IEEE Conf. on Computer Vision and Pattern Recognition, Miami, Florida, USA, pp. 248–255, 2009. [Google Scholar]

21. I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley et al., “Generative adversarial nets,” in Proc. Advances in Neural Information Processing Systems, Montreal, Canada, pp. 2672–2680, 2014. [Google Scholar]

22. T. Karras, S. Laine and T. Aila, “A Style-based generator architecture for generative adversarial networks,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 4401–4410, 2019. [Google Scholar]

23. T. Karras, S. Laine, M. Aittala, J. Hellsten, J. Lehtinen et al., “Analyzing and improving the image quality of stylegan,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Seattle, WA, USA, pp. 8110–8119, 2020. [Google Scholar]

24. T. Karras, M. Aittala, J. Hellsten, S. Laine, J. Lehtinen et al., “Training generative adversarial networks with limited data,” in Proc. Advances in Neural Information Processing Systems, Virtual, pp. 12104–12114, 2020. [Google Scholar]

25. Y. Sun, S. Ma, H. Jiang, Y. Liu and Z. Liu, “Highresolution sequence stratigraphy and sand body distribution in Putaohua reservoir of the Sanzhao sag,” Journal of Stratigraphy, vol. 34, no. 4, pp. 371–380, 2010. [Google Scholar]

26. K. He, G. Gkioxari, P. Dollár and R. Girshick, “Mask R-CNN,” in Proc. of the IEEE Int. Conf. on Computer Vision, Venice, Italy, pp. 2961–2969, 2017. [Google Scholar]

27. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, Nevada, USA, pp. 770–778, 2016. [Google Scholar]

28. S. Hochreiter and J. Schmidhuber, “Long short-term memory,” Neural Computation, vol. 9, no. 8, pp. 1735–1780, 1997 [Google Scholar] [PubMed]

29. T. Tran, T. Pham, G. Carneiro, L. Palmer and I. Reid, “A Bayesian data augmentation approach for learning deep models,” in Proc. Advances in Neural Information Processing Systems, Long Beach, CA, USA, pp. 2794–2803, 2017. [Google Scholar]

30. M. S. Esfahani and E. R. Dougherty, “Effect of separate sampling on classification accuracy,” Bioinformatics, vol. 30, no. 2, pp. 242–250, 2014. [Google Scholar]

31. X. Wang, R. Girshick, A. Gupta and K. He, “Non-local neural networks,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 7794–7803, 2018. [Google Scholar]

32. Z. Ji, K. Xiong, Y. Pang and X. Li, “Video summarization with attention-based encoder–decoder networks,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 30, no. 6, pp. 1709–1717, 2019. [Google Scholar]

33. D. Dowson and B. Landau, “The Fréchet distance between multivariate normal distributions,” Journal of Multivariate Analysis, vol. 12, no. 3, pp. 450–455, 1982. [Google Scholar]

34. Y. Akimoto, S. Shirakawa, N. Yoshinari, K. Uchida, S. Saito et al., “Adaptive stochastic natural gradient method for one-shot neural architecture search,” in Proc. of the 36th Int. Conf. on Machine Learning, Long Beach, CA, USA, pp. 171–180, 2019. [Google Scholar]

35. M. D. Bloice, C. Stocker and A. Holzinger, “Augmentor: An image augmentation library for machine learning,” Journal of Open Source Software, vol. 2, no. 19, pp. 432–433, 2017. [Google Scholar]

36. S. I. Amari, “Natural gradient works efficiently in learning,” Neural Computation, vol. 10, no. 2, pp. 251–276, 1998. [Google Scholar]

37. L. Bottou, “Large-scale machine learning with stochastic gradient descent,” in Proc. COMPSTAT’2010, Paris, France, pp. 177–186, 2010. [Google Scholar]

38. S. J. Pan and Q. Yang, “A survey on transfer learning,” IEEE Transactions on Knowledge and Data Engineering, vol. 22, no. 10, pp. 1345–1359, 2009. [Google Scholar]

39. T. Y. Lin, M. Maire, S. Belongie, J. Hays, P. Perona et al., “Microsoft coco: Common objects in context,” in Proc. of the European Conf. on Computer Vision, Zurich, Switzerland, pp. 740–755, 2014. [Google Scholar]

40. S. Barratt and R. Sharma, “A note on the inception score,” in Proc. of the 35th Int. Conf. on Machine Learning, Stockholm, Sweden, pp. 1–9, 2018. [Google Scholar]

41. A. Borji, “Pros and cons of GAN evaluation measures,” Computer Vision and Image Understanding, vol. 179, no. 2, pp. 41–65, 2019. [Google Scholar]

42. A. Radford, L. Metz and S. Chintala, “Unsupervised representation learning with deep convolutional generative adversarial networks,” in Proc. of the 4th Int. Conf. on Learning Representations, San Juan, Puerto Rico, pp. 1–16, 2015. [Google Scholar]

43. I. Gulrajani, F. Ahmed, M. Arjovsky, V. Dumoulin and A. C. Courville, “Improved training of wasserstein GANs,” in Proc. Advances in Neural Information Processing Systems, Long Beach, CA, USA, pp. 5769–5779, 2017. [Google Scholar]

44. X. Mao, Q. Li, H. Xie, R. Y. Lau, Z. Wang et al., “Least squares generative adversarial networks,” in Proc. of the IEEE Int. Conf. on Computer Vision, Venice, Italy, pp. 2794–2802, 2017. [Google Scholar]