Learning Noise-Assisted Robust Image Features for Fine-Grained Image Retrieval

1  Introduction

For the past two decades, extensive research has been done on image retrieval, which has proven useful [1]. In applications where classes have more significant inter-class variance, prior image retrieval methods work better, but not for classes with sizeable intra-class variance compared to inter-class variance. Conceptually, but in the real World, the search must be meticulous, that is, the relevant sub-category to be found by its definition, as a concept, in general, may not contain every single piece of data. For instance, a query for images like birds or dogs, or cars categories must have the same fine-grain subset of images returned. It becomes complex and challenging to search out. This is because, e.g., when looking at a single component of the bike or bird, only its textural details, such as the bird’s feathers and the bike’s headlight, are evident; only in detail comparison is anything identifiable, and therefore the problem is challenging to solve [2]. Learning robust descriptions is crucial in fine-grained image retrieval. If an efficient retrieval method is used, it enables images to be associated with similar features at the front and dissimilar ones at the end. In this regard, most of the prior works were based on deep metric learning (DML) paradigms. Several methods were built upon contrastive loss [3], triplet loss [4,5] and quadruplet loss [6,7]. The contrastive loss is usually based on the pair, i.e., a positive pair consists of images from the same class, while the negative pair consists of images of different classes. Contrastive loss aims to penalize the case when the negative pair distance is smaller than some margin and when the positive pair distance is greater. The disadvantage of this loss is that it does not take relative distances but only focuses on the pair. This was tackled by triplet loss, which is based on the triplets rather than pairs. A triplet is formed by choosing an anchor image, a positive image from the same anchor class, and a negative image from a different class. The Triplet loss aims to penalize the case when a positive pair (anchor-positive) distance is greater than the negative pair (anchor-negative) distance by some margin. Many previous works employed the triplet loss and improved it by including more negatives in the loss function [8–10]. These strategies were based on the common goal of DML, which aims to cluster all similar class images in the embedding space as closely as possible, resulting in more tightly clustered classes in the embedded space. However, this is not true for large intra-class variance databases since no image does not necessarily look like all the images within the same class. In addition, existing efforts [8–12] had limited efficiency since they hugely depended on sampling strategies. In contrast, this paper deals with instances sampled from the minibatch without requiring hard-mining strategies. This paper proposes an approach to create positive pairs inside the class cluster to diversify class instances while separating them from other class instances. The basic idea is illustrated in Fig. 1.

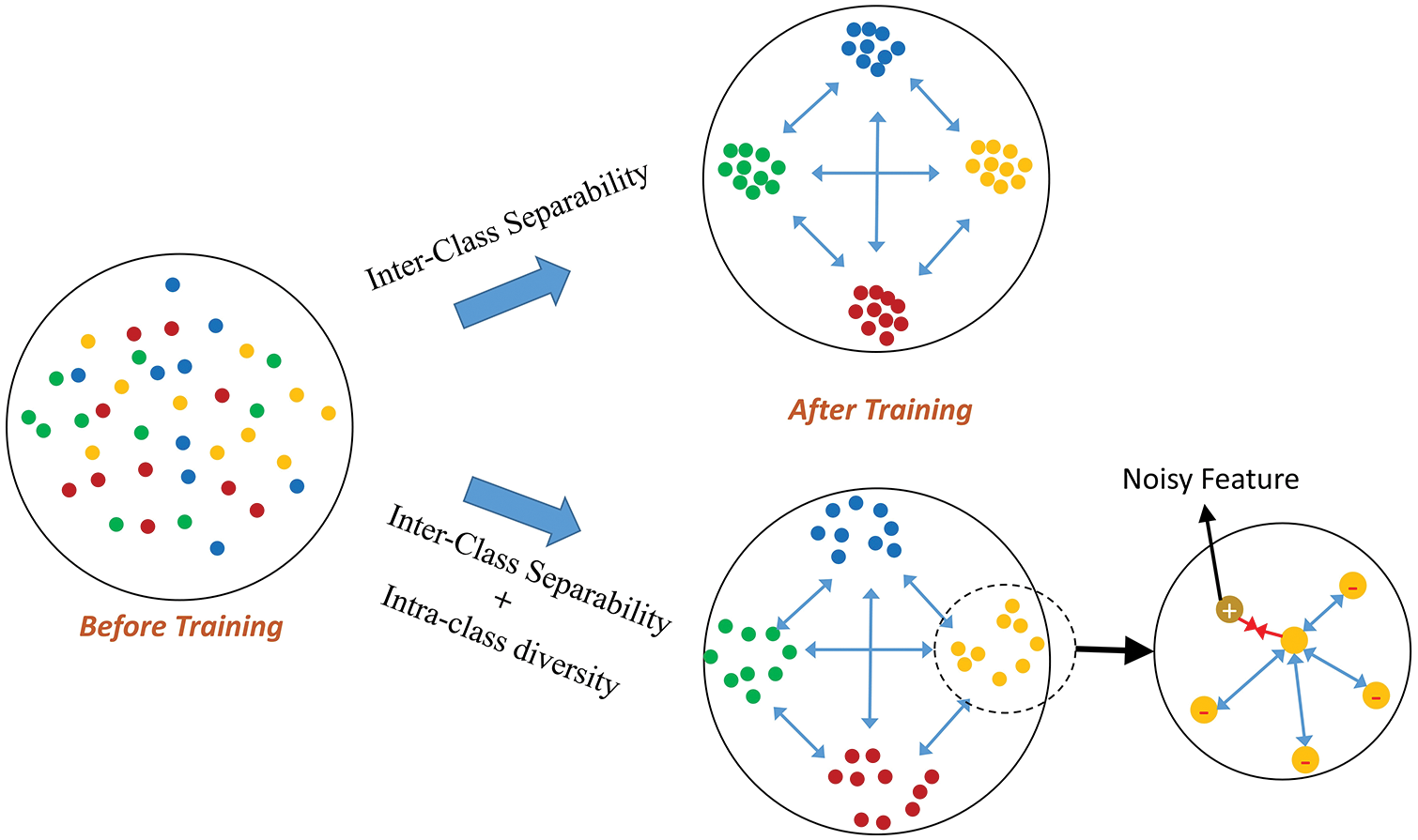
Figure 1: The proposed approach focuses on inter-class separability and intra-class diversity learning. The proposed work lies in the inclusion of intra-class diversity in embedded space. We aim to learn manifolds for each class because no query image necessarily looks identical to all instances of that class but only to the most similar instances

Contribution:

•   A noise-assisted feature learning approach for fine-grained image search is proposed, which aims to learn diverse features and reduce the costly sampling process of triple loss.

•   The main goal of the proposed work is to learn a manifold of each class instead of just class discriminative learning in the triplet-based loss. We do this by contrasting positive pairs (created by noise) in each class cluster in the embedded space.

•   The importance of intra-class diversity in the embedded space is studied as it helps in better generalization to unseen classes.

•   To include more diversity in the learned features, this paper exploits self-supervised constraint, which further helps to improve retrieval performance.

•   Finally, the proposed approach is validated with experiments conducted on well-known fine-grain datasets, which show improved performance compared to existing techniques.

2  Related Work

Research into image retrieval was also spurred by the success of the convolutional neural network (CNN) [13] and other deep learning techniques. For example, a pretrained CNN was used by Babenko et al. [14] for image retrieval and representation, and the CNN’s responses were used to fine-tune it on the target images. Using sum pooling on deep features, the feature aggregation method was proposed in [15,16]. According to Shakarami et al. [17], a descriptor for image retrieval was built on the fusion of three different features: local binary pattern (LBP), histogram of gradients (HOG), and CNN. To encode many locations with the convolutional layers’ encodings, Tolias et al. [18] described a method for producing compact features. A feature learning technique with a cross-batch reference strategy for picture retrieval was suggested by Yang et al. [19]. The bag-of-words approach was used by Mohedano et al. [20] to exploit CNN features, while CNN features with vector locally aggregated descriptors (VLAD) are utilized in [21]. These techniques were good at a coarse level, but fine-grained images require the detection of subtle locations.

Recently, research on fine-grained image tasks has been done using the deep learning paradigm. The challenge is how to locate and represent subtle details. An approach to fine-grained vehicle classification by Watkins et al. [22] is to first locate the item with a trained classifier and then deploy this detected border-box for vehicle classification. For object localization, the authors in [23] used pre-trained VGG-16 [24] and removed noise or background to pick its deep descriptors. The author of [25] made use of convolutional kernels to pick and represent the object’s sections. ResNet18 [26] was investigated by Kumar et al. [27] for the fine-grained image retrieval (FGIR) task, and its activations were employed for retrieval. For fine-grained categorization, Zhou et al. [28] investigated the label hierarchy to exploit rich associations through bipartite graphs and VGG-nets [24]. The centralized ranking loss was proposed by Zheng et al. [29] for weakly supervised object localization. The contours of the CNN response map were then used to extract the features.

In addition, some efforts were made to embed learning. Like, [4] utilized pairwise loss, and [5] utilized triplet loss on top of CNN for image embedding learning. Other extensions of these works are [8–12]. Most of these methods ignored inter-class diversity and were based on costly hard mining strategies. Further, Vasudeva et al. [30] looked for optimal hard mining. In addition, Xuan et al. [31] showed the importance of intra-class variance in learning embedding. To this end, we focus on incorporating intra-class diversity into the embedding space while minimizing the sampling costs.

3  Methodology

The main objective of our work is illustrated in Fig. 2. Here, the goal is to learn class manifold by including both Inter-Class separability and Intra-class diversity. To enhance a network’s potential for feature representation, noise can aid in the deep CNN’s learning of more accurate representations. Prior efforts such as [32,33] commonly used noisy labels to train feature representation networks, which requires a large dataset with noisy labels. Rather than of utilizing noisy labels, we train the network in this study by inserting randomness (noise) at the input and last layer. At the input layer, a noisy image is formed, and at the output layer, a noisy feature is created, both of which act as randomness to the network, which helps in achieving the model’s generalizability.

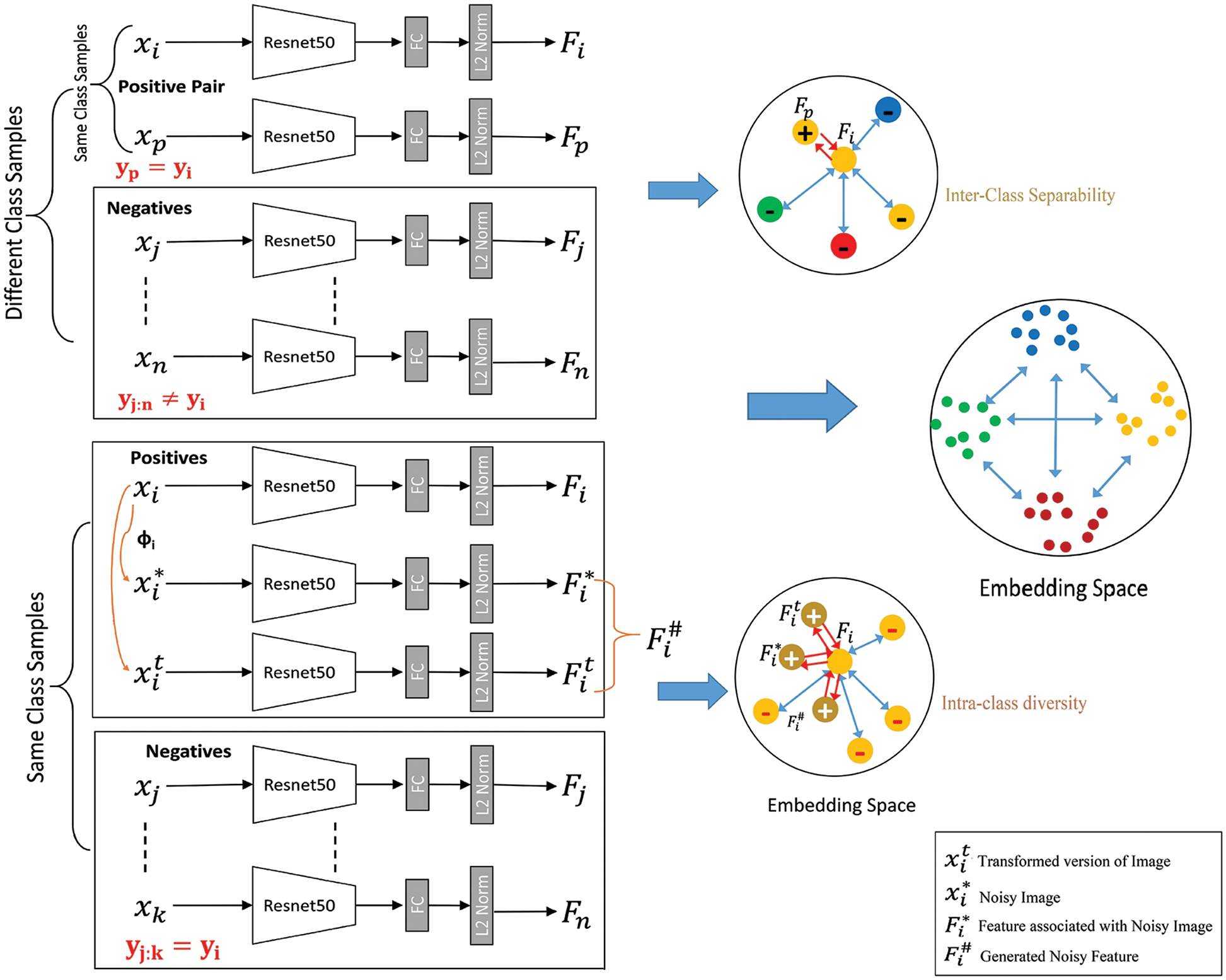
Figure 2: Overview of the proposed approach under FGIR

Let training images {x1,x2,…,xm}∈X with associated labels {y1,y2,…,ym}∈Y in the given minibatch for training the network. The goal is to learn low embedding for each image with the following constraint.

{Dy(fθ(xi),fθ(xj))→0, if yi=yj;Dy(fθ(xi),fθ(xj))>α, if yi≠ yj,(1)

where, fθ(xj) is the feature embedding of image xj, fθ is the feature extraction network, and Dy may be Euclidean or cosine distance.

Let fi=fθ(xi), I be the set of indices corresponding to the number of instances in a minibatch, A(i) be the set of indices of all positives to the ith image instance, and C(i) be the set of indices of all negatives to ith image instance.

For inter-class variance, the positives from simple transformation operations like rotation, cropping, flipping, etc., are considered. The metric constraint for (Xi,Xp,Xn):Yi=Yp,Yi≠Yn in terms of cosine similarity could be defined as:

(fi⊙fp)>(fi⊙fn),∀i,p,n∈I,yi=yp,yi≠yn(2)

and the loss for constraint (2) can be defined as:

Linter=∑i∈I1|A(i)|∑p∈A(i)(−log⁡exp⁡(fi⊙fp/τ)exp⁡(fi⊙fp/τ)+∑n∈C(i)exp⁡(fi⊙fn/τ))(3)

3.1 Noise-Assisted Feature Learning (NAFL)

Fine-grain images generally possess a large intra-class variance than an inter-class variance. Hence, the same should also be true in the embedding space. Prior works focused on separating class clusters as much as possible, neglecting intra-class variance and resulting in the tightening of class clusters.

Thus, to incorporate intra-class variance, class manifold learning should be utilized. For this, the positive pairs are formed as: given an input image xi, the positive candidate for xi computed as (4)

xI∗[a:a+k,b:b+k]=shuffle(xi[a:a+k,b:b+k](4)

Eq. (4) states that for each non-overlapping window of size k × k in the image xi, do shuffle the pixel values.

Fig. 3 depicts the noisy images with various-sized windows. On comparing to Gaussian noise, which adds noise all over the image, this work creates a noisy image by simply shuffling image intensities in the neighbor. This can be clearly visible in Fig. 3.

Figure 3: Noisy images under different window sizes (Best view during zoom and in color)

Now, consider the fi∗ be the L2 normalized feature embedding of the noisy image xi∗. Consider the cosine similarity (▪,⊙,▪) between fi and fi∗ as fi⊙fi∗, where ⊙ is the dot product. The goal is to maximize fi⊙fi∗ for all instances xi∈X. Similar to (1), the metric constraint for (xi,xi∗,xj):yi=y(xi∗)=yj could be defined as:

(fi⊙fi∗)>(fi⊙fj),∀xi,xj∈X,yi=y(xi∗)=yj(5)

where, xi∗ is a noised version of xi which is produced by applying (4).

For constraint (5), the loss can be defined as:

Lintra=∑i∈I[−log⁡exp⁡(fi⊙fi∗/ τ)exp⁡(fi⊙fi∗/ τ)+∑n∈A(i)exp⁡(fi⊙fn/τ)](6)

In addition to the noised image, noisy feature fi#=fi∗+fit is computed to further include it as the positive sample, where fit is the embedding of the transformed version. The loss Lintra can be rewritten as:

Lintra=∑i∈I∑p1∈(fi∗,fi#)(−log⁡exp⁡(fi⊙p1/τ)exp⁡(fi⊙p1/τ)+∑n∈A(i)exp⁡(fi⊙fn/τ))(7)

The network is trained with backpropagation to jointly minimize the two losses (3) and (7) over each minibatch m sampled from the database.

4  Implementation and Dataset Settings

The Imagenet pre-trained model Resnet-50 [26] is used as a base network. The embedding size is set to 1024. The learning rate is set to 10e-4, and the minibatch size is set to 64 images. For data augmentation, random rotation, reflection, crop, and color augmentation [34] are used. All the experiments are performed on MATLAB 2019b with NVIDIA Tesla K40c. Two widely used datasets, CARS-196 [35] and CUB-200 [36], are selected to evaluate the proposed method. The CUB-200 dataset consists of 11,788 images of 200 bird species. Following the state-of-the-art evaluation protocol [37], the first 100 species are used for training and the next 100 for testing. Similarly, the CARS-196 dataset consists of 198 car models and 16,185 images. The first 98 models are used for training, and the next 98 for testing.

5  Results

In this section, the FGIR results are reported, which includes an analysis of the effect of noise and the importance of intra-class diversity in retrieval performance.

5.1 Effect of Noise on the Network

To evaluate the influence of the noise on retrieval performance, the experiments are performed on the CARS-196 and CUB-200, and the results in the form of recall@k are depicted in Figs. 4 and 5. It can be observed from the figures that using a gaussian noise image improves retrieval performance compared to not using noise. Consequently, with the noisy image formed with the proposed method, performance is further improved, which is reflected in recall@k. This demonstrates that noise helps in learning the model generalization better.

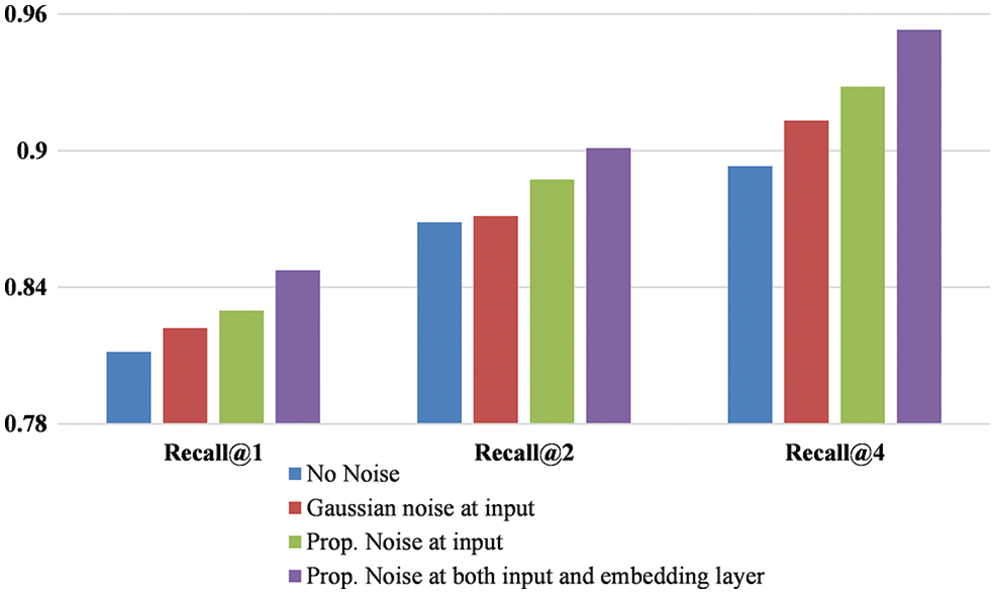
Figure 4: Recall@k for CARS-196 under different settings of noise

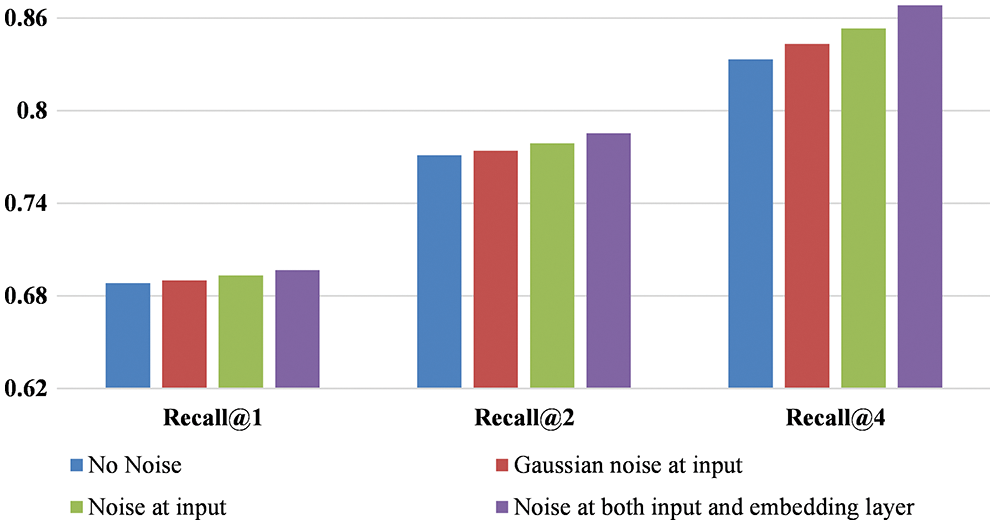
Figure 5: Recall@k for CUB-200 under different settings of noise

5.2 Importance of Intra-Class Diversity

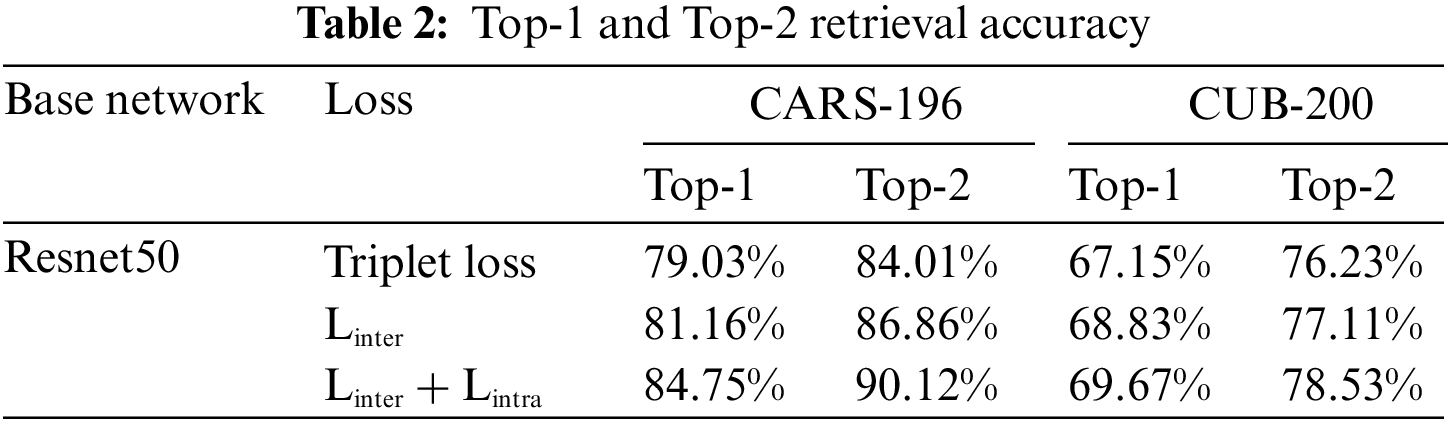
Next, the importance of intra-class diversity in the embedding space is examined. The fine-grained classification results by following standard training and testing protocol [35] are depicted in Table 1. In addition, the retrieval results are depicted in Table 2. As shown in Tables 1 and 2, when the inter-separability is included as a constraint in the embedding space, the classification accuracy improves for both datasets. For example, as in Table 1, for CARS-196, the accuracy of 90.2% is improved to 91.72% by training the model with the inter-separability loss compared to the cross entropy loss. Further, this too improved to 93.68% accuracy when the intra-diversity loss was also added. Therefore, this demonstrates the importance of intra-class diversity in the embedded space. Table 2 reports the retrieval results for both datasets where top-1 and top-2 retrieval accuracy improves with the inclusion of the intra-class diversity loss. This further confirms the importance of intra-class diversity.

5.3 Performance Enhancement with Self-Supervision Constraint

To further improve the model’s performance, the self-supervised learning approach can be explored. For this, the rotation [38], exemplar [39], and Jigsaw-puzzle [40] are tested. For the rotation task, the rotation angles in the range (0°, 90°, 180°, 270°) are considered. For the exemplar task, six transformations (translation, scaling, rotation, contrast, adding color intensity) are considered for each surrogate class. The results are depicted in Figs. 6 and 7, where it can be seen that one with the Jigsaw-puzzle as additional self-supervised learning (SSL) can improve retrieval performance compared to others. This appears to be because the jigsaw-puzzle task forces the model to focus on sub-parts or fine-grained parts of the image. However, rotation and exemplar tasks give the network a small amount of regularization.

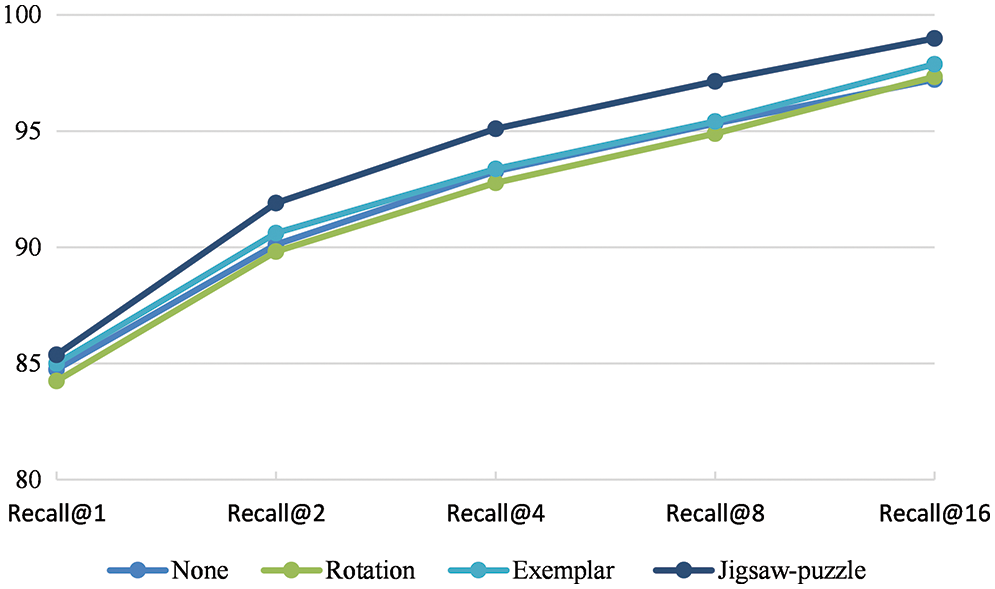
Figure 6: Recall@k for CARS-196 under different self-supervision tasks

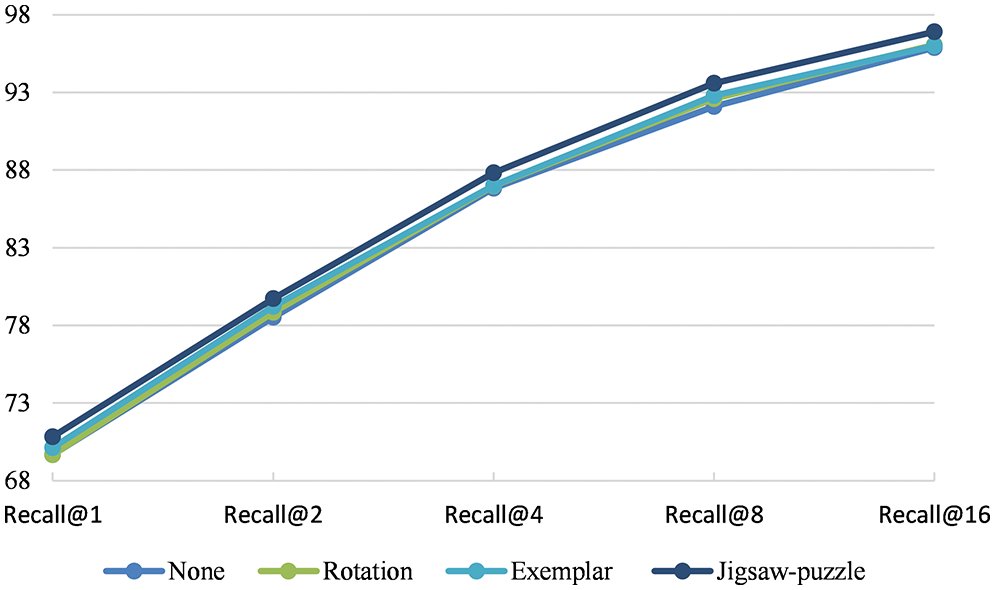
Figure 7: Recall@k for CUB-200 under different self-supervision tasks

5.4 Comparison to State-of-the-Arts

Next, the comparative analysis of the proposed method with other state-of-the-art are reported in Table 3, where the proposed method achieves better results with 84.75% Recall@1, 90.12% Recall@2, 93.27% Recall@4, 95.32% Recall@8, 97.21% Recall@16 for CARS-196. Further, this is improved by including self-supervision task (Jigsaw-puzzle), and the results are 85.38% Recall@1, 91.90% Recall@2, 95.1% Recall@4, 97.14% Recall@8, 98.99% Recall@16.

Similarly, for CUB-200, the proposed method NAFL achieves 69.67% Recall@1, 78.53% Recall@2, 86.82% Recall@4, 92.1% Recall@8, 95.87% Recall@16. In addition, this is further improved to 70.13% Recall@1, 78.88% Recall@2, 87.17% Recall@4, 92.4% Recall@8, and 96.8% Recall@16 by SSL. We also plot the retrieval results for the randomly sampled query from both datasets in Figs. 8 and 9.

Figure 8: Retrieval results on CARS-196 dataset. The green boundary box indicates the correct retrieved instance, and the red boundary box indicates the wrong retrieved instance

Figure 9: Retrieval results on the CUB-200 dataset. The green boundary box indicates the correct retrieved instance, and the red boundary box indicates the wrong retrieved instance

6  Conclusion

This paper presents a noise-assisted feature learning strategy for FGIR, which avoids the costly sampling process (as in triplet-based learning). This is accomplished by inserting noise into the input sample as well as the deep CNN’s embedding. The Resnet-50 architecture is used as the backbone network and trained jointly with a multi-loss objective, which deals with both class discriminative and intra-class diversity via noise-assisted learning. The CUB-200 and CARS-196 datasets are considered to validate our approach. Moreover, it showed that the proposed approach is able to improve over existing schemes. Future work will test the proposed method for large-scale datasets with the use of other deeper variants of CNN. In addition, it can be extended to deal with video analysis tasks like action classification and video retrieval. It can also be tested in the medical domain using both supervised and unsupervised learning strategies. In addition, it can be tested in self-supervised learning [41–45] mode.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. I. M. Hameed, S. H. Abdulhussain and B. M. Mahmmod, “Content-based image retrieval: A review of recent trends,” Cogent Engineering, vol. 8, no. 1, pp. 1–37, 2021. [Google Scholar]

2. L. Xie, J. Wang, B. Zhang and Q. Tian, “Fine-grained image search,” IEEE Transactions on Multimedia, vol. 17, no. 5, pp. 636–647, 2015. [Google Scholar]

3. S. Bell and K. Bala, “Learning visual similarity for product design with convolutional neural networks,” ACM Transactions on Graphics, vol. 34, no. 4, pp. 1–10, 2015. [Google Scholar]

4. J. Wang, Y. Song, T. Leung, C. Rosenberg, J. Wang et al., “Learning fine-grained image similarity with deep ranking,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Columbus, OH, USA, pp. 1386–1393, 2014. [Google Scholar]

5. F. Schroff, D. Kalenichenko and J. Philbin, “FaceNet: A unified embedding for face recognition and clustering,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Boston, MA, USA, pp. 815–823, 2015. [Google Scholar]

6. W. Chen, X. Chen, J. Zhang and K. Huang, “Beyond triplet loss: A deep quadruplet network for person re-identification,” in Proc.—30th IEEE Conf. on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, pp. 403–412, 2017. [Google Scholar]

7. C. Huang, C. C. Loy and X. Tang, “Local similarity-aware deep feature embedding,” Advances in Neural Information Processing Systems, vol. 29, pp. 1270–1278, 2016. [Google Scholar]

8. K. Sohn, “Improved deep metric learning with multi-class N-pair loss objective,” Advances in Neural Information Processing Systems, vol. 29, pp. 1857–1865, 2016. [Google Scholar]

9. H. O. Song, Y. Xiang, S. Jegelka and S. Savarese, “Deep metric learning via lifted structured feature embedding,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, pp. 4004–4012, 2016. [Google Scholar]

10. H. O. Song, S. Jegelka, V. Rathod and K. Murphy, “Deep metric learning via facility location,” in 2017 IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, pp. 2206–2214, 2017. [Google Scholar]

11. B. Yu, T. Liu, M. Gong, C. Ding and D. Tao, “Correcting the triplet selection bias for triplet loss,” in European Conf. in Computer Vision, ECCV, Munich, Germany, pp. 71–86, 2018. [Google Scholar]

12. C. Y. Wu, R. Manmatha, A. J. Smola and P. Krahenbuhl, “Sampling matters in deep embedding learning,” in 2017 IEEE Int. Conf. on Computer Vision (ICCV), Venice, Italy, pp. 2859–2867, 2017. [Google Scholar]

13. A. Krizhevsky, I. Sutskever and G. E. Hinton, “ImageNet classification with deep convolutional neural networks,” Advances in Neural Information Processing Systems, vol. 1, pp. 1097–1105, 2012. [Google Scholar]

14. A. Babenko, A. Slesarev, A. Chigorin and V. Lempitsky, “Neural codes for image retrieval,” in European Conf. on Computer Vision, Zurich, Switzerland, pp. 584–599, 2014. [Google Scholar]

15. A. B. Yandex and V. Lempitsky, “Aggregating local deep features for image retrieval,” in Proc. of the IEEE Int. Conf. on Computer Vision, Santiago, Chile, pp. 1269–1277, 2015. [Google Scholar]

16. Y. Kalantidis, C. Mellina and S. Osindero, “Cross-dimensional weighting for aggregated deep convolutional features,” in European Conf. on Computer Vision, Amsterdam, The Netherlands, pp. 685–701, 2016. [Google Scholar]

17. A. Shakarami and H. Tarrah, “An efficient image descriptor for image classification and CBIR,” Optik (Stuttg), vol. 214, pp. 164833, 2020. [Google Scholar] [PubMed]

18. G. Tolias, R. Sicre and H. Jégou, “Particular object retrieval with integral max-pooling of CNN activations,” in ICLR 2016-Int. Conf. on Learning Representations, San Juan, Puerto Rico, pp. 1–12, 2016. [Google Scholar]

19. H. F. Yang, K. Lin and C. S. Chen, “Cross-batch reference learning for deep classification and retrieval,” in Proc. of the 24th ACM Int. Conf. on Multimedia, Ottawa, ON, Canada, pp. 1237–1246, 2016. [Google Scholar]

20. E. Mohedano, K. Mcguinness, N. E. O’Connor, A. Salvador, F. Marqués et al., “Bags of local convolutional features for scalable instance search,” in Proc. of the 2016 ACM on Int. Conf. on Multimedia Retrieval, New York, USA, pp. 327–331, 2016. [Google Scholar]

21. J. Y. H. Ng, F. Yang and L. S. Davis, “Exploiting local features from deep networks for image retrieval,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, pp. 53–61, 2015. [Google Scholar]

22. R. Watkins, N. Pears and S. Manandhar, “Vehicle classification using ResNets, localisation and spatially-weighted pooling,” ArXiv., 2018. [Google Scholar]

23. X. S. Wei, J. H. Luo, J. Wu and Z. H. Zhou, “Selective convolutional descriptor aggregation for fine-grained image retrieval,” IEEE Transactions on Image Processing, vol. 26, no. 6, pp. 2868–2881, 2017. [Google Scholar] [PubMed]

24. K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” in 3rd Int. Conf. on Learning Representations, ICLR 2015, San Diego, CA, USA, 2015. [Google Scholar]

25. X. Zhang, H. Xiong, W. Zhou, W. Lin and Q. Tian, “Picking deep filter responses for finegrained image recognition,” in 2016 IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, pp. 1134–114, 2016. [Google Scholar]

26. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in 2016 IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, pp. 770–778, 2016. [Google Scholar]

27. V. Kumar, V. Tripathi and B. Pant, “Content based fine-grained image retrieval using convolutional neural network,” in 2020 7th Int. Conf. on Signal Processing and Integrated Networks (SPIN), Noida, India, pp. 1120–1125, 2020. [Google Scholar]

28. F. Zhou and Y. Lin, “Fine-grained image classification by exploring bipartite-graph labels,” in 2016 IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, pp. 1124–1133, 2016. [Google Scholar]

29. X. Zheng, R. Ji, X. Sun, Y. Wu, F. Huang et al., “Centralized ranking loss with weakly supervised localization for fine-grained object retrieval,” in Proc. of the 27th Int. Joint Conf. on Artificial Intelligence, Stockholm, Sweden, pp. 1226–1233, 2018. [Google Scholar]

30. B. Vasudeva, P. Deora, S. Bhattacharya, U. Pal and S. Chanda, “Loop: Looking for optimal hard negative embeddings for deep metric learning,” in IEEE/CVF Int. Conf. on Computer Vision (ICCV), Montreal, QC, Canada, pp. 10614–10623, 2021. [Google Scholar]

31. H. Xuan, A. Stylianou and R. Pless, “Improved embeddings with easy positive triplet mining,” in Proc. of the IEEE/CVF Winter Conf. on Applications of Computer Vision, Snowmass, CO, USA, pp. 2474–2482, 2020. [Google Scholar]

32. E. Rodner, M. Simon, R. B. Fisher and J. Denzler, “Fine-grained recognition in the noisy wild: Sensitivity analysis of convolutional neural networks approaches,” in British Machine Vision Conf. 2016, BMVC, York, UK, pp. 60.1–60.13, 2016. [Google Scholar]

33. J. Krause, B. Sapp, A. Howard, H. Zhou, A. Toshev et al., “The unreasonable effectiveness of noisy data for fine-grained recognition,” in European Conf. on Computer Vision, Amsterdam, The Netherlands, pp. 301–320, 2016. [Google Scholar]

34. M. Afifi and M. Brown, “What else can fool deep learning? addressing color constancy errors on deep neural network performance,” in 2019 IEEE/CVF Int. Conf. on Computer Vision (ICCV), Seoul, Korea (Southpp. 243–252, 2019. [Google Scholar]

35. J. Krause, M. Stark, J. Deng and L. Fei-Fei, “3D object representations for fine-grained categorization,” in 2013 IEEE Int. Conf. on Computer Vision Workshops, Sydney, NSW, Australia, pp. 554–561, 2013. [Google Scholar]

36. P. Welinder, S. Branson, T. Mita, C. Wah and F. Schroff, “Caltech-ucsd birds 200, caltech-UCSD,” Technical Report, California Institute of Technology, pp. 1–15, 2010. [Google Scholar]

37. X. Zheng, R. Ji, X. Sun, B. Zhang, Y. Wu et al., “Towards optimal fine grained retrieval via decorrelated centralized loss with normalize-scale layer,” in Proc. of the AAAI Conf. on Artificial Intelligence, vol. 33, no. 1, Honolulu Hawaii USA, pp. 9291–9298, 2019. [Google Scholar]

38. N. Komodakis and S. Gidaris, “Unsupervised representation learning by predicting image rotations,” in Int. Conf. on Learning Representations (ICLR), Vancouver, Canada, 2018. [Google Scholar]

39. A. Dosovitskiy, P. Fischer, J. T. Springenberg, M. Riedmiller and T. Brox, “Discriminative unsupervised feature learning with exemplar convolutional neural networks,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 38, no. 9, pp. 1734–1747, 2016. [Google Scholar] [PubMed]

40. M. Noroozi and P. Favaro, “Unsupervised learning of visual representations by solving jigsaw puzzles,” in European Conf. on Computer Vision, Amsterdam, Netherlands, pp. 69–84, 2016. [Google Scholar]

41. V. Kumar, V. Tripathi and B. Pant, “Unsupervised learning of visual representations via rotation and future frame prediction for video retrieval,” in Int. Conf. on Advances in Computing and Data Sciences (ICACDS 2021), Nashik, India, pp. 701–710, 2021. [Google Scholar]

42. V. Kumar, “Unsupervised learning of spatio-temporal representation with multi-task learning for video retrieval,” in 2022 National Conf. on Communications (NCC), Mumbai, India, pp. 118–123, 2022. [Google Scholar]

43. V. Kumar, V. Tripathi and B. Pant, “Enhancing unsupervised video representation learning by temporal contrastive modelling using 2d CNN,” in Int. Conf. on Computer Vision and Image Processing (CVIP-2021), Rupnagar, India, pp. 494–503, 2022. [Google Scholar]

44. V. Kumar, V. Tripathi, B. Pant, S. S. Alshamrani, A. Dumka et al., “Hybrid spatiotemporal contrastive representation learning for content-based surgical video retrieval,” Electronics, vol. 11, no. 9, pp. 1353, 2022. [Google Scholar]

45. V. Kumar, V. Tripathi and B. Pant, “Learning unsupervised visual representations using 3d convolutional autoencoder with temporal contrastive modeling for video retrieval,” International Journal of Mathematical, Engineering and Management Sciences, vol. 7, no. 2, pp. 272–287, 2022. [Google Scholar]