Solar Radiation Prediction Using Satin Bowerbird Optimization with Modified Deep Learning

1  Introduction

Renewable energy is focused on fulfilling the rising energy demand sustainably by decreasing greenhouse gas emissions and climate change risk reduction [1]. The most potential energy among renewable energy is solar energy because of its availability. As a result, there comes a rise in solar energy technology. But optimizing the utility and efficacy of solar energy will remain problematic because of its difficulty in gathering and precisely examining the solar radiations [2]. Solar energy projects could be very beneficial from reliable solar radiation data. Certainly, global solar radiation will be considered a very appropriate variable in predicting, monitoring, sizing, and simulating solar energy technology [3]. Currently, the study on solar radiation estimation is becoming more in-depth. Among several predictive techniques, the meekest is the persistence technique that would assume that the future solar radiations are equal to the present solar radiations [4]. Other solar radiation predictive techniques are categorized into 4 categories: machine learning (ML) approaches, physical techniques, hybrid techniques, and statistical approaches [5].

The physical technique accomplishes the solar power generation forecasting model under the geographical atmosphere and meteorological data (like pressure, temperatures, humidity, and so on) [6]. Such techniques are again clustered into 2 sub-categories: spatial correlation techniques and numerical weather prediction (NWP) techniques [7]. NWP techniques utilize numerical simulation for forecasting, i.e., physical and mathematical methods will be enforced on examining environmental circumstances, and high-speed computers were used for predicting solar radiations [8]. In normal circumstances, NWP techniques take a longer period to forecast. Furthermore, the weather and atmospheric elements in NWP techniques will take more work to make clear choices. In the present study, it is hard to enhance prediction accuracy [9]. The spatial correlation techniques harness spatial co-relation of solar radiations for estimating solar energy in numerous locations. It is noticed that spatial correlation approaches need rich historic data for simulating complicated temporal and spatial variations [10]. In summary, NWP approaches and other physical techniques are unsuitable for short-run and small regions because of long runtimes. In the meantime, they have more demands on computational sources.

This article develops an optimal Modified Bidirectional Gated Recurrent Unit Driven Solar Radiation Prediction (OMBGRU-SRP) for energy management. The presented OMBGRU-SRP technique mainly aims to accomplish an accurate and time SR prediction process. To accomplish this, the presented OMBGRU-SRP technique performs data preprocessing to normalize the solar data. Next, the MBGRU model is derived using BGRU with an attention mechanism and skip connections. At last, the hyperparameter tuning of the MBGRU model is carried out using the satin bowerbird optimization (SBO) algorithm to attain maximum prediction with minimum error values. Many experiments were conducted to demonstrate the enhanced SR prediction performance.

2  Literature Review

Reddy et al. [11], an elephant herd optimization approach presented with deep ELM (EHO-DELM) for predicting solar radiation through weather predictions. The proposed algorithm implements preprocessing to make the data consistent with the regression model. Furthermore, the presented method is employed for predicting the SR through the weather prediction dataset. In addition, the suggested algorithm is exploited to tune the biases and weights. The author in [12] developed two novel hybrid NN models, CNN-LSTM-ANN and CNN-ANN, for predicting global solar radiation (GSR). Also, the ANN model is established and compared to the efficiency of the hybrid NN mechanism. The study contributed to the search for a precise solar radiation prediction method. The hybrid NN model is tested or trained with the dataset from 10 different countries.

Zhu et al. [13] designed a novel LSTM-based attention module and GA (AGA-LSTM). The attention module allocates different weights to all the features, so the module can further focus on the main characteristics. In the meantime, the data selection and structure parameters are improved by using the GA system, and time sequence memory and processing abilities of LSTM are employed to forecast the direct normal irradiance and global horizontal irradiance after five, ten, and fifteen minutes. In [14], the author proposed a CNN and BiLSTM-based hybrid DL method for predicting efficient midterm solar radiation. The suggested method is tested under three distinct geo-location on similar latitudes since it approximately obtains similar solar radiation.

Zhu et al. [15] investigated direct normal irradiance (DNI) as a prediction target. They developed a Siamese CNN-LSTM (SCNN-LSTM) for predicting the inter-hour DNI via integrating the time-dependent spatial feature of historical meteorological observations and total sky images. Firstly, the features of overall sky images have been extracted automatically through an SCNN for describing the cloud data. Then, the meteorological observations and image features were integrated and later estimated, and the DNI was ten minutes in advance using an LSTM. Ghimire et al. [16] proposed a hybridized DL architecture, which incorporates the CNN for recognizing patterns with the LLSTM for forecasting half-hourly GSR. CNN is employed to strongly extract the input feature dataset from prediction parameters (antecedent input) while LSTM absorbs them for prediction. The suggested technique is benchmarked with a standalone model and other DL, Single Hidden Layer, and Tree-based methods.

3  The Proposed Model

This article has developed a new OMBGRU-SRP technique to forecast SR for energy management. The presented OMBGRU-SRP technique mainly aims to accomplish an accurate and time SR prediction process. It encompasses a three-stage process: data normalization, MBGRU-based forecasting, and SBO-based hyperparameter tuning. Fig. 1 defines the block diagram of the OMBGRU-SRP system.

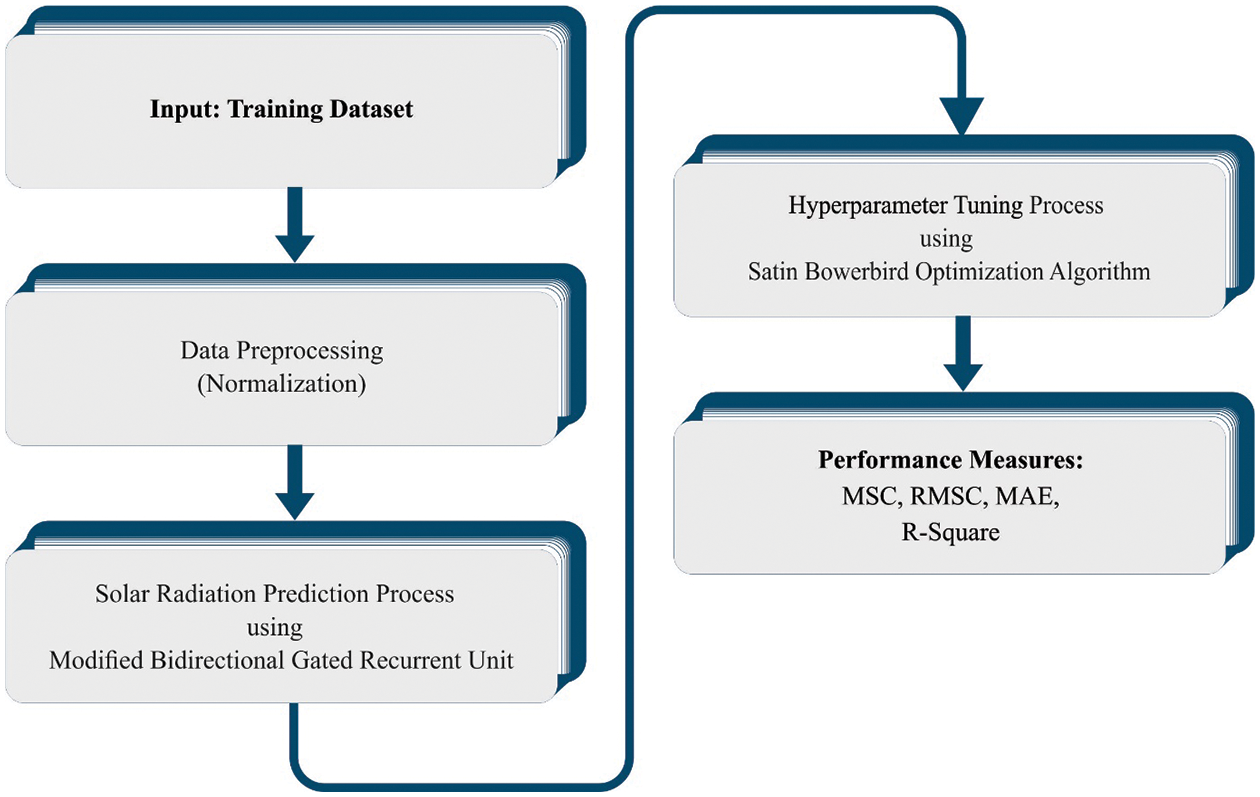
Figure 1: Block diagram of OMBGRU-SRP system

3.1 Data Preprocessing

In the beginning, the presented OMBGRU-SRP technique performs data preprocessing to normalize the solar data. Before utilizing the data for training and creating the ML technique, the data must endure normalized [17]. Data normalization is a usual approach executed for preparing the information for ML. The aim is to alter the numeric value from the dataset by utilizing an ordinary scale without changing variances in the ranges of values or losing data. With normalized data, it can create novel values in the data that continue the common distribution and ratios from the source data but keep value in a scale executed across every numeric column utilized during the model.

The meteorological data (input) were normalized by transforming them to values in the range [−1, 1] utilizing fundamental coding from MATLAB. The equation of normalized and log transformed is also demonstrated as under:

XN=X−XminXmax−Xmin(1)

YT=log⁡(1+Y)(2)

whereas X refers to meteorological data (wind speed, temperature, relative humidity), Xmin represents the minimal value of every accessible meteorological data, Xmax denotes the maximal value of every accessible meteorological data, XN implies the meteorological normalization data, YT denotes the log transformation outcome (solar radiation), and Y defines the actual outcome.

3.2 Solar Radiation Forecasting using MBGRU Model

In this study, the MBGRU model is derived using BGRU with an attention mechanism and skip connections. The BGRU includes two groups of GRUs in several directions that recognize the time dependency extracted from the backward and forward directions to input time series data [18]. Afterwards, the encoder ends, and the hidden encoding layer (HL) vector is considered an embedded vector in HL construction. The attention layer computes the weighted vector Att at distinct time steps. Next, the Att vector has multiplied by the encoding output resultant for obtaining the att-output vector, emphasizing the control of important time-steps data. During the decoder phase, att-output is directed to decoding BGRU as an input vector.

To provide a group of time consecutive dataset X=[x1,x2,x3,…,xt]T. Every xi comprises an m-dimension sensor reading. Considering that the hidden layer of BGRU is h, the encoding output vector and the final HL vector are attained with encoded BGRU units:

(He1×2h,Oet×2h)=fe(Xt×m)

He1×2h=Hf1×h⊕Hb1×h(3)

whereas fe(.) defines the abstract function of encoder BGRU. Hf, Hb determines the forward and backward final HLs, He defines the concatenated HL vector in Hf and Hb, and Oe indicates the output vector of the encoder.

During the attention layer, it can be utilized He1×2h and Oet×2h for attention-weighted computation. Initially, the first dimensional of He1×2h was copied t times for supporting with the dimensional of the Oet×2h vector. Het×2h and Oet×2h indicate the input to the attention layer for calculating the attention weighted Att1×t at all steps. Afterwards, Att1×t is multiplied with Oet×2h to obtain the att−output1×2h vector that emphasizes the key encoder time-step data. att outcome is transported to the decoder BGRU unit to compute the resultant vector and HL:

He1×2h→copyHet×2hAtt1×t=attention(Het×2h⊕Oet×2h)att−output1×2h=Att1×t×Oet×2h(Hd1×2h,Od1×2h)=fd(att−output1×2h,He1×2h)(4)

Afterwards, the att-output has concatenated with Od and input to linear predictive layer to decoder xt' that was repeating t times for predicting every encoder inputs X'=[x1',x2',x3',…,xt']T. Therefore, the MBGRU system was trained to minimize the entire reconstruction error E:

E=12∑i=1t(||ei||1)2(5)

whereas ||ei||1 stands for the 1-norm function that quickly converges and creates a further robust system than the 2-norm function. If the MBGRU is trained effectively, then the last encoded HL He is assumed that compression representation of input X. Once the MBGRU has been collected from several BGRU layers, the embedded vector is achieved by concatenating the last HLs of every layer:

zt=He1⊕He2⊕…HeL(6)

Hel defines the lth layer’s last HL vector, zt demonstrates the embedded vector to an input time sequence dataset, and L defines the entire count of BGRU layers. Fig. 2 illustrates the architecture of BGRU.

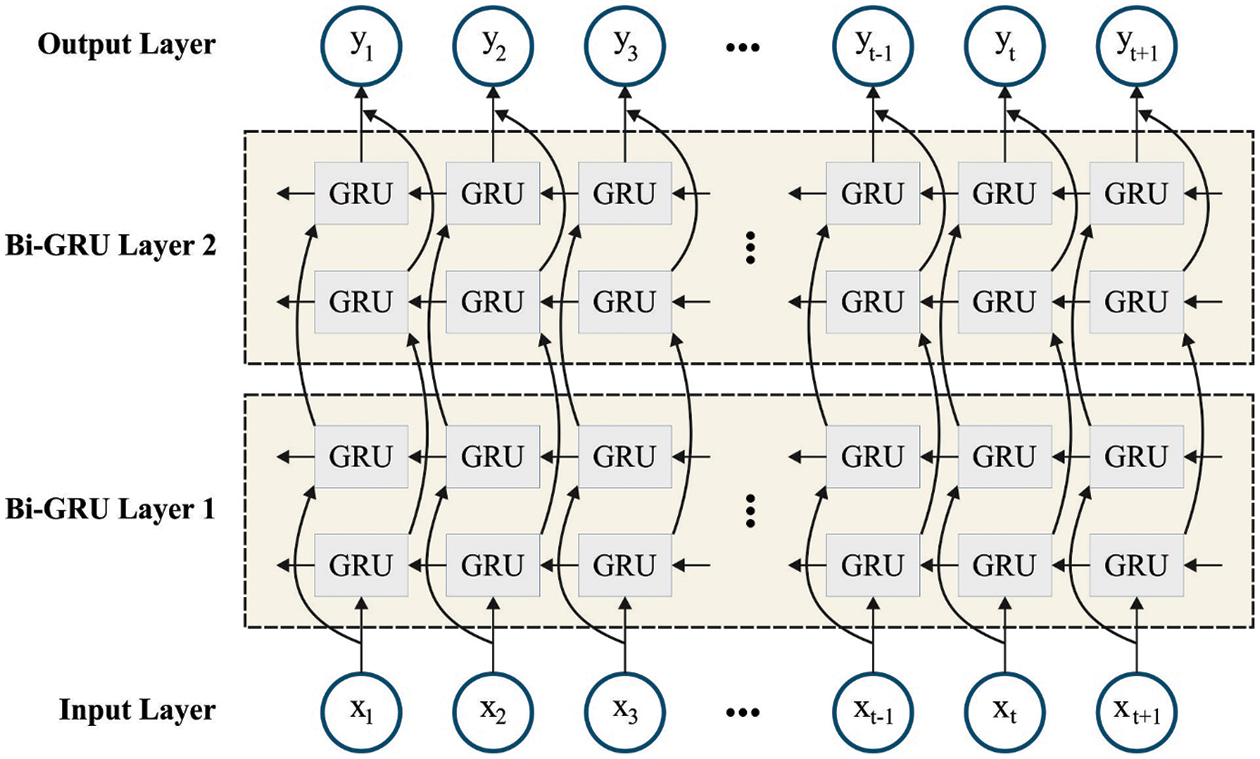
Figure 2: Structure of the BGRU model

3.3 Hyperparameter Optimization

At the final stage, the hyperparameter tuning of the MBGRU model is carried out using the SBO algorithm. The SBO process is a metaheuristic algorithm that determines the global optimal for the provided optimization issue [19]. It is a population-based, simple, robust, and efficient method. Initially, the arbitrary bowers procedure starts with creating the population of arbitrary even distribution by considering the maximal and minimal bounds. Next, every location can be defined using the variable which should be enhanced. The probability of parameter characterizes the attractive nature of bower. A female Satin bower bird picks a bower according to the likelihood, and it could define the possibility of all the individual members in the population with the following equation:

Probi=fiti∑n=1NBfitn(7)

fiti={11+f(xi),f(xi)≥01+|f(xi)|,f(xi)<0(8)

whereas NB indicates bower population size, fiti represents the fitness values of ani-th solution, and f(xi) characterizes the fitness value of the bower.

The SBO approach exploits the notion of exclusivity that calculates the position of the optimum bower and consequently permits the optimum solution to be protected at all levels of the optimization procedure. The SBO method simulates the concept of bird-making nests according to the usual constitution. In mating, the male satin bower bird uses their instinct for decorating besides building the bower to attract female birds. It is suggested that the male bower relies on the acquaintance to impact the innovative conclusion while building the bower; hence, the extremely familiar bird can build an extremely attractive bower more than lower knowledgeable one.

The optimally created bower is regarded as the elite round in the presented method. Since the elite position includes maximal fitness, it can affect another location. The modification of each current bower, which defines the novel position calculated through the position of the optimum fit bower, is defined as follows.

xiknew=xikold+λk((xjk+xelite,k2)−xikold)(9)

whereas xi denotes the ith solution vector, xj is evaluated by the final solution amongst each solution in the existing round, j is defined through the roulette wheel procedure, and xik indicates the k-th members. xelite symbolizes the elite location. In Eq. (10), λk represents the attraction of the target bower, whereas α represents maximal step size and pj indicates the probability accomplished, with the target bower in pj∈(0,1).

λk=α1+pj(10)

In the mutation process that exists after all the rounds of the SBO approach, the arbitrary variation is applied xik with specific possibilities. The standard distribution (N) in the mutation procedure is exploited through an average of xikold, and the variance of σ2, as demonstrated below:

xiknew∼N(xikold,σ2)(11)

N(xikold,σ2)=xikold+(σ∗N(0,1))(12)

σ=Z∗(varmax−varmin)(13)

where σ describes the width proportion, varmin and varmax indicate the minimum and maximum boundaries assigned to the variables. The Z parameter denotes the % of the variations amongst the minimal and maximal limits. Eventually, the newly produced and early population are evaluated and incorporated and organized according to the fitness value. The novel population is produced according to the predetermined value, while the remaining are rejected.

The SBO technique will derive the main function related to mean square error (MSE) and can be leveraged to estimate the MBGRU method's testing output. It is expressed below.

MSE=∑Ni|yi−y^i|2N(14)

whereas y denotes the count of rounds, yi indicates the experimental value, and y^i signifies the estimated values correspondingly.

4  Results and Discussion

In this section, we investigate the solar radiation prediction performance of the OMBGRU-SRP model under different runs. Table 1 offers a comprehensive set of solar radiation prediction results of the OMBGRU-SRP model under five runs. The results represented that the OMBGRU-SRP model has reached enhanced prediction results.

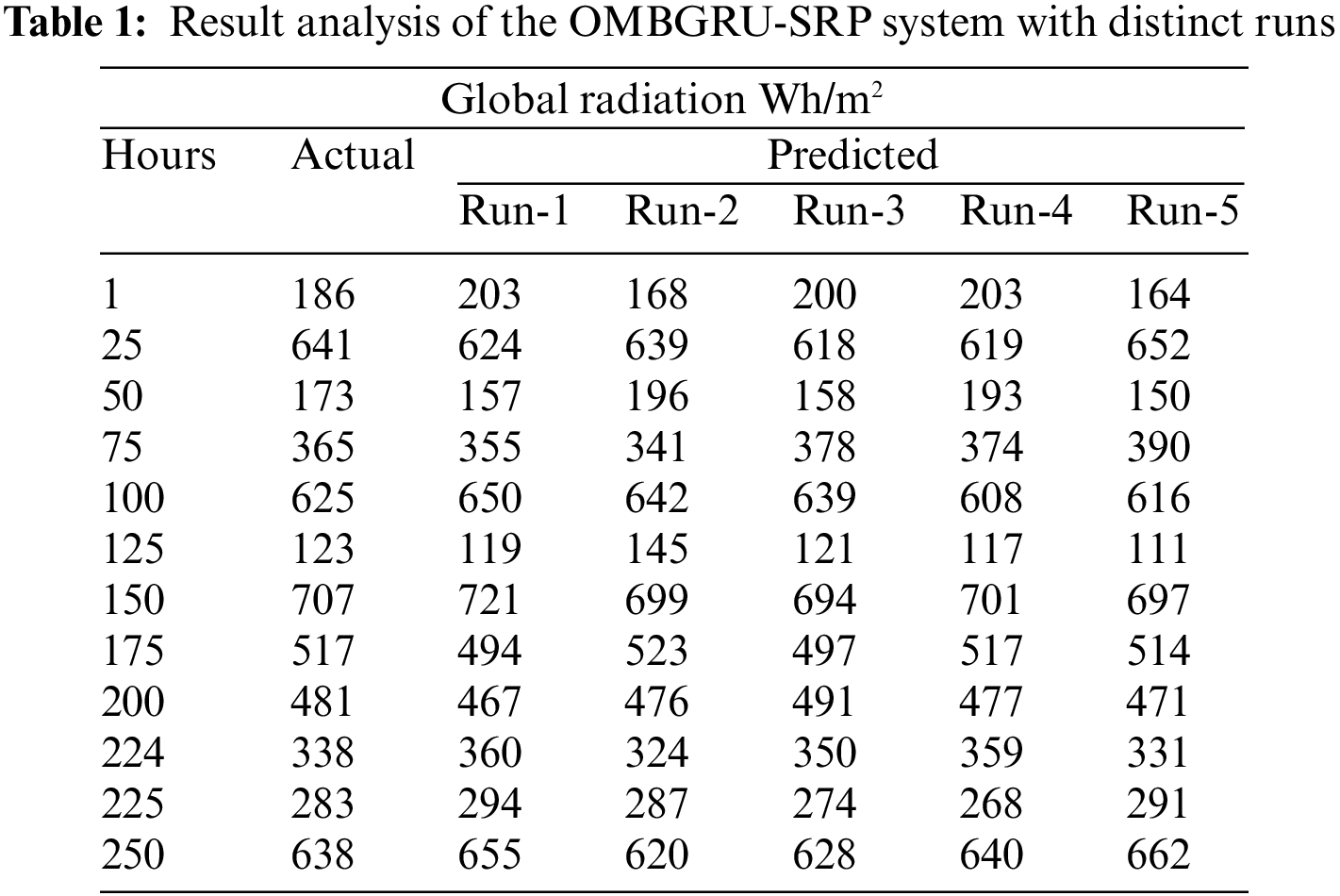
Fig. 3 represents the actual vs. prediction solar radiation forecasting results of the OMBGRU-SRP model under run-1. The figure reported that the OMBGRU-SRP model has shown enhanced forecasted outcomes under all hours of operation. It is also noted that the variance between the actual and predicted solar radiation values is considered a minimum.

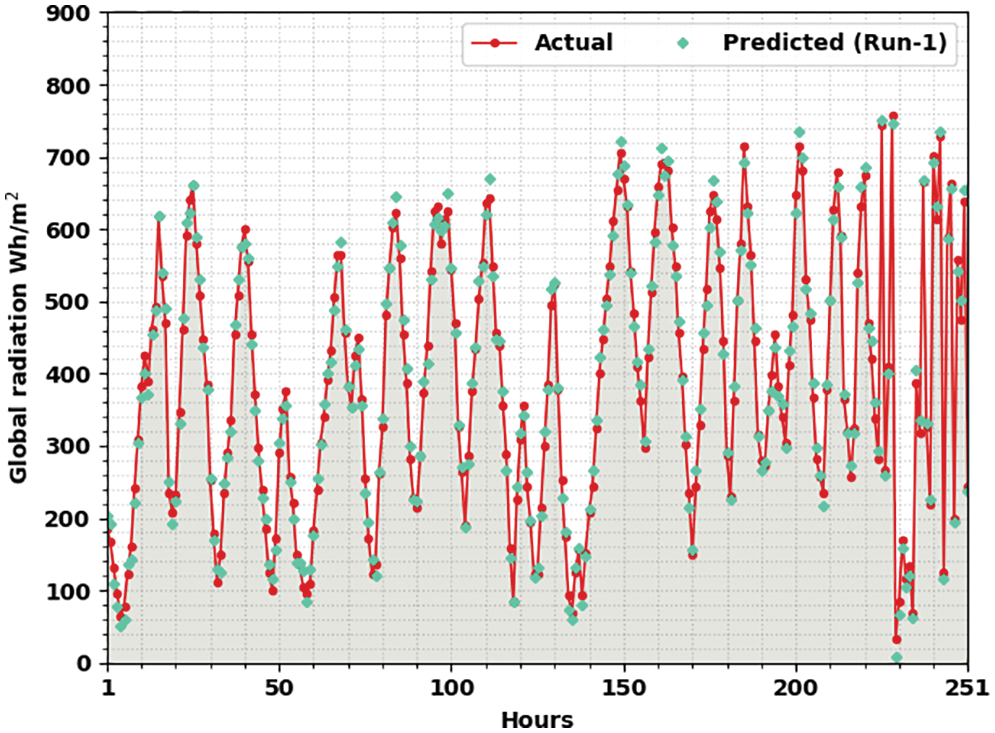
Figure 3: Actual vs. prediction analysis of OMBGRU-SRP system under Run1

Fig. 4 portrays the actual vs. prediction solar radiation predictive outcomes of the OMBGRU-SRP approach under run-2. The figure revealed the OMBGRU-SRP approach has displayed enhanced forecasted results under all hours of operation. It should be noted that the variance between the actual and predicted solar radiation values is minimum.

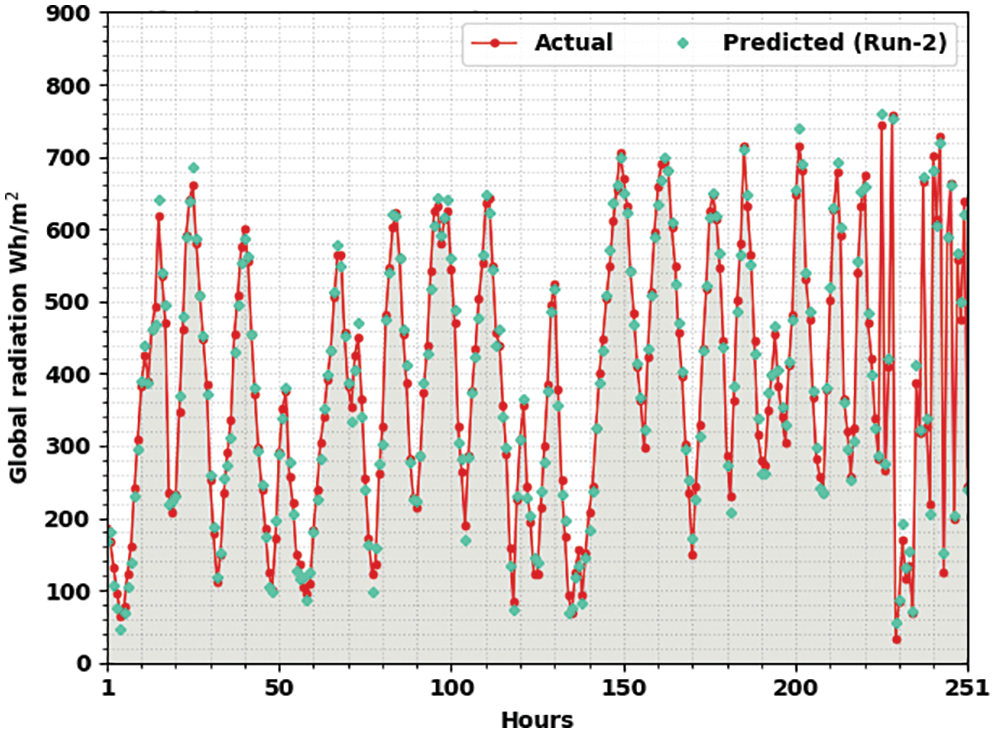
Figure 4: Actual vs. prediction analysis of OMBGRU-SRP system under Run2

Fig. 5 signifies the actual vs. prediction solar radiation forecasting outcomes of the OMBGRU-SRP method under run-3. The figure indicates the OMBGRU-SRP algorithm has exposed enhanced forecasted outcomes under all hours of operation. The variance between the actual and predicted solar radiation values will be considered a minimum.

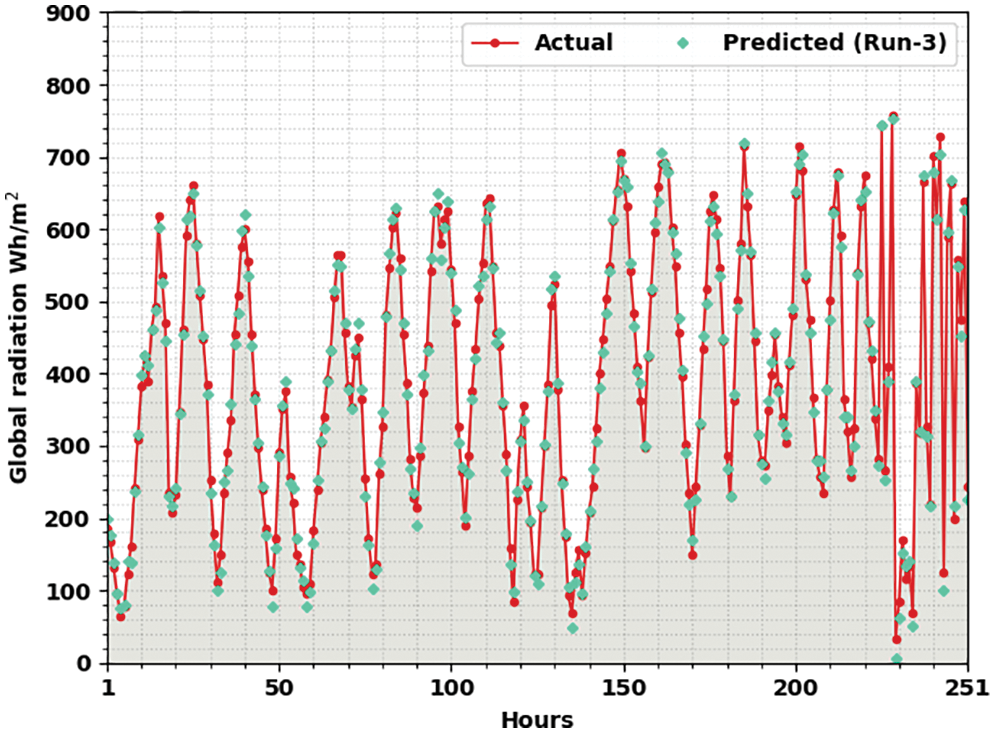
Figure 5: Actual vs. prediction analysis of OMBGRU-SRP system under Run3

Fig. 6 illustrates the actual vs. prediction solar radiation forecasting outcomes of the OMBGRU-SRP model under run-4. The figure signified the OMBGRU-SRP approach has exhibited enhanced forecasted outcomes under all hours of operation. The variance between the actual and predicted solar radiation values will be considered a minimum.

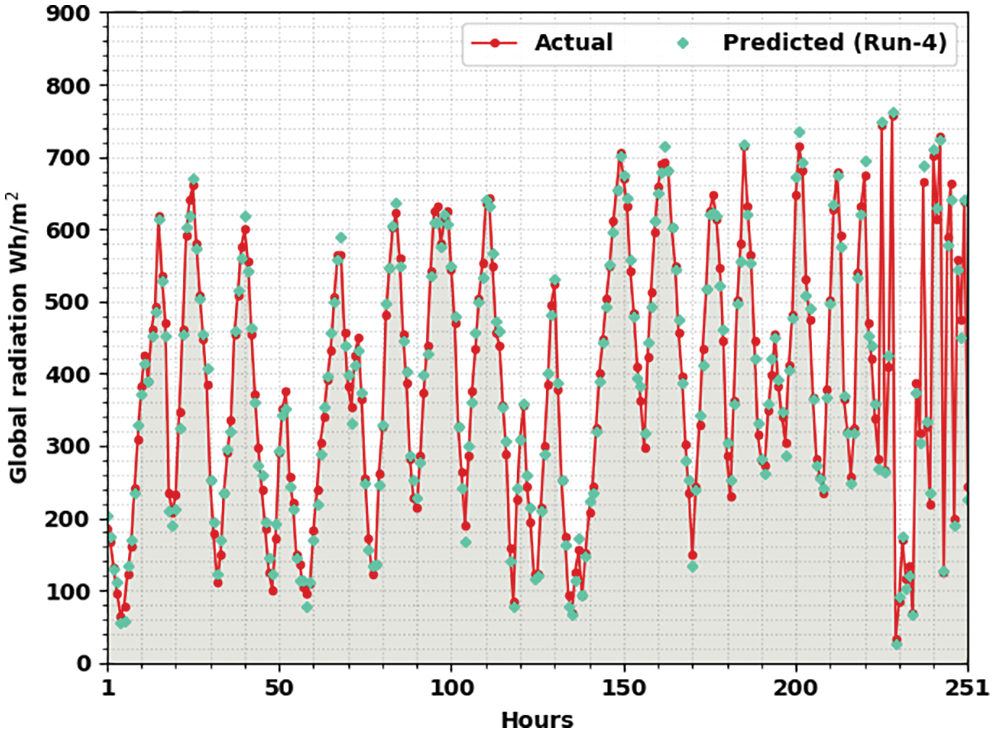
Figure 6: Actual vs. prediction analysis of OMBGRU-SRP system under Run4

Fig. 7 denotes the actual vs. prediction solar radiation forecasting outcomes of the OMBGRU-SRP method under run-5. The figure exhibited the OMBGRU-SRP approach has displayed enhanced forecasted results under all hours of operation. It is also noted that the difference between the actual and predictive solar radiation values will be minimum.

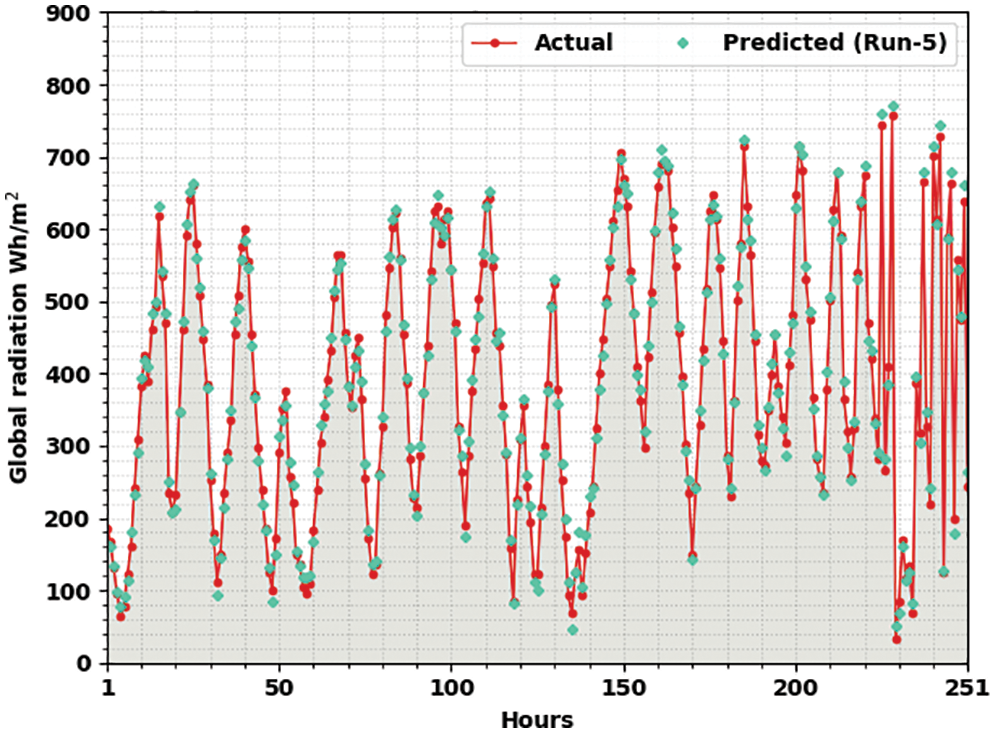
Figure 7: Actual vs. prediction analysis of OMBGRU-SRP system under Run5

Table 2 demonstrates the overall prediction results of the OMBGRU-SRP model with existing models.

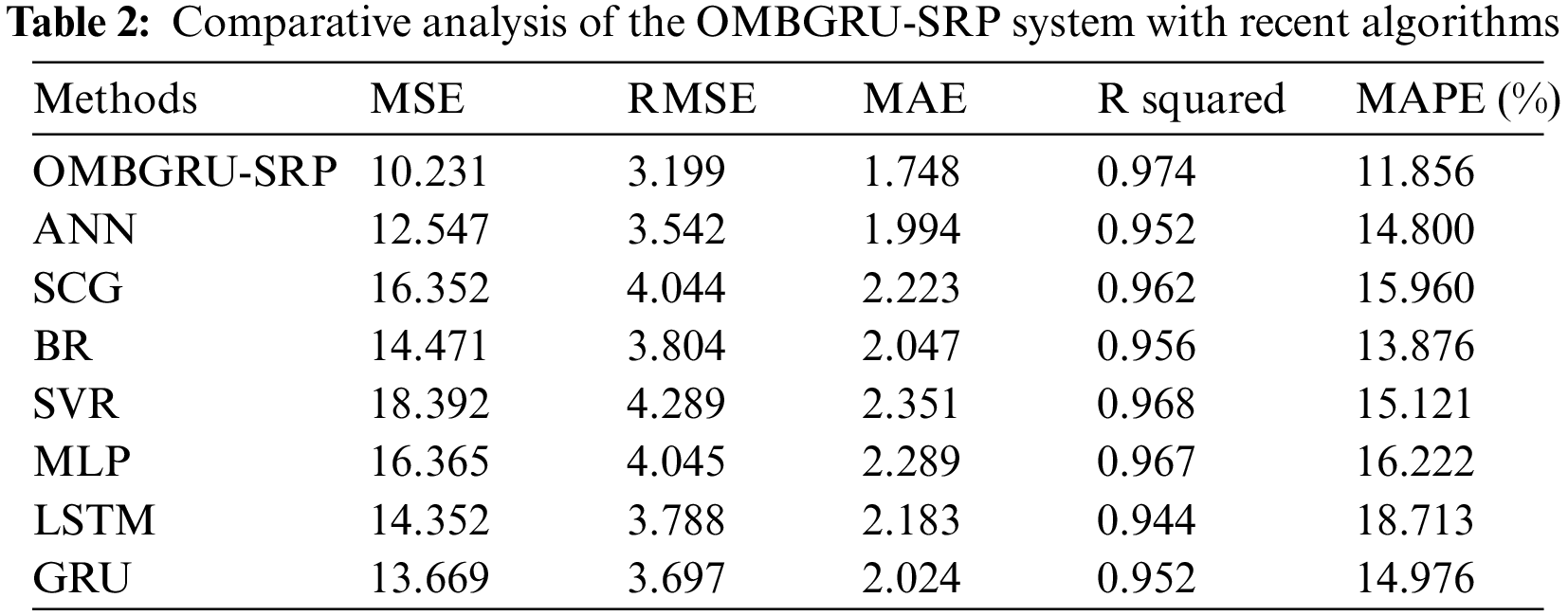
Fig. 8 reports a close MSE inspection of the OMBGRU-SRP model. The results denoted that the SVR model has reached an ineffectual MSE of 18.392 whereas the SCG and MLP models have reached closer MSE of 16.352 and 16.365 respectively. Along with that, the BR and LSTM models have resulted in reasonable MSE of 14.471 and 14.352. Although the ANN and GRU models have attained near optimal MSE of 12.547 and 13.669, the OMBGRU-SRP model has gained the least MSE of 10.231.

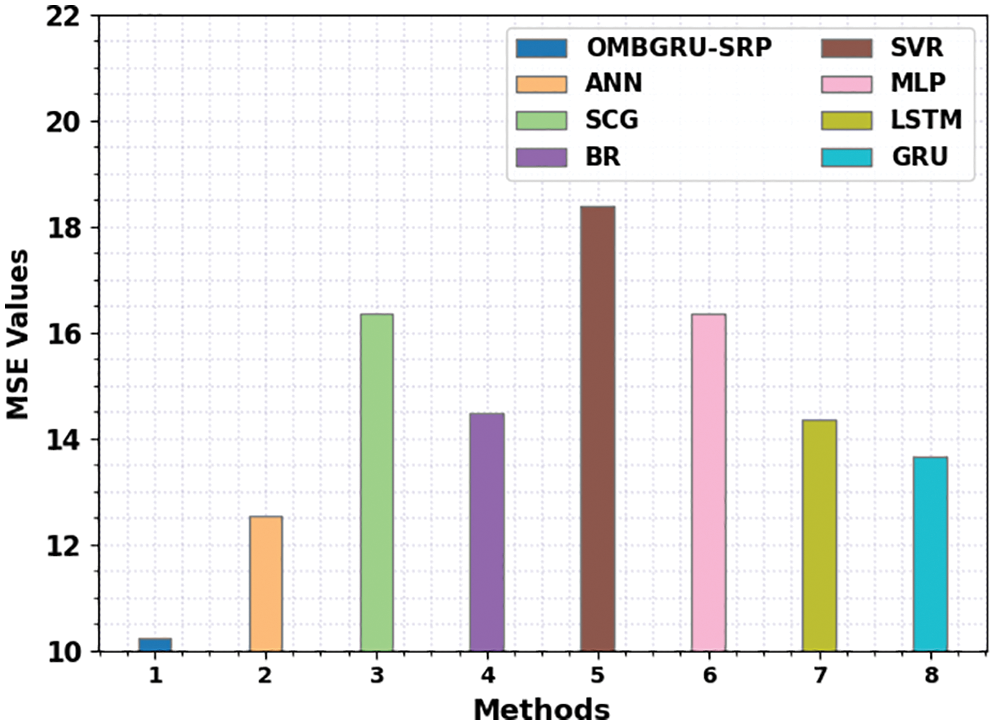
Figure 8: MSE analysis of OMBGRU-SRP system with recent algorithms

Fig. 9 reports a brief RMSE review of the OMBGRU-SRP method. The outcomes designated the SVR approach have attained an ineffectual RMSE of 4.289 whereas the SCG and MLP algorithms have reached closer RMSE of 4.044 and 4.045 correspondingly. Also, the BR and LSTM techniques have resulted in reasonable RMSE of 3.804 and 3.788. Although the ANN and GRU approaches have reached near optimal RMSE of 3.542 and 3.697, the OMBGRU-SRP method has attained the least RMSE of 3.199.

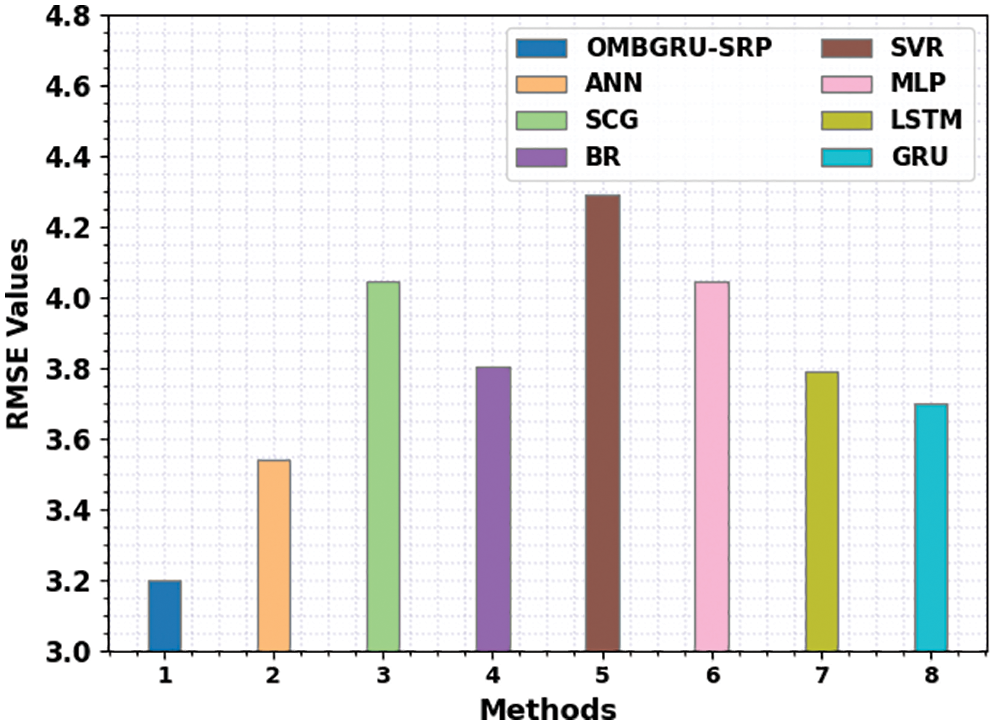
Figure 9: RMSE analysis of OMBGRU-SRP system with recent algorithms

Fig. 10 shows a detailed MAE review of the OMBGRU-SRP method. The outcomes denoted that the SVR algorithm has reached an ineffectual MAE of 2.351 whereas the SCG and MLP methodologies have reached closer MAE of 2.223 and 2.289 correspondingly. Also, the BR and LSTM techniques have resulted in reasonable MAE of 2.047 and 2.183. Although the ANN and GRU approaches have gained near optimal MAE of 1.994 and 2.024, the OMBGRU-SRP method has reached the least MAE of 1.748.

Figure 10: MAE analysis of OMBGRU-SRP system with recent algorithms

Fig. 11 portrays a brief MAPE review of the OMBGRU-SRP method. The results indicated that the LSTM algorithm had reached an ineffectual MAPE of 18.713%, whereas the SCG and MLP approaches have reached closer MAPE of 15.960% and 16.222%, respectively. Also, the SVR and GRU techniques have resulted in reasonable MAPE of 15.121% and 14.976%. Although the ANN and BR approaches have reached near optimal MAPE of 14.800% and 13.876%, the OMBGRU-SRP method has attained the least MAPE of 11.856%.

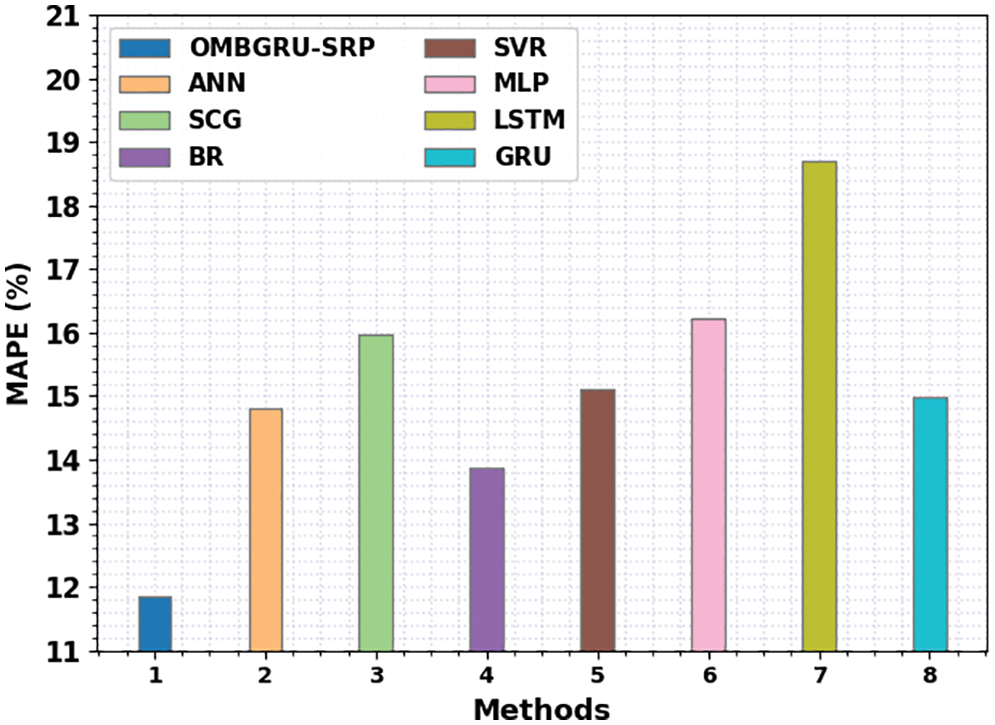
Figure 11: MAPE analysis of OMBGRU-SRP system with recent algorithms

Finally, a detailed R-squared examination of the OMBGRU-SRP model with recent models is given in Fig. 12. The results demonstrated that the OMBGRU-SRP model had shown effectual results with an increased R-squared value of 0.974. In contrast, the ANN SCG, BR, SVR, MLP, LSTM, and GRU models have reached reduced R-squared values. The detailed results affirm that the OMBGRU-SRP model has shown enhanced solar radiation prediction performance.

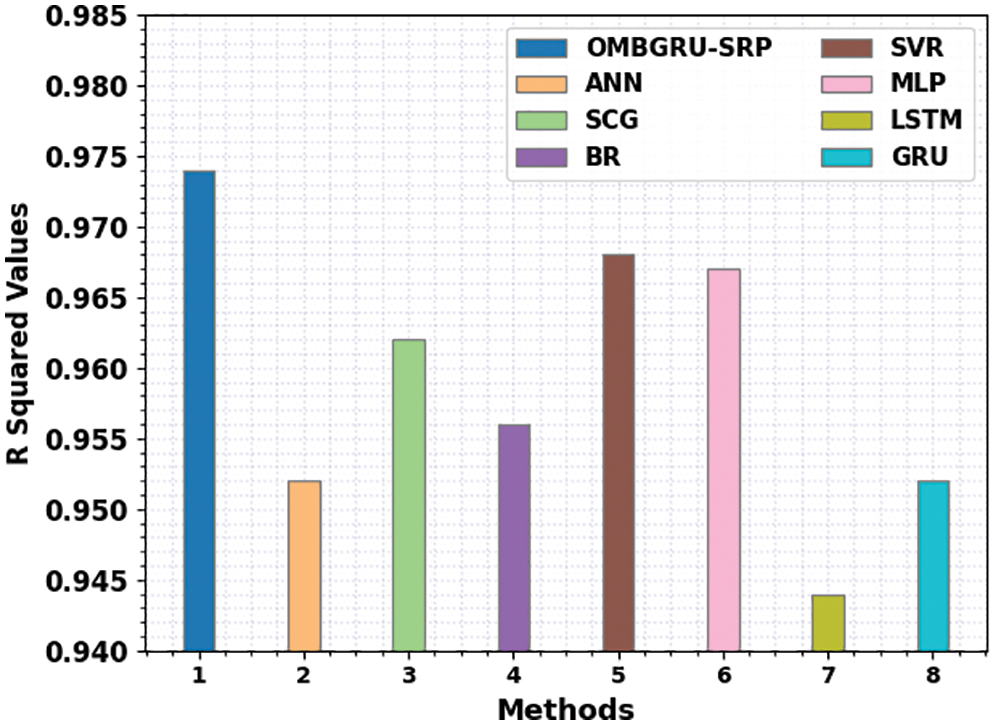
Figure 12: R squared analysis of OMBGRU-SRP system with recent algorithms

5  Conclusion

In this article, a new OMBGRU-SRP technique has been developed to forecast SR for energy management. The presented OMBGRU-SRP technique mainly aims to accomplish an accurate and time SR prediction process. Firstly, the presented OMBGRU-SRP technique performs data preprocessing to normalize the solar data. At the second level, the MBGRU model is derived using BGRU with an attention mechanism and skip connections. Finally, the hyperparameter tuning of the MBGRU model is carried out by using the SBO algorithm to attain maximum prediction with minimum error values. Many experiments were conducted to demonstrate the enhanced SR prediction performance. The experimental values highlighted the supremacy of the OMBGRU-SRP method over other existing models. Thus, the presented OMBGRU-SRP model can be employed for accurate SR forecasting. In future, hybrid DL models can be derived to extend the OMBGRU-SRP model for improved prediction outcomes.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. E. D. Obando, S. X. Carvajal and J. P. Agudelo, “Solar radiation prediction using machine learning techniques: A review,” IEEE Latin America Transactions, vol. 17, no. 4, pp. 684–697, 2019. [Google Scholar]

2. M. Aslam, J. M. Lee, H. S. Kim, S. J. Lee and S. Hong, “Deep learning models for long-term solar radiation forecasting considering microgrid installation: A comparative study,” Energies, vol. 13, no. 1, pp. 147, 2019. [Google Scholar]

3. S. Ghimire, R. C. Deo, N. Raj and J. Mi, “Deep learning neural networks trained with MODIS satellite-derived predictors for long-term global solar radiation prediction,” Energies, vol. 12, no. 12, pp. 2407, 2019. [Google Scholar]

4. M. Hou, T. Zhang, F. Weng, M. Ali, N. Al-Ansari et al., “Global solar radiation prediction using hybrid online sequential extreme learning machine model,” Energies, vol. 11, no. 12, pp. 3415, 2018. [Google Scholar]

5. S. Ghimire, R. C. Deo, H. Wang, M. S. Al-Musaylh, D. Casillas-Pérez et al., “Stacked LSTM sequence-to-sequence autoencoder with feature selection for daily solar radiation prediction: A review and new modeling results,” Energies, vol. 15, no. 3, pp. 1061, 2022. [Google Scholar]

6. Q. Zhang, X. Tian, P. Zhang, L. Hou, Z. Peng et al., “Solar radiation prediction model for the yellow river basin with deep learning,” Agronomy, vol. 12, no. 5, pp. 1081, 2022. [Google Scholar]

7. J. M. Han, E. S. Choi and A. Malkawi, “CoolVox: Advanced 3D convolutional neural network models for predicting solar radiation on building facades,” Building Simulation, vol. 15, no. 5, pp. 755–768, 2022. [Google Scholar]

8. H. Huang, S. S. Band, H. Karami, M. Ehteram, K. W. Chau et al., “Solar radiation prediction using improved soft computing models for semi-arid, slightly-arid and humid climates,” Alexandria Engineering Journal, vol. 61, no. 12, pp. 10631–10657, 2022. [Google Scholar]

9. O. A. Arqub and Z. Abo-Hammour, “Numerical solution of systems of second-order boundary value problems using continuous genetic algorithm,” Information Sciences, vol. 279, no. 6, pp. 396–415, 2014. [Google Scholar]

10. A. R. Hedar, M. Almaraashi, A. E. Abdel-Hakim and M. Abdulrahim, “Hybrid machine learning for solar radiation prediction in reduced feature spaces,” Energies, vol. 14, no. 23, pp. 7970, 2021. [Google Scholar]

11. K. N. Reddy, M. Thillaikarasi, B. S. Kumar and T. Suresh, “A novel elephant herd optimization model with a deep extreme learning machine for solar radiation prediction using weather forecasts,” The Journal of Supercomputing, vol. 78, no. 6, pp. 8560–8576, 2022. [Google Scholar]

12. M. Mukhtar, A. Oluwasanmi, N. Yimen, Z. Qinxiu, C. C. Ukwuoma et al., “Development and comparison of two novel hybrid neural network models for hourly solar radiation prediction,” Applied Sciences, vol. 12, no. 3, pp. 1435, 2022. [Google Scholar]

13. T. Zhu, Y. Li, Z. Li, Y. Guo and C. Ni, “Inter-hour forecast of solar radiation based on long short-term memory with attention mechanism and genetic algorithm,” Energies, vol. 15, no. 3, pp. 1062, 2022. [Google Scholar]

14. A. Rai, A. Shrivastava and K. C. Jana, “A CNN-BiLSTM based deep learning model for mid-term solar radiation prediction,” International Transactions on Electrical Energy Systems, vol. 31, no. 9, pp. e12664, 2021. [Google Scholar]

15. T. Zhu, Y. Guo, Z. Li and C. Wang, “Solar radiation prediction based on convolution neural network and long short-term memory,” Energies, vol. 14, no. 24, pp. 8498, 2021. [Google Scholar]

16. S. Ghimire, R. C. Deo, N. Raj and J. Mi, “Deep solar radiation forecasting with convolutional neural network and long short-term memory network algorithms,” Applied Energy, vol. 253, pp. 113541, 2019. [Google Scholar]

17. S. Y. Heng, W. M. Ridwan, P. Kumar, A. N. Ahmed, C. M. Fai et al., “Artificial neural network model with different backpropagation algorithms and meteorological data for solar radiation prediction,” Scientific Reports, vol. 12, no. 1, pp. 1–18, 2022. [Google Scholar]

18. J. Zhang, Y. Jiang, S. Wu, X. Li, H. Luo et al., “Prediction of remaining useful life based on bidirectional gated recurrent unit with temporal self-attention mechanism,” Reliability Engineering & System Safety, vol. 221, no. 4, pp. 108297, 2022. [Google Scholar]

19. A. M. Hemeida, O. M. Bakry, A. A. A. Mohamed and E. A. Mahmoud, “Genetic algorithms and satin bowerbird optimization for optimal allocation of distributed generators in radial system,” Applied Soft Computing, vol. 111, no. 5, pp. 107727, 2021. [Google Scholar]