 Open Access
Open Access
ARTICLE
A Novel Internet of Medical Thing Cryptosystem Based on Jigsaw Transformation and Ikeda Chaotic Map
1 Department of Computer Science, Najran University, Najran, 61441, Saudi Arabia
2 Department of Information Systems, Najran University, Najran, 61441, Saudi Arabia
3 Department of Electrical Engineering, Wah Engineering College, University of Wah, Wah Cantt, 47040, Pakistan
4 School of Computing, Edinburgh Napier University, Edinburgh, EH10 5DT, UK
* Corresponding Author: Mimonah Al Qathrady. Email:
Computer Systems Science and Engineering 2023, 46(3), 3017-3036. https://doi.org/10.32604/csse.2023.037281
Received 28 October 2022; Accepted 28 December 2022; Issue published 03 April 2023
Abstract
Image encryption has attracted much interest as a robust security solution for preventing unauthorized access to critical image data. Medical picture encryption is a crucial step in many cloud-based and healthcare applications. In this study, a strong cryptosystem based on a 2D chaotic map and Jigsaw transformation is presented for the encryption of medical photos in private Internet of Medical Things (IoMT) and cloud storage. A disorganized three-dimensional map is the foundation of the proposed cipher. The dispersion of pixel values and the permutation of their places in this map are accomplished using a nonlinear encoding process. The suggested cryptosystem enhances the security of the delivered medical images by performing many operations. To validate the efficiency of the recommended cryptosystem, various medical image kinds are used, each with its unique characteristics. Several measures are used to evaluate the proposed cryptosystem, which all support its robust security. The simulation results confirm the supplied cryptosystem’s secrecy. Furthermore, it provides strong robustness and suggested protection standards for cloud service applications, healthcare, and IoMT. It is seen that the proposed 3D chaotic cryptosystem obtains an average entropy of 7.9998, which is near its most excellent value of 8, and a typical NPCR value of 99.62%, which is also near its extreme value of 99.60%. Moreover, the recommended cryptosystem outperforms conventional security systems across the test assessment criteria.Keywords
Digital grayscale or color images are necessary data-carrying instruments. Images are used in various of critical applications such as biometric identification, online commerce, telemedicine, healthcare, military, and online banking. Concerns about the security of the storage and broadcast of medical images over public networks have grown in recent years. Organizations specializing in healthcare continue to publish mandatory requirements such as Picture Archiving and Communication Systems (PACS), Digital Imaging and Communications in Medicine (DICOM), and Health Insurance Portability and Accountability Act (HIPAA). Regarding medical image data storage, PACS is primarily meant to be used within the hospital network, which is typically secured by a firewall to keep out outsiders. Intruders, both accidental and evil, may have thousands of chances to tamper with private data if the conversation occurs on public networks. Public networks are rife with dangers to the security of medical image storage and transmission.
One of the leading security objectives is to ensure information confidentiality, considering the quickly expanding use of networks and multimedia capabilities. As they develop cutting-edge strategies to protect the privacy of image data both during storage and transmission, researchers continue to concentrate on image encryption. Image encryption differs from traditional text encryption because of images’ low entropy, high spatial correlation, and tremendous storage capacity [1]. Numerous cryptographic techniques have been proposed in the literature for attaining the goals of confusion and distribution. Chaotic maps have been used in cryptography to achieve both goals because of their predictability and high sensitivity to initial conditions. A few uses for chaotic maps in image encryption include histogram equalization, pixel scrambling, the generation of pseudorandom numbers, and the development of substitution boxes (S-boxes). Using techniques like steganography or even cryptography, which hides the message’s content from unauthorized readers, secret information is delivered. These techniques permit using text, audio, video, and picture for covert communication [2–5]. The image has grown in importance because of the development of the internet and digital multimedia capabilities.
Image data is far more significant and more spatially correlated than text data. Chaotic systems have been implemented in several image encryption techniques since they were first used, and their security capabilities were demonstrated. Non-linear, deterministic systems with properties that make them appropriate for image encryption are called chaotic maps. In other words, a chaotic system exhibits pseudorandom behavior and is susceptible to the beginning circumstances. This implies that a bit adjustment to the settings results in a different chaotic map output. Images sent or stored may be vulnerable to various security risks, including manipulation, eavesdropping, duplication, and noise. To make it easier to retrieve the original pixels during decryption, the scrambling technique must be reversible.
To achieve better encryption results, several methods integrate chaos theory with permutation algorithms. In [6], for instance, the authors suggest an encryption scheme with chaos that employs the Jigsaw procedure for the scrambling process. The method has three stages: pre-processing, encryption, and post-processing. In [7], an image-encryption technique with iterative cosine transform and the Jigsaw transform (JT) is described. To secure medical images, Hua et al. [8] first insert arbitrary data into the seed image and then use two steps of diffusion and pixel scrambling. The watermark is encrypted using the Jigsaw transform in a hybrid digital cryptosystem, which was presented in [9]. An input image was first permuted using a chaotic map, and then the watermark was embedded using the Discrete Cosine Transform (DCT). A selective chaos-based image encryption approach was proposed by Kanso et al. [10], which includes a scrambling phase using chaotic cat maps and a masking phase using the same block-based structure. Contrastingly, Wang et al. [11] proposed Langton’s ant (LA), cellular automata, to permute the image, where an entwining logistic map specified the phases and subsequent location of the ant. The researchers also concluded the process of image diffusion by employing a Piecewise Linear Chaotic Map (PWLCM). Chebyshev map and rotation equation was presented as pseudo-random bit generators in an image encryption scheme by Stoyanov et al. [12]. Aryal et al. [13] suggested a block-shuffling-based encryption model using block shuffling, positive-negative transformation, rotation, and color module permutation.
Furthermore, a histogram fluctuating technique was utilized as invertible data concealment. With an examination of the dynamic and the circuit of the chaotic map, Gao et al. [14] recommended an encryption approach based on multi-image fusion and fractional-order hyperchaotic systems. A method for image scrambling and diffusion was proposed by Wang et al. [15], which mixes 1D and 2D chaotic map systems to construct chaotic structures. The image is then scrambled using an L-shaped technique based on the block, observed by a diffusion period at the bit level. Both the scrambling and diffusion phases of Wang et al. dynamic encryption scheme [16] were presented. To achieve the dynamic behavior, the chaotic system’s pseudo-random number is tweaked after each iteration. A nested sine map in several dimensions forms the chaotic system. A Henon map-based image encryption approach using elliptic curve cryptography and dynamic substitution box confusion was reported by Ibrahim et al. in [17]. The image encryption approach developed by Laiphrakpam et al. [18] uses an elliptic curve and chaotic structure. It features four distinct phases: a chaotic diffusion stage, an S-box-based substitution stage, a Logistic map-based diffusion stage, and a block permutation stage. Arnold transforms (AT) were reported to be enhanced by Liang et al. [19] via a double permutation encryption technique depending on AT that alters both the location of pixels and their grey values. This approach is faster than the standard AT and just as helpful.
Mehta et al. [20] suggested a robust scheme for fundus images based on chaos theory utilizing a grouping of permutation and substitution design, which has applications in medical image cryptography, such as the encryption of fundus images. Using robust adaptive control, Javan et al. [21] developed a solution based on hyper-chaotic systems’ multi-mode synchronization to encrypt medical images. On the contrary, Moafimadani et al. [22] offered a technique based on chaotic maps to secure medical images from hacking. It employs a rapid shuffling procedure, observed by a diffusion that is both fast and flexible. Xue et al. introduced an image protection technique in [23] that uses the varying lengths of deoxyribonucleic acid chains. Row chain and column chain operations in DNA, dynamic coding in DNA, are all used to encrypt the image using this method. The approach was evaluated using three different types of medical images. Medical image encryption employing a genetic system variant and a coupled lattice map was published by Nematzadeh et al. in [24]. The cipher is enhanced by the connected lattice map, and the updated genetic algorithm speeds up convergence with a recent local search approach and a stop condition. An approach combining the Integer Wavelet Transform, DNA computing, and randomization was proposed by Ravichandran et al. [25]. The 1D logistic system coupled with pseudo-random numbers was used by Kumar et al. [26] in their presentation of a medical image encryption scheme. The authors examined how the logistic map’s parameters and beginning values affect its reshuffling and replacement operations. Natural as well as medical images, including those of the human brain, magnetic resonance imaging (MRI), and lungs, were used to validate the procedure. To improve upon many preexisting biometric encryption schemes, Carey et al. [27] offered a system for encrypting medical images using the user’s iris and fingerprint. These fingerprints and iris scans are hashed with the Indexing First One algorithm and then utilized as keys in an AES-CBC cipher with two rounds of encryption. The technique is also lossless, which is essential in a healthcare encryption system. For a strategy that is more stealthy, secure, and robust than prior approaches, Salama et al. [28] combined the Discrete Wavelet Transform’s wavelet-induced multi-resolution decomposition capacity with the energy compaction of the Discrete Cosine Transform. Banik et al. [29] presented a method for encrypting a series of medical photos using the elliptic curve analog ElGamal encryption scheme and the Mersenne Twister PRNG. This method decreases the time needed for encryption while also fixing ElGamal’s bloatware issue. After applying an optimized Arnold map on grey images over a predetermined number of iterations, Ge [30] introduced an encryption technique dubbed ALC encryption that uses Chebyshev and Logistic map cross-diffusion. This updated Arnold map is generic for images of any dimension. A cross-diffusion of a double chaotic map is used to encrypt color images. Using the Rossler dynamical system and the Sine map, Sangavi et al. [31] suggested a Medical Image Encryption scheme that does the usage of the chaotic nature of the data. It was stated by Chai et al. [32] that a medical image encryption strategy was developed using a hybrid of the Latin square and a chaotic system. An encryption method for protecting individual identities in medical images was published by Elamir et al. [33]. Data is concealed in the least significant bits of image pixels using the Least Significant Bit method. Afterward, the image is compressed using a key devised using DNA encoding rules and chaotic systems. Shafai et al. [34] proposed a medical image encryption-based algorithm. Wang et al. [35] discussed ridge regression predictor-based high precision error prediction algorithm for data hiding. Ma et al. [36] prosed a code division multiplexing-based reversible data hiding scheme. Some other schemes were proposed by various researchers over time [37–41]. There are numerous encryption algorithms in the literature based on different domains. We have selected the combination of jigsaw transformation and chaotic map to get the highly random private keys.
There exist many encryption structures for the security of image data in the literature. All the cryptosystems do not ensure the robustness of image data. There exists sensitive information in the images, such as the Internet of Medical Things (IoMT); which needs special protection. Numerous chaos-based encryption algorithms are vulnerable to some classical attacks. To make the encryption structure robust, we added the concept of plaintext-based key generation. The change of private key at each time of encryption makes the system perfect from a security point of view. Therefore, we have presented a cryptosystem to offer secrecy to cloud storage in IoMT. As compared to the other complex chaotic structures, the 2D chaotic map yields highly random and unpredictable numbers with low computation costs. Therefore we have selected the combination of a 2D Ikeda map and a jigsaw puzzle to achieve low computational cost. The key contributions of this work are as follows:
1. It offers excellent performance as compared to the traditional cryptosystems
2. To provide a robust communication system using a 2D chaotic map and Jigsaw transformation.
3. To offer security on the Internet of Medical Things (IoMT) by providing services in cloud storage.
4. To get maximum security with minimal computational complexity.
5. Its efficacy is examined in several forms of differential assaults, and positive results are found.
The numerical results are compared with the state of the art to assure the standard security achievement.
The remaining manuscript is ordered as follows: Section 2 offerings some fundamental aspects of the encryption algorithm; Section 3 gives the structure of the anticipated cryptosystem; The simulation outcomes are shown in Second 4; The performance analyses are depicted in Section 5; A contrast with published work is performed in Section 6; Lastly, a conclusion is presented in the last section.
The illustration of an IoMT-based health cloud is shown in Fig. 1.
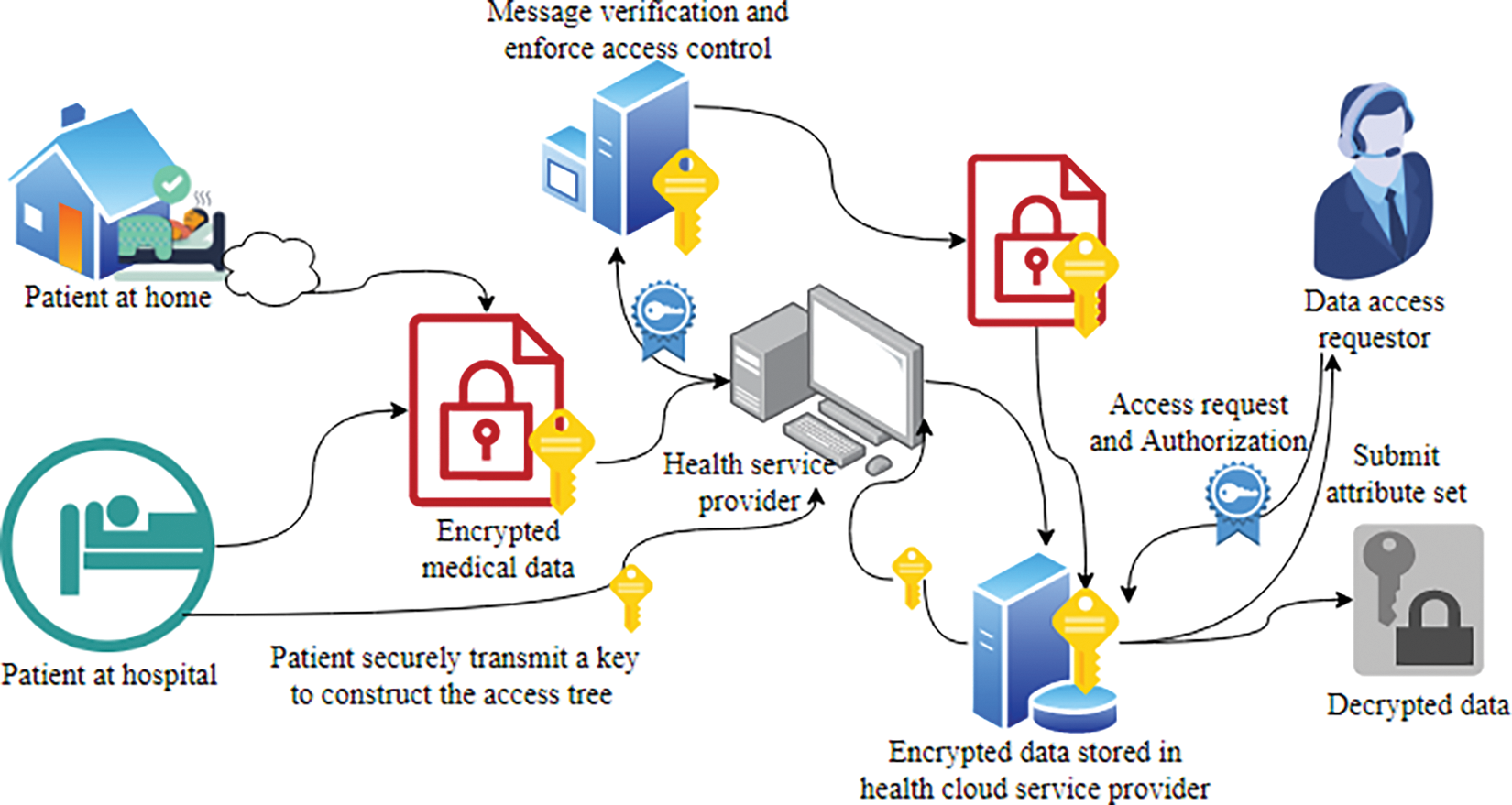
Figure 1: Secure data transmission at Health Cloud
A nonlinear operator
Consider
A sample implementation of Jigsaw transformation on the Skull X-ray image is depicted in Fig. 2.
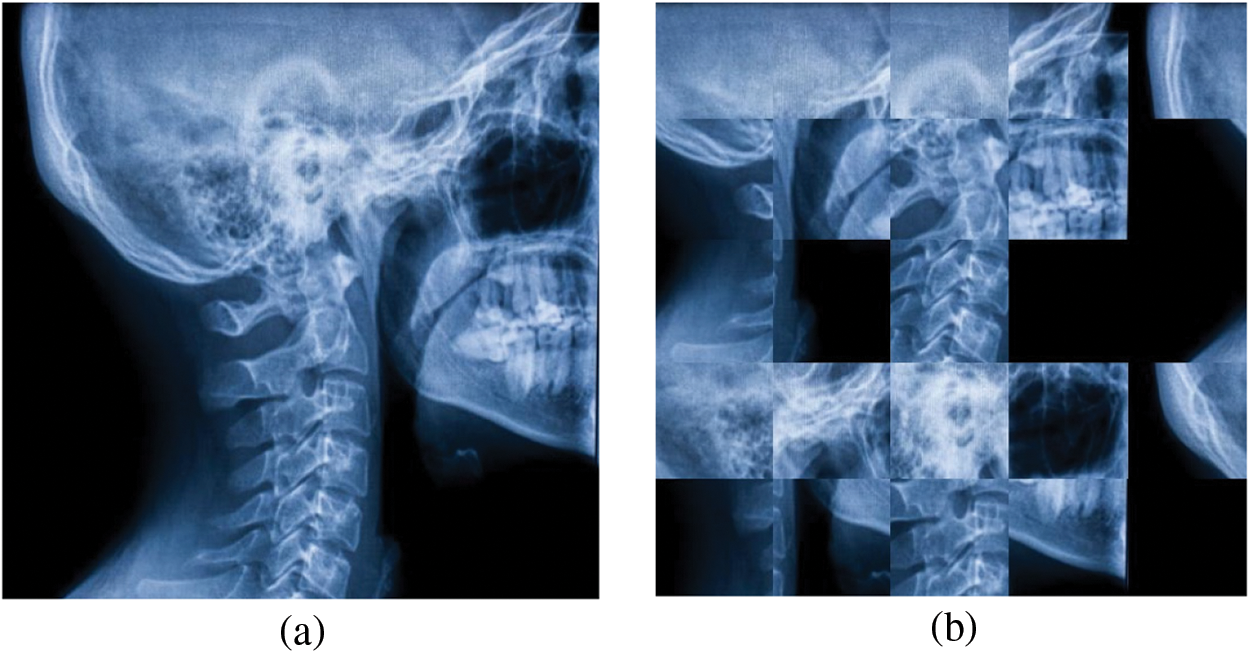
Figure 2: A sample implementation of Jigsaw transformation on Skull X-ray image
Kensuke Ikeda suggested the initial map as a model of light moving about a nonlinear optical cavity resonator. The 2D Ikeda map can be defined as:
where
The system shows chaotic behavior with
The point trajectories for the Ikeda map with 10000 iterations by variating the parameter
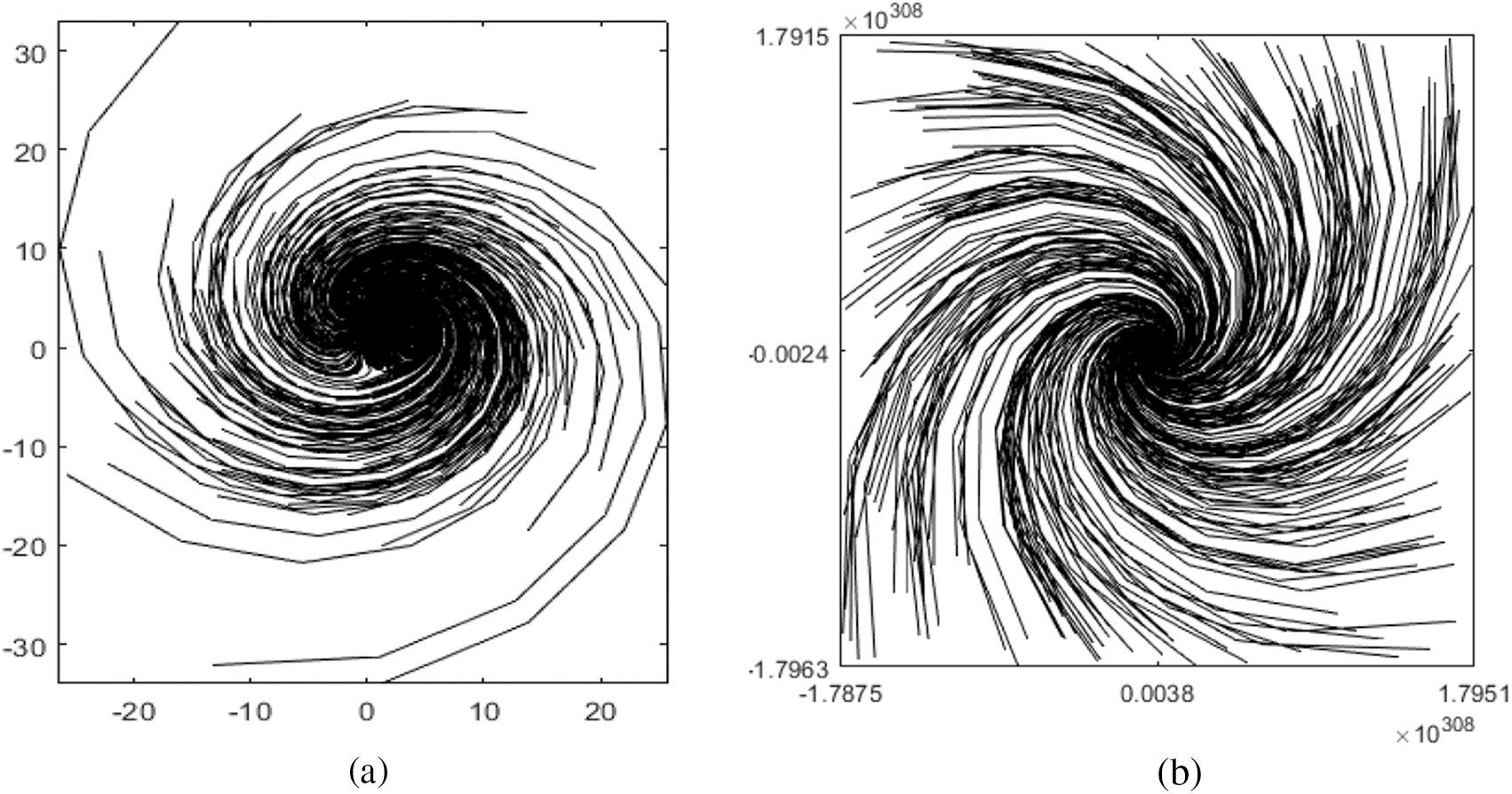
Figure 3: Point trajectories for (a)
3 Proposed Medical Image Cryptosystem
The maximum security in a cryptosystem is provided by the part of key generation. The unpredictability of the secret key of encryption algorithms makes it secure against all statistical and differential attacks. The simplest way to achieve randomness in the secret key is the dependency of key generation on the plaintext. The complete encryption with just a single pixel change in the plaintext gives rise to a robust structure. Therefore, we have utilized a formula for the parameters and initial conditions generation of the Ikeda chaotic map. As chaotic systems are highly sensitive to their initial conditions and chaotic parameters, a slight modification in the initial values causes an entirely distinct sequence of numerous iterations. The parameters for the chaotic map can be generated by:
where
3.2 Proposed Encryption Algorithm
The encryption structure involves the Ikeda map and Jigsaw transformation as primitives of the algorithm. The pseudo algorithm of the proposed algorithm is shown in Table 1. The working strides of the encryption scheme are as follows:

Step 1: Insert a plain medical image with dimensions
Step 2: Insert the original image in the key generation algorithm to construct the key parameters for the Ikeda chaotic map.
Step 3: The constructed initial conditions and parameter values are seeded in the Ikeda map and the chaotic sequences are stored for the encryption steps.
Step 4: The original image is initially permuted using the Jigsaw transformation with setting each block size
Step 5: The permuted image is then diffused with the Ikeda map
Step 6: The matrix data gained from step 5 is then shuffled row-wise and column-wise by implementing the
Step 7: The data attained from step 6 is again passed from the Jigsaw transformation to get the resultant matrix data.
Step 8: The final resultant is compiled as the enciphered image.
The flowchart diagram of the proposed medical image cryptosystem is shown in Fig. 4.
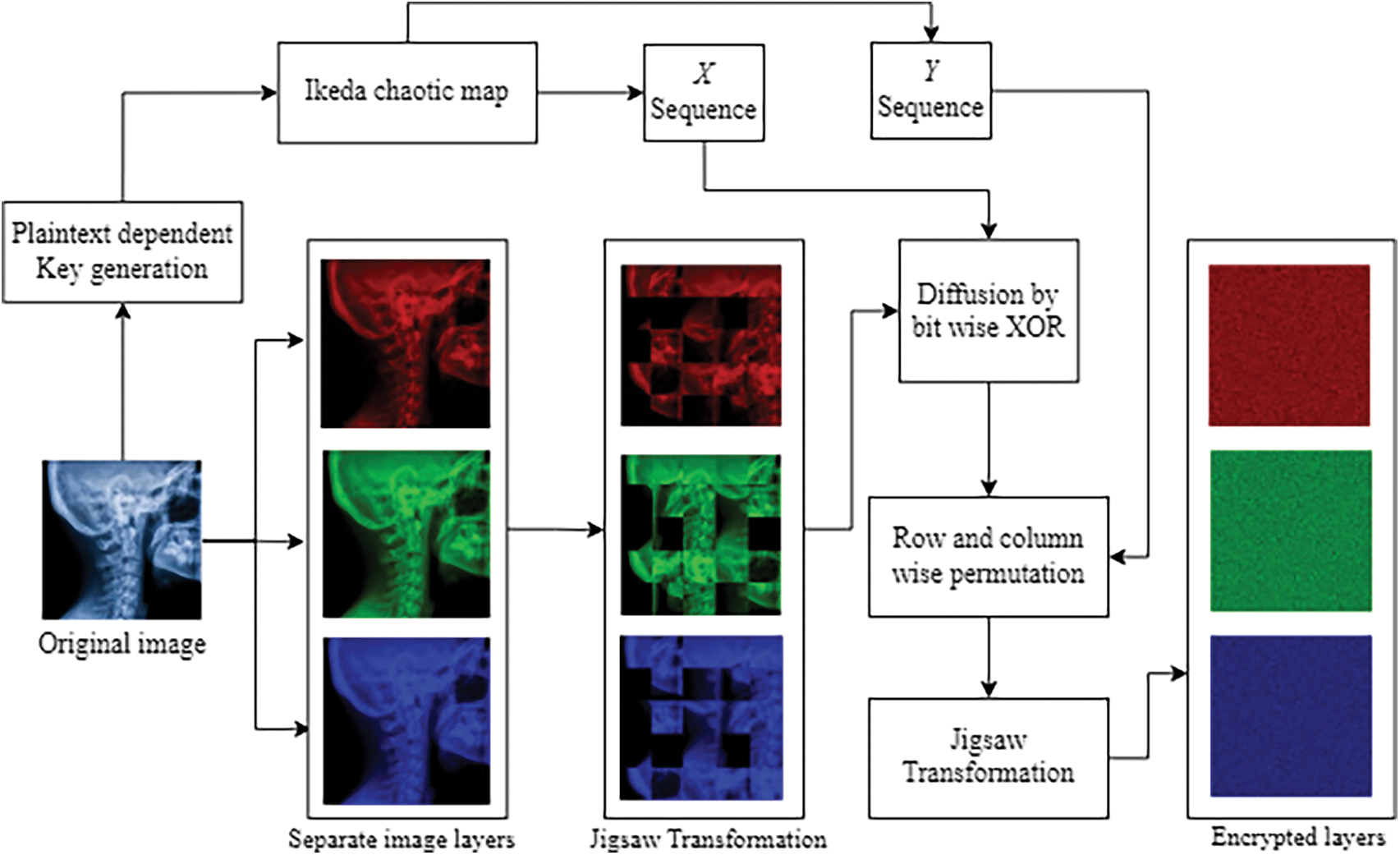
Figure 4: Flowchart of the proposed medical image cryptosystem
This section details the simulations that were carried out using Matlab 2020a on a 64-bit machine running Microsoft Windows 10 with an Intel(R) Core (TM) i3-3120M CPU running at 2.50 GHz and 8.00 GHZ RAM. The experimental images of the simulation outcomes incorporate abdominal Xray, Chest Xray, elbow Xray, hand Xray, knee Xray, and skull Xray with dimensions
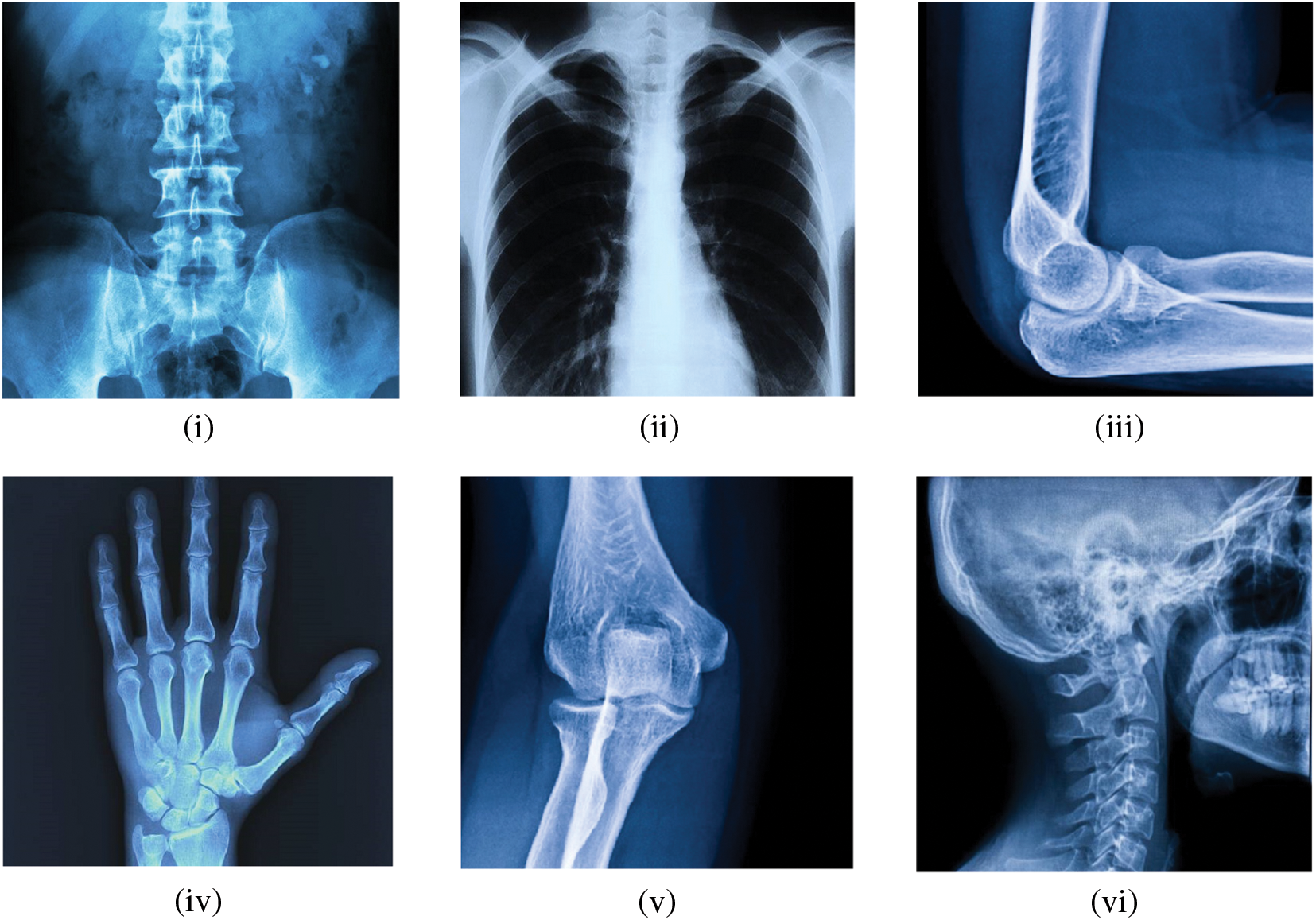
Figure 5: Experimental Xray images (i) Image 1; (ii) Image 2; (iii) Image 3; (iv) Image 4; (v) Image 5; (vi) Image 6
5 Security Performance Analyses
To check the efficiency of the proposed cryptosystem, we have performed some security analyses such as NIST, histogram, correlation coefficient, statistical histogram deviation, statistical irregular deviation, information entropy, differential attack, and key sensitivity analysis.
The National Institute of Standards and Technology (NIST) test is used for the encrypted data to examine the pseudo-randomness in the suggested method. The encrypted is tested using the NIST-800-22 technique, which contains 15 separate tests, in this study. All derived p-values must be higher than the predetermined significance level of 0.01 to qualify as a satisfactory pseudo-randomness sequence. Table 2 is a list of the NIST test results. As we can see, all the p-values are higher than 0.01, indicating that the hyperchaotic system passes all 15 of the NIST tests. As a result, the sequence employed in the suggested method behaves in a very unpredictable manner.
The dispersal of pixels in the plain and enciphered images serves as the histogram’s representation. It could reveal the spreading characteristics of the image pixel values by reflecting the frequency with which each grey level occurs. A standard image’s histogram typically has an uneven distribution, but an encrypted image using a robust encryption method will have a histogram that is as uniform as feasible. The histogram of the original images and their respective encrypted images are displayed in Fig. 6. Fig. 6 shows the histograms of the plain images (a–d) and the cipher images (e–h).
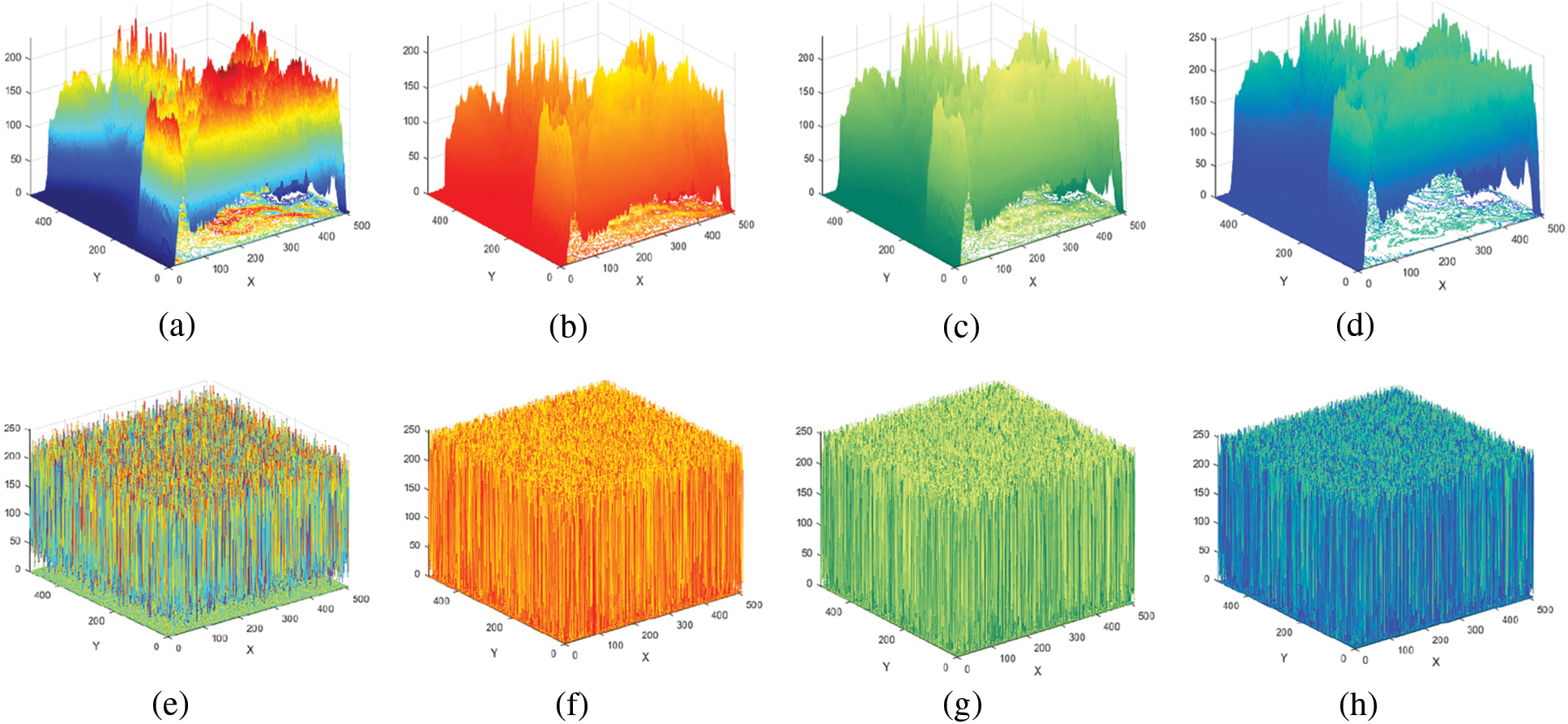
Figure 6: 3D histograms for Image 6 (a–d) Original layers; (e–h) Encrypted layers
Since the histograms of enciphered images vary from those of original images and the amount of every pixel value in the enciphered image is nearly equivalent, enciphered images cannot provide any statistical data about the plain image by examining their histograms. The suggested technique may, therefore, statistically evaluate assaults.
The correlation coefficient can be used to assess the unpredictability of ciphers produced by the offered cryptosystem. Each pair of contiguous pixels in the plain image have a robust association with one another. This association must be destroyed within the ciphered image by an effective cryptosystem. The diagonal, vertical, and horizontal correlations for the analyzed images are portrayed in Fig. 7.
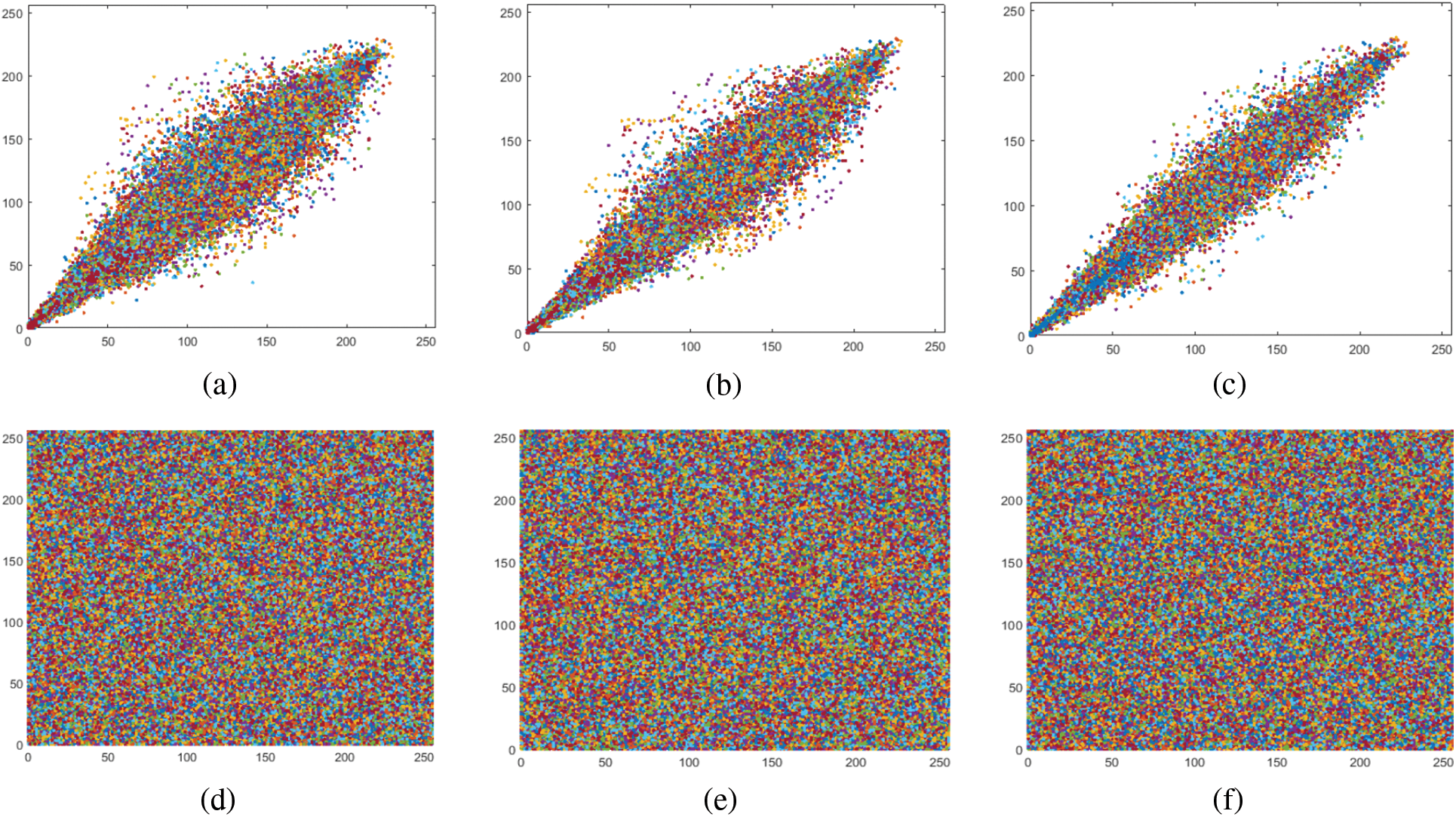
Figure 7: Correlation diagram for Image 1 (a–c) Original diagonal, horizontal, and vertical direction; (d–f) Encrypted diagonal, horizontal, and vertical direction, respectively
Using Eq. (7), the values of the correlation coefficients
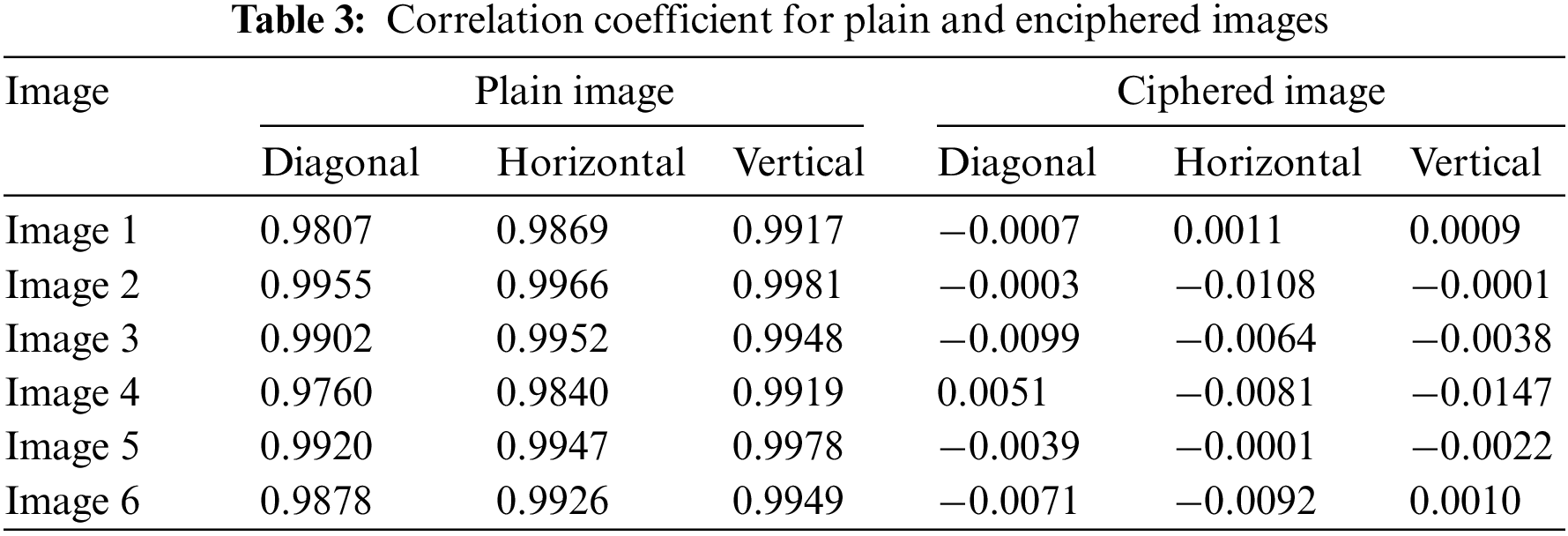
where
• The
• The
The results show a strong connection among contiguous pixels in the original experimental images, as expected. To put it another way, a low correlation coefficient value between the surrounding pixels of the evaluated cipher images shows that our suggested cryptosystem is quite efficient.
5.4 Statistical Histogram Deviation (
The histogram deviation, which represents the difference among the ciphered and plain images, may be used to assess ciphering quality. The value of the histogram deviation is calculated by (11).
where
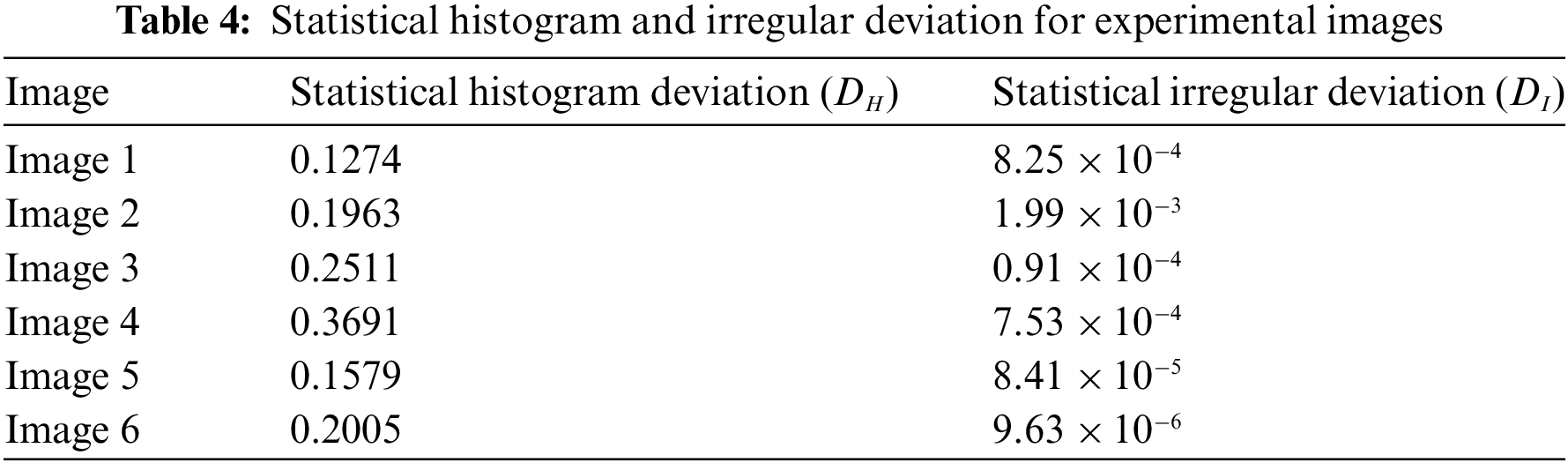
5.5 Statistical Irregular Deviation (
The irregular deviation, which reflects the value of the indiscretion of the eccentricity coming from the enciphering procedure, may be used to evaluate the ciphering quality. The value of irregular deviation is determined by (12).
where
The smallest value of statistical irregular deviation indicates the excellent quality of the cipher. The results of
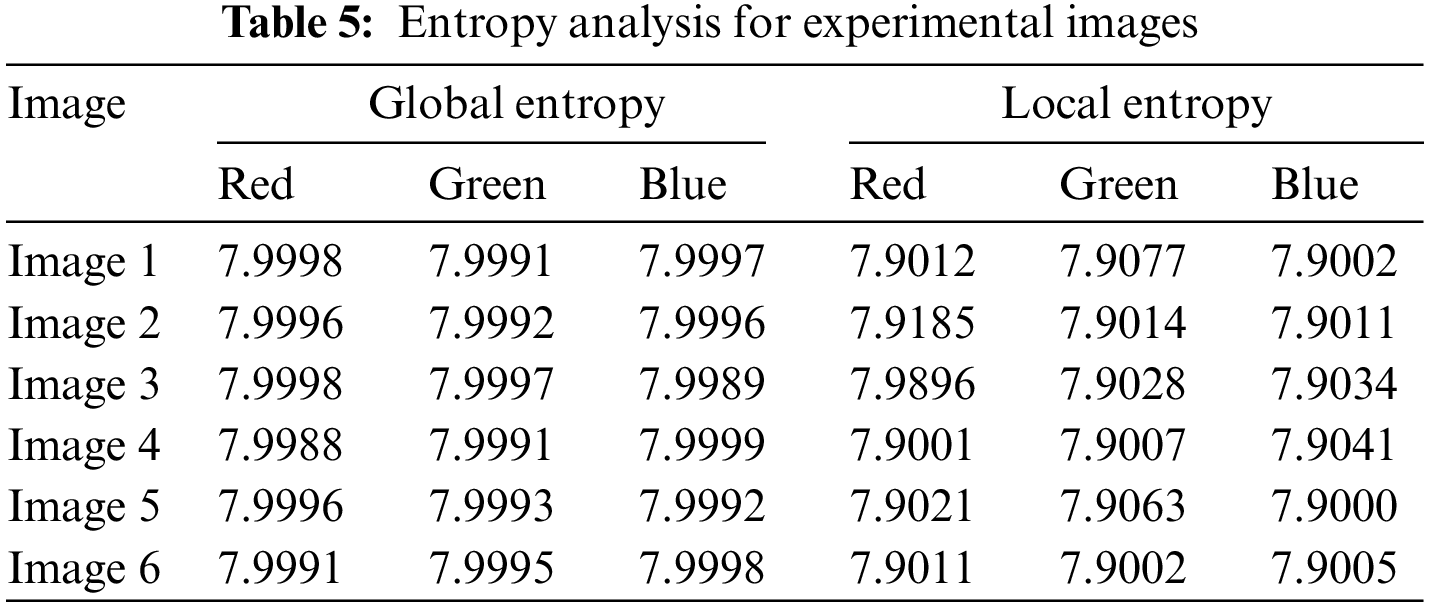
Shannon identified entropy as a crucial feature that expresses the uncertainty and irregularity of a data source 1949. Eq. (14) describes the entropy
The results of global and local entropy for encrypted medical images are depicted in Table 5. The ciphered results of global entropy are near the ideal value of 8 and local entropy also lies within the acceptance rate which indicates a lower risk of attacks related to entropy.
5.7 Differential Attack Analysis
The number of pixel change rates (NPCR), which refers to the proportion of various pixel numbers among two enciphered contents, is applied to quantify the unlikeness among two encrypted images. The number of averaged changing intensities among two enciphered images is counted using the Unified Average Changing Intensity (UACI). For 8-bit coded images, the idyllic NPCR and UACI values are 99.61 percent and 33.46 percent, correspondingly. The NPCR and UACI are specified as follows:
where
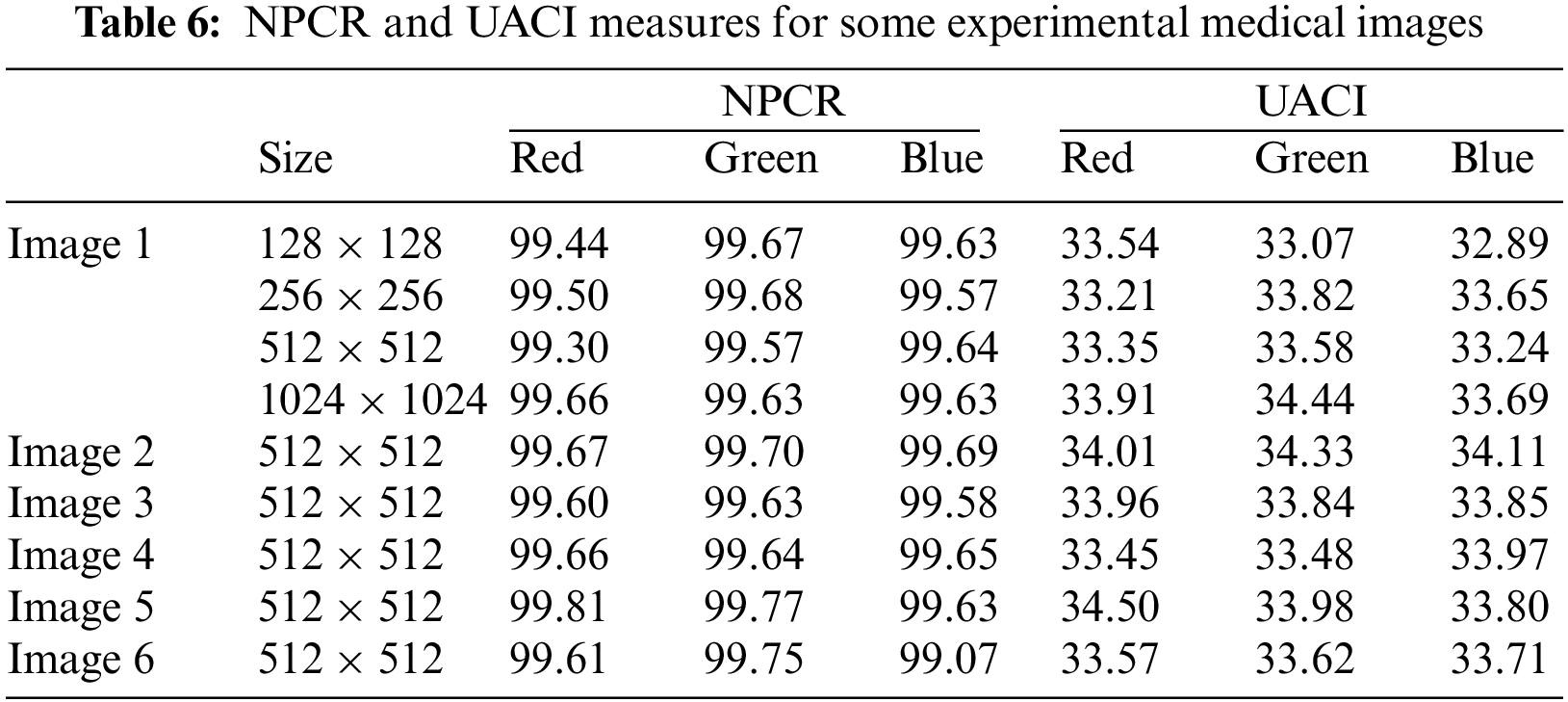
Table 6 shows that the suggested algorithm’s NPCR and UACI are also near standard values, at 99.6% and 33.5%, respectively.
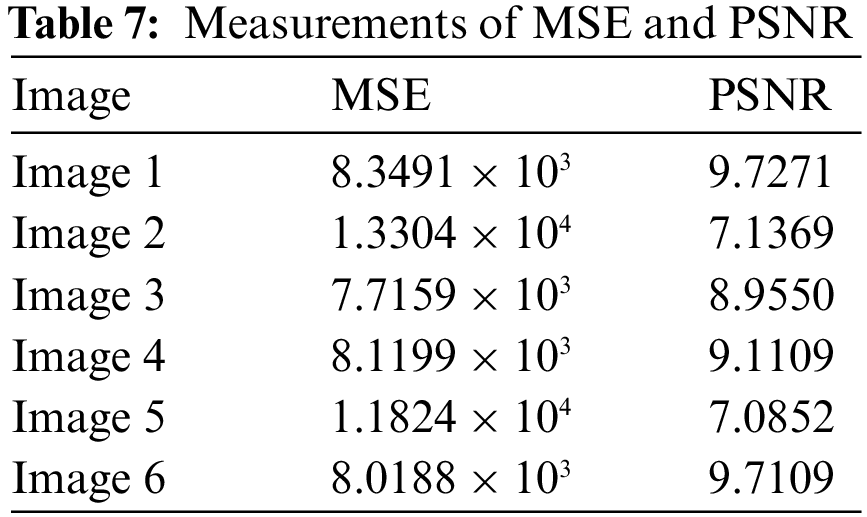
Mean-Square-Error (MSE) and Peak Signal-to-Noise Ratio (PSNR) are used to evaluate the efficiency of the decryption process. Typically, the PSNR of an encrypted image will be lower. Grayscale values for pixels in the
The low PSNR values in Table 7 demonstrate the difficulties in recovering the plain image from the cipher image without knowing the secret key.
5.9 Key Sensitivity and Space Analysis
Any data encryption structure’s effectiveness and toughness be contingent on the private keys that are used, which are regarded as the main elements of the ciphering technique. The wide keyspace and high sensitivity of the encryption technique to key variations are the two most crucial characteristics of the secret keys. The keyspace is controlled by the key size. It is preferable to have a private key that is as big as possible so that it is challenging for an attacker to guess. The key sensitivity shows that even if the attacker can obtain the private key with just one bit of change, the plain image will continue to be unexpected. Therefore, even with little differences in the secret key, a trustworthy and robust image ciphering approach must be susceptible to modest changes in the decoding key. If an image encryption method has a secret key that is larger than

Figure 8: (a–c) Images retrieved through the wrong key; (d) Image retrieved by the correct key
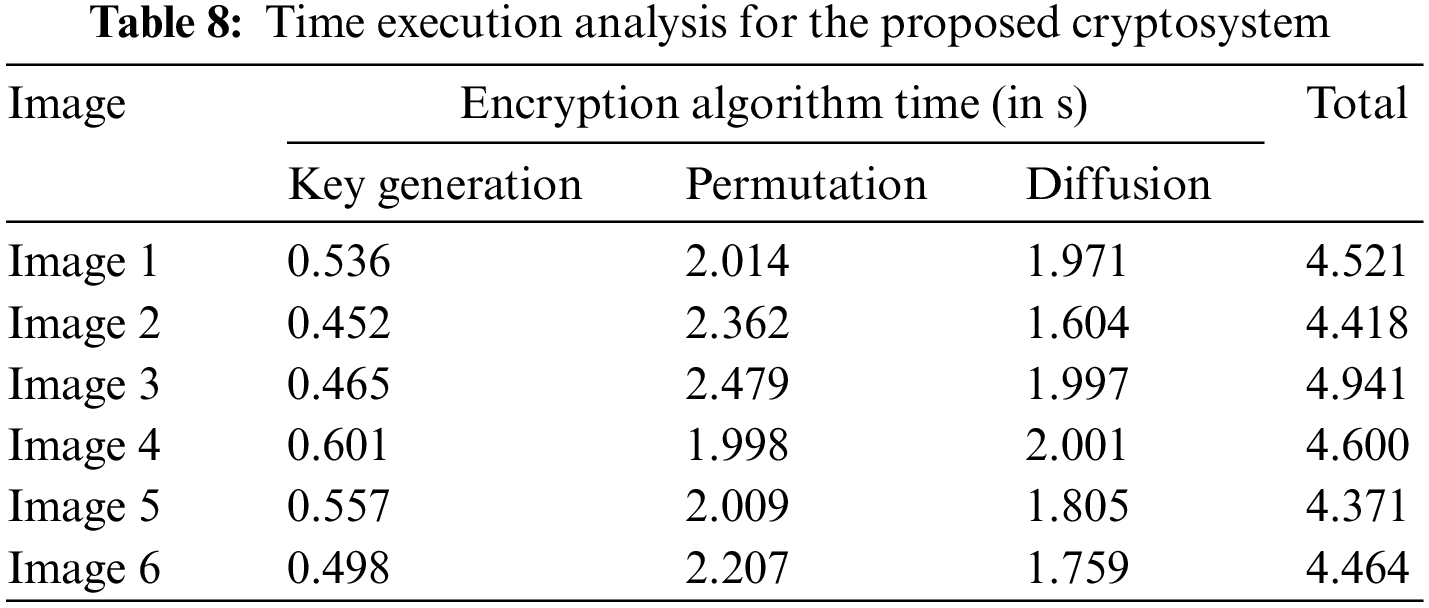
The algorithm’s performance concerning time reveals the reliability of the cryptosystem. Many algorithms offer high security with complex encryption structures but require a lot of time for execution which results in an increment in cost and time waste. Therefore, to examine the efficacy of the encryption algorithm, the time execution analysis plays a vital role in making it a reliable source of communication tool. The time execution analysis (in seconds) for the proposed cryptosystem is shown in Table 8. The results depict that the suggested cryptosystem offers higher security with reliable execution time.
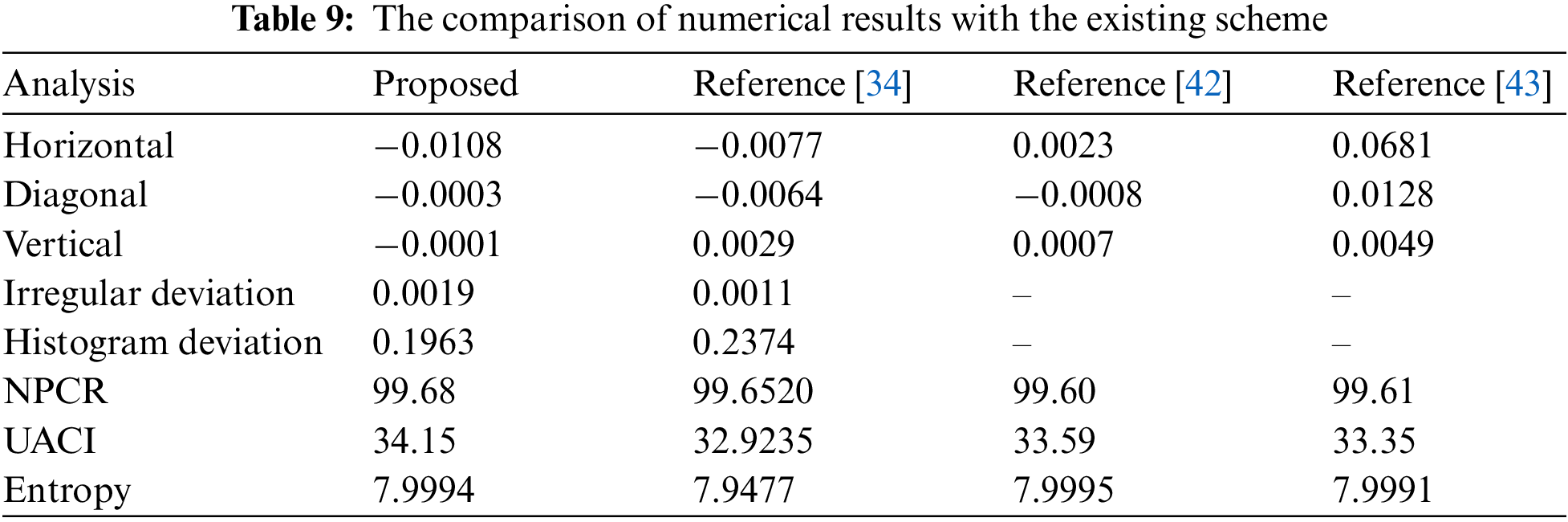
This section of the manuscript provides a brief comparison of the numerical statical analyses obtained from the proposed cryptosystem. The results of the correlation coefficient, entropy, statistical irregular deviation, statistical histogram deviation, NPCR, and UACI are compared with an already existing medical encryption scheme. The numerical results of “Image 2” are utilized for comparison with References [34,42,43]. The comparative results are shown in Table 9. The comparison of correlation shows that our proposed cryptosystem meets the standard results as the results in References [34,42,43]. The values of irregular deviation and irregular histogram are also up to the mark. The NPCR and UACI of our proposed algorithm are better than the scheme in References [34,42,43]. The entropy of the cipher produced by our cryptosystem is near the standard value which is 8. Other the other hand, the entropy of the exiting scheme is less. Therefore, we can say that our proposed structure meets the analysis criteria as compared to the existing work, which indicates the robustness of the algorithm.
In this work, Jigsaw transformation and Ikeda chaotic map-based medical image cryptosystem were proposed. It depends on a combination of value diffusion and position permutation algorithms. The results of the experiments performed on various medical images show that the offered cryptosystem is both robust against differential assaults and highly sensitive to initial conditions. It offers a high level of protection with little computational overhead. The entropy results also show how practical the proposed cryptosystem is. The comparative study performed in Table 8 also depicts that the algorithm meets the existing standards. As a result, the proposed 2D chaotic cryptosystem can be suggested for essential and sensitive IoMT applications in healthcare and telemedicine. To enhance the security performance of medical picture broadcasts and develop a multi-level security system for these images, we will combine additional security methods including steganography and watermarking in our subsequent study. Further study could investigate testing the anticipated 2D chaotic map cryptosystem with the NIST benchmark, using the proposed hybrid security techniques on large databases of color medical images, and suggesting a robust medical image encryption method based on DNA encoding in addition to chaos encryption.
Acknowledgement: The authors are thankful to the Deanship of Scientific Research at Najran University for funding this work under the Research Collaboration Funding program grant code (NU/RC/SERC/11/5).
Funding Statement: The authors are thankful to the Deanship of Scientific Research at Najran University for funding this work under the Research Groups Funding program grant code (NU/RC/SERC/11/5).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Q. Zhou, K. W. Wong, X. Liao, T. Xiang and Y. Hu, “Parallel image encryption algorithm based on discretized chaotic map,” Chaos Solitons Fractals, vol. 38, no. 4, pp. 1081–1092, 2008. [Google Scholar]
2. H. Gao, Y. Zhang, S. Liang and D. Li, “A new chaotic algorithm for image encryption,” Chaos Solitons Fractals, vol. 29, no. 2, pp. 393–399, 2006. [Google Scholar]
3. L. Xiong, Z. Xu and Y. Q. Shi, “An integer wavelet transform based scheme for reversible data hiding in encrypted images,” Multidimensional Systems and Signal Processing, vol. 29, no. 3, pp. 1191–1202, 2018. [Google Scholar]
4. R. Punidha and M. Sivaram, “Integer wavelet transform based approach for high robustness of audio signal transmission,” International Journal of Pure and Applied Mathematics, vol. 116, no. 23, pp. 295–304, 2017. [Google Scholar]
5. R. Huang, K. H. Rhee and S. Uchida, “A parallel image encryption method based on compressive sensing,” Multimedia Tools Application, vol. 72, no. 1, pp. 71–93, 2014. [Google Scholar]
6. Z. Li, C. Peng, W. Tan and L. Li, “An effective chaos-based image encryption scheme using imitating jigsaw method,” Complexity, vol. 2021, no. 11, pp. 1–18, 2021. [Google Scholar]
7. O. Vilardy, J. L. M. Barba and C. O. Torres, “Image encryption and decryption systems using the jigsaw transform and the iterative finite field cosine transform,” Photonics, vol. 6, no. 4, pp. 121, 2019. [Google Scholar]
8. Z. Hua, S. Yi and Y. Zhou, “Medical image encryption using high-speed scrambling and pixel adaptive diffusion,” Signal Processing, vol. 144, no. 1, pp. 134–144, 2018. [Google Scholar]
9. M. Arora and M. Khurana, “Secure image encryption technique based on jigsaw transform and chaotic scrambling using digital image watermarking,” Optical and Quantum Electronics, vol. 52, no. 59, pp. 13, 2020. [Google Scholar]
10. A. Kanso and M. Ghebleh, “An efficient and robust image encryption scheme for medical applications,” Communications in Nonlinear Science and Numerical Simulation, vol. 24, no. 1–3, pp. 98–116, 2015. [Google Scholar]
11. X. Wang and D. Xu, “A novel image encryption scheme using chaos and Langton’s Ant cellular automaton,” Nonlinear Dynamics, vol. 79, no. 4, pp. 2449–2456, 2015. [Google Scholar]
12. B. Stoyanov and K. Kordov, “Image encryption using Chebyshev map and rotation equation,” Entropy, vol. 17, no. 4, pp. 2117–2139, 2015. [Google Scholar]
13. A. Aryal, S. Imaizumi, T. Horiuchi and H. Kiya, “Integrated model of image protection techniques,” Journal of Imaging, vol. 4, no. 1, 2018. [Google Scholar]
14. X. Gao, J. Yu, S. Banerjee, H. Yan and J. Mou, “A new image encryption scheme based on fractional-order hyperchaotic system and multiple image fusion,” International Journal of Scientific Reports, vol. 11, 2021. [Google Scholar]
15. X. Wang and Y. Chen, “A new chaotic image encryption algorithm based on L-shaped method of dynamic block,” Sensing and Imaging, vol. 22, no. 1, pp. 503, 2021. [Google Scholar]
16. X. Wang and M. Zhang, “An image encryption algorithm based on new chaos and diffusion values of a truth table,” Journal of Information Science, vol. 579, no. 4, pp. 128–149, 2021. [Google Scholar]
17. S. Ibrahim and A. Alharbi, “Efficient image encryption scheme using Henon map, dynamic s-boxes and elliptic curve cryptography,” IEEE Access, vol. 8, pp. 194289–194302, 2021. [Google Scholar]
18. D. Laiphrakpam and M. Khumanthem, “A robust image encryption scheme based on chaotic system and elliptic curve over finite field,” Multimedia Tools Applications, vol. 77, no. 7, pp. 8629–8652, 2018. [Google Scholar]
19. R. Liang, Y. Qin, C. Zhang, J. Lai, M. Liu et al., “An improved Arnold image scrambling algorithm,” in IOP Conf. Series: Materials Science and Engineering, Bristol, UK, IOP Publishing, vol. 677, 2019. [Google Scholar]
20. G. Mehta, M. Dutta and P. Kim, “An efficient and lossless cryptosystem for security in tele-ophthalmology applications using chaotic theory,” International Journal of E-Health and Medical Communications, vol. 7, pp. 28–47, 2016. [Google Scholar]
21. A. A. K. Javan, M. Jafari, A. Shoeibi, A. Zare, M. Khodatars et al., “Medical images encryption based on adaptive-robust multi-mode synchronization of chen hyper-chaotic systems,” Sensors, vol. 21, no. 11, pp. 3925, 2021. [Google Scholar] [PubMed]
22. S. S. Moafimadani, Y. Chen and C. Tang, “A new algorithm for medical color images encryption using chaotic systems,” Entropy, vol. 21, no. 6, pp. 577, 2019. [Google Scholar] [PubMed]
23. X. Xue, H. Jin, D. Zhou and C. Zhou, “Medical image protection algorithm based on deoxyribonucleic acid chain of dynamic length,” Frontiers in Genetics, vol. 12, no. 266, pp. 1021, 2021. [Google Scholar]
24. H. Nematzadeh, R. Enayatifar, H. Motameni, F. G. Guimarães and V. N. Coelho, “Medical image encryption using a hybrid model of modified genetic algorithm and coupled map lattices,” Optics and Lasers in Engineering, vol. 110, pp. 24–32, 2018. [Google Scholar]
25. D. Ravichandran, S. A. Banu, B. Murthy, V. Balasubramanian, S. Fathima et al., “An efficient medical image encryption using hybrid DNA computing and chaos in transform domain,” Medical and Biological Engineering and Computing, vol. 59, no. 589, pp. 589–605, 2021. [Google Scholar] [PubMed]
26. M. Kumar and P. Gupta, “A new medical image encryption algorithm based on the 1D logistic map associated with pseudo-random numbers,” Multimedia Tools and Applications, vol. 80, no. 12, pp. 18941–18967, 2021. [Google Scholar]
27. A. Carey and J. Zhan, “A cancelable multi-modal biometric based encryption scheme for medical images,” in Proc. of the 2020 IEEE Int. Conf. on Big Data (Big Data), Atlanta, GA, USA, pp. 3711–3720, 2020. [Google Scholar]
28. A. Salama, M. Mokhtar, M. Tayel, E. Eldesouky and A. Ali, “A triple-channel encrypted hybrid fusion technique to improve security of medical images,” Computers, Materials & Continua, vol. 68, no. 1, pp. 431–446, 2021. [Google Scholar]
29. A. Banik, Z. Shamsi and D. Laiphrakpam, “An encryption scheme for securing multiple medical images,” Journal of Information Security and Applications, vol. 49, no. 4, pp. 102398, 2019. [Google Scholar]
30. J. Ge, “ALCencryption: A secure and efficient algorithm for medical image encryption,” Computer Modeling in Engineering and Sciences, vol. 125, no. 3, pp. 1083–1100, 2020. [Google Scholar]
31. V. Sangavi and P. Thangavel, “An exotic multi-dimensional conceptualization for medical image encryption exerting Rossler system and Sine map,” Journal of Information Security and Applications, vol. 55, no. 8, pp. 102626, 2020. [Google Scholar]
32. X. Chai, J. Zhang, Z. Gan and Y. Zhang, “Medical image encryption algorithm based on Latin square and memristive chaotic system,” Multimedia Tools and Applications, vol. 78, no. 24, pp. 35419–35453, 2019. [Google Scholar]
33. M. Elamir, W. Al-atabany and M. Mabrouk, “Hybrid image encryption scheme for secure E-health systems,” Network Modeling Analysis in Health Informatics and Bioinformatics, vol. 10, no. 1, pp. 1727, 2021. [Google Scholar]
34. W. E. Shafai, F. Khallaf, E. S. M. El-Rabaie and F. E. A. E. Samie, “Proposed 3D chaos-based medical image cryptosystem for secure cloud-IoMT eHealth communication services,” Journal of Ambient Intelligence and Humanized Computing, 2022. [Google Scholar]
35. X. Wang, X. Wang, B. Ma, Q. Li and Y. Q. Shi, “High precision error prediction algorithm based on ridge regression predictor for reversible data hiding,” IEEE Signal Processing Letters, vol. 28, pp. 1125–1129, 2021. [Google Scholar]
36. B. Ma and Y. Q. Shi, “A reversible data hiding scheme based on code division multiplexing,” IEEE Transactions on Information Forensics and Security, vol. 11, no. 9, pp. 1914–1927, 2016. [Google Scholar]
37. W. Xingyuan, G. Suo, Y. Xiaolin, Z. Shuang and W. Mingxu, “A new image encryption algorithm with cantor diagonal scrambling based on the PUMCML system,” International Journal of Bifurcation and Chaos, vol. 31, no. 1, pp. 2150003, 2021. [Google Scholar]
38. X. Wang and S. Gao, “A chaotic image encryption algorithm based on a counting system and the semi-tensor product,” Multimedia Tools and Applications, vol. 80, no. 7, pp. 10301–10322, 2021. [Google Scholar]
39. X. Wang, S. Gao, L. Yu, Y. Sun and H. Sun, “Chaotic image encryption algorithm based on bit-combination scrambling in decimal system and dynamic diffusion,” IEEE Access, vol. 7, pp. 103662–103677, 2019. [Google Scholar]
40. S. Gao, R. Wu, X. Wang, J. Wang, Q. Li et al., “A 3D model encryption scheme based on a cascaded chaotic system,” Signal Processing, vol. 202, no. 1, pp. 108745, 2022. [Google Scholar]
41. R. Wu, S. Gao, X. Wang, S. Liu, Q. Li et al., “AEA-NCS: An audio encryption algorithm based on a nested chaotic system,” Chaos Solitons & Fractals, vol. 165, no. 1, pp. 112770, 2022. [Google Scholar]
42. F. Masood, M. Driss, W. Boulila, J. Ahmad, S. U. Rehman et al., “A lightweight chaos-based medical image encryption scheme using random shuffling and XOR operations,” Wireless Personal Communications, vol. 127, no. 2, pp. 1405–1432, 2022. [Google Scholar]
43. R. Rhouma, S. Meherzi and S. Belghith, “Ocml-based colour image encryption,” Chaos Solitons & Fractals, vol. 40, no. 1, pp. 309–318, 2009. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools