 Open Access
Open Access
ARTICLE
Heap Based Optimization with Deep Quantum Neural Network Based Decision Making on Smart Healthcare Applications
1 Department of Computer Science, Faculty of Computing and Information Technology, King Abdulaziz University, Jeddah, 21589, Saudi Arabia
2 Information Technology Department, Faculty of Computing and Information Technology, King Abdulaziz University, Jeddah, 21589, Saudi Arabia
* Corresponding Author: Mahmoud Ragab. Email:
Computer Systems Science and Engineering 2023, 46(3), 3749-3765. https://doi.org/10.32604/csse.2023.036796
Received 12 October 2022; Accepted 02 February 2023; Issue published 03 April 2023
Abstract
The concept of smart healthcare has seen a gradual increase with the expansion of information technology. Smart healthcare will use a new generation of information technologies, like artificial intelligence, the Internet of Things (IoT), cloud computing, and big data, to transform the conventional medical system in an all-around way, making healthcare highly effective, more personalized, and more convenient. This work designs a new Heap Based Optimization with Deep Quantum Neural Network (HBO-DQNN) model for decision-making in smart healthcare applications. The presented HBO-DQNN model majorly focuses on identifying and classifying healthcare data. In the presented HBO-DQNN model, three stages of operations were performed. Data normalization is applied to pre-process the input data at the initial stage. Next, the HBO algorithm is used in the second stage to choose an optimal set of features from the healthcare data. At last, the DQNN model is exploited for healthcare data classification. A series of experiments were carried out to portray the promising classifier results of the HBO-DQNN model. The extensive comparative study reported the improvements of the HBO-DQNN method over other existing models with maximum accuracy of 97.05% and 95.72% under the colon cancer and lymphoma dataset.Keywords
Smart Health can be referred to as a field that grows as a subsection of Electronic Health (e-Health) and smart cities [1]. Smart cities are defined as “cities strongly originated on information and communication technology that invest in social and human capital for enhancing the standard of life of people by efficient mobility participatory governance, sustainability and wise management of resources, at the same time they guarantee the security and privacy of the people. "e-Health is defined as “an evolving domain in the incorporation of public health business and medical informatics, denoting to health services and data enhanced or delivered via the Internet and related technology [2]. Broadly, the term symbolizes not just a technical expansion but also an attitude, a state of mind, a commitment to networked and a way of thinking, and global thinking, for the improvement of health care globally, locally, and regionally by utilizing information and communication technology [3]. As a result, computational medicine seems to be an innovative subject. Depending on computer technology and large biomedical data, computational medicine was a disciplinary subject merging mathematics, medicine, biology, computer science, and many more [4]. It employs the technique of artificial intelligence (AI) to perceptively comprehend the principle and physiological system of human illnesses through analyses in big data. It offers valuable data and direction for disease estimation, medical services, and clinical diagnosis [5–9].
Considering the pharmaceutical sector, conventionally, novel drug research will suffer from a high failure rate, long periods, and substantial investment [10]. Conversely, the research related to computing medicine could complete the preclinical drug research and expansion in approximately 1 to 2 years, with low resource consumption and a high success rate denoting that the domain of medicinal health was progressively entering the time of digitization and intelligence. But biomedical data can be sparse, high-dimension, loud, and messy, making it tough to extract the rich data behind such data efficiently [11]. Then, a suitable technique was required to process great totals of bio-medical data to gain effectual data. In machine learning (ML), DL is an optimistic gem in artificial intelligence (AI). As a division of ML, it was shown that DL was a potential technique and exceeded conventional ML in areas like speech recognition, CV, and NLP [12]. The main step of the ML technique, termed feature engineering, was to utilize domain insincerely and expert knowledge to distil attributes from data and examine the attributes by ML techniques (like SVM, RF, and so on). In the period of big data, the physical abstraction was biased and insufficient such that it could not accomplish a high-performance method for particular errands [13]. Dissimilar to conventional ML methods, DL spares the physical need to derive features, enhancing resource and time efficacy. DL was applied by a neural network (NN) containing neurons. Every layer of NNs has more neurons, and the output of the upper layer was taken as input for the successive layer [14]. The NN will transform the actual input to the output through the link among layers and the non-linear processing approach.
This study designs a new Heap Based Optimization with Deep Quantum Neural Network (HBO-DQNN) model for decision-making in smart healthcare applications. The presented HBO-DQNN model majorly focuses on identifying and classifying healthcare data. In the presented HBO-DQNN model, three stages of operations were performed. Data normalization is applied to pre-process the input data at the initial stage. Next, the HBO algorithm is used in the second stage to choose an optimal set of features from the healthcare data. At last, the DQNN model is employed for healthcare data classification. A series of experiments were carried out to portray the promising classifier results of the HBO-DQNN model.
Praveen et al. [15] introduce an innovative Oppositional GSO (OGSO) method related to clustering with DNNs termed the OGSO-DNN technique for distributed healthcare mechanisms. The OGSO technique has been implemented in this paper for choosing the Cluster Head (CH) from presented IoT gadgets. The chosen CH sends data to the cloud server, which then accomplishes DNN-related classification procedures for medical diagnosis. In [16], the capsule network was implemented for ECG signal categorization in this study. Depending on the original network structure, 1D convolutional neural network (CNN) and LSTM network were included as a parallel feature extracting layer for extracting the spatial and temporal attributes of ECG signal. Moreover, the improvised routing technique was modelled, employing the prior probability of sub-capsules as a weighting factor for routing method categorization to weaken the effect of noise capsules.
In [17], dynamic and interoperable communication frameworks (DICFs) to regulate the functions of wearable medical gadgets were presented. The structure was accountable for monitoring, decision-making, and controlling the functionality and functioning period of the wearable sensor (WS) as a portion of smart healthcare trailing applications. In this structure, the nature of the wireless sensing gadgets and their basic attributes were accountable for devising a fully operative and continuous functioning of the sensing gadgets. Hoang et al. [18] devise a new technique utilizing a novel segmentation method and wide-ShuffleNet for classifying skin lesions. Firstly, the author computes the entropy-related weighting and first-order cumulative moment (EW-FCM) of the skin image. To separate the lesions from the background, such values were employed. After that, the author input the segmentation outcome into a novel DL framework wide-ShuffleNet and determined the type of skin lesion.
Mohapatra et al. [19] devise a smart healthcare system to detect numerous gastrointestinal (GI) abnormalities by utilizing time-frequency studies and CNNs. The initial stage of the work includes an image pre-processing stage, then extracting approximate DWT coefficients. Every class of decomposed images can be later given as input to certain concerned CNN techniques to train and test in 2 distinct classifier levels for recognizing its estimated value. In [20], a wearable sensor-related mechanism was modelled for activity estimation utilizing RNN on an edge device (i.e., laptop or personal computer). The input data of the mechanism can be gained from many wearable healthcare sensors like ECG, gyroscope sensors, magnetometers, and accelerometers. In [21], skin data will be accumulated through dedicated hardware. The gathered samples will be uploaded to the cloud for more processing utilizing a new multimodal data fusion structure, which executes skin lesion segmentation after classification. A hybrid structure was modelled, which uses the complementary strengths of 2 CNN structures for generating the segmented images for lesion segmentation.
This study designed a new HBO-DQNN method for decision-making in smart healthcare applications. The presented HBO-DQNN method primarily concentrates on detecting and classifying healthcare data. In the presented HBO-DQNN model, three stages of operations were performed, as elaborated below. Fig. 1 represents the block diagram of the HBO-DQNN system.

Figure 1: Block diagram of HBO-DQNN system
Normalization has distinct meanings in statistics, the simple utility of which was to regularize variables or data. It can be a technique that presents data in a similar field when they are not [22]. Otherwise, a data miner can face circumstances where the data properties add values in various domains or ranges. Large-value features will have a higher impact on cost function than low-value features. In building a metamodel from data, earlier model training starts. Information was divided into equivalent values normalized to values among one and zero scales to minimize the effect of the total scale and have nearly every input in the same range. The min-max method was a popular and simple normalizing technique in medicinal imaging. Through the assumption of attribute X, such it has a mapping from the dataset among
3.2 Feature Selection Using HBO Algorithm
In this stage, the HBO algorithm selects an optimal feature set from the healthcare data. Askari et al. [23] recommended a new MH called HBO based on the job description titles and employee responsibilities. The corporate rank hierarchy (CRH) was considered the common basis used in the corporation. The HBO depends on the 4 main phases; 1) employee self-contribution, 2) interaction between colleagues, 3) communication with the immediate boss, and 4) CRH. The mathematical modelling of HBO phases is listed as follows.
CRH: It can be modelled through the heap data structure. Here, searching agent fitness is defined using the index of the search agent, and key nodes in the population can be implemented by node value in a heap.
Communication with immediate boss: usually, the upper level in the central organizational structure is in charge of imposing restrictions and strategies; subordinates (children) will follow the immediate boss (parental node). To model these behaviours, the position of all search agents
In Eq. (2), the existing iteration can be characterized as r, the
From the expression, the parameter
Now, C and T correspondingly symbolize variable and
Communication among colleagues: In HBO, colleagues were agents, and the positions of all the agents are given below.
From the expression, the objective function (f) aims to estimate the fitness of the search agents. If
Employee’s self-contribution: now, the self-contribution is executed by storing the preceding employee’s location as;
A roulette wheel can be applied to separate the population into
A common methodology to upgrade the searching agent location is as follows;
Now, p in
Whereas error rate refers to the classification error rate employing particular features. The error rate has been calculated as the percentage of incorrect classifiers (by DQNN technique) to the count of classifiers made, written as a value betwixt zero and one. (ErrorRate was the complement of classifier accuracy),
3.3 Healthcare Data Classification
Finally, the DQNN model is exploited for healthcare data classification. The quantum network comprises many quantum perceptrons [25]. Every perceptron parallels the arbitrary unitary operator having n output rubies and
The quantum network comprises the input layer (input density matrix), L hidden layer (the unitary operator), and an output layer
Whereas the trace is taken over each layer except the output layer,

Figure 2: Architecture of QNN
The symbol
Consequently, the net positive is formulated by the composition of 0 & a series of completely positive transition maps
Whereas the transition map over layer l can be equivalent to
And the trace being taken over layer
Here, t denotes a specific sample of the trained set (time later at time
Afterwards the training iteration, the cost function differs as
Whereas
is the density matrix for layer
And (P) indicates the adjoint channel of the wholly positive map (
The training model is defined. Firstly, a first unitary operator is randomly selected. Then, the density matrices are recursively evaluated for each layer and training pair. Then, the variable matrixes
where
This section examines the performance of the HBO-DQNN method on two datasets, namely colon cancer and Lymphoma datasets. Table 1 represents the details of two datasets.

Table 2 and Fig. 3 illustrate the overall classification outcomes of the HBO-DQNN technique on the Colon Cancer Dataset. The outcomes inferred that the HBO-DQNN method had reached effectual outcomes under all aspects. For example, on 80% of the TR database, the HBO-DQNN model has obtained an average
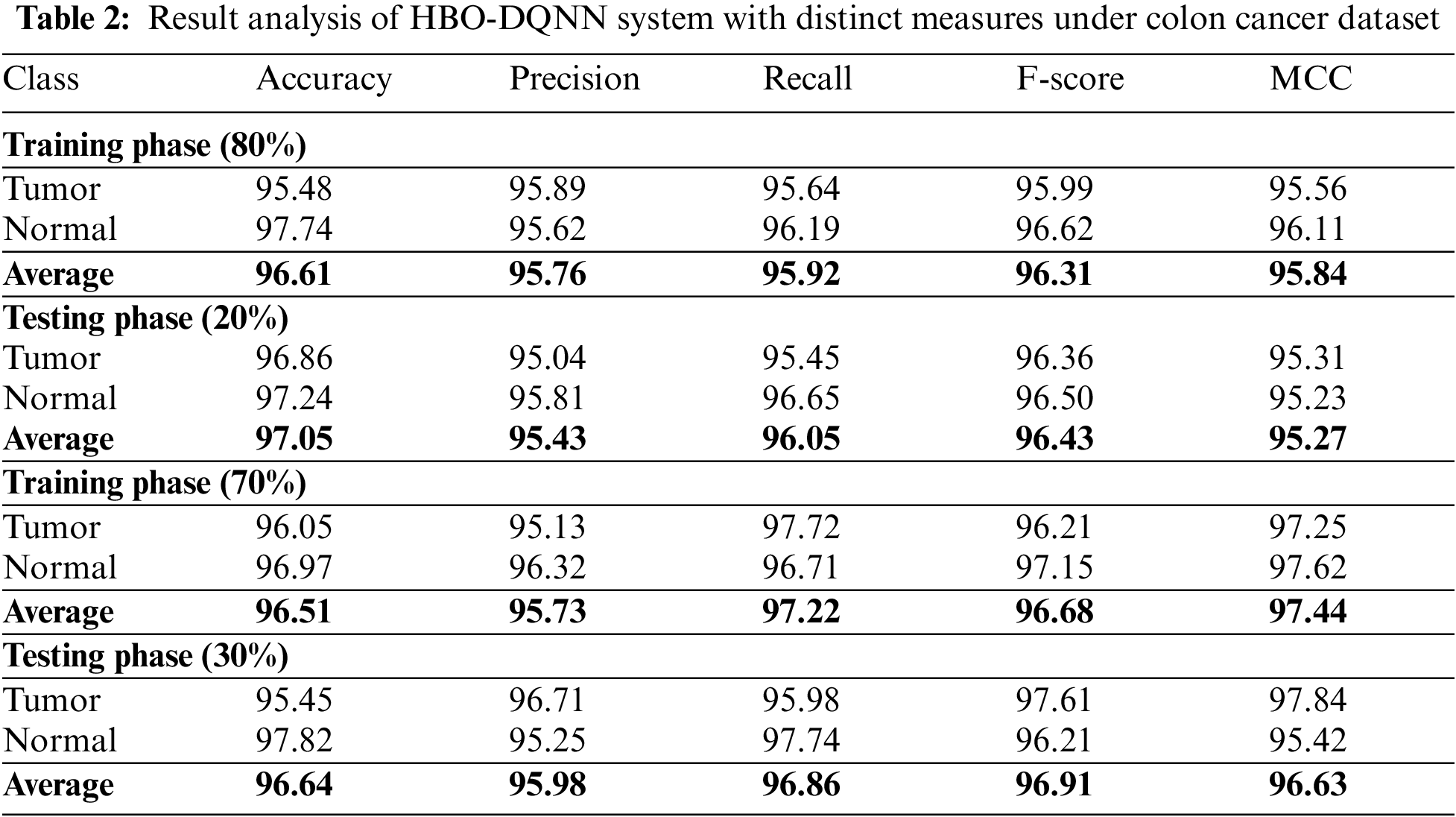

Figure 3: Average analysis of HBO-DQNN system under colon cancer dataset (a and b) TR and TS database of 80:20 and (c and d) TR and TS database of 70:30
The training accuracy (
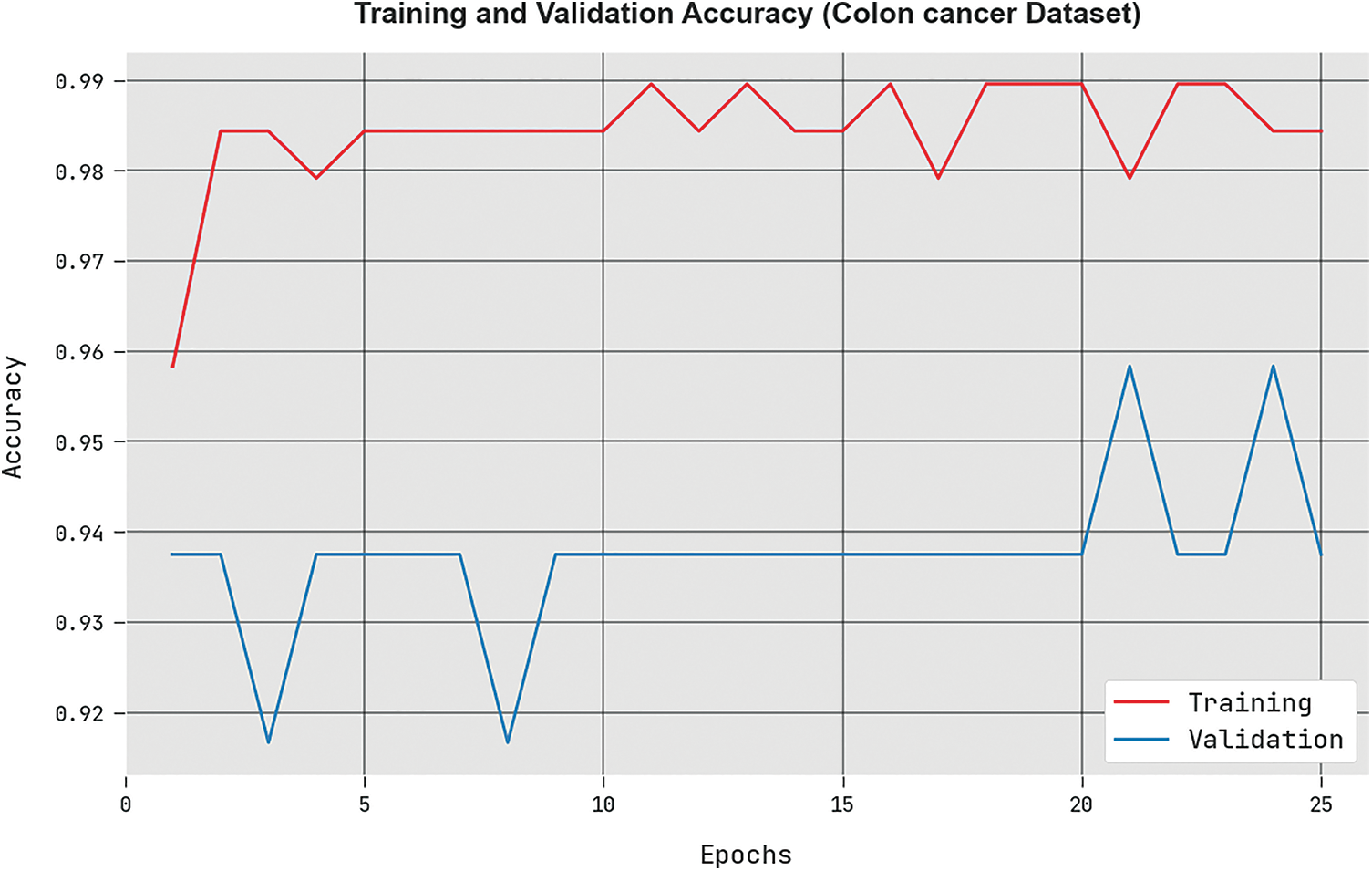
Figure 4:
The training loss (
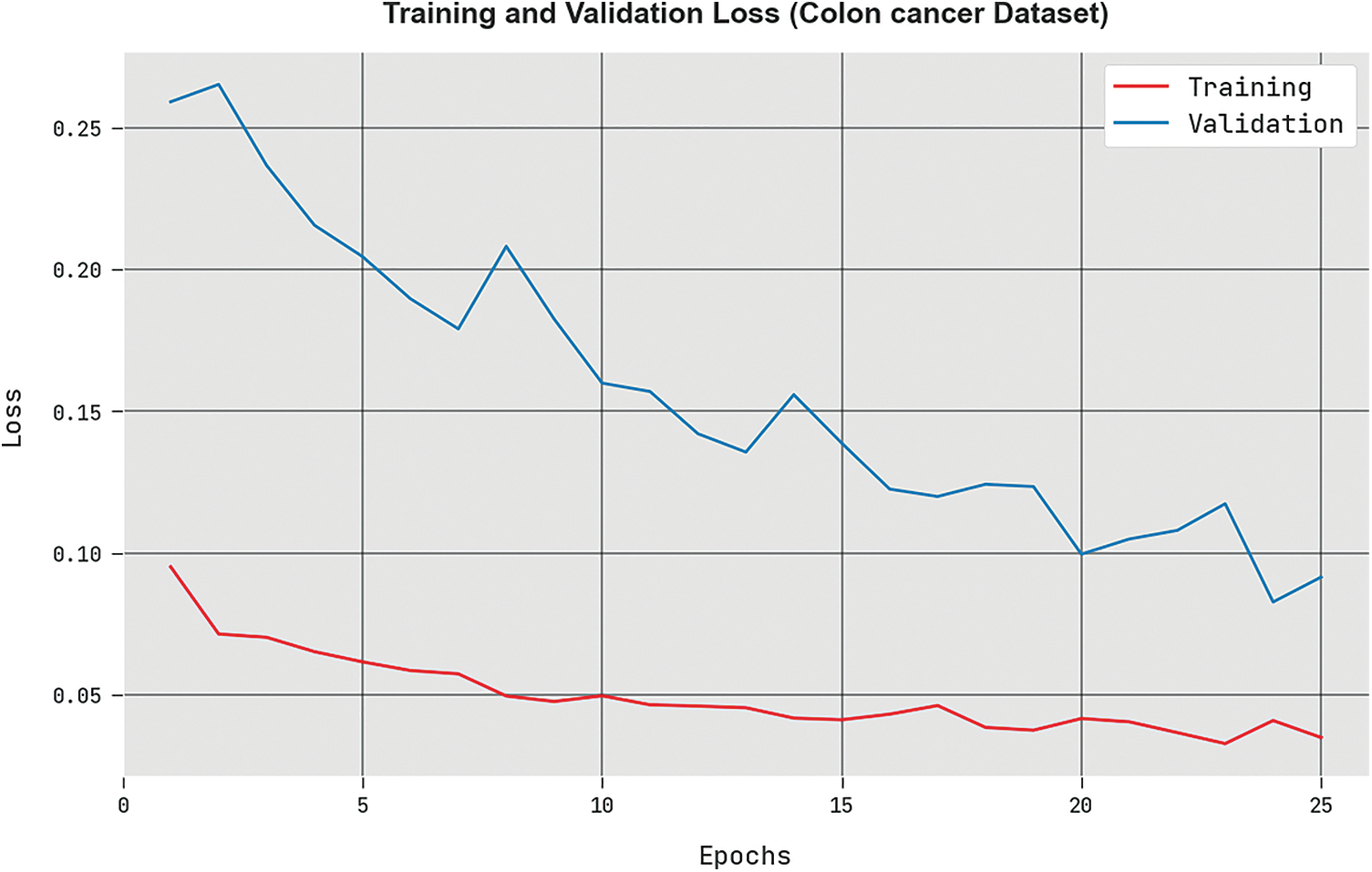
Figure 5:
A detailed ROC analysis of the HBO-DQNN technique under the Colon cancer database is displayed in Fig. 6. The outcomes displayed the HBO-DQNN method’s capability in classifying different classes in the test database.
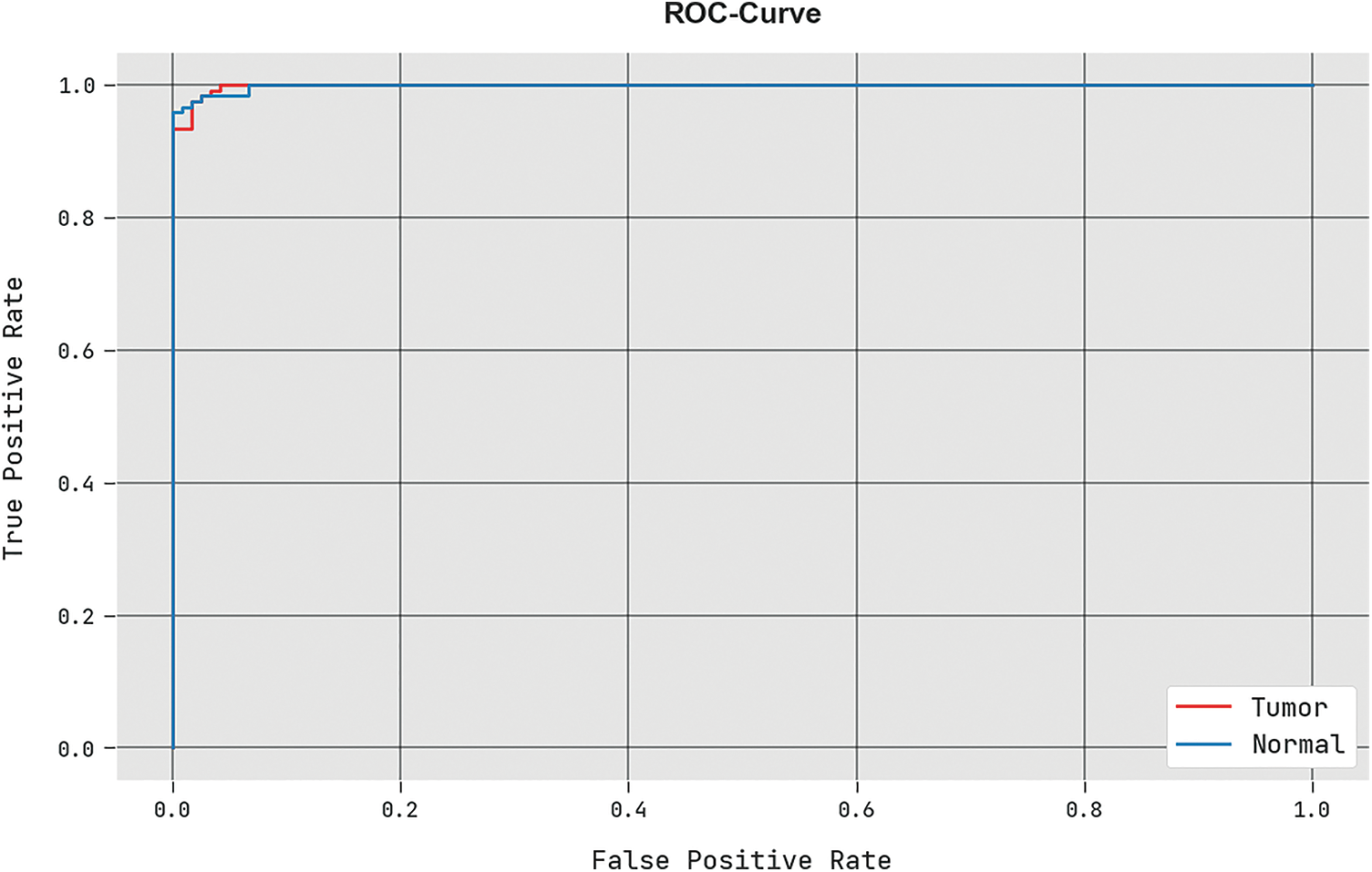
Figure 6: ROC analysis of HBO-DQNN system under colon cancer dataset
Table 3 and Fig. 7 demonstrate the overall classification outcomes of the HBO-DQNN method on the Lymphoma Dataset. The results show the HBO-DQNN technique has reached effectual outcomes in all aspects. For instance, on 80% of the TR database, the HBO-DQNN method has gained an average
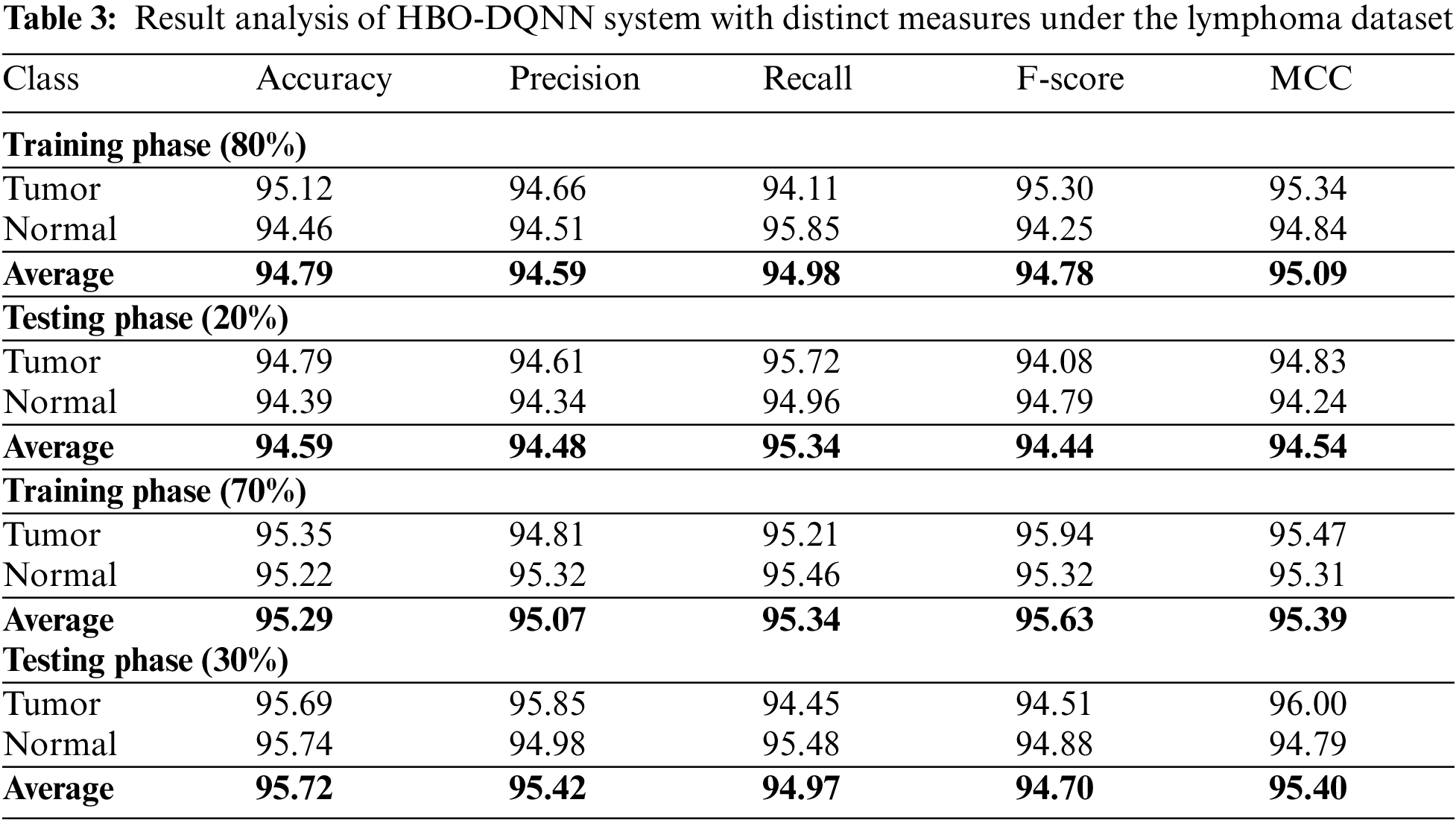
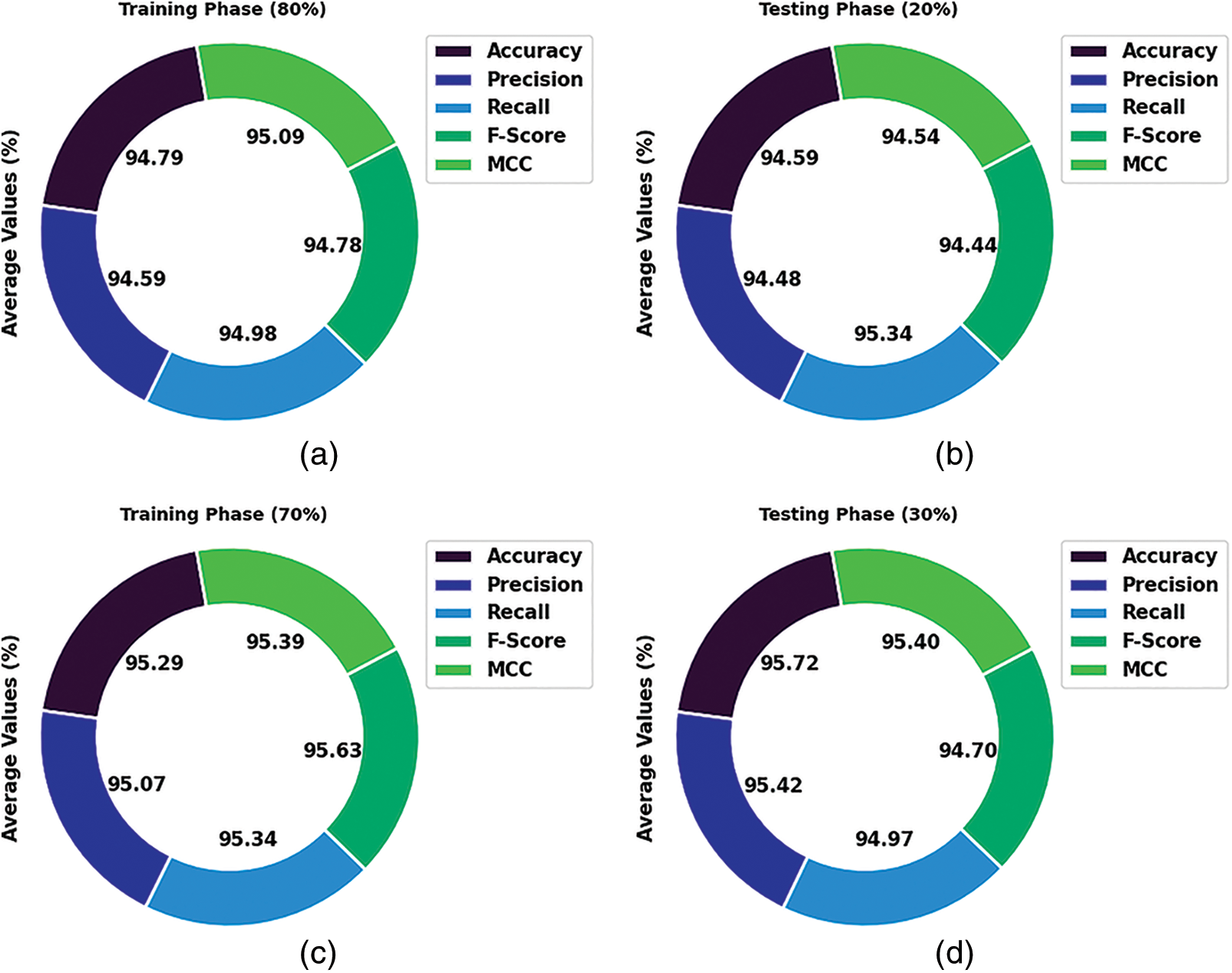
Figure 7: Average analysis of HBO-DQNN system under lymphoma dataset (a and b) TR and TS database of 80:20 and (c and d) TR and TS database of 70:30
In the meantime, on 20% of the TR database, the HBO-DQNN technique has achieved an average
The
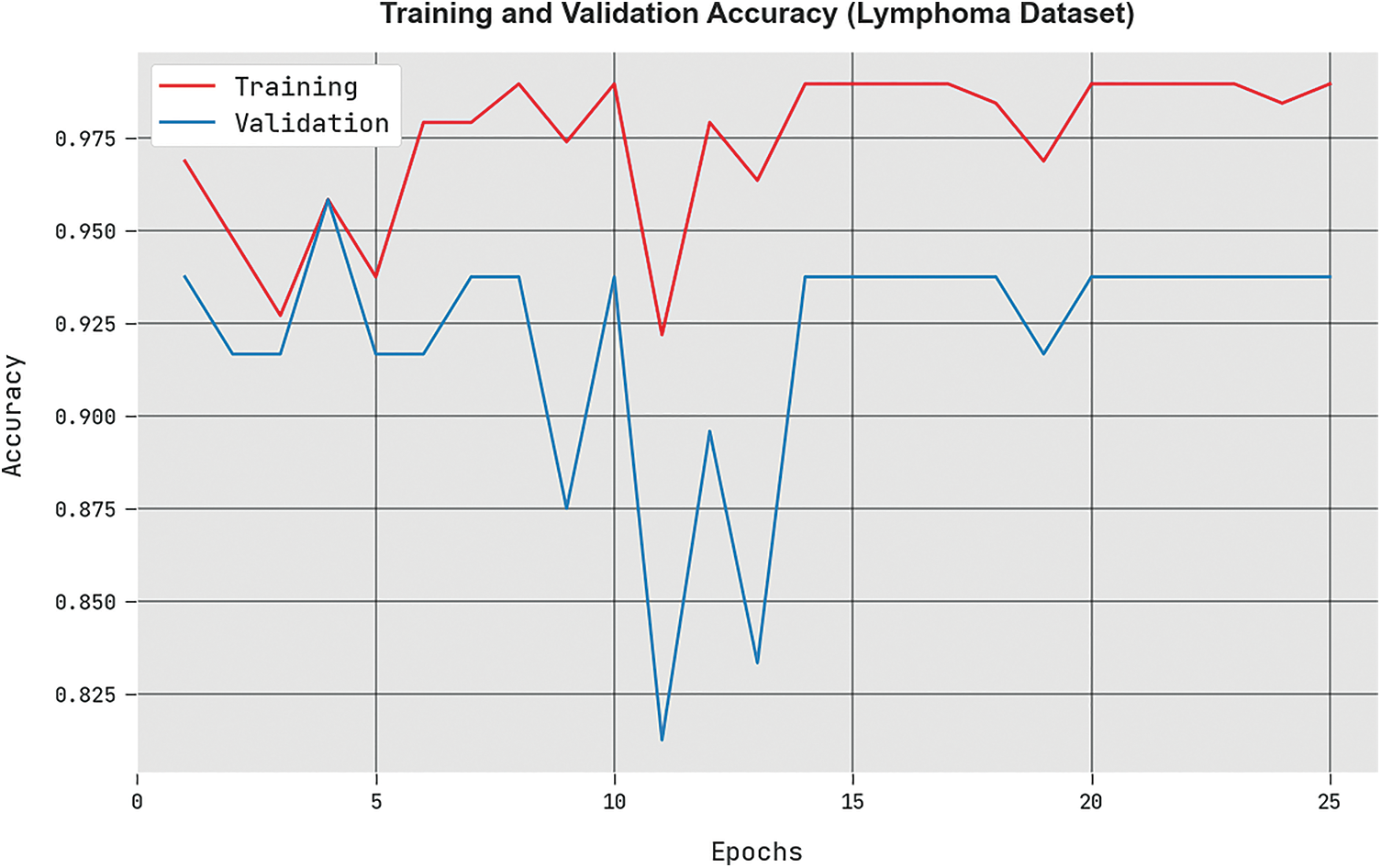
Figure 8:
The
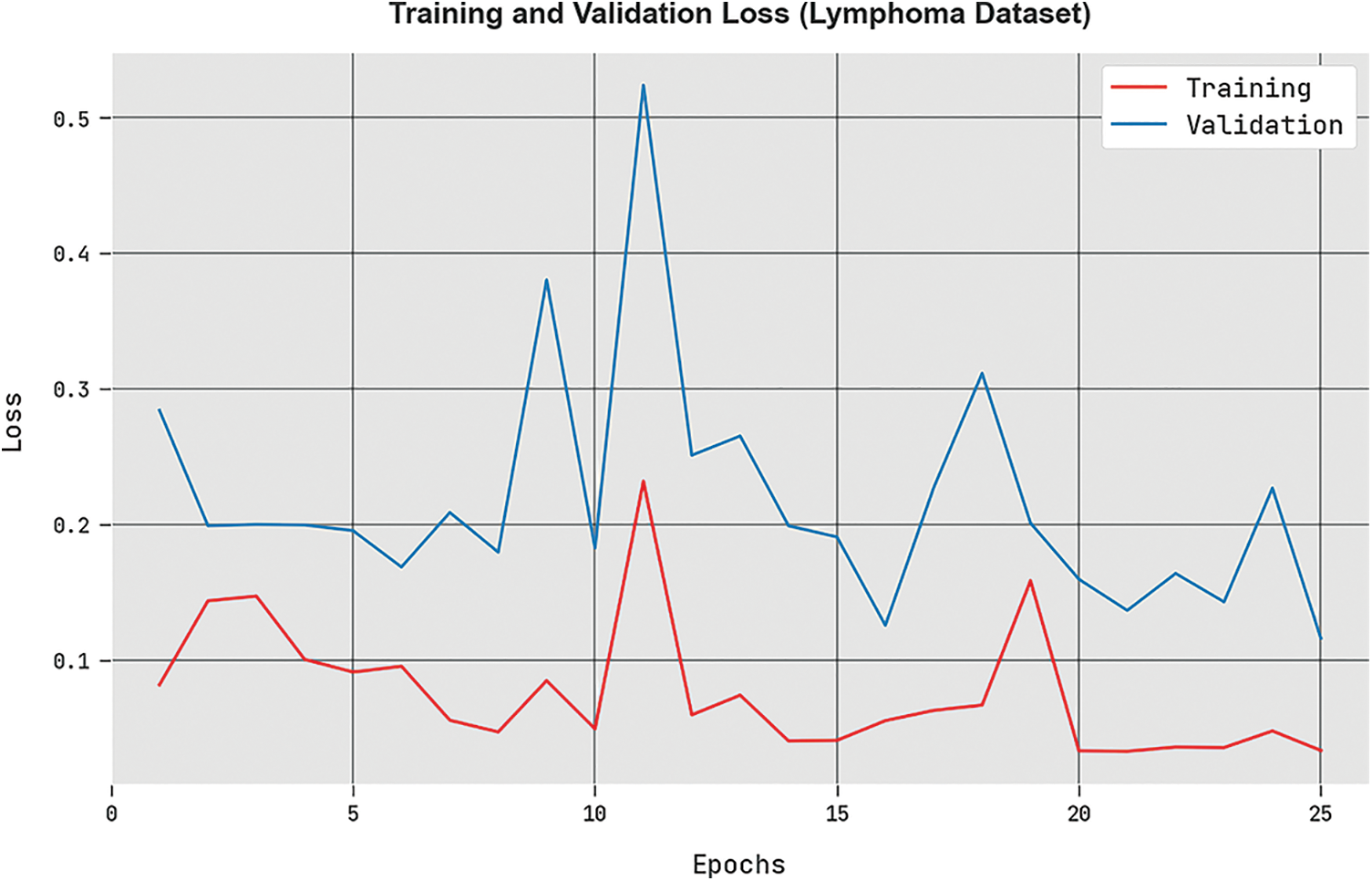
Figure 9:
A brief ROC study of the HBO-DQNN approach under the Lymphoma database is portrayed in Fig. 10. The outcomes denoted the HBO-DQNN technique has displayed its capability in classifying different classes in the test database.
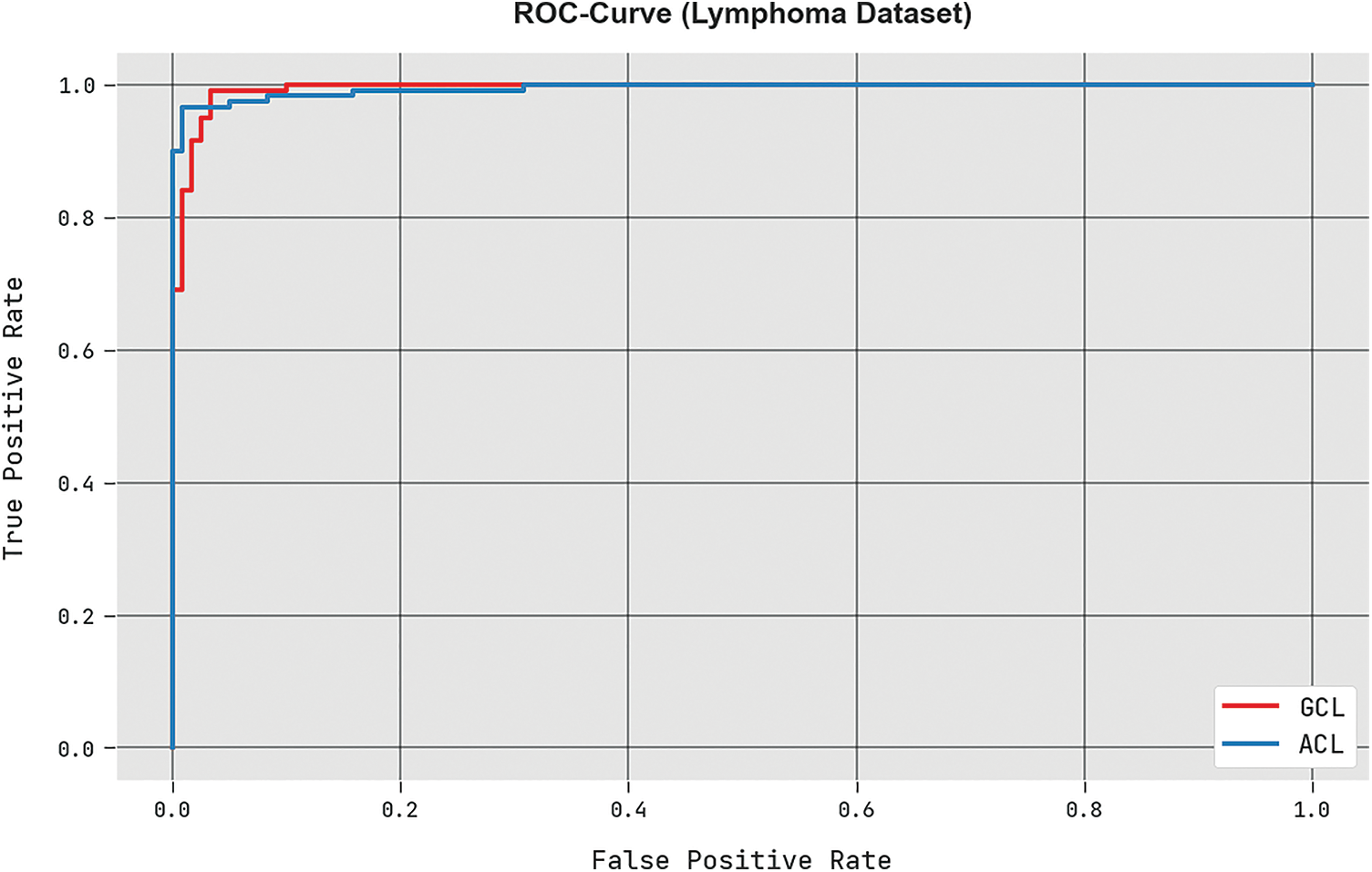
Figure 10: ROC analysis of HBO-DQNN system under the lymphoma dataset
A comprehensive comparison study of the HBO-DQNN method with contemporary techniques is given in Table 4 [27]. Fig. 11 examines a close
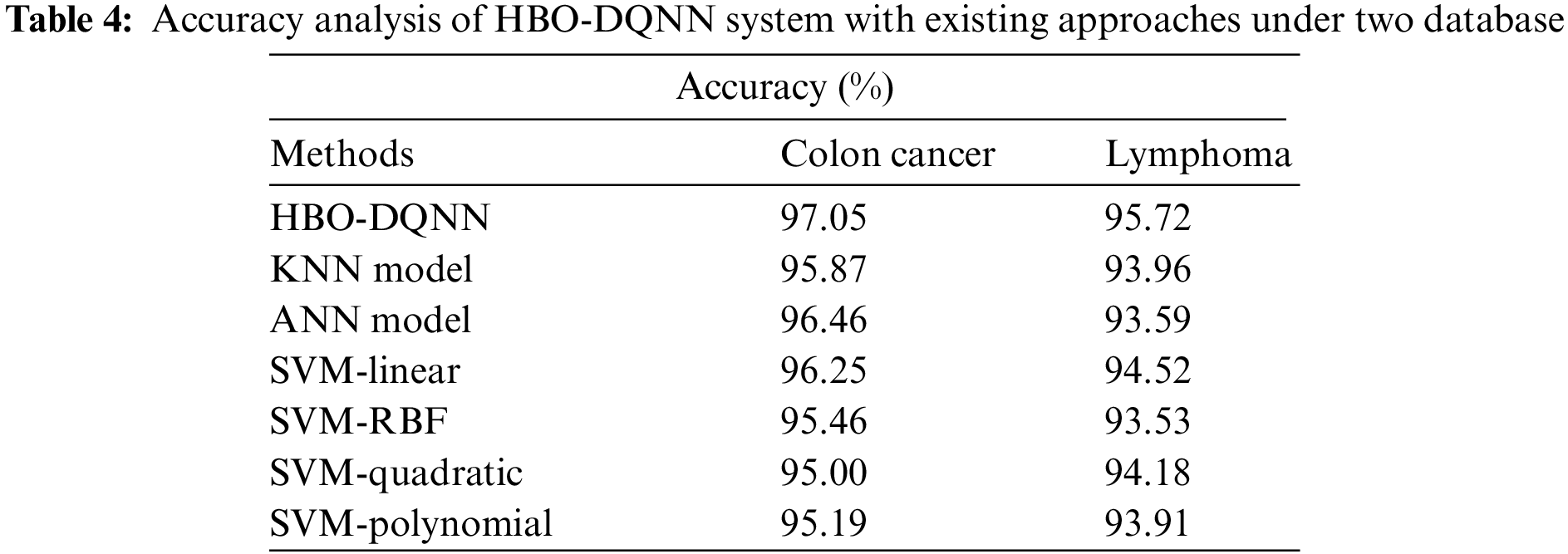
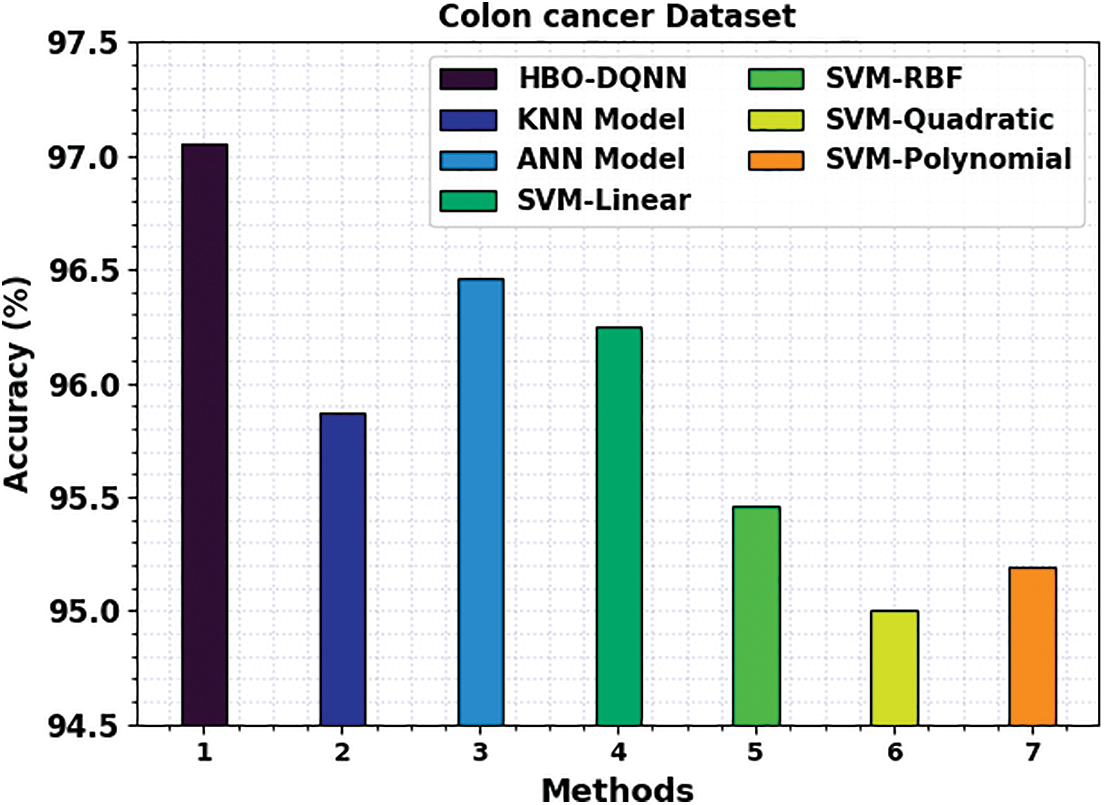
Figure 11:
Finally, Fig. 12 examines a comparative

Figure 12:
In this study, a new HBO-DQNN method was designed for decision-making in smart healthcare applications. The presented HBO-DQNN method primarily concentrates on detecting and classifying healthcare data. In the presented HBO-DQNN model, three stages of operations were performed. Data normalization is applied to pre-process the input data at the initial stage. Next, the HBO algorithm is used in the second stage to choose an optimal set of features from the healthcare data. At last, the DQNN model was used for healthcare data classification. A series of experiments were carried out to depict the promising classifier results of the HBO-DQNN model. The extensive comparative analysis reported the improvements of the HBO-DQNN method over other existing models with maximum accuracy of 97.05% and 95.72% under the colon cancer and lymphoma dataset. In future, hybrid DL classifiers can be involved to boost overall performance.
Funding Statement: This research work was funded by Institutional Fund Projects under grant no. (IFPIP: 488-611-1443). Therefore, the authors gratefully acknowledge technical and financial support provided by Ministry of Education and Deanship of Scientific Research (DSR), King Abdulaziz University (KAU), Jeddah, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. K. Muhammad, S. Khan, J. D. Ser and V. H. C. De Albuquerque, “Deep learning for multigrade brain tumor classification in smart healthcare systems: A prospective survey,” IEEE Transactions on Neural Networks and Learning Systems, vol. 32, no. 2, pp. 507–522, 2020. [Google Scholar]
2. L. Liu, J. Xu, Y. Huan, Z. Zou, S. C. Yeh et al., “A smart dental health-IoT platform based on intelligent hardware, deep learning, and a mobile terminal,” IEEE Journal of Biomedical and Health Informatics, vol. 24, no. 3, pp. 898–906, 2019. [Google Scholar] [PubMed]
3. A. A. Nancy, D. Ravindran, P. D. Raj Vincent, K. Srinivasan and D. G. Reina, “IoT-cloud-based smart healthcare monitoring system for heart disease prediction via deep learning,” Electronics, vol. 11, no. 15, pp. 2292, 2022. [Google Scholar]
4. W. Li, Y. Chai, F. Khan, S. R. U. Jan, S. Verma et al., “A comprehensive survey on machine learning-based big data analytics for IoT-enabled smart healthcare system,” Mobile Networks and Applications, vol. 26, no. 1, pp. 234–252, 2021. [Google Scholar]
5. M. Arabahmadi, R. Farahbakhsh and J. Rezazadeh, “Deep learning for smart healthcare—a survey on brain tumor detection from medical imaging,” Sensors, vol. 22, no. 5, pp. 1960, 2022. [Google Scholar] [PubMed]
6. M. Ragab, A. Albukhari, J. Alyami, and R. Mansour, “Ensemble deep-learning-enabled clinical decision support system for breast cancer diagnosis and classification on ultrasound images,” Biology, vol. 11, no. 3, pp. 439, 2022. [Google Scholar] [PubMed]
7. S. A. Alsuhibany, S. Abdel-Khalek, A. Algarni, A. Fayomi, D. Gupta et al., “Ensemble of deep learning based clinical decision support system for chronic kidney disease diagnosis in medical internet of things environment,” Computational Intelligence and Neuroscience, vol. 2021, Article ID 4931450, pp. 13, 2021. https://doi.org/10.1155/2021/493145 [Google Scholar] [CrossRef]
8. S. Althubiti, J. Escorcia-Gutierrez, M. Gamarra, R. Soto-Diaz and R. Mansour, “Improved metaheuristics with machine learning enabled medical decision support system,” Computers, Materials and Continua, vol. 73, no. 2, pp. 2423–2439, 2022. [Google Scholar]
9. M. Ragab, E. Ashary, W. Aljedaibi, I. Alzahrani, A. Kumar et al., “A novel metaheuristics with adaptive neuro-fuzzy inference system for decision making on autonomous unmanned aerial vehicle systems,” ISA Transactions, vol. 132, pp. 16–23, 2023. https://doi.org/10.1016/j.isatra.2022.04.006 [Google Scholar] [PubMed] [CrossRef]
10. H. Firdaus, S. I. Hassan and H. Kaur, “A comparative survey of machine learning and meta-heuristic optimization algorithms for sustainable and smart healthcare,” African Journal of Computing & ICT, vol. 11, no. 4, pp. 1–17, 2018. [Google Scholar] [PubMed]
11. Z. Lv, Z. Yu, S. Xie and A. Alamri, “Deep learning-based smart predictive evaluation for interactive multimedia-enabled smart healthcare,” ACM Transactions on Multimedia Computing, Communications, and Applications (TOMM), vol. 18, no. 1s, pp. 1–20, 2022. [Google Scholar]
12. W. H. Bangyal, J. Ahmed, and H. T. Rauf, “A modified bat algorithm with torus walk for solving global optimization problems,” International Journal of Bio-Inspired Computation, vol. 15, no. 1, pp. 1, 2020. [Google Scholar]
13. W. H. Bangyal, K. Nisar, A. A. B. A. Ibrahim, M. R. Haque, J. J. P. C. Rodrigues et al., “Comparative analysis of low discrepancy sequence-based initialization approaches using population-based algorithms for solving the global optimization problems,” Applied Sciences, vol. 11, no. 16, pp. 7591, 2021. [Google Scholar]
14. F. Teng, Z. Ma, J. Chen, M. Xiao and L. Huang, “Automatic medical code assignment via deep learning approach for intelligent healthcare,” IEEE Journal of Biomedical and Health Informatics, vol. 24, no. 9, pp. 2506–2515, 2020. [Google Scholar] [PubMed]
15. K. V. Praveen, P. J. Prathap, S. Dhanasekaran, I. H. Punithavathi, P. Duraipandy et al., “Deep learning based intelligent and sustainable smart healthcare application in cloud-centric IoT,” Computers, Materials and Continua, vol. 66, no. 2, pp. 1987–2003, 2021. [Google Scholar]
16. Y. Jiao, H. Qi and J. Wu, “Capsule network assisted electrocardiogram classification model for smart healthcare,” Biocybernetics and Biomedical Engineering, vol. 42, no. 2, pp. 543–555, 2022. [Google Scholar]
17. S. Baskar, P. M. Shakeel, R. Kumar, M. A. Burhanuddin and R. Sampath, “A dynamic and interoperable communication framework for controlling the operations of wearable sensors in smart healthcare applications,” Computer Communications, vol. 149, pp. 17–26, 2020. [Google Scholar]
18. L. Hoang, S. H. Lee, E. J. Lee and K. R. Kwon, “Multiclass skin lesion classification using a novel lightweight deep learning framework for smart healthcare,” Applied Sciences, vol. 12, no. 5, pp. 2677, 2022. [Google Scholar]
19. S. Mohapatra, J. Nayak, M. Mishra, G. K. Pati, B. Naik et al., “Wavelet transform and deep convolutional neural network-based smart healthcare system for gastrointestinal disease detection,” Interdisciplinary Sciences: Computational Life Sciences, vol. 13, no. 2, pp. 212–228, 2021. [Google Scholar] [PubMed]
20. M. Z. Uddin, “A wearable sensor-based activity prediction system to facilitate edge computing in the smart healthcare system,” Journal of Parallel, Distributed Computing, vol. 123, pp. 46–53, 2019. [Google Scholar]
21. M. A. Khan, K. Muhammad, M. Sharif, T. Akram and S. Kadry, “Intelligent fusion-assisted skin lesion localization and classification for smart healthcare,” Neural Computing and Applications, vol. 123, pp. 1–16, 2021. [Google Scholar]
22. A. Pandey and A. Jain, “Comparative analysis of KNN algorithm using various normalization techniques,” International Journal of Computer Network and Information Security, vol. 9, no. 11, pp. 36, 2017. [Google Scholar]
23. Q. Askari, M. Saeed and I. Younas, “Heap-based optimizer inspired by corporate rank hierarchy for global optimization,” Expert Systems with Applications, vol. 161, pp. 113702, 2020. [Google Scholar]
24. V. Bassetti, S. S. Rangarajan, C. K. Shiva, S. Verma, R. E. Collins et al., “A quasi-oppositional heap-based optimization technique for power flow analysis by considering large scale photovoltaic generator,” Energies, vol. 14, no. 17, pp. 5382, 2021. [Google Scholar]
25. E. Paquet and F. Soleymani, “QuantumLeap: Hybrid quantum neural network for financial predictions,” Expert Systems with Applications, vol. 195, pp. 116583, 2022. [Google Scholar]
26. M. Zhou, “Evaluation of financial risk efficiency based on big data and quantum neural network,” in 2022 6th Int. Conf. on Intelligent Computing and Control Systems (ICICCS), Madurai, India, pp. 944–947, May 2022. [Google Scholar]
27. C. Vanitha, D. Devaraj and M. Venkatesulu, “Gene expression data classification using support vector machine and mutual information-based gene selection,” Procedia Computer Science, vol. 47, pp. 13–21, 2015. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools