Battle Royale Optimization-Based Resource Scheduling Scheme for Cloud Computing Environment

1  Introduction

Cloud Computing (CC) is a creative technology that put forward a revolutionary change in how computing services are delivered. With the thriving progress of the Web and the Internet, CC has transformed how communication and information technology users access resources [1]. It has allowed driving the focus from local or personal computation to datacenter-centric computation by offering resources dynamically in a virtual manner through the Internet. CC converts computing as the 5th utility that can be charged on a pay-per-use provision similar to a conventional utility, namely, telephony, electricity, and gas [2]. Simply CC is a blooming technical trend that offers computing that is network, processing, applications, storage, and services in a managed, abstracted, and virtualized demand-driven manner utilizing the Internet. The sources which present the services were placed anywhere on the Internet instead of the local system [3]. Fig. 1 depicts the process of resource scheduling (RS) for the CC environment.

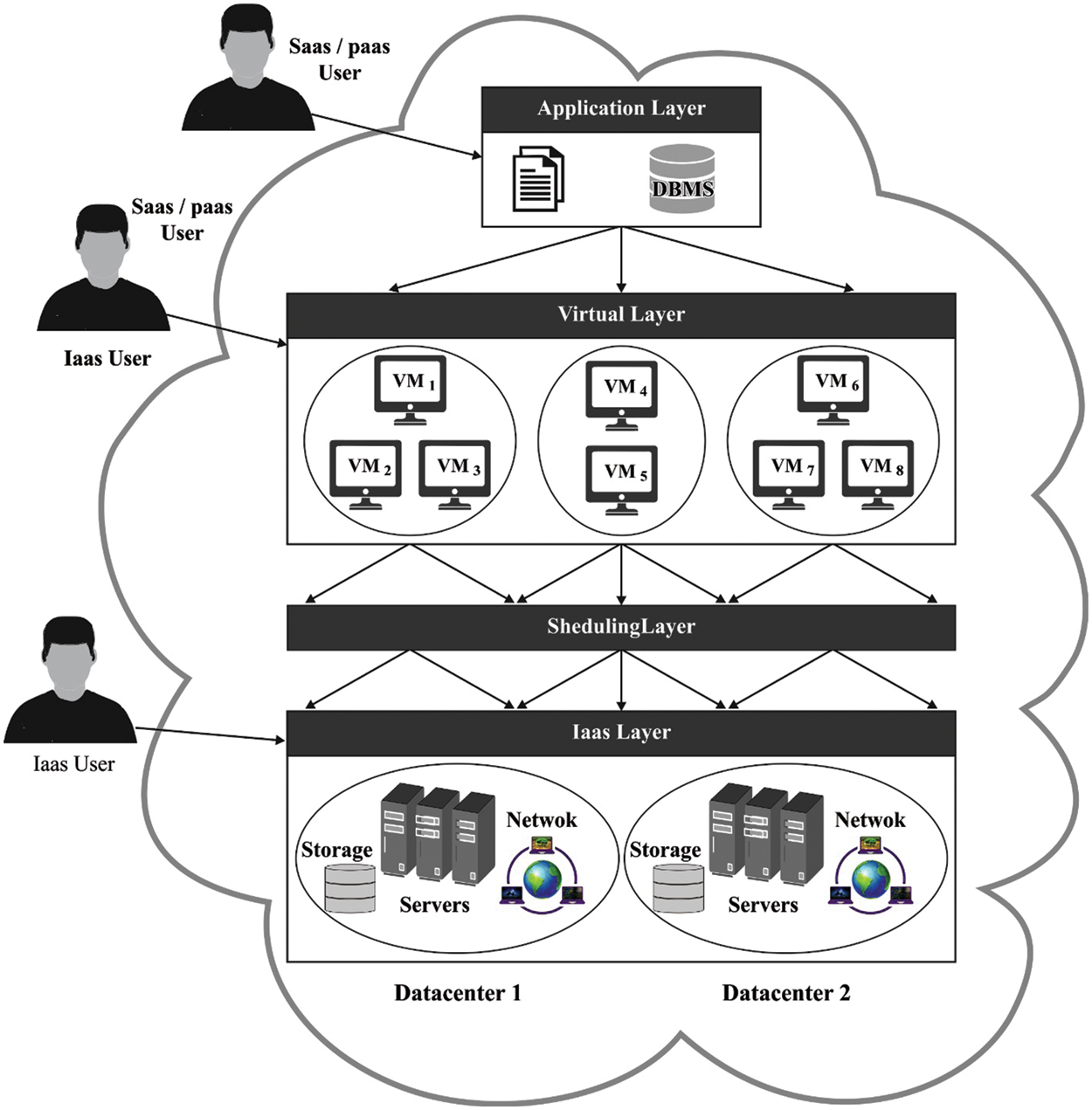
Figure 1: Resource scheduling for CC environment

CC indicates a well-known shared computing technology that conveys measurable on-demand services on the global network in a dynamic way. Fundamentally, CC provides end-users with diverse and limitless virtual sources acquired on-demand and with distinct billing standards (static-oriented and subscription) [4]. Task scheduling (TS) also draws an independent task mapping process on a set of acquired sources in a cloud context (for workflow application) for executing users’ specified quality of service (QoS) restrictions (cost and makespan). Workflow (common application linked with empirical study, including biology, astronomy, and earthquake) is shifted or migrated to the cloud for execution [5]. Even though optimal source detection for each workflow task to satisfy user-defined QoS has been broadly studied all these years, substantial intricacy needs more research. Firstly, the TS on a CC platform becomes an optimization issue; secondly, multiple TS optimization objectives were evident: high resource usage for the entire task queue and completion time reduction [6]; lastly, Cloud source dynamics, heterogeneity and measurability lead to high complexities. In CC, TS, resource selection, or jobs scheduling can be one such most considerable complexity which was garnered cloud service customers’ and providers’ attention. Moreover, particular studies on TS intricacy reflected promising results [7].

Studies on scheduling workflows and specifications focused on causality and temporal limits that identify order dependencies and existence among tasks [8]. Task Execution incurs a cost, which might change depending on the sources allotted. Resource allocation limitations describe restrictions on how the resources can be allotted, and scheduling in resource allocation limitations offers suitable resource allotment to tasks [9]. In CC, machines were positioned in various regions and contained disparate processing capabilities, costs, and features (amount of main memory, CPU cores count, etc.). The makespan cost linked with the TS and the sources allotted must be considered [10]. Thus, resource allocation and TS are prudently optimized and coordinated jointly to achieve a time-effective and overall cost schedule. Simply, for finding optimum task schedules through reducing makespan and cost.

This study introduces a Battle Royale Optimization-based Resource Scheduling Scheme for Cloud Computing Environment (BRORSS-CCE) technique. The BRORSS-CCE technique majorly schedules the available resources for maximum utilization and effectual makespan. In the BRORSS-CCE technique, the BRO is a population-based algorithm where all the individuals are denoted by a soldier/player who likes to go towards the optimal place and ultimate survival. The BRORSS-CCE technique can be employed to balance the load, distribute resources based on demand and assure services to all requests. The experimental validation of the BRORSS-CCE technique is tested under distinct aspects.

2  Related Works

In [11], the author devises an innovative hybrid gradient descent cuckoo search (HGDCS) technique related to cuckoo search (CS) methods and gradient descent (GD) techniques to resolve and optimize the issues based on resource scheduling (RS) in Infrastructure as a Service (IaaS) CC. This study will compare the load balancing (LB), makespan, performance improvement rate, and throughput of prevailing metaheuristic techniques with the presented HGDCS technique relevant to CC. Potu et al. [12] designed an extended PSO (EPSO) technique with a different gradient approach for optimizing the TS issue in cloud-fog atmospheres. The ultimate goal was to enhance resource efficiency and diminish the time consumed for task completion. The author conducted wide experimentations on the iFogSim simulators concerning total cost and makespan.

Devi et al. [13] utilize a GA related to encoded chromosomes (GEC-DRP) for managing dynamic RS. But the prevailing scheduling technique predicts the amount of physical machines (PM) required for the user in the future. This advanced scheduling technique will schedule the tasks on the cloud through computation of the amount of virtual machines (VMs) necessitated in the near future with its forecasted CPU and memory needs that can be considered as the main contribution of this study. The k-means approach would cluster the tasks related to memory usage and CPU as parameters. Belgacem et al. [14] offer a dynamic RS methodology that addresses users’ demand for resources with faster and improved responsiveness. It even modelled a multiobjective search method named Spacing Multi-Objective Antlion algorithm (S-MOAL) for reducing the cost and the makespan of utilizing virtual machines. Further, its impact on energy consumption and fault tolerance has been studied. Jena et al. [15] present a genetic algorithm (GA)-related Customer-Conscious RS and TS in multi-CC. This technique was split into 2 stages: the shortest task first scheduling and GA-related RS. The aim is to map the tasks to VMs of the multi-cloud federation to have maximal customer satisfaction and minimal makespan duration.

Madni et al. [16] introduce a new Multiobjective Cuckoo Search Optimization (MOCSO) approach to deal with the RS issue in CC. The ultimate goal of the RS issue was to diminish the cloud user’s cost and improve the performance through the reduction of makespan duration, which helps rise the profit or revenue for cloud providers to have maximal resource consumption. Thus, the MOCSO method is a technique to solve multiobjective RS issues in IaaS CC environment. Strumberger et al. [17] offer a hybrid whale optimization technique under swarm intelligence meta-heuristics, adapted to manage the RS complexity in cloud environments. To evaluate performance more precisely of the presented technique, original whale optimization has been adapted for RS.

3  Problem Formulation

To simplify the deliberation, the concept is that a group of cloud user tasks exists, and every task has several sub-tasks with superiority constraints. Every subtask is allowable to be managed on accessible resources [18]. A cloud resource has a capacity level (memory, CPU, storage, network). In this study, the discussion of CC emphasized that cloud task scheduling and resource allocation scenarios are real NP-Complete problems. Task scheduling of CC is shown below.

Input: It is assumed a tJ=(J1,J2, …,Ji, …,Jn) , where i∈[1,  n] and n refer to the quantity of independent tasks. A task Ji is generated using a series Ji1,Ji2,JijJiqO∈[1, q] , and q shows the amount of subtasks) to be implemented sequentially. A set of resources available is R=(R1,R2,Rk,Rm) , where k∈[1,  m] and m denote the available resources. Every subtask Jij is implemented on a subset RksubseteqR of resources available.

Output: An effectual Gantt chart of scheduling, comprising the task assignment on makespan and available resources. For three-task four-resource problems, its schedule is {(J11,  R2), (J31,  R4), (J21,  R2), (J12,  R4),(J22,  R1), (J32,  R2), (J23,  R4), (J33,  R3), (J13, R1)},  its Gantt chart and makespan.

Constraints: The runtime of every subtask is resource-reliant. Preemption is prohibited, viz., every subtask should be accomplished uninterrupted after being initiated. The resource could not consecutively implement multiple subtasks.

Objective: The challenge is to allocate every subtask to proper resources (routing problems) and sequence the subtask on the resource (sequencing problems) to minimalize the overall makespan and cost. The makespan is the overall length of the schedule (once each task has completed processing). The problem is that resource allocation and task scheduling must be coordinated carefully and jointly optimized for achieving a time-effective schedule and total cost.

4  The Proposed Model

This study introduces a new BRORSS-CCE technique for effectual resource allocation in the CC environment. The BRORSS-CCE technique majorly schedules the available resources for maximum utilization and effectual makespan.

4.1 Overview of BRO Algorithm

Battle Royale games simulated BRO technique. In this kind of fighting game, players (soldiers) fight against themselves in a competitive environment. In contrast, all the players try to endure initially and secondarily kill several other players as feasible [19]. When the player continuously obtains damage to a fixed (threshold) time, it is re-spawned from an arbitrarily selected area of game fields.

During the BRO technique, under the Battle Royale games, the primary candidate solution is arbitrarily distributed from the problem spaces. Afterwards, then relating all the solutions with their nearest neighbour, the optimum solutions concerning fitness values are termed winners and losers. The damage (lose) level of all the solutions is saved as a parameter from all the candidate solutions that are incremented than all the damages. When the solution sequentially obtains damage to threshold time-ranging in [3–6], depends upon the problem that is resolved-it is reallocated dependent upon Eq. (1). When their damage level doesn’t obtain the threshold, reallocation is obtained by Eq. (2). During all the reallocations, the candidate solution was reinitializing, for obtaining nearby to an optimum found already. During these formulas, r signifies the arbitrarily created number dependent upon uniform distribution from the range between zero and one, and xdam,d and xbest,d are the place of damaged and optimum solution (found so far) from dimensional d.lbd and ubd denote the corresponding lower and upper bounds of dimensional d from the problem space.

xdam,di+1=r(ubd−lbd)+lbd  (1)

xdam,di+1=xdam,di+r(xbest,d−xdam,di)  (2)

An important element of the technique is in every △ iteration of the searching procedure, the safe zone from the problem shrinks down nearby an optimum solution by △=△+round(△2) if i≥△ . Specificall0079, the zone shrinks down if i obtain the value of △ . For instance, assume that MaxCircle =500 ; before the primary value of △ ≈166 , and the zone shrinks down after 166 iterations. The next iteration value for shrinking down the field are ≈250 and 375. △ is initialization by △= Max Circleround(log10( Max Circle)) , and MaxCircle signifies the maximal amount of generations. Fig. 2 depicts the flowchart of the BRO technique.

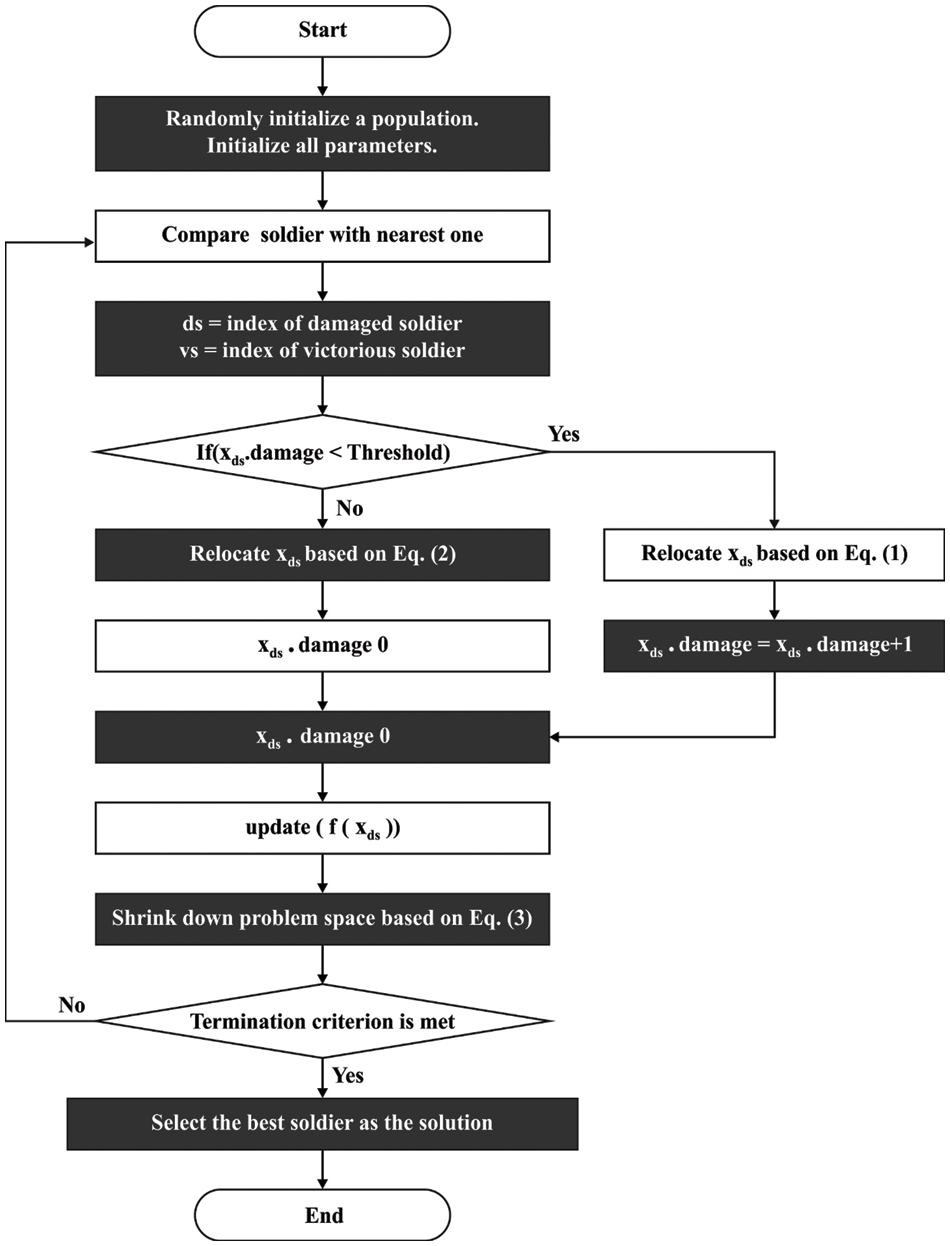
Figure 2: Flowchart of BRO technique

Noticeably the optimum solutions from all the iterations are saved for supporting elitism. Diminishing the problem space was able by Eq. (3), whereas SD(xd) implies the standard deviation of the entire population from dimensional d.

lbd=Xbest,d−SD(xd),   (3)

ubd=Xbest,d+SD(X)

4.2 Proposed Resource Scheduling Process

The BRORSS-CCE technique allocates initial and ends times to several implemented functions. As with other scheduling problems, RS from CC is a process that executes the distribution of appreciated cloud resources. Usually, processors, networks, stores, and VMs for fulfilling the demands of cloud users by cloud providers. It can be executed to balance the load, ensure equivalent distribution of resources based on the demand and offer any prioritization based on set rules [20]. It also ensures that CC can serve every cloud user request with specific service qualities. The RS problems are illuminated with utilize of Eq. (4).

RS=∑x=1m,n⁡(Rx+Sx…Nx)×Tx→UXZ  (4)

where as it allocates m needed counts of cloudlets or task T=(T1,  T2,  T3,  …,  Tm) onto n accessible physical to virtual resources from the cloud data centers R=(R1,  R2,  R3,  …,  Rn) , S=(S1,  S2,  S3,  …,  Sn) up to N=(N1,  N2,  N3,  …,  Nn) . The fitness of certain objective F=(F1,  F2,  F3,  …,  Fz) is improved to cloud user =(U1,  U2,  U3,  …,  Un) . If Z=1 , the fitness function F1 has been allocated to cloud users. If Z=2 , the fitness function F2 was allocated to cloud users, etc., based on its demands.

CC comprises several data centers, and every data centre is connected with VMs through distinct specifications. Assume that a group of cloudlets or tasks Ti=(T1,  T2,  T3,  …,  Tn) initiated in the cloud users as its needed demand. The cloud broker was responsible for allocating the cloudlets or tasks for requisite virtual resource Vj=(V1,  V2,  V3,  …,  Vm) as virtual resources with minimal completion time. The expected time to completion (ETC) was defined by the time of each cloudlet or task executed on a certain virtual resource attained through the ETC matrix. The overall amount of cloudlet or tasks multiplied by the overall amount of resources offers the ETC matrix dimension, and their components are described by ETC (Ti,  Vj) .

ETC(Ti,  Vj)=[T1V1T1V2T1V3……T1VmT2V1T2V2T2V3……T2VmT3V1T3V2T3V3……T3Vm⋮⋮⋮……⋮⋮⋮⋮……⋮TnV1TnV2TnVi3……TnVm] (5)

Hence, the primary aim is to hybridize the Gradient descent method to local search of enhanced CS approach to map the tasks or cloudlets on virtual resource with minimal ETC to minimal throughput and makespan using a balanced amount of imbalance via improving the rate of convergence.

5  Results and Discussion

This section inspects the scheduling efficiency of the BRORSS-CCE model under varying numbers of requests.

Table 1 and Fig. 3 report a comparative waiting time (WAITT) inspection of the BRORSS-CCE model with other recent models. The results indicated that the KHLBRS model has showcased poor performance with maximum WAITT values. Next, the IDSARS model has certainly attained reduced WAITT values. Followed by the HPSOMGARS and HMEERARS models have accomplished reasonable WAITT values. The experimental values inferred that the BRORSS-CCE model had reported enhanced results with minimal WAITT values under all requests. For instance, on 500 requests, the BRORSS-CCE model has offered a lower WAITT of 971 ms, whereas the KHLBRS, IDSARS, HPSOMGARS, and HMEERARS models have accomplished higher WAITT of 1491, 1368, 1172, and 1068 ms respectively.

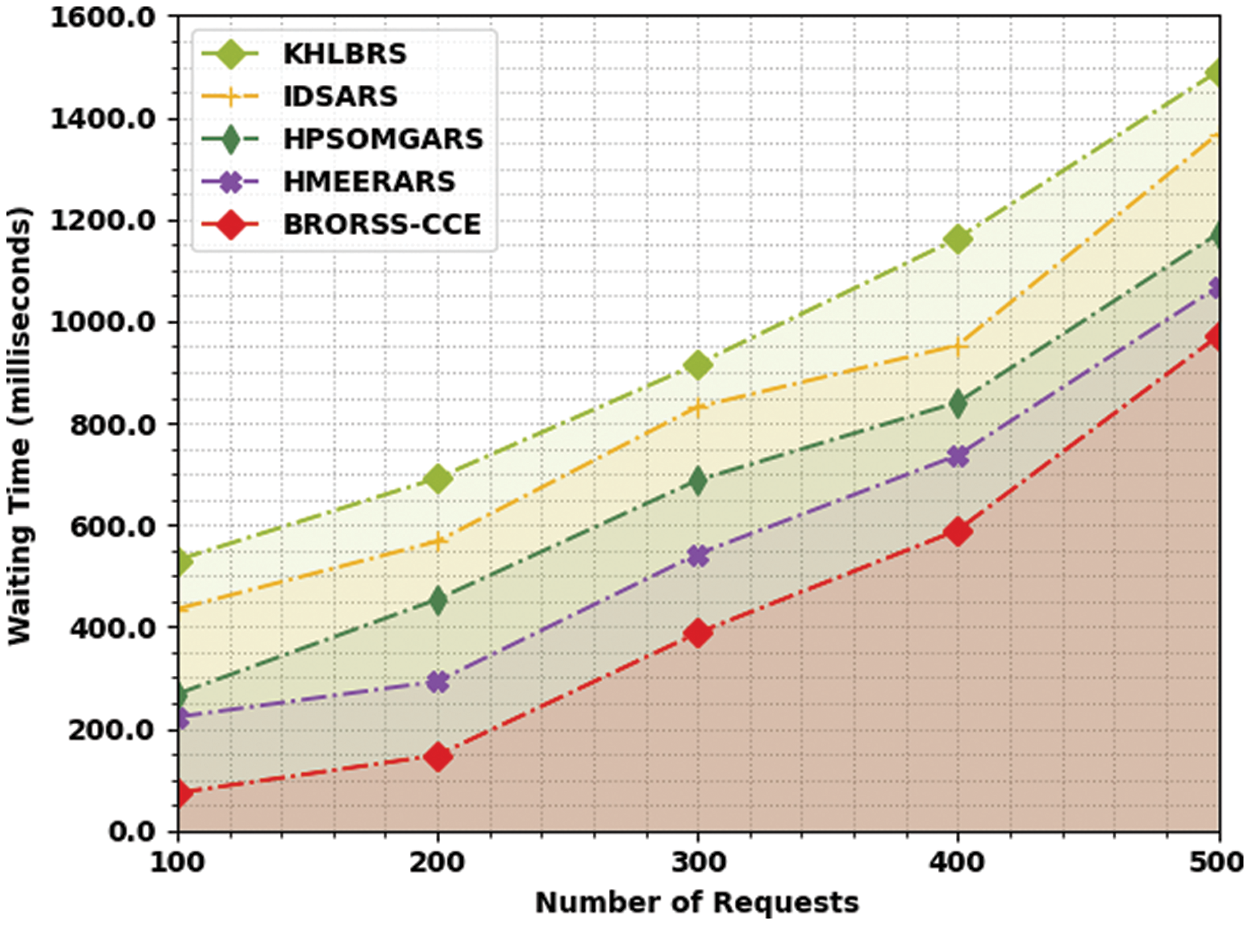
Figure 3: WAITT analysis of BRORSS-CCE approach under count of requests

Table 2 and Fig. 4 depict a comparative response time (RESPO) analysis of the BRORSS-CCE approach with other recent methods. The outcomes referred that the KHLBRS system has showcased poor performance with maximum RESPO values. Also, the IDSARS algorithm has certainly attained reduced RESPO values. Afterwards, the HPSOMGARS and HMEERARS techniques obtained reasonable RESPO values. The experimental values inferred that the BRORSS-CCE method had reported enhanced results with reduced RESPO values under all requests. For sample, on 500 requests, the BRORSS-CCE algorithm has offered minimal RESPO of 995 ms, whereas the KHLBRS, IDSARS, HPSOMGARS, and HMEERARS models have accomplished superior RESPO of 1574, 1326, 1114, and 1122 ms correspondingly.

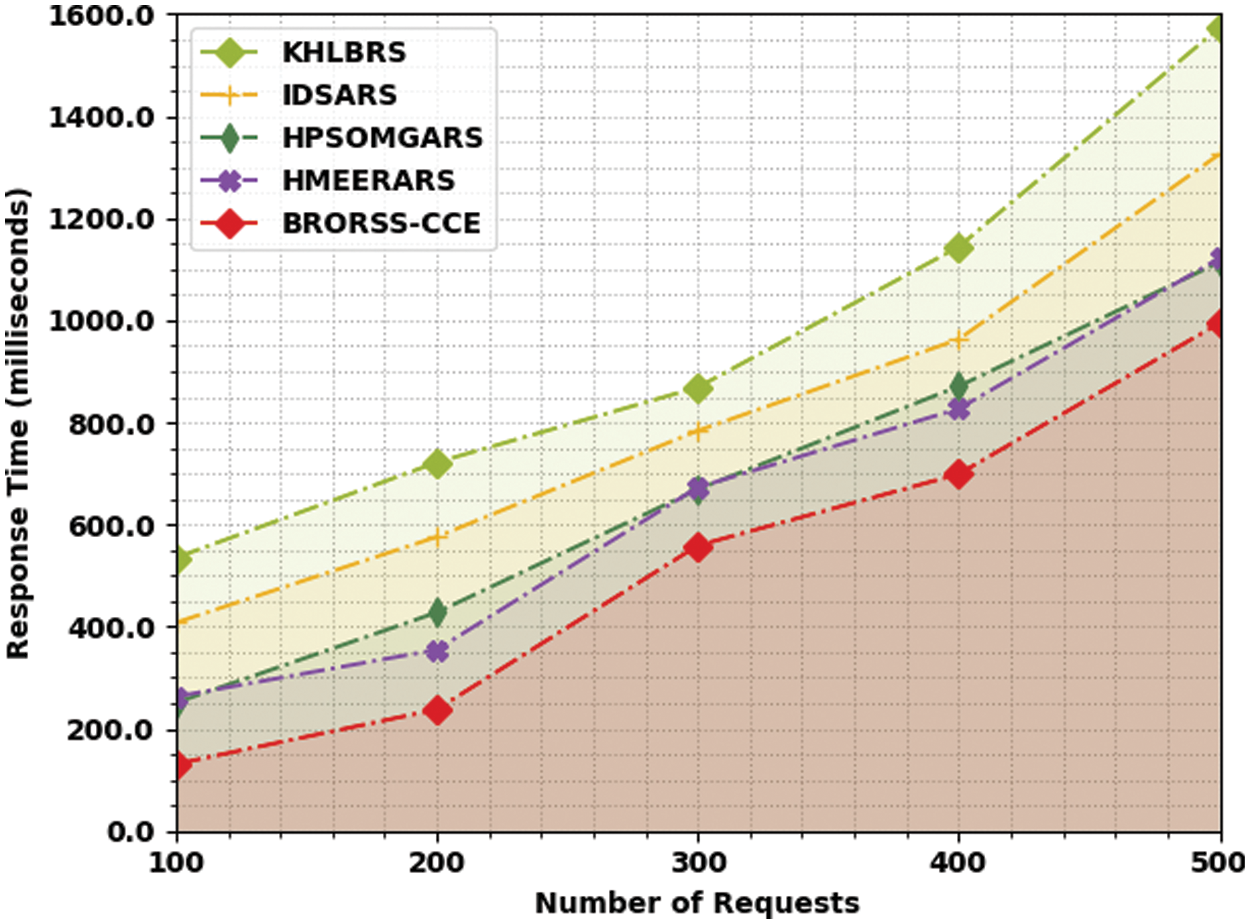
Figure 4: RESPO analysis of BRORSS-CCE approach under count of requests

Table 3 and Fig. 5 determine a comparative load balancing (LOADB) examination of the BRORSS-CCE methodology with other recent algorithms. The outcome indicated that the KHLBRS approach had showcased poor performance with minimal LOADB values. Along with that, the IDSARS technique has certainly attained higher LOADB values. Likewise, the HPSOMGARS and HMEERARS models have accomplished reasonable LOADB values. The experimental values inferred that the BRORSS-CCE system had reported enhanced results with higher LOADB values under all requests. For instance, on 500 requests, the BRORSS-CCE algorithm has offered a higher LOADB of 0.0901 ms, whereas the KHLBRS, IDSARS, HPSOMGARS, and HMEERARS systems have accomplished minimal LOADB of 0.0290, 0.0358, 0.0394, and 0.0618 ms correspondingly.

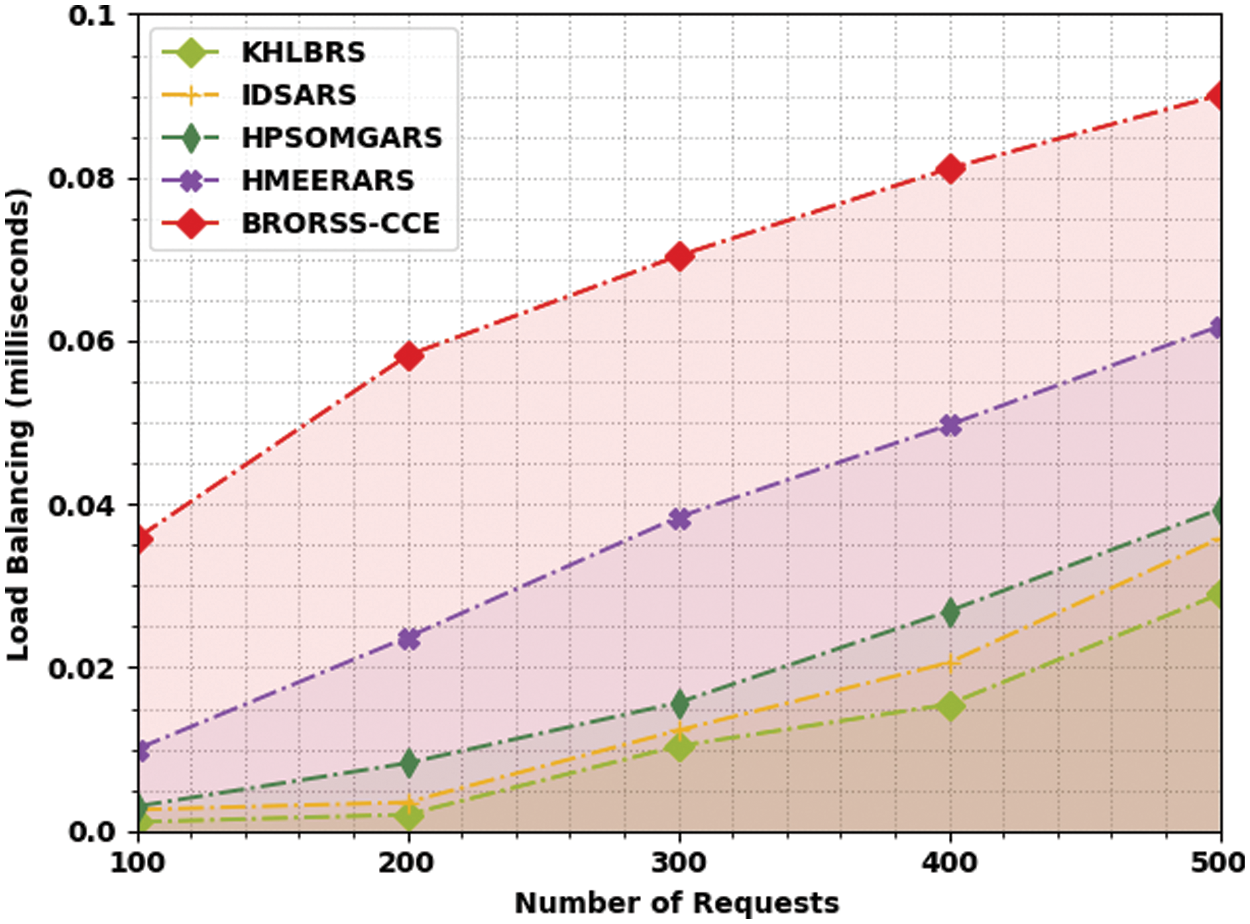
Figure 5: LOADB analysis of BRORSS-CCE approach under count of requests

Table 4 and Fig. 6 illustrate a comparative Throughout (THROU) investigation of the BRORSS-CCE model with other recent models. The outcome referred that the KHLBRS model has showcased poor performance with minimal THROU values. Besides, the IDSARS approach has certainly attained increased THROU values. Similarly, the HPSOMGARS and HMEERARS techniques have accomplished reasonable THROU values. The experimental values inferred that the BRORSS-CCE methodology has reported enhanced results with increased THROU values under all requests. For instance, on 500 requests, the BRORSS-CCE system has offered higher THROU of 442 ms, whereas the KHLBRS, IDSARS, HPSOMGARS, and HMEERARS algorithms have accomplished lower THROU of 93, 133, 168, and 203 ms correspondingly.

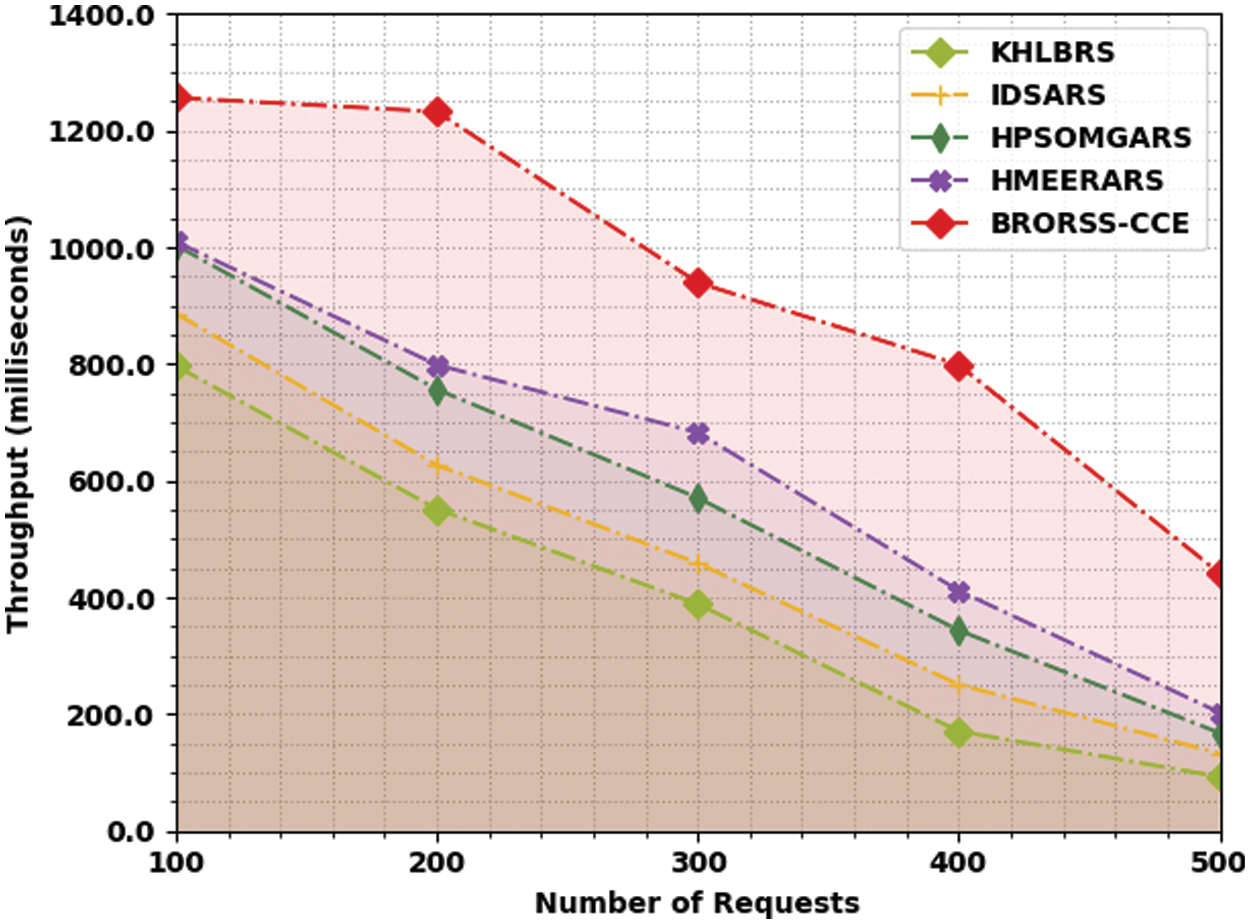
Figure 6: THROU analysis of BRORSS-CCE approach under count of requests

Table 5 and Fig. 7 showcases a comparative relative error (RELA) analysis of the BRORSS-CCE model with other recent algorithms. The results indicated that the KHLBRS methodology had showcased poor performance with maximum RELA values. Next, the IDSARS model has certainly attained reduced RELA values. At the same time, the HPSOMGARS and HMEERARS techniques have accomplished reasonable RELA values. The experimental values inferred that the BRORSS-CCE approach had reported enhanced results with minimal RELA values under all requests. For instance, on 500 requests, the BRORSS-CCE model has obtainable lower RELA of 0.035, whereas the KHLBRS, IDSARS, HPSOMGARS, and HMEERARS algorithms have accomplished higher RELA of 0.118, 0.097, 0.062, and 0.053, respectively.

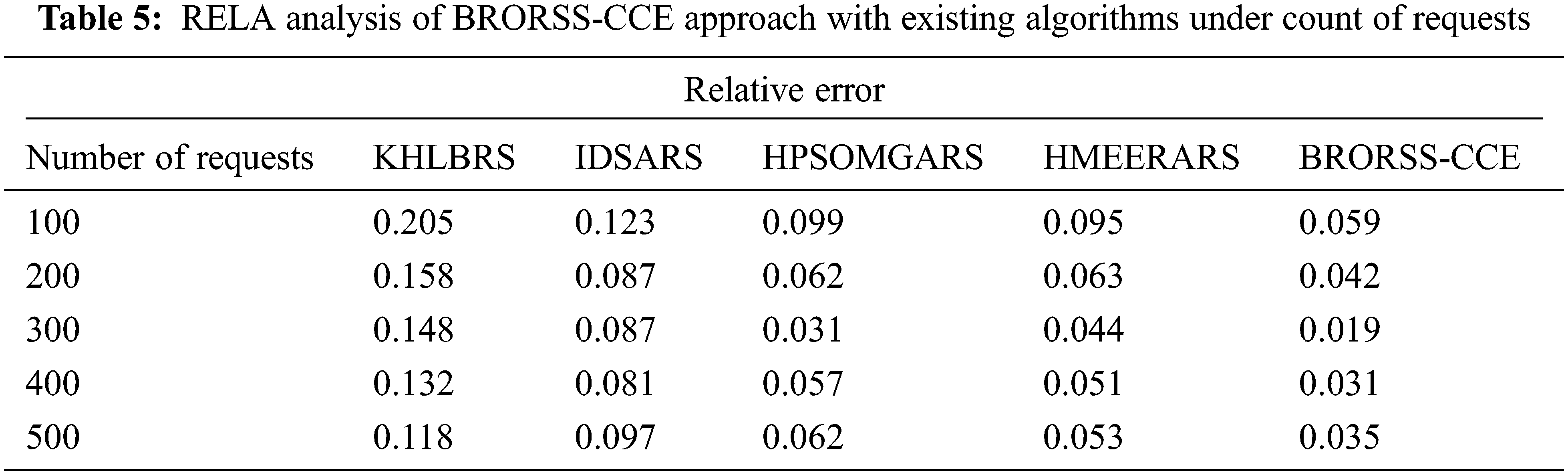
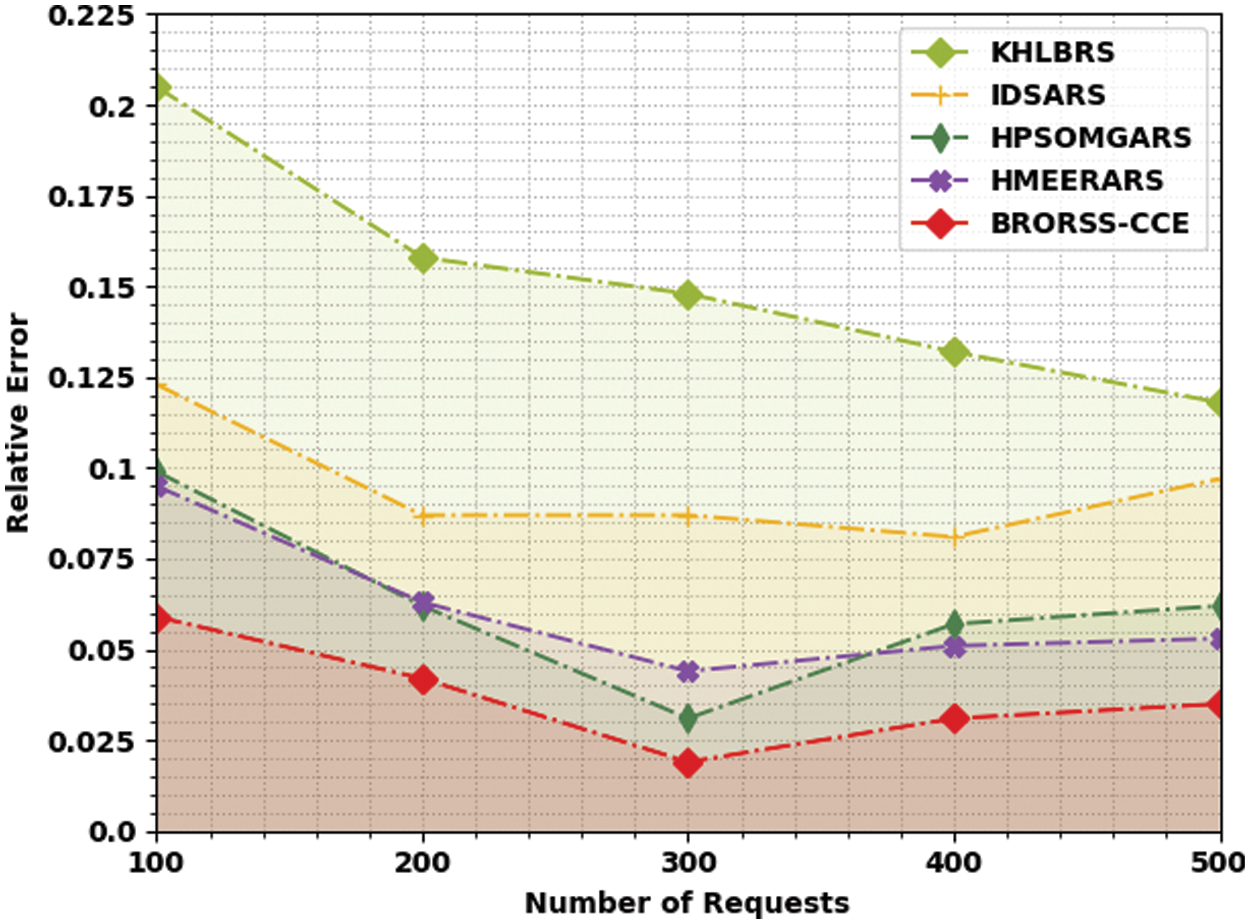
Figure 7: RELA analysis of BRORSS-CCE approach under count of requests

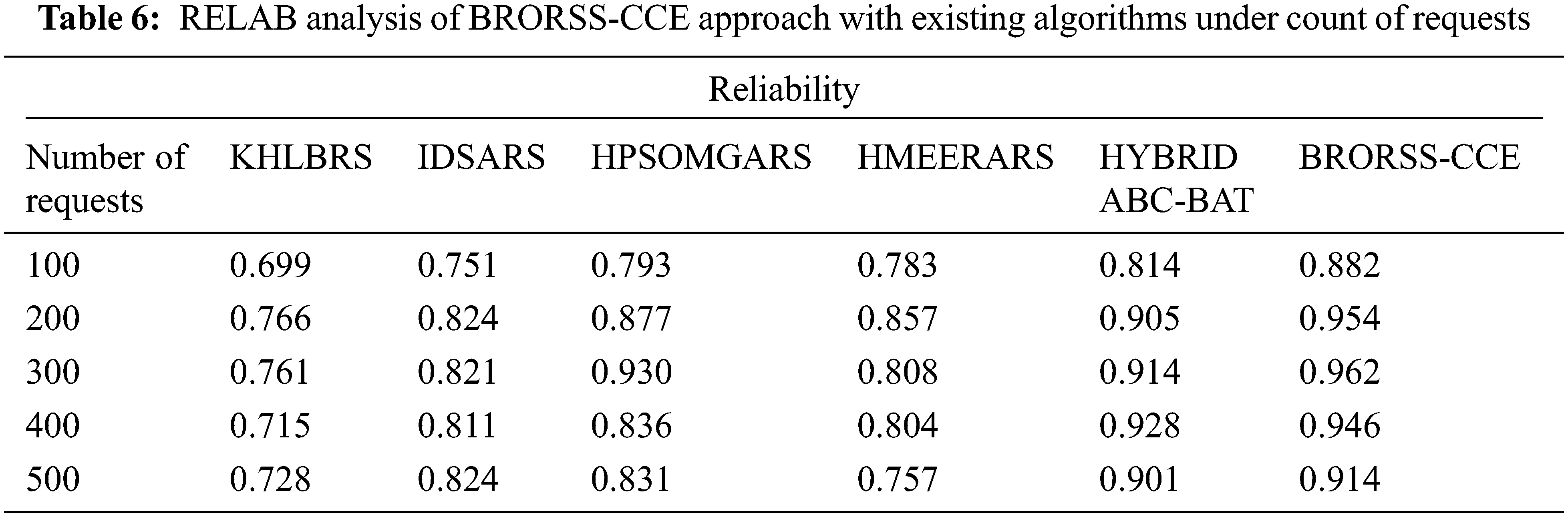
Table 6 depict comparative reliability (RELAB) inspection of the BRORSS-CCE technique with other recent approaches. The outcomes signified that the KHLBRS approach had showcased poor performance with minimal RELAB values. In line with this, the IDSARS algorithm has certainly attained increased RELAB values. Moreover, the HPSOMGARS, HMEERARS, and hybrid ABC-BAT systems have accomplished reasonable RELAB values. The experimental values inferred that the BRORSS-CCE technique had reported superior outcomes with enhanced RELAB values under all requests. For instance, on 500 requests, the BRORSS-CCE approach has offered a maximal RELAB of 0.914. In contrast, the KHLBRS, IDSARS, HPSOMGARS, hybrid ABC-BAT, and HMEERARS techniques have accomplished reduced LOADB of 0.728, 0.824, 0.831, 0.901, and 0.757, correspondingly.

6  Conclusion

This study introduces a new BRORSS-CCE technique for effectual resource allocation in the CC environment. The presented BRORSS-CCE technique majorly schedules the available resources for maximum utilization and effectual makespan. In the presented BRORSS-CCE technique, the BRO is a population-based algorithm where all the individuals are denoted by a soldier/player who likes to go towards the optimal place and ultimate survival. The BRORSS-CCE technique can be employed to balance the load, distribute resources based on demand and assure services to all requests. The experimental validation of the BRORSS-CCE technique is tested under distinct aspects. The experimental outcomes indicated the enhancements of the BRORSS-CCE technique over other models. Blockchain technology can be included to assure security in CC platform.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. P. Bal, S. Mohapatra, T. Das, K. Srinivasan and Y. Hu, “A joint resource allocation, security with efficient task scheduling in cloud computing using hybrid machine learning techniques,” Sensors, vol. 22, no. 3, pp. 1242, 2022. [Google Scholar] [PubMed]

2. R. Vijayalakshmi, V. Vasudevan, S. Kadry and R. L. Kumar, “Optimization of makespan and resource utilization in the fog computing environment through task scheduling algorithm,” International Journal of Wavelets, Multiresolution and Information Processing, vol. 18, no. 1, pp. 1941025, 2020. [Google Scholar]

3. M. B. Gawali and S. K. Shinde, “Task scheduling and resource allocation in cloud computing using a heuristic approach,” Journal of Cloud Computing, vol. 7, no. 1, pp. 4, 2018. [Google Scholar]

4. A. Belgacem and K. B. Bey, “Multiobjective workflow scheduling in cloud computing: Trade-off between makespan and cost,” Cluster Computing, vol. 25, no. 1, pp. 579–595, 2022. [Google Scholar]

5. Z. Peng, J. Lin, D. Cui, Q. Li and J. He, “A multiobjective trade-off framework for cloud resource scheduling based on the deep Q-network algorithm,” Cluster Computing, vol. 23, no. 4, pp. 2753–2767, 2020. [Google Scholar]

6. B. Dewangan, A. Agarwal and A. Pasricha, “Resource scheduling in cloud a comparative study,” International Journal of Computer Sciences and Engineering, vol. 6, no. 8, pp. 168–173, 2018. [Google Scholar]

7. R. G. Shooli and M. M. Javidi, “Using gravitational search algorithm enhanced by fuzzy for resource allocation in cloud computing environments,” SN Applied Sciences, vol. 2, no. 2, pp. 195, 2020. [Google Scholar]

8. J. Zheng and Y. Wang, “A hybrid multiobjective bat algorithm for solving cloud computing resource scheduling problems,” Sustainability, vol. 13, no. 14, pp. 7933, 2021. [Google Scholar]

9. V. Sathiyamoorthi, P. Keerthika, P. Suresh, Z. Zhang, A. Rao et al., “Adaptive fault tolerant resource allocation scheme for cloud computing environments,” Journal of Organizational and End User Computing, vol. 33, no. 5, pp. 135–152, 2021. [Google Scholar]

10. S. Varshney and S. Singh, “A survey on resource scheduling algorithms in cloud computing,” International Journal of Applied Engineering Research, vol. 13, no. 9, pp. 6839–6845, 2018. [Google Scholar]

11. S. H. H. Madni, M. S. Abd Latiff, S. M. Abdulhamid and J. Ali, “Hybrid gradient descent cuckoo search (HGDCS) algorithm for resource scheduling in IaaS cloud computing environment,” Cluster Computing, vol. 22, no. 1, pp. 301–334, 2019. [Google Scholar]

12. N. Potu, C. Jatoth and P. Parvataneni, “Optimizing resource scheduling based on extended particle swarm optimization in fog computing environments,” Concurrency and Computation: Practice and Experience, vol. 33, no. 23, pp. 1–13, 2021. [Google Scholar]

13. K. L. Devi and S. Valli, “Multiobjective heuristics algorithm for dynamic resource scheduling in the cloud computing environment,” The Journal of Supercomputing, vol. 77, no. 8, pp. 8252–8280, 2021. [Google Scholar]

14. A. Belgacem, K. Beghdad-Bey, H. Nacer and S. Bouznad, “Efficient dynamic resource allocation method for cloud computing environment,” Cluster Computing, vol. 23, no. 4, pp. 2871–2889, 2020. [Google Scholar]

15. T. Jena and J. R. Mohanty, “GA-Based customer-conscious resource allocation and task scheduling in multi-cloud computing,” Arabian Journal for Science and Engineering, vol. 43, no. 8, pp. 4115–4130, 2018. [Google Scholar]

16. S. H. H. Madni, M. S. A. Latiff, J. Ali and S. M. Abdulhamid, “Multi-objective-oriented cuckoo search optimization-based resource scheduling algorithm for clouds,” Arabian Journal for Science and Engineering, vol. 44, no. 4, pp. 3585–3602, 2019. [Google Scholar]

17. I. Strumberger, N. Bacanin, M. Tuba and E. Tuba, “Resource scheduling in cloud computing based on a hybridized whale optimization algorithm,” Applied Sciences, vol. 9, no. 22, pp. 4893, 2019. [Google Scholar]

18. J. -T. Tsai, J. -C. Fang and J. -H. Chou, “Optimized task scheduling and resource allocation on cloud computing environment using improved differential evolution algorithm,” Computers & Operations Research, vol. 40, no. 12, pp. 3045–3055, 2013. [Google Scholar]

19. S. Agahian and T. Akan, “Battle royale optimizer for training multi-layer perceptron,” Evolving Systems, vol. 13, no. 4, pp. 563–575, 2021. [Google Scholar]

20. S. H. H. Madni, M. S. A. Latiff, Y. Coulibaly and S. M. Abdulhamid, “Recent advancements in resource allocation techniques for cloud computing environment: A systematic review,” Cluster Computing, vol. 20, no. 3, pp. 2489–2533, 2017. [Google Scholar]