Enhancing the Adversarial Transferability with Channel Decomposition

1  Introduction

With the rapid development and remarkable success of deep neural networks (DNNs) in various tasks [1–3], the security of DNNs has received increasing attention. The robustness of DNNs is of great importance, especially in security-sensitive scenarios such as face recognition [4] and autonomous driving [5]. However, DNNs are vulnerable to adversarial examples [6], which are crafted by adding subtle perturbations to the original input examples. In recent years, a large number of adversarial attacks [7–10] have been proposed to generate more aggressive adversarial examples to study the robustness of DNNs.

Adversarial attacks can be divided into white-box and black-box attacks. In the white-box scenario, the attacker has access to the full knowledge of the target model, including the framework, parameters, and trainable weights. If the adversarial examples are crafted by accessing the gradient of the target model, it is called gradient-based attacks [11]. However, in practical applications, adversaries usually do not know or have limited knowledge of the target model. In this case, the adversarial attacks are called black-box attacks, which can be divided into query-based attacks [12–16] and transfer-based attacks [17,18]. In query-based attacks, it can be further divided into score-based and decision-based attacks depending on whether the adversary generates adversarial examples by querying the classification probability output or the hard label output of the target model. In transfer-based attacks, the adversarial examples are crafted by attacking a substitute model of the target model, then transferring attacks to the target model.

In this work, we propose a new transfer-based black-box attack, called the Channel Decomposition Attack Method (CDAM) to improve the transferability of adversarial examples. Specifically, it decomposes the three-channel of the original red-green-blue (RGB) image and uses zero-value padding. Each channel individually constitutes a three-channel image, which together with the original image forms a set of images for gradient calculation. CDAM tunes the current gradient by aggregating the gradients to stabilize the update direction. For escaping from local optima, CDAM adds or subtracts the random noise of the standard normal distribution to initialize the data point at each iteration. Besides, CDAM can be combined with other transfer-based black-box attacks [19,20] to further improve transferability. Empirical experiments on the standard ImageNet dataset show that the proposed CDAM can achieve higher success rates in the black-box scenario than the state-of-the-art transfer-based black-box attack [21]. For instance, CDAM improves the average success rate of the effective transfer-based attack by more than 8% using the adversarial examples crafted on Inception-v3. We also visualize the adversarial examples in Fig. 1. Our contributions are as follows:

1)   We propose a new transfer-based black-box attack method. Different from the others, it considers each channel of the input separately when attacking the substitute model, and calculates the aggregated gradient to tune the gradient direction and stabilize the gradient update.

2)   CDAM initializes the data point with random noise to escape from local optima, which reduces the dependence on substitute models and generates adversarial examples that can attack multiple black-box. Besides, it can combine with other transfer-based black-box attack methods, which could further enhance the transferability of crafted adversarial examples.

3)   Compared to the state-of-art method: CDAM obtains the highest average attack success rates; Under the ensemble-model setting, our integrated method achieves an average success rate of 96.6% on three adversarially trained black-box models, which is higher than the 85.6% of the current best method. The rest of the paper is organized as follows: Section 2 summarizes the related work; Section 3 introduces the implementation details of CDAM; Section 4 presents the experimental results and evaluates the performance of CDAM and Section 5 summarizes the work and describes the future work.

Figure 1: Adversarial examples generated by admix attack method (AAM) [21], Combined AAM (CAAM) [21], and our proposed CDAM, combined CDAM (CCDAM) with maximum perturbation ϵ  = 16. All adversarial examples are crafted on inception-v3 [22]. Our proposed CDAM and CCDAM generate visually similar adversaries as other attacks but have higher transferability

2  Related Work

Gradient-based Attacks: DNNs are vulnerable to adversarial attacks. Fast gradient sign method (FGSM) [11] generates adversarial examples that can deceive the neural network by adding increments to benign examples in the direction of the gradient. Due to the low attack success rate of FGSM, the Basic iterative method (BIM) [7] extends FGSM by multi-step iterations to improve the success rates of the attacks. Projected gradient descent (PGD) [8] introduces random initialization and projection based on BIM to improve the attack success rate further. Deepfool [9] uses l2 norm to limit perturbation size to minimize the adversarial perturbation. However, such attacks cannot be applied directly to the black-box models, and it is difficult to transfer the adversarial examples crafted on the white-box model to black-box models.

Query-based Attacks: Query-based attacks are divided into score-based attacks and decision-based attacks. In the score-based setting, the adversary can query the target model’s confidence score to guide the attack’s process [12,14]. Zeroth order optimization (ZOO) [14] is the first proposed score-based attack, which reduces the attack time and ensures the attack effect by approximating the first and second derivatives and hierarchical attacks. Natural evolution strategies (NES) [23] utilize natural evolution to estimate gradients. Random gradient-free (RGF) [24] samples distribution-independent random vectors to estimate the gradient. Prior-guided random gradient-free (P-RGF) [15] further improves the query efficiency of RGF with a transfer-based prior. Different from score-based attacks, decision-based attacks can only use hard labels fed by the target model to craft adversarial examples. For example, the first decision-based adversarial attack in Reference [13] makes the adversarial example travel along the boundary between the adversarial and non-adversarial regions. Simple black-box attack (SimBA) [16] updates the query sample by a greedy strategy without estimating the gradient explicitly. Query-efficient boundary-based black-box attack (QEBA) [17] uses the projection function to sample from a lower dimensional space to improve the sampling efficiency. However, query-based attacks require thousands of queries on the black-box model in practical black-box attack scenarios, which is inefficient and easily detectable.

Transfer-based Attacks: Different models trained on the same dataset may share similar decision boundaries. Adversarial examples can be transferred across models to some extent. Therefore, transfer-based attacks center on finding a substitute model and performing a white-box attack on the substitute model. Then the crafted adversarial examples are transferred into the inaccessible black-box target model. Attacking a set of substitute models [25,26] helps to improve transferability. However, it suffers from expensive computational costs. The poor transferability of the adversarial examples generated based on optimization and iterative methods leads to poor success rates in attacking black box models. Momentum iterative fast gradient sign method (MI-FGSM) [18] integrates momentum into the iterative method to enhance the transferability. It accumulates velocity vectors along the gradient direction of the loss function during the iterative process to stabilize the update direction and avoid undesirable local maxima. Diversity input method (DIM) [20] proposes randomly transforming the input samples with a certain probability and then using them as the classifier’s input for subsequent derivation operations. It can be combined with MI-FGSM to improve transferability. Translation-invariant method (TIM) [19] reduces the dependence of substitute models by translational invariance property; it convolves the gradient with a predefined Gaussian kernel to update the gradient to generate more transferable adversarial examples. Nesterov iterative fast gradient sign method (NI-FGSM) [27] proposes using the Nesterov Accelerated Gradient instead of momentum. Unlike MI-FGSM, it obtains the gradient information for the next iteration in advance, which means that NI-FGSM can look forward better and jump out of the local optima faster than MI-FGSM. AAM [21] is one of the best transfer-based attacks. It randomly selects a set of samples from different categories, which are added to the original input sample in a small proportion by linear interpolation to construct a set of input samples. AAM improves the transferability of adversarial examples by calculating the average gradient of a set of mixed input samples. Although these methods produce adversarial examples with good transferability, they treat the input samples as a whole without considering the sample channel-to-channel effects, which may be one of the reasons why there is still a considerable gap compared to white-box attacks.

3  Methodology

3.1 Attack Scenarios

Given a substitute model f with parameters θ and x∈X is a benign image with the ground-true label y, L(f(x;θ), y) denotes the loss function of f. Our goal is to find an adversarial image xadv∈X that satisfies Eq. (1):

f(x;θ)≠f(xadv;θ)s.t.||x−xadv||p≤ϵ, (1)

where ||⋅||p denotes p− norm distance and ϵ is the maximum upper bound allowed for the perturbation. The smaller ϵ , the smaller the difference between the adversarial image and the benign image.

In this work, we use the l∞ norm to restrict the adversarial perturbations, i.e., Eq. (2):

xadv=argmax||x−x′||∞≤ϵ⁡(L(x′, y;θ)). (2)

3.2 The Channel Decomposition Attack Method

Transfer-based attacks transfer adversarial perturbations on a substitute to target models. However, due to the high dependence on the substitute models, they are easy to fall into local optima, which is also called the ‘overfit’ of the substitute model.

The process of generating adversarial examples is also treated as the training process of a neural network. In this perspective, DIM, SIM, and AAM could all be treated as ways to improve transferability through data augmentation.

However, to the best of our knowledge, existing attacks treat the RGB channels as a whole at each iteration to improve the transferability, without considering the impact of each channel individually. During each iteration of the attack, we consider the impact of each channel of RGB input. The RGB input channels are decomposed and padded with a zero-value matrix, with each channel forming a separate three-channel input. We feed them into the model to calculate the gradients. Then we calculate the aggregated gradient to tune the gradient update direction. We formulate this as Eq. (3):

xR, xG, xB=CDP(x) (3)

where xR, xG, xB are the decomposed and padded images of the three R, G, and B channels respectively. CDP refers to the decomposition and padding of the input x. We show the entire attack framework in Fig. 2.

Figure 2: The framework of CDAM, where H denotes the image height and W denotes the image width, sgn is the sign function, xt−1adv is the adversarial example at t−1 -th iteration, ⊕ denotes element-wise add, ⊖ denotes element-wise minus. The adversarial examples generated by CDAM can attack multiple black-box models

PGD improves the attack success rate by adding random noise, essentially adding pixel values to the images. From this, we can infer that appropriate noise addition or reduction can effectively improve the success rate of adversarial attacks. As shown in Fig. 2, we initialize the data point by adding or subtracting random noise sampled from standard normal distribution during each iteration, to further improve the transferability. The formula can be expressed as Eq. (4):

xadd, xsub=x±p⋅N(0, 1),  (4)

where N(0, 1) is the standard normal distribution of random noise and p is the hyper-parameter.

With the above analysis, we propose the CDAM. It calculates the aggregated gradient to tune the direction of the update gradient. Its formula can be expressed as Eq. (5):

gt+1X1′=1n∑x1′∈X1′∑i=0n−1∇x1t′adv(L(f(γi⋅x1t′advy;θ))), (5)

where n is the scale copies of each input, γi∈[0, 1] control the portion of x1′tadv and X1′ is the first set of input obtained by Eq. (3), i.e., X1′=[x, xR, xG, xB] .

Adding or subtracting the random noise from the standard normal distribution, thus initializing the position of the input to escape from local optima. The gradient can be formulated as Eq. (6):

gt+1X2′=1n∑x2′∈X2′∑i=0n−1∇x2t′adv(L(f(γi⋅x2t′advy;θ))), (6)

where X2′ is obtained by Eq. (4).

In summary, gt+1X1′ is used to tune the gradient and stabilize the update direction. gt+1X2′ is used to initialize the position of input to escape from local optima. The final update gradient is obtained by the above two gradients as Eq. (7):

g^t+1=α⋅gt+1X1′+β⋅gt+1X2′,  (7)

where α and β control the portion of gt+1X1′ and gt+1X2′ . The CDAM is summarized in Algorithm 1.

4  Experiments

4.1 Experimental Setups

4.1.1 Dataset

ImageNet large scale visual recognition challenge (ILSVRC) 2012 dataset [28] is a lightweight version of the ImageNet dataset. We select 1000 categories from the ILSVRC 2012 validation set and randomly select one from each category, a total of 1000 images that can be correctly recognized by all models, to verify the effectiveness of the proposed method.

4.1.2 Comparison Method

We compare the state-of-the-art methods AAM [21] and CAAM, which is combined with TIM [19] and DIM [20]. All attack methods are combined with MI-FGSM [18].

4.1.3 Models

We validate the effectiveness of CDAM on four popular normally trained models, namely Inception-v3 (M1) [22], Inception-v4 (M2) [29], Inception-Resnet-v2 (M3) [29], and Resnet-v2-101 (M4) [30] as well as three ensemble adversarially trained models, i.e., Inc-v3ens3 (Ma), Inc-v3ens4 (Mb) and IncRes-v2ens (Mc) [31].

4.1.4 Evaluation Criteria

We use the attack success rate to compare the performance of different methods. The success rate is an important metric in adversarial attacks, which divides the number of misclassified adversarial examples by the total number of images.

4.1.5 Implementation Details

We follow the attack setting in MI-FGSM, the maximum perturbation of ϵ is set to 16, the number of iterations is set to 10, and the step size is set to 1.6. For MI-FGSM, the decay factor is set to 1.0. For DIM, the transformation probability is set to 0.5. For TIM, we adopt the Gaussian kernel with kernel size 7×7 . For SIM, the number of scale copies is set to 5 (i.e., i = 0, 1, 2, 3, 4). For AAM, the number of samples of different categories is set to 3, and images for mixing with η=0.2 . For the proposed method, we set n=5 , γi=1/2i , p=0.2 , α=0.2 and β=0.5 .

4.2 Single-Model Attack

We first perform two adversarial attacks i.e., AAM and our proposed CDAM on a single neural network. We craft the adversarial examples on four normally trained neural networks and test them on seven neural networks. Table 1 shows the success rates of these attacks.

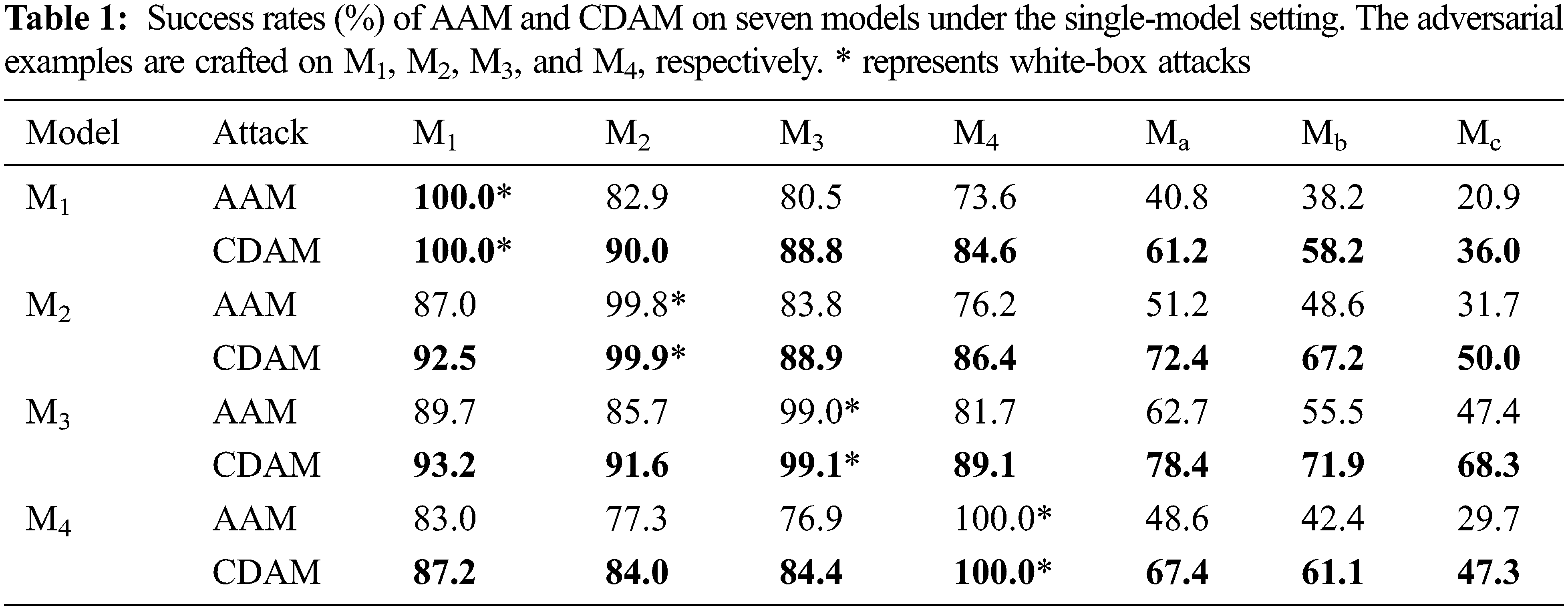
We can observe that CDAM outperforms both attacks on the normally trained black-box models and the adversarially trained black-box models while maintaining the success rates in the white-box scenario. In particular, when attacking the adversarially trained black-box model, CDAM outperforms AAM by a large margin, which is more practical for realistic scenarios.

For instance, when the attacked substitute model is M1, in the white-box scenario, both AAM and CDAM achieve success rates of 100.0%. However, in the black-box scenario, CDAM achieves an average success rate of 87.8%, which is 8.8% higher than AAM on the other three normally trained black-box models.

4.3 Combined with Other Transfer-Based Attack

We also validate the attack effectiveness of our proposed CDAM combined with other transfer-based attacks, such as TIM, DIM, and SIM. Since SIM is a special case of AAM and CDAM, we validate the effect achieved by combining TIM and DIM with AAM and CDAM, respectively. That is, CAAM and CCDAM. The results are shown in Table 2.

In general, attacks combined with CDAM achieved better transferability than AMM. Taking the substitute is M1 model for example, the success of CCDAM on three adversarially trained black-box models outperforms CAAM with a clear margin of 13.2%∼20.0%. Such remarkable improvements demonstrate the high effectiveness of the proposed method.

4.4 Ensemble-Model Attack

An adversarial example is more likely to be able to successfully attack another black-box model if it can attack multiple models at the same time. MI-FGSM has proved that attacking multiple models can effectively improve the transferability of adversarial examples. Therefore, to fully validate the effectiveness of the CDAM, we use the ensemble-model attack proposed in [18], which fuses the logit of multiple models for crafting adversarial examples. We attack four models, including M1, M2, M3, and M4, and verify the effectiveness of our method on three adversarially trained models.

Since adversarial examples are crafted on four normally trained models, all attacks have very similar success rates on these four models. Therefore, we only report the attack success rates on three adversarially trained black-box models.

As shown in Table 3, The average attack success rate achieved by CCDAM is higher than CAAM by 7.6%. This further convincingly demonstrates the high efficacy of CDAM.

4.5 Ablation Studies of Hyper-Parameters

For the number of input examples n and the portion of the input γi , we follow the setting in the [20] setup. We perform a series of ablation experiments to investigate the three hyper-parameters p, α and β of CDAM, and all the adversarial examples were crafted on the M1 model.

The portion of noise p : We report the attack success rates achieved by CDAM for different values of p, where α is fixed at 0.2 and β is fixed at 0.5. For the M1, i.e., the substitute model, CDAM achieves 100% attack success rates. As can be seen from Fig. 3a, the success rates increase as p increase, peaking at p.

Figure 3: Success rates (%) on the other six models with adversarial examples generated by CDAM on M1 model when varying hyper-parameters p, α and β

The weight of gtX1′α : We report the effect of the gradient weights calculated for the first set of images X1′ on the success rates, where p is fixed at 0.2 and β is fixed at 0.4. As can be seen from Fig. 3b, the success rates reach the highest when α=0.2 , and gradually decrease with the increase of α .

The weight of gtX2′β : We report the effect of the gradient weights calculated for the second set of images X2′ on the success rate, where p is fixed at 0.2 and α is fixed at 0.2. As can be seen from Fig. 3c, the success rates increase insignificantly as β continues to increase, reaching the highest rate when β=0.9 and near β=0.5 .

Through the above analysis, the change of p fluctuates a lot on the success rates, while the change of the values of α and β has less effect on the attack success rates. Therefore, we set p=0.2 , α=0.2 and β=0.5 .

5  Conclusion

In this work, we propose a new transfer-based black-box attack, called the CDAM to improve the transferability. Specifically, CDAM decomposes the channels and pads them with a zero-value matrix to generate a set of images for tuning the gradient direction and stabilizing the update gradient. During each iteration, it initializes the data point with random noise to escape from local optima, further improving the adversarial attacks’ transferability. Extensive experiments show that the proposed CDAM significantly improves the transferability of the adversarial attacks in the black-box scenario. In future work, we plan to reduce the memory and time overhead of CDAM and increase the speed of generating adversarial examples.

Funding Statement: This work was supported by Sichuan Science and Technology Program [No. 2022YFG0315, 2022YFG0174]; Sichuan Gas Turbine Research Institute stability support project of China Aero Engine Group Co., Ltd. [GJCZ-2019-71]; Key project of Chengdu [No. 2019-YF09-00044-CG].

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. Agrawal, M. Zarour, M. Alenezi, R. Kumar and R. A. Khan, “Security durability assessment through fuzzy analytic hierarchy process,” PeerJ Computer Science, vol. 5, no. 5, pp. 465–473, 2019. [Google Scholar]

2. L. Xiaolei, L. Xiaoyu, Z. Desheng, B. Jiayu, P. Yu et al., “Automatic selection attacks framework for hard label black-box models,” in Proc. INFOCOM, USA, pp. 1–7, 2022. [Google Scholar]

3. Z. Desheng, R. Ziyong, L. Zhifeng, L. Liang and T. Lulu, “An efficient bar code image recognition algorithm for sorting system,” Computers, Materials & Continua, vol. 64, no. 3, pp. 1885–1895, 2020. [Google Scholar]

4. Z. Yaoyao and D. Weihong, “Towards transferable adversarial attack against deep face recognition,” IEEE Transactions on Information Forensics and Security, vol. 16, no. 25, pp. 1452–1466, 2020. [Google Scholar]

5. Y. Cao, C. Xiao, B. Cyr, Y. Zhou, W. Park et al., “Adversarial sensor attack on lidar-based perception in autonomous driving,” in Proc. CCS, London, UK, pp. 2267–2281, 2019. [Google Scholar]

6. C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan et al., “Intriguing properties of neural networks,” in Proc. ICLR, Banff, CAN, pp. 142–153, 2014. [Google Scholar]

7. A. Kurakin, I. J. Goodfellow and S. Bengio, “Adversarial examples in the physical world,” in Proc. ICLR, Peurto Rico, PR, USA, pp. 99–112, 2016. [Google Scholar]

8. A. Madry, A. Makelov, L. Schmidt, D. Tsipras and A. Vladu, “Towards deep learning models resistant to adversarial attacks,” in Proc. ICLR, Vancouver, VAN, CAN, pp. 542–554, 2018. [Google Scholar]

9. S. Moosavi-Dezfooli, A. Fawzi and P. Frossard, “Deepfool: A simple and accurate method to fool deep neural networks,” in Proc. CVPR, Las Vegas, Nevada, USA, pp. 2574–2582, 2016. [Google Scholar]

10. N. Papernot, P. McDaniel, S. Jha, M. Fredrikson, Z. Berkay et al., “The limitations of deep learning in adversarial settings,” in Proc. EuroS&P, Saarbrucken, GER, pp. 372–387, 2016. [Google Scholar]

11. I. J. Goodfellow, J. Shlens and C. Szegedy, “Explaining and harnessing adversarial examples,” in Proc. ICLR, California, CA, USA, pp. 226–234, 2015. [Google Scholar]

12. A. N. Bhagoji, W. He, B. Li and D. Song, “Practical black-box attacks on deep neural networks using efficient query mechanisms,” in Proc. ECCV, Munich, GER, pp. 154–169, 2018. [Google Scholar]

13. W. Brendel, J. Rauber and M. Bethge, “Decision-based adversarial attacks: Reliable attacks against black-box machine learning models,” arXiv preprint arXiv: 1712.04248, 2017. [Google Scholar]

14. P. Chen, H. Zhang, Y. Sharma, J. Yi and C. Hsieh, “Zoo: Zeroth order optimization based black-box attacks to deep neural networks without training substitute models,” in Proc. AISec, Los Angeles, CA, USA, pp. 15–26, 2017. [Google Scholar]

15. S. Cheng, Y. Dong, T. Pang, H. Su and J. Zhu, “Improving black-box adversarial attacks with a transfer-based prior,” in Proc. NeurIPS, Vancouver, Canada, pp. 189–201, 2019. [Google Scholar]

16. C. Guo, J. Gardner, Y. You, A. G. Wilson and K. Weinberger, “Simple black-box adversarial attacks,” in Proc. ICML, Long Beach, CA, USA, pp. 2484–2493, 2019. [Google Scholar]

17. H. Li, X. Xu, X. Zhang, S. Yang and B. Li, “Qeba: Query-efficient boundary-based black-box attack,” in Proc. CVPR, Seattle, WA, USA, pp. 1221–1230, 2020. [Google Scholar]

18. Y. Dong, F. Liao, T. Pang, H. Su, J. Zhu et al., “Boosting adversarial attacks with momentum,” in Proc. CVPR, Salt Lake City, UT, USA, pp. 9185–9193, 2018. [Google Scholar]

19. Y. Dong, T. Pang, H. Su and J. Zhu, “Evading defenses to transferable adversarial examples by translation-invariant attacks,” in Proc. CVPR, Long Beach, CA, USA, pp. 4312–4321, 2019. [Google Scholar]

20. C. Xie, Z. Zhang, Y. Zhou S. Bai, J. Wang et al., “Improving transferability of adversarial examples with inputdiversity,” in Proc. CVPR, Long Beach, CA, USA, pp. 2730–2739, 2019. [Google Scholar]

21. X. Wang, X. He, J. Wang, and K. He, “Admix: Enhancing the transferability of adversarial attacks,” in Proc. ICCV, Montreal, Quebec, CAN, pp. 16158–16167, 2021. [Google Scholar]

22. C. Szegedy, V. Vanhoucke, S. Ioffe, J. Shlens and Z. Wojna, “Rethinking the inception architecture for computervision,” in Proc. CVPR, Las Vegas, NV, USA, pp. 2818–2826, 2016. [Google Scholar]

23. A. Ilyas, L. Engstrom, A. Athalye and J. Lin, “Black-box adversarial attacks with limited queries and information,” in Proc. ICML, Stockholm, SE, pp. 2137–2146, 2018. [Google Scholar]

24. Y. Nesterov and V. Spokoiny, “Random gradient-free minimization of convex functions,” Foundations of Computational Mathematics, vol. 17, no. 2, pp. 527–566, 2017. [Google Scholar]

25. J. Lu, T. Issaranon and D. Forsyth, “Safetynet: Detecting and rejecting adversarial examples robustly,” in Proc. ICCV, Venice, ITA, pp. 446–454, 2017. [Google Scholar]

26. N. Papernot, P. McDaniel, I. Goodfellow, S. Jha, Z. B. Celik et al., “Practical black-box attacks against machine learning,” in Proc. ASIACCS, Dubai, UAE, pp. 506–519, 2017. [Google Scholar]

27. J. Lin, C. Song, K. He, L. Wang and J. E. Hopcroft, “Nesterov accelerated gradient and scale invariance for adversarial attacks,” in Proc. ICLR, New Orleans, USA, pp. 681–696, 2019. [Google Scholar]

28. O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh et al., “Imagenet large scale visual recognition challenge,” International Journal of Computer Vision, vol. 115, no. 3, pp. 211–252, 2015. [Google Scholar]

29. C. Szegedy, S. Ioffe, V. Vanhoucke and A. A. Alemi, “Inception-v4, inception-resnet and the impact of residual connections on learning,” in Proc. AAAI, San Francisco, USA, pp. 1087–1097, 2017. [Google Scholar]

30. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. CVPR, Hawaii, USA, pp. 770–778, 2016. [Google Scholar]

31. F. Tramèr, D. Boneh, A. Kurakin, I. Goodfellow, N. Papernot et al., “Ensemble adversarial training: Attacks and defenses,” in Proc. ICLR, Toulon, FR, pp. 1021–1030, 2018. [Google Scholar]