Novel Metrics for Mutation Analysis

1  Introduction

Software testing provides instruments for verifying that predefined requirements are met and that the correct outputs are generated through the widespread use of software testing to eliminate potential bugs and ensure flawless software operation [1]. Formal method-based testing is one of the active research areas in software testing [2]. Formal methods are mathematical techniques used in computer science, specifically software and hardware engineering, to identify, develop, and validate software and hardware systems. The benefit of this modeling is to detect possible problems through pre-testing and to prevent future economic crises. In this respect, model-based methods such as FSM are widely used in critical systems such as the defense industry, and health, air, and space technologies. Formal methods permit demonstrating that a system or model satisfies the requirements.

Existing formal models for expressing software systems include finite state machines (FSM), Petri nets, and the Unified Modeling Language (UML). The Finite State Machine (FSM) is a widely used mathematical model with distinct inputs and outputs. It is primarily employed to model hardware and software systems. Various test-creation methods for FSMs have been suggested in the literature. The well-known algorithms are transition tour (CPP), W, Wp, UIO, UIOv, DS, HSI, H, SPY, and P [3]. Numerous studies compare these procedures. Typically, mutation analysis is used to evaluate the quality of tests designed for FSMs with these tools.

In software testing, mutation analysis is valuable for measuring defect detection capability and test effectiveness in formal models. Requirements, source code, models, and software products can be subject to mutation analysis. The software is systematically modified under certain error assumptions in mutation analysis to generate mutants. The created mutants are frequently used to evaluate a test set. Mutants are subjected to each test scenario in the test suite to assess their performance. Fault detection rate (FDR) is mutation analysis’s most current and widely used metric. FDR =M′M   is the formula used to calculate the fault detection rate. Here, M’ represents the mutant killed, whereas M represents the total number of mutants created.

Nonetheless, this metric has a few deficiencies. Although the FDR metric provides valuable information regarding the performance of test generation methods, it falls short of indicating efficacy. To resolve these issues, our study suggested three new metrics: “Fault detection rate per test set, fault detection rate per test scenario, and fault detection rate per time.”

When running the test scenario, it moves from the starting point to the point where the test will be started. Then the test is run, and finally, it returns from the endpoint to the starting point. The ways to get to the state where the test was to begin and return to the beginning after the test generates a significant amount of repetition. To avoid this situation, it is necessary to create fewer test cases [3]. In other words, the length of the test case is an important parameter. From this point of view, the “average mutant killing capacity per test scenario” (FDR |TC|) parameter has been developed to compare test quality in terms of showing the quality of the created test scenarios because the (FDR |TC|) metric allows for ranking in terms of mutant capture performance and scarcity of test cases.

The length of the test suite is an important performance parameter [3]. The long test suite runs slowly during execution. On the other hand, the shorter length has a higher performance than the two test suites with the same error detection rate. From this point of view, another metric we propose in the study and use to compare methods is the average mutant killing capacity divided by the length of the test set (FDR |TS|) . This metric also gives the average mutant killing capacity per pass of a test set.

With the developing technology, scaling has become essential to test extensive systems today [3]. Because in extensive systems, it may be necessary to test the entire system, compromising the detection rate. One of the essential effects of scalability is time. However, previous studies have yet to compare existing methods in terms of time. This study shows that many forms only work at a low scale. The biggest reason this reality is overlooked is that no parameter expressing the duration exists. Based on this, the time metric was developed in our study.

In our study, first of all, relevant studies are included. Afterward, FSM tests, test development methods, and mutation analysis are explained. Subsequently, the new metrics we developed within the scope of the study were discussed, and the study’s limitations were included. Finally, the results and evaluations related to the metrics we developed are given.

2  Related Work

Mutation testing is a standard evaluation technique for test suites [3]. The most significant issue with mutation analysis is that it complicates the computation of large systems [4]. Due to this, there has been a substantial increase in research on simplification in mutants [5]. It can be said that articles on mutant simplification, mutant equality [6], and effective mutants are concentrated in the literature [7,8]. On the other hand, there are also related articles in fields such as testing, the nuclear industry, the Internet of things, and deep learning [9]. This section provides comprehensive research on effective mutants and metrics. This is the result of our research focusing on improved mutant selection.

Kintis et al. created a new tool called iPITRV to improve the efficacy of mutation testing [10]. iPITRV outperforms the competition by discovering 6 percent more errors than combined. This method produces the best results overall. Wang et al. proposed using higher-order mutants to simulate complex failures [11]. Theoretically, these mutants apply to multiple failure scenarios. Experiments indicate that they can aid in enhancing the performance of high-order mutants. Zhang et al. proposed a low-cost, simple-to-implement method to improve the efficacy of mutation testing [12]. The proposed instrument can identify test suite flaws and generate new test cases accordingly. Experimental results demonstrate that the tool is highly competitive with contemporary supervised methods. Zhu et al. suggested additional research on reporting mutation testing in experiments [13]. Sánchez et al. examined the utility of mutation testing to evaluate and enhance performance testing [14]. Delgado-Pérez et al. investigated the viability of performing performance mutation testing at the source code level for general-purpose programming languages [15]. Zhu et al. proposed a collection of “mutation score antipatterns” that enable software engineers to refactor existing code or add tests to increase the mutation score [16]. When examining the studies, it is evident that numerous efforts have been made to improve the quality of mutants. However, no research has been conducted on defining a quality mutant.

To identify the most valuable operators, Delgado-Pérez et al. defined metrics [15]. Coverage data reduces the number of mutants at the expense of poor performance. Rani et al. investigated Java program operators and attempted to develop more efficient operators [17]. Examining these studies reveals that they concentrate on identifying operators in terms of metrics.

Another study presents an analytical and numerical analysis of a computer virus epidemic model. Features have been validated using test cases and computer simulations [18]. In a different study, a powerful tool has been developed for all nonlinear models of biomedical engineering problems with the structural preservation method [19]. Akgül et al. extended the classical computer virus model to the fractional fractal model in their study and then brought a solution to the model with the Atangana-Toufik method [20]. In a different study, the fractional order computer epidemic model was analyzed. In this context, a classical computer epidemic model has been extended to a fractional order model using Atangana-Baleanu fractional differential operator in the sense of Caputo [21]. Another study investigated the transmission dynamics of computer viruses interconnected via a global network. A numerical simulation example applied within the scope of the study confirmed the theoretical results of the designed technique [22]. In another study, a nonlinear delayed model was investigated to examine the dynamics of a virus in a computer network. In this framework, many significant results have been obtained for the stability of the model balances by using the Routh Hurwitz criterion, the Volterra Lyapunov function, and the Lasalle invariance principle [23].

As far as we know, no diagnosis has been made in any of the existing studies in the literature showing the relationship between test case length, test suite length, and duration length over performance. Thanks to this definition, the current errors of the parameters that may be faulty are eliminated, and an evaluation opportunity that can reveal higher performance is presented. For example, the test suite and case size must be short. But if the performance is terrible, the length evaluation is meaningless. The same is true for the time parameter. If the performance is too low, performing the test quickly will not be meaningful. For this reason, unlike the literature, it has been revealed that more information can be obtained about test suites thanks to the metrics we have developed.

3  Testing Finite State Testing

FSM is a mathematical model with discrete inputs and outputs. This model is used for modeling hardware and software systems. Some examples include text editors, compilers, synchronous sequential circuits, microprocessors, etc. Therefore, FSM is quite a standard model in computer science and engineering.

Test cases are test procedures that can be run successfully or unsuccessfully. Negative results should be obtained at the end of negative test cases, and positive results should be obtained in positive test cases. The test is considered successful if the expected test results match the results we have. The test case length represents the total processing steps required to run the test case.

Test suite refers to a set of test cases collectively. Here, the output of one test case can be the input of another test case. The test suite length represents the sum of the size of all test cases.

Moore and Mealy machines are the most common FSM models. A Mealy machine is defined as M (Q, Σ, Δ, δ, λ, q0)  where Q is a set of finite states, Σ is a set of input symbols, ∆ is a set of output symbols, δ: Q × Σ › → Q is the state transition function, λ: Q × Σ › → Δ is the output function, and q0 is the initial state.

3.1 Test Generation Methods

Finite State Machine (FSM), a formal modeling technique to represent circuits and software, has been widely used in testing. Even though there exist several test generation methods, the current increase in the demand for pervasive and safety-critical systems, as well as the increase in software size, calls for more rigorous ways that can produce better test suites, particularly in terms of test suite size, test case size, time spent for test generation, fault detection ratio and fault exposing potential.

In the literature, various methods are suggested to create test cases for FSMs. The most common are the Chinese Postman Problem (CPP), H-Switch-Cover (HSC), UIO, H, W, HSI, P, and SPY methods. This study examined CPP, HSC, SPY, P, HIS, and W methods. CPP and HSC methods are included in our comparison set because they produce small test cases in transition covers. On the other hand, W, HSI, P, and SPY methods were included in the study because of their up-to-date and widespread use.

3.1.1 Chinese Postman Method (Transition Tour)

A Chinese mathematician first studied CCP and came out as a postman who wanted to distribute the letters he received from the post office by stopping by all the streets in the city as quickly as possible. After delivering the letters, the postman had to return to the post office, where he had started. Thus, this problem is referred to as CPP in the literature. The purpose of the CCP is to find the shortest laps/tours that pass through the edges of a given network a minimum of once. This problem is focused on non-balanced graphs. The number of entry and exit edges on a vertex is different. The CPP method takes place in three stages. The algorithms used in these stages are the Floyd-Warshall algorithm, the Hungarian Method, and the Hierholzer algorithm. If the graph is balanced, an Euler cycle search algorithm can be used to find the minimum path visiting all edges.

For more information, see the article [24].

3.1.2 W Method

Let a given FSM be minimal and complete. W-set defines a string s (input sequences that distinguishes every two different states) such that O(qi, s) = O(qj, s) . A distinguishable (characterization) W-set always exists for each complete reduced FSM. The test generation method consists of two phases:

     i)  Characterization Sequence For Each Pair of States which provides O(qi, s) = O(qj, s)

    ii)  Creating Transition Cover Set which contains strings that are used to excite an FSM to ensure the coverage of all transitions.

For more information, see the article [25].

3.1.3 HSI Method

W method works only in completely-specified and deterministic FSMs. This is a limiting situation in many ways. The first method which is developed to overcome this is the HSI method. This method also works in partially-specified, nondeterministic FSMs. Our experiments have shown that the HSI method has a high performance in terms of runtime. Therefore, it also works well in terms of scalability. However, it has low performance in the fault detection ratio. In the worst case, the HSI method has the same test suite size as the W method.

For more information, see the article [26].

3.1.4 SPY Method

This method can be used in entirely and partially-specified FSMs, such as the HSI method. SPY aims to reduce test suite size. While creating the test suite, it does not create new branches. In the SPY method, these operations are calculated on the fly.

As presented later, our experiments show that the SPY method provides a 40% smaller test pack than the W and HSI methods. Besides, fewer test cases, as well as more prolonged test cases, are also possible. In most cases, SPY has a better error detection rate than the W and HSI methods. In contrast, the SPY method requires a longer time and more space to create test suites than traditional methods, making it unusable for large FSMs.

It can be referred to the article [27] for more information.

3.1.5 P Method

P method creates an n-complete test suite, meaning it is complete for all implementations with at most n states. The n-complete test suite guarantees to find all faulty implementations in FSMs with a bounded number of states. When creating an n-complete test suite, the P method uses user-defined test suites. P method handles most of the calculations on-the-fly.

The P method works in two steps. In the first step, test suites are created that can distinguish between states. In the second step, test cases are checked using the necessary rules for the n-complete test suite. Test cases suitable for this situation are added to the test suite.

According to the experiments, the test suite size of P is less than the traditional methods. However, the P method, like SPY, cannot produce results in relatively larger FSMs due to the lack of time and space.

It can be referred to the article [28] for more information.

3.1.6 HSC Method

HSC is a method based on the classic Switch Cover, which specifies that all transition pair criteria should be executed at a minimum once. One of the main features of Switch Cover is that it first converts FSM to the dual graph. The converted graph is balanced. After converting FSM to a dual graph, the Eulerian Cycle algorithm ensures that all edges are visited precisely once. The critical point of the HSC method is the usage of the Hierholzer algorithm as the Eulerian Cycle algorithm. The complexity of the Hierholzer algorithm is linear time.

It can be referred to the article [29] for more information.

3.1.7 Mutation Analysis

In mutation analysis, it is assumed that minor program modifications are sufficient to introduce complex errors [30]. The original model is systematically modified during mutation testing based on incorrect assumptions. These error assumptions represent potential programming errors. The mutant operators are aware of the erroneous beliefs that allow the mutants to mutate. According to Fabbri and Li [31], the following are potential mutation operators for FSMs: State-missing, State-extra, transition-missing, transition-extra, and Output-changed. The most prevalent application of mutation is measuring the effectiveness of test suites [12]. The mutant is destroyed if a test suite can differentiate a mutant from the original program. If it cannot determine, the mutant is considered to be alive. A mutant must be identical to the original program, or the test set must be insufficient to kill it for survival.

Mutation analysis establishes the sufficiency of a test set. These mutants are used to test the test set. The effectiveness of the tests is proportional to the total number of mutants eliminated. The most efficient test suite is the one that removes the most significant number of mutants at the optimal time. In practice, however, measuring the error detection rate of a system is complex. Because it is difficult to identify the system’s potential flaws precisely. FDR = M′ M  is the formula for determining the sufficiency of a test set. Where M represents the total number of mutants and M’ represents the number of mutants identified in the test set.

Mutation testing is a valuable technique. On the other hand, many mutants in a large model can present time and space constraints. The analysis must be conducted within reasonable time and space to avoid this issue. To accomplish this, techniques for reducing the number of mutants are utilized.

4  Novel Metrics

In this article, six basic metrics are examined. Three of these are the metrics we recommend in this study (fault detection ratio/test scenario length, fault detection ratio/test suite length, and fault detection ratio/test time). The other three are metrics from traditional methods (test case length, test suite length, and fault detection ratio), which we prefer because they’re widely used to compare with the metrics we’ve developed.

For example, test case length, test suite length, and duration alone don’t make sense in traditional metrics. Because the test scenario, test suite length, or test time may be short, it may not catch any mutant. In such a case, the test scenario, test set, or time does not give a meaningful result. Using these metrics with FDR reveals an effect related to its performance. This way, how much the metrics affect the performance can be easily seen.

If the test suite, test case, and test time are normalized between 0 and 1, the performance formula will be:

Performance =FDR |TS| + |TC| + |TIME|

5  Threats to Validity

There can be four threats to checking the study’s validity [32]: Conclusion, construct, and internal and external threats.

The study aims to compare FSM test generation methods in terms of time, killed mutants per test case, killed mutants per transitions, and other parameters. Evaluation results prove that this goal has been achieved.

Conclusion threat is mitigated by generating a possibly significant number of FSMs and concluding upon the averages. Regarding construct validity, the results are compared concerning the literature’s most common and adopted metrics. In the evaluations, the graph method often used in comparison studies is preferred to mitigate construct threats. To ensure the study’s internal validity, we utilized the same tool used in our previous works. Moreover, the methodology and the tool are tested by comparing the results of our tool and the existing tools.

For example, all methods have been compared to verify their performance. Hence, it ensured internal validity by realizing the study’s purpose.

FSMs are randomly generated to ensure the external validity of the study. 1500 FSMs are created. According to the literature, the quantity is sufficient for such a work made FSM [2,32]. This shows that the study can be generalized.

Although random FSMs were created, tests were made through many methods, tests were carried out by creating many mutants, and an attempt was made to select a sample as large as possible; it should be noted that our study reflects the results of a specific model.

Finding FDR can take time. For this reason, when a quick evaluation is desired, it may be necessary to use test time alone and test case and test suite length. However, such approaches will have a more significant potential for error.

6  Results

The metrics we recommend in this study are compared with traditional metrics such as Test Case Size (TCS), Test Suite Size (TSS), and Fault Detection Ratio (FDR) through HSC, CPP, SPY, P, HSI, and W methods. Random FSMs with varying numbers of states, inputs, outputs, and transitions were generated to compare the metrics. The error detection rate was evaluated using the mutation test. When comparing the scalability metric, the ISCAS’95 benchmark dataset is used.

Real-time systems can be tested thanks to Timed Automata. The metrics we developed can also be used for Timed Automata. The performance of the technique is not different from FSM. Therefore, using metrics in FSM or Timed Automata will produce the same results [27,28].

Performance metrics are calculated to compare the methods. To this end, the following five standard metrics are considered: Test Case Size (|TC|), Test Suite Size (|TS|), Fault Detection Ratio (FDR), FDR/|TC|, FDR/|TS|, and FDR/|TIME|.

All these performance metrics are measured against varying state, input, and output numbers. To this end, we use the following three configurations for each metric:

1.    Input is variable, the output is 10-valued, and the state is 10-valued

2.    Output is variable, input is 10-valued, and the state is 10-valued

3.    State is variable, input is 10-valued, the output is 10-valued

FSMs are randomly generated by a built-in tool called fsm-gen-fsm [2]. fsm-gen-fsm allows the definition of parameters such as the number of inputs, the number of outputs, and the number of transitions. Each FSM is produced five times, and the mean values of outcomes are calculated. This procedure is repeated 300 times. In other words, 1500 FSMs are created in total. According to similar studies, this amount seems sufficient and cannot be considered a serious threat to validity. Similarly, the random generation of values eliminates another validation threat. FSMs are reduced, deterministic, and connected.

We exploit mutation analysis to measure the effectiveness, i.e., the fault detection ratios of different test suites. In mutation analysis, several mutants of FSM are generated against some fault hypotheses. For example, according to the missing transition fault hypothesis, a mutant FSM can be obtained by removing an arbitrary transition from the original FSM. If we limit the number of missing transitions to some number k, one can generate k *number of transition mutants. Mutation analysis can therefore be a costly operation. In our experiments, the number of mutants generated for each FSM is approximately 20,000. We implemented the following mutation operators: (i) Change Initial State, (ii) Missing transition, (iii) Input-Exchanged (Avoiding Non-Determinism), (iv) Origin-Exchanged (avoiding non-determinism), (v) Extra transition, and (vi) Extra State (ES).

All the experiments are performed on an Ubuntu/GCC system with Intel Core i7, Nvidia Geforce 940 mx, and 16 GB of RAM.

6.1 Test Metrics in FSM Testing

6.1.1 Fault Detection Ratio (FDR)

The fault detection ratio comparison of methods as per the graph reveals the same character concerning the state, input, and output. In this study, fault detection ratio is another parameter that we attach importance to when comparing methods. Looking at Fig. 1, it is seen that the CPP method has a lower fault detection ratio compared to other methods. In other words, the performance of the CPP method in terms of fault detection ratio is lower than other methods. On the other hand, the performance of different methods is close.

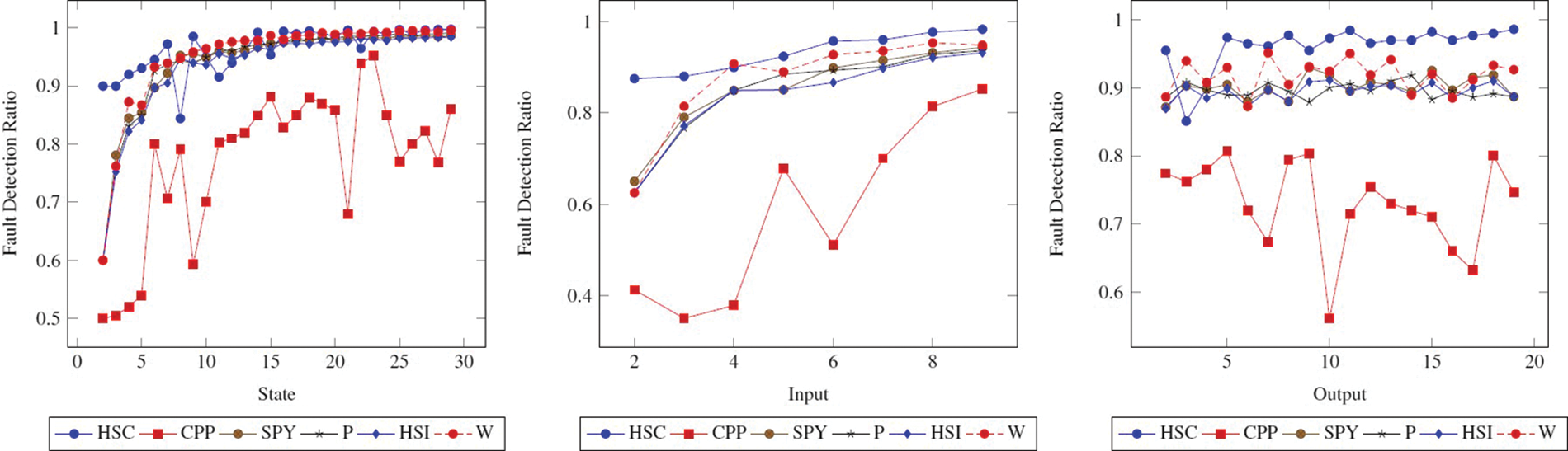
Figure 1: Fault detection ratio (FDR) comparison of methods. The figure shows how the FDR changes when the State, Input, and Output values of the State FSM increase

However, interpreting using only FDR does not give accurate results because many factors affect performance. For example, |TC|, |TS|, FDR|TC| , FDR|TS| , FDR|TIME| , parameters are not included in the FDR parameter. Only when these parameters are checked holistically can the actual quality of the test set be understood.

6.1.2 Test Case Size vs. FDR|TC|

When the FDR|TC|  metric we developed is compared with the traditional |TC| metric, it is seen that the results are very different from each other. For example, the values of the HSI method are high in Fig. 2 but low in the Fig. 3. The W method shows a similar picture. On the other hand, the CPP method presents the opposite view. This is because CPP creates one test case, and its FDR is close to 70%. Input and output graphs can also be characterized similarly to the state graph.

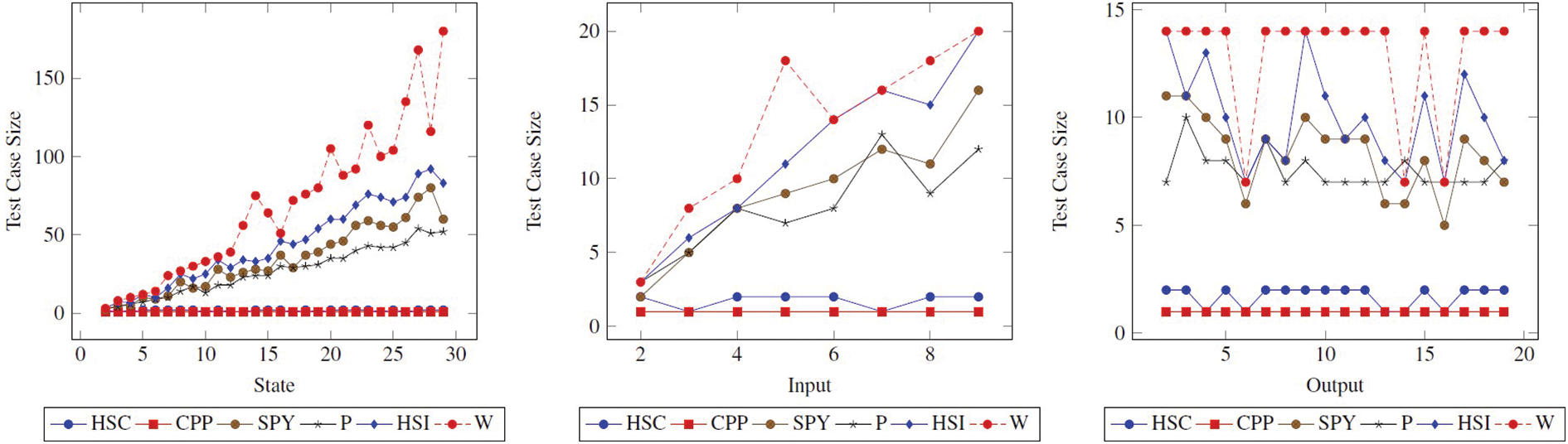
Figure 2: Test suite size (|TC|) comparison of methods. The figure shows how the |TC| changes when the State, Input, and Output values of the State FSM increase

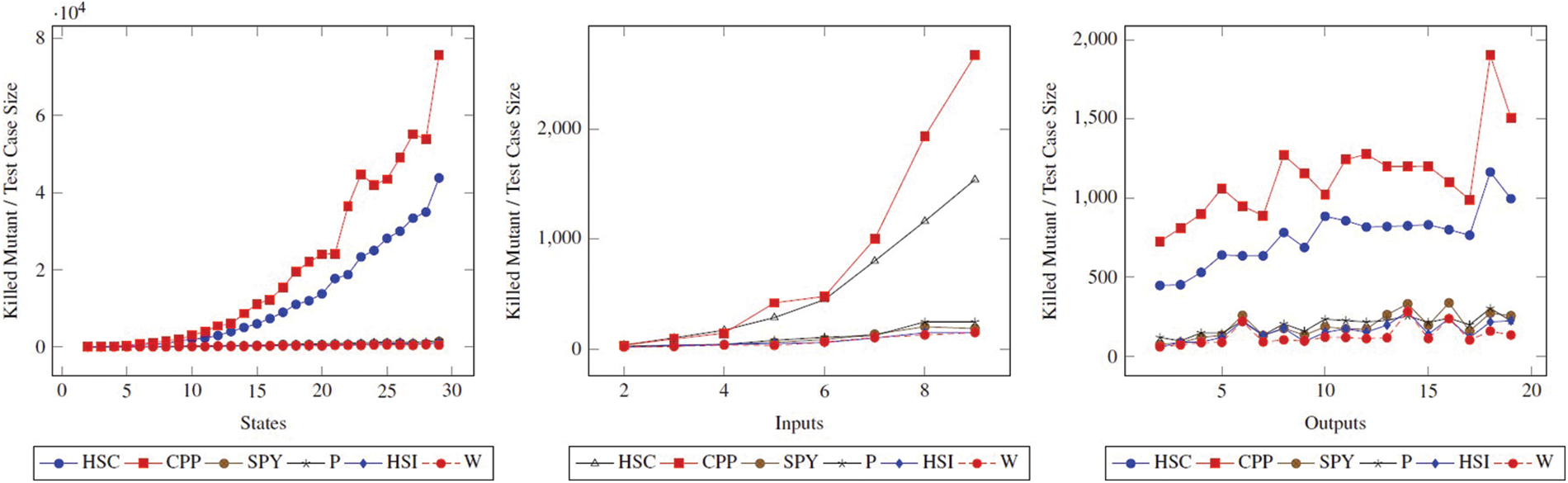
Figure 3: FDR|TC|  . The figure shows how the FDR|TC|  changes when the state, Input, and output values of the state FSM increase

As can be seen from all the graphs, it is seen in the test case size graphs, the HSC and CPP methods will have high values in the Fig. 3. The remarkable thing here is that this difference between the other methods in the test case size is not found in Fig. 3. This shows us that the FDR values of the W and HSI methods, which have significant values in Fig. 2, are small. This is also not preferred. It is not possible to do this analysis with traditional metrics.

6.1.3 Test Suite Size vs. FDR|TS|

When the FDR|TS|  metric we developed is compared with the traditional |TS| metric, it is seen that the results are very different from each other. For example, since the CPP method consists of a single test case and has an FDR of 70%, it stands out as the most performance method according to the FDR|TS|  metric we developed in Fig. 5. In addition, although the distributions of other forms are very different according to the |TS| metric (Fig. 4), they have very close values according to the FDR|TS| metric. This allows us to comment on FDR. For example, it is possible to conclude that the P and SPY methods with low values have high FDRs.

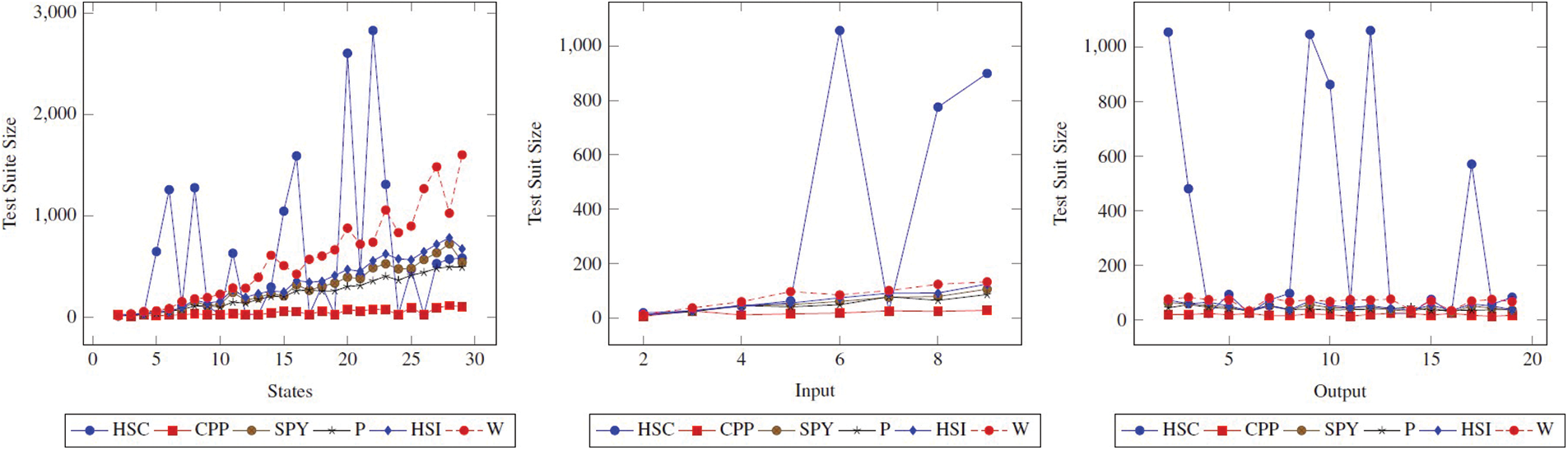
Figure 4: Test suite size (|TS|) comparison of methods. The figure shows how the |TS| changes when the state, input, and output values of the state FSM increase

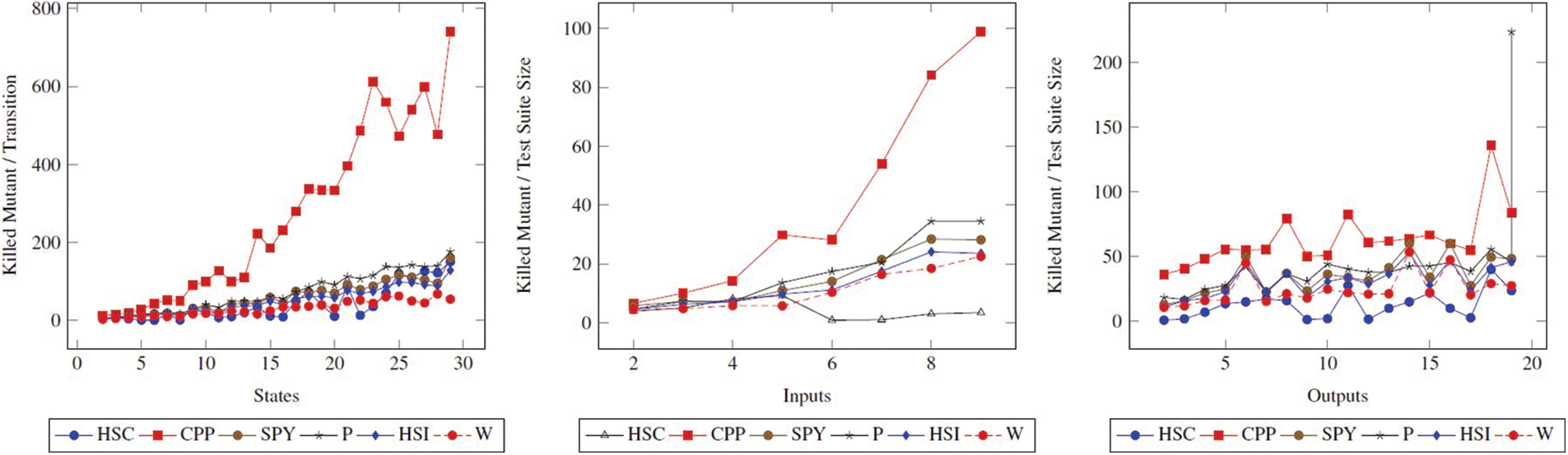
Figure 5: FDR|TS| . The figure shows how the FDR|TS| changes when the state, input, and output values of the state FSM increase

As can be seen, the ranking of P, SPY, HSI, and W according to the metric (FDR|TS|) is consistent with the literature [3]. This shows that the metric (FDR|TS|) we developed shows successful results.

6.1.4 FDR|TIME|

FSMs from the Collection of Digital Design Benchmarks1 1. https://ddd.fit.cvut.cz/prj/Benchmarks. (ISCAS’ 95) site were used as a real experimental validation. Using these FSMs, methods have been evaluated in terms of time complexity. Here it is seen that the time complexity of the P method is considerably higher than the other methods. On the other hand, the method with the least time complexity is the HSI method.

The FSM files in Table 1 were created by selecting the appropriate ones (reduced, deterministic) among hundreds of FSMs in ISCAS’95 Benchmarks. The majority of the files chosen consist of small FSMs. In experiments, it has been seen that the methods we have covered in this study do not work in larger FSMs.

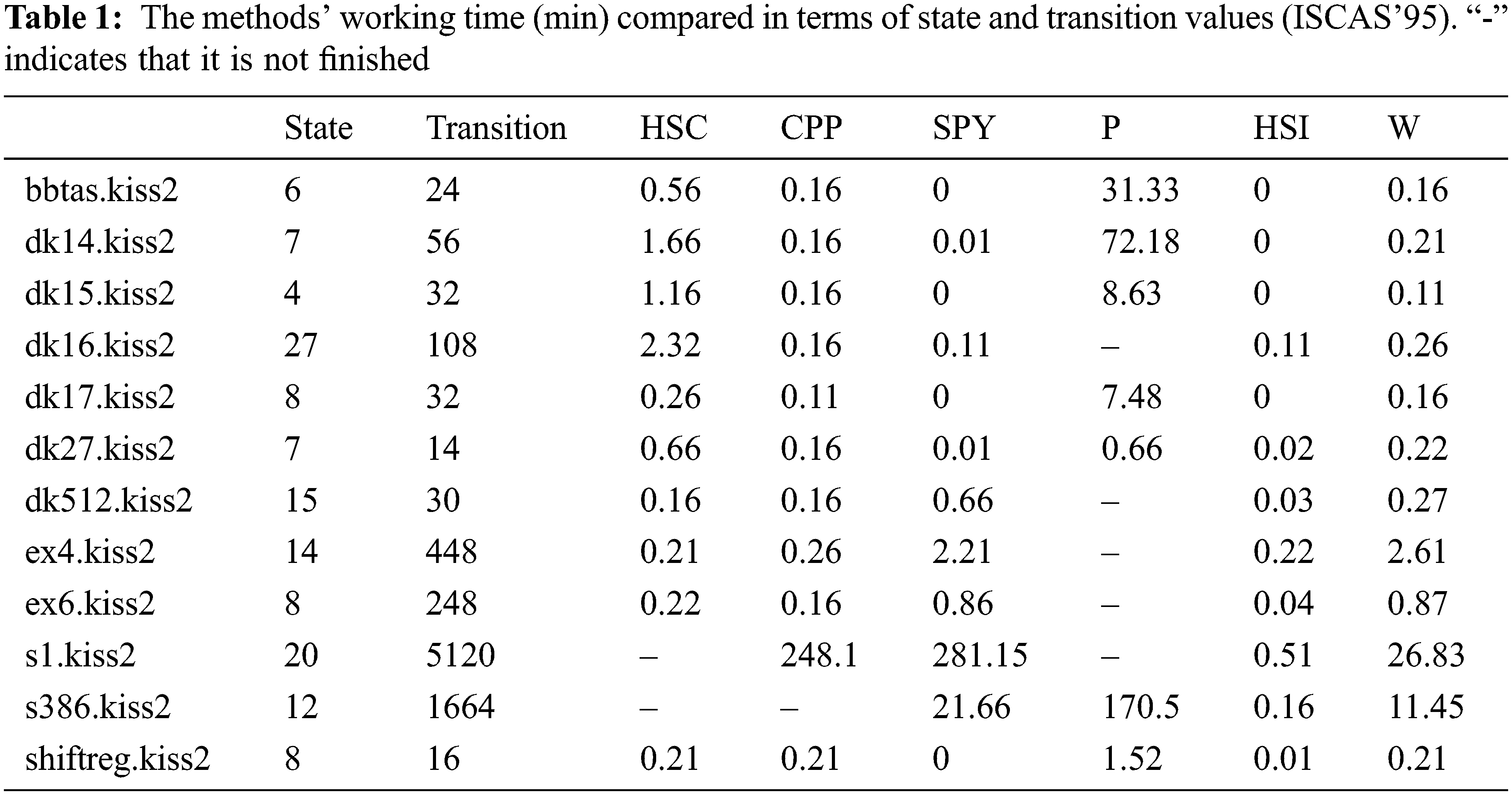
As can be seen in Table 1, it turns out that many methods only work or give results for a very long time in an FSM with approximately 20 states. Although the FSMs in Table 1 do not have high state and transition values, they are very slow. To our knowledge, this has not been reported in any previous study. This is because traditional metrics do not have a metric such as FDR|TIME| .

6.2 The Averages of the Methods

Table 2 contains the averages of the methods compared in terms of state values. In terms of state values, although FDR values are low, the rate of FDR per test case (FDR|TC|) of the CPP method is the highest. The same applies to the FDR rate (FDR|TS|) per test suite. On the other hand, the lowest efficiency in terms of FDR|TC|  and FDR|TS| belongs to the W method.

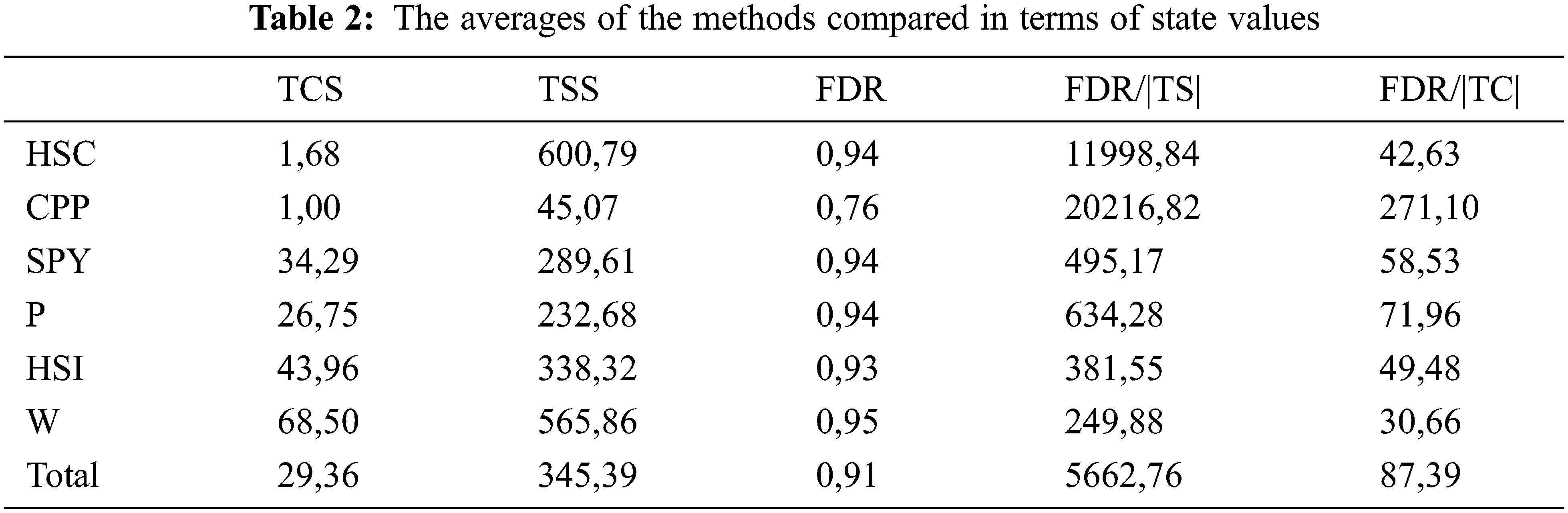
Table 3 contains the averages of the methods compared in terms of input values. In terms of input values, although FDR values are low, the rate of mutant killing per test case (FDR|TC|) of the CPP method is still the highest. The same applies to the mutant kill rate (FDR|TS|) per test suite. According to the average input values, the lowest efficiency in FDR|TC|  and FDR|TS| belongs to the W method.

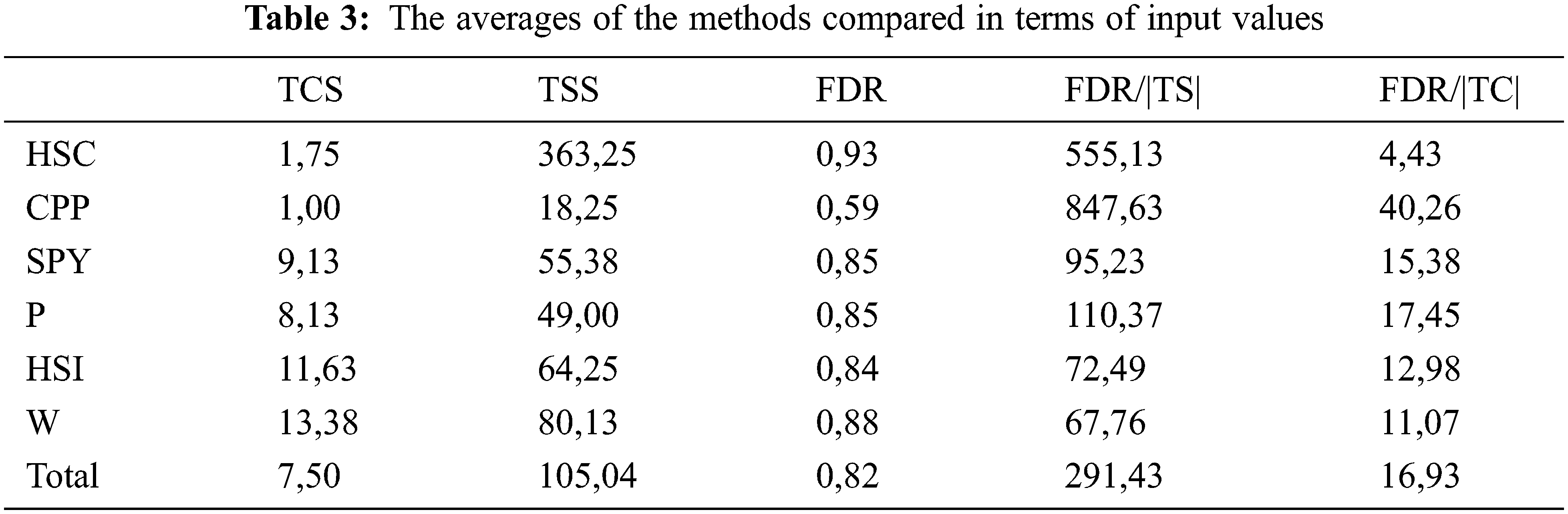
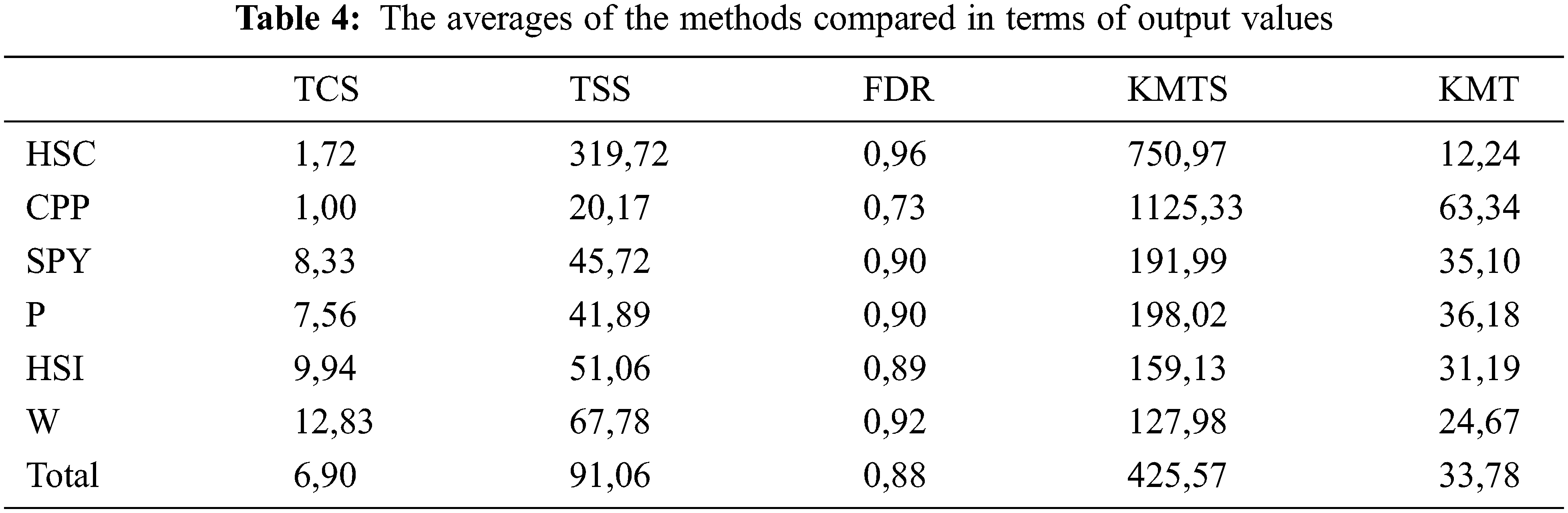
Table 4 contains the averages of the methods compared in terms of output values. In terms of output values, although the FDR values are low, the rate of mutant killing per test case (FDR|TC|) of the CPP method is still the highest. The same is true for the CPP method’s rate of mutant killing per test suite (FDR|TS|) . On the other hand, according to the average output values, the lowest efficiency in terms of FDR|TC| belongs to the W method. According to the average output values, the lowest efficiency in FDR|TS| belongs to the HSC method.

7  Conclusions

Three new metrics named FDR|TS| , FDR|TC| , and FDR|TIME| have been developed to eliminate the deficiencies of the Fault Detection Ratio (FDR), test case size, and test suite size metrics, which are the most widely used metrics to determine the quality of the test suites.

To validate our generated metrics, randomly generated FSMs and ISCAS’ 95 Benchmarks data, which are FSM data from the real world, were used. Thus, our advanced metrics have been tested using random and real-world data. CPP, HSC, W, HSI, P, and SPY methods were used to create the FSM test set. Initially, traditional metrics such as test case size, test suite size, and error detection rate (FDR) were applied to the test sets created by these tools. The metrics developed within the scope of the study were then used for identical test sets made with the same tools.

Ultimately, with the metrics we developed, it has been shown that it is possible to observe results that cannot be detected using traditional metrics. Thanks to the metrics we have developed, the existing errors of the parameters that may be faulty are eliminated, and an evaluation opportunity that can reveal higher performance is offered. For example, the test suite and case size must be short. But if the performance is terrible, the length evaluation is meaningless. The same is true for the time parameter. If the performance is too low, performing the test quickly will not be meaningful. For this reason, unlike the literature, it has been revealed that more information can be obtained about test suites thanks to the metrics we have developed.

Model-based methods such as FSM are widely used in critical systems such as the defense industry, and health, air, and space technologies. In this respect, the importance of our study is that it presents practical test set evaluation parameters to prevent future economic problems by detecting possible problems through pre-testing.

Considering real-time systems, Timed Automata are frequently preferred modeling methods. The metrics we developed within the scope of this study can also be used in Timed Automata as they have the same logic as FSMs. Therefore, using metrics in FSM or Timed Automata will produce the same results.

As a result, our study is expected to contribute to the relevant literature on obtaining quality test suites thanks to three new parameters. In future studies, it is considered that these metrics will be tested with other modeling methods.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

    1. B. S. Ainapure, Software Testing and Quality Assurance. Maharashtra, India: Technical Publications, 2014. [Google Scholar]

    2. A. T. Endo and A. Simao, “Evaluating test suite characteristics, cost, and effectiveness of FSM-based testing methods,” Information and Software Technology, vol. 55, no. 6, pp. 1045–1062, 2013. [Google Scholar]

    3. A. Mathur, Foundations of Software Testing, 2nd ed., Delhi, India: Pearson, 2013. [Google Scholar]

    4. R. Pelánek, “Properties of state spaces and their applications,” International Journal on Software Tools for Technology Transfer, vol. 10, no. 5, pp. 443–454, 2008. [Google Scholar]

    5. X. Devroey, G. Perrouin, M. Papadakis, A. Legay, P. -Y. Schobbens et al., “Model-based mutant equivalence detection using automata language equivalence and simulations,” Journal of Systems and Software, vol. 141, no. 8, pp. 1–15, 2018. [Google Scholar]

    6. I. Marsit, A. Ayad, D. Kim, M. Latif, J. Loh et al., “The ratio of equivalent mutants: A key to analyzing mutation equivalence,” Journal of Systems and Software, vol. 181, pp. 111039, 2021. [Google Scholar]

    7. C. Wei, X. Yao, D. Gong and H. Liu, “Spectral clustering based mutant reduction for mutation testing,” Information and Software Technology, vol. 132, no. 4, pp. 106502, 2021. [Google Scholar]

    8. N. Kushik, N. Yevtushenko and J. López, “Testing against non-deterministic FSMs: A probabilistic approach for test suite minimization,” Testing Software and Systems, vol. 13045, pp. 55–61, 2022. [Google Scholar]

    9. Q. Hu, L. Ma, X. Xie, B. Yu, Y. Liu et al., “DeepMutation++: A mutation testing framework for deep learning systems,” in 2019 34th ACM Int. Conf. on Automated Software Engineering (ASE), San Diego, CA, USA, pp. 1158–1161, 2019. [Google Scholar]

  10. M. Kintis, M. Papadakis, Y. Jia, N. Malevris, Y. Le Traon et al., “Detecting trivial mutant equivalences via compiler optimisations,” IEEE Transactions on Software Engineering, vol. 44, no. 4, pp. 308–333, 2018. [Google Scholar]

  11. H. Wang, Z. Li, Y. Liu, X. Chen, D. Paul et al., “Can higher-order mutants improve the performance of mutation-based fault localization?,” IEEE Transactions on Reliability, vol. 71, no. 2, pp. 1157–1173, 2022. [Google Scholar]

  12. J. Zhang, L. Zhang, M. Harman, D. Hao, Y. Jia et al., “Predictive mutation testing,” IEEE Transactions on Software Engineering, vol. 45, no. 9, pp. 898–918, 2019. [Google Scholar]

  13. Q. Zhu, A. Panichella and A. Zaidman, “A systematic literature review of how mutation testing supports quality assurance processes, software testing,” Verification and Reliability, vol. 28, no. 6, pp. e1675, 2018. [Google Scholar]

  14. A. B. Sánchez, P. Delgado-Pérez, S. Segura and I. Medina-Bulo, “Performance mutation testing: Hypothesis and open questions,” Information and Software Technology, vol. 103, no. 1, pp. 159–161, 2018. [Google Scholar]

  15. P. Delgado-Pérez, L. M. Rose and I. Medina-Bulo, “Coverage-based quality metric of mutation operators for test suite improvement,” Software Quality Journal, vol. 27, no. 2, pp. 823–859, 2019. [Google Scholar]

  16. Q. Zhu, A. Zaidman and A. Panichella, “How to kill them all: An exploratory study on the impact of code observability on mutation testing,” Journal of Systems and Software, vol. 173, no. 11, pp. 110864, 2021. [Google Scholar]

  17. S. Rani and B. Suri, “Investigating different metrics for evaluation and selection of mutation operators for Java,” International Journal of Software Engineering and Knowledge Engineering, vol. 31, no. 3, pp. 311–336, 2021. [Google Scholar]

  18. Z. Iqbal, M. A. Rehman, M. Imran, N. Ahmed, U. Fatima et al., “A finite difference scheme to solve a fractional order epidemic model of computer virus,” AIMS Mathematics, vol. 8, no. 1, pp. 2337–2359, 2023. [Google Scholar]

  19. A. Raza, M. Rafiq, D. Alrowaili, N. Ahmed and I. Khan, “Design of computer methods for solving cervical cancer epidemic model,” CMC-Computers Materials & Continua, vol. 70, no. 1, pp. 1649–1666, 2022. [Google Scholar]

  20. A. Akgül, U. Fatima, M. S. Iqbal, N. Ahmed, A. Raza et al., “A fractal fractional model for computer virus dynamics,” Chaos, Solitons & Fractals, vol. 147, pp. 110947, 2021. [Google Scholar]

  21. A. Akgül, M. Sajid Iqbal, U. Fatima, N. Ahmed, Z. Iqbal et al., “Optimal existence of fractional order computer virus epidemic model and numerical simulations,” Mathematical Methods in the Applied Sciences, vol. 44, no. 13, pp. 10673–10685, 2021. [Google Scholar]

  22. U. Fatima, D. Baleanu, N. Ahmed, S. Azam, A. Raza et al., “Numerical study of computer virus reaction-diffusion epidemic model,” 2021. [Google Scholar]

  23. A. Raza, U. Fatima, M. Rafiq, N. Ahmed, I. Khan et al., “Mathematical analysis and design of the nonstandard computational method for an epidemic model of computer virus with delay effect: Application of mathematical biology in computer science,” Results in Physics, vol. 21, no. 10, pp. 103750, 2021. [Google Scholar]

  24. S. Naito, “Fault detection for sequential machines by transition tours,” in Proc. 11th IEEE Int. Symp. on Fault Tolerant Computing (FTCS-11), New York, NY, USA, pp. 238–243, 1981. [Google Scholar]

  25. T. S. Chow, “Testing software design modeled by finite-state machines,” IEEE Transactions on Software Engineering, vol. 4, no. 3, pp. 178–187, 1978. [Google Scholar]

  26. N. Yevtushenko and A. Petrenko, Test derivation method for an arbitrary deterministic automaton, automatic control and computer sciences. in Automatic Control and Computer Sciences, Vol. 24. Allerton Press New York, pp. 65–68, 1990. [Google Scholar]

  27. A. Simão, A. Petrenko and N. Yevtushenko, “Generating reduced tests for FSMs with extra states,” Testing of Software and Communication Systems, vol. 5826, pp. 129–145, 2009. [Google Scholar]

  28. A. Simao and A. Petrenko, “Checking completeness of tests for finite state machines,” IEEE Transactions on Computers, vol. 59, no. 8, pp. 1023–1032, 2010. [Google Scholar]

  29. É. F. D. Souza, V. A. D. Santiago Júnior and N. L. Vijaykumar, “H-Switch Cover: A new test criterion to generate test case from finite state machines,” Software Quality Journal, vol. 25, no. 2, pp. 373–405, 2017. [Google Scholar]

  30. M. Papadakis and R. Just, “Special issue on mutation testing,” Information and Software Technology, vol. 81, pp. 1–2, 2017. [Google Scholar]

  31. S. C. Pinto Ferraz Fabbri, M. E. Delamaro, J. C. Maldonado and P. C. Masiero, “Mutation analysis testing for finite state machines,” in Proc. of 1994 IEEE Int. Symp. on Software Reliability Engineering, Monterey, CA, USA, pp. 220–2291984 [Google Scholar]

  32. C. Wohlin, P. Runeson, M. Höst, M. C. Ohlsson, B. Regnell et al., “Experimentation in software engineering,“ Springer Science & Business Media, 2012. [Google Scholar]