Cryptanalysis of 2D-SCMCI Hyperchaotic Map Based Image Encryption Algorithm

1  Introduction

Nowadays, digital images are an important way to share information, and when compared to text information, images are more vivid, easy to understand, and have more information. However, information security has been the biggest concern for users in the digital age. When seen from the perspective of a nation or a corporation, a great deal of sensitive information is at risk of being attacked or stolen. This includes, but is not limited to, scientific research and financial and military secrets. Photographs play an essential role in people’s private life since they allow them to document and share their everyday activities and thoughts. Cybercriminals can steal sensitive data by exploiting network weaknesses if precautions are not taken [1]. Consequently, digital image data must be safeguarded both in principle and in practice. Encrypting the original image is the most apparent method of security. Traditional encryption techniques for photos, while effective, have poor encryption efficiency [2,3]. That’s why it’s so important to learn about safe and practical algorithms.

The techniques that researchers have presented in recent years to encrypt images have been mainly based on chaos theory, optical transformation, DNA encoding, and compressed sensing, respectively. These ideas are utilized in developing numerous image encryption procedures to alter pixel placements and values. Munazah et al. [4] recommended an image encryption approach based on double chaotic maps. The chaotic sequence that is formed by the chaotic system is utilized to alter the locations of the image’s pixels. An optical image cryptosystem was devised by Wang and colleagues. After the phase-only hologram has been generated using the quadratic phase and double phase procedures, it is subsequently encrypted. Phase-only holograms cannot be decrypted. Learning the probability distribution [5] allows one to eventually retrieve the encrypted image. An image encryption technique based on genetic processes and chaotic DNA encoding was suggested by Younes et al. [6]. This algorithm used the biological DNA theory to the algorithm and built a one-of-a-kind encoding mechanism to modify pixel values. An image encryption method that depends on compressive sensing has been developed by Yang et al. This method initially compresses the image before proceeding to encrypt it. The amount of space that is used up by the image transmission is cut down to some degree, so that the effectiveness of the scheme may be improved [7].

Benefits of the chaotic system that align with those of cryptography include sensitivity to the initial value, excellent unpredictability, and resistance to cracking [8]. In image encryption, the chaotic system has seen extensive use and research [9–11]. Mathematician Matthews invented and elucidated the idea of chaotic cryptography [12] in 1989, making the first use of chaos in encryption systems. The encryption approach depending on the chaotic system is more secure than more conventional methods, mainly when used with images. Because of this, several researchers [13–15] have suggested chaotic system-based image encryption techniques. Wang et al. [16] utilized a reworked version of the 1D Logistic map to jumble up the coordinates of individual pixels. Naskar et al. [17] performed a diffusion operation using the Logistic map. However, criminal hackers’ cracking technology is also maturing. The encryption algorithm is vulnerable to unlawful attackers if just one chaotic system is employed [18–20]. A safe and efficient image encryption algorithm must thus use the chaotic system with other encryption techniques [21–23]. Even while several image encryption techniques have been presented up to this point, most of them only use a single grayscale image as the study object, and it is impossible to ensure either the safety or the efficiency of the algorithm [24–26].

The key contributions of the suggested work are defined in the following points.

1.    In this research, we have performed the cryptanalysis of a recently proposed cryptosystem [22].

2.    The central theme of the algorithm was the combination of diffusion and permutation for robustness depending on the 2D-SCMCI hyperchaotic map.

3.    The vulnerabilities of the cryptosystem were detected against a chosen-plaintext attack.

4.    The proposed attack can retrieve the secret keys of the system by inserting 258 chosen images in the understudy encryption algorithm.

5.    Moreover, the quality of the recovered data is assured with the help of some statistical analysis.

6.    We have also suggested some improvements in the existing system to certify the robustness against the proposed attack.

The rest of the work is arranged as follows; Section 2 presents the review of the originally proposed encryption technique; Section 3 offers cryptanalysis of the algorithm by listing the vulnerabilities account. Some quality assurance statistical analyses are performed on retrieved data in Section 4. Improvements to the existing encryption model are suggested in Section 5. Finally, a conclusion is drawn in the last section.

2  Review of the Originally Proposed Cryptosystem

In this section, we provide the basic structure of the initially offered algorithm. Also, we develop an equivalent structure to determine the vulnerabilities in the implementation. The encryption structure entirely depends on the hyperchaotic map.

2.1 2D-SCMCI Hyperchaotic Map

By considering the principal cascade modulation couple, the authors in [22] proposed a 2D-SCMCI map which can be stated as follows:

{x(n+1)=rsin⁡(π[(y(n)+h)ksin⁡(aπx(n))]),  y(n+1)=rsin⁡(π[(kx(n+1)+h)sin⁡(aπx(n))]),  (1)

where k signifies the modulation parameter, r, a and h denotes the chaotic parameters, x(n) and y(n) depicts two values at step n. The randomness of the elements of the 2D-SCMCI hyperchaotic map is examined by plotting the values against the total iterations. Fig. 1 shows the iterations plot of the hyperchaotic map for the first 300 values of x and y sequences.

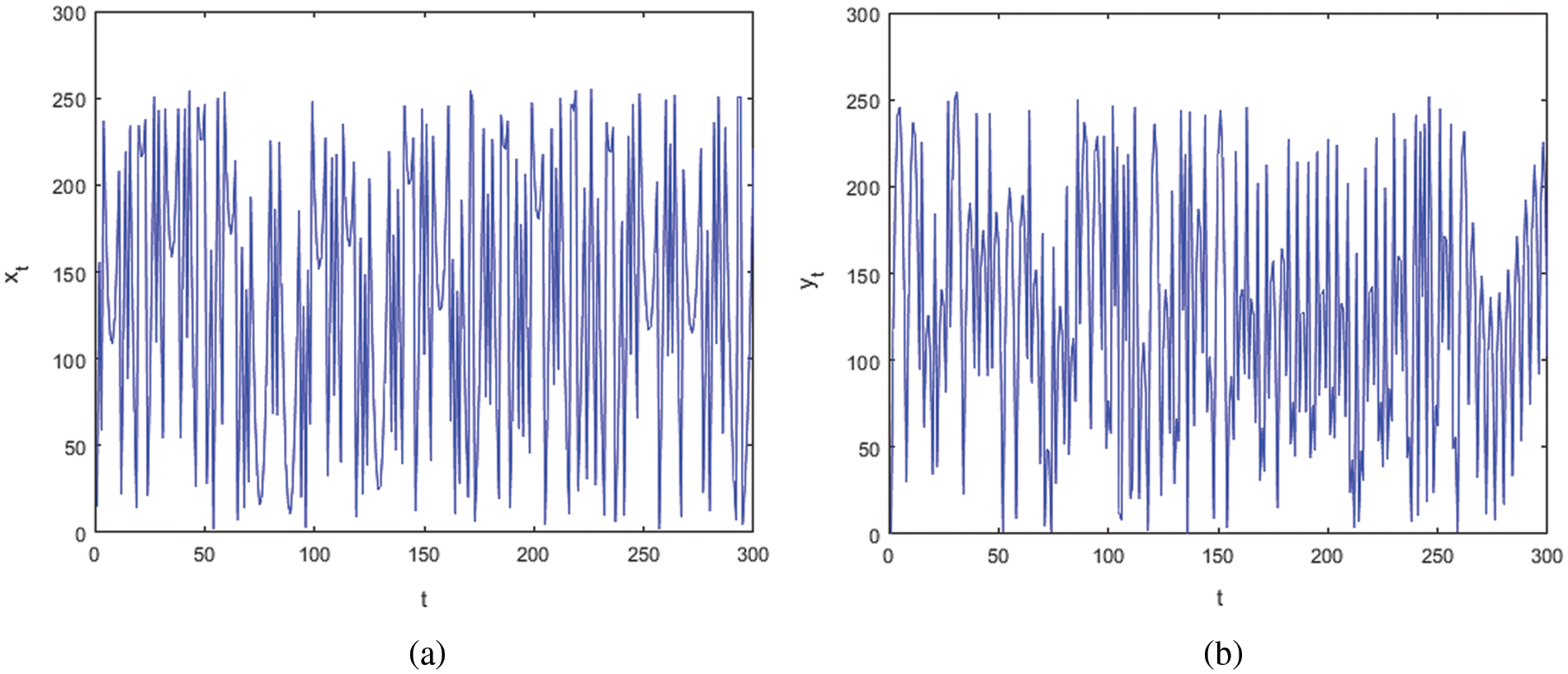
Figure 1: Iteration values plot for (a) x sequence (b) y sequence

2.2 Encryption Scheme

The encryption scheme proposed in [22] was entirely dependent on two operations, the first one the bit-based scrambling, and the second one is the diffusion operation carried by the bitwise XOR. The random number generator utilized to generate the private key was based on the SCMCI hyperchaotic map only. The working strides of the understudy encryption procedure are as follows:

1.    Insert a plain image P of size A×B as the input of the algorithm.

2.    The hyperchaotic map is iterated (n+R) times with R=max(A, B) and two chaotic sequences x and y of length n+R are attained.

3.    First, n values are discarded to get the highly random sequences X and Y.

4.    The histogram equalization is performed on the sequences x and y by using the vectors a and b by

{a=mod (floor(|x(i)|×1016), A2), b=mod (floor(|y(i)|×1016), B2). (2)

5.    The image scrambling operation by row is performed by using the vectors a,  b,  X,  and Y. If X>0,  then three left bits of the pixel are shifted to the right side, and if X<0,  then five left bits are shifted to the right side. The detailed phenomenon is explained in Fig. 2.

6.    Like step 5 the same operation is executed by using the array Y to shuffle the image pixels column-wise.

7.    New sequences x1 and y1 are generated by inserting different initial values and parametric values into the 2D-SCMCI hyperchaotic map with ( m+A+B ) iterations.

8.    The histogram equalization is applied to the sequences x1 and y1 and the sequences X2 and Y2 are obtained as

{X2(i)=mod((round(1000(|x1(i)×1016|−floor(|x2(i)×1016|)))), 256), Y2(i)=mod((round(1000(|y1(i)×1016|−floor(|y2(i)×1016|)))), 256). (3)

9.    From the above step the sequences M1 and M2 are generated as diffusion keys.

10.   Forward diffusion is applied using the sequence M1 as

{F(1, 1)=mod(D(1, 1)+M1(1, 1), 256), F(1, j)=mod(D(1, j)+M1(1, j)+F(1, j−1), 256), F(i, 1)=mod(D(i, 1)+M1(i, 1)+F(i−1, 1), 256),  F(i, j)=mod(D(i, j)+M1(i, j)+F(i, j−1)+F(i−1, j), 256). (4)

11.   Backward diffusion is applied using the sequence M2 by

{C(A, B)=mod(F(A, B)+M2(1, 1), 256), C(A, j)=mod(F(A, j)+M2(A, j)+C(A, j−1), 256), C(i, B)=mod(F(i, B)+M2(i, B)+C(i−1, B), 256), C(i, j)=mod(F(i, j)+M2(i, j)+C(i, j−1)+C(i−1, j), 256). (5)

12.   The result of step 11 is compiled as an encrypted image.

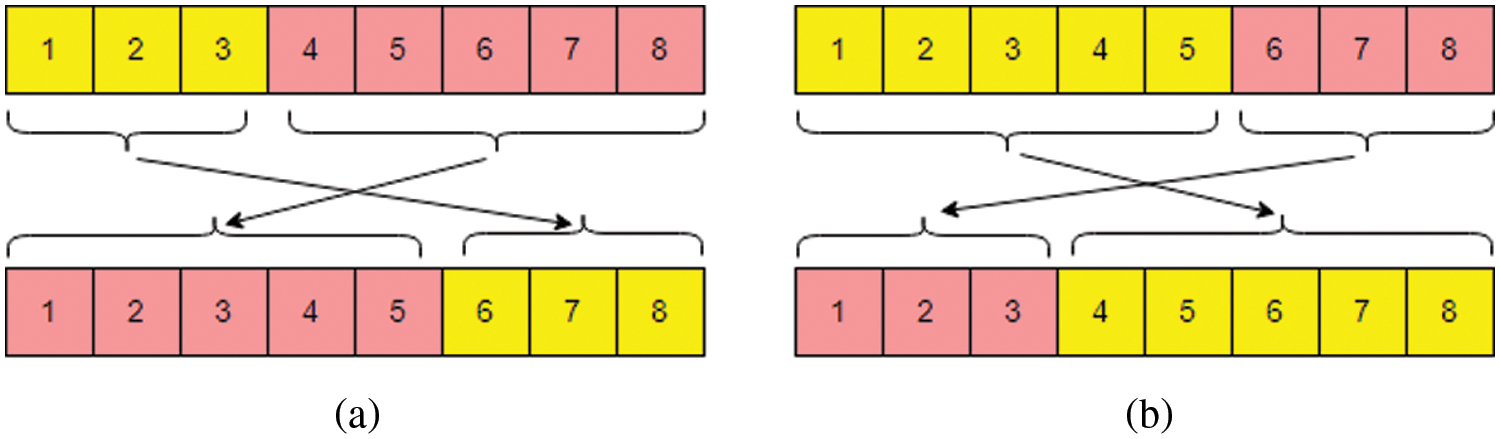
Figure 2: Bit-wise permutation for (a) X > 0; (b) X < 0

The description of the understudy cryptosystem is shown in Fig. 3.

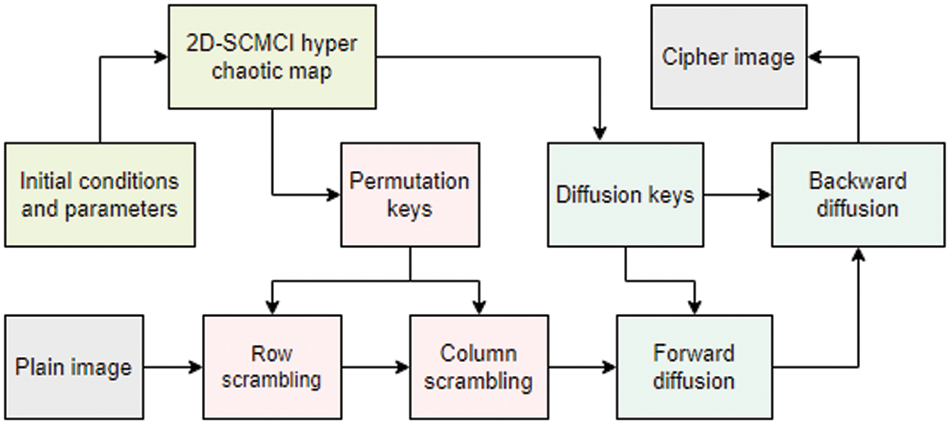
Figure 3: Flowchart diagram of the understudy cryptosystem

2.3 Equivalent Description

The originally proposed cryptosystem utilizes the concept of permutation and diffusion with just a 2D-SCMCI hyperchaotic map. The combination of permutation and diffusion is executed by four different keys column-wise permutation, row-wise permutation, forward diffusion, and backward diffusion. The equivalent encryption cipher can be developed for the originally proposed structure to get the loopholes and vulnerabilities. Suppose the keys applied for row-wise and column-wise permutations are renamed as kR and kC respectively and each permutation operation is denoted by P1 and P2 . Consider I denotes the original image to be inserted in the encryption algorithm. Therefore, we can write

C1=P1(I, kR),  (6)

C2=P2(C1, kC). (7)

The cipher C1 and C2 are the row-wise and column-wise permuted images. The next operation of forward diffusion DF and DB is performed by the keys kF and kB. Hence the operation can be written as

C3=DF(C2, kF),  (8)

C4=DB(C3, kB). (9)

The cipher C4 is considered the final encrypted version. All these four Eqs. (6)–(9) can be written into one equation by using the property of composition of functions as

C=DB(DF(P2(P1(I, kR), kC), kF),  kB). (10)

Eq. (10) is the equivalent description of the complete understudy encryption cipher.

3  Cryptanalysis

This section explains the vulnerabilities in the originally proposed model in [22]. It also demonstrates how a chosen-plaintext attack was used to break the encryption model. Finally, the experimental results are illustrated.

3.1 Vulnerabilities in the Exiting Model

The secure key generation leads to a robust encryption algorithm, but the implementation of the key in the structure also plays an important role. A weak combination of security primitives generates a cryptosystem that can be easily attacked with the help of some classical cryptanalysis assaults. In our case, the combination of permutation and diffusion with input-independent key generation generates the possibility of attack. The cryptanalysis of the cryptosystem is possible only if there exist some vulnerabilities in the implementation structure. The loopholes are determined by examining the encryption operations combinations and key generation of the algorithm. The existing understudy cryptosystem lacks the following points in its structure:

1.    The key generation is only dependent on the 2D-SCMCI hyperchaotic map and does not use any other domain to get the variety of PRNGs for the secret key.

2.    The independency of the key generation from the plaintext makes the secret extractable in cryptanalytical attacks.

3.    The combination of diffusion and permutation is considered a weak encryption structure.

4.    The direct implementation of the permutation operation with the chaotic keys makes it predictable against some classical attacks.

5.    The diffusion operation is invariant as opposed to just one full black image and the resultant may help in the prediction of the secret keys as well as the original image.

The vulnerabilities listed above make it breakable by some standard cryptanalysis attacks.

3.2 Chosen-Plaintext Attack

The chosen plaintext attack works on the principle that the attacker gets temporary access to the encryption machine and inserts some desired plaintext [20]. The resultant output from these attacks leads to information about the private key. Firstly, the combined operations of the entire structure are detected and then prioritized to make one of them invariant against the encryption procedure. The invariance varies for each cipher operation and gives different outputs according to the implemented operation. The flowchart of the offered chosen-plaintext attack is displayed in Fig. 4.

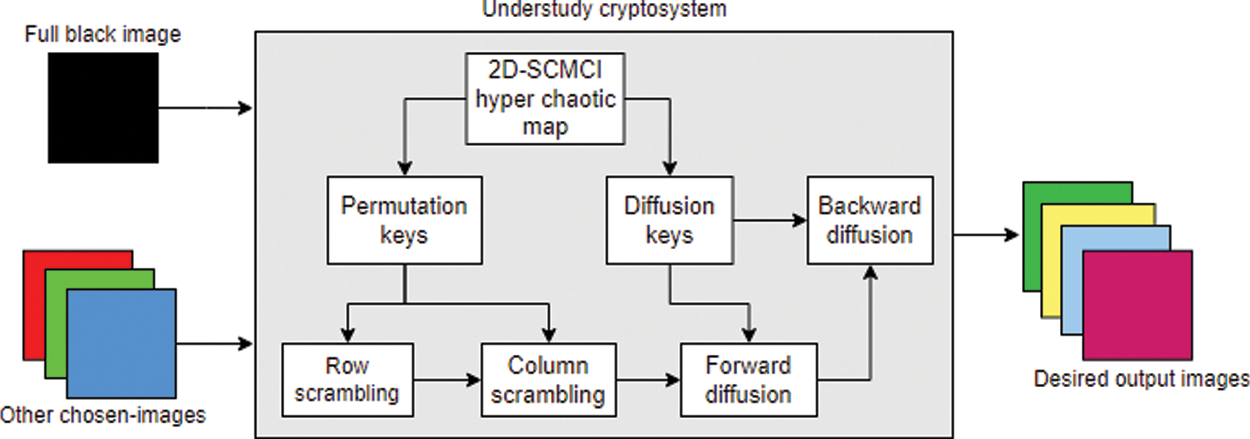
Figure 4: Flow chart of proposed chosen-plaintext attack

The full black image with all zero entries makes the diffusion operation invariant. Therefore, we insert a full black image as

I=(0⋯0⋮⋱⋮0⋯0)A×B,  (11)

The further attack is executed with the insertion of Eq. (11) into the system (10) and we get

C=DB(DF(P2(P1((0⋯0⋮⋱⋮0⋯0), kR), kC), kF),  kB). (12)

The row-wise and column-wise permutation according to the bit arrangement, becomes invariant because all the zero bit remains zero after the permutation operation. Therefore, Eq. (12) can be modified as

C=DB(DF((0⋯0⋮⋱⋮0⋯0), kF),  kB),  (13)

C=DB((0⋯0⋮⋱⋮0⋯0)⊕kF,  kB ),  (14)

C=(0⋯0⋮⋱⋮0⋯0)⊕kF⊕ kB,  (15)

The forward and backward diffusion keys kF⊕ kB can be combined as k. Hence, Eq. (15) can be written as

C=(0⋯0⋮⋱⋮0⋯0)⊕k=k. (16)

The diffusion key makes the utilization of the previous bits. Therefore, the process of decryption of forward and back diffusion is applied to the original diffusion key K. The retrieved diffusion key eliminates the effect of forward and backward diffusion. Hence, after getting the diffusion key, the system (10) is reduced to only a permutation-based system, which can be written as:

C=P2(P1(I, kR), kC),  (17)

The following procedure involves the insertion of other plain images into the exact permutation keys. The permutation keys are extracted accurately with the insertion of 257 plain images. The first plain image is inserted as

I1=(01⋯01⋯⋮0⋮1⋱⋯ 255255⋮255)A×B. (18)

All the other plain images are inserted by shuffling I1 in row and column direction 256 times. After the insertion of all the images, the resultant gives all the possible permutation positions of the understudy cryptosystem.

3.3 Experimental Results

The experimental outcomes are performed on grayscale images used in the originally proposed algorithm in [22], with dimensions 256 × 256. The visual results are shown in Fig. 5. From the depicted results we can see that the retrieved data is the same as the original data. The exactness of the retrieved data depicts the vulnerability of the cryptosystem against cryptanalysis attacks. The images in Figs. 5a–5d are termed “Image 1”, “Image 2”, “Image 3”, and “Image 4” respectively.

Figure 5: (a–d) Original images; (e–h) Encrypted images; (i–l) Recovered images

4  Security Measurement of Recovered Data

The quality of the recovered data can be measured by carefully examining the statistical analysis results of the original and recovered data. In this section, we have executed the histogram analysis, correlation analysis, and entropy analysis.

4.1 Histogram Analysis

In digital images, the histogram can be used to directly represent the distribution of all pixel values by counting the number of pixels with the same pixel value. Histograms of meaningful images typically show fluctuations because of the unequal distribution of pixel values. We can say that if two images visually look the same and their histograms are also equivalent then we can say that the original and retrieved possess zero error. By comparison, the encrypted image has a relatively flat histogram with a consistent distribution of pixel values. The results of the histogram for original, encrypted, and recovered “Images 1” to “Image 4” are shown in Fig. 6. The same sharp peaks in the original and retrieved data depict the exactitude of the proposed attack and the vulnerabilities of the cryptosystem.

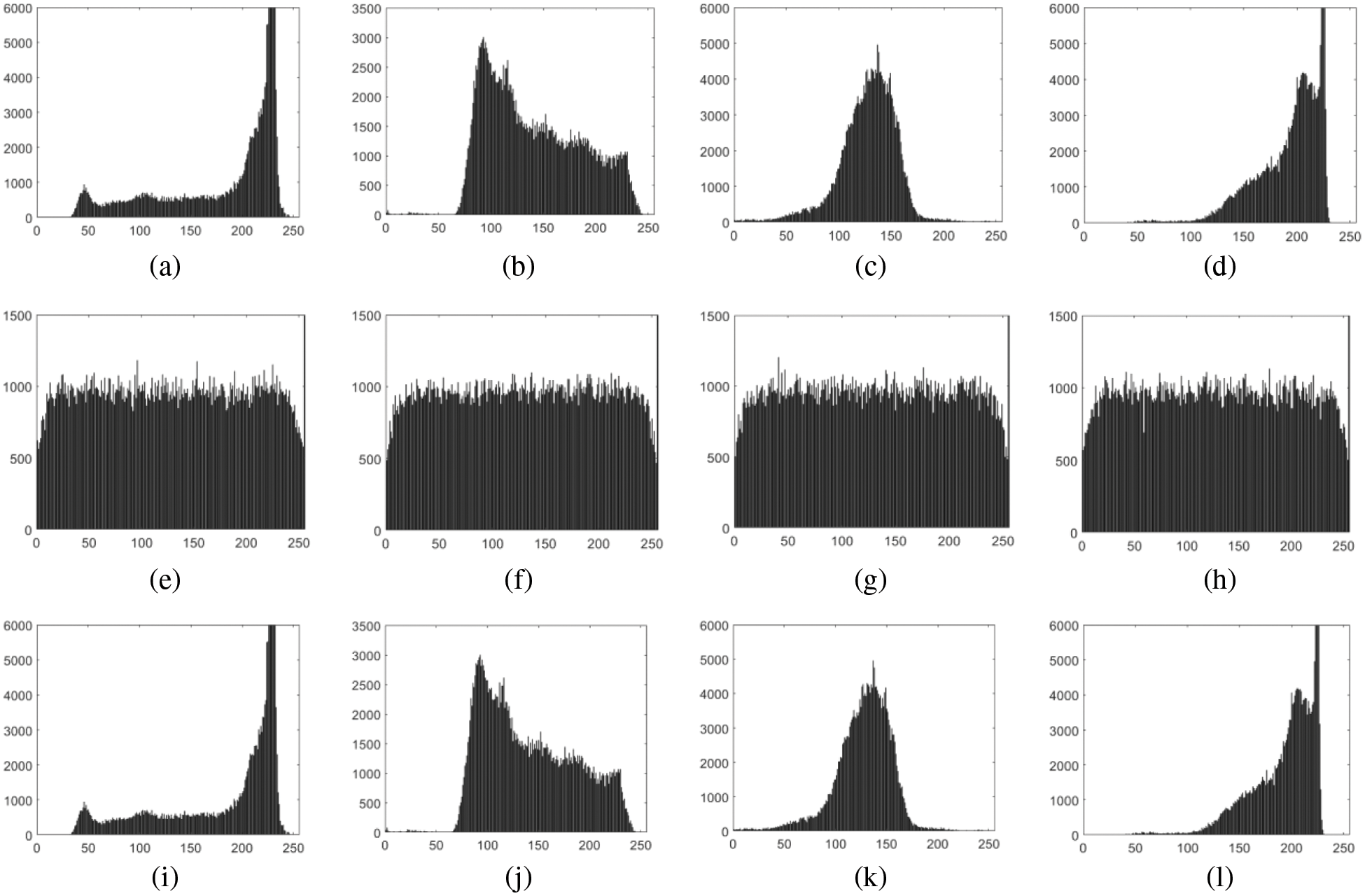
Figure 6: Histogram of (a–d) original images; (e–h) Encrypted images; (i–l) Recovered images

4.2 Correlation Analysis

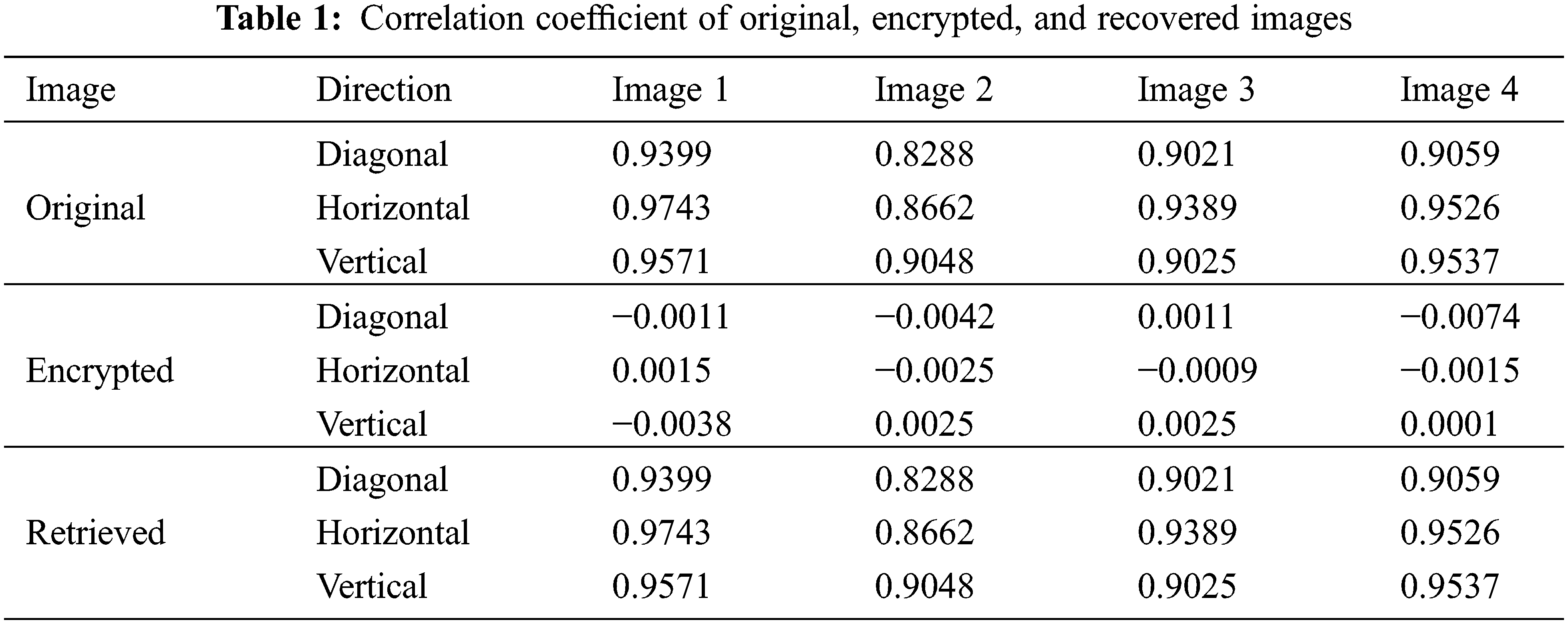
There is a high connection between neighboring pixels in meaningful images, and the images include much redundant information. Instead, cipher images are entirely devoid of redundancy and have no association with neighboring pixels. To prevent cracking the encryption technique by analysis of the correlation between neighboring pixels, an image encryption algorithm should be designed to break this strong correlation. The correlation coefficients of the original, encrypted, and retrieved images are listed in Table 1. From the enumerated values, we can observe that the correlation between original and recovered images is very similar. Therefore, we can say that the pixel of the recovered image is the same as the pixel of the original image.

The correlation diagram for the original and recovered “Image 1” are displayed in Fig. 7. The patterns in the correlation diagram of the original and retrieved images indicate the error-free recovery of the data applying the proposed attack.

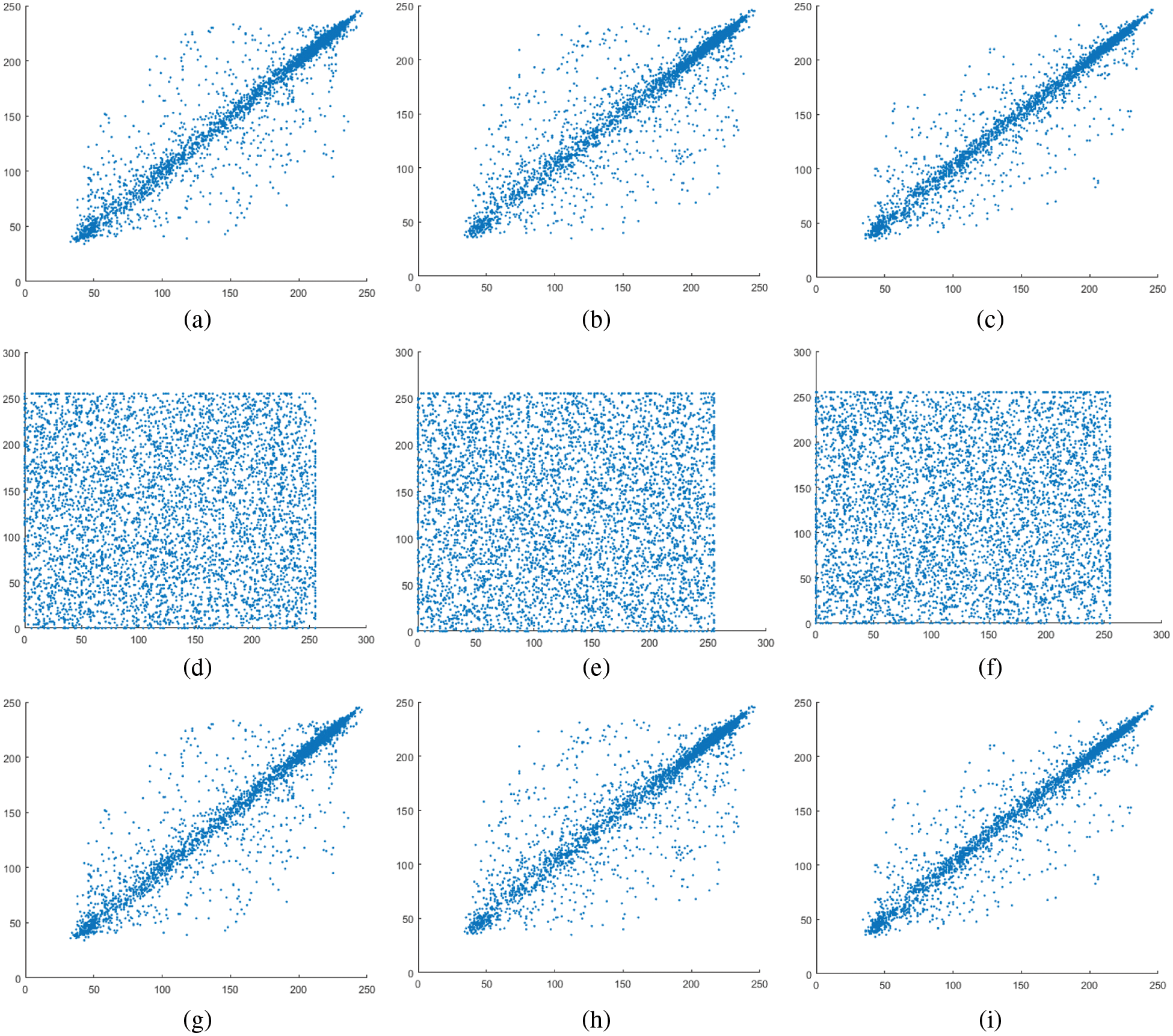
Figure 7: Correlation diagram in horizontal, diagonal, and vertical direction for (a–c) original image; (d–f) Encrypted image; (g–i) Retrieved image

4.3 Entropy Analysis

The entropy of an image is an effective metric for identifying the unpredictability of the distribution of pixel values since it signifies the uncertainty of the information contained within the image. The formula for determining the entropy of image data is

H(m)=∑i=02n−1⁡p(mi)log1p(mi),  (19)

where p(mi) shows the probability of the symbol mi . The ideal value for entropy is 8. The results of the entropy analysis are shown in Table 2. In the case of our understudy scheme, the entropy of encrypted result approaches 8. After the successful implementation of the suggested attack, the entropy of the original and recovered becomes the same due to the exact recovery of the image pixels.

4.4 Time Execution Analysis

In this segment of the manuscript, we have performed the time execution analysis of the proposed chosen plaintext on different sizes of images. The proposed attack can be retrieved the key from different sizes of images in very less time. The results are shown in Table 3. The depicted results indicate that our proposed attack can retrieve private keys in very less time, which indicates the reliability of our proposed algorithm.

5  Improvement Suggestions

In this section, we have proposed some improvements to the cryptanalyzed cryptosystem. The existing scheme is not vastly sensitive to the slight change in the plaintext. Therefore, we have suggested some advances in the encryption structure to improve its robustness as follows:

•   The sensitivity to the plaintext can be augmented by improving the key generation with its dependency on the input data.

•   The key space can be increased by adding more domains with hyperchaotic systems such as DNA coding, neural networks, compressing sensing, wavelet transforms, lattice-based structures, etc.

•   The primary security flaw in the encryption structure can be removed by enlightening the implementation operations of the algorithm.

•   The combination of diffusion and permutation can be transformed into a robust amalgamation with the inclusion of substitution operation.

•   The concept of multiple rounds can be added to the primary notion to avoid security breaches against standard attacks.

The proposed improvements can lead to the construction of a robust cryptosystem as compared to the original algorithm [22]. The encryption structure constructed on the suggested points can resist the proposed attack as well as other classical cryptographic attacks.

6  Conclusion

This work proposes a novel cryptanalysis approach to break a recently developed cryptosystem. The original structure depends only on the hyperchaotic map which makes the key space low due to a single domain. This article demonstrates that the method under investigation is unsuitable for cryptographic applications as it now stands and may require more improvements in the future. However, the approach in concern has several significant issues as well as poor security measures for protecting information privacy. The system passed various statistical tests; however, it is susceptible to attacks like chosen-plaintext and chosen-ciphertext, which are more often used. Additionally, the cryptosystem is entirely vulnerable due to its susceptibility to cycle attacks (successive encryptions) and the availability of multiple weak keys. All the results in this cryptanalysis paper have inspired us to come up with new systems that are more secure and don’t have the same problems. For this purpose, we have suggested some security improvement points which can be considered for the construction of a robust data communication system. Furthermore, the proposed attack can be implemented for other cryptosystems with similar encryption structures.

Funding Statement: The authors are thankful to the Deanship of Scientific Research at Najran University for funding this work under the Research Groups Funding program grant code (NU/RG/SERC/11/4).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. H. C. Chen, J. I. Guo, L. C. Huang and J. C. Yen, “Design and realization of a new signal security system for multimedia data transmission,” EURASIP Journal on Applied Signal Processing, vol. 2003, no. 13, pp. 1291–1305, 2003. [Google Scholar]

    2. Q. Zhang and J. Han, “A novel color image encryption algorithm based on image hashing, 6D hyperchaotic and DNA coding,” Multimedia Tools and Applications, vol. 80, pp. 13841–13864, 2021. [Google Scholar]

    3. T. J. Chuang and J. C. Lin, “A new algorithm for lossless still image compression,” Pattern Recognition, vol. 31, no. 9, pp. 1343–1352, 1998. [Google Scholar]

    4. L. Munazah, S. Parsa and A. P. Shabir, “Adaptive image encryption based on twin chaotic maps,” Multimedia Tools and Applications, vol. 2, pp. 1–20, 2022. [Google Scholar]

    5. F. Wang, R. Ni, J. Wang, Z. Zhu and Y. Hu, “Invertible encryption network for optical image cryptosystem,” Optics and Lasers in Engineering, vol. 149, pp. 106784, 2022. [Google Scholar]

    6. Q. Younes, J. Abdeltif, E. Mohamed and B. Abdelhamid, “Image encryption algorithm based on genetic operations and chaotic DNA encoding,” Soft Computing, vol. 9, pp. 1–10, 2021. [Google Scholar]

    7. K. L. Chung and L. C. Chang, “Large encryption binary images with higher security,” Pattern Recognition Letters, vol. 19, no. 5, pp. 461–468, 1998. [Google Scholar]

    8. X. Wang and Y. Su, “Security enhancement of image encryption method based on Fresnel diffraction with chaotic phase,” Optics Communications, vol. 506, pp. 127544, 2022. [Google Scholar]

    9. Y. Chen, S. Xie and J. Zhang, “A hybrid domain image encryption algorithm based on improved Henon map,” Entropy, vol. 24, pp. 287, 2022. [Google Scholar]

  10. W. Zhou and X. Wang, “A new combination chaotic system and its application in a new Bit-level image encryption scheme,” Optics and Lasers in Engineering, vol. 149, pp. 10–32, 2022. [Google Scholar]

  11. C. P. Wu and C. C. J. Kuo, “Design of integrated multimedia compression and encryption systems,” IEEE Transactions on Multimedia, vol. 7, no. 5, pp. 828–839, 2005. [Google Scholar]

  12. R. Matthews, “On the derivation of a chaotic encryption algorithm,” Cryptologia, vol. 13, pp. 29–42, 1989. [Google Scholar]

  13. B. F. Zaid, A. M. Asim, A. K. Muhamad, E. U. H. Muhammad and A. Waqar, “Highly dispersive substitution box (S-box) design using chaos,” ETRI Journal, vol. 42, pp. 619–632, 2020. [Google Scholar]

  14. N. Ying, Z. Zheng and X. Zhang, “An image encryption approach based on chaotic maps and genetic operations,” Multimedia Tools and Applications, vol. 79, pp. 13–33, 2020. [Google Scholar]

  15. T. S. Attaullah and S. J. Sajjad, “An improved chaotic cryptosystem for image encryption and digital watermarking,” Wireless Personal Communications, vol. 110, pp. 1429–1442, 2020. [Google Scholar]

  16. W. Wang, N. Guan and J. Yang, “Image encryption algorithm with random scrambling based on one-dimensional logistic selfembedding chaotic map,” Chaos, Solitons and Fractals, vol. 150, pp. 111–129, 2021. [Google Scholar]

  17. P. Naskar, B. Surojit, C. M. Kailash, G. D. Krishna and C. Atal, “An efficient block-level image encryption scheme based on multichaotic maps with DNA encoding,” Nonlinear Dynamics, vol. 105, pp. 3673–3698, 2021. [Google Scholar]

  18. Z. Hua and Y. Zhou, “Exponential chaotic model for generating robust chaos,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 51, no. 6, pp. 3713–3724, 2021. [Google Scholar]

  19. B. Ma and Y. Q. Shi, “A reversible data hiding scheme based on code division multiplexing,” IEEE Transactions on Information Forensics and Security, vol. 11, no. 9, pp. 1914–1927, 2016. [Google Scholar]

  20. X. Wang, X. Wang, B. Ma, Q. Li and Y. -Q. Shi, “High precision error prediction algorithm based on ridge regression predictor for reversible data hiding,” IEEE Signal Processing Letters, vol. 28, pp. 1125–1129, 2021. [Google Scholar]

  21. S. Gaoa, R. Wua, X. Wangb, J., Wanga, Q. Li et al., “A 3D model encryption scheme based on a cascaded chaotic system,” Signal Processing, vol. 202, 2022. https://doi.org/10.1016/j.sigpro.2022.108745 [Google Scholar]

  22. J. Sun, “2D-SCMCI hyperchaotic map for image encryption algorithm,” IEEE Access, vol. 9, pp. 59313–59327, 2021. [Google Scholar]

  23. X. Wang and S. Gao, “A chaotic image encryption algorithm based on a counting system and the semi-tensor product,” Multimedia Tools Applications, vol. 80, pp. 10301–10322, 2021. [Google Scholar]

  24. W. Xingyuan, G. Suo, Y. Xiaolin, Z. Shuang and W. Mingxu, “A new image encryption algorithm with cantor diagonal scrambling based on the PUMCML system,” International Journal of Bifurcation and Chaos, vol. 31, no. 1, pp. 1–30, 2021. [Google Scholar]

  25. C. Wang, B. Ma, Z. Xia, J. Li, Q. Li et al., “Stereoscopic image description with trinion fractional-order continuous orthogonal moments,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 32, no. 4, pp. 1998–2012, 2022. [Google Scholar]

  26. R. Wu, S. Gao, X. Wang, S. Liu, Q. Li et al., “AEA-NCS: An audio encryption algorithm based on a nested chaotic system,” Chaos, Solitons and Fractals, vol. 165, no. 1, pp. 112770, 2022. [Google Scholar]