Picture-Neutrosophic Trusted Safe Semi-Supervised Fuzzy Clustering for Noisy Data

1  Introduction

The finding of underlying connections between the human brain and events has made the development of sophisticated clustering algorithms fashionable in cognitive research [1,2]. Dealing with noisy data is one of the most intriguing clustering difficulties. Incorrect data with noises that affect the quality of results could be seen in many applications, such as satellite images [3], medical image processing [4,5], control systems [6], etc.

Semi-supervised fuzzy clustering techniques were introduced with additional information provided by users [7–9] to enhance the range of applications and the quality of clusters. The differences in incorporating various supplementary information forms were demonstrated in [10] which provided a summary of the semi-supervised fuzzy clustering technique. Accordingly, object segmentation using semi-supervised fuzzy clustering is effective as long as the proper supplementary information, also known as “safe information” and clean data are supplied. However, real-world data are frequently unreliable, noisy and inaccurate. These situations require more effective clustering methods.

The safe semi-supervised fuzzy clustering approach introduced in [11–13] is the typical method to deal with safe information in semi-supervised fuzzy clustering. There are two primary phases in their strategy after the core concept. The confidence weights for labeled data are calculated in the first phase. Then, the high confidence weights are used to generate and identify centers of clusters and fuzzy element values under the labeled data in the second phase. Safe semi-supervised Fuzzy C-Means clustering (S3FCM) approach was firstly presented in [11]. By balancing semi-supervised and unsupervised clustering, this technique investigated the incorrectly classified data. A local homogeneous graph was employed in the first phase [12]. The Local Homogeneous Consistent Safe SSFCM (LHC-S3FCM) method performed effectively on datasets with a large percentage of incorrectly categorized data by utilizing this graph. The CS3FCM, an enhanced safe semi-supervised clustering model, based on confidence weights, was put out in [13]. This approach provides good results in minimizing the negative impact of incorrectly labeled samples on the clustering process, assuming each data sample has its own safe confidence weight.

To establish the safe level of each sample in the data set, Guo et al. [14] have recently suggested a safe semi-supervised clustering with a safe degree. The model provides the essential procedures to reduce the adverse effects of risk in both labeled and unlabeled samples based on the safe degree value. Despite performing better than other approaches when dealing with “safe information”, safe semi-supervised fuzzy clustering algorithms can still not solve the challenge of clustering inaccurate data with noises. Noisy data division can lead to incorrect object detection and inference. Data points, isolated or at the edge of some clusters, are considered to contain noisy data. It is a must to improve safe semi-supervised fuzzy clustering algorithms for dealing with noisy data.

This research aims to develop a new clustering method to remove the noise from data and increase the performance of the clustering method. This method integrates the semi-supervised clustering method and the picture fuzzy set [15]. There are four membership degrees in the PFS [3] with Neutrosophic set [16], including the positive degree, neutral degree, negative degree and rejection degree. Noisy data typically have a high rejection rate. Additionally, the neutral degree is used to determine the data points belonging to the boundary of clusters. It is clear that PFS could be used to identify noisy data in datasets.

Based on the original Fuzzy C-Means (FCM) model, a fuzzy clustering algorithm for images (a.k.a. FC-PFS) introduced in [17] outperforms the other fuzzy clustering techniques in terms of average clustering indices such as the mean accuracy and computational time. As an extension of collaborative distributed fuzzy clustering (CDFCM) [18] on PFS, a form of FC-PFS on distributed computing known as DPFCM was demonstrated in [19]. As stated in the paper, a strategy to reduce computational time and increase clustering quality is the idea of semi-supervised clustering using distributed and cloud computing. Wu and Chen presented an adaptive picture fuzzy clustering technique based on entropy weight [20]. This approach improved accuracy, addressed noisy data in image segmentation and overcame the time-consuming limitation in existing picture fuzzy clustering algorithms. Two practical, robust picture fuzzy clustering techniques for decreasing computational time were also introduced [21,22]. Nonetheless, those fuzzy clustering algorithms struggle with managing both the “safe information” and the “noisy data” because if labeled data has noise, the clustering quality will be seriously affected.

To handle problems with enhancing “safe information” and reducing the effect of “noisy data”, Picture-Neutrosophic Trusted Safe Semi-Supervised Fuzzy Clustering (PNTS3FCM) is introduced. This is a new technique to address the issue of data partition with noisy information. The PNTS3FCM approach includes picture fuzzy and neutrosophic set concepts in the semi-supervised fuzzy clustering with a safe information procedure. The research proposes a new optimization model consisting of four essential components: a clustering component, an outlier-solving component and a safe semi-supervised fuzzy clustering using labeled and unlabeled data. The first two parts employed FC-PFS and the last two are the new parts to enhance safe information and reduce noisy data. An iterative technique from the formulation is also provided to construct the cluster centers and memberships. In fact, the survey has revealed a new field of study: safe, semi-supervised clustering on the picture fuzzy set. To compare PNTS3FCM with other available methods on benchmark datasets, two similar algorithms-FC-PFS [17] and CS3FCM [13], are chosen.

The remaining paper is structured as follows: Section 2 offers the essential information underpinning our study. The proposed approach is introduced in Section 3 and the experimental results are presented in Section 4. Some conclusions are given in the last section.

2  Preliminaries

In this section, some fundamental concepts and methods of semi-supervised clustering are presented, including Safe semi-supervised clustering and Picture fuzzy set and picture fuzzy clustering.

2.1 Safe Semi-Supervised Clustering

Safe semi-supervised fuzzy clustering approaches, including S3FCM [11], LHC-S3FCM [12] and CS3FCM [13] are proposed by Gan et al. Herein, we present the fundamental knowledge of these approaches.

For S3FCM, consider the dataset X={X1,X2,…,Xk,…,Xn} where n is the number of data elements. C is denoted for the number of clusters. The cluster center V is defined by {V1,V2,…,Vj,…,VC}. The membership degree of kth element belonging to the ith cluster is characterized by uik and m is the fuzzifier parameter. The value bk expresses a label indicator; the value bk=1 if Xk is labeled and bk=0 otherwise. fik are the fuzzy degrees of labeled samples. The objective function of S3FCM [11] is as below:

Jsa=∑k=1n∑i=1Cuikmdik2+λ1∑k=1n∑i=1C(uik−fikbk)2dik2+λ2∑k=1n∑i=1C(uik−u^ikbk)2dik2→Min(1)

with: ∑i=1cuik=1,∀k=1,n¯, uik∈[0,1],∀k=1,n¯. Where λ1 and λ2 are the regulatory factor in which U^=[u^ik]c×n is the partition matrix after using FCM on unlabeled data, dik is the distance between the kth element and ith cluster. The final cluster labels are determined through the algorithm [11] and the value uik is specified as follows:

uik=11+λ1+λ2(1+λ1+λ2−∑j=1CΔik∑j=1Cdik2djk2+Δik)(2)

where Δik=λ1fikbk+λ2u^ikbk.

The below function calculates the center vi:

vi=∑k=1nuik2xk+λ1∑k=1n(uik−fikbk)2xk+λ2∑k=1n(uik−u^ikbk)2xk∑k=1nuik2+λ1∑k=1n(uik−fikbk)2+λ2∑k=1n(uik−u^ikbk)2(3)

On the other hand, the LHC-S3FCM [12] is expected to deal with wrong labels from additional information. The objective function is defined as follows:

Jsa=∑k=1n∑i=1Cuikmdik2+λ1∑k=1l∑i=1C(uik−fik)mdik2+λ2∑k=1l∑r=l+1nwkr∑i=1C(uik−uir)2→Min(4)

with the constraints: ∑i=1cuik=1,∀k=1,n¯

Therefore, the cluster centers vi, the value uik for labeled data xk and the value uir for unlabeled data xr correspond to the below functions:

vi=∑k=1nuik2xk+λ1∑k=1l(uik−fik)2xk∑k=1nuik2+λ1∑k=1l(uik−fik)2;uik=pik+1−∑j=1Cpjkqjk∑j=1C1qjkqikanduir=Sir+1−∑j=1Csjrtjr∑j=1C1sjrtir(5)

Another approach of FCM is Confidence-weighted Safe Semi-supervised Clustering (CS3FCM) [13] by using confidence weights. The confidence weights show various effects of samples on performance degradation. The following is the goal:

Jc=∑k=1n∑i=1Cuikmdik2+λ1∑k=1lsk∑i=1C(uik−fik)2dik2+λ2∑k=1l1sk∑r=l+1nwkr∑i=1C(uik−uir)2→Min(6)

with ∑i=1cuik=1,∀k=1,n¯; λ1 and λ2 are the regulatory factors. Therefore, the value of vi, uik and uir are determined by the following functions:

vi=∑k=1nuik2xk+λ1∑k=1lsk(uik−fik)2xk∑k=1nuik2+λ1∑k=1lsk(uik−fik)2;uik=pik+1−∑j=1Cpjkqjk∑j=1C1qjkqikanduir=zir+1−∑j=1Czirtir∑j=1C1tirtir(7)

The methods of Gan [11–13] (S3FCM, LHC-S3FCM, CS3FCM) achieved good clustering accuracy. However, if there may be data outliers, they would affect the determination of the final clusters.

2.2 Picture Fuzzy Set and Picture Fuzzy Clustering

By generalizing the fuzzy set in [9] and the intuitionistic fuzzy set [23], Cuong et al. introduced a definition of the picture fuzzy set [15] in 2014 and have the form as follows:

S={(x,μS(x),ηS(x),γS(x))|x∈X}(8)

where μS(x), ηS(x) and γS(x) correspond to the positive degree, the neutral degree and the negative degree of each element. And these degrees satisfy the following conditions:

0≤μS(x),ηS(x),γS(x)≤1;0≤μS(x)+ηS(x)+γS(x)≤1(9)

Then, the refusal degree is computed by function:

ξS(x)=1−(μS(x)+ηS(x)+γS(x))(10)

The objective of FC-PFS [17] aims to group the data in clusters and reduce the outliers through the concept of entropy as follows:

Jm(U,η,ξ,V)=∑i=1n∑j=1C(μij(2−ξij))m‖xi−vj‖2+∑i=1n∑j=1Cηij(log⁡ηij+ξij)→Min(11)

with the constraints:

μij,ηij,ξij∈[0,1],μij+ηij+ξij∈[0,1],∑j=1Cμij(2−ξij)=1,∑j=1C(ηij+1Cξij)=1,i=1,n¯andj=1,C¯(12)

The values of μS(x),ηS(x) and γS(x) correspond to the positive, neutral and negative degrees of PFS [15]. The vector of the cluster centers denotes V.

For the above objective function, the cluster centers vj, the membership degrees μij and non-membership degrees ηij are computed using the following formulas:

vj=∑i=1n(μij(2−ξij))mxi∑i=1n(μij(2−ξij))m(13)

μij=1(2−ξij)∑k=1C(‖xi−vj‖2‖xi−vk‖2)1/(m−1)(14)

ηij=exp⁡(−ξij)∑k=1Cexp⁡(−ξik)(1−1C∑k=1Cξik)(15)

In [15], the refusal degree ξij is calculated using the Yager complement operator as follows:

ξij=1−(μij+ηij)−(1−(μij+ηij)α)1/α(16)

where α∈(0,1) is a regulatory factor and it is often chosen within [0.6–0.8].

The detailed steps for the FC-PFS algorithm are shown below.

3  The Proposed Picture-Neutrosophic Trusted Safe Semi-Supervised Fuzzy Clustering

3.1 Main Ideas

The idea behind the proposed method (PNTS3FCM) is the combination between PFS and safe semi-supervised fuzzy clustering by introducing a novel objective function with four primary components. The first and the second stages are employed from the original picture fuzzy clustering method [17]. The two last stages are the semi-supervised component used to orient the clustering process by labeled and unlabeled data. The main idea is represented in Fig. 1 and the detailed steps are described in Fig. 2.

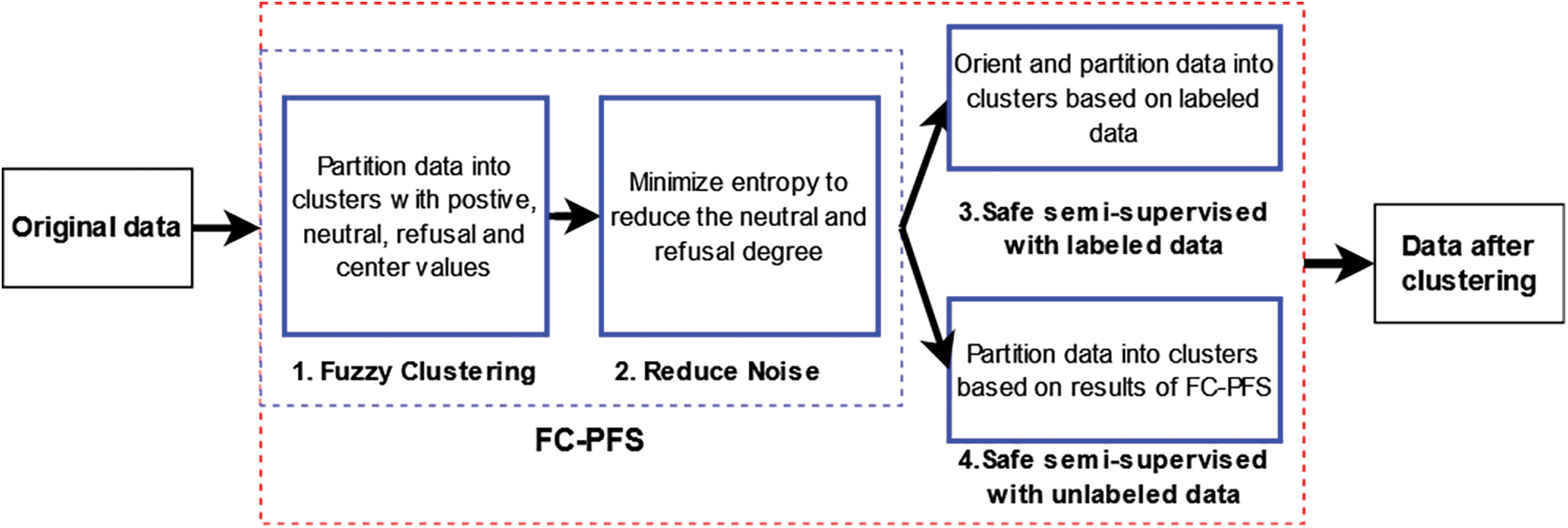
Figure 1: The main idea of the PNTS3FCM

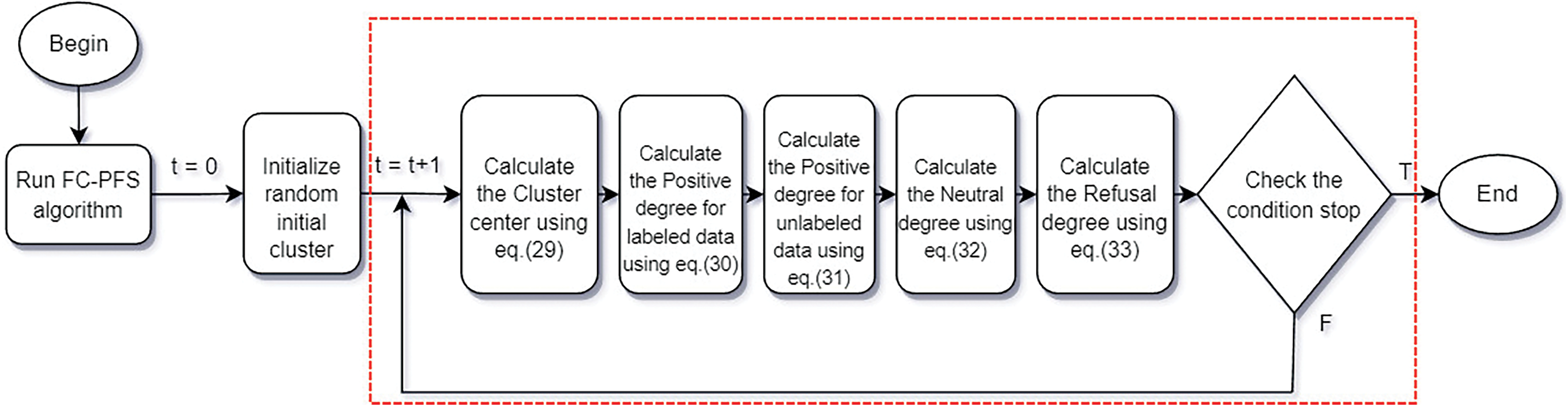
Figure 2: The details of the PNTS3FCM

Fig. 1 illustrates the method and concept in which the input data are provided to the block of PNTS3FCM. Through the use of picture fuzzy degrees, the first step of PNTS3FCM is to reduce the distance between data components and cluster centers. The picture fuzzy set model’s second step involves processing the “noisy data” by integrating the entropy quantity between the neutral and refuse degrees. The refusal degree plays an important role in reducing the effect of noise data in the objective function because of its higher value relating to noise data following [17].

To deal with “safe information”, the two last stages coordinate the safe semi-supervised fuzzy clustering using both labeled and unlabeled data. PNTS3FCM has two phases: Firstly, FC-PFS is used to partition all data to get the clustering result with positive, neutral and refusal values. The second phase uses all data with these values to partition data to archive better clustering quality by enhancing safe data information and reducing noisy data.

The technique produces final clusters that are reliable and confident. We will discuss the formulation and algorithm for this concept in the next section.

3.2 Details of PNTS3FCM

As illustrated by the main idea above, this section will describe the details of the proposed model. The objective function is stated by the following formula:

J=∑k=1n∑j=1C(μkj(2−ξkj))2‖Xk−Vj‖2+∑k=1n∑j=1Cηkj(log⁡ηkj+ξkj)+∑k=1L∑j=1C(μkj(2−ξkj)−fkj)21+(μ¯kj(2−ξ¯kj)−fkj)2‖Xk−Vj‖2+∑k=L+1n∑j=1C(μkj(2−ξkj))21+ξkj¯‖Xk−Vj‖2→Min(17)

With the constraints (k=1,n¯;j=1,C¯):

μkj,ηkj,ξkj≤1,∑j=1C(ηkj+ξkjC)=1,and∑j=1C(μkj(2−ξkj))=1(18)

where data set X={X1,X2,…,Xn} having n elements, the number of labeled data in X:L<n; the number of clusters C; the values of positive, neutral and refusal degrees of element Xk belong to cluster j:μkj,ηkj and ξkj. Each part of the objective function has its own meaning. The first two parts of Eq. (17), as shown, are those of the original picture fuzzy clustering (FC-PFS) [14]. The safe semi-supervised fuzzy clustering on the picture fuzzy set is covered in the last two parts.

•   The first part represents fuzzy clustering on the PFS.

•   The second part represents entropy information which helps to reduce noisy data through the neutral and refusal degrees of a data point.

•   The third part is the component for labeled data elements, where k=1..L and L is the number of labeled data elements. The numerator (μkj(2−ξkj)−fkj)2 describes semi-supervised fuzzy clustering, in which fkj is a given constant that has a value of 1 or 0.

fkj={1iftheelementkisinclusterj0iftheelement kisn′tincluster j(19)

The denominator 1+(μ¯kj(2−ξ¯kj)−fkj)2 describes the safe semi-supervised clustering. The meaning of this component is as follows: After clustering, if any data point is assigned to the correct label, the weight will be increased; otherwise, the weight will be decreased.

•   Finally, the fourth part is the component of the unlabeled data elements, where the numerator is the same as the first part and the denominator (1+ξ¯kj) is added to the component ξ¯kj. The meaning of this value is that after applying clustering to all data points, the denominator (1+ξ¯kj) will be greater than 1 for unlabeled data elements with high refusal value of ξ¯kj. Indeed, the weights of these data elements are reduced.

•   The additional information for semi-supervised fuzzy clustering is the prior picture membership degrees. We use the original FC-PFS algorithm to cluster all data, including labeled and unlabeled data. From that, we calculate four values (μ¯kj,η¯kj,ξ¯kj,V¯) that guide the calculation for all data elements.

Using the Lagrangian method, the optimal solutions to the stated problem are presented in Eqs. (20)–(24) below.

Vj=∑k=1n(μkj(2−ξkj))2Xk+∑k=1L(μkj(2−ξkj)−fkj)21+(μ¯kj(2−ξ¯kj)−fkj)2Xk+∑k=L+1n(μkj(2−ξkj))2(1+ξ¯kj)2Xk∑k=1n(μkj(2−ξkj))2+∑k=1L(μkj(2−ξkj)−fkj)21+(μ¯kj(2−ξ¯kj)−fkj)2+∑k=L+1n(μkj(2−ξkj))2(1+ξ¯kj)2(20)

The positive degree u of the labeled data elements is

μkj=fkj(2−ξkj)(2+(μ¯kj(2−ξ¯kj)−fkj)2)++1−∑i=1Cfki2+(μ¯ki(2−ξ¯ki)−fki)2(2−ξkj)(2+(μ¯kj(2−ξ¯kj)−fkj)2)(1+(μ¯kj(2−ξ¯kj)−fkj)2)∑i=1C‖Xk−Vj‖2(1+(μ¯ki(2−ξ¯ki)−fki)2)‖Xk−Vi‖2(2+(μ¯ki(2−ξ¯ki)−fki)2)(21)

The positive degree u of the unlabeled data elements is

μkj=1(2−ξkj)∑i=1C(1+1ξ¯kj1+1ξ¯ki)‖Xk−Vj‖2‖Xk−Vi‖2(22)

Other degrees are shown below:

ηkj=(1−1C∑i=1Cξki)e−ξkj∑i=1Ce−ξki(23)

ξkj=11+e3−(μkj+ηkj)−(3−(μkj+ηkj)α)1α(24)

Details of the FPNTS3FCM algorithm are below.

3.3 Remarks

Advantages of the PNTS3FCM algorithm:

a) PNTS3FCM has better clustering quality than the related methods, such as FC-PFS and CS3FCM algorithm, due to the capability to handle noisy data.

b) PNTS3FCM produces more information about the clusters, such as the cluster centers and the picture fuzzy degrees (positive, neutral, negative, refusal). It deals with both “safe information” and “noisy data”.

c) PNTS3FCM is the combination of three major concepts: SAFE, SEMI Clustering and PICTURE Fuzzy Set. The combination is the first trial in the literature toward practical problems.

Disadvantages of the PNTS3FCM algorithm

a) PNTS3FCM takes more computational time than the other algorithms due to the calculation of two additional parts in the objective function (24).

b) The model contains many parameters which need to be tuned in some real-world applications.

4  Experimental Results

4.1 Environmental Configuration

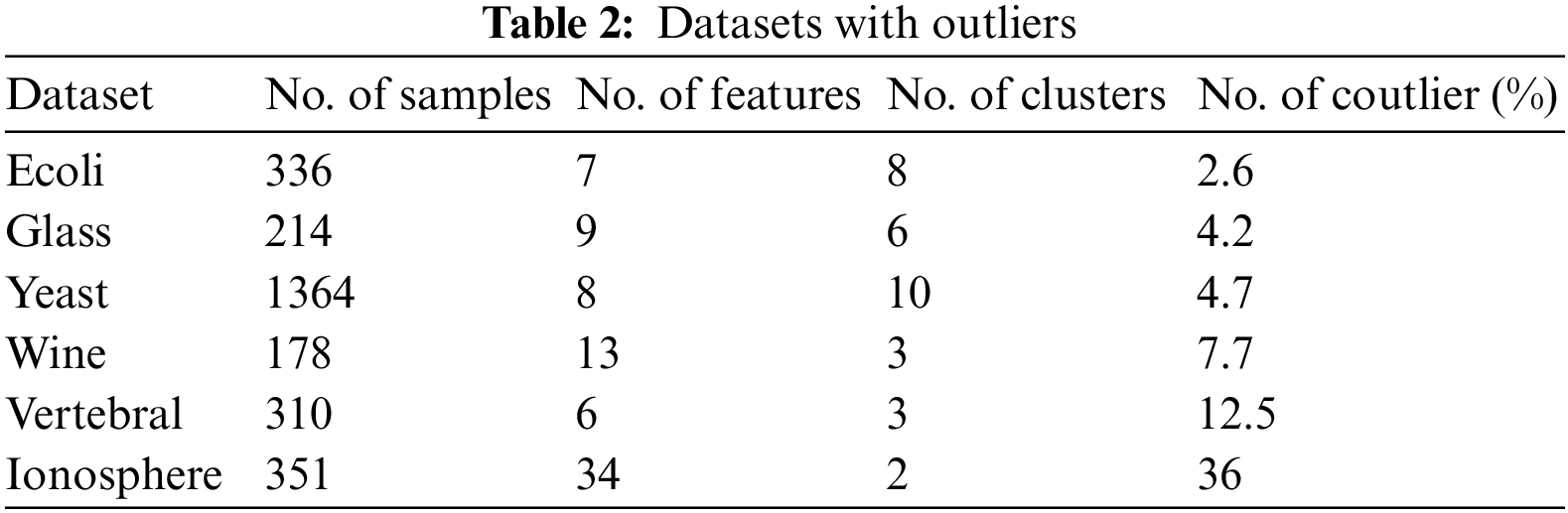
The experiments are performed on a Core i5-powered HP laptop using the C programming language. The selected benchmark UCI datasets [24] are described in Table 1. Outlier Detection DataSets (ODDS) [25] are given in Table 2.

Experiments are executed to compare the proposed PNTS3FCM approach and the state-of-art methods, CS3FCM [13] and FC-PFS [17]. The classification accuracy (CA), computing time (CT) and clustering quality indicators, including DB, PBM and ASWC [26], are the criteria for evaluation. The CT is the amount of time needed to complete the computation. Value CT is computed as in (25).

CT=T2−T1(25)

where T1, T2 is the starting time and ending time of the algorithm, respectively. The smaller value of CT reaches, the better performance of the method is. The calculation of CA [13] is given by the below equation.

CA=∑k=1nδ(yk,map(y~k))n(26)

where map(y~k) is the function that determines the equivalent label for y~k using the Kuhn–Munkres algorithm [12]. The function δ(x,y) gets two values (0 if x≠y and 1 if x=y). The performance of the CA index is better when it has a higher value.

The value of ASWC is computed by Eq. (27).

sxj=bp,jap,j+ε(27)

where ap,j is the average distance from ith element to all other parts in pth cluster; bp,j is the average distance from ith element to all other elements in pthcluster. ε is a tiny constant. It is added to make the denominator differ from zero (when ap,j=0). The higher value of the ASWC index leads to better performance.

The value of PBM [26] is determined by:

PBM=(1CE1EKDK)2(28)

where E1=∑i=1n‖Xi−X¯‖, EK=∑j=1C∑Xi∈clusterj‖Xi−X¯j‖, DK=maxj,l=1,…,C‖X¯j−X¯l‖ with X¯jis the average value of all elements in the jth cluster, j=1,C¯. The higher value of the PBM index has, the better performance is.

The DB [27] is determined by (29)

DB=1C∑i=1C(maxj:j≠i{Si+SjMij})(29)

where Ti is the size of ith cluster. In which Si and Mij are computed by

Si=1Ti∑j=1Ti|Xj−Vi|2;Mij=‖Vi−Vj‖withi,j=1,C¯,i≠j(30)

The average value and standard deviation value in experimental results are denoted as Ave and STD Dev, respectively.

4.2 Experimental Results

4.2.1 Classification Accuracy

Herein, the proposed method is assessed by classification accuracy in two situations, including on all data and labeled data. Herein, the experimental results are presented following two of these cases.

Evaluation by classification accuracy on all data

Using all the data elements of 15 datasets, the classification accuracy of PNTS3FCM, FC-PFS and CS3FCM are calculated and presented as follows. Table 3 shows the classification accuracy of all data without outliers.

As shown in Table 3, PNTS3FCM gets the best results of CA on 7/9 datasets (except Australian and WDBC). FC-PFS has not achieved the highest CA on all datasets. CS3FCM is the best model on 2/9 datasets (Australian, WDBC).

From the results in Table 4, it is clear that PNTS3FCM gives correct classification results in 4 out of 6 datasets (Glass, Yeast, Vertebral, Ionosphere). The other FC-PFS is only better on the Wine dataset and CS3FCM only gives good results on the Ecoli dataset.

Summary: During the evaluation by classification accuracy on all data, including outlier and non-outlier (15 datasets), PNTS3FCM is the best on 11 datasets (Balance-scale, Dermatology, Heart, Iris, Spambase, Tae, Waveform, Glass, Yeast, Vertebral, Ionosphere). FC-PFS is the best model on the Wine dataset. CS3FCM is the best model on three datasets (Australian, WDBC, Ecoli).

Evaluation by classification accuracy on labeled data

By using the labeled data elements of 15 datasets, the classification accuracy (CA) of PNTS3FCM, FC-PFS and CS3FCM are calculated and presented as follows. Table 5 shows the classification accuracy of labeled data without outliers.

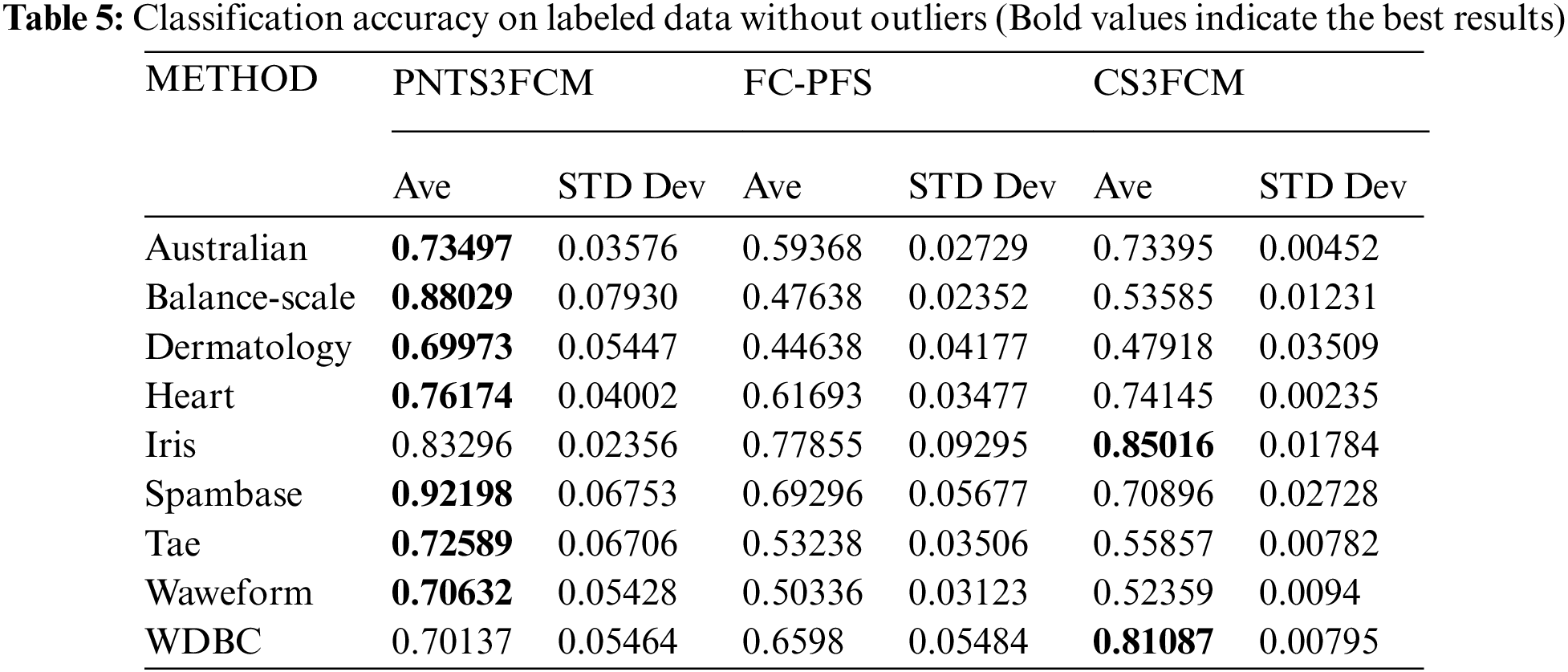
In Table 5, PNTS3FCM gets the best results of CA on 7/9 datasets (except Iris and WDBC). FC-PFS has no highest value on all datasets. CS3FCM is the best model on 2/9 datasets (Iris, WDBC). As shown in Table 6, PNTS3FCM shows the highest values on 4/6 datasets (Ecoli, Glass, Yeast, Vertebral). FC-PFS has no highest CA on all datasets. CS3FCM is the best model on 2/6 datasets (Wine, Ionosphere).

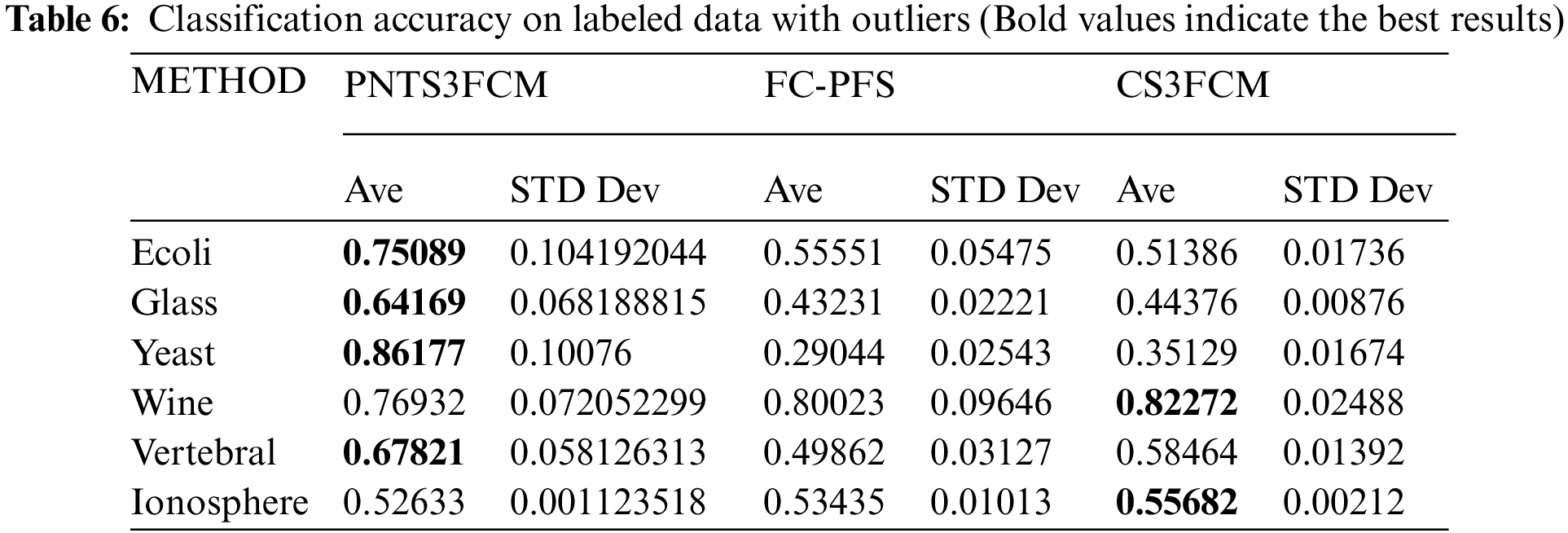
Summary: During the evaluation by classification accuracy on labeled data, including outlier and non-outlier (15 datasets), PNTS3FCM has better results on 11 datasets (Australian, Balance-scale, Dermatology, Heart, Spambase, Tae, Waveform, Ecoli, Glass, Yeast, Vertebral). FC-PFS has not had the highest CA on all datasets. CS3FCM is the best model on four datasets (Iris, WDBC, Wine, Ionosphere).

4.2.2 Evaluation by Clustering Quality

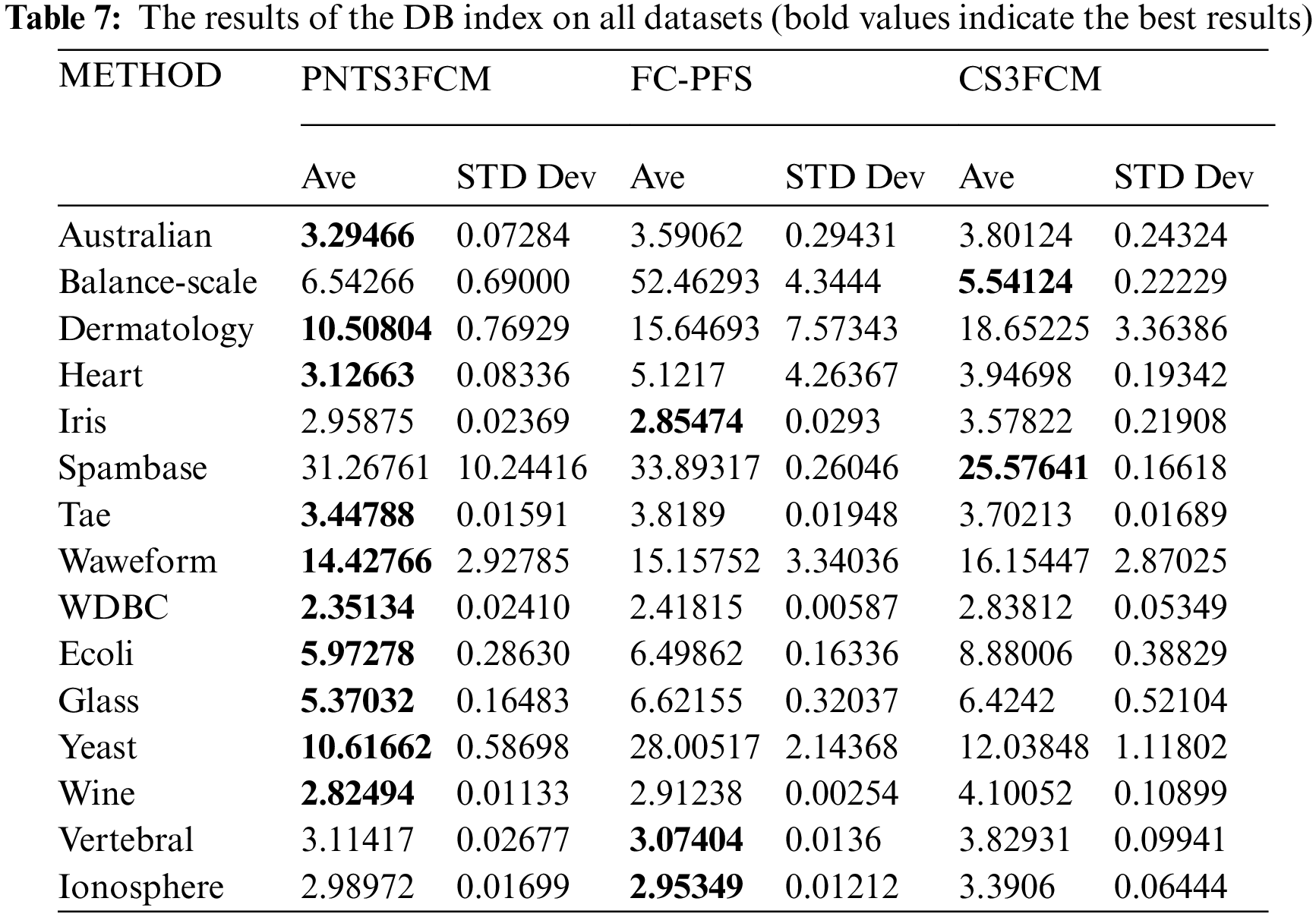
Summary: As in Table 7, During the evaluation clustering quality by DB index on all data, including outlier and non-outlier (15 datasets), PNTS3FCM gets the best results on ten datasets (Australian, Dermatology, Heart, Tae, Waveform, WDBC, Ecoli, Glass, Yeast, Wine). FC-PFS is the best model on three datasets (Iris, Vertebral, Ionosphere). CS3FCM is the best model on 3 datasets (Balance-scale, Spambase). This pointed out that the proposed method was better in clustering quality in not only outlier not also non-outlier data compared to others.

4.2.3 Evaluation by Computational Time (in seconds)

We compare PNTS3FCM and CS3FCM on 15 datasets using computational time. Table 8 shows the results of evaluation clustering quality by computational time on data without outlier datasets.

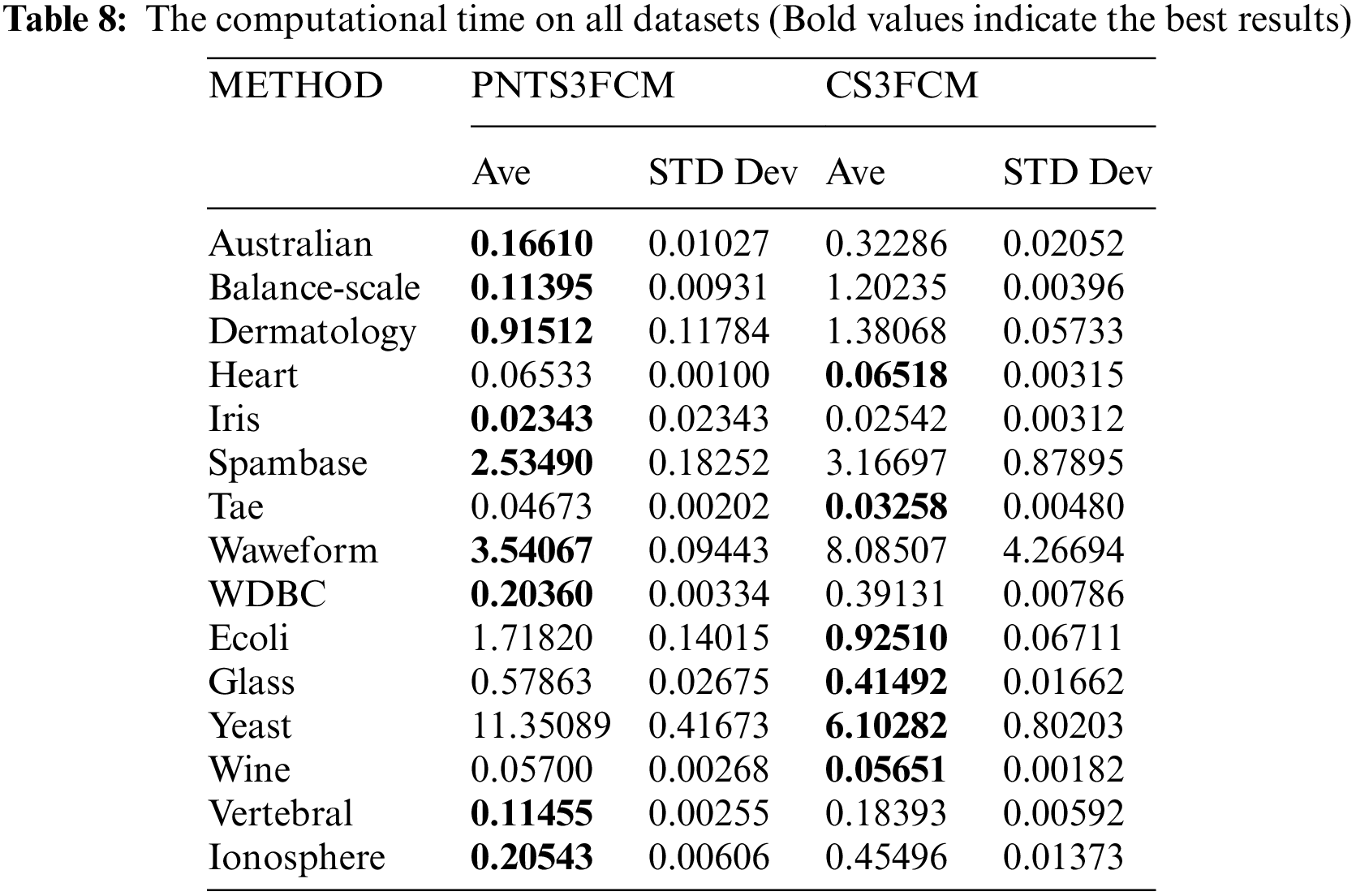
Summary: During the evaluation of computational time on all data, including outlier and non-outlier (15 datasets), PNTS3FCM has better results on nine datasets. CS3FCM is the best model on six datasets. The proposed method seems to be better with a more significant number of data clusters. To get better results, the proposed method is firstly based on Picture fuzzy set that has more information to reduce the noise or hesitation in partitioning data. Secondly, PNTS3PFCM has a safe semi-supervised part for labeled and unlabeled data that can cope with the doubt labeled data, then reduce their effectiveness in the clustering process.

5  Conclusion

This research suggested a novel technique called Picture-Neutrosophic Trusted Safe Semi-Supervised Fuzzy Clustering (PNTS3FCM) to address the issue of data clustering with high confidence and noisy information. PNTS3FCM is constructed based on combining Picture Fuzzy Sets, Neutrosophic Sets and safe fuzzy semi-supervised clustering (PFS). This method consists of 4 critical parts: the clustering portion, the outlier solution part and the safe semi-supervised fuzzy clustering with labeled and unlabeled data. Through the use of PFS, the first stage of PNTS3FCM aims to reduce the distance between data components and cluster centers. The model’s second step involves processing the “noisy data” by integrating the entropy quantity between the neutral and refuse degrees. The third and fourth stages coordinate the safe semi-supervised fuzzy clustering using both labeled and unlabeled data to solve the safety information. We also provide an iterative technique from the formulation to construct the cluster centers and memberships. The method produces final clusters that are reliable and confident.

PNTS3FCM has illustrated its effectiveness by comparing it with two related methods, including FC-PFS and CS3FCM algorithm. The experiment results show that PNTS3FCM is better than the others in terms of computational time and clustering quality. Even though the proposed PNTS3FCM mainly focuses on eliminating or reducing noisy data elements, this method still has some limitations. First of all, PNTS3FCM takes a long time to compute. Secondly, it needs an increased number of parameters. In the future, an effective optimization algorithm will be studied and introduced to overcome these limitations.

Acknowledgement: We are grateful for the support from the staff of the Institute of Information Technology, Vietnam Academy of Science and Technology.

Funding Statement: This research is funded by Graduate University of Science and Technology under grant number GUST.STS.ĐT2020-TT01.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. X. Ji, S. Liu, P. Zhao, X. Li and Q. Liu, “Clustering ensemble based on sample’s certainty,” Cognitive Computation, vol. 13, no. 4, pp. 1034–1046, 2021. [Google Scholar]

    2. J. Zhang, H. Wang, S. Huang, T. Li, P. Jin et al., “Co-adjustment learning for co-clustering,” Cognitive Computation, vol. 13, no. 2, pp. 504–517, 2021. [Google Scholar]

    3. P. H. Thong, “Some novel hybrid forecast methods based on picture fuzzy clustering for weather nowcasting from satellite image sequences,” Applied Intelligence, vol. 46, no. 1, pp. 1–15, 2017. [Google Scholar]

    4. A. Khosravanian, M. Rahmanimanesh, P. Keshavarzi and S. Mozaffari, “Fuzzy local intensity clustering (FLIC) model for automatic medical image segmentation,” The Visual Computer, vol. 37, no. 5, pp. 1185–1206, 2021. [Google Scholar]

    5. S. A. Kumar, B. S. Harish and V. M. Aradhya, “A picture fuzzy clustering approach for brain tumor segmentation,” in 2016 Second Int. Conf. on Cognitive Computing and Information Processing (CCIP), Mysuru, India, pp. 1–6, 2016. [Google Scholar]

    6. G. Bode, T. Schreiber, M. Baranski and D. Müller, “A time series clustering approach for building automation and control systems,” Applied Energy, vol. 238, no. 11, pp. 1337–1345, 2019. [Google Scholar]

    7. J. C. Bezdek, Pattern recognition with fuzzy objective function algorithms. New York: Plenum Press. http://dx.doi.org/10.1007/978-1-4757-0450-1. [Google Scholar]

    8. N. Grira, M. Crucianu and N. Boujemaa, “Active semi-supervised fuzzy clustering,” Pattern Recognition, vol. 41, no. 5, pp. 1834–1844, 2008. [Google Scholar]

    9. L. A. Zadeh, “Fuzzy sets,” Information and Control, vol. 8, no. 3, pp. 338–353, 1965. [Google Scholar]

  10. P. H. Thong and L. H. Son, “An overview of semi-supervised fuzzy clustering algorithms,” International Journal of Engineering and Technology, vol. 8, no. 4, pp. 301–306, 2016. [Google Scholar]

  11. H. Gan, “Safe semi-supervised fuzzy C-means clustering,” IEEE Access, vol. 7, pp. 95659–95664, 2019. [Google Scholar]

  12. H. Gan, Y. Fan, Z. Luo and Q. Zhang, “Local homogeneous consistent safe semi-supervised clustering,” Expert Systems with Applications, vol. 97, pp. 384–393, 2018. [Google Scholar]

  13. H. Gan, Y. Fan, Z. Luo, R. Huang and Z. Yang, “Confidence-weighted safe semi-supervised clustering,” Engineering Applications of Artificial Intelligence, vol. 81, pp. 107–116, 2019. [Google Scholar]

  14. L. Guo, H. Gan, S. Xia, X. Xu and T. Zhou, “Joint exploring of risky labeled and unlabeled samples for safe semi-supervised clustering,” Expert Systems with Applications, vol. 176, pp. 114796–114803, 2021. [Google Scholar]

  15. B. C. Cuong and V. Kreinovich, “Picture fuzzy sets,” Journal of Computer Science and Cybernetics, vol. 30, no. 4, pp. 409–420, 2014. [Google Scholar]

  16. F. Smarandache, Neutrosophy: Neutrosophic probability, set and logic: analytic synthesis & synthetic analysis. Santa Fe, Rehoboth, MA, USA: American Research Press, 1998. [Google Scholar]

  17. P. H. Thong and L. H. Son, “Picture fuzzy clustering: A new computational intelligence method,” Soft Computing, vol. 20, no. 9, pp. 3549–3562, 2016. [Google Scholar]

  18. J. Zhou, C. P. Chen, L. Chen and H. X. Li, “A collaborative fuzzy clustering algorithm in distributed network environments,” IEEE Transactions on Fuzzy Systems, vol. 22, no. 6, pp. 1443–1456, 2013. [Google Scholar]

  19. L. H. Son, “DPFCM: A novel distributed picture fuzzy clustering method on picture fuzzy sets,” Expert Systems with Applications, vol. 42, no. 1, pp. 51–66, 2015. [Google Scholar]

  20. C. Wu and Y. Chen, “Adaptive entropy weighted picture fuzzy clustering algorithm with spatial information for image segmentation,” Applied Soft Computing, vol. 86, no. 4, pp. 105888–105927, 2020. [Google Scholar]

  21. C. Wu and Z. Kang, “Robust entropy-based symmetric regularized picture fuzzy clustering for image segmentation,” Digital Signal Processing, vol. 110, no. 1, pp. 102905–102933, 2021. [Google Scholar]

  22. C. Wu and N. Liu, “Suppressed robust picture fuzzy clustering for image segmentation,” Soft Computing, vol. 25, no. 5, pp. 3751–3774, 2021. [Google Scholar]

  23. K. Atanassov, “Intuitionistic fuzzy sets,” International Journal Bioautomation, vol. 20, pp. S1–S6, 2016. [Google Scholar]

  24. UCI Machine learning repository, “Data,” 2021. [Online]. Available: https://archive.ics.uci.edu/ml/index.php. [Google Scholar]

  25. Outlier detection datasets (ODDS“Data,” 2016. [Online]. Available: http://odds.cs.stonybrook.edu/. [Google Scholar]

  26. L. Vendramin, R. J. Campello and E. R. Hruschka, “Relative clustering validity criteria: A comparative overview,” Statistical Analysis and Data Mining: The ASA Data Science Journal, vol. 3, no. 4, pp. 209–235, 2010. [Google Scholar]