Structural Interval Reliability Algorithm Based on Bernstein Polynomials and Evidence Theory

1  Introduction

Structural reliability is an essential tool to measure the safety performance of structures under the influence of uncertain factors. It is necessary to judge whether the reliability of traditional limit state calculation is reliable and the calculation cost is very high. In the existing methods, the deterministic mathematical model with safety coefficients is often adopted to complete the structural design. A complex deterministic model like the fractal fractional model [1] can be built by computer modeling, but it cannot accurately describe the uncertainty in engineering problems. Stochastic extension of the deterministic model [2] can address the above issue; however, various assumptions are imposed to simplify the calculation, which limits this method. To solve this problem, the method of fitting the probability density function of uncertain variables is often adopted. However, this method requires a lot of sampling, and the calculation cost sometimes exceeds that of the original method. Evidence theory [3] uses an interval composed of a pair of upper and lower probability values to describe the reliability of the problem and the uncertainty of the proposition. This interval contains the real probability value calculated by the traditional probability method. Thus, the problem of solving reliability is transformed into the problem of solving an interval value range [4]. Although it may cause conflicts in the evidence combination rule, some appropriate methods can avoid this problem [5]. Evidence theory uses probability bounds to reflect confidence in the collective power set of all possible outcomes. Evidence theory can deal with uncertain problems well in line with people’s habits of thinking, which can reasonably describe and deal with all kinds of incomplete information, uncertain information, unreliable information, and even conflicting information, so it is applied to various fields [6,7]. Therefore, the motivation of this research is to find an effective, low-cost method for structural interval reliability.

In this paper, a method to solve the reliability probability interval by using Bernstein polynomials is proposed. The value range of limit state function is obtained by Bernstein polynomial approximation, and then the reliability interval of the problem is obtained based on evidence theory [8]. This method has higher efficiency and accuracy for implicit limit states and complex explicit expressions [9,10].

The rest of the paper is organized as follows: Section 2 briefly reviews some specific measures and open issues in the literature. Section 3 elaborates on our proposed method. Section 4 presents the experiments, and Section 5 describes the results and discussion. Section 6 concludes the paper.

2  Review of Typical Uncertainty Measures

In this section, we first introduce some basic concepts of evidence theory and then summarize its application model in structural reliability analysis. In addition, the current research status with the structural reliability analysis is illustrated by pieces of literature.

2.1 Basic Principles of Evidence Theory

Evidence theory was first proposed and developed by Dempster and Shafer, which is also called Dempster–Shafer theory. The Frame of Discernment (FD) is the most fundamental concept in evidence theory [11] which is the set of all possible results that can be recognized for a particular decision problem. The FD is similar to the sample of random variables in probability theory, which consists of a finite number of essential elements. As an essential concept of evidence theory, the Basic Probability Assignment (BPA) is used to describe the credibility of propositions. Θ is regarded as the FD if the set function (m: 2X→[0,1] is the power set of Θ) satisfies the following three properties:

m(A)≥0,∀A∈2Xm(∅)=0∑A∈2Xm(A)=1(1)

Then m is called the BPA on the FD of Θ. For all A∈2X, m(A) is called the primary credible number of A, where the set A of m(A)≥0 is called the focal element of m. The primary credible number reflects the support of the evidence for the proposition that an element of X belongs to set A, or the degree to which the decision-maker has reason to believe in proposition A under this evidence, which is similar to the probability density function in the random model [12–14]. The belief function (Bel) and plausibility function (Pl) represent the degree of truth of proposition A. Bel(A) is the sum of the basic credible numbers of evidence that fully support proposition A, and Pl(A) is the sum of the basic credible numbers that fully or partially support proposition A, that is:

Bel(A)=∑C⊆Am(C)Pl(A)=∑C∩A≠∅m(C)(2)

The two measures, one upper bound and the other lower bound, form an upper and lower probability interval to describe the uncertainty of proposition A [15,16].

2.2 Structural Reliability Analysis Based on Evidence Theory

Evidence theory uses an interval composed of a pair of upper and lower probability values to describe the reliability of the problem. This interval contains the true probability value P calculated by the traditional probability method. With the increased uncertain variable information, the upper probability Pl(A), lower probability Bel(A) and P will approach the same value [17]. For a single evidence variable, the above method can be used to convert the variable into an interval variable. For the case of multiple independent evidence variables, the Cartesian product method should be used to combine all evidence variables.

For a two-dimensional limit state equation g(a,b), a∈A and b∈B are two independent evidence variables. The reliability domain of the structure is defined as follows:

G={g:g(a,b)≥g0},(a,b)∈dk,dk=[ai,bj]⊂D(3)

D=A×B={dk=[ai,bj],ai∈A,bj∈B}(4)

where g0 is the allowable response value, D is the Cartesian product of A and B, and ai,bj,dk are the focal elements of A, B and D respectively. Multiple independent evidence variables are combined by the Cartesian product and shown as a multi-dimensional cube structure in geometry.

Based on the combination of BPA and reliability domain G, the reliability measures Bel(G) and Pl(G) of the structure can be calculated. These two measures will contain the probability reliability value R=P{g(a,b)≥g0} under complete information:

Bel(G)≤R≤Pl(G)(5)

Bel(G) and Pl(G) are obtained from Eq. (2), where set A is replaced by G, and C becomes the focal element of the n-dimensional FD:

Bel(G)=∑dk⊆Gmd(dk)Pl(G)=∑dk∩G≠∅md(dk)(6)

The term md(dk) represents two joint BPAs. It can be seen that dk⊆G or dk∩G≠∅ is a necessary determiner when calculating Bel(G) and Pl(G); dk⊆G means that the focal element is entirely within the reliability domain, while dk∩G≠∅ indicates that the focal element is completely or partially within the reliability domain. To judge accurately, it is necessary to calculate the extreme value of the limit state equation g on each focal element dk:

[gmin,gmax]=[minX∈dkg(X),maxX∈dkg(X)](7)

If both gmin−g0 and gmax−g0 are positive, it indicates dk⊆G, and BPA is included in Bel(G) and Pl(G). If both gmin−g0 and gmax−g0 are negative, BPA is included in neither Bel(G) nor Pl(G). If gmin−g0 is negative but gmax−g0 is positive, it indicates dk∩G≠∅, and BPA is only included in Pl(G). By performing the above analysis on all focal elements, Bel(G) and Pl(G) can finally be obtained.

2.3 Related Works

In recent years, reliability research based on evidence theory has become a hot spot in the reliability research of high-tech equipment. The combination method proposed by Yang et al. [18] and Jiang et al. [19] considers multiple dimensions when fusing conflict evidence. However, there is still a problem that the consideration is not comprehensive or the probability subtraction method is used to measure the consistency of evidence at the decision-making level. In response to this problem, many experts and scholars have improved the evidence combination rules by modifying the evidence combination rules [20] and the actual evidence [21,22], respectively. However, the method of modifying the evidence combination rules fails to preserve the exchange laws and association law of the classical Dempster combination rules, which is not convenient for complex combination operations. Most of the previous methods to modify the actual evidence only consider the consistency of evidence at the reliability level. In contrast, the reliability evaluation depends on the probability distribution of indicators, so there is a lack of consistent measurement of evidence at the decision-making level. In literature [23], the conflict degree of evidence at the decision-making level is measured by the sum of the absolute values of the difference between the evidence and the Pignistic probability values of the same focal element, to define the correction weight of each evidence. However, the results of the consistency measurement between evidence by this method are often affected by the probability interval segmentation and are not accurate enough.

3  Methodology

In this method, the value range of the limit state function is obtained by Bernstein polynomial approximation, and then the reliability interval of the problem is obtained based on evidence theory. As seen from the above section, the key to reliability analysis of evidence theory is to solve the extreme value of the limit state function on each focal element [24]. There are two forms of limit state function for structural reliability analysis under cognitive uncertainty, namely, explicit limit state function and implicit limit state function. The explicit limit state function is divided into polynomial expressions and complex expressions. For complex expressions and implicit expressions, the response surface method is first used to establish the polynomial response surface approximation.

3.1 Response Surface Methodology

In this paper, the quadratic response surface method without cross terms is adopted. It approximates the actual limit state function g(x) in the following form:

g(x)≈G(x)=a+∑i=1nbixi+∑i=1ncixi2(8)

where x=[x1,x2,…,xn]T is an uncertain variable and a,bi,ci(i=1,…,n) are 2n + 1 unknown coefficients to be determined, which can be obtained by fitting some test points. In this method, the first test point is taken as the mean point xμ=[μ1,μ2,…,μn]T of uncertain variables, and the remaining 2n test points are taken as the maximum and minimum values of each uncertain variable. From this (2n + 1)th test point, the (2n + 1)th unknown coefficient can be obtained. Then the quadratic approximate limit state function without cross terms can be obtained.

3.2 Bernstein Polynomials for Extreme Values

After obtaining the approximate limit state function, the reliability analysis is transformed into the solution of the range of polynomials. Traditional optimization methods are complex in solving multi-dimensional and high-order problems, and there are optimal local problems. In this paper, a method based on Bernstein polynomials is proposed to obtain the value range of the limit state function. By using the properties of Bernstein polynomials [25], it is possible to solve Bernstein coefficients instead of finding the range directly.

Bernstein polynomials have the following properties for a given multivariate polynomial:

h(u)=∑0≤i≤naiui(9)

where i=[i1,i2,…,is], ui=u1i1⋅u2i2⋅…⋅usis and n=[n1,n2,…,ns], represent the highest values of each variable. If u1∈[0,1],u2∈[0,1],⋯,us∈[0,1] is satisfied, the original polynomial can be expanded into Bernstein polynomial form:

h(u)=∑0≤i≤nbi(D,g)Bin(u)(10)

and

min(bi(D,g))≤h(u)≤max(bi(D,g))(11)

Among

Bin(u)=Bi1n1(u1)⋅Bi2n2(u2)⋅……Bisns(us),(12)

Biknk(uk)=(nkik)(1−uk)nk−ikukik(13)

is called the ith Bernstein term, and

bi(D,g)=∑j≤i∏k=1s(ikjk)(nkjk)aj(14)

is called the term’s Bernstein coefficient, where aj corresponds to ai in the original polynomial one-to-one. Considering that (ij) is the probability of simply extracting j elements from i elements, the key to calculating the Bernstein coefficient is the coefficient ai in the original polynomial.

Expanding the approximate polynomial of the limit state function into a Bernstein polynomial, the value range of the limit state function is obtained from the properties of the Bernstein polynomial coefficients:min(bi(D,g))≤h(u)≤max(bi(D,g)). The evidence theory is used to complete the reliability analysis.

3.3 Algorithm Design

Based on the above contents, the specific algorithm for interval reliability analysis based on Bernstein polynomials and evidence theory can be obtained, as shown in Fig. 1.

Figure 1: Algorithm flow chart

4  Example

4.1 Numerical Examples

For the composite beam shown in Fig. 2, the elastic modulus of the beam is E, the length, width, and height are L (mm), A (mm) and B (mm) respectively, and the elastic modulus of the aluminum plate on the lower surface of the beam is Ea, and the width and height of the effective section are C (mm) and D (mm) respectively. Six external vertical forces P1, P2, P3, P4, P5 and P6 are applied to six different positions of the beam, L1, L2, L3, L4, L5 and L6 respectively. The limit state function is defined as the difference between the allowable stress and the maximum stress:

Y=g(x)=S−σmax(x)(15)

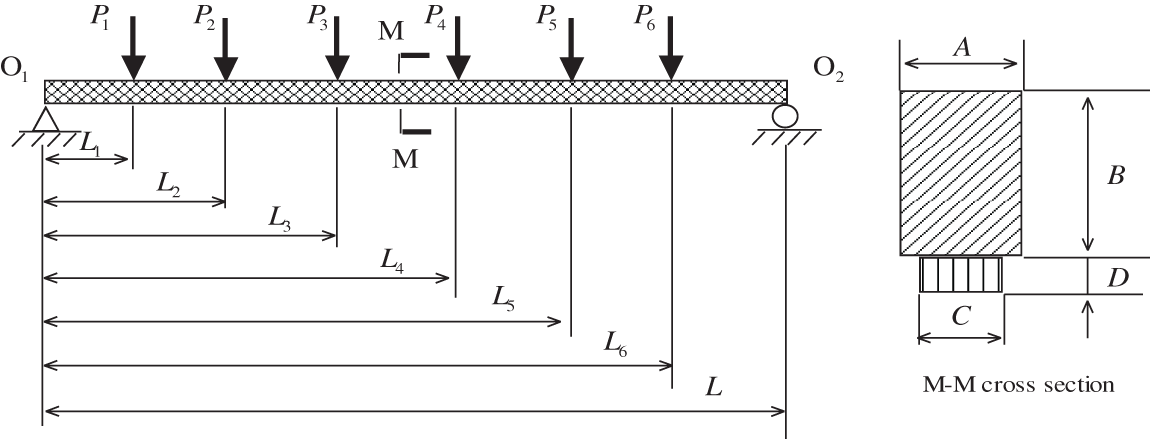
Figure 2: Composite beam diagram

Among them, S is the allowable stress, and σmax(x) represents the maximum stress and its expression is:

σmax(x)=max{σk(x):k=1,…,6}(16)

The stress σk(x) applied to the cross section at Pk can be expressed as follows:

σ1(x)=[L1∑i=16Pi(L−Li)/L]Ymax(x)W(x)(17)

σk(x)=[Lk∑i=16Pi(L−Li)/L−∑i=1k−1Pi(Lk−Li)]Ymax(x)W(x),k=(2,…,6)(18)

where Pi represents the external vertical force applied to the corresponding position of the beam, Li is the length of the beam at this position, and

Ymax(x)=0.5AB2+DC(B+D)Ea/EwAB+DCEa/Ew(19)

W(x)=AB312+AB[Ymax(x)−B2]2+CD3Ea12Ew+CDEaEw[D2+B−Ymax(x)]2(20)

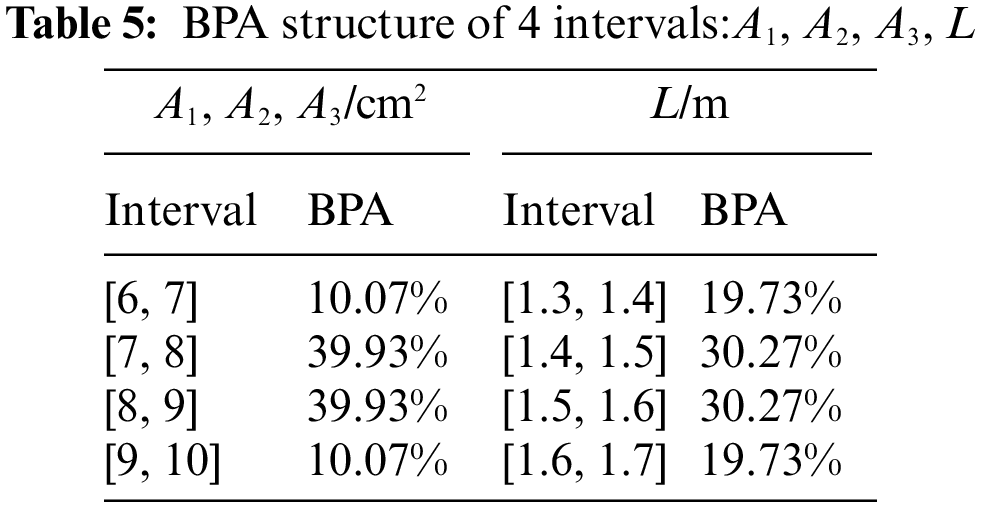
The values of the 15 fixed parameters in the model are: L1=200mm, L2=400mm, L3=600mm, L4=800mm, L5=1000mm, L6=1200mm, L=1400mm, P1=P2=P3=P4=P5=P6=15kN, Ea=70GPa and Ew=8.75GPa. Assume that variables A, B, C and D all obey normal distribution with mean values μA=100mm, μB=200mm, μC=80mm and μD=20mm and standard deviations σA=1mm, σB=2mm, σC=0.8mm and σD=0.2mm. The BPA of each variable is obtained through the probability model. Tables 1–3 show the BPA of each variable divided into four segments, eight segments and sixteen segments, respectively.

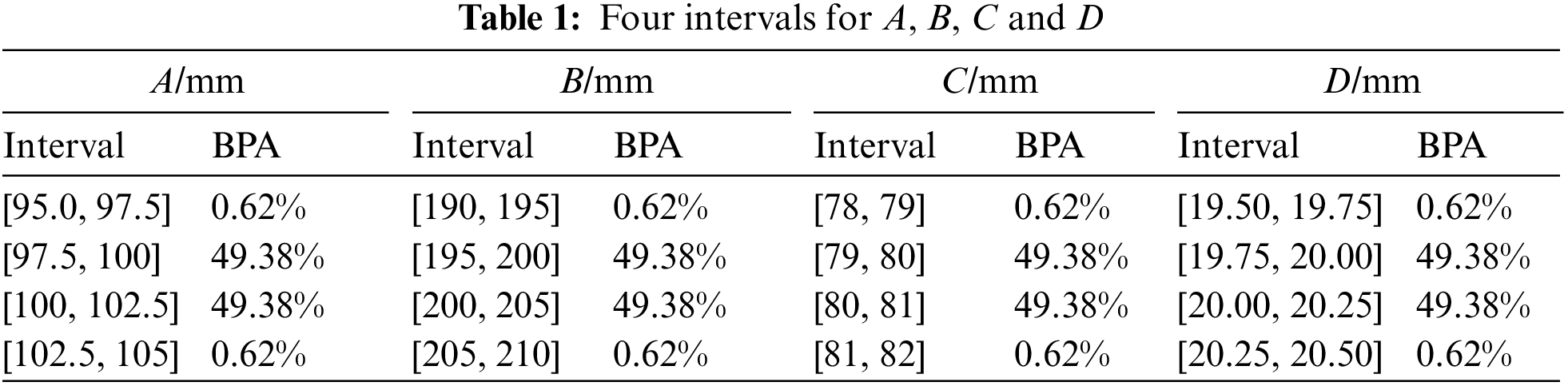
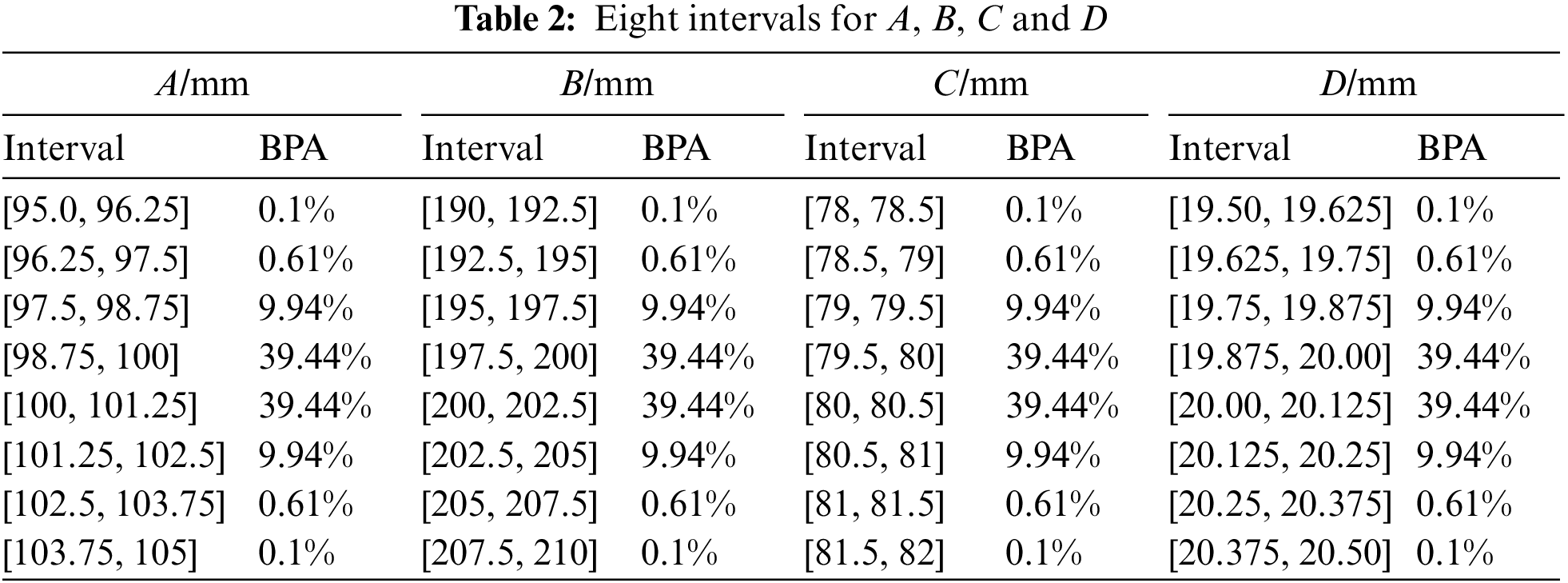
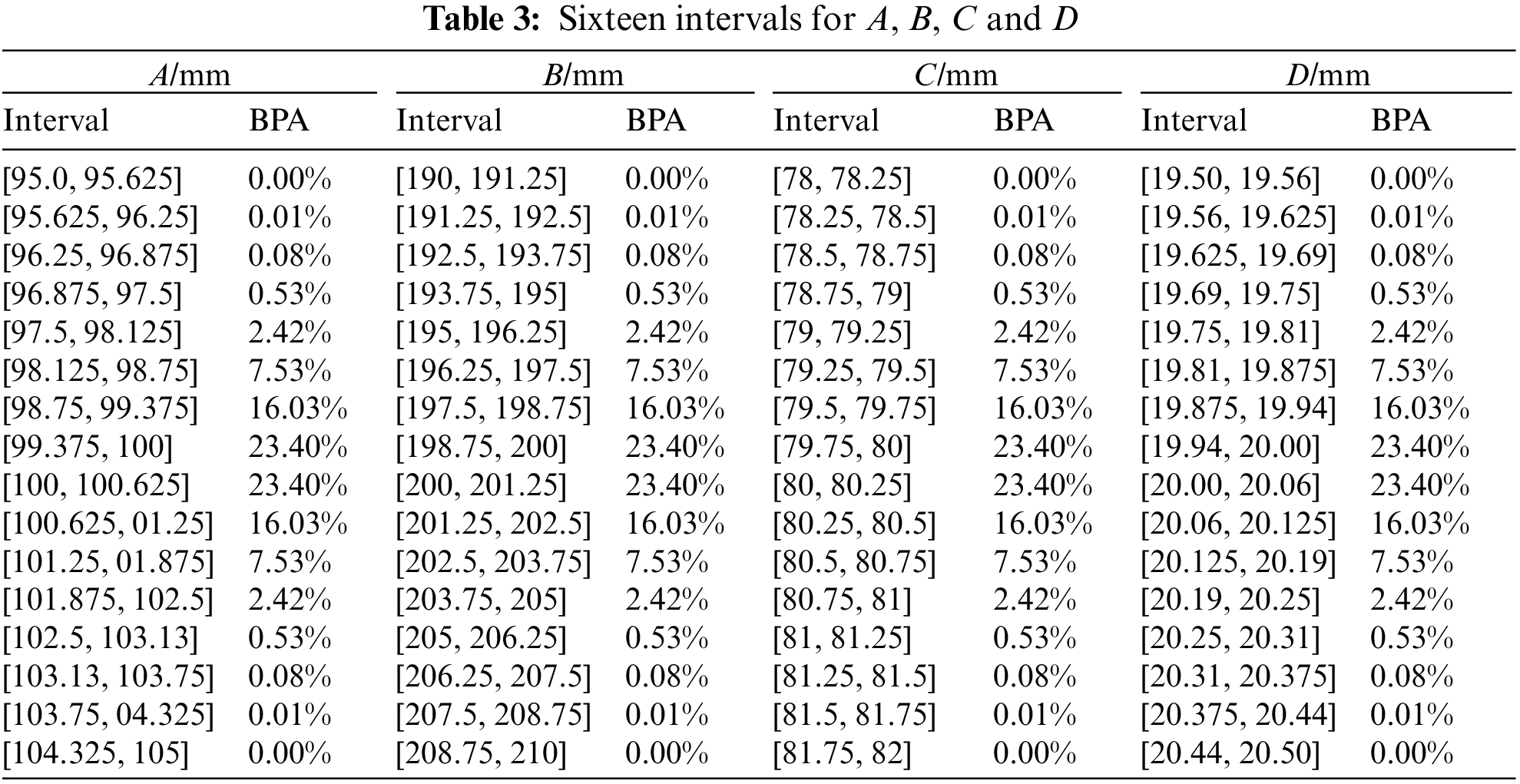
Taking the allowable stress S=0.0164, the Bernstein approximation method and linear approximation method proposed in this paper are used to analyze the reliability problem. They are compared with the safety results calculated directly by the genetic algorithm. The results are shown in Table 4. Case 1 represents the Bernstein approximation method, case 2 represents the linear approximation method, and case 3 represents the genetic algorithm. It can be seen from Table 4 that the interval probability obtained by dividing each variable into four segments, eight segments and sixteen segments by the method proposed in this paper is included in the safety probability interval, and the finer the number of variable segments, the smaller the interval probability span and the closer it is to the actual probability value (the real probability value is obtained by the Monte Carlo method, and the number of samples is 106), which shows that the method proposed in this paper is effective. The proposed method has lower computational efficiency compared with the linear approximation method, but the results are closer to the actual value. It can be seen that the proposed method has higher accuracy, especially for reliability problems with high nonlinearity. At the same time, the computational efficiency of the proposed method and the linear approximation method is related to the number of evidence uncertainties. The less uncertain the quantification of evidence, the higher the computational efficiency, and vice versa. The calculation efficiency and accuracy are related to the interval number of variable divisions. The larger the interval number, the lower the efficiency and the higher the accuracy. Therefore, the method proposed in this paper is more suitable for the implicit limit state with less evidence uncertainty and the explicit complex expression. The appropriate interval score should be selected during the calculation.

4.2 Engineering Examples

Fig. 3 shows the ten-bar structure. All horizontal and vertical bars are of length L, and Pi(i=1,2,3) is the concentrated load. The cross-sectional area and elastic modulus of each bar are Ai(i=1,2,…,10) and E, respectively.

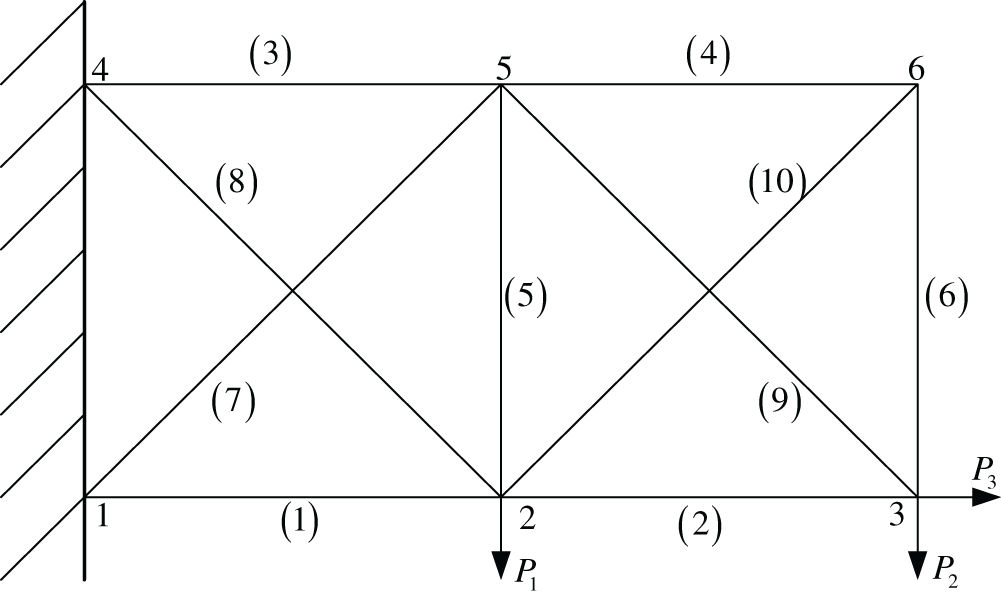
Figure 3: Schematic diagram of a ten-bar structure

Of these, the cross-sectional areas are A1∈[6,10] cm2 for bar 1 and A2∈[6,10] cm2 for bar 2, L∈[1.3,1.7]m is the evidence uncertainty, and the BPA structure is shown in Table 5. The rest are fixed parameters, and the values are: A4−10=8cm2, E=70GPa, L=1.5m , P1=500N and P2=P3=100N. The limit state equation can be defined as g(x)=D−dy(x), where dy(x) is the displacement in the vertical direction of node 3 and D is the allowable maximum displacement value, which is set as D=0.03m in this example.

5  Results and Discussion

To display the comparison results more clearly and accurately, the curves of Bel and Pl with the allowable stress S obtained by the two methods are given in this paper and compared with the actual probability curve obtained by the Monte Carlo method (the number of samples is 106). Figs. 4–6 show the results obtained by dividing the variables into four segments, eight segments and sixteen segments, respectively. As can be seen from the figure, in the whole process of S change, the Bel curve and Pl curve obtained by the two methods always include the actual probability P curve. With the increase of variable segmentation, i.e., the increase of information, the Bel curve and Pl curve gradually approach the actual probability curve. The Bel and Pl curves obtained by the Bernstein method are closer to the actual probability curve than those obtained by the linear method.

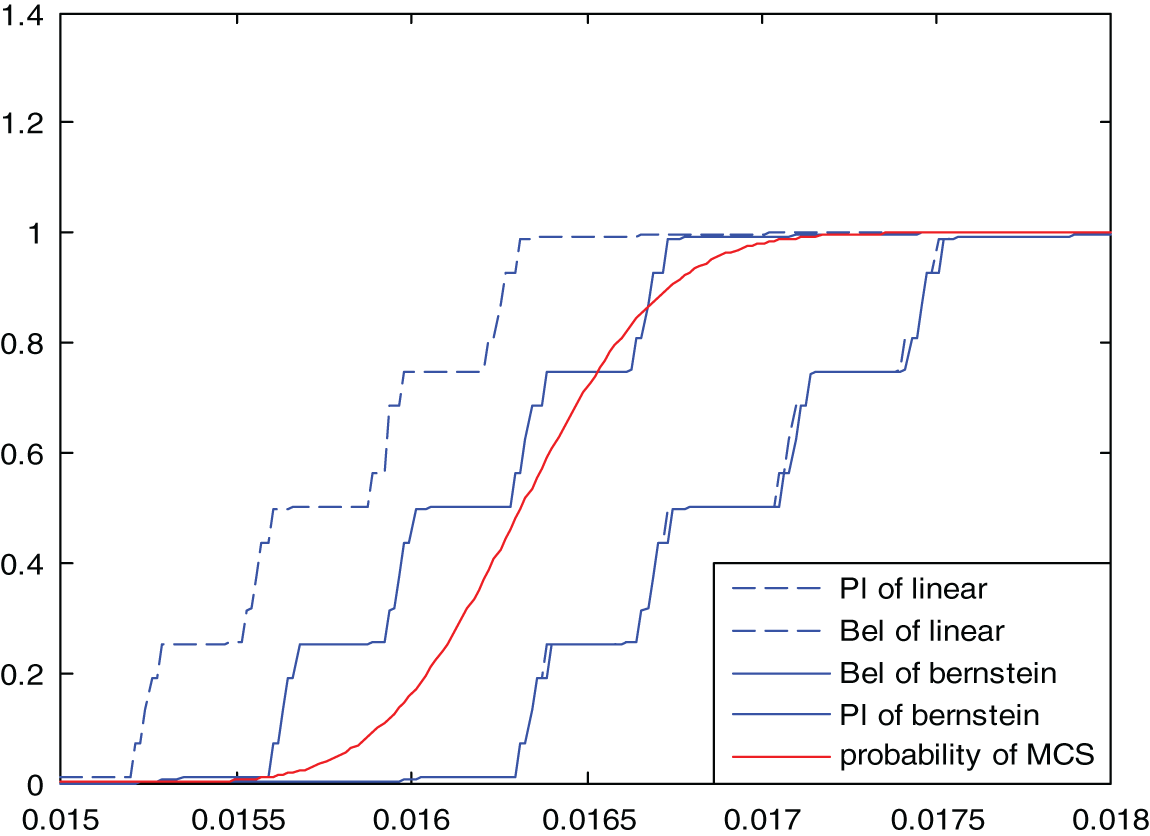
Figure 4: 4-interval cumulative distribution results

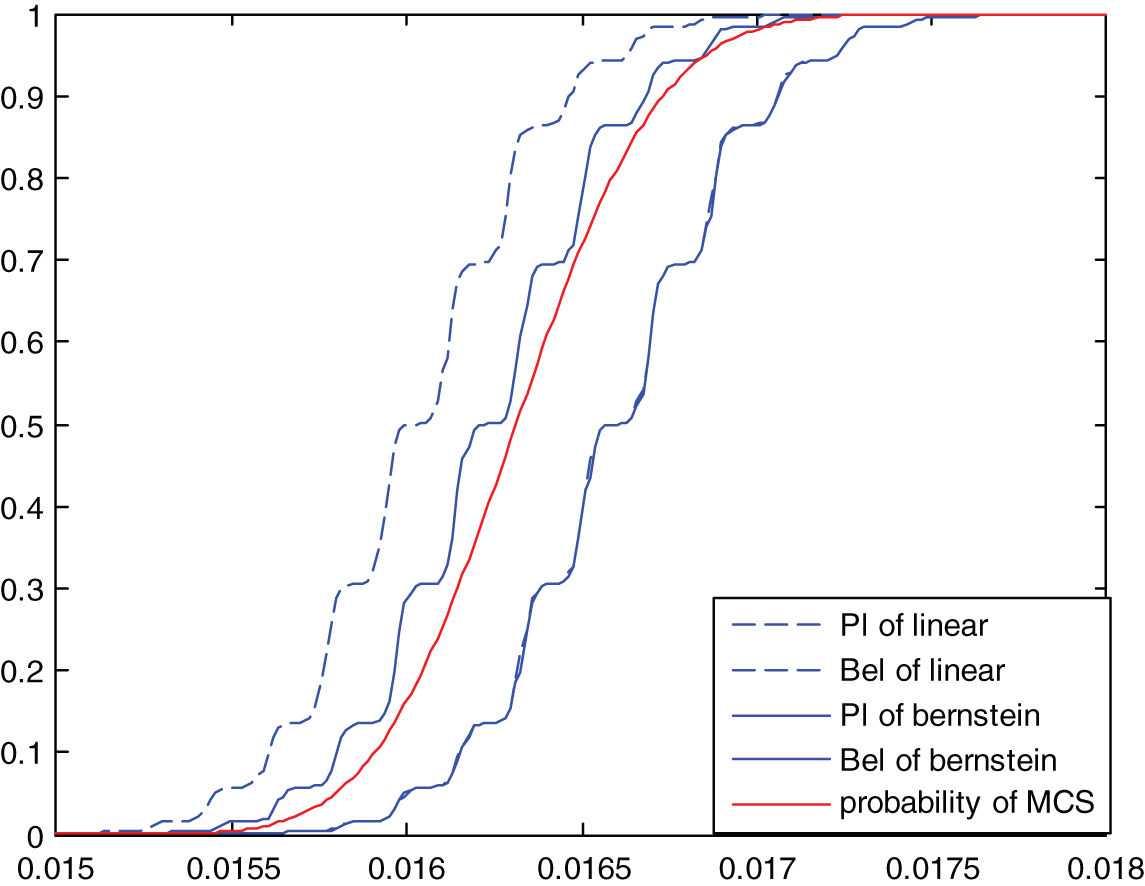
Figure 5: 8-interval cumulative distribution results

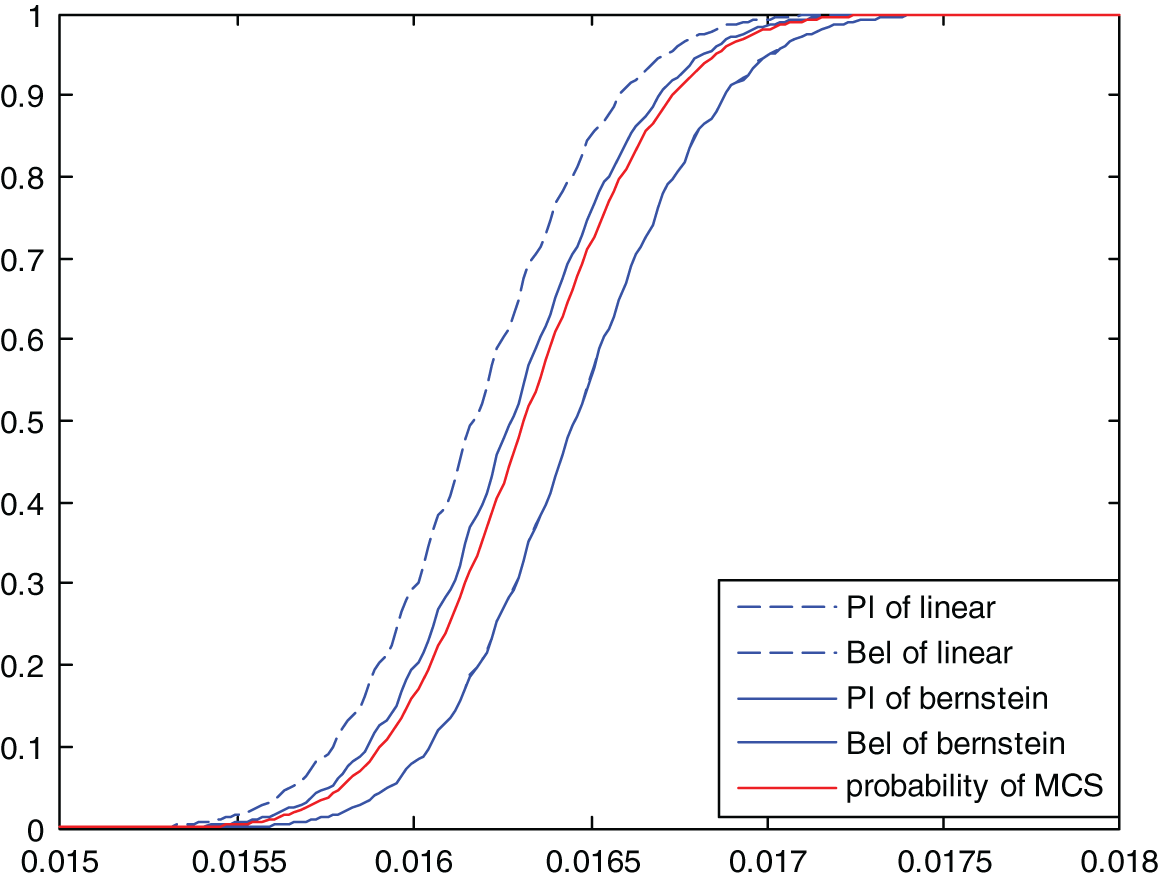
Figure 6: 16-interval cumulative distribution results

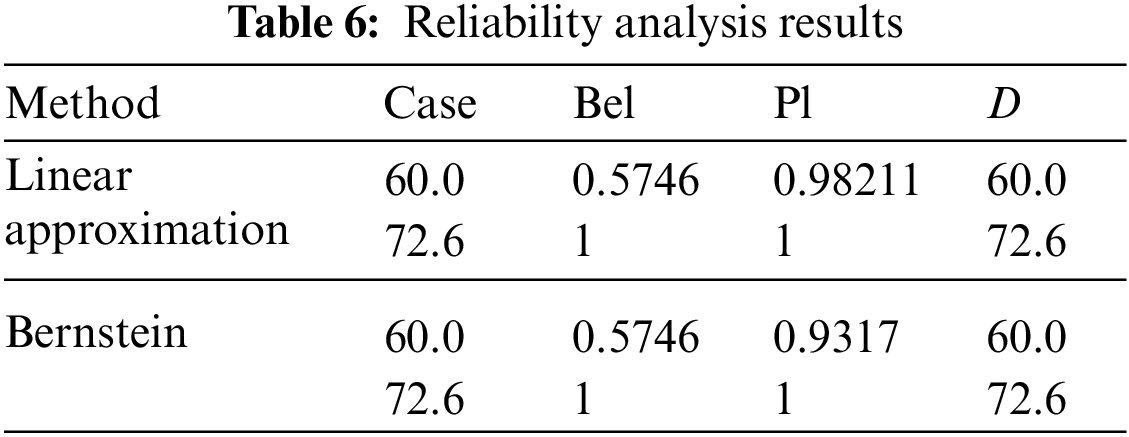
Table 6 shows the obtained reliability analysis results. When the allowable maximum displacement D of node 3 is D = 60.0 mm, the plausibility Pl = 0.9821 is obtained by linear approximation. According to this result, structural safety is ideal. However, the plausibility obtained by the Bernstein approximation is Pl = 0.9317, which is relatively small, indicating an excellent possibility of structural failure under the design requirements of this displacement value. It can be seen that the accuracy of the proposed method is higher than that of the linear approximation method. When the maximum allowable displacement D of node 3 is D = 72.6 mm, the reliability and plausibility obtained by the two methods are 1. It can be seen that the safety index always meets the design needs; that is, the structure is entirely reliable.

6  Conclusion

In this paper, a reliability analysis method based on evidence theory is proposed. Based on the non-probabilistic reliability index method, the extreme value of the limit state function is obtained by using the properties of the Bernstein polynomial to avoid large sampling.

The proposed method has been applied to a numerical example and an engineering application. The calculation results have shown that the proposed method has high calculation efficiency and accuracy, especially for some reliability problems with high nonlinearity. Compared with the linear approximation method, the proposed method in this paper has higher accuracy. Unfortunately, this study has not yet included large-scale reliability problems with many evidence uncertainties. It is expected that this method will be extended to the mixed reliability problem with cognitive uncertainty and random uncertainty in future.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. A. Akgul, U. Fatima, M. S. Iqbal, N. Ahmed, A. Raza et al., “A fractal fractional model for computer virus dynamics,” Chaos, Solitons and Fractals, vol. 147, no. 1, pp. 1–9, 2021. [Google Scholar]

    2. J. E. M. Diaz, A. Raza, N. Ahmed and M. Rafiq, “Analysis of a nonstandard computer method to simulate a nonlinear stochastic epidemiological model of coronavirus-like diseases,” Computer Methods and Programs in Biomedicine, vol. 204, no. 1, pp. 1–10, 2021. [Google Scholar]

    3. Y. Deng, “Uncertainty measure in evidence theory,” Science China Information Sciences, vol. 63, no. 11, pp. 5–23, 2020. [Google Scholar]

    4. X. Y. Chen, J. P. Fan and X. Y. Bian, “Theoretical analysis of non-probabilistic reliability based on interval model,” Acta Mechanica Solida Sinica, vol. 30, no. 6, pp. 638–646, 2017. [Google Scholar]

    5. B. Limboo and P. Dutta, “A Q-rung orthopair basic probability assignment and its application in medical diagnosis,” Decision Making: Applications in Management and Engineering, vol. 5, no. 1, pp. 290–308, 2022. [Google Scholar]

    6. D. N. Chen, H. S. Li and C. Y. Yao, “Reliability analysis based on evidence theory and Bayesian network for hydraulic drive system,” Chinese Hydraulics & Pneumatics, vol. 1, no. 4, pp. 8–14, 2017. [Google Scholar]

    7. C. Jiang, W. Zhang and W. X. Han, “A copula function based evidence theory model for correlation analysis and corresponding structural reliability method,” Journal of Mechanical Engineering, vol. 53, no. 16, pp. 199–209, 2017. [Google Scholar]

    8. R. Ghosal, S. Ghosh, J. Urbanek, J. A. Schrack and V. Zipunnikov, “Shape-constrained estimation in functional regression with Bernstein polynomials,” Computational Statistics & Data Analysis, vol. 178, no. 1, pp. 1–20, 2023. [Google Scholar]

    9. B. Jin, W. Zhou, L. Y. Tang, Z. Y. Li and Z. L. Jiang, “Calculation of structural reliability of implicit function under serviceability limit state,” Journal of Hunan University (Natural Sciences), vol. 47, no. 1, pp. 116–122, 2020. [Google Scholar]

  10. G. S. Su, L. F. Peng and L. H. Hu, “A Gaussian process-based dynamic surrogate model for complex engineering structural reliability analysis,” Structural Safety, vol. 68, no. 1, pp. 97–109, 2017. [Google Scholar]

  11. Z. Liu, J. Duan, L. Huang, J. Dezert and Y. Zhao, “Combination of classifiers with incomplete frames of discernment,” Chinese Journal of Aeronautics, vol. 35, no. 5, pp. 145–157, 2022. [Google Scholar]

  12. Z. Liu, X. Zhang, J. Niu and J. Dezert, “Combination of classifiers with different frames of discernment based on belief functions,” IEEE Transactions on Fuzzy Systems, vol. 99, no. 1, pp. 1, 2020. [Google Scholar]

  13. H. J. Shi, J. H. Li, H. Chang and L. L. Liu, “Research on passive localization method of shallow water acoustic source with single hydrophone based on hierarchical grid histogram filtering,” Applied Acoustics, vol. 194, no. 1, pp. 108812, 2022. [Google Scholar]

  14. H. Y. Dui, Y. Li and G. H. Bai, “An improved uncertainty importance analysis method for reliability,” Operations Research and Management Science, vol. 31, no. 3, pp. 100–104, 2022. [Google Scholar]

  15. S. T. Liu, X. J. Li, Z. J. Zhou, J. P. Yao and J. Wang, “A review of the application of evidence theory in pattern classification,” Journal of China Academy of Electronics and Information Technology, vol. 17, no. 3, pp. 247–258, 2022. [Google Scholar]

  16. C. Andrea, C. Davide and D. Thierry, “Belief functions and rough sets: Survey and new insights,” International Journal of Approximate Reasoning, vol. 143, no. 1, pp. 192–215, 2022. [Google Scholar]

  17. S. A. Solovyev and A. A. Soloveva, “Structural reliability analysis using evidence theory and fuzzy probability distributions,” Magazine of Civil Engineering, no. 107, pp. 10704, 2022. [Google Scholar]

  18. Y. X. Yang, X. Pan and Q. D. Cui, “An evidence combination rule based on transferable belief model and application in reliability assessment with multi-source data,” IEEE Access, vol. 8, no. 8, pp. 69096–69104, 2020. [Google Scholar]

  19. B. Jiang, X. A. Ling, L. Zhang and Y. J. Gao, “Evidence combination method based on improved modified weight,” Computer Engineering and Applications, vol. 57, no. 24, pp. 100–106, 2021. [Google Scholar]

  20. Q. Sun, X. Q. Ye and W. K. Gu, “A new combination rules of evidence theory,” Acta Electronica Sinica, vol. 28, no. 8, pp. 4, 2000. [Google Scholar]

  21. Z. Wang and F. Xiao, “An improved multi-source data fusion method based on the belief entropy and divergence measure,” Entropy, vol. 21, no. 6, pp. 611, 2019. [Google Scholar]

  22. P. J. Lv, X. J. Shi and Y. F. Qin, “An improved D-S algorithm for correcting evidence conflicts,” Electronic Measurement Technology, vol. 42, no. 19, pp. 96–100, 2019. [Google Scholar]

  23. B. Li, “Synthesis assessment method based on pignistic similarity and improved DS evidence theory,” Application Research of Computers, vol. 35, no. 12, pp. 3682–3684, 2018. [Google Scholar]

  24. Q. Liu and H. L. Zhang, “Reliability evaluation of weighted voting system based on D–S evidence theory,” Reliability Engineering and System Safety, vol. 217, no. 1, pp. 108079, 2022. [Google Scholar]

  25. J. Wu, J. G. Zhang, L. F. You and N. Ye Nan, “Structural reliability calculation method based on improved weighted response surface,” Journal of Beijing University of Aeronautics and Astronautics, vol. 47, no. 8, pp. 1638–1645, 2021. [Google Scholar]