Modified Garden Balsan Optimization Based Machine Learning for Intrusion Detection

1  Introduction

Recently, security in the Internet of Things (IoT) becomes a hot research topic among research communities and business people. There exist two fundamental clarifications for many security issues and wide privacy concerns. One is the IoT objects limited concerning processing capability, memory capacity, and power consumption. Due to such constraints, conventional Internet techniques such as RSA and Advanced Encryption Standards (AES) become complex in implementing directly in IoT [1,2]. End-to-end secure interactions in rich source substances, namely laptops, tablets, and phones, could be attained at the transport layer via Transport Layer Security (TLS) or else at the network layer through Internet Protocol Security (IPsec). However, such techniques are not straight away implemented in constrained source objects, and their unavailability can result in eavesdropping, network side-channel assaults, and tracking, amongst other privacy and security menaces [3,4]. So, integrating machine learning (ML) related intrusion detection (ID) in the IoT pattern becomes critical to resist such attacks whereas still meeting IoT criteria [5]. The IoT is ubiquitous in everyday lives, linking physical objects to e-services [6]. In other words, the IoT refers to an engine that powers modern health, home automation, and advanced manufacturing smart cities [7,8]. An intrusion detection system (IDS) becomes a security system which functions majorly in the network layer of an IoT mechanism [9]. An IDS positioned for an IoT mechanism must make the analysis of data packets and produce a response practically, scrutinize data packets presented in various IoT layers having diverse protocol stacks, and acclimatize to several technologies in an IoT setting [10]. An IDS designed for IoT-related smart environments should work in difficult circumstances of low processing abilities, quick response, and high-volume data processing. Thus, classical IDSs does not completely suitable for IoT settings [11]. IoT security has become an ongoing and serious issue; hence, the latest understanding of the security susceptibilities of IoT and the advancement of respective mitigation techniques were needed [12].

Attack detection in IoT was distinct when compared with the past because of its exclusive IoT service needs, which a central cloud does not meet: scalability, source limitations, mobility, distribution, low latency, and so on [13]. This denotes that neither cloud-related nor standalone threat discovery technologies were sufficient for addressing the security issues of IoT. So, an IDS must analyse for bridging the gap [14]. It was increasingly essential for continually studying the ID field in IoT networks. The latest method integrates the sensor with an alarm facility and is expected to provide superior security compared to the classical method. Henceforth, the latest system allows ML methods with IoT to fault diagnose from its initial levels. The ML approach could be offered superior outcomes than human professionals provide. Artificial neural network (ANN) is one of the ML approaches to detect a fault in the IoT environment. The most used ML approach to predict fault in a system was support vector machine (SVM), ANN, and Radial Basis Function (RBF) [15]. But several studies were being used to improve the act of the prevailing mechanism and high concentration in reducing the fault by using advanced methods.

This paper introduces a modified garden balsan optimization-based machine learning model for intrusion detection (MGBO-MLID) technique in the IoT cloud atmosphere. The presented MGBO-MLID technique applies min-max normalization that can be employed for scaling the features in a uniform format. Besides, the MGBO-MLID model exploits the MGBO algorithm to choose the optimal subset of features. The attention-based bidirectional long short-term (ABiLSTM) algorithm was leveraged for the recognition and classifying of intrusions. Finally, the Aquila optimization (AO) algorithm was applied as a hyperparameter optimizer to fine-tune the ABiLSTM technique. The performance evaluation of the MGBO-MLID model was tested with the help of a benchmark dataset.

2  Related Works

Alkadi et al. [16] suggested a deep blockchain framework (DBF) projected for presenting security-related distributed intrusion detection (ID) and privacy-related blockchains having smart contracts in IoT networks. A bidirectional (BiLSTM) algorithm can use the ID technique for dealing with sequential network data. Atul et al. [17] examined such issues and offered the pattern about enhanced transmission patterns, particularly suggesting Energy Aware Smart Home (EASH) structure. In this study, the issues in transmission failures and forms of network assaults were examined in EASH. Using ML methods, the abnormality resources of the transmission pattern were distinguished. In [18], the NSLKDD can be utilized for evaluating ML techniques for ID. But not everyone’s features enhance performance in huge datasets. Thus, selecting and reducing a particular feature set improvise accuracy and speed. Then, features were chosen by using Recursive Feature Elimination (RFE). Rigorous experimentation on IDS is conducted, which employs ML techniques like random forest (RF) and SVM. Almiani et al. [19] provided an artificially fully automated ID system for Fog security towards cyberattacks. The suggested method employs a multi-layer RNN devised to be applied for Fog computing security near users and IoT gadgets.

Yahyaoui et al. [20] suggested an anomaly detection technique employing SVM for wireless sensor network (WSN) ID and deep learning (DL) for gateway ID. And suggest a detection protocol that performs the on-demand SVM classifier orderly when an intrusion is suspected. The combination of an ML classifier with a statistical technique for malicious node localization is carried out. In [21], a new hybrid weighted deep belief network (HW-DBN) method was suggested for building an effective and dependable IDS (DeepIoT.IDS) method for detecting prevailing and new cyber-attacks. The HW-DBN method compiles an enhanced Gaussian–Bernoulli Restricted Boltzmann Machine (Deep GB-RBM) feature learning operator having a weighted deep neural network (WDNN) classifier. Kareem et al. [22] provide a new FS technique by increasing the activity of the Gorilla Troops Optimizer (GTO) depending on a system for bird swarms (BSA). This BSA can be utilized for boosting performance exploitation of GTO in recently advanced GTO-BSA due to its strong ability in finding feasible regions having optimum solutions.

3  The Proposed Model

In this paper, a novel MGBO-MLID technique was projected for the effectual recognition and classification of intrusions in the IoT cloud atmosphere. At the preliminary level, the presented MGBO-MLID model applied min-max normalization for scaling the features in a uniform format. Following this, the MGBO-MLID model exploits the MGBO algorithm to choose the optimal subset features. Besides, the MGBO with ABiLSTM method is utilized for the recognition and classification of intrusions. Fig. 1 portrays the overall flow of the MGBO-MLID approach.

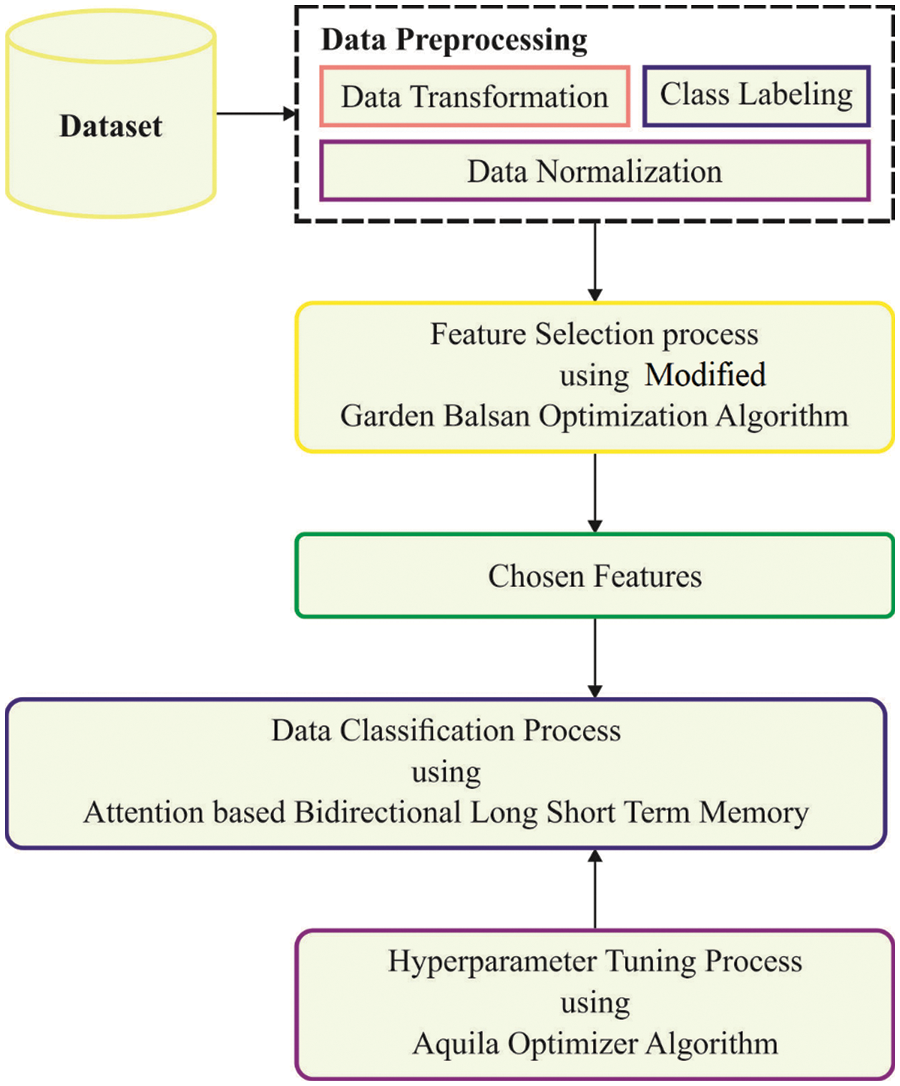
Figure 1: Overall flow of MGBO-MLID technique

3.1 Data Pre-Processing

At the introductory level, the presented MGBO-MLID model applied min-max normalization for scaling the features in a uniform format. Min-max normalization approach to scale the feature in [0,1] range by applying Eq. (1).

 ν′=v−minAmaxA−minA (1)

Herein, minA and maxA represent the minimal and maximal values of feature A . The original and normal value of an attribute, A , can be denoted by ν and ν′ correspondingly. It is noticed from the equation which is mentioned above that maximal and minimal feature values were mapped to 1 and correspondingly.

3.2 Design of MGBO-Based Feature Selection Model

Once the input data is pre-processed, the MGBO-MLID model exploits the MGBO algorithm to select the optimal subset features. During the simulation of garden balsam expansion and propagation, this process iterates at the start. In the procedure, the mechanical and second propagator, a mapping rule, and a selective method were implemented in turn; still, the end criteria were fulfilled, viz., both the accuracy requirement of the problem was fulfilled, and maximal iteration was obtained.

At this point, the steps contained from the dispersal of garden balsam populations:

1) The initialisation of populations is because of some seeds scattered arbitrarily on a particular region developing roots and constructing a 1st-generation population;

2) Progeny reproduction: The natural states of the developing region caused all the plants from the 1st-generation population to show different development rates. The stronger plants bear further fruit and spawn other seeds.

While the consequence of individual x , the subsequent amount of seeds were created:

S= fmax −f(x)fmax −fmin ×(Smax−Smin)+Smin                 (2)

whereas f(x) refers to the fitness value, fmax denotes the present population’s maximal fitness value, fmin denotes the present population’s minimal fitness value, smax indicates the upper limits on the amount of seeds, and Smin implies the minimal amount of seeds.

3) Mechanical transmission: The plants from optimum developing states bear completely grown fruits, further powerful ejection force, and, accordingly, distant ejections of seeds.

The range of seed diffusions is computed as follows:

A=(itermax −iteritermax )n×fmax −f(x)fmax −fmin ×Ainit              (3)

If fmax−f(x)=0 , or itermax−iter=0, A=ϵ. ϵ refers to the min value; iter signifies the evolutionary iterations at Present, itermax implies the max iteration and n proposes the non-linear harmonic factor.

4) Second transmission: To population diversity for increasing, the seed is arbitrarily transported from place to place by animals, water, and wind.

Its appearance is as follows:

x1′=xB+F(x2−x3)                  (4)

whereas x1′ denotes the novel place of x1 afterwards the secondary broadcast, xB signifies the optimum place, F represents the zoom factor, and x2 and x3 indicate the places of 2 dissimilar seeds.

5) Competition-based elimination: The population size of a particular area was restricted by Nmax . Once the population size attains the upper limit, an elite seed is taken, and a redundant seed is arbitrarily removed. The amount of elite seeds is computed utilizing Eq. (5).

Nbest=iteritermaxNmax                   (5)

Nbest signifies the number of elite solutions, and iter and itermax  are related to individuals.

The chaotic tent map has the characteristics of orderliness, randomness, and ergodicity. Based on the distinct characteristics, numerous researchers have proposed a chaotic tent map into the optimization technique that could significantly improve the diversity of the population and speed up the convergence rate at an earlier stage. In this work, the EGBO algorithm is designed by using the chaotic tent map to replace the original random population initialisation technique to improve the presented technique's population diversity as follows.

zk+1={2zk′0≤zk<0.52 (1−zk),0.5≤zk≤1                     (6)

The equation transformed from Eq. (7) using the Bernoulli shift is as follows.

zk+1=(2Z)mod1                               (7)

The step of utilizing the chaotic tent map for generating values is as follows.

Step 1: Randomly produce z0 within the range of zero and one (avoid z0 in a smaller period

(0.2, 0.4, 0.6, 0.8), y(1)=z0, i=j=1.

Step 2: Iterate through Eq. (7) to attain a sequence of zi, i=i+1.

Step 3: Once the maximal iteration count is reached, return to Step 4. Or else, if zi= {0, 0.25, 0.5, 0.75} or χj=χj−k, k={0 , 1, 2, 3, 4 } , changes the initial value of iteration by the formula x(i)=y(j+1)=y(j)+c , whereby c refers to a random number, j=j+1 . Or else return to Step 2.

Step 4: The process is halted, and the χ sequence is maintained.

The distribution histogram of tent chaotic and logistic chaotic maps lies in the range of zero and one with the primary value of 0.32 and the iteration times of 500, correspondingly. The stimulation outcome indicates that the sequence produced by tent chaos maps has considerably good uniformity compared to the logistic chaos sequence. As a result, the chaotic tent map is applied for initializing the position of the searching agent, which can improve the searching ability and reduces the impact of initial value on the optimization accuracy.

The fitness function (FF) takes the classifier’s accuracy and the number of selected features. It increases the classifier accurateness and reduces the selected features set size. Therefore, the FF mentioned below was leveraged for assessing individual solutions, as given in Eq. (8).

Fitness=α∗ ErrorRate+(1−α)∗#SF#All_F                           (8)

Wherein ErrorRate refers to a classifier error rate by making use of selected features. The error rate can be computed as the per cent of faulty classified (by 5-ANN classifier) to the number of classifications performed, exhibited as a value within 0 and 1. (Error Rate was a complement of the classifier accurateness), #SF represents the quantity of feature which is selected and #All_F means the total sum of attributes in an original set of data. α can be employed for managing the worth of classifier excellence and subsets length. In this test, α was fixed to 0.9.

3.3 Intrusion Detection and Classification Using ABiLSTM Model

In this study, the ABiLSTM model is utilized for the recognition and classification of intrusions. The main disadvantage of recurrent neural networks (RNN) was the incapability of learning contextual data to an extensive duration produced by vanishing gradient problems [23]. It was mostly attributed to the extended temporal gap range in the time input was attained for decision-making. Weakening the capability of RNNs for learning in long-distance dependency. Thus, the long short-term memory (LSTM) technique, an expanded version of RNNs utilized the model of gates to compare units. It overcomes vanishing gradient problems, so permits the preservation of extended periods of contextual data.

During this case, the opinion of BiLSTM was created in bidirectional RNNs (BiRNN). BiRNN manages orders of input from forwarding and backward input directions by utilizing 2 distinct hidden layers (HLs). The BiLSTMs link every HLs to a similar resultant layer. The restriction of classical RNNs was that it only utilizes the preceding context of input data sequences. BiLSTMs compensate for this by permitting data flow from either forward or backward directions.

The BiLSTM network evaluates the forward HL sequence outcome h→(t) , the resultant sequence of backward HL h→(t) and resultant layer y(t) with repeating the forward layer starting t=1 to tf , backward HL while t=tf to 1, and then upgrading the last value utilizing the subsequent formulas:

h→(t)=H(Wj→Xt+Vj→hj→(t−1)+bj→) (9)

h←(t)=H(Wj←Xt+yj←hj←(t−1)+bj←) (10)

y(t)=Uj→hj→(t)+Uj←hj←(t)+by. (11)

The last resultant vector, y(t) , is computed as:

y(t)=σy(h→,h←). (12)

The σy function concatenates the outcome sequence of neurons from the HL, and cloud is one of 4 functions like concatenate, multiply, add, and average. Fig. 2 depicts the framework of BiLSTM.

Figure 2: Structure of BiLSTM

To overcome the issue of Multihead attention (MHA), the block can be used from the presented technique, which calculates the numerous attention weighted sum previously considering single attention pass-on values. Thus, it is called “MHA”. Here, numerous attention heads are used. The resultants of such 2 heads are fed to drop-out layers and subsequently combined using a concatenation layer, and the resultant was given to the LSTM layer. The attention procedure allows weighted to context words to determine the word which is exacted was used to determine the sentiment of given input series.

a1=w1+w2+w3+…+wn                           (13)

a2=w1+w2+w3+…+wn                           (14)

3.4 Hyperparameter Tuning

At the last stage, the AO algorithm is applied as a hyperparameter optimizer to fine-tune the ABiLSTM model. Abualigah et al. 2021 developed an Aquila Optimizer (AO), a novel metaheuristic optimization technique [24]. This technique comprises four different kinds of hunting behaviour for the species of prey Aquila that could flexibly switch the hunting strategy for different prey species beforehand it is attacking the prey with the help of their sturdy feet and claws as well as rapid speed. It is mathematically modelled in the following subsection. At the expanded exploration (X) stage, Aquila identifies the prey area and chooses the better region to hunt by soaring higher in a vertical dive. AO extensively explores from higher altitude soaring to determine the range of searching space where the prey is situated. This behaviour can be mathematically expressed in the following:

X1(t+1)=Xbest(t)×(1−tT)+(XM(t)−Xbest(t)×rand)      (15)

XM(t)=1N∑i=1N⁡Xj(t)                                         (16)

From the equation, X1(t+1) refers to the location of the t+1 iteration produced by the extended exploration. Xbest(t) illustrates the best-obtained solution that could reflect the approximate location of prey X(t) indicates the average solution at t−th iterations. rand denotes a random value that lies within [0,1]. t and T denote the existing iteration count and the maximal iteration; correspondingly, N indicates the population count. Once the prey area is located at a higher altitude, they hover above the targeted prey, prepare to land, and eventually attack. For prey attacking, they explore a certain region for prey, and the mathematical expression can be explained in the following.

X2(t+1)=Xbesi(t)×Levy(D)+XR(t)+(y−x)×rand       (17)

In Eq. (17), D refers to the dimension size, Levy (D) indicates the Levy flight distribution function evaluated as follows, and X(t) represents a random solution that lies in the interval of [ 1, N] at i - th iteration.

Levy (D)=s×u×σ|v|1β                                      (18)

σ=(Γ(1+β)×sin⁡(πβ2)Γ(1+β2)×β×2(β−12)1) (19)

In the above equation, s and β are, correspondingly, constant values equivalent to 0.01 and 1.5; u and v denote random values lying within zero and one, y, and χ is evaluated to render the spirals in the search.

y=r×cos (θ)                                             (20)

x=r×sin (θ)                                            (21)

r=r1+U×D1                                               (22)

θ=−ω×D1+θ1,θ1=3×π2                                (23)

From the expression, r1 denotes the search cycle count that has a value from 1 to 20, D1 is comprised of integer numbers from 1 to dimension size (D), U, and ω refers to a fixed value of 0.00565 and 0.005.

In the expanded exploitation (X) phase, the prey region is precisely allocated, and they are prepared for the landing and attack. Aquila vertically descends and makes the first attack to observe the prey’s reaction. This technique is called a lower-altitude slow descent attack. Now, they approach the prey using a target region and perform the attack. The mathematical expression of this behaviour can be explained in the following.

X3(t+1)=(Xbest(t)−XM(t))×α−rand+((ub−lb)×rand+lb)×δ    (24)

In Eq. (24), Xbest(t) represents the optimal location and X(t) implies the average value of the existing position. α and δ are adjustment parameters fixed to 0.1, rand refers to a random number that lies within [0,1], and ub and lb denote the upper and lower limits.

Once Aquila approaches the prey, they attack the prey on land based on random movement. Finally, they attack the prey in the last location. The mathematical formula for these behaviours is given below.

X4(t+1)=QF×Xbesi(t)−(G1×X(t)×rand)−G2×Levy(D)+rand×G1      (25)

 QF(t)=t2×r8−1(1−T)2                                         (26)

G1=2×rand−1                                   (27)

G2=2×(1−tT)                                                 (28)

From the expression, X(t) denotes the existing location. QF(t) indicates the quality function values that are utilized for balancing the searching strategy, and G1 signifies the tracking prey movement that is a random value within [1,1]. G2 symbolizes the flight slope while chasing the prey that linearly reduces from 2 to . The rand denotes a random integer within [0,1].

The AO method makes a derivation of a fitness function for achieving improvised classifier performance. It sets a positive digit for indicating superior execution of candidate resolutions. In this work, the reduction of the classifier error rate was taken as a fitness function, as presented in Eq. (24). The optimum solution contains the least error rate, and the poor solution gets a higher error rate.

fitness(xi)=ClassifierErrorRate(xi)=number of misclassified samplesTotal number of samples∗100                   (29)

4  Performance Validation

This section reviews the experimental validation of the MGBO-MLID model utilizing a benchmark dataset, namely the NSL-KDD dataset. The results are investigated under distinct aspects.

4.1 Result Analysis on NSL-KDD Dataset

The performance validation of the MGBO-MLID model on the test NSL-KDD dataset is given in Table 1. The dataset holds 148417 samples with five class labels.

Fig. 3 exhibits the confusion matrices produced by the MGBO-MLID model on the NSL-KDD dataset. With the entire dataset, the MGBO-MLID model has identified 52745 samples in the denial of service (DoS) class, 12787 samples in the Probe class, 10 samples in R2L class, 3260 samples in the user to root (U2R) class, 76084 samples in a normal class. In addition, with 70% of training (TR) data, the MGBO-MLID method has identified 36892 samples in the DoS class, 8923 samples in the Probe class, 5 samples in R2L class, 2265 samples in U2R class, 53342 samples in the normal class. Along with that, with 30% of testing (TS) data, the MGBO-MLID approach has identified 15853 samples in the DoS class, 3864 samples in the Probe class, 5 samples in the R2L class, 995 samples in U2R class, and 22742 samples in the normal class.

Figure 3: Confusion matrices of MGBO-MLID approach under NSL-KDD dataset (a) Entire dataset, (b) 70% of TR data, and (c) 30% of TS data

Table 2 and Fig. 4 highlight the classification results offered by the MGBO-MLID model on the NSL-KDD dataset. The experimental values pointed out that the MGBO-MLID model has accomplished improved results in all aspects. For instance, on the entire dataset, the MGBO-MLID model has offered an average accuy of 99.05%, precn of 83.02%, recal of 76.34%, specy of 99.26%, Fscore of 76.53%, and FPR of 0.74. Also, on 70% of TR data, the MGBO-MLID technique has rendered an average accuy of 99.05%, precn of 81.30%, recal of 76.14%, specy of 99.26%, Fscore of 76.13%, and FPR of 0.74. Meanwhile, on 30% of TS data, the MGBO-MLID approach has provided an average accuy of 99.04%, precn of 85.93%, recal of 76.76%, specy of 99.25%, Fscore of 77.37%, and FPR of 0.75.

Figure 4: Result analysis of the MGBO-MLID approach under the NSL-KDD dataset

The training accuracy (TA) and validation accuracy (VA) acquired by the MGBO-MLID algorithm on the NSL-KDD dataset is portrayed in Fig. 5. The experimental outcome denoted the MGBO-MLID method has attained higher values of TA and VA. In Particular, the VA is greater than TA.

Figure 5: TA and VA analysis of the MGBO-MLID approach under the NSL-KDD dataset

The training loss (TL) and validation loss (VL) obtained by the MGBO-MLID approach on the NSL-KDD dataset were illustrated in Fig. 6. The experimental outcome implied that the MGBO-MLID methodology has reached minimal values of TL and VL. Specifically, the VL seems to be lesser than TL.

Figure 6: TL and VL analysis of the MGBO-MLID approach under the NSL-KDD dataset

A comparative result analysis of the MGBO-MLID model with recent models such as fuzzy (F-SVM), RNN, ensemble deep neural network (DNN), deep belief network (DBN), DMM, DNN, CVT, and deep learning model with rule-based feature selection (DL-RBFS) on NSL-KDD dataset was illustrated in Table 3 [25]. The obtained values pointed out that the MGBO-MLID model has reached enhanced performance over the other models. Concerning detection rate (DR), the MGBO-MLID model has gained a higher DR of 99.04% whereas TANN, F-SVM, RNN, Ensemble-DNN, DBN, ADS-DL, DMM, DNN, CVT, and DL-RBFS models have reached lower DR of 90.54%, 92.42%, 72.43%, 97.49%, 95.15%, 99.31%, 97.26%, 76.11%, 95.30%, and 98.84% respectively. Also, for FPR, the MGBO-MLID methodology has obtained a higher DR of 0.75% whereas TANN, F-SVM, RNN, Ensemble-DNN, DBN, ADS-DL, DMM, DNN, CVT, and DL-RBFS technique have attained lower FPR of 8.70%, 5.60%, 2.40%, 9.40%, 4.50%, 3.60%, 15%, 14.70%, 1.80%, and 1.10% correspondingly.

5  Conclusion

In this paper, a new MGBO-MLID technique was developed for the effectual recognition and classification of intrusions in the IoT cloud environment. At the preliminary level, the presented MGBO-MLID model applied min-max normalization for scaling the features in a uniform format. Following this, the MGBO-MLID model exploits the MGBO algorithm to choose the optimal subset feature. Besides, the MGBO with ABiLSTM model is utilized for the recognition and classification of intrusions. The experimental validation of the MGBO-MLID model is tested with the help of a benchmark dataset. The extensive comparative study reported the betterment of the MGBO-MLID model over recent approaches. In future, data clustering and outlier reduction algorithms can be applied to improve the classification outcome.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R114), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: 22UQU4340237DSR48.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. K. A. P. da Costa, J. P. Papa, C. O. Lisboa, R. Munoz and V. H. C. de Albuquerque, “Internet of Things: A survey on machine learning-based intrusion detection approaches,” Computer Networks, vol. 151, no. 22, pp. 147–157, 2019. [Google Scholar]

    2. J. Asharf, N. Moustafa, H. Khurshid, E. Debie, W. Haider et al., “A review of intrusion detection systems using machine and deep learning in internet of things: Challenges, solutions and future directions,” Electronics, vol. 9, no. 7, pp. 1177, 2020. [Google Scholar]

    3. M. A. Alohali, F. N. Al-Wesabi, A. M. Hilal, S. Goel, D. Gupta et al., “Artificial intelligence enabled intrusion detection systems for cognitive cyber-physical systems in industry 4.0 environment,” Cognitive Neurodynamics, vol. 16, no. 5, pp. 1045–1057, 2022. http://dx.doi.org/10.1007/s11571-022-09780-8. [Google Scholar]

    4. K. V. V. N. L. S. Kiran, R. N. K. Devisetty, N. P. Kalyan, K. Mukundini and R. Karthi, “Building a intrusion detection system for iot environment using machine learning techniques,” Procedia Computer Science, vol. 171, no. 7, pp. 2372–2379, 2020. [Google Scholar]

    5. A. M. Hilal, M. A. Alohali, F. N. Al-Wesabi, N. Nemri, J. Hasan et al., “Enhancing quality of experience in mobile edge computing using deep learning based data offloading and cyberattack detection technique,” Cluster Computing, vol. 76, no. 4, pp. 2518, 2021. http://dx.doi.org/10.1007/s10586-021-03401-5. [Google Scholar]

    6. A. M. Hilal, J. S. Alzahrani, I. Abunadi, N. Nemri, F. N. Al-Wesabi et al., “Intelligent deep learning model for privacy preserving IIoT on 6G environment,” Computers, Materials & Continua, vol. 72, no. 1, pp. 333–348, 2022. [Google Scholar]

    7. G. Singh and N. Khare, “A survey of intrusion detection from the perspective of intrusion datasets and machine learning techniques,” International Journal of Computers and Applications, pp. 1–11, 2021. http://dx.doi.org/10.1080/1206212X.2021.1885150. [Google Scholar]

    8. M. A. Hamza, S. B. Haj Hassine, I. Abunadi, F. N. Al-Wesabi, H. Alsolai et al., “Feature selection with optimal stacked sparse autoencoder for data mining,” Computers, Materials & Continua, vol. 72, no. 2, pp. 2581–2596, 2022. [Google Scholar]

    9. A. A. Albraikan, S. B. H. Hassine, S. M. Fati, F. N. Al-Wesabi, A. Mustafa Hilal et al., “Optimal deep learning-based cyberattack detection and classification technique on social networks,” Computers, Materials & Continua, vol. 72, no. 1, pp. 907–923, 2022. [Google Scholar]

  10. M. A. Rahman, A. T. Asyhari, L. S. Leong, G. B. Satrya, M. H. Tao et al., “Scalable machine learning-based intrusion detection system for IoT-enabled smart cities,” Sustainable Cities and Society, vol. 61, no. 1, pp. 102324, 2020. [Google Scholar]

  11. K. Mandal, M. Rajkumar, P. Ezhumalai, D. Jayakumar and R. Yuvarani, “Improved security using machine learning for IoT intrusion detection system,” Materials Today: Proceedings, pp. S2214785320377889, 2020. [Google Scholar]

  12. M. A. Alsoufi, S. Razak, M. M. Siraj, I. Nafea, F. A. Ghaleb et al., “Anomaly-based intrusion detection systems in IoT using deep learning: A systematic literature review,” Applied Sciences, vol. 11, no. 18, pp. 8383, 2021. [Google Scholar]

  13. R. H. Mohamed, F. A. Mosa and R. A. Sadek, “Efficient intrusion detection system for IoT environment,” International Journal of Advanced Computer Science and Applications, vol. 13, no. 4, pp. 572–578, 2022. [Google Scholar]

  14. A. Raghuvanshi, U. K. Singh, G. S. Sajja, H. Pallathadka, E. Asenso et al., “Intrusion detection using machine learning for risk mitigation in IoT-enabled smart irrigation in smart farming,” Journal of Food Quality, vol. 2022, no. 7, pp. 1–8, 2022. [Google Scholar]

  15. E. Gyamfi and A. Jurcut, “Intrusion detection in internet of things systems: A review on design approaches leveraging multi-access edge computing, machine learning, and datasets,” Sensors, vol. 22, no. 10, pp. 3744, 2022. [Google Scholar]

  16. O. Alkadi, N. Moustafa, B. Turnbull and K. K. R. Choo, “A deep blockchain framework-enabled collaborative intrusion detection for protecting IoT and cloud networks,” IEEE Internet Things Journal, vol. 8, no. 12, pp. 9463–9472, 2021. [Google Scholar]

  17. D. J. Atul, R. Kamalraj, G. Ramesh, K. S. Sankaran, S. Sharma et al., “A machine learning based IoT for providing an intrusion detection system for security,” Microprocessors and Microsystems, vol. 82, no. 4, pp. 103741, 2021. [Google Scholar]

  18. R. Patgiri, U. Varshney, T. Akutota and R. Kunde, “An investigation on intrusion detection system using machine learning,” in 2018 IEEE Symp. Series on Computational Intelligence (SSCI), Bangalore, India, pp. 1684–1691, 2018. [Google Scholar]

  19. M. Almiani, A. A. Ghazleh, A. Al-Rahayfeh, S. Atiewi and A. Razaque, “Deep recurrent neural network for IoT intrusion detection system,” Simulation Modelling Practice and Theory, vol. 101, pp. 102031, 2020. [Google Scholar]

  20. A. Yahyaoui, T. Abdellatif and R. Attia, “Hierarchical anomaly based intrusion detection and localization in IoT,” in 2019 15th Int. Wireless Communications & Mobile Computing Conf. (IWCMC), Tangier, Morocco, pp. 108–113, 2019. [Google Scholar]

  21. Z. K. Maseer, R. Yusof, S. A. Mostafa, N. Bahaman, O. Musa et al., “DeepIoT.IDS: Hybrid deep learning for enhancing IoT network intrusion detection,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3945–3966, 2021. [Google Scholar]

  22. S. S. Kareem, R. R. Mostafa, F. A. Hashim and H. M. El-Bakry, “An effective feature selection model using hybrid metaheuristic algorithms for IoT intrusion detection,” Sensors, vol. 22, no. 4, pp. 1396, 2022. [Google Scholar]

  23. Y. Bin, Y. Yang, F. Shen, X. Xu and H. T. Shen, “Bidirectional long-short term memory for video description,” in Proc. of the 24th ACM Int. Conf. on Multimedia, Amsterdam, The Netherlands, pp. 436–440, 2016. [Google Scholar]

  24. A. M. AlRassas, M. A. A. Al-qaness, A. A. Ewees, S. Ren, M. A. Elaziz et al., “Optimized ANFIS model using aquila optimizer for oil production forecasting,” Processes, vol. 9, no. 7, pp. 1194, 2021. [Google Scholar]

  25. J. B. Awotunde, C. Chakraborty and A. E. Adeniyi, “Intrusion detection in industrial internet of things network-based on deep learning model with rule-based feature selection,” Wireless Communications and Mobile Computing, vol. 2021, no. 2, pp. 1–17, 2021. [Google Scholar]