Sensor Network Structure Recognition Based on P-law

1  Introduction

The sensor graph network is a sensor network model organized according to the structure of the graph network (the sensors are the nodes of the graph network, the connections between the sensors serve as the edge of the graph network), and it is a distributed intelligent network system composed of sensor nodes interconnected through wireless communication deployed in the area of action, which can perform the specified tasks independently according to the environment. The self-organizing behavior of the sensor network is manifested as the clustering of sensor nodes in the sensor graph network. In the sensor graph network, there is a sensor network unit subgroup structure composed of several sensors with the core node (such as the gateway of the Internet of things (IoT)) as the center. These unit subgroups can be regarded as the basic organization module of a sensor network. The central node is the organizational core of the unit subgroup and has an aggregation effect. For example, the IoT gateway generally undertakes the tasks of data exchange, storage, processing and so on. These unit subgroups can be further combined to form more complex and larger sensor network subgroups. The unit and centrality of the sensor network are identified as the core of sensor network subgroup structure.

As a type of graph network, sensor networks widely exist in the real world, such as meteorological monitoring station network, energy consumption monitoring network, urban brain infrastructure network and so on. Many problems of sensor networks are essentially graph network structure problems. For example, the urbanization control of energy consumption of buildings, control of electric energy between high-rise and low-rise buildings, which is a graph network structure problem; There are many resource scheduling problems in the infrastructure of urban brain, including hardware resource management, capturing resource bottlenecks, system changes of user dynamic graph, etc. These are structural problems such as graph decomposition and graph synthesis.

At present, the research on sensor networks involves sensor network routing protocol [1–3], sensor network security [4,5], internet of things resource scheduling [6,7], energy consumption management [8] and so on. However, there is little research on sensor network structure recognition. The research of sensor graph network structure and graph network structure comes down in one continuous line. In recent years, the research on the structure of graph network has attracted widespread attention. Many graph network structure recognition algorithms have been developed in many disciplines such as computer science, physics and mathematics, and are widely used in specific problems in various scientific fields [9,10]. The existing methods for graph network structure recognition mainly include modularity maximization algorithm [11,12], spectral clustering algorithm [13,14] and label propagation algorithm [15,16]. Due to the large scale of large-scale graph networks, it is difficult to find global structure information. Therefore, the discovery of local structure has attracted the attention of researchers. The basic idea is to start from a few known nodes in the target structure and gradually expand to the remaining nodes in the structure. Research shows that the method based on seed set expansion [17,18] can effectively find local structures, including local spectrum method [19], personalized PageRank method [20,21], thermonuclear diffusion method [22], etc. Considering the unit characteristics and the connection mode between units which are based on core node signal transmission in sensor graph networks, a method based on unit patulousness and core node signal propagation (called p-law) is proposed to achieve the global structure recognition of sensor graph networks. This method first decomposes the sensor graph network according to the graph network units, and then combines the graph network units by the signal transmission path of the core node to form the sensor graph network subgroup. Specifically, the ideas of the proposed method are as follows: take the graph network unit subgroup as the basic construction module of the graph network subgroup. Then, take the central node as the signal organization center of the subgroup structure, and quickly generate the subgroup by the unit expansion method.

In summary, the main contributions of this paper are as follows:

(1)   The concepts of unit subgroup and k-order subgroup are provided, and the k-order subgroup model of graph network is established.

(2)   A k-order subgroup structure recognition method of graph network based on p-law is proposed.

(3)   The typical application of graph network subgroup structure identification method in sensor networks is presented.

2  Graph Network K-order Subgroup Model

2.1 K-order Subgroups of Graph Networks

Convention: let G = (V, E) be a graph, where V = {v1, v2, …, vn} is the node-set of graph G, and

E = {e1, e2, …, em} is the set of edges of graph G, and j(vi, vj) is the order (HOPS) of node vi reaching node vj, and deg(v) is the degree of node v (the number of edges connected to node v).

Definition 1: 1-order unit subgroup

Let H = (V′, E′) be a subgraph of G = (V, E), having V′⊆ V,  E′⊆ E and nodes v ∈ V, so that given any other nodes v′′ in H, j(v′′, v) = 1 is satisfied. Then H is the unit subgroup with node v as the core in graph G. which is recorded as:

g(v,1)=g(G|H, v, k=1) (1)

In Eq. (1), v is the core of the 1-order unit subgroup g in the graph network G, and k is the order of the subgroup in the graph network G.

Definition 2: 1-order extension of subgroups:

If g(v,1) = g(G|H, v, 1) is a unit subgroup with v as the core, gi(vi,1)=gi(G|Hi, vi, 1) is the i-th unit subgroup of the graph network G with vi as the core, H = (V′, E′),  Hi=(Vi′, Ei′) ,v′ ∈ V′, vi′∈Vi′ . If vi′∈V′ , vi′≠v′ , then gi(vi,1) is the 1-order extension of g(v,1) and vi′ is the extended core of g(v,1). The expanded subgroup is a 2-order subgroup, which is recorded as:

g(v,sk,2)=g(v,[v1,v2,…,vi],2)=g(v,1)∪⁡(g1(v1,1)∪⁡g2(v2,1)∪⁡…∪⁡gi(vi,1)) (2)

In Eq. (2): sk = [v1, v2, …, vi], v is the core of the graph network subgroup g, and sk is the set of 1-order extended cores of the graph network subgroup g.

The unit subgroups of the graph network and the 1-order extension of subgroups defined in definitions 1 and 2 are shown in Fig. 1.

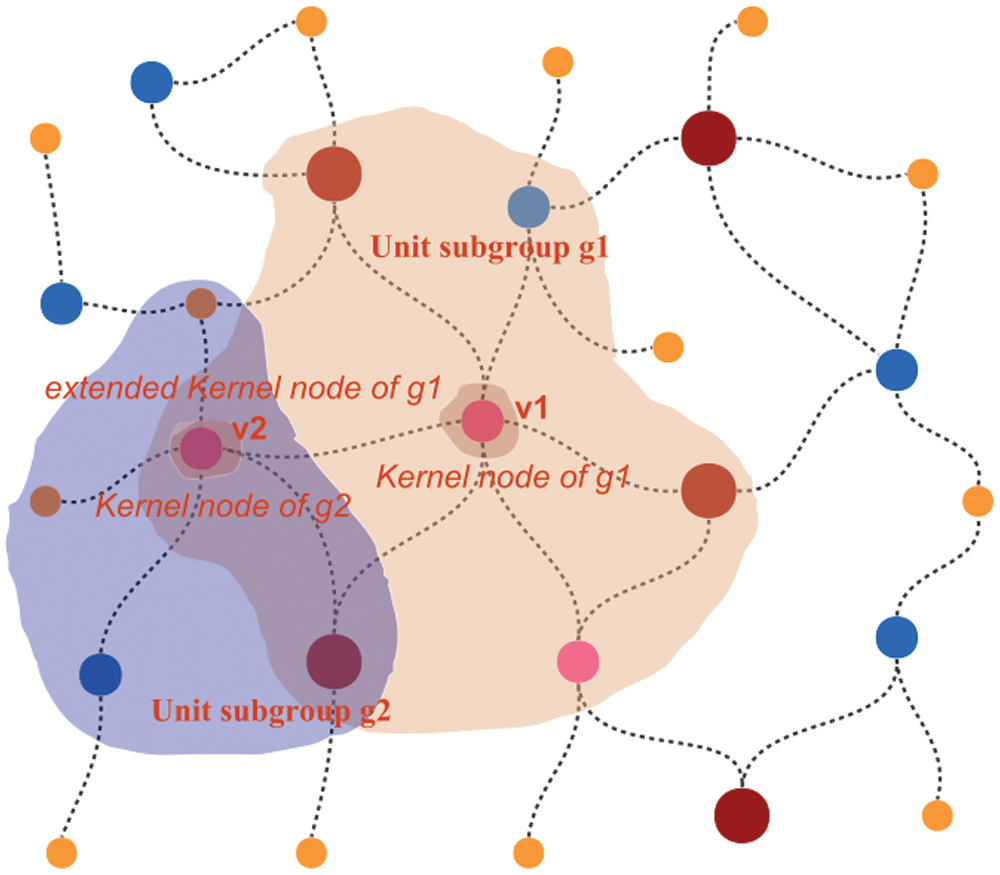
Figure 1: Schematic diagram of unit subgroups and 1-order extensions of graph network

Definition 3: k-order subgroup of graph network

if g(v,sk,1) is a 1-order subgroup with v as the core, and g(v,s1,s2,…,sj,k) satisfies: g(vhi,sh+1,1) is a 1-order subgroup with vhi as the core, sh+1 is its 1-order extended core, where vhi ∈ sh,h = 1, 2, …, k − 2, then, the following equation is called a k-order subgroup:

g(v,s1,s2,…,sk−1,k)=g(v,s1,1)∪⁡g(v1i,s2,1)∪⁡…∪⁡g(vhi,sh+1,1) (3)

In Eq. (3), s1, s2, …, sk−1 is the set of k-th order extended cores of the graph network subgroup G.

Fig. 2 is a schematic diagram of the extension of k-order subgroup and k-order subgroup.

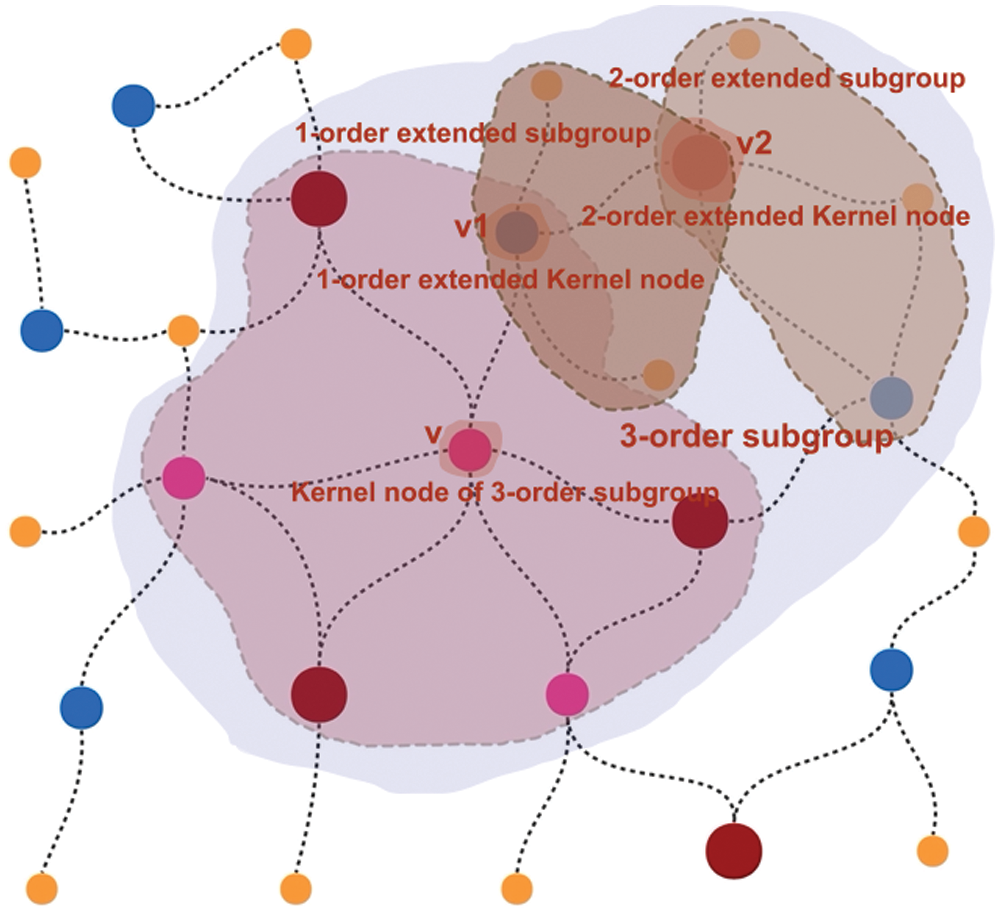
Figure 2: Schematic diagram of k-order subgroup extension and k-order subgroup

2.2 Related Properties of K-order Subgroup in Graph Network

Property 1:The k-order subgroup g(v,s1,s2,…,sk−1,k) of graph network has an extension chain l(v, s1, s2, …, sk−1) with v, s1, s2, …, sk−1 as the extension core series, and has a hierarchical structure corresponding to the extension chain l(v, s1, s2, …, sk−1).

According to the definition of k-order subgroup, k-order subgroup expands gradually according to the core node series v, s1, s2, …, sk−1, and the extension core expands step by step to form the extension chain l(v, s1, s2, …, sk−1), and the extension forms k-order subgroup. Therefore, it has a k-layer hierarchy corresponding to the extension chain l(v, s1, s2, …, sk−1).

Property 2: The order (hops) of any two nodes vi and vj in the k-order subgroup g(v,s1,s2,…,sk−1,k) of the graph network through the core v satisfies:

jv(vi, vj)≤2k (4)

Proof: According to property 1, the k-order subgroup of the graph network is hierarchical. If vi and vj are just on the k-th layer of subgroup g, at this time, the core v of the subgroup is the farthest from vi and vj, that is, j(vi, v)=k, j(vj, v) = k.

According to definition 3, vi must reach vj through the core v. At this time, if vi and vj are in layer K or within layer K, then: j(vi, v) ≤ k, j(vj, v) ≤ k. So, there is: jv(vi, vj) = j(vi, v) + j(vj, v) ≤ 2k.

End of proof.

Properties 1-2 are shown in Fig. 3.

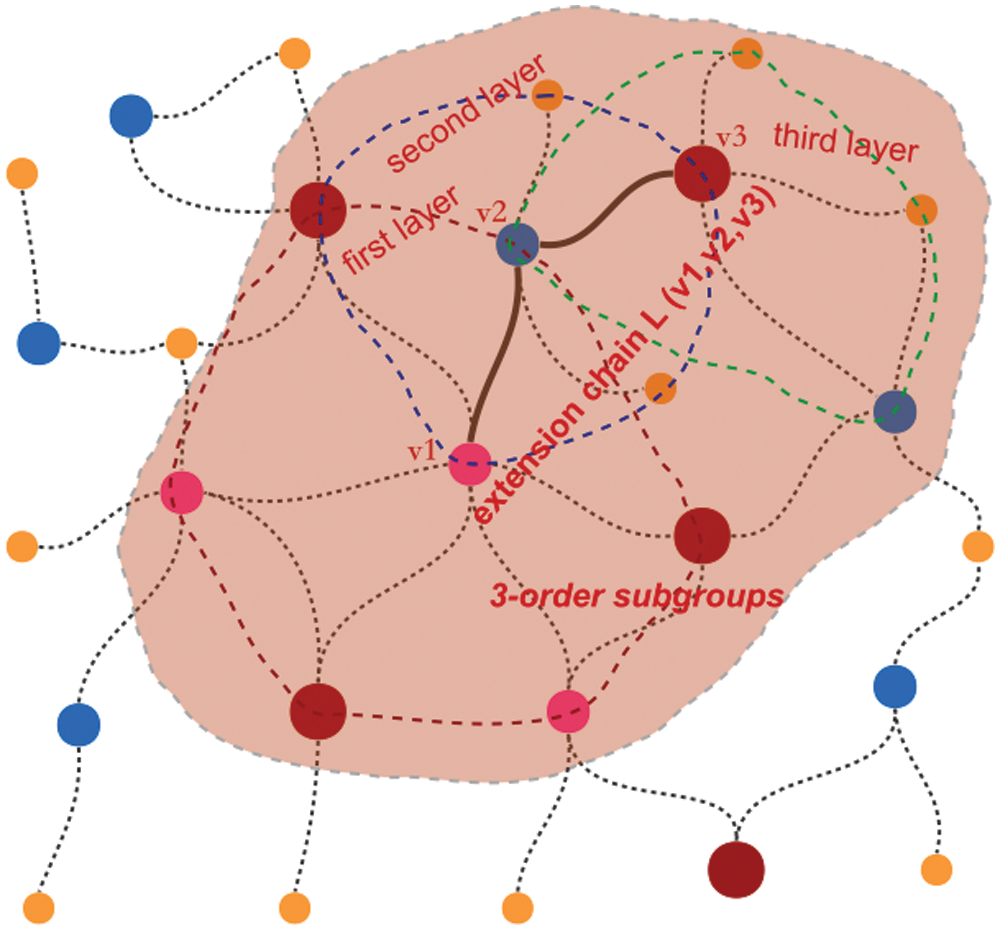
Figure 3: Schematic diagram of hierarchical structure of k-order subgroup

Theorem 1: Core reachability theorem of k-order subgroup of graph network

Any node vi in k-order subgroup g(v,s1,s2,…,sk−1,k) of graph network can reach any other node vj through the core node v.

Proof: According to definition 3 and property 1, the nodes of any layer in k-order subgroup of graph network are directly connected with the extension core of the layer. Because there is an extension chain in k-order subgroup of graph network, and the extended core on the extended chain is interconnected, any node in any layer of subgroup can reach the core v of the subgroup along the extended chain. Then, it reaches any other node in the subgroup through the extended chain. Therefore, any nodes in the subgroup can reach each other through the core and the extended chain, which has core reachability.

End of proof.

Fig. 4 shows the reachability of the core node of k-order subgroup. The node v4 in the 3-order subgroup reaches the core v1 through the extended chain L (v1, v2, v3), and then reaches the node v5 through the core v1.

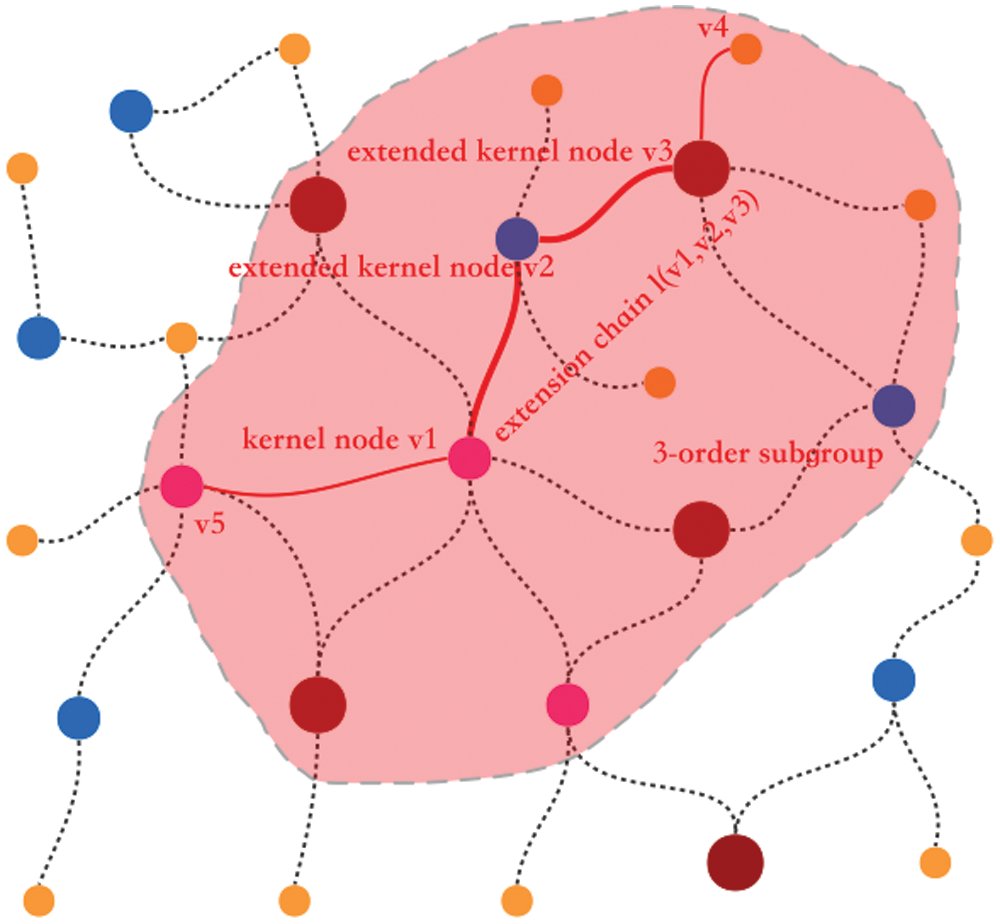
Figure 4: Schematic diagram of core reachability of k-order subgroup

Theorem 2: Node reachability theorem between subgroups of graph network

Let g1(v,s1,s2,…,sk−1,k)=g1(G|H1, v, s1, s2, …, sk−1, k) , g2(v′,s1′,s2′,…,sl−1′,l)=g2(G|H2, v′, s1′, s2′, …, sl′, l)

be two subgroups of graph network G respectively. If H1∩H2≠∅ , any node between g1(v,s1,s2,…,sk−1,k) and g2(v′,s1′,s2′,…,sl−1′,l) can reach each other.

Proof:

According to the meaning, because H1∩H2≠∅ , g1(v,s1,s2,…,sk−1,k) and g2(v′,s1′,s2′,…,sl−1′,l) must have a common node v′′.

Let vi and vj be arbitrary nodes of subgroups g1(v,s1,s2,…,sk−1,k) and g2(v′,s1′,s2′,…,sl−1′,l) respectively. According to theorem 1, vi can reach the common node v′′ through the core v of g1(v,s1,s2,…,sk−1,k) , and vj can reach the common node v′′ through the core v′ of g2(v′,s1′,s2′,…,sl−1′,l) .

That is:vi ⇔ v ⇔ v′′, vj ⇔ v′  ⇔ v′′, so there is:vi ⇔ v ⇔ v′′ ⇔ v′ ⇔ vj.

Therefore, vi and vj can reach the common node v′′ through their respective core and reach each other through the common node v′′.

End of proof.

Fig. 5 shows the case where any node among subgroups can reach each other. Node v3 in subgroup 2 reaches node v4 in subgroup 1 through the common node v1 of subgroup 1 and subgroup 2.

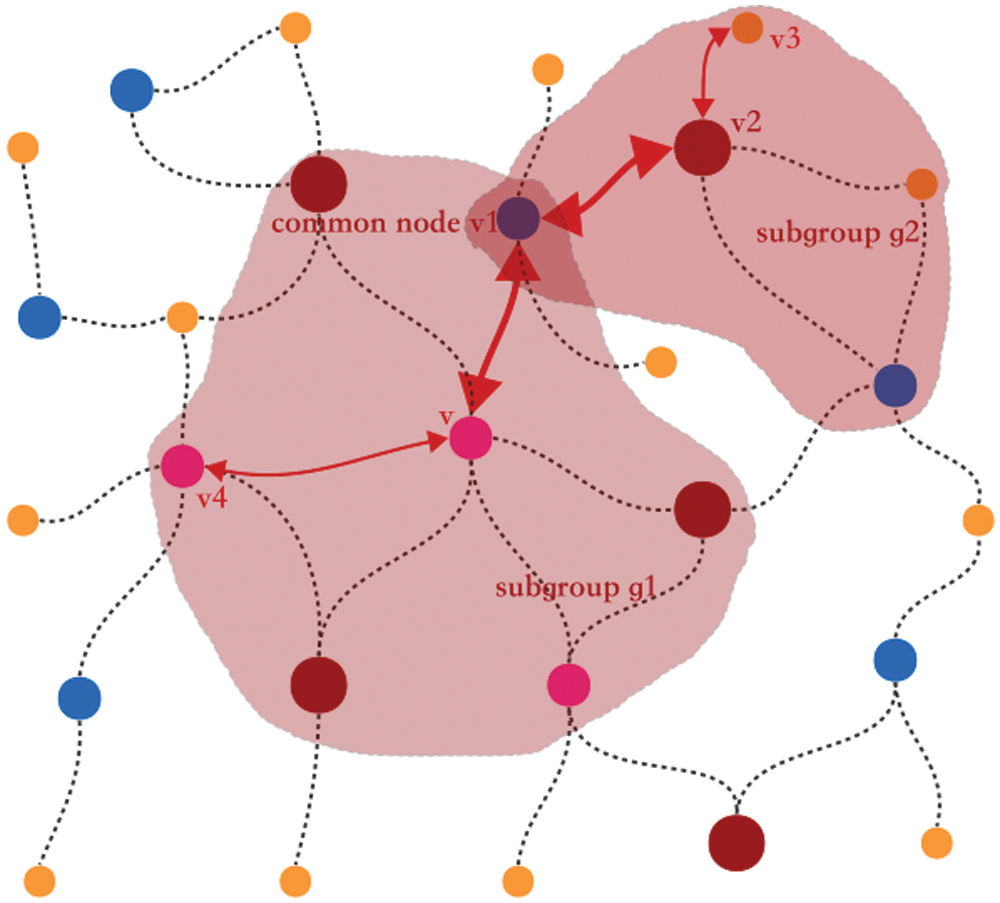
Figure 5: Schematic diagram of mutual accessibility of any nodes among subgroups

Theorem 3: Extension Theorem of Subgroup in Graph Network

K-order subgroup of graph network is expansion of 1-order subgroup based on (k-1)-order subgroup

Proof:

Let g(v,s1,s2,…,sk−2,k−1) be a (k-1)-order subgroup and l(v, s1, s2, …, sk−2) be its extended chain. sk−2 is the set of the end extended core nodes of the extension chain of the subgroup. Let v′ ∈ sk−2, sv′ be the associated node set of v′, and let v′′∈sv′ , g(v′′,1) be the 1-order unit subgroup with core v′′.

According to Definition 2:

1-order extension of g(v,s1,s2,…,sk−2,k−1) , that is, g(v,s1,s2,…,sk−2,k−1)∪⁡g(v′′,1) . At this time, the extended chain is extended to l(v, s1, s2, …, sk−2, v′′), and the original (k-1)-order subgroup g(v,s1,s2,…,sk−2,k−1) is extended to k-order subgroup g(v,s1,s2,…,sk−2,v′′,k) .

End of proof.

Theorem 4: Contraction theorem of subgroup in graph network

Contraction of k-order subgroup in graph network is by removing 1-order unit subgroup associated with the end extension core node in the extension chain (except the core node).

Proof:

Let g(v,s1,s2,…,sk−1,k) be a k-order subgroup and l(v, s1, s2, …, sk−1) be its extended chain. Select the end extended core node sk−1 from l(v, s1, s2, …, sk−1). Let vi ∈ sk−1, g(vi,1) be a 1-order unit subgroup with vi as the core. According to Theorem 3, if the subgroup is to be contracted, only remove the 1-order unit subgroup g(vi,1) from g(v,s1,s2,…,sk−1,k) (except the core node vi).

Namely:  (g(v,s1,s2,…,sk−1,k)−g(sk−1,1))∪sk−1 . At this time, the k-order subgroup g(v,s1,s2,…,sk−1,k) shrinks to k-1-order subgroup g(v,s1,s2,…,sk−2,k−1) and the extension chain l(v, s1, s2, …, sk−1) shrinks to l(v, s1, s2, …, sk−2).

End of proof.

3  Recognition Algorithm for K-order Subgroup Structure of Graph Network

3.1 The Basic Flow of Subgroup Structure Recognition of Graph Network

The basic flow of k-order subgroup structure recognition algorithm of graph network is as follows:

(1)   Determine the order of subgroup structure. You can set the default value to 3. According to the general law, if the order is too large, the subgroup scale may be too large, the compactness of the subgroup structure will be reduced, and the control force of the core node of the subgroup structure on the subgroup will be weakened.

(2)   The unit subgroups are generated in the order of the degree of the nodes with which as core of unit subgroups in graph network (from high to low), until the generated unit subgroups contain all the nodes of the graph network.

(3)   Select the unit subgroup with high degree of core node from the unit subgroups in turn for k-order expansion until it cannot be extended.

(4)   If necessary, the generated k-order subgroups can be further synthesized and optimized.

3.2 Generation Algorithm for K-order Subgroups of Graph Network

3.3 Synthesis and Optimization Algorithm for K-order Subgroups of Graph Network

3.4 Analysis of Recognition Algorithm for K-order Subgroup Structure of Graph Network

The key points of recognition algorithm for k-order subgroup structure of graph network are as follows:

(1)   Unit subgroup generation: the 1-order unit subgroup generation method used in the algorithm is to sort the nodes from high to low according to the degree of nodes, and then take out the nodes in order to generate 1-order unit subgroup until the nodes contained in the generated 1-order unit subgroups cover all the nodes in the graph network. In the generation of 1-order unit subgroups, this method ensures the clustering centrality and cohesion of nodes, that is, the nodes with higher degree give priority to the generation of 1-order unit subgroups.

(2)   Generation of k-order subgroup: select the 1-order unit subgroup with the highest centrality and cohesion as the subgroup to be expanded firstly, and then select the corresponding unit subgroup from the rest 1-order unit subgroup to expand until it can no longer be expanded.

(3)   Synthesis and optimization of k-order subgroups: for the previously generated k-order subgroups, further synthesis and optimization can be carried out as needed. If two k-order subgroups have high similarity (a coefficient can be set here for similarity control), that is, there are more common nodes, they can be combined to ensure their cohesion.

(4)   After subgroups synthesis and optimization, there may be common nodes between subgroups, which are the channels to realize signal transmission between subgroups. If you want to define the subgroup attribution of these coincident nodes, the following principles can be adopted: 1) If the common node is the core node, it can be determined according to the subgroup attribution of the core node (the core node can only belong to one subgroup); 2) If the common node is not a core node, it can be determined by the number of associated edges of the node and each subgroup; 3) Adjustment of subgroup belonging of core nodes: the associated nodes of core nodes may belong to multiple subgroups, which can be determined by the number of associated nodes between the core node and each subgroup.

4  Experiments and Analysis

4.1 Data Description

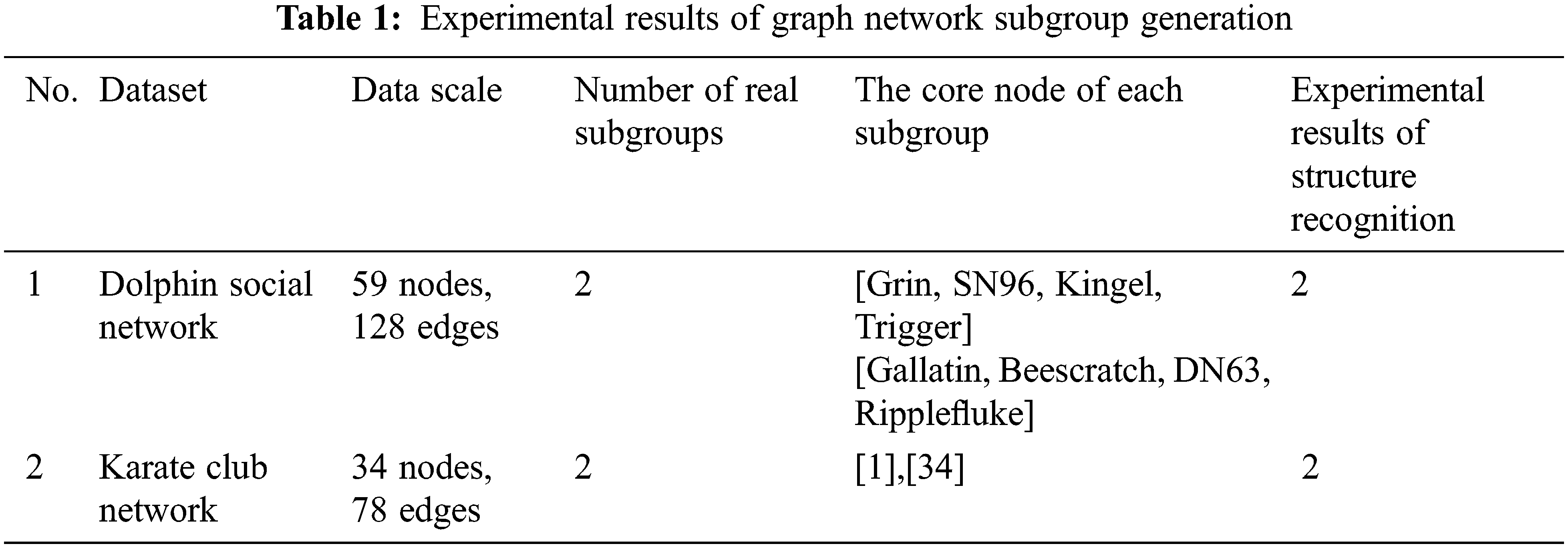
The following is the simulation experiment of sensor graph network structure recognition using the general real data set of graph networks: Dolphin network and karate club network. The two graph networks have 62 nodes, 128 edges, 34 nodes and 78 edges respectively. The real subgroup structure is two subgroups. The network diagram is shown in Fig. 6. The following experiments are carried out on these two real data sets to analyze and verify the above theories and algorithms.

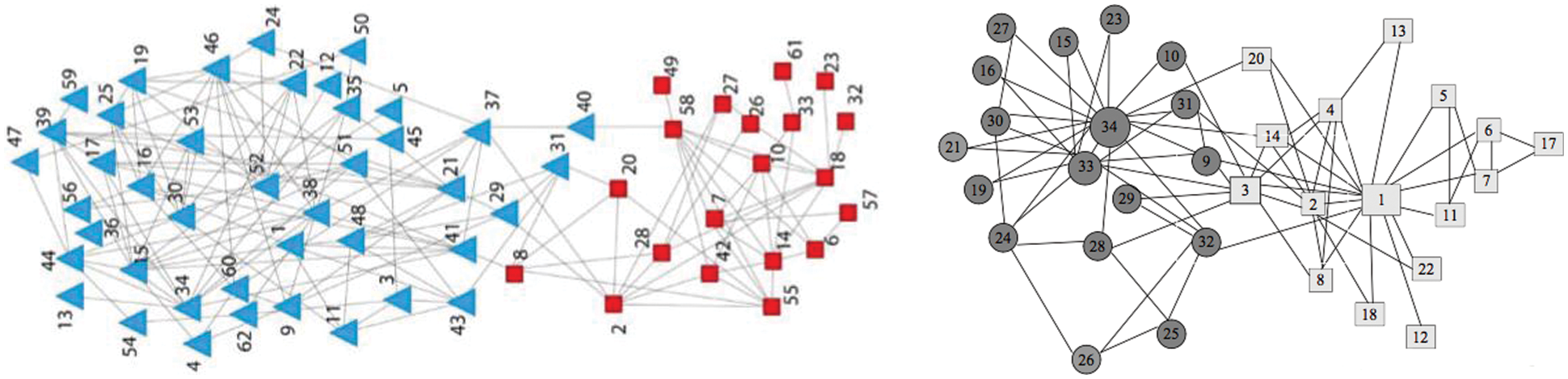
Figure 6: Dolphin social network and karate club network

4.2 Experimental Process

4.2.1 Unit Subgroup Generation

According to algorithm 1, based on the degree of nodes in the graph network, from the high to low order, the unit subgroup with the node as the core is generated successively until all nodes in the graph network are contained in the unit subgroups. Dolphin social network generates 43 unit subgroups, and karate club network generates 13 subgroups. As shown in Fig. 7.

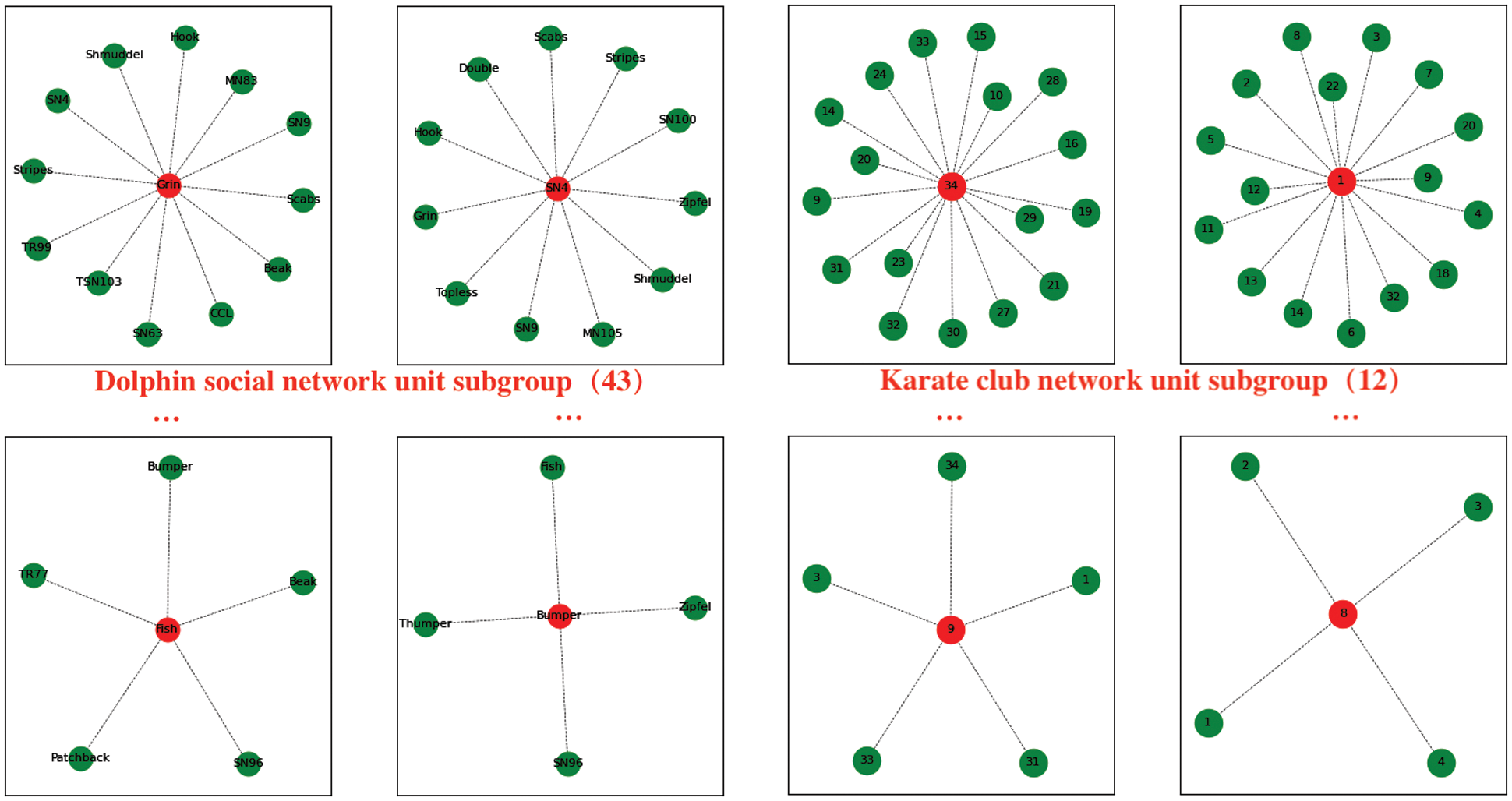
Figure 7: Unit subgroups of dolphin social network and karate club network

These unit subgroups are generated according to the clustering centrality (node degree), covering all nodes in the graph network. They are the basic elements of graph network subgroups.

4.2.2 Graph Network Subgroup Extension

According to algorithm 1, based on unit subgroups, the unit subgroups with high aggregation degree are selected in the order of node degree from high to low, and the k-order expansion is carried out until it can no longer be extended. After expansion, the dolphin network is expanded from 43 unit subgroups to 8 subgroups, of which 6 are 2-order subgroups and 2 unit subgroups are not expanded, indicating that the two unit subgroups tend to be separate groups, as shown in Fig. 8; The Karate club network is expanded from 12 unit subgroups to two 2-order subgroups. The expanded results are shown in Fig. 9.

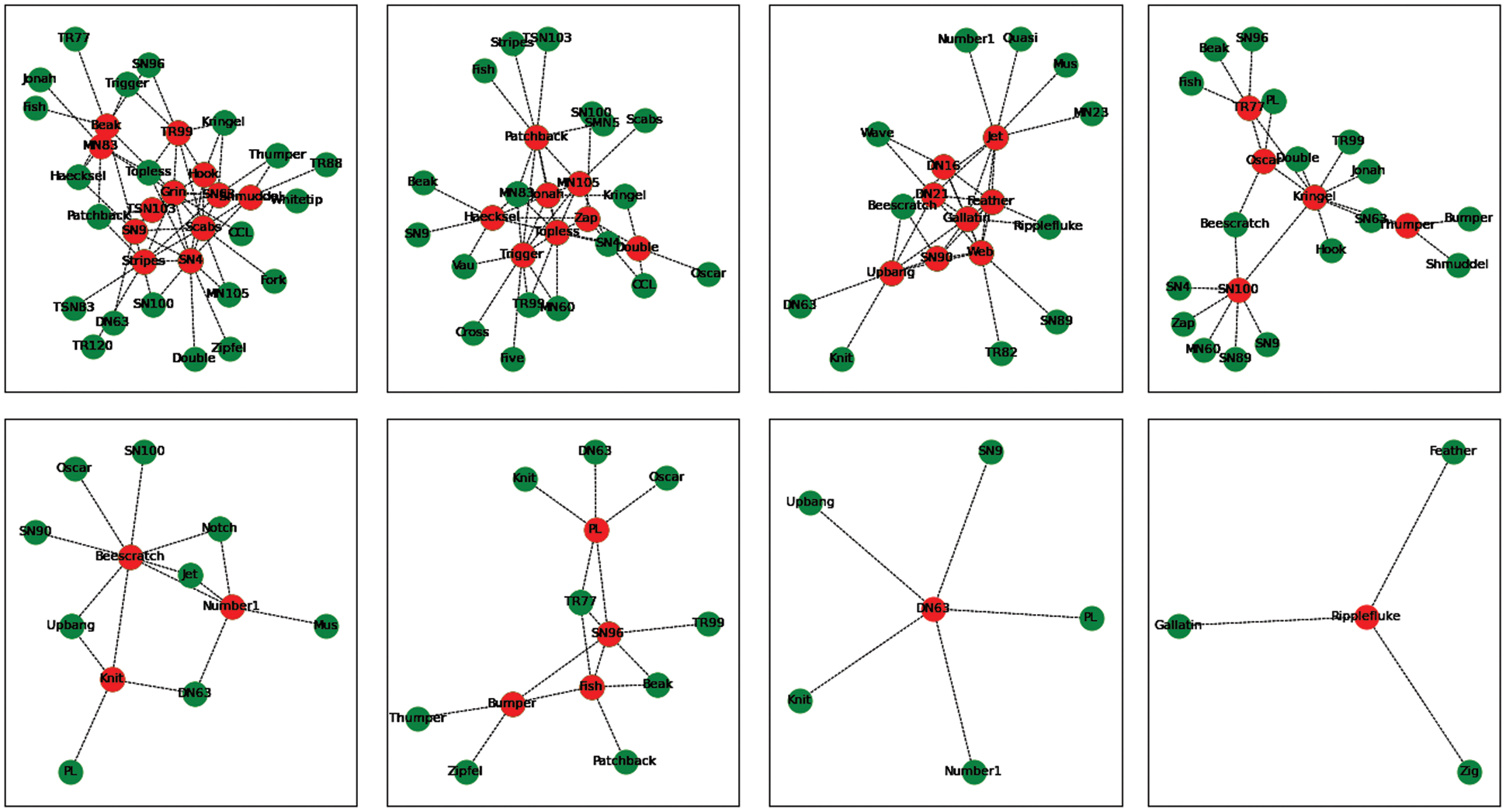
Figure 8: Eight subgroups of dolphin social network(after expansion)

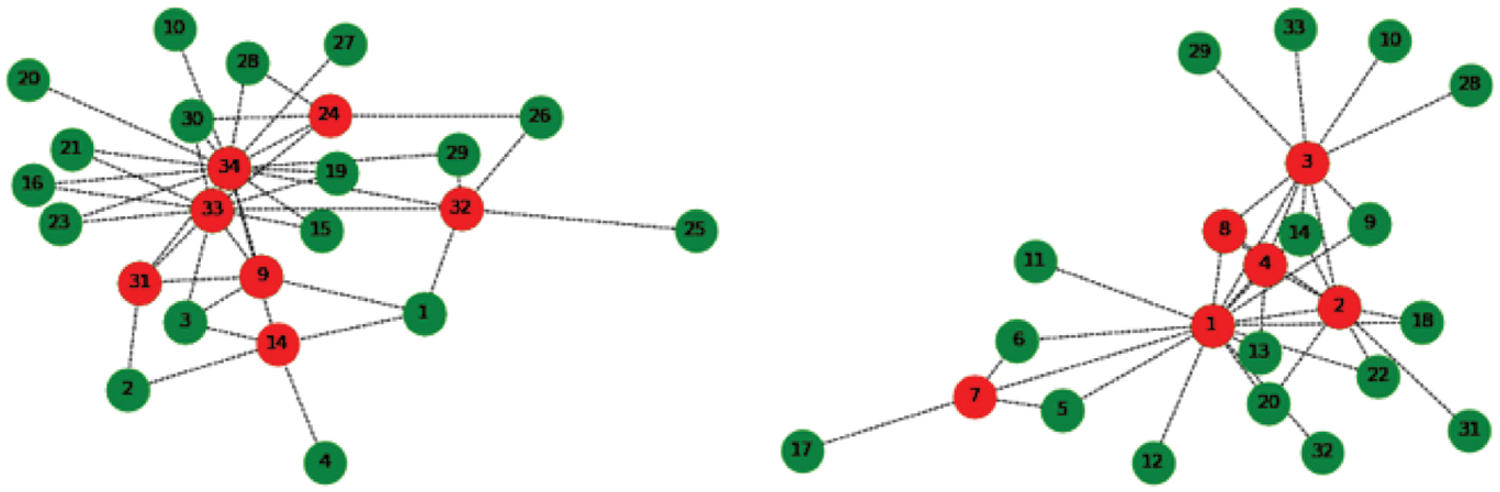
Figure 9: Two subgroups of the karate club network(after expansion)

4.2.3 Synthesis and Optimization of K-order Subgroups

If the generated k-order subgroups have more common nodes, further synthesis and optimization of k-order subgroups can be considered. The synthesized and optimized subgroups should have less connectivity, that is, there are fewer common nodes among subgroups. For Karate clubs, since the generated 2-order subgroups have reached the minimum number of graph network divisions, they will not be merged, and only the nodes between subgroups will be adjusted and optimized. The adjustment and optimization algorithm and idea are shown in the previous section. Subgroup structure recognition results are shown in Fig. 10.

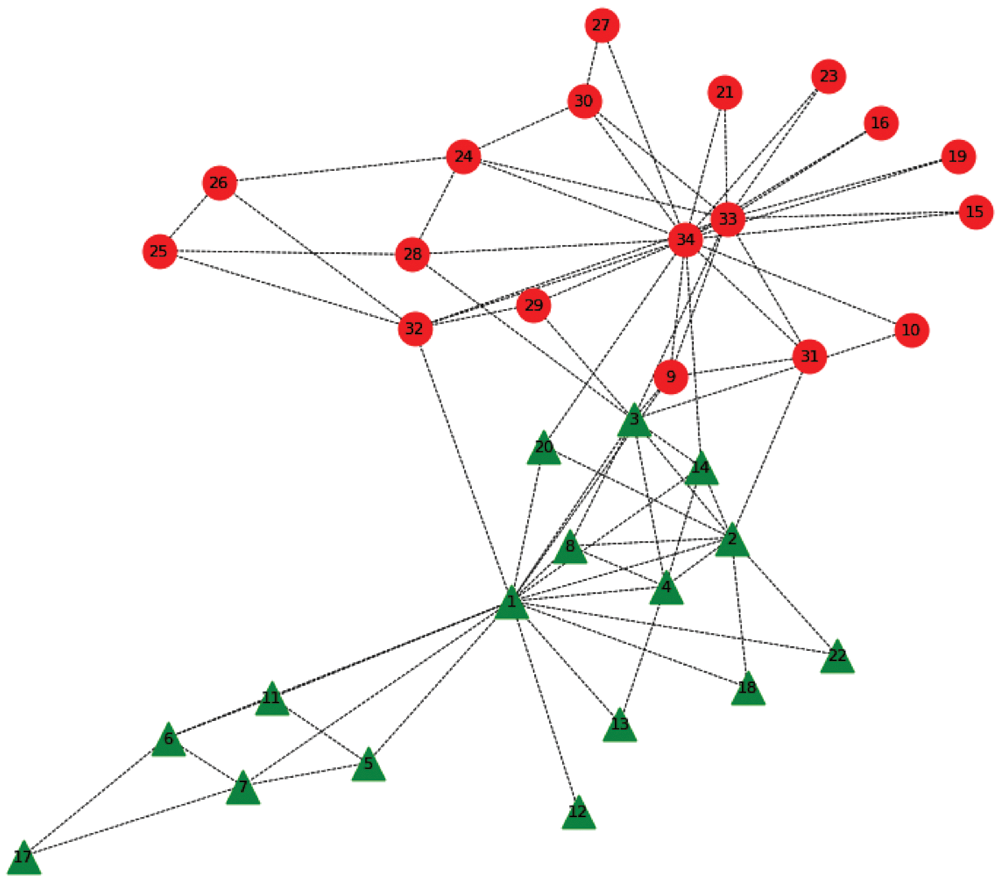
Figure 10: Two subgroup structures of the karate club network

For dolphin social network, eight subgroups are further merged into four subgroups by aggregation coefficient K(K = 0.6, K is a hyperparameter, it can be determined by observing the common nodes among subgroups in advance), two of which are unexpanded unit subgroups. According to algorithm 2, the number of common nodes of two unit subgroups and composite subgroups are compared respectively, and the unit subgroup is merged with the subgroup with more common nodes. After optimization and adjustment, eight subgroups are combined into two subgroups. The results are shown in Fig. 11. The coincident nodes among subgroups are processed according to the principle of coincident node processing. Subgroup structure recognition results are shown in Fig. 12.

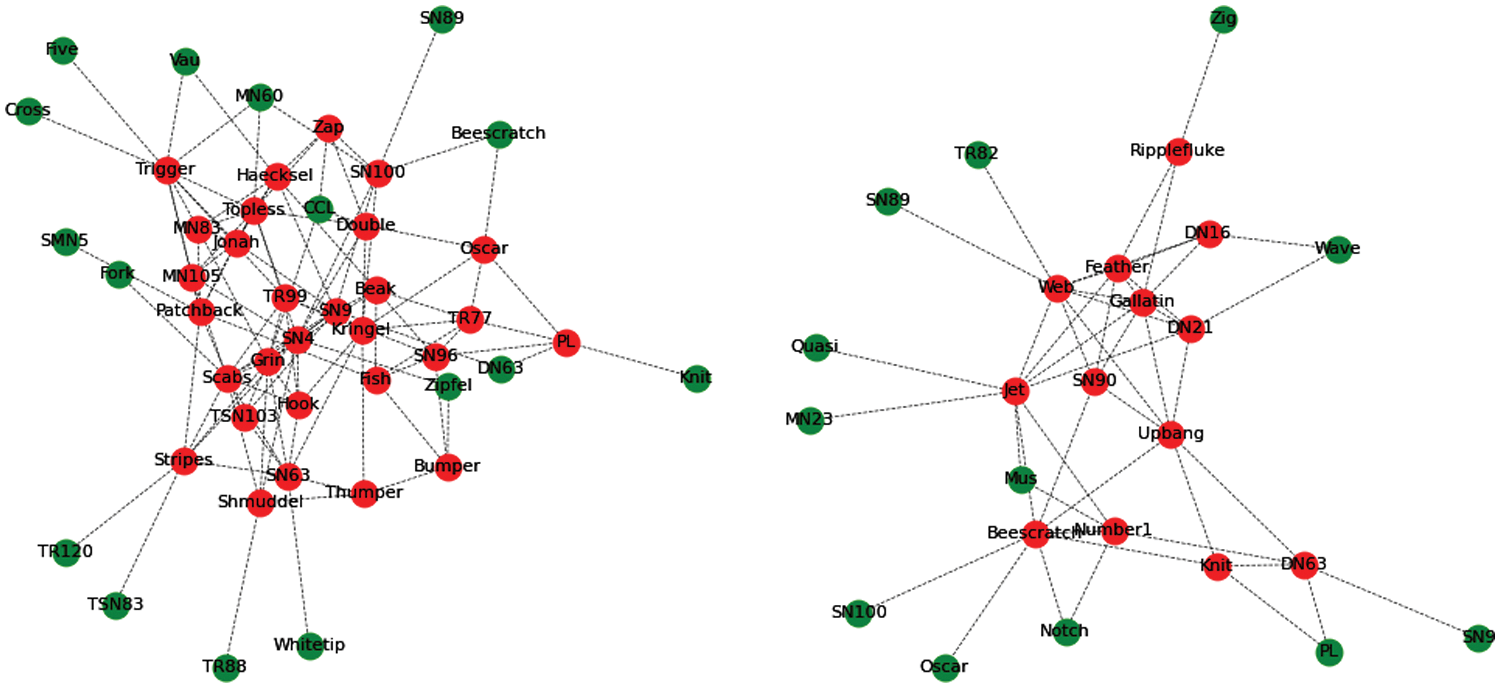
Figure 11: Two subgroups of the dolphin social network(after combined)

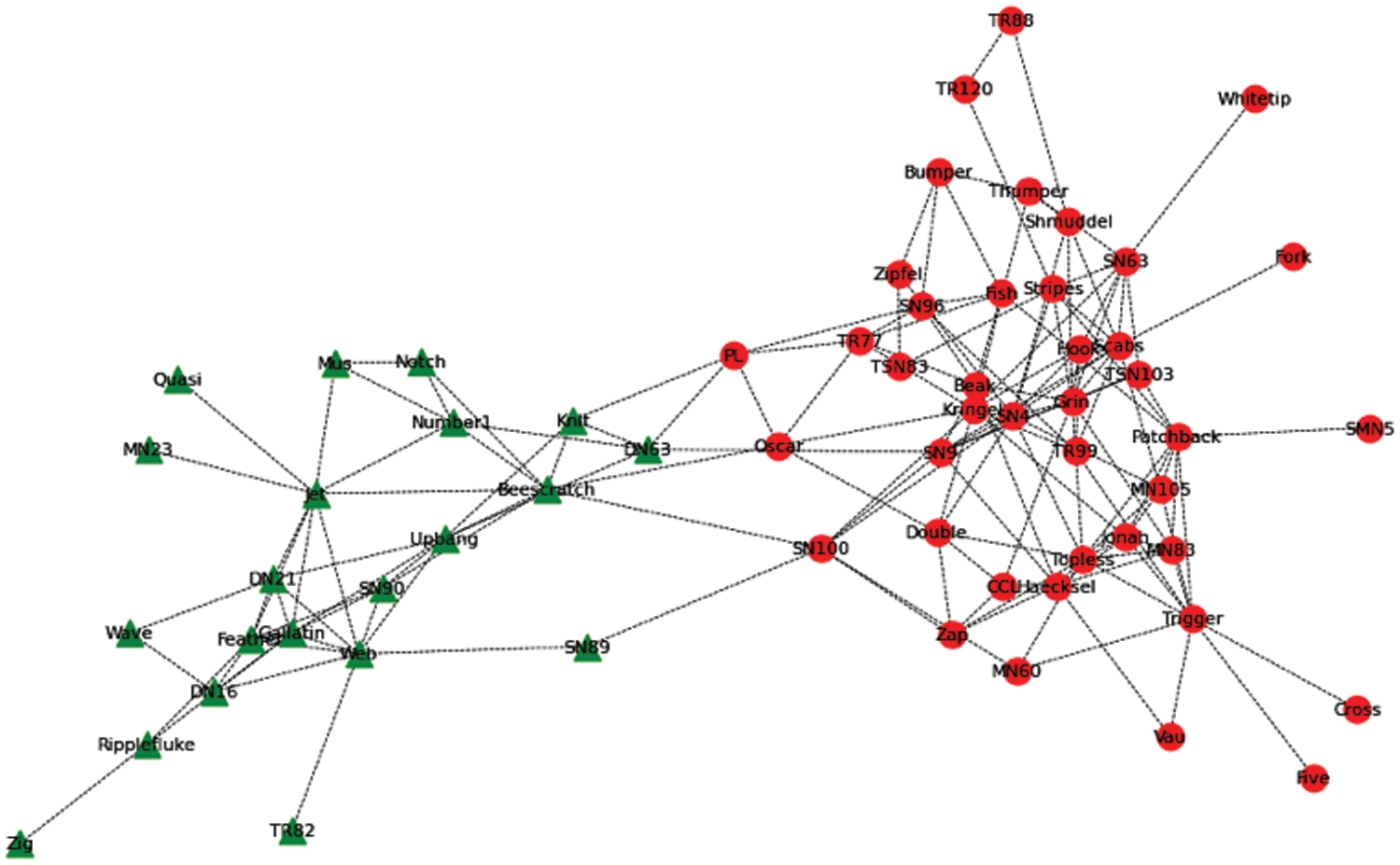
Figure 12: Two subgroup structures of the dolphin social network

4.3 Analysis of Experimental Results

The experimental results show that the method based on unit subgroup expansion and core node signal propagation can effectively recognize the subgroup structure of the sensor graph network. The identification results are consistent with the actual subgroup structure of graph network. At the same time, the core node expansion chain of subgroup (shown by red dots in each subgroup) are identified. The extension chain is a fast channel for signal transmission in subgroups, and the signal transmission between subgroups is carried out through the common nodes between subgroups. The experimental results are shown in Tab. 1.

5  Conclusion

Driven by the new generation of information technologies such as artificial intelligence, the IoT and cloud computing, the sensor network based on sensor technology has penetrated all aspects of the social industry, promoted the integration of human, machine and object space, such as intelligent medical treatment, intelligent transportation, ecological monitoring, urban brain, etc. To enable each unit of a sensor network to work cooperatively, accurately, and efficiently, it is necessary to involve the identification, optimization, decomposition and combination of sensor graph network structure. Starting from the objective phenomenon of sensor networks, this paper analyzes and studies them from the perspective of the graph network model. Experimental results reveal the objectivity of the existence of unit structure and core nodes in graph network, and the universal significance of unit patulousness and the continuous propagation of the core node signals in the process of subgroup structure identification, which can be well interpreted. The research results can be used in the identification of sensor network structure and the core node transmission path discovery and so on. Compared with existing similar studies, the research process, methods and results of this paper are better interpretable and enlightening. In the future, further research and attempts will be made in the following aspects: dynamic adjustment and optimization of sensor network structure, message exchange model among sensor network subgroups, intelligent cooperation among sensor network subgroups and so on.

Funding Statement: This research is supported by the Natural Science Foundation Project of Fujian Provincial Department of Science and Technology (Grant No. 2020J01385), Digital Fujian Industrial Energy Big Data Research Institute (Grant No. KB180045), Provincial Key Laboratory of Industrial Big Data Analysis and Application (Grant No. KB180029).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. S. Kaur and V. K. Joshi, “Hybrid soft computing technique based trust evaluation protocol for wireless sensor networks,” Intelligent Automation & Soft Computing, vol. 26, no. 2, pp. 217–226, 2020. [Google Scholar]

    2. A. A. Hady, “Duty cycling centralized hierarchical routing protocol with content analysis duty cycling mechanism for wireless sensor networks,” Computer Systems Science and Engineering, vol. 35, no. 5, pp. 347–355, 2020. [Google Scholar]

    3. L. Kou, Y. Shi, L. Zhang, D. Liu and Q. Yang, “A lightweight three-factor user authentication protocol for the information perception of iot,” Computers, Materials & Continua, vol. 58, no. 2, pp. 545–565, 2019. [Google Scholar]

    4. C. T. Poomagal, G. A. Sathish Kumar and D. Mehta, “Multi level key exchange and encryption protocol for internet of things (iot),” Computer Systems Science and Engineering, vol. 35, no. 1, pp. 51–63, 2020. [Google Scholar]

    5. J. Wang, W. Chen, L. Wang, Y. Ren and R. S. Sherratt, “Blockchain-based data storage mechanism for industrial internet of things,” Intelligent Automation & Soft Computing, vol. 26, no. 5, pp. 1157–1172, 2020. [Google Scholar]

    6. W. He, S. Guo, Y. Liang, R. Ma, X. Qiu et al., “Qos-aware and resource-efficient dynamic slicing mechanism for internet of things,” Computers, Materials & Continua, vol. 61, no. 3, pp. 1345–1364, 2019. [Google Scholar]

    7. M. Okhovvat and M. R. Kangavari, “Tslbs: A time-sensitive and load balanced scheduling approach to wireless sensor actor networks,” Computer Systems Science and Engineering, vol. 34, no. 1, pp. 13–21, 2019. [Google Scholar]

    8. W. Zhang, W. Fang, Q. Zhao, X. Ji, “Energy efficiency in internet of things: An overview,” Computers, Materials & Continua, vol. 63, no. 2, pp. 787–811, 2020. [Google Scholar]

    9. D. Stavros I, M. Eirini and K. J. Derek, “The impact of graph construction scheme and community detection algorithm on the repeatability of community and hub identification in structural brain networks,” Human Brain Mapping, vol. 42, no. 13, pp. 4261–4280, 2021. [Google Scholar]

  10. J. S. Hossein, A. Qomi, A. Mahdi, A. Masoud and Y. Naser, “An information theoretic approach to link prediction in multiplex networks,”Scientific Reports, vol. 11, no. 1, pp. 1–21, 2021. [Google Scholar]

  11. J. Zhang, H. Liu and Z. Wen, “A sparse completely positive relaxation of the modulatiry maximization for community detection,” SLAM Journal on Scientific Computing, vol. 40, no. 5, pp. A3091–A3120, 2018. [Google Scholar]

  12. K. He, Y. Li, S. Soundarajan and J. E. Hopcroft, “Hidden community detection in social networks,” Information Sciences:An International Journal, vol. 425, pp. 92–106, 2018. [Google Scholar]

  13. Y. T. Cui, Q. Niu and Z. X. Wang, “Semi-supervised spectral clustering approach for community detection based on signal transmission,” Computer Engineering & Design, vol. 39, no. 5, pp. 9–13, 2018. [Google Scholar]

  14. X. Q. Zhang, X. D. An and F. Y. Cao, “Detection community from bipartite network based on spectralclustering,” Computer Science, vol. 46, no. 4, pp. 216–221, 2019. [Google Scholar]

  15. W. P. Zhang, C. H. Che and Y. H. Qian, “A Two-stage community detection algorithm based on label propagation,” Computer Research and Develoment, vol. 55, no. 9, pp. 1959–1971, 2018. [Google Scholar]

  16. L. Li and L. Ni, “Community detection for label propagation with modularity optimization,” Computer Systems & Applications, vol. 25, no. 9, pp. 212–215, 2016. [Google Scholar]

  17. J. J. Whang, D. F. Gleich and I. S. Dhillon, “Overlapping community detection using neighborhood-inflated seed expansion,” IEEE Transaction on Knowledge and Data Engineering, vol. 28, no. 5, pp. 1272–1284, 2016. [Google Scholar]

  18. Y. Li, J. He, Y. X. Wu and R. J. Lv, “Overlapping community discovery method based on Two expansions of seeds,” Symmetry, vol. 13, no. 1, pp. 1–19, 2020. [Google Scholar]

  19. Y. X. Li, K. He, D. Bindel and J. E. Hopcroft, “Uncovering the small community structure in large networks: A local spectral approach,” in Proc. Proc. of the 24th Int. Conf. on World Wide Web, Geneva, Switzerland, pp. 658–668, 2015. [Google Scholar]

  20. F. Chung and O. Simpson, “Distributed algorithms for finding local clusters using heat kernel pagerank,” in Proc. Intertional Workshop on Algorithms and Models for the Web-Graph, Springer, Cham, pp. 177–189, 2015. [Google Scholar]

  21. I. M. Kloumann, J. Ugander and J. Kleingerg, “Block models and personalized PageRank,” Proceedings of the National Academy of Sciences of the United States of America, vol. 114, no. 1, pp. 33–38, 2017. [Google Scholar]

  22. F. Chung and O. Simson, “Computing heat kernel pagerank and a local clusering algorithm,” European Journal of Combinatorics, vol. 68, pp. 96–119, 2018. [Google Scholar]