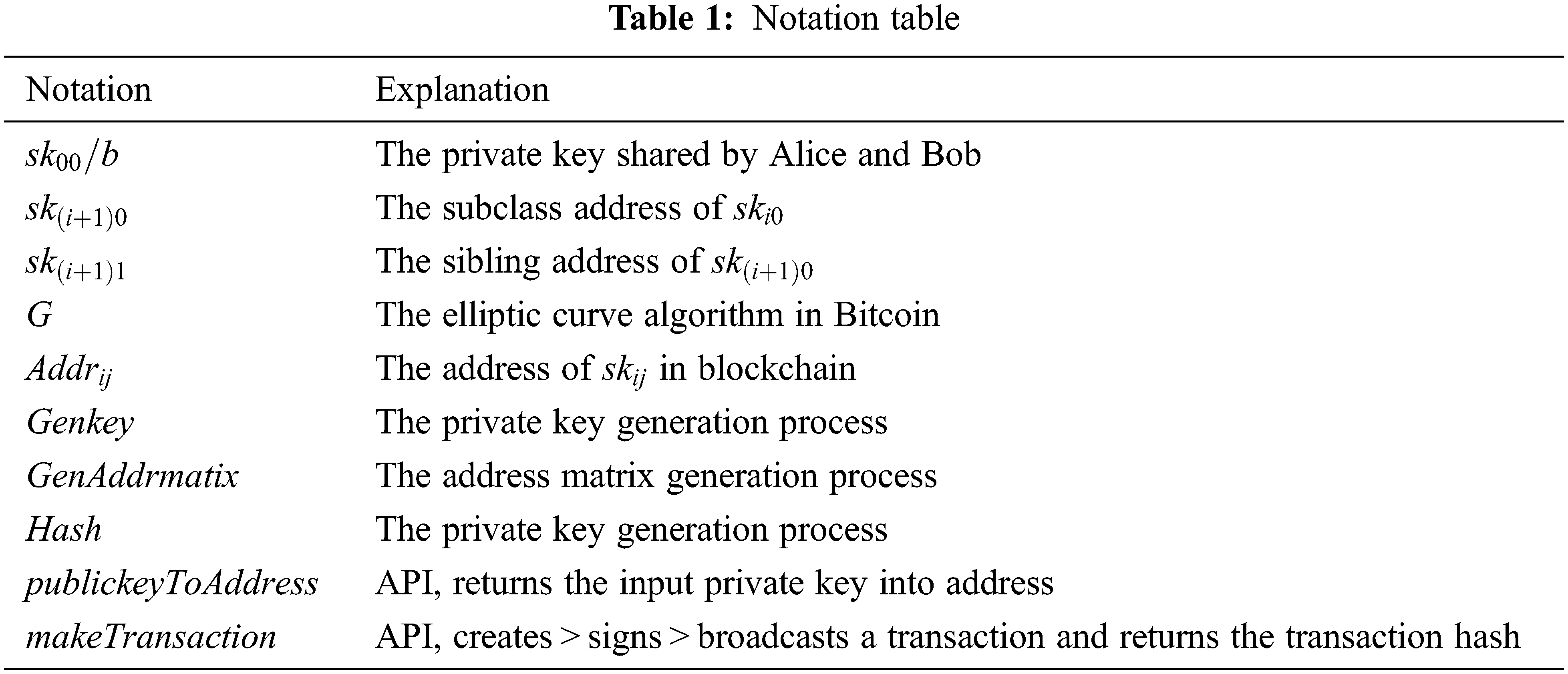
 Open Access
Open Access
ARTICLE
A Derivative Matrix-Based Covert Communication Method in Blockchain
1
School of Computer and Software, Nanjing University of Information Science & Technology, Nanjing, 210044, China
2
School of Hydrology and Water Resources, Nanjing University of Information Science & Technology, Nanjing, 210044, China
3
Wuxi Research Institute, Nanjing University of Information Science & Technology, Wuxi, 214100, China
4
Key Laboratory of Hydrometeorological Disaster Mechanism and Warning of Ministry of Water Resources, Nanjing, 210044, China
5
Engineering Research Center of Digital Forensics, Ministry of Education, Jiangsu Engineering Center of Network Monitoring,
School of Computer and Software, Nanjing University of Information Science & Technology, Nanjing, 210044, China
6
Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology (CICAEET), Nanjing,
University of Information Science & Technology, Nanjing, 210044, China
7
School of Automation, Nanjing University of Information Science & Technology, Nanjing, 210044, China
8
School of Computer Science Engineering, Nanyang Technological University, Singapore
* Corresponding Author: Xiaona Zhang. Email:
Computer Systems Science and Engineering 2023, 46(1), 225-239. https://doi.org/10.32604/csse.2023.034915
Received 01 August 2022; Accepted 08 October 2022; Issue published 20 January 2023
Abstract
The data in the blockchain cannot be tampered with and the users are anonymous, which enables the blockchain to be a natural carrier for covert communication. However, the existing methods of covert communication in blockchain suffer from the predefined channel structure, the capacity of a single transaction is not high, and the fixed transaction behaviors will lower the concealment of the communication channel. Therefore, this paper proposes a derivation matrix-based covert communication method in blockchain. It uses dual-key to derive two types of blockchain addresses and then constructs an address matrix by dividing addresses into multiple layers to make full use of the redundancy of addresses. Subsequently, to solve the problem of the lack of concealment caused by the fixed transaction behaviors, divide the rectangular matrix into square blocks with overlapping regions and then encrypt different blocks sequentially to make the transaction behaviors of the channel addresses match better with those of the real addresses. Further, the linear congruence algorithm is used to generate random sequence, which provides a random order for blocks encryption, and thus enhances the security of the encryption algorithm. Experimental results show that this method can effectively reduce the abnormal transaction behaviors of addresses while ensuring the channel transmission efficiency.Keywords
Covert communication technology is a branch of information security, which aims to covertly embed secret information into the original carriers, such as image [1], video [2] and audio [3], and then hides the communication behaviors and communication content in public channels. The carrier containing secret information generated by information hiding technology is often very similar to the original carrier, making it difficult to attract the attention of adversaries [4–6]. Therefore, the covert transmission of information between the two sides of communication can be performed to prevent malicious tampering or eavesdropping of information. However, in the current complex network context, the existence of third-party tends to cause the exposure of identity information of the communicating parties once the information is known to be abnormal [7]. In addition, the secret information uploaded by the sender may suffer from malicious tampering from social networks [1]. Therefore, it is crucial to find a decentralized and robust communication method [8]. Blockchain technology has attracted extensive attention from the community for the characteristics of decentralization, tamper resistance [9–12]. These characteristics make the blockchain a natural carrier for covert communication [13].
Bitcoin is a typical blockchain system, which has allowed users to push any sequence of data using OP_RETURN output scripts (OP) since March 2014. OP is a script opcode containing 80 bytes of data, which is specifically designed to carry additional transaction information [14]. In addition to the OP, secret information is also embedded into Bitcoin addresses by the least significant bit (LSB) embedding method [15]. However, these embedding methods are usually heuristic and empirical, and the adversaries can analyze the carriers through statistical methods or machine learning algorithms. The secret information will be subject to a high risk of leakage once the embedded carrier is detected. In contrast, the blockchain coverless covert communication methods have better concealment. Because these methods creatively use address transactions to map secret information without modifying or customizing the transactions themselves [16,17]. Thus, the adversaries cannot collect data for analysis. However, current coverless methods still have some limitations. First, compared with the traditional covert communication, the coverless covert communication, limited by the inherent channel structure, has less space to embed secret information in a single transaction; Second, current coverless methods do not consider the problem of the reuse of fixed addresses, and the more times the transaction addresses are reused, the greater the probability of the covert channel to be detected is.
To solve the above problems, this study proposes a derivation matrix-based covert communication method in blockchain. The construction of address matrix can make full use of the redundancy of the address transactions to increase the mapping number of a single transaction. In addition, a matrix encryption method based on random number is proposed. The matrix is divided into several blocks, and then the corresponding blocks are scrambled in order of the random sequence generated by the random generator. This can not only improve the anti-detection of the transaction address, but also improve the security of the channel encryption algorithm.
Our contributions are summarized as follows.
1. A derivation matrix-based covert communication method in blockchain is proposed. Generated blockchain addresses are divided into sibling addresses and subclass addresses, and subscripts are assigned to all addresses to construct an address matrix. By means of hierarchical transaction of addresses, the capacity of a single transaction is increased.
2. To further improve the concealment of the model, a matrix encryption method based on random number is proposed. The rectangular address matrix is divided into multiple square blocks. Then, the linear congruence algorithm is used to provide a random sequence. And finally, corresponding square blocks are encrypted in order of the random sequence. This manner of change relative relationship of addresses can effectively enhance the anti-detection of transaction addresses, and the random sequence also provides higher security for the channel encryption algorithm.
The rest of the paper is organized as follows. Section 2 presents the related work. Section 3 dwells on the proposed method and procedure. Section 4 presents the experimental results. Section 5 concludes the paper finally.
This section dwells on the related work of our algorithm from three aspects: covert communication technology in blockchain, encryption technology of digital matrix, and random algorithm.
2.1 Covert Communication Technology in Blockchain
To embed messages into Bitcoin system, the most straightforward and efficient way is to use the properties of transactions. Partala [15] designed a method of embedding and extracting reliably into a blockchain following the model by submitting payments (BLOCCE). BLOCCE is the first attempt to establish provably blockchain secure covert communication. Gao et al. [16] designed a secret data transmission scheme in blockchain, which uses thief cryptography to achieve highly concealed and high-performance data transmission in the context of open networks. However, the essence of embedding information in the transaction properties is by modifying or customizing the transaction itself, which will expose the secret communication behavior of the transactions. In other words, adversaries may suspect that the secret information is hidden in the fixed transaction data, and then similar transactions can be continuously collected, which increases the risk that the information is decrypted.
In contrast, coverless blockchain covert communication technology creatively uses transactions between addresses to embed secret information, rather than manually modify or customize the transaction itself. Therefore, it has strong concealment. In recent years, some researchers have tried to use coverless methods to implement convert communication in blockchain. Cao et al. [17] proposed a chain-based covert data embedding scheme in blockchain to achieve convert communication. The scheme first uses the transactions between addresses as the carrier of secret information, rather than manually modifying the properties. However, in the channel constructed by this scheme, the percentage of the parent addresses is very small, and the channel capacity depends on the subclass addresses. Zhang et al. [18] proposed a model of covert communication based on smart contracts. The scheme uses options in voting contracts to map the secret information and transmit information through contract execution. However, due to the anti-tamper to the contract, the channel of this model is not scalable.
Obviously, due to the channel structure, current covert communication methods cannot make full use of the redundancy of address transactions. Therefore, this paper uses dual-key to generate two types of blockchain addresses, and use the derivation relationship between addresses to construct the address matrix. This can make full use of the redundancy of address transactions, thereby increasing the mapping number of a single transaction.
2.2 Encryption Technology of Digital Matrix
In the blockchain covert communication, the reuse of addresses tends to cause the decrease of channel concealment. Therefore, the channel needs to be encrypted before covert communication. As an encryption technique, the main purpose of scrambling technique is to transform a meaningful two-dimensional matrix into a chaotic two-dimensional matrix [19]. At present, there are many scrambling algorithms, among which the Arnold transform algorithm is simple, easy to understand and implement, and has been well applied in information hiding. Arnold-based encryption schemes have been widely studied. Mishra et al. [20] proposed an encryption scheme based on Fibonacci and Lucas. Batool et al. [21] proposed a new image encryption scheme based on Arnold scrambling and Lucas, which encrypts the standard image using the Lucas sequence in different iterations of the image after the Arnold transform.
However, the above methods are all for the square matrix structure, and do not apply to the rectangular matrix structure whose length and width are not equal in this paper. Min et al. [22] proposed an image scrambling algorithm based on the Arnold transform. This algorithm proposes a multi-region algorithm for image scrambling encryption model, which divides the rectangular image into multiple square regions and scrambles each region. This paper follows their idea to block the generated address matrix. It aims to optimize the transaction behaviors of the addresses in the channel, and enhance the concealment of the channel.
Although the rectangular Arnold transform can achieve the purpose of encryption and provide stronger concealment for the communication channel. However, when the Arnold transform is used for simple sequence scrambling, the security of the encrypted channel algorithm is still not high, and one of the improvements is to optimize the scrambling sequence. Therefore, this paper introduces random numbers to ensure the randomness of the channel scrambling sequence in each round, increasing the difficulty of adversaries cracking them.
The distribution probabilities of random number should be random, and the result should be unpredictable and invisible. Currently, most methods use computer programs to generate uniformly distributed random numbers. Although these are not truly random numbers, they have statistical properties of truly random numbers [23–25].
The linear congruence algorithm is a pseudo-random number algorithm with fast generation speed and long output sequence cycle [26]. The basic idea is to obtain the next number by performing linear operations on the previous number and taking the modulus from it. François et al. [27] proposed a secure pseudo-random number generator triple mixer using permutations, and its positions are calculated and indexed by standard chaotic functions and linear congruences. The performance of the scheme is evaluated by statistical analysis. Such a cryptosystem can bring significant cryptographic quality for high security level. This paper uses the linear congruence generator (LCG) to provide random scrambling sequences for channel encryption, thereby improving the security of the channel encryption algorithm in this paper.
To improve the transmission efficiency of the blockchain coverless covert communication and ensure the concealment of the channel addresses after multiple transmissions, in this work, this paper establishes the blockchain covert channel based on the derivation matrix and encrypt the channel.
The implementation flow of our covert communication is illustrated in Fig. 1, which contains three main parts: dual-key based covert channel, random sequence-based matrix encryption, and derivation matrix-based covert communication. The first part is to derive new addresses combined with the existing addresses and dual-key, and group all addresses. The number of transactions needed is calculated according to the length of the embedded information, and then the address matrix is constructed. The operation object of the second part is the address matrix constructed in the previous step. The address matrix is encrypted with the random sequence generated by random generator to solve the concealment problem caused by the channel reuse. The third part is to embed the secret information using the transaction behaviors of the addresses, which requires the sender and receiver to agree on the mapping relationship between the address transactions and the secret information. Meanwhile, these addresses are monitored. Once the transaction occurs, since the receivers share the embedding process, the secret information can be extracted based on the address transactions by receiver. Table 1 shows the notations and explanations that appear in this paper.
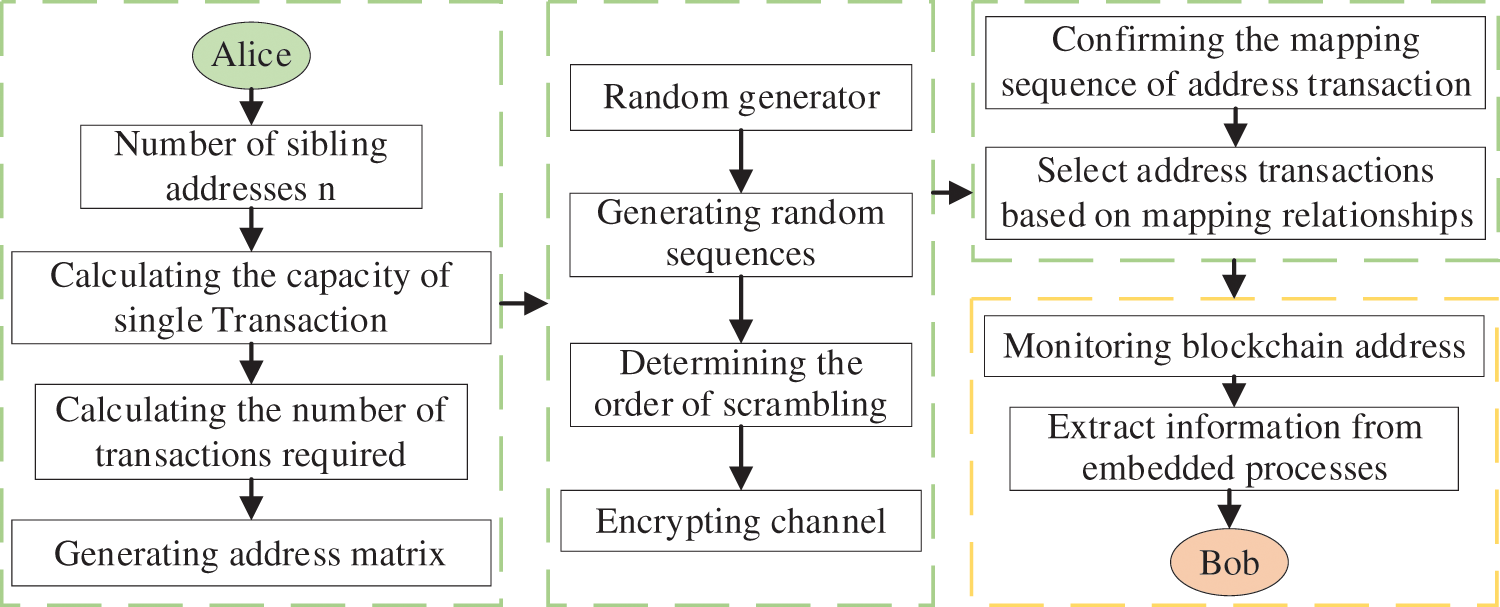
Figure 1: Overall process of covert communication
3.1 Dual-Key Based Covert Channel
The mapping number of a single transaction in the chain-based method depends on the number of the subclass addresses, and the capacity is limited. The covert communication model based on the smart contracts deploys a voting contract once to covertly transmit information by repeated voting. However, the capacity of this channel is limited by the number of the contract addresses. Since the contract cannot be tampered with, the covert channel does not have scalability. Inspired by the above methods, this paper uses dual-key to divide the generated blockchain addresses into sibling addresses and subclass addresses. Compared with the chain-based method where the capacity depends on the number of the subclass addresses, this paper combines the design idea of voting to transmit information, and make full use of the redundancy of address transactions. Therefore, the capacity depends on both subclass addresses and sibling addresses, which can increase the mapping number of a single transaction.
Fig. 2 depicts the covert channel framework based on dual-key.
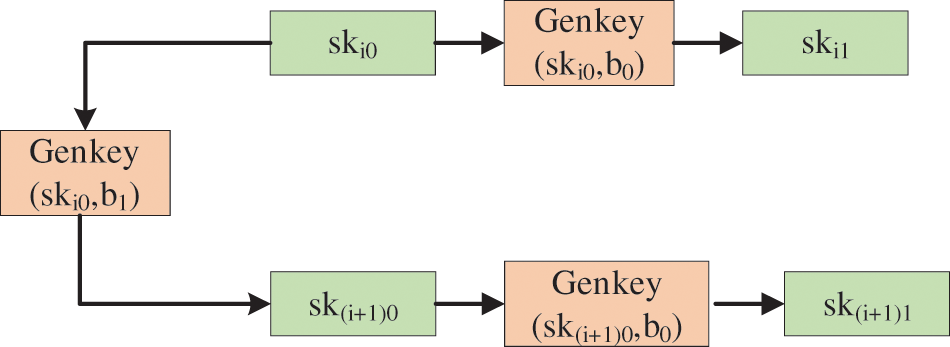
Figure 2: Dual-key based covert channel

After computing the new private key with Genkey, Alice uses the GenAddrmatrix method to construct a two-layer address matrix, which maps secret information by transactions between different layers. To continue embedding the secret information, this paper combines the scalability of the chain-based method by entering the private key

3.2 Random Sequence-Based Matrix Encryption
For the addresses after reuse, the fixed structure of the channel often leads to the formation of fixed transaction behaviors of the addresses, and thus reduces the concealment of the channel. In order to solve this problem, before transmitting a message, this paper first divides the address matrix into square blocks with the same size, and then randomly select blocks to scramble. The purpose is to change the relative relationship between addresses when transmitting a message and then optimize the transaction behaviors of addresses after multiple transmissions to improve the concealment of the channel.
For any rectangular matrix, it can always be divided into a finite number of square blocks with overlapping regions. The side of the square matrix is the width of the rectangular matrix.
Fig. 3 shows the division diagram based on a rectangular matrix. Where M is the short edge of the matrix, N is the long edge of the matrix, and the overlap length between blocks is fixed at t,
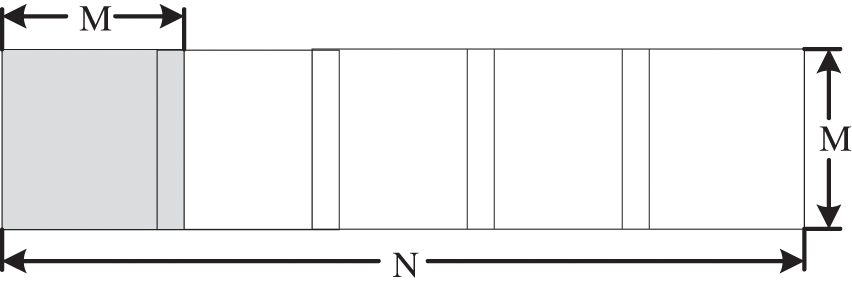
Figure 3: Order division of non-equal matrices
The Arnold transform, as an encryption technique, can transform a meaningful two-dimensional matrix into a chaotic two-dimensional matrix, thus enhancing the resistance to illegal attacks. In this paper, the security of the encryption channel algorithm is still not high. Therefore, this paper uses random numbers to improve the security of the encryption algorithm. The LCG is derived from the linear congruence method and uses the congruence operation to generate random numbers. The random number recurrence formula is as follows.
whereas
whereas
Fig. 4 shows the channel encryption process in this paper, unlike the sequential Arnold encryption, this paper encrypts the matrix in order of the generated random sequence.
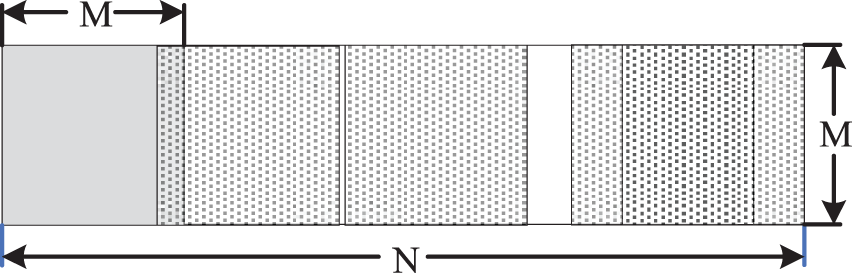
Figure 4: Order division of non-equal matrices
3.3 Covert Communication Based on Derivation Matrix
The communicating parties need to agree on a mapping relationship
The mapping relationship is portrayed in Fig. 5. The
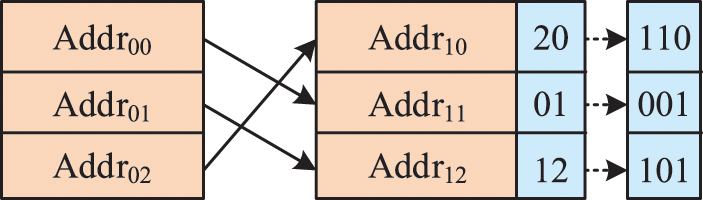
Figure 5: Mapping relationship between transaction and message sequences
To embed the secret information, Alice needs to enter the private key

Bob is the receiver of the communication and the sender of the communication. So Bob can extract the secret information through the embedding process. Algorithm 3 shows the pseudo-code of the extraction process of this scheme. Bob uses the GenAddrmatrix algorithm to obtain the address matrix, and monitors all transactions sent from

In this model, in order to achieve covert communication, both Alice and Bob need to know the private keys. In other words, all private keys are shared by Alice and Bob. Therefore, Alice and Bob must have a high degree of trust so that there is no one transfers all the money.
In this section, the setting of the parameters of the proposed method is first introduced. Subsequently, this paper does the simulation experiment form the perspective of transmission efficiency and anti-detection. Finally, the security of the channel encryption algorithm is analyzed.
The secret message this paper uses is a randomly generated 36-bit binary sequence. The number of sibling addresses n is set to 3. Sets m in the random algorithm to 64. The number of encrypted channels during a single communication is set to 4. In order to make the random sequence generated by the random generator have a period of m, we set a to 13 and c to 11.
This paper tests in the Bitcoin test-net. Testnet is an alternate chain of Bitcoin for development. The coin used for testing is distinguished from the actual coin, which has no real value and is used only for development. Thus, it reduces the cost of covert communication. Another difference is that the test networks less difficult than the main network, making block generation faster and shortening the time of covert communication. The following experiments compare the results in terms of transmission efficiency, resistance to detection, and security.
To facilitate the reader’s understanding and express the scheme more clearly, in the experiment,
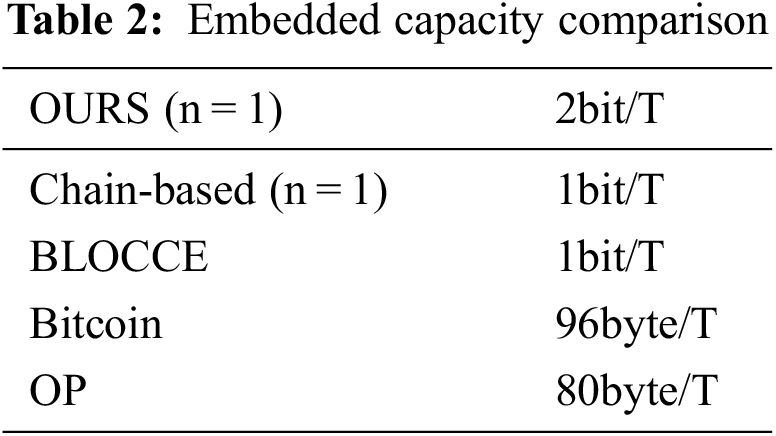
In Table 2, T represents a transaction, and the capacity of the chain-based method depends on the subclass addresses because it does not use the redundancy of the parent addresses. BLOCCE [17] uses the least significant bit of the address name as the embedding position, and the embedding efficiency is only 1 bit/T. The embedding capacity of the Bitcoin transaction and the script of OP [14] is higher, but these two schemes directly upload the encrypted secret information to the blockchain, which is easy to cause the adversaries’ suspicion, and the concealment is not guaranteed.
Since both the chain-based scheme and this paper’s scheme use transaction mapping information, Fig. 6 showcases the mapping number of a single transaction compared with the chain-based method [19]. It can be seen that as n increases, the mapping number of a single transaction is significantly higher than that of the chain-based method. To further increase the embedding capacity, this paper can also change the mapping relationship. For example, if n is set to 6, 36 one-to-one mappings can be formed, and this paper can use the first 26 pairs as the mapping from “a” to “z”. Compared with embedding information in binary which can only embed 5-bit information, after changing the mapping relationship, this paper can embed a lowercase alphabet, and the effective information can be greatly increased.
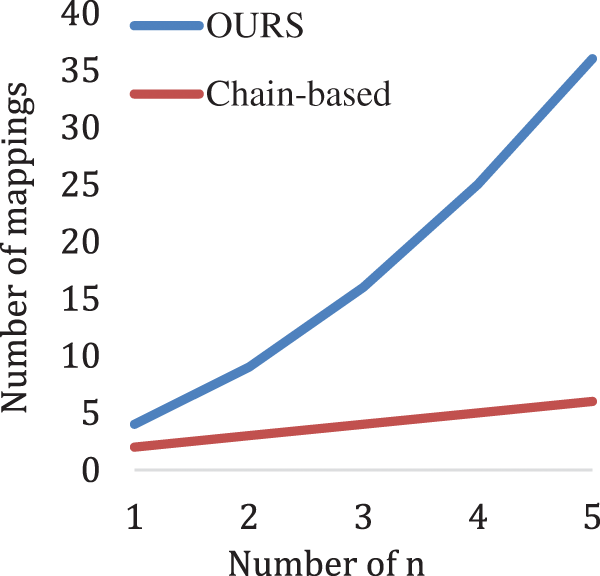
Figure 6: Mapping number of a single transaction compared with the chain-based method
4.2.2 Computational Complexity, Number of Transactions and Overall Spend
This paper uses
Eqs. (3) and (4) shows the computational complexity with the chain-based method and the BLOCCE method. It can be seen that the consumed time depends on the channel encryption process, key generation process, and the time to call the blockchain API for creating the transaction.
Fig. 7 shows the overall number of transactions required by the BLOCCE method [17], chain-based method [19], and our proposed method when the length of the passed secret information is from 10 to 100 bits. Since the number of transactions is inversely related to the embedding capacity, this means that the lower the embedding capacity is, the higher the number of transactions required. It can be seen that the number of transactions required by all three increases with the length of the secret information, but the number of transactions required by our scheme is smaller than that of the BLOCCE method and the chain-based method for the same information, and it becomes more obvious with the increase of the information length.
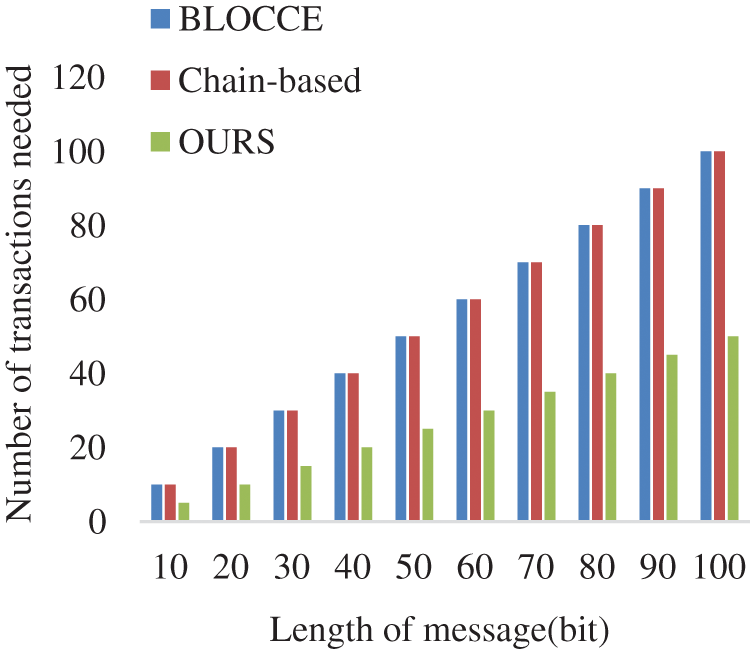
Figure 7: The overall number of transactions required by the BLOCCE, chain-based, and our method when the length of the passed secret information is from 10 to 100 bits
In fact, the system cost of the above methods can also be represented in terms of the number of transactions. Regardless of which method is used, the address used in the whole process belongs to Alice because Alice controls the generation of the private-public key pair. Thus, the transactions actually transferred from Alice to himself, and the transfer process does not result in a reduction of the total amount of the sender. So the system cost is mainly the miner’s fee for the transactions. Assuming that the miner’s fee is the same for each transaction, the system cost of the above method is proportional to Fig. 7. It can be seen that the transaction cost required by this method is also less than that of the BLOCCE method and chain-based method.
From the embedding capacity, the number of transactions and overall cost, it can be seen that the method in this paper has better transmission efficiency.
To make it easier to understand, this paper randomly generates 20 binary sequences with 16 bits and embed them in the blockchain network. The number of sibling addresses is set to 3.
Fig. 8 shows the comparison of interactive numbers of 10 addresses randomly selected before and after 20 covert communications. It can be seen that the interactive number of randomly selected addresses in the encrypted channel is significantly higher than that before channel encryption. For example, the number of interactions before and after encryption is 2 and 6 for the address with coordinates 02. This is due to the fact that the total number of interactive addresses before encryption depends on the number of sibling addresses n, which is up to
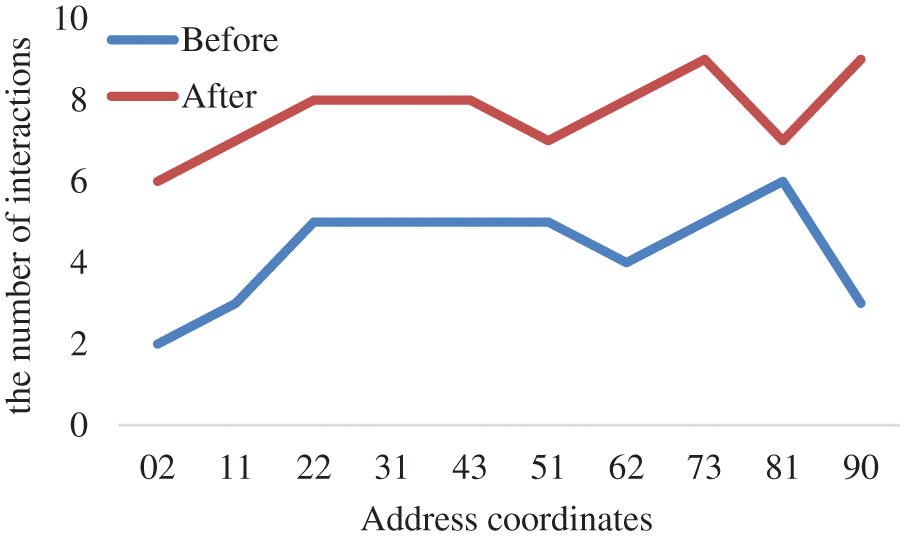
Figure 8: Comparison of interactive numbers of 10 addresses randomly selected before and after 20 covert communications
The security of the channel encryption algorithm remains low when using sequential scrambled encryption algorithms. For this reason, this paper uses a random sequence generated by a linear congruence generator to determine the encryption order of the blocks, which makes it difficult to collide with the true sequence since the adversaries do not know the order of the encryption.
If the sequential encryption is used, since the encryption order is fixed, the adversaries can obtain the correct channel structure as long as the order is successfully obtained once. Assuming that the encryption method is known to the adversaries, the probability
where M is the short edge of the address matrix and N is the long edge of the address matrix. Assume that the number of encryption required for the channel encryption is k,
Obviously, the probability of successful decryption using a random sequence is always lower than that using sequential encryption.
Moreover, since the initial value
In this paper, we propose a derivation matrix-based covert communication method in blockchain. First, we use the dual-key to construct an address matrix, and the transactions between different layers map different secret message sequences, which improves the capacity of a single transaction. Finally, the information is delivered through the broadcast of the transactions. To further improve the concealment, this paper scrambles the location relationship between the addresses and optimized the transaction behaviors of addresses. For the security of the encryption algorithm, we provide a random sequence for the scrambling order, which improves the security of the encryption algorithm. The receiver shares the embedding method and thus requires high loyalty to the sender. The experimental results demonstrate that the method can not only consume a reasonable cost to ensure the transmission efficiency of the message, but also protect the concealment and security of the channel. This paper will further improve our work in the following aspects in the future: (1) channel encryption is a random process, and can use a clustering optimization algorithm to obtain a better address distribution [28] to improve the channel crypticity. (2) this paper can use machine learning and deep learning methods to extract the transaction characteristics of the blockchain secret communication addresses [29] to enhance the anti-detection of the covert channel.
Funding Statement: This work was supported, in part, by the National Nature Science Foundation of China under grant numbers 62272236; in part, by the Natural Science Foundation of Jiangsu Province under grant numbers BK20201136, BK20191401; in part, by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) fund.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]
2. A. Bhaskar, C. Sharma, K. Mohiuddin, A. Singh, O. A. Nasr et al., “A robust video watermarking scheme with squirrel search algorithm,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3069–3089, 2022. [Google Scholar]
3. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]
4. W. Sun, G. Z. Dai, X. R. Zhang, X. Z. He and X. Chen, “TBE-Net: A three-branch embedding network with part-aware ability and feature complementary learning for vehicle re-identification,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 9, pp. 14557–14569, 2022. [Google Scholar]
5. S. Zander, G. Armitage and P. Branch, “Covert channels and countermeasures in computer network protocols,” IEEE Communications Magazine, vol. 45, no. 12, pp. 136–142, 2007. [Google Scholar]
6. W. Sun, L. Dai, X. R. Zhang, P. S. Chang and X. Z. He, “RSOD: Real-time small object detection algorithm in UAV-based traffic monitoring,” Applied Intelligence, vol. 52, no. 8, pp. 8448–8463, 2022. [Google Scholar]
7. T. Chen, Z. Qiu, G. Xie, L. Yuan, S. Duan et al., “A image copyright protection method using zero-watermark by blockchain and IPFS,” Journal of Information Hiding and Privacy Protection, vol. 3, no. 3, pp. 131–142, 2021. [Google Scholar]
8. X. R. Zhang, X. Sun, W. Sun, T. Xu and P. P. Wang, “Deformation expression of soft tissue based on BP neural network,” Intelligent Automation & Soft Computing, vol. 32, no. 2, pp. 1041–1053, 2022. [Google Scholar]
9. Y. J. Ren, Y. Leng, J. Qi, P. K. Sharma, J. Wang et al., “Multiple cloud storage mechanism based on blockchain in smart homes,” Future Generation Computer Systems, vol. 115, no. 2, pp. 304–313, 2021. [Google Scholar]
10. Z. L. Zhou, M. M. Wang, Z. W. Ni, Z. H. Xia and B. B. Gupta, “Reliable and sustainable product evaluation management system based on blockchain,” IEEE Transactions on Engineering Management, pp. 1–13, 2021. https://doi.org/10.1109/TEM.2021.3131583. [Google Scholar]
11. P. Chinnasamy, C. Vinothini, S. A. Kumar, A. A. Sundarraj, S. V. A. Jeba et al., “Blockchain technology in smart-cities,” Sensors, vol. 203, pp. 179–200, 2021. https://doi.org/10.1007/978-3-030-69395-4_11. [Google Scholar]
12. Y. J. Ren, F. J. Zhu, P. K. Sharma, T. Wang, J. Wang et al., “Data query mechanism based on hash computing power of blockchain in internet of things,” Sensors, vol. 20, no. 1, pp. 1–22, 2020. [Google Scholar]
13. P. Chinnasamy, B. Vinothini, V. Praveena, C. Vinothini and B. B. Sujitha, “Blockchain based access control and data sharing systems for smart devices,” Sensors, vol. 1767, no. 1, pp. 1–22, 2021. [Google Scholar]
14. J. Tian, G. P. Gou, C. Liu, Y. G. Chen, G. Xiong et al., “DLchain: A covert channel over blockchain based on dynamic labels,” in Proc. of the 2019 Conf. on Int. Conf. on Information and Communications Security, Cham, Switzerland, pp. 814–830, 2019. [Google Scholar]
15. J. Partala, “Provably secure covert communication on blockchain,” Cryptography, vol. 2, no. 3, pp. 18, 2018. [Google Scholar]
16. F. Gao, L. H. Zhu, K. K. Gai, C. Zhang and S. Liu, “Achieving a covert channel over an open blockchain network,” IEEE Network, vol. 34, no. 2, pp. 6–13, 2020. [Google Scholar]
17. H. T. Cao, H. Yin, F. Gao, Z. J. Zhang, B. Khoussainov et al., “Chain-based covert data embedding schemes in blockchain,” IEEE Internet of Things Journal, pp. 1–1, 2020. https://doi.org/10.1109/JIOT.2020.3040389. [Google Scholar]
18. L. J. Zhang, Z. J. Zhang, W. Z. Wang, Z. L. Jin, Y. S. Su et al., “Research on a covert communication model realized by using smart contracts in blockchain environment,” IEEE Systems Journal, pp. 2822–2833, 2021. https://doi.org/10.1109/JSYST.2021.3057333. [Google Scholar]
19. L. Sun, J. C. Xu, S. W. Liu, S. G. Zhang, Y. Li et al., “A robust image watermarking scheme using arnold transform and BP neural network,” Neural Computing and Applications, vol. 30, no. 8, pp. 2425–2440, 2018. [Google Scholar]
20. M. Mishra, P. Mishra, M. C. Adhikary and S. Kumar, “Image encryption using fibonacci-lucas transformation,” arXiv preprint arXiv: 1210.5912, 2012. [Google Scholar]
21. S. I. Batool and H. M. Waseem, “A novel image encryption scheme based on arnold scrambling and lucas series,” Multimedia Tools and Applications, vol. 78, no. 19, pp. 27611–27637, 2019. [Google Scholar]
22. L. Min, L. Ting and Y. J. He, “Arnold transform based image scrambling method,” in Proc. of the 3rd Int. Conf. on Multimedia Technology (ICMT-13), Paris, France, pp. 1302–1309, 2013. [Google Scholar]
23. W. Sun, Y. T. Du, X. Zhang and G. C. Zhang, “Detection and recognition of text traffic signs above the road,” International Journal of Sensor Networks, vol. 35, no. 2, pp. 69–77, 2021. [Google Scholar]
24. S. M. Hosseini, H. Karimi and M. V. Jahan, “Generating pseudo-random numbers by combining two systems with complex behaviors,” Journal of Information Security and Applications, vol. 19, no. 2, pp. 149–162, 2014. [Google Scholar]
25. W. Sun, X. R. Zhang, S. Peeta, X. Z. He and Y. F. Li, “A Real-time fatigue driving recognition method incorporating contextual features and two fusion levels,” IEEE Transactions on Intelligent Transportation Systems, vol. 18, no. 12, pp. 3408–3420, 2017. [Google Scholar]
26. A. Akhshani, A. Akhavan, A. Mobaraki, S. C. Lim and Z. Hasson, “Pseudo random number generator based on quantum chaotic map,” Communications in Nonlinear Science and Numerical Simulation, vol. 19, no. 1, pp. 101–111, 2014. [Google Scholar]
27. M. François, T. Grosges, D. Barchiesi and R. Erra, “Pseudo-random number generator based on mixing of three chaotic maps,” Communications in Nonlinear Science and Numerical Simulation, vol. 19, no. 4, pp. 887–895, 2014. [Google Scholar]
28. W. Sun, G. C. Zhang, X. R. Zhang, X. Zhang and N. N. Ge, “Fine-grained vehicle type classification using lightweight convolutional neural network with feature optimization and joint learning strategy,” Multimedia Tools and Applications Multimedia Tools and Applications, vol. 80, no. 20, pp. 30803–30816, 2021. [Google Scholar]
29. W. Sun, X. Chen, X. R. Zhang, G. Z. Dai, P. S. Chang et al., “A Multi-feature learning model with enhanced local attention for vehicle re-identification,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3549–3561, 2021. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools